Abstract
The estimation of thermodynamic parameters of N-Acetyl-L-cysteine (NAC) protonation were determined in NaCl(aq), (CH3)4NCl(aq), (C2H5)4NI(aq), employing various temperature and ionic strengths conditions, by potentiometric measurements. The interaction of NAC with some essential metal cations (e.g., Ca2+, Mg2+ and Zn2+) was investigated as well at 298.15 K in NaCl(aq) in the ionic strength range 0.1 ≤ I/mol dm−3 ≤ 1.0. The values of protonation constants at infinite dilution and at T = 298.15 K are: log K1H = 9.962 ± 0.005 (S—H) and log K2H = 3.347 ± 0.008 (COO-H). In the presence of a background electrolyte, both log K1H and log K2H values followed the trend (C2H5)4NI ≥ (CH3)4NCl ≥ NaCl. The differences in the values of protonation constants among the three ionic media were interpreted in terms of variation of activity coefficients and formation of weak complexes. Accordingly, the determination of the stability of 4 species, namely: NaL−, NaHL0(aq), (CH3)4NL−, (CH3)4NHL0(aq) was assessed. In addition, as regards the interactions of Mg2+, Ca2+ and Zn2+ with NAC, the main species where the ML0(aq), ML(OH)−, and ML22−, that were found to be important in the chemical speciation of NAC in real multicomponent solutions. The whole set of the data collected may be crucial for the development of NAC-based materials for natural fluids selective decontamination from heavy metals.
Keywords: N-acetylcysteine, Chemical speciation, Weak complexes, Modeling, Natural fluids, Sequestration, Ionic strength
Graphical abstract
Highlights
-
•
Interaction of N-Acetyl-L-cysteine with H+, Na+, Ca2+, Mg2+ and Zn2+ is studied.
-
•
Data are modeled according to SIT and weak interaction models.
-
•
Complexation occurs through sulfur and oxygen.
-
•
Speciation of Zn2+ in sea water and blood plasma is proposed.
-
•
Results aid in the design of new materials to remove pollutants from natural fluids.
1. Introduction
N-Acetyl-L-cysteine (NAC, Scheme 1 ) is an amino-acid derivative of cysteine, a precursor of the antioxidant enzyme glutathione. In medicine, NAC has been used for more than 30 years [1,2], mostly as a mucolytic, since it may be used to help clear mucus in cystic fibrosis, pneumonia, and in tracheostomy care [3,4]. Looking for the topic “N-acetylcysteine” on scientific databases more than 10,000 papers can be found, meaning that NAC is involved in various active fields of investigation.
Scheme 1.
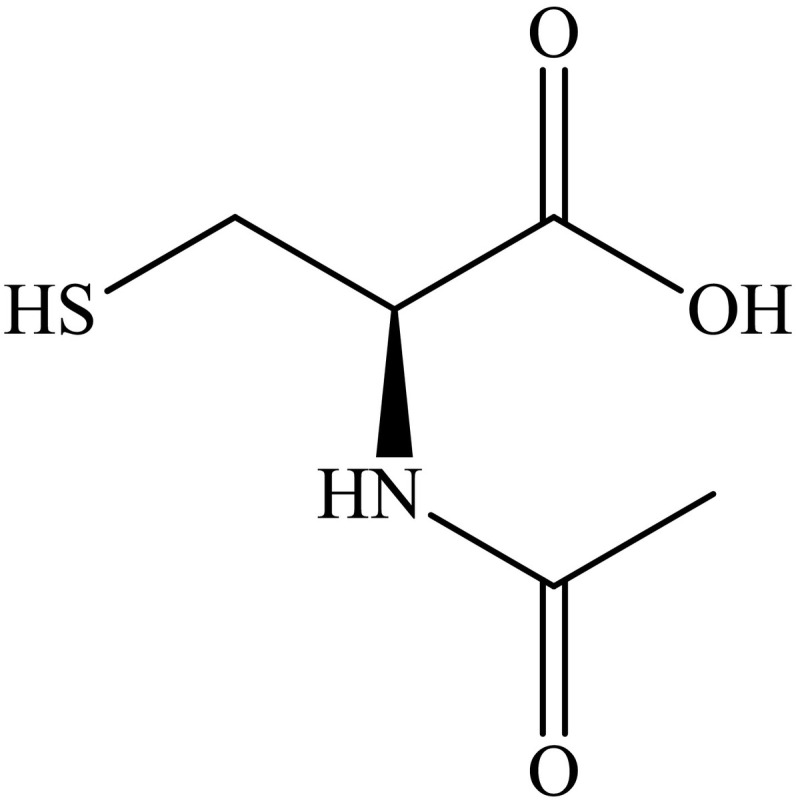
Chemical structure of N-Acetyl-L-cysteine (NAC).
Currently, NAC is used in treatment for acute poisoning with acetaminophen, restoring protective levels of glutathione (GSH) [5], yet NAC is employed in many other pharmaceuticals applications: NAC produces antiviral activity in HIV patients [6]; as antioxidant [7], it is used in combination with sodium bicarbonate in the prevention of contrast-induced nephropathy after cardiac catheterization, although this is still controversial [8], in several psychiatric disorders [[9], [10], [11]] or liver cirrhosis treatments [12]. In addition, NAC has been studied also in other medical correlated fields, such as in [13] where NAC zinc salt is described as therapeutic agent of type 2 diabetes mellitus in place of synthetic pharmaceuticals, or in [14] regarding the generation of contrast through chemical exchange saturation transfer (CEST). Recent studies showed potential use of N-Acetyl-L-cysteine as dietary supplements to protect high-risk populations from the carcinogenicity of aristolochic acids [15], from toxicity of silver nanoparticles [16,17], and as inhibitor of muscle fatigue in humans [18]. Among the large amount of studies on NAC biological activity [[19], [20], [21], [22]], some researchers envisaged its potential as a supplementary nutraceutical to provide protection against influenza and other RNA viruses, including coronavirus, mitigating the symptoms of infections [23]. Furthermore, NAC is also known to limit damages coming from heavy metals exposure of humans, both by reducing oxidative stress, being, as said, a strong free radicals scavenger, as well as by promoting the toxicants excretion by chelation [[24], [25], [26]]. It is also worth to note that, although NAC has been found to remove heavy and radioactive metals from tissues, it does not seem to enhance the releasing of essential metals, such as calcium, magnesium, zinc etc., from body [[26] and references therein]. Since no significant side effects have been ascertained in the use of NAC as a drug, and due to its capability to interact with metals and other chemicals, it is being tested for environmental applications. Accordingly, it has been assessed that NAC displays a great potential as efficient and safe agent for organic contaminants removal from shellfish [27]. However, few examples are available, yet very promising, where NAC-functionalized materials were easily synthesized and investigated in the separation of uranyl ions from radioactive effluents [28], in the sequestration of Hg2+ from petrochemical wastewater [29] and for Cd2+ and Pb2+ removal from biological and environmental media [30]. With the aim of exploring the potential of NAC as active compound to be implemented in new materials to mitigate heavy metals contamination, a preliminary investigation has been carried out, to ascertain and quantify the nature and extent of its interactions with naturally occurring metal cations and at specific conditions of real multicomponent solutions. A suitable extraction strategy should involve the use of an extractant that can efficiently compete with other ligands present in the specific aquatic system, while being both able to concentrate extremely diluted contaminants and to be selective towards the target species over other essential cations. From this viewpoint, it is clear how crucial is the estimation of all the possible interactions, including the weakest, and their relative extent, in a complex mixture, to develop a remediation material applicable in real systems. Thermodynamic studies on the complexation of heavy metals and other important cations by NAC may address this issue and help to design more selective and robust sorbents. Unfortunately, not so many investigations are reported on the chemistry of NAC, mostly on the thermodynamic equilibria in aqueous systems. Few and quite scattered are the investigations on Hg2+, Zn2+, Pb2+ and other metal cations [[31], [32], [33], [34], [35]]. Bearing this in mind, this study is focused on the potentiometric determination of the protonation constants in three different media (NaCl(aq), (CH3)4NCl(aq), (C2H5)4NI(aq)) at different ionic strengths and temperatures, aiming to assess the stability of weak species that NAC may form with Na+. In addition, the stability constants of NAC with Ca2+, Mg2+ and Zn2+ were also determined in similar experimental conditions. The data reported in this work may be very important to elucidate the chemical speciation of NAC in real multicomponent solutions (e.g. sea water) and the possible role of its complexes with Na+, Ca2+, Mg2+ and Zn2+, in order to provide useful information to develop specific sorbents able to selectively interact with heavy metals avoiding essential metals depletion in natural fluids.
2. Experimental section
2.1. Chemicals (see sample table)
The NAC solutions were prepared by weighing pure N-Acetyl-L-cysteine. The solutions of metal cations were prepared weighting the proper chloride salts (CaCl2·2 H2O, MgCl2·6 H2O and anhydrous ZnCl2) and the concentration of metals was checked by titration with standard EDTA solution. Sodium chloride (NaCl) was prepared by weighing the pure salt dried in an oven at T = 383 ± 2 K for 2 h. Tetramethylammonium chloride ((CH3)4NCl) and tetraethylammonium iodide ((C2H5)4NI) were recrystallized from methanol [36]. Hydrochloric acid (HCl), sodium hydroxide (NaOH), tetramethylammonium hydroxide ((CH3)4NOH) and tetraethylammonium hydroxide ((C2H5)4NOH) solutions were prepared from concentrated ampoules and standardized using sodium carbonate and potassium biphthalate, respectively, previously dried at T = 383 ± 2 K in an oven at least for 1 h. NaOH, (CH3)4NOH and (C2H5)4NOH solutions were stored in dark bottles and preserved by CO2(g) through soda lime traps. Grade A glassware and CO2-free analytical grade water (ρ = 18 MΩ cm) were employed in the preparation of all the solutions. The chemicals were purchased from Merck Italy at the highest purity available (see Table 1 ).
Table 1.
Description of the chemical used (all purchased from Sigma-Aldrich). Purity (mass) as stated by the supplier.
| Chemical | CAS n° | Purification | Assay (mass) |
|---|---|---|---|
| Sodium chloride | 7647-14-5 | NO | ≥99% |
| Tetramethylammonium chloride | 75-57-0 | [36] | ≥99% |
| Tetraethylammonium iodide | 68-05-3 | [36] | 98% |
| Hydrochloric acid | 7647-01-0 | NO | ≥99% |
| Tetramethylammonium hydroxide | 10424-65-4 | NO | ~10%a |
| Tetraethylammonium hydroxide | 77-98-5 | NO | ~10%a |
| Sodium hydroxide | 1310-73-2 | NO | ≥99% |
| Potassium phthalate monobasic | 877-24-7 | NO | ≥99.95% |
| Sodium carbonate | 497-19-8 | NO | 99.995% |
| Calcium chloride dihydrate | 10035-04-8 | NO | ≥99% |
| Magnesium chloride hexahydrate | 7791-18-6 | NO | ≥99% |
| Zinc chloride anhydrous | 7646-85-7 | NO | ≥98% |
| N-acetyl-L-cysteine | 616-91-1 | NO | ≥99% |
Value refers to the concentration in the solutions. On the dry basis, their assay is ≥99.5% (mass).
2.2. Potentiometric equipment and procedure
Potentiometric measurements were performed by using two independent automatic titration systems described elsewhere [37], following the guidelines reported by Bottari et al. [38]. The estimated accuracy for both systems was ±0.15 mV for e.m.f. and ± 0.002 cm3 for titrant volume readings. Devices were connected to a PC and the titrations were carried out using the Metrohm TIAMO 2.5 software to control titrant delivery, data acquisition and e.m.f. stability. For the evaluation of the protonation constants, a volume of 25 cm3 of the titrand solution, containing NAC ligand (5 ≤ c L/mmol dm−3 ≤ 15), HCl (2 ≤ c H/mmol dm−3 ≤ 10) and the supporting electrolyte (NaCl, or (CH3)4NCl, (C2H5)4NI at different ionic strengths) was titrated with standard NaOH (or (CH3)4NOH or (C2H5)4NOH) up to pH ~ 11.0. For the determination of stability constants, the same procedure was followed, but the metal chloride (0.5 ≤ c M/mmol dm−3 ≤ 2.0) was added into the titrand solution. All measurements were performed into glass jacket cells thermostated at the desired temperature (u T = 0.1 K), at p = 0.1 MPa under magnetic stirring, bubbling pure N2 through the solutions to avoid O2 and CO2 inside. Glass electrode calibration was performed with the Gran's method by independent titrations of strong acid solutions with standard base under the same medium and ionic strength conditions of the systems under investigation, in order to determine the standard electrode potential (E 0) and the acidic junction potential (E j = j a [H+]). Accordingly, the pH scale used was the free one, pH ≡ − log [H+], where [H+] is the free proton concentration. The reliability of the calibration in the alkaline range was checked by calculating the appropriate pK w values. For each titration, 70 to 90 data points were collected. All the potentiometric titrations performed are available as Supporting information (MS Excel file).
2.3. Calculations
The computer program BSTAC4 [39], that minimizes the sum of square errors in electromotive force values, was used to refine the protonation and formation constants. To draw speciation diagrams and to calculate species formation percentages, HySS program was used [40]. To fit linear and non-linear equations for the dependence on ionic strength, LIANA program was used [39]. ES2WC software [41] was employed to determine the stability of the weak species formed between the ligand and the supporting electrolyte inputting the values of the protonation constants at various ionic strengths obtained in different ionic media in the molar concentration scale.
Along the text, for simplicity, units of measurement of the arguments of logarithms will be omitted. However, it remains implied that the arguments relating to equilibrium constants (K ijk) are divided by their unit of measurement, i.e. mol kg−1 (H2O).
All the equilibrium constants determined in this work refer to the equilibria:
| (1) |
| (1a) |
| (1b) |
| (1c) |
where Eqs. (1), (1a) regards protonation constants and Eqs. (1b), (1c) are related to metal complex formation constants. When i < 0 and no ligand is involved, Eq. (1b) refers to metal hydrolysis constant (β i ⁎). Throughout the paper, errors associated to directly measured variables (e.g., temperature, ionic strength, pH) are given as standard uncertainties, those associated to quantities derived from fitting procedures are given as 95% confidence interval (1.96 · s.d.). The conversion from the molar (mol dm−3) to the molal [mol kg−1(H2O)] concentration scale was performed using the appropriate density values [42].
The sequestering ability of N-Acetyl-L-cysteine towards Zn2+ has been assessed by means of pL0.5 calculations in various conditions. As detailed elsewhere [43], pL0.5 is a semiempirical parameter representing the total concentration of a ligand (L, as -log c L) required to bind the 50% (as mole fraction, x M = 0.5) of a given component (M) in a given solution when c M → 0. By plotting the fraction of M (fixing c M = 10−10 mol dm−3) bound to L vs. -log c L a sigmoidal curve is obtained (sequestration diagram), and can be fitted to the Boltzmann-type equation:
| (2) |
where pL = −log c L, and pL0.5 is the only adjustable parameter. Like other “p” functions (e.g. the pM), the higher the pL0.5, the greater the sequestering ability.
2.4. Data analysis
The experimental data of this work and the literature findings constitute the dataset on which all the calculations are carried out. The differences in the values of protonation or complex formation constants obtained at different temperatures, ionic strengths and ionic media may be interpreted in two ways: the first one is a hybrid chemico-physical model in which the dependence of the equilibrium constants on ionic strength and ionic medium is a function of the variation of activity coefficients. Accordingly, their values depend on the nature of the species and on the molal concentration of the background electrolyte (e.g. Debye-Hückel, SIT [[44], [45], [46], [47], [48]]). This approach can be considered the best choice for the modeling in a single ionic medium (e.g. NaCl(aq)) or when ionic strength is very high. The second approach is a purely chemical model (“weak complex model”), in which the activity coefficients vary with ionic strength according to an equation that is independent of the nature of a species (generally for I < 1 mol dm−3), but only on its charge and the medium effect is interpreted in terms of formation of weak species between the molecule under study and the ions of the supporting electrolyte. From this basis, a background electrolyte, that it is assumed to be not (or very weakly) interacting with the molecule under study, is required; for this purpose, when dealing with O- and S- donor ligands, the choice falls on (C2H5)4NI(aq) or, more rarely, on (CH3)4NCl(aq) [[49], [50], [51], [52], [53], [54], [55], [56], [57], [58], [59]]. Moreover, since this approach is based on the direct comparison of data obtained in different media (the so-called ΔpK method), the use of the molar concentration scale is more reliable [60,61].
The two approaches, although coming from different theoretical backgrounds, provide the same modeling ability and can be used indifferently, yet separately, i.e. paying attention on avoiding their overlapping.
2.4.1. Debye-Hückel and SIT equations
According to the first approach, the dependence of equilibrium constants on ionic strength can be expressed in terms of activity coefficients. As an example, for the protonation constants in Eq. (1):
| (3) |
where log K i0 0 is the value of the protonation constants of the ith step at infinite dilution (superscript “0”) and γ is the activity coefficient of each species (H+, L2− and HiLi−2) of charge z. The dependence of the activity coefficient of each species on ionic strength can be expressed according to a simple Debye-Hückel type equation:
| (4) |
| (4a) |
When both ionic strength and equilibrium constants are expressed in the molal concentration scale (mol kg(H2O) −1), Eq. (4) becomes the SIT (Specific ion Interaction Theory) [[44], [45], [46], [47], [48]] equation and f (I) = Δεi · I (the subscript “i” refers to the ith protonation step). SIT theory assumes that in Eq. (4) the linear term f (I) depends only on interaction between ions of opposite charge, and this can be expressed as (only for 1:1 salts):
| (5) |
where ε is the specific ion interaction coefficient and the sum covers the interactions between the ion under examination and all the ions (M or X) of opposite charge multiplied for their molal concentration (m). When the single activity coefficients of Eq. (3) are as expressed as in Eq. (4), the general equation for the dependence of equilibrium constants on ionic strength is:
| (6) |
| (6a) |
The temperature dependence of the protonation constants was considered by means of the well-known following equation:
| (7) |
| (7a) |
| (7b) |
where log β θ i H 0 is the protonation constant ad infinite dilution (“0” superscript) and at the reference temperature, θ (in our case θ = 298.15 K). ∆H i0 0 is the enthalpy change of the ith step at infinite dilution, 52.23 = 1/(R·ln10) in kJ mol−1, A' and ∆ε i′ are given in Eqs. (7a), (7b) and the latter is the ionic strength dependence parameters of ∆H i 0.
Combination of Eqs. (6), (7) leads to the fitting equation:
| (8) |
| (8a) |
where log β i H is the protonation constant value at any temperature and ionic strength. Eqs. (6), (6a), (7), (7a), (7b), (8) are also valid for metal complex formation constants and in the molar concentration scale. In the latter case, ∆ε i is substituted by C i, ∆H i 0 0 by A T, and ∆ε i ' by C i '.
Further details on this equation are given elsewhere [57].
2.4.2. Weak interaction model
As above reported, the weak interaction model adopts the so-called Δlog K H or ΔpK method, to interpret the differences of the “apparent” protonation constants in “non-interacting” ((C2H5)4NI(aq) in this work) aqueous media and those in an interacting medium (NaCl(aq) and (CH3)4NCl(aq) in this work). A direct determination of the stability of these species is often hard since they rarely exceed the value of log K = 1.0. A detailed description of the basic principles of this approach [41,49,51,54] and some examples can be found, for example, in refs [50, 52, 55–59]. Briefly, for a simple monoprotic acid (HL), the lowering effect of the “apparent” protonation constant (log K i H app) in an “interacting” medium (e.g., NaCl(aq)) with respect to a non-interacting one (log K i H) can be interpreted in terms of formation of a weak complex (whose stability constant is K MHiL) between the deprotonated ligand and the cation of the supporting electrolyte (at the concentration c M):
| (9) |
For polyprotic ligands, a slightly more complicated calculation should be used, even if starting from the basic assumption that the average number of protons bound to a ligand () is fixed in given conditions, independently of its expression. This means that it can be indifferently calculated using only the “apparent” overall protonation constants (β i H app, referred to Eq. (1))
| (10) |
or by the “effective” protonation and complex formation constants (β 0i ≡ β i H):
| (11) |
the equivalence of the two expressions means that the formation constants (of weak complexes) can be calculated by minimizing the function
| (12) |
According to this approach, ionic strength dependence of equilibrium constants is given in Eq. (13):
| (13) |
| (13a) |
where log K can be the protonation constant (K H) or the weak complex formation constant (K MHiL), log K 0 is the same quantity at infinite dilution, c 0 and c 1 are the ionic strength dependence parameters common to all the species and z* is given in Eq. (6a). It is worth mentioning that this approach is valid at I < 1.0 mol dm−3.
Whenever data at different temperatures are available, adjustable parameters of Eq. (13) (i.e., log K 0, c 0, c 1) can be written as follows:
| (14) |
where YT is the value of the parameters at the temperature T, Yθ is the value at the reference temperature θ (298.15 K) and the partial derivative accounts for the temperature dependence.
This approach seems to be more complex than the previous one since it requires the estimation of the stability of many species in order to cover all the possible interactions occurring in a specific solution (at given T and I values). For example, to study the chemical speciation of the Zn2+/NAC2− system in sea water at S = 35 and T = 298.15 K, the stability constants of the sea water species (H+, Na+, K+, Ca2+, Mg2+, Cl−, SO4 2−, CO3 2−, OH− just to mention the most relevant) and the ones coming from any other possible species involving Zn2+ (e.g., Zn2+/Cl−) and NAC (e.g., Ca2+/NAC2−) should be known at S = 35 (~ 0.72 mol dm−3) and T = 298.15 K. However, according to this approach the ionic strength dependence for these species is often very similar and, for some species with unknown stability, predictive equations are also available (e.g., [54]). For example, in this work the stability of the K+/NAC2− species is estimated using the corresponding values for the Na+/NAC2− ones.
3. Results and discussion
3.1. Protonation constants of N-acetyl-L-cysteine
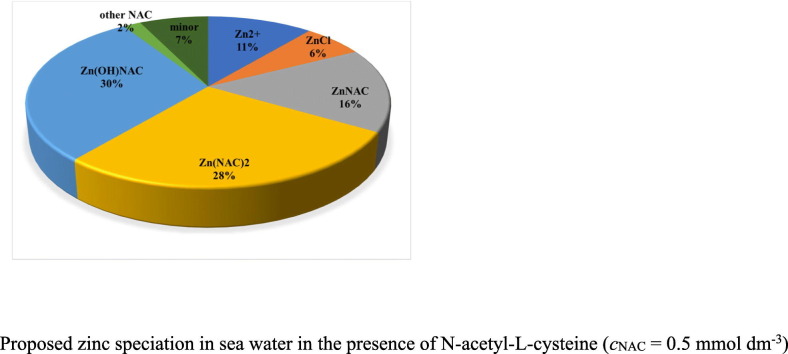
The values of “apparent” protonation constants of NAC obtained in the three ionic media at different temperatures and ionic strengths are reported as Supporting information (Tables S1–S2). During all the steps of the data analysis, the literature data from refs. [33, 34, 62] (see Table S3) were used together with new experimental results here commented for the first time. The dependence of protonation constants on ionic strength obtained in the three ionic media are shown in Fig. 1(a–b) for the first and second step, respectively. Experimental data are displayed as open symbols, literature ones as solid symbols.
Fig. 1.
Medium effect on the dependence of the first (a) and second (b) protonation constants of NAC in different background electrolytes at T = 298.15 K: NaCl(aq) (□), (CH3)4NCl(aq) (○), (C2H5)4NI(aq) (Δ). Solid symbols refer to literature data.
From the data here shown it can be argued that protonation constants values decrease with increasing of ionic strength up to I ~ 0.3 mol dm−3, whereas, above this value, the trend is inverted. In both cases, literature data at I = 1 mol dm−3 seems to be quite low, yet they were considered into the data analysis. As regards the medium effect, the protonation constants in (C2H5)4NI(aq) are much higher than the ones found in (CH3)4NCl(aq), in turn higher, in a lower extent, than in NaCl(aq). This behavior, which is typical of O-donor ligand, indicates that the deprotonated ligand (L2−) interacts with both Na+ and (CH3)4N+, whereas it does not with (C2H5)4N+. The second protonation step shows similar trend, indicating that also the protonated HL− species has the same behavior.
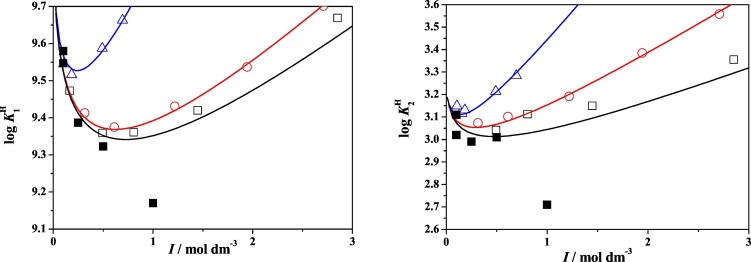
In Fig. 2(a–b), the dependence of the values of the two protonation constants on ionic strength in NaCl(aq) at three different temperatures is given.
Fig. 2.
Temperature effect on the dependence of the first (a) second (b) protonation constant of NAC in NaCl(aq) at different temperatures: T = 283.15 K (□), T = 298.15 K (○) and T = 318.15 K (Δ).
Fig. 2 shows that the first protonation constant, which refers to the thiol group, is much more affected by the temperature variation; accordingly, an intense decrease of stability is observed when temperature is increased, as a result of an exothermic process. Moreover, the difference among the curves at the three temperatures is quite independent of ionic strength. The second protonation step, involving the carboxylate group, is much less affected by the temperature variation if compared to log K H 1. However, considering all the curves depicted in Fig. 2b, the presence of a slightly exothermic process can be argued. In fact, data at 318.15 K are undoubtedly lower than the ones found at other temperatures. Contrarily to the first protonation step, this process is more affected by the ionic strength variation.
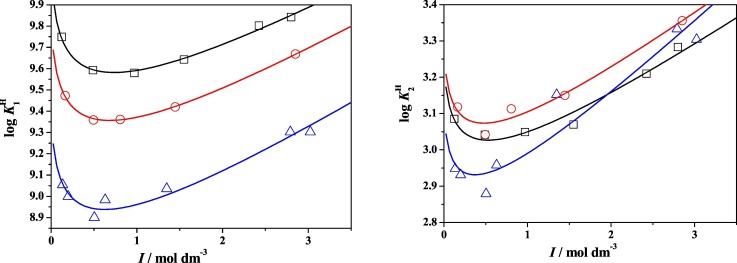
The influence of temperature in the speciation of NAC in NaCl(aq) is shown in Fig. 3 , where the distribution diagram of the NAC species at T = 288.15 K (blue line), 298.15 K (green line) and 310.15 K (red line) is reported at I = 0.5 mol dm−3.
Fig. 3.
Distribution diagram of the NAC (L) species as function of the pH in NaCl(aq) at I = 0.5 mol dm−3 and different temperatures: (blue) = 288.15 K, (green) = 298.15 K, (red) = 310.15 K. Experimental condition cL = 2 mmol dm−3.
The diprotonated H2L species is present at pH < 4.5 with similar formation percentages at the three temperatures. The monoprotonated HL species reaches 50% of formation at pH ~ 3 and it is the predominant species at 4 ≤ pH ≤ 9, which is the pH range including the most important natural fluids. The formation of the free L species starts at pH ~ 8.0 and reaches the 50% of formation species at pH ~ 9, ~ 9.5 and ~ 10, respectively at T = 318.15, 298.15 and 283.15 K.
The experimental and literature data (Tables S1–S3) obtained from BSTAC4 in the three ionic media were fitted to Eq. (8) according the data analysis described in Section 2.4.1, and the refined parameters are reported in Table 2 . Using 69 datapoints, the mean deviation resulted m.d.e = 0.04 (in log K units), like the experimental errors associated, the mean of the residues is me = −0.002.
Table 2.
Ionic strength and temperature dependence parameters according to Debye-Hückel (EDH, molar concentration scale) and SIT (molal concentration scale) models (p = 0.1 MPa).
| EDH | log Kθ iH0 |
Ci |
ATi |
C'i |
||
|---|---|---|---|---|---|---|
| NaCl | (CH3)4NCl | (C2H5)4NI | NaCl | |||
| i=1a | 9.937 ± 0.008b | 0.226 ± 0.005b | 0.271 ± 0.005b | 0.69 ± 0.02b | −27.4 ± 0.9b | 2.0 ± 0.8b |
| i = 2 | 3.274 ± 0.008 | 0.180 ± 0.006 | 0.287 ± 0.008 | 0.58 ± 0.03 | −2.9 ± 0.9 | 3.1 ± 0.7 |
| SIT | log Kθ iH0 |
∆εi |
∆Hi 00 |
∆εi′ |
||
|---|---|---|---|---|---|---|
| NaCl | (CH3)4NCl | (C2H5)4NI | NaCl | |||
| i = 1 | 9.947 ± 0.009 | 0.204 ± 0.006 | 0.173 ± 0.009 | 0.55 ± 0.02 | −27.4 ± 0.9 | 1.7 ± 0.9 |
| i = 2 | 3.284 ± 0.010 | 0.158 ± 0.006 | 0.179 ± 0.011 | 0.43 ± 0.03 | −2.9 ± 1.0 | 2.7 ± 0.8 |
Protonation step, see Eq. (1a).
95% confidence interval (C.I.) = 2ur (relative standard uncertainty on log10KH); standard uncertainties: u(T) = 0.1 K, u(p) = 1 kPa.
Protonation constants calculated at some relevant values of temperatures and ionic strengths are reported in Tables S4–S5.
As regards the data analysis according to the weak interaction model, tetraethylammonium iodide was assumed to be the non-interacting medium and some parameters were fixed. In particular, the value of c 0 was kept constant to c 0 = 0.1, according to previous findings [[50], [51], [52],55,56,58,59], the protonation constants at infinite dilution were set to log K 1 H0 = 9.937 and log K 2 H0 = 3.274 and the gradient for their temperature dependence was obtained by dividing the parameter A Ti (Table 2) by 1702 [57], thus ∂ log K 1 H 0/∂T = − 27.4/1702 = −0.016 and ∂ log K 2 H 0/∂T = − 2.9/1702 = −0.002. The dataset used for this analysis is the same as above (only data at I < 1 mol dm−3), but the refinement of the results was carried out, with ES2WC software [41], in two steps: the first one with the data in the three ionic media at 298.15 K, to obtain the stability constants of the weak species at infinite dilution and the ionic strength dependence parameter, c 1, common to all the species (m.d.e = 0.027); the second step regarded only the data in NaCl(aq) at the three temperatures, once the parameters previously determined were fixed, in order to calculate only the temperature dependence ones (m.d.e = 0.011). In this way, the four weak species were determined, namely: NaL−, NaHL0 (aq), (CH3)4NL−, (CH3)4NHL0 (aq). The whole set of parameters is given in Table 3 .
Table 3.
Equilibrium constants at infinite dilution, temperature and ionic strength dependence parameters of the weak species for NAC at T = 298.15 K and p = 0.1 MPa.
| Equilibrium | z* | Yθ (log β0) | |
|---|---|---|---|
| H+ + L2− = HL− | 4 | 9.936a | −0.016a |
| 2H+ + L2− = H2L0(aq) | 6 | 13.210a | −0.018a |
| Na+ + L2− = NaL− | 4 | 0.77b ± 0.06c | −0.0008d ± 0.0005c |
| Na+ + H+ + L2− = NaHL0(aq) | 6 | 9.83b ± 0.03 | −0.019d ± 0.003 |
| (CH3)4N+ + L2− = (CH3)4NL− | 4 | 0.61b ± 0.03 | – |
| (CH3)4N+ + H+ + L2− = (CH3)4NHL0(aq) | 6 | 9.55b ± 0.13 | – |
Taken from Table 2 and kept constant during calculations.
Results of the first refinement step.
95% C.I.
Results of the second refinement step.
Kept fixed during calculations; standard uncertainties: u(T) = 0.1 K, u(p) = 1 kPa.
To demonstrate that in terms of chemical speciation the two approaches are absolutely equivalent, two distribution diagrams obtained in the same conditions, namely I = 1.0 mol dm−3 in NaCl(aq), T = 298.15 K are reported in Fig. 4 . The first diagram is drawn with “apparent” protonation constants calculated from data in Table 2 (log K H 1 app = 9.35 and log β H 2 app = 12.39), the second with “effective” protonation constants and sodium complexes computed from data in Table 3 (log K H 1 = 9.88 and log β H 2 = 13.18, log K NaL- = 0.72, log β NaHL = 9.80). As it can be observed, the two diagrams show essentially the same chemical information. In fact, in the diagram a the amount of HL− is 100% from pH ~ 4 to pH ~ 8 and the curve relative to the fraction L2− begins at pH ~ 8 reaching the maximum of 100% at pH ~11. In the diagram b there are also the sodium species, whose formation percentage is very high, the NaHL0 (aq) reaches 45% from pH ~ 4 to 8 and the NaL− achieves ~80% at pH = 11.
Fig. 4.
Distribution diagram of the NAC (cL = 2 mmol dm−3) species as function of the pH in NaCl(aq) at I = 1.0 mol dm−3 and T = 298.15 K (solid black), 310.15 K (dotted red). a) “apparent” approach; b) “effective” approach.
The red dotted lines represent the sum of the species containing the ligand at the same protonation step. Thus, HL− and NaHL0 (aq) are summed up as well as NaL− and L2−. In this way, the diagram b drawn only with the curves relative to the H2L0 (aq), (HL− + NaHL0 (aq)) and (NaL− + L2−) is identical to the diagram a. But if the chemical information is apparently the same, the meaning is not, because with the approach b it is possible to consider also species often neglected, which may become important in condition of real multicomponent solutions.
3.2. Stability constants of N-acetyl-L-cysteine with Ca2+, Mg2+ and Zn2+
The potentiometric titrations performed in the presence of metal cations were analyzed with BSTAC computer program [39]. To assess a correct speciation scheme, the NAC protonation constants and the metal hydrolysis constants are required. The former were determined from data in Table 2, the latter were derived from literature [[63], [64], [65]]. In both cases, the data were calculated at the experimental ionic strength value. Regarding the zinc hydrolysis constants, it must be remarked that published data are based on very few experimental values and a systematic work is still necessary. In this work, data from Baes and Mesmer were analyzed and used because they worked quite well for many of the other papers with which our experimental results must be compared. Thermodynamic quantities are taken from Brown and Ekberg [64].
The results of the data analysis allowed to determine several complex species, whose values are reported in Table 4 (data converted to the molal concentration scale are given in Table S6).
Table 4.
Overalla equilibrium constants of the M2+/NAC2− species in NaCl(aq) in the molar concentration scale at T = 298.15 K and at p = 0.1 MPa.
| I/mol dm−3 | CaL0(aq) | CaHL+ | CaL22− |
|---|---|---|---|
| 0.098 | 1.36 ± 0.04b | 10.22 ± 0.03b | 3.82 ± 0.02b |
| 0.135 | 1.29 ± 0.03 | 10.16 ± 0.03 | 3.75 ± 0.02 |
| 0.485 | 1.13 ± 0.02 | 10.04 ± 0.04 | 3.64 ± 0.03 |
| 0.736 | 1.17 ± 0.04 | 10.12 ± 0.06 | 3.71 ± 0.05 |
| 0.960 | 1.25 ± 0.06 | 10.22 ± 0.07 | 3.82 ± 0.07 |
| I/mol dm−3 | MgL0(aq) | MgHL+ |
|---|---|---|
| 0.113 | 2.05 ± 0.02 | 11.38 ± 0.02 |
| 0.148 | 2.01 ± 0.02 | 11.34 ± 0.02 |
| 0.385 | 1.93 ± 0.02 | 11.31 ± 0.01 |
| 0.854 | 2.13 ± 0.06 | 11.61 ± 0.06 |
| 1.052 | 2.26 ± 0.07 | 11.78 ± 0.09 |
| I/mol dm−3 | ZnL0(aq) | ZnLH+ | ZnL(OH)− | ZnL22− | ZnL2(OH)3− | ZnL34− |
|---|---|---|---|---|---|---|
| 0.134 | 5.58 ± 0.04 | 11.28 ± 0.07 | −2.96 ± 0.15 | 11.22 ± 0.03 | 1.42 ± 0.05 | 14.87 ± 0.09 |
| 0.495 | 5.59 ± 0.05 | 11.04 ± 0.09 | −2.99 ± 0.19 | 11.09 ± 0.03 | 1.47 ± 0.06 | 14.81 ± 0.12 |
| 0.742 | 5.76 ± 0.05 | 11.03 ± 0.11 | −2.89 ± 0.22 | 11.15 ± 0.04 | 1.55 ± 0.07 | 14.77 ± 0.14 |
| 1.057 | 6.03 ± 0.07 | 11.08 ± 0.14 | −2.72 ± 0.28 | 11.30 ± 0.05 | 1.66 ± 0.09 | 14.71 ± 0.18 |
log βMHiL values refer to Eq. (1b).
95% Confidence interval; standard uncertainties u are: u(c) = 0.001 mol dm−3, u(T) = 0.1 K, u(p) = 1 kPa.
From the data here reported, it can be observed that there are two common species, ML0 (aq) and MHL+, for which the relative stability follows the trend: Zn2+ >> Mg2+ > Ca2+. The ML2 2− species was assessed for Ca2+ and Zn2+, not for Mg2+, whereas the ML3 4−, ML(OH)− and ML2(OH)3− were only found for Zn2+. This kind of speciation is quite common for amino-acids, which generally form polydentate complexes through N,O- five-membered rings [66]. In this case, the amino group is not available but there is an extra thiol group on the side chain. Thus, it is reasonable to assume that the complexation occurs through a S,O- six-membered ring, as also suggested by Santoso et al. [33] by molecular modeling. The stability of all the metal complexes is much lower with respect to the cysteine one, since the latter has three binding sites (N,S,O), even if often acts as five-membered bidentate (N,S) ligand [35,67]. For example, in the same conditions (T = 310.15 K and I = 0.15 mol L−1), the stability of the ZnL0 (aq) species is log K = 9.11 and 5.40 for cysteine and NAC, respectively [68]. Similarly, Zucconi et al. [69] found log K CaL = 2.98 for cysteine (T = 310.15 K and I = 0.15 mol dm−3 in KNO3) much higher than the value here reported for NAC, log K CaL = 1.29, even at T = 298.15 K and I = 0.135 mol dm−3 in NaCl(aq).
However, the stability of the Zn2+/NAC2− species is also lower than the one displayed by 3-mercaptoproprionic acid (3-MPA): both molecules bear the moiety −OOC-CH (R)-CH2-S− and may form a the six-membered ring involving a carboxylate and a thiol group (R = H for 3-MPA and N(H)COCH3 for NAC). According to NIST [62], the stability of the ZnL2 2− species for 3-MPA is log β ML2 2− = 12.2 (at I = 0.5 mol dm−3 and T = 298.15 K), one order of magnitude higher than NAC for the same species (log β ML2 2− = 11.12, see Table 4). A similar discussion applies for the ZnL0 (aq) species. de Brabander rejected this species giving a value of 3.44 that appears to be too low [70]; in the Jess database [71] a value of log K ZnL = 6.43 is reported at T = 303.15 and I = 0.1 mol dm−3 in KNO3(aq) that is higher than our value, which can be roughly calculated to be log K ZnL ~ 5.6 in similar conditions.
Therefore, it may be speculated that the N-acetyl residue of NAC does not provide any complexing ability, and, in addition, may also disturb the formation of complex species, probably due to steric hindrance. A similar comparison for Ca2+ and Mg2+ cannot be made since data for cysteine and 3-MPA are not available to our knowledge. Moreover, it is interesting to note that the stability of the ML2 2− species, expressed as stepwise, sometimes exceeds the stability of the simple ML0 (aq) species. For example, log K CaL = 1.31 and log K CaL2 2-− = 2.46 (as CaL0 (aq) + L2− = CaL2 2−), a quite common behavior for S-donor ligands [67].
Santoso [33] and Quyoom [31] reported two species, ZnL and ZnL2 2−, at 318.15 and 298.15 K, respectively and at I = 0.1 mol dm−3. Cardiano et al. [34] evidenced the formation of three species, namely ZnL0 (aq), ZnL2 2− and ZnL(OH)− at different ionic strengths, in NaCl(aq) and at T = 298.15 K. NIST database [62] reports five complexes, such as ZnL0 (aq), ZnL2 2−, ZnL3 4−, ZnL(OH) − and ZnL2(OH)3−, at I = 0.15 mol dm−3 and T = 310.15 K in Na+ medium; Gockel et al. [35] found four species, namely ZnL0 (aq), ZnL2 2−, ZnL2H− and ZnL2(OH)3−. As it can be noticed, all authors reported the formation of the ZnL0 (aq) and ZnL2 2− species, which can be considered as the most important ones in the Zn2+/NAC2− system. In addition, many papers proposed the formation of a mixed hydrolytic species, some propending for the simple ZnL(OH)− and others for the ZnL2(OH)3−, NIST reports both [62]. ZnL3 4−, ZnHL+ and ZnHL2 − can be considered as minor species, probably formed only in particular conditions and negligible in the speciation studies of natural fluids.
During the data analysis, several attempts to check for other species, such as the ZnL2H−, ZnL(OH)2 2−, ZnL(OH)3 3−, ZnL2(OH)2 4− were performed. In one attempt, the ZnL(OH)2 2− has been determined as an alternative to the ZnL2(OH)3−, but the statistical parameters of the fits worsened significantly and the model containing the ZnL2(OH)3− instead of the ZnL(OH)2 2− was chosen. For the selection of the best speciation scheme, some usual procedures were adopted [72,73].
The data analysis of the complex formation constants, according to the “apparent” approach, was performed by fitting the experimental data in Table 4 together with the literature ones [[33], [34], [35],62,74], reported in Table S7, to Eq. (8). Thus, a list of parameters to estimate the value of each equilibrium constant as a function of ionic strength is obtained and is given in Table 5 . Using a total of n = 70 datapoints, the global mean deviation of the fit is quite satisfying (m.d. = 0.25 log K units).
Table 5.
Summary of the ionic strength dependence parameters of Eq. (8) for all the M2+/NAC2− species obtained analyzing experimental and literature data at T = 298.15 K and at p = 0.1 MPa.
| Species | log βMHiL0a | z* | p* | Cij | Δεij |
|---|---|---|---|---|---|
| CaL0(aq) | 2.18 ± 0.06b | 8 | 1 | 0.71 ± 0.09b | 0.68 ± 0.08b |
| CaHL+ | 11.11 ± 0.06 | 8 | 2 | 0.66 ± 0.12 | 0.64 ± 0.11 |
| CaL22− | 4.71 ± 0.06 | 8 | 2 | 0.66 ± 0.12 | 0.64 ± 0.11 |
| MgL0(aq) | 2.99 ± 0.13 | 8 | 1 | 0.71 ± 0.09 | 0.68 ± 0.08 |
| MgHL+ | 12.41 ± 0.15 | 8 | 2 | 0.66 ± 0.12 | 0.64 ± 0.11 |
| ZnL0(aq) | 6.46 ± 0.12 | 8 | 1 | 0.71 ± 0.09 | 0.68 ± 0.08 |
| ZnHL+ | 12.09 ± 0.07 | 8 | 2 | 0.66 ± 0.12 | 0.64 ± 0.11 |
| ZnL22− | 12.09 ± 0.09 | 8 | 2 | 0.66 ± 0.12 | 0.64 ± 0.11 |
| ZnL34− | 14.87 ± 0.17 | 0 | 3 | −0.16 ± 0.09 | −0.12 ± 0.08 |
| ZnL2(OH)3− | 1.89 ± 0.16 | 2 | 1 | 0.14 ± 0.09 | 0.14 ± 0.08 |
| ZnL(OH)− | −1.86 ± 0.14 | 6 | 0 | 0.57 ± 0.09 | 0.54 ± 0.08 |
log β0MHiL values refer to Eq. (1b).
95% Confidence interval; standard uncertainties u are: u(T) = 0.1 K, u(p) = 1 kPa.
Apart from experimental data and the ones reported by Cardiano et al. [34], other information are fragmentary in terms of dependence on ionic strength and temperature. Thus, the ionic strength dependence parameters were constrained to be dependent on the stoichiometry of the reaction for all the metal cations, and temperature dependence parameters were estimated (at I = 0.15 mol dm−3) by comparing calculated data from Table 5 and NIST data only for the common species, namely: ZnL0 (aq) (ΔH 0 = −17 kJ mol−1), ZnL(OH)− (ΔH 0 = −26 kJ mol−1), ZnL2 2− (ΔH 0 = 9.9 kJ mol−1), ZnL2(OH)3− (ΔH 0 = −119 kJ mol−1) and ZnL3 4− (ΔH 0 = −7 kJ mol−1).
The data analysis according to the “effective” approach was performed also in this case. To make the data independent of the ionic medium, the entire dataset was corrected according to Eq. (9). For example, the value of the “apparent” complex formation constant of the ZnL0 (aq) species should be corrected by the formation of the NaL− (values in Table 3) and the ZnCl+ [73] species. If more than one ligand is present in the species this must be considered, as well as in case of protonated species. The results are reported in Table 6 .
Table 6.
Summary of the ionic strength dependence parameters of Eq. (13) for all the M2+/NAC2− species obtained analyzing experimental and literature data at T = 298.15 K and at p = 0.1 MPa.
| Species | p* | z* | Yθ (log β0)a | |
|---|---|---|---|---|
| CaL0(aq) | 1 | 8 | 2.17 ± 0.08b | – |
| CaHL+ | 2 | 8 | 10.77 ± 0.12 | – |
| CaL22− | 2 | 8 | 4.80 ± 0.16 | – |
| MgL0(aq) | 1 | 8 | 3.01 ± 0.14 | – |
| MgHL+ | 2 | 8 | 12.14 ± 0.10 | – |
| ZnL0(aq) | 1 | 8 | 6.49 ± 0.09 | −0.010c |
| ZnHL+ | 2 | 8 | 11.76 ± 0.10 | – |
| ZnL22− | 2 | 8 | 12.23 ± 0.09 | 0.006c |
| ZnL34− | 3 | 0 | 15.2 ± 0.2 | −0.004c |
| ZnL2(OH)3− | 1 | 2 | 2.7 ± 0.2 | −0.070c |
| ZnL(OH)− | 0 | 6 | −1.0 ± 0.2 | −0.015c |
| Yθ | ||
|---|---|---|
| c0 | 0.76 ± 0.09 | – |
| c1 | 0.11 ± 0.02 | – |
3.3. Speciation in natural fluids
To understand the importance of the “weak interaction” approach, let us assume one wants to study the chemical speciation of N-acetylcysteine in a real multicomponent solution, such as sea water or human blood plasma. They are both aqueous solutions containing many ions (apart of neutral molecules, macromolecules, and biota), all concurring to the total ionic strength (I = 0.72 and 0.1506 mol dm−3 for sea water and human blood plasma, respectively). Neither sea water nor human blood plasma can be approximated to a simple NaCl(aq) solution, since they both contain significant amounts of Ca2+, Mg2+, Na+, SO4 2− and other interacting ions that influence the equilibrium constant values. Among the possible solutions to deal with this problem (e.g., measure stability constants in that specific medium), the use of the “effective” approach with the explicit presence of “weak complexes” is the one here selected. As described in the Experimental section, the values of the “apparent” equilibrium constants are “depurated” by the influence of the interacting ions, becoming independent of the background medium and used together with all the weak interactions with the ions in the fluid.
As an example, the chemical speciation of NAC in the condition of sea water (at S = 35) is shown in Fig. 5 , in the following experimental condition: T = 298.15 K, c Zn = 1 μmol dm−3, c NAC = 0.5 mmol dm−3, the concentration of sea water components is reported by Bretti et al. [53] and is given in Table S8, the whole set of stability constants used is given in Table S9. The chemical speciation of Ca2+ and Mg2+ is not affected by the presence of NAC, due to their high concentration compared to NAC. On the contrary, Zn2+ is present in trace amount and in sea water is distributed among ZnCl+ (44%), Zn2+ (16%), ZnCl2 0 (aq) (15%), Zn(OH)Cl0 (aq) (13%) and other minor species (12%) [75]; in the presence of NAC 76% of the total zinc concentration is present as NAC species (as sum of ZnL0 (aq), ZnL2 2− and ZnL(OH)−), free Zn2+ is 11% and ZnCl+ only 6%. By the way, NAC is distributed among: free NAC2− (0.2%), HNAC− (7.6%), Na+/NAC2− species (2.3%), Ca2+/NAC2− species (0.9%), Mg2+/NAC2− species (87%) and Zn2+/NAC2− species (1.5%).
Fig. 5.
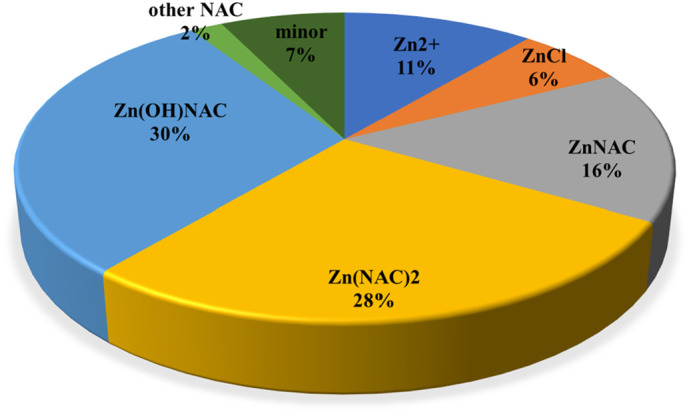
Pie chart of the zinc species in sea water in the following experimental condition: T = 298.15 K, cZn = 1 μmol dm−3, cNAC = 500 μmol dm−3. Concentration of components in Table S8, equilibrium constants in Table S9.
In human blood plasma, zinc is known to be distributed among histidine and cysteine complex species [67,76]. In this work, N-acetylcysteine was added to the model build by Hallman et al. [76] in order to evaluate the influence on the speciation of Zn2+. The speciation model has been slightly simplified: the seventeen amino-acids considered by Hallman were reduced to only 3: histidine (His), cysteine (Cys) and glycine (Gly), the latter including: glycine, alanine, arginine, cystine, glutamine, glutamic acid, isoleucine, leucine, methionine, ornithine, proline, serine, threonine, tryptophan and valine. The equilibrium constants of histidine, cysteine and their ternary mixed species were taken from Hallmann [76], as well as the simple species of Zn2+ with the third amino-acid, indicated as Gly− but accounting for all the others; for the mixed species the following were considered (log β in parenthesis): Zn(Gly)(His)0 (aq) (11.6), ZnH(Gly)(His)+ (19.55), ZnH2(Gly)(His)2+ (26.35), ZnH(Gly)2(His)0 (aq) (23.10) and ZnH(Gly)(His)2 0 (aq) (22.79). As regards the other ligands, data of H+/Ca2+/Mg2+ with OH−, Cl−, SO4 2−, CO3 2−, PO4 3− and Gly− were calculated from [73], data for Zn2+/PO4 3− and Zn2+/CO3 2− systems were elaborated from [65], those of Zn2+/Cit3− from [77], glutathione protonation constants and interaction with Ca2+ and Mg2+ from [78]. The concentration of low molecular weight ions in blood plasma was taken from Lentner [79] and it is reported in Table S8, the values of the equilibrium constants of all the species considered in Table S10.
In the abovementioned conditions, the amount of Zn2+/NAC2− species starts to become important when concentration of NAC exceeds 0.4 mmol dm−3; however even if c NAC was 0.01 mol dm−3, the formation percentage of the Zn(NAC)2 2− species would have been lower than the corresponding Zn(Cys)2 2−, that remains the most relevant species in human blood plasma, among the low molecular weight ligands. To give an example, the zinc distribution when c NAC = 1 mmol dm−3 is provided in Fig. 6 (only species with percentage greater than 1%).
Fig. 6.
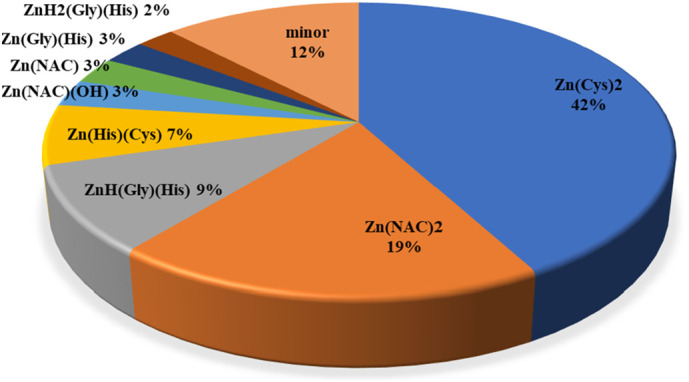
Pie chart of the zinc species in blood plasma in the following experimental condition: T = 310.15 K, cNAC = 1.0 mmol dm−3. Concentration of components in Table S8, equilibrium constants in Table S10.
The sequestering ability was evaluated computing the pL0.5 values in different condition. This parameters is strongly dependent on the condition in which it is determined, since it is able, because of its calculation [43], to measure the ability of the ligand under investigation to sequester the target cation also taking into account the side reactions present in that specific conditions. To underline this aspect, the trend of the calculated pL0.5 in sea water and in NaCl(aq) at I = 0.72 mol dm−3 is given in Fig. 7 .
Fig. 7.
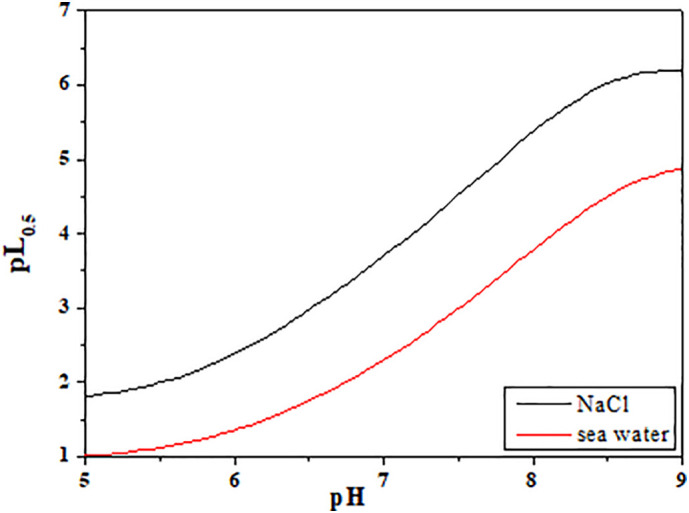
Trend of pL0.5vs. pH at T = 298.15 K in sea water and in NaCl(aq) (at I = 0.7 mol dm−3).
The pH range investigated is 5 to 9, which is of course not very informative for sea water, but it is useful to demonstrate what claimed. The stability constants used, the “effective” ones, are identical, because the total ionic strength is the same in both cases. However, the composition of the solutions is different: in the case of NaCl(aq) the ions concurring to the ionic strength are only Na+ and Cl−, whereas for sea water much more components are involved, including sulfate, potassium etc. In other words, the shift between the two diagrams, which is about one order of magnitude, measures the lowering of the ability of NAC to sequester Zn2+ due to the presence of sea water components. The pL0.5 calculated in the conditions of sea water (pH = 8.1, I = 0.72 mol dm−3) is 3.9, meaning that the amount of NAC required to sequester 50% of total Zn2+ (at c Zn = 10−10 mol dm−3) is 10−3.9 mol dm−3 = 0.13 mmol dm−3. In the same condition, but in NaCl(aq) the value is lower being 0.0035 mmol dm−3, indicating that NAC can be considered as a good sequestering agent in the pH range 7 to 9. In human blood plasma this calculation was not performed considering that the concentration ranges cannot be considered to vary that much.
4. Conclusions
This work represents an advance in the knowledge of the acid-base properties of N-Acetyl-L-cysteine and its interaction with metal cations of great relevance in biological and environmental fields, such as Ca2+, Mg2+ and Zn2+. NAC shows two well separated protonation steps, and the main species in the pH window of natural fluids is the monoprotonated HL−, with a protonated thiol group and a deprotonated carboxylate group. Calculating the stepwise thermodynamic functions, ΔG 0, ΔH 0 and TΔS0, it results that both processes are exothermic (negative ΔH 0 values) and entropic in nature, even if the first only by few kJ mol−1. For example, at infinite dilution, the values are: ΔG 0 1 = −56.7 kJ mol−1; ΔH 0 1 = −27.4 kJ mol−1; TΔS 0 1 = 29.3 kJ mol−1 and ΔG 0 2 = −18.7 kJ mol−1; ΔH 0 2 = −2.9 kJ mol−1; TΔS 0 2 = 15.8 kJ mol−1. The determination of the protonation constants in NaCl(aq), (CH3)4NCl(aq) and (C2H5)4NI(aq) enabled the determination of four weak species by means of the so-called ΔpK method, namely NaL−, NaHL0 (aq), (CH3)4NL− and (CH3)4NHL0 (aq), whose presence is useful in the speciation modeling of real multicomponent solutions. Metal complexation is relevant in all the pH range, but the speciation scheme of the M2+/NAC2− system is still under debate: most authors agree about the presence of ML0 (aq) and ML2 2− species, with the second one to be the most relevant. In addition, the MHL+, ML3 4−, M(OH)L− and ML2(OH)3− were also determined, but only the mixed hydrolytic ones resulted to be important in natural fluids with pH > 8 (see Fig. 5, for example). As regards the speciation in natural fluids, NAC was found to form complexes with Zn2+ especially when it is present at a trace level, for example in sea water, with c Zn = 10−6 mol dm−3 and c NAC = 5·10−4 mol dm−3, more than 70% of total zinc is present as a complex species with NAC; in blood plasma, NAC resulted to be important in zinc speciation when it is present at c NAC > 3·10−4 mol dm−3, but the main species remain the Zn(Cys)2 2−.
In conclusion, in this paper the analysis of the data was performed according to two approaches, a first one in which data in NaCl(aq) were processed with Debye-Hückel and SIT equations and another in which the data were compared to ionic media that do not interact with the ligand, allowing to determine stability constants that are independent of the medium, to be used in combination with stability constants of “weak species” between the ions under study (e.g., Zn2+, Ca2+, Mg2+ and NAC) and the components of the solution (e.g., Na+, K+, Cl−, SO4 2−). This last aspect was found to be very promising in the study of the chemical speciation in natural fluids, where many components are present with different concentrations. It was also shown that the two approaches display the same modeling ability, but the second one is designed to also consider species that generally are considered to be negligible. The great advantage of the “effective” model is that the conversion from one model to another can be done, with a good approximation as shown in Fig. 4, without doing experiments in each specific ionic medium but “just” knowing the thermodynamic equilibrium constants and the weak complexes between the ligand and the cation under study and the component of the solution. The whole of the results coming from this thermodynamic study, especially those coming from the pL0.5 calculation, may aid in the design of new materials able to selectively remove target cationic pollutants in specific conditions, from natural fluids. In this sense, for example, being Na+, Ca2+ and Mg2+ the most abundant metal cations in sea water, the assessment of their interactions with NAC ought to be considered as an essential tool to develop NAC-based sorbents for other trace contaminants removal.
Funding
We thank UniME (Research & Mobility2017, Prot. 009041).
CRediT authorship contribution statement
Clemente Bretti: Conceptualization, Validation, Investigation, Writing - original draft. Paola Cardiano: Methodology, Project administration, Resources, Visualization. Anna Irto: Validation, Investigation, Visualization. Gabriele Lando: Methodology, Writing - review & editing, Formal analysis, Data curation. Demetrio Milea: Conceptualization, Project administration, Formal analysis. Silvio Sammartano: Conceptualization, Methodology, Software, Supervision, Funding acquisition, Resources, Formal analysis.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
Authors wish to thank reviewers and editor for helpful discussion during the peer-review process.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.molliq.2020.114164.
Appendix A. Supplementary data
Supplementary tables
Supplementary material
References
- 1.Berk M., Frye R.E. Springer Nature Singapore Pte Ltd; Singapore: 2019. The Therapeutic Use of N-Acetylcysteine (NAC) in Medicine. [Google Scholar]
- 2.Šalamon Š., Kramar B., Marolt T.P., Poljšak B., Milisav I. Antioxidants (Basel) 2019;8:111. doi: 10.3390/antiox8050111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ziment I. Biomed. Pharmacother. 1988;42:513. [PubMed] [Google Scholar]
- 4.Holdiness M.R. Clin. Pharmacokinet. 1991;20:123. doi: 10.2165/00003088-199120020-00004. [DOI] [PubMed] [Google Scholar]
- 5.Kerksick C., Willoughby D. J. Int. Soc. Sports Nutr. 2005;2:38. doi: 10.1186/1550-2783-2-2-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.S K.G. Altern. Med. Rev. 1998;3:114. [PubMed] [Google Scholar]
- 7.Aldini G., Altomare A., Baron G., Vistoli G., Carini M., Borsani L., Sergio F. Free Radic. Res. 2018;52:751. doi: 10.1080/10715762.2018.1468564. [DOI] [PubMed] [Google Scholar]
- 8.Brown J.R., Block C.A., Malenka D.J., O'Connor G.T., Schoolwerth A.C., Thompson C.A. JACC Cardiovasc Interv. 2009;2:1116. doi: 10.1016/j.jcin.2009.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dean O G.F., Berk M.J. Psychiatry Neurosci. 2011;36:78. doi: 10.1503/jpn.100057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gadallah A.-H.A., Ebada M.A., Gadallah A., Ahmed H., Rashad W., Eid K.A., Bahbah E., Alkanj S. J. Obsess.-Compuls. Rel. 2020;25 [Google Scholar]
- 11.McQueen G., Lay A., Lally J., Gabay A.S., Collier T., Lythgoe D.J., Barker G.J., Stone J.M., McGuire P., MacCabe J.H., Egerton A. Psychophar. 2020;237:443. doi: 10.1007/s00213-019-05382-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mohamed D.I., Khairy E., Khedr S.A., Habib E.K., Elayat W.M., El-kharashi O.A. Neurochem. Int. 2020;132:104602. doi: 10.1016/j.neuint.2019.104602. [DOI] [PubMed] [Google Scholar]
- 13.Adachi Y., Yoshikawa Y., Sakurai H. Biofactors. 2007;29:213. doi: 10.1002/biof.5520290405. [DOI] [PubMed] [Google Scholar]
- 14.Chen J., Yadav N.N., Stait-Gardner T., Gupta A., Price W.S., Zheng G. NMR Biomed. 2020;33 doi: 10.1002/nbm.4188. [DOI] [PubMed] [Google Scholar]
- 15.Zhang J., Chan C.-K., Ham Y.-H., Chan W. Chem. Res. Toxicol. 2020;33:1374–1381. doi: 10.1021/acs.chemrestox.9b00488. [DOI] [PubMed] [Google Scholar]
- 16.Mendonça M.C.P., Rodrigues N.P., Scott-Fordsmand J.J., Jesus M.B.d., Amorim M.J.B. Environ. Pollut. 2020;256 doi: 10.1016/j.envpol.2019.113484. [DOI] [PubMed] [Google Scholar]
- 17.Mendonça M.C.P., de Jesus M.B., van Gestel C.A.M. Sci. Tot. Environ. 2020;715 doi: 10.1016/j.scitotenv.2020.136797. [DOI] [PubMed] [Google Scholar]
- 18.Reid M.B., Stokić D.S., Koch S.M., Khawli F.A., Leis A.A. J. Clin. Invest. 1994;94:2468. doi: 10.1172/JCI117615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stamler J., Mendelsohn M.E., Amarante P., Smick D., Andon N., Davies P.F., Cooke J.P., Loscalzo J. Circ. Res. 1989;65:789. doi: 10.1161/01.res.65.3.789. [DOI] [PubMed] [Google Scholar]
- 20.Notartomaso S., Scarselli P., Mascio G., Liberatore F., Mazzon E., Mammana S., Gugliandolo A., Cruccu G., Bruno V., Nicoletti F., Battaglia G. Mol. Pain. 2020;16:1. doi: 10.1177/1744806920904292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.De Flora S., Bennicelli C., Camoirano A., Serra D., Romano M., Rossi G.A., Morelli A., De Flora A. Carcinogene. 1985;6:1735. doi: 10.1093/carcin/6.12.1735. [DOI] [PubMed] [Google Scholar]
- 22.Gregory S., Kelly N.D. Altern. Med. Rev. 1998;3:114. [PubMed] [Google Scholar]
- 23.McCarty M.F., Di Nicolantonio J.J. Prog. Cardiovasc. Dis. 2020;63:383–385. doi: 10.1016/j.pcad.2020.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Colak N., Torun H., Gruz J., Strnad M., Ayaz F.A. Ecotoxicol. Environ. Safety. 2019;181:49. doi: 10.1016/j.ecoenv.2019.05.052. [DOI] [PubMed] [Google Scholar]
- 25.Unsal V., Dalkıran T., Çiçek M., Kölükçü E. Adv. Pharm. Bull. 2020;10:184. doi: 10.34172/apb.2020.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rossignol Daniel A. In: The Therapeutic Use of N-Acetylcysteine (NAC) in Medicine. Frye R.E., Berk M., editors. Springer; 2019. [Google Scholar]
- 27.Pena-Llopis S., Serrano R., Pitarch E., Beltrán E., Ibáñez M., Hernández F., Peña J.B. Aquatic Toxicol. 2014;154:131. doi: 10.1016/j.aquatox.2014.05.006. [DOI] [PubMed] [Google Scholar]
- 28.Han X., Xu M., Yang S., Qiana J., Hua D. J. Mater. Chem. A. 2017;5:5123. [Google Scholar]
- 29.Kazemi A., Bahramifar N., Heydari A., Olsen S.I. J. Taiwan Inst. Chem. Eng. 2019;95:78. [Google Scholar]
- 30.Evli S., Karagözler A.A., Güven G., Orhan H., Uygun M., Uygun D.A. Bull. Mater. Sci. 2020;43:107. [Google Scholar]
- 31.Quyoom S., Khan B. J. Chem. 2009;9:S117. [Google Scholar]
- 32.Jalilehvand F., Parmar K., Zielke S. Metallomics. 2013;5:1368. doi: 10.1039/c3mt00173c. [DOI] [PubMed] [Google Scholar]
- 33.Santoso S.P., Chandra I.K., Soetaredjo F.E., Angkawijaya A.E., Ju Y.H. J. Chem. Eng. Data. 2014;59:1661. [Google Scholar]
- 34.Cardiano P., Foti C., Giuffrè O. J. Mol. Liquids. 2016;223:360. [Google Scholar]
- 35.Gockel P., Vahrenkamp H., Zuberbühler A.D. Helv. Chim. Acta. 1993;76:511. [Google Scholar]
- 36.Perrin D.D., Armarego W.L.F. 3rd ed. Pergamon Press; Oxford (UK): 1988. Purification of Laboratory Chemicals. [Google Scholar]
- 37.Cigala R.M., Crea F., De Stefano C., Lando G., Manfredi G., Sammartano S. J. Mol. Liquids. 2012;165:143. [Google Scholar]
- 38.Bottari E., Braibanti A., Ciavatta L., Corrie A.M., Daniele P.G., Dallavalle F., Grimaldi M., Mastroianni A., Mori G., Ostacoli G., Paoletti P., Rizzarelli E., Sammartano S., Severini C., Vacca A., Williams D.R. Ann. Chim. (Rome) 1978;68:813. [Google Scholar]
- 39.De Stefano C., Sammartano S., Mineo P., Rigano C. In: Marine Chemistry - An Environmental Analytical Chemistry Approach. Gianguzza A., Pelizzetti E., Sammartano S., editors. Kluwer Academic Publishers; Amsterdam: 1997. pp. 71–83. [Google Scholar]
- 40.Alderighi L., Gans P., Ienco A., Peters D., Sabatini A., Vacca A. Coord. Chem. Rev. 1999;194:311. [Google Scholar]
- 41.De Robertis A., De Stefano C., Sammartano S., Rigano C. Talanta. 1987;34:933. doi: 10.1016/0039-9140(87)80132-7. [DOI] [PubMed] [Google Scholar]
- 42.De Stefano C., Foti C., Sammartano S., Gianguzza A., Rigano C. Ann. Chim. (Rome) 1994;84:159. [Google Scholar]
- 43.Crea F., De Stefano C., Foti C., Milea D., Sammartano S. Curr. Med. Chem. 2014;21:3819. doi: 10.2174/0929867321666140601160740. [DOI] [PubMed] [Google Scholar]
- 44.Brønsted J.N. J. Am. Chem. Soc. 1922;44:938. [Google Scholar]
- 45.Bjerrum N. Mat. Fys. Medd. K. Dan. Vidensk. Selsk. 1926;7:1. [Google Scholar]
- 46.Guggenheim E.A. Philos. Mag. 1935;19:588. [Google Scholar]
- 47.Biederman G. Dahlem Konferenzen; Berlin: 1975. Dahlem Workshop on the Nature of Seawater; p. 339. [Google Scholar]
- 48.Grenthe I., Puigdomenech I. OECD; Paris: 1997. Modelling in Aquatic Chemistry. [Google Scholar]
- 49.Daniele P.G., Foti C., Gianguzza A., Prenesti E., Sammartano S. Coord. Chem. Rev. 2008;252:1093. [Google Scholar]
- 50.Bretti C., De Stefano C., Lando G., Sammartano S. Fluid Phase Equilibr. 2010;292:71. [Google Scholar]
- 51.Berto S., Daniele P.G., Lando G., Prenesti E., Sammartano S. Int. J. Electrochem. Sci. 2012;7:10976. [Google Scholar]
- 52.Bretti C., Cukrowski I., De Stefano C., Lando G. J. Chem. Eng. Data. 2014;59:3728. [Google Scholar]
- 53.Bretti C., Cigala R.M., De Stefano C., Lando G., Sammartano S. Chemosphere. 2016;150:341. doi: 10.1016/j.chemosphere.2016.02.023. [DOI] [PubMed] [Google Scholar]
- 54.Crea F., De Stefano C., Foti C., Lando G., Milea D., Sammartano S. Met. Ions Life Sci. 2016;16:133. doi: 10.1007/978-3-319-21756-7_5. [DOI] [PubMed] [Google Scholar]
- 55.Bretti C., Cigala R.M., De Stefano C., Lando G., Sammartano S. Fluid Phase Equilibr. 2017;434:63. [Google Scholar]
- 56.Majlesi K., Bretti C., Cigala R.M., De Stefano C., Majlesi K., Sammartano S. J. Solut. Chem. 2018;47:528. [Google Scholar]
- 57.Bretti C., De Stefano C., Lando G., Sammartano S. J. Chem. Thermodyn. 2018;123 [Google Scholar]
- 58.Arena G., Bretti C., Grasso G.I., Lando G., Sammartano S., Sgarlata C. J. Chem. Thermodyn. 2019;139 [Google Scholar]
- 59.Bretti C., Cigala R.M., De Stefano C., Lando G., Sammartano S. J. Mol. Liquids. 2019;274:68. [Google Scholar]
- 60.Pytkowicz R.M. vol. 1. CRC Press, Inc.; 1979. Activity Coefficients in Electrolyte Solutions. [Google Scholar]
- 61.Pytkowicz R.M. vol. 2. CRC Press, Inc.; 1979. Activity Coefficients in Electrolyte Solutions. [Google Scholar]
- 62.Martell A.E., Smith R.M., Motekaitis R.J. 2004. NIST Standard Reference Database 46, vers.8. Gaithersburg. [Google Scholar]
- 63.Baes C.F., Mesmer R.E. Wiley; New York: 1976. The Hydrolysis of Cations. [Google Scholar]
- 64.Brown P.L., Ekberg C. Wiley-VCH Verlag GmbH & Co; Weinheim (Germany): 2016. Hydrolysis of Metal Ions. [Google Scholar]
- 65.Powell K.J., Brown P.L., Byrne R.H., Gajda T., Hefter G., Leuz A.K., Sjöberg S., Wanner H. Pure Appl. Chem. 2013;85:2249. [Google Scholar]
- 66.Kiss T., Sòvago I., Gergely A. Pure Appl. Chem. 1991;63:597. [Google Scholar]
- 67.Berthon G. Pure Appl. Chem. 1995;67:1117. [Google Scholar]
- 68.Arena G., Musumeci S., Rizzarelli E., Sammartano S., Rigano C. Transit. Met. Chem. 1980;5:297. [Google Scholar]
- 69.Zucconi T.D., Janauer G.E., Donahe S., Lewkowicz C. J. Pharma. Sci. 1979;68:426. doi: 10.1002/jps.2600680409. [DOI] [PubMed] [Google Scholar]
- 70.de Brabander H.F., Creyf H.S., Goeminne A.M., van Poucke L.C. Talanta. 1976;23:405. doi: 10.1016/0039-9140(76)80059-8. [DOI] [PubMed] [Google Scholar]
- 71.May P.M., Muray K. Talanta. 1991;38:1419. doi: 10.1016/0039-9140(91)80290-g. [DOI] [PubMed] [Google Scholar]
- 72.Crea F., Milea D., Sammartano S. Ann. Chim. (Rome) 2005;95:767. doi: 10.1002/adic.200590090. [DOI] [PubMed] [Google Scholar]
- 73.Crea F., De Stefano C., Milea D., Pettignano A., Sammartano S. Bioinorg. Chem. Appl. 2015;2015:12. doi: 10.1155/2015/267985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Inczédy J., Maróthy J. Acta Chim. Acad. Sci. Hung. 1975;86:1–2. [Google Scholar]
- 75.Kester D., Ahrland S., Beasley T., Bernhard M., Branica M., Campbell I., Eichhorn G., Kraus K., Kreinling K., MIllero F.J., Nuernberg H., Piro A., Pytkowicz R.M., Steffan L., Stumm W. 1975. Dahlem Workshop on the Nature of Seawater, Berlin. [Google Scholar]
- 76.Hallman P.S., Perrin D.D., Watt A.E. Biochem. J. 1971;121:549. doi: 10.1042/bj1210549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Cigala R.M., Crea F., De Stefano C., Foti C., Milea D., Sammartano S. Monat. Chem. 2015;146:527. [Google Scholar]
- 78.Cigala R.M., Crea F., De Stefano C., Lando G., Milea D., Sammartano S. Amino Acids. 2012;43:629. doi: 10.1007/s00726-011-1110-0. [DOI] [PubMed] [Google Scholar]
- 79.Lentner C. 8th ed. CIBA-Geigy; Basilea, Switzerland: 1983. Geigy Scientific Tables. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary tables
Supplementary material