Estimating the genome-wide contribution of selection to temporal allele frequency change

Significance

A long-standing problem in evolutionary biology is to understand the processes that shape the genetic composition of populations. In a population without migration, two processes that change allele frequencies are selection, which increases beneficial alleles and removes deleterious ones, and genetic drift, which randomly changes frequencies as some parents contribute more or fewer alleles to the next generation. Previous efforts to disentangle these processes have used genomic samples from a single time point and models of how selection affects neighboring sites (linked selection). Here, we use genomic data taken through time to quantify contributions of selection and drift to genome-wide frequency changes. We show that selection acts over short timescales in three evolve-and-resequence studies and has a sizable genome-wide impact.

Abstract

Rapid phenotypic adaptation is often observed in natural populations and selection experiments. However, detecting the genome-wide impact of this selection is difficult since adaptation often proceeds from standing variation and selection on polygenic traits, both of which may leave faint genomic signals indistinguishable from a noisy background of genetic drift. One promising signal comes from the genome-wide covariance between allele frequency changes observable from temporal genomic data (e.g., evolve-and-resequence studies). These temporal covariances reflect how heritable fitness variation in the population leads changes in allele frequencies at one time point to be predictive of the changes at later time points, as alleles are indirectly selected due to remaining associations with selected alleles. Since genetic drift does not lead to temporal covariance, we can use these covariances to estimate what fraction of the variation in allele frequency change through time is driven by linked selection. Here, we reanalyze three selection experiments to quantify the effects of linked selection over short timescales using covariance among time points and across replicates. We estimate that at least 17 to 37% of allele frequency change is driven by selection in these experiments. Against this background of positive genome-wide temporal covariances, we also identify signals of negative temporal covariance corresponding to reversals in the direction of selection for a reasonable proportion of loci over the time course of a selection experiment. Overall, we find that in the three studies we analyzed, linked selection has a large impact on short-term allele frequency dynamics that is readily distinguishable from genetic drift.

A long-standing problem in evolutionary genetics is quantifying the roles of genetic drift and selection in shaping genome-wide allele frequency changes. Selection can affect allele frequencies, both directly and indirectly, with the indirect effect coming from the action of selection on correlated loci elsewhere in genome [e.g., linked selection (1–4); ref. 5 has a review]. Previous work has mostly focused on teasing apart the impacts of drift and selection on genome-wide diversity using population samples from a single contemporary time point, often by modeling the correlation between regional recombination rate, gene density, and diversity created in the presence of linked selection (6, 7). This approach has shown that linked selection has a major role in shaping patterns of genome-wide diversity across the genomes of a range of sexual species (8–16) and has allowed us to quantify the relative influence of positive selection (hitchhiking) and negative selection (background selection) (8, 9, 16–19). However, we lack an understanding of both how linked selection acts over short time intervals and its full impact on genome-wide allele frequency changes.

There are numerous examples of rapid phenotypic adaptation (20–23) and rapid, selection-driven genomic evolution in asexual populations (24–26). Yet, the polygenic nature of fitness makes detecting the impact of selection on genome-wide variation over short timescales in sexual populations remarkably difficult (27–29). This is because the effect of selection on a polygenic trait (such as fitness) is distributed across numerous loci. This can lead to subtle allele frequency shifts on standing variation that are difficult to distinguish from background levels of genetic drift and sampling variance. Increasingly, genomic experimental evolution studies with multiple time points, and in some cases multiple replicate populations, are being used to detect large-effect selected loci (30, 31) and differentiate modes of selection (32–34). In addition, these temporal–genomic studies have begun in wild populations, some with the goal of finding variants that exhibit frequency changes consistent with fluctuating selection (35, 36). In a previous paper, we proposed that one useful signal for understanding the genome-wide impact of polygenic linked selection detectable from temporal genomic data is the temporal autocovariance (i.e., covariance between two time points) of allele frequency changes (37). These covariances are created when the loci that underly heritable fitness variation perturb the frequencies of linked alleles; in contrast, when genetic drift acts alone in a closed population, these covariances are expected to be zero for neutral alleles. Mathematically, temporal covariances are useful because it is natural to decompose the total variance in allele frequency change across a time interval into the variances and covariances in allele frequency change between generations. Furthermore, biologically, these covariances reflect the extent to which allele frequency changes in one generation predict changes in another due to shared selection pressures and associations with selected loci.

Here, we provide empirical analyses to quantify the impact of linked selection acting over short timescales (tens of generations) across two evolve-and-resequence studies (33, 38) and an artificial selection experiment (39). These sequencing selection experiments have started to uncover selected loci contributing to the adaptive response; however, it is as yet far from clear how much of genome-wide allele frequency changes are driven by selection or genetic drift. We repeatedly find a signal of temporal covariance, consistent with linked selection acting to significantly perturb genome-wide allele frequency changes across the genome in a manner that other approaches would not be able differentiate from genetic drift. We estimate a lower bound of the fraction of variance in allele frequency change caused by selection, as well as the correlation between allele frequency changes between replicate populations caused by convergent selection pressures. Overall, we demonstrate that linked selection has a powerful role in shaping genome-wide allele frequency changes over very short timescales in experimental evolution.

Results

We first analyzed the dataset of Barghi et al. (33), an evolve-and-resequence study with 10 replicate populations exposed to a high-temperature laboratory environment, evolved for 60 generations, and sequenced every 10 generations. Using the seven time points and 10 replicate populations, we estimated the genome-wide $6\times 6$ temporal covariance matrix $\mathbf{Q}$ for each of the 10 replicates. Each row of these matrices represents the temporal covariance Cov(Δ₁₀p_s,Δ₁₀pt) between the allele frequency change (in 10-generation intervals, denoted Δ₁₀p_t) of some initial reference generation $s$ (the row of the matrix) and some later time point $t$ (the column of the matrix). We corrected these matrices for biases created due to sampling noise and normalized the entries for heterozygosity (SI Appendix, sections S1.2 and S1.4). These covariances are expected to be zero when only drift is acting, as only heritable variation for fitness can create covariance between allele frequency changes in a closed population (37). Averaging across the 10 replicate temporal covariances matrices, we find temporal covariances that are statistically significant (95% block bootstraps CIs do not contain zero), consistent with linked selection perturbing genome-wide allele frequency changes over very short time periods. The covariances between all adjacent time intervals are positive and then decay toward zero as we look at more distant time intervals (Fig. 1A), as expected when directional selection affects linked variants’ frequency trajectories until ultimately linkage disequilibrium (LD) and the associated additive genetic variance for fitness decays (which could occur as a population reaches a new optimum and directional selection weakens) (37). The temporal covariances per replicate are noisier, but this general pattern holds (SI Appendix, Fig. S23).

Fig. 1.

(A) Temporal covariance, averaged across all 10 replicate populations, through time from the Barghi et al. (33) study. Each line depicts the temporal covariance $\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_s,\mathrm{\Delta }{p}_t\right)$ from some reference generation $s$ to a later time $t$, which varies along the x axis; each line corresponds to a row of the triangle of the temporal covariance matrix with the same color (Right). The ranges around each point are $95\%$ block bootstrap CIs. (B) A lower bound on the proportion of the total variance in allele frequency change explained by linked selection, $G\left(t\right)$, as it varies through time $t$ along the x axis. The black line is the $G\left(t\right)$ averaged across replicates, with the $95\%$ block bootstrap CI. The other lines are the $G\left(t\right)$ for each individual replicate, with colors indicating what subset of the temporal covariance matrix in Right is being included in the calculation of $G\left(t\right)$.

Since our covariances are averages over loci, the covariance estimate could be strongly affected by a few outlier regions. To test whether large outlier regions drive the genome-wide signal we see in the Barghi et al. (33) data, we calculate the covariances in 100-kb windows along the genome (we refer to these as windowed covariances throughout) and take the median windowed covariance (and trimmed-mean windowed covariance) as a measure of the genome-wide covariance robust to large-effect loci. These robust estimates (SI Appendix, Table S1 and Fig. S24) confirm the patterns we see using the mean covariance, establishing that genomic temporal covariances are nonzero due to the impact of selection acting across many genomic regions.

While the presence of positive temporal covariances is consistent with selection affecting allele frequencies over time, this measure is not easily interpretable. We can calculate a more intuitive measure from the temporal covariances to quantify the impact of selection on allele frequency change: the ratio of total covariance in allele frequency change to the total variance in allele frequency change. We denote the change in allele frequency as $\mathrm{\Delta }{p}_t=p_{t+1}-p_t$, where $p_t$ is the allele frequency in generation $t$. Since the total variation in allele frequency change can be partitioned into variance and covariance components, $\mathrm{\text{Var}}\left(p_t-p_0\right)={\sum }_{i=0}^{t-1}\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_i\right)+{\sum }_{i=0}^{t-1}{\sum }_{j\ne i}^{t-1}\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_i,\mathrm{\Delta }{p}_j\right)$ (we correct for biases due to sequencing depth), and the covariances are zero when drift acts alone, this is a lower bound on how much of the variance in allele frequency change is caused by linked selection (37). We call this measure $G\left(t\right)$, defined as

$$G\left(t\right)=\frac{{\sum }_{i=0}^{t-1}{\sum }_{j\ne i}^{t-1}\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_i,\mathrm{\Delta }{p}_j\right)}{\mathrm{\text{Var}}\left(p_t-p_0\right)}.$$ [1]

This estimates the impact of selection on allele frequency change between the initial generation 0 and some later generation $t$, which can be varied to see how this quantity grows through time. When the sum of the covariances is positive, this measure can intuitively be understood as a lower bound on relative fraction of allele frequency change normally thought of as “drift” that is actually due to selection. Additionally, $G\left(t\right)$ can be understood as a short-timescale estimate of the reduction in neutral diversity due to linked selection (or equivalently, the reduction in neutral effective population size needed to account linked selection) (SI Appendix, section S7). Since the Barghi et al. (33) experiment is sequenced every 10 generations, the numerator uses the covariances estimated between 10-generation blocks of allele frequency change; thus, the strong, unobservable covariances between adjacent generations do not contribute to the numerator of $G\left(t\right)$. Had these covariances been measurable on shorter timescales, their cumulative effect would likely have been higher yet (SI Appendix, sections S2 and S8.4 have more details). Additionally, selection inflates the variance in allele frequency change per generation; however, this effect cannot be easily distinguished from drift. For both these reasons, our measure $G\left(t\right)$ is quite conservative (we demonstrate this through simulations in SI Appendix, section S8.4). Still, we find a remarkably strong signal. Greater than $20\%$ of total, genome-wide allele frequency change over 60 generations is the result of selection (Fig. 1B). This proportion of variance attributable to selection builds over time in Fig. 1B as the effects of linked selection are compounded over the generations unlike genetic drift. Our G(t) starts to plateau to a constant level as the covariances from earlier generations have decayed and so, no longer contribute as strongly (Fig. 1).

Additionally, we looked for a signal of temporal autocovariance in Bergland et al. (35), a study that collected Drosophila melanogaster through spring–fall season pairs across 3 years. If there was a strong pattern of genome-wide fluctuating selection, we might expect a pattern of positive covariances between similar seasonal changes (e.g., spring–fall in two adjacent years) and negative covariances between dissimilar seasonal changes (e.g., spring–fall and fall–spring in two adjacent years). However, we find no such signal over years, and in reproducing their original analysis, we find that their number of statistically significant seasonal polymorphisms is not enriched compared with an empirical null distribution created by permuting seasonal labels (we discuss this in more depth in SI Appendix, section S6).

The replicate design of Barghi et al. (33) allows us to quantify another covariance: the covariance in allele frequency change between replicate populations experiencing convergent selection pressures. These between-replicate covariances are created in the same way as temporal covariances: alleles linked to a particular fitness background are expected to have allele frequency changes in the same direction if the selection pressures are similar. Intuitively, where temporal covariances reflect that alleles associated with heritable fitness backgrounds are predictive of frequency changes between generations, replicate covariances reflect that heritable fitness backgrounds common to each replicate predict (under the same selection pressures) frequency changes between replicates; we note that there is not a direct one-to-one correspondence between temporal and replicate covariances since the latter are driven by a shared selection pressure and the stochastic genetic backgrounds across replicate populations. We measure this through a statistic similar to a correlation, which we call the convergent correlation: the ratio of average between-replicate covariance across all pairs to the average SD across all pairs of replicates:

$$\mathrm{c}\mathrm{o}\mathrm{r}\left(\mathrm{\Delta }{p}_s,\mathrm{\Delta }{p}_t\right)=\frac{{\mathbb{E}}_{A\ne B}\left(\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_{s,A},\mathrm{\Delta }{p}_{t,B}\right)\right)}{{\mathbb{E}}_{A\ne B}\left(\sqrt{\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{s,A}\right)\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{t,B}\right)}\right)},$$ [2]

where $A$ and $B$ here are two replicate labels, and for the Barghi et al. (33) data, we use Δ₁₀p_t.

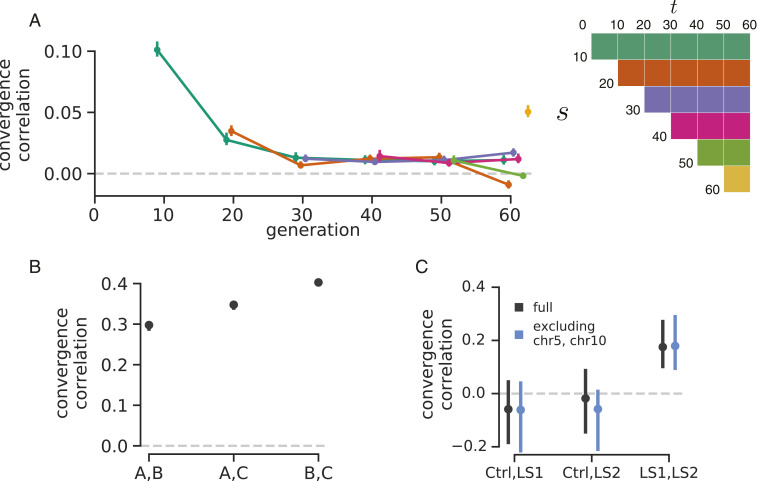
We have calculated the convergent correlation for all rows of the replicate covariance matrices. Like temporal covariances, we visualize these through time (Fig. 2 A, Left), with each line representing the convergent correlation from a particular reference generation $s$ as it varies with $t$ (shown on the x axis). In other words, each of the colored lines corresponds to the like-colored row of the convergence correlation matrix (Fig. 2 A, Right). We find that these convergent correlation coefficients are relatively weak and decay very quickly from an initial value of about 0.1 (95% block bootstrap CIs $\left[0.094,0.11\right]$) to around 0.01 (95% CIs [0.0087, 0.015]) within 20 generations. This suggests that while a substantial fraction of the initial response is shared over the replicates, this is followed by a rapid decay, a result consistent with the primary finding of the original Barghi et al. (33) study: that alternative loci contribute to longer-term adaptation across the different replicates.

Fig. 2.

(A) The convergence correlations, averaged across Barghi et al. (33) replicate pairs, through time. Each line represents the convergence correlation $\mathrm{c}\mathrm{o}\mathrm{r}\left(\mathrm{\Delta }{p}_s,\mathrm{\Delta }{p}_t\right)$ from a starting reference generation $s$ to a later time $t$, which varies along the x axis; each line corresponds to a row of the temporal convergence correlation matrix depicted on Right (where the diagonal elements represent the convergence correlations between the same time points across replicate populations). We note that convergent correlation for the last time point is an outlier; we are unsure as to the cause of this (e.g., it does not appear to be driven by a single pair of replicates). (B) The convergence correlations between individual pairs of replicates in the Kelly and Hughes (38) data (note that the CIs are plotted but are small on this y-axis scale). (C) The convergence correlations between individual pairs of replicates in the data from Castro et al. (39) for the two selection lines (LS1 and LS2) and the control (Ctrl); gray CIs are those using the complete dataset, and blue CIs exclude chromosome 5 (chr5) and chr10, which harbor the two regions Castro et al. (39) found to have signals of parallel selection between LS1 and LS2. Through simulations, we have found that the differences in convergence correlation CI widths between these Drosophila studies and the Longshanks study are due to the differing population sizes.

A benefit of between-replicate covariances is that unlike temporal covariances, these can be calculated with only two sequenced time points and a replicated study design. This allowed us to assess the impact of linked selection in driving convergent patterns of allele frequency change across replicate populations in two other studies. First, we reanalyzed the selection experiment of Kelly and Hughes (38), which evolved three replicate wild populations of Drosophila simulans for 14 generations adapting to a novel laboratory environment. Since each replicate was exposed to the same selection pressure and shared LD common to the original natural founding population, we expected each of the three replicate populations to have positive convergence correlations. We find that all three convergent correlation coefficients between replicate pairs are significant (Fig. 2B) and average to 0.36 ($95\%$ CI $\left[0.31,0.40\right]$). Additionally, we can calculate the proportion of the total variance in allele frequency change from convergent selection pressure, analogous to our $G\left(t\right)$, where the numerator is the convergent covariance and the denominator is the total variance (SI Appendix, section S4). We find that 37% of the total variance is due to shared allele frequency changes caused by selection (95% CI [29%, 41%]); these are similar to the convergence correlation since the variance is relatively constant across the replicates.

Next, we reanalyzed the Longshanks selection experiment, which selected for longer tibiae length relative to body size in mice, leading to a response to selection of about 5 SDs over the course of 20 generations (39, 40). This study includes two independent selection lines, Longshanks 1 (LS1) and Longshanks 2 (LS2), and an unselected control line (Ctrl) where parents were randomly selected. Consequently, this selection experiment offers a useful control to test our convergence correlations: we expect to see significant positive convergence correlations in the comparison between the two Longshanks selection lines but not between each of the control and Longshanks line pairs. We find that this is the case (gray CIs in Fig. 2C), with convergence correlations between each of the Longshanks lines and the control not being statistically different from zero, while the convergence correlation between the two Longshanks lines is strong (0.18) and statistically significant (CIs [0.07, 0.25]).

One finding in the Longshanks study was that two major-effect loci showed parallel frequency shifts between the two selection lines. We were curious to what extent our genome-wide covariances were being driven by these two outlier large-effect loci, so we excluded them from the analysis. Since we do not know the extent to which LD around these large-effect loci affects neighboring loci, we took the conservative precaution of excluding the entire chromosomes these loci reside on (chromosomes 5 and 10) and recalculating the temporal covariances. We find that excluding these large-effect loci has little impact on the CIs (blue CIs in Fig. 2C), indicating that these across-replicate covariances are indeed driven by a large number of loci. This is consistent with a signal of selection on a polygenic trait driving genome-wide change, although we note that large-effect loci can contribute to the indirect change at unlinked loci (41, 42).

The presence of an unselected control line provides an alternative way to partition the effects of linked selection and genetic drift: we can compare the total variance in allele frequency change of the control line (which excludes the effect of artificial selection on allele frequencies) with the total variance in frequency change of the Longshanks selection lines. This allows us to estimate the increase in variance in allele frequency change due to selection, which we can further partition into the effects of selection shared between selection lines and those unique to a selection line by estimating the shared effect through the observed covariance between replicates (Materials and Methods and SI Appendix, section S4 have more details). We estimate at least 32% (95% CI $\left[21\%,48\%\right]$) of the variance in allele frequency change is driven by the effects of selection, of which 14% (95% CI $\left[3\%,33\%\right]$) is estimated to be unique to a selection line, and 17% (95% CI $\left[9\%,23\%\right]$) is the effect of shared selection between the two Longshanks selection lines.

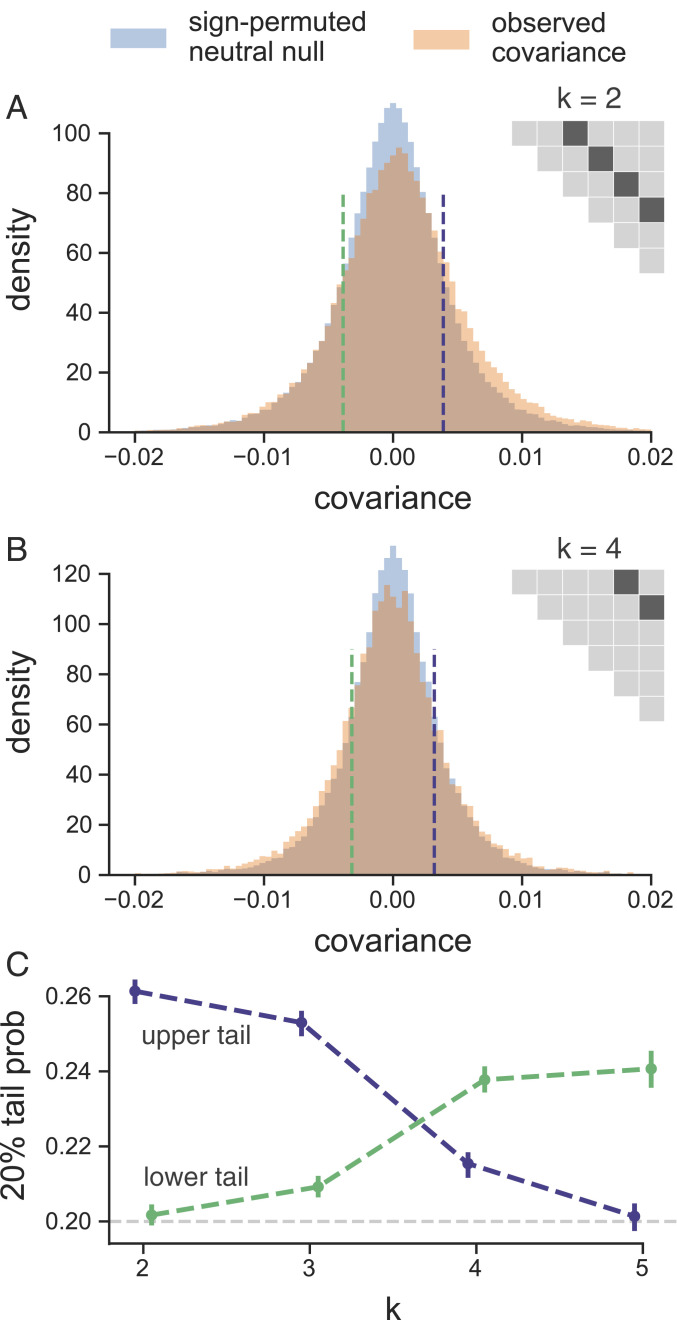
We observed that in the longest study we analyzed (33), some genome-wide temporal covariances become negative at future time points (the first two rows in Fig. 1 A, Left). This shows that alleles that were on average going up initially are later going down in frequency (i.e., that the average direction of selection experienced by alleles has flipped). This might reflect either a change in the environment or the genetic background, due to epistatic relationships among alleles altered by frequency changes (which can occur during an optima shift; ref. 43) or recombination breaking up selective alleles. Such reversals in selection dynamics could be occurring at other time points, but the signal of a change in the direction of selection at particular loci may be washed out when we calculate our genome-wide average temporal covariances. To address this limitation, we calculated the distribution of the temporal covariances over 100-kb windowed covariances (Fig. 3 shows these distributions pooling across all replicates, and SI Appendix, Fig. S26 shows individuals replicates). The covariance estimate of each genomic window will be noisy, due to sampling and genetic drift, and the neutral distribution of the covariance is complicated due to LD, which can occur over long physical distances in evolve-and-resequence and selection studies (44, 45). To address this, we have developed a permutation-based procedure that constructs an empirical neutral null distribution by randomly flipping the sign of the allele frequency changes in each genomic window (i.e., a single random sign flip is applied to all loci in a window). This destroys the systematic covariances created by linked selection and creates a sampling distribution of the covariances spuriously created by neutral genetic drift while preserving the complex dependencies between adjacent loci created by LD. This empirical neutral null distribution is conservative in the sense that the variances of the covariances are wider than expected under drift alone, as selection not only creates covariance between time intervals but also, inflates the magnitude of allele frequency change within a time interval. We see (Fig. 3 A and B) that there is an empirical excess of windows with positive covariances between close time points compared with the null distribution (a heavier right tail) and that this then shifts to an excess of windows with negative covariances between more distant time points (a heavier left tail).

Fig. 3.

(A and B) The distribution of temporal covariances calculated in 100-kb genomic windows from the Barghi et al. (33) study plotted alongside an empirical neutral null distribution created by recalculating the windowed covariances on 1,000 sign permutations of allele frequency changes within tiles. The number of histogram bins is 88, chosen by cross-validation (SI Appendix, Fig. S25). In A, windowed covariances $\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_t,\mathrm{\Delta }{p}_{t+k}\right)$ are separated by $k=2\times 10$ generations, and in A, the covariances are separated by $k=4\times 10$ generations; each $k$ is an off diagonal from the variance diagonal of the temporal covariance matrix (cartoon of upper triangle of covariance matrix in A and B, where the first diagonal is the variance, and the dark gray indicates which off diagonal of the covariance matrix is plotted in the histograms). (C) The lower and upper tail probabilities of the observed windowed covariances, at 20 and 80% quintiles of the empirical neutral null distribution, for varying time between allele frequency changes (i.e., which off diagonal $k$). The CIs are $95\%$ block bootstrap CIs, and the light gray dashed line indicates the 20% tail probability expected under the neutral null. Similar figures for different values of $k$ are in SI Appendix, Fig. S27.

We quantified the degree to which the left and right tails are inflated compared with the null distribution as a function of time and see excesses in both tails in Fig. 3C. This finding is also robust to sign-permuting allele frequency changes on a chromosome level, the longest extent that gametic LD can extend (SI Appendix, Fig. S29). We see a striking pattern that the windowed covariances not only decay toward zero but in fact, become negative through time, consistent with many regions in the genome having had a reversed fitness effect at later time points.

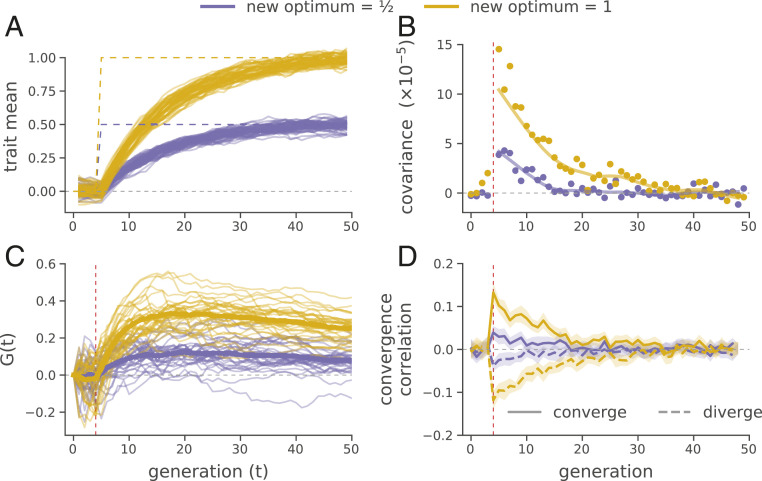
Finally, we used forward-in-time simulations to explore the conditions under which temporal and convergent correlations arise. We show a subset of our results for a model of stabilizing selection on a phenotype where directional selection is induced by a sudden shift in the optimum phenotype of varying magnitudes (Fig. 4A). We find that positive temporal covariances are produced by such selection (Fig. 4B) and that these positive temporal covariances can compound together to generate a large proportion of allele frequency change being due to selection [i.e., large $G\left(t\right)$] over the relatively short time periods similar to our analyzed selection datasets span (Fig. 4C). The magnitude of $G\left(t\right)$ increases with the strength of selection (i.e., the variance in fitness) such that stronger selection generates larger proportions of allele frequency change. We find a similar picture of stronger convergent selection pressures generating larger convergence correlations (Fig. 4D; SI Appendix, Fig. S12 shows how other factors impact convergence correlations).

Fig. 4.

Forward-in-time simulations demonstrate how temporal covariance, $G\left(t\right)$ trajectories, and convergence correlations arise during optima shifts of two different magnitudes, under GSS. (A) Trait means across 30 replicates before and after optima shifts (solid lines) for two different magnitudes (indicated by color). The new optimal trait values are indicated by the purple and yellow dashed lines. (B) Mean temporal covariance $\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_5,\mathrm{\Delta }{p}_t\right)$ across 30 simulation replicates, where $t$ varies along the x axis (points), with a loess-smoothed average (solid lines). (C) $G\left(t\right)$ trajectories through time for 30 replicate simulations across two optima shifts. The solid lines are loess-smoothed averages. (D) The convergence correlations between two populations (each 1,000 diploids) split from a common population that underwent an optima shift in either the same direction (converge) or opposite directions (diverge) at generation 5. In B–D, directional selection begins at generation 5, when the optima shifts; this is indicated by the vertical dashed red lines (SI Appendix, section S8.2 has details on these simulations).

Averaging across replicates, these simulation results show $G\left(t\right)$ is relatively insensitive to the number of loci underlying the trait. However, if only a small number of loci influence the trait, the $G\left(t\right)$ trajectories are typically much more stochastic across replicates. This reaffirms that the genome-wide linked selection response we see in the Barghi et al. (33) data is highly polygenic (compare Fig. 1B with SI Appendix, Fig. S6). Furthermore, using our simulations we find that sampling only every 10 generations does indeed mean that our estimates of $G\left(t\right)$ are an underestimate of the proportional effect of linked selection as they cannot include the covariance between closely spaced generations (SI Appendix, Fig. S14).

Additionally, we explored other modes of selection with simulations. We find that the long-term dynamics of the covariances under directional truncation selection, which generates substantial epistasis, are richer than we see under Gaussian stabilizing selection (GSS) and multiplicative selection (SI Appendix, Fig. S18). We also conducted simulations of purifying selection alone (i.e., background selection) and find that this can also generate positive temporal covariances (SI Appendix, Fig. S16) and under some circumstances, can even generate convergence correlations (SI Appendix, Fig. S17). Thus, it is unlikely that the signatures of linked selection we see are entirely the result of the novel selection pressure the populations are exposed to, and some of this signature may be ongoing purifying selection. Only in the case of the Longshanks experiment does the presence of a control line allow us to conclude that selection that is almost entirely due to the novel selection pressure.

While none of our experiments have selected the populations in divergent directions, in our simulations we find that such selection can generate negative convergent correlations (Fig. 4D). This suggests that selection experiments combining multiple replicates, control lines, as well as divergent selection pressures might be quite informative in disentangling the contribution of particular selection pressures from genome-wide allele frequency changes.

Discussion

Since the seminal analysis of Smith and Haigh (1) demonstrating that linked neutral diversity is reduced as an advantageous polymorphism sweeps to fixation, over four decades of theoretical and empirical research has bettered our understanding of linked selection. One underused approach to understand the genome-wide effects of selection on polygenic trait (e.g., on standing variation) stems from an early quantitative genetic model of linked selection (41) and its later developments (42, 46–48; ref. 5 has a comparison of these models with classic hitchhiking models). Implicit in these models is that autocovariance between allele frequency change is created when there is heritable fitness variation in the population, a signal that may be readily detected from temporal genomic data (37). Depending on how many loci affect fitness, even a strong effect of linked selection may not be differentiable from genetic drift using only single contemporary population samples or looking at temporal allele frequency change at each locus in isolation. In this way, averaging summaries of temporal data allows us to sidestep the key problem of detecting selection from standing variation: that the genomic footprint leaves too soft of a signature to differentiate from a background of genetic drift. In fact, we find that the temporal covariance signal is detectable even in the extremely difficult to detect case of selection on highly polygenic traits (37).

It is worth building some intuition why temporal covariance allows us to detect such faint signals of polygenic linked selection from temporal genomic data. Variance in allele frequency change is subject to both drift and sampling noise, which at any single locus, may swamp the temporal covariance signal due to selection or create spurious covariances when selection is not acting. However, these spurious covariances do not share a directional signal, whereas the covariances created by linked selection do; consequently, averaging across the entire genome, the temporal signal exceeds sampling noise.

Our analyses reveal that a sizable proportion of allele frequency change in these experimental evolution populations is due to the (likely indirect) action of selection. Capitalizing on replicated designs, we characterized the extent to which convergent selection pressures lead to parallel changes in allele frequencies across replicate populations and found that a substantial proportion of the response is shared across short timescales. These likely represent substantial underestimates of the contribution of linked selection because the studies we have reanalyzed do not sequence the population each generation, preventing us from including the effects of stronger correlations between adjacent generations. Furthermore, our estimation methods are intentionally conservative: for example, they exclude the contribution of selection that does not persist across generations and selection that reverses sign; thus, they can be seen as a lower bound of the effects of selection, which we have confirmed through forward-in-time simulations. Finally, through simulation results, we show that for a given level of additive genetic variance, the strengths of temporal and replicate covariances depend on the mode of selection, the details of the populations or selection experiment, and the level of LD, yet the level of temporal covariance is relatively invariant to the number of loci underlying fitness, as long as fitness is sufficiently polygenic.

These estimates of the contribution of selection could be refined by using patterns of LD and recombination, which would allow us to more fully parameterize a linked selection model of temporal allele frequency change (37). The basic prediction is that regions of higher LD and lower recombination should have greater temporal autocovariance than regions with lower LD and higher recombination. However, one limitation of these pooled sequence datasets is that none of the studies we reanalyzed estimated LD data for the evolved populations. While there are LD data for a natural population of D. simulans (49, 50), we did not find a relationship between temporal covariance and LD. We believe that this is driven by the idiosyncratic nature of LD in evolve-and-resequence populations, which often extends over large genomic distances (38, 44). Future studies complete with LD data and recombination maps would allow one to disentangle the influence of closely linked sites from more distant sites in causing temporal autocovariance and allow the fitting of more parametric models to estimate population parameters such as the additive genetic variance for fitness directly from temporal genomic data alone (37). Future work could refine our $G\left(t\right)$ estimates by including selection’s impact on the variance in allele frequency terms (e.g., equation 26 of ref. 37) and possibly quantifying the covariances missed when sequencing is not done each generation; both would lead to less conservative estimates that could show a large impact of selection.

Our primary focus here has been on evolution in laboratory populations. It is unclear whether we should expect a similar impact of selection in natural populations. In some of these experiments, selection pressures may have been stronger or more sustained than in natural populations (51, 52). Conversely, these laboratory populations were maintained at relatively small census sizes (Table 1), which will amplify the role of genetic drift, and increase the frequency of rare deleterious alleles in selection lines due to founder effects. The advantage of laboratory experiments is that they are closed populations; in natural populations, temporal covariance could also arise from the systematic migration of alleles from differentiated populations. Adapting these methods to natural populations will require either populations that are reasonably closed to migration or the effect of migration to be accounted for possibly either by knowledge of allele frequencies in source populations or the identification of migrant individuals.

Table 1.

Summary of the main selection studies we analyzed

Study	Species	Selection	Replicates	Population size*	Generations	Time points
Kelly and Hughes (38)	D. simulans	Laboratory adaptation	3	$\sim$1,100	14	2
Barghi et al. (33)	D. simulans	Laboratory adaptation	10	$\sim$1,000	60	7
Castro et al. (39)	Mus musculus	Tibiae length	2	32	17	2
	Mus musculus	Control	1	28	17	2

^*Approximate census population size during experiment.

While it challenging to apply temporal methods to natural populations, there is a lot of promise for these approaches (35, 36). Efforts to quantify the impact of linked selection have found that obligately sexual organisms have up to an 89% reduction in genome-wide diversity over long time periods (16, 18, 53–55) Thus, linked selection makes a sizable contribution to long-term allele frequency change in some species, and there is reason to be hopeful that we could detect this from temporal data, which would help to resolve the timescales that linked selection acts over in the wild. In our reanalysis of the Barghi et al. (32) study, we find evidence of complex linked selection dynamics, with selection pressures flipping over time due to environmental change, the breakup of epistatic combinations, or advantageous haplotypes. Such patterns would be completely obscured in samples from only contemporary populations. Thus, we can hope to have a much richer picture of the impact of selection as temporal sequencing becomes more common, allowing us to observe the effects of ecological dynamics in genomic data (52).

Furthermore, understanding the dynamics of linked selection over short timescales will help to unite phenotypic studies of rapid adaptation with a detectable genomic signature to address long-standing questions concerning linked selection, evolutionary quantitative genetics, and the overall impact selection has on genetic variation.

Materials and Methods

Datasets Analyzed.

We used available genomic data data from four studies: pooled population resequencing data from Barghi et al. (33), Kelly and Hughes (38), and Bergland et al. (35) and individual-level sequencing data from Castro et al. (39). In all cases, we used the variants kept after the filtering criteria of the original studies.

Variance and Covariance Estimates.

To remove systematic covariances in allele frequency change caused by tracking the reference or minor allele, we randomly choose an allele to track frequency for each locus. Then, we calculate the variance–covariance matrix of allele frequency changes using a Python software package we have written, available at http://github.com/vsbuffalo/cvtk. This simultaneously calculates temporal variances and covariances and replicate covariances and uses the sampling depth and number of diploid individuals to correct for bias in the variance estimates and a bias that occurs in covariance estimates between adjacent time points due to shared sampling noise (SI Appendix, sections S1.2–S1.4 have mathematical details of these estimators). We assess that our bias correction procedure is working adequately through a series of diagnostic plots that ensure that the procedure removes the relationship between sampling depth and uncorrected variance and covariances (SI Appendix, Fig. S4). Through our simulations we find that our estimates can differ based on how fixations and losses are handled in long time series (SI Appendix, section S8.7), but none of our findings in the text are qualitatively altered by this decision (SI Appendix, Figs. S19 and S20).

Estimating Uncertainty with a Block Bootstrap.

To infer the uncertainty of covariance, convergence correlation, and $G\left(t\right)$ estimates, we used a block bootstrap procedure. This bootstrap procedure resamples blocks of loci, rather than individual loci, to infer the uncertainty of a statistic in the presence of unknown correlation between loci. As most estimators in this paper are ratios [e.g., covariance standardized by sample heterozygosity, $G\left(t\right)$, and the convergence correlation], which we estimate with a ratio of averages, we exploit the linearity of expectation for efficient computation of bootstrap samples (SI Appendix, Fig. S3 shows details).

Partitioning Unique and Shared Selection Effects in the Longshanks Study.

The unselected control line in the Longshanks experiment allows us to additionally partition the total variance in allele frequency change into drift, shared effects of selection, and unshared effects of selection between selected replicates. We begin by decomposing the allele frequency change in LS1 as $\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}={\mathrm{\Delta }}_D{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}+{\mathrm{\Delta }}_U{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}+{\mathrm{\Delta }}_S{p}_{t,\mathrm{L}\mathrm{S}}$, where these terms are the drift in LS1 (${\mathrm{\Delta }}_D{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}$), selection unique to the LS1 replicate (${\mathrm{\Delta }}_U{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}$), and selection response shared between the two Longshanks replicates (${\mathrm{\Delta }}_S{p}_{t,\mathrm{L}\mathrm{S}}$; and similarly for LS2). By construction, this decomposition assumes that each of these terms is uncorrelated within replicates, so the contribution of each term to the total variance in allele frequency change, $\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}\right)$, is the variance of that term’s allele frequency change.

We estimate the effects of selection by first calculating the fraction of the total variance explained by drift. We assume that the variance in allele frequency change observed in the unselected control [$\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{t,\mathrm{C}\mathrm{t}\mathrm{r}\mathrm{l}}\right)$] is driven entirely by neutral genetic drift, and since an identical breeding scheme was used across all three replicates (except that breeders for the Ctrl line were chosen at random), we can use this as an estimate of the contribution of neutral genetic drift in the selected lines, $\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{t,\mathrm{C}\mathrm{t}\mathrm{r}\mathrm{l}}\right)=\mathrm{\text{Var}}\left({\mathrm{\Delta }}_D{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}\right)=\mathrm{\text{Var}}\left({\mathrm{\Delta }}_D{p}_{t,\mathrm{L}\mathrm{S}\mathrm{2}}\right)$. Then, we can estimate the increase in variance in allele frequency change due to selection as $\left(\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}}\right)+\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{2}}\right)\right)/2-\mathrm{\text{Var}}\left(\mathrm{\Delta }{p}_{t,\mathrm{C}\mathrm{t}\mathrm{r}\mathrm{l}}\right)$ and the shared effect of selection across selected lines as $\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}},\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{2}}\right)$. Finally, the covariance in allele change between replicates is used to estimate the shared effects of selection between lines, $\mathrm{C}\mathrm{o}\mathrm{v}\left(\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{1}},\mathrm{\Delta }{p}_{t,\mathrm{L}\mathrm{S}\mathrm{2}}\right)=\mathrm{\text{Var}}\left({\mathrm{\Delta }}_S{p}_{t,\mathrm{L}\mathrm{S}}\right)$.

Windowed Covariance and the Empirical Neutral Null.

Throughout the paper, we use genomic windows for the block bootstrap procedure. For the D. simulans and D. melanogaster data from the Barghi et al. (33), Kelly and Hughes (38), and Bergland et al. (35) studies, we used large megabase windows for the block bootstrap procedure, while we used a 10-Mb window for the large mouse genome data from the Castro et al. (39) study.

Given evidence of a reversal in the direction of selection at later time points in the Barghi et al. (33) study, we calculated windowed temporal covariances on 10-kb windows and looked at the distribution of these covariances through time. We compare these distributions of windowed covariances with an empirical neutral null created by randomly permuting the sign of allele frequency change at the block level (to preserve the correlation structure between loci due to LD). This destroys the systematic covariances in allele frequency change created by linked selection, which emulates a frequency trajectory under drift. This approach is conservative since heritable fitness variation also inflates the magnitude of allele frequency change more than expected under drift, but we do not change these magnitudes. Using this empirical neutral null distribution of windowed covariances, we calculate how much of the observed windowed covariance distribution falls outside of empirical null distribution for different tail probabilities. While the comparison between the distribution of 10-kb windowed covariances and the empirical neutral null created from sign-permuting 10-kb windows is most natural, we wanted to ensure that our finding that the shift from mostly positive to mostly negative windowed covariances through time (Fig. 3) was robust to LD extending beyond the range of these 10-kb windows. We took the conservative approach of also sign permuting at the chromosome level and found the same qualitative shift (SI Appendix, Fig. S29).

Forward-in-Time Simulations.

To explore how aspects of genetic architecture, models of selection, and experimental design impact temporal covariance, the $G\left(t\right)$ trajectories, and convergence correlations, we ran extensive forward-in-time simulations using SLiM (56); here, we discuss the GSS simulations in Fig. 4, but SI Appendix, section S8 describes these simulation routines and others in detail.

We simulated directional selection on a trait by first evolving each population of $N=\mathrm{1,000}$ diploids to equilibrium (we will refer to this as the burn-in hereafter) under GSS for $10N$ generations with the stabilizing selection variance $V_s=1$ and an optima set at 0. We note that the small burn-in population size means that these simulations should not be taken as reflecting any specific natural population, and they are for illustrative purposes only. We simulated a polygenic architecture by setting the trait mutation rate to $10^{-8}$ per base pair, per generation, in addition to having a separate neutral mutation of $10^{-8}$, which created neutral mutations that we used to calculate the temporal covariances. Our simulated region was 50 Mb in length (about one-quarter of a Drosophila chromosome), and trait alleles were randomly selected to have a $\pm 0.01$ effect size. By tracking the trait mean through the burn-in, we found that it converged to the optimum as expected. After the burn-in, the population was split into two different replicate populations to capture the effect of bottlenecks in selection experiments (these population sizes varied between 50, 500, and 1,000 diploids, the latter representing no bottleneck). Each population then underwent an optima shift of 0.1, 0.5, or 1 on generation 5, with the first four generations serving as a control. These optima shifts were in the same direction (converging), different directions (diverging), or only one optima shifted (as a control). By tracking the trait mean, we saw that it converged as expected during burn-in, and the trait showed the expected directional response to selection (SI Appendix, Fig. S7). Using the neutral population frequency data from these simulations, we calculated the temporal covariances, $G\left(t\right)$ trajectories, and convergence correlations.

Data Availability.

All analyses were done in Python using numpy, matplotlib, and Jupyter notebooks (57–60); reanalysis code and notebooks to reproduce these analyses are available on GitHub, https://github.com/vsbuffalo/cvtk/ (61). All data are from previous studies and available; Barghi et al. (33, 62) data were downloaded from https://datadryad.org/resource/doi:10.5061/dryad.rr137kn, Kelly and Hughes (38, 63) data were downloaded from https://gsajournals.figshare.com/articles/Supplemental_Material_for_Kelly_and_Hughes_2018/7124963, Bergland et al. (35, 64) data were downloaded from https://datadryad.org/stash/dataset/doi:10.5061/dryad.v883p, and Castro et al. (39, 65) data were downloaded from http://ftp.tuebingen.mpg.de/fml/ag-chan/Longshanks/.