Optical properties of metasurfaces infiltrated with liquid crystals

Significance

Nanostructured metamaterials have been engineered to generate a wide range of optical phenomena, allowing an unprecedented control over the propagation of light. However, they are generally designed as single-purpose devices without a modifiable optical response, which can be a barrier to applications. In this work, we report the nontrivial infiltration of a nanostructured planar silica metalens with nematic liquid crystals. We then demonstrate a measurable change in the metalens optical response after infiltration. Since the orientation-dependent optical properties of liquid crystals can be controlled with external stimuli, this technology could potentially enable dynamic control of the metalens optical response.

Abstract

Optical metasurfaces allow the ability to precisely manipulate the wavefront of light, creating many interesting and exotic optical phenomena. However, they generally lack dynamic control over their optical properties and are limited to passive optical elements. In this work, we report the nontrivial infiltration of nanostructured metalenses with three respective nematic liquid crystals of different refractive index and birefringence. The optical properties of the metalens are evaluated after liquid-crystal infiltration to quantify its effect on the intended optical design. We observe a significant modification of the metalens focus after infiltration for each liquid crystal. These optical changes result from modification of local refractive index surrounding the metalens structure after infiltration. We report qualitative agreement of the optical experiments with finite-difference time-domain solver (FDTD) simulation results. By harnessing the tunability inherent in the orientation dependent refractive index of the infiltrated liquid crystal, the metalens system considered here has the potential to enable dynamic reconfigurability in metasurfaces.

Metasurfaces for flat optics have spurred a wide deal of interest as a photonic technology enabling manipulation of the wavefront of light on an unprecedented scale (1–6). These devices offer control over the phase, amplitude, and polarization state of the wavefront traversing the structured plane via the local interaction of light with metaatoms arranged at the nanoscale (7–12). With current fabrication techniques it is possible to engineer phase, amplitude, and polarization landscapes, allowing localized control of the scattered field and molding the flow of light to create optical effects which are unparalleled in natural materials (13, 14). This technology has shown promise as a radical change in the form–function relationship compared with conventional refractive optical elements (15–18).

Most engineered metasurfaces have a prescribed geometry which has been designed to fulfill a single functionality, and as such these devices are necessarily passive optical elements. This presents a barrier to potential application where differing optical responses may be necessary. The opportunity to enable reconfigurability in optical materials through the application of external stimuli has been a longstanding goal of photonics. In recent years, there have been numerous attempts to design reconfigurable systems, including mechanical (11, 19), thermal (20–23), and external voltage-based approaches (24). In this work, we report the infiltration of nanopillared planar metasurfaces with various nematic liquid crystals (NLCs) by harnessing the wetting properties of the metasurface. This infiltration is explained by a combination of competing forces, namely the capillary and the resisting hydrodynamic forces (25). Since the LC is a birefringent complex fluid, wetting of the metasurface induces a modification of the refractive index map with local and global order, in turn modifying the phase and amplitude of the transmitted electromagnetic field.

It is well known that LCs respond to external stimuli (e.g., electric field, magnetic field, temperature, strain, etc.,) by undergoing a molecular reorientation which is responsible for refractive index changes of the LC (26, 27). Recent studies on reconfigurable optics created with conventional sandwiched LC cells with one of the two plates coated with a metasurface have been reported (28–30). Opposed to these implementations involving a bulky LC cell, we propose in this work to harness the wetting properties of the metalens to replace the air between the planar nanostructures with optically active birefringent and viscoelastic LCs. This implementation allows for controlling phase and amplitude distribution in the metalens plane, thereby limiting the optical changes that are unavoidable with thick LC slabs laying above the metasurface. By harnessing the infiltrated LC optical properties the transmitted field can be significantly modified, and furthermore potentially controlled.

Metalens Infiltration

Phenomenology.

Infiltration of the metalens system has been investigated for three different common thermotropic rod-shaped nematic LCs: MBBA (Sigma-Aldrich), E7 (Merck), and BL009 (Beam Co.). As we expect the lensing ability in our metalens system to be mainly affected by the refractive index of the infiltrate material, these NLCs have been chosen to represent a wide range of effective refractive index (n) and birefringence (n). The presence of long-range order in the LC means that for fixed light propagation direction the NLC acts as a material with a modifiable local birefringence. Refractive index data at room temperature are given in Table 1 (31). The wetting of nanopatterned surfaces is in general nontrivial and heavily dependent upon the geometrical properties of the patterned array and hydrophilic attraction between the liquid and the substrate material, as well as viscous properties of the wetting liquid (25). As such, the three NLCs were chosen for their predicted infiltration properties, as explained below.

Table 1.

Infiltrated LC optical properties

LC	no	ne	∆n
MBBA	1.56	1.68	0.12
E7	1.52	1.74	0.23
BL009	1.59	1.87	0.28

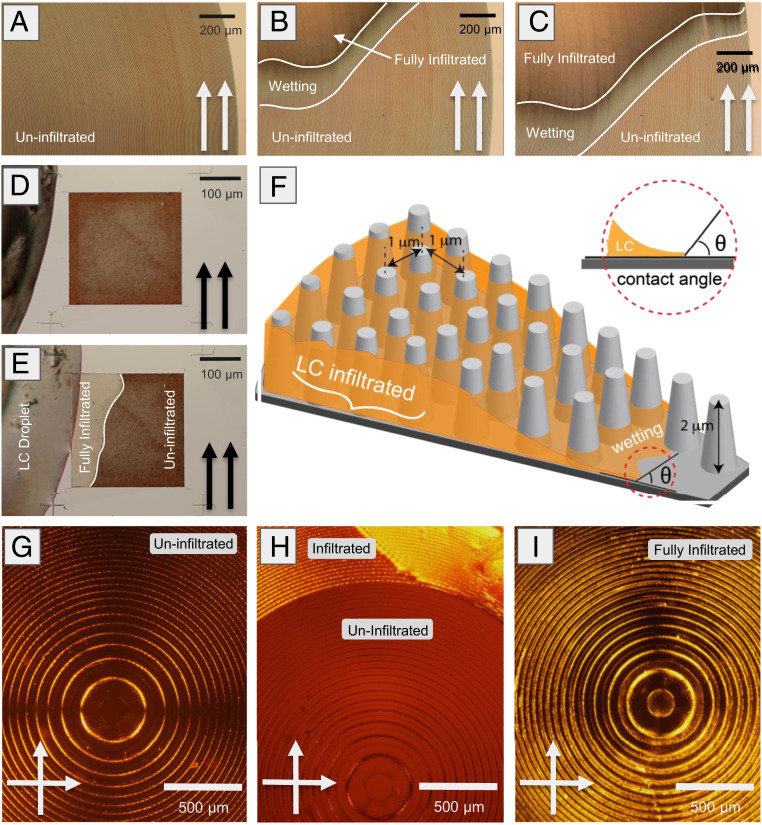
A droplet of wetting liquid placed on top of a nanopatterned array typically remains in at equilibrium, either in the Cassie-Baxter state (32), by forming a droplet on the surface without wetting the structure, or the Wenzel state (33), by displacing the air infiltration and filling the structure below the droplet. However, there exists a third state in which the liquid exceeds the equilibrium Wenzel state, propagating an infiltrating film around the droplet and throughout the microstructure, leading to a full infiltration of the nanopatterned array with the wetting material (34, 35). See Fig. 2F for an illustration of this case where the fully infiltrated and wetting layers are shown during the infiltration process. This state has been previously observed in nanopatterned structures infiltrated with conventional fluids (36–38).

Fig. 2.

Characterization of LC infiltration in the metalens system. (A–C) Progression of LC (MBBA) infiltration for the metalens (1 cm diameter, glass on glass) system in parallel polarization: (A) uninfiltrated, and (B) partially infiltrated. (C) Infiltrating film progresses circumferentially throughout the structure. (D and E) LC (MBBA) infiltration for a structured substrate composed of TiO₂ pillars. The film progresses from D to E at full infiltration outward from the initial contact point without a visible wetting layer, still resulting in full infiltration. Here the same infiltrate LC leads to different wetting behavior based on the substrate properties. (F) Illustration of LC infiltration into a regular array of the metalens’ SiO₂ pillars. The wetting layer is seen preceding full infiltration. The contact angle is measured at the edge of the infiltrated film droplet. (G–I) Optical analysis of metalens central region in crossed polarization during the infiltration process: (G) uninfiltrated, (H) partially infiltrated, (I) fully infiltrated.

The infiltration state arises as the system responds to the introduction of a liquid droplet by attempting to minimize the free-energy differential in the air–liquid–substrate system. Free energy is a function of the interfacial energy in the air–liquid, liquid–substrate, and air–substrate interfaces, which are dependent upon the substrate and infiltrating material parameters (25, 34). A more extended theoretical discussion about our current understandings of the infiltration process has been provided (SI Appendix, Fig. S1).

We have characterized the infiltration process in our metalens system through measurements of the contact angle and scanning electron microscopy measurements of the metalens geometrical parameters (39). Based on these measurements, our wetting model predicts that the metalens structure will favor infiltration of the selected LCs. We predict an equilibrium stable film fully infiltrating the metalens with the film height at the pillar height (2 μm). This analysis assumes a regular array of flat-topped cylindrical pillars (measured sidewall angle at 2.8°). In reality the pillar spacing and size is highly nonuniform throughout the metalens, as can be seen in Fig. 1. This nonuniform geometry can give rise to complex infiltration behavior which is difficult to predict on the scale of the metalens, and which is not contained within the simplified model.

Fig. 1.

SEM images of the metalens at different magnification; metalenses are composed of an array of nanopillars with controlled diameters. Top view of the (A) metalens center and (B) metalens outer edge. (C) Tilted and zoomed view of largest pillars on the edge of the second ring, and (D) a tilted and zoomed view of the same area.

Experimental Infiltration and Evaluation.

Infiltration of the metalens has been observed with polarized optical microscopy by comparing optical transmission in the infiltrated and uninfiltrated cases. Concurrent observation of the infiltration under parallel polarization (0° polarizers) and crossed polarization (90° polarizers) gives information about both the state of infiltration and local alignment of the LC. In particular, when the lens is observed between parallel polarizers the change in transmitted light intensity indicates a change in LC film thickness. However, when viewed between crossed polarizers, bright and dark regions show different levels of molecular alignment in the LC.

The infiltration process for the metalens system is illustrated in Fig. 2. Three subsequent images during infiltration with MBBA, observed under parallel polarizations, are seen in Fig. 2 A–C. The fully infiltrated and wetting regions are clearly distinguished from the uninfiltrated region by a decrease in transmission intensity with increasing film height. A boundary line between these regions has been added for clearer distinction. Between the second (Fig. 2B) and third (Fig. 2C) panels there is a clear circumferential progression of the wetting front around the metalens, which is indicative of the observed infiltration.

The infiltration of another optical metasurface composed of titanium dioxide (TiO₂) nanopillars (40) is shown in Fig. 2 D and E for reference. In this case the infiltration appears as an increase in intensity under parallel polarization, but the infiltrated region and propagating front are still clearly visible. Inclusion of the TiO₂ metasurface is intended to show that certain other structures and materials can be infiltrated using a similar technique, leading to different optical results after infiltration. This can be incorporated in a wider range of designed optical response and potentially reconfigurable devices.

A similar progression can be seen under cross-polarization for the metalens infiltration in Fig. 2 G–I. For the initial uninfiltrated lens, the densely pillared regions are clearly visible while the open rings appear dark. This image also shows a clear maltese cross resulting from conoscopic interference in the focal plane. The conoscopic cross shows the variation, as function of the azimuthal angle, of the radiation intensity transmitted through the polarizer-metalens-analyzer. The isochrome circles with the minimum or maximum intensity of the transmitted light correspond to a definite phase difference between the ordinary and extraordinary rays. In particular, when the phase difference is equal to multiples of 2π, it results in a particular interference pattern known as maltese or conoscopic cross (26, 41). The infiltration proceeds in Fig. 2 H and I, leading to full infiltration of the metalens. In this case the fully infiltrated regions are visibly brighter during infiltration due to the disordered alignment of the LC. The final LC orientation is strongly disordered, with self-aligned domains extending over several rings.

During infiltration, the LC tends to fully infiltrate circumferential rings in the metalens before moving radially inward. We believe this effect is due to the radial nonuniformity present in the metalens microstructure, such that the liquid experiences energetically favorable infiltration in the relatively wide channels which becomes more difficult in the densely pillared regions. The disparity in ease of infiltration for the two regions is reflected in the infiltration dynamics, leading to the observed behavior (42).

The NLC equilibrium state following full infiltration has been observed for each of the sampled LCs. We have characterized both the local LC alignment and the state of filling following an infiltration process. The alignment information is obtained from cross-polarization intensity, as discussed above. A typical equilibrium infiltration state, observed for MBBA in cross-polarization, is shown in Fig. 2I. More examples are available (SI Appendix, Fig. S2). In this case the LC alignment is significantly disordered. This can be expected from the complex boundary interaction with the metalens without including an alignment medium for controlling this interaction. It is important to control the infiltration orientation state as a baseline for reconfigurable orientation controls and to maintain consistent refractive index across the metastructure.

Observation of the equilibrium following infiltration shows a relative change over the uninfiltrated case for every region of the metalens. This indicates that the LC has infiltrated into the entire metastructure, which is consistent with the theoretical infiltration behavior. The height of the LC film (t) infiltrated into the metalens has been measured with a tilt optical delay compensator, which relates the phase retardation ($\text{Γ}$) and birefringence ($\mathrm{\Delta }n$) to the film thickness ($\text{Γ}=t\mathrm{\Delta }n$). The measured average film height for the lens is less than 50% of the pillar height (0.8 μm) with local regions between 0.2 and 1.0 μm. The uneven infiltration height is indicative of the complex pillar geometry of the metasurface substrate (SI Appendix, Fig. S3).

Optical Properties.

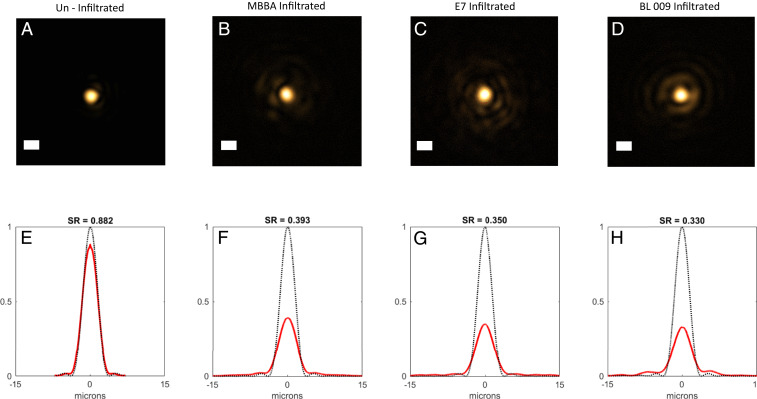
The focusing properties of the metalens have been characterized by the experimental point-spread function (PSF) at the focus plane. A diffraction-limited Airy pattern is expected for ideal focusing (39). The loss in focusing ability after LC infiltration is quantified by a widening of the Gaussian fitted full-width at half-maximum (FWHM) of the central focal point and an increase in the first sidelobe intensity, which translates to a decreased Strehl ratio. The PSF characterization is conducted for incident plane wave at $\lambda$ = 633 nm in accordance with design specifications (SI Appendix, Fig. S4).

FWHM of the central focal point from the ideal focusing metalens (numerical aperture = 0.1) is calculated at 3.25 μm in the focal plane; the ideal profile is plotted with black dotted line in Fig. 3E. Experimentally (Fig. 3 A–E), we obtain the FWHM at 3.4 ± 0.2 μm (SD), first sidelobe intensity at 2%, and Strehl ratio at 0.882, calculated from the two-dimensional (2D) integrated focal point. The focusing profiles obtained after LC infiltration with the three different LCs are shown in Fig. 3 B–D, with the ideal focusing profiles plotted in black dotted lines for reference. There is a significant increase in the central focal point FWHM after all three LCs are infiltrated. For each NLC, MBBA (Fig. 3B), E7 (Fig. 3C), and BL009 (Fig. 3D), the experimental focal-point FWHMs are found to be 4.1 ± 0.2, 4.1 ± 0.2, and 4.3 ± 0.2 μm (SD), respectively. Experimental Strehl ratios were found to be 0.393, 0.350, and 0.330, respectively. The FWHM of the center intensity is observed to increase with the increasing refractive index and birefringence of the LC, and this is a direct result of modification of the refractive index in the local environment of the individual metalens pillars by the NLC.

Fig. 3.

PSF of the metalenses (1 cm, glass on glass) taken at the focal plane, demonstrating the change in focusing quality between clean and infiltrated lenses. The first row (A–D) shows the images’ focal point, and the bottom row (E–H) shows the 2D integrated PSF. Infiltration of the lenses with LC results in a clear spreading of the central focal point and increase in first sidelobe intensity. Image brightness has been manipulated for viewing. (A and E) Focusing of the uninfiltrated metalens. (Scale bar, 5 μm.) Diffraction limiting Airy rings are less visible. FWHM for the central focal point, FWHM = 3.4 μm, Strehl ratio (SR) = 0.882. (B and F) MBBA infiltrated metalens (Scale bar, 5 μm.) FWHM = 4.1 μm, SR = 0.393. (C and G) E7 infiltrated metalens (Scale bar, 5 μm.) FWHM = 4.1 μm, SR = 0.350. (D and H) BL009 infiltrated metalens (Scale bar, 5 μm.) FWHM = 4.3 μm, SR = 0.330.

The metalens structures are designed for ambient conditions, corresponding to a sharp index contrast of approximately $\mathrm{\Delta }n$ = 0.5 at the air–glass boundary. They are not designed to accommodate the relatively small index contrast produced by infiltration of NLCs whose refractive indices are similar to the constituent material. This reduction of the index contrast leads to a corresponding decrease in the metalens focusing ability observed here. The quality of the focal spot is also dependent upon the degree and homogeneity of infiltration. The greatly increased first sidelobe intensity, at 200−500% for the NLC infiltrated lenses with respect to the uninfiltrated results (Fig. 3 B–D), is indicative of significant aberration within the metalens due to the infiltration. Specifically, spherical aberration of the metalenses increases significantly due to the reduced phase gradient when infiltrated with NLC (SI Appendix, Fig. S5). Further studies are needed, focusing on treating the metasurfaces with LC alignment layers to homogenize and control the local molecular orientation and redesigning the metasurfaces to better accommodate the NLC infiltration (43–45).

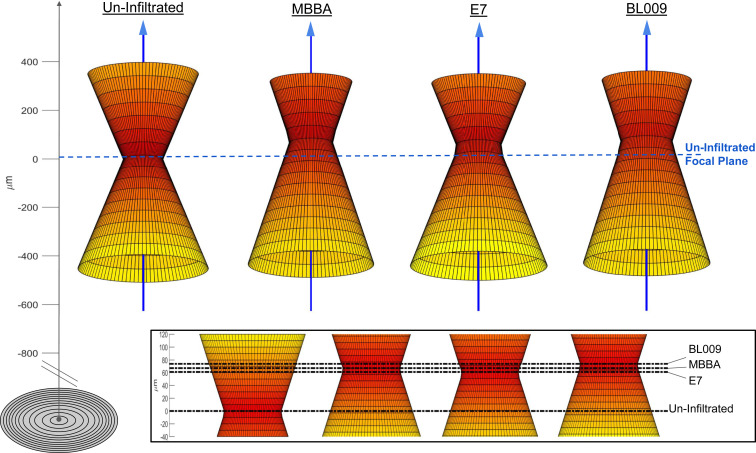
The focusing properties of the metalens can similarly be evaluated through a comparison of the three-dimensional spatial focusing profile produced by the metalens after modification by the NLC infiltration (Fig. 4). The spatial focusing profile has been characterized by imaging the through–focal-plane PSF while moving outward along the optical axis. A representation of the spatial profile has been reconstructed by calculating a radius of constant total intensity for the normalized PSF at each plane. Thus for the PSF at the metalens focal point, the representation radius reduces to the FWHM of the central intensity distribution in Fig. 3. A representation of this form disregards information about the Airy pattern and complex spatial phase interactions in any focal plane, and instead shows the general focusing behavior in the vicinity of the focal point.

Fig. 4.

Experimental diffraction-limited spatial focusing profile of the uninfiltrated and NLC fully infiltrated (MBBA, E7, BL009) lenses through the focal point seen in Fig. 3. The focusing behavior is qualitatively similar to standard refractive lensing. Beam radius measurements are taken at intervals of 50 ± 10 μm over a range of 800 μm about the focal point. This resolution is too low to observe Raleigh behavior in the region of the focal point. In each case NLC infiltration tends to extend the focal length of the lens by a small amount from the optical axis of the clean lens. Horizontal dashed line represents the focal plane of the uninfiltrated lens.

In Fig. 4, differences in experimentally measured beam waist can be seen, corresponding to the results of the central intensity’s FWHM after LC infiltration as seen in Fig. 3. Note that the profile is sampled in steps of 50 μm, which is on the order of the Raleigh length (∼30 μm). A measurable displacement of the focal point along the optical axis is observed after infiltration. In each case, LC infiltration tends to increase the focal length, along with a decrease in divergence of the focus. This can be seen in the Fig. 4 (Inset), which magnifies the focal region. Despite the large shift after infiltration, measured focal-point displacement is remarkably similar for all three NLCs, notwithstanding the differences in effective refractive index. This is possible due to the simultaneous effects of index contrast depression in the infiltrated region and inhomogeneous index contrast from partial infiltration. This can account for the large difference in focusing between infiltrated and uninfiltrated lenses, and smaller differences between infiltration with different LCs.

Optical Simulations.

Simulations of the metalens optical properties have been performed using a commercial finite-difference time-domain solver (Lumerical). The metalens was simulated at a reduced size (50-μm diameter, comprising two Fresnel zones) while maintaining a numerical aperture of 0.1, which was necessary due to limits on the computational resources. Since the phase profiles of the metalenses are not linear, this will result in the same external stimuli producing different degrees of perturbation to the focal spot. More details are given in SI Appendix. The near field was computed at a distance of 2$\lambda$ (1,266 nm), and far-field transform techniques were then used to obtain the theoretical PSF and focal-spot profile. This simulation was performed for the metalens in free space (uninfiltrated) and for the metalens with E7 NLC infiltration, accounting for light polarized along the ordinary and extraordinary axes. The infiltrated layer was assumed to be homogeneous at a constant height of h = 800 nm, in accordance with an average of the experimentally measured height of the infiltrated layer; however, this is an approximation to the actual wetting height profile.

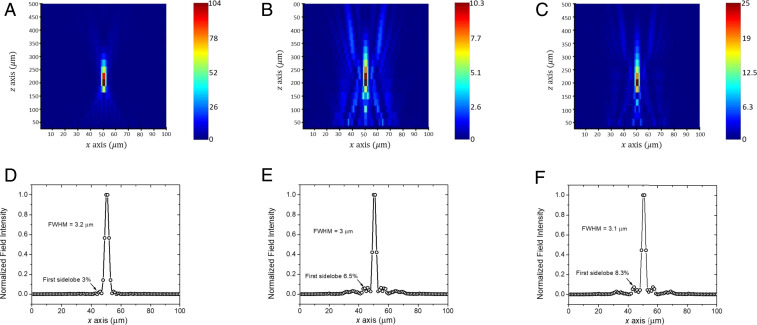
The resulting simulated PSFs over the simulation domain are shown in Fig. 5. We observe the focal length of the simulated metalens in air to be 200 μm, which is consistent with experiment. When subject to E7 infiltration, the observed focal length is modified by 5 and 10% for the extraordinary and ordinary refractive index, respectively. The maximum field intensity at the focus also drops significantly, accompanied by significantly increased background noise. These results are indicative of aberrations in the focal spot as significant energy is diverted beyond the main lobe of the focal point. The intensity of the first sidelobe is also seen to increase, along with an increase in the background noise strength, in Fig. 5 B and C.

Fig. 5.

Simulated focusing behavior of the metalens (A and D) uninfiltrated, and with E7 infiltration oriented along the (B and E) ordinary axis and (C and F) extraordinary axis, respectively. The first row (A–C) shows the PSF near the focus, while the second row (D–F) shows the theoretical focal-spot profile taken at the focal plane. LC was treated as a homogeneous layer with height h = 0.8 μm. For infiltrated E7, the maximum field intensity at the focus decreases accompanied by increases in the sidelobe intensity and a visible shift in focal point, which is indicative of aberrations in the focusing.

Interestingly, the focusing effect is seen to be stronger for the higher extraordinary refractive index of E7 (Fig. 5C), rather than the lower ordinary refractive index (Fig. 5B). This phenomenon can be understood as refractive index of the latter is closer to that of glass, which is the constituent material of both the nanostructure and substrate. This implies a significant reduction in the refractive index contrast for the ordinary index compared to the extraordinary index.

In these simulations we observe a steadily increasing amount of power diverted into the sidelobes of the PSF at the focal point, shown for the simulations in Fig. 5 D–F, which is consistent with what is observed for the experimental metalens in Fig. 3. First sidelobe intensities as obtained from the simulations are 3% for the uninfiltrated metalens, which corresponds well with the ideal Airy pattern and results obtained from the experimental uninfiltrated metalens. This intensity increases by 100 and 200% for the E7 infiltrated metalens illuminated along the ordinary and extraordinary axis, respectively. The increase in sidelobe intensity translates to a progressively lower Strehl ratio as the refractive index of the pillared region is increased. The trend of increasing sidelobe intensity and decreasing Strehl ratio with infiltration is consistent with experiment.

Concluding Remarks.

Taken together with the increase in focal-point FWHM and decrease in Strehl ratio for the infiltrated metalens, the increase of focal-point distance is evidence for a measurable modification of the optical properties with infiltration of LCs of different effective refractive indices. This is achieved without major modification of the initial metasurface function designed for working in air. The infiltration can still be improved, however, by smoothing orientational inhomogeneities and liquid height gradients within the metalens. Surfactants can work to homogenize the initial orientation state following infiltration, and provide a consistent index throughout the structure (43).

Control over the LC orientation state both during and after infiltration is essential for optical reconfigurability of the metasurface. A key benefit of LCs as an infiltration liquid are well-developed alignment and orientation control methods. These include traditional voltage and optical field bias methods, and chemical surface treatments designed for dynamic photoalignment. These hold promise as future methods to provide reconfigurable optical properties in the metalens system.

Materials and Methods

The metalenses considered in this work are 1 cm diameter, composed of fused silica nanopillars on a fused silica substrate, designed for lensing at $\lambda$ = 633 nm with focal length f = 5 cm and numerical aperture = 0.1. Metalenses were fabricated using deep-ultraviolet projection stepper lithography with a 248-nm source wavelength. Details on the metalens construction and designed optical response can be found in previous work (39).

Polarized optical microscopy was performed with a Leica DM2500P microscope. The metalenses were illuminated for optical characterization with a Cobalt 06-MLD diode laser at 633 nm and 5 mW, and expanded beam data were collected using a commercial complementary metal-oxide-semiconductor (CMOS) camera (SI Appendix, Fig. S4).

Data Availability.

All relevant data can be found herein or in SI Appendix.