Physical modeling of the heritability and maintenance of epigenetic modifications

Significance

Epigenetic regulation serves as the basis on which multicellular organisms differentiate genetically identical cells into various cell types, and aberrations in epigenetic modifications lead to a range of diseases. The specific biological mechanisms behind the heritability and maintenance of epigenetic modifications are currently not well understood. We develop a predictive theoretical model of the interplay between the proteins that control chromosomal compaction and those that confer posttranslational modifications to histone proteins within chromosomal DNA. Our model is built on the experimentally observed behavior for these individual biological contributions, resulting in a predictive framework that captures a robust mechanism for epigenetic heritability.

Abstract

We develop a predictive theoretical model of the physical mechanisms that govern the heritability and maintenance of epigenetic modifications. This model focuses on a particular modification, methylation of lysine-9 of histone H3 (H3K9), which is one of the most representative and critical epigenetic marks that affects chromatin organization and gene expression. Our model combines the effect of segregation and compaction on chromosomal organization with the effect of the interaction between proteins that compact the chromatin (heterochromatin protein 1) and the methyltransferases that affect methyl spreading. Our chromatin model demonstrates that a block of H3K9 methylations in the epigenetic sequence determines the compaction state at any particular location in the chromatin. Using our predictive model for chromatin compaction, we develop a methylation model to address the reestablishment of the methylation sequence following DNA replication. Our model reliably maintains methylation over generations, thereby establishing the robustness of the epigenetic code.

The sequence of DNA base pairs contains the genetic instructions for organisms to carry out life’s processes, and changes to the DNA sequence can lead to aberrant behavior. Differences in behavior can also arise in two genetically identical cells due to chemical modifications to the chromosomal DNA and posttranslational modifications to the proteins that package this DNA. Unusual patterns of such epigenetic markers result in atypical gene expression and a wide variety of diseases, including developmental disorders, diabetes, obesity, and cancers (1–3).

A nucleosome—the fundamental unit of chromosomal DNA—consists of DNA wrapped around a set of eight core histone proteins. Chemical modifications to the tails of the histone proteins control both the local and global organizational state of chromatin and thereby alter the availability of genes to transcription factors. During interphase, regions of DNA can be classified as densely packed heterochromatin or more loosely packed and transcriptionally accessible euchromatin (Fig. 1, Top). Methylation of histone proteins is essential for heterochromatin formation (4) and transcriptional repression of genes (5–7). Epigenetic methyl marks interact with heterochromatin protein 1 (HP1), which specifically binds to methylated H3K9 (with strongest affinity for trimethylated H3K9 or H3K9me3) (8–10). HP1 oligomerizes when bound to adjacent nucleosomes, leading to compaction (11, 12).

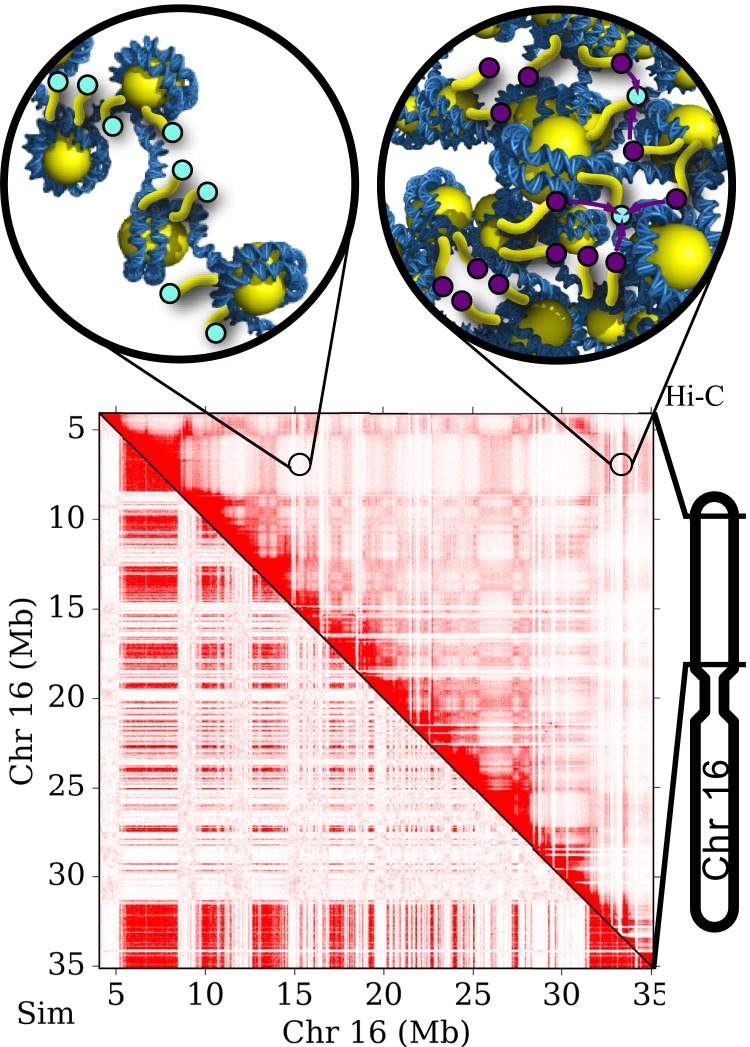
Fig. 1.

(Top) Images demonstrate the degree of chromosomal compaction in euchromatin (Left) and heterochromatin (Right). Cyan and purple circles represent histone tails that are unmethylated and methylated, respectively. (Bottom) Image shows results from Hi-C experiments (16, 17) (upper-right triangle) compared with our physical model for chromosomal organization (lower-left triangle) (22). Chromosome compartments within the Hi-C contact map indicate segregation into heterochromatin and euchromatin.

HP1 cooperatively interacts with H3K9 methyltransferases SUV39H1/2 (13–15). For epigenetic marks like H3K9me3 to be conferred within chromatin, DNA segments must come into close spatial proximity. Hi-C experiments display distinct patterns of epigenetic histone modifications, suggesting a connection between DNA organization and epigenetic regulation (16, 17) (see Fig. 1, Bottom for a Hi-C pattern). Furthermore, the formation of phase-separated liquid droplets by HP1$\alpha$ indicates that epigenetic gene silencing may be driven by the physical isolation and compact nature of heterochromatic regions (18, 19).

The epigenetic code must be reliably transferred to daughter cells during replication to ensure proper programming of the cell identity and expression of the genome. As the replication machinery progresses, newly replicated DNA is rapidly reassembled into chromatin (20). The parental nucleosomes are randomly positioned on one of the two daughter strands, and the gaps between parental nucleosomes are filled with unmarked, newly synthesized nucleosomes to maintain the same nucleosome density (21). Methylation of the daughter strands counteracts the initial reduction in methylation and returns the methylation density to its original level, maintaining the epigenetic code across generations.

The results of stable-isotope labeling experiments show that histone methylation levels are transiently reduced during S phase and gradually reestablished during subsequent stages of the cell cycle (23, 24). Reverón-Gómez et al. (25) developed a sequencing technique, chromatin occupancy after replication (ChOR-seq), that also measures histone modification occupancy following replication. They find that the genomic positioning of histone modifications is preserved in daughter strands and that the kinetics of modification restoration varies across epigenetic marks and loci.

A “buffer model” explanation has been proposed to account for both the imprecise inheritance of histone methylation on a nucleosome level and the reliable maintenance of gene silencing at a genomic scale (23). Theoretical models show that cooperativity and long-range interactions between nucleosomes are required to establish robust bistability (26–29). Models that incorporate physically motivated chromatin connectivity, for instance through experimental measurements of contact probabilities in human and Drosophila cells (30) or a semiflexible bead-spring polymer (31–33), agree with experimental results of the extent of epigenetic spreading and the stable coexistence of distinct epigenetic domains. They demonstrate that coupling between three-dimensional (3D) folding and one-dimensional epigenetic spreading leads to bistability and epigenetic memory. Some models find that barrier elements are necessary to keep epigenetic marks confined to a local domain (32–34).

These models lay the groundwork for understanding the connection between chromatin architecture and epigenetic heritability. We extend this foundation by including in our model differences in the density of nucleosomes per unit volume in heterochromatin and euchromatin, which have been observed experimentally. Measurements from orientation-independent differential interference contrast microscopy indicate that heterochromatin is 5.5 to 7.5 times as dense as euchromatin (35). The addition of differential densities in our model helps explain the mechanistic factors that cause epigenetic domains to phase-segregate and thereby preserve the epigenetic sequence.

We develop a theoretical model for the reestablishment of epigenetic modifications following DNA replication. Our theory is based on our current understanding of heterochromatin/euchromatin segregation and methylation spreading (22, 36). We capture both the relationship between methylation state and HP1 binding as well as the cooperative interaction between HP1 and methyltransferase. Our model reproduces the robustness of the epigenetic code over the course of multiple generations. These results qualitatively recapitulate experimental observations that large methylated regions are preserved over generations while small fluctuations are not passed on. Our results demonstrate how chromatin organization, together with methyltransferase activity, could serve as a mechanism for the heritability of the epigenetic code. Thus, our model offers the physical insight needed to draw meaningful biological conclusions about the relationship between epigenetic heritability and chromosome organization.

Methods

Our model for the heritability of the methylation sequence integrates chromosomal compaction and methyl spreading within chromatin. Our model for DNA segregation into heterochromatin and euchromatin is based on the methylation sequence and cooperative HP1 binding (22). We capture the thermodynamics and configuration statistics of this system using a polymer-based Monte Carlo (MC) simulation. We implement a coarse-graining interaction (37) that allows us to simulate an entire human chromosome with nucleosome-scale discretization. The initial methylation profile is determined from experimental chromatin immunoprecipitation followed by sequencing (ChIP-seq) data (38, 39). To decide which histone tails are methylated, a cutoff is applied to the ChIP-seq signal such that approximately 50% of the histone tails are methylated.

In our model, HP1 can bind and unbind to any histone tail, but it preferentially binds to methylated tails based on experimental measurements of the binding affinities (11). To capture the effect of the oligomerization of HP1, we include an experimentally derived energetic benefit for regions with higher concentrations of HP1 (11), which then leads to segregation and compaction. For a given HP1 concentration and methylation profile, our model predicts which genomic regions compact to form heterochromatin. Fig. 2, Top show the structural progression of the chromosome with increasing HP1 concentration (where Gen 0 indicates the initial methyl profile determined by ChIP-seq data), demonstrating the role that HP1 plays in modulating the chromosomal state. Our model exhibits a behavior similar to that in previous works (40–42) that treat chromatin as a block copolymer. Furthermore, polymer models constructed based on epigenetic data accurately predict many genomic contacts as measured by Hi-C experiments (43, 44). However, our model directly incorporates HP1 binding as an essential player in methylation due to the experimentally established connection between HP1 and methyltransferase (45, 46).

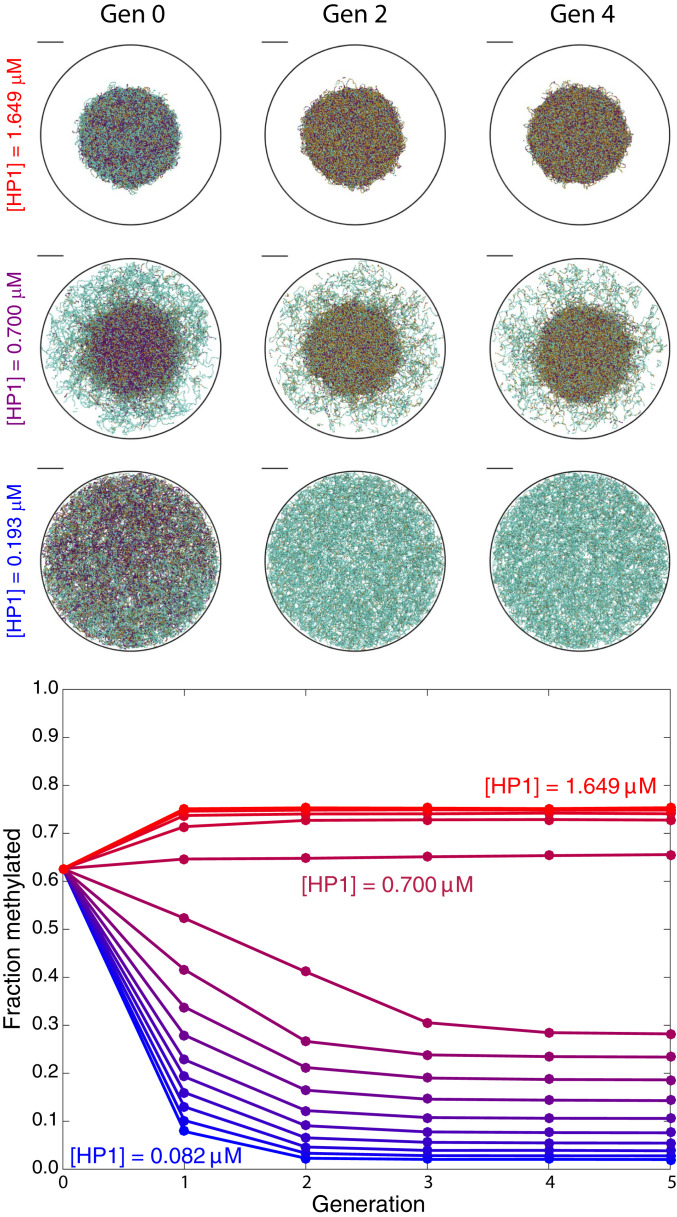
Fig. 2.

(Top) Images show representative configurations of the chromatin structure at generations 0, 2, and 4 for three concentrations of HP1. (Scale bars, $250\hspace{0.17em}\mathrm{n}\mathrm{m}$.) Cyan, gold, and purple colors designate nucleosomes that are unmethylated at both histone tails, methylated at one tail, and methylated at both tails, respectively. (Bottom) Plot shows the fraction of methylated nucleosomes versus generation of methylation conferral for a range of free HP1 concentrations from $\left[\mathrm{H}\mathrm{P}\mathrm{1}\right]=0.082\hspace{0.17em}\mathrm{\mu }\text{M}$ (blue) to $\left[\mathrm{H}\mathrm{P}\mathrm{1}\right]=1.649\hspace{0.17em}\mathrm{\mu }\text{M}$ (red).

Our methylation model captures loop-mediated spreading of methyl marks (36) and predicts which nucleosomes become methylated based on the spatial arrangement of the chromatin. Methylation may spread from methylated or unmethylated nucleosomes, based on the binding of HP1 to each site (11). We write a kinetic equation for the change in methylation probability with respect to time $\frac{d{p}_i}{dt}=k_m^{\left(0\right)}⟨n_{{\mathrm{H}\mathrm{P}\mathrm{1}}_i}⟩\left(1-p_i\right)-k_d{p}_i$, where $p_i$ is the probability that the $i$th nucleosome is methylated (i.e., trimethylated in our model), $k_m^{\left(0\right)}$ is the bare methyltransferase rate, and $k_d$ is the demethylation rate. We define $⟨n_{{\mathrm{H}\mathrm{P}\mathrm{1}}_i}⟩$ as the average number of HP1-bound tails within a cutoff distance $a$ of the $i$th nucleosome. The looping radius $a=15\hspace{0.17em}\mathrm{n}\mathrm{m}$ is chosen to approximately correspond to half the resolution of the MC simulation (similar results are obtained for values between $a=5\hspace{0.17em}\mathrm{n}\mathrm{m}$ and $a=35\hspace{0.17em}\mathrm{n}\mathrm{m}$). We specify the function of the methyltransferase based on experimental measurements of spreading around a nucleosome (45, 46) and define the parameter ${\alpha }_d=k_m^{\left(0\right)}/k_d$ as the relative rate of methylation to demethylation.

We combine the MC simulation for the 3D configurations and the methyl spreading calculation from the kinetic equation for methylation by alternating between predicting the chromatin organization and the methylation sequence. We use experimental ChIP-seq data as the methylation profile for an initial chromatin compaction simulation (identified as generation 0). We determine $⟨n_{{\mathrm{H}\mathrm{P}\mathrm{1}}_i}⟩$ from an average over 26 independent structures to obtain a representative nucleosome connectivity map. This map serves as the input to the methyl spreading master equation, which we solve for the steady-state methylation profile. We then convert the steady-state profile into a specific methylation sequence by selecting the methylation status of each nucleosome randomly based on the probabilities $p_i$ from the master equation. Next, we use the resulting methylation sequence as the input to another chromatin compaction simulation. We repeat this process to observe compaction and reestablishment over multiple generations, where a generation is one cycle through the MC simulation and reamplification calculation. The specific steps we take are as follows:

• 1)Divide the ChIP-seq data from ref. 39 into 200-bp sections corresponding to nucleosomes.
• 2)Apply cutoffs to the ChIP-seq signal so that 50% of histone tails are methylated.
• 3)Based on the methylation sequence, run an MC simulation to obtain equilibrium nucleosome positions and HP1 binding.
• 4)To mimic replication, randomly demethylate 50% of nucleosomes. (This step is only necessary for Fig. 6 since equilibrium of the master equation is independent of the initial condition.).
• 5)Solve the master equation for the methylation probabilities.
• 6)Randomly determine the methylation sequence based on the methylation probabilities.
• 7)Return to step 3.

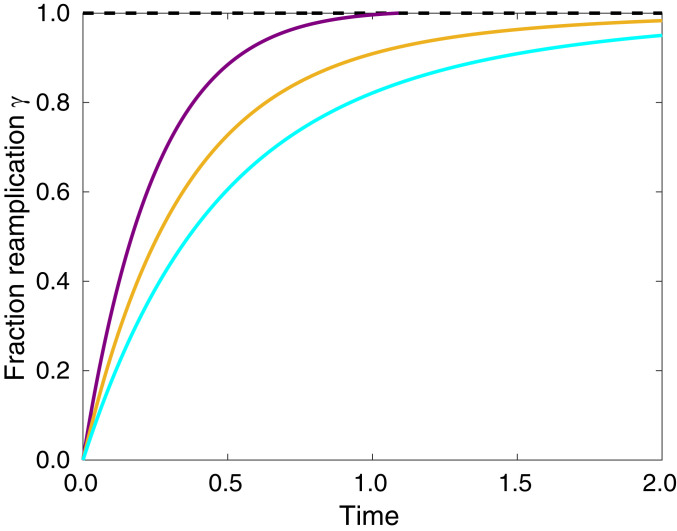
Fig. 6.

Plot of the fraction reamplification $\gamma$ versus time for nucleosomes categorized as high- (purple), intermediate- (gold), and low-methylation (cyan).

Since the in vivo concentration of HP1 is unknown, we perform this procedure over a broad range of concentrations to illustrate the full spectrum of possible epigenetic behavior. We select the value ${\alpha }_d=0.042$ so that the fraction of methylated nucleosomes returns to approximately the same value after each successive generation for a moderate concentration of unbound HP1 (0.700 $\mathrm{\mu }$M).

We also investigate the reestablishment kinetics after replication by solving the master equation for the methylation probability as a function of time. To determine the initial methylation profile, methylated nucleosomes from the original, ChIP-seq–derived methylation sequence are randomly selected to be demethylated with a probability of 50%. Then, the methylation kinetic equation is solved analytically based on the numerically determined looping contacts.

Our choice of methodology is informed by experimental data and our current understanding of the relevant timescales in the system. In using an averaged connectivity, we assume that the timescale for chromosome dynamics is much shorter than that for methyl transfer, as experimental measurements suggest is the case. Data from mass spectrometry experiments in HeLa cells fit to a simple mass-action model indicate that the order of the transfer rate for histone methylation may be between $10^{-2}$ per d and 1 per d (47). In vitro experiments of the kinetics of the murine H3K9 methyltransferase G9a find that methylation occurs on the order of hours (48). The diffusion coefficient of genetic loci in mammalian cells is approximately on the order of 1 $\mathrm{\mu }{\text{m}}^2$/min based on single-molecule optical tracking experiments (49). Together, these estimates for the methylation rate and diffusion coefficient suggest that DNA looping dynamics are much faster than methylation dynamics.

Cell cycles of replication and reestablishment occur on the order of many days, over which chromosomal DNA undergoes considerable dynamic rearrangement. Simultaneously capturing methylation kinetics and all facets of chromosomal dynamics over these time scales remains inaccessible for models with the level of detail that we aim to achieve for H3K9 methylation (i.e., single-nucleosome precision). We therefore focus our efforts on attaining accurate descriptions of methylation dynamics and chromosomal segregation into heterochromatin and euchromatin.

Methylation of H3K9 is shown experimentally to be confined to nucleosomes in close proximity (45, 46). Accordingly, we build a model that captures chromosomal condensation and methylation based on the experimentally observed function of methyltransferase (45) as well as our model of heterochromatin segregation (22). While chromosomal dynamics will influence large-scale chromosomal rearrangement, the effects we present here depend primarily on the local condensation of nucleosomes, which leads to an enhanced number of neighboring nucleosomes within heterochromatin. Considering an average connectivity allows us to represent a range of chromosomal structures and account for local fluctuations in nucleosome positions and HP1 binding.

Furthermore, experimental evidence of compartmentalization in Hi-C experiments suggests major differences between the large-scale chromosomal organization in conventional and inverted nuclei (50). However, both cell types exhibit compartmentalization into heterochromatin and euchromatin domains as well as compaction within heterochromatin. Since our model depends primarily on local compartmentalization, the mechanism that we present remains valid for both conventional and inverted nuclei despite the major differences in their large-scale organization.

Materials and Data Availability.

MC simulation code to predict chromosomal organization is found in the Spakowitz laboratory GitHub repository (https://github.com/SpakowitzLab) and code/documentation for the master equation solution for methylation dynamics is found on the Spakowitz group website (http://www.stanford.edu/∼ajspakow/).

Results and Discussion

We illustrate in Fig. 2, Top the effect of HP1 concentration on chromatin structure (note that generation 0 has the same methylation sequence for all HP1 concentrations). We observe that when the concentration of HP1 is low, the fraction of nucleosomes bound with HP1 is also low, and the chromosome is uncondensed. As the concentration of HP1 increases, the chromosome undergoes a phase transition, with some regions condensed and others uncondensed. At high concentrations of HP1, almost all nucleosomes are bound with HP1, and the chromosome is fully condensed.

Following the procedure described in the previous section, we study methylation reestablishment over generations of structural rearrangement and methyl spreading. Fig. 2 shows the progression of chromatin structure and the overall fraction of methylated nucleosomes over multiple generations. The average methylation level exhibits either amplification or reduction with generation, depending on whether the initial chromatin state is uncondensed (low HP1 concentration) or condensed (high HP1 concentration). An intermediate HP1 concentration of $\left[\mathrm{H}\mathrm{P}\mathrm{1}\right]=0.700\hspace{0.17em}\mathrm{\mu }\text{M}$ (purple) results in a fraction methylated that is approximately constant over the generations of reestablishment. At this optimal concentration, the structure maintains a “core” and “corona” with different degrees of nucleosome density. This difference in nucleosome density results in a disparate number of neighbors that participate in the conferral of methyl marks, causing the condensed core to reestablish its methylation and the uncondensed corona to maintain its unmethylated state. At low concentrations of HP1, the entire chromosome is uncondensed, resulting in the entire chromosome losing methylation. Conversely, the entire chromosome is condensed at high HP1 concentrations, leading to the entire chromosome reestablishing to a higher fraction methylated than in generation 0. This in turn leads to further compaction and methylation in subsequent generations.

The methylation level of a region of $\sim$100 nucleosomes is a better predictor of local compaction state (i.e., located in heterochromatin or euchromatin) than an individual nucleosome’s methylation state (22). We determine the fraction of methylated nucleosomes in sliding windows of 101 nucleosomes, with a window centered around each nucleosome. Throughout our current work, we focus our analysis on the fraction of nucleosomes methylated per window rather than the methylation state of individual nucleosomes.

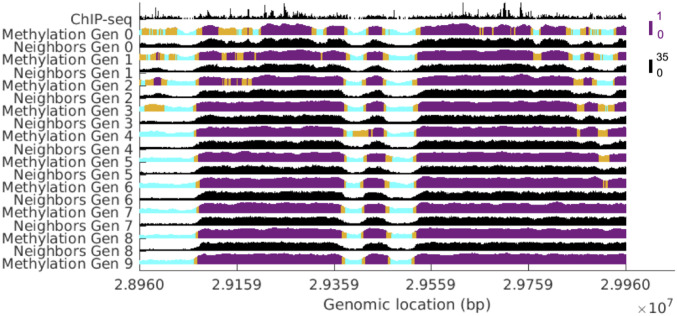
Fig. 3 shows the methylation profile and number of neighbors for each successive generation for a subsection of the chromosome for the optimal HP1 concentration $\left[\mathrm{H}\mathrm{P}\mathrm{1}\right]=0.700\hspace{0.17em}\mathrm{\mu }\text{M}$ (see SI Appendix, Fig. S1 for methylation profiles over a broader chromosomal region). The height of the methylation profile corresponds to the fraction of nucleosomes methylated in the surrounding window of 101 nucleosomes. The color represents the compaction state of the nucleosome as predicted by the window fraction methylated and cutoffs established from Fig. 5 (cutoff selection is described later in this section when Fig. 5 is introduced). Cyan, gold, and purple colors designate nucleosomes that are in euchromatin, the boundary, and heterochromatin, respectively. Regions with more neighbors tend to maintain their methylation over time and lie predominantly in heterochromatin or on the boundary. Notably, the window-averaged plots in Fig. 3 show the local state of the chromosome and do not reveal underlying fluctuations in the methylation sequence. The fact that window averaging is sufficient to capture the local state suggests that this mechanism for methylation is robust against local fluctuations in the methylation state. The shape of the methylation profile closely resembles that of the number of neighbors, demonstrating a clear connection between chromosomal organization and epigenetic state.

Fig. 3.

The evolution of the methylation profile and number of neighbors for a subsection of the chromosome at the optimal concentration of HP1. The height of the methylation profile corresponds to the fraction of methylated nucleosomes in the surrounding window of 101 nucleosomes. The color represents the compaction state of the nucleosome as predicted by the window fraction methylated and cutoffs established from Fig. 5. Cyan, gold, and purple colors designate nucleosomes that are in euchromatin, boundary between euchromatin/heterochromatin, and heterochromatin, respectively.

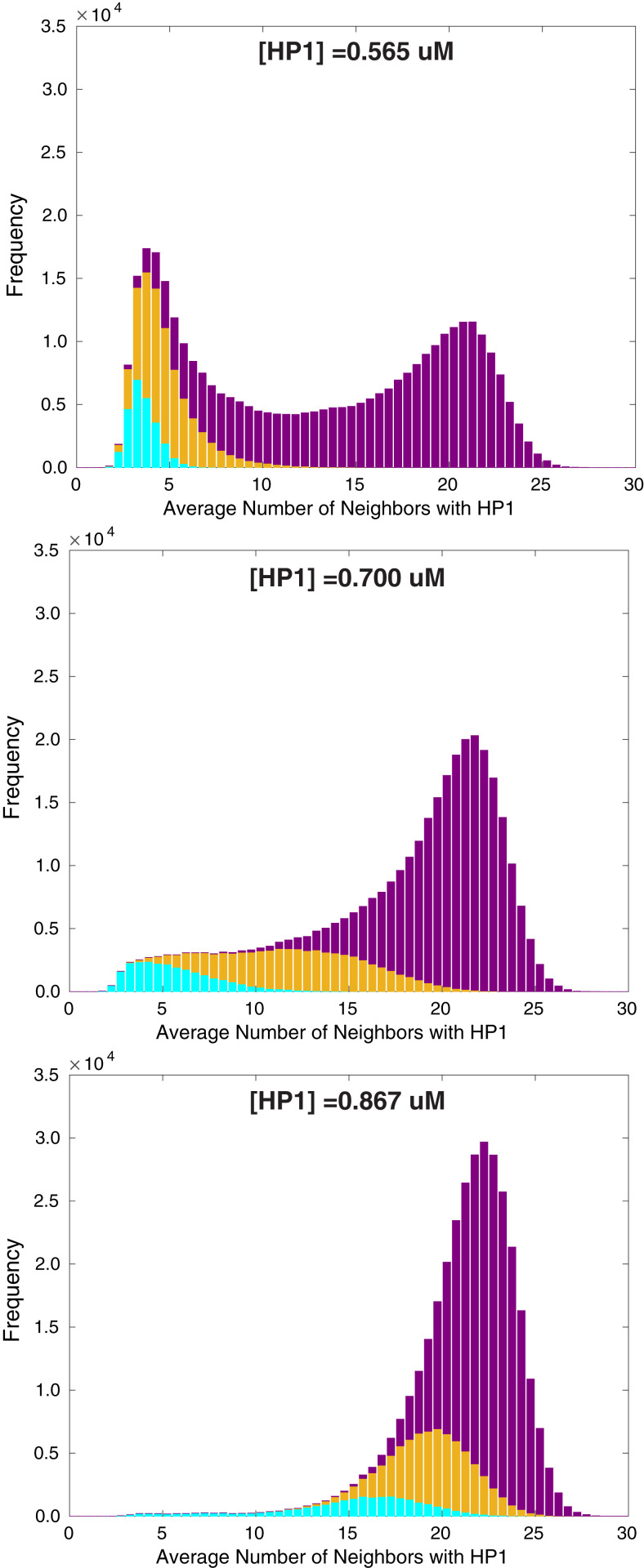
Fig. 5.

Histograms of the average number of neighboring nucleosomes with HP1 bound for three concentrations of HP1, given by 0.565 $\mathrm{\mu }$M, 0.700 $\mathrm{\mu }$M, and 0.867 $\mathrm{\mu }$M from top to bottom. Cyan, gold, and purple colors correspond to nucleosomes that are classified as originally residing in euchromatin, the boundary, and heterochromatin, respectively.

Experimental evidence shows that the epigenetic state is maintained at genomic length scales despite fluctuations at individual nucleosomes (23). As Fig. 3 demonstrates, the mechanism in our model allows for the overall preservation of condensed/methylated (i.e., transcriptionally repressed) regions and uncondensed/unmethylated (i.e., transcriptionally active) regions even as small fluctuations are not passed on. Our results reflect a mechanism of imprecise inheritance and thus exhibit a behavior similar to experimental observations.

While there is some small loss and gain of methylation, overall the domain boundaries are remarkably stable. The boundaries that do shift are those that border regions too small to maintain their original epigenetic state, whether methylated or unmethylated. We note that unlike experimental ChIP-seq profiles, which show heterogeneous methylation levels within domains, our methylation profile becomes increasingly homogeneous in both euchromatic and heterochromatic domains with each passing generation. One possible explanation for this difference is that we apply a cutoff to multicell ChIP-seq data to approximate a starting methylation profile for a single-cell simulation. The subsequent observed change in part represents relaxation away from the inherently inexact initial condition. In our determination of the methylation sequence, we applied a cutoff such that 50% of histone tails would be methylated, but this percentage is not well established and could be different from the number we prescribed. Furthermore, our model does not capture all processes in the cell, so it is possible that processes beyond the scope of our model are contributing to heterogeneity in the epigenetic profile. Another, perhaps less likely, explanation is that the actual methylation profile is more homogeneous than the inherently stochastic data produced by the ChIP-seq protocol.

In our model, the increasing homogeneity occurs because of entropic effects. Once a heterochromatic domain has enough methylation to maintain compaction and an elevated methylation level, then the lowest energy and highest entropy state will occur when methyl marks are more evenly spread among nucleosomes. Small euchromatic and heterochromatic domains cannot maintain their methylation level when surrounded by a much larger region of the opposite compaction state. Gradually these small domains are consumed by the larger ones, with entropy driving a homogenizing redistribution of methyl marks. That is, small domains that were initially euchromatic and heterochromatic gain or lose methylation, respectively, and as a result the overall methylation level within the larger domain equalizes.

We define the correlation coefficient $\chi$ (i.e., the Pearson correlation coefficient) for the current methylation state to the generation-0 methylation state

$$\chi =\frac{⟨m_i^{\left(j\right)}{m}_i^{\left(0\right)}⟩-⟨m_i^{\left(j\right)}⟩⟨m_i^{\left(0\right)}⟩}{{\sigma }_m^{\left(j\right)}{\sigma }_m^{\left(0\right)}},$$ [1]

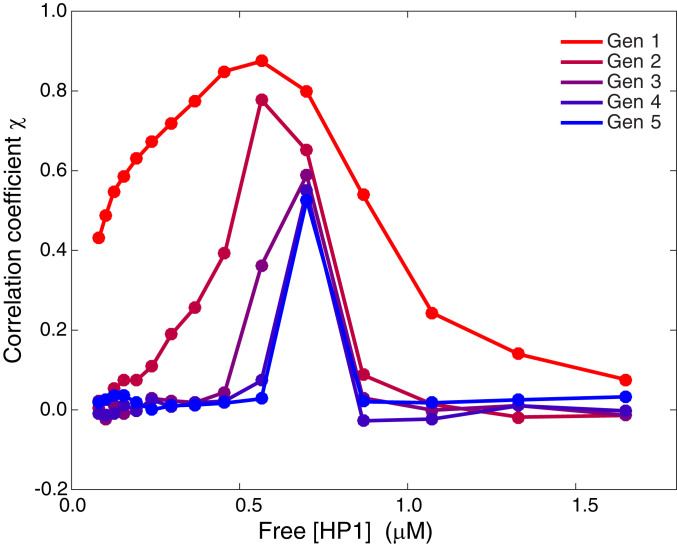
where $m_i^{\left(j\right)}$ is the window-averaged methylation (window size of 101 nucleosomes) centered at the $i$th nucleosome for the current state at the end of the methylation process for the $j$th generation (i.e., $m_i^{\left(0\right)}$ corresponds to the window-averaged methylation for generation 0). The methylation SDs ${\sigma }_m^{\left(j\right)}$ and ${\sigma }_m^{\left(0\right)}$ give the SD of the methylation sequence for the current generation and generation 0, respectively. Fig. 4 shows the correlation coefficient $\chi$ versus the concentration of HP1 for reestablishment over five generations. The recapitulation of the profile demonstrated in Fig. 3 for the optimal HP1 concentration is demonstrated in Fig. 4, since the correlation coefficient $\chi$ is a global indicator of sequence similarity between the current generation and generation 0. At the optimal concentration of HP1, the correlation decreases in the first couple of generations and stabilizes thereafter, indicating that the profile is maintained. With each successive generation, the correlation decreases slightly, but overall the methylation sequence is robust.

Fig. 4.

Plot of the correlation coefficient $\chi$ versus free HP1 concentration for five generations of reestablishment of the methylation sequence.

However, HP1 concentrations away from the optimal value exhibit a correlation coefficient that tends to zero, suggesting this mechanism relies on HP1 to control the differential compaction of the chromosome that is necessary to achieve robust conferral of the marks. For concentrations of HP1 below the optimal value, much of the original methylation is lost, and the correlation tends to zero over multiple generations. For concentrations above the optimal value, there is more methylation in the final state than in the initial one, so again the correlation tends to zero. Similar results are shown in SI Appendix, Fig. S2 for a correlation coefficient that compares the sequences to generation 1 (after one round of reestablishment).

The distribution of neighboring nucleosomes with HP1 bound (i.e., nucleosomes that are capable of spreading methyl marks) further illustrates the self-reinforcing relationship between chromatin structure and methylation. Fig. 5 shows the distribution of neighboring nucleosomes for HP1 concentrations coinciding with the optimal value $0.700\hspace{0.17em}\mathrm{\mu }\text{M}$ (middle plot) and two HP1 concentrations just above ($0.867\hspace{0.17em}\mathrm{\mu }\text{M}$, bottom plot) and below ($0.565\hspace{0.17em}\mathrm{\mu }\text{M}$, top plot) the optimal value. The peak that appears at low number of neighbors in the distributions corresponds to nucleosomes found in euchromatin, while the peak at high number of neighbors corresponds to those in heterochromatin. The coloring represents the classification of nucleosomes based on the original methylation sequence. To determine the classification, we first identify the midpoint between the peak at low number of neighbors and the peak at high number of neighbors. Two cutoffs in the window fraction methylated are selected such that less than 1.5% of nucleosomes classified as euchromatin or heterochromatin lie above or below the midpoint, respectively.

At the optimal concentration of HP1, we observe the greatest separation within the distribution between the unmethylated (cyan) and methylated (purple) regions (i.e., minimal overlap within the average number of neighboring nucleosomes). The left region of the histogram is primarily cyan, indicating that nucleosomes that are originally in euchromatin have a low number of neighbors and thus remain in euchromatin. Likewise, the right region is primarily purple, indicating that nucleosomes that are originally in heterochromatin have a high number of neighbors and thus remain in heterochromatin. As a result, nucleosomes will have roughly the same number of neighbors for the transfer of methyl marks and will retain their original methylation state, whether unmethylated or methylated. Below the optimal concentration of HP1, nucleosomes in heterochromatin move into euchromatin, losing both neighbors and methylation, as inferred from the presence of gold and purple in the left peak of Fig. 5, Top. For concentrations above the optimal value (bottom plot), the presence of gold and cyan in the right peak suggests that nucleosomes in euchromatin move into heterochromatin, gaining both neighbors and methylation. In both cases, the methylation sequence is not maintained. These results predict that it is the cooperative nature of chromatin compaction and methyl spreading that ensures the stability of the epigenetic sequence over generations.

In addition to recapitulating the long-term conservation of epigenetic domains over multiple cell cycles, our model also captures the dynamics of the restoration of methylation after a single replication event. We define the fraction reamplification:

$$\gamma ={⟨\frac{m_i\left(t\right)-m_i\left(t=0\right)}{m_i^{\left(j\right)}-m_i\left(t=0\right)}⟩}_{\hspace{0.17em}\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{h}},$$ [2]

where $m_i\left(t\right)$ is the window-averaged methylation of the $i$th nucleosome during reamplification, and $m_i^{\left(j\right)}=m_i\left(t\to \infty \right)$ is the final methylation state. The average ${⟨\dots ⟩}_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{h}}$ indicates an average over nucleosomes that are categorized as high-methylation (purple), intermediate-methylation (gold), and low-methylation (cyan). The predicted behavior suggests that degree of methylation is positively correlated with the kinetics of reamplification of the signal, resulting in regions of high methylation reaching their final methylation state faster than regions of low methylation. Although experimental data for H3K9me3 are lacking, the kinetics for H3K27me3, another repressive trimethylation modification, are available (25). Experimental ChOR-seq measurements find that highly methylated regions return to their original methylation level more quickly than less methylated regions (25), which is the same qualitative trend as our results.

Conclusion

Our work demonstrates that methyl spreading and chromatin compaction may act jointly as a mechanism for preserving the epigenetic code. Essentially, the proposed mechanism utilizes the phase transition associated with heterochromatin compaction as a template for the methylation sequence in the next generation. The preferential binding of HP1 to methylated nucleosomes results in cooperative compaction of chromosomal regions. HP1 molecules bind more prevalently in regions that are highly methylated, which causes those regions to condense into heterochromatin with more nucleosomes in close spatial proximity. The increase in neighboring nucleosomes then causes those highly methylated regions to maintain their methylation in the subsequent generation due to the cooperative interaction between locally bound HP1 and methyltransferase. In contrast, fewer HP1 molecules bind in regions that are less methylated, which causes those regions to decondense, driving nucleosomes farther apart. Those less-methylated regions maintain their unmethylated state due to the decrease in neighboring nucleosomes. By creating such a feedback loop, HP1 may serve as a global regulator for the overall methylation level in the chromosome and enable epigenetic domains to persist over generations at the optimal concentration of HP1. This proposed mechanism represents a robust strategy for maintaining the epigenetic code that is not sensitive to large-scale chromosomal dynamics and cell-to-cell variability in chromosomal organization. Our work illustrates how large methylated domains could be passed successfully from one generation to the next, while small fluctuations in the methylation profile would not be maintained in the next generation, thus reaffirming a trend seen in experiments. Our model proposes that physical mechanisms that operate globally and cooperatively contribute to long-term epigenetic heritability.