Data-Driven Motion Detection and Event-by-Event Correction for Brain PET: Comparison with Vicra

Abstract

Head motion degrades image quality and causes erroneous parameter estimates in tracer kinetic modeling in brain PET studies. Existing motion correction methods include frame-based image registration (FIR) and correction using real-time hardware-based motion tracking (HMT) information. However, FIR cannot correct for motion within 1 predefined scan period, and HMT is not readily available in the clinic since it typically requires attaching a tracking device to the patient. In this study, we propose a motion correction framework with a data-driven algorithm, that is, using the PET raw data itself, to address these limitations. Methods: We propose a data-driven algorithm, centroid of distribution (COD), to detect head motion. In COD, the central coordinates of the line of response of all events are averaged over 1-s intervals to generate a COD trace. A point-to-point change in the COD trace in 1 direction that exceeded a user-defined threshold was defined as a time point of head motion, which was followed by manually adding additional motion time points. All the frames defined by such time points were reconstructed without attenuation correction and rigidly registered to a reference frame. The resulting transformation matrices were then used to perform the final motion-compensated reconstruction. We applied the new COD framework to 23 human dynamic datasets, all containing large head motion, with ¹⁸F-FDG (n = 13) and ¹¹C-UCB-J ((R)-1-((3-(¹¹C-methyl-¹¹C)pyridin-4-yl)methyl)-4-(3,4,5-trifluorophenyl)pyrrolidin-2-one) (n = 10) and compared its performance with FIR and with HMT using Vicra (an optical HMT device), which can be considered the gold standard. Results: The COD method yielded a 1.0% ± 3.2% (mean ± SD across all subjects and 12 gray matter regions) SUV difference for ¹⁸F-FDG (3.7% ± 5.4% for ¹¹C-UCB-J) compared with HMT, whereas no motion correction (NMC) and FIR yielded −15.7% ± 12.2% (−20.5% ± 15.8%) and −4.7% ± 6.9% (−6.2% ± 11.0%), respectively. For ¹⁸F-FDG dynamic studies, COD yielded differences of 3.6% ± 10.9% in K_i value as compared with HMT, whereas NMC and FIR yielded −18.0% ± 39.2% and −2.6% ± 19.8%, respectively. For ¹¹C-UCB-J, COD yielded 3.7% ± 5.2% differences in V_T compared with HMT, whereas NMC and FIR yielded −20.0% ± 12.5% and −5.3% ± 9.4%, respectively. Conclusion: The proposed COD-based data-driven motion correction method outperformed FIR and achieved comparable or even better performance than the Vicra HMT method in both static and dynamic studies.

The spatial resolution of PET scanners has improved over the years. For instance, the dedicated brain scanner high-resolution research tomograph (HRRT; Siemens) has a resolution of less than 3 mm in full width at half maximum. However, head motion during brain PET studies reduces image resolution (sharpness), lowers concentrations in high-uptake regions, and causes bias in tracer kinetic modeling. Existing motion correction methods include frame-based image registration (FIR) (1) and correction using information from real-time hardware-based motion tracking (HMT) (2). FIR cannot correct for motion within 1 scan period (intraframe), and HMT is not routinely used in the clinic, since it typically requires attaching a tracking device to the patient. Thus, there is a need to develop a robust data-driven approach to detect and correct head motion.

Several data-driven approaches (3–5) have been proposed. Thielemans et al. (3) used principal-component analysis, and Schleyer et al. (6) compared principal-component analysis with an approach that used total-count changes with the aid of time-of-flight information. However, for the real patient studies of Thielemans et al. and Schleyer et al. (3,6), there lacked a comparison with a gold standard. In addition, the impact of motion correction on the accuracy of absolute quantification was not explored by those investigators (3,6). Feng et al. (5) proposed direct estimation of the head motion using the second-moment information, with a thorough validation study remaining to be performed. Additional articles (7,8) should be consulted to provide the reader with a more complete review.

Here, we propose a data-driven algorithm, centroid of distribution (COD), to detect head motion and perform motion correction within the list-mode reconstruction. A similar concept was previously proposed by other groups (9), and the COD method was also previously developed for respiratory motion detection (10) and voluntary body motion detection (11) with the aid of time-of-flight information. In this paper, we extended the use of COD to a non–time-of-flight scanner, HRRT, to detect head motion, followed by event-by-event correction (12). The proposed approach was compared with FIR and HMT using a Polaris Vicra (Northern Digital Inc.) optical HMT device (13,14). Vicra-based correction provided continuous head motion monitoring with event-by-event motion correction, which can be considered the gold standard. The proposed method was evaluated using both SUV and model-based quantification measures for 23 human dynamic scans, all containing large head motion, with ¹⁸F-FDG and ¹¹C-UCB-J ((R)-1-((3-(¹¹C-methyl-¹¹C)pyridin-4-yl)methyl)-4-(3,4,5-trifluorophenyl)pyrrolidin-2-one) (15).

MATERIALS AND METHODS

Human Subjects and Data Acquisitions

Twenty-three previously acquired human PET dynamic studies with 2 different radiotracers were analyzed. The subjects belonged to multiple diagnostic categories. These included 13 with ¹⁸F-FDG (injected activity, 184 ± 4 MBq) and 10 with ¹¹C-UCB-J (363 ± 178 MBq), a novel radiotracer that binds to the synaptic vesicle glycoprotein 2A (15), which has shown its potential as a synaptic density marker in Alzheimer disease (16). The 23 datasets for this study were chosen by identifying the subjects who exhibited the largest head motion of 290 examined subjects. The head motion magnitude of any point within the field of view was determined from the Vicra data as twice the SD of motion of that point. To describe the motion of the entire brain, 8 points were selected as the vertices of a 10-cm side-length cube centered in the scanner field of view. The final motion magnitude was the average of the values from the 8 points. More details have been previously published (13). This study was approved by the Yale University Human Investigation Committee and Radiation Safety Committee.

A transmission scan, used for attenuation correction, was performed before the PET emission acquisition. For both tracers, dynamic scans of 90-min duration were performed on the HRRT scanner, with the Vicra used for motion monitoring. Individual T1-weighted MR images were segmented using FreeSurfer (17) to generate regions of interest (ROIs), which were resliced to the individual PET space based on the MR–PET rigid registration using mutual information.

COD Motion Detection and Event-by-Event Motion Correction

Head motion information was extracted from the list-mode data using the COD algorithm. In COD, for every list-mode event i, the line of response is determined by the pair of detectors. The spatial coordinates of the 2 detectors were recorded in millimeters from the center of the scanner field of view, and the center of each event’s line of response, (X_i, Y_i, Z_i), was determined. The (X_i, Y_i, Z_i) for each event was averaged over a short time interval Δt—for example, 1 s in this study—to generate raw COD traces in 3 directions: C_X for lateral, C_Y for anterior–posterior, and C_Z for superior–inferior; a sample is shown in Figure 1A. Next, we implemented a semiautomatic motion-detection algorithm based on the assumption that sharp changes in COD represent head motion. The detection algorithm included 4 phases (the Discussion section provides details of the parameter settings in the algorithm).

FIGURE 1.

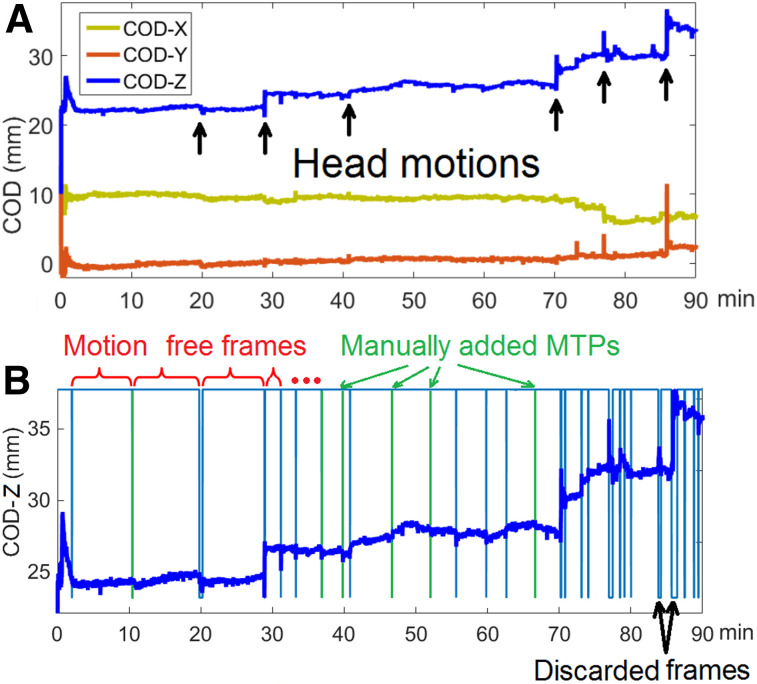
(A) COD traces in 3 directions of ¹⁸F-FDG study. Arrows denote abrupt changes in C_Z, which indicate head motion. (B) Motion detection results. Blue vertical lines indicate motion time points (MTPs) from automated detection, and green vertical lines indicate manually added points from visual assessment of undetected abrupt changes. Top horizontal line segments indicate preserved MFF, and short bottom line segments indicate discarded frames due to overly frequent motion.

The first phase was selection of the COD direction to use for motion detection. The variance of each COD directional value was calculated from 2 min after injection until the end of the scan. The direction with the highest variance was chosen for motion detection (denoted C(t)). An example is shown in Figure 1, where C_Z contained the largest variance.

The second phase was automatic detection of step motion. In this phase, the algorithm includes applying a 1-dimension 15-s median filter to obtain a new trace M(t); determining motion time points (t_i, times when motion occurs) by calculating the forward difference of M(t) (an example is shown in Supplemental Fig. 1A; supplemental materials are available at http://jnm.snmjournals.org) as D(t) = M(t + Δt) − M(t) and comparing D(t) with a user-defined threshold (as described in the Discussion section) (if D(t) exceeded the threshold, time t was chosen as a motion time point and added to a list t_i); labeling each frame between t_i and t_i+1 as a motion-free frame (MFF); and, if a MFF was shorter than 30 s, excluding data within this frame from further analysis. This step ensures that the preserved MFFs contain sufficient counting statistics for later motion estimation.

The third phase was visual assessment of the COD trace to identify additional motion. Since we considered only forward differences, that is, an abrupt change in COD over Δt = 1 s in the second phase, we may miss motion that was relatively slow, for example, lasting 2–3 s. For that obvious missed motion, we manually added t_i values based on the visual observation of the COD changes. An example can be found in Figure 1B.

The fourth phase was detection of slow motion. Some subjects exhibited slow motion, in which case a t_i value was automatically added in the middle of each MFF that was longer than 10 min (as described in the Discussion section).

Because of rapid changes in tracer distribution immediately after injection, COD alters rapidly. It is therefore challenging for the proposed method to detect motion within very early frames, such as within the first 2 min after injection (Fig. 1). Thus, we did not attempt to detect motion during the first 2 min of each study.

An example of the detection results is shown in Figure 1B. The horizontal lines at the top of the graph define each MFF, and the blue vertical lines indicate the automatically detected t_i values. Gaps in the horizontal lines at the top indicate frames discarded because of rapid motion. Green lines show the manually added t_i values in the third phase. As a reference, Supplemental Figure 1B shows the averaged distance of the 8 vertices of the reference cube (13) in the z direction in comparison to the position during the transmission scan, computed from the Vicra information.

Once the t_i values were determined, motion between MFFs was estimated and corrected using several steps. The first was to reconstruct each MFF using ordered-subsets expectation maximization without attenuation correction. The second was to smooth each MFF reconstruction using a 3 × 3 × 3 median filter followed by a gaussian filter of 5 mm in full width at half maximum. The third was to register each MFF image to a reference frame rigidly, that is, in the first 2 min. The fourth was to build a motion file for the entire study using each t_i and the transformation matrix to be used for all the events between t_i and t_i+1. The last was to use MOLAR (12) to perform event-by-event motion-compensated ordered-subsets expectation maximization reconstruction (2 iteration ×30 subsets), based on the chosen frame timing. For the COD method, no change in position is assumed during each MFF; however, because there may be multiple MFFs within each reconstructed frame, a final reconstructed frame may include data from multiple poses. In addition, if any of the discarded frame periods from the second detection phase overlap with each reconstructed frame, that portion of list-mode data was not included in the reconstruction of that frame. Therefore, COD results may be slightly noisier than other methods because of the discarded data.

Between-frame registrations were performed using FLIRT (18) with normalized mutual information as the similarity metric. Motion between the transmission and emission scans was corrected through manual registration between the MFF reference frame (without attenuation correction) and the transmission image. This transformation was incorporated into the motion file (the fourth step, above).

Motion Correction Methods for Comparison

In this study, the COD-based method was compared with conventional FIR and with Vicra-based event-by-event correction, which was treated as the gold standard. For the FIR method, predefined dynamic frames (10 × 30 s and 17 × 5 min) were first reconstructed using ordered-subsets expectation maximization (2 iterations × 30 subsets) and registered to a reference frame, that is, the first 10 min. For the Vicra method, subject motion was recorded with a Vicra optical tracking system at 20 Hz; that is, a rigid transformation matrix was determined every 50 ms, which was used for motion correction in the MOLAR reconstruction (12). Thus, all 3 methods used the same reconstruction pipeline with the same frame timing, just with different motion information, that is, none for FIR, 20 Hz for Vicra, and piecewise constant (during each MFF) with possible gaps for COD. For Vicra, mean position information during the transmission scan was used for correction between emission and attenuation images. For FIR, no motion correction (NMC) was performed between emission and attenuation images, consistent with typical practice.

Image Analysis

Twelve gray matter (GM) ROIs (17) were used to generate time–activity curves: amygdala, caudate, cerebellum cortex, frontal, hippocampus, insula, occipital, pallidum, parietal, putamen, temporal, and thalamus. The proposed COD-based approach was compared with NMC, FIR, and Vicra. The mean and SD of the SUV for the 0 to 10 min and the 60 to 90 min frames were computed for all GM ROIs. For each approach, the MR was registered to each frame, that is, 0–10 min and 60–90 min. For both ¹⁸F-FDG and ¹¹C-UCB-J, tracer concentrations are higher in GM than in white matter; SUV will therefore typically decrease in GM if motion is present during the frame and if attenuation correction mismatch is not considered. The effects of attenuation correction mismatch can be complicated, depending on the motion direction and tracer distribution. In other words, a better motion correction method will, in general, yield higher GM concentrations, unless large motion introduces inter-GM region-of-interest (ROI) cross talk.

Dynamic analysis was also performed, and the effect of residual motion was determined by its effect on fits to respective kinetic models. For both tracers, the time–activity curves (27 frames: 10 × 30 s, 17 × 5 min) for each ROI were computed for each correction method.

For ¹⁸F-FDG, Patlak analysis was performed (19), with t* set to 60 min and a 30-min scan duration being used. The slope K_i was calculated for each GM ROI. A population-based input function was used. To generate the population-based input function, arterial plasma curves (in SUV units) from 40 subjects (not included in this study) were averaged. The population-based input function was scaled for each subject using the injected dose normalized by body weight.

For ¹¹C-UCB-J, 1-tissue-compartment-model (20) fitting was applied to each ROI to generate the distribution volume, or V_T—the tissue-to-plasma concentration ratio at equilibrium, reflecting specific plus nonspecific binding. The rate of entry of tracer from blood to tissue, K₁, was also estimated. K₁ is governed mostly by the early tracer kinetics, whereas V_T is more affected by the late kinetics. Thus, K₁ is more sensitive to head motion in the early frames whereas V_T is affected more by late-frame motion. Metabolite-corrected arterial plasma curves were used as the input function.

The estimated kinetic parameters were compared between methods, using Vicra as the gold standard. In addition, the model-fitting normalized residual error was calculated for each ROI, as follows:

$$\text{Residual error}=100\%\sqrt{\frac{{\displaystyle \sum _i{w}_i{\left(C_{\text{T}}\left(t_i\right)-C_{\text{TF}}\left(t_i\right)\right)}^2}}{{\displaystyle \sum _i{w}_i{C}_{\text{T}}^2\left(t_i\right)}}},$$

where i is the frame number index, $C_{\text{T}}\left(t_i\right)$ represents the mean ROI concentration of frame i, $C_{\text{TF}}\left(t_i\right)$ is the mean concentration value of the fitted kinetic model of frame i, and w_i is the weighting factor used in the model fit. Uncorrected motion will cause increased residual error. Two ¹¹C-UCB-J studies underwent levetiracetam displacement at 60 min; these 2 studies were excluded from K₁, V_T, and residual error calculations.

RESULTS

COD computation time (mean ± SD) was 9.3 ± 5.1 min using a single-core 2.4-GHz central processing unit. C_X was selected for automatic detection in 7 subjects, and C_Z was selected for the other 16 subjects. The user-defined threshold in the second step of the first phase was 0.13 ± 0.03 mm (COD units do not correspond to actual distances) for ¹⁸F-FDG and 0.23 ± 0.12 mm for ¹¹C-UCB-J. The larger threshold variation for ¹¹C-UCB-J was due to greater variability in injected dose (¹¹C-UCB-J: 363 ± 178 MBq; ¹⁸F-FDG: 184 ± 4 MBq). During the 90-min scans, for ¹⁸F-FDG, there were 27 ± 7 MFFs (41 ± 14 for ¹¹C-UCB-J), which included 6.6 ± 3.7 manually added MFFs (8.0 ± 3.8 for ¹¹C-UCB-J). The fraction of scan time that was discarded was 6.4% ± 3.5% for ¹⁸F-FDG (7.1% ± 5.5% for ¹¹C-UCB-J).

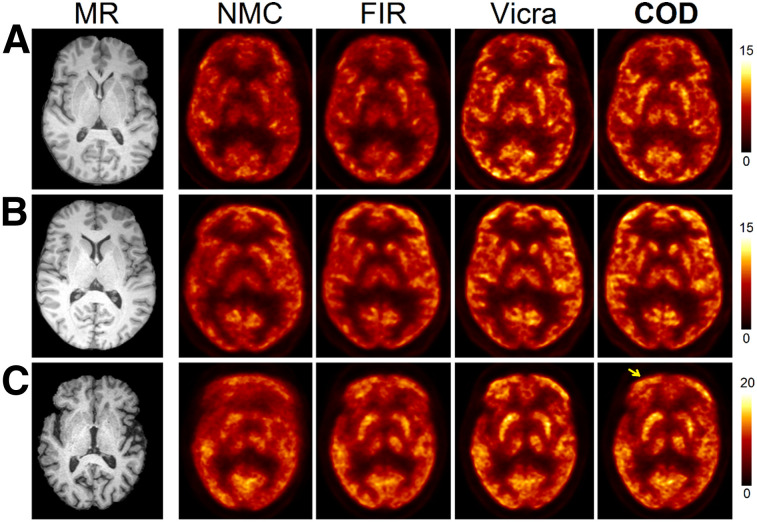
In Figure 2 (¹⁸F-FDG), transverse 60 to 90 min SUV images from 3 subjects are shown. A coronal view of these studies is shown in Supplemental Figure 2. In terms of SUV_mean compared with Vicra, the 3 subjects yielded +3.0% (ranked 2/13, second best), +0.6% (6/13), and −2.7% (13/13) for the COD method. Visually, COD and Vicra yielded very similar images for all 3 subjects. Detailed SUV results are shown in Supplemental Table 1. For the first 10 min, minimal SUV bias was observed among all methods, thus indicating that motion was minimal during the early scan. For the 60 to 90 min studies, NMC yielded a large negative bias (−15.7%) in SUV whereas FIR largely reduced the bias to −4.7% across all subjects and regions. The bias was calculated by averaging the percentage difference between a given method’s ROI results, for example, NMC, and the Vicra across all the subjects, and these values were then averaged over all the ROIs. The COD method yielded a positive bias for 9 of 12 ROIs, with the mean 1% higher than the Vicra, indicating that an excellent correction performance was achieved by COD. Furthermore, the ROI-level mean of intersubject variation (with respect to Vicra) was smallest for COD (3.2%), compared with FIR (6.9%) and NMC (12.2%).

FIGURE 2.

Sample slices in SUV units of motion-corrected reconstructions of ¹⁸F-FDG studies (60–90 min). Studies from A, B, and C ranked 2/13, 6/13, and 13/13 (worst) of COD-based approach, respectively. Subtle motion blur at frontal region (arrow) can be seen in COD (C).

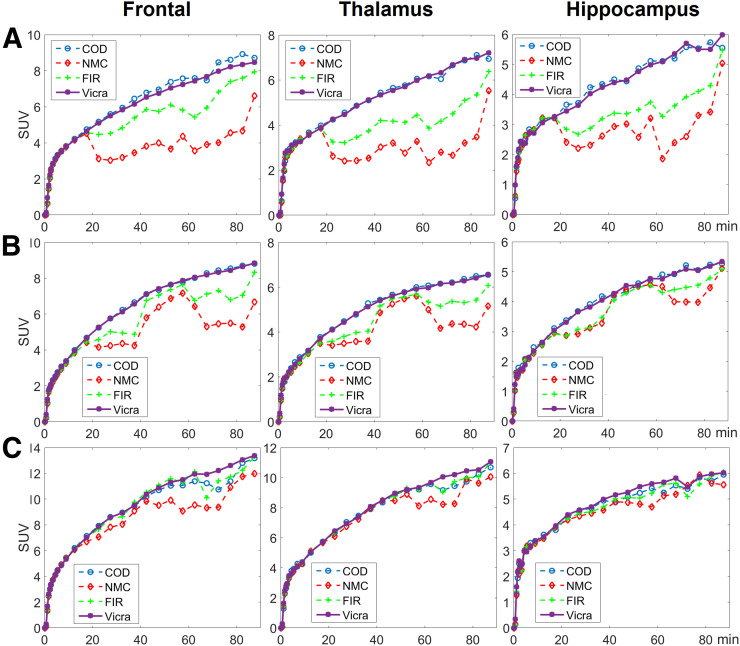
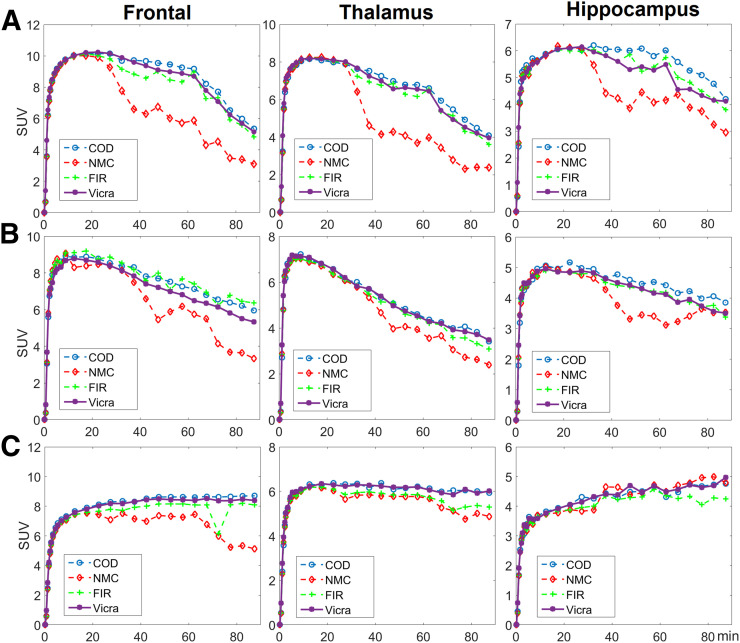
Time–activity curves for 3 representative ROIs, that is, frontal (large), thalamus (medium), and hippocampus (small), in the selected subjects are shown in Figure 3. For the first 10 min, the time–activity curves for all methods highly overlapped, indicating that minimal motion occurred, consistent with the numeric results in Supplemental Table 1. For all regions and for most frames, FIR, though outperforming NMC, yielded time–activity curves that were noisier and lower in value than those obtained with Vicra. COD yielded time–activity curves that highly overlapped with those of Vicra for the first 2 subjects. For the frontal region of the first subject, COD even exceeded Vicra. For the third subject, in which COD performed worst, COD was slightly worse than Vicra and similar to FIR for the last 30 min.

FIGURE 3.

Three time–activity curve examples of ¹⁸F-FDG studies for 3 regions (columns). Studies from A, B, and C ranked 2/13, 6/13, and 13/13 (worst) of COD-based approach, respectively.

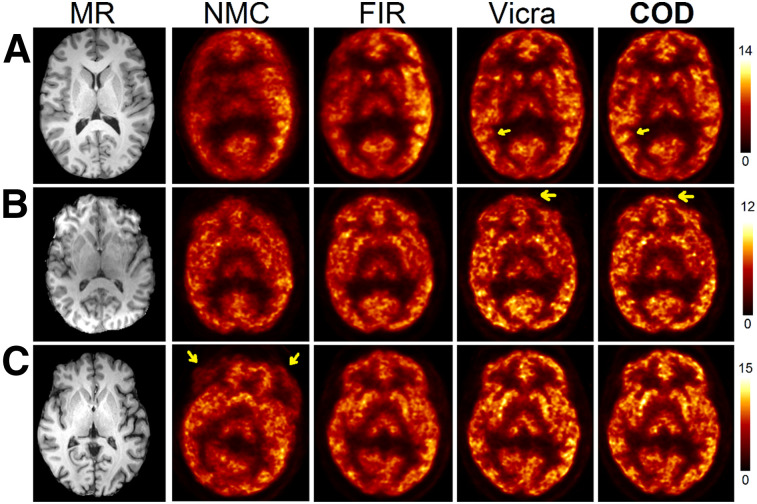
In Figure 4 (¹¹C-UCB-J), the 60 to 90 min transverse SUV images of 3 subjects are shown, ranking 2, 4, and 9 of 10 in the COD method in terms of SUV_mean bias compared with Vicra. A coronal view of these studies is shown in Supplemental Figure 3. Visually, compared with NMC, FIR substantially improved image sharpness for all subjects. For the third subject, the NMC image showed the large head motion, which was corrected by FIR. COD further improved sharpness and quantitation for all subjects. As compared with Vicra, COD yielded sharper and higher concentrations for the first and second subjects, as can be seen in cortical regions. For the Vicra method, the reflecting marker occasionally failed to maintain a rigid attachment to the subject’s head, as may explain the suboptimal performance of Vicra in these subjects (as described in the Discussion section). Detailed SUV results are provided in Supplemental Table 2. For the first 10 min, COD (−1.5%) slightly outperformed FIR (−3.4%) in terms of SUV bias compared with Vicra. For 60–90 min, FIR (−6.2%) yielded substantial improvement compared with NMC (−20.5%), whereas COD exceeded Vicra by 3.7%. Intersubject SD was smallest in COD (5.4%), compared with FIR (11.0%) and NMC (15.8%).

FIGURE 4.

Sample slices in SUV units of motion-corrected reconstructions of ¹¹C-UCB-J studies (60–90 min). Studies from A, B, and C ranked 2/10, 4/10, and 9/10 of COD-based approach, respectively. Arrows in A and B point to cortical regions, where COD showed sharper and higher concentration values than Vicra. Arrows in C show large magnitude of head motion in this subject.

In Figure 5, time–activity curves for the frontal, thalamus, and hippocampus regions of the 3 selected subjects in ¹¹C-UCB-J studies are shown. Consistent with the visual comparison shown in Figure 4, COD outperformed Vicra by yielding higher-value time–activity curves for the first and second subjects but comparable curves for the third subject. Bolus injection was used for only the first 2 subjects, whereas bolus plus infusion was used for the third.

FIGURE 5.

Three time–activity curve examples of ¹¹C-UCB-J studies for 3 regions (columns). Studies from A, B, and C ranked 2/10, 4/10, and 9/10 of COD-based approach, respectively. Subject A used bolus injection and underwent displacement at 60 min. Subject B used bolus injection, whereas C used infusion paradigm.

For ¹⁸F-FDG dynamic studies, K_i results are shown in Table 1. NMC yielded a large negative bias (−18%) with very high intersubject variation (39%) compared with Vicra. FIR substantially reduced the bias and intersubject variation to −2.6% ± 19.8%. The COD method outperformed FIR, with +3.6% mean bias and 10.9% intersubject SD. In terms of the residual error of Patlak fitting, averaging over all regions and subjects, NMC yielded 4.6%, FIR reduced the error by half (2.6%) whereas COD yielded better performance, comparable to Vicra, at 1.5% versus 1.2%, respectively. The residual error results are shown in Supplemental Table 3.

TABLE 1.

¹⁸F-FDG K_i Difference (%) Compared with Vicra

Site	NMC	FIR	COD
Amygdala	18.0 ± 60.4	−5.8 ± 22.4	3.1 ± 11.3
Caudate	−11.3 ± 39.0	−0.8 ± 29.8	6.3 ± 18.2
Cerebellum	−21.9 ± 38.2	−2.1 ± 12.4	2.6 ± 9.8
Frontal	−36.0 ± 43.4	−2.6 ± 25.4	8.5 ± 12.0
Hippocampus	−4.3 ± 40.9	−5.6 ± 19.7	−2.5 ± 13.3
Insula	−11.7 ± 19.3	−3.9 ± 14.1	4.7 ± 8.1
Occipital	−19.3 ± 27.5	3.4 ± 19.7	7.5 ± 11.8
Pallidum	−9.4 ± 47.6	0.2 ± 15.2	0.9 ± 12.9
Parietal	−27.6 ± 40.9	−1.4 ± 19.3	3.6 ± 8.6
Putamen	−35.0 ± 48.3	−1.3 ± 23.9	6.0 ± 9.7
Temporal	−27.5 ± 27.6	−3.6 ± 16.4	3.9 ± 7.4
Thalamus	−30.3 ± 38.0	−8.4 ± 19.0	−0.9 ± 7.3
Average difference (%)	−18.0	−2.6	3.6
Average SD (%)	39.2	19.8	10.9

SD is across all subjects.

For ¹¹C-UCB-J dynamic studies, K₁ and V_T results are shown in Table 2. For all methods, a very small K₁ bias was found because K₁ is sensitive to motion in the early frames, but there was minimal motion from 0 to 10 min (Supplemental Table 2). COD yielded the lowest intersubject variation (1.9%), compared with FIR (6.2%) and NMC (9.0%). For V_T, NMC yielded a large negative bias and intersubject variation (−20.0% ± 12.5%), whereas FIR showed great improvement in both (−5.3% ± 9.4%). COD yielded higher V_T values (3.7% ± 5.2%) than Vicra. Since COD yielded higher activity values than Vicra in SUV analysis (Supplemental Table 2), V_T estimated using COD will be higher, and is likely to be closer to the truth. In terms of model-fitting residual error, COD (2.5%) outperformed all other approaches, that is, NMC (7.3%), FIR (4.6%), and Vicra (2.8%) (Supplemental Table 4). Therefore, COD yielded the best performance in motion correction for the ¹¹C-UCB-J studies.

TABLE 2.

¹¹C-UCB-J K₁ and V_T Difference (%) Compared with Vicra

Parameter	NMC		FIR		COD
	K1	VT	K1	VT	K1	VT
Amygdala	0.8 ± 10.4	−24.6 ± 13.0	−1.2 ± 7.6	−7.5 ± 12.5	−0.7 ± 2.7	5.0 ± 6.2
Caudate	−3.5 ± 11.3	−29.9 ± 12.6	−3.9 ± 7.2	−6.6 ± 8.6	−0.8 ± 2.0	5.4 ± 5.3
Cerebellum	0.0 ± 5.5	−10.4 ± 9.9	−0.8 ± 3.6	−4.6 ± 6.8	−0.4 ± 1.5	2.1 ± 4.4
Frontal	1.2 ± 12.8	−37.8 ± 12.9	−3.1 ± 8.0	−5.2 ± 8.7	0.3 ± 1.1	3.5 ± 2.9
Hippocampus	−4.3 ± 6.7	−14.0 ± 12.9	−1.5 ± 6.5	−6.1 ± 10.2	0.5 ± 2.2	3.6 ± 5.7
Insula	2.1 ± 9.4	−21.1 ± 11.5	−0.7 ± 5.4	−6.7 ± 7.5	0.4 ± 0.7	2.1 ± 3.5
Occipital	0.3 ± 6.8	−10.5 ± 12.8	−0.3 ± 4.5	−0.6 ± 10.9	−0.9 ± 2.5	6.2 ± 7.5
Pallidum	−0.7 ± 6.4	7.7 ± 19.3	−0.2 ± 7.1	−5.1 ± 10.5	0.4 ± 3.2	0.5 ± 7.0
Parietal	0.2 ± 10.5	−25.8 ± 10.3	−1.6 ± 6.5	−1.3 ± 11.2	−0.8 ± 2.4	5.5 ± 6.2
Putamen	1.3 ± 8.5	−29.9 ± 9.7	−1.2 ± 5.2	−7.8 ± 7.3	0.2 ± 1.1	2.5 ± 4.2
Temporal	0.8 ± 10.9	−27.2 ± 10.9	−1.1 ± 6.2	−5.6 ± 12.7	−0.1 ± 1.8	5.8 ± 5.6
Thalamus	−2.4 ± 8.7	−16.7 ± 14.8	−2.2 ± 6.3	−6.0 ± 5.6	−0.6 ± 1.7	2.4 ± 4.2
Average difference (%)	−0.5	−20.0	−1.5	−5.3	−0.2	3.7
Average SD (%)	9.0	12.5	6.2	9.4	1.9	5.2

SD is across all subjects.

DISCUSSION

In this study, we proposed a data-driven head motion detection method followed by rigid motion correction. The proposed method was compared with a frame-based image registration method and a hardware-based event-by-event Vicra method, which was treated as the gold standard. For ¹⁸F-FDG and ¹¹C-UCB-J, the proposed method outperformed FIR and achieved results comparable to or better than those of Vicra for both static and dynamic data.

In theory, the Vicra method should yield the best possible performance. However, we found that COD yielded slightly higher GM SUVs (1% for ¹⁸F-FDG, 3.7% for ¹¹C-UCB-J), suggesting that Vicra HMT was not ideal for this patient cohort with large head motion. Ideally, the Vicra tool must be rigidly fixed to the head, but this may fail in several ways. For instance, the tool may permanently displace from its original location because of imperfect fixation. In this study, although we excluded scans containing obvious Vicra failure based on the technologist report, the positive percentage difference of COD over Vicra indicated that imperfect Vicra HMT still existed. Thus, the excellent performance by COD showed that a data-driven approach can be as effective as HMT.

In this study, the COD method discarded approximately 7% of the counts because of excessive and frequent motion. In contrast, Vicra used all the data. If these large-motion periods affect the Vicra tracking, such as by introducing nonrigid attachment between the marker and the subject’s head, then by excluding the same data, the performance of Vicra may improve. If so, a hybrid approach, that is, Vicra plus COD, could be implemented in the future to further improve Vicra tracking.

As an alternative to all the aforementioned approaches, markerless motion tracking using camera systems requires no attachment to a patient (21). However, the accuracy of such methods remains to be thoroughly tested, since the results can be affected by nonrigid facial expression changes (21) and performance may vary for different populations.

The success of the proposed method can be tracer-dependent. Here, we used ¹¹C-UCB-J and ¹⁸F-FDG for the following reasons: ¹⁸F-FDG is the most clinically used PET tracer, whereas ¹¹C-UCB-J, as a very novel tracer, has shown its efficacy for studying multiple neurologic disorders (16,22) and has great potential for wider clinical and research use. In addition, the 20-min half-life of ¹¹C added a challenge for the COD algorithm because of the high-noise condition for the late scan frames. However, we note that both tracers have a broad distribution in the brain, with patterns that do not vary substantially over time. This characteristic could make the image-registration step more robust than for tracers with a heterogeneous and time-varying distribution, such as ¹¹C-raclopride. In the future, we will evaluate COD with a wider variety of tracers.

In this implementation of the algorithm, several user-defined parameters were applied: the length of the median filter applied to the COD trace, the threshold for motion determination, the minimum duration of an MFF, the 5-min maximum length of an MFF for slow-motion detection, and the smoothing kernel for MFF reconstructions. These parameters were chosen empirically. Here, we clarify the rationale behind the choice of parameters for this algorithm: a 5-min maximum MFF was chosen as a tradeoff among the sensitivity to slow motion, the computational cost, and the registration accuracy, which is affected by noise and tracer distribution change. The 30-s shortest MFF was chosen to be the same length as the shortest dynamic frame. Another choice could be a count-level based approach, in which the threshold could be based on the minimal number of counts for each MFF. The 15-s median filter and threshold were tested against human detection of the abrupt changes in the COD curve for the same studies, and we adjusted the threshold to best match the human observations. In addition, in this study, we did not evaluate how much of the good performance of the COD method was due to manually added MFFs. In the future, further optimization of each parameter is required.

There are other limitations to this study. First, the COD method cannot accurately detect motion early after injection because of rapid changes in tracer distribution; therefore, data-driven motion correction during this period will remain challenging. Also, here we used list-mode reconstruction, but our approach can be extended to sinogram-based reconstruction (23) with minimal modification. In addition, we compared the COD-based approach with conventional FIR, in which each frame was reconstructed with attenuation correction. Thus, FIR suffered from not only intraframe motion but also attenuation mismatch artifacts. To minimize the latter effect, motion estimation could be performed using images without attenuation correction (13,24). In this study, we did not compare our approach with other data-driven approaches (3–5); such a comparison is important to clarify what method will provide the most robust and accurate method for motion detection and correction. The current detection method may detect some false-positive motion (in the absence of motion) purely due to noise in the COD. However, such false-positive detected motion should not substantially affect the reconstruction results despite the fact that small errors may still occur since the registration is subject to image noise. In addition, false-positive detection could also occur because of very rapid tracer kinetics.

CONCLUSION

We proposed a data-driven method to detect head motion followed by rigid motion correction. The proposed method was compared with a frame-based image registration method and the hardware-based Vicra method. For both ¹⁸F-FDG and ¹¹C-UCB-J, the proposed method outperformed FIR and achieved results comparable to or better than those for Vicra in both static and dynamic studies.

DISCLOSURE

This work was funded by National Institutes of Health (NIH) grants R01AG052560, R01NS094253 and R03EB027209 and by CTSA grant UL1 TR000142 from the National Center for Advancing Translational Science (NCATS), a component of the NIH. Its contents are solely the responsibility of the authors and do not necessarily represent the official view of the NIH. No other potential conflict of interest relevant to this article was reported.

KEY POINTS

• QUESTION: Can a data-driven head motion correction method achieve performance similar to that of HMT?

• PERTINENT FINDINGS: In a dynamic PET study of subjects with large head motion using ¹⁸F-FDG (n = 13) or ¹¹C-UCB-J (n = 10), both static and dynamic measures showed that the proposed data-driven head motion detection and correction method yielded results comparable to or better than those of the hardware-based approach.

• IMPLICATIONS FOR PATIENT CARE: Data-driven head motion correction can be reliably performed for clinical or research brain PET scans for tracers with broad distributions.