Abstract
Our purpose was to assess the performance of full-dose (FD) PET image synthesis in both image and sinogram space from low-dose (LD) PET images and sinograms without sacrificing diagnostic quality using deep learning techniques. Methods: Clinical brain PET/CT studies of 140 patients were retrospectively used for LD-to-FD PET conversion. Five percent of the events were randomly selected from the FD list-mode PET data to simulate a realistic LD acquisition. A modified 3-dimensional U-Net model was implemented to predict FD sinograms in the projection space (PSS) and FD images in image space (PIS) from their corresponding LD sinograms and images, respectively. The quality of the predicted PET images was assessed by 2 nuclear medicine specialists using a 5-point grading scheme. Quantitative analysis using established metrics including the peak signal-to-noise ratio (PSNR), structural similarity index metric (SSIM), regionwise SUV bias, and first-, second- and high-order texture radiomic features in 83 brain regions for the test and evaluation datasets was also performed. Results: All PSS images were scored 4 or higher (good to excellent) by the nuclear medicine specialists. PSNR and SSIM values of 0.96 ± 0.03 and 0.97 ± 0.02, respectively, were obtained for PIS, and values of 31.70 ± 0.75 and 37.30 ± 0.71, respectively, were obtained for PSS. The average SUV bias calculated over all brain regions was 0.24% ± 0.96% and 1.05% ± 1.44% for PSS and PIS, respectively. The Bland–Altman plots reported the lowest SUV bias (0.02) and variance (95% confidence interval, −0.92 to +0.84) for PSS, compared with the reference FD images. The relative error of the homogeneity radiomic feature belonging to the gray-level cooccurrence matrix category was −1.07 ± 1.77 and 0.28 ± 1.4 for PIS and PSS, respectively. Conclusion: The qualitative assessment and quantitative analysis demonstrated that the FD PET PSS led to superior performance, resulting in higher image quality and lower SUV bias and variance than for FD PET PIS.
Keywords: PET/CT, brain imaging, low-dose imaging, deep learning, radiomics
Molecular neuroimaging using PET is ideally suited for monitoring cell and molecular events early in the course of a neurodegenerative disease and during pharmacologic therapy (1). PET is a molecular imaging technique that produces a 3-dimensional (3D) radiotracer distribution map representing properties of biologic tissues, such as metabolic activity or receptor availability. PET images suffer from a relatively high noise level dictated by the Poisson nature of annihilation photon emission and detection. Apart from the technical aspects, PET image quality depends on the amount of injected radiotracer or acquisition time, which are proportional to the statistics of the detected events. The main argument in favor of a reduction of the injected radiotracer’s activity is linked to the potential risks of ionizing radiation (2). Albeit low, this increase in risk motivates precaution, particularly in pediatric patients, healthy volunteers, or in the case of multiple scanning for follow-up or monitoring of the response to treatment using different tracers. Therefore, there has always been a desire to moderate the injected activity to minimize the potential health hazards. A reduced acquisition time could have a positive impact on the patient’s comfort and on the scanner’s throughput. However, dose and time reduction can adversely affect image quality, inevitably leading to a lower signal-to-noise ratio (SNR) and thus hampering the quantitative and diagnostic value of PET imaging.
To address this issue, several approaches have been proposed in the literature to produce standard-dose and full-dose (FD) PET images from corresponding low-dose (LD) and low-count images (3). Formerly, iterative reconstruction algorithms with accurate statistical modeling (4) and postprocessing or filtering (5,6) were the 2 common methods. However, these approaches tend to reduced spatial resolution and quantitative accuracy by producing overly smooth structures (7,8). In the past few years, deep learning algorithms have witnessed notable growth in the fields of computer vision and medical image analysis (9,10). Contrary to other denoising approaches, which are applied directly on LD PET images, deep learning algorithms are capable of learning a nonlinear transformation to predict standard-dose images from LD inputs. In particular, convolutional neural network (CNN) models have demonstrated outstanding performance in cross-modality image synthesis, such as MRI-to-CT conversion (11,12), joint PET attenuation and scatter correction in image space (PIS) (13,14), and synthesis of FD PET images from LD images (15–21). Xiang et al. suggested a deep auto-context CNN architecture that estimates FD PET images on the basis of local patches in LD PET images (19). A major limitation of this work is that 2-dimensional (2D) transaxial slices were extracted from PET images and used for 2D training of the CNN model. Another group claimed that reliable FD PET could be estimated from a 200th LD image using a residual U-Net architecture (22). Other work from the same group used 2D slices of LD 18F-florbetaben PET images along with various MR sequences, such as T1-weighted, T2-weighted, and diffusion-weighted imaging (DWI), to predict FD images using a U-Net architecture (15). Häggström et al. (23) developed a deep encoder–decoder network for direct reconstruction of PET images from sinograms, whereas Hong et al. (24) proposed a data-driven, single-image superresolution technique for sinograms using a deep residual CNN to improve the spatial resolution and noise properties of PET.
A more recent work reported on the use of a 3D U-Net along with anatomic information from coregistered MRI to improve the SNR of PET without using higher-SNR PET images in the training dataset (25). Cui et al. (26) presented an unsupervised PET-denoising model that was fed by the patient’s prior high-quality images and used the noisy PET image itself as the training label. As such, this approach does not need any paired dataset for training. Furthermore, Lu et al. (27) investigated the effect of different network architectures and other parameters pertaining to both noise reduction and quantitative performance. The optimized fully 3D U-Net architecture is capable of reducing the noise in LD PET images while minimizing the quantification bias for lung nodule characterization.
Previous studies relied on deep learning–based approaches to establish an end-to-end pipeline to synthesize FD PET image space (15–21). As such, these approaches are optimized for a specific protocol, such as an image reconstruction algorithm or a postreconstruction filter. Therefore, adoption of a different reconstruction technique requires retraining of the CNN. Conversely, the prediction of FD PET images in projection space allows selection of any reconstruction or postreconstruction filter without the need for retraining the CNN. Furthermore, PSS provides a more comprehensive data representation than PIS, effectively containing detailed information about count statistics and spatial and temporal distributions. To take advantage of this fact, a 3D U-Net was trained to predict FD sinograms from LD sinograms in an end-to-end fashion. Thereafter, the synthesized sinogram can be reconstructed using any reconstruction algorithm. The results achieved using the proposed framework are compared with the PIS implementation using the same 3D U-Net architecture. LD PET imaging using the proposed approach would be beneficial in pediatric and adolescent clinical studies as well as in research protocols requiring serial studies.
MATERIALS AND METHODS
PET/CT Data Acquisition
The present study was conducted on 18F-FDG brain PET/CT studies collected between June 2017 and May 2019 at Geneva University Hospital. The database consisted of 140 patients presenting with cognitive symptoms of possible neurodegenerative disease (73 ± 8 y): 66 men and 74 women (73 ± 9 y and 72 ± 11 y, respectively). Detailed demographic information on the patients is summarized in Table 1. The study protocol was approved by the institution’s ethics committee, and all patients gave written informed content. The PET/CT acquisitions were performed on a Biograph mCT scanner (Siemens Healthcare) about 35 min after injection. An LD CT scan (120 kVp, 20 mAs) was performed for PET attenuation correction. The patients underwent a 20-min brain PET/CT scan after injection of 205 ± 10 MBq of 18F-FDG. PET data were acquired in list-mode format and reconstructed using e7 tool (an offline reconstruction toolkit provided by Siemens Healthcare) to produce FD PET sinograms and images. Subsequently, a subset of PET data containing 5% of the total events was extracted randomly from the list-mode data to produce LD sinograms (400 × 168 × 621 matrix) using a validated code (28). Both FD and LD PET images were reconstructed into a 200 × 200 × 109 image matrix (2.03 × 2.03 × 2.2 mm voxel size) using an ordinary Poisson ordered-subsets expectation-maximization (OP-OSEM) algorithm (5 iterations, 21 subsets). The PET images underwent postreconstruction gaussian filtering (2 mm in full width at half maximum), similar to the clinical protocol.
TABLE 1.
Demographics of Patients Included in This Study
| Demographic | Training | Test | Validation |
| Number | 100 | 20 | 20 |
| Sex (n) | |||
| Male | 45 | 11 | 8 |
| Female | 55 | 9 | 12 |
| Age, mean ± SD (y) | 73 ± 8 | 68 ± 18 | 73 ± 4.5 |
| Weight, mean ± SD (kg) | 70 ± 13 | 67 ± 12 | 71 ± 11 |
Indication/diagnosis: cognitive symptoms of possible neurodegenerative etiology.
U-Net Architecture
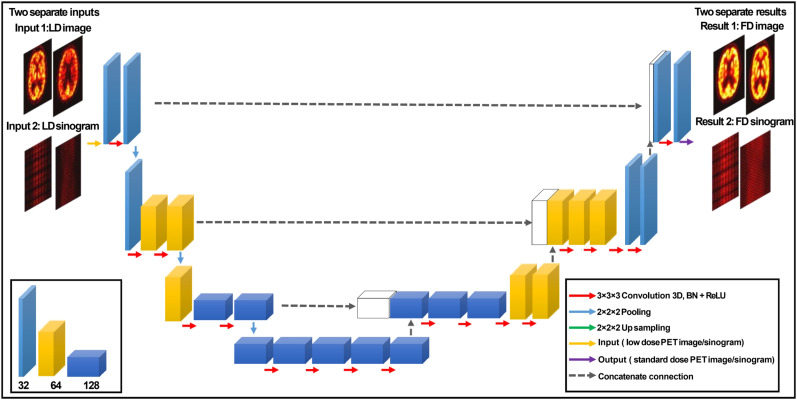
A modified 3D U-Net based on a model proposed previously (29) was developed to predict FD images (PIS) and sinograms (PSS) from their corresponding LD images and sinograms. Figure 1 shows the structure of the modified 3D U-Net, which consists of an encoder–decoder module. In the encoder part, each layer contains two 3D convolutions (30) followed by a rectified linear unit (ReLu) activation function and a 3D maxpooling with a stride size of 2. In the decoder part, each layer consists of 3D up-sampling with a stride of 2 followed by two 3D convolutions and a ReLu. The size of all convolutional kernels is 3 × 3 × 3 voxels in each convolutional layer. The shortcut connections between the outputs of each layer in the encoder network and the corresponding layer in the decoder network aimed at addressing the gradient vanishing problem that occurs in complex deep learning models. In CNN, the bottleneck is a layer that contains fewer neurons than its neighboring layers (31). To avoid this issue, the number of channels was doubled before maxpooling and before each ReLu function. The network input is either a 101 × 101 × 71 matrix (after cropping) in PIS or a 400 × 168 × 62 matrix in PSS.
FIGURE 1.
Schematic diagram of modified 3D U-net, consisting of encoder–decoder CNN. Tensors are indicated by boxes, whereas arrows denote computational operations. Number of channels is indicated beneath each box in bottom left panel. Input and output of this network are LD and FD image PET pairs either in image or sinogram space. BN = batch normalization; ReLU = rectified linear unit activation.
The modified 3D U-net architecture also includes a series of pooling options, dilated convolutional layers, and 16 convolutional layers. The Adam optimizer with a learning rate of 0.001 was used to minimize the loss function. A dataset of paired LD and FD images and sinograms of 100 subjects were used to train the network using the adaptive moment estimation implemented in the Keras open-source package (32,33), which computes adaptive learning rates for each parameter and saves an exponentially decaying average of past gradients using Equations 1 and 2:
| Eq. 1 |
| Eq. 2 |
where and indicate the estimation of the mean and the uncentered variance of the gradients, respectively; denotes the gradient at a subsequent time step ; and and are exponential decay rates with, ∈ [0, 1].
The model was implemented on NVIDIA 2080Ti GPU with 8 GB of memory running under a Microsoft Windows 10 operating system. The training was performed using mini-batch size of 5 for 250 epochs.
Data Augmentation
To increase the size of the training dataset while avoiding overfitting, 3 types of data augmentation methods were implemented. These included rotations, transformations, and zooming, which were randomly applied to the training dataset. Hence, the model was trained using the 300 augmented images along with the 100 original images. Applying such a rigid deformation to the training dataset assisted the network to learn features that are invariant to these transformations (34).
Training, Validation, and Testing
The training and hyperparameter fine tuning of the model were performed on 100 patients. Twenty patients were used for model evaluation, whereas a separate unseen dataset of 20 patients served as the test dataset. The mean squared error loss function was used for the training of the model.
Evaluation Strategy
Clinical Qualitative Assessment
The PSS and PIS FD PET images along with their corresponding reference FD and LD PET images were anonymized and randomly enumerated for qualitative evaluation by 2 nuclear medicine physicians. In total, 80 PET images were evaluated, including 20 reference FD, 20 LD, 20 PIS, and 20 PSS PET images belonging to the test dataset. The quality of PET images was assessed using a 5-point grading scheme, where 1 indicates uninterpretable; 2, poor; 3, adequate; 4, good; and 5, excellent (Supplemental Fig. 1; supplemental materials are available at http://jnm.snmjournals.org).
Quantitative Analysis
The accuracy of the predicted FD images from LD PET data were evaluated using 3 quantitative metrics, including the root mean squared error (RMSE), peak signal-to-noise ratio (PSNR), and structural similarity index metrics (SSIM) (Equations 3, 4, and 5, respectively). Moreover, these metrics were also calculated for the LD images to provide insight about the noise levels and significant signal in the LD images.
| Eq. 3 |
| Eq. 4 |
| Eq. 5 |
In Equation 3, is the total number of voxels in the head region, is the reference image (FD), and is the predicted FD image. In Equation 4, indicates the maximum intensity value of or , whereas MSE is the mean squared error. and in Equation 5 denote the mean value of the images and, respectively. indicates the covariance of and, which in turn represent the variances of and images, respectively. The constant parameters and (were used to avoid a division by very small numbers.
Region-based analysis was also performed to assess the agreement of the tracer uptake and 28 radiomic features between predicted and ground-truth images. Using the PMOD medical image analysis software (PMOD Technologies LLC) and the Hammers N30R83 brain atlas, 83 brain regions were delineated on the ground-truth FD PET images. Then, the delineated volume regions were mapped to LD, PIS, and PSS PET images to quantify 28 radiometric features using the LIFEx analysis tool (35). Moreover, the regionwise SUV bias and SD were calculated for the 83 brain regions on the predicted as well as LD PET images, with the FD PET images serving as a reference. A joint histogram analysis was also performed to depict the voxelwise correlation of the activity concentration between PIS and PSS and reference FD PET images.
Overall, 28 radiomic features were extracted for each brain region, including 7 conventional indices, 5 first-order features, 7 gray-level zone length matrix features, 6 gray-level run length matrix features, and 3 gray level cooccurrence matrix features. The list of these radiomic features is shown in Table 2. The relative error (RE%) was also calculated for the radiomic features using Equation 6.
| Eq. 6 |
TABLE 2.
Summary of 28 Radiomic Features Belonging to 6 Main Categories Estimated for 83 Brain Regions
| Radiomic feature category | Radiomic feature |
| Conventional indices | SUVmean |
| SUVSD | |
| SUVmax | |
| SUV Q1 | |
| SUV Q2 | |
| SUV Q3 | |
| TLG (mL) | |
| First-order features: histogram | Kurtosis |
| Entropy_log10 | |
| Entropy_log2 | |
| First-order features: shape | SHAPE_volume (mL) |
| SHAPE_volume (no. of voxels) | |
| Gray-level zone length matrix | Short-zone emphasis (SZE) |
| Long-zone emphasis (LZE) | |
| Short-zone low gray-level emphasis (SZLGE) | |
| Short-zone high gray-level emphasis (SZHGLE) | |
| Long-zone low gray-level emphasis (LZLGLE) | |
| Long-zone high gray-level emphasis (LZHGLE) | |
| Zone percentage (ZP) | |
| Gray-level run length matrix | Short-run emphasis (SRE) |
| Long-run emphasis (LRE) | |
| Short-run low gray-level emphasis (SRLGLE) | |
| Short-run high gray-level emphasis (SRHGLE) | |
| Run length nonuniformity (RLNU) | |
| Run percentage (RP) | |
| Gray-level cooccurrence matrix | Homogeneity |
| Energy | |
| Dissimilarity |
In Equation 6, denotes the value of a specific radiomic feature calculated in a brain region. The MedCalc software (36) was used for the calculation of the pairwise t test for statistical analysis of RMSE, SSIM, and PSNR between LD, PSS, PIS, and reference FD PET images. The significance level was set at a P value of less than 0.05 for all comparisons.
RESULTS
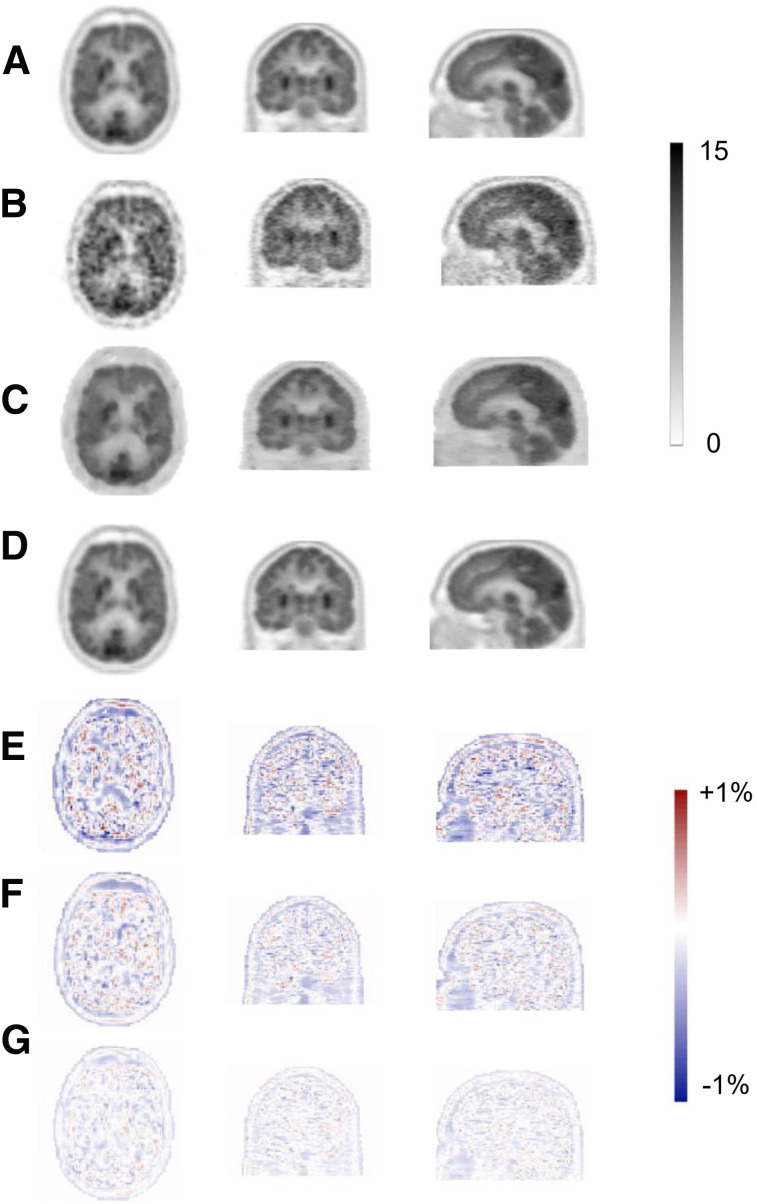
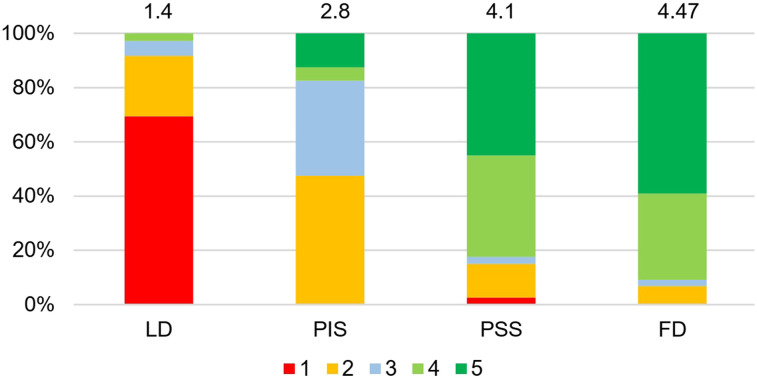
The predicted images in both PIS and PSS exhibited notable enhancement in image quality compared with LD images, providing almost similar appearance with respect to reference FD PET images. Figure 2 displays representative transverse, coronal, and sagittal views showing reference FD, LD, PIS, and PSS PET images along with their corresponding bias maps. The visual inspection revealed that the images derived from training in the PSS better reflected the underlying 18F-FDG uptake patterns and anatomy than those obtained from implementation in PIS. The image quality scores assigned by the 2 physicians to FD, LD, PIS, and PSS images are shown in Figure 3. The mean scores for each group are indicated at the top of each bar. The PIS images were scored as poor (score of 2) or better. The FD and PSS images exhibited comparable quality, with scores of 4.9 and 4.55 (good) or higher, respectively.
FIGURE 2.
Representative 18F-FDG brain PET images of 65-y-old male patient. Reference FD (A) and corresponding LD (B) and predicted FD images in image (C) and sinogram space (D) are presented. SUV bias maps for LD (E), PIS (F), and PSS (G) PET images with respect to reference FD PET image are also shown.
FIGURE 3.
Result of image quality assessment by 2 nuclear medicine specialists for LD, PIS, PSS, and FD PET images. Mean scores are presented on top of bar plots. 1 = uninterpretable; 2 = poor; 3 = adequate; 4 = good; 5 = excellent.
Table 3 summarizes the PSNR, SSIM, and RMSE calculated separately on the validation and test datasets for PIS, PSS, and LD PET images. Overall, the predicted images in PSS showed improved image quality, noise properties, and quantitative accuracy (Table 4), with statistically significant differences with respect to the implementation in PIS.
TABLE 3.
Comparison of Results Obtained from Analysis of Image Quality in LD PET Images and Predicted Images in PIS and PSS for Validation Dataset
| Dataset | SSIM | PSNR | RMSE |
| Validation | |||
| PIS | 0.97 ± 0.02 | 34.60 ± 1.08 | 0.18 ± 0.02 |
| PSS | 0.98 ± 0.01 | 38.25 ± 0.66 | 0.15 ± 0.03 |
| LD | 0.84 ± 0.04 | 29.00 ± 0.92 | 0.40 ± 0.03 |
| P (PIS vs. PSS) | 0.022 | 0.019 | 0.016 |
| P (PIS vs. LD) | 0.037 | 0.021 | 0.036 |
| P (PSS vs. LD) | 0.042 | 0.025 | 0.030 |
| Test | |||
| PIS | 0.96 ± 0.03 | 31.70 ± 0.75 | 0.18 ± 0.04 |
| PSS | 0.97 ± 0.02 | 37.30 ± 0.71 | 0.17 ± 0.01 |
| LD | 0.82 ± 0.15 | 29.92 ± 0.71 | 0.41 ± 0.04 |
| P (PIS vs. PSS) | 0.031 | 0.024 | 0.018 |
| P (PIS vs. LD) | 0.040 | 0.036 | 0.041 |
| P (PSS vs. LD) | 0.041 | 0.031 | 0.031 |
TABLE 4.
Average and Absolute Average SUV Bias ± SD Calculated Across 83 Brain Regions for LD, PIS, and PSS PET Images
| Bias (%) | PSS | PIS | LD |
| Average SUV | 0.24 ± 0.96 | 1.05 ± 1.44 | 0.10 ± 1.47 |
| Absolute average SUV | 0.69 ± 0.70 | 1.35 ± 1.15 | 1.12 ± 0.93 |
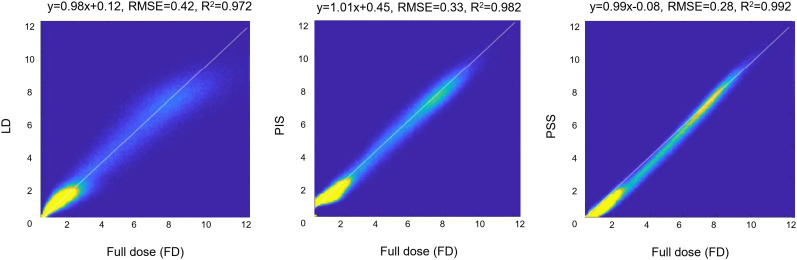
Figure 4 illustrates linear regression plots depicting the correlation between tracer uptake for LD, PIS, and PSS with respect to FD. The scatter and linear regression plots showed an increased correlation between PSS and FD (R2 = 0.99, RMSE = 0.28) compared with PIS (R2 = 0.98, RMSE = 0.33). A relatively higher RMSE (0.42) was obtained for LD PET images.
FIGURE 4.
Joint histogram analysis of LD PET images (left), predicted FD images in PSS (middle), and PIS (right) vs. FD PET images.
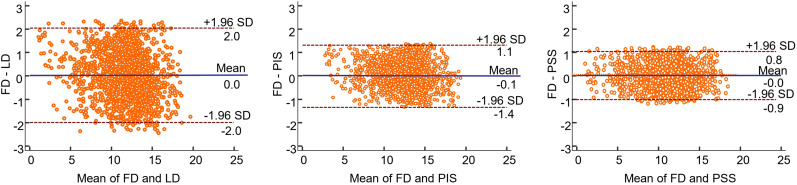
The Bland–Altman plots, in which each data point reflects a brain region, confirmed the results obtained from joint histogram analysis, with the lowest SUV bias (0.02) and smallest SUV variance (95% confidence interval, −0.92 to +0.84) being observed for PSS images (Fig. 5). Though the SUV bias is extremely low for LD images, increased variance compared with FD images was observed (95% confidence interval, −2 to +2), reflecting their poor image quality.
FIGURE 5.
Bland and Altman plots of SUV differences in 83 brain regions calculated for LD (left), PIS (middle), and PSS (right) PET images with respect to reference FD PET images in test dataset. Solid blue and dashed lines denote mean and 95% confidence interval of SUV differences, respectively.
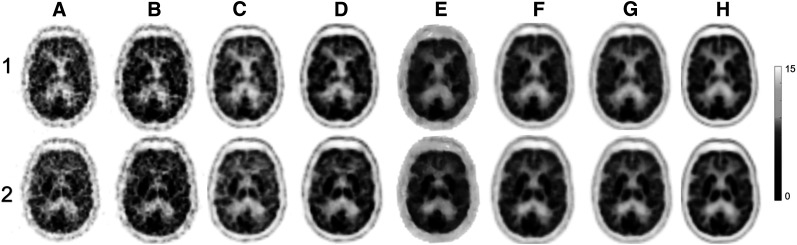
Figure 6 compares the deep learning predicted images (PIS and PSS) and images reconstructed from the LD sinogram using 4 state-of-the-art iterative reconstruction methods, including OSEM, OSEM + TOF, OSEM + PSF, and OSEM + TOF + PSF. The FD sinogram was also reconstructed using OSEM and OSEM + TOF + PSF as a reference.
FIGURE 6.
Comparison of images of 2 clinical 18F-FDG brain PET studies (1 and 2) reconstructed from 5% LD sinograms using 4 different reconstruction algorithms, including OSEM (A), OSEM + TOF (B), OSEM + PSF (C), and OSEM + TOF + PSF (D) with deep learning–based predicted images in PIS (E) and PSS (F). Reference FD images reconstructed using OSEM (G) and OSEM + TOF + PSF (H) are also shown.
Supplemental Figure 2 depicts the regionwise quantitative accuracy of the tracer uptake for LD, PSS, and PIS images. The SD of tracer uptake in all brain regions (Supplemental Fig. 3), SUV bias, and its SD within each brain region were calculated using the Hammers N30R83 brain atlas to delineate the 83 brain regions. It was shown that the SUV bias was below 4% for PSS, PIS, and LD images, with LD exhibiting a relatively high SD compared with PIS and PSS. The PSS approach led to the lowest absolute average SUV bias (0.69% ± 0.7%) across all brain regions, whereas PIS and LD resulted in an absolute average SUV bias of 1.35% ± 1.15% and 1.12% ± 0.93%, respectively (Table 4). Even though a very low SUV bias was observed in LD images, a remarkably increased SD was seen, reflecting the high noise level in LD images. The symmetric left and right sides of the brain regions were merged, reporting a single value to reduce the number of regions. Hence, the 83 brain regions were reduced to 44 in Figure 6. The higher SD of SUV bias was observed in LD images, reflecting the noisy nature of low-count images. Lower SDs were observed in PSS than in PIS.
Supplemental Figures 4 and 5 show the relative error (%) of 28 radiomic features calculated for PSS and PIS images across the 83 brain regions for the 20 subjects in the test dataset. The mean RE of SUVmean calculated across all brain regions was 0.24% ± 0.96% and 1.05% ± 1.44% for PSS and PIS, respectively. The largest SUVmean bias between PSS and PIS images with respect to reference FD images was observed in the brain stem (4.04%), corpus callosum (3.8%), pallidum (3.08%), caudate nucleus (1.6%), and superior frontal gyrus (3.38%). SUVmax had a mean RE of 1.18% ± 1.5% and 0.81% ± 0.51% for PIS and PSS, respectively. The mean RE of the homogeneity radiomic feature belonging to the gray-level cooccurrence matrix category was −1.07% ± 1.77% and 0.28% ± 1.4% for PIS and PSS, respectively. Only 12 and 5 regions had an RE greater than 2% for PIS and PSS, respectively. The middle frontal gyrus, medial orbital gyrus, and posterior orbital gyrus displayed substantial variances for dissimilarity radiomic feature of both PIS and PSS (3.68% vs. 4.89%, −1.7% vs. 2.91%, and −1.7% vs. 2.9%, respectively).
DISCUSSION
Table 5 summarizes the study design and outcomes of previous works reporting on the prediction of FD PET images from LD images based on deep learning approaches (15–21). In this work, we aimed to generate diagnostic-quality 18F-FDG brain PET images from LD PET data in PIS or PSS corresponding to only just 5% of injected activity compared with the regular FD scan. The neural network was trained using a 3D scheme, considering a batch of image slices as input, since there is a dependence of tracer distribution along the z-axis. Hence, by including the neighboring slices, the model would be able to capture the underlying morphologic information. In contrast to previous studies, we aimed to train the network in PSS and PIS to evaluate the performance of both approaches for estimation of FD PET images. It was shown that the synthesized FD images predicted from LD sinograms had a superior image quality and lower regional SUV bias and variance than either LD or FD images predicted in PIS. This finding highlights the value of using raw data in PSS (400 × 168 × 621 = 41,731,200) rather than the data in PIS (101 × 101 × 71 = 724,271). The data representation in PIS is different from that in PSS. Let us consider an ideal point source located at the center of the field of view, which would appear as a hot spot in the corresponding location in PIS. The same point source would be reflected in PSS by numerous correlated lines of response, conveying different data representations of the same element. The extended or detailed data available in PSS helped the convolutional network to better decode the underlying features, thus resulting in superior performance. The convolutional network trained in PIS applied simplistic noise reduction, thus leading to blurred, highly smoothed, and slightly biased FD images.
TABLE 5.
Summary of Previous Studies Focusing on LD-to-FD PET Conversion in Brain PET Imaging Using Deep Learning Techniques
| Study | Patients (n) | Input | Network architecture | Injected activity (MBq) | LD ratio (%) | Tracer | Scanning time (min) | Time from injection to scan (min) | Scanner model | Evaluation method and metrics |
| (16) | 11 | LD PET, MRI (T1) | Segmented brain tissues from MRI to build tissue-specific models to predict standard-dose plus iterative refinement strategy | 203 ± 12 | 25 | 18F-FDG | 12 | 36 | Siemens Biograph mMR | Leave-one-out cross-validation, SUV bias |
| (8) | 8 | LD PET, MRI (T1, DTI) | Sparse representation based on mapping strategy and incremental refinement scheme | 203 ± 12 | 25 | 18F-FDG | 12 | 60 | Siemens Biograph mMR | NMSE, PSNR, contrast recovery, quantification bias |
| (19) | 16 | LD PET MRI (T1) | Deep auto-context CNN architecture with 4 layers | 203 ± 12 | 25 | 18F-FDG | 12 | 60 | Siemens Biograph mMR | NMSE, PSNR, training and testing time comparison, training loss vs. iteration |
| (22) | 9 | LD PET | 2.5D U-Net (modified) | 370 | 0.5 | 18F-FDG | 40 | 45 | GE Signa PET/MRI | NRMSE, error maps |
| (15) | 40 | LD PET MRI (T1, T2, 3D) | 2D U-Net | 330 ± 30 | 1 | 18F-florbetaben | 20 | 90–110 | GE Signa PET/MRI | SSIM, PSNR, RMSE, clinical image quality scoring, Bland–Altman analysis |
| (20) | 16 | LD PET | 3D conditional GANs | 203 ± 12 | 25 | 18F-FDG | 12 | 36 | Siemens Biograph mMR | SSIM, PSNR, RMSE, quantification bias |
| (21) | 40 | LD PET | 2.5D GAN | 330 ± 30 | 1 | 18F-florbetaben | 20 | 90–111 | GE SIGNA PET/MRI | SSIM, PSNR, RMSE, clinical image quality scoring, error maps |
| This work in PIS | 140 | LD PET image | 3D U-Net (modified) | 205 ± 10 | 5 | 18F-FDG | 20 | 34 | Siemens Biograph mCT | SSIM, PSNR, RMSE, clinical image quality scoring, Bland–Altman analysis, quantification bias, radiomic features, joint histogram, error maps |
| This work in PSS | 140 | LD PET sinograms | 3D U-Net (modified) | 205 ± 10 | 5 | 18F-FDG | 20 | 34 | Siemens Biograph mCT | SSIM, PSNR, RMSE, clinical image quality scoring, Bland–Altman analysis, quantification bias, radiomic features, joint histogram, error maps |
DTI = diffusion tensor imaging; GAN = generative adversarial network; NMSE = normalized mean square error; NRMSE = normalized root mean square error.
The qualitative assessment of image quality performed by nuclear medicine specialists demonstrated the superior performance of the PSS approach, showing close agreement between PSS and the reference FD images. The RMSE calculated on LD and synthesized PSS and PIS images were 0.41 ± 0.03, 0.17 ± 0.01, and 0.18 ± 0.04, respectively, reflecting the effectiveness of model training in PSS (P < 0.05). Moreover, the SSIM improved from 0.84 ± 0.04 for LD to 0.96 ± 0.03 for PIS images and further to 0.97 ± 0.02 for PSS images. It would be enlightening to consider the resulting metrics in conjunction with those obtained from LD images for better interpretation of the extent of improvement achieved by the proposed methods. For instance, Ouyang et al. (21) claimed that only 1% of the standard dose was used, yielding LD images with better or at least comparable SSIM (0.86 vs. 0.84) and RMSE (0.2 vs. 0.4), compared with ours with 5% of the FD. This finding might partly stem from differences in sensitivity between PET scanners—differences that directly affect the quality of the PET images. In this regard, previous studies conducted on the GE Healthcare Signa PET/MRI device (1,2) took advantage of its higher sensitivity (21cps/kBq) and better count-rate performance characteristics (peak noise-equivalent count rate of 210 kcps at 17.5 kBq/cm3) than those of the Biograph mCT scanner used in this study, a scanner that had a considerably lower detection sensitivity (9.7 cps/kBq) and count-rate performance (noise-equivalent count rate, 180 kcps at 28 kBq/cm3). Furthermore, their technique relied on support from coregistered MR images, which could partly explain why a 5% LD image in the present study and a 1% LD in abovementioned studies resulted in a comparable RMSE (∼0.15).
The quantitative analysis of 83 brain regions in terms of 28 radiomic features showed high repeatability of the radiomic features for both PSS and PIS techniques. From the 2,324 data points corresponding to the number of regions multiplied by the number of radiomic features, only 3 and 9 data points for PIS and PSS, respectively, had an RE larger than 5%, with the remaining data points exhibiting no significant REs. The quantitative evaluation showed less than 1% mean absolute error in most brain regions for PSS. We involved both patients and healthy individuals to offer a heterogeneous dataset. Neurologic abnormalities present in our dataset included patients presenting with cognitive symptoms of possible neurodegenerative disease. Since the dataset for the training contained both patients and healthy individuals, data augmentation was applied to avoid overfitting and to guarantee robust and effective training. The Bland and Altman analysis showed reduced bias and variance in the 83 regional SUVmean values obtained from PSS and PIS PET images, compared with LD images. The Bland and Altman plots further demonstrated the superior performance of the PSS approach, resulting in SUVs that are comparable to the original FD images.
In terms of computation time, training in PIS is less demanding than training in PSS. Training in PIS took about 38 h, versus about 210 h in PSS. Moreover, synthesis of a single PET image (after training) in PIS takes about 100 s, versus the approximately 370 s required in PSS. This difference stems from the increased data size and consequently added processing burden for the PSS implementation.
One of the limitations of the present study was that during the clinical evaluation, the LD images were relatively easily identified by physicians. Hence, the physicians could have been subconsciously biased and could have assigned lower scores to these images. Moreover, patient motion during the PET/CT scan, particularly for patients with dementia, who are more susceptible to involuntary motion, may impair the quality of both LD and FD PET images. However, motion might affect LD and FD PET images differently since the randomly selected events for creation of the LD images might not exactly follow the same motion pattern as in the FD PET data.
CONCLUSION
We have demonstrated that high-quality 18F-FDG brain PET images can be generated using deep learning approaches either in PIS or in PSS. The noise was effectively reduced in the predicted PET images from the LD data. Prediction of FD PET images in sinogram space exhibited superior performance, resulting in higher image quality and minimal quantification bias.
DISCLOSURE
This work was supported by the Swiss National Science Foundation under grants SNRF 320030_176052 and SNF 320030_169876 and the Swiss Cancer Research Foundation under grant KFS-3855-02-2016. No other potential conflict of interest relevant to this article was reported.
KEY POINTS
QUESTION: Does implementation of deep learning–guided LD brain 18F-FDG PET imaging in PSS improve performance over implementation in PIS?
PERTINENT FINDINGS: Using a cohort study comparing 140 clinical brain 18F-FDG PET/CT studies, among which 100, 20, and 20 patients were randomly partitioned into training, validation, and independent validation sets, respectively, we demonstrated through qualitative assessment and quantitative analysis that the FD PET prediction in PSS led to superior performance, resulting in increased image quality and decreased SUV bias and variance compared with FD PET prediction in PIS.
IMPLICATIONS FOR PATIENT CARE: The proposed deep learning–guided denoising technique enables substantial reduction of radiation dose to patients and is applicable in a clinical setting.
Supplementary Material
REFERENCES
- 1.Zaidi H, Montandon M-L, Assal F. Structure-function based quantitative brain image analysis. PET Clin. 2010;5:155–168. [DOI] [PubMed] [Google Scholar]
- 2.Health Risks from Exposure to Low Levels of Ionizing Radiation: BEIR VII—Phase 2. Washington DC: National Research Council; 2006:155–189. [Google Scholar]
- 3.Gatidis S, Wurslin C, Seith F, et al. Towards tracer dose reduction in PET studies: simulation of dose reduction by retrospective randomized undersampling of list-mode data. Hell J Nucl Med. 2016;19:15–18. [DOI] [PubMed] [Google Scholar]
- 4.Reader AJ, Zaidi H. Advances in PET image reconstruction. PET Clin. 2007;2:173–190. [DOI] [PubMed] [Google Scholar]
- 5.Yu S, Muhammed HH. Comparison of pre-and post-reconstruction denoising approaches in positron emission tomography. Paper presented at the 1st International Conference on Biomedical Engineering (IBIOMED); October 5–6, 2016; Yogyakarta, Indonesia.
- 6.Arabi H, Zaidi H. Improvement of image quality in PET using post-reconstruction hybrid spatial-frequency domain filtering. Phys Med Biol. 2018;63:215010. [DOI] [PubMed] [Google Scholar]
- 7.Wang C, Zhenghui H, Pengcheng S, Huafeng L. Low dose PET reconstruction with total variation regularization. Conf Proc IEEE Eng Med Biol Soc. 2014;2014:1917–1920. [DOI] [PubMed] [Google Scholar]
- 8.Wang Y, Zhang P, An L, et al. Predicting standard-dose PET image from low-dose PET and multimodal MR images using mapping-based sparse representation. Phys Med Biol. 2016;61:791–812. [DOI] [PubMed] [Google Scholar]
- 9.Litjens G, Kooi T, Bejnordi BE, et al. A survey on deep learning in medical image analysis. Med Image Anal. 2017;42:60–88. [DOI] [PubMed] [Google Scholar]
- 10.Liu X, Faes L, Kale AU, et al. A comparison of deep learning performance against health-care professionals in detecting diseases from medical imaging: a systematic review and meta-analysis. Lancet Digit Health. 2019;1:e271–e297. [DOI] [PubMed] [Google Scholar]
- 11.Arabi H, Zeng G, Zheng G, Zaidi H. Novel adversarial semantic structure deep learning for MRI-guided attenuation correction in brain PET/MRI. Eur J Nucl Med Mol Imaging. 2019;46:2746–2759. [DOI] [PubMed] [Google Scholar]
- 12.Han X. MR-based synthetic CT generation using a deep convolutional neural network method. Med Phys. 2017;44:1408–1419. [DOI] [PubMed] [Google Scholar]
- 13.Bortolin K, Arabi H, Zaidi H. Deep learning-guided attenuation and scatter correction in brain PET/MRI without using anatomical images. Paper presented at: IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC); October 26 to November 2, 2019; Manchester, UK.
- 14.Yang J, Park D, Gullberg GT, Seo Y. Joint correction of attenuation and scatter in image space using deep convolutional neural networks for dedicated brain 18F-FDG PET. Phys Med Biol. 2019;64:075019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen KT, Gong E, de Carvalho Macruz FB, et al. Ultra-low-dose 18F-florbetaben amyloid PET imaging using deep learning with multi-contrast MRI inputs. Radiology. 2019;290:649–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kang J, Gao Y, Shi F, Lalush DS, Lin W, Shen D. Prediction of standard-dose brain PET image by using MRI and low-dose brain [18F]FDG PET images. Med Phys. 2015;42:5301–5309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kaplan S, Zhu YM. Full-dose PET image estimation from low-dose PET image using deep learning: a pilot study. J Digit Imaging. 2019;32:773–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schaefferkoetter JD, Yan J, Soderlund TA, et al. Quantitative accuracy and lesion detectability of low-dose FDG-PET for lung cancer screening. J Nucl Med. 2017;58:399–405. [DOI] [PubMed] [Google Scholar]
- 19.Xiang L, Qiao Y, Nie D, An L, Wang Q, Shen D. Deep auto-context convolutional neural networks for standard-dose PET image estimation from low-dose PET/MRI. Neurocomputing. 2017;267:406–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang Y, Yu B, Wang L, et al. 3D conditional generative adversarial networks for high-quality PET image estimation at low dose. Neuroimage. 2018;174:550–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ouyang J, Chen KT, Gong E, Pauly J, Zaharchuk G. Ultra-low-dose PET reconstruction using generative adversarial network with feature matching and task-specific perceptual loss. Med Phys. 2019;46:3555–3564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Xu J, Gong E, Pauly J, Zaharchuk G. 200x low-dose PET reconstruction using deep learning. arXiv.org website. https://arxiv.org/abs/1712.04119. Published December 12, 2017. Accessed March 14, 2020.
- 23.Häggström I, Schmidtlein CR, Campanella G, Fuchs TJ. DeepPET: a deep encoder-decoder network for directly solving the PET image reconstruction inverse problem. Med Image Anal. 2019;54:253–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hong X, Zan Y, Weng F, Tao W, Peng Q, Huang Q. Enhancing the image quality via transferred deep residual learning of coarse PET sinograms. IEEE Trans Med Imaging. 2018;37:2322–2332. [DOI] [PubMed] [Google Scholar]
- 25.Liu CC, Qi J. Higher SNR PET image prediction using a deep learning model and MRI image. Phys Med Biol. 2019;64:115004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cui J, Gong K, Guo N, et al. PET image denoising using unsupervised deep learning. Eur J Nucl Med Mol Imaging. 2019;46:2780–2789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lu W, Onofrey JA, Lu Y, et al. An investigation of quantitative accuracy for deep learning based denoising in oncological PET. Phys Med Biol. 2019;64:165019. [DOI] [PubMed] [Google Scholar]
- 28.Schaefferkoetter J, Nai YH, Reilhac A, Townsend DW, Eriksson L, Conti M. Low dose positron emission tomography emulation from decimated high statistics: a clinical validation study. Med Phys. 2019;46:2638–2645. [DOI] [PubMed] [Google Scholar]
- 29.Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. International Conference on Medical Image Computing and Computer-Assisted Intervention. Munich, Germany; Medical Image Computing and Computer Assisted Intervention Society; 2015:234–241.
- 30.Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: learning dense volumetric segmentation from sparse annotation. International Conference on Medical Image Computing and Computer-Assisted Intervention. Athens, Greece; Medical Image Computing and Computer Assisted Intervention Society; 2016:424–432.
- 31.Sandler M, Howard A, Zhu M, Zhmoginov A, Chen L-C. Mobilenetv2: inverted residuals and linear bottlenecks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE; 2018:4510–4520. [Google Scholar]
- 32.Keras: the python deep learning library. Astrophysics Source Code Library website. https://ascl.net/1806.022. Accessed March 14, 2020.
- 33.Kingma DP, Ba J. Adam: a method for stochastic optimization. arXiv.org website. https://arxiv.org/abs/1412.6980. Published December 22, 2014. Revised January 30, 2017. Accessed March 14, 2020.
- 34.Tanner MA, Wong WH. The calculation of posterior distributions by data augmentation. J Am Stat Assoc. 1987;82:528–540. [Google Scholar]
- 35.Nioche C, Orlhac F, Boughdad S, et al. LIFEx: a freeware for radiomic feature calculation in multimodality imaging to accelerate advances in the characterization of tumor heterogeneity. Cancer Res. 2018;78:4786–4789. [DOI] [PubMed] [Google Scholar]
- 36.Schoonjans F, Zalata A, Depuydt C, Comhaire F. MedCalc: a new computer program for medical statistics. Comput Methods Programs Biomed. 1995;48:257–262. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.