Complex dynamics in susceptible-infected models for COVID-19 with multi-drug resistance

Highlights

• •Complex dynamics in a susceptible-infected (SI) model for COVID-19 with multi-drug resistance (MDR) and its fractional-order counterpart are investigated.
• •New fractional Routh-Hurwitz (FRH) conditions are introduced and proved for the fractional case (0,2].
• •Local stability of the new SIMDR model is investigated for all the multi-drug resistance steady sates using the FRH scheme.
• •Chaotic attractors are obtained in both the integer and fractional-order SIMDR models.
• •This study helps to understand complex behaviors and predict spread of severe infectious diseases such as COVID-19.

Abstract

Nowadays, exploring complex dynamic of epidemic models becomes a focal point for research after the outbreak of COVID-19 pandemic which has no vaccine or fully approved drug treatment up till now. Hence, complex dynamics in a susceptible-infected (SI) model for COVID-19 with multi-drug resistance (MDR) and its fractional-order counterpart are investigated. Existence of positive solution in fractional-order model is discussed. Local stability based on the fractional Routh-Hurwitz (FRH) conditions is considered. Also, new FRH conditions are introduced and proved for the fractional case (0,2]. All these FRH conditions are also applied to discuss local stability of the multi-drug resistance steady states. Chaotic attractors are also found in this model for both integer-order and fractional-order cases. Numerical tools such as Lyapunov exponents, Lyapunov spectrum and bifurcation diagrams are employed to confirm existence of these complex dynamics. This study helps to understand complex behaviors and predict spread of severe infectious diseases such as COVID-19.

1. Introduction

Some diseases that were thought to have disappeared have reappeared. The family of Coronaviridae is a strong example to this observation; The outbreak of the Middle East Respiratory Syndrome Corona virus (MERS-CoV) was recorded in Saudi Arabia in 2012 [1]. Recently, the whole world suffers from the outbreak of a newer version of coronavirus disease (COVID-19) which becomes more dangerous and is currently considered to be the most pathogenic virus or a world wide pandemic [2], [3], [4], [5]. The MERS-CoV is transmitted from bats-to-human through camels, while COVID-19 has reptilians as intermediate hosts. Unfortunately, COVID-19 has neither a vaccine nor a fully approved drug treatment up till now. Moreover, COVID-19 is an RNA virus which means that it has high mutation rates and has highly conserved sequences in nucleic acids that is maintained by natural selection. In addition, the coronaviruses have the order Nidovirales which are enveloped, non-segmented positive-sense RNA viruses. Therefore, it is difficult to find its suitable vaccine quickly and the memory effect (or hereditary properties) has a vital role in recognizing its behaviors. However, some drugs such as Remdesivir shows promise to some patients and is granted emergency use authorization from US FDA [6]. In March 2020, the anti-malaria drug known as Hydroxychloroquine shows positive signs to reduce some of the symptoms of COVID-19 for some patients especially with adding Azithromycin [7]. In [8], it was recommended that Remdesivir can be used as the preferred agent, and Hydroxychloroquine could be used for patients who have resistance against Remdesivir or when Remdesivir is not available. However in [9], some kind of biological resistance to Hydroxychloroquine was reported. Recently, it has been recommended that the use of Hydroxychloroquine should be under medical supervision since it has some side effects on the heart [10]. Hence, studies of antiviral resistance, antimicrobial resistance (AMR), multi-drug resistance (MDR) and waning vaccination [11] may be useful in this context.

On the other hand, mathematical models are very useful to understand and predict spread of epidemics. In mathematical epidemiology, the Susceptible-Infected (SI) models, Susceptible-Infected-Recovered (SIR) models and Susceptible-Exposed-Infected-Recovered (SEIR) models are used to study the transmission of virus from human-to-human and the humanitarian diffusion of epidemics [12]. Indeed, the AMR and MDR models belong to the class of SIR epidemic models. In addition, the memory effects are also important for AMR and MDR phenomena since they depend on the exposure time. Recently, new mathematical models for COVID-19 have been introduced and studied by scientists (see for example, Sarkar et al. [13], Kucharski et al. [14], Bozkurt et al. [15], Ben Fredj and Chrif [16], Jiwei et al. [17], Ndaïrou et al. [18], Okuonghae and Omame [19], Aslan et al. [20], Chimmula and Zhang [21], Ivorra et al. [22], Çakan [23], Soukhovolsky et al. [24], Huang et al. [25], Cooper et al. [26], Wang et al. [27], Salgotra et al. [28], Saif Ullah and Khan [29], Asamoah et al. [30], Basu and Campbell [31], Annas et al. [32], Croccolo and Roman [33], Kaxiras et al. [34], Lee et al. [35], Mandal et al. [36], Bekiros and Kouloumpou [37], Reis et al. [38], Mahajan et al. [39], Bagal et al. [40], Papo et al. [41], Džiugys et al. [42], Samui et al. [43], Khan et al. [44], and Ghanbari [45]).

Recently, fractional calculus (FC) has been shown to have continuous progress [46], [47], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58]. Fractional-order modeling provides more adequacies in describing the natural phenomenon. FC can also be used to model complex systems with long term memory, hereditary properties and non-local behaviors since it generalizes the existing classical differentiation to arbitrary real-valued order. Therefore, scientists have recently presented some fractional-order mathematical models for COVID-19 (see for example, Atangana [59], Khan and Atangana [60], Tuan et al. [61], Higazy [62], Alkahtani and Alzaid [63], Zhang [64], Yadav and Verma [65], Baleanu et al. [66], Mohammad and Trounev [67], and Zhang and Jain [68]).

In this work, complex dynamics in Susceptible-Infected (SI) model [69] and its fractional-order counterpart are studied. This Susceptible-Infected (SI) model explores the dynamics of three classes of infected populations by COVID-19 and a susceptible one. The three infected classes are divided into three types; The first type is sensitive to Remdesivir but resistant to Hydroxychloroquine. The second type responds to Hydroxychloroquine but resistant to Remdesivir. The last type is resistant to both of Remdesivir and Hydroxychloroquine. The fractional model is considered in the interval (0,2] which enables us to achieve higher adequacy of modeling the system and higher degrees of freedom. Also, new applicable fractional Routh-Hurwitz (FRH) conditions are introduced and proved for four-dimensional systems in the case (0,2]. Finally, this kind of work helps to understand and predict complex dynamics arising from serious epidemiological diseases such as COVID-19.

2. Fractional calculus

The Caputo fractional differential operator [70] is defined as

$$D_{t_0}^{q}u\left(t\right)=J^{z-q}{u}^{\left(z\right)}\left(t\right),$$ (1)

$$J^p\epsilon \left(t\right)=\left[\underset{t_0}{\overset{t}{\int }}{(t-\mu )}^{p-1}\epsilon \left(\mu \right)d\mu \right]/\Gamma \left(p\right),$$ (2)

where q > 0, p > 0, z is an integer such that $z-1<q<z.$ When $t_0=0,$ the Caputo fractional differential operator is denoted by D^q. It is clear that $D_{t_0}^q$ is a non-local operator with singular kernel. So it can be used to describe complex dynamics of models involving hereditary properties and long term memory.

According to the well-known Matignon's inequalities, the linearized fractional-order n-dimensional system is locally asymptotically stable (LAS) if

$$\left|\arg \left({\lambda }_i\right)\right|>q\pi /2,i=1,...,n,$$ (3)

where q ∈ (0, 2] and λ_i are the eigenvalues of related Jacobian [71]. The associated stability region is illustrated in Fig. 1 .

Fig. 1.

Stability region of linearized system when the fractional parameter q satisfies (a) 0 ≤ q < 1, (b) 1 ≤ q < 2..

Remark 1

It is clear from Fig. 1 that the unstability region for q ∈ [1, 2] contains the entire unstability region for q ∈ (0, 1). So if an equilibrium point lies in the unstable region for q ∈ (0, 1) then it also lies in the unstable region for q ∈ [1, 2]. Therefore, any imperative condition for ensuring the local stability of the case q ∈ (0, 1) is also an imperative condition for ensuring the local stability of the case q ∈ [1, 2].

3. Models’ description

3.1. The integer-order SIMDR model

In [69], Elettreby and Ahmed introduced the following integer-order model for a multi-drug resistance (MDR) which explores the dynamics of the susceptible and three classes of infected populations. The proposed Susceptible-Infected (SIMDR) model is described as

$$\begin{array}{c}{\displaystyle \frac{d{x}_1}{dt}=r{x}_1(1-x_1)-b_1{x}_1{x}_2-b_2{x}_1{x}_3-b_{12}{x}_1{x}_4,}\hfill \\ {\displaystyle \frac{d{x}_2}{dt}=b_1{x}_1{x}_2-{\mu }_1{x}_2-b_4{x}_2{x}_4,}\hfill \\ {\displaystyle \frac{d{x}_3}{dt}=b_2{x}_1{x}_3-{\mu }_2{x}_3-b_5{x}_3{x}_4,}\hfill \\ {\displaystyle \frac{d{x}_4}{dt}=b_{12}{x}_1{x}_4+b_4{x}_2{x}_4+b_5{x}_3{x}_4-{\mu }_{12}{x}_4,}\hfill \end{array}$$ (4)

where the state variables x ₁, x ₂, x ₃, x ₄ refer, respectively, to the susceptible population, infected population that responding only to Remdesivir, infected population that responding only to Hydroxychloroquine and infected population that shows resistance to both of these drugs. All parameters r, b ₁, b ₂, b ₁₂, b ₄, b ₅, μ ₁, μ ₂ and μ ₁₂ are positive real numbers and their meaning is completely explained in Table 1 .

Table 1.

Meaning of parameters in the SIMDR model.

Parameters	Meaning
μ1	Natural death rate of the infected population x2 (infected population responding only to Remdesivir)
μ2	Natural death rate of the infected population x3 (infected population responding only to Hydroxychloroquine)
μ12	Natural death rate of the infected population x4 (resisting population to both drugs)
b1	Encounter rate of x1 with x2 per unit time
b2	Encounter rate of x1 with x3 per unit time
b12	Encounter rate of x1 with x4 per unit time
b4	Encounter rate of x2 with x4 per unit time
b5	Encounter rate of x3 with x4 per unit time
r	Rate of growth of the population x1

3.2. The fractional-order SIMDR model

In fact, involving the Caputo type ($D_{t_0}^q$) into the SIMDR model given by Eq. (4), enables us to achieve more realistic description of natural phenomena. Moreover, the resulting long-term memory effect and hereditary properties of $D_{t_0}^q$, are better candidate to handle the rich dynamics of the proposed model and give more adequate description of its natural behaviors. Therefore, the fractional-order form of the SIMDR model given by Eq. (4) is described as

$$\begin{array}{c}{D}^q{x}_1=r{x}_1(1-x_1)-b_1{x}_1{x}_2-b_2{x}_1{x}_3-b_{12}{x}_1{x}_4,\hfill \\ D^q{x}_2=b_1{x}_1{x}_2-{\mu }_1{x}_2-b_4{x}_2{x}_4,\hfill \\ D^q{x}_3=b_2{x}_1{x}_3-{\mu }_2{x}_3-b_5{x}_3{x}_4,\hfill \\ D^q{x}_4=b_{12}{x}_1{x}_4+b_4{x}_2{x}_4+b_5{x}_3{x}_4-{\mu }_{12}{x}_4,\hfill \end{array}$$ (5)

where q ∈ (0, 2]. Obviously, the SIMDR model given by Eq. (5) has greater degrees of freedom since the fractional parameter has higher arbitrary real-valued orders.

Both of SIMDR models given by Eqs. (4) and (5) have the same steady states

$$\begin{array}{c}{S}_0=(0,0,0,0),S_1=(1,0,0,0),S_2=({\gamma }_1,{\beta }_1,0,0),\hfill \\ S_3=({\gamma }_2,0,{\beta }_2,0),\hfill \\ S_4=({\gamma }_3,0,0,{\beta }_3),S_5=({\chi }_1,{\chi }_2,0,{\chi }_3),S_6=({\tilde{\chi }}_1,0,{\tilde{\chi }}_2,{\tilde{\chi }}_3),\hfill \\ S_7=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4),\hfill \end{array}$$ (6)

where

$$\begin{array}{c}{\displaystyle {\gamma }_1=\frac{{\mu }_1}{b_1},{\gamma }_2=\frac{{\mu }_2}{b_2},{\gamma }_3=\frac{{\mu }_{12}}{b_{12}},{\beta }_1=\frac{r}{b_1}\left(1-\frac{{\mu }_1}{b_1}\right),}\hfill \\ {\displaystyle {\beta }_2=\frac{r}{b_2}(1-\frac{{\mu }_2}{b_2}),{\beta }_3=\frac{r}{b_{12}}(1-\frac{{\mu }_{12}}{b_{12}}),}\hfill \\ {\displaystyle {\chi }_1=1-\frac{b_1{\mu }_{12}-b_{12}{\mu }_1}{r{b}_4},{\tilde{\chi }}_1=1-\frac{b_2{\mu }_{12}-b_{12}{\mu }_2}{r{b}_5},}\hfill \\ {\displaystyle {\chi }_2=\frac{{\mu }_{12}-b_{12}{\chi }_1}{b_4},{\tilde{\chi }}_2=\frac{{\mu }_{12}-b_{12}{\tilde{\chi }}_1}{b_5},}\hfill \\ {\displaystyle {\chi }_3=\frac{b_1{\chi }_1-{\mu }_1}{b_4},{\tilde{\chi }}_3=\frac{b_2{\tilde{\chi }}_1-{\mu }_2}{b_5},{\alpha }_1=\frac{b_5{\mu }_1-b_4{\mu }_2}{b_1{b}_5-b_2{b}_4},}\hfill \\ {\displaystyle {\alpha }_2=\frac{b_2(b_{12}{\alpha }_1-{\mu }_{12})+b_5(r(1-{\alpha }_1)-b_{12}{\alpha }_4)}{b_1{b}_5-b_2{b}_4},}\hfill \\ {\displaystyle {\alpha }_3=-\frac{b_1(b_{12}{\alpha }_1-{\mu }_{12})+b_4(r(1-{\alpha }_1)-b_{12}{\alpha }_4)}{b_1{b}_5-b_2{b}_4},}\hfill \\ {\displaystyle {\alpha }_4=\frac{b_2{\mu }_1-b_1{\mu }_2}{b_1{b}_5-b_2{b}_4}.}\hfill \end{array}$$

To discuss the existence of positive solution of SIMDR model given by Eq. (5), we prove the following theorem.

Theorem 1

Assume that a closed set $\Psi =\{(x_1,x_2,x_3,x_4)\in R_{+}^4:\zeta \le |x_i|<\xi ,{\sum }_{i=1}^4{x}_i\le \frac{\nu }{\eta }\},$ where ζ > 0 is very close to zero, $\nu =2r\xi$ and $\eta =\min (r,{\mu }_1,{\mu }_2,{\mu }_{12}).$ Hence, any solution of the SIMDR system (5) that starts in Ψ remains positive for all t > 0.

Proof

Let P(t) be the sum of all the state variables in the population, then we obtain

$$D^{q}P\left(t\right)<\nu -\eta P\left(t\right).$$ (7)

Recalling the well-known Mittag–Leffler functions $E_q\left(t\right)={\sum }_{m=0}^{\infty }\frac{t^m}{\Gamma (1+mq)}\ge 0$, and applying the Laplace transform to the inequality (7), we get

$$P\left(t\right)<\left(P\left(0\right)-\frac{\nu }{\eta }\right)E_q(-\eta t^q)+\frac{\nu }{\eta }.$$ (8)

It is clear that $E_q(-\eta t^q)$ has a bounded positive value. Clearly, $P\left(t\right)\le \frac{\nu }{\eta }$ when $P\left(0\right)\le \frac{\nu }{\eta }$. Hence, Ψ is positive closed invariant set for the fractional-order SIMDR system (5). Furthermore, if one defines a solution X(t) of the model (5) given that $P\left(0\right)>\frac{\nu }{\eta }$, one gets

$$\underset{t\to \infty }{lim}\mathrm{X}\left(P\left(t\right)\right)=\frac{\nu }{\eta }$$ (9)

since ${\lim }_{t\to \infty }{E}_q(-\eta t^q)=0.$ Therefore, any solution starts in the closed set Ψ will remain in Ψ. □

4. Local stability

Consider the following general fractional-order nonlinear system

$$D^q\mathrm{Y}\left(t\right)=\Omega \left(\mathrm{Y}\left(t\right)\right),$$ (10)

where q ∈ (0, 2],Y ∈ Rⁿ and Ω is a nonlinear vector function. Let $\overline{\mathrm{Y}}$ be a steady state of Eq. (10) with the following characteristic polynomial:

$$\upsilon \left(\lambda \right)={\lambda }^n+{\kappa }_1{\lambda }^{n-1}+...+{\kappa }_{n-1}\lambda +{\kappa }_n=0,$$ (11)

Here, we will recall the FRH conditions when the degree of polynomial $\upsilon \left(\lambda \right)$ is three and four, respectively [72], [73], [74]. Firstly, let $\Delta \left(\upsilon \right)$ be the discriminant of $\upsilon \left(\lambda \right)$. Hence, the three-dimensional case of FRH criterion is summarized as follows

• (i) $\overline{\mathrm{Y}}$ is LAS for q ∈ (0, 2] if $\Delta \left(\upsilon \right)>0$ along with κ ₁ > 0,  κ ₃ > 0 and κ ₃ < κ ₁ κ ₂.
• (ii)For $q<\frac{2}{3}$, $\overline{\mathrm{Y}}$ is LAS if $\Delta \left(\upsilon \right)<0$ in addition to κ ₃ > 0, κ ₁ ≥ 0 and κ ₂ ≥ 0.
• (iii) $\overline{\mathrm{Y}}$ is LAS when q ∈ (0, 1) if $\Delta \left(\upsilon \right)<0$ and the following conditions κ ₁ > 0,  κ ₂ > 0 and ${\kappa }_3={\kappa }_1{\kappa }_2$ hold.
• (iv)If 1 ≤ q < 2, ${\kappa }_3={\kappa }_1{\kappa }_2$ and $\Delta \left(\upsilon \right)<0$ then the Matignon's conditions (3) do not hold.
• (v)If 0 < q ≤ 2 then κ ₃ > 0 is an imperative condition for $\overline{\mathrm{Y}}$ to be LAS.

Also, according to Proposition 1 of [73] and conditions (3), the following four-dimensional FRH conditions are straightforwardly obtained

(1) Let Λ₁,  Λ₂,  Λ₃,  Λ₄ be Routh–Hurwitz determinants

$${\Lambda }_1={\kappa }_1,{\Lambda }_2=\left|\begin{array}{cc}{\kappa }_1& 1\\ {\kappa }_3& {\kappa }_2\end{array}\right|,{\Lambda }_3=\left|\begin{array}{ccc}{\kappa }_1& 1& 0\\ {\kappa }_3& {\kappa }_2& {\kappa }_1\\ 0& {\kappa }_4& {\kappa }_3\end{array}\right|,$$ (12)

then $\overline{\mathrm{Y}}$ is LAS for 0 < q ≤ 2 if ${\Lambda }_1>0,{\Lambda }_2>0,{\Lambda }_3=0,{\kappa }_4>0.$

If q > 2/3,$\Delta \left(\upsilon \right)>0,{\kappa }_1>0,{\kappa }_2<0$ then $\overline{\mathrm{Y}}$ does not satisfy Matignon's conditions (3).

If 0 < q < 1/3, $\Delta \left(\upsilon \right)<0,{\kappa }_i>0,i=1,2,3,4$ then $\overline{\mathrm{Y}}$ is LAS. However, if $0<q\le 2,\Delta \left(\upsilon \right)<0,$ κ ₁ < 0,  κ ₃ < 0,  κ ₂ > 0,   κ ₄ > 0 then $\overline{\mathrm{Y}}$ does not satisfy Matignon's conditions (3).

If $q\in (0,1),\Delta \left(\upsilon \right)<0,{\kappa }_i>0,i=1,2,3,4$ and $\frac{{\kappa }_3}{{\kappa }_1{\kappa }_2}+\frac{{\kappa }_1{\kappa }_4}{{\kappa }_2{\kappa }_3}=1$ then $\overline{\mathrm{Y}}$ is LAS.

(5) If 0 < q ≤ 1 then κ ₄ > 0 is an imperative condition for $\overline{\mathrm{Y}}$ to be LAS.

The following lemma can also be added to extend the above-mentioned FRH conditions.

Lemma 1

Consider the characteristic polynomial (11) with $n=4$ ;

• (a)If $1\le q\le 2,\Delta \left(\upsilon \right)<0$ and $\frac{{\kappa }_3}{{\kappa }_1{\kappa }_2}+\frac{{\kappa }_1{\kappa }_4}{{\kappa }_2{\kappa }_3}=1,$ then the Matignon's inequalities (3) are not satisfied;
• (b)If 1 < q ≤ 2 then κ ₄ > 0 is an imperative condition for $\overline{\mathrm{Y}}$ to be LAS.

Proof

To prove part (a), we recall that $\Delta \left(\upsilon \right)<0$ implies the existence of two real roots and a pair of complex conjugate eigenvalues ${\lambda }_{\pm }=\rho \pm iw,w>0.$ However, the condition $\frac{{\kappa }_3}{{\kappa }_1{\kappa }_2}+\frac{{\kappa }_1{\kappa }_4}{{\kappa }_2{\kappa }_3}=1$ implies that $\rho =0.$ So according to the Matignon's conditions (3), the eigenvalues are located in the unstable region for 1 ≤ q ≤ 2 (See Fig. 1b). The part (a) is now proved.

To prove (b), we recall that κ ₄ > 0 is an imperative condition for $\overline{\mathrm{Y}}$ to be LAS when 0 < q ≤ 1. So according to Remark 1, κ ₄ > 0 is also an imperative condition for $\overline{\mathrm{Y}}$ to be LAS when 1 < q ≤ 2. □

4.1. Applications to the SIMDR models

In the following, we will apply the above-mentioned stability results to the SIMDR models given by Eqs. (4) and (5). Although the system has eight equilibrium points, we only focus on the equilibrium states in which the component x ₄ is not vanished. Obviously, if the last component of the steady state is vanished then it does not have a multi-drug resistance which contradicts the biological meaning of this model.

Theorem 2

When 0 < q ≤ 2, the steady state $S_4=({\gamma }_3,0,0,{\beta }_3)$ of the fractional SIMDR system (5) is LAS if

$$r>\max \left(\frac{b_{12}}{b_4(1-{\gamma }_3)}\left[b_1{\gamma }_3-{\mu }_1\right],\frac{b_{12}}{b_5(1-{\gamma }_3)}\left[b_2{\gamma }_3-{\mu }_2\right]\right).$$ (13)

Proof

The steady state $S_4=({\gamma }_3,0,0,{\beta }_3)$ has the characteristic polynomial

$$\begin{array}{c}\upsilon \left(\lambda \right)=(\lambda -b_1{\gamma }_3+{\mu }_1+b_4{\beta }_3)({\lambda }^3+{\kappa }_1{\lambda }^2+{\kappa }_2\lambda +{\kappa }_3)=0,\hfill \\ {\kappa }_1=b_5{\beta }_3+{\mu }_2+{\gamma }_3(r-b_2),\hfill \\ {\kappa }_2={\gamma }_3(r{b}_5{\beta }_3-r{b}_2{\gamma }_3+r{\mu }_2+b_{12}^2{\beta }_3),\hfill \\ {\kappa }_3=b_{12}^2{\beta }_3{\gamma }_3({\mu }_2-b_2{\gamma }_3+b_5{\beta }_3),\hfill \end{array}$$

which has the four roots; ${\lambda }_1=b_1{\gamma }_3-{\mu }_1-b_4{\beta }_3,{\lambda }_2=b_2{\gamma }_3-{\mu }_2-b_5{\beta }_3,{\lambda }_{3,4}=\frac{-r{\gamma }_3}{2}\pm \frac{\sqrt{{\left(r{\gamma }_3\right)}^2-4b_{12}{\mu }_{12}{\beta }_3}}{2}.$ It is clear that λ _{3, 4} satisfy the conditions (3). Moreover, the following condition ensure the existence of $S_4=({\gamma }_3,0,0,{\beta }_3)$:

$$0\le {\gamma }_3<1$$ (14)

If conditions (13) hold then λ _{1, 2} also satisfy the Matignon's conditions (3) which also imply that $S_4=({\gamma }_3,0,0,{\beta }_3)$ is LAS for q ∈ (0, 2]. □

Obviously, the steady state $S_5=({\chi }_1,{\chi }_2,0,{\chi }_3)$ exists only if

$$r(1-{\gamma }_3)<\frac{b_1{\mu }_{12}-b_{12}{\mu }_1}{b_4}<r\left(1-\frac{{\mu }_1}{b_1}\right).$$ (15)

Also, $S_5=({\chi }_1,{\chi }_2,0,{\chi }_3)$ has the following eigenvalue equation

$$(\lambda +{\mu }_2-b_2{\chi }_1+b_5{\chi }_3)\vartheta \left(\lambda \right)=0,$$ (16)

where

$$\vartheta \left(\lambda \right)=({\lambda }^3+{\kappa }_1{\lambda }^2+{\kappa }_2\lambda +{\kappa }_3),$$

$$\begin{array}{ccc}\hfill {\kappa }_1& =& r{\chi }_1>0,{\kappa }_2={\chi }_1(b_{12}^2{\chi }_3+b_1^2{\chi }_2)+b_4^2{\chi }_2{\chi }_3>0,\hfill \\ \hfill {\kappa }_3& =& r{b}_4^2{\chi }_1{\chi }_2{\chi }_3>0.\hfill \end{array}$$

Obviously, Eq. (16) has negative eigenvalue if

$$-{\mu }_2+b_2{\chi }_1-b_5{\chi }_3<0.$$ (17)

Applying the conditions (3) and the three-dimensional FRH conditions to ϑ(λ), the following lemma is straightforwardly obtained.

Lemma 2

If conditions (15) and (17) hold, the steady state $S_5=({\chi }_1,{\chi }_2,0,{\chi }_3)$ of the fractional SIMDR system (5) is LAS when

• (i) q ∈ (0, 2] and $\Delta \left(\upsilon \right)>0;$
• (ii) q < 2/3 and $\Delta \left(\upsilon \right)<0;$
• (iii) q ∈ (0, 1), $\Delta \left(\upsilon \right)<0$ and $r=\frac{b_1{\mu }_{12}-b_{12}{\mu }_1}{b_4}.$

However, if q ∈ [1, 2), $\Delta \left(\upsilon \right)<0$ and $r=\frac{b_1{\mu }_{12}-b_{12}{\mu }_1}{b_4}$ then $S_5=({\chi }_1,{\chi }_2,0,{\chi }_3)$ is not LAS.

It is also clear that, the multi-drug resistance steady state $S_6=({\tilde{\chi }}_1,0,{\tilde{\chi }}_2,{\tilde{\chi }}_3)$ exists only if

$$r(1-{\gamma }_3)<\frac{b_2{\mu }_{12}-b_{12}{\mu }_2}{b_5}<r\left(1-\frac{{\mu }_2}{b_2}\right).$$ (18)

Also, $S_6=({\tilde{\chi }}_1,0,{\tilde{\chi }}_2,{\tilde{\chi }}_3)$ has the characteristic equation

$$(b_1{\tilde{\chi }}_1-{\mu }_1-b_4{\tilde{\chi }}_3-\lambda )\vartheta \left(\lambda \right)=0,$$ (19)

where

$$\vartheta \left(\lambda \right)=({\lambda }^3+{\kappa }_1{\lambda }^2+{\kappa }_2\lambda +{\kappa }_3),$$

$$\begin{array}{ccc}\hfill {\kappa }_1& =& r-\frac{b_2{\mu }_{12}-b_{12}{\mu }_2}{b_5},\hfill \\ \hfill {\kappa }_2& =& -\frac{r^2}{b_5}[({\mu }_2-b_2)(b_{12}^2+{\mu }_{12}{b}_5-b_5{b}_{12})+b_2^2(b_{12}-{\mu }_{12})]-\frac{r}{b_5^3}[-2b_2{b}_5{b}_{12}(b_2^2{\mu }_{12}+b_{12}^2{\mu }_2)\hfill \\ & & +(b_2+b_5)(b_2^2{\mu }_{12}^2{b}_5+2b_2{b}_5{b}_{12}^2{\mu }_2)+(b_{12}-b_5)({\mu }_2^2{b}_5{b}_{12}^2+2b_2^2{b}_{12}{b}_5{\mu }_{12})-b_2{b}_5{b}_{12}{\mu }_{12}{\mu }_2(b_2+b_{12})]\hfill \\ & & -\frac{1}{b_5^3}[(b_2-b_{12})(b_{12}{b}_2^3{\mu }_{12}^2-2b_2^2{\mu }_{12}{b}_{12}^2{\mu }_2)+b_{12}^3{b}_2{\mu }_2^2(b_2+b_5-b_{12})+b_5{\mu }_{12}{b}_2^2{b}_{12}(-2b_{12}{\mu }_2+b_2{\mu }_{12})],\hfill \\ \hfill {\kappa }_3& =& r^3({\mu }_2-b_2)(b_{12}-{\mu }_{12})+\frac{r^2}{b_5}({\mu }_{12}{b}_2-{\mu }_2{b}_{12})({\mu }_{12}{\mu }_2+3b_2{b}_{12}-2({\mu }_{12}{b}_2+{\mu }_2{b}_{12}))\hfill \\ & & \frac{-3b_2{b}_{12}(b_{12}^2{\mu }_2^2+b_2^2{\mu }_{12}^2)-b_2{b}_{12}{\mu }_{12}{\mu }_2({\mu }_{12}{b}_2+{\mu }_2{b}_{12})+6b_2^2{b}_{12}^2{\mu }_{12}{\mu }_2+b_{12}^3{\mu }_2^3+b_2^3{\mu }_{12}^3}{b_5^2}r\hfill \\ & & +\frac{3b_2^2{b}_{12}^2{\mu }_{12}{\mu }_2({\mu }_2{b}_{12}-{\mu }_{12}{b}_2)+b_2{b}_{12}(b_2^3{\mu }_{12}^3-b_{12}^3{\mu }_2^3)}{b_5^3}.\hfill \end{array}$$

Eq. (19) has a negative eigenvalue if $b_1{\tilde{\chi }}_1-{\mu }_1-b_4{\tilde{\chi }}_3<0$. Similarly, conditions for local stability of $S_6=({\tilde{\chi }}_1,0,{\tilde{\chi }}_2,{\tilde{\chi }}_3)$ can be obtained by the three-dimensional FRH conditions as shown above.

Indeed, the multi-drug resistance steady state $S_7=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)$ exists only if ${\alpha }_i>0,i=1,2,3,4.$ Also, the Jacobian computed at $S_7=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)$ yields the eigenvalue equation

$$\upsilon \left(\lambda \right)={\lambda }^4+{\kappa }_1{\lambda }^3+{\kappa }_2{\lambda }^2+{\kappa }_3\lambda +{\kappa }_4=0,$$ (20)

where

$$\begin{array}{c}{\kappa }_1=r{\alpha }_1>0,\hfill \\ {\kappa }_2=(b_4^2{\alpha }_2+b_5^2{\alpha }_3)+{\alpha }_1(b_1^2{\alpha }_2+b_2^2{\alpha }_3+b_{12}^2{\alpha }_4)>0,\hfill \\ {\kappa }_3=r{\alpha }_1{\alpha }_4(b_4^2{\alpha }_2+b_5^2{\alpha }_3)>0,\hfill \\ {\kappa }_4={\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4(b_2^2{b}_4^2+b_1^2{b}_5^2-b_1{b}_2{b}_4{b}_5)>0.\hfill \end{array}$$

So based on the four-dimensional FRH conditions and Lemma 1, the following lemma is straightforwardly proved.

Lemma 3

If ${\alpha }_i>0,i=1,2,3,4,$ then $S_7=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)$ exists and the following statements hold

• (i)If the Routh-Hurwitz determinants satisfy the FRH condition (1) then $S_7=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)$ is LAS for 0 < q ≤ 2.
• (ii)When $\Delta \left(\upsilon \right)<0,$ the steady state $S_7=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)$ is LAS for 0 < q < 1/3.
• (iii)When $\Delta \left(\upsilon \right)<0,$ $\frac{{\kappa }_3}{{\kappa }_1{\kappa }_2}+\frac{{\kappa }_1{\kappa }_4}{{\kappa }_2{\kappa }_3}=1;$ the steady state $S_7=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)$ is LAS for 0 < q < 1; however it is not LAS for 1 ≤ q ≤ 2.

Remark 2

The healthy steady state $S_1=(1,0,0,0)$ has the eigenvalues ${\lambda }_1=-r,{\lambda }_2=b_1-{\mu }_1,{\lambda }_3=b_2-{\mu }_2$ and ${\lambda }_4=b_{12}-{\mu }_{12}$ then it is LAS for all 0 < q ≤ 2 when μ ₁ > b ₁,μ ₂ > b ₂ and μ ₁₂ > b ₁₂.

4.2. Simulation results

The set $r={\mu }_{12}=b_1=b_5=0.1,b_{12}=0.09,b_2={\mu }_1=0.11,b_4=0.08,{\mu }_2=0.12$ satisfies the stability conditions in Remark 2. Simulation results using this data set show that the integer-order SIMDR system (4) converges to the healthy state faster than the corresponding fractional-order counterpart does. Fig. 2 depicts this observation.

Fig. 2.

Plots of susceptible and infective populations of the SIMDR models given by Eqs. (4), (5) with $r={\mu }_{12}=b_1=b_5=0.1,$$b_{12}=0.09,b_2={\mu }_1=0.11,b_4=0.08,{\mu }_2=0.12$ and using different values of q..

The set $r=b_{12}=0.1,$ $b_1=b_2=0.001,$ $b_4=0.8,$ $b_5=0.7,$ ${\mu }_1=0.11,$ ${\mu }_2=0.12,$ ${\mu }_{12}=0.01$ satisfies the stability conditions of $S_4=({\gamma }_3,0,0,{\beta }_3)=(0.1,0,0,0.9)$. Simulation results using this data set show that the fractional-order SIMDR system (5) converges to the multi-drug resistance (MDR) steady state faster than the corresponding integer-order counterpart does. Fig. 3 depicts these results.

Fig. 3.

Plots of susceptible and infective populations of the SIMDR models given by Eqns. (4), (5) with $r=b_{12}=0.1,$$b_1=b_2=0.001,$$b_4=0.8,$$b_5=0.7,$${\mu }_1=0.11,$${\mu }_2=0.12,$${\mu }_{12}=0.01$ and using different values of q..

The set $r=0.1847640761,b_1=0.3,$ $b_2=0.11,b_{12}=0.19,$ $b_4=0.08,$ $b_5=0.1,$ ${\mu }_1=0.11,$ ${\mu }_2=0.12,$ ${\mu }_{12}=0.1$ satisfies the stability conditions of $S_5=({\chi }_1,{\chi }_2,0,{\chi }_3)=(0.384,0.3372,0,0.0663)$ given in Lemma 2. Simulation results using this data set show that the fractional-order SIMDR system (5) converges to all the MDR steady state components faster than the corresponding integer-order counterpart does (except $x_3=0$). Fig. 4 illustrates these results.

Fig. 4.

Plots of susceptible and infective populations of the SIMDR models given by Eqns. (4), (5) with $r=.1847640761,b_1=0.3,$$b_2=0.11,b_{12}=0.19,$$b_4=0.08,$$b_5=0.1,$${\mu }_1=0.11,$${\mu }_2=0.12,$${\mu }_{12}=0.1$ and using different values of q..

According to these conditions, the obtained results show that the response of individuals to Hydroxychloroquine is vanishing after a course of time. Also, these results show that the fractional-order SIMDR model exhibits more resistance to both drugs comparing to its integer-order form. The results in the fractional case are more accurate since the memory effect erases the oscillations. Hence, in this case the fractional-order model is better candidate to describe the multi-drug resistance phenomena.

The set $r=0.9,b_1=0.2,$ $b_2=0.13,b_{12}=0.1,$ $b_4=0.01,$ $b_5=0.07,$ ${\mu }_1=0.22,$ ${\mu }_2={\mu }_{12}=0.1$ satisfies the stability conditions of $S_6=({\tilde{\chi }}_1,0,{\tilde{\chi }}_2,{\tilde{\chi }}_3)=(0.9524,0,0.06803,0.3401)$. Simulation results using this data set show that the fractional-order SIMDR system (5) tends to all components of the multi-drug resistance steady state faster than the corresponding integer-order counterpart does (except $x_2=0$). Fig. 5 summarizes these results. Moreover, the obtained results show that the response of individuals to Remdesivir is vanishing after some time. Also, these results show that the fractional-order SIMDR model exhibits more resistance to both drugs than its integer-order form. Therefore, this case also shows that the fractional-order model given by Eq. (5) is better candidate to describe the multi-drug resistance phenomena.

Fig. 5.

Plots of susceptible and infective populations of the SIMDR models given by Eqns. (4), (5) with $r=0.9,b_1=0.2,$$b_2=0.13,b_{12}=0.1,$$b_4=0.01,$$b_5=0.07,$${\mu }_1=0.22,$${\mu }_2={\mu }_{12}=0.1$ and using different values of q..

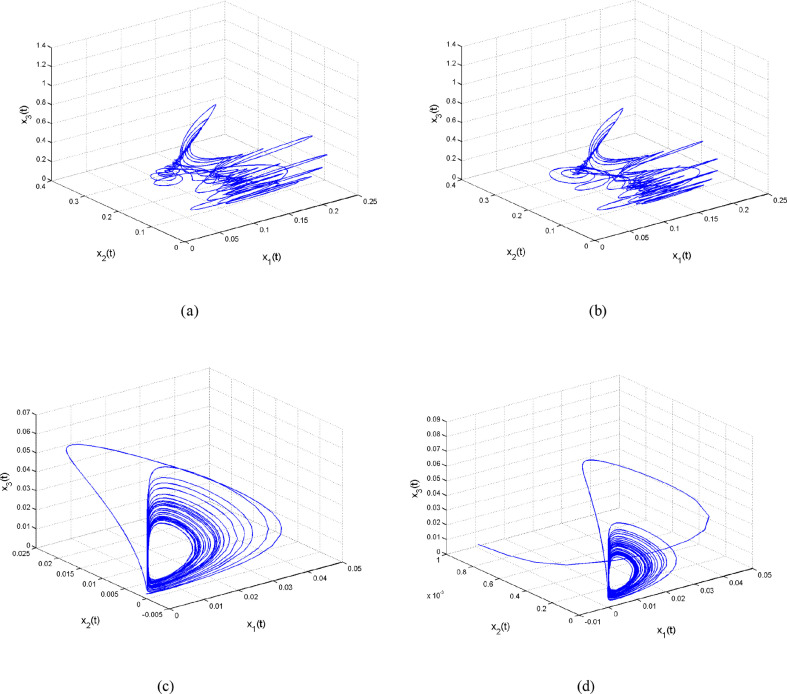
5. Chaos in the integer-order SIMDR model

Chaotic attractors are found in the SIMDR model given by Eq. (4). Calculations of Lyapunov exponents (LEs) corresponding to some chaotic behaviors are given in Table 2 . The calculations are based on Wolf's algorithm [75] and the corresponding chaotic attractors are depicted in Fig. 6 .

Table 2.

Calculations of LEs (Λ_{i, s}) of the SIMDR model given by Eq. (4).

Parameter Set	Λ1	Λ2	Λ3	Λ4
$r=3.3,b_1=11.5,b_2=2,b_{12}=75,{\mu }_1=1,b_4=1,{\mu }_2=0.1,b_5=10.3,{\mu }_{12}=11.5$	0.011391	0.005804	−0.090994	−0.156050
$r=6,b_1=300,b_2=300,b_{12}=0.1,{\mu }_1=2,b_4=1,{\mu }_2=1,b_5=2,{\mu }_{12}=0.5$	0.014493	−0.003904	−0.111544	−0.130222
$r=6,b_1=2,b_2=400,b_{12}=0.01,{\mu }_1=2,b_4=1,{\mu }_2=1,b_5=0.2,{\mu }_{12}=0.02$	0.061863	0.000212	−0.498306	−0.903541
$r=8,b_1=2,b_2=400,b_{12}=0.01,{\mu }_1=2,b_4=1,{\mu }_2=1,b_5=0.2,{\mu }_{12}=0.02$	0.087525	−0.124483	−0.061632	−1.872964

Fig. 6.

Chaotic attractors of SIMDR model given by Eq. (4) exist when (a) $r=3.3,b_1=11.5,b_2=2,b_{12}=75,{\mu }_1=1,$$b_4=1,{\mu }_2=0.1,b_5=10.3,{\mu }_{12}=11.5$; (b) $r=6,b_1=300,b_2=300,b_{12}=0.1,$${\mu }_1=2,b_4=1,{\mu }_2=1,b_5=2,{\mu }_{12}=0.5$; (c) $r=6,b_1=2,b_2=400,b_{12}=0.01,{\mu }_1=2,b_4=1,{\mu }_2=1,b_5=0.2,{\mu }_{12}=0.02$; (d) $r=8,b_1=2,b_2=400,b_{12}=0.01,{\mu }_1=2,b_4=1,{\mu }_2=1,b_5=0.2,{\mu }_{12}=0.02$.

Computations of the corresponding bifurcation diagrams are performed by varying the dynamical parameter r and using the parameter sets given in Table 2. The results are illustrated in Fig. 7 .

Fig. 7.

Bifurcations diagrams of SIMDR model given by Eq. (4) by varying the dynamical parameter r and using (a) $b_1=11.5,b_2=2,b_{12}=75,{\mu }_1=1,$$b_4=1,{\mu }_2=0.1,b_5=10.3,{\mu }_{12}=11.5$; (b) $b_1=300,b_2=300,b_{12}=0.1,$${\mu }_1=2,$$b_4=1,{\mu }_2=1,b_5=2,{\mu }_{12}=0.5$; (c) $b_1=2,b_2=400,b_{12}=0.01,{\mu }_1=2,b_4=1,{\mu }_2=1,b_5=0.2,{\mu }_{12}=0.02$; (d) $b_1=2,$$b_2=400,b_{12}=0.01,{\mu }_1=2,b_4=1,{\mu }_2=1,b_5=0.2,{\mu }_{12}=0.02$.

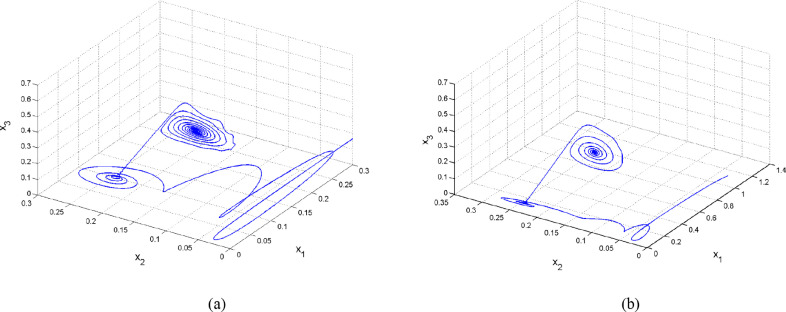
6. Chaos in the fractional SIMDR model

Chaotic attractors are found in the SIMDR model given by Eq. (5) when $r=3,b_1=11.5,b_2=2,b_{12}=75,{\mu }_1=1,b_4=1,{\mu }_2=0.1,b_5=10.3,{\mu }_{12}=11.5$ and fractional parameter $q=0.99$ and $q=0.97.$ These attractors are depicted in Fig. 8 . In addition, computations of Lyapunov spectrum as r and q are varied, are illustrated in Fig. 9 . These computations of Lyapunov spectrum verify the existence of wide range of unpredictable dynamical behaviors in the fractional-order model. Therefore, by studying this kind of complex dynamics, scientists can understand the mechanism of spreading diseases or infections.

Fig. 8.

Chaotic attractors of SIMDR model given by Eq. (5) exist when $r=3,b_1=11.5,b_2=2,b_{12}=75,{\mu }_1=1,$$b_4=1,{\mu }_2=0.1,b_5=10.3,{\mu }_{12}=11.5$ and (a) $q=0.99,$ (b) $q=0.97.$.

Fig. 9.

Lyapunov spectrum of SIMDR model given by Eq. (5) with $b_1=11.5,b_2=2,b_{12}=75,{\mu }_1=1,$$b_4=1,{\mu }_2=0.1,b_5=10.3,{\mu }_{12}=11.5$, (a) $q=0.99$ and varying r, (b) $r=3$ and varying q..

7. Conclusion

A Susceptible-Infected (SI) model describes the dynamics of three classes of infected populations by COVID-19 and a susceptible one has been suggested. The model has been called SIMDR. The infected populations of this model are assumed to have resistance against two drugs; Remdesivir and Hydroxychloroquine such that; The infected first class responds to Remdesivir but is resistant to Hydroxychloroquine. The second infected class responds to Hydroxychloroquine but is resistant to Remdesivir. The third infected class is resistant to both of Remdesivir and Hydroxychloroquine.

Dynamical behaviors in the SIMDR model for COVID-19 and its fractional-order counterpart have been explored. Existence of positive solution in the fractional-order model has been proved. Conditions of local stability based on the FRH criterion have been obtained. In addition, new FRH conditions have been proved for the case (0,2] and have also been applied to the fractional SIMDR model. Chaotic attractors have also been found in this model for both integer-order and fractional-order cases. These results help us to understand and control the spread of serious infectious diseases with multi-drug resistance when the dynamics becomes more complicated.

It has also been shown that the fractional-order SIMDR model is more adequate and realistic in describing natural phenomena than its integer-order counterpart since the former involves fractional differential operator with singular kernel which results in existence of long-term memory effect, hereditary properties. Therefore, it is better choice to handle complex dynamics. Moreover, comparisons between the integer-order and fractional-order SIMDR models show that the fractional model is better candidate to describe the multi-drug resistance phenomena since it exhibits greater resistance of both Remdesivir and Hydroxychloroquine than its integer-order form. These advantages are because of the fractional-order SIMDR has higher degrees of freedom that affect the spread of the disease. Furthermore, the values derived from the fractional model are closer to most of components of the multi-drug resistance steady states due to the existence of memory effect, which erase the oscillations in the fractional model after some time. Thus, it has been shown that the fractional-order SIMDR is more accurate and realistic to describe and explain the data of COVID-19 in some models with multi-drug resistance phenomena. In addition, the simulation results show also that if COVID-19 persists then the fractional-order SIMDR is better in modeling the cases with multi-drug resistance phenomena since it has been shown that the integer-order SIMDR model converges to the healthy state faster than the corresponding fractional-order counterpart does.

Declaration of Competing Interest

No competing of interest.