Abstract
Efficient delivery of multiple resources for emergency recovery during disasters is a matter of life and death. Nevertheless, most studies in this field only handle situations involving single resource. This paper formulates the Multi-Resource Scheduling and Routing Problem (MRSRP) for emergency relief and develops a solution framework to effectively deliver expendable and non-expendable resources in Emergency Recovery Operations. Six methods, namely, Greedy, Augmented Greedy, k-Node Crossover, Scheduling. Monte Carlo, and Clustering, are developed and benchmarked against the exact method (for small instances) and the genetic algorithm (for large instances). Results reveal that all six heuristics are valid and generate near or actual optimal solutions for small instances. With respect to large instances, the developed methods can generate near-optimal solutions within an acceptable computational time frame. The Monte Carlo algorithm, however, emerges as the most effective method. Findings of comprehensive comparative analysis suggest that the proposed MRSRP model and the Monte Carlo method can serve as a useful tool for decision-makers to better deploy resources during emergency recovery operations.
Keywords: Expendable resources, Non-expendable resources, Emergency recovery operations, Multi-resource scheduling, Heuristics algorithms, Clustering algorithm, Coronavirus outbreak case
1. Introduction
In emergency situations, such as major earthquakes or widespread outbreaks of infectious disease, quickly supplying diverse and critically needed rescue resources from various relief centres to many demand points can be a matter of life and death. A typical example is delivering urgent medical treatments\supplies from emergency recovery operation (ERO) control centres to various hospitals in a short period of time to treat a large number of injured patients when a destructive natural disaster strikes. For instance, in the ERO following the attack of Hurricane Katrina on New Orleans, USA, in 2005, delays in the treatment of victims occurred as a result of a shortage of nurses even though the medical supplies were distributed on time to those who needed them [1]. In another example, on Saturday, February 7, 2009, also known as Black Saturday, over 400 bushfires swept through parts of rural Victoria, Australia. The day is remembered for the deadliest and most devastating bushfires in the nation's history, with 173 deaths and 414 injuries. However, the Victorian emergency response teams' efforts were hampered by the fact that medical services were unavailable in local areas and some first aid services were uncoordinated in their initial response. It was reported that resources such as medical teams and medical supplies were poorly coordinated, especially in providing relief to smaller, remote communities and people who stayed on their properties [2]. Such delay and poor coordination could be avoided or minimised if scheduling of both expendable and non-expendable resources could be taken into consideration in the same optimisation process. However, scheduling problems for multiple resources during emergency situations have become more complicated than in the case of single resource scheduling [1,3,4]. The ERO will be more complex considering the fact that relief centre (RC) is usually subject to severe resource limitations and acute time pressures in deciding what resources are to be sent to which hospitals to rescue/save lives.
Since time is critical in emergency situations and short response time can help save more lives, appropriate schedule and routing plans for emergency vehicles in delivering multiple resources from RCs to hospitals are of utmost importance. Reducing human casualties and fatalities is critically dependent on the rapid deployment of resources for EROs at demand points. Failure to assign adequate resources in a timely manner has been the root cause of many disastrous situations [3,[5], [6], [7]]. This is a challenging task given the scarceness of resources and the uncertain scale of the disasters [8,9]. Hospitals in a city are usually dispersed in geographical location and diverse in their ability to handle a surge capacity. An unexpected flood of patients can overwhelm hospitals and exceed their surge capacities, thereby affecting their preparedness for responding to emergencies and disasters [10,11].
ERO often mandates many types of resources to serve the demand points. Both expendable resources, such as food, clothing, shelter, and medical items, and non-expendable resources, such as nurses, surgeons, and medical equipment, are required in a devastation scenario in order to reduce the number of casualties. Among the resources that can be delivered from RCs, some are expendable, such as medical supplies, which can be simply unloaded at the destination so that the delivery vehicle can continue with its journey to other stops. The unloading of these resources will not impact much on the total completion time of the trip. However, some resources are non-expendable, for instance specialist surgeons and special medical equipment, which can be needed at multiple locations. As such, the delivery vehicle will have to wait until the relief operation at one stop is finished before it can deliver the resources to another stop to provide relief. The wait can significantly impact on the total journey time of the vehicle hence its opportunities to operate another run. This being the case, optimisation of routes and schedules of vehicles supplying multiple resources to different locations, referred to as the Multi-Resource Routing and Scheduling Problem (MRRSP) for emergency relief, is paramount for disaster management to be effective. To the best of the authors’ knowledge, no previous studies have contextualised the ERO problem to address key operational challenges, such as timely distribution, by developing mechanisms to facilitate the coordination among resources. Both expendable and non-expendable items need to be examined with a consideration of collaboration between resources using various heuristics and clustering algorithms.
This paper, hence, aims to develop algorithms as a solution framework so that the emergency authorities can implement reasonably good to excellent solutions that generate, allocate and schedule resources for the EROs at an entire set of demand points in a disaster relief scenario within acceptable computational time. Hence, in this study, the MRSRP is modelled for disaster management centres to route and schedule emergency vehicles, in order to deliver expendable and non-expendable resources to hospitals. It will take into account the linear programming optimisation model, aiming to determine the routing of the demand points (e.g., hospitals) visited by chosen vehicle(s) to deliver requisite resources. At the same time, it will minimise completion times of recovery operations at individual demand points weighted by the severity level of EROs in each demand point.
Since MRSRP is related to the multiple Travelling Salesman Problem (mTSP) [12,13], involving both the routing and scheduling problems has proved to be NP-hard [14,15]. An efficient way to find a near-optimal schedule for multiple resources in emergency response facilitates the eventual attainment of effective resource management and ensures the welfare of disaster victims [16]. Six heuristics algorithms, namely, Greedy, Augmented Greedy, k-Node Crossover, Scheduling, Monte Carlo, and Clustering have been developed to obtain near-optimal solutions for the MRSRP. The heuristics are first validated, using small cases with only a few RCs, demand points and vehicles, against the exact solutions. Upon validation, ten large cases with a maximum of 15 RCs, 500 demand points and 50 vehicles, are implemented to evaluate the performance of the heuristics by comparing the solutions against those of the well-known genetic algorithm - a meta-heuristic approach.
The remainder of this paper is structured as follows: Section 2 reviews the relevant literature on vehicle routing and scheduling in EROs and identifies the research gap that this study attempts to address. Section 3 details the statement and formulation of the MRSRP. Section 4 shows the pseudo codes of the six heuristics used in this study. Section 5 empirically validates the six heuristics against the exact solutions for small instances. It then compares the performance of the six heuristics against that of the genetic algorithm for large instances and identifies the best heuristic. Section 6 concludes the study with a discussion on its limitations and what future research directions could pursue.
2. Related works
This study falls in the field of logistics and transportation operations spanning across the categories of routing or scheduling optimisation and emergency relief. There has been a substantial amount of work on vehicle routing and scheduling for emergency relief or related problems using mathematical programming. Some of the latest works include Pillac et al. [17]; Shahparvari et al. [18]; Bruni et al. [19]; Zhang et al. [20] and Schneider and Nurre [21].
In routing and scheduling, for example, Bertazzi et al. [22] develop a mixed-integer programming model to solve the Multi-Depot Inventory Routing Problem which minimises routing costs by determining how to serve the customers from different depots while managing their inventory levels to avoid stock-outs. A three-phase meta-heuristic algorithm is designed to solve the problem. The proposed algorithm performs better than a branch-and-cut algorithm for this type of problem. Li et al. [23] apply Whittle's restless bandits approach to develop an index policy to optimize the scheduling of limited resources to a large number of jobs, such as medical treatments, with uncertain lifetimes and service times, in the aftermath of a mass casualty incident. The new approach enables the development of state-dependent policy to prioritise jobs to better utilise the resource.
Jung et al. [24] develop a model for allocating operating room capacity in hospitals to scheduled patients while accommodating randomly arrived emergency patients without incurring excessive delays. The aim is to develop a framework for aggregating weekly schedules and generating detailed daily schedules that minimise the total cost of the expected operating time, idle time, and overtime of the operating rooms. Using the proposed approach, the optimal capacity allocation of operating rooms to elective patients can be determined as a function of the emergency arrival rate. Mahmoudi et al. [25] develop a new network data envelopment analysis model for the sustainable Urban Network Design Problem. By integrating data envelopment analysis, game theory and sustainability requirements, a bi-level model is proposed for selecting and scheduling urban road construction projects which is solved using a meta-heuristic algorithm. The model improves the environmental and social performance of the urban network during all evaluation periods. Shi et al. [26] formulate a model for a Home Health Care Routing and Scheduling Problem from the perspective of Robust Optimisation (RO) to take into account uncertain travel and service times. The non-deterministic variables are defined based on the theory of budget uncertainty and arrival time of each caregiver is rewritten as a complicated recursive function. The model overcomes the shortcomings of many deterministic models for this problem.
In emergency relief research, Bababeik et al. [27] investigate the optimal location and allocation of relief trains to enhance the resilience level of the rail network. Using link exposure measure which considers the operational attributes of links and accessibility to road system, a bi-objective programming model is formulated and solved using an augmented e-constraint method combined with a fuzzy-logic approach. The proposed framework shows superiority in providing an economical and effective layout compared to conventional maximal covering model. Wu et al. [28] propose to use microblogging data to identify waterlogging locations during urban rainstorm to optimize post-disaster rescue routes. By developing a location-routing problem model and solving it with NSGA-III algorithm, new routes to dissipate road traffic can be assigned timely which can be of great significance to the emergency rescue of victims during rainstorm disasters. The approach is novel in that it leverages social media data to obtain critical information on disasters to facilitate emergency relief. Zhu et al. [29] consider equity and priority issues in optimizing routing of rescue vehicles during emergency relief. Two models are developed taking into account the different levels of injury representing equity and the in-transit tolerable suffering duration representing rescue priority. The models excel in the fairness of human sufferings mitigation and outperform other models both in operational cost control and psychological sufferings alleviation.
While the above reviewed studies are successful in suggesting new approaches or formulating advanced strategies in solving routing and scheduling problems for emergency relief, one common shortcoming is that only single resource is considered or resource is not the focus of the optimisation. Reviews by Caunhye et al. [30]; Galindo and Batta [31]; Özdamar and Ertem [32] and Zhou et al. [33] reveal that most of the models developed for emergency relief only permit scheduling of one type of resource, either expendable or non-expendable. For example, optimisation models that consider only the resource scheduling of expendable resources include Haghani and Oh [34]; Özdamar et al. [35]; Chang et al. [36]; Balcik et al. [37]; Huang et al. [38]; Zokaee et al. [39]; among others. Another set of optimisation models consider only the resource scheduling of non-expendable resources in disaster emergencies. They include Rolland et al. [6]; Falasca and Zobel [40]; Wex et al. [15]; Lassiter et al. [41]; Schryen et al. [42]; Bodaghi and Palaneeswaran [43]; and so on.
To date, only a few studies, including Lee et al. [3]; Lei et al. [1] and Shahparvari and Bodaghi [44] have proposed models for emergency resource scheduling that include both expendable and non-expendable resources. Most of these studies put forward a mixed integer programming model (MILP) and applied heuristic algorithms for the assignment and scheduling of multiple resources in a supply network. Table 1 summarises the characteristics and limitations of some of the above mentioned vehicle routing and scheduling models for emergency relief distribution. It can be seen that many of them are deterministic in nature with minimisation of travel time as one of the objectives. Also, many of them assume that the sequence of the route is known beforehand and use heuristic methods to find a near-optimal rather than an exact solution. This is due to the NP-hard nature of the problem and it is especially so when delivery of both expendable and non-expendable resources in the same trip is considered. In practice, this assumption may not be valid and needs to be addressed in the optimisation model.
Table 1.
Summary of reviewed vehicle routing and scheduling optimisation models for emergency relief.
| Study | Resource | Sequence | Mode | Objective | Solution | Model Limitation |
|---|---|---|---|---|---|---|
| Chang et al. [36] | Expendable | – | Stochastic | To minimise transportation cost, facility set up cost, equipment cost | Exact method |
|
| Balcik et al. [37] | Expendable | Known | Stochastic | To maximise total expected demand | Exact method |
|
| ||||||
| Huang et al. [45] | Expendable | Unknown | Deterministic | To minimise total travel time, sums of arrival times and unsatisfied demand | Heuristic method |
|
| Falasca and Zobel [40] | Non-expendable | – | Deterministic | To minimise cost of task shortage, total number of undesired tasks and time blocks | Exact method |
|
| Lee et al. [3] | Both | Known | Deterministic | To minimise total weighted tardiness | Heuristic method |
|
| ||||||
| Wex et al. [15] | Non-expendable | Unknown | Deterministic | To minimise total weighted completion times | Heuristic method |
|
| ||||||
| Schryen et al. [42] | Non-expendable | Unknown | Stochastic | To minimise total weighted completion times | Heuristic method |
|
| ||||||
| Lei et al. [1] | Both | Known | Deterministic | To minimise total weighted tardiness | Heuristic method |
|
| ||||||
| Caunhye et al. [47] | Expendable | Unknown | Stochastic | To minimise cost of setting up warehouse, total response time | Exact method |
|
| ||||||
| Shahparvari and Bodaghi [44] | Both | Known | Deterministic | To minimise operational costs of the vehicle fleet | Heuristic method |
|
| ||||||
| Bodaghi et al. [48] | Both | Unknown | Probabilistic | To minimise weighted completion time | Exact method |
|
Vehicle routing problem (VRP) for emergency relief differs from other VRPs in that vehicles are often not required to return to the depots where they are dispatched (Open VRP (OVRP)). Or if they do, the final leg is not critical. Despite there being much less research when compared to classical VRP, studies have been undertaken on OVRP using various heuristics, such as evolutionary algorithm [49], particle swamp optimisation methodology [50], genetic algorithm [51], variable neighbourhood search algorithm [52], simulated annealing [53], and ant colony optimisation [54], among others, to generate near-optimal solutions. While OVRP can have one or more starting points, in practice, multiple depots are more common to accommodate a large fleet and the class of problems is referred to as multi-depot OVRP (MDOVRP). Research on MDOVRP is relatively limited because it is more challenging than the conventional MDVRP, which is a complex combinatorial problem. For example, Tarantilis and Kiranoudis [55] studied MDOVRP using the fresh meat industry in Greece as a case study. Liu et al. [56] proposed a MILP formulation for MDOVRP and used a hybrid genetic algorithm to find routes that minimise total travelling costs. Pichka et al. [57] also proposed a MILP model for the MDOVRP and developed a simulated annealing algorithm to establish near-optimal solutions for medium-sized and large instances. For the ERO, MDOVRP is akin to the MRSRP that is investigated in this present analysis as vehicles are sent from multiple RCs; they visit more than one demand point to deliver multiple resources.
As far as heuristic methods for solving VRP for emergency response are concerned, Wex et al. [15] have systematically categorised the different types of heuristic methods and compared computationally their performance. The different heuristic methods were used to solve a rescue unit assignment scheduling problem under randomly generated scenarios using data generated from the major earthquake in Japan in 2011. The heuristics examined include the Greedy method, construction heuristics, improvement heuristics, the Greedy randomised adaptive search procedure (GRASP), and the Monte Carlo-based heuristic method. Upon comparison, Wex et al. [15] reported that performance of the examined heuristic methods varies according to the size or context of the problem. Nevertheless, they concluded that using appropriate heuristic methods, reasonably feasible solutions for NP-hard routing and scheduling problem for emergency response could be obtained quickly. Table 2 summarises some of the other heuristics methods proposed by recent studies for solving the routing and scheduling problem in emergency relief distribution.
Table 2.
Heuristic methods for solving VRP in emergency relief proposed in recent studies.
| Study | Algorithm | Purpose | Approach | Merit |
|---|---|---|---|---|
| Duque et al. [58] | Iterated Greedy-randomise constructive procedure (IGRCP) | For scheduling and routing of a repair crew after a disaster | Based on the GRASP meta-heuristic method with multiple runs of the construction phase plus improvement routine | Overcomes the problem size limitation of dynamic programming and solves medium- to large-scale instances efficiently |
| Fontem et al. [59] | Decomposition-based method | To solve the Emergency Open Routing under Stochastic Travel Times and Deadlines (EORSTTD) Problem for quick relief during emergency | Renders the EORSTTD problem tractable by formulating a counterpart problem, and decomposes it into two sub-problems | Produces a solution that enables flexible decisions to be made according to the decision-maker's preference to avoid the risk of deadline violation |
| Osman and Ram [60] | Centralised Point-to-Point Look-Back (C-PTPLB) | To find evacuation routes from an urban building and out of its predetermined neighbourhood | Based on looking back from intermediate destination nodes at a current time T, and identifying the objects that can be point-to-point routed to reach there precisely at time T from preceding nodes | Provides point-to-point optimal route schedules while minimising the number of iterations when compared with other methods |
| Bruni et al. [19] | Iterated Greedy method | For routing of vehicles carrying critical supplies and to disaster victims | Implements an adaptive local search procedure and a destroy procedure to enable extensive searching for a solution space where near-optimal solutions can be employed | Flexible and applicable to various risk measures, can provide good solutions quickly |
| Faiz et al. [61] | Column generation and Path generation algorithm | For vehicle routing operations during a humanitarian crisis | Devises a task adjacency graph for a path-based integer linear program, using a column generation framework to solve large-scale instances | Outperforms the exact method (traditional arc-based mixed integer linear program) in solution time without sacrificing solution quality |
| Moreno et al. [62] | Branch-and-Benders-cut, construction and local search heuristics | To solve the Crew Scheduling and Routing Problem in road restoration after disasters | Decomposes an integrated problem into a master problem with scheduling decisions and sub-problems with routing decisions | Provides feasible solutions and optimality gaps where instances cannot be solved utilising exact methods |
As such, an optimisation model with appropriate heuristic algorithms could serve as an automated decision support system for decision-makers in emergency situations characterised by a high level of complexity and high time pressure. They could enhance human-based decision-making through rapid scenario analysis to maximise operational efficiency in emergency situations. Doing so will minimise losses in human lives. The MRSRP model and the heuristic algorithms proposed in this study are developed with reference to the above analyses and with such an objective in mind. It aims to supplement the inadequacies of the previous studies by considering multiple resources in the problem formulation. Using mixed integer programming and heuristics to find near-optimal solution like many of the previous studies, the study extends the previous work by accommodating in the model conditions closer to reality. It not only addresses inadequacies in the extant literature of multi-resource scheduling problem for EROs but also assists decision-makers in making better decisions during emergency situations. Based on an extensive literature review, six heuristic algorithms are developed and evaluated in this study, seeking the most appropriate method for solving the MRRSP in the context of supplying both expendable and non-expendable resources from relief centres to hospitals during emergency situations. The search for most efficient heuristics for solving the MRRSP aligns with the views many researchers in this field. For example, Bélanger et al. [63] review studies on the development of models to support decision making in emergency medical services (EMS) in the last decade. The need arises from the fact that dynamism inherent to EMS, as well as considerations of equity and patient medical outcomes, have demanded for new modelling approaches to address problems related to emergency vehicle location and relocation, in addition to dispatching decisions. While it is found that the size of the EMS problems under study is growing, and that there is an increasing use of stochastic and dynamic programming, they also opine that considerable efforts will need to be devoted to the development of more efficient solving methods.
Examples of previous efforts in this regard include Knight et al. [64]; which proposed new models for locating emergency medical services by incorporating survival functions for capturing multiple classes of heterogeneous patients, and Shahparvari et al. [18]; which developed a capacitated vehicle routing solution to evacuate short-notice evacuees with time windows and disruption risks under uncertainties during a bushfire. Bodaghi and Palaneeswaran [43]; Bodaghi et al. [4] have developed a bi-objective MILP model to address the problem where both expendable and non-expendable resources are considered. However, they did not consider the collaboration and quantity of different non-expendable resources. Wex et al. [15] have systematically categorised the different types of heuristic methods and compared computationally their performance for only the non-expendable resources. Also, they have not considered the collaboration between non-expendable resources. Table 3 gives an overview of the heuristic algorithms developed and evaluated in this study.
Table 3.
Overview of the heuristics developed in this study for solving the MRRSP for emergency response.
| Heuristic | Description | Related Works | Shortcomings |
|---|---|---|---|
| Greedy Algorithm |
|
Liu et al. [65]; Ceselli et al. [66]; Majzoubi [67]; Tang and Zhu [68]; Zhao et al. [69]; Ciancio et al. [70] |
|
|
|
||
| Augmented Greedy |
|
Li and Wang [71]; Almutairi [72]; Bettinelli et al. [73]; Kritikos and Ioannou [74] |
|
| Algorithm |
|
||
| k-Node Crossover Algorithm |
|
Baptista and Tavares [75]; Zhang et al. [76]; Zheng et al. [77] |
|
| |||
| Scheduling Algorithm |
|
Jaw et al. [78]; Weng et al. [79]; Ramchurn et al. [80]; Wex et al. [15] |
|
| |||
| Monte Carlo Algorithm |
|
Wex et al. [81]; Abdullah et al. [82]; Al-Harthei et al. [83]; Wu and Sioshansi [84] |
|
|
|
||
| Genetic Algorithm |
|
Baker and Ayechew [85]; Okhrin and Richter [86]; Zidi et al. [87]; Mguis et al. [88]; Zheng et al. [77]; Qin et al. [89] |
|
| |||
| Clustering Algorithm |
|
Özdamar and Demir [90]; He et al. [91]; Vargas-Florez et al. [92]; Pillac et al. [17]; Gharib et al. [93]; Penna et al. [94] |
|
|
|
3. Notations and formulation
The notations employed in the model are as follows:
Sets and Indices
| V | Set of vehicles |
| I | Set of n demand points + {0, n+1} where 0 and represent the dummy starting and ending nodes. |
| K | Set of relief centres (RCs) |
| G | Set of all resource types |
| T | Set of resource types for expendable resources |
| R | Set of resource types for non-expendable resources |
| Indices for demand points, | |
| v | Index for vehicle, |
| k | Index for RCs, |
| t | Index of resource types, |
Parameters
| Quantity of a resource type t required by a demand point i | |
| Capacity of vehicle v for carrying expendable and/or non-expendable resources | |
| Capacity of RC k for expendable and/or non-expendable resources | |
| Travel time required for vehicle v to transport resources from i to j | |
| Processing time for recovery operations at demand point i for a non-expendable resource | |
| Reduction factor to adjust the normal processing time of non-expendable resource t per extra resources at i | |
| Severity level of demand point i | |
| m | An arbitrary big positive number |
Variables
The decision variables can be defined as shown below:
| A binary variable to identify the sequence of demand points served by vehicle v. if demand point i is processed by vehicle v immediately before processing demand point j; 0 otherwise. | |
| A binary variable to identify an RC that can supply resources for demand point i with vehicle v. if the RC k supplies resources for demand point i with vehicle v; 0 otherwise. |
The auxiliary variables are:
| The quantity of resource type t shipped from the RC k with vehicle v; , . | |
| Starting time of relief operation at demand point i. | |
| Completion time of relief operation at demand point i. | |
| Required processing time for each non-expendable resource t at demand point i. |
With these notations, parameters, and variables, the objective function of the MRSRP model [48] is expressed as:
| (1) |
The objective function (1) minimises the weighted sum of completion times over all demand points. The weighted factor depends on the severity level of each demand point. The set of constraints considered in the MRSRP model is listed below:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Constraint sets (2) to (5) relate to determining the sequence of demand points visited by each vehicle to deliver the required resources for the recovery operations. Two additional dummy points (the starting and ending points) are defined for each vehicle (denoted by ‘0’ for the starting point and ’’ for the ending point). The processing times and transportation time from or to these dummy points are equal to zero (i.e. ). Constraint (2) guarantees that there is exactly one demand point instantly processed after each demand point for each vehicle to deliver resources. Constraint (3) ensures that each vehicle initially starts from its starting point (i.e. the RC in which the vehicle is located). Constraint (4) eliminates the loops in processing the demand points by a particular vehicle. Constraint (5) guarantees that if an instant predecessor is available for each demand point and each vehicle, it would be an immediate successor in this case, unless it is in fact the last demand point (demand point ).
Constraint (6) establishes the relationship between a covered incident, the vehicle (v), and the RC (k) from where the vehicle carried the resources. Constraint (7) calculates the total quantity of expendable resources delivered from k by vehicle v. Similarly, constraint (8) calculates the maximum quantity of non-expendable resources by a vehicle.
Constraint (9) establishes the relationship between variable and . Constraint (10) ensures that the total quantity of resources delivered by a vehicle does not exceed its capacity. Constraint (11) calculates the processing time required for each non-expendable resource to process each demand point. The non-expendable resource usage and the processing time of the relief operation at each demand point are assumed to have a linear relationship. Each demand point has associated with it a normal processing time for each type of non-expendable resource. If the quantity of a particular non-expendable resource carried by a vehicle is greater than the requirement of a specific demand point, the processing time for the demand point is adjusted by a factor as described in constraint (11). Since multiplication of two decision variables ( and ) makes this constraint non-linear, an auxiliary variable () with a positive real value is used to linearise this constraint as follows:
| (12a) |
| (12b) |
| (12c) |
The developed constraints can cover both possible cases. If binary variable , then . In this case, constraints (12a) and (12b) imply and , respectively. Since m has an arbitrary big positive value, constraint (12c) has always been satisfied in this situation, and then . In the second scenario, if binary variable , then . Since m has an arbitrary big positive value, constraints (12a) and (12b) have always been satisfied. Constraint (12c) implies and since has a strictly positive real value, constraint (12c) ensures that .
Constraints (12)-(13) are time-related constraints. Constraint (12) ensures that the starting time of a relief operation at each demand point is not earlier than the latest transportation of resources from RC to demand point i with vehicle v. Constraint (13) ensures that the starting time of the relief operation is not earlier than the earliest arrival time of the resources from the previous demand points. Constraint (14) calculates the completion time of the relief operation at each demand point. Constraints (15) and (16) define the domains of employed variables.
4. Solution approaches
If non-expendable resources are relaxed and assuming that the processing time of operations depends on vehicle rather than resources, our model falls into the category of VRP problem. Since the VRP model is NP-hard, our model's complexity is NP-hard too and an optimal solution cannot be found for large instances [95]. In addition, decision support must be provided quickly in real emergency situations [42] and an exact solution or exact solutions cannot be identified in a reasonable amount of time for our model even for small to medium cases. Hence, several heuristics are developed to provide a high-quality solution within the running time limitation in emergency situations. In this paper, six heuristics and a mixed heuristic and Clustering algorithm are constructed and compared with the genetic algorithm. The details of these heuristics are described in the subsections below.
4.1. Greedy algorithm
In the Greedy algorithm, we follow the problem-solving heuristic of identifying the least weighted completion time choice as a local optimal at each stage with the intent of finding a near global optimum. To reach the minimum total weighted completion time, it is obvious that demand of incidents with high severity value (weight) should be met as early as possible. To accommodate this into the algorithm, locations (e.g. incidents/demand points) are sorted by decreasing the order of their severity level (). Starting from location i with the highest severity weight, an incident is allocated to a node (RC or a visited hospital) where the node has the least total time.
In the Greedy algorithm, the decision rule for selecting the next incident is based on identifying a node with the least total time which incorporates two components: (a) transportation time from capable nodes with capable vehicles to the next incident (i), and (b) current completion time of capable vehicles. It is worth noting that in this method processing time of non-expendable resources for the next incident (i) is not considered in the decision-making process when selecting the most suitable node and vehicle to cover the demand of the next incident. However, after selecting the most suitable vehicle to cover the next incident (i), the vehicle's completion time is updated. This is conducted by considering the following elements: (a) transportation time from the most suitable node to the next incident (i), (b) current completion time of the vehicle, and (c) maximum processing time for non-expendable resources regarding incident i. Algorithm 1 describes the pseudo code for the Greedy heuristic algorithm.
Algorithm 1.
Greedy Algorithm.
The use of the Greedy algorithm in this study has its merit because at each level of recursion the size of the problem becomes smaller. The algorithm is fast, but there is the issue of “correctness†to overcome [96,97]. It is obvious that the obtained solution from the Greedy algorithm may not be the best, since the Greedy heuristic operates based on sorting the location for incidents by curtailing the severity level of the location. It also ignores the operations’ processing times in each location in the decision-making process where the next incident to cover has to be identified.
4.2. Augmented Greedy
As explained earlier, one of the main contributions of this study is to highlight that the number of available non-expendable resources affects the processing time and therefore planning of EROs. For example, if a vehicle carries three doctors and five nurses as non-expendable resources, and if the next incident requires only two nurses, since the remaining three nurses can help to expedite the operations, the processing time of this incident is reduced. Therefore, this adjustment should be performed on the Greedy algorithm to obtain a more accurate schedule.
Augmented Greedy (Algorithm 2) is developed to apply this adjustment on the output of the Greedy algorithm. In this method, the sequence of visiting incidents by each vehicle (which is the output of the Greedy algorithm) is considered as an input of the Augmented Greedy heuristic. To apply this adjustment, for each vehicle and for every non-expendable resource, the difference between the maximum number of non-expendable resources which have been used to cover all incidents (by the current vehicle) and the demand of each incident (covered by the current vehicle) is computed. Following this, the current processing time of each incident is updated by multiplying the computed value of the difference by which is a random reduction coefficient. It is obvious that updating the processing time of a node (i) affects the completion time of all subsequent nodes visited after node i. Consequently, this algorithm re-calculates the completion time of all succeeding nodes after making the adjustment on any node's processing time.
Algorithm 2.
Augmented Greedy Algorithm.
The Augmented Greedy algorithm addresses the correctness issue of the Greedy algorithm and can produce better result. Owing to the need to recalculate the completion time of all succeeding nodes upon adjustment of processing time at the proceeding node in every recursion, however, the overall processing time is much longer than that of the Greedy algorithm.
4.3. k-node crossover algorithm
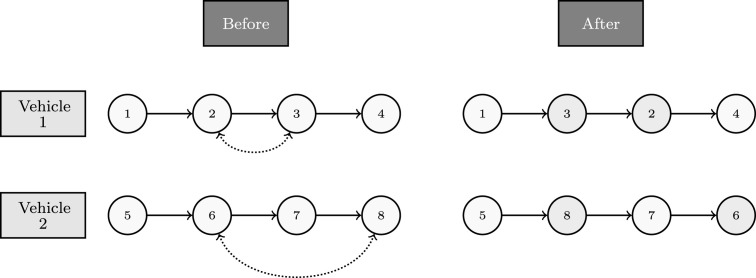
In the literature, Crossover procedure has been employed to improve the heuristic algorithms, where in each iteration the initial solution can be improved by applying the Crossover procedure [77]. Crossover methods can be implemented as a post-analysis improvement heuristic. In the Greedy-based algorithms it is quite possible that selecting the most optimal short-term solutions may lead to losing the chance of identifying the optimal outcome. Making the local optimal choice at each stage does not necessarily result in finding a global optimum and thus randomly exchanging the location of k number of nodes might improve the identified initial solution. After the scheduling of all incidents for each vehicle is determined, we apply the Crossover heuristic to randomly substitute the sequence of k number of locations in each iteration.
In this study, we apply 2-node and 3-node Crossover heuristics on the output of the Augmented Greedy algorithm to further improve the scheduling of available vehicles, in order to cover the incidents (Fig. 1 ). In a 2-node crossover algorithm, the sequence of each vehicle's routing and its corresponding values of completion time from the Augmented Greedy algorithm are imported as inputs. Then, vehicles which have been engaged in the recovery operations are identified. Out of all engaged vehicles, α per cent is randomly selected, where in our study. If no vehicle is selected, we select at least one vehicle. Afterwards, for each selected and engaged vehicle, the sequence of two nodes is exchanged randomly. The same process is used in the 3-node Crossover method with the exception that three nodes are randomly exchanged for each selected and engaged vehicle. Finally, the sum of weighted completion time of all vehicles is computed as the value of objective function (Z) for the first iteration. The Crossover heuristic is iterated for a predetermined number of iterations and the minimum value of total weighted completion time of all vehicles is reported as the output of this method (Algorithm 3).
Fig. 1.
k-Node Crossover algorithm.
The k-Node Crossover algorithm (Algorithm 3) overcomes the shortcoming of the Greedy and the Augmented Greedy algorithms by minimising the possibilities of trapping in a local optimum. Consequently, it can give better results than the previous two heuristics. Owing to the many iterations during the crossover, however, the running time can be much longer.
Algorithm 3.
k-Node Crossover Algorithm.
4.4. Scheduling algorithm
Up to this point, the processing time of the next visiting incident is not considered in the decision to identify the least weighted completion time choice as a local optimal. To incorporate the processing times of incidents for each type of non-expendable resource in the decision-making process, a Scheduling heuristic is developed. In this algorithm, three components constitute the total time which is the basis for making decisions on the next incident to be taken care of: (a) transportation time from the current node to the next incident (i), (b) current completion time of the vehicle at the current node, and (c) maximum processing time of non-expendable resources for incident i. The Scheduling heuristics have been previously suggested by [[15], [79]], however, no studies have taken the multi-resource scenarios into consideration.
In this method, we introduce an improved decision rule to provide a superior optimal solution. In the Greedy algorithm, the priority of an incident is determined using its severity level (). Since processing time of the non-expendable resources has a direct impact on the completion time of a vehicle and subsequently on the objective function (total weighted completion time of all vehicles), engaging both severity level of an incident and the corresponding average processing time of non-expendable resources to define the priority of an incident seems to be effective. Therefore, in the Scheduling algorithm, each incident's priority is determined by increasing the order of , where is the average processing time of non-expendable resources, and is the severity level of node i. This method addresses the trade-off between processing time and severity level for making decisions on the priority of incidents to cover.
Similar to the Augmented Greedy approach, in the Scheduling algorithm once a vehicle is allocated to cover an incident, processing time of non-expendable resources for all visited nodes by this vehicle is updated. In other words, for each non-expendable resource the maximum value of processing time that has been required for each visited incident is identified. Then, processing time of all visited nodes including the current incident is reduced by this term: a random reduction coefficient () times the difference between maximum value of demand for all visited incidents by the current vehicle and demand of each incident for non-expendable resources. Details concerning the Scheduling heuristic are explained in Algorithm 4.
Algorithm 4.
Scheduling Algorithm.
The Scheduling algorithm has the merit of completing more tasks in a given amount of time by running tasks which take less time to complete. It thus can have a higher throughput rate than the previous algorithms. The downside is that tasks that take longer time to complete might have a lower opportunity to run. The search can also be trapped in a local optimum instead of finding the global optimum.
4.5. Monte Carlo algorithm
The proposed Scheduling heuristic algorithm provides significant benefits that can solve parallel vehicle disaster recovery operations. However, due to the complexity of the problem, this method might get stuck in a local optima. To further improve this method and to overcome the informational uncertainties, we have customised the Monte Carlo method to deal with this problem. The structure of this method is similar to the Scheduling heuristic algorithm except for the decision-making process to select which vehicle is going to cover the next incident (i). Once a list of capable nodes with capable vehicles is identified, the vehicle with the lowest total time is selected to undertake the recovery operations for location i in the Scheduling method. The difference here is that instead of selecting the vehicle with the least total time, a list of all capable vehicles are sorted based on their estimated total time, and then of vehicles with least total time are screened. Afterwards, one vehicle is randomly selected from the screened list. By introducing randomness into the process of identifying the local optimal choice and repeating this process for a predefined number of iterations, the schedule with minimum total weighted completion time generally outperforms the Scheduling method, which seeks the near optimal solution in a single iteration. Algorithm 5 delineates the process of applying the Monte Carlo method.
Algorithm 5.
Monte Carlo Algorithm.
The Monte Carlo algorithm has all the merits of the Scheduling algorithm but minimising the bias against tasks with long completion time. As such, it reduces the possibility of trapping in a local optimum and can produce a better solution. Nonetheless, it can be challenging to determine the appropriate level of randomness and number of iterations. The algorithm can also have a long running time due to many iterations.
4.6. Meta-Heuristic algorithm (GA)
Meta-heuristic approaches are widely used as an alternative approach for heuristics in disaster relief operations [77]. In particular, a Genetic Algorithm (GA) can be designed as an alternative for proposed heuristics and compare the performance of heuristics against GA. An evolutionary optimisation algorithm, such as GA, conducts a search through the possible solutions by exploiting a population of points in parallel rather than a single point [98]. In this study, a chromosome represents the sequence of incidents that is assigned to each vehicle and it is generated randomly. As an iterative process, the evolution starts from a population of a randomly generated sequence of vehicles where the population in each iteration is referred to as a generation. In each generation, the fitness of every chromosome is evaluated based on: firstly, the total weighted completion time of all vehicles (value of objective function); and secondly, penalty values that are applied for exceeding the capacity of a corresponding RC or vehicle for both expendable and non-expendable resources.
The better fitting chromosomes are stochastically selected from the current population, and each individual's genome is modified to form a new generation. In other words, the chromosomes are sorted based on their fitness values and a proportion (i.e. survival rate) of chromosomes with the highest fitness are selected as the parents for the next generation. We have adopted the single-point crossover genetic operator in which genetic information of two parents is combined to generate new offspring. In this study, the crossover point is randomly selected from the range of incidents. To maintain genetic diversity from one generation of a population of chromosomes to the next, based on the defined mutation probability, sequences for visiting the incidents in a chromosome are altered from its initial state. This evolutionary process is iterated for a predefined period of time.
Although the genetic algorithms do not guarantee optimality, they are likely to provide a solution that is closest to the global optimum. The search is not easily trapped in local optima because of the probabilistic nature of the solution [99]. As such, the solution obtained using genetic algorithm can be used a benchmark for the other heuristics. The downside of the algorithm is that the running time can be long due to many iterations especially for large complex problems.
4.7. Clustering algorithm
Finding the optimal solution using the optimisation model may not be practical in some large and highly complex cases [100]. Therefore, most heuristic approaches try to improve the initial solution based on the predefined rules and identifying the local optimal choice with the hope of achieving the global optimal solution. Alternatively, clustering approaches have been introduced to manage the complexity of a large sized problem by assigning the demand points to a fixed number of clusters and then applying the exact mathematical model for the reduced number of incidents in each cluster. However, it is still possible that the size of a cluster's sub-problem would be large enough to make it NP-Hard and unable to be solved. To overcome this issue, Özdamar and Demir [90] proposed a hierarchical clustering and routing procedure for large-scale disaster relief logistics planning through an iterative process. Firstly, an attempt is made to solve the main problem within a predefined period of time. If no solution is identified, then the problem is divided into two sub-problems and another run is performed. If a solution is obtained for each cluster, solutions are aggregated to constitute the overall solution to the problem. In the case where a feasible solution is lacking for both sub-problems, clusters are further broken down into smaller sub-problems until the exact model can be solved for all sub-problems. This iterative clustering approach is adopted in this study. However, there is a major issue to address: how can the incidents be clustered to achieve the maximum precision for the aggregated solution?
We have developed a novel methodology to hierarchically cluster the recovery operations where the processing time of non-expendable resources is accounted for. First, for each pair of the nodes in the sequence of ( in the main problem (including RCs and incidents), a relatedness function () is defined by computing the ratio of the normalised severity level () over the normalised total completion time (TC) of covering incident i. Total completion time includes the transportation time from node to i and maximum processing time of non-expendable resources for incident i (i.e. ). This function addresses the trade-off between the processing time of an incident and its severity level when deciding to select an appropriate vehicle that covers the next incident. Given that the starting point of all vehicles is a RC, and a RC might have more than a single vehicle, the relatedness value is computed for each vehicle v that is available in a RC and an incident i. To obtain the relatedness value for two incidents (e.g. and i), since a single vehicle is available in the current incident (), there would be no need to consider the multi-vehicle scenario and can be computed from the ratio of .
Once the relatedness for each pair of nodes is obtained, incidents are tentatively allocated to a vehicle using a heuristic method. After ensuring that a RC (k) and its available vehicle(s) have sufficient capacity to supply expendable and non-expendable resources for an incident, one would be nominated to cover incident i which has the maximum relatedness to it. This process is repeated for all available vehicles. For covering the next set of incidents, similarly, an incident i is allocated to the vehicle that is located in node where is the highest. By using this method, total n number of incidents () are broken down to v number of collections () which will be potentially covered by the corresponding vehicle (v). Finally, the completion time () of each vehicle visiting the related nodes is computed and the weighted completion time of each node () is obtained. The total weighted completion time of each vehicle would be the sum of for all incidents that are visited by vehicle v. Aggregating the total weighted completion time of all vehicles gives the value of objective function ().
Similar to the Augmented Greedy method, completion time of each vehicle and the weighted completion time of each incident () should be updated to reflect the fact that where extra non-expendable resources are available in a vehicle, they definitely assist in processing the incident faster and the completion time of incidents decreases accordingly. Updating the processing time for all nodes is performed prior to creating sub-problems and their corresponding clusters.
Considering the fact that scheduling of EROs should be carried out in a fairly short time span, and since attempting to identify a solution for a cluster is a lengthy process, we limit the maximum number of trials to the number of vehicles in a problem. Therefore, for v number of vehicles, there are number of sub-problems in the most broken down sub-problem. Each sub-problem includes number of clusters. In each cluster, there are , , number of RCs, vehicles, and incident sets, respectively.
To form a larger problem which includes number of clusters, two clusters should be merged. We combine the two clusters with the lowest value of total weighted completion times () following the logic that an exact model can identify a better solution when more incidents are available in a pool. This process is repeated to form sub-problems with () number of clusters. It is obvious that a problem with ‘1’ cluster is the same as the original problem.
The process of identifying a solution starts with the problem which has a single cluster including all vehicles, in other words, the original problem. We attempt to solve this problem using the exact mathematical model for a predefined period of time to meet a target gap. If a solution is identified, the process is terminated; otherwise, the algorithm attempts to solve the sub-problem with two clusters. This process continues until either a solution is identified for all clusters of a sub-problem, or the last sub-problem including v number of clusters delivers no feasible solution. Algorithm 6 displays the detailed steps that are involved in the Clustering algorithm.
Algorithm 6.
Clustering Algorithm.
The Clustering algorithm has the advantage of finding a solution for a large complex vehicle routing and scheduling problem by splitting the problem into sub-problems of smaller clusters to solve, which is relatively easier, and combining the outcomes to form a total solution. It can provide a good balance between effort and quality of solution [101]. The shortcoming is that it can be challenging in splitting the original problem into an appropriate number of clusters to obtain optimality. Also, because of the spilt, running time can be long due to many iterations.
5. Numerical experiment
In this section, numerical experiments are developed to evaluate and compare the proposed algorithms. To reflect the impact and diversity of real-world natural disasters, ten scenarios have been generated. In the next section, settings of each experiment are explained. Next, the validity of the developed heuristics, meta-heuristic, clustering, and exact models are investigated. Finally, results of solving the developed scenarios using the proposed methods are presented.
5.1. Settings
Random variables and their distribution are presented in Table 4 . Since generating random numbers that follow a Normal distribution may result in negative values, a sub-routine has been developed to regenerate the random numbers when a negative value exists in a set. With regard to the capacity of RCs and vehicles for expendable and non-expendable resources, Normal distribution is adopted. However, the parameters () of this distribution for the aforementioned four random variables are selected in way that they suit the problem size. Without loss of generality, two expendable and two non-expendable resources have been considered in this study.
Table 4.
Random variables and their distribution.
| Random Variable | Distribution | Random Variable | Distribution |
|---|---|---|---|
| Processing time | Demand | ||
| Processing time | Demand | ||
| Travel time | Demand | ||
| Severity Level (Weight) | Demand | ||
| CP | CP |
The special settings of individual algorithms are presented below:
| k-Node Crossover | Α | 10% |
| Number of iterations (rep) | 10,000 | |
| Monte Carlo | Β | 30% |
| Number of iterations (rep) | 10,000 | |
| GA | Run time | 30 min |
| Population size | 1000 | |
| Number of generations | 500 | |
| Number of chromosomes | 100 | |
| Survival rate | 70% | |
| Mutation probability | 50% | |
| k-penalty cost | 100,000 | |
| Clustering | Run time | 2 h |
| Target Gap () | 1% | |
| BigM | 1,000,000 |
5.2. Validation
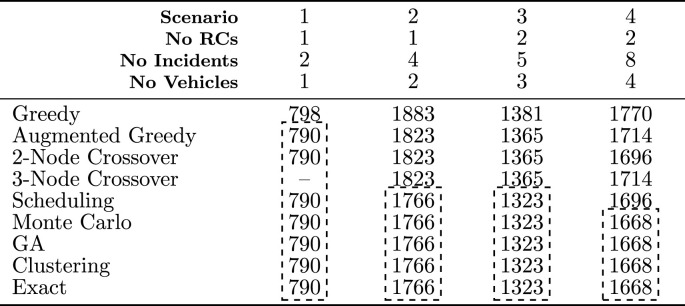
The developed exact mathematical model, heuristics, meta-heuristic, and Clustering algorithms should be validated prior to putting them into practice. Four small sized scenarios are considered for the validation process (Table 5 ): (1,2,1), (1,4,2), (2,5,3), and (2,8,4) in the format of (number of RCs, number of incidents, and number of vehicles). Python 3.6 is employed for evaluating the heuristics, meta-heuristic, and some parts of the Clustering algorithm. To program and solve the exact model, CPLEX 12.8 is used in conjunction with Python 3.6 API.
Table 5.
Assessing the validity of the exact, heuristic, and meta-heuristic models.
Results of the validation process indicate a satisfactory outcome and show consistent solutions for the developed methods. Greedy algorithm is not comparable with others as the processing time of a node is not adjusted for the cases where extra non-expendable resources are available to expedite the processing of an incident. However, the smallest scenario shows that when processing time of nodes is updated based on available non-expendable resources in a vehicle (i.e. Augmented Greedy), the total weighted completion time would be the same for all methods. The exception here is the 3-node crossover algorithm which did not provide a result. It makes sense as there are only two incidents in this scenario and applying the 3-node crossover is not possible. We have also manually solved the first two scenarios to ensure that the results of algorithms are valid. The outcomes of the remaining experiments demonstrate that the developed models and methods are valid.
5.3. Results
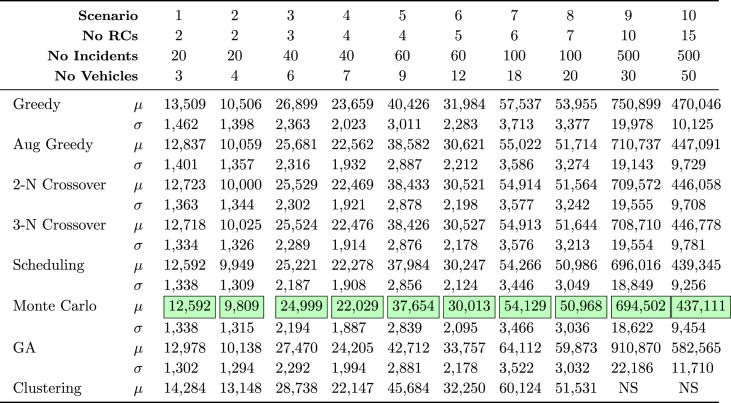
To assess effectiveness and accuracy of the developed methods for responding to the EROs, ten scenarios have been developed. To ensure that variations of the model inputs are captured in the objective function, each scenario is analysed under all heuristics for thirty iterations. The mean and standard deviation of thirty runs for all heuristics are presented in Table 6 . The only exception is the Clustering method which is evaluated once. Compared to other developed methods, computational time of Clustering method is so high that its usability for EROs is questionable. Results indicate that lack of updating the processing time (i.e. Greedy algorithm) where extra non-expendable resources are available, leads to ineffective planning of EROs. Furthermore, the k-Node Crossover algorithm generally makes some improvements to the output of the Augmented Greedy method. It can be observed that incorporating the updated processing time when deciding to select the next incident (i.e. Scheduling algorithm) is definitely effective. This algorithm is further improved by randomly selecting a capable vehicle among the candidates with the least total completion time (i.e. Monte Carlo method), in order to avoid trapping in a local optimum. Finally, neither GA nor Clustering demonstrates outstanding performance in planning of recovery operations.
Table 6.
Results of solving ten scenarios using the developed heuristics, GA, and Clustering algorithms.
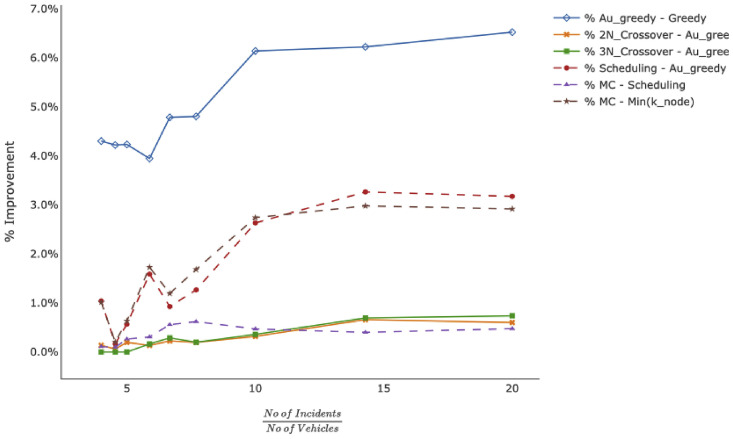
Considering the methods which have been used for developing the heuristics, the number of allocated incidents to each vehicle might affect the model's effectiveness. To further investigate this proposition, percentage of improvement for each pair of related heuristics against the ratio of number of incidents to number of vehicles for various problems is presented in Fig. 2 . When this ratio increases, it implies that vehicles visit a larger number of incidents in a given scenario. Results indicate that if more incidents are allocated to a vehicle, the Augmented Greedy algorithm can deliver a better solution. The logic behind this finding is that the process of adjusting the processing time for an incident in this method impacts on the completion time of all subsequent incidents which are visited by the same vehicle. Therefore, a vehicle visiting more incidents usually improves the total completion time so that all allocated incidents are in fact covered.
Fig. 2.
Percentage of improvement for developed heuristics.
The same pattern can be observed for both 2-Node and 3-Node Crossover methods. If more incidents are allocated to a vehicle, the k-Node Crossover algorithm has further opportunity to identify a better solution by exchanging the sequence of the higher number of visited incidents. It can also be observed that 3-Node method outperforms the 2-Node Crossover when more incidents are visited by a vehicle. Higher values of this ratio also lead to higher performance of the Scheduling algorithm compared to the Augmented Greedy. This is due to the fact that in the Scheduling algorithm, processing time of the next incident is involved in the decision making on identifying the next most suitable incident to cover. The improved decision making process has a positive impact on the total completion time as the required time to complete all incidents is reduced accordingly. The same logic applies when the magnitude of improvement regarding the Monte Carlo algorithm is assessed against the minimum improvement of k-Node Crossover algorithms. Compared to the Scheduling algorithm, the Monte Carlo post-analysis algorithm also works relatively better in scenarios that number of incidents is higher and thus more incidents are allocated to vehicles. However, this method is almost robust when changes in this ratio occur.
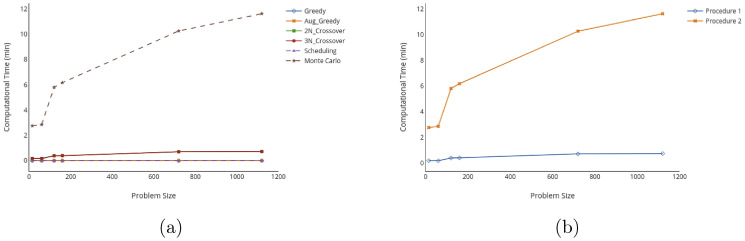
Given that this study investigates the decision support systems for ERO, probing the computational time for obtaining a near-optimal schedule is crucial. Fig. 3 presents the mean computational time of heuristic-based methods for thirty runs. Mean and 95% confidence interval of all runs are presented in A. It is observed that all base methods including Greedy, Augmented Greedy, and Scheduling algorithms are able to solve the examined scenarios using two Intel Xeon processors (2.5 GHz) with 16 GB of RAM in less than a minute. However, the post-analysis algorithms including k-Node Crossover and Monte Carlo methods where the schedule is being revisited for 10,000 iterations trigger the significant increase in computational time (Fig. 3a). Therefore, we have bundled the computational time of each base method with its post-analysis improvement algorithms in two procedures.
Fig. 3.
Comparison between the computational time of (a) heuristics, and (b) Procedure 1 (Greedy + Augmented Greedy + Min(K-Node Crossover) and Procedure 2 (Scheduling + Monte Carlo).
The first procedure includes the sum of computational times of Greedy, Augmented Greedy, and minimum computational time of 2-Node and 3-Node Crossover methods. The second procedure includes the sum of computational times of Scheduling and Monte Carlo algorithms. Although section 5.3 has shown that the second procedure is superior in terms of identifying the least total weighted completion time, Fig. 3b illustrates that the computational time of this procedure is more sensitive to the size of the problem (i.e. number of incidents number of RCs number of vehicles). Scheduling, however, can be performed without engaging the Monte Carlo as the post-optimal improvement algorithm, and thus Scheduling provides the best of two worlds in delivering a reasonable solution with a fair amount of computational time. It is worth noting that clustering has not been considered for this analysis as the computational time that is required for this method has a very wide range, starting from 30 min for smaller problems to more than two days for larger problems in the range of examined scenarios.
5.4. Case study
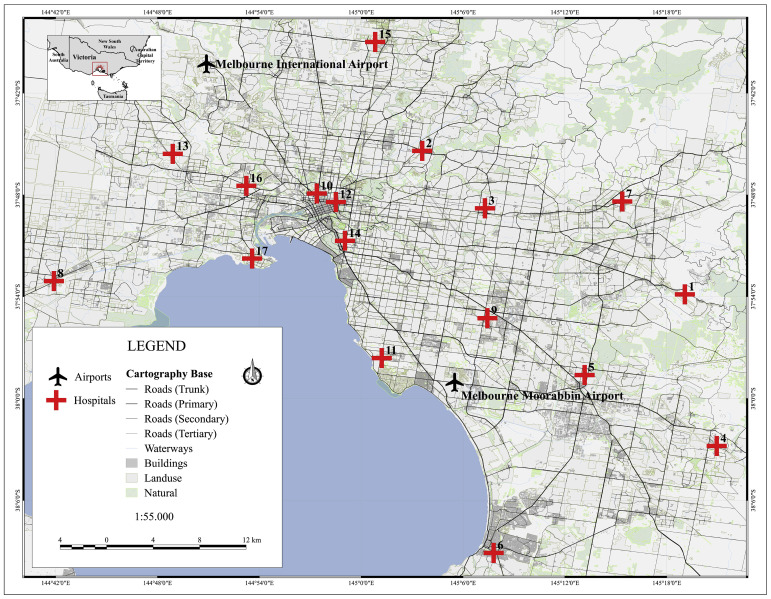
To enable the validation of the proposed model, a case study of multi-resource scheduling for emergency operations in the public hospital network in the Melbourne metropolitan area was brought forth for succinct analysis. The case study assumed a sudden outbreak scenario similar to the 2003 SARS coronavirus outbreak in Asia and other parts of the world Bodaghi et al. [4]. The Information regarding the hospitals in the Melbourne metropolitan area was obtained from the Department of Health, Victoria, Australia and the National Health Performance Authority [102]. The validation exercise included 17 hospitals (demand points) as listed in Table A2 and portrayed in Fig. 4 . Furthermore, the case study evaluation assumed two relief centres (RCs) for distributing resources. The stipulated RCs being Melbourne's Tullamarine Airport and Moorabbin Airport while transportation was by road for both expendable resources (e.g., medical supplies) and non-expendable resources (e.g., surgeons). The destinations were the emergency operations demand points i.e. hospitals. The simulated case study was deemed to be equivalent to emergency operations in a disaster relief scenario.
Fig. 4.
Case study area- Greater Melbourne metropolitan area.
In addition, it was assumed that four capable vehicles were available. Two vehicle types, namely heavy and light emergency vehicles with specific capacities, were included in this validation, i.e. light vehicle 1 and heavy vehicle 2 were available in Tullamarine Airport, and light vehicle 3 and heavy vehicle 4 were available in Moorabbin Airport. The release times of vehicles from Tullamarine Airport and Moorabbin Airport were randomly generated using a uniform distribution . The shortest travel time between nodes with an average speed of 40 km/h, was the basis for calculating resource transportation for emergency operations at the demand points.
In this case study, two types of non-expendable resources were considered: (a) health professionals (excluding surgeons) for non-surgery emergencies, and (b) surgeons for emergency surgery. The numbers of health professionals and surgeons available at the Tullamarine and Moorabbin Airports were considered (60, 35) and (40, 20), respectively. Alternatively, the modelling process made assumptions regarding the treatments undertaken by each health professional teams. In this sense, each team was stipulated to offer treatment to 40 emergency patients and three resuscitation patients. The two types of expendable resources considered for emergency operations were (a) medical supplies, and (b) surgical supplies. Also, the availability of these expendable resources at the Tullamarine and Moorabbin Airports were assumed as (6500, 300) and (3500, 200) units respectively. The assumption incorporated to the study concerning the demands (in units) for each type of resources at each hospital was based on the corresponding area's population and the average number of emergencies and resuscitation patients per month that visited the emergency department at each hospital. The processing time (in hours) for the relief operations at each hospital have been considered according to the demand, e.g. 10 min per emergency patient as per the National Health Performance Authority. Huber-Wagner et al. [103] studied the duration's necessary for emergency operations during mass casualty scenarios and revealed that a mean operation requires an average time of 130 min.
For the purpose of model validation, it was assumed that resuscitation patients require 130 min for treatment. Any extra volunteer or surgeon team member can reduce the processing time of an emergency operation to 10 and 15 min, respectively. The severity levels (importance levels of operations at each hospital) were generated randomly using discrete uniform distribution . The details of the case study are tabulated in Table A3.
Table 7 shows the results of applying the proposed algorithms on the area of interest. The results of the analysis indicates that both Monte Carlo and GA algorithm could outperform other algorithms to calculate the total completion time of the emergency operations weighted by the severity level. Computational time-wise, however, the results indicates that the Monte Carlo algorithm could outperform GA algorithm by 90% reduction in the CPU time. The Completion time of the case study is reported as 757 by Monte Carlo algorithm pertained in 187.92 s. The clustering algorithm could pertain objective value function of 838 within 7651 s which indicates that this algorithm is the less efficient method in the emergency response operations.
Table 7.
Results of the comparison of the algorithms on the real case study.
| Algorithms | Greedy | Updated Greedy | 2-N Crossover | 3-N Crossover | Scheduling | Monte Carlo | GA | Clustering |
|---|---|---|---|---|---|---|---|---|
| Objectives | 935 | 775 | 775 | 775 | 772 | 757 | 757 | 838 |
| CPU times(s) | 0.10 | 0.08 | 11.64 | 10.69 | 0.10 | 187.92 | 1800 | 7651 |
The detailed results of the case study is tabulated in Table 8 . For instance, picks up 25 health professionals and 20 surgeons with enough supply of the emergency expendable items from Melbourne airport to visit 5 hospitals including Western, Northern, St Vincent, Box hill, and Alfred hospitals, respectively. The generated visiting plan for the rest of points is shown in Table 8.
Table 8.
Case study resource allocation.
| Vehicle | RC | Sequence | Expandable Items |
Non-expandable Items |
||
|---|---|---|---|---|---|---|
| 3045 | 176 | 25 | 20 | |||
| 2978 | 102 | 31 | 14 | |||
| 1644 | 70 | 17 | 9 | |||
| 1692 | 100 | 20 | 10 | |||
6. Discussion and concluding remarks
At strategic level, during an emergency or disaster response, a relief centre is a central command and control facility that is responsible for preparing, planning, coordinating, and controlling the EROs. Strategic and operational decisions should be, however, made in a short time span to protect lives and properties. For this reason, it is crucial to employ effective tools and methods to facilitate swift and accurate planning for covering all incidents. In the majority of recovery operations, engaging non-expendable resources is inevitable. In bushfire emergency response, for example, both firefighters and medical crews should be dispatched to suppress the fire and assist injured people, simultaneously. A similar situation exists as part of the Flexible Home Aged Care package (hospital in home plan) where the operations team is required to attend a number of calls for assistance when several seniors require immediate attention.
In the vehicle routing problems that non-expendable resources are also involved in emergency response operations, the role of resource planning becomes utterly crucial. Based on collected data from incidents or direct communication with people who are urgently requiring help, the severity of incidents is assessed and the number of non-expendable resources are determined for each vehicle in a way that out of all allocated incidents, the one with the maximum demand is also covered. The implication of this arrangement is that for other incidents, extra non-expendable resources become available. It is obvious that extra available resources will not stay put and they will help provide assistance to process the incidents faster. This is where the main contribution of this study stands out: the estimated processing time of incidents should be updated in the planning process given that the objective function of scheduling models for this type of problem is generally formulated as the total weighted completion time of all vehicles. If this key factor is not taken into account, incompetent or poor planning will result in either over-supplying resources or delays in processing the incidents.
Adjusting processing time of recovery operations for each incident can be undertaken in different planning stages using various methods: (1) Solving the problem without adjusting the processing time (Greedy method) and then making the adjustments for all incidents and the total weighted completion times of all vehicles (Augmented Greedy method); (2) As a post-analysis technique and through an iterative method, the output of Augmented Greedy algorithm can be further improved (k-Node Crossover); (3) Incorporating the adjusted processing time in the decision-making process when selecting a vehicle to cover the next incident (Scheduling method); (4) Improving the decisions on incident selection in a post-analysis process via introducing a random process for choosing the best next incident to cover (Monte Carlo method); and (5) Breaking down the main problem into sub-problems (clusters) and using the exact method to solve the smaller sized problems. This is followed by aggregating the optimal values of objective function for all sub-problems, in order to obtain the optimal value for the main problem (Clustering algorithm).
Comparing the results of the Augmented Greedy method with the original Greedy algorithm clearly indicates that ignoring to update the processing time for non-expendable resources results in higher total weighted completion time. Therefore, this gap should be filled in planning and scheduling processes of recovery operations. The question here is whether updating the final schedule (Augmented Greedy method) and applying an improved methods such as k-Node Crossover is the most effective way to tackle this issue. Our results stipulate that although both k-Node Crossover methods demonstrate a superior performance compared to the Augmented Greedy algorithm, fine-tuning the decision-making process of identifying the local optimal choice by considering the updated processing time of the next incident (i.e. Scheduling method) wields a significant and positive impact on the schedule. We have also noticed that since the Scheduling algorithm inherits the negative properties of the Greedy method with the possibility of losing a better optimal solution as a result of stage-based decision-making, a post-analysis method in more effective to address this shortcoming. That is the reason Monte Carlo has outperformed all heuristics and delivered the most effective solution. Furthermore, the comparison between the percentage of improvement among each pair of heuristics reveals that heuristics with post optimal improvements provide superior performance compared to the original models. Moreover, introducing the randomness into the decision model results in an improved solution, especially for scenarios that the number of allocated incidents to vehicles is higher.
In addition to the aforementioned findings, we benchmarked the solutions against the meta-heuristic (GA) and clustering algorithms which have been cited many times for planning of EROs. It is, however, crucial to note that the planning process should be undertaken within a reasonable time span to address the requirements of managing recovery operations. From the computational time perspective, all scenarios have been successfully analysed by the six developed heuristics in less than 30 min, which is in the acceptable range. The only exception is the largest scenarios which took almost 48 min to analyse by the Monte Carlo method. That explains why we limit the GA to provide the solution in 30 min. As indicated in section 5.3, GA was not successful in providing a better solution compared to the heuristics within the specified time limit. Therefore, although GA provides a reasonable solution for planning of various operations across supply chains, for a limited planning time span, some reservations should be taken into consideration.
It is also recommended by several studies to use the Clustering algorithm for planning the recovery operations. The logic behind this recommendation is that although breaking down the main problem into sub-problems introduces sub-optimal routing solutions, using the exact method for solving each cluster might make up the sub-optimality of solutions for each portion of problem. Although we have developed a novel heuristic method to effectively cluster the problems into more relevant sub-problems using the relatedness function between incidents, results show no significant advantage of the Clustering algorithm to heuristics. In addition, it is worth mentioning that solving the problem using the iterative Clustering algorithm could take up more than two days to deliver the final solution. As a result, we recommend avoiding Clustering algorithms for scheduling of recovery operations where the planning period should be sufficiently short.
Probing the computational time of the defined bundle of base and post-analysis improving methods reveals that the first group including the combination of Greedy, Augmented Greedy, and k-Node Crossover methods is less affected by the size of the problem. Basically, the first procedure is recommended for the situations that time is pressing and the second procedure would be more appropriate when a superior solution is preferred at the cost of spending a little bit more time on the planning process. Scheduling, however, could be considered as a conservative approach whereby a reasonable solution is delivered within a short time span.
To summarise the findings of this study into a guideline, managers of emergency recovery operations are recommended to (i) apply the recommended adjustment on operating time. Availability of extra non-expendable resources for less severe incidents makes these incidents to be covered faster. In other word, one of the proposed algorithms of this study should be employed in the planning process; (ii) avoid using the clustering method to plan the recovery operations; (iii) employ the procedure 2 for planning when precision of solution is more important that the urgency of delivering the solution. If 30 min of computational time for planning process is within the acceptable range, managers of ERO are recommended to use the procedure 2 when the problem size is less than 1200; (iv) use procedure 1 for larger problem size or very short time frames of planning process. Following these recommendations provides significant benefits to managers of ERO such as optimal deployment of resources, obtaining more accurate processing time, decreasing the likelihood of over-supplying non-expendable resources and thus reducing the cost of operations, and effective selection of a solution approach based on the trade-off between the computational time and optimality of the solution.
To further improve the developed methods, future studies can extend the proposed algorithms by incorporating the stochastic variables and conducting stochastic optimisation to address the uncertainties involved in scheduling of recovery operations. Another promising pathway is to develop multi-objective models in which the trade-off between the processing time and severity level of incidents for selecting the next incident to cover is investigated. Furthermore, employing the decomposition methods to solve the exact model of this problem for large sized emergency scenarios might be of great value.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ijdrr.2020.101780.
Appendix A. Computational time of Heuristics
Table A.1
Computation time and 95% confidence interval of heuristics (in seconds)
| Scenario | Parameter | Greedy | Updated Greedy | 2-N Crossover | 3-N Crossover | Scheduling | Monte Carlo |
|---|---|---|---|---|---|---|---|
| 1 | μ | 0.06 | 0.05 | 10.50 | 10.34 | 0.07 | 165.09 |
| 95% CI - LB | 0.05 | 0.04 | 10.45 | 10.24 | 0.07 | 164.16 | |
| 95% CI - UB | 0.07 | 0.07 | 10.55 | 10.43 | 0.07 | 166.02 | |
| 2 | μ | 0.05 | 0.03 | 10.54 | 10.50 | 0.07 | 171.14 |
| 95% CI - LB | 0.05 | 0.03 | 10.49 | 10.43 | 0.07 | 170.30 | |
| 95% CI - UB | 0.05 | 0.03 | 10.58 | 10.56 | 0.07 | 171.98 | |
| 3 | μ | 0.08 | 0.06 | 23.37 | 23.20 | 0.12 | 347.76 |
| 95% CI - LB | 0.08 | 0.06 | 23.27 | 23.09 | 0.12 | 345.66 | |
| 95% CI - UB | 0.09 | 0.06 | 23.46 | 23.30 | 0.13 | 349.86 | |
| 4 | μ | 0.09 | 0.06 | 23.92 | 23.78 | 0.12 | 370.28 |
| 95% CI - LB | 0.09 | 0.06 | 23.85 | 23.69 | 0.12 | 368.13 | |
| 95% CI - UB | 0.09 | 0.06 | 23.98 | 23.87 | 0.13 | 372.44 | |
| 5 | μ | 0.14 | 0.09 | 42.28 | 41.99 | 0.18 | 615.43 |
| 95% CI - LB | 0.13 | 0.08 | 42.19 | 41.84 | 0.18 | 609.81 | |
| 95% CI - UB | 0.14 | 0.09 | 42.37 | 42.13 | 0.19 | 621.05 | |
| 6 | μ | 0.15 | 0.10 | 43.72 | 43.32 | 0.20 | 697.27 |
| 95% CI - LB | 0.15 | 0.09 | 43.61 | 43.17 | 0.20 | 693.75 | |
| 95% CI - UB | 0.16 | 0.10 | 43.82 | 43.47 | 0.21 | 700.79 | |
| 7 | μ | 0.30 | 0.18 | 99.10 | 99.28 | 0.39 | 1572.03 |
| 95% CI - LB | 0.29 | 0.17 | 98.76 | 98.99 | 0.38 | 1561.42 | |
| 95% CI - UB | 0.30 | 0.19 | 99.43 | 99.58 | 0.40 | 1582.63 | |
| 8 | μ | 0.32 | 0.18 | 102.08 | 101.91 | 0.40 | 1670.65 |
| 95% CI - LB | 0.31 | 0.18 | 101.79 | 101.68 | 0.40 | 1661.59 | |
| 95% CI - UB | 0.33 | 0.19 | 102.37 | 102.14 | 0.41 | 1679.71 | |
| 9 | μ | 1.85 | 0.28 | 175.93 | 175.89 | 2.13 | 1847.72 |
| 95% CI - LB | 1.80 | 0.27 | 175.44 | 175.22 | 2.10 | 1827.60 | |
| 95% CI - UB | 1.90 | 0.29 | 176.42 | 176.56 | 2.17 | 1867.84 | |
| 10 | μ | 2.99 | 0.36 | 207.51 | 207.92 | 3.22 | 2833.32 |
| 95% CI - LB | 2.91 | 0.33 | 206.68 | 207.01 | 3.17 | 2812.78 | |
| 95% CI - UB | 3.07 | 0.39 | 208.35 | 208.82 | 3.27 | 2853.87 |
Table A.2
Summary of 17 public hospitals considered in the case study simulation.
| No. | Hospital name | No. of beds | Address | Location | Post Code |
|---|---|---|---|---|---|
| 1 | Angliss Hospital | 100–199 | Albert Street | Upper Ferntree Gully | 3156 |
| 2 | Austin Hospital | 145 Studley Road | Heidelberg | 3084 | |
| 3 | Box Hill Hospital | 200–500 | 51 Nelson Road | Box Hill | 3128 |
| 4 | Casey Hospital | 200–500 | 52 Kangan Drive | Berwick | 3806 |
| 5 | Dandenong Hospital | 200–500 | 105-135 David Street | Dandenong | 3175 |
| 6 | Frankston Hospital | 200–500 | Hastings Rd | Frankston | 3199 |
| 7 | Maroondah Hospital | 200–500 | 1 Mt Dandenong Rd | East Ringwood | 3135 |
| 8 | Mercy Hospital | 100–199 | 300 Princes Highway | Werribee | 3030 |
| 9 | Monash M.C. | 500 | 246 Clayton Road | Clayton | 3168 |
| 10 | Royal Melbourne | 500 | 300 Grattan Street | Parkville | 3050 |
| 11 | Sandringham Hospital | 100–150 | 193 Bluff Road | Sandringham | 3191 |
| 12 | St Vincent's Hospital | 500 | 41 Victoria Parade | Fitzroy | 3065 |
| 13 | Sunshine Hospital | 200–500 | 176 Furlong Road | St. Albans | 3021 |
| 14 | Alfred Hospital | 55 Commercial Road | Melbourne | 3004 | |
| 15 | The Northern Hospital | 200–500 | 185 Cooper Street | Epping | 3076 |
| 16 | Western Hospital | 200–500 | 160 Gordon Street | Footscray | 3011 |
| 17 | Williamstown Hospital | 50–99 | 77b Railway Crescent | Williamstown | 3016 |
Table A.3
Details of the case study.
| H. No. | Expendable resources |
Non-expendable resources |
Processing times |
Severity |
|||
|---|---|---|---|---|---|---|---|
| Medical supplies |
Surgical supplies |
Health professionals |
Surgeons |
Non-surgery emergencies |
Surgery resuscitation |
||
| 1 | 337 | 12 | 8 | 4 | 7.02 | 6.51 | 6 |
| 2 | 790 | 29 | 20 | 10 | 6.58 | 6.29 | 3 |
| 3 | 664 | 25 | 17 | 8 | 6.51 | 6.78 | 2 |
| 4 | 467 | 9 | 12 | 3 | 6.49 | 6.51 | 1 |
| 5 | 690 | 28 | 17 | 9 | 6.76 | 6.75 | 5 |
| 6 | 1238 | 33 | 31 | 11 | 6.66 | 6.51 | 6 |
| 7 | 464 | 19 | 12 | 6 | 6.44 | 6.87 | 2 |
| 8 | 176 | 3 | 4 | 1 | 7.33 | 6.51 | 1 |
| 9 | 920 | 41 | 23 | 14 | 6.67 | 6.36 | 6 |
| 10 | 572 | 62 | 14 | 21 | 6.81 | 6.41 | 4 |
| 11 | 154 | 4 | 4 | 1 | 6.42 | 8.68 | 6 |
| 12 | 311 | 25 | 8 | 8 | 6.48 | 6.78 | 3 |
| 13 | 356 | 9 | 9 | 3 | 6.59 | 6.51 | 2 |
| 14 | 657 | 60 | 16 | 20 | 6.84 | 6.51 | 1 |
| 15 | 997 | 40 | 25 | 13 | 6.65 | 6.68 | 5 |
| 16 | 416 | 26 | 10 | 9 | 6.93 | 6.27 | 6 |
| 17 | 150 | 21 | 4 | 7 | 6.25 | 6.51 | 2 |
Appendix B. Supplementary data
The following is the Supplementary data to this article:
References
- 1.Lei L., Pinedo M., Qi L., Wang S., Yang J. Personnel scheduling and supplies provisioning in emergency relief operations. Ann. Oper. Res. 2015;235:487–515. [Google Scholar]
- 2.Teague B., McLeod R., Pascoe S.M. Government Printer; 2009. 2009 Victorian Bushfires Royal Commission: Interim Report 2: Priorities for Building in Bushfire Prone Areas. [Google Scholar]
- 3.Lee K., Lei L., Pinedo M., Wang S. Operations scheduling with multiple resources and transportation considerations. Int. J. Prod. Res. 2013;51:7071–7090. [Google Scholar]
- 4.Bodaghi B., Palaneeswaran E., Abbasi B. Bi-objective multi-resource scheduling problem for emergency relief operations. Prod. Plann. Contr. 2018;29:1191–1206. [Google Scholar]
- 5.Arora H., Raghu T., Vinze A. Resource allocation for demand surge mitigation during disaster response. Decis. Support Syst. 2010;50:304–315. [Google Scholar]
- 6.Rolland E., Patterson R.A., Ward K., Dodin B. Decision support for disaster management. Oper. Manag. Res. 2010;3:68–79. [Google Scholar]
- 7.Hasanzadeh H., Bashiri M. An efficient network for disaster management: model and solution. Appl. Math. Model. 2016;40:3688–3702. [Google Scholar]
- 8.Hu C., Liu X., Hua Y. A bi-objective robust model for emergency resource allocation under uncertainty. Int. J. Prod. Res. 2016;54:7421–7438. [Google Scholar]
- 9.Sahebjamnia N., Torabi S.A., Mansouri S.A. A hybrid decision support system for managing humanitarian relief chains. Decis. Support Syst. 2017;95:12–26. [Google Scholar]
- 10.Traub M., Bradt D.A., Joseph A.P. The surge capacity for people in emergencies (scope) study in australasian hospitals. Med. J. Aust. 2007;186:394–398. doi: 10.5694/j.1326-5377.2007.tb00971.x. [DOI] [PubMed] [Google Scholar]
- 11.Sheikhbardsiri H., Raeisi A.R., Nekoei-Moghadam M., Rezaei F. Surge capacity of hospitals in emergencies and disasters with a preparedness approach: a systematic review. Disaster Med. Public Health Prep. 2017;11:612–620. doi: 10.1017/dmp.2016.178. [DOI] [PubMed] [Google Scholar]
- 12.Bektas T. The multiple traveling salesman problem: an overview of formulations and solution procedures. Omega. 2006;34:209–219. [Google Scholar]
- 13.Laporte G. A concise guide to the traveling salesman problem. J. Oper. Res. Soc. 2010;61:35–40. [Google Scholar]
- 14.Campbell A.M., Vandenbussche D., Hermann W. Routing for relief efforts. Transport. Sci. 2008;42:127–145. [Google Scholar]
- 15.Wex F., Schryen G., Feuerriegel S., Neumann D. Emergency response in natural disaster management: allocation and scheduling of rescue units. Eur. J. Oper. Res. 2014;235:697–708. [Google Scholar]
- 16.Rodríguez-Espíndola O., Albores P., Brewster C. Disaster preparedness in humanitarian logistics: a collaborative approach for resource management in floods. Eur. J. Oper. Res. 2018;264:978–993. [Google Scholar]
- 17.Pillac V., Van Hentenryck P., Even C. A conflict-based path-generation heuristic for evacuation planning. Transp. Res. Part B Methodol. 2016;83:136–150. [Google Scholar]
- 18.Shahparvari S., Abbasi B., Chhetri P. Possibilistic scheduling routing for short-notice bushfire emergency evacuation under uncertainties: an australian case study. Omega. 2017;72:96–117. [Google Scholar]
- 19.Bruni M., Beraldi P., Khodaparasti S. A fast heuristic for routing in post-disaster humanitarian relief logistics. Transport. Res. Procedia. 2018;30:304–313. [Google Scholar]
- 20.Zhang S., Ruan X., Xia Y., Feng X. Foldable container in empty container repositioning in intermodal transportation network of belt and road initiative: strengths and limitations. Marit. Pol. Manag. 2018;45:351–369. [Google Scholar]
- 21.Schneider K., Nurre S.G. A multi-criteria vehicle routing approach to improve the compliance audit schedule for food banks. Omega. 2019;84:127–140. [Google Scholar]
- 22.Bertazzi L., Coelho L.C., De Maio A., Laganà D. A matheuristic algorithm for the multi-depot inventory routing problem. Transport. Res. E Logist. Transport. Rev. 2019;122:524–544. [Google Scholar]
- 23.Li D., Ding L., Connor S. When to switch? index policies for resource scheduling in emergency response. Prod. Oper. Manag. 2020;29:241–262. [Google Scholar]
- 24.Jung K.S., Pinedo M., Sriskandarajah C., Tiwari V. Scheduling elective surgeries with emergency patients at shared operating rooms. Prod. Oper. Manag. 2019;28:1407–1430. [Google Scholar]
- 25.Mahmoudi R., Shetab-Boushehri S.N., Hejazi S.R., Emrouznejad A., Rajabi P. A hybrid egalitarian bargaining game-dea and sustainable network design approach for evaluating, selecting and scheduling urban road construction projects. Transport. Res. E Logist. Transport. Rev. 2019;130:161–183. [Google Scholar]
- 26.Shi Y., Boudouh T., Grunder O. A robust optimization for a home health care routing and scheduling problem with consideration of uncertain travel and service times. Transport. Res. E Logist. Transport. Rev. 2019;128:52–95. [Google Scholar]
- 27.Bababeik M., Khademi N., Chen A. Increasing the resilience level of a vulnerable rail network: the strategy of location and allocation of emergency relief trains. Transport. Res. E Logist. Transport. Rev. 2018;119:110–128. [Google Scholar]
- 28.Wu X., Cao Y., Xiao Y., Guo J. Finding of urban rainstorm and waterlogging disasters based on microblogging data and the location-routing problem model of urban emergency logistics. Ann. Oper. Res. 2018:1–32. [Google Scholar]
- 29.Zhu L., Gong Y., Xu Y., Gu J. Emergency relief routing models for injured victims considering equity and priority. Ann. Oper. Res. 2018:1–34. [Google Scholar]
- 30.Caunhye A.M., Nie X., Pokharel S. Optimization models in emergency logistics: a literature review. Soc. Econ. Plann. Sci. 2012;46:4–13. [Google Scholar]
- 31.Galindo G., Batta R. Review of recent developments in or/ms research in disaster operations management. Eur. J. Oper. Res. 2013;230:201–211. [Google Scholar]
- 32.Özdamar L., Ertem M.A. Models, solutions and enabling technologies in humanitarian logistics. Eur. J. Oper. Res. 2015;244:55–65. [Google Scholar]
- 33.Zhou L., Wu X., Xu Z., Fujita H. Emergency decision making for natural disasters: an overview. Int. J. Disaster Risk Reduct. 2018;27:567–576. [Google Scholar]
- 34.Haghani A., Oh S.C. Formulation and solution of a multi-commodity, multi-modal network flow model for disaster relief operations. Transport. Res. Pol. Pract. 1996;30:231–250. [Google Scholar]
- 35.Özdamar L., Ekinci E., Küçükyazici B. Emergency logistics planning in natural disasters. Ann. Oper. Res. 2004;129:217–245. [Google Scholar]
- 36.Chang M.S., Tseng Y.L., Chen J.W. A scenario planning approach for the flood emergency logistics preparation problem under uncertainty. Transport. Res. E Logist. Transport. Rev. 2007;43:737–754. [Google Scholar]
- 37.Balcik B., Beamon B.M., Smilowitz K. Last mile distribution in humanitarian relief. J. Intell. Transport. Syst. 2008;12:51–63. [Google Scholar]
- 38.Huang K., Jiang Y., Yuan Y., Zhao L. Modeling multiple humanitarian objectives in emergency response to large-scale disasters. Transport. Res. E Logist. Transport. Rev. 2015;75:1–17. [Google Scholar]
- 39.Zokaee S., Bozorgi-Amiri A., Sadjadi S.J. A robust optimization model for humanitarian relief chain design under uncertainty. Appl. Math. Model. 2016;40:7996–8016. [Google Scholar]
- 40.Falasca M., Zobel C. An optimization model for volunteer assignments in humanitarian organizations. Soc. Econ. Plann. Sci. 2012;46:250–260. [Google Scholar]
- 41.Lassiter K., Khademi A., Taaffe K.M. A robust optimization approach to volunteer management in humanitarian crises. Int. J. Prod. Econ. 2015;163:97–111. [Google Scholar]
- 42.Schryen G., Rauchecker G., Comes T. Resource planning in disaster response. Bus. Inf. Syst. Eng. 2015;57:243–259. [Google Scholar]
- 43.Bodaghi B., Palaneeswaran E. Proceedings of the International Conference on Industrial Engineering and Operations Management, Detroit, Michigan. 2016. An optimization model for scheduling emergency operations with multiple teams; pp. 436–442. [Google Scholar]
- 44.Shahparvari S., Bodaghi B. Risk reduction for distribution of the perishable rescue items; a possibilistic programming approach. Int. J. Disaster Risk Reduct. 2018;31:886–901. [Google Scholar]
- 45.Huang M., Smilowitz K., Balcik B. Models for relief routing: equity, efficiency and efficacy. Transport. Res. E Logist. Transport. Rev. 2012;48:2–18. [Google Scholar]
- 47.Caunhye A.M., Zhang Y., Li M., Nie X. A location-routing model for prepositioning and distributing emergency supplies. Transport. Res. E Logist. Transport. Rev. 2016;90:161–176. [Google Scholar]
- 48.Bodaghi B., Palaneeswaran E., Shahparvari S., Mohammadi M. Probabilistic allocation and scheduling of multiple resources for emergency operations; a victorian bushfire case study. Comput. Environ. Urban Syst. 2020;81:101479. [Google Scholar]
- 49.Repoussis P.P., Tarantilis C.D., Ioannou G. The open vehicle routing problem with time windows. J. Oper. Res. Soc. 2007;58:355–367. [Google Scholar]
- 50.MirHassani S., Abolghasemi N. A particle swarm optimization algorithm for open vehicle routing problem. Expert Syst. Appl. 2011;38:11547–11551. [Google Scholar]
- 51.Yu S., Ding C., Zhu K. A hybrid ga–ts algorithm for open vehicle routing optimization of coal mines material. Expert Syst. Appl. 2011;38:10568–10573. [Google Scholar]
- 52.Fleszar K., Osman I.H., Hindi K.S. A variable neighbourhood search algorithm for the open vehicle routing problem. Eur. J. Oper. Res. 2009;195:803–809. [Google Scholar]
- 53.BañOs R., Ortega J., Gil C., FernáNdez A., De Toro F. A simulated annealing-based parallel multi-objective approach to vehicle routing problems with time windows. Expert Syst. Appl. 2013;40:1696–1707. [Google Scholar]
- 54.Tang J., Ma Y., Guan J., Yan C. A max–min ant system for the split delivery weighted vehicle routing problem. Expert Syst. Appl. 2013;40:7468–7477. [Google Scholar]
- 55.Tarantilis C., Kiranoudis C. Distribution of fresh meat. J. Food Eng. 2002;51:85–91. [Google Scholar]
- 56.Liu R., Jiang Z., Geng N. A hybrid genetic algorithm for the multi-depot open vehicle routing problem. OR spectrum. 2014;36:401–421. [Google Scholar]
- 57.Pichka K., Ashjari B., Ziaeifar A., Nickbeen P. Open vehicle routing problem optimization under realistic assumptions. Int. J. Res. Ind. Eng. 2014;3:46–55. [Google Scholar]
- 58.Duque P.A.M., Dolinskaya I.S., Sörensen K. Network repair crew scheduling and routing for emergency relief distribution problem. Eur. J. Oper. Res. 2016;248:272–285. [Google Scholar]
- 59.Fontem B., Melouk S.H., Keskin B.B., Bajwa N. A decomposition-based heuristic for stochastic emergency routing problems. Expert Syst. Appl. 2016;59:47–59. [Google Scholar]
- 60.Osman M.S., Ram B. Routing and scheduling on evacuation path networks using centralized hybrid approach. Comput. Oper. Res. 2017;88:332–339. [Google Scholar]
- 61.Faiz T.I., Vogiatzis C., Noor-E-Alam M. A column generation algorithm for vehicle scheduling and routing problems. Comput. Ind. Eng. 2019;130:222–236. [Google Scholar]
- 62.Moreno A., Munari P., Alem D. A branch-and-benders-cut algorithm for the crew scheduling and routing problem in road restoration. Eur. J. Oper. Res. 2019;275:16–34. [Google Scholar]
- 63.Bélanger V., Ruiz A., Soriano P. Recent optimization models and trends in location, relocation, and dispatching of emergency medical vehicles. Eur. J. Oper. Res. 2019;272:1–23. [Google Scholar]
- 64.Knight V.A., Harper P.R., Smith L. Ambulance allocation for maximal survival with heterogeneous outcome measures. Omega. 2012;40:918–926. [Google Scholar]
- 65.Liu D., Han J., Zhu J. Vehicle routing for medical supplies in large-scale emergencies. Lecture Notes Oper. Res. 2007;8:412–419. [Google Scholar]
- 66.Ceselli A., Righini G., Tresoldi E. Combined location and routing problems for drug distribution. Discrete Appl. Math. 2014;165:130–145. [Google Scholar]
- 67.Majzoubi F. University of Louisville; 2014. A Mathematical Programming Approach for Dispatching and Relocating EMS Vehicles. Ph.D. thesis. [Google Scholar]
- 68.Tang P., Zhu S. Emergency logistics distribution vrp based on differential evolution optimization. J. Software Eng. 2015;9:105–113. [Google Scholar]
- 69.Zhao J., Guo Y., Duan X. Dynamic path planning of emergency vehicles based on travel time prediction. J. Adv. Transport. 2017;2017 [Google Scholar]
- 70.Ciancio C., Laganà D., Musmanno R., Santoro F. An integrated algorithm for shift scheduling problems for local public transport companies. Omega. 2018;75:139–153. [Google Scholar]
- 71.Li T., Wang X. Logistics: the Emerging Frontiers of Transportation and Development in China. 2009. Study on the vehicle routing problem based on improved ga-greedy algorithm; pp. 2814–2822. [Google Scholar]
- 72.Almutairi A. University of Portsmouth; 2016. Sim-heuristic Algorithms for Robust Vehicle Routing Problem with Stochastic Demand. Ph.D. thesis. [Google Scholar]
- 73.Bettinelli A., Santini A., Vigo D. A real-time conflict solution algorithm for the train rescheduling problem. Transp. Res. Part B Methodol. 2017;106:237–265. [Google Scholar]
- 74.Kritikos M., Ioannou G. A greedy heuristic for the capacitated minimum spanning tree problem. J. Oper. Res. Soc. 2017;68:1223–1235. [Google Scholar]
- 75.Baptista F., Tavares J. v INEGI, Panorama sociodemográfico de Morelos. México. Springer; 2009. Bio-inspired algorithms for the vehicle routing problem; pp. 35–40. [Google Scholar]
- 76.Zhang Z., Liu M., Lim A. A memetic algorithm for the patient transportation problem. Omega. 2015;54:60–71. [Google Scholar]
- 77.Zheng Y.J., Chen S.Y., Ling H.F. Evolutionary optimization for disaster relief operations: a survey. Appl. Soft Comput. 2015;27:553–566. [Google Scholar]
- 78.Jaw J.J., Odoni A.R., Psaraftis H.N., Wilson N.H. A heuristic algorithm for the multi-vehicle advance request dial-a-ride problem with time windows. Transp. Res. Part B Methodol. 1986;20:243–257. [Google Scholar]
- 79.Weng M.X., Lu J., Ren H. Unrelated parallel machine scheduling with setup consideration and a total weighted completion time objective. Int. J. Prod. Econ. 2001;70:215–226. [Google Scholar]
- 80.Ramchurn S.D., Polukarov M., Farinelli A., Truong C., Jennings N.R. vol. 3. International Foundation for Autonomous Agents and Multiagent Systems; 2010. Coalition formation with spatial and temporal constraints; pp. 1181–1188. (Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems). [Google Scholar]
- 81.Wex F., Schryen G., Neumann D. A fuzzy decision support model for natural disaster response under informational uncertainty. Int. J. Inf. Syst. Crisis Response Manag. 2012;4:23–41. [Google Scholar]
- 82.Abdullah S., Sabar N.R., Nazri M.Z.A., Ayob M. An exponential monte-carlo algorithm for feature selection problems. Comput. Ind. Eng. 2014;67:160–167. [Google Scholar]
- 83.Al-Harthei H., Toth V.T., Garib A., Mahmoud S.A. 2017. Efficient real-time allocation of patrol cars in traffic management; pp. 1–8. (Proceedings of the 2nd World Congress on Civil, Structural, and Environmental Engineering (CSEEÃ-17)). ICTE–105. [Google Scholar]
- 84.Wu F., Sioshansi R. A two-stage stochastic optimization model for scheduling electric vehicle charging loads to relieve distribution-system constraints. Transp. Res. Part B Methodol. 2017;102:55–82. [Google Scholar]
- 85.Baker B.M., Ayechew M. A genetic algorithm for the vehicle routing problem. Comput. Oper. Res. 2003;30:787–800. [Google Scholar]
- 86.Okhrin I., Richter K. Vehicle routing problem with real-time travel times. Int. J. Veh. Inf. Commun. Syst. 2009;2:59–77. [Google Scholar]
- 87.Zidi K., Mguis F., Borne P., Ghedira K. Distributed genetic algorithm for disaster relief planning. Int. J. Comput. Commun. Contr. 2013;8:769–783. [Google Scholar]
- 88.Mguis F., Zidi K., Ghedira K., Borne P. Distributed approach for vehicle routing problem in disaster case. IFAC Proc. Vol. 2012;45:353–359. [Google Scholar]
- 89.Qin J., Ye Y., Cheng B.r., Zhao X., Ni L. The emergency vehicle routing problem with uncertain demand under sustainability environments. Sustainability. 2017;9:288. [Google Scholar]
- 90.Özdamar L., Demir O. A hierarchical clustering and routing procedure for large scale disaster relief logistics planning. Transport. Res. E Logist. Transport. Rev. 2012;48:591–602. [Google Scholar]
- 91.He Y., Wen J., Huang M. 2015 11th International Conference on Computational Intelligence and Security (CIS), IEEE. 2015. Study on emergency relief vrp based on clustering and pso; pp. 43–47. [Google Scholar]
- 92.Vargas-Florez J., Medina-Rodríguez R., Alva-Cabrera R. Information Management and Big Data. Springer; 2015. A clustering optimization approach for disaster relief delivery: a case study in lima-Peru; pp. 69–80. [Google Scholar]
- 93.Gharib Z., Bozorgi-Amiri A., Tavakkoli-Moghaddam R., Najafi E. A cluster-based emergency vehicle routing problem in disaster with reliability. Sci. Iran. Trans. E, Ind. Eng. 2018;25:2312–2330. [Google Scholar]
- 94.Penna P.H.V., Santos A.C., Prins C. Vehicle routing problems for last mile distribution after major disaster. J. Oper. Res. Soc. 2018;69:1254–1268. [Google Scholar]
- 95.Arnold F., Sã¶rensen K. What makes a vrp solution good? the generation of problem-specific knowledge for heuristics. Comput. Oper. Res. 2018 [Google Scholar]
- 96.Bellur U., Kulkarni R. IEEE International Conference on Web Services (ICWS 2007), IEEE. 2007. Improved matchmaking algorithm for semantic web services based on bipartite graph matching; pp. 86–93. [Google Scholar]
- 97.Jiang W. Advances in Computer Communication and Computational Sciences. Springer; 2019. Analysis and discussion of radar construction problems with greedy algorithm; pp. 303–312. [Google Scholar]
- 98.Shahparvari S., Abbasi B., Chhetri P., Abareshi A. Transportation Research Part D: Transport and Environment; 2017. Fleet Routing and Scheduling in Bushfire Emergency Evacuation: A Regional Case Study of the Black Saturday Bushfires in australia. [Google Scholar]
- 99.Mardle S., Pascoe S. An overview of genetic algorithms for the solution of optimisation problems. Comput. High. Educ. Econ. Rev. 1999;13:16–20. [Google Scholar]
- 100.BarbarosoÄŸlu G., Özdamar L., Çevik A. An interactive approach for hierarchical analysis of helicopter logistics in disaster relief operations. Eur. J. Oper. Res. 2002;140:118–133. [Google Scholar]
- 101.Perez-Ortega J., Almanza-Ortega N.N., Romero D. Balancing effort and benefit of k-means clustering algorithms in big data realms. PloS One. 2018;13:1–19. doi: 10.1371/journal.pone.0201874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Bodaghi B. SWINBURNE UNIVERSITY OF TECHNOLOGY Melbourne, Australia; 2017. Optimisation Approaches for Scheduling Disaster Emergency Operations with Multiple Resources. Ph.D. thesis. 2017. [Google Scholar]
- 103.Huber-Wagner S., Lefering R., Qvick L.M., Körner M., Kay M.V., Pfeifer K.J., Reiser M., Mutschler W., Kanz K.G., on Polytrauma of the German Trauma Society, W.G. Effect of whole-body ct during trauma resuscitation on survival: a retrospective, multicentre study. Lancet. 2009;373:1455–1461. doi: 10.1016/S0140-6736(09)60232-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.