Abstract
Diffusion tensor imaging (DTI) based group analysis has helped uncover the impact of white matter injuries in a wide range of studies involving subjects from preterm neonates to adults. The application of these methods to fetal cohorts, however, has been hampered by the challenging nature of in utero fetal DTI caused by unconstrained fetal motion, limited scan times, and limited signal-to-noise ratio. We present a framework that addresses these issues to systematically evaluate group differences in fetal cohorts. A motion-robust DTI computation approach with a new unbiased DTI template construction method is unified with kernel-regression in age and tensor-specific registration to normalize DTI volumes in an unbiased space. A robust statistical approach is used to map region-specific group differences to the medial representation of the tracts of interest. The proposed approach was applied and showed, for the first time, differences in local white matter fractional anisotropy based on in utero DTI of fetuses with congenital heart disease and age-matched healthy controls. This paper suggests the need for fetal-specific pipelines to be used for DTI-based group analysis involving fetal cohorts.
1. Introduction
Diffusion Tensor Imaging (DTI) is widely used to image brain microstructure and to compare groups of subjects and patients based on the diffusion properties of the white matter (WM). Unlike ex utero imaging where methods such as immobilization devices or sedation can be employed to limit motion, in utero fetal DTI is hampered by motion, low SNR, and fewer gradient directions applied to minimize maternal discomfort and the adverse impact of fetal motion.
To account for fetal motion, DTI computation methods that utilize volume-to-volume registration (VVR) and slice-to-volume registration (SVR) have been proposed [5,6,9]. Compared to VVR-based methods, SVR methods have shown more accurate reconstruction of the microstructure in moving subjects [5,9]. The resulting DTIs, however, would still be noisier than those obtained from motion-free scans since a large number of fetal DWI scans or slices are dropped and the remaining motion-corrected slices are interpolated. This raises challenges and a critical need for robust and unbiased processing of fetal DTI for group analysis. Moreover, in addition to the data being scarce in this domain, there are no publicly available in utero fetal DTI templates or atlases. As a result, DTI-based group comparison of fetal cohorts remains largely unreported.
In related work, the Tract-Based Spatial Statistics (TBSS) approach [13] has been used in neonatal studies to evaluate impact of preterm birth on WM development [2], among many other applications. Small region-of-interest (ROI) based comparisons, though frequently reported, are inadequate for generalization over the tracts of interest and are prone to operator-induced placement errors. An improved ROI-based strategy called Tract-Specific Analysis (TSA) [15] that considers entire tract of interest has also been proposed and recently applied to preterm cohorts [11].
In this study, we use an outlier-robust motion-tracking based SVR approach for fetal DTI computation, and tensor-specific registration to construct unbiased kernel-regressed templates for TSA. Kernel-regression in age is necessary given the fast changing shape of the fetal brain and the proposed template construction approach was needed as part of the group analysis pipeline because no existing DTI template construction approaches integrate kernel-regression in age with tensor-specific registration. Our approach accounts for gestational age (GA) and computes an unbiased template; this is followed by GA-adjusted group statistical TSA. The proposed approach was applied to evaluate group differences, for the first time, between in utero congenital heart disease (CHD) and healthy control fetuses. The results show differences that extend the previous findings in neonates and adolescents [10,12] suggesting that WM alterations in CHD start in-utero as early as 28 weeks GA.
2. Methods
Given multiple motion-corrupted, low-SNR diffusion-weighted imaging (DWI) volumes of fetuses in different planes, we aim to study differences present in the DTIs of fetal cohorts. A DTI-based group analysis pipeline including TBSS, ROI-based, and TSA comprises: (1) DTI computation in a standard space, (2) registration of subject DTIs with an existing or study-specific template, and (3) statistical analysis following DTI volume normalization. Our proposed pipeline for fetal brain DTI group analysis comprising these three steps is shown in Fig. 1.
Fig. 1.
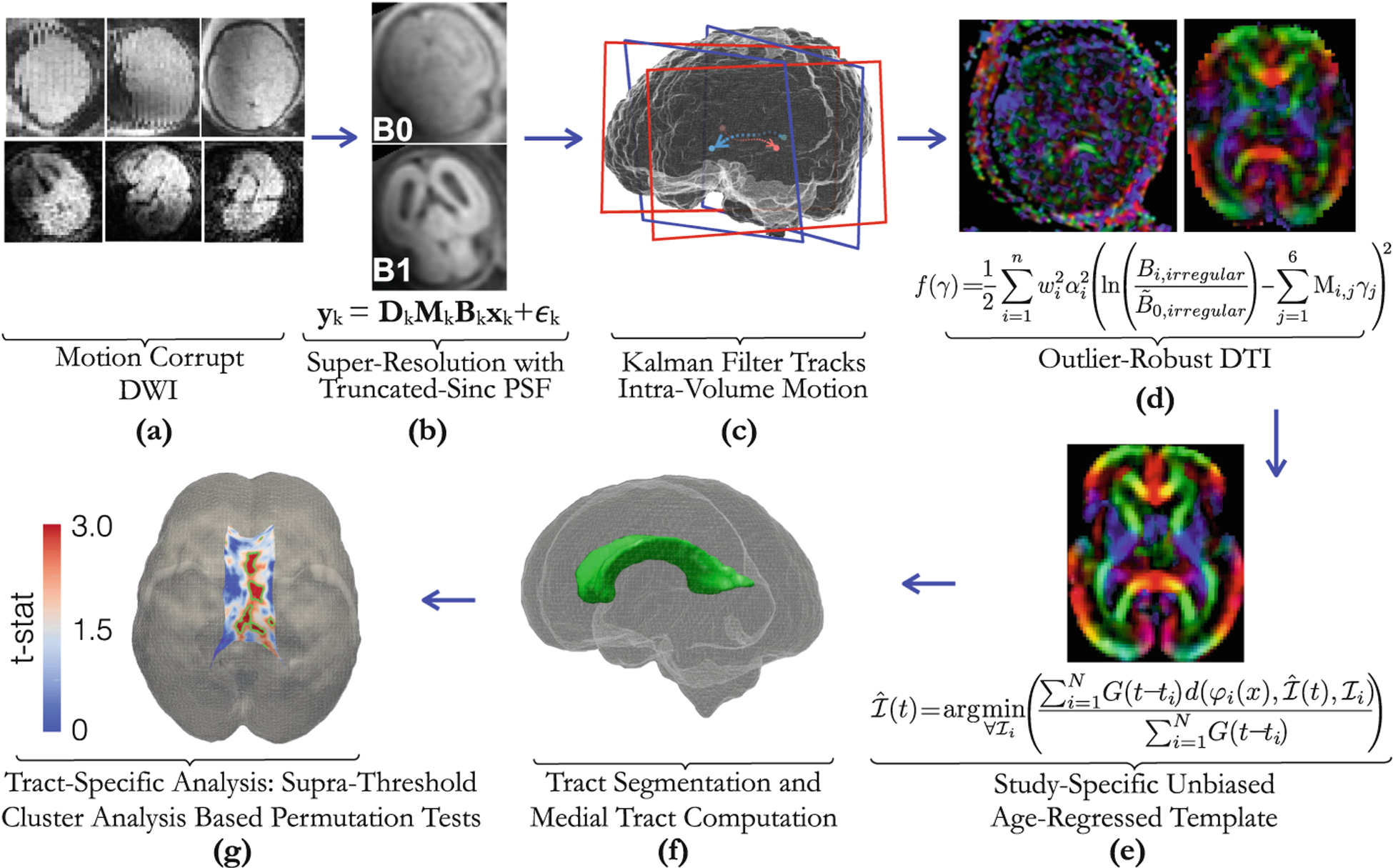
Proposed fetal brain DTI group analysis pipeline: The acquired DWI data (often multi-planar), (a) is used to compute composite super-resolved B0 and B1 images (b). Motion-tracking based slice-to-volume registration (c) is used to map b = 0 and b ≠ 0 slices to standard space [9] where DTI (d) is computed directly from motion-corrected data (shown next to a color FA image obtained directly from the scanner without motion correction). Template construction (e) provides an unbiased spatial frame where group statistical differences (f) are computed and localized (g).
2.1. DWI Processing and DTI Computation
Fetal DTIs are computed using a motion and outlier-robust method that computes tensors using motion-corrected diffusion data in a standard space. The slices from b = 0 and b ≠ 0 images are first used to compute composite B0 and B1 images using an SVR-based super-resolution reconstruction approach with a truncated Sinc point spread function (PSF) [7]. A rigid transformation is computed between the composite B0 and B1 images and the T2w image of the fetal brain reconstructed using the SVR approach. Slice-level motion correction is performed for the b ≠ 0 slices through a robust registration-based state-space motion tracking algorithm [9]. Using the slice to B0, B0 to T2w, and T2w to standard space transformations, each slice from b = 0 and b ≠ 0 image set is rigidly mapped to the standard space. A constrained weighted locally linear least squares method is used to fit single tensor per voxel directly from scattered data, obtained using slice-level motion-corrected DWI, with a Gaussian PSF [9].
2.2. Study-Specific Template and Normalization
To spatially normalize DTI volumes to an unbiased space, an age-regressed template is computed by applying a large deformation diffeomorphic metric mapping that optimizes a tensor metric to register DTIs, as described below.
DTI Registration:
Registration of two DTIs is defined as a mapping of a manifold under a transformation that lies in the infinite-dimensional space of diffeomorphism . A diffeomorphism exists with a smooth inverse and satisfies the Lagrangian ordinary differential equation: where υt(φ(x)) ∈ R3 represents smooth velocity fields that are integrated forward in time to compute the transformations; a corresponding inverse φ−1(x) can be computed by integrating velocity fields backwards in time. The image registration cost function (ξ) can thus be defined as follows:
| (1) |
where Ψ is a matching metric computed between the fixed DTI and the moving DTI , and D(φ(x)) is a metric on the transformation that is formulated based on the exact model of deformation used to approximate diffeomorphism and is used in 1 to regularize ξ. We choose Ψ to be a tensor similarity metric, i.e. the Euclidean Distance Squared between Deviatoric tensors (DDS).
Template Construction:
Since the anatomic variability among fetuses and across age cannot be characterized in Hilbert space, the set of DTIs are considered time-indexed observations in a Riemannian manifold . A time-regressed template at time t = τ can be computed as an empirical Fréchet mean, under the distribution of manifold-valued DTIs, using generalized Nadaraya-Watson kernel regression in age [4]. To do this, we use a minimum-distance template computation approach: Given N DTIs denoted as , we express the template computation at time t as the following minimization problem:
| (2) |
where for t ≤ κ and 0 otherwise, κ is a time bandwidth parameter; and is a DTI matching metric. This minimization problem is solved using the iterative algorithm described below:
Initialize and .
Initialize using a 3D rigid and affine transform.
Estimate φi(x): time domain is discretized into T steps and φi(x) is computed by integrating velocity fields computed at each time step t(t = 1…T).
Compute optimal .
Update .
Repeat steps 3 to 5 until φi(x) and converge (change less than thresholds).
Spatial Normalization:
The DTIs are registered to the computed template using the tensor-specific approach. The rigid and affine transforms are computed using normalized mutual information (NMI) metric and used to initialize the nonrigid transform. All transformations are applied to DTIs in a single step.
2.3. Statistical Analysis
We apply TSA for group analysis, which is based on a general linear model and evaluates the distribution of DTI scalars over medial template of interest [16]. TSA was shown to be more robust to errors in registration than other group comparison methods such as TBSS [11]. To perform TSA, a tract of interest is segmented in the template space and its medial template is computed using continuous medial representation [14]. The spatially normalized DTIs are sampled along normals to the medial template and the DTI-scalars are computed. The data from cohorts being compared are projected on the medial template and compared using permutation-based non-parametric suprathreshold cluster analysis that controls the family-wise error rate (FWER). This analysis reveals clusters that are deemed significant at cluster-size threshold α under the null hypothesis. A t-statistic threshold is used to construct the null distribution.
3. Application and Results
Application:
We used our framework to compare a cohort of healthy fetuses (control) to a cohort of fetuses identified with congenital heart disease (CHD). Fetal MRIs were acquired in utero at Boston Children’s Hospital using an Institutional Review Board approved protocol, with informed consent from pregnant women volunteers. Subjects with at least 2 DWI scans without extreme motion-induced or distortion artifacts were chosen for this study. The MRIs were acquired on 3T Siemens Skyra scanners without maternal sedation or breath-hold. Each scan session included multiple orthogonal T2 HASTE scans using TR/TE = 1.4–2 s/100–120 ms, 0.9–1.1 mm in-plane and 2 mm out-of-plane resolution with 2/4-slice interleaved acquisition, and DWI comprising 2–4 scans in axial or coronal planes with respect to the fetal head with 1 or 2 b = 0 s/mm2 images, and 12-direction b = 500 s/mm2 acquired using TR/TE = 3–4 s/60 ms, 2 mm in-plane and 2–4 mm out-of-plane resolution. Total imaging time was <45 min (3–10 min for DWI).
Processing:
We computed DTIs for 8 control and 9 CHD subjects scanned at GAs between 26 week 4 days (26w4d) and 30w0d. A template of control DTIs was computed at τ = 28w3d with 1.2 mm isotropic resolution. The time-bandwidth κ was set to 1w6d and φ(x) was computed using T = 6. Ten iterations of the template construction algorithm were completed to compute with error minimization in (1) solved at step 3. We used DTITK [17] for tensor-to-tensor registration. The final template was computed by composing linear and non-linear transformations and transforming DTIs in a single step to reduce interpolation error. All DTIs were non-linearly registered to this template and subsequently transformed to the template space in one step.
Tract Medial Representation:
In this study, we evaluated the differences in Corpus Callosum (CC) – a large tract that develops early in the 1st trimester. Since the cortical projections in late 2nd trimester are early in their development, we only segmented the anterio-posteriorly oriented region of the CC. Figure 2 shows the segmented CC region along with cmrep-fit [14] computed medial template.
Fig. 2.
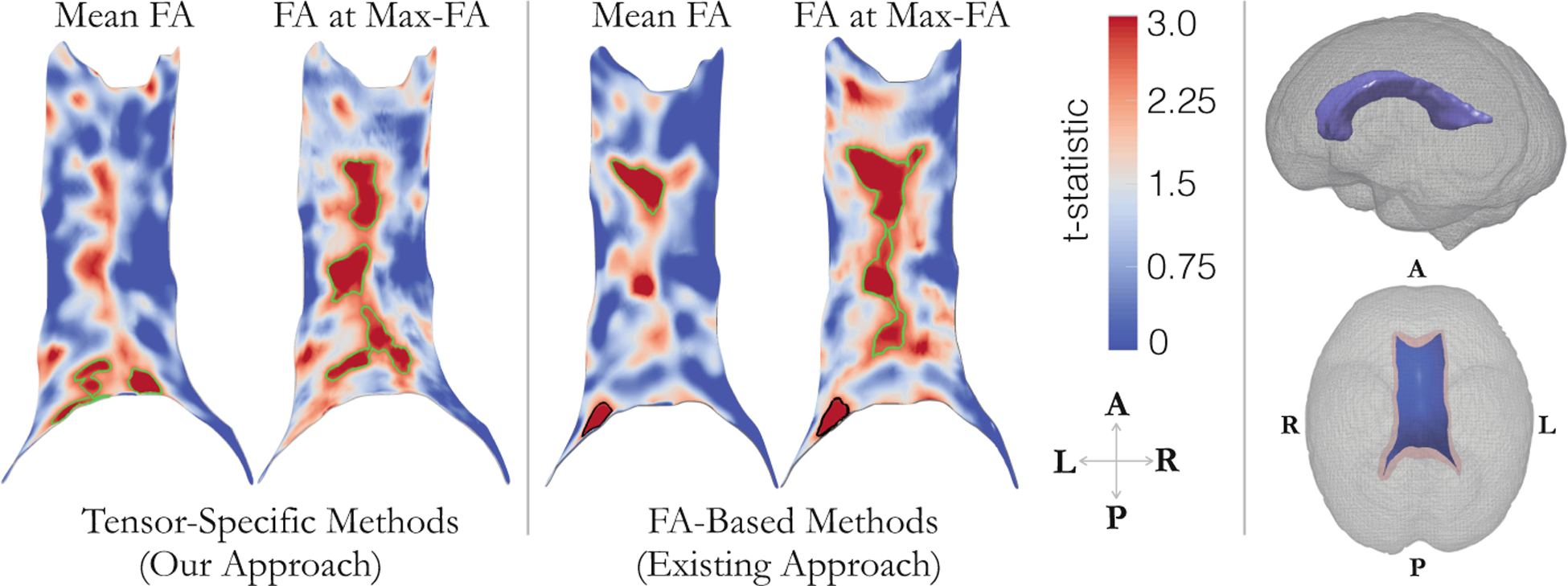
TSA: Significant clusters (green edge) in t-statistic maps computed over the CC medial template for mean-FA and max-FA comparisons in medial templates obtained using tensor-based (proposed) and FA-based (existing) pipelines. These results suggest that the FA near splenium and the body of CC is likely lower in subjects suffering from CHD in comparison to the controls within the clusters shown. FA-based method missed the differences near splenium observed using tensor-specific approach. The segmented CC region (top) and fitted (cmrep) medial template (bottom) is shown in the right.
Statistical Analysis:
As described earlier, we used permutation tests for group comparison. A contrast of [1 −1 0] was used to compare control against CHD group while adjusting for age as a covariate. Clusters were obtained from the t-statistic image computed for the contrast using t-threshold = 2.62. Permutation tests were done with number of permutations N = 10000, and α = 0.05. Clusters computed for true labeling of the data larger than αN percentile of the null distribution were marked significant. Summary statistics of DTI-derived metrics over CC comparing control and CHD groups have been shown in Table 1. Using TSA, projections of group differences in DTI scalars on the CC medial template were computed. We evaluated differences using mean and max-FA projections.
Table 1.
Summary statistics of the DTI-derived scalars: significant differences in mean of DTI scalars between control and CHD groups were observed.
| Control(μa ± σa) | CHD (μb ± σb) | p-value (Ho : μa = μb) | 95% CI (μa − μb) | |
|---|---|---|---|---|
| FA | 0.25 ± 0.08 | 0.21 ± 0.07 | <1e-4 | (0.039, 0.048) |
| MD | 1.41 ± 0.16 | 1.44 ± 0.16 | <1e-4 | (−0.036, −0.017) |
| AD | 1.82 ± 0.20 | 1.77 ± 0.20 | <1e-4 | (0.033, 0.058) |
| RD | 1.20 ± 0.17 | 1.27 ± 0.17 | <1e-4 | (−0.073, −0.052) |
The summary statistics in Table 1 were computed using the control and CHD DTI templates. Consistent with a previous study of neonates [10], we observed that in comparison to control group, CHD group exhibited lower FA and AD but higher MD and RD. This observation suggests that the CC tracts in control group were likely more mature than the CC tracts in CHD group, as it has been shown [3] that brain maturation results in increased FA and reduced MD in CC.
In TSA, we found significant clusters (encircled by green line, Fig. 2) only in FA projections over the medial template along the body of the CC and near the splenium using max-FA projection, and in the splenium using mean projection. For comparison, results obtained by using existing FA-based registration and template construction methods have been shown as well. FA maps from DTIs were computed and used to construct an FA template that was registered to the FA map of the DTI template computed using our method. Linear and non-linear transformations from FA registrations were applied in one step to DTIs. ANTS was used for FA-based processing [1] and TSA was applied exactly as described previously. Only 1 large cluster was found significant in comparisons using the FA-based approach in the body of the CC. Compared to the proposed approach, FA-based approach results in larger clusters during permutation tests and leads to larger threshold for significance for true labeling of the data. This results in smaller, more focal differences to be missed; the differences near splenium observed using the proposed pipeline were missed by the FA-based approach even though the t-statistic image shows presence of hyper-intense clusters.
The posterior region of the CC (including splenium) has been reported to develop slower than the anterior region in 2nd trimester of pregnancy [6]. One hypothesis to explain these results is that the altered cardiac physiology of CHD results in impaired oxygenation and nutrient delivery to the developing brain, leading to alterations in the typical trajectory of microstructural development. While similar observations were made in a recent study that reported migrating neurons were delayed in CHD neonates [8], these differences were not studied by in utero DTI. We present the first evidence to warrant further studies using DWI to investigate altered brain development in fetuses with CHD and provide a unique, unified framework that addresses many of the challenges of fetal DTI.
4. Conclusion
We present comprehensive methods to evaluate tract-specific group differences within the developing fetal brain. DTIs reconstructed using an outlier-robust motion-tracking method were co-registered to construct a study-specific unbiased template incorporating kernel-regression in age. Tract-specific analysis (TSA) was applied to the volume-normalized fetal DTIs and permutation tests were used to evaluate the group differences between CHD and healthy in utero fetal cohort while adjusting for age. Significant clusters were found in the body and splenium of corpus callosum. The methods presented in this study enable group-comparison studies using in utero acquired DWI of the fetal brain.
Acknowledgments
This work was supported by the McKnight Foundation, the Fetal Health Foundation, NIH R01 EB018988, NIH K23NS101120, and Mend A Heart Foundation.
References
- 1.Avants BB, Epstein CL, Grossman M, Gee JC: Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal 12(1), 26–41 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ball G, et al. : An optimised tract-based spatial statistics protocol for neonates: applications to prematurity and chronic lung disease. NeuroImage 53(1), 94–102 (2010) [DOI] [PubMed] [Google Scholar]
- 3.Braga RM, et al. : Development of the corticospinal and callosal tracts from extremely premature birth up to 2 years of age. PLoS ONE 10(5), 1–15 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Davis BC, Fletcher PT, Bullitt E, Joshi S: Population shape regression from random design data. Int. J. Comput. Vis 90, 255–266 (2010) [Google Scholar]
- 5.Fogtmann M, et al. : A unified approach to diffusion direction sensitive slice registration and 3-D DTI reconstruction from moving fetal brain anatomy. IEEE Trans. Med. Imaging 33(2), 272–289 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jiang S, et al. : Diffusion tensor imaging (DTI) of the brain in moving subjects: application to in-utero fetal and ex-utero studies. Mag. Reson. Med 62(3), 645–655 (2009) [DOI] [PubMed] [Google Scholar]
- 7.Kainz B, et al. : Fast volume reconstruction from motion corrupted stacks of 2D slices. IEEE Trans. Med. Imaging 34(9), 1901–1913 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kelly CJ, et al. : Impaired development of the cerebral cortex in infants with congenital heart disease is correlated to reduced cerebral oxygen delivery. Sci. Rep 7(1), 15088 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Marami B, et al. : Temporal slice registration and robust diffusion-tensor reconstruction for improved fetal brain structural connectivity analysis. NeuroImage 156, 475–488 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Miller SP, et al. : Abnormal brain development in newborns with congenital heart disease. New Engl. J. Med 357(19), 1928–1938 (2007) [DOI] [PubMed] [Google Scholar]
- 11.Pecheva D, et al. : A tract-specific approach to assessing white matter in preterm infants. NeuroImage 157, 675–694 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rollins CK, et al. : White matter microstructure and cognition in adolescents with congenital heart disease. J. Pediatr 165(5), 936–944 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Smith SM, et al. : Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage 31(4), 1487–1505 (2006) [DOI] [PubMed] [Google Scholar]
- 14.Yushkevich PA: Continuous medial representation of brain structures using the biharmonic PDE. NeuroImage 45(1), S99–S110 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yushkevich PA, Zhang H, Simon TJ, Gee JC: Structure-specific statistical mapping of white matter tracts. NeuroImage 41(2), 448–461 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang H, et al. : A tract-specific framework for white matter morphometry combining macroscopic and microscopic tract features. Med. Image Anal 14(5), 666–673 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang H, Yushkevich PA, Alexander DC, Gee JC: Deformable registration of diffusion tensor MR images with explicit orientation optimization. Med. Image Anal 10(5), 764–785 (2006) [DOI] [PubMed] [Google Scholar]


