The role of computational fluid dynamics tools on investigation of pathogen transmission: Prevention and control

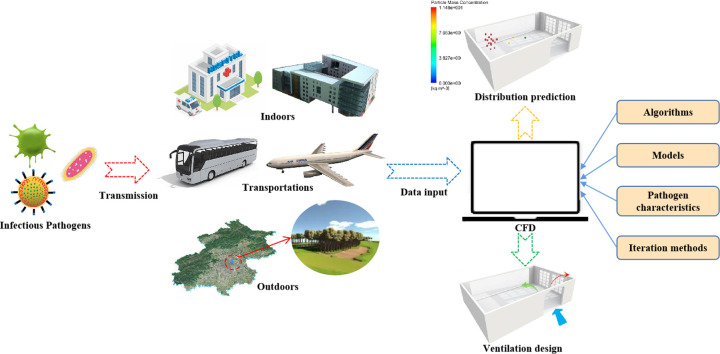
Abstract

Transmission mechanics of infectious pathogen in various environments are of great complexity and has always been attracting many researchers' attention. As a cost-effective and powerful method, Computational Fluid Dynamics (CFD) plays an important role in numerically solving environmental fluid mechanics. Besides, with the development of computer science, an increasing number of researchers start to analyze pathogen transmission by using CFD methods. Inspired by the impact of COVID-19, this review summarizes research works of pathogen transmission based on CFD methods with different models and algorithms. Defining the pathogen as the particle or gaseous in CFD simulation is a common method and epidemic models are used in some investigations to rise the authenticity of calculation. Although it is not so difficult to describe the physical characteristics of pathogens, how to describe the biological characteristics of it is still a big challenge in the CFD simulation. A series of investigations which analyzed pathogen transmission in different environments (hospital, teaching building, etc) demonstrated the effect of airflow on pathogen transmission and emphasized the importance of reasonable ventilation. Finally, this review presented three advanced methods: LBM method, Porous Media method, and Web-based forecasting method. Although CFD methods mentioned in this review may not alleviate the current pandemic situation, it helps researchers realize the transmission mechanisms of pathogens like viruses and bacteria and provides guidelines for reducing infection risk in epidemic or pandemic situations.

Graphical abstract

1. Introduction

At the end of 2019, cases of viral pneumonia with highly infectious were found in Wuhan, China. Within just several weeks, this disease has swept right through Hubei province and spread to other cities and countries. This new and readily contagious virus named COVID-19 was the culprit of disease which has been already caused more than three thousand deaths in China rapidly. According to the last statistics provided by WHO, global cases of infection exceeded 19 million including more than 72 thousand deaths (WHO Coronavirus Disease (COVID-19), n.d.).

It is not the first time these epidemics or pandemics happened: SARS virus in 2003 caused 774 deaths (Yasui et al., 2014); Ebola Virus Disease lead to more than 11,000 deaths in the world during 2014–2016 (Prescott et al., 2017), etc. Several diseases caused by viruses have already be conquered like Smallpox vaccine was successfully created over 20 years (Weltzin et al., 2003), there are various kinds of viruses are remaining unknown and may bring the global crisis.

Eliminating the infectious source and controlling the transmission of the pathogen are the main methods to mitigate the infection risk. However, sometimes it is impossible to eliminate the source thoroughly while controlling its transmission is more practicable. The transmission routines of the pathogen can be various such as droplet transmission, airborne diffusion, and so on. Pathogens can even spread in wild waterfowl (Richard et al., 2013) and transport through aerosols. Generally, the fluid as air, water is the main media of pathogen transmission, investigating the mechanisms of pathogen spread in different fluid conditions is helpful for predicting the pathogen's distribution and controlling the infectious risk.

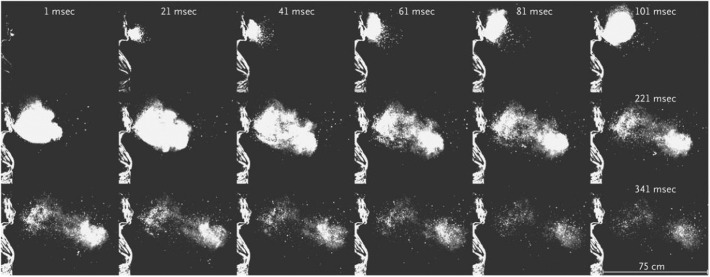
Pathogens can be always carried by droplets from coughing or sneezing and they can spread through the air rapidly. At MIT, Dr. Bourouiba et al. (Bourouiba and Bush, 2014) analyzed the spouted droplets from people's mouth. By using the Particle Image Velocimetry (PIV), they captured the transient spreading process of droplets and indicated that droplet can travel even 20 ft as the sneezing picture caught by high speed photography shown in Fig. 1 .

Fig. 1.

Transient motion of droplets with high speed (Richard et al., 2013).

It can be observed that the droplets spouted out from the mouth of the experimenter and generated a foggy form immediately. Small droplets were diluted in the air with million particles which may cause diseases within 6 m in theory. Moreover, in Busco et al. (2020) research work, the sneezing zone which may contain virus carriers like droplets or aerosols was modeled by using CFD method. It was proved in this investigation that the biomechanics of sneezing can be predicted by the signal generated from contractions or relaxations of head muscles; Dbouk and Drikakis (2020a) analyzed the effect of the wind speed on the transmission of coughing droplets and found 2 m social distance may not sufficiently prevent pathogen transmission.

As a carrier, droplets from sneezing play an important role in spreading pathogens and increasing attention have been paid on different mechanisms of it. Such as the analysis provided by Bhardwaj and Agrawal (2020), the drying time of respiratory droplets was predicted by calculating. Droplet volume, contact angle and environmental temperature were analyzed and the lifetime of droplets under those conditions was investigated. The evaporation of droplets will also be affected by the dust in the air, and this factor should be also considered in the future.

Different from other particles, pathogens are much smaller and their diameters are generally no more than 100 nm and their motion is largely affected by flowing air, hence it is difficult to analyze their trajectories directly in the atmospheric environment. With the development of computer science, a new method based on Computation Fluid Dynamics (CFD) can be used to solve this problem and it has been already well developed over the years.

By solving the nonlinear Navier-Stokes equation, CFD can be used to simulate complex fluid flow in various areas and it has been applied since the 1940s (Roache, 1972; Chu, 1979; Lomax et al., 2001). Based on finite difference method (FDM), finite element method (FEM), finite volume method (FVM), etc., CFD tools show a good performance on simulating various fluid in different engineering field such as the flight simulations (Boelens and O.J., n.d.; Cao and Ziwen, n.d.; Jia et al., n.d.), multiphase fluid in oil and gas industry (Peng et al., 2019a; Peng et al., 2019b; Liu et al., 2018; Su et al., 2019), etc. The applications of CFD method in the biological field and environmental field are also common. As early as in 1944, a new FORTRAN code of CFD which was based on transport equations was developed in order to simulate the diffusion case (Ginger, 1944) and in the next decades, an increasing number of investigations about air pollution, atmosphere environment and pathogen transmission can be found.

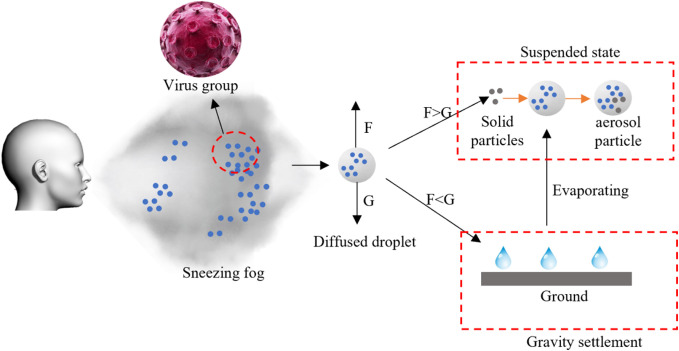
As mentioned above, the droplet can bring the pathogen into the airflow and hence cause infectious diseases due to the spread of it. Normally the droplet with pathogens is generated by coughing or sneezing from the infected and the procedure of droplets generated by sneezing is shown in Fig. 2 .

Fig. 2.

Sneezing fog and diffusion of droplets diffusion.

Sneezing fog with numerous droplets is generated firstly. Some larger droplets from the fog fell down after a short period due to the gravity; Other smaller droplets suspended in the air by virtue of buoyancy. Suspending droplet absorbed on small solid particles to gradually form aerosols. In addition, droplets deposited on the ground may rise into the air again as a result of the evaporation. The moving mechanisms of the droplet in this procedure are of great complexity and there are various researches about them can be found which are listed in Table 1 .

Table 1.

Investigations of droplet in different environment.

	Authors	CFD tools	Models
Droplets in fog	Pinilla et al. (2015)	STAR-CCM+	Lagrange
	Sun et al. (2020)	User-defined	Multiphase Eulerian
	Delele et al. (2012)	Ansys	Eddy-viscosity Turbulence models
Diffused droplets	Ryan et al. (n.d.)	DQMOM	Time-dependent Eulerian Model
	Padoin et al. (2015)	PRO/II	Turbulence model
	Sazhin et al. (2011)	Ansys (Fluent),	Coupled model
Aerosol particle	Albriet et al. (2010)	A CFD code	Modal aerosol model
	Hoque et al. (2011)	CFD-ACE+	ANN, HSS
	Igor and Novosselov (2014)	ADL	DES model

The impact of COVID-19 is global and the pandemic situation is closely related to the health of every individual. It does not mean that there is no way to prevent or control it effective vaccines are unavailable though. Understanding the transmission of infections such as COVID-19 in various media is of great importance. In this review, the principles of different CFD algorithms are described concisely and intuitively; Theories and applications of CFD in investigations of pathogen transmission are summarized. The objective of this research work is to indicate the important role of CFD method in analyzing pathogen transmission. Through summarizing various applications of CFD method, the transmission mechanism of pathogens and prevention methods are also concluded in this work.

2. Features of the CFD method

Three steps are necessary for numerical analysis by using CFD tools:

• (1)Generating the mesh model with high quality is the key to ensure the accuracy of calculation;
• (2)Boundary conditions are required to define variables at the boundary.
• (3)Different algorithms that can be selected in CFD determine the way of iteration.

This work carried out in this section is to summarize the feature of CFD from three aspects: simplification, algorithms diversity and maneuverability.

2.1. Simplification

Different from experimental methods, the CFD method based on mathematical models that can be operated on computers is effective and cost-saving. In numerical simulations, the pathogens are carried by small particles like solid particles or droplets can be defined by calculation models. Although the biological properties of the pathogen are complicated and various, the shape feature of the pathogen carrier is relatively simple to describe. In CFD, those particles can be defined as spheres, tetrahedrons, hexahedrons and even by the shape factor, then the pathogen transmission in different environmental fluids can be solved by utilizing multiphase models. Moreover, the transport species model can be also applied to simulations of it. In this model, the infectious pathogen in the air is defined as the pollutant source with a constant concentration (generally measured by the field experiment). Characteristics of fluid such as turbulence intensity, velocity are required in simulating the diffusion of “pollutant source”.

Generalized transportation is widely used in multiple source problems and it can be calculated by three exchange law:

Newton viscosity law used to describe the momentum exchange:

$$\tau =-\mu \frac{\partial u}{\partial x_j},\mathrm{N}/{\mathrm{m}}^2$$ (1)

Fourier heat transfer law used to describe the heat exchange:

$$\mathrm{q}=-\mu \frac{\partial T}{\partial x_j},\mathrm{W}/{\mathrm{m}}^2$$ (2)

Fick law used to describe the mass exchange: (J _1j is the source diffusion relative to coordinates, D ₁₂ is the diffusion coefficient between two sources)

$$J_{1j}=-D_{12}\frac{\partial {\rho }_1}{\partial x_j}=-D_{12}\frac{\partial \left(\rho Y_1\right)}{\partial x_j}=-\rho D_{12}\frac{\partial Y_1}{\partial x_j}$$ (3)

Reynolds transportation law calculates the source quantity in control volume at time “t”, which can be described as:

$$\varphi \left(t\right)={\int }_V\phi \left(x_i,t\right)\mathit{\delta V}={\int }_V\mathit{\phi \delta V}$$ (4)

Introducing the continuous equation:

$$\frac{\mathit{D\rho }}{\mathit{Dt}}+\rho \frac{\partial v_j}{x_j}=0$$ (5)

And Guass law (divergence law)

$${\int }_S{\rho }_S{V}_{\mathit{Sn}}\mathit{dS}={\int }_V\frac{\partial }{\partial x_j}\left({\rho }_S{V}_{\mathit{Sj}}\right)\mathit{\delta V}=-{\int }_V\frac{\partial }{\partial x_j}\left(\rho D_S\frac{\partial Y}{\partial x_j}\right)\mathit{\delta V}$$ (6)

Then, the improved transportation can be written as:

$$\frac{\partial \left(\rho Y_S\right)}{\partial t}+\frac{\partial }{\partial x_j}\left(\rho Y_S{v}_{\mathrm{j}}\right)=\frac{\partial }{\partial x_j}\left(\rho D_S\frac{\partial Y_S}{\partial x_j}\right)-w_s$$ (7)

This equation of CFD models can greatly describe the diffusion under different time and space, more, the convection term and chemical reaction are taken into account in the calculation.

Compared with defining pathogen carriers as particles in simulation, the transport species model is simpler with less time-consuming in calculation; Another advantage of the transport species model is that chemical reactions can be added in it. However, the multiphase simulation which describes the actual motion of particles is more accurate in simulating the distribution and transmission routes of pathogens.

Steps of simulating the particle are shown as follow:

Solving the particle's position in space:

$$\frac{\mathit{dx}}{\mathit{dt}}=u_p$$ (8)

Combining the balance equation of forces:

$$\frac{d\overline{u_p}}{\mathit{dt}}=F_D\left(\overline{u}-\overline{u_p}\right)+\frac{g\left({\rho }_p-\rho \right)}{{\rho }_p}+\overline{F}$$ (9)

Then, the equation can be written as the form shown below:

$$\frac{d{u}_p}{\mathit{dt}}=\frac{1}{{\tau }_p}\left(u-u_p\right)+\alpha$$ (10)

Considering the acceleration caused by forces except the drag force and solving the particle motion in each step by iterative calculation:

$$u_p^{n+1}=u^{n+1}+e^{-\frac{\mathit{\Delta t}}{{\tau }_p}}\left(u_p^n-u^n\right)-\alpha {\tau }_p\left(e^{-\frac{\mathit{\Delta t}}{{\tau }_p}}-1\right)$$ (11)

$$x_p^{n+1}=x_p^n+\mathit{\Delta t}\left(u_p^n+\alpha {\tau }_p\right)+{\tau }_p\left(1-e^{-\frac{\mathit{\Delta t}}{{\tau }_p}}\right)\left(u_p^n-u^n-\alpha {\tau }_p\right)$$ (12)

Besides, the Volume of Fluent (VOF) model performs well in simulating pathogen transmission, especially in the gas-liquid interface. In a control volume, the total value of each phase equals 100% and there are three situations in VOF:

If the volume fraction of “q” phase is α,then:

• (1)α = 0, no “q” phase in this cell;
• (2)α = 1, the cell is full of “q” phase;
• (3)0<α<1, interface between “q” phase and other phases can be found in the cell.

The momentum equation and the energy equation of VOF are determined and shared by each phase.

The momentum equation mainly depends on characteristics and volume fraction of each phase and it can be written as below:

$$\frac{\partial }{\partial t}\left(\rho \overrightarrow{v}\right)+\nabla •\left(\overrightarrow{v}\overrightarrow{v}\right)=\nabla •\left[\mu \left(\overrightarrow{v}+\nabla {\overrightarrow{v}}^T\right)\right]+\rho \overrightarrow{g}+\overrightarrow{F}$$ (13)

Energy equation of VOF can be written as:

$$\frac{\partial }{\partial t}\left(\mathit{\rho E}\right)+\nabla •\left[\overrightarrow{v}\left(\mathit{\rho E}+p\right)\right]=\nabla •\left[k_{\mathit{eff}}\nabla T-\sum _q\sum _j{h}_{j,q}{J}_{j,q}+\left({\tau }_{\mathit{eff}}•\overrightarrow{v}\right)\right]+s_h$$ (14)

K_eff is Effective Thermal Conductivity; J _j,q is diffusion flux of “J” phase in “q” phase while the h _j,q represents the enthalpy of it; S _h is the volume of the heating source defined by users. The energy was defined as a variable relating to the average quality in VOF:

$$E=\frac{{\sum }_{q=1}^n{\alpha }_q{\rho }_q{E}_q}{{\sum }_{q=1}^n{\alpha }_q{\rho }_q}$$ (15)

$$E_q=\mathit{hq}-\frac{p}{{\rho }_q}+\frac{v^2}{2}$$ (16)

More, Porous media has also been widely used to simulate the fluid flow or multiphase flow in porous materials. Porous Media was simplified to a special fluid zone with the source of flowing resistance. The momentum equation in Porous Media model includes two loss items: Viscous loss and inertia loss. The equation can be written as:

$$S_i=-\left(\sum _{j=1}^3{D}_{\mathit{ij}}\mu v_j+\frac{1}{2}\sum _{j=1}^3{C}_{\mathit{ij}}\rho |v|v_j\right)$$ (17)

Resistance characteristics in all directions are assumed the same, and the equation can be written as:

$$S_i=-\left(\frac{\mu }{\alpha }{v}_i+\frac{1}{2}{C}_2\rho |v|v_i\right)$$ (18)

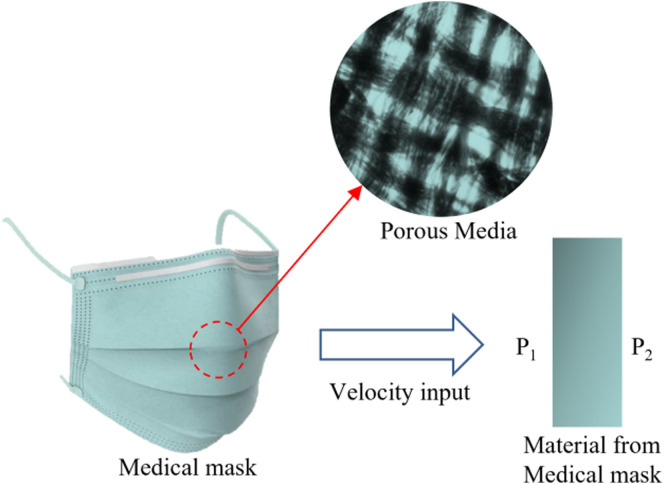
Generally, the inertia resistance coefficient C ₂ and viscous coefficient $\frac{\mu }{\alpha }$ are needed as the parameter of the boundary condition. Taking the medical mask as an example and the way of obtaining these parameters are shown in Fig. 3 .

Fig. 3.

Sketch Map of calculation.

The pressure difference (P ₁ -P ₂) between both ends of material from the mask as shown in Fig. 3 can be measured under a velocity input (V _i). The relationship between pressure difference and the input velocity can be described by the equation as:

$$\mathit{\Delta P}=\frac{1}{2}{C}_2\mathit{\rho \Delta n}{v}^2+\frac{\mu }{\alpha }\mathit{\Delta nv}$$ (19)

Then the coefficient C ₂ and $\frac{\mu }{\alpha }$ can be calculated in the case of density ρ and thickness Δn are known.

Some of investigations about transport species model and multiphase model are listed in Table 2 .

Table 2.

Applications of multiphase model and transport species model.

	Author	Method	Investigation content
Multiphase model	Yu et al. (2017)	CFD-DEM	Dust diffusion in working area under forced-exhaust ventilation.
	Wen et al. (2018)	CFD-DPM	Diffusion of coal particles in the mine.
	Kumar et al. (2017)	Fluidyn-PANACHE	Plume diffusion in various atmospheres.
	Zhang et al. (2016)	OpenFOAM	The effect of Brownian motion on particles extraction.
	Marchioli et al. (2007)	DNS code	The effect of gravity and lift on particles diffusion and deposition.
Transport species model	Sabatino et al. (2007))	Fluent	Investigation about the diffusion of urban pollutant.
	Li et al. (2016)	Fluent	Depression mechanisms of vegetation barriers on pollutant diffusion.
	Vyskocil et al. (2014)	CFD code	Diffusion of steam in the vessel.
	Yang et al. (2016a)	ANSYS 12.0	Investigation of mass diffusion and species transport of suspensions in turbulence.
VOF model	Mirzaee et al. (2016)	Ansys 14.0	Analysis of capturing airborne particles from the air into the liquid.
	Li et al. (2020a)	Ansys-Fluent 19.2	Investigation of the virus transmission through the siphon toilet.
	C et al. (2020)	DEM solver	Research on simulating a single bubble behavior in fluidized bed.
Porous Media	Dbouk and Drikakis (2020b)	OpenFOAM	Numerical analysis on droplets spreading through a face mask
	Li, (2009a)	FLUENT 6.2.16	Simulation of the aerodynamic behavior of a gas mask which consists of two filter layers

2.2. Algorithms diversity

There are various CFD algorithms can be chosen from different CFD tools. Finite Volume Method (FVM), Finite Difference Method (FDM) and Finite Element Method (FEM) methods are in common use in recent years, they can solve most problems of fluid at present and are already been commercialized. Besides, Particle Method (PM) including Smooth Particle Hydrodynamics (SPH), Moving Particle Semi-implicit (MPS) method and Finite Volume Particle (FVP) method and Lattice Boltzmann Method (LBM) based a meshless method have been greatly developed in these years. The characteristics of these algorithms are summarized in Table 3 :

Table 3.

Characteristics of different CFD algorithms.

CFD algorithms	Advantages	Disadvantages
FVM	1. Good adaptability to mesh file, can be applied on complex engineering problems	1. Truncation error is uncertain
	2. Good performance at fluid-solid interaction	2. Computational accuracy is relatively low
	3. Conservative calculation
FEM	1. Can adapt to most irregular calculation area	1. Big cost on calculation
	2. Application scope is wide	2. Relatively poor at highlighting the characteristics of object
FDM	1. Easy to program and parallel operation	1. Difficult to adjust the irregular area of mesh
	2. Fast calculating speed	2.Computational accuracy is relatively low
PM	1. Fast calculating speed	1. Inaccurate calculation of weak point pressure field
	2. Can be used to simulate the large-scale scene	2. Large amounts of particles are needed
LBM	1. High effective at computational calculation	1. Not suitable for simulating the heat transfer at Nano-scale
	2. Can be used to analyze the mesoscopic problems by linking with molecular dynamics	2. Can be only applied on incompressible laminar flow at low Knudsen

Several algorithms are mainly used in recent as summarized in Table.3. Although the mechanism of pathogen transmission in the fluid is complex, the motion of pathogens still follows the hydrodynamics law and can be solved by mathematics models of CFD algorithms. For example, the LBM method can be used to solve pathogen transmission in small-scale while FDM method can be applied on the large-scale transmission of the pathogen.

2.3. Maneuverability

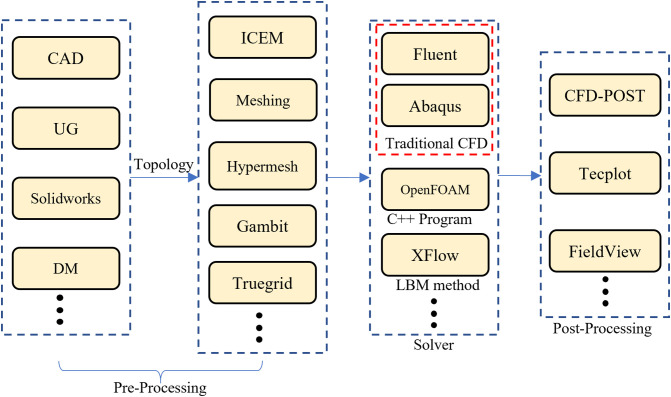
CFD tools are in high compatibility and their computing files can be transferred in a variety of software. In general, the structure of CFD software consists of three parts: pre-processing, solver and post-processing and Fig. 4 below shows some options of each part.

Fig. 4.

Structure of CFD tools and various options.

Users can build the model by using the modelling module of CFD tools such as the DM in Ansys Workbench and they can also use professional modelling software like CAD, UG, etc. Then, different solvers can be chosen to conducting calculation and program codes such as User Defined Function (UDF) is allowed in operation of CFD tools. For example, Fluent is one of the most common CFD solvers based on FVM algorithms, there are four methods can be chosen. These methods can be divided into two categories: (1) Segregated solver; (2) Coupled solver. Advantages, principles and applicability of these methods are summed up in Table 4 .

Table 4.

Principles and applicability of fluent solvers.

Solver categories	Methods	Principles	Applicability
Segregated	SIMPLE	Instead of solving the N-S equation directly, the momentum equation is modified by pressure.	Suitable for solving the compressible flow
	SIMPLEC		Suitable for solving the incompressible flow
	PISO
Couple	Coupled	Simultaneously solving the N-S equations directly.	Suitable for solving the compressible flow

3. Epidemic theories and experimental methods

Pathogen transmission in the environment is a complex process. For the sake of the accurate simulation result, the calculation model and parameters of the simulation are necessary. Furthermore, epidemic models should be taken into account in numerical simulations. By using experimental methods to get the data that is required in the boundary condition is important, besides, experimental data are also needed to validate the simulation result. This section summarizes various epidemic models that should be used in the simulation. Moreover, experimental methods which can be applied to analyzing pathogen transmission are presented in this section as well. Although some of the experiments summarized were not used in combination with CFD methods, they can provide valuable references for similar studies by using numerical simulations (Fig. 5).

Fig. 5.

Volumetric flow rate.

3.1. Application of epidemic model on CFD method

Poussou et al. (2010) investigated the effects of moving people on pollutant diffusion and airflow. By combining the PIV experiment technology, they used CFD method with a second-order upwind scheme to simulate the airflow. The Re-Normalization Group (RNG) k-ε was used in simulation in order to solve the turbulence with the good performance of accuracy, efficiency and robustness; In Gao and Niu (Gao and Niu, 2006) study, RNG k-ε model including the effect of low-Reynolds-number is used to solve the airflow and the diffusion of tracer gas which can represent the contaminant transmission are calculated by the equation below:

$$\frac{\partial }{\partial t}\left(\mathit{\rho \varphi }\right)+\mathit{div}\left(\rho \stackrel{\Rightarrow }{U}\varphi -{\Gamma }_{\varphi }\times \mathit{grad\varphi }\right)=S_{\varphi }$$ (20)

Where t, ρ and ϕ are time, air density and tracer gas concentration respectively.

Unsteady flow is a big challenge in accurate simulation as Zhang et al., 2014) indicated. Flow in the environmental channel is always unsteady, and it hence increases the complexity of simulation on pathogen transmissions. How to treat an unsteady flow as the steady flow in practice is still a difficulty. By defining the wave in hydraulic calculation can effectively simplify the disturbance in unsteady flow. Capillary wave (Mahmood and Khalid, 1975) can reflect the disturbance brought by some factors to surface of fluid which can be written as:

• (1)For shallow waves:

$$C^2=\left(\frac{\mathit{gL}}{2\pi }+\frac{2\mathit{\pi \sigma }}{\mathit{\rho L}}\right)tanh\frac{2\mathit{\pi y}}{\mathit{\rho L}}$$ (21)

• (2)For deep waves:

$$C^2=\left(\frac{\mathit{gL}}{2\pi }+\frac{2\mathit{\pi \sigma }}{\mathit{\rho L}}\right)$$ (22)

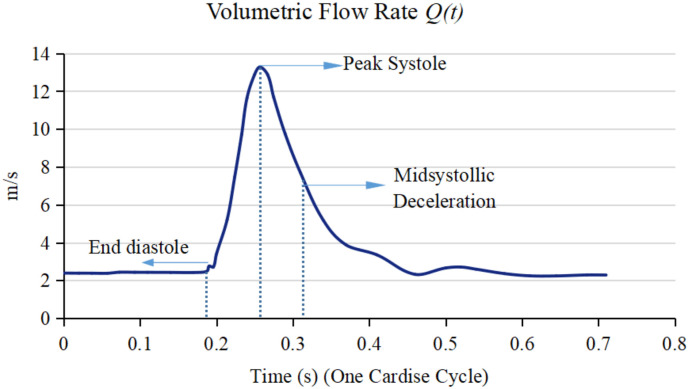
Ku (1997) presented a “waveform” method to model unsteady flow in blood which reflects the relationship between time and volumetric flow rate:

Mantha et al. (2006) used this method in the simulation of biological flows and found the relationship between wall shear stress and the location of the aneurysm; Nanduri et al. (2009) also used “waveform” to solve the unsteady laminar flow and the objective of this study is to build a human body surface model to simulate the airflow around the body. Although this method is useful for analyzing particle transportation in biological flows, it is not suitable for simulating unsteady flow in the atmosphere due to greater disturbance.

More, in order to simplify the model for analyzing the airflow in building, Axley (1989) presented a Multi-zone model which allows users to calculate the hourly rate of airflow between various rooms and Dols et al. (2003) improved this model by providing the equation of mass conversion as:

$$\frac{d{m}_{\mathit{ci}}}{\mathit{dt}}=\sum _j{F}_{j,i}\left(1-{\eta }_{\mathit{ji}}\right)C_j-\sum _j{F}_{i,j}+\mathit{Gi}$$ (23)

Based on the dispersal theory which is not limited to the wall-mixed region, Multi-zone model idealized the flow system as assembles of each element. This method has been applied to various research in building environments: Li et al. (2005a) studied the SARS virus transmission in 19 high-rise apartments of an estate. They have studied the effect of clinical and environmental factors on pathogen transmission in order to confirm the airborne hypothesis. Their investigation is comprehensive and it illustrated the transmission routine of the virus in buildings though, they did not provide a specific measure to control this in a single room.

In Jiang et al. (2010) study, ventilation schemes were quantitively analyzed. By using CFD technique and Multi-zone model, the ventilation in a hospital was simulated and a “safe ventilation rate” was defined. Through PHOENICS, they simulated the effect of airflow on SARS virus dilution and pointed out: (1) Diluting the viral air emitted by SARS infectious by 10,000 times fresh air can achieve the requirement of “safe ventilation rate” and hence will reduce the transmission risk; (2) Lower volumes of dilution air cannot protect the non-infected people.

Particle contaminant such as PM₁₀ is always a carrier of the pathogen. Lee et al. (2017) analyzed particles' transport and penetration in a multi-story building by using CONTAMW. It was indicated in their analysis that particles with a diameter smaller than 1 micro can easier penetrate the lower floor of a building. Moreover, because of the airflow in the vertical zone such as elevator, particles may transport to higher floor as they indicated. Although the investigation presented in this article is comprehensive, only the situation in winter has been simulated. Seasonal factors such as various temperatures, air humidity are important in the simulation of pathogen transmission and these parameters should also be considered as well.

Airflow caused by temperature difference will affect pathogen transmission. Chao et al. (2017) simulated the three cases by combing the Multi-zone model and two-way air flow effect in order to demonstrate the effect of temperature difference on air quality of indoor. It can be found from one of the cases they studied, the airflow generated by the temperature difference between bathroom and corridor can transport infectious pathogens, and hence the door of infected zoom should be closed as they suggested.

Closing doors and windows in a room is not equivalent to obtaining a closed space. The crack of the door and windows is always ignored by researchers when simulating the airflow or pathogen spreading in the building or a single room. By using Multi-zone method in CFD simulation, Yang and Gao (2015) analyzed the effect of stack and wind effect on contaminating dispersion and found that these factors will cause the contamination horizontally or vertically spread. Their research also indicated that the pollutant gas can be transported through cracks of doors and windows and may cause infectious disease.

Because of the great effectiveness, Multi-zone method was widely used in many cases which can be found in Wu et al. (2017), Zhai and Liu (2008), Lai et al. (2008), Ge et al. (2011) and Zhai et al. (2012) studies. Although the assumption of this model (to define a zone filled with fully mixed air and ignore the disturbance in airflow) reduces the accuracy of simulation, it provides an effective method to illustrate the airflow pattern in the building environment.

Investigations based on CFD models or aerodynamics theories can only describe the transmission on physical characteristics of the pathogen, however, the biological characteristics of it cannot be ignored such as its replication and infectiousness. The Wells-Riley model which is in common use was provided in 1955 (Dutra and Frank, 1955). This model can predict the new infection in a period of time and can be written as:

$$N_C=S\left(1-e^{-\frac{\mathit{Iqpt}}{Q}}\right)$$ (24)

Where S is the susceptible people in an area, I is the number of infectious people and p represents the pulmonary ventilation rate of susceptible people.

Zhu et al. (2012) investigated the potential risk of infection in public transportation by using Wells-Riley model in CFD simulations. It was proved in their study that the closer to the operating exhaust in the bus the infected person is, the smaller the infection risk bringing to others is. Besides, this study indicated that the ventilation system of most of buses is not effective because there is only one single exhaust was located in the middle of the cabin or the back wall. Yan et al. (2017) studied the transmission of coughing particles in the breathing zone of people. In their investigation, the method that combines the Wells-Riley model and the Lagrange model in CFD was used. It was illustrated from this study that the location of releasing particles will affect the particle travel distance. Based on the Well-Riley model, this research work has also presented a quantifiable approach to assess the infection risk of passengers. These studies are helpful for improving the design of the vehicle ventilation system and hence reduce the infection risk though, they did not consider the effect of altitude on airflow patterns in vehicles.

The Wells-Riley model can also be applied to building simulation. Niu and Gao (2010) analyzed the natural ventilation which may cause infectious disease spread in high rise buildings by using the Wells-Riley model in CFD simulation. It is worth mentioning that the concentration of infectious pathogens is not equivalent to the infection risk. It was indicated in this study that the concentration level of the upper room is two orders of magnitude lower than the adjacent lower room, but the difference of infection risk between them is only one order of magnitude. Wells-Riley model plays an important role in transforming pathogen concentration to the infection risk and increasing researches which applied Wells-Riley model to CFD simulation can be found: Noakes et al. (n.d.) studied transmission method of the airborne pathogen in an enclosed space and Tung and Hu (2008) simulated the airborne transmission of the indoor environment in multiple spaces; Moreover, Aliabadi et al. (2014), Gupta et al. (2012), Villafruela et al. (2013) and You et al. (2019) used this model in the simulations of their research.

Since Wells-Riley model proposed, it has been modified and improved. The key assumption of the original equation is that the concentration of infectious particles is at a steady-state after suspending for a long time in the air. However, it is not suitable for calculating the infection risk in unsteady-state conditions. In order to solve this problem, Rudnick and Milton (2003) improved Wells-Riley equation which considered steady-state exposure, and the infectious probability for susceptible individuals can be written as:

$$P=\frac{D}{S}=1-e^{-\frac{\mathit{Iqpt}}{Q}}\times \left[1-\frac{V}{\mathit{Qt}}\left(1-e^{-\frac{\mathit{Qt}}{V}}\right)\right]$$ (25)

This modified model was used in Liao et al. (2005) investigation which studied the relationship between infectivity and volume of inhaled air. Besides, this model was proved to be well performing in studies of Heffernan et al. (2005), Li et al. (2005b), Fabian et al. (2008), Mendell et al. (2013), Atkinson and Wein (2008). Compared with researches using original Wells-Riley, those using improved equation are more convincing.

Based on physical characteristics like aerodynamics of respiration droplets, Chaudhuri et al. (2020) proposed a numerical model for the early state of Covid-19 pandemic by integrated the chemical mechanism and pandemic evolution equations. The “τ” this work derived by using the theory of collision rate represents the lifetime of the droplet. It can be written as:

$$\tau =min\left\{t_{\mathit{evap}}|t_{\mathit{evap}}\ge t_{\mathit{settle}}\forall D_{s,0}\right\}$$ (26)

t _evap is the evaporation time of the droplet and t _settle is the setting time of it. It can be found from the study that the impact of respiratory droplets on infection growth parameters and infection growing rate is obvious.

Susceptible-Infected-Recovered (SIR) model was proposed by Mckendrick (1927) can be used to analyze the spread rate, range and transmission route of pathogens. The population can be divided into three groups in assumptions of this model: (1) S level: susceptible people; (2) R level: recovered people but may become susceptible people if the time is out of immunity; (3) I: infectious people. Based on this model, a Susceptible-Exposed-Infected-Recovered (SEIR) model which considers the exposed people in the equation was defined by Anderson and Mary (1991).

Some investigations based on these models are listed below in Table 5 :

Table 5.

Investigations based on epidemic models.

Sources	Contents
SIR model: $\frac{\mathit{dS}}{\mathit{dt}}=-\mathit{\beta SI}$,$\frac{\mathit{dI}}{\mathit{dt}}=\mathit{\beta SI}-\mathit{\gamma I}$,$\frac{\mathit{dR}}{\mathit{dt}}=\mathit{\gamma I}$
Stone et al. (2007))	Analyzed the nonlinear dynamics of recurrent diseases by referring the SIR model.
Zaman et al. (2008)	Presented a helpful model for controlling the infections based on the SIR model.
Kar and Batabyal (2011)	Studied a vaccination case by using nonlinear mathematical method of the epidemic model.
SIRS model: $\frac{\mathit{dS}}{\mathit{dt}}=-\mathit{\beta SI}+\mathit{\alpha R}$,$\frac{\mathit{dI}}{\mathit{dt}}=\mathit{\beta SI}-\mathit{\gamma I}$,$\frac{\mathit{dR}}{\mathit{dt}}=\mathit{\gamma I}-\mathit{\alpha R}$
Xu et al. (2010)	Investigated saturation incidence and temporary immunity by using a delayed SIRS model.
Xia et al., 2009)	Analyzed how nonuniform transmission affects the critical threshold of SIRS model on scale free networks.
Agiza et al. (2003)	Studied phase transitions in some epidemic models like SIRS which is defined on small-world networks.
SEIR model: $\frac{\mathit{dS}}{\mathit{dt}}=-\mathit{\beta SI}$, $\frac{\mathit{dI}}{\mathit{dt}}=\mathit{\alpha E}-{\gamma }_{2}I$, $\frac{\mathit{dE}}{\mathit{dt}}=\mathit{\beta SI}-\left(\alpha +{\gamma }_1\right)E$, $\frac{\mathit{dR}}{\mathit{dt}}={\gamma }_{1}E+{\gamma }_{2}I$
Li et al. (1999)	Investigated transmission of infection in people who directly contacted the host
Dukic et al. (2012)	Tracked the evolution of the infectious disease over time based on an epidemic model.
Lekone and Finkenstädt (n.d.)	Investigated the daily incidence and mortality time of Ebola virus based on SEIR model

More, Hathway and Abigail (2008) combined the CFD method and SIR model in order to analyze pathogen transmission in hospital space and Asanuma and Ito (n.d.) predicted the exposure risk of the population in the hospital by using CFD with considering the SIR model. From these investigations, it can be found that this epidemic model is well performed in simulating the spread of infectious diseases. However, the number of researches that applied these models to CFD simulation is still a small amount due to the complexity of modelling and calculation in simulating the airflow or particle transport among a crowd of people.

3.2. Experiments of airborne transmission

In CFD simulation, not only the mesh model is crucial but also the parameter of simulation is of great importance to let users obtain the results they require. Generally, the boundary condition such as velocity, pressure, turbulence intensity can be measured from experiments. In recent, micro-particles experiments and tracer gas experiments are most used in investigations of airborne transmission.

Romano et al. (2015) simulated the airflow pattern and concentration of airborne particles in an operating theater (OT) by using CFD method. They also conducted an experiment in order to verify the accuracy of simulation results and in their experiment, a six-way aerosol distributor was used to convey the generated aerosol particles; OPC (optical particles counter) equipped with a dilution system was used to measure the particle concentration; A rotating vane anemometer and a thermo-anemometer were used to measure the velocity and temperature respectively. They also validated the simulation result by comparing the data measured from the experiment and found that the experimental and numerical data were well coincided (Error is less than 2% for temperature and 10% for velocity). The value of mean absolute percentage error for particle concentration is 42% though, the experimental curve and the numerical curve are similar in changing trends. Therefore, experiments involving particle-fluid flow are more suitable for qualitative analysis, because it is hard to accurately control conditions such as temperature, pressure, stable velocity of flow.

Zhou et al. (2018a) established a model which can be used to predict the distribution of negative ions produced by the air ionizer and the efficiency of this device. In their experiment, an emission system consisting of a compressor and nebulizer was used to compress the filtered air and aerosolize the bacteria; An ion counter was used to test the emission concentration. In order to present their experiment clearly, the installed experimental system is shown below in Fig. 6 :

Fig. 6.

The detailed experimental setup (Chaudhuri et al., 2020).

The objective of the experiment carried out in this work was to measure the susceptibility constant of the bacteria and the distribution of the negative ions. More, the experimental data were used to validate the simulation and the result showed that the data of simulation had a good agreement with that of the experiment. By combining the experiment and numerical simulation, this research analyzed the effect of air ion on disinfection and provided the removal mechanisms for various bacteria. The use of negative ions was proved useful in inactivating bacteria and can be implemented in the ventilation system of the hospital or residence.

Estrada-Perez et al. (2017) used the Particle Tracking Velocimetry (PTV) technique to extract information from flow in an analysis of droplet distribution and airborne bacteria in residential showers. Through a combination of the visualization algorithm, this study intuitively showed the trajectories of the droplet. Besides, it was proved that the bacterial load in the shower air will increase while turning on the shower spray. The effect of droplet velocity and distribution on aerosolized bacterial groups was not given this study, more, the parameter of shower such as water temperature, nuzzle structures should be also considered in the experiment as well.

Choi et al. (2018) classified the airborne particle according to their optical properties by using experimental methods. Ink-jet aerosol generator (IJAG) was used to generate, dry the airborne particle, the light-scattering signal was used to estimate the correlation value in the classification analysis of airborne particles. The correlation value proposed in this work is helpful for particle detection and classification though, how to apply this method to detect other airborne pathogens with more complicated biological characteristics is required to be furthered.

Mei and Gong (2018), Couch et al. (1970), Yan et al. (2009) and Petersen (1980) used various experiments to measure the particles. From those investigations, two factors are important to ensure the accuracy of the experiment:

• (1)Conveyed air from experiment needs to be filtered;
• (2)Particles should be uniformly delivered.

Experiments to analyzed the particle are useful for understanding the motion law of it. However, it is difficult to massively measure the characteristic of nano-scale particles. The tracer gas method is also a common method in analyzing the pollution diffusion and airflow patterns. Tracer gas can be mixed with air without any changes and it can be easily detected because of special physical characteristics. Helium, nitrogen, argon and carbon dioxide are always chosen to carry out the experiment as a tracer gas.

Gao et al. (2008) combined the use of experiment and CFD method to study airborne transmission in different flats of a high-rise building and to verify their simulation, the data of tracer gas experiment from Denmark Aalborg University (Heiselberg et al., 2003) is used. The analysis of this work is comprehensive by illustrating the transmission mechanism of the airborne virus and how to control virus transmission in a high building based on this investigation is needed to be furthered.

To investigate airborne transmission between horizontal adjacent units, Wu et al. (2019) analyzed influence factors of transmission route especially the contribution of wind force and thermal buoyancy force and found from the result that the wind force is the main driving force to affect the inter-unit dispersion. The experiment conducted in this work is conducted in a slab-type building in Hongkong, SF₆ was used as the tracer gas and injected by the air samples; CO₂ was used to calculate the ventilation rate and monitored by TSI Q-Trak and CO₂ Sensor. Although the spread risk may be overestimated in the analysis because the crack of the door and windows can cause the pathogens aerosol deposit, this work still provides a valuable study in identifying the possible transmission route of the airborne.

Ai et al. (2019) used a tracer gas (NO₂) experiment to examine the characteristics of airborne transmission of the exhaled droplet between two people in an experimental room. Two manikins were used to represent an exposed people and an infected people; Air velocity was measured by the Swema 3000 omnidirectional anemometer; PT100 sensor was used to monitor the air temperature; To test the tracer gas concentration, a Faster Concentration Meter (FMC) and INNOVA Multi-gas sampler and Monitor are used. This work has indicated an interaction between exhaled gas and supply flow and analyzed the impact of these factors on infection risk for an exposed person facing an infectious person. Although the experiment carried out in this work was based on a steady-state condition without taking the impact factor of time into consideration, it provided an effective method for researches afterward.

Villafruela et al. (2016) also used manikins in the tracer gas experiment in their investigation of cross risk through airborne infection. In their experiment, the breathing systems of manikins were conducted by artificial lungs which allow their breath with a sinusoidal airflow shape. Using manikins to simulate the infection transmission between populations can reduce the risk of the experiment and it has been widely used over the years which can be found in investigations of Yang et al. (2016b), Seto (2014), Luo et al. (2018), etc.

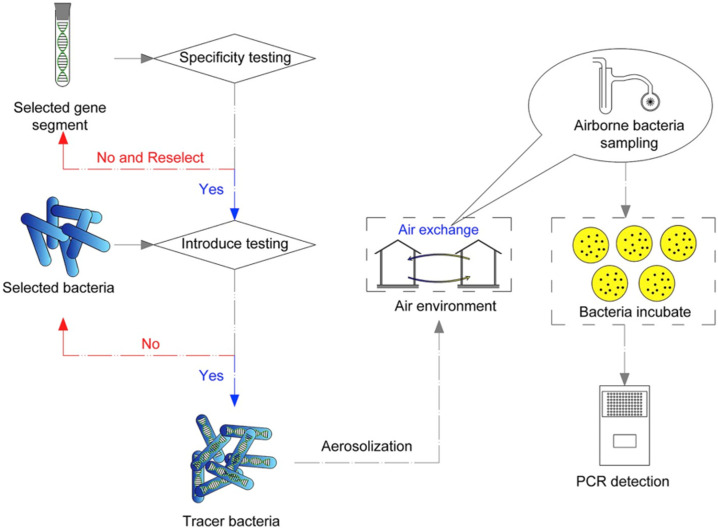
Although the tracer gas experiment has been widely used in various studies, few researchers focused on the transporting process of microorganisms in the transport media. Simplifying the transmission process of pathogens by defining them as particles or gaseous pollutants is an effective method, however, ignoring the biological characteristics of microorganisms may prevent researchers from understanding the migration of pathogens. In Li et al. (2019a) investigation, they used a tracing method to analyze the bacteria transmission in the building environment. It can be divided into three steps in their research:

• (1)Culturing and filtering the suitable bacteria;
• (2)Aerosolizing the bacteria particles and conveying into measuring environment;
• (3)Analyzing the airborne transmission of E. coli by using PCR.

And the flow chart given by them is shown below in Fig. 7 :

Fig. 7.

Experiment process of tracing bacteria (Li et al., 2019a).

It will be more persuasive if this process can be carried out in an experiment of researches by using the tracer gas method or particle experiment. However, it will also increase the risk in conducting experiments if the bacteria or virus are highly infectious.

Overall, both the particle experiment and tracer gas experiment can help people understand the process of pathogen transmission, moreover, it provides crucial information for CFD users. On the one hand, the information including experimental data can be used as boundary conditions in CFD simulation; On the other hand, the results of the experiment can be quantitively or qualitatively verified to ensure the accuracy of CFD simulation. Therefore, designing an effective experiment in analyzing pathogen transmission is necessary, it makes the simulation result more convincing.

4. Applications and potential chances

4.1. Applications of CFD on airborne transmission

4.1.1. Transmission in building environment

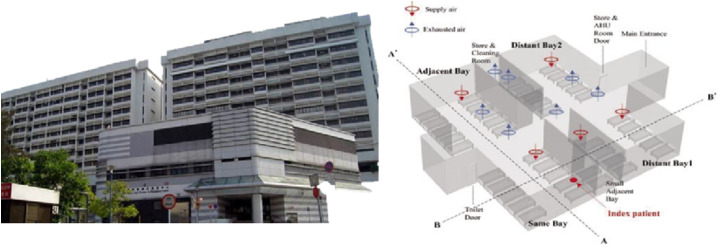
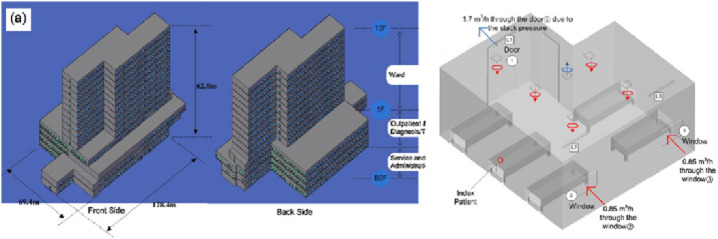
Transmission of pathogens can be different in various spaces and when the epidemic outbreaks caused by infectious pathogens, hospitals will become a high-risk place and may lead to a second infection. How to control the pathogen in hospitals by using an effective ventilation system becomes a great concern. Kao and Yang (2006) established a CFD model of cough and simulated the spread of droplets with the virus in an isolated room of the hospital. Their investigation indicated that parallel flow can effectively control the virus transmission and staggering the position of air inlet and outlet is also an effective way. Lim et al. (2010a) used the tracer gas and CFD coupled method to analyze the characteristics of the airborne virus in their article published in 2010. They indicated that the spread of the virus can be considered as the gas diffusion because the size of it is nano-scale, Brownian motion can be used to describe the virus transmission in air. Their simulation model in this research was based on the Prince of Wales Hospital in Hong Kong as shown in Fig. 8 :

Fig. 8.

The Prince of Wales Hospital and the simulation model of it (Lim et al., 2010a).

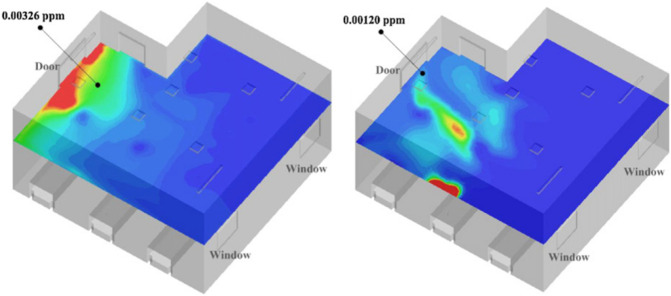
They used the tracer gas NO₂ to replace the viral gas emitted from the patient and simulated three cases under different volumes of supplied air and exhausted air, the simulation results presented the diffusion process of tracer gas as in Fig. 9 :

Fig. 9.

The simulation of tracer gas diffusion (Lim et al., 2010a).

In the same year, this research group studied a similar topic by using the tracer gas and CFD method. In this analysis, the stack effect of high rise building on airflow is considered and the simulation model is based on the General Hospital K in Korea as shown in Fig. 10 .

Fig. 10.

The Prince of Wales Hospital and the simulation model of it (Lim et al., 2010b).

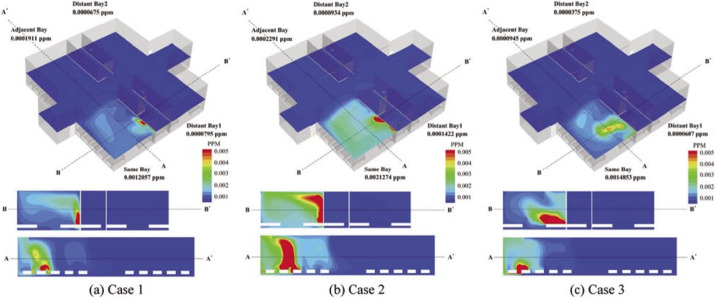
They have simulated the spread of tracer gas in the wards of both on the lower floor (5F) and higher floor (15F) to demonstrate the stack effect. Some of the simulation results are shown as shown in Fig. 11 :

Fig. 11.

Simulation results of the tracer gas transmission in wards of different floors (Lim et al., 2010b).

These researches above mainly investigated pathogen transmission inside the hospital and they are meaningful in protecting patients and hospital staff. However, not only pathogen transmission inside the hospital is dangerous, but the pollutant emission from the hospital is also a great concern for public health. Chang et al. (2011) by using CFD modeled the atmospheric environment out the hospital and simulated the spread of the viral (SARS) gas emitted from the hospital. The mesh model of simulation is shown in Fig. 12 :

Fig. 12.

Mesh model of simulation (Chang et al., 2011).

This model was generated by tetrahedral grids; The wind velocity as a boundary parameter was measured by the hot-film probe and anemometry equipment; 16 wind directions were considered in the calculation. Moreover, in order to verify this model, tracer gas was used in the experiment model with a 1:50 scale. The simulation result below in Fig. 13 respectively shows the concentration contour of pollutant gas at both the height of the roof chimney (right) and 1.5 m (left) above the ground.

Fig. 13.

Diffusion of pollutant gas emitted from hospital (Chang et al., 2011).

By the simulation results, they indicated that both the maximum concentration and mean concentration of pollutant gas in small and would not affect residents' health. However, when a large number of SARS patients were arranged in the hospital, it is still a bit risky for people who actives in the high-concentration area on the ground level.

Research works above were mainly focused on the airflow pattern or impact of ventilation on pathogen transmission. However, cross-infection frequently happened in hospitals and should be paid attention to in case studies of pathogen transmission. Based on Eulerian-Lagrangian method, a case study proposed by Wang et al. (2020a) has illustrated that the sneezing process from a virus carrier is responsible for the occurrence of cross-infection. This research provided two evaluation parameters: Total Maximum Time(TMT) and Overall Particle Concentration(OPC) which can be used to reflect the motion of particles and the probability of cross-infection. Through the simulation and numerical analysis, authors suggested a bottom-in and top-out ventilation method which can effectively minimize the cross-infection.

It can be found from those investigations that the ventilation strategy is very important in controlling pathogen transmission in hospitals. Compared with the open-air environment, indoor ventilation is easier to be controlled, hence, it is necessary to ensure safety when emitted the viral gas from the exhausted system from the hospital. Without professional medical equipment, the buildings with high population density such as residential buildings, commercial buildings and campus buildings are in higher infection risk.

Li et al., 2019b studied natural ventilation in teaching buildings by using CFD method. In their investigation, PHOENICS with RANS model was used to simulate the ventilation; The SIMPLE algorithm was used to calculate and PRESTO scheme was used to staggered the pressure interpolation; The wind profile at inlet boundary of the simulation was determined by the equation of ASHRAE (ASHRAE Handbook, 2009) as:

$$\frac{U\left(y\right)}{U_{\mathit{ref}}}={\left(\frac{y}{H}\right)}^{0.22}$$ (27)

Through the simulation, they indicated that the ventilation of the teaching building with a “line-type” corridor is better than that of the inside corridor; They have also presented an optimization design for better ventilation in teaching buildings by determining the best wind angle.

Moreover, Cuce et al. (2019) studied the natural ventilation in school buildings based on its working principles and limitation of passive ventilation; In a crowded room, the concentration of volatile organic substances generated by human skin oil is high, Xiong et al. (2019) analyzed the concentration change of products from reactions of ozone with squalene in a University classroom. The CFD method was used, and the time-dependent concentration of chemicals in the classroom was defined in simulation.

Some kinds of viruses such as COVID-19 are tenacious and can survive a long period in the digestive system. As Wu et al. (2020) indicated, the survival time of SARS-Cov-2 in faeces is longer and hence the toilet can be a high-risk zone to spread the infection pathogens. However, people often ignore this situation. To solve this problem, Li et al. (2020b) simulated the motion of droplets escaping from the siphon toilet which may cause the virus spread. By using CFD, a combination of the VOF model and the DPM model was used to simulate the fluid flow and the movement of particles.

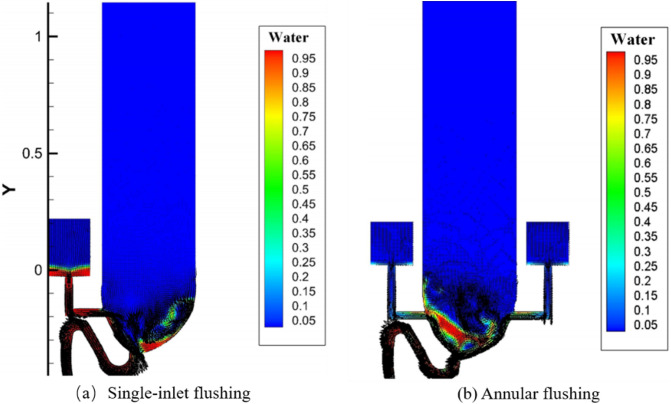
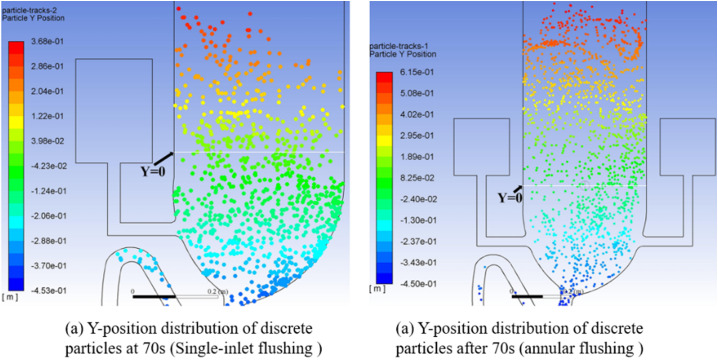
The droplets transmission and fluid flowing under two kinds of flushing process were simulated and the simulation results are shown in Fig. 14 and Fig. 15 :

Fig. 14.

Flushing process of two kinds of siphon toilets.

Fig. 15.

Y-position distribution of discrete particles in two siphon toilets (flushing time of 70s).

It can be observed from simulations that particles will spread in flushing because of the turbulence generated by the high speed of flowing water. More, it was obtained that 40% ~ 60% of particles can reach above the toilet seat. The research of this work is meaningful and it was indicated that before flushing, laying down the lid is useful for preventing the virus transmission. More, washing the seat of the toilet is necessary because the floating virus may deposit on the surface of it. This research group has also analyzed the movement of a virus-laden particle in the process of urinal flushing (Wang et al., 2020b). Without the prevention, over 57% of particles can escape from the urinal and the particle can reach the highest position of 0.84 m at only 5.5 s. So it is mandatory to wear a mask in public to reduce infection risk.

Furthering this study about virus transmission in the squat toilet by applying the method proposed in this work is important because, in many places such as China, the use of the squat toilet is higher than that of the sitting toilet in public.

Some investigations of CFD simulations of ventilation or pathogen transmission in the building environment are summarized below in Table 6 :

Table 6.

Investigations of various cases in building environment (“-” represents unavailable data).

Sources	CFD tool	Model	Algorithm	Contribution
Cho (2019)	STAR-CCM+	Renormalization group k-ε	SIMPLE	Explored a new ventilation strategy by laying out the exhaust air grilles
King et al. (2013))	Fluent	RSM, RNG k-ε	SIMPLE	Predicted the bioaerosols deposition by using CFD based Lagrange particle method
Shen et al. (2013))	Fluent	Standard k-ε, S2S	SIMPLE	Investigated the pollutant transmission under various ventilation method especially the Personal ventilation (PV)
Wong et al. (n.d.))	Fluent	–		Analyzed the aerosol transmission of A/H3N2 virus in an acute ward
Qian et al. (2009))	Fluent	RNG k-ε	Solving Navier-stokes	Established a new simulation model for predicting the airborne transmission in enclosed wards
Noakes et al. (2004))	CFX	Standard k-ε	–	Simulated the biological inactivation in airflow under UVGI
Zhou et al. (2018b)	Fluent	Renormalization group k-ε model	SIMPLE	Provided suggestions for improving Chinese standard GB 51039-2014 in ventilation layout

It can be obtained from these investigations:

• (1)Ventilation is one of the most effective methods to control the pathogens transmission and the reasonable arrangement of the ventilation system is necessary.
• (2)The effect of the stack effect should be considered when analyzing the ventilation in high-rise buildings.
• (3)Rooms with infected patients need to be diluted with plenty of fresh air.

4.1.2. Transmission in public transportation

Traffic vehicles are also dangerous when there are infectious patients. Under the high personnel density and weak ventilation system, it is difficult to control the pathogen such as the airborne virus. According to this problem, more and more researchers investigated airflow in various kinds of vehicles by using CFD methods.

Zhang and Chen (2007a) provided a new method for improving the airflow distribution system of the Boeing 767; Yan et al. (2009) studied the contaminated air in a cabin of Boeing 767–300 by using CFD simulation and to understand the mechanism of transmission, they quantified the droplet and air transmission by modelling the sneezing, coughing and breathing. Due to the special ventilation in the cabin of the airplane, the airflow patterns are different from those in rooms. The path-line of the velocity field in the cabin was simulated and can be found in their research as shown in Fig. 16 :

Fig. 16.

Path-line of the velocity field in both the whole cabin (left) and the horizontal breathing plane(right) (Yan et al., 2009).

They indicated that: The pollutant was divided into two halves by the ventilation system of the cabin; The longitudinal airflow may let the pollutant longitudinally transport. They also emphasized that because of the unavailable data, the effect of the multiphase jet on the microenvironment was still an unknown complexity.

Zhang, et al. (Zhang and Chen, 2007b; Zhang and Chen, 2007c; Zhang and Chen, 2007d); Liu, et al. (Liu and Chen, 2013), Bady et al. (n.d.) and Wang et al. (2017) studied the diffusion of contaminant sources (including virus, bacteria, etc) in a cabin by using CFD method based on Quasi–reversibility equation provided by Lattes and Lions in 1969 (Lattès et al., 1969). Due to the complexity of fluid flow patterns in the airplane, it is more difficult to control pathogen transmission compared with other non-enclosed vehicles. Therefore, keeping the larger distance between passengers in an epidemic situation is necessary.

Not only many researchers investigated the ventilation or pathogen transmission in cabins, but also a large number of investigations of that in carriages of buses or trains were provided. Based on shuttle bus system of Harvard University, Zhu et al. (2010) simulated the lifetime of air in the bus environment and evaluated the ventilation efficiency, moreover, they analyzed the effect of ventilation on pollutant concentration which revealed the risk of infectious disease; Li et al. (2017) analyzed the airflow patterns inside and outside a bus and investigated the effect of windows opening on ventilation rate; Wang et al. (2014) studied the air distribution and the diffusion of droplets from coughs in China high-speed railway; Knibbs et al. (2012) analyzed the transmission of infectious virus in passenger cars.

Compared with the simulation of ventilation or airborne transmission in the building environment, the motion of transportation should be considered in the simulation of that in the transportation system. Moreover, the risk of infection transmission is higher in enclosed vehicles like airplanes or high-speed trains. So, during the epidemic time, the regular disinfection in traffic vehicles is necessary except keeping enough ventilation volume.

4.2. Advanced methods in analysis of pathogens transmission

4.2.1. Lattice Boltzmann Method (LBM) applications

LBM is a new computational method of CFD that has been developed in recent years. Since 1992, various researchers have been devoting to the development of LBM theory. Chen and Doolen (1998) presented a thermal model based on functions of energy distribution and promoted the development of double distribution function to simulate problems of the convection and the diffusion; Qian and Lallemand (1992) proposed the simplest equation of discrete Boltzmann which satisfying the conservation law; Succi (2001) applied LBM on porous media flow, turbulence, reaction flow and flow of soft matter system.

Different from the traditional CFD algorithm, fluid is defined as a large number of particles by LBM and the calculation is based on statistical mechanics. There are three important assumptions in LBM simulation:

• (1)Two particles collisions are mainly considered;
• (2)The velocity distribution of each particle exists independently;
• (3)The external force does not affect the dynamic behavior of the local collision.

By using LBM, Mu et al. (2016) studied the transmission mechanism of SVOCs in small particles like PM 2.5 and investigated the adsorption and desorption process of SVOCs; Mao et al. (2019) also analyzed the mass transfer of SVOCs with suspended particles by using LBM. In their investigation, the interaction between particles and SVOCs was considered; Cai and Zhang (2016) established a model for simulating the deposition and filtration process of airborne particles based on Boltzmann and discrete element method.

There are various models that can be used in the simulation of LBM and these models can be defined by the layout of lattice, some models which are in common use are shown in Fig. 17 (2D) and Fig. 18 (3D):

Fig. 17.

2D model: D2Q9 (left), D2Q5 (right).

Fig. 18.

12 3D model: D3Q18 (left), D3Q15 (right).

Different models lead to different iteration method in the calculation and can be applied to various investigations. Table 7 lists some investigations based on these models:

Table 7.

LBM cases in various field.

Sources	Models	Contributions
H. et al. (2017))	D2Q9, D3Q19, k-ɛ, turbulence model	Analyzed some kinds of turbulence flow and transport/deposition of particles in different channels
Liu et al. (2013)	D2Q5	Presented model coupling the LABSWE with the LABADE2D.
Maslo et al. (2014))	D2Q5, D2Q9	Applied the LBM on oil spilling in large-scale.
Hao and Cheng (2009))	D3Q19	Analyzed the anisotropic permeabilities of gaseous diffusion in a fuel cell
Bogner et al. (2015)	D3Q19	Investigated the drag correlation in both dilute and moderately dense flow
Kim et al. (2015))	D2Q9	Simulated the water transport and gas diffusion in one kind of fuel cell
Navidbakhsh et al. (2012)	D2Q9	Studied the invasion and occupation process of Plasmodium falciparum in blood cell

Although many investigations in various fields based on LBM have been presented, there are few investigations about pathogen transmission. Moreover, it is difficult to analyze the mass transfer case at the mesoscopic level by using the traditional method, hence, it is still a great chance for developing the LBM in the field of epidemiology.

4.2.2. Porous media model applications

Face masks have been used to prevent virus transmission and it is necessary for the epidemic situation. Li (Li, 2009b) simulated the aerodynamic behavior of a gas mask which consists of two filter layers. The low-Reynolds number k–ε turbulent model was used in the simulation to solve the fluid and the Porous Media model with Forchheimer's equation was used to solve the flowing in filter layers. Based on the index of the air age, they replaced the adsorption time of toxic gaseous by the residence time of air in the canister. The model of the gas mask and the simulation results in their research are shown below in Fig. 19 :

Fig. 19.

Grid model of the gas mask (left) and the flow field of simulation (right) (Li, 2009b).

This research indicated that the design of the mask such as the hole properties is important: Larger hole area and greater hole distribution lead to a lower pressure drop, a smaller dead zone, and so on. Theoretical analysis was mainly studied in this work and it has also provided a reference in designing a sufficient mask.

Dbouk and Drikakis (2020c) analyzed the role of the mask in preventing the droplet transmission by utilizing OpenFOAM with a combination of the use of turbulence model and porous model. In the simulation model, the mask fitting to the face was considered which is shown as in Fig. 20 :

Fig. 20.

Model of the mask and face.

More, the interaction between the mask and the droplet was defined to three modes: stick, splash/rebound and penetrate. Droplets escaped from a human with and without a surgical mask were simulated and the simulation results at the fifth second are shown in Fig. 21 :

Fig. 21.

Droplet transmission in situations with and without a mask.

It was obtained from the research work that wearing a mask can effectively prevent the droplet from spreading in large quantities though, many droplets can still penetrate the mask and travel more than 1.2 m. This could explain why doctors and nurses can be infected even with masks and as mentioned in this study, it is so important for a mask to fit face which can block more droplets from the mouth and hence reduce the infection risk.

Li et al. (2009) designed three passageways for a gas mask and simulated the aerodynamic behaviors of gas it; Khanafer et al. (2012) investigated the fluid flow in an artificial lung by defining it as a porous media. It can be found from these investigations that Porous media can perform well on simulating the mass transfer in porous media. However, there are few studies about pathogen transmission by using the Porous Model.

4.2.3. Web-based forecasting system for pathogen transmission

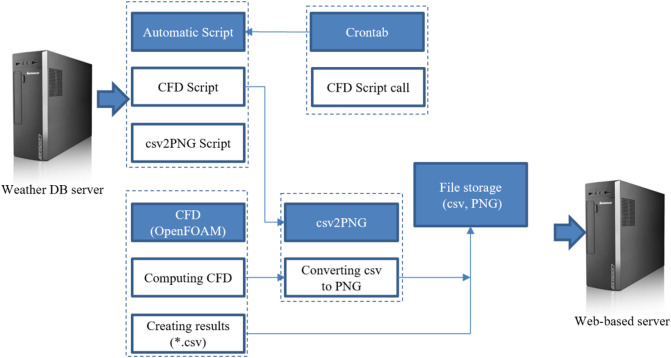
Turbulent flow in the atmosphere is unsteady due to the changing weather and it is difficult to measure the airborne transmission in the atmospheric environment directly. Although aerodynamics models of airborne transmission based on CFD method have been greatly developed, it is still a big challenge for applying them to the large-scale environment. Seo et al. (2015) presented a method based on meteorological information from web-system that can help for solving this problem.

This research group analyzed the relationship between foot-and-mouth disease (FMD) spread and hourly wind in Anseong. Moreover, they collected the infection data and built a model by using the GIS method. Then, they used a code division multiple access (CDMA) to send the weather data to a weather data acquisition server (WDAS) in every 10 min and interlock the data with geographical information. The OpenFOAM code was used to simulate the spread of the airborne virus the simulation result can well describe the virus transmission. The process of the CFD simulation based on web-based forecasting system can be described as below in Fig. 22 :

Fig. 22.

Detailed process of CFD simulation based on web-based forecasting system.

The Web-based forecasting system has been widely used in various cases such as flooding (Li et al., 2006), tourism demand (Song et al., 2008), monitoring of marine pollution (Kulawiak et al., 2010), etc. However, there are few studies about pathogen transmission based on combing the Web-based forecasting system and CFD method. Hence, more databases of pathogen transmission and meteorological information are needed to develop the Web-based forecasting system in the analysis of pathogen transmission.

5. Summary

CFD methods have a good performance in solving complex fluid and are widely used in the study of pathogen transmission in recent years. In this review, different algorithms, models and solvers are introduced and the applicability of CFD under various conditions is summarized. Moreover, investigations of pathogen transmission through CFD are summed up, including the application of an epidemic model on CFD method and transmission process in different environments. In order to obtain the simulation and verify the accuracy of calculation, experimental methods are widely used such as particle experiments and tracer gas experiments. However, most researches simplify the pathogen as particles or gaseous without considering their biological characteristics. Although some investigations have defined the epidemic models in CFD simulation of pathogen transmission, biological characteristics (like propagation and survival rate, etc) of a pathogen are still a gap in recent studies.

From investigations summarized in this review, it can be found that ventilation is one of the most effective methods to control pathogen transmission in the air. Different environments require different ventilation systems, the building environment such as teaching building and residential building and the natural ventilation method is the main way to dilute the concentration of the pathogen. However, in high-risk zones such as hospitals, not only the reasonable ventilation of indoor is required, but also the infectious risk due to emission needs to be considered. Besides, pathogen transmission in different vehicles is distinct, a proper strategy of ventilation is necessary for transportation especially the airplane and high-speed train with an enclosed environment.

This review also presented some advanced methods for CFD application on pathogen transmission according to recent investigations as:

• (1)LBM simulation allows researchers to investigate pathogen transmission from the mesoscale level;
• (2)Based on the Porous Media model, researchers can better analyze the transport of pathogens in complex media, such as medical masks, human organs, etc.
• (3)Web-based forecasting system can be combined with the CFD method to analyze the transmission of infectious pathogens in the atmospheric environment and predict the cross-regional transmission of pathogens.

Declaration of competing interest

The authors declared that they have no conflicts of interest to this work as:

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Editor: Yifeng Zhang