Computational methods for exploring protein conformations

Abstract

Proteins are dynamic molecules that can transition between a potentially wide range of structures comprising their conformational ensemble. The nature of these conformations and their relative probabilities are described by a high-dimensional free energy landscape. While computer simulation techniques such as molecular dynamics simulations allow characterisation of the metastable conformational states and the transitions between them, and thus free energy landscapes, to be characterised, the barriers between states can be high, precluding efficient sampling without substantial computational resources. Over the past decades, a dizzying array of methods have emerged for enhancing conformational sampling, and for projecting the free energy landscape onto a reduced set of dimensions that allow conformational states to be distinguished, known as collective variables (CVs), along which sampling may be directed. Here, a brief description of what biomolecular simulation entails is followed by a more detailed exposition of the nature of CVs and methods for determining these, and, lastly, an overview of the myriad different approaches for enhancing conformational sampling, most of which rely upon CVs, including new advances in both CV determination and conformational sampling due to machine learning.

Introduction

It is now generally accepted that in their biological environment, proteins exist not in a single, rigid structure, but as a dynamic ensemble of conformations distributed across a free energy landscape according to their Boltzmann-weighted probability of occurrence. The structure of this landscape is typically rugged, comprising a large number of conformations of similar energy and possible transition pathways between these, due to proteins having numerous degrees of freedom. The nature of the conformational ensemble and associated energy landscape depend on the protein and its environment, and may change in response to events such as interaction with cellular binding partners. Characterisation of the free energy landscape and thus the accessible conformational ensemble is essential in order to understand the function and malfunction of proteins.

Experiments that report on protein structure, such as X-ray diffraction [1], nuclear magnetic resonance [2] and Förster resonance energy transfer [3], generally provide either the average values of a large number of structural properties or distributions of a small number of structural properties. Neither is sufficient to fully characterise the conformational ensemble, which requires knowing not only the distributions of a large number of property values, but also which combinations of property values occur simultaneously, and the likelihood of each of these combinations. Molecular simulation can, at least in principle, provide this type of information. There are also myriad ways to bias simulations towards conformations that fit the experimental data [4–6].

The physico-chemical properties and molecular connectivity of a molecule or group of molecules are described by a ‘force field’, a mathematical relationship for the potential energy of the system in terms of the coordinates of its substituent particles (often atoms). The coordinates define the molecular conformation, and the potential energy relates to its probability of occurrence. In Markov chain Monte Carlo (MCMC), conformational space is stochastically sampled, whereas in molecular dynamics (MD) simulations, the main focus here, conformational space is deterministically sampled by propagating Newton's equations of motion. In its simplest formulation, this generates time-dependent conformational dynamics, although many of the methods described here trade time continuity for enhanced sampling.

The quality of the force field determines whether the conformations that are sampled in a simulation are realistic. The usefulness of a simulation, however, depends primarily on three factors:

• 1) The molecules included in/excluded from the simulation.

• 2) The level of detail required to examine the biological process or properties of interest.

• 3) The degree of sampling (in terms of temporal and spatial scale).

These three factors are inextricably linked: inclusion of more molecules, representation at a higher level of detail, and more extensive conformational sampling all increase the computational cost. The optimal choice, therefore, is always a trade-off, and depends on the available computational resources.

With regard to the first factor, historically, MD simulations of proteins typically comprised a single protein molecule in vacuum [7] and, later, in aqueous solution [8]. Nowadays, increases in computing power mean that large protein complexes comprising multiple subunits and/or ligands and protein-membrane systems can be simulated [9]. There is also increasing interest in simulating proteins in crowded conditions reminiscent of the interior of a cell [10,11]. While these developments are exciting, the trade-off between system size, the temporal and spatial scale of the motions of interest, and the computational effort required remains.

The choice of the most appropriate level of detail at which to run a simulation depends on the system and process of interest. Force fields are constantly being improved [12–14], but must always balance accuracy with computational efficiency. Standard atomic-level protein force fields, such as AMBER [15], CHARMM [16], and OPLS [17], explicitly model each atom or, in the case of the GROMOS [18] force fields, all heavy and non-aliphatic hydrogen atoms. The interactions between bonded and non-bonded atoms are described using simple mathematical functions, the parameters for which are fitted to structural or thermodynamic quantum-mechanical (QM) or experimental data [19].

To study the reaction mechanism of an enzyme, a mixed QM/MM representation is required. The reaction site is modelled using a QM description, allowing bond breaking and formation, and the remainder of the system is modelled at an atomic (molecular mechanics, MM) level. The QM part of the simulation is extremely computationally expensive, however, limiting the applicability of QM/MM approaches to small systems or short time-scales [20].

To model larger-scale processes with a high dependence on electronic polarisation, such as computing the binding free energy of a ligand to a protein, a polarisable model may be most appropriate [19,21]. Both approaches are too computationally expensive to be a good choice when these aspects are not of interest, however.

At the other end of the scale, coarse-grained representations [22,23], in which multiple atoms are subsumed into beads, allow much larger systems to be simulated for longer time-scales and thus sample larger-scale conformational motions. They can be limited, however, by the common need for additional terms to maintain native structure [24] (e.g. an elastic network model (ENM) [25]), which can limit conformational sampling. The recent implementation of a Gō model as an alternative structural restraint for the Martini coarse-grained model appears to hold much promise in this light [26]. As with QM/MM, mixed resolution or multi-scale simulations provide a compromise between the limitations and benefits of atomic-level and coarse-grained representations [27]. The different resolutions may be deployed sequentially, or concurrently [28]; in the latter, the resolution of each particle can be fixed, adaptable, or decoupled via virtual sites. These various strategies and their different implementations were recently reviewed by Machado et al. [29].

The main focus of this review is the third factor, the degree of sampling. An MD simulation can be considered ergodic if it samples all conformations accessible under the conditions in which it is run (e.g. temperature, pressure) at the correct probability of occurrence. Ergodicity is required if the goal is to determine the underlying free energy landscape. If the aim is to sample only part of the free energy landscape, for example, to follow a particular process, then the extent of sampling of the relevant regions of conformational space becomes important. Convergence of the sampling of conformational space towards the correct Boltzmann-weighted conformational ensemble is unfortunately difficult to measure, although a number of potential methods have been proposed [30]. Convergence may also refer to the approach of the estimated value of a quantity (e.g. the time-average of a structural property calculated from the simulation) to its true value (e.g. the ensemble-average of the same structural property determined experimentally). Often, however, a simulation is being run because the true value is not known, in which case, the overlap between independent estimates (e.g. derived from multiple independent simulations or statistically independent segments of a single simulation) and their associated confidence intervals can be used as a proxy for convergence [30]. A simulation is then said to be converged when the estimated value of a property or properties no longer depends substantially on the length of the simulation or on its initial conditions.

Convergence is in principle possible using MD or MC, but in practice, even just sampling of biologically relevant time-scales (microseconds–milliseconds) is seldom achieved. In general, this is due to the rugged nature of the conformational free energy landscape, on which different regions, representing pools of accessible conformations, may be separated by high free energy barriers that are unlikely to be traversed on the simulation time-scale achievable using available computing resources. For example, an MD simulation with an atomistic force field requires an integration time steps on the order of femtoseconds (10⁻¹⁵ s), whereas biologically interesting events such as protein folding take milliseconds (10⁻³ s) or longer, and so require >10¹² integration time steps. At each step, the interactions between tens or hundreds of thousands of atoms must be evaluated, such that it typically requires weeks or months of simulation on a high-performance computing system to obtain microsecond-millisecond length simulations. Even this may not be enough to assess the probability of all possible events or to estimate the relative population of all possible conformations, that is, to determine the free energy landscape. The sampling problem is exacerbated if the initial coordinates are of poor quality or structurally distant from the region(s) of the free energy landscape that are of interest, and is particularly fraught for intrinsically disordered proteins and protein regions [31,32].

One solution to the sampling problem has been to increase the speed of MD software packages through parallelisation and use of GPUs [33–37]. Another is to build dedicated hardware specifically designed for MD simulation, such as Anton [38] and MDGRAPE-4 [39]. Anton provided the first millisecond all-atom MD simulation of a protein, and its successor can perform multi-microsecond simulation of even larger systems in a single day [40].

MD simulations themselves can also be run in parallel. An early proponent of this, and of citizen science, is the folding@home project, in which a huge number of MD simulations are run on computers volunteered by private citizens [41]. Methods and software aimed at allowing scientists to easily run multiple simulations in parallel are also emerging [42–44]. Each simulation is typically much shorter than the time-scales of interest and covers just a tiny fraction of the complete conformational ensemble, and so must be combined and reweighted. An increasingly popular way of doing so is to construct Markov state models (MSMs), memoryless transition networks describing the populations and kinetics of interconversion between metastable conformational states [45,46]. MSMs have been used to study slow dynamical processes that would otherwise only be accessible using specialised computing infrastructure, including protein folding and conformational transitions. There are also path-based methods that use many short simulations to study slow processes and rare events, such as transition path sampling [47] and milestoning [48], although for the former, the simulations often need to be run sequentially.

Another approach, which forms the basis of this review, is the development of algorithmic methods for enhancing conformational sampling during an MD simulation. It is impossible to discuss modern methods for enhancing sampling without discussing collective variables (CVs), however. CVs are useful for both interpreting the huge amount of detailed data produced during an MD simulation, and directing conformational sampling to efficiently cover the underlying free energy landscape. This review therefore begins by discussing the nature of collective variables and methods for determining these, before describing different approaches to enhancing conformational sampling either to follow a particular process or to sample the free energy landscape, including the flurry of new methods that leverage machine learning techniques. The goal is to provide a general overview of the field rather than delve too deep into technical details.

Collective variables

Conformational ensembles are inherently high dimensional, which makes them difficult to visualise and analyse. Each conformation generated during an MD simulation, for instance, is represented by the coordinates of the N atoms comprising the system, meaning that the conformational ensemble that is produced exists on a 3N-dimensional free energy landscape. Only some of these dimensions are likely to be informative, however. Dimensionality reduction methods are increasingly being used to organise conformational ensembles, and in doing so, to determine which properties are important for organising the conformations or to a biological process of interest, and which are simply noise [49,50]. The generalised coordinates produced by dimensionality reduction are often called collective variables (CVs) (Figure 1), but are also referred to as reaction coordinates, order parameters, and features.

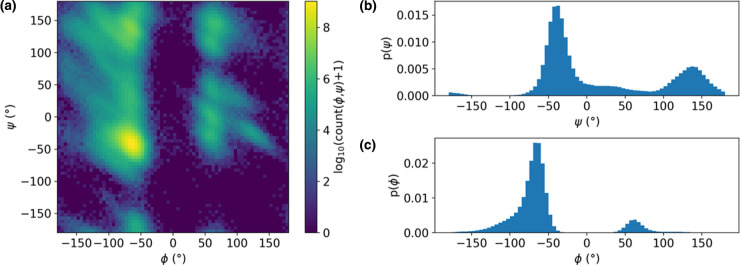
Figure 1. Illustration of projection of a free energy landscape onto commonly used CVs.

(a) Ramachandran maps project the conformational free energy landscape onto the backbone φ and ψ dihedral angle values. The example shown here is for a 100 ns MD simulation of hen egg white lysozyme (PDB ID: 1aki). (b,c) Projections of the conformational free energy landscape onto a single CV: (b) ψ and (c) φ. All angle values are in degrees. Projection of the free energy landscape onto the combination of both backbone dihedral angles is useful because it clearly separates the two major regions of secondary structure, namely (right-handed) α-helices and β-strands, although it is less effective at providing a more detailed degree of separation, such as between parallel and antiparallel β-strands — for this, additional CVs are required. ψ alone (b) could be a useful CV, as it preserves this separation, whereas projection onto φ (c) conflates α-helical and β-strand structure.

A CV is useful if conformational states of interest can be distinguished when the conformational ensemble is projected onto it. For instance, where the goal is to exhaustively sample a conformational ensemble, the conformational states of interest are the metastable states between which transitions are rare. For a process that involves transition between an initial and final conformation, a change in the CV represents progression along the path connecting the initial and final states. Sometimes more than one CV may be required to completely distinguish conformational states.

In addition to aiding the analysis and interpretation of conformational ensembles and MD simulation data, sampling can be directed along one or more CVs to enhance conformational sampling. To effectively enhance sampling, a CV should satisfy the following properties [51–53]:

• Clearly demarcate (meta)stable states of the system that are of interest;

• Account for the highest-variance or slowest conformational transitions;

• Limited in number (to allow the conformations along each CV to be exhaustively sampled);

• Be calculable as an explicit function of the system coordinates.

It is very difficult to intuit good CVs that will usefully enhance sampling, and accelerating irrelevant CVs may not improve the sampling over standard MD. Because of this, there is an enormous literature on CV design, including several recent reviews [52–56]. It is also important to consider interpretability of CVs—this is not necessary to enhance sampling, but is desirable for understanding mechanisms. It may be possible to, however, enhance sampling on one CV and then reweight the trajectory according to another more easily interpretable CV for analysis. Conceptually simple CVs include inter-atomic distances, angles or dihedrals, or the radius of gyration, of a subset of atoms in the system. Even in combination, these may not be adequate to describe the often complex conformational changes that take place during a biologically important event or across the entirety of a free energy landscape, however. In some cases, prior knowledge of the system or process can be used to determine appropriate CVs. It is also possible to use experimental observables directly as CVs [57,58]. In other cases, analysis of a preliminary simulation, or simulations of the end states of a transition, can provide clues. CV choice is delicate, however, and a poor choice can add user bias and reduce the reliability of the CV-enhanced sampling. This concern has stimulated the development of methods for using machine learning, with differing degrees of user input, to determine CVs, although in some cases, this may come at the expense of interpretability [55].

An early but still popular machine learning approach to determining high-variance CVs is to run a preliminary MD simulation and analyse it using principal component analysis (PCA). This identifies linear projections along which the conformational variance is maximal. The first few eigenvectors of the correlation matrix, which represent the leading high-variance modes, can be used as CVs [59]. More recently, harmonic linear discriminant analysis (HLDA) has been used to obtain CVs that are linear combinations of a small set of user-specified descriptors thought to be capable of discriminating between metastable states, based on short unbiased simulations of each state [60]. Combination of HLDA with neural networks allows compression of a larger number of descriptors into a lower-dimensional space [61].

Methods for learning CVs that describe slow modes from preliminary simulations have largely arisen from the MSM field, where they are critical to MSM construction. A key development was that of the variational approach to conformational dynamics (VAC) [62,63] and the more general variational approach of Markov processes (VAMP), which allow iterative assessment of many input functions i.e. CVs or linear combinations thereof, describing possible state decompositions. Input functions with the highest eigenvalue correspond to the indicator function whose eigenfunctions best approximate those of the continuous transfer operator describing transitions between metastable states [62–64].

A popular special case of VAC [65] is time structure-based (or time-lagged) independent component analysis (tICA) [65–68]. tICA allows creation of slow CVs suitable for enhanced sampling methods such as metadynamics [69] by linearly combining potentially simple CVs such as dihedral angles or pairwise contact distances such that their decorrelation time is maximised [45,70]. Importantly, it uses the tICs, which are the time equivalent of the principal components, to explicitly encode kinetic correspondence rather than using structural similarity as a proxy. Kernel tICA [71] and landmark kernel tICA [72] broaden the range of applicable input functions by removing the need for linearity.

Neural networks [73], including nonlinear [50,74,75] and time-lagged variational [76] autoencoders, and a Bayesian framework that operates according to similar principles [77], have also been developed to find the optimal slow CVs. In some cases (e.g. VAMPnets [73]), these methods map directly from molecular coordinates to Markov states, and so are not useful for identifying CVs for other purposes. Additionally, the slowest modes are not always the modes of interest [45,78], although a solution to this problem was recently provided by the deflated variational approach to Markov processes (dVAMP) [79].

Other recent approaches to learning CVs for enhanced sampling include spectral gap optimisation of order parameters (SGOOP) [80], which estimates the best combination of low-dimensional candidate CVs according to the maximum path entropy estimate of the spectral gap for dynamics viewed as a function of those CVs; EncoderMap, based on a neural network autoencoder [81]; and identification of the essential internal coordinates by using supervised machine learning to assign molecular structures to metastable states [82].

Machine learning and related methods are increasingly being used to provide a less heuristic approach to CV discovery. The success of machine learning, however, relies upon abundant and suitable training data; a chicken and egg situation in the case of the rare events for which enhanced sampling is required. A solution is to iterate between sampling and machine learning; such adaptive methods are discussed towards the end of this review.

Enhanced sampling algorithms

Enhanced sampling algorithms speed up sampling of rare events, typically by adjusting the simulation temperature or Hamiltonian, with the latter including tuning the existing terms or adding bias potentials. While use of an enhanced sampling algorithm does not guarantee convergence, done correctly, it will improve conformational sampling and thus increase the likelihood of convergence. A huge number of enhanced sampling algorithms are available, and various methods for categorising these have been suggested [83,84]. Here, the different methods are divided into four categories, depending on whether sampling is enhanced along a CV, how the CV is determined, and whether or not the biasing and/or the CV adapt during the simulation:

1. Sampling enhanced by scaling the temperature

2. Sampling enhanced along one or more CVs

3. Sampling adaptively enhanced along one or more CVs

4. Sampling adaptively enhanced along one or more CVs learnt on-the-fly

Sampling enhanced by scaling the temperature

Notwithstanding the space dedicated to determining CVs, the simplest way to enhance sampling is to increase the temperature and thus the kinetic energy of the system, effectively lowering the heights of barriers between conformations (Table 1). Such approaches will only improve convergence if the major barriers to conformational sampling are not temperature-dependent [85].

Table 1. Category 1: Sampling enhanced by scaling the temperature.

Category 1. No/general CV
Name	Description	Citations
Simulated annealing	System is heated and then gradually cooled. May involve multiple iterations to sample different minima on the free energy landscape. One of the oldest techniques, but recently shown to increase sampling by at least an order of magnitude. Does not sample from a Boltzmann distribution.	[107,108]
Simulated tempering	Like simulated annealing, but samples from a Boltzmann distribution.	[109,110]
T-REMD: Temperature replica exchange MD	Multiple independent replicas in parallel, with coordinates exchanged at regular intervals. Sensitive to the choice of control parameters; substantial literature regarding their optimisation.	[86,91,111–117]
R-REMD: Reservoir REMD	T-REMD with the highest temperature replica replaced with a pre-generated reservoir of structures. Dependent on reservoir adequately covering conformational space.	[118–121]
M-REMD: Multiplexed REMD	T-REMD with several independent simulations at each temperature. Exchanges can occur between these and between temperatures. Takes advantage of highly parallel computing.	[122]
TAMD: Temperature-accelerated MD	Explores free-energy landscape of a large set of CVs at the physical temperature using an artificially high fictitious temperature.	[123]
REST and REST2: Replica exchange with solute tempering	Only the temperature of the solute differs between replicas. Increases the probability of exchanges by reducing the effective system size compared at each exchange attempt.	[91,124]
SGLD: Self-guided Langevin dynamics	SGLD increases the temperature of low-frequency motions only, with the SGLD temperatures scaled across replicas. The implementation of Wu et al. uses the SGLD partition function to remove the problems caused by the ad hoc force term of Lee and Olson [125].	[125,126]

Of these methods, Temperature replica exchange MD (T-REMD, parallel tempering), which combines MD and MC [86], deserves explanation, as it forms the basis for a wide range of methods. Multiple independent MD simulations are run in parallel across a ladder of different temperatures (Figure 2a). Exchange of coordinates between two temperatures is attempted at regular intervals and accepted or rejected according to the Metropolis criterion. Only the lowest temperature simulation, run at the temperature of interest, is kept and analysed. The exchanges mean that sampling is discontinuous, so special analysis methods are required to extract kinetic information and follow processes [87–89]. T-REMD was one of the earliest enhanced sampling methods and remains widely used. For small systems, the increase in computational resources required to run multiple simulations in parallel is compensated for by the increase in sampling. Unfortunately, however, efficient exchange between neighbouring replicas requires sufficient overlap of their energy distributions, and, as a consequence, the number of replicas required to cover a given temperature range grows according to the square root of the number of particles in the system [90].

Figure 2. Schematic illustration of three key enhanced sampling methods.

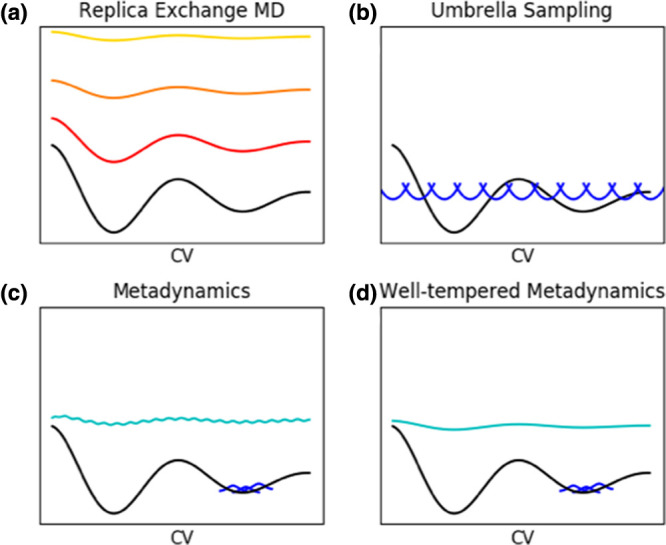
In all cases, the black line represents a free energy landscape projected onto a single CV, for simplicity. (a) Replica exchange MD, in which multiple independent replicas are run under different conditions, such as at increasingly high temperatures (red to yellow lines), which smooth the free energy landscape; (b) Umbrella sampling, where the blue harmonic potentials represent the ‘umbrellas’ that restraint conformational sampling along the CV; (c) metadynamics, where the potential energy surface is smoothed along one or more CVs by adding Gaussian functions (blue) to regions of the conformational space that have already been visited until ultimately (cyan) the entire surface is filled; (d) well-tempered metadynamics, where the rate and size of the Gaussian functions (blue) are reduced as sampling progresses, resulting in a smooth free energy surface (or a pre-specified distribution function, cyan) and avoiding over-filling.

Sampling enhanced along one or more CVs

Perhaps the conceptually simplest approaches to CV-based enhanced sampling are those in which sampling is directed or restrained along a CV that describes a particular process (Table 2 and Figure 2b). These can be useful when the start and end point are known, and if a CV that describes the transition between these can be defined. They are less useful, however, for global exploration of conformational space.

Table 2. Category 2: Sampling enhanced along one or more CVs.

Name	Description	Citations
SMD: steered MD	An external force is applied to induce rare transitions along a CV to occur at a faster rate. Computational analogy to atomic force microscopy. Added force may induce physically unrealistic conformational transitions, and in general, does not sample from a Boltzmann distribution.	[127–129]
US: umbrella sampling	Uses a harmonic biasing potential to restrain the simulation to a series of windows along a pre-defined CV. If reweighted, can be used to determine the free energy surface and thus the change in free energy along the CV.	[130]
H-REMD: Hamiltonian REMD	Like T-REMD, but each replica is simulated under a different Hamiltonian. Classic versions involve scaling the protein backbone and side chain dihedral angle potentials or the non-bonded interactions.	[90,131–137]
Resolution H-REMD	Each replica is simulated at a different level of resolution, e.g. atomic-level to coarse-grained.	[119,138,139]
Partial- and local-H-REMD	Only terms of the Hamiltonian involving the part of the system for which sampling is slow are exchanged.	[140]
2D-REMD	Two-dimensional H-REMD with scaling of temperature and inter-molecular interactions. Also used coarse-grained representation to calculate Kd for an IDP allosteric regulator.	[141]
REAMD: Replica exchange of aMD	Combination of aMD with REMD; each replica has a different level of acceleration. Avoids the statistical reweighting problem of aMD.	[85,142]
ENM-H-REMD: Elastic network model H-REMD.	Each replica is simulated with a different degree of a distance-dependent biasing potential that drives the structure away from its initial conformation in directions compatible with an ENM. Primarily enhances sampling around the initial structure.	[143]
HS-H-REMD: hydrogen bond switching H-REMD	Exchanges take place between three replicas; two with either an attractive or repulsive hydrogen bonding potential added to the Hamiltonian. Similar performance to T-REMD with fewer replicas.	[144]

Hamiltonian REMD (H-REMD) refers to REMD with each replica simulated under a different Hamiltonian (Figure 2a). T-REMD is a special case of H-REMD in which the scaling of the temperature is equivalent to scaling the whole Hamiltonian simultaneously [90]. The benefit of H-REMD is that only the part(s) of the Hamiltonian that limit conformational sampling can be scaled. In this way, H-REMD, like replica exchange with solute tempering (REST) [91], solves the T-REMD problem of the rapidly increasing numbers of replicas required as system size increases [90]. A wide variety of different modifications of the Hamiltonian have been suggested (Table 2). H-REMD is useful when there is little prior knowledge of the nature of the conformational ensemble or free energy landscape and, in particular, what the barriers to conformational sampling might be. Substantial simulation effort can be expanded on sampling modified Hamiltonians that are not of interest, however[55]. Additionally, the choice of how to modify the Hamiltonian can rely on and thus be biased by prior knowledge.

Sampling adaptively enhanced along one or more CVs

Adaptive approaches to enhanced sampling (Table 3) learn about the underlying free energy surface during a simulation and use that knowledge to drive the simulation away from conformations (in CV-space) that have already been visited. In some cases, the size or nature of the added biasing potential may change during the simulation. These approaches not only enhance sampling, but also allow reconstruction of the free energy surface as a function of the chosen CVs [51,53]. Early approaches include accelerated MD [92], adaptive variations of umbrella sampling (US), and methods such as local elevation [93] and conformational flooding [94] that add a history-dependent potential to one or a few system properties, thus constructing the bias potential on-the-fly. Local elevation and conformational flooding are similar to what has become the primary method for adaptive enhanced sampling along CVs: metadynamics [95] (Figure 2c). Its main novelties were adaptation of the free energy rather than potential energy surface, and generalisation of the bias potential to act upon any CV or multidimensional set of CVs. These CVs may be as simple as the backbone dihedral angles, or can be almost arbitrarily complex. There are a huge number of variations of metadynamics, many of which involve combining it with other enhanced sampling techniques. Others, such as well-tempered metadynamics (Figure 2d), adjust the weight of the biasing potential as the biased free energy landscape approaches some target distribution (most simply, a uniform distribution), with the most recent versions doing so via machine learning. The underlying free energy landscape can then be reconstructed as the mirror image of the ultimate bias potential. Table 3 focuses on approaches aimed at increasing conformational sampling rather than calculation of kinetic properties. Interested readers are directed to recent comprehensive reviews dedicated to metadynamics for further details [51–53].

Table 3. Category 3: Sampling adaptively enhanced along one or more CVs.

Name	Description	Citations
aMD: accelerated MD	‘Boost’ potential applied when potential energy drops below a user-specified cut-off to increase rate of escape from minima. Reweighting of the resulting conformational ensemble to account for the applied bias is not always straightforward.	[92,145,146]
aUS: adaptive US	Iterates between sampling along a CV according to an umbrella potential and updating the umbrella potential according to an estimate of the probability distribution along the CV to improve sampling of under-sampled regions.	[147,148]
SH-US: self-healing US	Automatically updates the umbrella potential on-the-fly until the umbrella potentials cancel out the free energy profile.	[149]
Multidimensional aUS	Like aUS, but with the umbrella potentials applied across more than one CV.	[150]
Local elevation	Generates a history-dependent bias potential by adding Gaussians centred on the currently occupied value of one or more system properties to persuade the system to visit new areas of conformational space.	[93]
Conformational flooding	Like local elevation but formulated more generally to act on coarse-grained conformational coordinates.	[94]
LEUS: Local elevation umbrella sampling	A short LE build-up phase is used to construct an optimized biasing potential along conformationally relevant degrees of freedom that is then used in a (comparatively longer) US sampling phase.	[83]
Metadynamics	Like local elevation, but the biases are added to the free energy rather than potential energy surface, and the bias potential is generalised to act upon any CV or multidimensional set of CVs.	[95]
Multiple walkers (altruistic) metadynamics	Many metadynamics runs are performed in parallel, all of which contribute to filling in the free energy landscape.	[151]
WTE metadynamics: well-tempered ensemble metadynamics	The energy is used as collective variable to sample the well-tempered ensemble. Note that this is different to well-tempered metadynamics.	[152]
Bias-exchange metadynamics	A number of independent metadynamics simulations are run in parallel, each biasing a different CV, with exchange of coordinates between biases. The REMD and metadynamics act synergistically to overcome barriers.	[153]
Parallel-bias metadynamics	Single-replica variant of bias-exchange metadynamics in which the CV that is biased is switched during the simulation according to the Metropolis criterion, avoiding the need to have as many replicas as CVs.	[154]
T-REMD (parallel tempering) metadynamics	Multiple metadynamics simulations are performed in parallel at different temperatures, all of which contribute to filling in the free energy landscape. Improves the exploration of low probability regions and sampling of degrees of freedom not included in the CV, but requires a large number of replicas for all but very small systems.	[155]
REST metadynamics	Like T-REMD metadynamics, but only the solute experiences different temperatures.	[156]
WTE-metadynamics REMD	Combines WTE-metadynamics with T-REMD by running WTE-metadynamics at each temperature. Overlap and thus exchange between replicas is increased, and canonical averages of properties of interest can be obtained with reweighting.	[157]
Metadynamics with on-the-fly adjustment of the biasing frequency or weight
WT-metadynamics: well-tempered metadynamics	The height of the Gaussian functions and the rate at which they are deposited decreases during the simulation and inversely to the time spent at a given value of the CV(s) to prevent over-filling.	[158]
TT metadynamics: transition-tempered metadynamics	Like WT-metadynamics, but decreases the height of the Gaussians according to the number of round trips between basins in the free energy landscape. Useful for calculating the free energy surface along a few well-chosen collective variables (CVs) at a time, but requires a priori estimation of the basin positions.	[159]
µ-tempered metadynamics	Like WT-metadynamics, but allows use of wide Gaussians and a high filling rate without slowing convergence.	[160]
WT-metadynamics-REMD	Multiple WT-metadynamics simulations are run in parallel, each biasing multiple CVs simultaneously. The degree of bias increases across the ladder of replicas.	[161]
Metabasin metadynamics	The energy level to which the metadynamics can fill the free energy landscape is restricted, to either a pre-defined level or relative to unknown barrier energies, with both these and the Gaussian shape estimated on-the-fly. Reduces need to carefully choose CVs to avoid sampling irrelevant high-energy regions.	[162]
Metadynamics with on-the-fly adjustment of the biasing frequency or weight to achieve a target probability distribution function
OPES: on-the-fly probability-enhanced sampling	A recent reconsideration of metadynamics that begins with a coarse-grained estimate of the free energy landscape and converges towards a more detailed representation using a weighted kernel density estimation and on-the-fly compression algorithm.	[163]
VES: variationally enhanced sampling; deep-VES	Use an artificial neural network to determine a smoothly differentiable bias potential as a function of a pre-selected small number of CVs that drives the system towards a user-defined target probability distribution in which free energy barriers are lowered.	[164] [165]
TALOS: targeted adversarial learning optimized sampling	Uses a generative adversarial network competing game between a sampling engine and a virtual discriminator to construct the bias potential.	[166]

Sampling adaptively enhanced along one or more CVs learnt on-the-fly

While traditionally, CVs are defined prior to running an enhanced sampling simulation, more recently developed adaptive sampling methods (compared here [96]) iterate between or combine these two phases, making them more applicable to systems where there is little prior knowledge from which to estimate appropriate CVs (Table 4). The learning phases utilise MSMs, tICA, and a variety of machine learning techniques.

Table 4. Category 4: Sampling enhanced along one or more CVs learnt on-the-fly.

Name	Description	Citations
On-the-fly HTMD: on-the-fly high-throughput MD	Iterates between multiple short MD simulations (HTMD) and use of an MSM to learn a simplified model of the system to decide from where to respawn the next batch of simulations.	[167]
Extended DM-d-MD: extended diffusion-map-directed MD; iMapD: intrinsic map dynamics	Uses diffusion maps, a non-linear manifold machine learning technique for dimensionality reduction to select regions of conformational space from an initial unbiased MD simulation from which to launch new rounds of MD simulations. Unbiased simulations are used because CVs based on diffusion maps do not explicitly map to atomic coordinates, and so cannot be used in US or metadynamics, which require calculation of the gradient of the CV with respect to the atomic coordinates [55]	[168,169]
VAC-metadynamics	Uses tICA to analysis an initial WT-metadynamics simulation to obtain more effective CVs that are used in a second WT-metadynamics simulation. Not strictly iterative.	[70]
RAVE: reweighted autoencoded variational Bayes for enhanced sampling	Iterates between enhanced sampling simulations and deep learning using variational autoencoders to learn an optimum but still physically interpretable reaction coordinate, as well as the probability distribution along this coordinate, which are then used to bias the enhanced sampling simulations.	[170]
REAP: reinforcement learning based adaptive sampling	Uses reinforcement learning to estimate the importance of CVs on-the-fly while exploring the conformational landscape. Requires an initial unbiased MD simulation from which to generate a dictionary of CVs and their trial weights.	[171]
MESA: molecular enhanced sampling with autoencoders	Iterates between umbrella sampling along trial CVs and using an auto-associative artificial neural network with a nonlinear encoder and decoder to learn CVs.	[172]

Emerging approaches to conformational sampling

In addition to being used to learn CVs, machine learning has been used to do away with the need to run MD or MC simulations or determine CVs almost entirely.

Deep generative MSMs (DeepGenMSMs) [97] use a generative neural network to learn a model that maps the high-dimensional conformational space to a low-dimensional latent space, describes transitions between metastable states in this latent space, and maps the latent space back to conformations. This model can then predict the future evolution of a system, including previously unseen conformations.

Boltzmann generators [98] use a deep generative neural network to construct invertible transformations between the conformational landscape and a simple Gaussian coordinate system. Sampling of the equilibrium conformational probability distribution, including states not included in the training, can then take place in the simple coordinate system, and the Gaussian coordinates transformed back into conformations. Training the neural network requires furnishing of high- and low-probability states, and thus requires some preliminary, possibly enhanced, conformational sampling [99]. Additionally, this method will require further development to be applicable to the high dimensional space of, e.g. a protein in explicit water [99]. Regardless, this is a very promising approach.

Another new method capable of predicting conformations not incorporated into the training data are dynamic graphical models (DGMs) [100]. The global molecular conformation is partitioned into local substructures, changes to which depend only on themselves and their neighbours. DGMs seem particularly well suited to IDPs and other systems with a very large number of metastable states.

In contrast with the general trend towards removing, as much as possible, human influence on the choice of CVs and thus the directions in which conformational sampling is enhanced, one intriguing method for enhancing sampling that takes the opposite approach is interactive MD, in which the user can add force directly by interacting with the simulation while it is running. While this functionality is not new [101,102], it has recently been given a new lease of life by taking advantage of virtual reality (VR) has been used to allow the user to interact directly with the molecule [103]. A recent update allows interactive ensemble MD simulations, and provides output suitable for MSM workflows [104].

Perspectives

• Converged sampling of the entire free energy landscape, and thus conformational ensemble, is crucial to properly estimate equilibrium properties of molecular systems and to assess the likelihood of states and transition pathways between them.

• Current efforts increasingly use machine learning to determine optimal CVs along which to direct sampling and project the free energy landscape, and iterate between learning CVs and adaptive enhanced sampling techniques, thus reducing the impact of poor CV choice. The latest techniques do away with the need to learn CVs or carry out enhanced sampling altogether, other than to provide training data.

• As has long been the case in the method development field, there remains an urgent need to prove the potential of new methods on the types of complex biological systems that users are interested in, not just simple model systems. There is an increasing focus on improving the reproducibility and reliability of simulations [105]; ideally, use of multiple different force fields and simulation methods should become the norm, aided by tools for improving interoperability between different MD codes [106], and convergence should be monitored, for which robust and widely applicable tools are required. Together, these will greatly improve the quality of investigations of protein conformational dynamics.

Abbreviations

aMD

accelerated MD

aUS

adaptive US

CV

collective variables

DeepGenMSMs

Deep generative MSMs

DGM

dynamic graphical model

DM-d-MD

diffusion-map-directed MD

dVAMP

deflated variational approach to Markov processes

ENM

elastic network model

GPU

graphical processing unit

HLDA

harmonic linear discriminant analysis

H-REMD

Hamiltonian REMD

HS-H-REMD

hydrogen bond switching H-REMD

HTMD

high-throughput MD

iMapD

intrinsic map dynamics

LEUS

Local elevation US

MCMC

Markov chain Monte Carlo (MCMC)

MD

molecular dynamics

MESA

molecular enhanced sampling with autoencoders

MM

molecular mechanics

M-REMD

Multiplexed REMD

MSM

Markov state models

OPES

on-the-fly probability-enhanced sampling

PCA

principal component analysis

QM

quantum-mechanical

RAVE

reweighted autoencoded variational Bayes for enhanced sampling

REAMD

Replica exchange of aMD

REAP

reinforcement learning based adaptive sampling

REMD

replica exchange MD

REST

Replica exchange with solute tempering

R-REMD

Reservoir REMD

SGLD-H-REMD

Self-guided Langevin dynamics H-REMD

SGOOP

spectral gap optimisation of order parameters

SH-US

self-healing US

SMD

steered MD

TALOS

targeted adversarial learning optimised sampling

TAMD

Temperature-accelerated MD

tICA

time structure-based (or time-lagged) independent component analysis

T-REMD

Temperature REMD

TT

transition-tempered

US

umbrella sampling

VAC

variational approach to conformational dynamics

VAMP

variational approach of Markov processes

VES

variationally enhanced sampling

VR

virtual reality

WT

well-tempered

WTE

well-tempered ensemble.

Competing Interests

The author declares that there are no competing interests associated with this manuscript.

Open Access

Open access for this article was enabled by the participation of University of Auckland in an all-inclusive Read & Publish pilot with Portland Press and the Biochemical Society under a transformative agreement with CAUL.

Funding

J.R.A. is supported by a Rutherford Discovery Fellowship (15-MAU-001/UOA-1508).

Author Contribution

J.R.A. designed, drafted and revised this work and approved it for publication.