Comparison of Hexahedral and Tetrahedral Elements in Finite Element Analysis of the Foot and Footwear

Abstract

Finite element analysis has been widely used in the field of foot and footwear biomechanics to determine plantar pressures as well as stresses and strains within soft tissue and footwear materials. When dealing with anatomical structures such as the foot, hexahedral mesh generation accounts for most of the model development time due to geometric complexities imposed by branching and embedded structures. Tetrahedral meshing, which can be more easily automated, has been the approach of choice to date in foot and footwear biomechanics. Here, we use the nonlinear Finite Element program Abaqus (Simulia, Providence, RI) to examine the advantages and disadvantages of tetrahedral and hexahedral elements under compression and shear loading, material incompressibility, and frictional contact conditions which are commonly seen in foot and footwear biomechanics. This study demonstrated that for a range of simulation conditions, hybrid hexahedral elements (Abaqus C3D8H) consistently performed well while hybrid linear tetrahedral elements (Abaqus C3D4H) performed poorly. On the other hand, enhanced quadratic tetrahedral elements with improved stress visualization (Abaqus C3D10I) performed as well as the hybrid hexahedral elements in terms of contact pressure and contact shear stress predictions. Although the enhanced quadratic tetrahedral element simulations were computationally expensive compared to hexahedral element simulations in both barefoot and footwear conditions, the enhanced quadratic tetrahedral element formulation seems to be very promising for foot and footwear applications as a result of decreased labor and expedited model development.

Introduction

Accurate prediction of stresses under the foot in barefoot and shod conditions provides insight into the biomechanics of normal and pathological feet and is especially useful in people with diabetes and peripheral neuropathy (Erdemir et al. 2005, Morag et al. 1997, Shaw et al. 1997, Cavanagh et al. 2000, Bus et al. 2008, Owings et al. 2009). Various experimental and computational methods have been previously developed to measure or estimate the contact pressure and shear stress patterns in the foot during gait (Bus et al. 2009, Sacco et al. 2009, Rao et al. 2010, Maluf, & Mueller 2003, Yavuz et al. 2007, Yavuz et al. 2009). The finite element (FE) method is one such computational tool that is widely used in foot biomechanics for predictive simulations of plantar pressures (Erdemir et al. 2005, Gefen et al. 2000, Gefen 2002, Goske et al. 2006, Chen et al. 2010, Cheung & Zhang 2008, Cheung et al. 2004, Cheung et al. 2005).

In three-dimensional (3D) finite element analysis, two types of element shapes are commonly utilized for mesh generation: tetrahedral and hexahedral. While tetrahedral meshing is highly automated, hexahedral meshing commonly requires user intervention and is labor intensive (Mitchell 2002). As a result, most finite element models of the foot developed to date are built using tetrahedral elements (Chen et al. 2010, Gefen et al. 2000, Cheung, & Zhang 2008, Cheung et al. 2004, Cheung et al. 2005). Nonetheless, hexahedral elements are generally preferred over tetrahedral elements because of their superior performance in terms of convergence rate and accuracy of the solution. The preference for hexahedral elements can be attributed to the fact that linear tetrahedral elements are very stiff and exhibit the phenomena of volumetric and shear locking (Benzley et al. 1995, Cifuentes, & Kalbag 1992). The convergence behavior of tetrahedral and hexahedral elements have also been compared (Ramos & Simões 2006, Benzley et al. 1995) but to our knowledge, no study has yet examined the relative performance of tetrahedral and hexahedral elements when combined with material and geometric nonlinearities such as material incompressibility, large deformation, and frictional contact. All these conditions are common in foot and footwear biomechanics.

The objective of the present study was to evaluate the performance of linear and quadratic tetrahedral and hexahedral elements under conditions such as material incompressibility, frictional contact, and complex loading (compression and shear loads) which are often necessary in barefoot (deformable-rigid contact) and footwear (deformable-deformable contact) simulations. Our specific aims were to assess: (1) the contact pressure and shear stress distributions; (2) the computational cost of simulations using linear and quadratic tetrahedral and linear hexahedral elements under full and relaxed material incompressibility and frictional conditions for barefoot and shod simulations.

Materials and Methods

A simplified geometric model, representative of the human heel pad in contact with the floor or in contact with the insole (in the case of footwear simulations) was created. This model is an approximation of the human heel pad in terms of its shape and size (Erdemir et al. 2006). The model consisted of four components: bone, soft tissue, insole, and floor (Table 1). Bone and floor were modeled as rigid bodies to decrease the computational time. Plantar soft tissue was modeled as a hyperelastic material with a strain energy function represented by a first order Ogden material model of the form:

$$\mathrm{U}=\sum _{\mathrm{i}=1}^{\mathrm{N}}\frac{2{\mu }_i}{{\alpha }_i^2}({\overline{\lambda }}_1^{\alpha i}+{\overline{\lambda }}_2^{\alpha i}+{\overline{\lambda }}_3^{\alpha i})+\sum _{\mathrm{i}=1}^{\mathrm{N}}\frac{1}{D_i}{(J^{el}-1)}^{2i}$$

where λ̄_i are the deviatoric principal stretches, N is the order which was set to 1, μ_i, α_i, D_i are the hyperelastic material constants, and J^el is the elastic volume ratio. The effective Poison’s ratio is dictated by the value of D_i. The hyperelastic constants for the full incompressibility case (effective Poisson’s ratio 0.5) were adapted from Erdemir et al. (2006) (Table 1). In the case of relaxed incompressibility of the soft tissue, the value of D_i was increased to 12.6 leading to an effective Poisson’s ratio of 0.45. The insole was modeled as Microcell Puff using a nonlinear hyperfoam material with a strain energy function represented by:

$$\mathrm{U}=\sum _{\mathrm{i}=1}^{\mathrm{N}}\frac{2{\mu }_i}{{\alpha }_i^2}({\overline{\lambda }}_1^{\alpha i}+{\overline{\lambda }}_2^{\alpha i}+{\overline{\lambda }}_3^{\alpha i}-3)+\frac{1}{{\beta }_i}\left({(J^{el})}^{-{\alpha }_i{\beta }_i}-1\right)$$

Table 1.

Model components and dimensions. R: radius (major axis, along horizontal direction); r: radius (minor axis, along vertical direction); L: length; W: width; D: Depth.

Mesh Entity	Material type	Geometry
Bone	Rigid Shell	Revolution of Quarter Ellipse (R = 20 mm, r = 10 mm)
Floor	Rigid Shell	Planar Surface
Soft Tissue	Hyperelastic, Ogden (Erdemir et al. 2006) μ1 = 0.01645 MPa; α1 = 6.82 ; D1 = 0 or 12.5	Solid Geometry Revolution of Quarter Ellipse (Inner Surface) (R = 20 mm, r = 10 mm) Revolution of Quarter Circle (Outer Surface) (R = r = 30 mm)
Insole	Hyperfoam, Microcell puff (Goske et al. 2006) μ1 = 1.32 MPa; α1 = 28.16; ν1 = 0.054	Rectangular Prism (120 mm (L) × 120 mm (W) × 5 mm (D)

Where λ̄_i are the deviatoric principal stretches, N is the order which was set to 1, and μ_i, α_i, ϑ_i are the material constants. The compressibility coefficient β_i is related to the Poisson’s ratio by the ϑ_i expression: ${\beta }_i=\frac{{\vartheta }_i}{1-2{\vartheta }_i}$.

The material constants were obtained from Goske et al. (2006) (Table 1). Bone and floor surfaces were meshed using 3D triangular (3 node, R3D3) and quadrilateral (4 node, R3D4) rigid shell elements. Soft tissue was meshed and modeled using; a) 4 node hybrid tetrahedron with linear pressure (C3D4H); b) 10 node hybrid tetrahedron with constant pressure (C3D10H); c) 10 node modified hybrid tetrahedron with linear pressure and hourglass control (C3D10MH); d) 10-node general-purpose quadratic tetrahedron with improved surface stress visualization (C3D10I) and; e) 8 node linear hybrid hexahedral element with constant pressure (C3D8H). The insole was meshed using 8 node linear hexahedral elements (C3D8). The boundaries of the bone and soft tissue were tied to prevent any relative motion during the analysis while surface to surface “hard” contact was defined between soft tissue (slave) and floor (master) in barefoot simulations; soft tissue (slave) and insole (master), and insole (slave) and floor (master) in footwear simulations (Abaqus 6.10, 2010). Contact with a coefficient of friction of 0.3 and frictionless conditions were both modeled.

To determine appropriate mesh size, a mesh convergence analysis was performed with simulations conducted under a 300 N compressive load. Five meshes of varying element sizes were modeled. A mesh was deemed to be acceptable when a further increase in mesh density did not change the output variables (contact pressure, von Mises stresses, and hydrostatic pressure by more than 5%. Mesh sizes determined in this manner were: 33,120 elements for hexahedral, 106,261 elements for linear tetrahedral and 39,732 elements for quadratic tetrahedral.

Two loading conditions were considered for idealized barefoot and footwear simulations. In the first case, a compressive load of 300N was applied to the bone to simulate single leg standing. The bone was allowed to move only vertically. In the second case, a compressive load of 700N and a shear force of 100N were applied to the bone simulating the conditions at heel strike during walking. The bone was allowed to move vertically and horizontally. All the simulations were performed using Abaqus Standard 6.10 (Simulia, Providence, RI) on 16 cores of an 8 x Dual Core AMD Opteron computer with 64 GB RAM.

Results

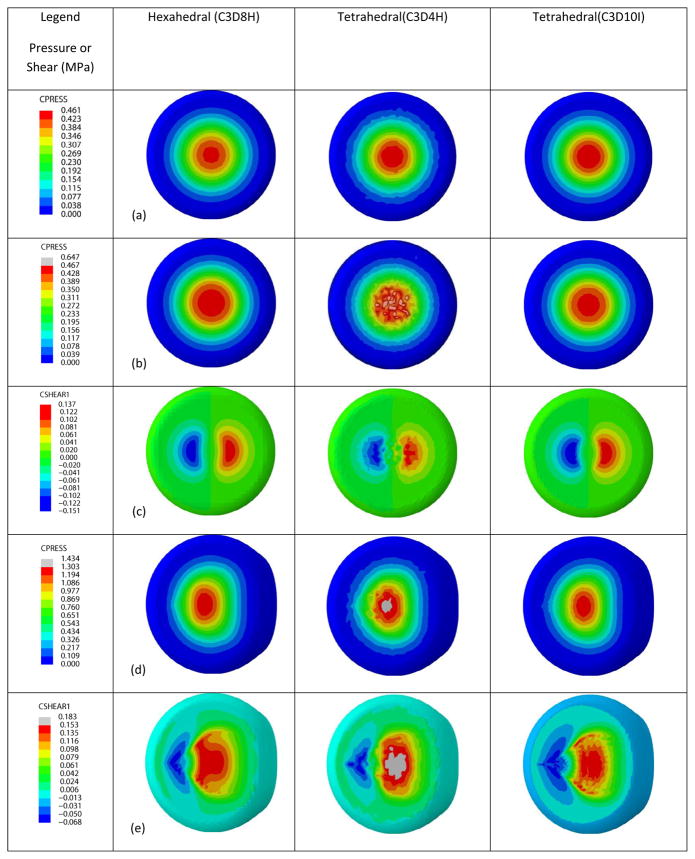
A total of 31 simulations were performed in which the soft tissue was modeled using various element types. Only completely converged finite element solutions are reported and discussed here. Simulations utilizing element types C3D10H and C3D10MH all ended prematurely. For the remaining tetrahedral simulations (C3D4H, “linear tetrahedral”, and C3D10I, “quadratic tetrahedral”) and “hexahedral elements” (C3D4H), the peak contact pressures, contact shear stresses, and computational times are reported in Tables 2 and 3. Contact stress distributions for barefoot conditions (including simulations with the relaxed incompressibility assumption) are presented in Figures 1 and 2. Figure 3 illustrates contact distributions for footwear conditions.

Table 2.

Mesh metrics, loading conditions, material type, peak contact pressure, and simulation times for various barefoot simulations. μ: Coefficient of friction; C: compression; S: shear; Pos: Positive value of shear stress; Neg: Negative value of shear stress. Simulation times were reported by finite element analysis package, Abaqus (Simulia, Providence, RI).

Type of Mesh	No of Elements	No of Nodes	Element Length (mm)	Poisson’s Ratio	Load (N)	μ	Contact Pressure (kPa)	Contact Shear Stress (Pos/Neg, kPa)	CPU Time (Sec)	Wall Clock Time (Sec)
Frictionless contact and compressive load
Linear Hexahedral (C3D8H)	33120	37235	1.1	0.5	300 (C)	0	439.1	-	5408.7	597
Linear Tetrahedral (C3D4H)	106261	20206	1.35	0.5	300(C)	0	466	-	6598.5	790
Quadratic Tetrahedral (C3D10I)	39732	60858	0.8–2.5	0.5	300(C)	0	461.2	-	26081	2239
Frictional contact and compressive load
Linear Hexahedral (C3D8H)	33120	37235	1.1	0.5	300(C)	0.3	434.4	104.2/−104.2	9256.4	842
Linear Hexahedral (C3D8H)	33120	37235	1.1	0.45	300(C)	0.3	516	183.2/−183.2	13061	1170
Linear Tetrahedral (C3D4H)	106261	20206	1.35	0.5	300(C)	0.3	647.2	137.3/−150.8	14154	1433
Linear Tetrahedral (C3D4H)	106261	20206	1.35	0.45	300(C)	0.3	538.6	18.03/−17.74	16883	1690
Quadratic Tetrahedral (C3D10I)	39732	60858	0.8–2.5	0.5	300(C)	0.3	467.1	122.4/−122.4	52420	4063
Frictional contact and combined compression and shear load
Linear Hexahedral (C3D8H)	33120	37235	1.1	0.5	700(C) + 100(S)	0.3	1303	153.3/−65.77	66555	5724
Linear Hexahedral (C3D8H)	33120	37235	1.1	0.45	700(C) + 100(S)	0.3	1475	213.5/−22.30	32347	2826
Linear Tetrahedral (C3D4H)	106261	20206	1.35	0.5	700(C) + 100(S)	0.3	1434	182.9/−68.08	44032	4499
Linear Tetrahedral (C3D4H)	106261	20206	1.35	0.45	700(C) + 100(S)	0.3	1654	225.7/−56.25	35070	3478
Quadratic Tetrahedral (C3D10I)	39732	60858	0.8–2.5	0.5	700(C) + 100(S)	0.3	1389	163/−50.94	162973	12525

Table 3.

Model dimensions, loading conditions, material type, peak contact pressure and simulation times for various footwear simulations. μ: Coefficient of friction; C: compression; S: shear; Pos: Positive value of shear stress; Neg: Negative value of shear stress. Simulation times were reported by finite element analysis package, Abaqus (Simulia, Providence, RI).

Type of Mesh	No of Elements	No of Nodes	Element Length (mm)	Poisson’s Ratio	Load (N)	μ	Contact Pressure (kPa)	Contact Shear Stress (Pos/Neg, kPa)	CPU Time (Sec)	Wall Clock Time (Sec)
Frictional contact and compressive load
Linear Hexahedral (C3D8H)	33120	37235	1.1	0.5	300 (C)	0.3	337.7	65.93/−66.2	27337	2322
Linear Tetrahedral (C3D4H)	106261	20206	1.35	0.5	300 (C)	0.3	434.8	70.18/−67.57	24896	2389
Quadratic Tetrahedral (C3D10I)	39732	60858	0.8–2.5	0.5	300 (C)	0.3	350.2	70.38/−71.05	90732	6765
Frictional contact and combined compressive and shear load
Linear Hexahedral (C3D8H)	33120	37235	1.1	0.5	700 (C) + 100 (S)	0.3	968.9	138.9/−49.15	156195	13000
Linear Tetrahedral (C3D4H)	106261	20206	1.35	0.5	700 (C) + 100 (S)	0.3	1028	148.2/−49.82	115958	10762
Quadratic Tetrahedral (C3D10I)	39732	60858	0.8–2.5	0.5	700 (C) + 100 (S)	0.3	993.5	141.9/−55.02	342181	25874

Figure 1.

Contact pressure and contact shear stress distribution predicted by hexahedral, linear, and quadratic tetrahedral meshes under barefoot simulation conditions. (a) Contact pressure distribution under frictionless contact, compressive load, and full tissue incompressibility. (b) Contact pressure distribution under frictional contact, compressive load, and full tissue incompressibility. (c) Contact shear stress distribution under frictional contact, compressive load, and full tissue incompressibility. (d) Contact pressure distribution under frictional contact, compressive combined with shear load, and full tissue incompressibility. (e) Contact shear stress distribution under frictional contact, compressive combined with shear load, and full tissue incompressibility. Only one component of shear distribution was shown. This direction corresponded to direction of shear loading, if existed. In frictional contact, without shear loading, theoretical focalization of shear distribution should be equal in magnitude but opposite in direction. Color scale for shear was adjusted for comparison purposes, where linear tetrahedral mesh was exhibiting discrepancies from the theoretical focalization.

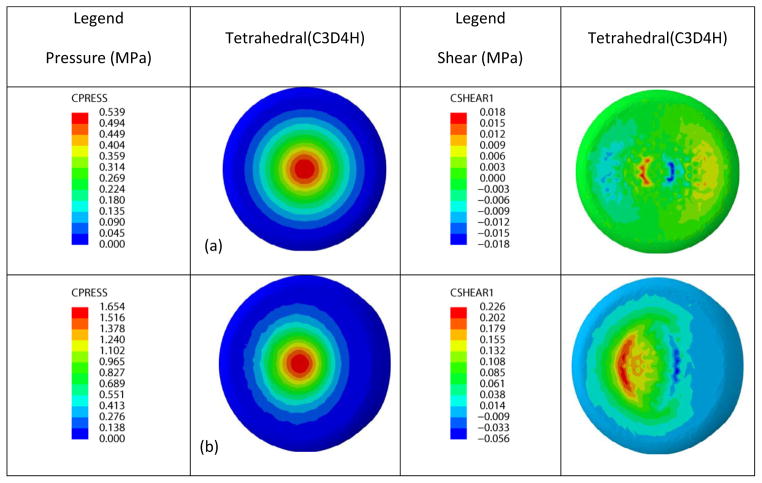
Figure 2.

(a) Contact pressure and contact shear stress distribution predicted by linear tetrahedral mesh under frictional contact, compressive load, and relaxed incompressibility condition (effective Poisson’s ratio 0.45). (b) Contact pressure and contact shear stress distribution predicted by linear tetrahedral mesh under frictional contact, compressive combined with shear load, and relaxed incompressibility condition (effective Poisson’s ratio 0.45).

Figure 3.

Contact pressure and contact shear stress distribution predicted by hexahedral, linear, and quadratic tetrahedral meshes under footwear simulation conditions. (a) Contact pressure distribution under frictional contact, compressive load, and full tissue incompressibility. (b) Contact shear stress distribution under frictional contact, compressive load, and full tissue incompressibility. (c) Contact pressure distribution under frictional contact, compressive combined with shear load, and full tissue incompressibility. (d) Contact shear stress distribution under frictional contact, compressive combined with shear load, and full tissue incompressibility. Only one component of shear distribution was shown. This direction corresponded to direction of shear loading, if existed. In frictional contact, without shear loading, theoretical focalization of shear distribution should be equal in magnitude but opposite in direction. Color scale for shear was adjusted for comparison purposes, where linear tetrahedral mesh was exhibiting discrepancies from the theoretical focalization.

Discussion

Various FE simulations were performed to study the effect of element type on relative prediction of contact pressure and contact shear stress distributions, and solution time (CPU and wall clock). Apart from contact pressures, it is essential to accurately capture the contact shear stresses since a number of authors have suggested that elevated shear stress may play a crucial role in diabetic foot ulceration (Mueller et al. 2008, Yavuz et al. 2007). Since model predictions and computational cost depend on the mesh size, we attempted to determine an adequate mesh size (for each element type) that provided consistent model predictions without further need for an increase in mesh density. In barefoot simulations with frictionless contact under compressive loading conditions, models comprising of hexahedral elements (C3D8H), linear tetrahedral (C3D4H) and quadratic tetrahedral (C3D10I) elements resulted in smooth, uniform, and comparable pressure distributions (Figure 1). Although the peak pressure value predicted by the linear tetrahedral mesh was higher (Table 2), the pressure distribution was acceptable for practical use. In barefoot and footwear conditions, and under compressive loading conditions, when frictional contact was included between the interacting surfaces (soft tissue, insole and floor) contact pressure distribution and contact shear stress distribution predicted by linear tetrahedral mesh was noisy and mesh dependent as illustrated by patches of locally elevated peak pressures (Figure 1b–c,3 a–b). However the pressure distribution predicted by hexahedral and quadratic tetrahedral meshes were smooth and uniform (Figure 1b–c, 3 a–b) and qualitatively similar to the pressure distribution of a heel pad obtained via a commercial pressure platform (Novel North America, St. Paul, MN Figure 4). Under combined compressive and shear loading conditions, the contact pressure and contact shear stress distributions predicted by linear tetrahedral elements were noisy with locally elevated peak pressures compared to the smooth and uniform pressure distributions predicted by quadratic tetrahedral and hexahedral elements (Figure 1d–e, 3c–d). Though the contact pressure distributions predicted by linear tetrahedral elements under footwear conditions were not as noisy as those observed in the barefoot simulations, the peak pressures were considerably higher compared to the solutions using other element types (Table 3). In barefoot simulations, when the material incompressibility of the soft tissue was relaxed, the contact pressure distribution predicted by linear tetrahedral elements under compression and combined compression with shear loading was smooth and uniform (Figure 2). However, the peak contact pressure values were higher by 24% and 26% under compression and compression combined with shear loading conditions compared to hexahedral mesh (Table 2). More importantly, contact shear stress distribution under both compression and compression combined with shear loading still remained noisy (Figure 2) and the peak contact shear stress values decreased by 82–85% compared to those observed using the hexahedral mesh (Table 2).

Figure 4.

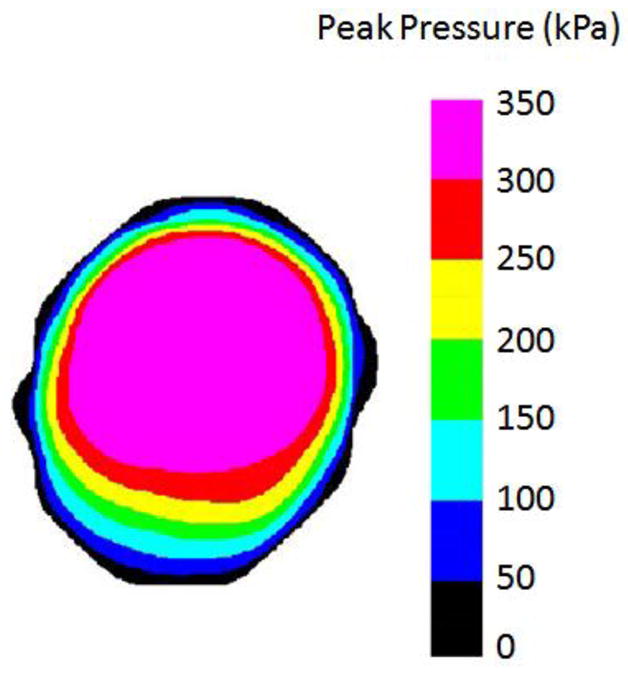
Representative pressure distribution under a human heel pad during barefoot walking obtained using an Emed pressure platform (novel North America, St. Paul, MN). Data collected following Institutional Review Board approval of the University of Washington.

In summary, hexahedral elements consistently predicted reasonable contact pressures and contact shear stresses regardless of loading conditions, material incompressibility, contact, friction, and footwear condition (barefoot or with insole). However, the result from models with linear tetrahedral elements indicated that these elements should only be used under frictionless contact conditions or when the material incompressibility condition can be relaxed. It is clear from our results that a model solved on Abaqus using linear tetrahedral elements to simulate barefoot conditions results in very poor shear stress predictions. We believe that, although future foot and footwear analysts should ideally utilize hexahedral meshes, novel tetrahedral element formulations can provide a reliable solution albeit with the disadvantage of increased computational cost (Tables 2 and 3). Studies which repeat the present study with other finite element analysis software are warranted and to encourage this, we have included access details to the models used in this study in the Appendix.

Appendix

Full data set, including models and input files are freely accessible in the ‘Downloads’ section of the project web site, https://simtk.org/home/meshcomparison (last accessed March 25, 2011).