Quantum Mechanics/Molecular Mechanics Study of Resting-State Vanadium Nitrogenase: Molecular and Electronic Structure of the Iron–Vanadium Cofactor

Abstract

The nitrogenase enzymes are responsible for all biological nitrogen reduction. How this is accomplished at the atomic level, however, has still not been established. The molybdenum-dependent nitrogenase has been extensively studied and is the most active catalyst for dinitrogen reduction of the nitrogenase enzymes. The vanadium-dependent form, on the other hand, displays different reactivity, being capable of CO and CO₂ reduction to hydrocarbons. Only recently did a crystal structure of the VFe protein of vanadium nitrogenase become available, paving the way for detailed theoretical studies of the iron–vanadium cofactor (FeVco) within the protein matrix. The crystal structure revealed a bridging 4-atom ligand between two Fe atoms, proposed to be either a CO₃^2– or NO₃^– ligand. Using a quantum mechanics/molecular mechanics model of the VFe protein, starting from the 1.35 Å crystal structure, we have systematically explored multiple computational models for FeVco, considering either a CO₃^2– or NO₃^– ligand, three different redox states, and multiple broken-symmetry states. We find that only a [VFe₇S₈C(CO₃)]^2– model for FeVco reproduces the crystal structure of FeVco well, as seen in a comparison of the Fe–Fe and V–Fe distances in the computed models. Furthermore, a broken-symmetry solution with Fe2, Fe3, and Fe5 spin-down (BS7-235) is energetically preferred. The electronic structure of the [VFe₇S₈C(CO₃)]^2– BS7-235 model is compared to our [MoFe₇S₉C]⁻ BS7-235 model of FeMoco via localized orbital analysis and is discussed in terms of local oxidation states and different degrees of delocalization. As previously found from Fe X-ray absorption spectroscopy studies, the Fe part of FeVco is reduced compared to FeMoco, and the calculations reveal Fe5 as locally ferrous. This suggests resting-state FeVco to be analogous to an unprotonated E₁ state of FeMoco. Furthermore, V–Fe interactions in FeVco are not as strong compared to Mo–Fe interactions in FeMoco. These clear differences in the electronic structures of otherwise similar cofactors suggest an explanation for distinct differences in reactivity.

Short abstract

A quantum mechanics/molecular mechanics study of the iron−vanadium cofactor (FeVco) of vanadium nitrogenase was performed, starting from the recent X-ray structure containing a new 4-atom XO₃ ligand. Multiple structural models for the cofactor were explored, considering both CO₃²⁻ and NO₃⁻ ligands, three different redox states, and many broken-symmetry states. We find that only a [VFe₇S₈C(CO₃)]²⁻ model is consistent with the experimental structure, discuss the electronic structure in detail, and compare to the iron−molybdenum cofactor.

Introduction

Nitrogenases are nature’s solution to the difficult problem of converting atmospheric nitrogen into a bioavailable form.^1,2 These enzymes catalyze the reaction of dinitrogen to two molecules of ammonia in an adenosine triphosphate (ATP)-dependent process according to the stoichiometry

as recently established for all three types of nitrogenase.³ For each molecule of reacted dinitrogen, a molecule of dihydrogen is produced. This obligatory dihydrogen formation was hypothesized early on^4,5 as being related to a catalytically active state that included hydrides. Now it is well established that the reductive elimination of two hydrides to form dihydrogen is a part of the mechanism.⁶

Three different types of nitrogenase enzymes exist: molybdenum nitrogenase (Mo-nitrogenase),^7,8 vanadium nitrogenase (V-nitrogenase)⁹⁻¹¹ and iron-only nitrogenase (Fe-nitrogenase),^12,13 which differ in their catalytic activity. Mo-nitrogenase is the most active at ambient temperature¹⁴ and is preferably expressed by organisms. It is also the nitrogenase that has been most extensively studied. V-nitrogenase, on the other hand, has received less attention because of difficulties in expressing it, as it is only produced in Mo-deficient conditions.^10,15 While V-nitrogenase is less active under ambient conditions than Mo-nitrogenase, at cooler temperatures, V-nitrogenase is more active than Mo-nitrogenase.¹⁵ In recent years, V-nitrogenase has gained more attention because of its capability of binding CO in its resting state,¹⁶ reducing CO to hydrocarbons,¹⁷ and even reducing CO₂ to CO.¹⁸ Little is known about the third type of nitrogenase, the iron-only nitrogenase. It is even less active than V-nitrogenase and seems to be only expressed in Mo- and V-deficient conditions.^19,20

Mo-nitrogenase consists of the molybdenum–iron protein (MoFe protein), an α₂β₂ heterotetramer, and the iron protein (Fe protein), which is a δ₂ homodimer. The MoFe protein contains a catalytically active site, the iron–molybdenum cofactor (FeMoco) a [MoFe₇S₉C-homocitrate] cluster, and the P-cluster an [Fe₈S₇] cluster.²¹ In the dithionite reduced state (resting state), FeMoco exhibits an S = ³/₂ spin state, as revealed via electron paramagnetic resonance (EPR) spectroscopy, whereas the P-cluster is EPR-silent (in an integer spin state).^1,22−24 The Fe protein is a reductase containing an [Fe₄S₄] cluster, which shuttles electrons to FeMoco through the P-cluster in an event driven by the hydrolysis of ATP.²⁵

Like Mo-nitrogenase, V-nitrogenase is a heteromultimeric protein complex comprised of the vanadium–iron protein (VFe protein) and the Fe protein. The Fe protein of V-nitrogenase shows high similarity to the Fe protein of Mo-nitrogenase, as recently revealed by crystallography.²⁶ However, the VFe protein, as it appears in the 1.35 Å resolution X-ray structure (PDB 5NY6),²⁷ is an α₂β₂γ₂ heterohexamer, containing two more peptide chains than the MoFe protein. The role of these additional chains is currently not clear. The VFe protein contains an iron–vanadium cofactor (FeVco) and a P-cluster, with the latter being more or less structurally identical with its MoFe counterpart but with different redox behavior.²⁸ While the P-cluster of the MoFe protein is EPR-silent in a dithionite solution, there have been reports on S = ¹/₂²⁹ and ⁵/₂³⁰ EPR signals in similar VFe dithionite preparations, which have usually been attributed to a singly oxidized VFe P-cluster, suggesting that a VFe P-cluster is more easily oxidized than a MoFe one.^28,30

FeMoco of the MoFe protein is now well characterized via high-resolution crystallography and spectroscopy. The cofactor resembles two fused iron–sulfur cubanes ([MoFe₃S₃] and [Fe₄S₃]) but with seven Fe ions, nine sulfides, a Mo ion, and a central carbide. It contains a Mo-bound homocitrate ligand and is bound to the protein via a cysteine residue (to one of its Fe atoms) and a histidine residue (to the Mo atom). The overall oxidation state of FeMoco, and the local oxidation state of individual metals, has been a subject of debate. In recent years, the literature has converged on a [MoFe₇S₉C]⁻ resting state via analysis of the ⁵⁷Fe Mössbauer isomer shifts,^31,32 Spatially resolved anomalous dispersion (SpReAD) refinement of the MoFe protein³³ and a computational study by us³⁴ [we found that quantum mechanics/molecular mechanics (QM/MM)-optimized structures only favored this charge state when compared to the 1.0 Å crystal structure of the MoFe protein (PDB 3U7Q)].³⁵ A Mo(III) oxidation state was discovered in FeMoco via Mo X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism experiments and theoretical calculations.³⁶⁻³⁸ A 3Fe(II)4Fe(III) oxidation state is suggested by SpReAD³³ and Se XAS³⁹ experiments, while theoretical calculations suggest more delocalization of electrons.^32,34

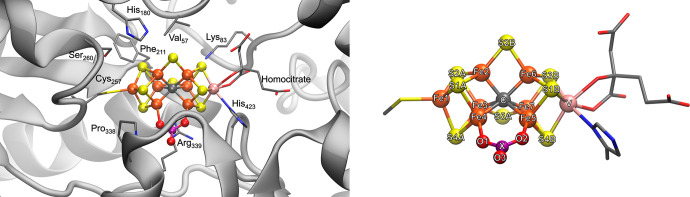
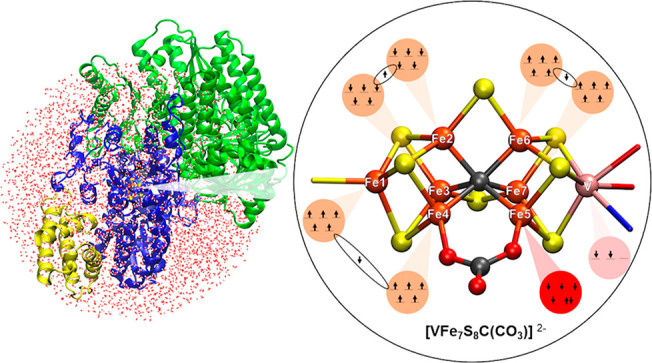
Through multiple spectroscopic studies, FeVco was found to be structurally similar to FeMoco, with a proposed VFe₇ metal core⁴⁰⁻⁴³ and also featuring a central carbide, as evidenced by Fe X-ray emission spectroscopy.⁴⁴ While the first crystal structure of the VFe protein confirmed the overall similar nature of FeVco compared to FeMoco, the crystal structure surprisingly revealed a 4-atom bridging ligand between two Fe atoms (Fe₄ and Fe₅) instead of a bridging sulfide. The electron density map suggested that either a nitrate (NO₃^–) or a carbonate (CO₃^2–) is present (Figure 1),²⁷ and this same ligand also appears in another crystal structure of the VFe protein.⁴⁵ While spectroscopic confirmation of the carbonate/nitrate ligand is lacking for the VFe protein in solution, it will be assumed for the purposes of this study that the carbonate/nitrate ligand, as revealed by the X-ray structure, is an integral part of FeVco that is always present.

Figure 1.

Left: FeVco within the protein matrix as it appears in the PBD5N6Y X-ray structure.²⁷ Right: FeVco with atoms labeled. The 4-atom bridging ligand (shown as XO₃) that is proposed to be either carbonate or nitrate.²⁷

FeVco, like FeMoco, appears to have a noninteger spin of S = ³/₂ in a dithionite solution (in its resting state),^29,46 analogous to synthetic [VFe₃S₄]²⁺ cubanes synthesized by Holm and co-workers.^47,48 This assignment is complicated, however, by the occurrence of multiple S = ³/₂ EPR signals with different rhombicities as well as additional S = ¹/₂ and ⁵/₂ signals. Although these are plausibly attributed to one-electron-oxidized P-clusters, some debate remains about the origin of these signals.²⁸

In the synthetic V-cubanes, the V atom is in a V(III) oxidation state and the Fe atoms in Fe(2.5) and Fe(II) oxidation states according to ⁵⁷Fe Mössbauer studies.⁴⁸ From V XAS, comparing FeVco and a [VFe₃S₄]²⁺ cubane, the V ion of FeVco was also found to be in a V(III) oxidation state.^40,41 A V(III) oxidation state results in a d² configuration, in contrast to the d³ configuration for Mo(III) in FeMoco and [MoFe₃S₄]³⁺ cubanes.^36,49 A joint Fe high-energy-resolution fluorescence detection (HERFD)-XAS and density functional theory (DFT) study comparing [MoFe₃S₄]³⁺/[VFe₃S₄]²⁺ cubanes and MoFe/VFe proteins suggests a more reduced Fe part in FeVco compared to FeMoco.⁵⁰

In our previous theoretical studies^34,51 of FeMoco in the MoFe protein, we demonstrated that the geometric structure of FeMoco is well described by our computational protocol by comparison to the 1.0 Å X-ray structure of the MoFe protein. Our protocol accounts for the protein environment via a systematically improvable QM/MM model and describes the electronic structure via broken-symmetry DFT (BS-DFT) calculations using the TPSSh exchange-correlation functional, which we have found to describe the complex electronic structure of the cofactor better than other functionals.⁵¹ Furthermore, we have shown that the calculated structures are highly sensitive to the redox state of the cofactor and that the charge state of FeMoco could be unambiguously determined by the structural comparison. The analysis furthermore indicated a specific electronic state (BS determinant) to be in better agreement with the experimental structure than the other low-lying states.³⁴

In comparison to FeMoco, few computational studies have focused on FeVco,^{44,50,52−55} and to the best of our knowledge, only a single study⁵⁵ from our own group has presented calculations on FeVco that included the new 4-atom ligand (carbonate or nitrate). Our previous study presented calculations on a nonresting ligand-bound state and focused primarily on the assignment of a light-atom ligand (NH or OH) bridging Fe₂ and Fe₆ of FeVco in a recent crystal structure.⁴⁵ Our QM/MM calculations found a structure with an OH ligand to be more consistent with the crystal structure than an NH ligand. The results were not as clear-cut, however, for the identity of the 4-atom ligand bridging Fe₄ and Fe₅, with calculated structures slightly favoring carbonate over nitrate.

In this study, we present QM/MM calculations of FeVco in the VFe protein in its resting state. The aim is to characterize the electronic structure of the cofactor and compare it to the resting state FeMoco in the MoFe protein. Thus, we seek to critically examine, via comparison to the recent crystal structure,²⁷ whether the calculations are more consistent with a carbonate or a nitrate ligand and whether the Fe redox state of the cofactor is more reduced or oxidized than that in FeMoco. We also set out to understand the differences in the electronic structures between both cofactors that are known to give rise to different reactivities.

Computational Details

MM Model Preparation

The VFe protein was first modeled classically using the 1.35 Å X-ray structure of the VFe protein from Azotobacter vinelandii as a starting point.²⁷ The protocol is similar to that of our previous model for the MoFe protein.³⁴ All molecules and residues present in the crystal structure were included, and no attempt was made to model missing residues. GROMACS, version 5.1.4,⁵⁶⁻⁵⁸ was used to prepare the MM model and add missing H atoms. The VFe protein is an α₂β₂γ₂ heterohexamer (it contains two VnfDKG trimers), and the protonation state of titrable residues was determined in a single αβγ trimer by visual inspection of the hydrogen-bonding patterns [see the Supporting Information (SI) for specific assignments]. It is assumed here that the protonation state of the titrable residues is the same in both αβγ subunits. The CHARMM36 protein force field⁵⁹ was used in all MM and QM/MM calculations (see the SI for details on force-field parameters for inorganic residues). The protein was solvated in a cubic periodic box and as the overall charge of the protein was 62 -, the charge was neutralized by adding 62 Na ions ions, giving a total system size of 531080 atoms. The MM model was then simulated in the NVT ensemble at 300 K for 5 ns. Further details on the MM setup are given in the SI.

QM/MM Preparation and Calculations

A spherical QM/MM model (Figure 2) was generated from a snapshot from the MM molecular dynamics trajectory). All residues from a single αβγ trimer (VnfDKG) and all residues from the second β monomer (VnfK) of the VFe protein are in the QM/MM model (chains A–C and E, as labeled in PDB 5N6Y),²⁷ i.e., an αβ₂γ heterotetramer. Additionally, all water molecules and other crystallographically determined ions within ∼42 Å of the carbide of a single FeVco unit, as well as 35 Na ions, are included to keep the system charge-neutral. See the SI for further information. The QM/MM model size is 32562 atoms. An alternative QM/MM model consisting of the full protein was also prepared, as detailed in the SI and discussed in the Results and Discussion section.

Figure 2.

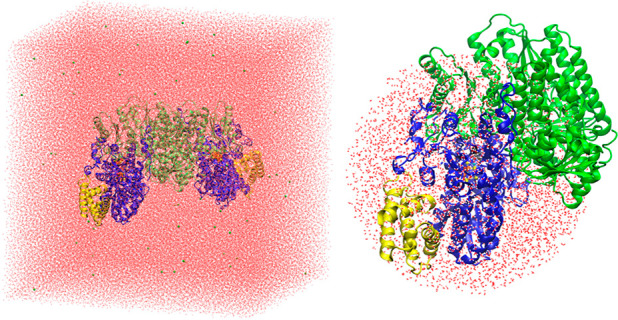
Left: 531080-atom MM model. Right: 32562-atom QM/MM model.

Chemshell, version 3.7,^60,61 was used for all QM/MM calculations using ORCA, version 4.1.0^62,63 (unless otherwise stated), as the QM code within an electrostatic embedding QM/MM coupling scheme. Broken-symmetry solutions of FeVco were found with the spin-flipping procedure, as implemented in ORCA from a high-spin ferromagnetic state (M_S = ³⁵/₂, ³⁴/₂, or ³³/₂, depending on the redox state).

Link atoms were used to terminate the QM/MM border using a charge shift scheme, as implemented in Chemshell.⁶⁰ For the QM calculations, we used the same methodology as that in previous studies,^34,51,55 the TPSSh hybrid density functional^64,65 with a relativistically recontracted def2 Ahlrichs basis set^66,67 with a triple-ζ ZORA-def2-TZVP for V, Fe, S, carbide, and the XO₃ ligand, whereas a double-ζ ZORA-def2-SVP was used for other atoms.⁶⁷ The RIJCOSX approximation^68,69 was used with the default grid setting to speed up the Coulomb and exchange integrals. The D3BJ dispersion correction^70,71 and ZORA relativistic approximation^72,73 were also used. The MM calculations used the CHARMM36 force field within the DL_POLY program,⁷⁴ as implemented in Chemshell, and QM/MM geometry optimizations were performed with DL-FIND.⁷⁵

The QM/MM optimizations used an active region of 1038 atoms (except where otherwise stated), with all other atoms of the model frozen. Three QM regions were used, with the smallest region being 57 atoms, the intermediate region being 83 atoms, and the largest region being 181 atoms (link atoms are not included in the atom count); see Figures S1–S3. Single-point QM/MM calculations on the crystal structure geometry were calculated using ORCA with the MM point charges included. The VMD program⁷⁶ was used to render the figures of molecular structures in this Article and to calculate RMSDs of the structures. Polarized QM energies (i.e., QM energies polarized by the MM point charges) are primarily discussed instead of total QM/MM energies.

Results and Discussion

A computational model of the resting state FeVco depends on the identity of the 4-atom ligand, redox state, total spin state (M_S value in BS-DFT), and actual spin-coupling configuration (an electronic or a broken-symmetry state in BS-DFT). We are describing the spin coupling of this complicated system via BS-DFT, which unfortunately is not capable of describing pure spin states. Nonetheless, for the related FeMoco system, BS-DFT has been rather successful for describing its various geometric and spectroscopic properties,^32,44,50,77 and the landscape of broken-symmetry solutions has been extensively explored in multiple studies.^53,78,79 This, however, is not the case for FeVco since the discovery of the 4-atom ligand. We will thus start our discussion by exploring the broken-symmetry landscape of FeVco via single-point calculations on the X-ray crystal structure for various models (section 1), before moving on to QM/MM geometry optimizations for the most plausible broken-symmetry states compared to the crystal structure (section 2). We note that the X-ray structure of the VFe protein has a resolution of 1.35 Ų⁷ compared to the X-ray structure of the MoFe protein with 1.0 Å resolution.³⁵ As will be shown, the lower resolution is still sufficient for distinguishing between different cofactor models. The electronic structure of the final FeVco model is then analyzed in detail and compared to the more studied FeMoco (section 3). Finally, we discuss the problem of redox stability of FeVco in these calculations (section 4)

1. Broken-Symmetry Solutions of FeVco (Using the X-ray Structure)

Noodleman and co-workers originally proposed 10 different BS solutions for FeMoco,⁷⁹ assuming 3-fold symmetry of the cofactor. For FeMoco and FeVco, this symmetry is broken, both by the ligation on Mo/V and by the protein environment. In recent studies that account for the protein environment,^51,80−82 it has become common to consider all 35 BS ways of flipping the Fe ions in FeMoco, and as shown in our QM/MM study on FeMoco,³⁴ spin-isomeric solutions (i.e., solutions equivalent under 3-fold symmetry) give important geometric differences. In the case of FeVco, the new 4-atom bridging ligand further breaks the symmetry, and hence it becomes necessary to consider all possible broken-symmetry solutions. We label the broken-symmetry solutions according to the Noodleman classification⁷⁹ but also according to which Fe ions are spin-down, e.g., “BS7-235” (BS7 class according to Noodleman), and where Fe₂, Fe₃, and Fe₅ (crystal-structure numbering) are spin-down. Because the V ion is part of the spin coupling in the cluster, it could also be considered part of the spin-flipping problem. In practice, we have found (similar to FeMoco) that the V ion will always flip to its lowest configuration on its own (see the SI for more information).

Because the charge, ligand, and metal oxidation states of FeVco in the X-ray structure are not completely clear, we will consider three different redox states for each carbonate and nitrate ligand model: [VFe₇S₈C(CO₃)]^0,1–,2– and [VFe₇S₈C(NO₃)]^1–,0,1+. We note that an Fe XAS study showed that FeVco (in the VFe protein) in its S = ³/₂ resting state likely contains a more reduced Fe part compared to FeMoco.⁵⁰ While the protein crystals in the X-ray crystallography study were not subject to an EPR investigation, the dithionite conditions employed in crystallization of the protein should result in crystallized resting state (i.e., the S = ³/₂ state). We considered two redox states compatible with S = ³/₂ ([VFe₇S₈C(CO₃)]^0,2– and [VFe₇S₈C(NO₃)]^1–,1+) and one integer-spin redox state ([VFe₇S₈C(CO₃)]⁻ and [VFe₇S₈C(NO₃)]⁰) for comparison. All models with different redox states, different ligands, and different total spins (M_S in BS-DFT) and their energies are tabulated in Table S1.

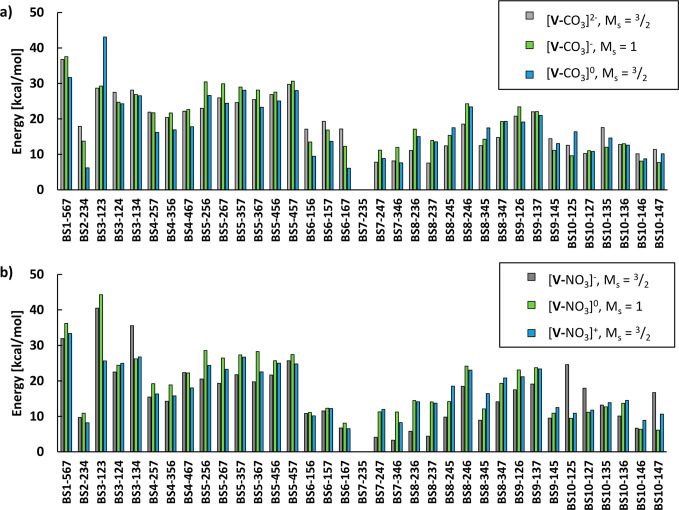
The electronic energies of the 35 broken-symmetry solutions (single-point QM/MM energies on the X-ray structure; QM region of 57 atoms) for each model are shown in Figure 3. For simplicity, only the lowest-energy total spin states (M_S), where the lowest-energy BS solution is found, are shown (see Figures S4–S18 and Table S1 for data on other spin states). In the following discussion, we use the abbreviation [V-XO₃]ⁿ, where V indicates the VFe₇S₈C part of the cofactor, X is either C or N in the 4-atom ligand, and n indicates the total charge.

Figure 3.

Relative energies (polarized QM energies) of all 35 broken-symmetry solutions of FeVco. All calculations were performed on the crystal structure geometry of the cofactor, with MM point charges included.²⁷ In all cases, the BS7-235 state was found to be favored, and all energies are therefore relative to the BS7-235 solution for each redox state and ligand model. (a) Relative energies for carbonate models. (b) Relative energies if nitrate is the 4-atom ligand. The QM-region size in the QM/MM model is 57 atoms.

In the case of [V-CO₃]⁰, the M_S = ³/₂ BS7-235 solution is favored, while M_S = ¹/₂ BS7-235 (+3.27 kcal/mol), BS10-147 (+4.95 kcal/mol), and BS10-146 (+5.06 kcal/mol) are the second, third, and fourth lowest in energy, respectively. The BS solution that is the second lowest for M_S = ³/₂ is BS6-167 (+6.09 kcal/mol), whereas the BS7-346 (+7.63 kcal/mol) and BS7-247 (+8.30 kcal/mol) with M_S = ³/₂ are even higher in energy.

For the integer-spin redox state [V-CO₃]⁻, BS7-235 with M_S = 1 is favored, followed closely by M_S = 2 BS7-235 (+1.51 kcal/mol; Figure S5), M_S = 2 BS7-346 (+8.67 kcal/mol; Figure S5), and M_S = 2 BS7-247 (+9.37 kcal/mol; Figure S5). For [V-CO₃]^2–, BS7-235 with M_S = ³/₂ is favored, followed by BS8-237 (+7.58 kcal/mol), BS7-247 (+7.83 kcal/mol), and BS7-346 (+8.18 kcal/mol). The M_S = ¹/₂ BS8-236 (+11.08 kcal/mol) is the lowest M_S = ¹/₂ solution.

Exchanging the CO₃ ligand for a NO₃ ligand results in some changes to the energy landscape. The BS7-235 solution with M_S = ³/₂ is still preferred for [V-NO₃]⁺, followed by M_S = ¹/₂ solutions BS7-235 (+2.51 kcal/mol), BS10-146 (+4.22 kcal/mol), and BS10-147 (+4.70 kcal/mol), whereas the BS6-167 (+6.50 kcal/mol) solution with M_S = ³/₂ is the fifth lowest in energy.

For [V-NO₃]⁰, the M_S = 1 BS7-235 is favored, with M_S = 1 BS10-147 (+6.10 kcal/mol) being the second lowest in energy, whereas M_S = 1 BS10-146 (+6.38 kcal/mol) and M_S = 1 BS6-167 (8.10 kcal/mol) are the third and fourth lowest in energy, respectively.

For [V-NO₃]⁻, M_S = ³/₂ BS7-235 is the lowest in energy, with BS7-346 (+3.30 kcal/mol) being second lowest, whereas BS7-247 (+4.09 kcal/mol) and BS8-237 (+4.41 kcal/mol) are the third and fourth lowest in energy, respectively.

Overall, the BS7-235 broken-symmetry solution is always favored, regardless of whether a CO₃ or a NO₃ ligand is considered or what the redox state is. Unlike FeMoco, the other spin-isomeric BS7 solutions (BS7-247 and BS7-346) are usually higher in energy for FeVco than other non-BS7 solutions. For FeMoco ([MoFe₇S₉C]⁻; M_S = ³/₂), the BS7 class of solutions is the lowest in energy^34,79 and energetically indistinguishable but does result in distinct geometric differences. As discussed in our previous study,³⁴ the FeMoco BS7-235 solution yields a calculated structure in very good agreement with the geometry of the crystal structure (and captures trends in the metal–metal distances not seen for the other BS solutions) but is not quite the lowest in energy (being 0.7 kcal/mol higher in energy than BS7-346).

The functional dependence of these single-point energy calculations was explored by redoing the calculations on [V-CO₃]^2– with the nonhybrid TPSS functional and the 20% Hartree–Fock (HF) exchange hybrid B3LYP functional (Figure S19); BS7-235 was still always preferred. Calculations were also performed without an explicit protein environment using a continuum solvation model (CPCM with a dielectric constant of 4) instead of QM/MM (Figure S20), but the preference for BS7-235 was retained.

Mulliken spin populations of the different [VFe₇S₈CXO₃]ⁿ models are tabulated in Tables S4–S17. We note that if the self-consistent field did not converge to the specific BS solution attempted but rather another one, then no attempt was made to force convergence.

2. QM/MM-Optimized Models

As discussed, the BS7-235 solution is overall favored by a few kilocalories per mole for all redox states and ligands considered. When considering the other BS7 solutions, this preference for BS7-235, compared to BS7-346 and BS7-247, seems to be an effect exerted by both V and XO₃, which stabilize this particular BS solution (see “the BS7 solutions” chapter in the SI). Because of this strong preference, we will only discuss the BS7-235 solution from now on. QM/MM geometry optimizations were performed for the BS7-235 solution for each ligand and each redox state considered: [V-CO₃]^0,1–,2– and [V-NO₃]^1+,0,1–. For the noninteger spin redox states, we only considered a M_S = ³/₂ spin state due to the strong preference for this spin state (and due to the experimental spin state being S = ³/₂), as previously discussed, while for [V-CO₃]⁻, both M_S = 1 and 2 spin states were considered (because of the small energy gap between these states).

The root-mean-square deviations (RMSDs) of the optimized cofactors (the [VFe₇S₈C(XO₃)] part) with respect to both cofactors in the crystal structure are shown in Table 1 for two different QM regions. This RMSD definition is used throughout the Article.

Table 1. RMSDs^b (in Å) of Different QM/MM-Optimized Geometries Compared to the Experimentally Determined X-ray Structure^a,27.

structure and spin	57-atom QM region	181-atom QM region
[V-CO3]2–, MS = 3/2	0.082	0.079
[V-CO3]−, MS = 1	0.085	0.079
[V-CO3]−, MS = 2	0.111	0.104
[V-CO3], MS = 3/2	0.104	0.091
[V-NO3]−, MS = 3/2	0.095	0.085
[V-NO3], MS = 1	0.095	0.082
[V-NO3]+, MS = 3/2	0.093	0.088

^aThe BS7-235 solution is used for all calculations.

^bThe RMSD is defined as the deviation of the [VFe₇S₈C(XO₃)] part with respect to both cofactors in the X-ray structure.

For a small 57-atom QM region, the optimized [V-CO₃]^2– model yields a structure that is in best agreement with the X-ray structure, based on the RMSDs. The M_S = 1 [V-CO₃]⁻ model, however, gives an RMSD value of only 0.003 Å higher. Other models give larger deviations and appear at first glance less likely. The M_S = 2 [V-CO₃]⁻ model is interestingly in worst agreement with the crystal structure, despite the previous single-point calculations showing the M_S = 1 and 2 states as close in energy (1.51 kcal/mol in favor of M_S = 1). Once optimized, the energy difference between the two M_S states increases to 8.60 kcal/mol for the 57-atom QM-region QM/MM model and further increases to 13.08 kcal/mol for the 181-atom QM-region QM/MM model.

As the QM-region size is increased from 57 to 181 atoms, the spread in the RMSD values for the models becomes smaller. [V-CO₃]^2– and [V-CO₃]⁻ now yield equally good structures, and [V-NO₃]⁰ is only 0.003 Å worse. The simple RMSD metric thus appears to not be beneficial in distinguishing between different FeVco models. However, if instead we focus on comparing individual metal–metal distances of the optimized structures to the X-ray structure (presented in Figure 4 and Table 2), a clear distinction between models becomes apparent.

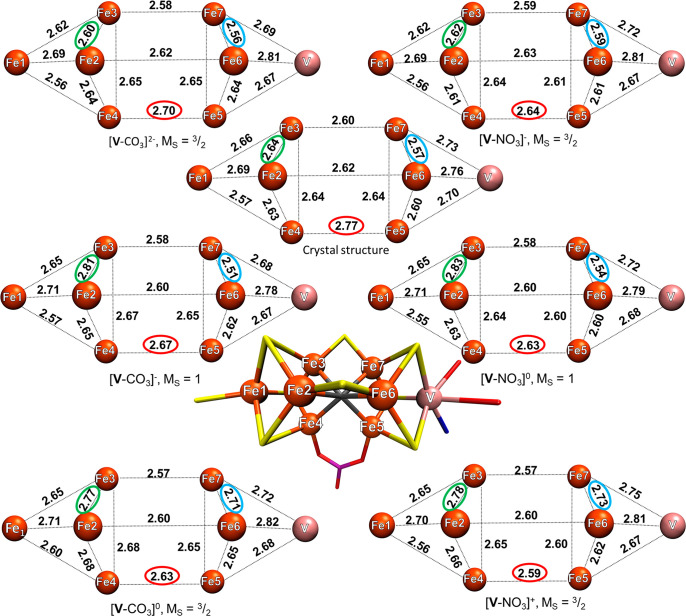
Figure 4.

Metal–metal distances of six QM/MM models (QM region: 181 atoms) calculated using the BS7-235 solution compared to the X-ray structure. The green and blue ellipsoids highlight the Fe₂–Fe₃ and Fe₆–Fe₇ distances that are strongly affected by the redox state. The red ellipsoid highlights the change in the Fe₄–Fe₅ distance with the bridging XO₃ ligand. The metal–metal distances of the crystal structure are the average of the two cofactors found in the 5N6Y crystal structure. All distances are in angstroms.

Table 2. Various Bond Lengths (Å), Atom–Atom Distances (Å), and a Dihedral Angle (deg) of the Two Instances of FeVco in the PBD 5N6Y Crystal Structure and Values from Relaxed QM/MM (181 QM-Region Atoms) Structures.

model	crystal A	crystal B	[V-CO3]2–	[V-CO3]−	[V-CO3]	[V-NO3]−	[V-NO3]	[V-NO3]+
spin (MS)	N/A	N/A	3/2	1	3/2	3/2	1	3/2
BS	N/A	N/A	BS7-235	BS7-235	BS7-235	BS7-235	BS7-235	BS7-235
Fe1–Fe2	2.71	2.68	2.69	2.71	2.71	2.69	2.71	2.70
Fe1–Fe3	2.66	2.65	2.63	2.65	2.65	2.62	2.65	2.65
Fe1–Fe4	2.58	2.57	2.58	2.57	2.60	2.56	2.55	2.56
V–Fe5	2.70	2.69	2.67	2.67	2.68	2.67	2.68	2.67
V–Fe6	2.77	2.75	2.81	2.78	2.82	2.81	2.79	2.81
V–Fe7	2.73	2.74	2.69	2.68	2.72	2.72	2.72	2.75
Fe2–Fe3	2.63	2.65	2.60	2.81	2.77	2.62	2.83	2.78
Fe2–Fe4	2.62	2.63	2.64	2.65	2.68	2.61	2.63	2.66
Fe3–Fe4	2.63	2.64	2.65	2.67	2.68	2.64	2.64	2.65
Fe5–Fe6	2.60	2.60	2.64	2.62	2.65	2.61	2.60	2.62
Fe5–Fe7	2.63	2.64	2.65	2.65	2.65	2.61	2.60	2.60
Fe6–Fe7	2.57	2.57	2.56	2.51	2.71	2.59	2.54	2.73
V–Fe1	7.11	7.09	7.05	7.00	7.00	7.04	7.01	6.99
C–Fe1	3.48	3.49	3.47	3.39	3.44	3.45	3.38	3.42
C–V	3.63	3.60	3.59	3.61	3.57	3.59	3.63	3.57
Fe2–Fe6	2.61	2.63	2.62	2.60	2.60	2.63	2.60	2.60
Fe3–Fe7	2.60	2.60	2.58	2.58	2.57	2.59	2.58	2.57
Fe4–Fe5	2.76	2.78	2.70	2.67	2.63	2.64	2.63	2.59
Fe4–O1XO3	1.97	1.93	1.96	1.93	1.90	2.05	2.04	2.01
Fe5–O2XO3	1.93	1.94	1.97	1.94	1.91	2.05	2.02	2.00
∠Fe4–O1XO3-O2XO3-Fe5	–11.30	–10.93	–13.85	–14.42	–15.09	–11.15	–10.76	–10.74
V–Oalcohol	2.17	2.17	2.16	2.14	2.12	2.15	2.12	2.07
V–Ocarboxy	2.12	2.10	2.08	2.05	2.03	2.06	2.03	2.02
V–NHis423	2.30	2.31	2.21	2.21	2.20	2.21	2.21	2.21
Fe1–SCys257	2.29	2.32	2.29	2.27	2.25	2.28	2.26	2.25
Fe2–S2B	2.21	2.23	2.21	2.17	2.17	2.19	2.16	2.16
Fe6–S2B	2.17	2.21	2.19	2.17	2.15	2.17	2.17	2.14
Fe3–S5A	2.23	2.23	2.20	2.17	2.16	2.19	2.16	2.15
Fe7–S5A	2.27	2.25	2.21	2.19	2.17	2.20	2.18	2.15

We note in this context that there is little variation in the metal–metal distances of FeMoco in X-ray structures of the MoFe protein of differing resolution, as is shown in Table S26. In the comparison of a 1.0-Å-resolution X-ray structure (PDB 3U7Q) to a 1.43-Å-resolution X-ray structure (PDB 4TKU),⁸⁴ there is a maximum of 0.04 Å difference in the metal–metal distance, whereas the mean absolute deviation is only 0.01 Å. We therefore consider the 1.35 Å resolution of the VFe protein sufficient for our comparison of computed models to X-ray geometries.

Considering first the X-ray structure, a comparison of distances involving Fe₁ and Fe₂, Fe₃, and Fe₄, respectively (in the Fe₄S₃C cubane part of FeVco), reveals Fe₁–Fe₄ as the shortest (2.57 Å), Fe₁–Fe₃ in the middle (2.66 Å), and Fe₁–Fe₂ as the longest (2.69 Å). All computed models also show this trend, revealing an asymmetry in the Fe–Fe interactions. Turning our attention to the Fe₂–Fe₃ distance next, for [V-CO₃]⁻ and [V-NO₃]⁰, the Fe₂–Fe₃ distance is significantly overestimated compared to the experiment by 0.17 and 0.19 Å, respectively. The same applies for the [V-CO₃]⁰ and [V-NO₃]⁺ models, where the same distance is overestimated by 0.13 and 0.14 Å, respectively, whereas the more reduced [V-CO₃]^2– and [V-NO₃]⁻ models underestimate it by only 0.04 and 0.02 Å, respectively. Hence, a clear sensitivity of the cofactor geometry with respect to the redox state is revealed.

In the VFe₃S₃C cubane, the X-ray structure reveals the trend of Fe₅–Fe₇ being longer (2.64 Å) than the Fe₅–Fe₆ (2.60 Å) and Fe₆–Fe₇ (2.57 Å) distances. This trend is not captured at all for the more oxidized models, [V-CO₃]⁰ and [V-NO₃]⁺, which instead show Fe₆–Fe₇ as the longest distance. The carbonate models [V-CO₃]⁻ and [V-CO₃]^2– capture the trend reasonably well and the nitrate models less well.

These redox-dependent structural changes for the Fe₂–Fe₃ and Fe₆–Fe₇ pairs are particularly significant and can be understood. The [V-CO₃]^2– and [V-NO₃]⁻ models are in good agreement with the X-ray structure for these distances. For Fe₂–Fe₃, the deviations are only 0.04 and 0.02 Å, respectively, but when an electron is removed, the distance increases by 0.21 Å for both the [V-CO₃]⁻ and the [V-NO₃]⁰ models.

Similarly, the Fe₆–Fe₇ distance is affected as the cluster is further oxidized. Upon going from the [V-CO₃]⁻ and [V-NO₃]⁰ models to the more oxidized models [V-CO₃]⁰ and [V-NO₃]⁺, this distance is increased by ∼0.2 Å. Clearly, these redox-dependent structural changes correspond to the removal of electrons at specific parts of FeVco and, as discussed later, correlate well with the presence or absence of the mixed-valence delocalized electrons of FeVco.

As for the V–Fe₅, V–Fe₆, and V–Fe₇ distances in the crystal structure, the V–Fe₅ distance is the shortest (2.70 Å), V–Fe₇ is in the middle (2.73 Å) and V–Fe₆ is the longest (2.76 Å). All models capture this trend, but the models do not capture the absolute values well.

Overall, only the [V-CO₃]^2– model reproduces both the metal–metal distances well enough as well as captures all of the observed trends within the cofactor. On the basis of the specific redox-dependent structural changes, the more oxidized [V-CO₃]^1–,0 and [V-NO₃]^0,1+ models can all be safely ruled out. Additionally, the 0.13 Å shorter Fe₄–Fe₅ distance in [V-NO₃]⁻ makes this model an unlikely candidate. Therefore, we conclude that the model that best reproduces the crystal structure is [V-CO₃]^2–.

3. Electronic Structure of the E₀ State of FeVco in Comparison to the E₀ State of FeMoco

Until now, we have not discussed the electronic structure of FeVco in any detail. The electronic structure of iron–sulfur cofactors is complicated⁸⁵⁻⁸⁷ with FeMoco and FeVco probably being the most complicated examples. Because of the many unpaired electrons, spin coupling, strong covalency, mixed-valence spin delocalization, unusual ligand environment (interstitial carbide), and metal–metal bonding interactions, the electronic structure of these clusters is truly exotic, presenting a true challenge to current quantum chemistry approaches. While the ability of the single-determinant BS-DFT strategy to describe these complex systems should be continuously scrutinized, the good agreement previously obtained for the structure of FeMoco^34,55 and now for the [V-CO₃]^2– model of FeVco compared to the high-resolution X-ray structure, especially in reproducing trends in metal–metal distances, suggests that we are describing at least aspects of the complicated electronic structure correctly. A simple analysis of the spin density via atomic spin populations of the cofactors is typically not very informative. However, as our previous work on FeMoco^32,34,36 has revealed, utilizing localized orbital analysis of the broken-symmetry determinant allows one to gain detailed insight into the cofactor, and approximate oxidation state assignments are possible despite extensive spin delocalization. As discussed in our QM/MM study of FeMoco, the approximate oxidation state assignments from localized orbital analysis could be correlated well with both the experimental and calculated metal–metal distances. We now present a localized orbital analysis of FeVco and compare it to a localized orbital analysis of FeMoco utilizing the intrinsic atomic orbital–intrinsic bond orbital (IAOIBO) method.⁸⁸ While previous work by us used Pipek–Mezey localization,⁸⁹ the use of better-behaved IAO charges should reduce possible artifacts in the localization procedure arising from maximizing the atomic charge (with the basis set dependence of Mulliken charges being the major issue) of each orbital.

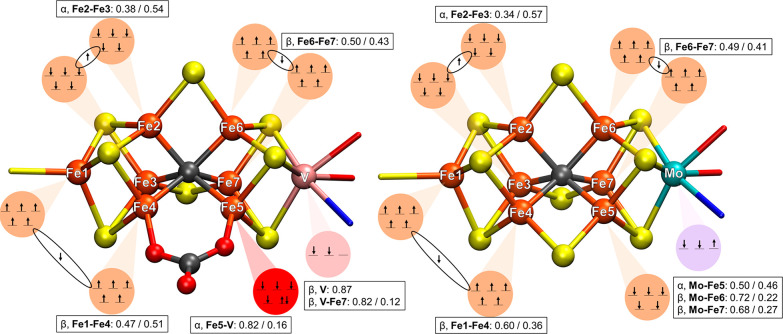
Figure 5 shows our interpretation of the BS7-235 electronic state of [V-CO₃]^2– (181-atom QM/MM model) and the BS7-235 electronic state of FeMoco (247-atom QM/MM model from a previous study by us³⁴) based on assignment of the IAOIBO localized orbitals to specific atoms. Isosurfaces of the localized orbitals themselves are shown in Figures S21–S23.

Figure 5.

Proposed electronic structure as interpreted from IAOIBO localized orbitals of the BS7-235 broken-symmetry determinant for both FeVco and FeMoco computational models. Left: [V-CO₃]^2– 181-atom-QM-region-optimized QM/MM model. Right: 254-atom-QM-region-optimized QM/MM model of FeMoco (from a previous study).³⁴ The values in the boxes give the population of the localized orbitals (see Figures S21–23 for the localized orbitals) that indicate the magnitude of delocalization of the minority spin electrons between atoms as well as delocalization between the heterometal (Mo/V) and Fe ions.

The Fe ions in FeMoco/FeVco are all high-spin Fe(III) or Fe(II). Assigning the five majority-spin electrons (either α or β depending on the spin coupling) on each Fe ion is unambiguous because they are always well-localized, and the only difficulty is in assigning the minority-spin electrons.

The minority-spin electrons can either localize on a specific Fe ion [making it localized Fe(II)] or alternatively delocalize between two Fe ions (if the majority spins of both ions are parallel) to create a mixed-valence Fe(2.5)–Fe(2.5) pair. However, depending on competing interactions in the cofactor or the effect of the protein environment, one also observes partial delocalization, which is, furthermore, sensitive to the theory level.

Starting with Fe₁ in FeVco and FeMoco, five α electrons are easily assigned via the localized orbital analysis. Additionally, there is a β electron delocalized between Fe₁ and Fe₄ for both cofactors. In FeMoco, the electron is only partially delocalized (Fe₁–Fe₄: 0.60/0.36), whereas in FeVco, the analogous β electron is more delocalized with even slightly more Fe₄ character than Fe₁ (Fe₁–Fe₄: 0.47/0.51). For FeMoco, the Fe₁–Fe₂, Fe₁–Fe₃, and Fe₁–Fe₄ distances are more or less equal (∼2.66 Å) in the PBD 3U7Q X-ray structure,³⁵ whereas for FeVco, we observe distinctly different distances. Fe₁–Fe₄ (X-ray: 2.57 Å) is the shortest distance, Fe₁–Fe₃ (X-ray: 2.66 Å) is in the middle, and Fe₁–Fe₂ (X-ray: 2.69 Å) is the longest. This difference between FeMoco and FeVco can be rationalized as being due to the Fe₁–Fe₄ β electron being more delocalized in FeVco than in FeMoco, resulting in stronger Fe–Fe bonding and a shorter Fe₁–Fe₄ distance in FeVco than in FeMoco. We speculate that the carbonate ligand, bound to Fe₄, is behind this increased delocalization of the β electron, possibly by increased back-bonding between Fe₄ and the carbonate.

The minority-spin β electron between Fe₆ and Fe₇ is almost equally delocalized in FeMoco (Fe₆–Fe₇: 0.49/0.41) as in FeVco (Fe₆–Fe₇: 0.50/0.43). When the experimental Fe₆–Fe₇ distances in both cofactors are compared, they are very similar, but FeVco has a 0.03 Å shorter Fe₆–Fe₇ distance (X-ray: 2.57 Å) compared to FeMoco (X-ray: 2.60 Å).

The minority-spin α electron between Fe₂ and Fe₃ is somewhat more localized on Fe₃ in FeMoco (Fe₂–Fe₃: 0.34/0.57) than in FeVco (Fe₂–Fe₃: 0.38–0.54), but classifying Fe₂–Fe₃ as a Fe(2.5)–Fe(2.5) delocalized pair still seems appropriate. However, the distance between Fe₂ and Fe₃ in both FeVco (X-ray: 2.64 Å) and FeMoco (X-ray: 2.65 Å) is longer or about equal to those in Fe₂–Fe₄ and Fe₃–Fe₄ in the Fe₂–Fe₃–Fe₄ triangle, which is seemingly in disagreement with the assignment of Fe₂–Fe₃ being a mixed-valent pair but Fe₂–Fe₄ and Fe₃–Fe₄ not. We note, however, that calculations of both cofactors are still in good agreement with the respective X-ray structures.

The localized orbital analysis allows us to rationalize the redox-dependent structural changes shown in Figure 4 for the [V-CO₃]^2–, [V-CO₃]⁻, and [V-CO₃]⁰ models. As electrons are removed from [V-CO₃]^2–, we get first a 0.21 Å elongation of the Fe₂–Fe₃ distance in [V-CO₃]⁻, and this is followed by a 0.20 Å elongation of Fe₆–Fe₇ in [V-CO₃]⁰. These changes obviously correspond to removal of the minority-spin delocalized electrons between these two pairs of Fe ions. A localized orbital analysis of the [V-CO₃]⁻ and [V-CO₃]⁰ models confirms this interpretation (Figures S22 and S23). Interestingly, the minority-spin on Fe₅ remains in these models. This suggests that the delocalized electrons in FeVco occupy higher energy levels than the localized electron on Fe₅.

Analyzing the heterometal orbitals, we see first that the oxidation state assignment of V in FeVco appears to be unambiguous based on the presence of two strongly localized β-spin electrons (and no appreciable V–Fe delocalization) to give a V(III) 3d² assignment. This is in contrast to Mo in FeMoco, where an unusual Mo(III) 4d³ configuration is observed with an appreciable Mo–Fe delocalization. As previously discussed, the Mo(III) 4d³ configuration is a highly unusual one, breaking Hund’s rule, and has been referred to as a “non-Hund” configuration.^34,36,50 Furthermore, the 4d electrons of Mo are not as localized compared to the 3d electrons of V, with slightly more pronounced Fe character of the β orbital; Mo–Fe₆, 0.72/0.22; Mo–Fe₇, 0.68/0.27. The α electron on Mo in FeMoco is even more delocalized (Mo–Fe₅: 0.50/0.46), which is suggestive of Mo–Fe bonding. The electronic structure of Mo in FeMoco is thus more ambiguous from the localized orbital analysis than that of V in FeVco. We note that V K-edge XAS of the VFe protein supports the V(III) assignment in FeVco,⁴¹ and Mo K- and L-edge XAS supports the Mo(III) assignment.^36,37 More recently, experimental support for the unusual non-Hund configuration at Mo comes from Mo L-edge X-ray magnetic circular dichroism spectroscopy of a related [MoFe₃S₄] model cubane that shares the unusual electronic structure of FeMoco.³⁸

In the X-ray structure of FeMoco (PDB 3U7Q), the Mo–Fe₅ distance (X-ray: 2.73 Å) is longer than the Mo–Fe₆ (X-ray: 2.67 Å) and Mo–Fe₇ (X-ray: 2.68 Å) distances. In our 247-atom QM-region QM/MM model of FeMoco, the calculated Mo–Fe₅ distance is also longer (2.71 Å) than the Mo–Fe₆ and Mo–Fe₇ distances (2.65 and 2.62 Å, respectively). Although the α electron of Mo is somewhat more delocalized than the β electrons of Mo, in our computed model, the Mo–Fe₅ distance ends up being the longest of the three. This may be related to the higher effective charge at Fe₅ [being assigned as Fe(III) rather than Fe₆/Fe₇ (assigned as Fe(2.5)–Fe(2.5)] or possibly the overall ferromagnetic alignment of Fe₅ and Mo.

While V in FeVco lacks a third d electron, an additional localized α electron is instead present on Fe₅ (Fe₅–V: 0.82/0.16), making it of primarily localized Fe(II) character. In the PBD 5N6Y crystal structure, the V–Fe₅ distance (X-ray: 2.70 Å) is shorter than the V–Fe₆ (X-ray: 2.76 Å) and V–Fe₇ (X-ray: 2.73 Å) distances, in contrast to the analogous Mo–Fe distances in FeMoco. In our 181-atom QM-region QM/MM model of FeVco, the V–Fe₅ distance is also shorter (2.67 Å) than the V–Fe₆ and V–Fe₇ distances (2.81 and 2.69 Å, respectively).

The Mayer bond order (MBO)⁹⁰ is a useful metric for the magnitude of bonding between two atoms. The absolute values of MBO between the metals in FeVco and FeMoco are tabulated in Table S20. In the 247-atom QM-region QM/MM model of FeMoco and 181-atom QM-region QM/MM model of FeVco, we observe similar and relatively low MBO values between Fe atoms that do not have a delocalized minority-spin electron (values ranging from 0.21 to 0.31).

Fe atoms that are ferromagnetically aligned and have a delocalized minority-spin electron, on the other hand, show higher MBO values (ranging from 0.41 to 0.47), indicating more bonding character between these Fe atoms compared to Fe interactions with no delocalized electrons.

The MBOs for the heterometal and Fe interaction in FeVco and FeMoco paint a starkly different picture between the two cofactors. The MBOs for V–Fe₅ (0.37), V–Fe₆ (0.18), and V–Fe₇ (0.30) are much lower than the MBOs for Mo–Fe₅ (0.47), Mo–Fe₆ (0.45), and Mo–Fe₇ (0.49), indicating that Mo in FeMoco interacts more strongly with the Fe atoms of FeMoco than V in FeVco.

This difference in interaction between the heterometal and Fe ions in the cofactor is intriguing because the average Mo–Fe distance in FeMoco is shorter than the average V–Fe distance in FeVco. This difference between the average Mo–Fe and V–Fe distances is seemingly in contradiction because one would expect Mo, a larger ion than V, to have longer Mo–Fe distances than the V–Fe distances. In the 1.0-Å-resolution X-ray structure of the MoFe protein (PDB 3U7Q),³⁵ the average Mo–Fe distance is 2.69 Å, whereas it is 2.70 Å according to extended X-ray absorption fine structure (EXAFS).⁹¹ In comparison, the average V–Fe distance in the 1.35-Å-resolution X-ray structure of the VFe protein (PDB 5N6Y) is 2.73 Å, whereas it is 2.76 Å as interpreted from EXAFS.⁴⁰ In our models of FeMoco and FeVco, we underestimate these distances. The average Mo–Fe distance is 2.66 Å (underestimation of 0.03 or 0.04 Å) and the average V–Fe distance is 2.72 Å (underestimation of 0.01 or 0.04 Å). However, the average M–Fe (M = Mo, V) distance agrees with the EXAFS data, where the increase in the average M–Fe (M = Mo, V) distance between Mo–Fe and V–Fe is 0.06 Å, which we capture exactly in our computed models. This difference between EXAFS and the crystal structure for V–Fe may be attributed to the lower-resolution crystal structure (1.35 Å for VFe).

The delocalization or bonding interactions that we observe between the Mo ion and the Fe ions but less so between the V ion and the Fe ions in our computed models are a likely explanation for the difference between the Mo–Fe and V–Fe distances. It seems likely that this effect is at least partially due to more diffuse 4d orbitals of Mo, resulting in larger overlap between Mo and Fe orbitals than V and Fe orbitals.

These differences in the electronic structure between the two cofactors, which are subsequently reflected in the molecular structure, are likely one of the contributing factors to the difference of the catalytic activity between the two cofactors. Aside from differences in the catalytic activity, another important difference between the two cofactors is that FeVco is capable of binding CO in its resting state, whereas FeMoco can only do so under turnover conditions.⁹² One hypothesis is that the more ferrous iron environment in FeVco aids CO binding to an Fe ion in the resting state, something not possible in FeMoco. In fact, the resting state FeVco can be interpreted as being analogous to an unprotonated E₁ state in FeMoco, and it has been proposed in a recent joint EXAFS–QM/MM study that the MoFe₃S₃ subcubane of FeMoco receives the added electron when reduced to the E₁ state,⁹³ which is analogous to the reduced VFe₃S₃ subcubane of our resting state FeVco model.

4. Stability of the [VFe₇S₈(CO₃)]^2– Redox State

The previously discussed results, in our view, clearly establish the resting state structure of FeVco as containing a bound CO₃ ligand and a redox state consistent with [VFe₇S₈(CO₃)]^2– and a formal oxidation state distribution as V(III)Fe(II)₄Fe(III)₃. Furthermore, the calculated electronic state according to a BS-DFT description is M_S = ³/₂ (which is consistent with the experimental S = ³/₂ spin state) and having a lowest-energy BS7-235 solution with spin delocalization, as indicated in Figure 5. Only this specific ligand (CO₃), this specific redox state ([V-CO₃]^2–), and this specific alignment of spins (BS7-235) can account for the specific geometric properties of FeVco seen in the experimental X-ray structure.

Until now, we have, however, not discussed a problem that arises from this more negative charge of the resting state FeVco ([VFe₇S₈(CO₃)]^2–) compared to the resting state FeMoco ([MoFe₇S₉]⁻), namely, that of unbound electrons. The QM/MM model discussed (calculated using a 181-atom QM region and the TPSSh functional) results in 12 α and 11 β electrons residing in orbitals with positive orbital energies (Figures S25–S27). Positive orbital energies are unphysical in this context because they suggest that spontaneous detachment of the electrons from the cofactor should occur. While unbound electrons are sometimes an indication of an inflexible basis set, because of the large polarized triple-ζ basis set used here, this is unlikely to be the case. We considered three possible reasons for the presence of unbound electrons in the [V-CO₃]^2– computational model: (i) the cofactor is, unlike FeMoco, protonated in the resting state, (ii) the unbound electrons arise because of the DFT self-interaction error (SIE), and (iii) the cofactor is insufficiently stabilized by the QM/MM model.

i. Protonated Cofactor

A QM/MM model (58-atom QM region) with an additional proton on the longer carboxylate arm of the homocitrate ligand was found to result in a reduction in the number of unbound electrons to 2 α and 3 β electrons (with a subsequent increase in the RMSD to 0.095 Å compared to 0.080 Å for an unprotonated model). Models with protonated belt sulfides S2B or S5A (Table S25) were found to have no unbound electrons. However, the protonation of a belt sulfide was accompanied by a 0.10–0.13 Å elongation of the Fe–S2B/S5A distances, a difference that would likely be resolved in the crystal structure if it were present. Additionally, the RMSD was considerably worse than the unprotonated model (0.106 and 0.121 Å for S2B and S5A protonation, respectively, compared to 0.080 Å for an unprotonated model). Thus, we consider a protonated resting state FeVco model unlikely.

ii. Self-Interaction Error

The unbound electrons could arise because of the approximate nature of the density functional used. Approximate density functionals do not show the correct long-range asymptotic behavior of the potential and suffer from SIEs.⁹⁴⁻⁹⁷ While hybrid density functionals reduce the SIE via the inclusion of exact HF exchange and range-separated hybrids can enforce the correct long-range behavior, the low amount employed in most popular hybrid functionals used for transition-metal chemistry (typically 0–25%) is usually not sufficient to resolve the issues. As revealed in Figure S28, while increasing the global HF exchange in the standard hybrid DFT form results in a decrease of unbound electrons of FeVco, this is not a realistic strategy for describing FeVco because the quality of the geometry deteriorates significantly, as revealed by the strong increase in RMSD with respect to the crystal structure. The 50–70% HF exchange required to remove unbound electrons results in an unacceptable RMSD (>0.20 Å), suggesting that the electronic structure is very poorly described with those functionals. This problem of high HF exchange functionals deteriorating the electronic structure of nitrogenase cofactors has been noted previously by us and others for FeMoco.^51,98

iii. Environmental Effects

Because the spherical QM/MM model does not account for mutual polarization between the QM and MM regions and does not contain the whole VFe protein, we considered the possibility of protein polarization or longer-range bulk electrostatics playing a role in stabilizing the cofactor.

The protein and solvent environment clearly play a role in describing the cofactor, as can be seen by considering a simple 59-atom cluster model of the cofactor in a vacuum; this results in a very unstable cofactor with 195 unbound electrons. Such a vacuum model, furthermore, gives a poor geometric structure (RMSD of 0.166 Å). Using a simple continuum solvation model, COSMO⁹⁹ with a dielectric constant of 4, the electronic structure is stabilized considerably, yet 13 unbound electrons remain. A different continuum model, CPCM (using a Gaussian charge scheme and a scaled vdW cavity^100,101), however, stabilizes the electronic structure, resulting in no unbound electrons. These results thus clearly reveal a sensitivity of the computational model to bulk electrostatics and polarization effects. These continuum model calculations, however, clearly result in cofactor structures inferior to the QM/MM models, as can be judged by the relatively high RMSDs of the cofactor geometries (Table 3), being not much better than the vacuum-optimized geometry.

Table 3. Unbound Electrons and RMSD (with Respect to the X-ray Geometry) in Cluster and QM/MM Models of FeVco.

	system size (atoms)	QM-region size (atoms)	charge (QM region)	unbound electrons	RMSDc (Å)
vacuumb	59	59	–6	195	0.166
COSMOb	59	59	–6	13	0.140
CPCMa,b	59	59	–6	0	0.141
QM/MM	32562	57	–6	29	0.082
QM/MM	32562	83	–3	32	0.085
QM/MM	32562	181	–3	23	0.079
QM/MM	47516	57	–6	62	0.084
QM/MM	531080	57	–6	0	0.085
QM/MM	47516	181	–3	70	0.080
QM/MM	531080	181	–3	0	0.079

^aUsing a Gaussian charge scheme and a scaled van der Waals surface.¹⁰¹

^bAn additional two protons are added to cap residues 423^His and 257^Cys.

^cThe RMSD is defined as the deviation of the [VFe₇S₈C(XO₃)] part with respect to both cofactors in the crystal structure.

The lack of protein polarization by the MM environment in the QM/MM models could only be partially explored in this study via a systematic increase of the QM-region size in the calculations. Upon going from a 57-atom QM-region model to a 181-atom model, the number of unbound electrons is only reduced from 29 to 23. Longer-range polarization effects affecting the electronic structure stability can presently not be ruled out and could be explored using even larger QM regions or via polarizable QM/MM methods.

The effect of long-range bulk electrostatics was explored in more detail by the creation of an additional QM/MM setup. Instead of a spherical model (Figure 2, right), centered on the cofactor of half of the hexameric protein, a new QM/MM model consisting of the whole VFe protein was cut from the periodic MM-box model (Figure 2, left) of the whole solvated VFe protein. A 3 Å solvation shell and all Na⁺ ions were additionally included in the model, resulting in an overall neutral model of 47516 atoms. This model (Figure S29), consisting of the whole protein, is slightly larger than the spherical model of half of the protein. Interestingly, however, this larger model that avoids cutting protein chains and includes the whole protein and all Na⁺ ions (as MM point charges) actually results in an increase in unbound electrons to 62 (for a 57-atom QM region). This unfavorable result, nonetheless, suggests a strong sensitivity to the bulk electrostatic environment through the presence and/or distribution of MM point charges. When the size of the MM point-charge environment was increased even further, a model where all 531080 atoms (additional water molecules) of the solvated protein box (Figure 2, left) were included in the electrostatic embedding was calculated. Remarkably, this results in complete stabilization of all electrons. QM/MM geometry optimizations at this level of theory further revealed almost negligible structural changes compared to the 47516-atom model, demonstrating that these unphysical unbound electrons do not affect the local structure of the cofactor. Calculations with an even larger 181-atom QM region with the extended MM region resulted in a very similar geometry and no unbound electrons.

The problem of unbound electrons in computational models of FeVco thus appears primarily to be a question of insufficient solvent bulk electrostatic effects. Fortunately, insufficient account of this bulk effect has little consequence for the quality of the cofactor geometry (Table 3) or the spin-density distribution (see the Mulliken spin populations in Table S26). Clearly, however, a proper account of solvent bulk electrostatics needs to be carefully considered in future calculations of the redox properties of these cofactors.

Conclusion

We have performed, to our knowledge, the first extensive computational study on the resting state FeVco of V-nitrogenase from A. vinelandii using a QM/MM model starting from the 1.35-Å-resolution X-ray structure (PDB 5N6Y). We systematically explored 35 different broken-symmetry solutions for all plausible oxidation states of FeVco, using either nitrate or carbonate as a possible 4-atom bridging ligand, and found that the BS7-235 solution (with Fe atoms labeled 2, 3, and 5 being spin-down) is energetically favored in all cases. Through a careful comparison of the QM/MM-optimized structures to the X-ray structure by analysis of the Fe–Fe and V–Fe distances, we find that only the [VFe₇S₈C(CO₃)]^2– model is in good agreement with the X-ray structure. Analysis of the electronic structure of [VFe₇S₈C(CO₃)]^2– via the localized orbitals reveals a reduced VFe₃ subcubane compared to the MoFe₃ subcubane in FeMoco. This is in good agreement with a previous Fe K-edge XAS study of MoFe and VFe proteins⁵⁰ and, interestingly, suggests that the Fe electronic structure of the resting state FeVco is analogous to the E₁ state of FeMoco, recently characterized by a joint Fe/Mo EXAFS and QM/MM study.⁹³ The additional electron in the VFe₃ subcubane is localized on Fe₅, making it locally ferrous, in contrast to the ferric Fe₅ in the analogous computational model of FeMoco (as interpreted from the BS7-235 solution). The oxidation state of V is found to be V(III), in agreement with experimental V K-edge XAS studies,⁴¹ and the V(III) ion is found to have less bonding interactions with Fe ions than Mo(III) in FeMoco.

These electronic structure differences between FeVco and FeMoco are proposed as a likely reason for the experimentally observed differences in the reactivity and catalytic activity.

Finally, we discussed the stability of the electronic structure of the FeVco model with respect to unbound electrons. It is found that the more reduced FeVco model (compared to FeMoco) is highly sensitive to solvent bulk electrostatic effects and that a large number of explicit solvent molecules are required to stabilize the highest electron energy levels of the cofactor.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.0c01320.

• Additional data on computational details, broken-symmetry energies, Mulliken spin populations, figures of localized orbitals, and electron structure as well as optimized geometries (PDF)

Author Contributions

The manuscript was written through contributions of all authors.

R.B. acknowledges support from the Icelandic Research Fund (Grants 141218051 and 162880051) and University of Iceland Research Fund. Open Access funding was provided by the Max Planck Society.

The authors declare no competing financial interest.