Hot-Carrier Generation in Plasmonic Nanoparticles: The Importance of Atomic Structure

Abstract

Metal nanoparticles are attractive for plasmon-enhanced generation of hot carriers, which may be harnessed in photochemical reactions. In this work, we analyze the coherent femtosecond dynamics of photon absorption, plasmon formation, and subsequent hot-carrier generation through plasmon dephasing using first-principles simulations. We predict the energetic and spatial hot-carrier distributions in small metal nanoparticles and show that the distribution of hot electrons is very sensitive to the local structure. Our results show that surface sites exhibit enhanced hot-electron generation in comparison to the bulk of the nanoparticle. Although the details of the distribution depend on particle size and shape, as a general trend, lower-coordinated surface sites such as corners, edges, and {100} facets exhibit a higher proportion of hot electrons than higher-coordinated surface sites such as {111} facets or the core sites. The present results thereby demonstrate how hot carriers could be tailored by careful design of atomic-scale structures in nanoscale systems.

Plasmon-enhanced technologies enabled by metal nanoparticles (NPs) provide promising avenues for harvesting and converting sunlight to chemical energy¹ and driving photochemical reactions.² The underlying processes rely on the decay of plasmonic excitations and the subsequent generation of high-energy non-equilibrium electrons and holes.³ These electrons and holes are often collectively referred to as hot carriers (HCs), but their distributions can vary substantially with time after excitation.^4,5 HCs generated by plasmon decay can, in principle, be transferred to a chemically attached acceptor such as a semiconductor or a molecule, a process that is potentially useful for technologies such as photovoltaics,⁶ photodetection,^7,8 photon up-conversion,⁹ and photocatalysis^2,10−13 and possibly relevant for NP growth processes.¹⁴

It can be challenging to develop comprehensive understanding of plasmon-generated hot carriers via purely experimental approaches both due to time constraints and the difficulty associated with disentangling different contributions.¹⁵⁻¹⁷ In this context, complementary theoretical and computational approaches can provide highly valuable insight as they enable scrutinizing the relevant microscopic processes. The present theoretical understanding of plasmonic HC generation is mostly based on flat metal surfaces^18,19 or jellium NPs neglecting the underlying atomic structure.^4,5,20−26 Whereas atomic-scale effects in nanoplasmonics, in general, have been increasingly addressed in recent years,²⁷⁻³² atomic-scale modeling of plasmonic HC generation is only emerging.³³⁻³⁵ In particular, detailed atomic-scale distributions of plasmon-generated HCs, to our knowledge, have not yet been scrutinized. In the context of photocatalysis detailed understanding of plasmonic HC generation at the atomic scale is, however, of paramount importance as chemical reactions take place at this size scale.

In this work, we analyze the effect of local atomic-scale structure on plasmonic HC generation and demonstrate that the distribution of HCs after plasmon decay is sensitive to the atomic-scale details. Using a series of NPs, we analyze quantitatively the spatial distribution of plasmon-generated HCs at the atomic scale with respect to surface orientation as well as for edge and corner sites. As the trends are consistent across NPs of different size and shape, the trends obtained here are expected to be transferable to more general nanoscale structures. For this study, we have developed a fully atomistic, parameter-free, and generally applicable description of plasmonic HC generation based on Kohn–Sham (KS) density functional theory (DFT)^36,37 and time-dependent density functional theory (TDDFT).³⁸

Results and Discussion

Real-Time Dynamics of Localized Surface Plasmon

To introduce our approach for modeling plasmonic HC generation, we start with a comprehensive characterization of plasmon formation and subsequent dephasing. We consider an icosahedral Ag₅₆₁ silver NP as an example system with a clear plasmon resonance in the photoabsorption spectrum (Figure 1a).³⁹ The ground-state electronic structure of the NP is calculated with DFT using the Gritsenko–van Leeuwen–van Lenthe–Baerends–solid-correlation (GLLB-sc) exchange-correlation (XC) potential^40,41 for an improved d-band description.^28,42 The time-dependent response is then calculated with TDDFT using either the random-phase approximation (RPA) or the adiabatic GLLB-sc²⁸ (see Methods for details).

Figure 1.

Real-time dynamics of a localized surface plasmon in a silver nanoparticle. (a) Photoabsorption spectrum of the Ag₅₆₁ NP (shaded) and the intensity profile of an impacting electric field pulse (green). Photoabsorption is determined by the imaginary part of the polarizability, α, and the corresponding real part, Re[α], is shown as a dotted line. (b) Electric field pulse impacting the plasmon resonance of the NP. (c) Time-dependent dipole moment response of the NP. (d) Electron density oscillations in the NP at selected time instances (red and blue isosurfaces denote density increase and decrease, respectively). (e) Time evolution of the energy stored in the excited electronic system. The total energy (black) is divided into the energy of nonresonant electron–hole transition contributions constituting screened plasmon excitation (purple) and that of resonant transition contributions constituting mainly hot carriers (orange). A part of the plasmon energy is in the form of Coulomb energy (gray).

To excite the localized surface plasmon resonance (LSPR) in the NP, we use a monochromatic ultrafast Gaussian light pulse

1

that induces real-time dynamics of electrons in the system. The pulse frequency ω₀ = 3.6 eV is tuned to the plasmon resonance, the pulse duration is determined by τ₀ = 3 fs, and the pulse is centered at t₀ = 10 fs (Figure 1b). The pulse strength is weak, 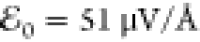, putting the response in the linear-response regime. In the frequency space, the pulse is wide enough to cover the whole plasmon resonance (Figure 1a).

The interaction between electrons and light is described in the dipole approximation, within which the light pulse creates a time-dependent external potential, 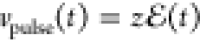, that causes the time evolution of the KS states |ψ_n(t)⟩ and excitation of the LSPR. The light pulse induces a strong dipole-moment response [Figure 1c(1–3)]. The corresponding electron density oscillations [Figure 1d(1–3)] are composed of a surface-to-surface component associated with delocalized valence electrons near the Fermi energy and atom-localized contributions that correspond to screening due to virtual excitations from the d-band.³⁹ As time proceeds to t ≈ 17 fs, the excited electrons start to lose their collective plasmonic motion via a dephasing process commonly referred to as Landau damping.⁴³ As the plasmon dephases, the dipole moment decays [Figure 1c(4,5)] corresponding to vanishing surface-to-surface density oscillation [Figure 1d(4,5)].³³ Whereas the density oscillations and dipole moment response gives an illustrative picture of the plasmon formation and decay, they seem not to provide a tractable way for scrutinizing HC contributions to the response. To this end, we consider the time-dependent energy contributions of different KS transitions.

Time-Dependent Energy Contributions

As the pulse is tuned to the LSPR, the electronic system absorbs energy from the incident light and remains in an excited state after the pulse has vanished. To analyze the distribution of this energy, we first consider the total time-dependent energy of the system given by

2

where E_tot⁽⁰⁾ is the ground-state energy, ΔE(t) is the time-dependent energy stored in the excited state (Figure 1e, black line), and 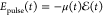is the potential energy of the system under the external electric field.

The incident light pulse pumps energy into the system; that is, it does work on the system as 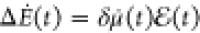, where dots indicate time derivatives and δμ(t) = μ(t) – μ⁽⁰⁾ is the induced dipole moment. Thus, the total accumulated electronic energy can be written as

3

The electronic energy increases through absorption in a stepwise manner following the pulse intensity (Figure 1e, t ≈ 5...15 fs). After the pulse has ended (t ≳ 15 fs), the absorbed energy remains in the system and the total energy has attained a new constant value given by the photoabsorption cross section (Figure 1a and eq 11 in Methods).

Although the total energy remains constant, the electronic energy does not stay equally distributed among the electron–hole transitions i → a excited by the light pulse. To quantify this effect, we consider the decomposition of the energy in electron–hole transition contributions. This decomposition is based on the linear response of the KS density matrix, δρ_ia(t), expressed in the basis of the eigenstates (ϵ_n, ψ_n⁽⁰⁾) of the ground-state Hamiltonian. The electron–hole decomposition of energy is (see Supplementary Note S1 for derivation)

4

where the sum is restricted by ground-state occupation numbers f_n so that the indices i and a correspond to the created hole and electron states, respectively. Here, ω_ia = ϵ_a – ϵ_i is the electron–hole transition energy (the KS eigenvalue difference), P_ia(t) is the transition probability defined as

5

and E_ia^C(t) is the Coulomb energy as obtained from the Hartree–XC kernel (defined in Supplementary Note S1).

Plasmon formation and dephasing can be scrutinized by considering the energy stored in the electronic system in terms of the electron–hole transition energy, ω_ia, with respect to the pulse frequency ω₀ (Supplementary Figure S1). The plasmon is formed by constructive coupling of low-energy transitions [ω_ia ≲ 2 eV; see Figure 2a and time instances (1–3) in Figure 2b].^39,43,44 Simultaneously, high-energy virtual d-electron transitions (ω_ia ≳ 4 eV) screen the plasmonic density oscillation, decreasing the total induced field. The energy stored in the screening is similar to the energy stored in the polarization of a dielectric in general; that is, as the total field strength decreases, energy is instead stored in the polarization of the d-electron states as in ω_iaP_ia(t) in eq 4. The nonresonant low- and high-energy transitions carry most of the energy during plasmon excitation (Figure 1e, purple line). As the plasmon dephases, the absorbed energy is redistributed to electron–hole transitions that are resonant with the pulse [Figure 1e, orange line; corresponding to the diagonal in the transition contribution maps in Figure 2b; see time instances (4,5)]. After dephasing, the energy remains almost exclusively stored in these transitions constituting the plasmon-generated HCs. The transitions comprising the plasmon are active in photoabsorption (Figure 2a), and hot holes and electrons are generated through plasmon decay, instead of the HC transitions absorbing the light directly (shown in detail in Supplementary Figure S2).

Figure 2.

Electron–hole transition contributions to plasmon formation and decay. (a) Electron–hole contributions to the photoabsorption at the resonance energy visualized as a transition contribution map (TCM). Density of states is also shown along the energy axes. (b) Electron–hole contributions to the time-dependent electronic energy visualized as TCM on a logarithmic color scale. The solid diagonal line corresponds to the transition energies matching with the pulse frequency ω₀ and the dotted diagonal lines are drawn at ω₀ ± 2σ to indicate the pulse width 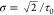, defining the boundaries for resonant and nonresonant transitions for Figure 1e. (c) Occupation probabilities of hole and electron states. Solid blue and red lines denote state occupations from resonant transitions, and dashed lines denote occupations from all transitions (resonant and nonresonant). The figure columns (1–5) show panels (b) and (c) for the time instances labeled in Figure 1. The color scale and axis limits are the same in all of the columns.

At longer time scales, the electronic system would dissipate the absorbed energy to the environment via radiation, atomic motion, or other processes, but such decay pathways are not included within the description used here. Thus, in the present picture, there appears no significant dynamics in Ag₅₆₁ at time scales beyond t ≳ 30 fs after the fast dephasing of the LSPR through Landau damping, which takes place due to the presence of multiple excitation eigenstates forming the broadened plasmon peak in the photoabsorption spectrum⁴³ (Supplementary Figure S3). However, the dynamics can be very different in small clusters with a discrete excitation spectrum. In contrast to a single broad plasmon peak in Ag₅₆₁, for example, in the Ag₅₅ cluster, individual electron–hole transitions couple strongly to the plasmon,³⁹ a process that is referred to as plasmon fragmentation.^45,46 Correspondingly, the time-domain response exhibits Rabi oscillations and energy transfer back from the resonant transitions to the plasmon^33,47 (Supplementary Figure S4).

As the coupling of transitions via Coulomb interaction is recognized as an essential characteristic of plasmonic excitations,^39,43,44,48 it is instructive to consider the Coulomb energy, 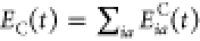. This energy exhibits strong oscillations (Figure 1e, gray line) analogous to the dipole moment (Figure 1c) as only the electron density oscillation contributes to the Coulomb energy. At the maxima of the surface-to-surface density oscillation [time instances (1) and (3) in Figure 1d,e], the Coulomb contribution is a significant part of the plasmon energy, but at the minima between [e.g., time instance (2)], the Coulomb energy is vanishing as the electronic energy is stored in the electron current flowing through the particle (Supplementary Figure S5).

Temporal Evolution of Hot-Carrier Distributions

Having established a real-time picture of plasmon formation and decay, we are in the position to analyze the distributions of electrons and holes during the process. The probabilities for creating a hole in an initially occupied state i or an electron in an initially unoccupied state a are given directly by the transition probability of eq 5 as

6

respectively. P_i^h and P_a determine exactly the diagonal elements of the second-order response of the density matrix (Supplementary Note S1); in other words, they correspond to the increase of the occupation of the initially unoccupied state a and the decrease of the occupation of the initially occupied state i.

The occupation probabilities given by eq 6 show strong oscillations during the time evolution [Figure 2c(1–3), dashed lines]. These oscillations are explained by the oscillation of the Coulomb energy. As the Coulomb energy contribution is carried mainly by nonresonant transitions (Supplementary Figure S6), the occupation probabilities of the electron and hole states contributing to these nonresonant transitions oscillate analogously to the Coulomb energy. The oscillations are especially visible in the occupations of electron and hole states that form the plasmon,³⁵ that is, the states near the Fermi energy, often referred to as Drude carriers.⁴⁹ The oscillatory population and depopulation of these states indicate that they would not likely be individually separable while they are a part of the plasmon as the Coulomb interaction is an essential part of the excitation itself.⁵⁰

The contributions of the resonant transitions to the Coulomb energy are relatively small (Supplementary Figure S6), and the occupations of the corresponding electron and hole states grow steadily as the plasmon decays (Figure 2c, solid lines). At the end of the dynamic evolution studied here [Figure 2c(5)], electrons and holes are still coupled in the form of electron–hole transitions, and the distributions at t = 30 fs can be considered as the initial nonthermal HC distributions. After their generation, these carriers would separate and interact via electron–electron and electron–phonon scattering processes^3,5,19,51 that are not captured in the present description. The slight asymmetry between the hole and electron distributions is caused by a nonzero width of the pulse in the frequency space (Figure 1a).

Energetic and Atomic-Scale Spatial Distributions of Hot Carriers

We now analyze the distribution of plasmon-generated hot carriers and the impact of local atomic-scale structure. We start by considering the series of icosahedral silver NPs Ag₁₄₇, Ag₃₀₉, and Ag₅₆₁, the photoabsorption properties of which we have described in detail in previous work^28,39 (see Supplementary Figure S7 for photoabsorption spectra and densities of states). The light pulse is tuned to the plasmon resonance of the NPs, and the initial HC distributions are analyzed after the plasmon has dephased at a time t = 30 fs. The HC distributions show a pronounced dependence on NP size (Figure 3a) and local structure (Figure 3b,c) as discussed in the following.

Figure 3.

Hot-carrier distributions after plasmon decay. (a) Occupation probabilities of hole and electron states in icosahedral silver NPs of 147–561 atoms. (b) Occupation probabilities at different atomic sites of Ag₅₆₁. All the panels use the same axis limits (normalized by the number of atoms). (c) Spatial density profiles of all induced holes and electrons and induced electrons with energy of more than 1 eV in Ag₅₆₁. Plots show isosurfaces corresponding to 10 and 20% of maximum value, and slices are taken through the center of the NP.

As particle size increases, the HC distributions are increasingly dominated by interband d-electron transitions²⁶ (hole ∼ −4 eV → electron ∼0 eV) converging toward the distributions obtained for flat surfaces.^18,19 In contrast to extended systems, geometry confinement effects are significant for plasmonic HC generation in nanoscale systems.⁵² Due to the broken crystal symmetry, additional “intraband” transitions are available for plasmonic HC generation in NPs, which results in the population of higher-energy electron and hole states (Figure 3a; electron states of >0.5 eV, hole states of >−3.5 eV). The relative contribution of these sp-states is most pronounced in the smallest NPs²⁶ (Ag₁₄₇, Ag₃₀₉), but they are non-negligible also in Ag₅₆₁. Similar size-dependent trends are also present in silver NPs of other shapes, whereas the detailed relative contributions of different transitions vary (Supplementary Figure S8).

The calculated probability distributions of plasmon-generated electrons and holes (see Methods) exhibit strong spatial variance (shown for the icosahedral Ag₅₆₁ NP in Figure 3b,c): Holes are localized at atomic sites throughout the particle, which is expected as the majority of holes originates from the atom-localized d-states. As a result, their energy distribution is very similar for core and surface sites. Hot electrons, on the other hand, are more delocalized and reside to larger extent in the surface region. The surface contribution is even more pronounced for higher-energy hot electrons (>1 eV electrons in Figure 3c). The probability density of these hot electrons is strongly enhanced especially at low-coordinated edge and corner sites compared to sites in the core and on flat surfaces (Figure 3b). The energetic distributions of plasmon-generated holes and electrons are not necessarily symmetric when projected onto a particular site (Figure 3b and Supplementary Figure S8). This asymmetry is especially pronounced for the corner site in Ag₅₆₁, which reflects the fact that the hot-electron density at corner sites originates likely from throughout the particle due to the uniformity of the hole density.

A more quantitative view is obtained by considering the total per-atom occupation probability of hot electrons at a particular atomic site in comparison to the total per-atom occupation probability throughout the system (Figure 4). These data suggest that in the icosahedral Ag₅₆₁ NP, hot electrons with more than 1 eV are almost three times more likely to be found in the vicinity of a corner site than a uniform spatial distribution would correspond to. We emphasize that these are per-atom considerations; that is, as the 12 corner atoms constitute only around 2% of the atoms in the particle, it is expected that about 6% of the electrons with more than 1 eV would be generated in the vicinity of the corner atoms. Overall, hot electrons with more than 1 eV constitute 30–60% of all hot electrons depending on system (Supplementary Figure S8). The absolute total number of HCs generated depends on the light energy that is absorbed, which is in turn determined by the photoabsorption cross section and light intensity.

Figure 4.

Atomic-scale distributions of hot electrons in silver nanoparticles. Spatial distribution of hot electrons generated on different atomic sites in icosahedral (Ih), cuboctahedral (Cub-Oh), and regularly truncated octahedral (RTO) NPs. Sites with lower coordination exhibit a higher proportion of hot electrons than core sites. A spatially uniform distribution corresponds to a normalized probability of unity. The insets show the atomic structures with the different atomic sites colored.

Similarly to icosahedral shapes, hot electrons in the cuboctahedral and regularly truncated octahedral NPs are more likely to be generated at a surface site than at a core site (Figure 4). The preference for surface sites is even more pronounced for hot electrons with more than 1 eV. The corner sites of the cuboctahedral and regularly truncated octahedral NPs, however, do not show as enhanced distribution of hot electrons as those sites of the icosahedral Ag₅₆₁ particle. This further underlines the sensitivity of HC generation to atomic-scale details and the exact electronic structure of the NP and site(s) in question.

As a general trend, lower-coordinated sites seems to exhibit an enhancement of hot electrons compared to higher-coordinated sites. This trend is observed for corner and edge sites, but the data for cuboctahedral and regularly truncated octahedral NPs suggest also that more hot electrons are generated on the lower-coordinated {100} surface than on the {111} surface. In contrast to strong spatial variation of hot electrons, plasmon-generated holes do not show strong spatial dependence in the considered NPs (Supplementary Figure S9).

For practical utilization, HCs need to be transferred to the environment. The HC distributions obtained in the present work can be considered as the initial nonthermal HC distributions before any electron–electron scattering^19,51 has taken place. Thus, these HC distributions could serve as an initial condition for subsequent dynamics^3,5 that is not included in the present approach. In general, HC transfer to environment can occur indirectly (i.e., carriers are first produced in the metal and subsequently transferred to the acceptor) or directly (i.e., plasmon dephasing leads directly to the injection of HCs in empty acceptor, or occupied donor, states).^2,53−62 However, both experiments⁶³⁻⁶⁵ and calculations^51,52,65,66 indicate that HCs generated in the metal can quickly relax through electron–electron scattering, which renders the indirect pathway inefficient. The direct-transfer process, on the other hand, presents an opportunity to obtain more efficient plasmonic HC devices.^54,56,62 The prevalence of hot electrons on lower-coordinated surface sites described in the present work seems favorable for their utility through the direct transfer processes. It is, however, crucial to also consider the hybridization of the surface electronic states with acceptor states, where the latter can originate, for example, from an adsorbed molecule⁶⁷ or a semiconductor.^68,69 To maximize the efficiency for direct excitation transfer, the emitting and receiving states should be energetically aligned and spatially overlapping. In addition, hot-electron generation can be affected by the dielectric environment, for example, by red-shifting the plasmon resonance so that d-band electrons are not excited. The framework presented here enables analysis and quantification of these aspects at the atomic scale with material specificity and without resorting to empirical parameters.

Conclusions

In conclusion, we presented a comprehensive first-principles account of the real-time dynamics of plasmon formation and dephasing into HCs and analyzed quantitatively the impact of atomic-scale structure on the HC generation. Our results on silver NPs indicate that lower-coordinated surface sites exhibit a larger proportion of hot electrons, especially those with higher energy, than the bulk of the nanoparticle or higher-coordinated surface sites. In contrast, the distribution of hot holes is relatively homogeneous within each considered NP. These features can be traced to the electronic structure as hole and electron states exhibit localized d- and delocalized sp-type character, respectively. We would therefore expect the present insight to be qualitatively transferable to other late transition metals that exhibit similar electronic structure. The observed trends are present in NPs of different shapes and sizes with varying prevalence. We therefore envision that the obtained atomic-scale insights could be applicable to nanoscale structures in general. First-principles predictions of plasmonic HC generation, as presented here, can thereby facilitate tuning and optimizing photocatalytic systems down to the atomic scale, for example, by enabling identification of promising surface-acceptor combinations.

Methods

Computational Details

The ground-state electronic structures were calculated with KS-DFT^36,37 using the GLLB-sc exchange-correlation potential.^40,41 The time-domain responses were calculated with TDDFT³⁸ starting from the ground state. The dynamical response was described with RPA for the data in Figures 1 and 2 and in Supplementary Figures S1–S6, whereas all the other data were calculated with the adiabatic GLLB-sc.²⁸ The two response kernels yield very similar results (Supplementary Figure S10), but the GLLB-sc potential is not suitable for obtaining the total energies.

All of the calculations were carried out with the open-source GPAW code package⁷⁰ using localized basis sets⁷¹ and the real-time propagation TDDFT implementation.²⁸ We used 11-electron projector-augmented wave⁷² setups for Ag, treating the remaining electrons as a frozen core. We used an extended “p-valence” basis set that includes diffuse 5p functions, which are important for describing plasmon resonances.⁷³ The basis set is similar to the ones used in refs (28) and (39).

The photoabsorption spectra were calculated using the δ-kick technique,⁷⁴ yielding linear impulse response. The photoabsorption of icosahedral particles is isotropic, and the electric field was aligned along the x direction. The resulting HCs do not exhibit a strong variation between different sites (Figure 3c). For the time propagation, we used a time step of 10 as and total propagation time of at least 30 fs. The spectra were broadened using Gaussian damping with σ = 0.07 eV corresponding to a full width at half-maximum of 0.16 eV. The real-time response to a pulse was calculated as a postprocessing step through convolution as described below in detail. In the convolution Fourier transforms or time-domain response, there is no artificial damping.

A grid spacing parameter of h = 0.3 Å was chosen to represent densities and potentials, and the nanoparticles were surrounded by a vacuum region of at least 6 Å. The Hartree potential was evaluated with a Poisson solver using the monopole and dipole corrections for the potential. Fermi–Dirac smearing was applied to the occupation numbers to facilitate convergence. The KS electron–hole basis included electron–hole pairs with occupation number difference f_i – f_a ≥ 10^–3.

Before the response calculations, all geometries were relaxed using the BFGS optimizer in the open-source ASE package.⁷⁵ The relaxation calculations used the Perdew–Burke–Ernzerhof (PBE)⁷⁶ functional, double-ζ polarized (dzp) basis sets, and h = 0.2 Å.

Pulse Response from Convolution

The photoabsorption spectrum can be efficiently calculated from real-time propagation using the δ-kick perturbation⁷⁴ as in the linear-response regime all the frequencies are independent of each other. We utilize this property in the present work for calculating the linear response of the density matrix to the Gaussian pulse of eq 1 as a postprocessing step. First, the time propagation is carried out for perturbation v_kick(t) = zK₀δ(t), yielding the impulse response of the system and the corresponding time-dependent density matrix δρ_ia^kick(t). Then, in the linear-response regime, the response to the pulse of eq 1 is obtained as a convolution

7

which can be very efficiently calculated in frequency space by employing the convolution theorem and inverse Fourier transform

8

where δρ_ia^kick(ω) and 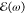are Fourier transforms of the respective time-domain quantities. Here, δρ_ia(ω) can be efficiently calculated from the impulse response by using the computational framework developed in ref (39). The time derivatives required for calculating the energy (Supplementary Note S4) are obtained similarly as

9

10

In practice, is nonvanishing only on a finite frequency interval (see Figure 1a), which narrows the integration limits.

It is emphasized that the time-dependent density matrix, δρ_ia(t), is a complex quantity in time domain, so in practical calculations, it is convenient to carry out Fourier transform for the real Reδρ_ia(t) and imaginary Imδρ_ia(t) parts separately to utilize the properties of Fourier transform of real quantities.

We also note in passing that the impulse response δρ_ia^kick(ω) can be equivalently calculated from the Casida linear-response frequency-space formalism.^39,77 Hence, the linear real-time response to any pulse can also be calculated from the Casida solutions by using the convolution of eq 8.

Total Absorbed Energy

By invoking Fourier transform, the total absorbed energy after the pulse has vanished is obtained as

11

where is the dipole strength function, which equals the photoabsorption cross section safe for a constant multiplier.

Hot-Carrier Distributions

The hot-electron energy distributions corresponding to the state occupation probabilities P_a^e of eq 6 are obtained as (time dependence is not explicitly marked)

12

where

and

that is, they correspond to the real and imaginary parts of δρ_ia (see Supplementary Note S2 for details). For visualization purposes, Gaussian smoothing (convolution) is applied with respect to the ϵ axis.

The spatial probability density of hot electrons is given by the full electron–electron part of the second-order density matrix as (see Supplementary Note S1 and note that only the real part contributes due to the hermiticity of the density matrix)

13

The diagonal and degenerate states dominate the spatial density contributions, which allows us to define a spatio-energetic distribution

14

which is used to calculate the spatial density of hot electrons with more than 1 eV as 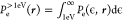, and the energy distribution of hot electrons in a spatial volume V as . The distribution at a specific atomic site (e.g., corner atoms) is obtained by integration over the Voronoi cell associated with the site.

The spatial and energetic distributions of hot holes are calculated analogously to the electrons.

Software Used

The GPAW package^70,78 with linear combination of atomic orbitals (LCAO) mode⁷¹ was used for DFT calculations. The real-time propagation LCAO-TDDFT implementation in GPAW²⁸ was used for the TDDFT calculations. Density-matrix-based analysis tools in frequency space³⁹ and in real time (present work) were used for analysis. The ASE library⁷⁵ was used for constructing atomic structures and geometry relaxation. The NumPy⁷⁹ and Matplotlib⁸⁰ Python packages and the VMD software^81,82 were used for processing and plotting data.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c03004.

• Figures S1–S10 displaying supporting data, notes S1–S4 deriving equations, and supporting reference (PDF)

The authors declare no competing financial interest.

Notes

Scripts, input and data files are also available on Zenodo (https://doi.org/10.5281/zenodo.3927527).