Abstract
Background
The novel coronavirus (coronavirus disease 2019 [COVID-19]) outbreak began in China in December last year, and confirmed cases began occurring in Korea in mid-February 2020. Since the end of February, the rate of infection has increased greatly due to mass (herd) infection within religious groups and nursing homes in the Daegu and Gyeongbuk regions. This mass infection has increased the number of infected people more rapidly than was initially expected; the epidemic model based on existing studies had predicted a much lower infection rate and faster recovery.
Methods
The present study evaluated rapid infection spread by mass infection in Korea and the high mortality rate for the elderly and those with underlying diseases through the Susceptible-Exposed-Infected-Recovered-Dead (SEIRD) model.
Results
The present study demonstrated early infection peak occurrence (-6.3 days for Daegu and -5.3 days for Gyeongbuk) and slow recovery trend (= -1,486.6 persons for Daegu and -223.7 persons for Gyeongbuk) between the actual and the epidemic model for a mass infection region compared to a normal infection region.
Conclusion
The analysis of the time difference between infection and recovery can help predict the epidemic peak due to mass (or normal) infection and can also be used as a time index to prepare medical resources.
Keywords: Coronavirus, COVID-19, Mass infection, SEIRD model, Korea
Graphical Abstract
INTRODUCTION
The novel coronavirus (coronavirus disease 2019 [COVID-19]) outbreak began in Wuhan, China in December 2019 and has spread to at least 177 countries.1 According to the World Health Organization (WHO) report,2 as of 5 August 2020, COVID-19 has killed more than 696,147 people so far, with more than 18.3 million confirmed cases globally.
Symptoms of COVID-19 are not specific and the disease manifestation can vary from no symptoms (asymptomatic) to severe pneumonia and death. According to a WHO report based on 55,924 laboratory-confirmed cases,3 typical signs and symptoms include fever, dry cough, fatigue, sputum production, shortness of breath, and sore throat. In the case of fatality, the patient may die from a cytokine storm, the body's rapid immune response caused by the virus.4 Even after COVID-19 is cured, the antibody may not last for a long time, and the possibility that COVID-19 can recur in many treated patients is being investigated.5 Also, current diagnostic kits are not perfect and show false negatives of about 3%.6 However, failure to detect a small number of cases of the potentially deadly viral infection causes virus spread. The current real-time reverse-transcriptase-polymerase chain reaction (rRT-PCR) test detects SARS-CoV-2-related genetic material, the COVID-19 disease-causing virus.7 Also, on the inspection side, if the patient is inspected too early or the amount of virus is insufficient, the inspection result may be negative, and the kit reagent also has some defects.6
Researchers at UT-Austin in the US analyzed about 450 cases of infection in 93 cities in China and found that more than 10% of the confirmed cases were asymptomatic.8 The period of serial interval (continuous infection) of the virus, which was the time taken from the time the infected person showed symptoms until the second infected person showed symptoms, was only 4 days on average. As a measure of the transmission rate of infectious diseases, the shorter the serial interval, the faster the transmission rate. In the study, the rate of transmission of COVID-19 was analyzed to be as fast as the seasonal flu. In order to respond to the rapid spread of COVID-19, appropriate virus spread models should be established for each country, and accordingly, inspection kits, screening clinics, and infectious disease treatment hospitals should be equipped more rapidly and aggressively.
Unlike the general spread of viruses, the new coronavirus spread rapidly in Korea, mainly from religious groups and nursing homes.9 Through these collective infections, the new virus spread rapidly within a much shorter time than the infectious disease spreading curve of the infectious disease spread model. In particular, most of the elderly patients in nursing homes have significant underlying diseases, and due to additional COVID-19 infection, the mortality rate in Korea was higher compared to the mortality rate for common COVID-19 infection.
In this paper, we analyzed the rapid virus spread and recovery trend by mass infection in Korea using the Susceptible-Exposed-Infected-Recovered-Dead (SEIRD) model.10 By analyzing the inconsistency between the SEIRD model and the trend of infection caused by mass infections, this study derives the infection reproduction number, the date of the inflection point, the mortality rate of the elderly with underlying disease, and the difference between the epidemic peak and recovery for each region.
METHODS
This section describes the basic SEIRD model,10,11 important parameter settings in published epidemic models,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32 and the infection-reproduction equation.
SEIRD model
The individuals of the SEIRD model are classified into four types, S(t), E(t), I(t), R(t) and D(t) which denote the number of people susceptible, exposed, infected, and recovered on day t (Supplementary Fig. 1). The SEIRD model is defined by a system of 5 ordinary differential equations as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where β, δ, and γ denote the transmission rate, the infection (onset) rate, and the recovery rate, respectively. β(= R0γ) is obtained by R0, the initial infection-reproduction number. δ(= 1/c) and γ(= 1/h) are calculated by c, the incubation (latent) period, and h, the hospitalization (infectious) period, respectively. ρ(= 1/d) is the rate at which people die and d is the infection-death period (i.e. days from infection to death). α is the death fatality rate.
Setting of parameters
The estimated values of important parameters of COVID-19 was analyzed in recently studied epidemic models (Supplementary Table 1).12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32 The parameters for the SEIRD model were set by the data analysis results for Wuhan city, China and Gyeongbuk, Daegu, Korea. We assumed no further transmission would occur once a person entered into the status of R. S was set to (P-I[0]-E[0]), total city population (P) excluding the initially infected and exposed population.9 E was set as 20 times that of I in accordance with Wang et al.12 and Read et al.13 R(0) and D(0) were set as 0. The mean incubation period of the new coronavirus was determined to be 5.2 days according to previously published studies.14,15,16,17 Therefore, δ was set as 0.1923(= 1/5.2) with reference to previously published studies.14,15,16,18,20 In some12,22 though not all21 previous studies, the average hospitalization period including the mean time from pathogenesis (disease onset) to diagnosis was calculated as 18 days. The median time from disease onset to diagnosis among confirmed patients was previously found to be 5 days.23 On this basis, our γ was set as 0.0556(= 1/18) while various γ were presented in earlier research.12,14,15,16,21,24 And d was set as 14 days according to the existing research result.20 α is strongly influenced by elapsed time, age, and underlying disease from the date of virus spread.25,26 The values used in our model were based on mortality rates for those over 60 years of age as of May 4, 2020.27
The infection-reproduction number, R0, represents the average number of new infections spread by each infected person. The average number of secondary infections (reproduction function) at time t is expressed as R0(t). R0 should be carefully selected because it greatly affects the spread curve of the spread model.15,21,28,29 The number of secondary infections at time t is given as follows:
| (6) |
where (= 3.7 and 2.7 for Daegu and Gyeongbuk respectively) and (= 0.5 for both regions) are the reproduction number at the beginning and end of the spread of infectious diseases. The td(= 12 and 9 days for Daegu and Gyeongbuk respectively) represent the date of the inflection point and the steepest decline of R0. It could be thought of as the main lockdown date and was set based on the date that infection rates began to decrease after the explosion of infection rates in Daegu and Gyeongbuk. The k(= 0.5) indicates the declination rate of R0. In addition, the declination rate was set in consideration of the rapid increase and decrease of infection. In a previous study, β was used as an inferred value via a least-square-based procedure with Poisson noise15 and Markov Chain Monte Carlo29 or preset constants.30 In this paper, β(= R0γ) is obtained by R0 and γ.
RESULTS
Parameter setting used for SEIRD model
Table 1 shows the basic information and infection-reproduction parameters used for our SEIRD model in the mass infection region (Daegu and Gyeongbuk) and the normal infection region (Seoul and Gyeonggi). The population of each city was set based on current data. The respective I(0) was set to 13, the number of infected people found in Daegu as of February 19, 2020.9 I(0) also was set to 14 for Gyeongbuk (on February 22), Seoul (on February 20), and Gyeonggi (on February 21).9,33 Daegu and Gyeongbuk are mass infection regions, while Seoul and Gyeonggi are normal infection regions. Therefore, Daegu and Gyeongbuk regions show more confirmed cases and recovery than Seoul and Gyeonggi. The reproduction number at the beginning of the epidemic and the data for the inflection point of each city was set taking into account mass and normal infection rates.
Table 1. Basic information and infection-reproduction parameters for our Susceptible-Exposed-Infected-Recovered-Dead model.
| Area | Population | I(0) | td | α, % | ||
|---|---|---|---|---|---|---|
| Daegu | 2,433,568 | 13 | 3.7 | 0.0 | 15 | 2.82 |
| Gyeongbuk | 2,653,418 | 14 | 2.6 | 0.0 | 15 | 4.34 |
| Seoul | 9,726,787 | 1 | 1.5 | 0.0 | 50 | 0.55 |
| Gyeonggi | 13,311,254 | 1 | 1.3 | 0.0 | 45 | 2.88 |
Mass infection analysis in Daegu and Gyeongbuk
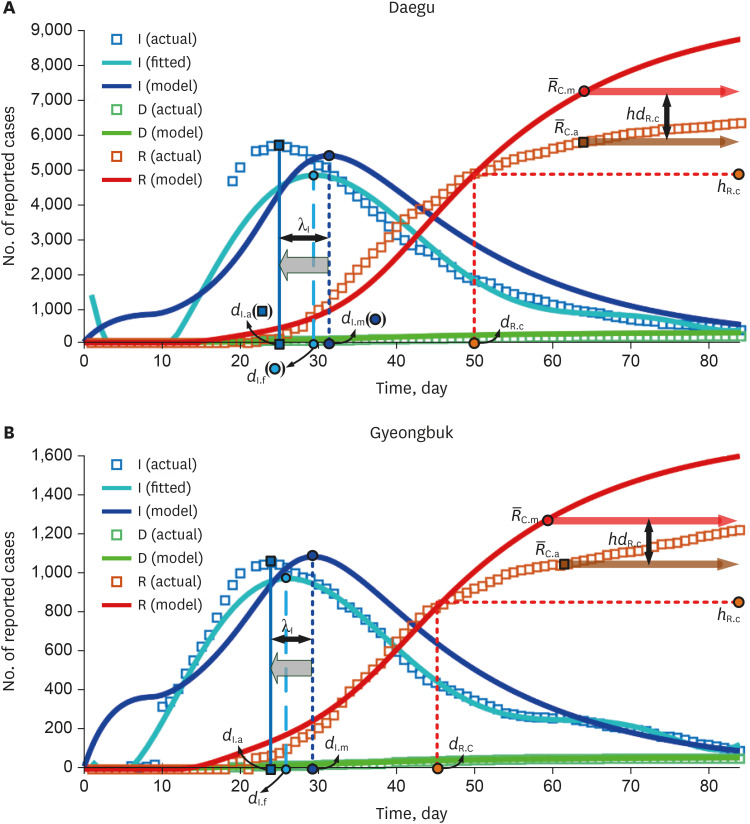
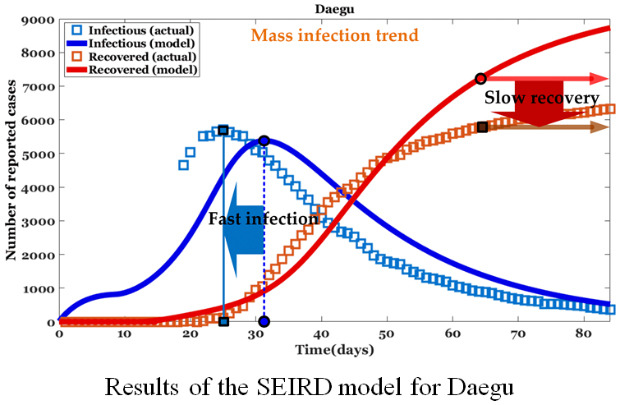
Results from the SEIRD model for the Daegu-Gyeongbuk region are shown in Fig. 1. The graph was modeled based on actual data from the start of infection and for an 84-day period. The figure shows the distribution of I (infections) and D (deaths) for the left Y-axis and R (recovered) for the right Y-axis. From the actual data for Daegu and Gyeongbuk, the number of infected persons exploded after the 10th day from the start of the spread of the infectious disease. This is due to the collective infections that occurred through Sinchonji religious groups and nursing homes. To quantitatively confirm the actual infection curve, 6th order polynomial curve fitting was also applied.
Fig. 1. Results of the Susceptible-Exposed-Infected-Recovered-Dead model for mass infection. (A) λI = −6.3 days for Daegu was obtained by the difference between the actual epidemic peak dI.a = 25 days and the modeled epidemic peak dI.m = 31.3 days. (B) λI = −5.3 days for Gyeongbuk was obtained by the difference between the actual epidemic peak dI.a = 24 and the modeled epidemic peak dI.m = 29.3 days.
It is not easy to estimate the rapid increase in the number of infected people due to the (incidental) collective infection as an existing SEIRD model. In the case of mass infections, such as in religious groups or nursing homes in Korea, epidemic peaks may occur earlier compared to predictions made by common SEIRD models. In other words, collective infection means that the time to prepare health care resources before the spread of infectious diseases can be much shorter than we thought. Although the td was set considering the period of the mass infection described in Fig. 1A, it can be seen that there is a time difference λI(= dI.a − dI.m) between the actual (fitted) and the estimated (modeled by our model) infection trends. λI(= −6.3 days for Daegu and −5.3 days for Gyeongbuk) was obtained by the difference between the actual epidemic peak dI.a(= 25 days for Daegu and 24 days for Gyeongbuk) and the modeled epidemic peak dI.m(= 31.3 days for Daegu and 29.3 days for Gyeongbuk). Also, in order to find differences in the actual and estimated trends for those recovering from COVID, the date dR.C occurs when the actual and estimated numbers of those recovering are equal and the number of those recovering hR.C at that time is defined. The averages, and , of the actual and modeled recovery numbers are compared. It was found that mass infection by COVID-19 may cause a difference hdR.C( − ) in the number of those recovering after dR.C. hdR.C(= −1486.6 persons for Daegu and −223.7 persons for Gyeongbuk) is determined by the difference in dates in the actual ( = 5781.7 persons for Daegu and 1,058.7 persons for Gyeongbuk) and modeled ( = 7,268.3 persons for Daegu and 1,291.4 persons for Gyeongbuk) recovery trends. The experimental results indicate that in the case of mass infection, the actual recovery trend may occur later than the modeled recovery trend.
The delay of actual recovery can be confirmed in a recent report on the release of containment in Daegu city.9 In the simulation of this paper, the hospitalization period was set to 18 days based on the results of existing COVID-19 studies,12,22 but the actual recovery trend was not accurately predicted. The results of these recovery simulations indicate that recovery delays may occur by country and region. According to Daegu city,9 as a result of investigating the treatment period of about 5,000 diagnosed patients, the average treatment period was 24.8 days. It was found that it took more than 20 days for 73% of all confirmed cases in Daegu to be cured. In addition, the average treatment period for people who healed completely from COVID-19 and were under the age of 30 was 24.7 days, and the treatment period between the ages of 30 and 69 years was 24.8 days; thus there was little difference in treatment period by age group observed in our study. We further note that the treatment period for patients aged 70 or older was 25.6 days, similar to other treatment periods. As shown in Table 2, the average duration of release of sequestered patients by management type was 25.3 days for hospitals, 24.4 days for living treatment facilities, and 22.7 days for self-isolation. In addition, it took a little longer for the relatively severe patients admitted to the hospital to be released from quarantine.
Table 2. Period of release of quarantine by management type of confirmed coronavirus disease 2019 patients on May 4, 20209.
| Management | No. of patients | Less than 20 days | 20–29 days | 30–39 days | 40 days or more |
|---|---|---|---|---|---|
| Hospital | 2,413 | 553 (23) | 1,174 (49) | 593 (24) | 93 (4) |
| Living treatment facility | 2,391 | 729 (31) | 1,062 (44) | 547 (23) | 53 (2) |
| Self-isolation | 177 | 41 (23) | 129 (73) | 7 (4) | - |
| Total | 4,981 | 1,323 (27) | 2,365 (47) | 1,147 (23) | 146 (3) |
Data are presented as number (%).
Daegu ( = 3.7) has a much higher reproduction number than other regions due to group infections among the Shincheonji religious group, while Gyeongbuk ( = 2.6) has the next highest reproduction number due to group infections in nursing hospitals where senior citizens are hospitalized. The number of infected people in Gyeongbuk increased rapidly from the date of infection, similar to Daegu, but the reproduction number was smaller than that of Daegu.
Normal infection analysis in Seoul and Gyeonggi
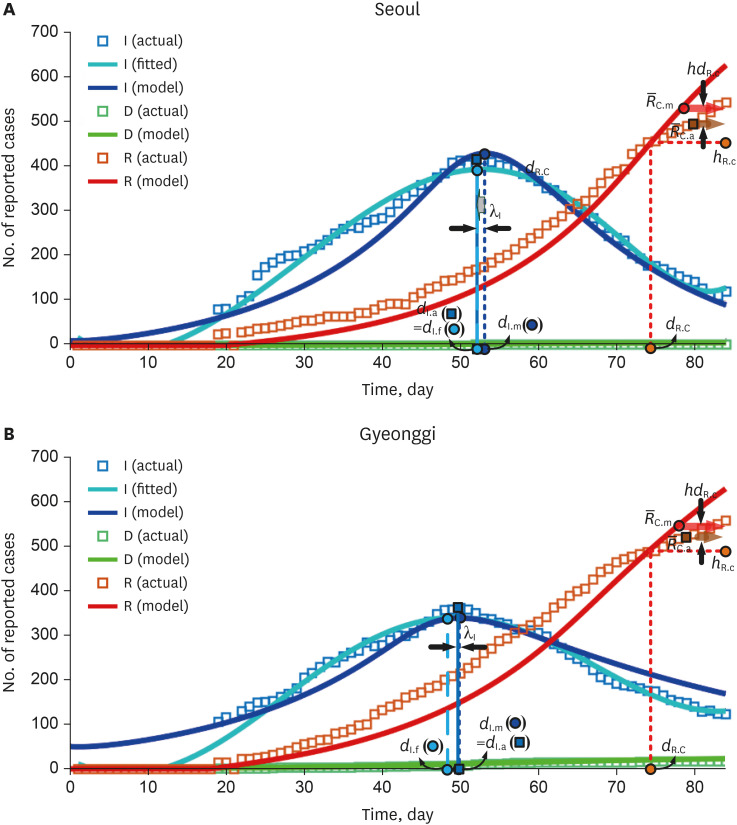
Fig. 2 shows the actual data and the modeling results by SEIRD model for Seoul and Gyeonggi. Unlike the short-term explosive mass infections in the Daegu-Gyeongbuk regions, the number of infected people in the Seoul-Gyeonggi regions increased and decreased sporadically on a small scale via general spread. As shown in the fitted infection trend curve, the spread of infection increased slowly and there were three to four small spreads in both regions shown in Fig. 1. Although the td was established considering the duration of a small-scale infection outbreak, it can be seen that the actual (fitted) and estimated (modeled) infection trends in our model are somewhat different compared to those for mass infection. λI(= −0.1 days for Seoul and 0.1 days for Gyeonggi) is calculated as the difference between the actual epidemic peak dI.a(= 53 days for Seoul and 50 days for Gyeonggi) and the modeled epidemic peak dI.m(= 53.1 days for Seoul and 49.9 days for Gyeonggi). Unlike Daegu-Gyeongbuk, in Seoul-Gyeonggi, the modeled infection trend is similar to the actual infection trend with a small λI. hdR.C(= −38.5 persons for Seoul and −32.9 persons for Gyeonggi) is determined by the difference in dates in the actual ( = 496.0 persons for Seoul and 520.0 persons for Gyeonggi) and modeled ( = 534.5 persons for Seoul and 552.9 persons for Gyeonggi) recovery trends. In addition, normal infection in Seoul-Gyeonggi made a small difference between the averages of actual and modeled recovery numbers after dR.C, unlike the mass infection in Daegu-Gyeongbuk. The recovery period of COVID-19, regardless of whether it was a mass infection or a normal infection, was quite long in Korea as described in Table 2, resulting in a delay in the actual recovery trend. While Gyeonggi had a high mortality rate compared to the number of confirmed patients, Seoul's mortality rate was significantly lower than in other regions.
Fig. 2. Results of the Susceptible-Exposed-Infected-Recovered-Dead model for normal infection. (A) λI = −0.1 days for Seoul is calculated as the difference between the actual epidemic peak dI.a = 53 days and the modeled epidemic peak dI.m = 53.1 days. (B) λI = 0.1 days for Gyeonggi is calculated as the difference between the actual epidemic peak dI.a = 50 days and the modeled epidemic peak dI.m = 49.9 days.
In Seoul and Gyeonggi, the reproduction number is small due to the small number of general infections, and the td is high (gentle descent) due to a long-term irregular small-scale spread. Using the reproduction equation (equation 6), it was found that the reproduction number and td are inversely related ( ∝ 1/td) regardless of the mass infection and the general infection. This implies that when sufficient COVID-19 infection data is available, the td corresponding to the reproduction number can be deduced.
Full analysis in Korea
In this section, we comprehensively analyzed the difference of epidemic peaks and the number of those recovering in the actual trend and the epidemic model for cities in Korea. Table 3 shows the result of parameters related to infections and recoveries for the actual and modeled trend of COVID-19 in the cities of Korea. It is necessary to note that the actual (as well as modeled) epidemic peaks and the cross date (dR.C) of the actual and modeled recovery curves were different in Daegu-Gyeongbuk, where small mass infection occurred, and Seoul-Gyeonggi, where small-scale general infection occurred. Despite the fact that td was set considering the actual duration of infection, λI in Daegu-Gyeongbuk with mass infection showed a time leading phenomenon of epidemic peaks, while λI in Seoul-Gyeonggi with normal infection showed little difference. The fitting curve of Daegu-Gyeongbuk (dI.a − dI.f = −5, 2) did not express the actual infection trend due to the rapid increase in the number of infected people compared to Seoul-Gyeonggi (dI.a − dI.f = 0, 1). The average epidemic peaks of each region are = −5.8 days for Daegu-Gyeongbuk and = −0.1 days for Seoul-Gyeonggi. The parameters used in this paper were analyzed based on the resulting trends. If only the initial infection trend is given without prior information of the mass infection, the actual epidemic peak may appear much faster than the epidemic peak predicted by the model.
Table 3. Parameters related to infections and recovery for the actual and modeled trend of coronavirus disease 2019 in several cities of Korea.
| Type of infection | Area | λI | dI.m | dI.f | dI.a | hdR.c | dR.c | hR.c | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Mass | Daegu | −6.3 | 31.3 | 30 | 25 | −1,486.6 | 7,268.3 | 5,781.7 | 50 | 4,859 |
| Gyeongbuk | −5.3 | 29.3 | 26 | 24 | −232.7 | 1,291.4 | 1,058.7 | 45 | 823 | |
| Normal | Seoul | −0.1 | 53.1 | 53 | 53 | −38.5 | 534.5 | 496.0 | 75 | 455 |
| Gyeonggi | −0.1 | 49.9 | 49 | 50 | −32.9 | 552.9 | 520.0 | 74 | 487 |
The infection trend predicted in the SEIRD model10,11 was greatly influenced by the transmission rate and incubation period, and these two variables were dominant factors in the actual infection trend. As a result, actual and predicted infection trends had morphological similarities. Therefore, it is easy to compare actual and predicted infection trends based on infection peaks. On the other hand, recovery trend prediction was affected by the recovery rate and fatality rate, but it was not easy to apply the values of these variables to any region or country to predict. Actually, for COVID-19, the recovery rates investigated in several studies12,14,15,16,18,21,24 had the largest minimum-to-maximum ratio compared to other variables. In addition, the recovery trend, unlike the infection trend, had no characteristic points that can be used as a reference point. For this reason, in the comparison of recovery trends, the difference in the number of recoverers was used, not the time (day).
In the recovery trend, the crossing date and the number of those recovering at that time were used to analyze whether the model follows the actual recovery trend. The fast crossing time meant that the model deviated faster from the actual recovery trend. The crossing dates of Daegu-Gyeongbuk and Seoul-Gyeonggi were dR.C = 50, 45 and dR.C = 75, 74, respectively. The recovery crossing dates in the Daegu-Gyeongbuk (mass infection) were earlier than in the Seoul-Gyeonggi (normal infection). This was because the actual recovery in the Daegu-Gyeongbuk region was slower than what was predicted by the epidemic model due to the long hospitalization period, while the used epidemic model for Seoul-Gyeonggi followed the actual recovery trend. In conclusion, the faster crossing time in Daegu-Gyeongbuk could lead to a large discrepancy between the actual number of those recovering and the number of recovering COVID-19 patients predicted by the model, as described in the mass infection analysis.
DISCUSSION
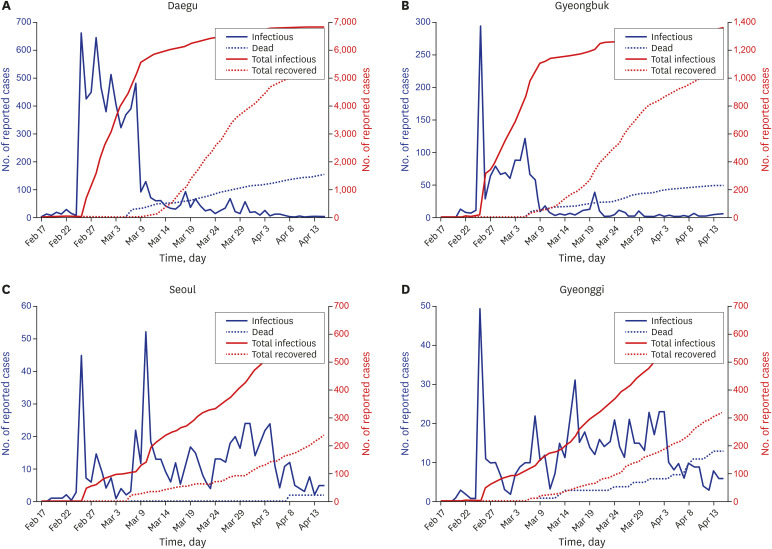
According to the Korea Centers for Disease Control and Prevention in Korea, during the first 4 weeks after the first outbreak on January 20, the disease spread slowly with less than 100 confirmed cases.33 However, the number of patients rapidly surged after that, exceeding 5,000 within 6 weeks, most of them in the Daegu and Gyeongbuk regions.33 This surge overcrowded regional hospital resources and forced some confirmed patients to stay at home. Fig. 3 shows the trend of daily (infections and deaths) and cumulative (total infections and total recovered) COVID-19 confirmed patients in Daegu, Gyeongbuk, Seoul, and Gyeonggi.9 Since national patient number 31, belonging to a religious group, was reported on February 18, there was a surge of confirmed cases with hundreds of new cases per day, mainly in Daegu and Gyeongbuk area. Korea's virus cases topped 7,000 on Saturday with most new virus infections in the southeastern city of Daegu, the epicenter of the virus outbreak, and neighboring Gyeongbuk as of March 7. Of 94 new cases, 27 were reported in the southeastern city of Daegu, which became the epicenter of the virus following a mass infection of people linked to a church of the Shincheonji religious sect in February. So far, 6,761 people have been diagnosed with the respiratory disease in the city located some 300 kilometers from Seoul, with an additional 1,310 people diagnosed with the virus in the surrounding Gyeongbuk. As of March 10, 2020, 54 out of the 7,513 confirmed patients with COVID-19 in Korea had died.
Fig. 3. Trend of daily (infections and deaths) and cumulative (total infections and total recovered) coronavirus disease 2019 confirmed patients. (A) The cumulative confirmed cases in Daegu rapidly exceeded 6,000 through mass infection by the religious groups within a month. (B) The cumulative number of confirmed cases in Gyeongbuk has steeply exceeded 1,100 through mass infection at nursing hospitals within a month. (C) The number of confirmed cases in Seoul gradually reached 250 due to general infection within a month. (D) The number of confirmed patients in the game gradually reached 230 due to general infection within a month.
Table 4 shows the number of deaths and mortality rates by age among confirmed patients in Korea.27 The mortality rate applied to Gyeongbuk was set to 4.34%, which was much higher than the rates in previous reports.25,26 This value was higher than the mortality rate for participants in their 60s (60–69), which was also due to the mass infection of the elderly with underlying diseases in nursing homes, the main infectious factor in the Gyeongbuk. In addition, the relatively high mortality rate in Daegu was due to mass infections among religious groups, and it was estimated that the age range of infected people in Daegu was rather high. Mortality rates from previous studies did not adequately estimate the death curve for the elderly with mass infection and underlying disease, because most of the deaths in Korea were those with underlying disease who were over 60 years of age. Because the number of infected people in Seoul and Gyeonggi was much lower than that of Daegu and Gyeongbuk, it was not easy to infer the correlation between mortality rate due to normal infection and age and underlying disease in their region.
Table 4. Status of confirmed patients in Korea by age27.
| Age, yr | Confirmed case | Dead | Fatality rate, % |
|---|---|---|---|
| ≥ 80 | 488 (4.52) | 120 (47.62) | 24.59 |
| 70–79 | 710 (6.57) | 76 (30.16) | 10.7 |
| 60–69 | 1,353 (12.53) | 36 (14.29) | 2.66 |
| 50–59 | 1,956 (18.11) | 15 (5.95) | 0.77 |
| 40–49 | 1,435 (13.29) | 3 (1.19) | 0.21 |
| 30–39 | 1,164 (10.78) | 2 (0.79) | 0.17 |
| 20–29 | 2,964 (27.44) | 0 (0.00) | - |
| 10–19 | 591 (5.47) | 0 (0.00) | - |
| 0–9 | 140 (1.3) | 0 (0.00) | - |
Data are presented as number (%).
Unlike the general virus outbreak, the spread of COVID-19 in Korea has been rapid, particularly in closed spaces such as religious organizations and nursing homes in Daegu-Gyeongbuk. In contrast, general community infections excluding such closed spaces progressed slowly due to the active use of masks and disinfectants by citizens. Therefore, the rapid spread in the early stages of infection was limited to specific religious groups and nursing hospital communities rather than representing all of Daegu-Gyeongbuk (or Korea). It may be difficult to estimate the spread of the virus due to such an unusual mass infection using a general epidemic model.
The spread and status of COVID-19 in Daegu-Gyeongbuk was as follows. First, the number of infected people in Daegu-Gyeongbuk accounted for 76% of the total number of infected people in Korea, and it had spread to specific communities within Daegu-Gyeongbuk. Second, the explosion of infection occurred within 10 days after the initial infection and lasted for 2 weeks, and then began to fade. Third, due to active social distance and the use of masks, the proliferation of communities with COVID-19 outbreaks other than specific communities that were sources of infection had progressed relatively slowly. Fourth, large-scale examinations through screening clinics and drive-through examinations in the early stages of the spread of infection enabled accurate statistics of the increase in confirmatory patients. Fifth, Korea has a high patient acceptance rate of treatment facilities that can cope with the rapidly growing confirmed infection rates.
Table 5 shows the analysis for infection peak date of various countries. Many studies predicted infection peaks or trends of COVID-19 using various epidemic models.12,34,35,36,37 Most infection epidemic studies were conducted before the spread of infection, and studies analyzing the difference between the actual and predicted infection peaks after the spread of infection were not active. Analyzing these differences is very important in determining the characteristics of the epidemic itself, such as asymptomatic infection, the population density of the affected area, and social distancing. In this paper, the characteristics of mass infection and asymptomatic infection were inferred by analyzing the difference between the actual and predicted infection peaks as well as the accuracy of the used epidemic model. Table 5 shows the time taken from first infected person to peak infection in various countries. The time taken to peak infection in Daegu and Gyeongbuk was achieved in a very short time compared to other countries. It may be due to mass infections through religious groups and nursing hospitals and asymptomatic infection of COVID-19. And this rapid infection peak also occurred in China and Italy. In China, the actual peak date of infection in the public data34 and the trend of 3-day average of new confired cases37 was much faster than the estimated peak date in the phase-adjusted estimation method.12 And in the case of Italy as well, the actual infection peak time in the trend of 3-day average of new confired cases37 was much faster than the predicted infection peak time in the improved epidemic dynamics model.35 This early infection peak is likely related to asymptomatic infection of COVID-19.35 used a modified SEIR model including an asymptomatic infection variable to predict the epidemic peak in Italy. As a result, the method shows a relatively small peak date difference between the actual and predicted peaks despite the large infection scale in Italy. As a result, this paper infers that in Daegu-Gyeongbuk, the high population density of religious organizations and nursing hospitals and the amplification of infections caused by asymptomatic infection of COVID-19 (long incubation period) significantly advanced the epidemic peak date compared to other countries or cities.
Table 5. Analysis for infection peak date of various countries.
| Time from first confirmed to infection peak | Method | References |
|---|---|---|
| 25 days (Daegu), 24 days (Gyeongbuk), 53 days (Seoul), 50 days (Gyeonggi) | Actual | Proposed (This paper) |
| 31 days (Daegu), 29 days (Gyeongbuk), 53 days (Seoul), 50 days (Gyeonggi) | SEIRD | Proposed (This paper) |
| 82 days (Wuhan, China) | SEIR | 12 |
| 31 days (Hubei, China) | Actual | 34 |
| 68 days (Italy) | Modified SEIR | 35 |
| 36 days (first peak, Greece) | Actual | 36 |
| 60 days (China), 40 days (Korea), 40 days (Japan), 58 days (Italy) | Actual | 37 |
SEIRD = Susceptible-Exposed-Infected-Recovered-Dead.
It is not easy to explain the mass infections in Daegu-Gyeongbuk described above as a general epidemic model. Although the parameters used in the SEIRD model were set based on the results of a recent COVID-19 study, the model used did not accurately describe the spreading characteristics within Daegu-Gyeongbuk. Nevertheless, this paper analyzed the early appearance of epidemic peaks and slow recovery trends by mass infection by comparing the difference between epidemic peaks and recovery trends between the actual trend and the epidemic model. This characterization of mass infection is useful for inferring the preparation time of necessary medical resources in the future, and can also be used to derive the hospitalization period of the infectious group (older in this paper than in previous research) that directly affects the recovery trend.
Mass infection was the largest factor affecting the COVID-19 spread in Korea and occurred intensively in a short period of time, earlier than the epidemic peak date predicted in the existing SEIRD model. Modeling studies of mass infections have more variables to be considered compared to general virus outbreaks. When a mass infection occurs, the initial virus response time is much shorter than for normal spread. Therefore, in order to prepare for the second epidemic of COVID-19, rapid research on collective infections by country and region is essential, and a command system should be established to prepare medical resources within the predicted epidemic peak date.
Footnotes
Funding: This work was supported by Electronics and Telecommunications Research Institute (ETRI) grant funded by the Korean government (20ZD1100, Development of ICT Convergence Technology for Daegu-Gyeongbuk Regional Industry).
Disclosure: The authors have no potential conflicts of interest to disclose.
- Conceptualization: Bae TW, Kwon KK.
- Data curation: Bae TW.
- Formal analysis: Bae TW.
- Funding acquisition: Kwon KK.
- Investigation: Bae TW, Kim KH.
- Methodology: Bae TW.
- Project administration: Kwon KK.
- Resources: Bae TW.
- Software: Bae TW.
- Supervision: Kwon KK.
- Validation: Bae TW, Kwon KK.
- Visualization: Bae TW.
- Writing - original draft: Bae TW.
- Writing - review & editing: Bae TW.
SUPPLEMENTARY MATERIALS
Estimated values of important parameters of COVID-19 in a published epidemic model
Transition configuration of Susceptible-Exposed-Infected-Recovered-Dead model.
References
- 1.Mackenzie JS, Smith DW. COVID-19: a novel zoonotic disease caused by a coronavirus from China: what we know and what we don't. [Updated 2020]. [Accessed May 9, 2020]. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7086482/pdf/MA20013.pdf. [DOI] [PMC free article] [PubMed]
- 2.World Health Organization. Coronavirus disease (COVID-19) pandemic. [Updated 2020]. [Accessed May 9, 2020]. https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
- 3.World Health Organization. Report of the WHO-China joint mission on coronavirus disease 2019 (COVID-19) [Updated 2020]. [Accessed May 9, 2020]. https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf.
- 4.Mehta P, McAuley DF, Brown M, Sanchez E, Tattersall RS, Manson JJ, et al. COVID-19: consider cytokine storm syndromes and immunosuppression. Lancet. 2020;395(10229):1033–1034. doi: 10.1016/S0140-6736(20)30628-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen D, Xu W, Lei Z, Huang Z, Liu J, Gao Z, et al. Recurrence of positive SARS-CoV-2 RNA in COVID-19: a case report. Int J Infect Dis. 2020;93:297–299. doi: 10.1016/j.ijid.2020.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.MedicineNet. Are coronavirus tests accurate? [Updated 2020]. [Accessed May 9, 2020]. https://www.medicinenet.com/script/main/art.asp?articlekey=228250.
- 7.Long C, Xu H, Shen Q, Zhang X, Fan B, Wang C, et al. Diagnosis of the coronavirus disease (COVID-19): rRT-PCR or CT? Eur J Radiol. 2020;126:108961. doi: 10.1016/j.ejrad.2020.108961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Du Z, Xu X, Wu Y, Wang L, Cowling BJ, Meyers LA. Serial interval of COVID-19 among publicly reported confirmed cases. Emerg Infect Dis. 2020;26(6):1341–1343. doi: 10.3201/eid2606.200357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Daegu Metropolitan City. Trend of reported cases. [Updated 2020]. [Accessed May 9 2020]. http://www.daegu.go.kr/dgcontent/index.do?menu_id=00936642.
- 10.Chowell G, Hengartner NW, Castillo-Chavez C, Fenimore PW, Hyman JM. The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. J Theor Biol. 2004;229(1):119–126. doi: 10.1016/j.jtbi.2004.03.006. [DOI] [PubMed] [Google Scholar]
- 11.Piccolomiini EL, Zama F. Monitoring Italian COVID-19 spread by an adaptive SEIRD model. medRxiv. [Updated 2020]. [Accessed May 9, 2020]. https://www.medrxiv.org/content/10.1101/2020.04.03.20049734v1.
- 12.Wang H, Wang Z, Dong Y, Chang R, Xu C, Yu X, et al. Phase-adjusted estimation of the number of coronavirus disease 2019 cases in Wuhan, China. Cell Discov. 2020;6(1):10. doi: 10.1038/s41421-020-0148-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Read JM, Bridgen JR, Cummings DA, Ho A, Jewell CP. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv. [Updated 2020]. [Accessed May 9, 2020]. https://www.medrxiv.org/content/10.1101/2020.01.23.20018549v1.full.pdf. [DOI] [PMC free article] [PubMed]
- 14.Liu T, Hu J, Kang M, Lin L, Zhong H, Xiao J, et al. Transmission dynamics of 2019 novel coronavirus (2019-nCoV) Lancet. 2020 [Google Scholar]
- 15.Kuniya T. Prediction of the epidemic peak of coronavirus disease in Japan, 2020. J Clin Med. 2020;9(3):1–7. doi: 10.3390/jcm9030789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 2020;382(13):1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Backer JA, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Euro Surveill. 2020;25(5):1–6. doi: 10.2807/1560-7917.ES.2020.25.5.2000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhou T, Liu Q, Yang Z, Liao J, Yang K, Bai W, et al. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV. J Evid Based Med. 2020;13(1):3–7. doi: 10.1111/jebm.12376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Linton NM, Kobayashi T, Yang Y, Hayashi K, Akhmetzhanov AR, Jung SM, et al. Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: a statistical analysis of publicly available case data. J Clin Med. 2020;9(2):1–9. doi: 10.3390/jcm9020538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Baker R. Reactive Social distancing in a SIR model of epidemics such as COVID-19. arXiv. [Updated 2020]. [Accessed May 9, 2020]. https://arxiv.org/abs/2003.08285.
- 22.Chen N, Zhou M, Dong X, Qu J, Gong F, Han Y, et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: a descriptive study. Lancet. 2020;395(10223):507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yang Y, Lu Q, Liu M, Wang Y, Zhang A, Jalali N, et al. Epidemiological and clinical features of the 2019 novel coronavirus outbreak in China. medRxiv. [Updated 2020]. [Accessed April 24, 2020]. https://www.medrxiv.org/content/10.1101/2020.02.10.20021675v2.
- 24.Sun H, Qiu Y, Yan H, Huang Y, Zhu Y, Chen SX. Tracking and predicting COVID-19 epidemic in China mainland. medRxiv. [Updated 2020]. [Accessed April 24, 2020]. https://www.medrxiv.org/content/10.1101/2020.02.17.20024257v1.
- 25.Korean Society of Infectious Diseases; Korea Centers for Disease Control and Prevention. Analysis on 54 mortality cases of coronavirus disease 2019 in the Republic of Korea from January 19 to March 10, 2020. J Korean Med Sci. 2020;35(12):e132. doi: 10.3346/jkms.2020.35.e132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Korean Society of Infectious Diseases. Report on the epidemiological features of coronavirus disease 2019 (COVID-19) outbreak in the Republic of Korea from January 19 to March 2, 2020. J Korean Med Sci. 2020;35(10):e112. doi: 10.3346/jkms.2020.35.e112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ministry of Health and Welfare. Domestic occurrence status. [Updated 2020]. [Accessed May 9 2020]. http://ncov.mohw.go.kr/bdBoardList_Real.do.
- 28.Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds J, Funk S, et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020;20(5):553–558. doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Imperial College London. Report 3: transmissibility of 2019-nCoV. [Updated 2020]. [Accessed May 9 2020]. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-transmissibility-25-01-2020.pdf.
- 30.Tang B, Wang X, Li Q, Bragazzi NL, Tang S, Xiao Y, et al. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J Clin Med. 2020;9(2):1–13. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Iwata K, Miyakoshi C. A simulation on potential secondary spread of novel coronavirus in an exported country using a stochastic epidemic SEIR model. J Clin Med. 2020;9(4):1–7. doi: 10.3390/jcm9040944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Boldog P, Tekeli T, Vizi Z, Dénes A, Bartha FA, Röst G. Risk assessment of novel coronavirus COVID-19 outbreaks outside China. J Clin Med. 2020;9(2):1–12. doi: 10.3390/jcm9020571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Korea Centers for Disease Control and Prevention. Press release. [Updated 2020]. [Accessed May 9, 2020]. https://www.cdc.go.kr/board/board.es?mid=a20501000000&bid=0015.
- 34.Wikipedia. COVID-19 pandemic in Hubei. [Updated 2020]. [Accessed August 8, 2020]. https://en.wikipedia.org/wiki/COVID-19_pandemic_in_Hubei.
- 35.Wang H, Xu K, Li Z, Pang K, He H. Improved epidemic dynamics model and its prediction for COVID-19 in Italy. Appl Sci. 2020;10(14):1–12. [Google Scholar]
- 36.COVID-19 pandemic in Greece. [Updated 2020]. [Accessed August 8, 2020]. https://en.wikipedia.org/wiki/COVID-19_pandemic_in_Greece.
- 37.Chen YT, Yen YF, Yu SH, Su EC. An examination on the transmission of COVID-19 and the effect of response strategies: a comparative analysis. Int J Environ Res Public Health. 2020;17(16):1–14. doi: 10.3390/ijerph17165687. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Estimated values of important parameters of COVID-19 in a published epidemic model
Transition configuration of Susceptible-Exposed-Infected-Recovered-Dead model.