Application of Graphene as a Nanoindenter Interacting with Phospholipid Membranes—Computer Simulation Study

Abstract

Synthesis of graphene (GN) in 2004 stimulated wide interest in potential applications of 2D materials in catalysis, optoelectronics, biotechnology, and construction of sensing devices. In the presented study, interactions between GN sheets and phospholipid bilayers are examined using steered molecular dynamics simulations. GN sheets of different sizes were inserted into a bilayer and subsequently withdrawn from it at two different rates (1 and 2 m/s). In some cases, nanoindentation led to substantial damage of the phospholipid bilayer; however, an effective self-sealing process occurred even after significant degradation. The average force and work, deflection of the membrane during indentation, withdrawal processes, and structural changes caused by moving sheets are discussed. These quantities are utilized to estimate the suitability of GN sheets for targeted drug delivery or other nanomedicine tools. The results are compared with those obtained for other nanostructures such as homogeneous and heterogeneous nanotubes.

Introduction

Graphene (GN) has received such attention in the last decade and a half that there is little need for description. The sheets possess a distinct set of properties leading to extensive applications. In electronics, for example, its superior electrical and thermal conductivity combined with a huge specific 2D area have made it an attractive material for current transport in lithium batteries and supercapacitors. Its zero band gap has been manipulated to advantage in photovoltaic devices. High tensile and shear strengths coupled with a large Young’s modulus make it suitable for mechanical resonators.^1,2 Some GN-based materials are also flexible enough to replace indium tin oxide as a transparent conductor, creating potential for high-quality flexible displays.³ GN’s chemical properties are similarly promising. GN materials improve the overall performance of polymer composites when added as a reinforcing agent.^4,5 It has been found to enhance the bulk physical properties of polymers when added as a reinforcing agent.^4,5 GN and its derivatives, such as GN oxide, also hold promise as functional materials in water purification.⁶ Many of GN’s properties are superior to those found in other carbon-based materials, such as nanotubes.^7,8

Research on GN has also stimulated major progress in the application of two-dimensional atomic materials.^4,9,10 Its useful physical properties combined with its biomolecular interactions make GN highly attractive for low-cost disposable biosensors.¹¹⁻¹³ Research into biocompatibility has shown that at least some GN-family nanomaterials may be problematic, even degrading in human blood plasma,^14,15 and there have also been reports that the sheets may reduce cell proliferation.¹⁶ On the other hand, GN may have applications in systems with a high concentration of phospholipids, such as osteoarthritic synovial fluid.¹⁷ In this disease, GN’s affinity for lipids may help target problematic hyaluronan–lipid interactions or fortify the membranes on articular surfaces against degeneration.

In recent years, micro- and nanodevices were successfully tested as potential nanoknives in neurosurgeries¹⁸ or cell cutters.¹⁹ The fabrication of structures that could perform the roles of nanoknives or nanoneedles has also been realized.²⁰ The properties of GN suggest that it may become an important material in such medical devices. Recent simulation studies have shown that the GN sheets are able to extract the cholesterols from the protein clusters or bilayers.^21,22 In order to find novel therapies based on targeted drug delivery using nanostructures or to test the suitability of GN in future medical devices, it is crucial to deeply examine the impact of GN on the phospholipid bilayer, especially during the process of forced GN movement through the bilayer. Our previous studies show that carbon-based materials [i.e., carbon nanotubes (CNTs) or silicon-carbide nanotubes] can effectively and less invasively penetrate the bilayer.²³⁻²⁶ In this study, we examine the use of GN sheets as phospholipid bilayer nanoindenters and discuss the impact of various-sized GN sheets on the phospholipid bilayer during indentation and withdrawal processes.

Although the information on the bending characteristics can be inferred from phenomenological models of continuous media, information on molecular aspects—such as molecular extraction from the membrane or self-healing following nanoindentation—can only be obtained from an atomistic model. The average force and work, bilayer deflection, and number of molecules permanently removed from the membrane are analyzed. Also, a comparison with earlier obtained results with the CNT²³⁻²⁵ and the silicon-carbide nanotube (SiCNT)²⁶ is provided. Finally, we present the unexpectedly high degree to which the phospholipid bilayer can self-seal following significant damage to its structure.

Computational Details

Molecular dynamics (MD) simulations were performed at a physiological temperature in an aqueous environment. NAMD 2.8²⁷ simulation software with the all atom–atom CHARMM force field^28,29 and standard TIP3P water model³⁰ were used. The phospholipid bilayer consists of 232 1,2-dimyristoyl-sn-glycero-3-phosphocholines (DMPC) and 48 cholesterols.³¹ Atomic charges and the model for phospholipid and cholesterol molecules were taken from ref (32). All simulations were repeated 15 times to ensure sufficient sampling of the configuration space. The results presented here are averages of these simulation runs.

Table 1 presents the sizes of the GN sheets. Periodic boundary conditions were applied to all examined systems. The size of the box after equilibration was approximately 98 × 81 × n Å, with n equal to 116, 128, and 155 Å for the shortest to longest GN sheet lengths. The maximum width of 96 Å was chosen such that the GN could be treated as infinite along the x-axis.

Table 1. Sizes of GN Sheets Used (m × n [Å]).

GN size (m × n) [Å]	96 × 52	56 × 52	16 × 52
simulation cell	111.6 × 96 × 160	111.6 × 96 × 160	111.6 × 96 × 160
no. of water molecules	32,961	33,339	33,714
GN size	96 × 32	56 × 32	16 × 32
simulation cell	111.6 × 96 × 140	111.6 × 96 × 140	111.6 × 96 × 140
no. of water molecules	27,693	27,931	28,171
GN size	96 × 12	56 × 12	16 × 12
simulation cell	111.6 × 96 × 120	111.6 × 96 × 120	111.6 × 96 × 120
no. of water molecules	22,479	22,576	22,675

The initial configurations of the systems were obtained from a series of NPT and subsequent NVT simulations. During NPT equilibration processes, the pressure was controlled using the Langevin barostat implemented in NAMD, with the decay time set to 100 ps, the piston set to 200 ps, and the reference pressure set to 1 atm. During this phase, GN planes were fixed with the lower edge at approximately 9 Å from the bilayer for all sizes. To prevent the entire membrane from being pushed during the indentation process, the movement of atom C2 in phospholipids near the simulation cell edge was restrained. These additional constraints are added to represent the insertion of a larger membrane, a fragment of which is the simulated system. Each equilibration process lasted for 1 ns, and 0.5 fs time steps were used for all simulations. After equilibration, the main simulations were started and the sheets allowed to move.

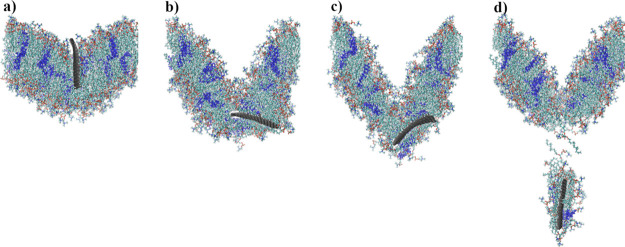
Steered MD (SMD)^27,34 were utilized to facilitate the indentation of the phospholipid bilayer by GN and its subsequent withdrawal out of the membrane. During the indentation process, virtual springs were added in two different ways—to the atoms closest to the bilayer surface (along the m-axis, cf. Figure 1a,b) and to the atoms on both sides of the GN sheet (along the n-axis) up to the half-height of the GN plane (Figure 1c). The springs were connected to imaginary points, which moved downward at one of two constant speeds (1 or 2 m/s). During the withdrawal of the GN nanoindenter, springs were added to the furthest edge of the GN (along the m-axis) and connected to points moving upward (Figure 1d). The force constant for each spring was set to 10 kcal mol^–1 Å^–2. For all SMD simulation runs, necessary data were collected every 50 simulation steps to calculate the average force, work, and indentation depth, and the trajectory was stored every 10⁵ steps.

Figure 1.

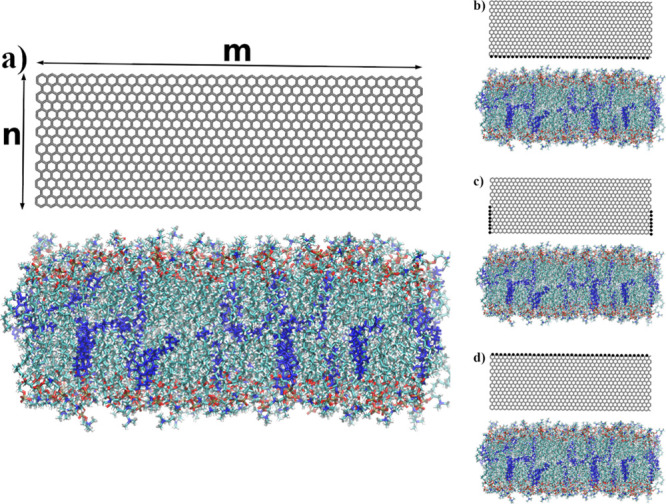
Visualization of positions of SMD atoms (system with 96 × 32 GN) via VMD 1.9.2.³³ (a) Initial configuration of the system, (b) springs added to the GN atoms closest to the bilayer surface, (c) springs added on both sides of GN along the n-axis, and (d) springs added to the GN atoms farthest to the bilayer surface. Atoms with associated SMD springs were additionally marked. Cholesterols are colored blue.

The indentation/withdrawal rates of 1 and 2 m/s are in general much higher than those used in experimental studies, such as atomic force microscopy or single-molecule force spectroscopy.^35,36 These choices are a result of the compromise between computation time and a faithful reproduction of membrane behavior. The rates are, however, comparable to those in previous studies^{25,26,35,37,38} and with those in SMD simulations of other biological phenomena, such as protein folding.^39,40 Ultimately, the accuracy will vary depending on the problem under study,⁴¹ but this approach provides useful insights into the dynamic properties of molecular systems, for example, drug design and protein folding,^37−39,42 which could not be accomplished in reasonable time alternatively.

Indentation simulations were also attempted with the GN sheet driven by springs attached to its furthest edge from the membrane. However, many of these attempts were discarded as they caused the GN sheet to rotate or fold even before reaching the membrane itself. Table 2 shows the number of attempts (30 for each system varying in GN size, 15 for 1 m/s, and 15 for 2 m/s) where GN was able to reach the glycerol backbones of DMPCs from the first layer without folding for this setup.

Table 2. Number of Attempts for Which GN Sheets Varying in Size Were Able To Reach the Glycerol Backbones of DMPCs Located in the First Layer of the Membrane without Folding.

size of GN	number of successful attempts (from 30)
96 × 52	3
96 × 32	23
96 × 12	0
56 × 52	0
56 × 32	25
56 × 12	0
16 × 52	0
16 × 32	13
16 × 12	0

Unfortunately, even if the GN was able to penetrate the membrane, it folded between the first and second layers of the membrane or after cutting through the second layer (as shown in Figure 2). In only four cases (from 270 studied) was GN able to go through the membrane in the desired way, without folding or rotating.

Figure 2.

Example of an indentation process in the case when SMD dummy atoms were attached to the top edge of the GN plane. The system with 96 × 32 GN was chosen as a representative one.

Results and Discussion

Indentation Process

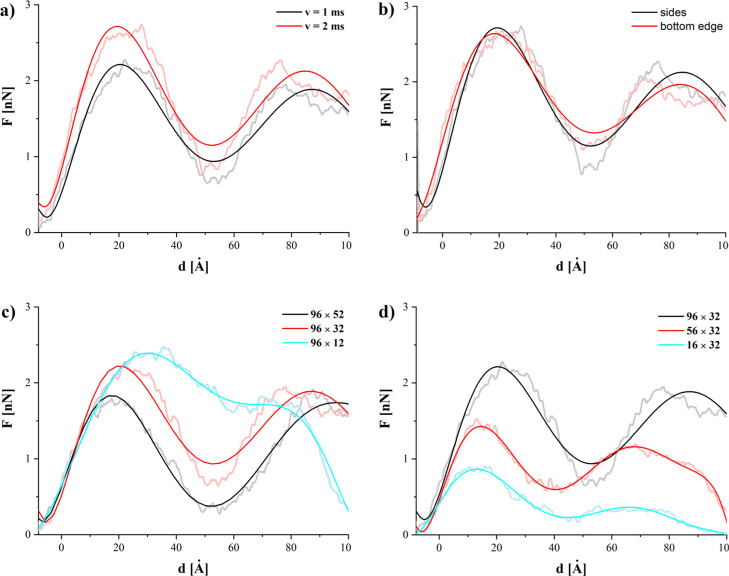
The force required to move GN is shown in Figure 3 as a function of depth d below the upper surface of the membrane. Depth d = 0 is defined at the end of equilibration as the average depth of all N atoms in the upper membrane. Obtained force values (max. 2.72 nN) are similar in magnitude to those reported for different nanotubes^{24,26,43−45} and the distribution of SMD-pulled atoms does not significantly affect the shape of the obtained force curves (see Figure 3b). The consequent stages of the nanoindentation process are clearly visible in the average force curves. The initial stage (below 0 Å) is associated with the movement through a water environment. As the GN reaches the polar part of the first layer of phospholipids, a drastic increase of required force can be observed. This is associated with the first contact between the GN and membrane, and the forced separation of the interacting polar heads as they are pushed from the path of GN. The increase of force remains almost linear until it reaches the first maximum at approximately 20 Å. This maximum can be associated with the breach of the strongly interacting glycerol backbones of the first-layer DMPC phospholipids. Visual inspection of the trajectories shows that in some cases, especially for the wider GNs (higher m values), single DMPC molecules are fully dislodged by GN. The GN is able to slide through the bilayer, but some phospholipids, because of reduced available free volume, are not able to escape the GN path and are effectively stuck on the leading edge of the GN sheets. After the glycerol backbones are separated, in all studied systems, the force begins to diminish.

Figure 3.

Force required during the indentation process. Zero on x-axis corresponds to the point where GN sheet reaches phospholipid heads of the first layer. To improve the clarity of the figures, the high-noisy curves were approximated with the seven-degree polynomials.

Direct contact between GN and the lipid hydrocarbon tails is energetically favorable to GN in contact with water. Similar behavior has been previously reported for carbon and SiCNTs, where the average force began to diminish after penetration of the first hydrophilic part of the bilayer.^25,26 It should be noted that the force decrease is inversely proportional to the GN height (cf. Figure 3c). What is also quite interesting is that the membrane significantly bends during this stage of the indentation process. Van der Waals interactions (represented by Lennard-Jones 12–6 potential) introduce significant adhesion between the GN and the bilayer, causing the GN to attract the membrane to itself.

The force again begins to increase as the GN reaches the second layer of DMPCs. The second occurring maximum generally corresponds, again, to the interaction with the polar heads of the DMPCs but on the lower surface of the membrane. Significant membrane bending should also be noted at this stage. Differences also manifest for sheets of different widths (cf. Figure 1d). As could be expected, nanoindentation using a wider plane means higher required force—0.86, 1.42, and 2.21 nN—for the narrowest to widest planes. Moreover, there is a shift of the second maximum on the force plot for 96 × 32 GN. This results from the deformation induced by strong interactions between GN and the bilayer, as described in the previous paragraph.

The work required to perform the nanoindentation can be defined as

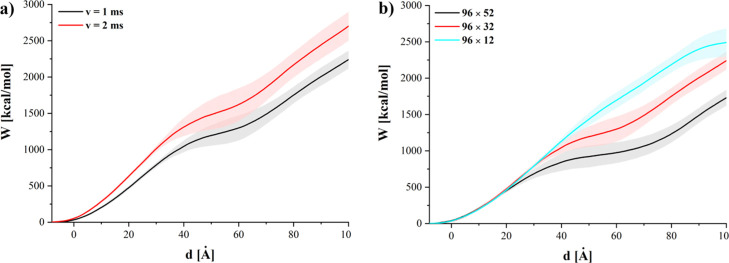
where the force F is a function of indentation depth d and d₀ represents the initial position of the GN. Figure 4 shows the selected average work curves obtained by averaging work as a function of indentation depth over all available simulation runs for a particular system. The data selection presented in Figure 4 correspond to the force curves shown in Figure 3a,c, respectively. Figure 5 presents the work required to reach a certain indentation depth for different GNs.

Figure 4.

Average work required to push various GN sheets (b) with different speeds (a) into the membrane.

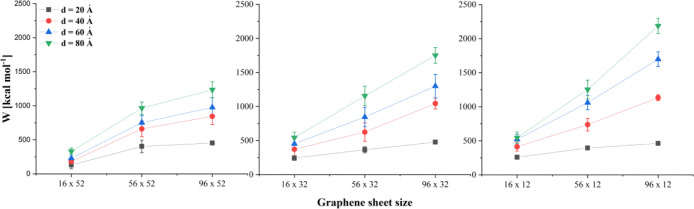
Figure 5.

Average work required to reach selected indentation depths for different sizes of GN nanosheets (lines are guides for the eyes only).

For GNs of the same height (52, 32, or 12 Å), the amount of work increases with the width of the GN. It can be also seen that for GN sheets of the same width, the required work decreases with the increase of the GN surface. This result suggests that the amount of work required to insert the GNs into the membrane is a counterbalance of two factors. The hydrophobic GN surface facilitates insertion into the membrane and leads to a decrease of overall work. However, the work required to first penetrate the membrane increases with the initial contact surface and, hence, the GN sheet width. This is further evidenced by the strong dependence of energy on width for the shallowest indentation depth (d = 20 Å, Figure 5 black squares), while the variation with height is minimal. Similarly, for the tallest sheets (Figure 5, left), there is the least increase in work required to reach successive depths for any individual width. These results indicate that the process of nanoindentation is not simply driven by interactions between the GN surface and phospholipid heads or tails alone but is also associated with the affinity of the GN surface for the lipid tails and its ability to overcome to drag caused at the leading edge of the GN sheet.

We would also like to discuss the impact of the GN sheet on the membrane structure. In Figure 6, the average deflection of the bilayer is shown as a function of the distance from the surface of GN. The C2 glycerol backbone atoms from the DMPC molecule’s top layer were chosen to assess the average dislocation of the DMPC as it is the atom located in the most inflexible part of the phospholipid molecule. The atoms for which we calculated deflection and the indentation depth of 56 Å are similar as in our previous studies²⁴⁻²⁶ to allow for comparison with results obtained for CNTs and SiCNTs. The selected indentation depth corresponds to the configuration in which GN reaches the glycerol backbones in the second layer of phospholipids.

Figure 6.

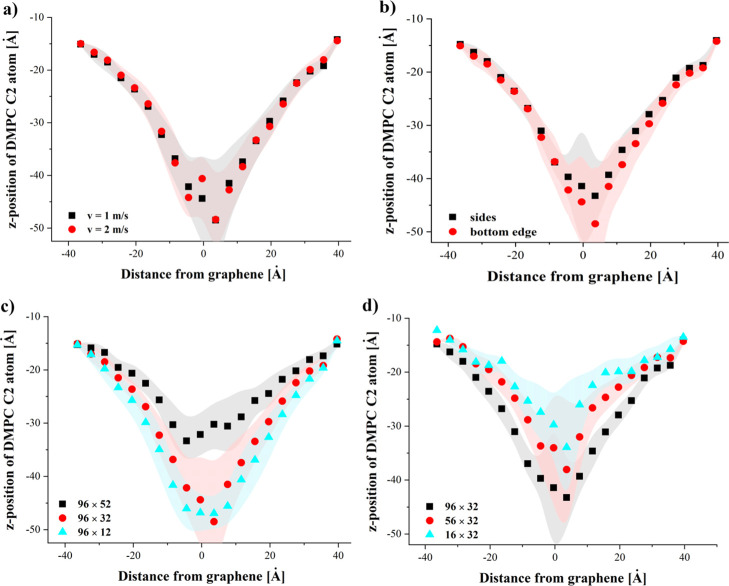
Average dislocation of the C2 phospholipid atoms during the indentation process. The following systems were chosen: 96 × 32 and springs at the bottom edge—(a); 96 × 32 and v = 1 m/s—(b); 96 × ..., v = 1 m/s and springs at the bottom edge—(c); ... × 32, v = 1 m/s and springs on sides—(d).

The deflection during the indentation process does not practically depend on the speed of GN (see Figure 6a) or on the method of pulling (see Figure 6b). A similar behavior could be observed in case of the nanoindentation of the membrane with silicon-carbide or CNTs where the membrane bending was nearly independent of indentation speed.^25,26 It should be noted that the membrane bending in case of GN is significantly higher (up to 35 Å in the most pronounced case) than in case of CNTs (approximately 13 Å)²⁵ or SiCNTs (approximately 9 Å).²⁶

Significant differences can be observed between GN sheet heights. For the 96 × 52 GN, the membrane bending is not as pronounced as with 96 × 32 and 96 × 12 GNs. In the case of 96 × 52, the contact time between GN and the membrane is longest and the phospholipid molecules are able to slide along the GN surface. This allows the membrane to partially reduce the perturbation induced by the nanoindentation process. The largest GN sheet best facilitates this reordering as DMPC and cholesterol molecules can easily move along the GN side surfaces. The bending of the membrane is correlated with the initial contact surface between the membrane and GN (see Figure 6d), yielding greater bending for wider GN sheets. Similar results were observed for CNTs of different diameters.²⁵ With the increase of the nanotube circumference and the number of carbon atoms in the nanotube ring, the bending also increased.

Membrane deflection is visualized in Figure 7, where the snapshot of the initial system (Figure 7a) and the snapshot of the same system (Figure 7b) during the indentation process are shown. The average deflection presented in Figure 6 was calculated for the same nanoindentation stage as presented in Figure 7b. The bending of the membrane is also affected by the size of the simulation cell in the direction perpendicular to the GN surface. The larger cell could lead to overall lower deflection, as the modeled membrane of larger surface could more easily accommodate the GN. It should be noted that the bending and overall structural impact of indentation is reduced as the membrane size increases, so our model represents a pessimistic forecast of the indentation process of GN on a bilayer.

Figure 7.

Comparison between a 96 × 32 initial system and the same system during the indentation process. Springs were added on the sides of GN and the indentation speed was equal to 1 m/s.

As an additional representation of membrane disturbance, Table 3 lists the average number of phospholipids or cholesterols which were permanently removed during the indentation process. A lipid was considered removed if, when the GN exits the far side of the membrane, the molecule is separated from the rest of the membrane atoms by at least 4 Å.

Table 3. Average Number of Permanently Removed Lipids during the Indentation Process.

size of GN [Å] and pulling method	average number of removed lipids (std. dev.)
springs at both sides	v = 1 m/s	v = 2 m/s
96 × 52	8.1 (2.9)	4.3 (3.0)
96 × 32	8.0 (3.4)	4.7 (2.4)
96 × 12	5.3 (3.8)	4.4 (2.8)
56 × 52	2.5 (1.6)	1.4 (1.2)
56 × 32	3.6 (1.8)	2.5 (1.5)
56 × 12	2.1 (1.5)	2.1 (1.6)
16 × 52	0.7 (0.6)	0.7 (0.6)
16 × 32	0.3 (0.4)	0.4 (0.6)
16 × 12	0.3 (0.6)	0.5 (0.6)
Springs at Bottom Edge
96 × 52	8.5 (3.8)	4.5 (2.8)
96 × 32	9.1 (4.0)	4.1 (3.2)
96 × 12	3.5 (2.2)	3.6 (1.7)
56 × 52	1.8 (1.4)	2.0 (1.5)
56 × 32	3.5 (2.3)	3.5 (3.2)
56 × 12	1.9 (1.4)	1.2 (0.9)
16 × 52	0.7 (0.7)	0.4 (0.5)
16 × 32	0.6 (0.7)	0.3 (0.6)
16 × 12	0.3 (0.6)	0.5 (0.6)

The obtained results suggest that the higher indentation speed (2 m/s) is less intrusive. This result is in good agreement with our previous study.²⁵ For the largest studied GNs, the number of lipids extracted for an indentation speed v = 2 m/s is almost halved in comparison to v = 1 m/s. The data presented in Table 3 clearly show that the number of extracted lipids is proportional to the GN width and side surface. The method of modeling the indentation process (pulling the GN by the bottom or side edges) does not affect the obtained results. It should be also noted that we did not observe the process of extraction of cholesterols from the membrane as reported previously by Zhang et al.²² although the perturbation of the membrane by moving GN might have prohibited it. Also, the longer simulation time in previous studies of interactions between GN and a bilayer (t > 24 ns) may be a major factor.

Meaningful comparison can be made between these GN results and the results for CNTs²⁵ and SiCNTs²⁶ of our previous work. A direct comparison shows a higher maximal force for GN (2.88 nN) compared to CNTs (1.93 nN) and SiCNTs (1.52 nN). However, the width of this sheet is such that it essentially cuts the membrane in half. Some of the dimensions provide for a more sensible comparison. For instance, the SiCNT nanotube is 55.16 Å in circumference and 72 Å tall. This closely matches the contact area of a 56 × 52 GN sheet, and the discrepancy in height should cause minimal difference at the point of maximal force. Comparison in this way shows a much more modest increase in maximal force: F_max = 1.37, 1.52, and 1.67 nN for (12, 12) CNT, (10, 10) SiCNT, and the 56 × 52 GN systems, respectively. It should be noted that the studied speed for GN is slightly slower (2 vs 2.5 m/s), which may also slightly attenuate the difference in force.

Figure 7b shows that indentation using GN can cause significant deflection (equal to 28.5 Å for the system shown in Figure 7b). Again, comparing with the 56 × 52 sheet yields similar values as the other structures—13.2 Å for (12, 12) CNT and 7.7 Å for SiCNT compared to 13.8 Å for the GN sheet. Significantly, the largest deflection does not occur for the CNT with the largest diameter studied previously.²⁵ Moreover, in the case of SiCNT, the largest deflection occurs for the largest speed studied, as opposed to systems with CNT,²⁶ where smaller speed means larger deflection. These are both in contrast to GN, which did not show a pronounced difference in speed and led to the greatest deflections for the widest systems.

Finally, we would like to compare the number of lipids which were permanently removed from the membrane. The (12, 12) homogeneous nanotube was, on average, able to remove 7.4 lipids during indentation process at a speed of 2.5 m/s, but the most destructive for the membrane was (15, 15) CNT.²⁵ The heterogeneous nanotube was able to remove 6.26 lipids for the highest speed tested.²⁶ Comparable GN (56 × 52 with side springs) is much less destructive, removing 2.47 lipids from the membrane. In contrast to nanotubes, it was for the lower speed (v = 1 m/s). This behavior is connected with the fact that with GN we indent along one axis, whereas the nanotube ring presents a 2D surface to the membrane. For GN sheets, it is more difficult to merely push the molecules and their binding plays a crucial role. During indentation at smaller speeds, more lipid molecules can attach to the GN surface because of the longer time of contact between them. This conclusion can be confirmed by the values presented in Table 3 where, in most cases, a smaller indentation velocity leads to a larger number of removed lipids.

Removal Process

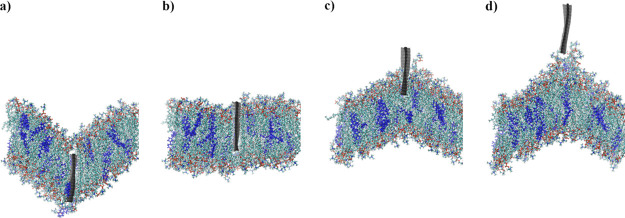
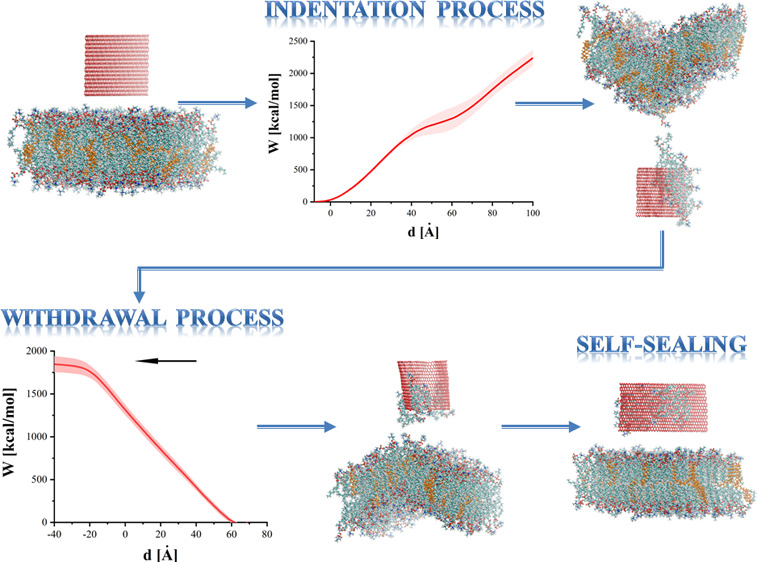
To reduce computational cost, only the cases with the most pronounced membrane damage, where the largest number of removed lipids occurred, were taken into account. The four most destructive cases were taken from simulations of 96 × 52 and 96 × 32 GN. For example, for the system with 96 × 52 GN, where springs were at the bottom edge, the speed was equal to 1 m/s; run no. 13 was a basis for GN extraction simulation, because in this case, up to 15 lipids (instead of the average value of 8.47) were permanently removed during indentation process. Each of these was then repeated 4 times, for a total of 16 independent simulation runs. Because an indentation speed of 1 m/s seems to be more destructive (see Table 3), this speed was used for simulations of the removal process. In the discussed process, springs were added only on the upper edge of the GN sheet (see Figure 1d). In the initial configurations, the z-position of these SMD GN atoms was approximately equal to −40 Å, corresponding to an indentation depth d = 72 Å and d = 92 Å for 96 × 32 and 96 × 52 GN, respectively. In the following, zero depth corresponds to the bottom edge of the GN, reaching the original position of the membrane surface before indentation.

A series of instantaneous configurations during the removal process is shown in Figure 8. Figure 8a shows the initial configuration and further stages are shown in subsequent figures (Figure 8b–d). Figure 8d does not show the final configuration—the run was continued to properly assess the number of removed lipids. Instead, Figure 8d presents the configuration at which GN started to detach from the membrane.

Figure 8.

Instantaneous configurations of the system with the 96 × 32 GN plane.

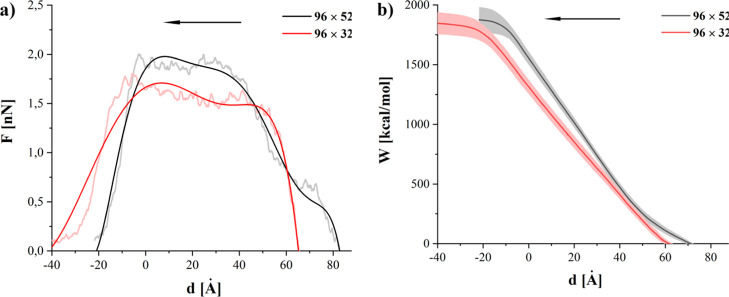
Figure 9a shows the comparison of the average force required to remove GN from the membrane. Although the maximal force required to remove GN is smaller for the systems with 96 × 32 GN (1.9 and 1.7 nN for 96 × 52 and 96 × 32 system, respectively), the average work (Figure 9b) is larger. As in the case of the indentation process, the longer sheet (96 × 52) is able to slide longer. This leads to significantly lower required force in the initial stage of the removal process, after the initial ballistic area. It also elongates the escape from the polar surface, but shortens the force plateau as the membrane is able to rebound from its deformation by sliding along the GN during extraction. The larger contact area, coupled with GN’s affinity for the inner membrane, is also responsible for the slightly higher maximum of the required force in case of the 96 × 52 GN. These observations are also confirmed by the shape of work curves (Figure 9b). The initial slope is lower for the 96 × 52 GN. Overall, the total work required to remove the GN is slightly higher (1876 ± 107 vs 1842 ± 93 kcal/mol) for larger GN.

Figure 9.

Comparison of average force (a) and work (b) during the removal process.

Work and force curves, supported by visual inspections of the simulated systems, indicate that the 96 × 52 GN separates completely after reaching a position approximately 20 Å above the initial (before the indentation) position of the bilayer. The shorter GN is completely separated from the bilayer when it reaches position 35 Å above the initial membrane location.

As can be seen in Figure 8c,d, the membrane is quite strongly pulled upward by the sheets during removal. In Figure 10, the average dislocation of the DMPC C2 atom is shown. The deflection was estimated for the indentation depth d for which the GN was physically disconnected from the membrane.

Figure 10.

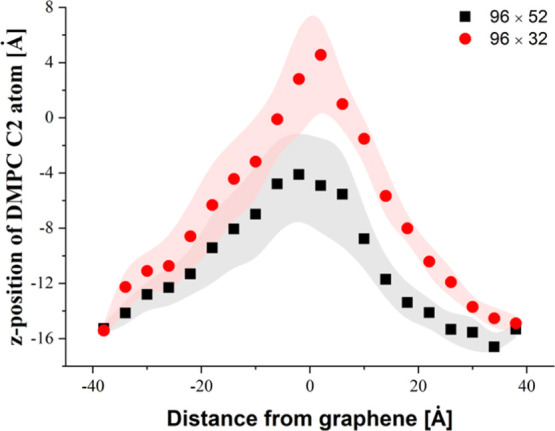
Average dislocation of C2 phospholipid atoms from the membrane upper layer.

Similar to the indentation process, the membrane displacement is less pronounced for the larger GN sheet (max −4.1 vs 4.7 Å). The difference in the maximal value of the z-position of C2 atoms is equal to 8.8 Å. By taking into account the average bending of the membrane during the indentation process (see Figure 6c), the average z-distance covered by phospholipids is ∼60 and ∼30 Å for systems with 96 × 32 and 96 × 52 GN, respectively. The deflection graphs confirm our previous finding concerning the required work and force, indicating that the contact between the membrane and GN is terminated faster in case of GN with a lower side surface. As it could be expected, the work required to pull the GN out from the membrane increases with the GN side surface because of the adhesion of hydrophobic phospholipid tails (see Figure 9b).

It is also surprising that removal, compared to the indentation process, is less harmful in terms of number of lipids removed from the membrane. For the systems with 96 × 52 GN, no cases of molecule extractions from the bilayer were observed. In case of systems with a 96 × 32 GN plane, the average number of extracted molecules is equal to 1.27, which is a factor of 7 lower than the equivalent indentation process.

Again, the system with 56 × 52 GN has a similar surface area as (12, 12) CNT²⁵ and (10, 10) SiCNT,²⁶ so the extraction processes should be comparable. For all nanostructures studied, the average force is larger for higher removal speeds. For systems with GN, the average maximal force is equal to 1.15 and 1.2 nN for removal speeds of 1 and 2 m/s, respectively. Comparing these results with results calculated for systems with homogeneous and heterogeneous nanotubes, we can conclude that force is higher than in systems with (12, 12) CNT (maximal force for 2.5 m/s is equal to 0.68 nN) and in good agreement with SiCNT (maximal force for 2.5 m/s is equal to 1.17 nN and for v = 1.5 m/s F_max = 1.08 nN). Maximal average dislocation of C2 DMPC atoms is smaller for a higher removal speed (10.9 Å for GN at v = 1 m/s and 7.16 Å for GN at v = 2 m/s). This is consistent with results obtained for systems with nanotubes. Also, the values of dislocation are comparable; even when taking into account a smaller extraction speed of v = 0.5 m/s for systems with nanotubes, the largest average displacement of C2 atoms is equal to 14.6 Å for systems with (12, 12) CNT and 12.2 Å for systems with SiCNT.

The effect of indentation on the membrane is lower with GN sheets than with nanotubes when taking into account the number of lipids removed from the membrane. Only in one case out of thirty studied (15 independent simulation runs for v = 1 m/s and 15 for v = 2 m/s) was 56 × 52 GN able to remove phospholipids (one DMPC molecule was pulled out of the membrane). Compared with the, on average, 3.9 removed lipids for systems with SiCNT and 1.9 lipids for (12, 12) CNT, the significantly less destructive nature of GN is quite apparent.

Self-Sealing Process

Membrane damage during indentation was significantly larger when SMD dummy atoms were attached to the upper edge of the GN sheets. Two examples can be seen in Figures 2d and 11. As can be seen in Figure 2d, lipids densely crowd the GN after indentation (in this example, 35 lipids were removed by GN from the bilayer). The top view, side view, and the position of water molecules after indentation are shown for this system in Figure 11a–c. These show how the membrane was torn and a water tunnel (approximately 75 Å long and up to 10 Å wide) inside the membrane was created. Even greater distortion can be observed for another selected case shown in Figure 11d–f, where two water channels (76 Å long by 14 Å wide and 20 Å long by 6 Å wide) were created.

Figure 11.

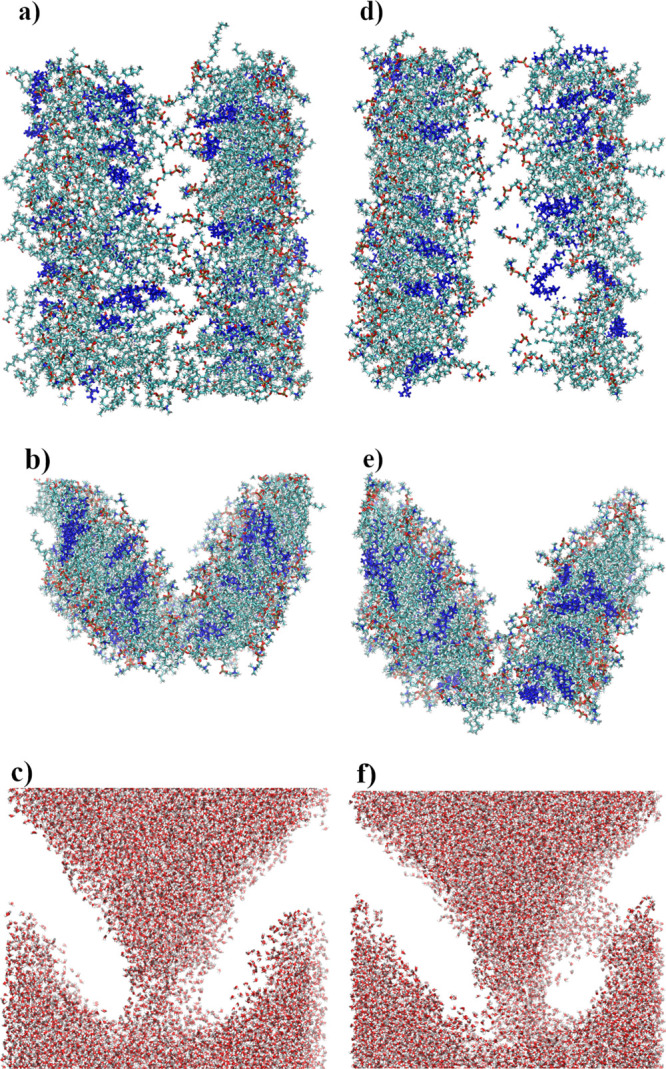
Examples of distortion caused by a moving 96 × 32 GN sheet—two selected cases. Upper snapshots—top view, middle snapshots—side view, and bottom snapshots—water configurations.

For the two basic SMD protocols tested, the membrane does not lose its functionality. Only in two cases from the 540 studied were small water tunnels through the membrane (no longer than 25 Å) observed (systems with 96 × 32 GN). Moreover, even in the most intrusive case of pushing GN into the membrane by applying force to the top edge atoms, only in systems using 96 × 32 GN sheets were water channels created. Eight examples with 96 × 32 GNs, where the largest water tunnels were created, were further analyzed. Longer simulations were additionally performed. The GNs were immobilized at positions similar to the one shown in Figure 2d and the simulations continued for 50 ns.

During these simulations, membrane regeneration was observed. In each case, the deflection caused by the indentation returned to normal. Moreover, the water channels were closed. Only in one case, shown in Figure 11f, was one of two channels observed after 50 ns, but its size was reduced to about 12 Å length. The simulation of this system was extended for additional 50 ns (100 ns in total) and led to a closing of the second channel after 74 ns.

The self-sealing process is independent from the number of lipids permanently removed from the membrane. Even when the largest number of lipids was removed from membrane (35 lipids, or 12.5% of total number of lipids used, see Figures 2d and 10d), the self-sealing process occurred. The time required for the membrane regeneration process is rather loosely dependent on the size of the water channel, as shown in Table 4.

Table 4. Approximate Size of Water Channels and Time Required by the Membrane To Remove Them.

size of channel (length × width) [Å]	time required to seal the water channel [ns]
13 × 8	34
24 × 10	19
25 × 10	20
25 × 12	7
40 × 27	42
55 × 16	38
75 × 10	41
20 × 10	6
76 × 14	74

Figure 12 depicts the same systems as shown in Figure 11 but after 50 ns of additional simulation. It confirms the efficiency of the self-sealing process, although some local density changes can be observed in the membrane.

Figure 12.

Configurations of systems shown in Figure 11 after the self-sealing process.

Creation of water channels is concerning as the entrance of water into the membrane represents a significant impairment of membrane function. In contrast to previously obtained results for nanotubes,^25,26 such water channels were not observed. However, it should be noted that the size of the GN that caused the most crippling changes in the membrane was comparable with the membrane length. For comparison, GN sheets of comparable size to nanotubes, that is 56 × 52, should be considered. In this case, the structural changes in the membrane do not exceed the impact of the homogeneous or heterogeneous nanotubes.^25,26

Conclusions

Nanoindentation of phospholipid bilayers using GN planes of different sizes as well as their subsequent withdrawal and membrane self-sealing processes were examined using classical MD simulation methods. The average force required to cut through the membrane with GN or withdraw it from the membrane is of the order of nanonewtons, in good agreement with previous reports, where various nanotubes were used as indenters. Also, the average work is comparable with values reported for different nanostructures. Force and work depend strongly on the size of the GN sheet and indentation/withdrawal rate; however, those quantities seem not to depend on the method used to pull the GN. Membrane deflection depends significantly on the height of GN where, additionally, sliding of the GN through the bilayer has noticeable impact. As could be expected, the number of lipids permanently removed from the membrane is the highest for the GN sheets with the largest surface. For removal processes, the number of extracted lipids is definitely smaller than for indentation. The number of lipids extracted from the membrane during the indentation process is on the same level as in case of carbon and SiCNTs.

The obtained results suggest that even for the worst case scenarios, when the GN causes significant damage, the membrane structure was able to regenerate. Water molecules were not able to permanently penetrate the membrane hydrophobic core. The self-sealing process is quite efficient, and the membrane was able to remove water molecules and close the water channels introduced by indentation in less than 50 ns. Also, deflection caused by GN sheets is levelled quickly. Our studies may be of importance for new trends in nanomedicine. The GN sheets may be considered as potential candidates for nanoknives or nanoblades in specialized medical devices operating on the cell level. Also, in the case of targeted drug delivery, GN could be considered as one of the potential carriers if the issue of GN biotoxicity could be resolved by specific functionalization. One can hope that the presented results will aid in understanding the interactions between biomembranes and carbon-based nanostructures. Both nanotubes and GN sheets seem to be good candidates for further experimental studies; however, indentation using GNs may require additional caution to avoid excessive trauma to lipid membranes.

The authors declare no competing financial interest.