Bioinspired Multiresonant Acoustic Devices Based on Electrospun Piezoelectric Polymeric Nanofibers

Abstract

Cochlear hair cells are critical for the conversion of acoustic into electrical signals and their dysfunction is a primary cause of acquired hearing impairments, which worsen with aging. Piezoelectric materials can reproduce the acoustic-electrical transduction properties of the cochlea and represent promising candidates for future cochlear prostheses. The majority of piezoelectric hearing devices so far developed are based on thin films, which have not managed to simultaneously provide the desired flexibility, high sensitivity, wide frequency selectivity, and biocompatibility. To overcome these issues, we hypothesized that fibrous membranes made up of polymeric piezoelectric biocompatible nanofibers could be employed to mimic the function of the basilar membrane, by selectively vibrating in response to different frequencies of sound and transmitting the resulting electrical impulses to the vestibulocochlear nerve. In this study, poly(vinylidene fluoride-trifluoroethylene) piezoelectric nanofiber-based acoustic circular sensors were designed and fabricated using the electrospinning technique. The performance of the sensors was investigated with particular focus on the identification of the resonance frequencies and acoustic-electrical conversion in fibrous membrane with different size and fiber orientation. The voltage output (1–17 mV) varied in the range of low resonance frequency (100–400 Hz) depending on the diameter of the macroscale sensors and alignment of the fibers. The devices developed can be regarded as a proof-of-concept demonstrating the possibility of using piezoelectric fibers to convert acoustic waves into electrical signals, through possible synergistic effects of piezoelectricity and triboelectricity. The study has paved the way for the development of self-powered nanofibrous implantable auditory sensors.

Introduction

Piezoelectric materials possess the special ability to produce an electrical voltage in response to a mechanical force, which makes them particularly suitable for a wide range of applications, including sensors, transducers, energy harvesting, and biomedical devices.¹⁻⁴ Some of these are based on acoustic resonators, which enable the conversion of acoustic sound into electricity and, eventually, can be designed to resonate at specific frequencies when stimulated with acoustic waves, thereby achieving the desired sound frequency selectivity. These conversion mechanisms can be used to restore the auditory function, in the case of sensorineural hearing loss, by developing artificial basilar membranes with piezoelectric properties. The basilar membrane traverses the length of the coiled cochlea, the hearing organ of the inner ear, separating two of the three compartments or scalae: scala media (filled with endolymph fluid) and scala tympani (filled with perilymph fluid). The basilar membrane is able to selectively respond to acoustic waves of different frequencies because of a gradation in stiffness along its length, arising from graded changes in its width and thickness.⁵ Sound waves drive pistonlike movements of the ossicles and the oval window that generate propagating deformations of the basilar membrane with maxima dependent on the original sound frequency. The frequency-dependent deformations occurring in specific locations where shear strain is generated on the stereocilia of the hair cells result in the flow of ions and the generation of a receptor potential in inner hair cells. This triggers the release of neurotransmitters at the base of the inner hair cells, activating the cochlear spiral ganglion neurons, which transfer the signal along the cochlear nerve and the auditory pathway via action potentials.⁶ Damage to hair cells leads to a disruption of hearing function, with severe and often underestimated consequences on quality of life; however, these can be alleviated, at least in part, by a cochlear prosthesis or implant.

The majority of commercially available cochlear implants are based on external microphones and signal processing units that digitize the incoming sound waves and transmit the signals to spiral ganglion neurons via a small array of electrodes lined along the length of the implant. The electrodes can then activate the surviving spiral ganglion neurons resident at specific points in the cochlea, and these can be mapped to the processor so that the correct sound activates the correct place.⁷ Although in many cases the implant allows the user to hear speech and to communicate, the fidelity of the hearing is low and there are difficulties in hearing speech-in-noise. In addition, there are issues with the amount of energy required and power consumption, as well as with the presence of external elements, which is often uncomfortable for patients and mostly regarded as aesthetically blemishing. Therefore, new implantable devices are being developed based on different transduction mechanisms. Among these, devices based on piezoelectric systems represent the most promising option and a number of potential piezo-acoustic devices for cochlear implants have been already reported in the literature.⁸⁻¹⁵

The majority of these devices are usually based on piezoelectric thin films, with lead-zirconate-titanate (PZT),¹⁵ aluminum nitride,^16,17 polyvinylidene fluoride (PVDF),^18,19 and its copolymer poly(vinylidene fluoride-trifluoroethylene) (PVDF-TrFE)⁸ being the materials mostly used as artificial basal membranes. However, these compounds present a number of limitations, related to toxicity (in the case of lead zirconate titanate (PZT)), high stiffness (PZT and aluminum nitride), insufficient frequency selectivity, and low sensitivity (PVDF and PVDF-TrFE), as reported in the relative previous studies. Therefore, the simultaneous realization of biocompatibility, wide frequency selectivity, and high sensitivity represent an acknowledged challenge for cochlear implantable devices.⁷ In the attempt to overcome these issues, polymeric nanofibers with piezoelectric properties become appealing²⁰ because of the possibility of tuning the nanoconfined crystallinity and fiber orientation. This potentially modulates the mechanical compliance and piezoelectricity, achieving the desired frequency selectivity and sensitivity. PVDF and P(VDF-TrFE) piezoelectric fibers fabricated by electrospinning have recently attracted significant interest because of their flexibility, high specific properties, and biocompatibility at relatively low cost²¹⁻²⁵ and are potential candidates for developing novel implantable hearing devices. It has been reported that PVDF electrospun fibers possess high sensitivity to acoustic signals, which is about five times higher than that of PVDF solid films.²⁶ Additionally, it is believed that electrospinning allows for the simultaneous fabrication and poling of fibers with sizable piezoelectric activity, as high voltage is applied during processing.^27,28 On the basis of these superior characteristics, PVDF-based fibers could potentially overcome the limitations of piezoelectric polymer thin films for artificial cochlear implant systems evidenced in previous reports. However, the design and optimization of these acoustic sensors can be achieved only by a full understanding of the relationships between the multiscale structure of the fibrous membranes, the device geometry, and acoustic-electrical conversion properties.

Inspired by the fibrous nature of the basilar membrane microstructure,²⁹ in this paper, we investigate the correlation between structure, morphology, and size effect of the piezo-acoustic response of electrospun membranes made up of random and aligned P(VDF-TrFE) fibers, in circular devices with different diameters (Figures 1a, 1b), with the aim of tuning resonance frequencies and developing a frequency map, or tonotopy. It was found that the frequency response varies by changing geometrical size and microstructural morphology of the fibrous membrane. The present results provide a proof of principle to drive the downscaling engineering of electrospun fiber-based sensors toward more suitable designs of implantable devices.

Figure 1.

(a) Schematic picture of the human cochlea and the bioinspired size effect for frequency selectivity. (b) Schematic picture of the acoustic device with fibrous membranes. (c) Schematic picture of laser vibrometer testing system. (d) Light microscopy image of 30 mm diameter device with random P(VDF-TrFE) fibers. (e) SEM image of random P(VDF-TrFE) fibers. (f) Light microscopy image of a 30 mm diameter device with aligned P(VDF-TrFE) fibers. (g) SEM image of aligned fibers. (h) Distribution of the diameters of random and aligned fibers; (i) Quantification of alignment in random and aligned fibers. (j) Typical stress–strain curves of samples with random and aligned fibers. (k) Strain at break, maximum stress, and tensile modulus of samples with random and aligned fibers.

Results and Discussion

Circular Acoustic Devices with Tailored Fibrous Structure and Mechanical Properties

The devices developed and tested (Figure 1a–c) represent prototypal shapes to reproduce the varying cross-sectional size and fibrous structure of the basilar membrane, with dimensions that are convenient to optimize the processing and the testing conditions, as a proof of concept for potential piezo-acoustic devices. Each circular device is fabricated and assembled by electrospinning of P(VDF-TrFE) random and aligned fibers sandwiched between two 3D-printed frames with copper stripes as electrodes into a drumlike structure (Figure 1b), with the thickness of both types of membranes kept around 60 μm in all devices (more details in Experimental Methods). Figure 1d, e and f, g show optical microscopy and SEM images of random and aligned P(VDF-TrFE) fibers, respectively. Measurements on more than 100 individual fibers revealed a distribution of diameter with a mode value of ∼0.74 ± 0.45 μm in random fibers (Figure 1h) and no preferential orientation (Figure 1i). Aligned P(VDF-TrFE) fibers present a mode diameter of ∼0.60 ± 0.35 μm (Figure 1h) and an orientation between ±20° (Figure 1i) with respect to the direction indicated with “0°” in Figure 1g. The fiber orientation affects the mechanical properties of the membranes, as shown in Figure 1j, k. It can be observed that aligned fibers possess lower ultimate strain at break, higher apparent tensile strength and higher tensile modulus, calculated as the slope of the initial linear part of the stress (apparent)–strain curve (Figure 1j, k).

Compared to the case of PVDF, the phase analysis on P(VDF-TrFE) copolymers is often more challenging, because of the lack of standard XRD cards and the disagreement in the existing literature on the assignment of diffraction peaks and FTIR bands belonging to the α, β, and γ polymorphs. The phase identification is frequently accomplished referring to the PVDF system, whose crystallographic structures have been more widely characterized. The X-ray diffraction carried out on the P(VDF-TrFE) powder reveals the presence of a main peak at 2θ = 19.9° (Figure 2a), which according to various previous studies can be assigned to the (110)/(200) planes of the orthorhombic β phase (space group Amm2).³⁰⁻³⁴ The shoulder at about 2θ = 17.7° is difficult to assign, as evidenced by the disagreement found in the available literature. In a previous publication, it has been attributed to amorphous regions,³² whereas in a different study, it has been assigned to the (100) plane of the nonpolar monoclinic α-phase (space group P2₁/c).³³ The main diffraction peak in both the random and aligned fibers (Figure 2a) is consistent with the main peak in the starting powder, denoting the main presence of the β phase in both membranes. The diffraction pattern of the random fibers presents a broad hump at about 2θ = 18.3° (Figure 2a), less visible in the aligned fibers, which could be attributed to the monoclinic γ phase (space group C2), whose corresponding peak could possibly overlap with another peak belonging to the α-phase, as previously reported for the case of PVDF.³⁵ The aligned fibers present an additional visible shoulder at about 2θ = 22.5°, which is significantly suppressed in the random fiber membrane (Figure 2a). A similar shoulder was observed in a previous study on P(VDF-TrFE) powder purchased from the same supplier, but it could not be fully resolved and was labeled as “an isolated diffraction line”.³⁶ However, according to other authors,³⁷ this shoulder can be interpreted as an equatorial peak of the β phase, which appears as a consequence of a reduced distance between carbon chains because of the stretching experienced by the fibers during alignment, justifying the absence of this peak in the random membrane. The other possibility is that this shoulder belongs to the γ phase, according to the following discussion.

Figure 2.

Structural characterization of PVDF-TrFE powder and electrospun fibers. (a) XRD of starting powder, random, and aligned fibers; (b) FTIR of PVDF-TrFE starting powder; (c) polarized FTIR of PVDF-TrFE random fibers; (d) polarized FTIR of PVDF-TrFE aligned fibers.

The uncertainty on the presence of different phases could be eventually solved with the aid of FTIR spectroscopy; however, in PVDF-based polymers, the precise assignment of the absorption bands is also challenging because of the overlapping of vibrational modes belonging to different polymorphs within narrow wavenumber ranges.³⁸⁻⁴⁰ On the basis of the affinity between the infrared spectra of PVDF and P(VDF-TrFE), the band assignment has been mainly carried out following the considerations reported in ref (39). Accordingly, the absorption bands exclusively belonging to the β and γ phases are respectively located at 1285 cm^–1 (symmetric stretching of CF₂, antisymmetric stretching of CC, bending of CCC^41,42) and 1245 cm^–1 (asymmetric stretching of CF₂, rocking of CH₂, twisting of CH₂⁴³), which ascertain the presence of both phases in the pristine powder (Figure 2b), as well as in both electrospun membranes (Figure 2c, d). Because of the absence of bands solely belonging to the α phase (for instance, at 975 and 1209 cm^–1 as in PVDF³⁹) in the spectrum of both electrospun membranes, the presence of the α phase in the fibers can be ruled out with a certain degree of confidence. The band labeled with L_M (linkages mode) can be assigned to localized modes of head-to-head (−CH₂–CF₂–CF₂–CH₂−) and tail-to-tail (−CF₂–CH₂–CH₂–CF₂−) linkages, and is found at 1340 cm^–1 in the powder, 1341 cm^–1 in the random fibers and at 1334 cm^–1 in the aligned fibers, denoting the largest shifts in wavenumbers compared to all of the other observed bands. For all other remaining bands, there are significant controversies in the literature regarding their precise assignment as reviewed in ref (39), but it is likely that they contain the convolution of various modes belonging to the different polymorphs. However, on the basis of the XRD and FTIR combined analysis, it can be concluded that the initial powder and both electrospun membranes contain a mixture of β and γ phases.

The polarized FTIR spectra of the random membrane show a weak dichroism (Figure 2c), whereas the absorption bands of the aligned fibers significantly vary with the polarizer angle (Figure 2d). In particular, the bands at 845, 883, 1186, 1287, and 1430 cm^–1 increase intensity from 0° (incident beam polarized parallel to fibers direction) to 90° (incident beam polarized perpendicular to fibers direction), whereas the bands at 946, 1075, and 1398 cm^–1 decrease intensity from 0 to 90° (Figure 2d). The band at 1334 cm^–1 shows a slight shift toward higher wavenumbers and a slight intensity decrease with increasing angle, whereas the bands at 1118 and 1245 cm^–1 do not show a major intensity change. The trends observed are in agreement with previous studies.⁴⁴⁻⁴⁶ According to ref (45), the transition moments of the modes at 1075 and 1398 cm^–1 are parallel to the lattice parameter c of the β phase unit cell, along which the carbon chains are oriented. Therefore, it can be inferred that carbon chains of the β phase are oriented along the fibers’ length and the dipoles are oriented along the radial direction, in agreement with previous reports.³³ The increasing intensity of the bands at 845 and 883 cm^–1 from 0 to 90° confirms that the polar b axis is perpendicular to the fiber axis. The dichroism evidenced in the polarized spectra has been quantified by estimating the dichroic ratio R for each band, here calculated as

1

where ΔA_∥ and ΔA_⊥ indicate the differences between the values of each absorbance peak and the very first neighboring valley, at 0 and 90° polarizer angle, respectively. Because of the possible contribution of different phases in various absorption bands, the actual orientation of the transition moment 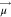corresponding to each vibrational mode can be determined following the approach proposed by Fraser in ref (47). The method allows estimating the minimum fractions f_m of molecular segments perfectly oriented and the range of the angle α formed by their long axis with the transition moment vectors, directly from the dichroic ratio R relative to each band. According to Fraser, the following conditions hold:

2

3

The results for both random and aligned fibers are summarized in Table 1. It can be observed that in the random membrane, the dichroic ratios present tiny deviations from unity, except for the modes at 1076 and 1398 cm^–1, which show the highest dichroicity, likewise in the aligned fibers. In the latter, the dichroic ratio relative to the mode at 1075 cm^–1 ideally goes to infinity, as there is no observable absorption band at 90° (ΔA_⊥ ≈ 0). The largest finite dichroic ratio is found at 1398 cm^–1 (R = 4.55), where the angle α is restricted within the interval 0° ≤ α ≤ 33.54°, with a minimum fraction of aligned molecular segments of 54%. The other modes with strong dichroicity are those at 946 cm^–1 (R = 0.24) and 1430 cm^–1 (R = 0.05), which display a small range of variation of the angle α and large values of f_m, indicating a pronounced degree of alignment of the relative molecular segments, compared to the random membrane.

Table 1. Analysis of Polarized FTIR Spectra of Random and Aligned Fibers^a.

		random fibers			aligned fibers
wavenumbers (cm–1)	approximate normal modes assignment	estimated dichroic ratio R	estimated α intervals	fm	estimated dichroic ratio R	estimated α intervals	fm
845	νs(CF2)+νs(CC) [45]	1.10	0° ≤ α ≤ 53.41°	0.03	1.06	0° ≤ α ≤ 53.88°	0.02
882	ρ(CH2)+νas(CF2)+ρ(CF2) [45]	1.10	0° ≤ α ≤ 53.46°	0.03	1.01	0° ≤ α ≤ 54.51°	0.006
944	-t(CH2)-νas(CF2) [43]	1.22	0° ≤ α ≤ 52.03°	0.06	0.24	72.29° ≤ α ≤ 90°	0.72
1076	νas(CC)+w(CH2)+w(CF2) [45]	2.48	0° ≤ α ≤ 41.94°	0.33	-	-	-
1121	νs(CC)+νas(CC) [43]	1.27	0° ≤ α ≤ 51.40°	0.07	1.76	0° ≤ α ≤ 46.80°	0.20
1185	νas(CF2)+ρ(CF2)+ρ(CH2) [45]	1.09	0° ≤ α ≤ 53.57°	0.03	0.83	57.15° ≤ α ≤ 90°	0.11
1245	νas(CF2) [41]	1.27	0° ≤ α ≤ 51.46°	0.08	2.02	0° ≤ α ≤ 44.82°	0.25
1284	νs(CF2)+νs(CC)+δ(CCC) [45]	0.97	55.09° ≤ α ≤ 90°	0.01	0.34	55.09°≤α≤90°	0.56
1341	head-to-head and tail-to-tail linkages [41]	1.43	0° ≤ α ≤ 49.79°	0.12	0.72	67.53° ≤ α ≤ 90°	0.20
1398	w(CH2)+νs(CC) [45]	1.44	0° ≤ α ≤ 49.63°	0.12	4.55	0° ≤ α ≤ 33.54°	0.54
1428	δ(CH2)-w(CH2) [45]	1.14	0° ≤ α ≤ 52.95°	0.04	0.05	80.94° ≤ α ≤ 90°	0.92

^aThe symbol indicate ν_s, symmetric stretching; ν_as, antisymmetric stretching; δ, bending; ρ, rocking; t, twisting; w, wagging. The sign ± indicates in-phase and out-of-phase vibration

Electromechanical Behavior of Electrospun Fibers at the Nanoscale

Figures 3a–c and 4a–c show representative amplitude and phase images of random and aligned fibers acquired in tapping mode, indicating smooth surface morphology in both cases. The cantilever tuning in dual AC resonance tracking piezo-force microscopy (DART) mode shows the presence of a resonance peak at around 280 kHz in both cases (see Figure S1). Figures 3d–m and 4d–m present the typical evolution of the off-field and on-field hysteresis loops (amplitude/phase-bias voltage) for different applied bias voltage in both fiber types. In the low-voltage regime (±10 V), the off-field amplitude response of random fibers shows a linear dependence on the bias voltage with a positive slope (Figure 3e), which may indicate that the polarization at that particular location of the fiber is parallel to the positive bias. The on-field amplitude loop has a V-like shape (Figure 3e), with a vertex at around −1 V, maybe signifying that beyond −1 V bias, a tiny polarization reorientation begins, as also shown by the on-field phase change (Figure 3d). In the range ±50 V, there is already a significant polarization reorientation, as proved by the minimum points of the off-field amplitude plot located at about 30/40 V and −35 V, and by the corresponding off-field phase changes (Figures 3f, g). The presence of amplitude minima during the beginning of electrical loading may indicate the recovery of the strain imposed during the previous electrical loading, as typically observed in ferroelectric/ferroelastic materials on the macroscale⁴⁸ and at the microscale.^49,50 The on-field amplitude loop shows a butterfly-like shape, with minimum points at the bias voltage corresponding to about 180° shift of the on-field phase (Figure 3f). The loops at ±100 V (Figures 3h, i) appear more saturated, with minimum off-field amplitudes at about ±60 V, which can be considered as the off-field coercive voltage, as it does not significantly shift in the loops at higher voltage bias. This is consistently coincident with an inflection point in the on-field amplitude plot. At the minimum points of both off- and on-field amplitude plots, the phase switches of about 180° in both off- and on-field responses. The loops at higher voltage bias (Figures 3j–m) show similar trends, but with the presence of more complicated features, consisting of local maximum points in the off-amplitude loops that cannot be currently fully justified but might be related to a departure from cantilever resonance conditions at high applied voltage, with consequent lower amplitude response.

Figure 3.

Atomic/piezoelectric force microscopy on random fibers. (a–c) Amplitude and phase images; (d–m) evolution of off- and on-field amplitude and phase response as a function of voltage bias.

Figure 4.

Atomic/piezoelectric force microscopy on aligned fibers. (a–c) Amplitude and phase images; (d–m) evolution of off- and on-field amplitude and phase response as a function of voltage bias.

In the low-voltage range (±10 V), aligned fibers show a linear amplitude–voltage loop observed in both the off- and on-field amplitude hysteresis loops (Figure 4e). It can be noticed that the off-field response decreases with increasing the positive bias, whereas it increases with increasing negative bias; in other words, the amplitude–voltage linear response has a negative slope. This may be due to two reasons: (i) the initial polarization direction in which that particular fiber’s location is oriented along the negative direction of the bias voltage; (ii) the negative piezoelectric effect, which characterizes the electromechanical behavior of PVDF-based piezoelectric polymers.^51,52 In order to fully clarify this, more detailed studies are needed. Figures 4f, g shows the hysteresis loops in the range ±50 V, whereby the on-field plot appears symmetric, but with nonlinear and hysteretic behavior in both amplitude and phase. The amplitude off-field loop shows the largest response at the maximum applied bias voltage, and minimum values at about ±25 V bias voltage. The off- and on-field phase loops might already reflect polarization reversal. Beyond ±50 V bias voltage (Figures 4h–m), the trend of both on-field amplitude and phase loops does not present significant alterations, whereas the off-field loops shows interesting changes, probably related to a change in the poling state during the application of an increasing bias voltage. In particular, in the range −100 V/+100 V, the maximum in the off-field amplitude appears around zero bias voltage and the minima around ±70 V, where the maximum rate of the off-field phase change is observed (Figures 4h, i). Similar comments apply to the off-field amplitude loops in the range −150 V/+150 V (Figure 4k), which show an additional anomaly represented by an inversion of trend in the high applied bias range, beyond which the amplitude response starts decreasing with increasing bias. This is coincident with a step change in the phase loop. The loops generated at ±200 V bias voltage also present interesting features: (i) the off- and on-field phase loops have very similar phase values (around 0°) in the high-bias region, probably suggesting that the polarization induced in the fibers is oriented along the positive bias; (ii) in the high-bias region, the off-field amplitude response approaches the value obtained around zero bias voltage; (iii) the minima in the off-field amplitude loop are located in the same bias region, where the on-field amplitude presents an inflection point and where the off-field phase switches, suggesting that the corresponding field might identify the off-field coercive bias. However, the negative slope of the off-field amplitude loop in the high bias regime may suggest that the loops are not entirely saturated, although the response to the cantilever tuning shows much higher amplitude compared to the initial tuning (Figure S1), indicating that a higher degree of poling might have been induced during the application of high DC bias. Despite the additional factors not related to ferroelectricity that can influence the PFM response,^53,54 the present results may confirm that the electrospun P(VDF-TrFE) fibers are ferroelectric (and therefore piezoelectric), and their polarization can be locally enhanced and reversed by external applied voltages of appropriate magnitude. The PFM loops generated resemble those reported in various previous studies on PVDF-based fibers,⁵⁵⁻⁵⁸ adding confidence about the ferroelectric nature of the electrospun membranes here fabricated.

Response to Acoustic Stimuli

Laser vibrometry measurements provided important insights into the acoustic response of the electrospun membranes. Monitoring the displacement of the center point of each membrane during the application of a sweep of acoustic sine waves with constant amplitude and decreasing frequency over the human audible frequency range (10 kHz to 100 Hz) enabled identifying of the frequencies corresponding to the maximum displacements, i.e., the resonance frequencies. The results here reported are relative to tests carried out with acoustic waves with an average sound pressure level of 78 dB. The data are analyzed by computing the short-time Fourier transform (STFT), the power spectral density (PSD), and the spectrograms, and by comparing the values of resonance frequencies, displacement, and voltage at resonance reported in Figures 5 and 6 and Table 2.

Figure 5.

Response of random fibers and aligned fibers in the last ∼18.5 s of the sound wave sweep (input frequency in the range 1500–100 Hz) and corresponding STFT frequency spectra in circular devices with 30, 20, and 10 mm diameter. (a1–f1) Displacement, (a2–f2) displacement STFT, (a2–f3) voltage output, and (a4–f4) voltage STFT of random fibers and aligned fibers.

Figure 6.

STFT, PSD, windowed spectral power of displacement, and voltage of 30 mm diameter devices with (a–c) random and (e–g) aligned fibers within the input frequency sweep. Resonance frequency, displacement of center point, and voltage output as a function of device diameter in (d) random and (h) aligned fibers.

Table 2. Resonance Frequency, Displacement of Center Point, and Voltage Output as a Function of Device Diameter in Random and Aligned Fibers.

	circle diameter (mm)	resonance frequency (Hz)	displacement (μm)	voltage output (mV)
random fibers	30	140	240	17
	20	167	133	8
	16	302	120	5
	10	330	76	1
aligned fibers	30	186	78	10
	20	222	45	5
	16	230	11	3
	10	220	9	3

Figure 5 shows the response of displacement and voltage output, along with STFT of the devices with 10, 20, and 30 mm diameter consisting of random and aligned membranes, approximately in the last ∼18.5 s of the sweep (input frequencies below 1600 Hz), where the major resonance effects have been observed. In random membranes, the frequency corresponding to the maximum displacement decreases with increasing the diameter of the electrospun membranes (Figures 5a1–c1, a2–c2, and 6d), whereas the voltage output increases as expected because of the larger deformation experienced by the vibrating electrospun membranes in larger diameter devices (Figures 5a3–c3, 5a4–c4 and 6d). The maximum displacement values in random membranes are found in the last 3–4 s of the sweep (input frequencies below 500 Hz, see Figures 5a1–c1), with the presence of minor peaks in time intervals corresponding to input frequencies between 1250 and 500 Hz (Figures 5a1–c1). The displacement values in random membranes are higher than those in the aligned membranes (Figures 5a1–f1 and 6d, h and Table 2), probably because of their lower elastic modulus (see Figure 1j, k). By reducing the diameter of the electrospun membranes with aligned fibers, the variation in the displacement during the frequency sweep is significantly suppressed (see Figures 5d1–f1 and 6h and Table 2), making the identification of the resonance frequency more difficult and less diameter-dependent compared to the random fiber membranes (see also Figure 6d and Table 2). Displacement peaks in the time interval 105–107 s, in which the input frequency is around 1160 Hz, are often observed in both random (see Figures 5a1–c1) and aligned devices (see Figure 5d1–f1). It has been experimentally verified that these peaks can be mainly attributed to the resonance of the frame-clamp parts used in the experiments. However, in some cases, the peak around 1160 Hz overlaps with other peaks corresponding to vibrations experienced by the membranes (see, for instance, 10 mm diameter devices with aligned fibers in Figure 5f1).

All the tested electrospun membranes presented a measurable voltage output, which shows maximum values corresponding to the largest displacements (resonance conditions), as can be observed in Figure 5 and Figure S2. For small diameter devices (10 mm diameter), the voltage output at resonance is not clearly visible in the graph scales in Figure 5; therefore, the relevant intervals have been replotted in Figure S2, which shows the comparison between the voltage–time signals far from resonance, where they appear as random noise (Figure S2a1–c1 for random fibers and Figure S2d1–f1 for aligned fibers), and nearby resonance, where they present a more regular and periodic pattern (Figures S2a2–c2 for random fibers and Figures S2d2–f2 for aligned fibers).

In the STFT plots in Figure 5, there are two main peaks: a broad/skewed peak in the low-frequency range in the displacement (Figures 5a2–f2) and voltage (Figures 5a4–f4), and a rather sharp peak at around 740 Hz only in the STFT of the displacement signals (Figures 5a2–f2). Figure 6a, e displays the PSD plots of the displacement and voltage signals relative to 30 mm diameter device with random and aligned membranes, respectively. One can notice that the peaks in the low-frequency range (in this case, at 140 Hz in random and at 186 Hz in aligned fibers) are stronger than the peak around 740 Hz, suggesting that the peaks in the low-frequency range correspond to the resonance frequencies. The peaks around 740 Hz are consistent with those observed in the STFT and PSD plots obtained on a 30 mm device with random fibers in the absence of acoustic input (Figure S3a, b), suggesting that the peak is not related to the acoustic sweep input. The STFT and PSD plots of the electrospun membranes with aligned fibers generally display slightly broadened spectra compared to the random fibers, with the main frequency components of displacement and voltage output signals located just above 200 Hz (Figures 5 and 6a, e).

The spectrograms in Figure 6 depict the time evolution of the spectral components of the displacement-time (Figure 6b, f for random and aligned fibers, respectively) and voltage–time signals (Figures 6c, g for random and aligned fibers, respectively) obtained on the 30 mm diameter device in the last 20 s of the sweeps (input frequencies below 1750 Hz), which contain the most relevant acoustic-mechanical and acoustic-electrical conversion effects. The spectrograms relative to the entire duration (120 s) of the tests (input frequencies in the range 10 kHz to 100 Hz) are shown in Figure S4a–d. All spectrograms indicate that as the PSD of the displacement increases, the voltage output becomes higher. A color change from blue to red in the scale bar indicates an increasing power spectral density of the spectral components identified in the displacement and voltage output signals.

The spectrograms (Figure 6b, c and f, g) show that the vibration frequencies of both random and aligned fibers reduce in a linear fashion with reducing the input frequencies. The highest power spectral densities attributed to the largest displacement of the membrane, highlighted by red color, are mainly observed below 1750 Hz in both random and aligned fibers. The horizontal lines indicate the spectral components of the signals whose frequency is constant during the entire time interval considered. To identify the frequency components due to the background noise present in the testing environment during the entire frequency sweep, we also obtained the spectrograms from the displacement–time and voltage–time signals recorded for 2 min in the absence of any acoustic sound wave input (Figure S4e, f). Worthy of note are the intense horizontal lines around 4500 Hz (Figure S4). Additionally, as shown in Figure S4b, d, the power densities of the voltage output are low at frequencies higher than 1750 Hz; this occurs probably because the vibration amplitudes of the membranes are not high enough to produce a considerable electrical output, which can be attributed to a possible lower response at high frequency and to the possible stiffening of the PVDF-TrFE fibrous membranes at high-frequency dynamic conditions because of their viscoelastic nature. The storage modulus of PVDF was reported to increase more than 1 × 10⁴ times under oscillatory dynamic stress with increasing frequency from 0.1 to 1000 Hz.⁵⁹ As the input frequency increases, the membranes become stiffer and less viscous because of the fast response and relaxation of the polymer chains. The main responsive line in the spectrograms is accompanied by a series of minor lines with different slopes (see white arrows in Figure 6b, c and f, g), whose PSD increases with decreasing input frequency; these possibly correspond to overtones of the main frequency response.

The resonance frequencies and the corresponding displacement and voltage output of the electrospun membranes with different diameter were extrapolated from the analysis of the plots and summarized in Figures 6d, h and Table 2. As expected, the resonance frequency increased, whereas displacement and voltage output decreased with decreasing the diameter of random membranes in which the area of the electrodes and electrical contact was kept unchanged in the relative devices. In the case of aligned fibrous membrane, a similar trend appeared at relatively large diameters (16, 20, and 30 mm) except for the device of 10 mm diameter, where the resonance frequency could not be neatly identified.

By testing several devices with the same diameter, it was noticed that the displacement values and the resonance frequencies can vary from sample to sample and from test to test. This is due to a number of factors that are difficult to be precisely controlled, such as interconnection between fibers, packing density, fiber diameter, and thickness of the membranes (which all affect membrane bending stiffness), as well as the clamping conditions on the devices and their position in the mounting stage of the laser vibrometer (see ref (60) for a discussion on similar effects in PVDF ribbons⁶⁰). In the efforts to minimize data scatter by keeping the processing and testing conditions as consistent as possible, good data repeatability could be obtained.

It should also be mentioned that a significant scatter in the voltage output has been observed throughout all the tests carried out, which can be attributed to a series of factors that are difficult to fully control. These include (i) the difficulty of electrospinning membranes with exactly the same thickness; (ii) variation in orientation degree in membranes with aligned fibers; (iii) the inhomogeneous degree of poling in fibers throughout the membranes; (iv) the generation of triboelectric charges during vibration due to the friction between fibers and electrodes, as explained in detail in ref (61); (v) the accumulation and migration of surface electrical charges present between fibers and at the membrane–electrode interface during the device fabrication; (vi) possible inhomogeneity in the membrane–electrode contacts.

The displacement maps reported in Figure 7 depict the vibrational modes of the electrospun membranes at selected input frequencies. More specifically, these maps represent snapshots of the instant values of the displacement of each point of the membranes at a fixed value of the input frequency and for a particular phase value of the input wave at which the gradient in the vertical displacement between different parts of the membranes was the greatest. Red-colored areas correspond to positive out-of-plane displacement, whereas blue color indicates areas with negative out-of-plane displacement. Two characteristic displacement patterns were visualized, namely circular and striped. It is believed that the circular patterns correspond to the main vibration mode attributed to the circular shape of the sensor, whereas the other striped ones may relate to vibration harmonics in different phase sequences, as well as the anisotropic structure and property of the nanofibrous membranes.

Figure 7.

Displacement maps at selected frequencies in devices with (a) random and (b) aligned fibers with different diameters. Scale bar: 5 mm. Displacement maps of sections of 16 mm diameter membranes with (c) random and (d) aligned fibers with respect to the reference plane (zero vertical displacement). Mesh widths: 220 μm.

It can be observed that the random membrane-based sensors show little variations in the displacement maps within the entire range of frequency considered, suggesting that the main vibrational circular modes and harmonic stripes hardly change with the input frequencies in the range considered (Figure 7a). The displacement maps of the aligned fibers instead show a more significant effect of the diameter variation on the vibrational modes in the range of frequency selected (see Figure 7b). The circular modes appeared to be more elongated and different sequence phases of harmonic patterns were generated especially at higher frequency (>1000 Hz). In particular, multiordered stripes of about 0.5–1 mm in width with opposite vibrations to each other were visualized in the device with 16 mm diameter at 1470 and 1150 Hz (Figure 7b).

An enlarged view of a section of the 16 mm diameter membranes with random and aligned fibers is shown in Figure 7c, d, respectively, which better highlights the characteristics of localized vibrations with respect to the reference plane (placed at zero vertical displacement). It can be seen that random membranes show the same sign of displacement above and below the reference plane in the entire area scanned, whereas the sign of the displacement in aligned fibers periodically changes in direction perpendicular to the fiber direction. A qualitative explanation for this relies on the idea that entangled random fiber membranes may vibrate like an integrated continuous membrane with more or less isotropic behavior, whereas aligned fibers could vibrate more like “anisotropic strings or belts”. Despite the circular symmetry of the devices, the variety of vibrational modes and their variation/sequence observed in the displacement maps of random and aligned membranes reflect the high level of complexity involved in structure, morphology (entanglement and alignment), uniformity, and thickness of the fibrous structure at multiscales, as well as the reproducibility of the device fabrication and variation in the data tested, as explained above.

Correlation between Microstructure, Electromechanical Properties, and Acoustic–Electric Conversion

The extent of fiber alignment induced during electrospinning has a clear effect on the orientation of molecular segments, as shown by the analysis of the FTIR spectra. This might help to slightly increase the degree of poling compared to random fibers, although no strong evidence could be found in the PFM tests or from the electrical output values obtained in the acoustic-electrical conversion tests. However, based on the similar voltage outputs obtained in random and aligned membranes and on the reduced vibration amplitudes of the latter, it could be argued that aligned fibers present better piezoelectric and triboelectric performance. This agrees with the view that a higher degree of poling would determine not only higher piezoelectric activity but also enhanced triboelectric performance.^62,63 Additionally, aligned fibers would allow a better control of the membranes microstructure, which can be purposely engineered to achieve higher triboelectric conversion (i.e., in PVDF-TrFE-based composites,⁶⁴ and PVDF-TrFE-multiwall nanotubes-poly(dimethylsiloxane) heterostructures⁶⁵), thereby turning particularly useful for miniaturized devices. The smaller displacement values and thus narrow range of resonance frequency obtained in the acoustic sweep tests of the aligned fibers are in agreement with the lower strain and the higher tensile modulus.

Conclusions

In this research, the structural characteristics, the local electromechanical properties, and the response to acoustic stimuli of piezoelectric membrane devices based on P(VDF-TrFE) random and aligned fibers produced by electrospinning have been thoroughly investigated. The results suggest that P(VDF-TrFE) fiber-based acoustic sensors are capable of generating electric signals up to 17 mV in response to low frequency between 100 and 400 Hz, depending on the size of the sensors and alignment of the fibers when resonating under acoustic stimuli. The sensors with random nanofibers demonstrated a wider range of frequency selectivity and higher sensitivity as evidenced by the downshift of the resonance frequency and by the higher voltage output with increasing the circular diameter, compared to those with aligned nanofibers. As a result of the possible combined action of piezoelectric and triboelectric effects, the sensors could be potentially suited to engineer in vitro cochlea models and replacement system in vivo with the needed functions and resolution. The proof-of-concept here developed in macroscale indicates that major challenges for developing implantable devices relate to miniaturization, the fabrication of a fibrous network microstructure with consistent homogeneity, and the reproducible electrical contacts. To address the challenges of downscaling, while maintaining desirable electro-acoustical responses, researchers should pursue specific modifications of the fiber properties and opportune geometrical variations of the devices.

Methods

Design and Fabrication of Nanofiber-Based Acoustic Devices

P(VDF-TrFE) powder (75/25% mol, Piezotech, France) was added to a solution (20 wt % concentration) of dimethylformamide (DMF) and acetone (Sigma-Aldrich) in a 3:2 volume ratio and stirred at 300 rpm in glass vials for 2 h on a hot plate at 70 °C to ensure homogeneous mixing. The polymer solution was transferred into a plastic 10 mL syringe, which was placed into a pump (Chemyx, Fusion 100) and connected to a 14-gauge steel needle (1.6 mm inner diameter), via a tube of polytetrafluoroethylene (PTFE) with an inner diameter of 0.8 mm (Cole Palmer). The needle was inserted in a purpose-built electrospinning machine, in which the static voltage between the needle and a ground collector was supplied by a DC voltage power supply (Glassman High Voltage Inc.). The effects of the distance from the needle tip to the grounded electrodes, the flow rate, and applied voltage on fiber deposition were investigated and determined to be optimal at 15 cm, 3 mL/h, and 15 kV, respectively, for a stable deposition. To generate random fibers, we used a steel plate ground electrode to collect the fibers, whereas to obtain aligned fibers, we used two parallel conductive metal rods (8 cm in distance) acting as counter electrodes to the needle. The fibrous membranes (∼60 μm in thickness) were collected on and clamped between two copper electrodes on poly(lactic acid) (PLA) frames with circular holes of 10, 16, 20, and 30 mm diameter, respectively, fabricated by a 3D FDM printer (Figure 1c). Electrospinning was carried out at room temperature 22–25 °C in a hospital lab with a central ventilation system and a dehumidifier.

Characterization of Mechanical Properties, Structure, and Orientation of Electrospun P(VDF-TrFE) Nanofibers

The tensile mechanical properties of the membranes with random and aligned fibers were tested. Fiber membranes (∼60 ± 20 μm thickness) were electrospun on paper frames and were subsequently cut into rectangular samples (4 cm width and 23 cm length using a laser cutter (Trotec, Speedy100R), adapted from the method described in ref (66). The sample thickness was determined by averaging among five different thickness values across the sample cross-section edges taken with a micrometer. Five samples of random and aligned fibers were stretched at a rate of 5 mm/min until failure using an Instron 5564. The samples with aligned fibers were stretched along the direction of the fibers.

The phases, structure, and molecular orientation in both random and aligned fibers were studied by X-ray diffraction and polarized Fourier transform infrared (FTIR) spectroscopy. The X-ray diffraction patterns were obtained using a 2D Vantec (Brooker, Germany), with a Cu Kα X-ray source (λ = 1.54 Å) operated at 50 kV and 1 mA. The data were collected in the range 2θ = 15–25° at a 0.05° step size. Polarized FTIR spectroscopy was carried out in transmission mode on fibers deposited on the devices with 30 mm diameter using a Jasco FTIR 4200 spectrometer equipped with a polarizer (PL 82, Jasco, UK). Scans were generated with four different polarizer orientations, namely, 0, 30, 60, and 90°, where 0 and 90° indicate directions parallel and perpendicular to the orientation of the aligned fibers, respectively. For comparison, a spectrum of the P(VDF-TrFE) starting powder was obtained in attenuated total reflectance (ATR) mode, using a diamond reflectance accessory (Diamond MIRacle ATR, Pike Technologies, US). All spectra were obtained at 4 cm^–1 resolution over the range 600–4000 cm^–1 wavenumbers. A background scan was performed before each measurement.

Fiber morphology was assessed by scanning electron microscopy (SEM, ZEISS EVO MA10) and the topology by atomic force microscopy (AFM) in tapping mode using an MFP-3D system (Asylum Research, USA), with conductive cantilevers (∼2.9 N/m spring constant and 16–40 quality factor) driven by a voltage of about 1.2 V amplitude, with a scan frequency of 0.3 Hz.

Characterization of the Nanoscale Electromechanical Behavior of Electrospun P(VDF-TrFE) Nanofibers

The ferroelectric properties of single fibers were characterized using the dual AC resonance tracking piezo-force microscopy (DART-PFM) technique,⁶⁷ by generating hysteresis loops in various locations on the surface of different fibers to identify repeated trends. Amplitude and phase responses were obtained on fibers deposited on gold-coated silicon wafers, by driving the cantilever at around 280 kHz (resonance frequency in DART mode), with a feedback frequency window of 10 kHz and an applied voltage of 4 V. Off- and on-field hysteresis loops were extrapolated by applying varying DC bias voltages using triangular-square waveforms of 0.1 Hz frequency and varying amplitudes in the range 5–200 V.

Characterization of Piezo-Acoustic Performance of the Piezo-Nanofiber-Based Devices

A piezo-acoustic-laser-vibrometer system was custom-built by assembling a laser vibrometer (MSA-050 Microsystem Analyzer, Polytech, Germany), mouth stimulator (Type 4227-A, Brüel & Kjær, Denmark) and multichannel high impedance JFET input voltage buffers through a data acquisition device (DAQ) (Powerlab 16, ADInstruments). The laser vibrometer was used to monitor the vibration of the center point of each circular membrane in response to an acoustic stimulus consisting of sound sine waves with frequency swept in the range 10 kHz to 100 Hz within 2 min, with a rate of approximately 82.5 Hz/s. Tests were conducted at five different constant sound intensities of 0.01, 0.05, 0.1, 0.5, and 1 V nominal values, corresponding to average sound pressure levels (SPL) of 70, 78, 84, 106, and 111 dB, which presented variations of ±15 dB due to the frequency change during the sweep. Tests with an average SPL > 78 dB caused irreversible displacement biases (drift of the center point original position), especially in the large diameter devices, which would not allow for a consistent comparison of the devices. Therefore, only sweeping at 78 dB SPL has been discussed here. The acoustic waves were generated by the mouth simulator held at about 6 cm beneath the devices. The electrodes on the devices being tested were first connected to high-impedance JFET input voltage buffers before being connected to the DAQ. The voltage buffers were found to be needed due to the high impedance nature of the devices being tested. The buffers allowed removing the capacitive cross-talk when testing multiple channel devices simultaneously and obtaining a reproducible/reliable recording of the voltage output from the piezoelectric devices. The displacement and the voltage signals were synchronized and recorded by the Powerlab LabChart program using a sampling frequency of 40 000 data points per second on each channel. The displacement data were collected by taking the output from the laser vibrometer to the DAQ and applying a conversion factor within software to get the real-time displacement data. Displacement maps were generated from all tested devices using Polytech software which allowed fine scanning of the devices, where the distance between neighboring scanned points was set at 220 μm. The displacement of each point was monitored during the application of the acoustic stimulus, consisting of a frequency sweep from 10 kHz to 100 Hz in 1 s with an average sound pressure level of 84 dB.

Data Analysis

A Matlab code was programmed to compute the short-time Fourier transform, the power spectral density, and the spectrograms. A spectrogram algorithm was applied to achieve STFT with a sampling frequency of 40 k/s, which gives better frequency plots based on discrete-time signals. The trend from the original data was removed by using the “detrendData” function, enabling us to focus on the fluctuations in the data. To remove the noise, we used a channel that recorded the background signal as reference data, together with a “notchFilter”. Hanning window was used for PSD, where the window length was 4096, hop size 256, and number of points 262 144.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.0c09238.

• Figure S1, PFM cantilever tuning; Figure S2, voltage–time signals of random and aligned fibers with 10, 20, and 30 mm diameters at far-from resonance and near-to resonance conditions, as indicated in the legends; Figure S3, STFT and PSD of a 30 mm device with random fibers without acoustic wave input; Figure S4, displacement and voltage output spectrograms of 30 mm device with random fibers (a, b) and aligned fibers (c, d) with a wider range of frequency sweep up to 10 kHz; displacement and voltage output spectrogram of 30 mm device with random fibers without input sweep (e, f) (PDF)

Author Present Address

^■ School of Instrumentation and Optoelectronic Engineering, Beihang University, Beijing 100083, China (S.G.)

Author Present Address

^● Current address: School of Information Science and Technology, Fudan University, 220 Handan Road, Shanghai, 200433, China (X.L.)

Author Contributions

^† G.V. and J.C. contributed equally to this work.

Author Contributions

G.V. and J.C. contributed equally to the design, fabrication, characterization, analyses of the devices. T.M. integrated the acoustic-laser vibrometer testing system and contributed with measurement and data analysis. F.S., M.J., J.S., J.E., D.Z., S.G., and H.Z. participated in the preliminary work. W.S. initiated and mentored the work. All authors contributed to the preparation of the manuscript.

The authors declare no competing financial interest.