The first MICCAI challenge on PET tumor segmentation

Abstract

Introduction:

Automatic functional volume segmentation in PET images is a challenge that has been addressed using a large array of methods. A major limitation for the field has been the lack of a benchmark dataset that would allow direct comparison of the results in the various publications. In the present work, we describe a comparison of recent methods on a large dataset following recommendations by the American Association of Physicists in Medicine (AAPM) task group (TG) 211, which was carried out within a MICCAI (Medical Image Computing and Computer Assisted Intervention) challenge.

Materials and methods:

Organization and funding was provided by France Life Imaging (FLI). A dataset of 176 images combining simulated, phantom and clinical images was assembled. A website allowed the participants to register and download training data (n=19). Challengers then submitted encapsulated pipelines on an online platform that autonomously ran the algorithms on the testing data (n=157) and evaluated the results. The methods were ranked according to the arithmetic mean of sensitivity and positive predictive value.

Results:

Sixteen teams registered but only four provided manuscripts and pipeline(s) for a total of 10 methods. In addition, results using two thresholds and the Fuzzy Locally Adaptive Bayesian (FLAB) were generated. All competing methods except one performed with median accuracy above 0.8. The method with the highest score was the convolutional neural network-based segmentation, which significantly outperformed 9 out of 12 of the other methods, but not the improved K-Means, Gaussian Model Mixture and Fuzzy C-Means methods.

Conclusion:

The most rigorous comparative study of PET segmentation algorithms to date was carried out using a dataset that is the largest used in such studies so far. The hierarchy amongst the methods in terms of accuracy did not depend strongly on the subset of datasets or the metrics (or combination of metrics). All the methods submitted by the challengers except one demonstrated good performance with median accuracy scores above 0.8.

Graphical Abstract

Introduction

Positron Emission Tomography (PET) / Computed Tomography (CT) is established today as an important tool for patients management in oncology, cardiology and neurology. In oncology especially, fluorodeoxyglucose (FDG) PET is routinely used for diagnosis, staging, radiotherapy planning, and therapy monitoring and follow-up (Bai et al., 2013). After data acquisition and image reconstruction, an important step for exploiting the quantitative content of PET/CT images is the region of interest (ROI) determination that allows extracting semi-quantitative metrics such as mean or maximum standardized uptake values (SUV). SUV is a normalized scale for voxel intensities based on patient weight and injected radiotracer dose (other variants of SUV normalization exist) (Visser et al., 2010).

More recently, the quick development of the radiomics field in PET/CT imaging also involves the accurate, robust and reproducible segmentation of the tumor volume in order to extract numerous additional features such as 3D shape descriptors, intensity- and histogram-based metrics and 2^nd or higher order textural features (Hatt et al., 2017b).

Automatic segmentation of functional volumes in PET images is a challenging task, due to their low signal-to-noise ratio (SNR) and limited spatial resolution associated with partial volume effects, combined with small grid sizes used in image reconstruction (hence large voxel sizes and poor spatial sampling). Manual delineation is usually considered poorly reproducible, tedious and time-consuming in medical imaging, and this is especially true in PET and for 3D volumes (Hatt et al., 2017a). This imposed the development of auto-segmentation methods. Before 2007, most of these methods were restricted to selecting some kind of binary threshold of PET image intensities, such as for example a percentage of the SUV_max, absolute threshold of SUV, or adaptive thresholding approaches taking into account the background intensity and/or the contrast between object and background (Dewalle-Vignion et al., 2010). Adding dependency on the object volume resulted in the development of iterative methods (Nehmeh et al., 2009). However, most of these approaches were designed and optimized using simplistic objects (mostly phantom acquisitions of spherical homogenous objects in homogeneous background) and usually fail to accurately delineate real tumors (Hatt et al., 2017a). After 2007 studies began investigating the use of other image processing and segmentation paradigms to address the challenge and over the last 10 years, dozens of methods have been published relying on various image segmentation techniques or combinations of techniques from broad categories (thresholding, contour-based, region-based, clustering, statistical, machine learning…) (Foster et al., 2014; Hatt et al., 2017a; Zaidi and El Naqa, 2010). One major issue that has been identified is the lack of a standard (or benchmark) database that would allow comparing all methods on the same datasets (Hatt et al., 2017a). Currently, most published methods have been optimized and validated on a specific, usually home-made, dataset. Such validations, considering only a single class of data amongst clinical, phantom or simulated images is lacking rigor due to the imperfections inherent for each class: unreliable ground-truth (e.g. manual delineation of a single expert or CT-derived volumes in clinical images) or unrealistic objects (perfect spheres, very high contrast, low noise, no uptake heterogeneity) (Hatt et al., 2017a). Typically, no evaluation of robustness versus scanner acquisition or reconstruction protocols and no evaluation of repeatability are performed (Hatt et al., 2017a). The reimplementation of methods by other groups can also be misleading (Hatt and Visvikis, 2015).

As a result, there is still no consensus in the literature about which methods would be optimal for clinical practice, and only a few commercial products include more advanced techniques than threshold-based approaches (Hatt et al., 2017a). In order to improve over this situation, task group n° 211¹ (TG211) of the American Association of Physicists in Medicine (AAPM) has worked since 2011 on the development of a benchmark as well as on proper validation guidelines, suggesting appropriate combination of datasets and evaluation metrics in its recently published report (Hatt et al., 2017a). Another paper was also published to describe the design and the first tests of such a benchmark that will eventually be available to the community (Berthon et al., 2017).

To date there has been a single attempt at a challenge for PET segmentation. It was organized by Turku University Hospital (Finland) and the results were published as a comparative study (Shepherd et al., 2012). Although 30 methods from 13 institutions were compared, the dataset used had limited discriminative power as it contained only 7 volumes from 2 images of a phantom using glass inserts with cold walls, which can lead to biased results (Berthon et al., 2013; Hofheinz et al., 2010; van den Hoff and Hofheinz, 2013) and 2 patient images. On the other hand, MICCAI (Medical Image Computing and Computer Assisted Intervention) has organized numerous segmentation challenges² over the years, but none of them addressed tumor delineation in PET images.

France Life Imaging (FLI)³, a national French infrastructure dedicated to in vivo imaging, decided to sponsor two segmentation challenges for the MICCAI 2016 conference. One was dedicated to PET image segmentation for tumor delineation. It was funded by FLI and jointly organized with TG211 members, who provided datasets from the future AAPM benchmark as well as evaluation guidelines. One novel aspect of these FLI-sponsored challenges was the development and exploitation of an online platform to autonomously run the algorithms and generate segmentation results automatically without user intervention. The main goals of this challenge was to compare state-of-the-art PET segmentation algorithms on a large dataset following recommendations by the TG211 in terms of datasets and evaluation metrics, and to promote the online platform developed by FLI.

The present paper aims at presenting this challenge and its results.

Materials and methods

1. Challenge organization and sponsorship

The sponsorship and funding source for the challenge and the development of the platform used was the IAM (Image Analysis and Management) taskforce of FLI. Members of TG211 provided methodological advice, evaluation guidelines, as well as training and testing datasets. A scientific/clinical advisory board and a technical board were appointed (table 1).

Table 1:

members of the scientific/clinical and technical boards.

Name	Institution
Scientific / clinical advisory board
Dimitris Visvikis	INSERM, Brest, France - TG211 and FLI
Mathieu Hatt	INSERM, Brest, France - TG211 and FLI
Assen Kirov	MSKCC, New-York, USA (Chair of TG211)
Federico Turkheimer	King’s College, London, UK
Technical board
Frederic Cervenansky	Université Claude Bernard, Lyon, France
Tristan Glatard	CNRS, Lyon, France (VIP) Concordia University, Montreal, Canada
Michael Kain	INRIA, Rennes, France - FLI-IAM
Baptiste Laurent	INSERM, Brest, France - FLI-IAM

A web portal⁴ was built to present and advertise the challenge and to allow participants to register and download training data. Shanoir (SHAring NeurOImaging Resources)⁵ served as central database to store all datasets, all processed results and scores. Shanoir is an open source platform designed to share, archive, search and visualize imaging data (Barillot et al., 2016). It provides a user-friendly secure web access and a workflow to collect and retrieve data from multiple sources, with a specific extension to manage PET imaging developed for this challenge. The pipeline execution platform was developed within the Virtual Imaging Platform⁶ (VIP) (Glatard et al., 2013) by FLI-IAM engineers. VIP is a web portal for medical simulation and image data analysis. In this challenge, it provided the ability to execute all the applications and the metrics computation in the same environment, ensuring equity among challengers and results reproducibility.

2. Datasets and evaluation methodology

2.1. Overall objectives and methodology

The present challenge was focused on PET-only segmentation (no PET/CT multimodal segmentation) and on the evaluation of the accuracy (not robustness or repeatability) in delineating isolated solid tumor (no diffuse, multi-focal disease). It was also focused on static PET segmentation (no dynamic PET).

TG211 recommends the combined use of three types of datasets for PET segmentation validation: synthetic and simulated images, phantom acquisitions, and real clinical images (Berthon et al., 2017; Hatt et al., 2017a). Each category of image has a specific associated ground-truth (or surrogate of truth), with advantages and drawbacks, which make them complementary for a comprehensive and rigorous evaluation of the methods accuracy (table 2).

Table 2:

A summary of the types of PET images used for validation.

Type of images	Associated ground-truth or surrogate of truth	Realism of image characteristics	Realism of tumors	Computational time	Convenience
Synthetic images (no simulation of physics beyond addition of blur and noise to the ground-truth)	Perfect (voxel-by-voxel)	Low	Low to high. Depends on the digital phantom used.	Low	Easy to produce in large numbers.
Simulated images (e.g. with GATE (Le Maitre et al., 2009; Papadimitroulas et al., 2013) or SIMSET (Aristophanous et al., 2008))	Perfect (voxel-by-voxel)	Medium to High	Low to high. Depends on the digital phantom used.	High	Implementation is not straightforward. Time consuming. A proprietary reconstruction algorithm is not easily available.
Physical phantom acquisitions	Imperfect (relies on known geometrical properties + associated high resolution CT).	High (real)	Usually simplified objects. Depends on the physical phantom used.	N/A	Requires access to a real scanner and phantom. Can be time consuming.
Clinical images	Approximate	High (real)	High (real)	N/A	Rare datasets, difficult to generate. Digitized histopathology measurements are full of potential errors.
	Approximate (Consensus of manual delineations by several experts).	High (real).	High (real).	N/A	At least three manual contours are recommended. Time consuming.

With the help from contributing members of TG211, the following dataset was assembled: 70 synthetic and simulated (GATE, SIMSET) images (Aristophanous et al., 2008; Le Maitre et al., 2009; Papadimitroulas et al., 2013), 75 physical zeolites physical phantom images (different acquisitions of the same phantom containing 11 different zeolites, for which the ground-truth is obtained by thresholding the associated high resolution CT) (Zito et al., 2012) and 25 clinical images, 19 with volumes reconstructed from histopathology slices (Geets et al., 2007; Wanet et al., 2011) and 6 with statistical consensus (generated with the STAPLE algorithm (Warfield et al., 2004)) of three manual delineations (Lapuyade-Lahorgue et al., 2015). All the 176 tumors were isolated in a volume of interest (VOI) containing only the tumor and its immediate surrounding background. For simulated cases as well as for clinical cases with manual segmentation, the ground-truth was generated for the metabolically active volume, i.e. excluding areas with uptake similar as the background or without uptake. The training dataset contained such cases. Table 3 provides more details for each category.

Table 3:

Details of the dataset

Type of images	Number of images			Details	Provided by
	Training19	Testing157
Synthetic and simulated	2		12	Synthetic	M. Hatt and D. Visvikis, LaTIM, France
	2		10	Simulated with GATE (Papadimitroulas et al., 2013)	M. Hatt and D. Visvikis, LaTIM, France
	2		48	Simulated with SIMSET (Aristophanous et al., 2008)	M. Aristophanous, MD Anderson, Texas, USA
Physical phantom	9(3×3)	66(6×11)		Six different acquisitions of 11 zeolites (no cold walls) of various shapes and sizes (Zito et al., 2012)	E. De Bernardi, Italy
Clinical images	3	16		Images of head and neck or lung tumors with histopathology (Geets et al., 2007; Wanet et al., 2011)	J. A. Lee, UCL, Belgium
	1	5		Images of lung tumors with consensus of manual delineations (Lapuyade-Lahorgue et al., 2015)	Catherine Cheze Le Rest, CHU de Poitiers, France

2.2. Challengers pipelines integration

Contrary to testing data which was never available to challengers, a training subset representative of the whole dataset (6 synthetic and simulated, 9 phantom and 4 clinical images provided with their associated ground-truth) was made available for download to all registered participants so they could evaluate and optimize their algorithm(s) offline, on their own systems. All submitted methods had to be fully automated, including for parameters initialization, as they had to be run automatically without user intervention on the platform.

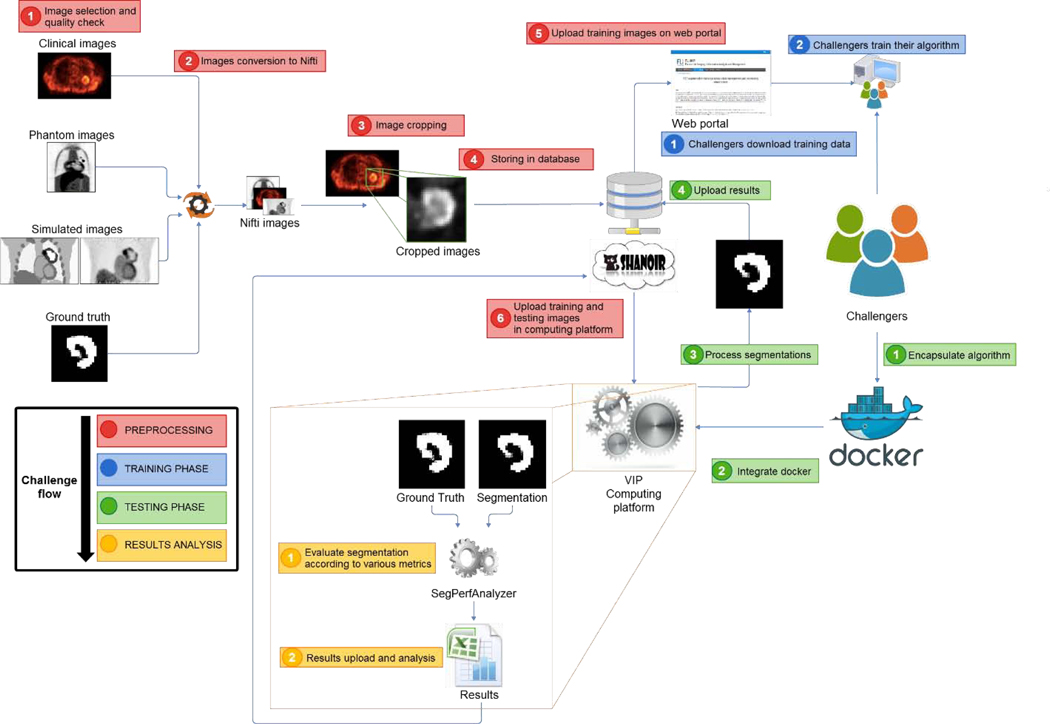
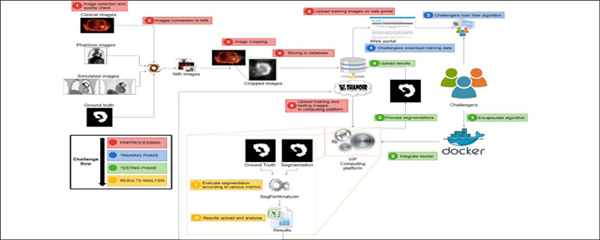
Pipeline integration and validation in VIP happened as follows. First, challengers bundled their applications in Docker containers⁷ (Merkel, 2014), to facilitate installation on the remote platform and to ensure reproducibility. Docker containers were annotated with JSON (JavaScript Object Notation) files complying with the Boutiques format⁸. JSON is a versatile format, allowing for a standard description of the command line used to launch applications, enabling thus their automated integration in VIP. The VIP team transferred input data from the Shanoir database⁹ and executed the pipelines on training data (available to the challengers) to ensure that the results were consistent with the ones computed by the challengers in their own environments. Finally, the VIP team executed the pipelines on the evaluation data without intervention from the challengers, computed the associated accuracy metrics, and transferred the results back to the Shanoir database. Data were transferred between VIP and Shanoir because VIP was exploited as a computing platform. Figure 1 illustrates the overall workflow.

Figure 1:

Illustration of the overall challenge workflow. In red, the preparation of the data by the FLI and VIP engineers. In blue, the training phase (challengers download training data and train algorithms). In green, the actual testing phase: challengers encapsulate their algorithm(s) to be run on the platform, which automatically extracts the segmentation results and evaluates them with the various metrics, then uploads them back into Shanoir.

2.3. Accuracy evaluation and comparison of methods

In order to evaluate the accuracy of each method, numerous metrics can be considered, including volume difference, barycenter distance, Jaccard and Dice coefficients, contour mean distance (CMD), or the combination of sensitivity (SE) and positive predictive value (PPV). As recommended by the TG211 we used the combination of SE and PPV as it provides the most comprehensive information on location, size and shape, as well as information regarding false positives and false negatives, for a moderate complexity (Hatt et al., 2017a).

Without consideration for a specific clinical application, both SE and PPV are equally important. Creating a single accuracy score to rank the methods thus led us to use the score=0.5×SE+0.5×PPV. On the other hand, the use of PET functional volumes for different clinical applications could lead to consider either SE or PPV to be more important (Hatt et al., 2017a). For instance, in radiotherapy planning, the objective is to reduce the risk of missing the target, even if it means delivering higher dose to the surrounding healthy tissues and organs-at-risk. Therefore in that case SE could be considered more important than PPV. We thus considered an alternative score_RT=0.6×SE+0.4×PPV. On the contrary, for therapy follow-up the goal is to obtain consistent volume measurements in sequential PET scans and to avoid including background/nearby tissues in the quantitative measurements used to quantify the tumor characteristics, even if it means risking under-evaluation of the true spatial extent of the volume of interest. As a result, PPV could be considered more important than SE, and we thus considered a third score denoted score_FU=0.4×SE+0.6×PPV. The values 0.4 and 0.6 were chosen arbitrarily on the basis that 0.45 and 0.55 would not lead to substantial changes in the scores, whereas 0.35 and 0.65 or 0.3 and 0.7 would put too much emphasis on one metric. Since neither of these 3 scores have clinical backing at present, they should be regarded as examples for potential clinically derived scores in analogy with the medical consideration functions (Kim et al., 2015). Results according to these alternate weights, as well as Jaccard, Dice and CMD are provided in the appendix (table A1).

The following analyses were carried out: comparing the methods on the entire dataset, as well as separately on each category of images (simulated, phantom, clinical), according to score, SE and PPV. Finally, two different consensuses of the segmentations were generated through majority voting and STAPLE (Dewalle-Vignion et al., 2015; McGurk et al., 2013).

Ranking of the methods and statistical superiority was determined with the Kruskal-Wallis test. This is an extension of the Man-Whitney rank-sum tests for more than 2 groups that does not assume a normal distribution and is not based only on the mean or median accuracy but takes into account the ranking of all points. Hence methods can be ranked higher even with a slightly lower mean or median accuracy, if they achieve more consistent (tighter distributions) accuracy. P-values below 0.01 were considered significant.

3. Challengers and methods

Sixteen different teams from 7 countries initially registered and downloaded the training dataset. Only 4 teams from 4 countries (2 from France, 1 from Poland, and 1 from China and USA) submitted papers and thereby provided a commitment to continue with the testing phase (table 4). Out of the 12 teams that did not continue after the training phase, 5 justified their choice by the fact they did not have the time and/or manpower to deal with the pipeline integration and following up the various tasks. The 7 others did not provide explanation. Some teams submitted several different methods and as a result 10 pipelines were integrated. In addition, the results of three additional methods were generated (in fully automatic mode without user intervention for a fair comparison) for reference: two fixed thresholding at 40% and 50% of the maximum, and the fuzzy locally adaptive Bayesian (FLAB) algorithm (Hatt et al., 2009, 2010). FLAB was included in addition to both fixed thresholds in order to provide a comparison with a well-known method that has previously demonstrated higher accuracy than fixed-thresholds, as it was not possible to include an adaptive threshold method due to the heterogeneity of the datasets in terms of image characteristics. In total, the results of 13 methods were produced and compared in the present analysis.

Table 4:

Team members, affiliations, country and implemented methods.

Team	Members	Institution(s)	Country	Implemented methods
1	A. Ouahabi V. Jaouen M. Hatt D. Visvikis H. Fayad	LaTIM, INSERM UMR 1101, Brest	France	Ant colony optimization (ACO) algorithm (Fayad et al., 2015) With two different initialization schemes
2	S. Liu X. Huang L. Li	Key Laboratory of Image Processing and Intelligent Control of Ministry of Education of China. School of Automation,Huazhong University of Science and Technology, Wuhan 430074	China USA	Random forest (RF) exploiting image features (Breiman, 2001)
	W. Lu S. Tan	Memorial Sloan-Kettering Cancer Center, New-York		Adaptive region growing (ARG) (Tan et al., 2017)
3	V. Jaouen M. Hatt	LaTIM, INSERM UMR 1101, Brest	France	Gradient-aided region-based active contour (GARAC) (Jaouen et al., 2014)
	H. Fayad
	C. Tauber
	D. Visvikis
4	J. Czakon F. Drapejkowski	Stermedia Sp. z o. o., ul. A. Ostrowskiego 13, Wroclaw Lower Silesian Oncology Center, Department of Nuclear Medicine - PET-CT Laboratory, Wroclaw	Poland	Spatial distance weighted fuzzy C-Means (SDWFCM)
	G. Żurek			(Guo et al., 2015)
	P. Giedziun			Convolutional neural network (CNN)
	J. Żebrowski W. Dyrka			(Duchi et al., 2011; Krizhevsky et al., 2012)
				Dictionary model (DICT)
				(Dahl and Larsen, 2011)
				Gaussian mixture model (GMM)
				(Aristophanous et al., 2007)
				K-Means (KM) clustering
				(Arthur and Vassilvitskii, 2007)
FLI	B. Laurent	LaTIM, INSERM UMR 1101, Brest	France	Fixed threshold at 40 and 50% of SUVmax FLAB (Hatt et al., 2009, 2010)

3.1. Short description of each method

3.1.1. Methods implemented by challengers

a. Ant colony optimization (ACO)

ACO is a population-based model that mimics the collective foraging behavior of real ant colonies. Artificial ants explore their environment (in the present case the PET volume) in quest for food (the aimed functional volume) and exchange information through iterative update of pheromone quantitative information, which attracts other ants along their path. The food source was initialized in two different ways. The ACO(s) is the static version initializing the food as a r-radii neighborhood Nr(o) around voxels of intensity 70% of the maximum of the SUV. The ACO(d) is the dynamic version of the algorithm relying on the Otsu thresholding (Otsu, 1979) for the initialization to extract a case-specific food comparison value (70% in the case of the static version). Unlike global thresholding, local neighborhood analysis is exploited to enhance the spatial consistency of the final volume. After convergence, a pheromone map is obtained with highest density in the estimated volume. The method was initially developed using 2 classes (Fayad et al., 2015), which was the version entered in the present challenge. The algorithm was applied with its original parametrization without optimization on the training data, which was simply analyzed to verify the algorithm generated expected results.

b. Random forest (RF) on image features

This is a supervised machine learning algorithm using Random Forest (RF). The core idea is to consider the PET segmentation problem as a two-class classification problem, in which each voxel is classified as either the tumor or the background based on image features. The RF is a combination of tree predictors such that each tree depends on the values of a random vector sampled independently and with the same distribution for all trees in the forest (Breiman, 2001). The algorithm follows three steps: feature extraction, training and classification. A total of 30 features were extracted for each voxel from its 27-neighborhood including one 27-dimension gray-level feature (concatenating intensities of its 27-neighborhood), one 27-dimension gradient feature (concatenating the gradient magnitude of its 27-neighborhood) and 28 textural features (the mean and standard deviation of 14 attributes, i.e. Angular Second Moment (Energy), Contrast, Correlation, Variance, Inverse Difference Moment (Homogeneity), Sum Average, Sum Variance, Sum Entropy, Entropy, Difference Variance, Difference Entropy, Information Measure of Correlation I and II, Maximal Correlation Coefficient) (Haralick et al., 1973). The building and training of the RF was performed using the training dataset.

c. Adaptive region growing (ARG)

ARG is an adaptive region-growing algorithm specially designed for tumor segmentation in PET (Tan et al., 2017). Particularly, the ARG repeatedly applies a confidence connected region-growing (CCRG) algorithm with an increasing relaxing factor f. A maximum curvature strategy is used to automatically identify the optimal value for f as the transition point on the f-volume curve, where the volume just grows from the tumor into the surrounding normal tissues. This algorithm was based only on the assumption of a relatively homogeneous background without any assumptions regarding uptake within the tumor, and did not require any phantom calibration or any a priori knowledge. It is also insensitive to changes in the discretization step Δf. In the present challenge, the Δf was set to be 0.001. There was therefore no specific tuning or training using the training dataset.

d. Gradient-aided region-based active contour (GARAC)

The GARAC model is a hybrid level-set 3D deformable model driven by both global region-based forces (Chan and Vese, 2001) and Vector Field Convolution (VFC) edge-based force fields (EBF) (Li and Acton, 2007). The originality of the approach lies in a local and dynamic weighting of the influence of the EBF term according to a blind estimation of its relevance for allowing the model to evolve toward the tumor boundary. Due to their local nature, EBF are more sensitive to noise and are thus not well defined everywhere across the PET image domain. The EBF term is locally weighted proportionally to the degree of collinearity between inner and outer net edge forces in the vicinity of each node of the discretized interface. By doing so, the model takes advantage of both global statistics for increased robustness while making a dynamic use of the more local edge information for increased precision around edges (Jaouen et al., 2014). For all images, the model was initialized as an ellipsoid located at the center of the field of view. The lengths of its semi-principal axes were set to one third of the corresponding image dimension. It was observed on the training data that the method tends to underestimate volumes resulting in high PPV but low SE. A 1-voxel dilatation of the resulting contour was considered but finally not implemented for the challenge.

e. Spatial distance weighted fuzzy C-Means (SDWFCM)

The SDWFCM method is a 3D extension of the spatial fuzzy C-means algorithm (Guo et al., 2015). In contrast to the regular fuzzy C-means, SDWFCM adjusts similarities between each voxel and class centroids by taking into account their spatial distances. The initialization was naive random. Parameters of the algorithm, including number of clusters c=2, degree of fuzzy classification m=2, weight of the spatial features λ=0.5, and size of the spatial neighborhood nb=1 (Guo et al., 2015) were tuned by maximizing the DSC in the training set.

f. Convolutional neural network (CNN)

CNN is a variant of the multilayer perceptron network specialized for image processing and widely used in deep learning (Krizhevsky et al., 2012; LeCun et al., 2015). Informally, CNN classifies an input image based on higher-level features extracted from the input using several layers of convolutional filters. In the current work, the input of the network is a 3D patch from the image. To account for a relatively small number of samples, the training dataset was artificially augmented with rotationally transformed samples. The network was trained using the AdaGrad stochastic gradient descent algorithm (Duchi et al., 2011). The final binary segmentation was reconstructed from binary labels of the overlapping 3D patches using the Otsu thresholding (Otsu, 1979). The best network architecture was selected in the 5-fold cross-validation process maximizing the DSC in the training dataset.

g. Dictionary model (DICT)

The DICT model is a 3D extension of a method for learning discriminative image patches (Dahl and Larsen, 2011). The core of the model is the dictionary of patch-label pairs learned by means of the vector quantization approach. The labeling algorithm assigns each image patch the binarized label of the most similar dictionary patch. In the present implementation, the labeling window walks voxel by voxel, hence the final label of each voxel is the binarized average from all labels overlapping the voxel.

h. Gaussian mixture model (GMM)

The GMM model is a well-established probabilistic generalization of the K-means clustering, which assumes that each class is defined by a Gaussian distribution (Aristophanous et al., 2007). Parameters of the distributions are estimated using the Expectation-Maximization (EM) algorithm. Means of the n=4 distributions were initialized using the K-means algorithm in four tries. Then, the EM procedure updated the distribution means during at most 100 iterations. At the end of the process the single most intense class was labeled as the tumor.

i. K-Means (KM)

The K-means clustering algorithm was implemented with 2 clusters (k=2). The cluster means were initialized using the K-means++ algorithm (Arthur and Vassilvitskii, 2007). Then, the EM procedure was repeated 10 times for at most 100 iterations to find the best fit in terms of inertia (the within-cluster sum-of-squares).

Note: In the SDWFCM, DICT, GMM and KM pipelines, images with sharp intensity peaks were considered grainy. They were pre-processed with the Gaussian filter (except GMM) and post-processed with the binary opening and closing, the approach which was found to maximize DSC in the training set.

3.1.2. Additional methods implemented by FLI engineers for comparison

a. Fixed threshold at 40% and 50% of the maximum

Simple binary thresholds of intensities at respectively 40% or 50% of the single maximum value in the tumor. SUV_max was chosen over SUV_peak as the use of SUV_max is still more widely used in the literature and clinical practice.

b. Fuzzy locally adaptive Bayesian (FLAB)

FLAB relies on a combination of Bayesian-based statistical segmentation and a fuzzy measure to take into account both the spatial blur and noise characteristics of PET images when classifying a voxel in a given class (e.g. tumor and background). The algorithm relies on a fuzzy C-means initialization followed by an iterative estimation of the parameters of each class (mean and standard deviation of the Gaussian distribution of each class and fuzzy transition, as well as local spatial correlation between neighboring voxels). FLAB was initially published as a 2-class version (Hatt et al., 2009) and then expanded to 3 classes for highly heterogeneous lesions (Hatt et al., 2010). Most of previous studies relied on the user for the choice of 2 or 3 classes. In the present work, an automated detection of the number of classes was implemented so it could be run without user intervention, as the other methods implemented as pipelines. The algorithm was applied with the original parametrization (Hatt et al., 2010) without re-optimization using the training data.

Results

The quantitative results are presented with raw data (all points) over box-and-whisker plots that provide values for minimum and maximum, median, 75 and 25 percentiles, as well as outside values (below or above lower/upper quartile ± 1.5 × interquartile range) and far out values (below or above lower/upper quartile ± 3 × interquartile range) that appear in red in the graphs. Results in the text are provided as “mean±standard deviation (median)”.

We present the results according to accuracy score (figure 2), SE (figure 3) and PPV (figure 4). The results by image category are provided for each metric in figures 2b, 3b and 4b. Figure 5 shows the results of the two consensuses with respect to the best method. Figure 6 shows visual examples.

Figure 2:

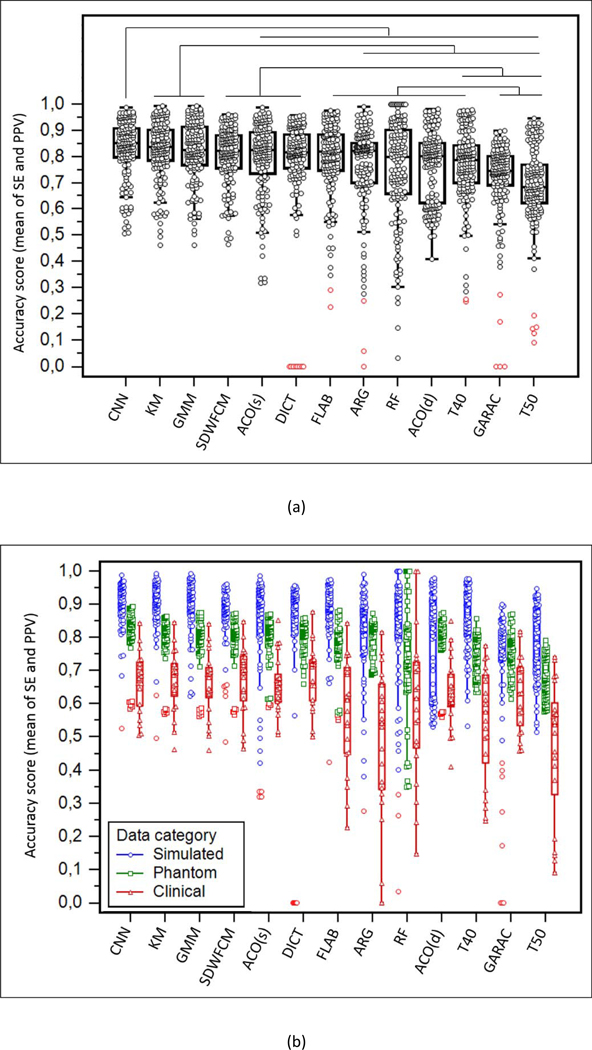
Ranking of the 13 methods according to score=0.5×SE+0.5×PPV for (a) the entire dataset and (b) by data category. The methods are ranked from highest to lowest performance from left to right according to the Kruskal-Wallis test result. Lines on top of (a) show the statistically significant superiority (p<0.01).

Figure 3:

Ranking of the 13 methods according to SE for (a) the entire dataset and (b) by data category. The methods are ranked from highest to lowest performance from left to right according to the Kruskal-Wallis test result. Lines on top of (a) show the statistically significant superiority (p<0.01).

Figure 4:

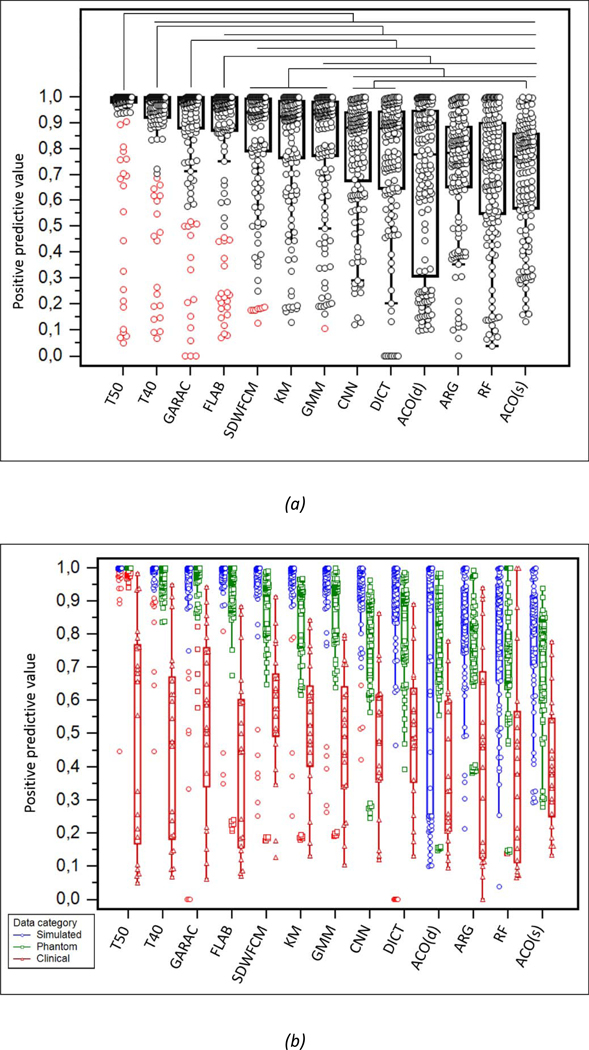
Ranking of the 13 methods according to PPV for (a) the entire dataset and (b) by data category. The methods are ranked from highest to lowest performance from left to right according to the Kruskal-Wallis test result. Lines on top of (a) show the statistically significant superiority (p<0.01).

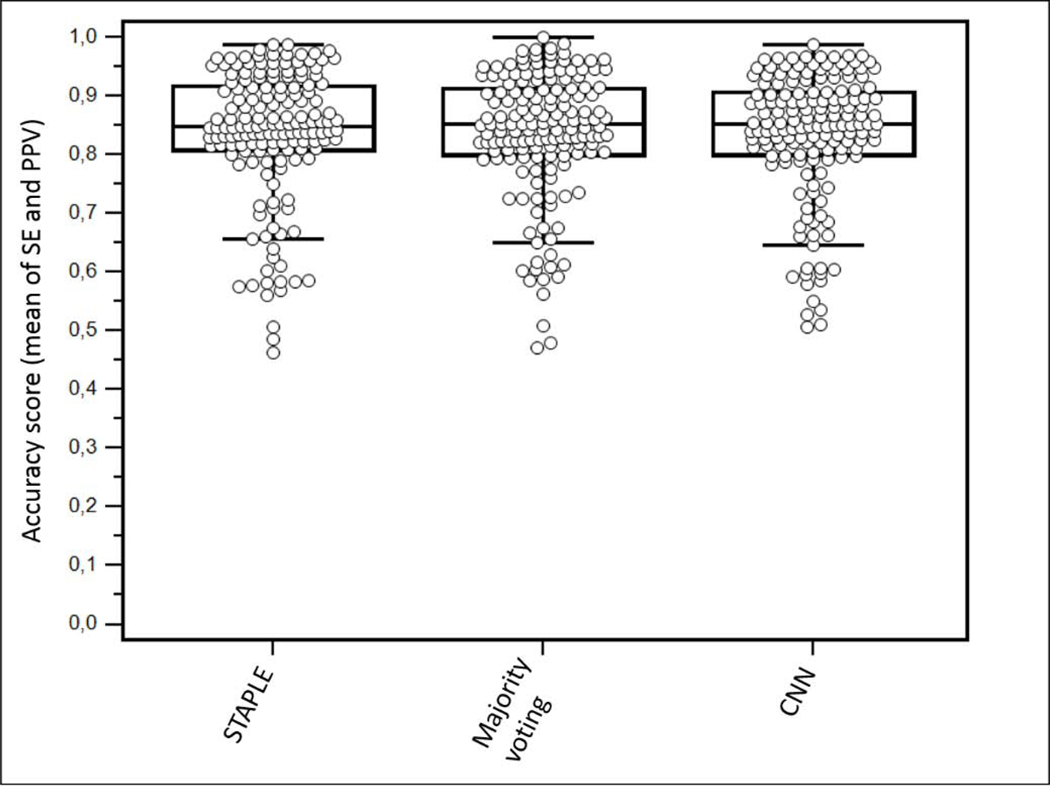
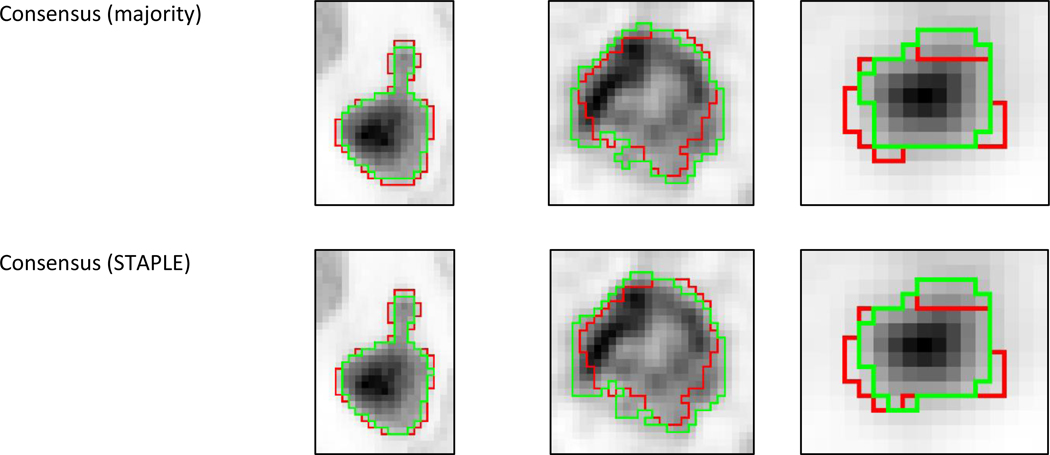
Figure 5:

Comparison of the consensuses using majority voting and STAPLE, with the best method (CNN). The results are ranked from highest to lowest performance from left to right according to the Kruskal-Wallis test result.

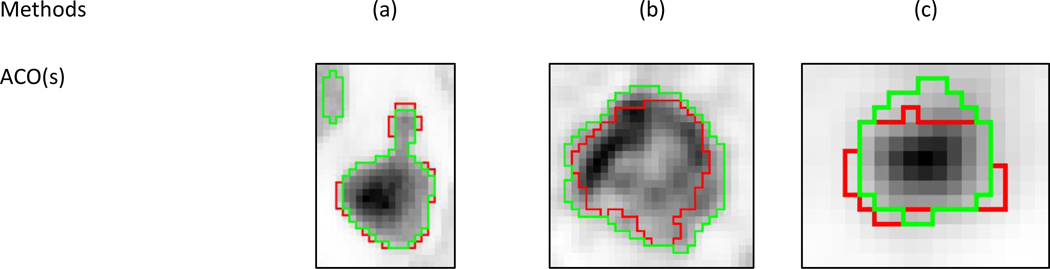
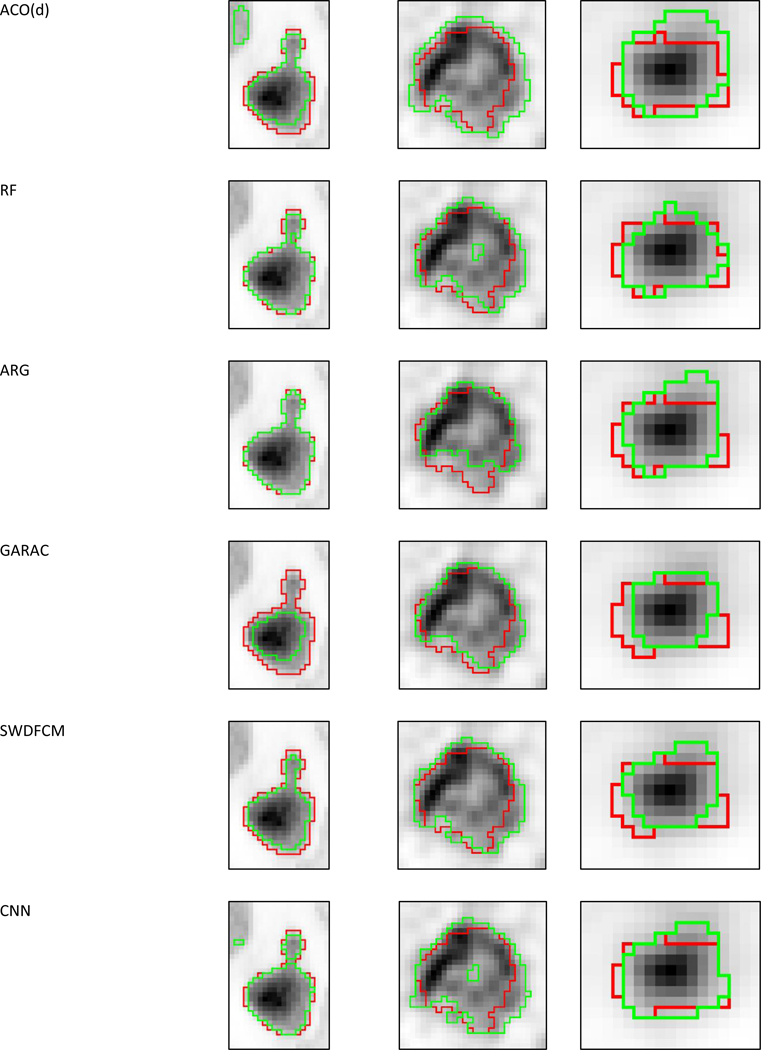
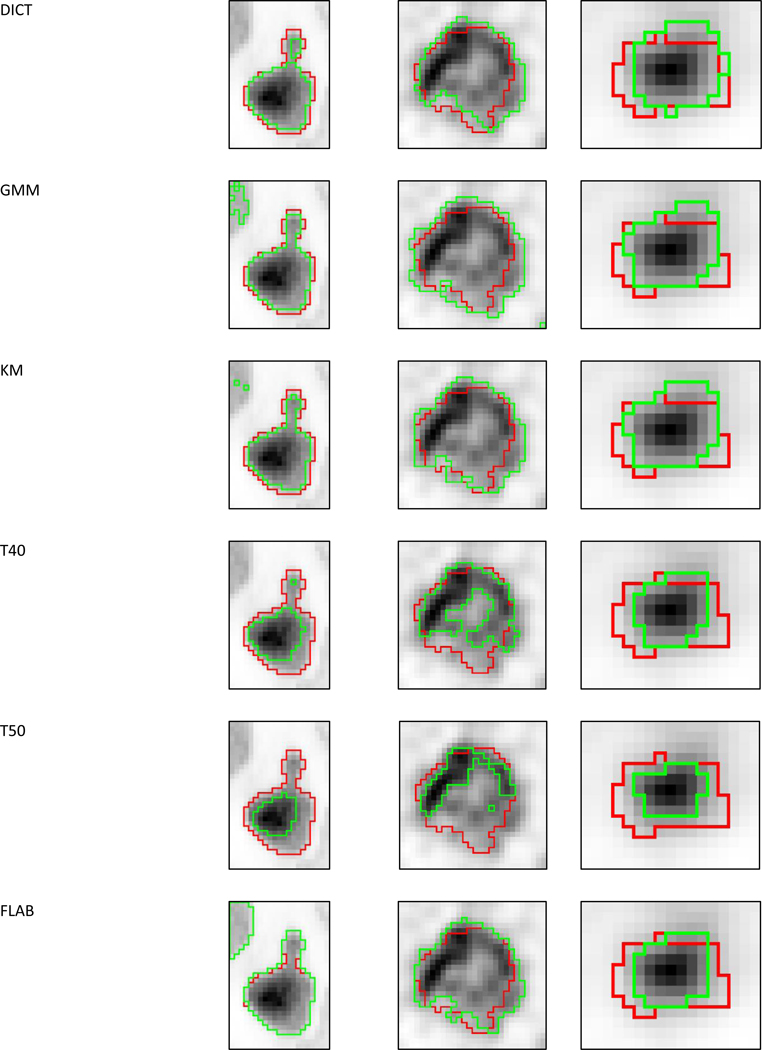
Figure 6:

Visual examples of segmentation (green contours) results from all methods and the two consensuses on cases with (a) high (simulated), (b) intermediate (clinical) and (c) low (phantom) disagreement. The red contours correspond to the ground-truth.

Table A1 in the appendix contains statistics for all the metrics including Dice and Jaccard coefficients, CMD, Score_RT and Score_FU.

Ranking according to accuracy score, SE and PPV

Table 5 shows the ranking of the 13 methods according to SE, PPV and accuracy score.

Table 5:

Ranking of the 13 methods according to SE, PPV, and accuracy score.

Methods	Ranking
	SE	PPV	Score
CNN	2	8	1
KM	8	6	2
GMM	7	7	3
SDWFCM	9	5	4
DICT	6	9	5
ACO(s)	1	13	6
FLAB	10	4	7
ARG	4	11	8
RF	5	12	9
ACO(d)	3	10	10
T40	11	2	11
GARAC	12	3	12
T50	13	1	13

According to accuracy score, CNN was ranked first, and had a significantly higher score than the nine methods ranked 5^th to 13^th. KM, GMM and SWDFCM had slightly lower scores than CNN, but the difference was not significant. Both significantly outperformed ARG, RF, ACO(d), GARAC and the thresholds, but not SDWFCM, ACO(s), DICT and FLAB. The first four best methods had no accuracy result below 0.45 in the entire testing dataset and provided consistent accuracy, whereas most of the other methods were penalized by low accuracy for several cases and exhibited much larger spread. Regarding the MICCAI challenge, the methods implemented by team 4 trusted the first four places. Team 1 came second with ACO(s), followed by team 2 with ARG and RF and team 3 was last with GARAC that performed better than T50 but not T40.

As shown in figures 3 and 4, the low accuracy of GARAC and thresholds is explained by a high PPV at the expense of a low SE. The most accurate methods reached a better compromise between both metrics. Except thresholds in the first two places, the method with the highest PPV was GARAC (significantly higher than all methods below except FLAB, ranked 4^th). SWDFCM, KM and GMM were ranked 6^th, 7^th and 8^th with significantly higher PPV than the other methods ranked below. ACO (both versions), RF and ARG came last in terms of PPV. The ranking according to SE was almost exactly the opposite of PPV, with thresholds and GARAC having the lowest values, whereas ACO(s) and CNN ranked 1^st and 2^nd, with statistically higher performance than the 10 methods below. FLAB and SWDFCM were in 12^th and 11^th position, with statistically lower SE than all methods above, but significantly higher than GARAC and the thresholds.

Interestingly, the outliers and cases for which each method provided the lowest accuracy in each data category were almost never the same, highlighting different behaviors of the methods in their failures, and hinting at the potential interest of a consensus approach. Some methods also completely failed in some cases, which was mostly due to unexpected configurations compared to the training data, leading to failed initialization and/or empty (or filled) segmentation maps, leading to 100% specificity and 0% sensitivity (or vice-versa).

Consensus

The majority voting consensus was just above the best method with a score of 0.835±0.109 (0.853) vs. 0.834±0.109 (0.852) for CNN. The statistical consensus using STAPLE (Warfield et al., 2004) led to an accuracy of 0.834±0.114 (0.848), with a slightly better ranking according to Kruskal-Wallis test compared to majority voting, thanks to a larger standard deviation despite slightly smaller median and mean values. However, both differences were small and not statistically significant (p>0.9).

Ranking of methods by data category

As shown in figure 2b, the methods reached the highest accuracy on the simulated images (despite some outliers with very low accuracy in some instances), whereas lower performance was observed on phantom images (although with a smaller spread due to the smaller range of size and shapes included) and even lower performance on clinical images, with the largest spread. For example, CNN accuracy in simulated, phantom and clinical images was 0.901±0.074 (0.921), 0.818±0.076 (0.835) and 0.665±0.091 (0.678) respectively, with significant differences between the three (p<0.0001). Similar observations (p≤0.0007 between simulated and phantom, p<0.0001 for clinical with respect to both phantom and simulated) were made for all methods except two (ACO(d) and GARAC) for which the differences in accuracy between simulated and phantom images were not significant. ACO(d) had accuracy 0.781±0.156 (0.843) on simulated and 0.791±0.075 (0.806) on phantom (p=0.13). GARAC similarly exhibited levels of accuracy that were not significantly different between simulated and phantom datasets (0.710±0.206 (0.775) vs. 0.750±0.059 (0.756), p=0.19). In both cases however, the level of accuracy achieved in clinical images (0.633±0.104 (0.628) for ACO(d) and 0.633±0.111 (0.632) for GARAC) was significantly lower (p≤0.0008) than in both simulated and phantom datasets.

The hierarchy between the methods observed on the entire dataset remained the same whatever category of images was considered, although on clinical images the differences were less striking because of the larger variability of accuracy. Although some methods exhibited similar (ACO(s) and DICT) or even better (GARAC and ACO(d)) sensitivity for clinical images than on phantom and simulated ones, all methods exhibited low PPV on clinical images.

The disagreement amongst the methods was quantified with the standard deviation (SD) of the accuracy score. Across the entire dataset this SD was 0.098±0.066 (0.075) and again varied strongly between simulated, phantom and clinical images: it was the highest and with the largest spread for simulated images (0.123±0.080 (0.097)), whereas for phantom images the disagreement was the lowest and also much tighter (0.069±0.022, (0.066)). For clinical images it was intermediate but with a larger spread (0.108±0.074, (0.102)). Figure 5 shows representative examples of segmentation results with low, intermediate and high disagreement between methods that correspond to phantom, clinical and simulated cases respectively.

Ranking of methods according to other performance metrics

The hierarchy amongst methods was not strongly altered when considering Dice and Jaccard coefficients or CMD (see appendix table A1 for statistics). According to accuracy score with alternative weights (score_RT and score_FU for emphasis on SE or PPV respectively), the hierarchy between the methods remained the same although the differences between methods were either increased or reduced, methods with high PPV being favored according to score_FU whereas those with high SE were favored according to score_RT.

Qualitative visual comparison

Runtime

The pipelines were not optimized for fast execution since it was not an evaluation criterion for the challenge. In order to accurately measure execution times, a benchmark in controlled conditions after the end of the challenge was conducted: a server with 1 Intel Xeon E5-2630L v4 processor (1.8GHz, 10 cores, 2 threads per core) and 64GB of RAM was dedicated to the benchmark. All pipelines were executed on all images of the testing dataset. Pipelines were executed sequentially to ensure no interference or overlap between executions. Execution time, CPU utilization and peak memory consumption were measured using Linux command “/bin/time”. Tables A2, A3 and A4 in the appendix show the corresponding statistics. The average execution time by image across all pipelines was 18.9s. However, the execution time across images varied substantially as shown by the min and max values. On average, KM was the fastest method and ARG was the slowest. Memory consumption remained reasonable, although RF used more than 2 GB of RAM. ACO, on the contrary, used only 4MB. CPU utilization shows that some pipelines were able to exploit multiple CPU cores. Overall, all pipelines can run on a state-of-the-art computer.

Discussion

This challenge was the first to address the PET segmentation paradigm using a large dataset consisting of a total of 168 images including simulated, phantom and clinical images with rigorous associated ground-truth, following an evaluation protocol designed according to recent recommendations by the TG211 (Berthon et al., 2017; Hatt et al., 2017a). Despite the small number of challengers, several observations can be derived from the results.

All the methods under comparison but three performed quite well (median accuracy scores above 0.8) given the size, heterogeneity and complexity of the testing dataset. GARAC, T40 and T50 were the only methods with median accuracy scores below 0.8 (0.747, 0.786 and 0.685 respectively). This relatively poorer performance was explained by very high PPV at the expense of low SE. Although some methods were clearly superior to others, overall all methods implemented by challengers provided satisfactory segmentation in most cases, which is encouraging regarding their potential transfer to clinical use. One particularly important point is that the disagreement between the methods was high for simulated images, but lower for clinical images. For phantom cases that are mostly small homogeneous uptakes, the agreement amongst methods was the highest, as could be expected. Our results highlight the limited performance of fixed thresholds. We hope it will contribute in convincing clinicians and researchers to stop using them and rely instead on more sophisticated methods already available in clinical practice, such as gradient-based contours and adaptive thresholding approaches. Amongst the best methods in the present comparative study, some are quite complex to implement (e.g. CNN), but for others (e.g. GMM or KM with associated pre- and post-processing steps) the implementation is quite straightforward. These could be made rapidly available to the clinical community to favourably replace basic thresholds currently still widely used in clinical workstations. Nonetheless, the variable level of accuracy across cases observed for all methods including the best ones, suggests that expert supervision and guidance is still necessary in a clinical context (Hatt et al., 2017a). The present results cannot be used to directly discuss a clinical impact of the differences between accuracy levels achieved by the methods, as this would require a “level III analysis”, i.e. with metrics that evaluate the clinical relevance of the disagreement between segmentation and ground-truth, such as the dosimetry impact in radiotherapy planning (Berthon et al., 2017).

It is important to emphasize that the methods accuracy was seen to decrease along with the reliability of ground truth (and as the realism increased), with overall better performance on simulated images, compared to phantom acquisitions, and clinical images. This can be related with the relatively higher realism and complexity of shapes and heterogeneity of clinical images, and the small size of zeolites in the phantom images, compared to simulated cases. At the same time the relatively lower reliability of the associated ground-truth (or surrogate of truth in the case of clinical images) information for phantom and clinical images compared to simulated ones surely also played a role in this trend. In particular, the surrogate of truth from the histopathology in some of the clinical images appears clearly to be off with respect to the actual voxels grey-levels distribution (see for example in figure 6 where the contour does not seem to accurately cover the uptake of the tumor especially at the borders), and it is thus not fair to expect an automatic algorithm to reach a high accuracy in such cases. The definition of the ground-truth for simulated and clinical cases with manual delineation excluded areas with uptake similar as (or lower than) the background uptake. Thus for the few cases with necrotic cores or areas with low uptake, methods that were able to exclude such areas were at an advantage. Note that the training dataset contained such a case, so challengers had the opportunity to take this into account. The dataset nonetheless allowed to highlight statistically significant differences between most of the methods. The resulting hierarchy did not strongly depend on either the metrics used, on the alternative weights for sensitivity and positive predictive values, or on the category of images (although the differences were less pronounced for clinical data).

Some of the best performing methods were not necessarily the most complex ones, as SWDFCM, GMM and KM can be considered older and less complex than CNN, RF, FLAB or ACO. However these were not the “standard” versions of the algorithms, as additional pre- and post-processing steps (filtering before segmentation and morphological opening/closing operations after segmentation) were implemented and parameters were optimized on the training dataset, which was representative of the testing data. According to training data, the methods that benefited the most from these additional steps were KM and GMM that lack spatial consistency modeling. Similar improvements could be applied to the more sophisticated methods. For example, GARAC with a simple 1-voxel expansion in all directions led to significantly improved accuracy scores of 0.765±0.192 (0.811), vs. 0.717±0.152 (0.747) (p<0.0001). This simple post-processing step would allow the method to rank in 8^th position (just below FLAB) instead of 12^th. Ideally, a more explicit modelling of partial volume effects in the method’s functions could lead to similar or even better improvement. Similarly, it was observed that the CNN segmentation results sometimes presented holes or irregular contours, owing to its lack of explicit spatial consistency constraints, however this occurred in a small number of cases and closing these holes had no statistically significant impact on its score.

The various methods under comparison often provide different segmentation results for a given case (figure 6). Therefore the approaches combining various different segmentation paradigms, either through consensus (McGurk et al., 2013) or by learning automatically to choose the most appropriate method on a case-by-case basis such as in the ATLAAS (automatic decision tree-based learning algorithm for advanced image segmentation) method (Berthon et al., 2016), appear as promising developments for the future. In order to provide insights regarding the potential of the consensus approach, we generated a consensus using majority voting and STAPLE. Both were ranked just above the best method and STAPLE was slightly better than majority voting, in line with previous observations (Dewalle-Vignion et al., 2015). However, the differences were not significant, highlighting the fact that although complementary, the best methods may already be close to the accuracy limits for the present dataset, which can also be related to the limited reliability of the ground-truth in some cases, especially the clinical data with histopathology surrogate of truth. It would also be interesting in the future to investigate if the use of the alternative approach (ATLAAS) could improve the results over a simple consensus. We determined that if an algorithm similar to ATLAAS could perfectly select the best method amongst the 13 in each case, this would lead to an accuracy of 0.885±0.096 (0.894), significantly higher than CNN alone or both consensuses (p<0.0001).

We would like to emphasize that only a small subset of existing methods for PET segmentation (Foster et al., 2014; Hatt et al., 2017a) have been evaluated and our results do not presume about the potential performance of other, recently developed approaches. We can only regret that so few challengers confirmed their initial registration to the challenge, and we hope that in the near future the benchmark developed by the TG211, which will contain the same dataset as the present challenge, but also additional data, will provide the means for a more comprehensive evaluation and comparison with other methods. Although the present challenge was organized with the help of the TG211, the future benchmark will likely not be organized as a challenge, but rather as a tool provided to the community to facilitate development, evaluation and comparison of segmentation methods. This benchmark is expected to continuously evolve with the contributions of the community (new methods, data and/or evaluation metrics). Nonetheless its development will benefit from lessons learned in this challenge.

The present challenge was the first to allow for running the methods on a platform without the possibility for the challengers to tamper with the results or optimize parameters on case-by-case basis, thereby ensuring a high reliability of the comparison results and conclusions. It was also guaranteed that the challengers’ pipelines would be run without modifications, due to their execution in Docker containers in a remote platform, allowing for a most rigorous comparative study. This obviously penalized methods that may benefit from user-intervention, such as FLAB for the choice of the number of classes that had to be automatized for the present implementation. ACO on the other hand was implemented with 2 classes only which may have hindered its performance on the most heterogeneous cases. Other methods could also benefit from user-guidance, especially regarding initialization of parameters and exclusion of non-tumor uptakes in the background. However, this would also introduce some user-dependency and thus potentially reduce reproducibility.

The present challenge had some limitations. Algorithms had to be implemented as non-interactive, automatic pipelines, which is much more time-consuming than simply downloading data for processing them in-house. This discouraged several challengers who had initially registered. It is also possible that some teams renounced participation in the challenge after observing poor performance of their methods on the training set. As a result, only 13 methods were included in the present comparative study. This is less than the previous comparative study that included 30 methods (Shepherd et al., 2012). However, this previous comparison was carried out on only 7 volumes from 2 images of a phantom with cold walls glass inserts and 2 clinical images. In addition, the 30 methods actually consisted mostly of variants of distinct algorithm types, including for example 13 variants of thresholding.

We could not include adaptive thresholds that usually provide more reliable segmentation than fixed thresholds because they require optimization for each specific configuration of scanner model, reconstruction algorithm, reconstruction parameters and acquisition protocol, which was not possible here given the high heterogeneity of the evaluation dataset. The future developments of the benchmark by the TG211 will provide new opportunities to carry out further comprehensive comparisons of existing methods, on an even larger training/testing database.

Although we focused on the combination of PPV and SE to evaluate accuracy, other quantitative metrics were calculated and are provided in the appendix for completeness, although they did not lead to important changes in the ranking. Alternative metrics (Shepherd et al., 2012) or alternative combinations of the available metrics could be further explored in future attempts to even better discriminate methods.

The present comparative analysis was also limited to accuracy evaluation, as we did not include evaluation of robustness and repeatability. In order to investigate these two criteria rigorously, numerous acquisitions of the same object with varying levels of noise, different scanner models and reconstruction algorithms are needed (Berthon et al., 2017; Hatt et al., 2017a). Although data exist that could form the basis of such benchmark, it is still insufficient at the moment to carry out a rigorous and comprehensive comparison like the one performed here for accuracy. For instance, the 66 images of zeolites used in the present analysis are 6 different acquisitions of the same 11 zeolites. We included all 66 images in order to increase the testing samples without specifically exploiting them to evaluate robustness. Similarly, this was a single phantom acquired in a single scanner, and other types of phantom acquired in several scanners models could thus provide additional data for a more complete evaluation. Regarding repeatability, although we do not have specific results for analysis and this would require an additional study, the pipelines were all run several times each on the online platform for practical reasons, as well as to measure runtimes, and no significant differences in performance were measured from one run to the next.

Finally, all algorithms were run without any user intervention on images that were pre-cropped, containing the tumor only. In most cases, the PET segmentation algorithms assume that such a pre-selection of the tumor to segment in the whole-body image has been performed by an expert as a pre-processing step, and this usually involves graphical interface and user intervention for tumor detection and isolation in a 3D region of interest. The present challenge did not address the issue of determining this ROI (automatically or manually), or the impact of the variability of its determination on the segmentation end results, which remains very important for clinical implementation and usability of the methods (Hatt et al., 2017a). Some of the methods performance could be enhanced by additional user intervention in defining the initial VOI, for instance to exclude nearby non-tumor uptake that can end up as part of the final segmented volume (see examples in figure 6).

Conclusions

The MICCAI 2016 PET challenge provided an opportunity to carry out the most rigorous comparative study of recently developed PET segmentation algorithms to date on the largest dataset (19 images in training and 157 in testing) so far. The hierarchy amongst the methods in terms of accuracy did not depend strongly on the subset of datasets or the metrics (or combination of metrics) used to quantify the methods accuracy. All the methods submitted by the challengers but one demonstrated good accuracy (median accuracy above 0.8). The CNN-based method won the challenge by achieving a sensitivity of 0.88±0.09 (0.90) and a positive predictive value of 0.79±0.22 (0.88). We hope the present report will encourage more teams to participate in future comparisons which will rely on the benchmark currently developed by the TG211 to better understand the advantages and drawbacks of the various PET segmentation strategies available to date. Such standardization is a necessary step to tackle more successfully the difficult problem of segmenting PET images.

Highlights.

A comparative study of 13 PET segmentation methods was carried out within a MICCAI challenge.

The evaluation methodology followed guidelines recently published by the AAPM task group 211. Accuracy was evaluated on a testing dataset of 157 simulated, phantom and clinical PET images. Most of the advanced algorithms performed well and significantly better than thresholds.

A method based on convolutional neural networks won the challenge.

Vitae

Mathieu Hatt is an INSERM junior research associate and is based within the LaTIM UMR 1101 where he is in charge of research activities dedicated to multimodal image analysis and processing, radiomics and machine learning for oncology applications. He received his Master degree in computer sciences from the University of Strasbourg in 2004, his PhD and habilitation to supervise research degrees from the University of Brest in 2008 and 2012 respectively.

Baptiste Laurent is a FLI-IAM engineer at INSERM. He received his Engineer degree from ISEN, Brest, and his “Signal and Image for Biology and Medicine” Master degree from UBO, Brest in 2013. He is based within the LaTIM UMR 1101.

Hadi Fayad is an associate professor with the University of Western Britanny. He is based within the LaTIM UMR 1101 and is on charge of research activities dealing especially with motion management in radiotherapy and in multi-modality imaging such as PET/CT and PET/MR. Hadi Fayad is in charge of the SIBM (Signal and Image in Biology and Medicine) master and is responsible for the computer and internet certificate at the faculty of Medicine of the UBO. He obtained an engineering degree in computer communication (2006), a master degree in computer science (2007), and a PhD in medical image processing (2011).

Shan Tan is a professor with the School of Automation, Huazhong University of Science and Technology, China. His research interests include biomedical image reconstruction and analysis, pattern recognition, and inverse problem in image processing. He obtained his PhD degree in pattern recognition and intelligent system from Xidian University in 2007.

Laquan Li is a Ph.D student at the School of Automation, Huazhong University of Science and Technology, China. Her research interests include medical image processing and analysis, and variational method for inverse problem. She obtained her Bachelor degree in mathematics in 2011.

Wei Lu is an associate attending physicist in the Department of Medical Physics, Memorial Sloan Kettering Cancer Center, US. His research interests include PET/CT for cancer diagnosis and response evaluation, image guided radiation therapy (IGRT), 4D-CT for tumor motion compensation, and medical image analysis. He received his PhD in biological engineering from the University of Missouri in 2003.

Vincent Jaouen is a post-doc fellow with the University of Western Britanny. He is based within the LaTIM UMR 1101 where he conducts his research activity on the development of new medical image processing techniques. His current research interests are in segmentation and filtering approaches for PET and Ultrasound modalities. He received his Master degree in applied physics from the University of Rennes 1 in 2012, and his PhD degree from the University of Tours in 2016.

Clovis Tauber is an associate professor with the Université François Rabelais in Tours, France. He is in charge of the Vector-valued image processing project in the Inserm Imaging and Brain UMRS U930. His research interests include the development of medical image filtering, segmentation and quantification approaches to process PET, MRI and ultrasound images. He received his PhD degree from the Institut National Polytechnique of Toulouse in 2005.

Jakub Czakon was a data scientist at Stermedia Sp. z o.o. in Wroclaw, Poland where he worked on various data-scientific projects such as facial recognition, cancer detection and classification, and text mining of labor market data. He holds a Master’s degree in theoretical physics (University of Silesia, 2009) and the international master title in chess. Currently, he is a Data Scientist at deepsense.io in Warsaw, Poland.

Filip Drapejkowski is a deep learning engineer at Stermedia Sp. z o.o. and Cancer Center Sp. z o.o. in Wroclaw, Poland. He holds a Master’s degree in computer science (Wroclaw University of Science and Technology, 2017) He is a founder of medical.ml, a students’ research club focused on machine learning for medical applications.

Witold Dyrka is a research assistant professor in the Department of Biomedical Engineering, Faculty of Fundamental Problems of Technology, Wroclaw University of Science and Technology, Poland, and a co-founder of Cancer Center Sp z o.o. He was a Scientist at Stermedia Sp. z o.o. within the Support Programme of the Partnership between Higher Education and Science and Business Activity Sector of City of Wroclaw. His research interests focus on bioinformatics and development of intelligent computational methods for this domain. He holds Master’s degrees in computer science (Wroclaw University of Technology, 2005), biomedical engineering (2006) and bioinformatics (Kingston University, 2007), and a PhD degree in biocybernetics and biomedical engineering from the Polish Academy of Sciences (2012).

Sorina Camarasu-Pop is a CNRS research engineer at the CREATIS laboratory in Lyon, France. She received her Engineering degree in Telecommunications in 2007 and her Ph.D degree (on exploiting heterogeneous distributed systems for Monte-Carlo simulations in the medical field) in 2013, both from the National Institute for Applied Sciences of Lyon (INSA-Lyon, France). She is currently in charge of the Virtual Imaging Platform. Her activity is focused on optimizing the execution of medical image processing applications on heterogeneous distributed systems.

Frédéric Cervenansky obtained a PhD on brain’s autoregulation from the University of Clermont-Ferrand, France in 2002. He worked for 7 years on different commercial software in medical image processing: for Philips Medical System on their new nuclear platform, for Segami on renal and pulmonary protocols, and for Medasys on epilepsy problems. He joined CREATIS in 2009 to integrate Virtual Physiological-Human Network of Excellence (VPH-NOE) Imaging Tools subgroup as an expert on medical imaging data and medical imaging processing. He is involved in several national projects: the Virtual Imaging Platform (VIP), the national infrastructure France Life Imaging (in the Information Analysis and Management node) and the OFSEP cohort for example, and also in international challenges (technical and scientific board). Since 2016, he is responsible for the informatic and developments department and the medical databases management at CREATIS.

Pascal Girard is a CNRS computer engineer at the CREATIS laboratory in Lyon, France. He received his Engineering degree in software development in 2009, after being a medical doctor (1999). He worked on several IT projects, mainly medical and scientific IT projects. He currently works for the national France Life Imaging (FLI) infrastructure on the Virtual Imaging Platform (VIP), which is a web platform for the processing and simulation of medical images. His activity is focused on VIP IT developments, computer maintenance, pipeline import in VIP and user support.

Michael Kain is an INRIA software engineer, based within VisAGeS UMR 1228. He received his Master of Computer Science from the University of Ulm, Germany (2006). Since 09/2013 he is the technical manager of the French research infrastructure project FLI-IAM. His main activities are project management, web based software architectures, embedded in the environment of medical imaging storage and analysis.

Yao Yao is a FLI-IAM engineer at INRIA in Rennes, France. She received her Engineering degree in Telecommunications in 2010 from TELECOM Bretagne. She is now based within the VisAGeS UMR 1228.

Christian Barillot got his Ph.D. thesis from the University of Rennes 1 on “Information Processing” in 1984 and his “Habilitation” thesis on Computer Sciences in 1999. From 1986, he was a research associate at the Signals and Images in Medicine Laboratory (University of Rennes 1). In 1986, he was appointed by the CNRS. In 1987, 1988 and again partially in 1991, he was a research fellow at Mayo Clinic (Rochester, MN) in the Biomedical Imaging Resources. Between 1988 and 1996 he worked for the SIM Laboratory and the INSERM U335 unit (University of Rennes I). In 2003, he was a visiting professor at the Robarts Research Institute (University of Western Ontario, Canada). In 1996, he joined IRISA, collaborating first with the VISTA Team. Since 2004, he is the scientific leader of the VisAGeS research unit, and since 2010 he is the director of the Neurinfo imaging platform. Between 2007 and 2010, he was appointed by French National Agency for Scientific Evaluation as a scientific delegate for the supervision of research units evaluation in life sciences. Since 2011, he is member of the scientific committee of the CNRS Institute for Information Sciences and Technologies, and the chairman since 2015.

Assen Kirov is an associate attending physicist at Memorial Sloan-Kettering Cancer Center and chair of AAPM Task Group No. 211. He completed his PhD in Nuclear Physics at Sofia University “St. Kliment Ohridsky” in 1993 based on research performed at Washington University in Saint Louis, Moscow State University and the Joint Institute for Nuclear Research in Dubna. Before joining MSKCC he was a post-doctoral fellow instructor of radiology and research assistant professoir at Mallinckrodt Institute of Radiology at Washington University and assistant professor at Case Western Reserve University in Cleveland.

Dimitris Visvikis is a director of research with the INSERM in France. He is based within the LaTIM UMR 1101, where he is in charge of a group on quantitative multi-modality imaging for diagnosis and therapy in oncology. He obtained his PhD degree from the University of London in 1996. After that he has worked as a Senior Research Fellow in the Wolfson Brain Imaging Centre of the University of Cambridge and spent five years as a principal physicist in the Institute of Nuclear Medicine in University College London.

Appendix

Table A1:

Statistics for SE, PPV, score, score_RT, score_FU, Dice and Jaccard coefficients and CMD.

Methods	Teams	Sensitivity			Positive predictive value			Score			ScoreRT			ScoreFU			Dice			Jaccard			Contour mean distance (mm)
		Mean	SD	Median	Mean	SD	Median	Mean	SD	Median	Mean	SD	Median	Mean	SD	Median	Mean	SD	Median	Mean	SD	Median	Mean	SD	Median
ACO (static)	1	0.887	0.152	0.934	0.698	0.222	0.769	0.792	0.141	0.825	0.811	0.134	0.837	0.773	0.152	0.822	0.754	0.185	0.822	0.637	0.214	0.698	2.20	2.27	1.32
ACO (dynamic)		0.860	0.139	0.907	0.670	0.316	0.779	0.765	0.131	0.803	0.784	0.104	0.809	0.746	0.164	0.797	0.681	0.237	0.781	0.561	0.251	0.640	3.22	3.93	1.63
RF	2	0.806	0.189	0.869	0.695	0.262	0.756	0.750	0.196	0.800	0.761	0.189	0.806	0.739	0.205	0.781	0.720	0.234	0.783	0.608	0.259	0.643	3.20	3.27	2.10
ARG		0.804	0.230	0.886	0.722	0.233	0.784	0.763	0.167	0.823	0.772	0.169	0.829	0.755	0.170	0.807	0.721	0.208	0.802	0.598	0.216	0.670	3.63	4.21	2.26
GARAC	3	0.556	0.202	0.563	0.877	0.232	0.988	0.717	0.152	0.747	0.685	0.151	0.712	0.749	0.159	0.796	0.641	0.193	0.691	0.497	0.179	0.527	2.56	1.95	1.95
SWDFCM	4	0.777	0.124	0.776	0.838	0.229	0.941	0.807	0.107	0.823	0.801	0.093	0.812	0.813	0.126	0.843	0.773	0.156	0.806	0.652	0.179	0.675	1.70	1.53	1.31
CNN		0.881	0.091	0.903	0.787	0.215	0.882	0.834	0.109	0.852	0.844	0.093	0.851	0.825	0.128	0.858	0.807	0.158	0.847	0.702	0.189	0.734	1.89	2.20	1.03
DICT		0.793	0.227	0.861	0.763	0.258	0.878	0.778	0.202	0.818	0.781	0.200	0.827	0.775	0.207	0.826	0.752	0.217	0.806	0.638	0.215	0.675	2.23	2.68	1.36
GMM		0.816	0.132	0.852	0.821	0.239	0.936	0.818	0.114	0.826	0.818	0.100	0.816	0.819	0.134	0.845	0.782	0.170	0.810	0.669	0.201	0.681	1.81	1.78	1.29
KM		0.819	0.113	0.821	0.828	0.228	0.926	0.823	0.111	0.837	0.822	0.095	0.829	0.824	0.130	0.848	0.793	0.161	0.823	0.682	0.190	0.700	1.65	1.66	1.18
T40	Reference	0.634	0.204	0.635	0.898	0.214	0.994	0.766	0.140	0.786	0.740	0.142	0.753	0.793	0.145	0.812	0.705	0.189	0.745	0.575	0.214	0.594	2.12	2.15	1.58
T50		0.458	0.219	0.414	0.925	0.209	1.000	0.691	0.154	0.685	0.645	0.158	0.623	0.738	0.156	0.745	0.572	0.214	0.555	0.433	0.219	0.384	2.81	2.54	2.45
FLAB		0.738	0.146	0.768	0.848	0.258	0.965	0.793	0.139	0.819	0.782	0.126	0.794	0.804	0.158	0.835	0.751	0.188	0.793	0.632	0.209	0.657	1.87	1.87	1.33
Majority voting	Consensus	0.852	0.112	0.885	0.818	0.211	0.905	0.835	0.109	0.853	0.839	0.096	0.851	0.832	0.125	0.856	0.810	0.152	0.839	0.704	0.185	0.723	1.67	1.89	1.11
STAPLE		0.889	0.087	0.913	0.782	0.228	0.865	0.834	0.114	0.848	0.846	0.096	0.857	0.825	0.134	0.847	0.805	0.171	0.839	0.701	0.201	0.723	1.64	1.77	1.14

Table A2:

pipeline CPU usage per image. Values above 100 % indicate that the pipeline used multiple computing cores.

Pipeline (method)	CPU usage (%)
	Average	Min	Max
RF	83	81	87
GARAC	98	74	135
DICT	99	97	99
ACO	99	99	99
ARG	100	84	104
KM	119	95	317
GMM	264	149	672
SWDFCM	312	111	511
CNN	515	291	847

Table A3:

pipeline execution time per image.

Pipeline (method)	Execution time (seconds)
	Average	Min	Max
KM	2.1	1.8	3.3
GMM	2.5	1.9	5.4
SWDFCM	7.7	2.4	53.7
ACO	8.6	0.9	83.9
RF	10.5	9.3	13.6
DICT	12.6	3.6	110.2
GARAC	15.7	7.0	159.5
CNN	25.5	16.6	78.5
ARG	84.9	14.4	699.4

Table A4:

pipeline peak RAM use per image.

Pipeline (method)	Peak RAM usage (Mbytes)
	Average	Min	Max
ACO	4.5	4.1	8.7
GMM	102.3	99.9	114.9
KM	103.1	101.4	126.4
SWDFCM	104.1	101.9	114.0
CNN	128.7	127.0	139.2
DICT	152.5	152.3	152.9
GARAC	169.4	160.9	177.9
ARG	220.3	211.1	251.9
RF	2 280.0	1 430.8	3 159.8