Advancing statistical analysis of ambulatory assessment data in the study of addictive behavior: A primer on three person-oriented techniques

Abstract

Ambulatory assessment (AA) methodologies have the potential to increase understanding and treatment of addictive behavior in seemingly unprecedented ways, due in part, to their emphasis on intensive repeated assessments of an individual's addictive behavior in context. But, many analytic techniques traditionally applied to AA data - techniques that average across people and time - do not fully leverage this potential. In an effort to take advantage of the individualized, temporal nature of AA data on addictive behavior, the current paper considers three underutilized person-oriented analytic techniques: multilevel modeling, p-technique, and group iterative multiple model estimation. After reviewing prevailing analytic techniques, each person-oriented technique is presented, AA data specifications are mentioned, an example analysis using generated data is provided, and advantages and limitations are discussed; the paper closes with a brief comparison across techniques. Increasing use of person-oriented techniques will substantially enhance inferences that can be drawn from AA data on addictive behavior and has implications for the development of individualized interventions.

1. Introduction

The naturalistic, time intensive nature of data collected via ambulatory assessment (AA) uniquely facilitates studying the complexity of addictive behavior. By repeatedly measuring moment-to-moment addictive behaviors in the physical and psychological contexts in which they occur, AA data capture an individual's patterns of use, symptoms, and potential treatment targets. Unfortunately, a large proportion of the empirical work utilizing AA data reduces their richness by collapsing across people and time. To support the growing popularity of more sophisticated statistical analyses being applied to AA data, we present three underutilized analytic techniques ideal for exploiting the individualized, temporal nature of AA data on addictive behavior: multilevel modeling (MLM), p-technique, and group iterative multiple model estimation (GIMME). Application of these techniques will help identify the mechanisms subserving addictive behavior and offer ways to better utilize AA data in clinical addiction treatment settings.

AA methodologies span assessment types (e.g., self-report, behavioral observation, and biological/physiological measurement) and time intervals to ecologically capture addictive behavior in real time. Generally, an event- or interval-based approach is employed wherein, for example, participants report addictive behavior alongside co-occurring factors (e.g., affect, stress, peers) via portable device. Additional methods include physiological monitoring (e.g., via fitbit) during everyday activity and regular diaries. The frequency of assessment varies widely. Some studies utilize a daily approach (Shapiro, Jamner, Davydov, & James, 2002; Shiffman et al., 2002), while others cue responses many times a day (Delfino, Jamner, & Whalen, 2001), and still others utilize continuous recordings (Weinstock, Farney, Elrod, Henderson, & Weiss, 2017).

Through these strategies, AA methodologies largely circumvent the pitfalls of retrospective or dispositional report (Solhan, Trull, Jahng, & Wood, 2009) that are reliant on accurate recall of distal events and mental aggregation of experiences (e.g., “how much do you feel [a target emotion] on average?”). Minimizing the time interval between a behavior and its report is also known to reduce “digit bias” (i.e., inappropriate rounding) on counts of addictive behaviors (Shiffman, 2009). Additionally, new technologies (e.g., smartphone or actigraphy) have dramatically improved the logistics of collecting AA data while also increasing compliance and sampling rates. Clearly, AA methods are an increasingly critical complement to traditional research methods in the social and medical sciences.

2. Prevailing analytic techniques for AA data

Two key strengths of AA methods – the repeated assessments and the person-oriented nature of the data – can be leveraged by currently available, but underemployed, analytic techniques to advance the content and quality of insights into addictive behavior. Below, we first discuss analytic techniques typically applied to AA data, review their strengths and limitations, and then propose three additional techniques with undeniable advantages for AA-related research and eventual clinical translation.

Historically, AA data have often been analyzed by pooling (via means or sums) data across time or selecting specific data points (single values or time windows in relation to an event) to model differences between periods in which addictive behaviors did and did not occur. For instance, to test the hypothesis that negative mood predicts alcohol use, researchers have tracked both negative affect and use via AA throughout periods where affect undergoes frequent shifts but no use event occurs (e.g., throughout a week day). Often, negative affect data is subsequently pooled or focused temporally to estimate its influence on use events that occur proximally (e.g., later that day; Epstein et al., 2009) or distally (e.g., the following weekend; Hussong, Hicks, Levy, & Curran, 2001).

Sometimes collapsing or narrowing assessments across time is reasonable; combining repeated assessments of the same construct increases reliability and minimizes measurement error relative to a single cross-sectional assessment (Hamdi & Iacono, 2014). For instance, large scale, between-person data reduction approaches (e.g., factor analyses) that combine items into meaningful subscales have facilitated understanding of the role of negative affect in substance use (Shiffman & Waters, 2004). But, this approach works best for modeling phenomena with no variation over time (Birkhoff, 1931; Molenaar, 2004). This is rarely the case for AA data as many effects are transient (e.g., mood). Moreover, aggregating or narrowing information across time may eliminate or occlude meaningful temporal variation.

Similarly, collapsing assessments across people is a reasonable way to increase reliability and reduce error, but between-person results require people to be homogenous (Birkhoff, 1931; Molenaar, 2004). In most research using AA methods, however, analyses average across heterogeneous people, yielding results that may not apply to even a single individual. In some AA research, attempts are made to account for heterogeneity by comparing effects between groups (e.g., negative affect effects on smoking in those with and without PTSD; Beckham et al., 2008). Even though this work accounts for addictive behavior variation, it presupposes within-group homogeneity.

For heterogeneous samples or subsamples (which is often the case in addiction etiology, phenomenology, and treatment outcomes; Vrieze, Iacono, & McGue, 2012; Wong & Schumann, 2008), traditional between-person techniques are also limited in their ability to test hypotheses about what effects are consistently present for all individuals with addictive behavior problems (Beltz, Wright, Sprague, & Molenaar, 2016). This is evident in clinical settings where a treatment effect detected in a cross-sectional group has uncertain effects for individuals presenting for care. Not surprisingly, treatment effects are modest and individuals experience wide variation in treatment outcomes, including unacceptable rates of relapse (Cutler & Fishbain, 2005; Moos & Moos, 2006; Piasecki, 2006).

Individualized, intensive longitudinal AA methods – and in particular the applications of the analytic methods discussed below – provide an exceptional opportunity to build upon growing interest in analytic techniques that move beyond averages of AA data (e.g., (Chow, Witkiewitz, Grasman, Hutton, & Maisto, 2014; Treloar, Piasecki, McCarthy, Sher, & Heath, 2015) and with potential to improve the precision of etiological and treatment models of addiction across individuals.

3. Underutilized analytic techniques for AA data

One way to leverage the strengths of AA methods is to apply analysis techniques – such as multilevel modeling, p-technique factor analyses, and GIMME – that utilize all observed data across time and individuals. These person-oriented techniques uniquely allow within-person modeling of addictive behavior. For each technique, we describe mathematics and specific data requirements, followed by an illustrative analysis with interpreted results, and end with a discussion of advantages and disadvantages.

4. Data generation

We generated a data set amenable to all techniques. When using empirical data, it is assumed that all preprocessing (e.g., handling of missing data) has occurred prior to analysis. The generated data represent a 60-day diary study of negative affect (operationalized by 10 items) and the addictive behavior of alcohol use (operationalized by 1 item) for a sample of 25 women and 25 men. Data were generated in Matlab according to a structural vector autoregressive model with linear trends. Each replication (i.e., participant's data set) consisted of 60 observations of 11 variables. The data were generated to reflect sex differences, associations between key variables, and patterns of change over days. Specifically, data were generated for: 1) a group of men (n = 20) with one general negative affect factor inversely associated with alcohol use across days; 2) a group of men (n = 5) and women (n = 20) with two negative affect factors, with one positively associated with alcohol use increasingly over days; and 3) a group of women (n = 5) with three negative affect factors, with one positively associated with alcohol use increasingly over days.

5. Multilevel modeling

Multilevel modeling (MLM) is a parametric approach for modeling continuous outcomes in nested data, such that measurements are repeated within an individual (growth curve model) or across members of naturally occurring groups (e.g., people sharing a family or school). To account for dependencies – which violate independent observation assumptions required for techniques like regression – MLMs adjust the error structure of the data, parceling out random effects (e.g., variance common to an individual over repeated measurements) from fixed effects (i.e., mean-level main effects and interactions). MLM is equipped to characterize trajectories of addictive behavior across time and can estimate whether time-invariant grouping factors (e.g., sex) and timevariant psychological processes (e.g., fluctuations in negative affect) moderate those trajectories. In this case, correlated observations within an individual (i) are first modeled in a Level-1, time-varying (t) equation:

$$\begin{gathered} {\mathbf{OUTCOME}}_{\mathit{ti}}={\pi }_{0\mathit{i}}{\mathbf{INTERCEPT}}_{\mathit{ti}}+{\pi }_{\mathrm{1i}}{\mathbf{TIME}}_{\mathit{ti}}+{\pi }_{\mathrm{2i}}{\mathrm{LEVEL}1}_{\mathit{ti}} \\ {+\pi }_{\mathrm{3i}}{{\mathbf{TIME}}_{\mathit{ti}}}^{\ast }{\mathrm{LEVEL}1}_{\mathit{ti}}+{\epsilon }_{\mathit{ti}} \end{gathered}$$

An individual's score on an outcome measure (e.g., alcohol use) at a given time point is explained by the initial level of the outcome for that individual (i.e., intercept; π_0i), the slope of the outcome over the time series (π_1i), and the slope (π_2i) of their score on a Level-1 (i.e., time-varying) predictor (e.g., negative affect), the Level-1 interaction of time and the time-varying predictor (π_3i), and some within-person error (ε_ti). The Level-1 equation is then added to the specified Level-2, time-invariant equations:

$$\begin{gathered} {\pi }_{0\mathit{i}}={\beta }_{00}\mathbf{INTERCEPT}+{\beta }_{01}{\mathbf{INTERCEPT}}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}}+{\mathbf{r}}_{0i}\mathbf{INTERCEPT} \\ {\pi }_{1\mathit{i}}={\beta }_{10}\mathbf{TIME}+{\beta }_{11}{\mathbf{TIME}}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}}+{\mathbf{r}}_{1\mathit{i}}\mathrm{SLOPE}(\mathrm{TIME}) \\ {\pi }_{2\mathit{i}}={\beta }_{20}\mathrm{LEVEL}1+{\beta }_{21}{\mathrm{LEVEL}1}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}}+{\mathbf{r}}_{2\mathit{i}}\mathrm{SLOPE}(\mathrm{LEVEL}1) \\ {\pi }_{3\mathit{i}}={\beta }_{30}{\mathbf{TIME}}^{\ast }\mathrm{LEVEL}1+{\beta }_{31}{\mathbf{TIME}}^{\ast }{\mathrm{LEVEL}1}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}} \end{gathered}$$

The individual's intercept is a combination of the sample mean for the outcome (i.e., fixed effect for the intercept, β₀₀), time-invariant, fixed effects for a group (e.g., gender, β₀₁), and random effects for between-person variation in the outcome (r_0i). Additional estimates include a fixed slope parameter for time (β₁₀) and the other time-varying predictor (e.g., negative affect; β₁₀). Level-2, time-invariant effects (e.g., gender) are also estimated as predictors of the rate of change in the Level-1 slopes (i.e., cross-level interactions; β₁₁ and β₂₁). While no random term was specified for the interaction between time and the Level-1 parameter in the equation above, such parameters can be included based on hypothesized effects. Random slopes are included to account for between-person variation in rate of change over time (i.e., random slope for time; r_1i) and rate of change in the other time-varying predictor (e.g., random slope for change in negative affect; r_2i). Importantly, inclusion of random effects in MLM affords person-centered adjustment of the model based on inter-individual variation. Together, the equations yield the full random coefficients MLM:

$$\begin{gathered} {\mathbf{OUTCOME}}_{\mathit{ti}}={\beta }_{00}\mathbf{INTERCEPT}+{\beta }_{01}{\mathbf{INTERCEPT}}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}} \\ +{\mathbf{r}}_{0i}\mathbf{INTERCEPT}+{\beta }_{10}\mathbf{TIME}+{\beta }_{11}{\mathbf{TIME}}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}} \\ +{\mathbf{r}}_{1\mathit{i}}\mathrm{SLOPE}(\mathrm{TIME})+{\beta }_{20}\mathrm{LEVEL}1 \\ +{\beta }_{21}{\mathrm{LEVEL}1}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}}+{\mathbf{r}}_{2\mathit{i}}\mathrm{SLOPE}(\mathrm{LEVEL}1) \\ +{\beta }_{30}{\mathbf{TIME}}^{\ast }\mathrm{LEVEL}1+{\beta }_{31}{\mathbf{TIME}}^{\ast }{\mathrm{LEVEL}1}^{\ast }{\mathrm{LEVEL}2}_{\mathit{i}} \\ +{\epsilon }_{\mathit{ti}} \end{gathered}$$

Thus, results of MLMs combine average effects (i.e., fixed effects; analogous to regression results corrected for dependent observations) across people with the degree of individual deviation from that group average by random variation in the levels (i.e., intercepts) and change over time (i.e., slopes) in the outcome.

Through additional specifications of MLMs (not shown here), researchers can model different functional forms and bidirectional relationships. MLMs can estimate non-linear functional forms (e.g., quadratic or cubic relations) across the sample (i.e., fixed effect) with corresponding random effects (i.e., covariance estimates) to identify person-centered variation. Though not within a single model, MLMs can be used to make inferences about the bi-directionality of effects. That is, an initial model regressing Y_t on X_t-1 can be fit in conjunction with a separate model regressing X_t on Y_t-1 to model how each factor earlier in time predicts the other later in time (Duckworth, Tsukayama, & May, 2010). In all MLMs (but especially in the case of novel model specifications), comparisons of relative model fit (i.e., Akaike Information Criterion and change in χ²) can be helpful for determining which parameters should be retained in nested models. As terms are added, model fit should incrementally increase. Additionally multiple computational tools are available for guiding interpretation of MLM interactions (Preacher, Curran, & Bauer, 2006) and extending the multilevel framework to test lagged associations (Preacher, Zyphur, & Zhang, 2010).

5.1. Data specifications

Most statistical software packages support MLM (e.g., most commonly R, HLM, MPlus, SAS, SPSS, STATA). Analyses require a minimum of two observations (three for growth curves) and permit unequal spacing between assessments and different numbers of repeated observations within individuals through full information maximum likelihood. More information on MLMs (also called Linear Mixed Models and Hierarchical Linear Models) is available elsewhere (Bolger & Laurenceau, 2013; Ram & Grimm, 2009; Raudenbush & Bryk, 2002; Singer & Willett, 2003; West, Welch, & Galecki, 2014).

5.2. Illustration of MLM

Generated data were submitted to SPSS to answer the research question: “Does negative affect predict alcohol use differently for men and women over time?” (i.e., a three-way interaction of Day, Affect, and Sex predicting Use). Fixed effects were estimated for time-varying (Level-1) predictors Day and Negative Affect (10-item composite) and the time-invariant (Level-2) effect of Sex. Two- and three-way interactions were also estimated.

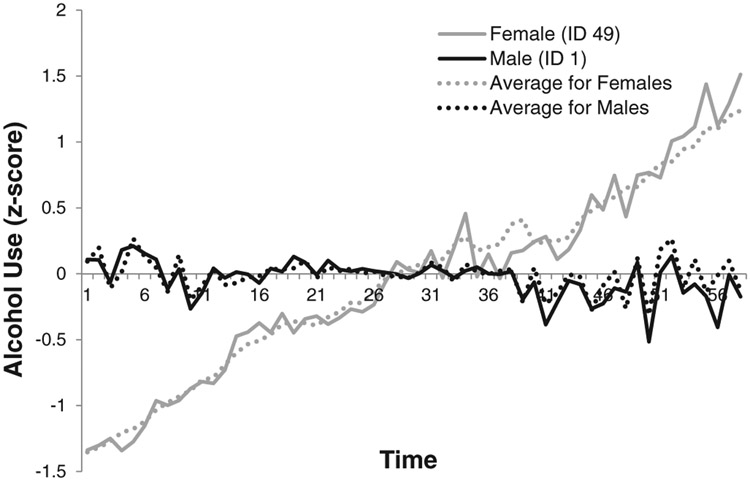
Results are presented in Table 1 and Fig. 1. The three-way interaction between Day, Affect, and Sex (i.e., β₃₁) significantly predicted change in Alcohol Use after adjusting for the significant main effects of each. Specifically, increases in Negative Affect concomitantly increased Alcohol Use over time in women but not in men, irrespective of daily fluctuation in affect. For expository purposes, Fig. 1 presents the model-predicted growth trajectory for average alcohol use in both genders alongside observed values for exemplary male and female participants.

Table 1.

Standardized betas for multilevel model-predicted daily change in alcohol use as a function of negative affect and sex.

Level-1 parameters				Interactions & Level-2 parameters
Intercept (β00)	Day (β10)	Negative affect (β10)		Predicting intercept	Predicting time effect
− 1.01*****	0.34***	0.03***	Female (vs. male)	β01 = 1.08***	β11 = 0.04***
			Negative affect	β20 = 0.07***	β30 = − 0.003***
			Sex × negative affect	β21 = − 0.04*	β31 = 0.003***

Time effect (i.e. “Days”) over 60 days; AIC = 8973.12; BIC = 8997.13.

Model: ALCOHOL_ti = β₀₀INTERCEPT + β₀₁INTERCEPT * SEX_i + r_0iINTERCEPT + β₁₀DAYS + β₁₁DAYS *SEX_i + r_1iSLOPE(DAYS) + β₂₀AFFECT + β₂₁ AFFECT * SEX_i + r_2iSLOPE (AFFECT) + β₃₀DAYS * AFFECT + β₃₁DAYS * AFFECT * SEX_i + ε_ti.

^***p < 0.001.

^**p < 0.01.

^*p < 0.05.

Fig. 1.

Multilevel model predicted change In alcohol use (z-score across Level-1 variance using all Individuals to standardize across male and female drinkers) by average negative affect In each gender. Gray lines depict trajectory of alcohol use given specific values for negative affect for the exemplary female case (solid gray line; ID 49) and on average across females (dotted gray line). Black lines depict trajectory of alcohol use given specific values for negative affect for the exemplary male case (solid black line; ID 1) and on average across males (dotted black line). The high degree of similarity between Individual and average gender trajectories for alcohol use Illustrates that MLM pools Information across Individuals to estimate effects.

5.3. Advantages of MLM

Regarding individuals, MLM takes into account the nested structure of AA data (i.e., repeated observations within individuals) and allows for estimation of both group averages (fixed effects) and individual variation from those averages (random effects). The inclusion of random effects can account for between-person variation in the levels of a factor (e.g., at the intercept) and within-person variation in a factor over time (e.g., in the slope). This is paramount for addiction research, in which there is evidence for heterogeneity in the potency of risks across people (e.g., Foster, Hicks, Iacono, & McGue, 2015).

Regarding time, MLMs implemented as growth curves can identify patterns of linear and non-linear change across occasions and do not force data aggregation or narrowing of the time window. Inclusion of non-linear polynomial effects (e.g., quadratic or cubic) can facilitate answering research questions like “Is fluctuation in negative affect during an alcohol drinking episode related to changes in the rate of consumption?”. Furthermore, between-person heterogeneity can be estimated by leveraging group-level data to derive predictions for the parameters characterizing each individual's trajectory. Other advantages include the ability of MLMs to utilize data from subjects with relatively few observations (e.g., 3 time points), and to accommodate differences in the numbers of observations per person.

5.4. Limitations of MLM

Despite these advantages, MLM has notable restrictions. For instance, MLM does not permit individual-level heterogeneity in the direction of prediction. That is, in one model, effects are estimated in a single direction (i.e., the effect of negative affect on alcohol use) without accounting for reciprocal effects (i.e., negative affect increases alcohol use and alcohol use, in turn, increases negative affect). Additionally, though individual-level estimates can be derived from MLMs, they rely on group-level data and researcher-imposed parameters (i.e., a priori choice to include linear and polynomial functional forms) that may not uniformly apply to all individuals in the sample. Consider, for instance, a data set in which 90% of individuals follow a linear trajectory and the other 10% follow a quadratic trajectory. If only a linear trajectory is modeled (which is likely because the quadratic term may not contribute much to overall model fit), individual-level estimates will be provided for the 10%, but they will not be good reflections of their quadratic data. Individual-level estimates, then, reflect variation in average sample trajectories (e.g., linear, quadratic, logistic), so if an individual qualitatively (vs. quantitatively) differs from others, their uniqueness may go unnoticed. The consequences of this misfit are considerable since treatment outcome models would not distinguish between individuals with progressive improvement (linear effect) from those with a relapsing trajectory (quadratic effect).Finally, item variance between and within people is often treated as noise rather than variability that could inform estimation and interpretation. For instance, negative affect items in a composite may have person-specific or time-varying effects on alcohol use. That is, “sadness” may drive one person's alcohol use, while “anger” is responsible for another's. Analytic techniques that offer a means of testing multivariate effects could facilitate more person-specific questions of AA data.

6. P-technique factor analysis

P-technique is a multivariate approach for analyzing intra-individual variation. Initially introduced by Cattell (1943), it uses intensive longitudinal data (e.g., AA data), from a single individual to identify relations among variables in order to reduce the variables into a smaller set of latent (i.e., unobserved) factors. Counter to traditional factor analysis (r-technique) that results in a latent structure that generalizes across people, p-technique results in a structure that generalizes across time for an individual, as seen in their comparable equations:

R-Technique (standard)	P-technique
yi = Ληi + ςi	y(t) = Λη(t) + ς(t)

Here, y is a zero-centered p-variate matrix of observations across individuals (i), where i = 1, 2, 3, …, N, or time (t), where t = 1, 2, 3, …, T, η is the q-variate latent factor series, whose relation to y is specified in the (p,q)-dimensional matrix of factor loadings Λ, and ς is the p-dimensional vector of measurement errors.

Studying addictive behaviors with p-technique facilitates detection of person-specific heterogeneity that is occluded by standard factor analysis or by techniques for AA data that require pooling. For example, the application of p-technique in the study of personality revealed that the Five Factor model, though well replicated across people, was not detected for even one participant (Borkenau & Ossendorf, 1998; Molenaar & Campbell, 2009). Most participants had fewer than 5 factors. This insight into the heterogeneity of personality was achieved by leveraging AA methods (i.e., 90-day diaries of a personality inventory), and we hypothesize that this parallels yet-to-be uncovered findings for addictive behaviors and related constructs.

6.1. Data specifications

Standard software packages that support r-technique factor analysis can implement variants of p-technique, including R, MPlus, SAS, SPSS, STATA, and LISREL. Separate data sets are used for each participant (repeated assessments in rows and variables in columns). Optimal data come from variables that show variation (e.g., a vector of 1’s cannot covary with other vectors) measured at equally spaced intervals, with the number of necessary assessments depending upon features of the model and data set. Though simulations find robust estimation against lagged effects (e.g., between two measurement occasions; Molenaar & Nesselroade, 2009), the time series is assumed to be stationary – containing no time point-specific relations or trends across the entire time series. Time effects detected across occasions must be accounted for (e.g., through regression and analysis of residuals) prior to running p-technique. More information and details on p-technique are available elsewhere (Jones & Nesselroade, 1990; Russell, Jones, & Miller, 2007; Stephenson, 1936).

6.2. Illustration of p-technique factor analysis

The structural equation modeling software LISREL was used to illustrate p-technique with the generated data sets of one woman and one man (same individuals in Fig. 1) to answer the research question: “What is the nature of the relations between (potentially) different aspects of negative affect and alcohol use for this individual?”. An exploratory approach using Lagrange Multiplier Equivalents tests determined the appropriate number of factors, wherein fit of a one-factor model was followed by fit of two- and three-factor models until two of four fit indices were excellent (see Brown, 2015): root mean squared error of approximation (RMSEA) ≤ 0.05; standardized root mean residual (SRMR) ≤ 0.05; comparative fit index (CFI) ≥ 0.95; non-normed fit index (NNFI) ≥ 0.95. An oblique rotation was conducted and a confirmatory model was fit.

Results are presented in Fig. 2; both models fit well. For the male participant, a one-factor solution including all 11 variables was optimal with each negative affect loading positively and the alcohol use item loading negatively. Therefore, aspects of negative affect (e.g., sadness and anxiety) were indistinguishable, as all affect items related strongly and positively to the latent Internalizing factor. Negative affect is unlikely to coincide with alcohol use for this male, as evidenced by its inverse relationship with the Internalizing factor. For the female participant, a three-factor solution (i.e., Depressed, including alcohol use; Withdrawn, and Anxious) was optimal. The alcohol use item loaded strongly and positively onto the latent Depressed factor. When this female experienced high levels of sadness (but not necessarily when she experienced isolation or nervousness), concurrent alcohol use was likely.

Fig. 2.

Exemplary p-technique factor structure by sex; NA1–10 denote negative affect item indicators; AU1 denotes single alcohol use item indicator; ***p < 0.001, **p < 0.01, *p < 0.05.

6.3. Advantages of p-technique factor analysis

Regarding individuals, p-technique captures intra-individual variation in associations within a multivariate time series, creating a network of indicators for latent factors that characterizes the behavior of each participant. As with prior research in the structure of personality, a standard (i.e., group-level) factor model ignores person-specific variation and answers a population-level research question that occludes potential misfit for individuals. P-technique has particular advantages for addiction research using AA methods. It can use multilevel, multimethod constructs (e.g., alcohol use, symptoms, and craving) to create person-specific profiles of addiction severity. For some people, alcohol use may not be strongly associated with craving, but this unique etiology may go undetected in group-level analysis. Person-specific associations of this type could reduce treatment effectiveness when time is devoted to addressing craving across individuals whose craving operates relatively independently of their heavy use.

Regarding time, p-technique utilizes multiple, consecutive measurement occasions to estimate item associations for a single person. In the study of addictive behavior, one analytic difficulty with AA data is that the focal behavior is characterized by occasional or less frequent use events spaced in between longer periods in which no use event occurs. Thus, individuals differentially contribute to the group averages that characterize a sample. P-technique readily uses multiple measurements within each individual to capture person-specific patterns of use that are not disproportionally weighted by others.

6.4. Limitations of p-technique factor analysis

The traditional p-technique factor model has two clear limitations for answering some hypotheses regarding temporal variation (Lee & Little, 2012). First, both the factor loadings and the effects of one observed item on another are assumed to be stationary or time-invariant, such that the effect of time from one measurement to the next is the same early and late in the time series. Consequently, p-technique is not suitable for determining dynamic associations, or relations that vary across time. In fact, any systematic variation over time, such as the linear trends previously identified in the generated data (see Fig. 1), must be statistically removed prior to conducting analyses. Moreover, p-technique considers only contemporaneous relations among indicators, meaning that lagged effects of one indicator on others (i.e., the extent to which today's negative mood influences tomorrow's alcohol use) go unmodeled (and can lead to spurious results; see Gates, Molenaar, Hillary, Ram, & Rovine, 2010).

7. Group iterative multiple model estimation (GIMME)

GIMME is a multivariate approach for modeling intra-individual temporal covariation in a group-informed network. It identifies multivariate associations prominent for everyone in a sample (i.e., group-level) and person-specific associations (i.e., individual-level). Mathematically, GIMME implements unified structural equation models (uSEMs; Gates et al., 2010; Kim, Zhu, Chang, Bentler, & Ernst, 2007), which are a type of structural vector autoregressive model that estimates both contemporaneous (same measurement occasion) and lagged (e.g., between two consecutive measurement occasions) directed associations between variables by combining structural equation and vector autoregressive models, respectively. For a zero-centered p-variate time series, GIMME is defined as:

$${\eta }_{\mathit{i}}(\mathit{t})=({\mathbf{A}}_{\mathit{i}}+{{\mathbf{A}}_{\mathit{i}}}^{\mathrm{g}}){\eta }_{\mathit{i}}(\mathit{t})+({\Phi }_{1i}+{{\Phi }_{1i}}^{\mathrm{g}}){\eta }_{\mathit{i}}(\mathit{t}-1)+{\zeta }_{\mathit{i}}(\mathit{t})$$

The observed time series, η(t), for an individual (i) is a combination of the pxpA matrix of contemporaneous associations (at the same t) and the pxpΦ matrix of first order lagged associations (at the previous t), with a p-variate vector of errors in ζ (i.e., diagonal covariance matrix without sequential dependencies). GIMME is typically fit via a data-driven procedure in which Lagrange Multiplier Equivalents tests are used to iteratively add associations to the networks of all individuals that are significant for some criterion of the sample (usually 75%), and then to add associations that are significant for each individual (Gates & Molenaar, 2012). All associations (in the A and Φ matrices) are estimated at the individual-level (i.e., have a person-specific β-weight), with some contained in networks for everyone in the group (g) and some only contained in networks of individuals. GIMME originated in neuroimaging literature had has been used to estimate alcohol-related brain networks, but has promise for all types of AA data (Beltz et al., 2013).

7.1. Data specifications

GIMME can be run using an R package by the same name (Lane and Gates, in press; Lane, Gates, Molenaar, Hallquist, & Pike, 2017), but standard SEM software (i.e., the programs listed above for p-technique analyses) can be used to run the person-level uSEMs GIMME implements. Data requirements are similar to p-technique, with unique data input files for each participant, containing 3–20 continuous variables with noteworthy variance measured at equally spaced intervals, and the number of necessary assessments depending upon features of the data and model; stationarity is assumed. GIMME networks are evaluated using alternative model fit indices (Brown, 2014). More information and details on GIMME are available elsewhere (Lane and Gates, in press; Beltz & Gates, in press; Gates et al., 2010).

7.2. Illustration of GIMME

Generated data for all 50 individuals and the GIMME package in R were used to answer the research question: “What behavioral network (i.e., features of negative affect) underlies alcohol use? How common is it across individuals?”. A data-driven implementation of GIMME was used, wherein group-level network connections were first estimated if they significantly contributed to the network for 75% of the sample, and individual-level connections were then added until the network for a single participant fit well.

Results of the group-level structure (black lines) and individual-level networks for exemplary participants are presented in Fig. 3 and Table 2; all networks fit the data well. At the group-level, negative affect (NA1-10) and alcohol use (AU) were associated via two connections. First, AU contemporaneously predicted one aspect of negative affect (NA3), such that use today was associated with elevated negative affect measured by this item (e.g., ashamed) (β_ID49 = 0.95, β_ID1 = − 0.55). Second, another aspect of negative affect (NA4) contemporaneously predicted AU, such that this negative affect item (e.g., upset) was associated with same-day elevation in alcohol use (β_ID49 = 0.75, β_ID1 = − 0.41). All other group-level associations linked individual NA items with one another on the same day or reflected autoregression (lagged prediction of the same variable). These findings are reasonable, respectively reflecting concordance among aspects of negative affect and a persistence of affect and use day-to-day.

Fig. 3.

GIMME group and exemplary individual network model. NA1–10 denotes negative affect item 1–10; AU1 denotes single alcohol use item. Solid and dashed lines denote contemporaneous and lagged effects, respectively; black (significant in at least 75% of individuals in the sample) and gray lines denote group- and individual-level effects, respectively; red and blue lines denote positive and negative effects, respectively. Models for exemplary male (Chi-squared = 157.41, p = 0.16, RMSEA = 0.04, SRMR = 0.08, CFI = 0.96, NNFI = 0.93) and female (Chi-squared = 152.65, p = 0.14, RMSEA = 0.05, SRMR = 0.08, CFI = 0.97, NNFI = 0.95) fit well. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Group and individual parameters for exemplary female and male cases.

Group level parameters
			Exemplary female (ID 49)		Exemplary male (ID 1)
DV		IV	β		β
AU1		AU1t-1	− 0.06		0.26**
AU1		NA4	0.75***		− 0.41***
NA1		NAlt-1	0.29**		0.05
NA1		NA8	− 0.49***		0.51***
NA2		NA10	0.031		0.11
NA2		NA2t-1	0.08		− 0.20*
NA3		AU1	0.95***		− 0.55***
NA3		NA3t-1	0.07		0.02
NA4		NA2	0.55***		0.54***
NA4		NA4t-1	0.28**		0.13
NA5		NA5t-1	0.022		0.00
NA5		NA9	0.091		0.39**
NA6		NA6t-1	0.24**		− 0.16*
NA6		NA8	0.44***		0.20*
NA7		NA7t-1	0.20*		− 0.02
NA8		NA7	0.64***		0.13
NA8		NA8t-1	− 0.05		0.026
NA9		NA6	0.18		0.27*
NA9		NA9t-1	− 0.07		− 0.02
NA10		NA1	− 0.17		0.34***
NA10		NA10t-1	0.07		0.012
Individual level parameters
Exemplary female (ID 49)			Exemplary male (ID 1)
DV	IV	β	DV	IV	β
AU1	NA10	− 0.51***	AU1	NA1	− 0.34***
AU1	NA2	0.47**	AU1	NA7t-1	0.28**
AU1	NA3	− 0.81***	NA2	NA1	0.41***
NA1	NA8t-1	0.21*	NA4	NAlt-1	− 0.26**
NA1	NA9t-1	0.26**	NA5	AU1	− 0.42***
NA2	NA1	0.33**	NA6	NA2	0.34***
NA2	NA4t-1	0.45***	NA6	NA3	0.43***
NA2	NA9t-1	0.29**	NA6	NA7t-1	0.22**
NA3	NA6t-1	0.30**	NA6	NA8t-1	− 0.23**
NA5	NA10	0.31*	NA7	NA2	0.54***
NA5	NA8	0.40***	NA8	NA4	0.43***
NA5	NA9t-1	− 0.22*	NA9	NA2	0.34**
NA6	NA10t-1	− 0.22**	NA9	NA7	0.25*
NA6	AU1t-1	− 0.26**	NA10	NA4	0.42***
NA6	NA4	− 0.30***
NA7	NA10	0.36**
NA7	NA9	0.38**
NA9	NA4	− 0.46***
NA10	NA6	0.24*
NA10	NA9	0.55***

The group level model depicts effects that are significant in at least 75% of individuals in the sample, but that are estimated for all; NA1-10 denotes negative affect items; AU1 denotes single alcohol use item; DV denotes dependent variable; IV denotes independent variable; t-1 subscript identifies predictor earlier in time (i.e., yesterday's NA predicting today's AU); only individual path common to both cases is NA1 predicting NA2.

^***p < 0.001

^**p < 0.01

^*p < 0.05.

Inspection of the exemplary networks reveals different associations between negative affect and alcohol use for these two individuals. For the exemplary male, all associations between alcohol use and negative affect items are negative (in blue), suggesting that higher levels of alcohol use were generally associated with lower levels of same-day negative affect. By contrast, the exemplary female exhibited positive (in red) contemporaneous associations between alcohol use and some of those same affect items (NA3 and NA4), indicating substantial elevation in negative affect on higher alcohol use days. One association – the link between AU and NA6 – was lagged, indicating that alcohol use predicted decreases in one aspect of negative affect the next day, as would be reflective of self-medication. Not surprisingly, other network connections (Table 2) were more uniform across all NA items in the male participant who had one negative affect factor, while negative affect items clustered more in the female participant who had three factors (see p-technique results).

7.3. Advantages of GIMME

Regarding individuals, GIMME models both inter-individual similarity (via group-level connections) and intra-individual variation (via person-specific models with individual-level connections) to permit sample-level inferences while accurately capturing the heterogeneity characteristic of AA data. By modeling heterogeneity directly, GIMME has unprecedented benefit for research in the etiology and treatment of addictive behaviors. Rather than condensing between-person variation into average effects expected to apply uniformly, GIMME prioritizes identification of the degree to which effects (e.g., mechanistic cycles that reinforce addictive behavior) meaningfully describe a sample or just a subset of individuals. Furthermore, unique network features can be leveraged for individualized clinical care (see examples in Beltz et al., 2016). For instance, a randomized controlled trial exploring a treatment for an addictive behavior could use AA data in combination with GIMME to estimate homogeneity of treatment effects and, by extension, heterogeneity in the likelihood of treatment failure, providing insights into personalized medicine.

Regarding time, GIMME utilizes a person-specific approach accounting for contemporaneous and lagged relations among variables. Consequently, it is possible to model the extent to which candidate antecedents – yesterday's negative affect, for example – account for daily variation in addictive behavior and also the extent to which current addictive behavior begets consequences later. Models can even be extended to consider lagged effects spanning measurement occasions (Beltz & Molenaar, 2015). For instance, a lag of 7 would capture weekly effects in a daily diary study examining weekend binge drinking (in a way similar to vector autoregressive models).

7.4. Limitations of GIMME

Despite its substantial advantages, GIMME also has some critical limitations. First, the requirement for equally-spaced measurements limits GIMME's application to some types of AA data, such as those collected via burst designs (although subsampling or binning could be used to generate equally-spaced intervals amenable to GIMME). Second, GIMME assumes stationarity, or that the lagged effect of one factor on the other across days is uniform across time; these are longterm (across all measurements) trends, and not short-term (e.g., day-to-day) cycles estimated by lagged connections. Although data can be statistically detrended prior to GIMME analyses, this assumption may prevent GIMME from capturing dynamic patterns, such as treatment effects or relapse in a single model. Third, GIMME does not model the means of variables. Consequently, research questions aimed at differentiating levels of a factor (e.g., alcohol consumption by gender) may require complementary techniques.

8. Discussion

Person-oriented analysis techniques can provide inimitable insights into how addictive behaviors unfold across people over time and, consequently, offer unparalleled potential for personalizing prevention and intervention. Regarding individuals, both p-technique and GIMME estimate person-specific, multivariate networks while MLM considers individual heterogeneity with respect to group effects. P-technique is particularly useful for determining whether a mean-level finding holds at the individual-level, while MLM facilitates group-level inferences. GIMME combines the benefits of both techniques (unlike MLM, it estimates group effects through common features rather than averages).

Regarding time, both MLM and GIMME explicitly estimate crossassessment temporal effects. Whereas GIMME considers lagged, measurement-to-measurement variation (e.g., day-to-day), MLM examines the pattern of variation across all measurements (e.g., span of two months). Though p-technique is comparatively limited in the estimation of time, in that it estimates contemporaneous covariation, dynamic modeling extensions are available (see Lee & Little, 2012).

Despite the apparent draw of person-oriented techniques for basic and applied investigations in addictive behavior, some points of emphasis are warranted. First, person-oriented techniques are not necessarily superior to the prevailing, group-level analysis techniques for AA data; the best technique is always one that matches the research question. Person-oriented techniques help to address different types of questions, especially those concerning heterogeneity in addictive behavior patterns, along with their antecedents and consequences. Evidence of heterogeneity (e.g., in etiology) across cases can then complement nomothetic, group-level inferences (e.g., in the threshold for clinically-relevant alcohol use) to broadly classify clinical vulnerability or to identify a potential intervention, which could then be individualized through the incorporation of idiographic data and analyses (Schneider & Stone, 2016). Second, researchers must carefully select an analysis technique based not only on their question, but also on the realities of their data (e.g., spacing and number of assessments and levels). For instance, a one-week burst design with 20 measurements would probably not be well-suited to p-technique or GIMME, but would be a candidate for MLM, and a diary study of use carry-over effects in 30 adults would be ideal for GIMME. Third, the techniques presented here are generally for inferential analyses; data-specific preprocessing, including missing data imputation and time trend detection, may be necessary.

Beyond the three techniques presented, others are also available to uniquely enhance understanding of addictive behaviors through AA data. For example, latent transition models show how individuals change patterns (e.g., of substance use) over time (Collins & Lanza, 2010; Muthen & Muthen, 2000). Dynamic factor models extend p-technique to lagged data (Browne & Zhang, 2007, 2010; Molenaar, 1985; Wood & Brown, 1994). Vector autoregressive models permit inferences about temporal ordering (Granger, 1969; Lütkepohl, 2005). Multilevel structural equation models parse within- and between-person variance in estimation of multivariate associations like mediation (Preacher et al., 2010). State space and Markov models for regime shifting can be used for multi-level and dynamic data, including studies of relapse (e.g., Chow et al., 2014; Chow, Hamaker, Fujita, & Boker, 2009).

When thoughtfully implemented, person-oriented analysis techniques maximize the inferences that can be drawn from AA data. They handle inter- and intra-individual heterogeneity directly to characterize addiction etiology (i.e., nomothetic knowledge of multifarious causes) and - one day - will improve the precision of addiction treatment (i.e., idiographic knowledge of particular cases).

HIGHLIGHTS.

• Ambulatory assessment (AA) data are often collapsed across people and time.

• Person-oriented analysis is rare, but ideal for capturing heterogeneity in AA data.

• Multilevel modeling estimates individual deviation from group effects over time.

• P-technique examines the person-specific covariation (factor) structure of AA data.

• Iterative multiple model estimation creates individual-level temporal networks.