Emergency decision support modeling for COVID‐19 based on spherical fuzzy information

Abstract

Significant emergency measures should be taken until an emergency event occurs. It is understood that the emergency is characterized by limited time and information, harmfulness and uncertainty, and decision‐makers are always critically bound by uncertainty and risk. This paper introduces many novel approaches to addressing the emergency situation of COVID‐19 under spherical fuzzy environment. Fundamentally, the paper includes six main sections to achieve appropriate and accurate measures to address the situation of emergency decision‐making. As the spherical fuzzy set (FS) is a generalized framework of fuzzy structure to handle more uncertainty and ambiguity in decision‐making problems (DMPs). First, we discuss basic algebraic operational laws (AOLs) under spherical FS. In addition, elaborate on the deficiency of existing AOLs and present three cases to address the validity of the proposed novel AOLs under spherical fuzzy settings. Second, we present a list of Einstein aggregation operators (AgOp) based on the Einstein norm to aggregate uncertain information in DMPs. Thirdly, we are introducing two techniques to demonstrate the unknown weight of the criteria. Fourthly, we develop extended TOPSIS and Gray relational analysis approaches based on AgOp with unknown weight information of the criteria. In fifth, we design three algorithms to address the uncertainty and ambiguity information in emergency DMPs. Finally, the numerical case study of the novel carnivorous (COVID‐19) situation is provided as an application for emergency decision‐making based on the proposed three algorithms. Results explore the effectiveness of our proposed methodologies and provide accurate emergency measures to address the global uncertainty of COVID‐19.

1. INTRODUCTION

Throughout the 21st century, along with the accelerated cycle of economic globalization and integration, human beings face numerous challenges, such as the terrorist attacks of September 11, 2001 in the United States, March 24–28, 2004 Catalina hurricane tropical cyclone the South Atlantic Ocean, October 8, 2005 Kashmir earthquake in Pakistan, May 12, 2008 Sichuan earthquake in China, and now December 2019 novel coronavirus (COVID‐19) in Wuhan, China, could cause serious economic damage, risk people's living standards and lead to social disorder.

Since December 2019, in Wuhan, China, there have been several unidentified cases of pneumonia with cough, dyspnea, exhaustion, and fever as the major symptoms reported in a short time. ¹ The Chinese health officials and CDC immediately identified the pathogen of these cases as a new form of coronavirus which was called COVID‐19 by the World Health Organization (WHO) on January 10, 2020. ² The Chinese government's information department held a press conference on pneumonia prevention and control of new coronavirus infections on January 22, 2020. The same day, a strategy for the prevention and control of pneumonitis of new coronavirus infection was announced by the People's Republic of China, along with COVID‐19 epidemic research, sample collection and testing, monitoring and management of close contacts, and public propaganda, education and risk communication. ³

Usually, the virus infects during close touch and through respiratory droplets emitted when people sneeze or cough. Respiratory droplets can arise during respiration but the virus is not assumed to be airborne. This can also be transmitted if you touch an infected surface, and then your face. It is most infectious when people are symptomatic, but it may be possible to transmit them before start showing symptoms. Usually, the time among exposure and appearance of symptoms is about 5 days but can extend from 2 to 14 days. Fever, cough, and chest tightness are symptoms of depression. Pneumonia and acute respiratory distress syndrome may also be symptoms. There is still no proven vaccine or antiviral treatment available. Symptomatic and supportive therapy is primary care. Recommended protective measures include hand washing, covering the mouth when coughing, keeping distance from other people, and monitoring and self‐isolation of people suspected of being infected. The transmission of COVID‐19 and various interventions also had an unprecedented negative effect on the routine lives of people and the healthy functioning of society. Cities around the world have declared varying rates of closures and restrictions on traffic.

However, there are several upcoming concerns about COVID‐19 spread outbreak. Tomorrow how many people would get infected? When will the inflection point of the infection rate appear? How many individuals during the peak time will get infected? Could current treatments, technologies control COVID‐19 successfully? What mathematical models can help us to understand these concerns?

Many researchers contribute to prevent and control the emergency situation of COVID‐19. Yang and Wang ⁴ propose the mathematical model to show the outbreak of COVID‐19. Toğaçar et al., ⁵ presented the deducting method of COVID‐19 using fuzzy color and stacking approaches. Tuite et al., ⁶ propose the COVID‐19 transmission and mitigation strategies based mathematical model among Canada's population, Ciufolini and Paolozzi ⁷ presented the Gauss error function based Mathematical prediction model of COVID‐19 outbreak in Italy. Sohail and Nutini ⁸ introduced the novel mathematical model of forecasting the timeframe of COVID‐19. Khan and Atangana ⁹ propose the fractional derivative‐based dynamics mathematical model for COVID‐19.

The COVID‐19 is a novel coronavirus which was identified in December 2019, so data on the epidemic is still inadequate, and medical technologies such as clinical trials are still in a critical phase of exploration. Until now, disease data have been hard to apply directly to current mathematical models, and questions need to be answered about how successful the ongoing emergency response is and whether health care services can be spent more scientifically in the future, and so forth. In the case of an emergency, decision‐makers, or disaster response departments should implement strategies or select an appropriate emergency strategy to avoid further escalation of the crisis. It is a matter for the evolving strategy sector to take rapid and effective decisions. Emergency decision‐making as an integral part of the disaster response has been a significant task for many governments and a subject of discussion in academic circles. Under this scenario, when making decisions, people are usually bound logical rather than completely reasonable. It is therefore important to establish decision‐making approaches that understand human actions to provide people with efficient means of responding to emergency situations.

Tackling ambiguous and uncertain data in real‐life situations has always been a difficulty. Several approaches have been explored to address the complexity and ambiguity found in real‐life processes, such as the theory of fuzzy set (FS). The implementation of FS ¹⁰ has been widely used in several uncertain circumstances, like networking, decision taking, clustering, pattern recognition and many other similar artificial intelligence studies. FS operated with occurrences by defining them with values in [0,1] as membership grade. Through using this type of mathematical framework, the researcher can numerically analyze the uncertainty of an event that only allows us to convey the degree of involvement in an event that is the degree of satisfaction but does not give us any information of the degree of dissatisfaction. To address this issue, the concept of intuitionistic FS introduced ¹¹ that describes the positive and negative membership functions of an event on the [0,1], given the sum of these grades is ≤1. Intuitionistic FS has been used in many real‐life applications. ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ Due to the limited constraints in intuitionistic FS, the Pythagorean FS has been introduced ¹⁷ by utilizing intuitionistic FS, in which the positive and negative membership functions squares sum should be ≤1. In other words, all the intuitionistic FS are the subsets of Pythagorean FS, which have more powerful ¹⁸ , ¹⁹ , ²⁰ , ²¹ solving abilities in uncertain problems in real‐life applications.

Intuitionistic FS and Pythagorean FS theories have been effectively applied in various field, but still there are numerous circumstances that cannot be presented by these theories in real‐world, for example, casting a vote, we may face human judgment including more answers of a sort: yes, no, abstain and refuse. For example, in the election station, the chambers issue 600 voting papers for the applicants. The voting outcomes are distributed into four categories to gather with the number of papers that are vote in favor (276), abstain (124), vote in against (145), and refuse to vote (55). Here, abstain means the voting paper is blank, nobody gives the vote in favor and against yet at the same time takes the vote, group of refusal of the vote means if a person did not cast the vote. The candidate is viewed as effective in light of the fact the quantity of supportive papers is larger than the vote in against. Such sort of models (in which the number of abstain is a key role and the group of “refusal of vote” in reality exists) occurred and FS, intuitionistic FS, and Pythagorean FS could not deal it. In this way picture, FS ²² is presented to enhanced the structure of Pythagorean FS. For more study, we refer to References [23, 24, 25, 26, 27].

But, with the constant complexity of human knowledge modeling and theory development, picture FS will be invalid in some decision‐making problems (DMPs). Recently, to address this, the spherical FSs ²⁸ , ²⁹ initially established, have proved to be an effective way for determining ambiguity more impressively than the existing FS frameworks. The information is represented in the spherical FS with three membership grades, $\rho ,\daleth$, and $\tilde{n}$, whose sum of the squares of the membership grades is atmost 1, that is, ${\rho }^2+{\daleth }^2+{\tilde{n}}^2\le 1$. Spherical FS is acknowledged to become more general than traditional FS frameworks. Come up with an example to illustrate the notion of spherical FS, which consists of an expert giving priority relating to attribute values with positive, neutral, and negative grades 0.7, 0.5, and 0.5, so obviously $0.7+0.5+0.5=1.7>1$ and So picture FS cannot handle this kind of information, but we do have spherical FS 0.7² + 0.5²+ 0.5²= 1.7 > 1 and so spherical FS can handle such situation very effectively. The notion of spherical FS extend to present the novel aggregation operators ³⁰ (AgOp) using algebraic norm‐based operational laws (OLs) for spherical FS. These AgOp are generalized to established Dombi norm‐based list of Dombi AgOp ³¹ and explore their applicability in DMPs. To engage the logarithm function, Jin et al. ³² proposed logarithmic OLs based logarithmic AgOp and also link the spherical fuzzy information to linguistic present linguistic AgOp ³³ and discussed the applicability in DMPs. List of decision‐making techniques are established to contribute to spherical FS like cosine similarity measure ³⁴ are discussed to tackle the uncertain information in DMPs. To find out the distance measure between the spherical FSs ³⁵ and proposed their representation to spherical fuzzy norm ³⁶ are explore and implemented to determine the uncertain information in real‐life DMPs. TOPSIS under spherical fuzzy rough set ³⁷ are establish successfully to deal DMPs. Spherical fuzzy symmetric sum based AgOp ³⁸ is proposed to deal with real‐life DMPs more effectively.

Decision‐making for people and organizations, is one of the most critical activities and it an interdisciplinary research area that involves psychologists, economists, mathematicians, computer scientists from nearly all fields. Multiple attribute decision making (MADM) has achieved great reputation as an interesting research division of decision‐making theory. There are actually two categories of methodology involved with continuous and discrete decision making issues, respectively. And those are methodologies of decision‐making with multiple objective (MO) and multiple attribute (MA). The range of alternatives in MODM problems is infinite, and the trade‐offs between design requirements are usually characterized by continuous functions. MADM problems only provide for the determination of the “best” alternative by recognizing trade‐offs within a set of attractive design parameters. MADM leads to determining between possible actions in the presence of several typically conflicting attributes. Emergency decision making is one of the important and crucial branch of the decision‐making theory. Under this scenario, to understand human actions to provide people with efficient means of responding to emergency situations.

The main objective of this study is to establish emergency decision making with the help of FS theory. To solve the environmental, economic, and social issues, we will develop the new tool to describe the actually information and based on the proposed tool, we construct the emergency decision support system for environmental problem of COVID‐19. We will apply the emergency decision support model of COVD‐19 in this emergency situation. The main objective of this study is to develop the emergency decision support system for environmental and economic issue of COVD‐19 under spherical fuzzy information. This study has following contributions:

• (1)Discuss the deficiency of existing operational laws of spherical FS and propose novel operational laws using Algebraic t‐norm and t‐conorm.
• (2)Discussed the novel operational laws using Einstein t‐norm and t‐conorm using spherical fuzzy environment.
• (3)Introduced the list of aggregation operators based on the Einstein operational laws to aggregate the uncertainty in decision making problems.
• (4)Establish two techniques (1) analytical hierarchy process and (2) spherical fuzzy entropy measure to determine the unknown weight information of the considered attributes.
• (5)Technique for order preference by similarity to ideal solution (TOPSIS) and grey relational analysis (GRA) methods are introduce to tackle the uncertainty in emergency decision‐making problems under spherical fuzzy information.
• (6)We design three different algorithm to tackle emergency decision‐making problems.
• (7)We shall collect the exact data disaster during the COVD‐19 and then construct the mathematical model of emergency decision support systems for COVD‐19 under the generalized structure of spherical FSs and compare our proposed three techniques with existing techniques to shows the validity and effectiveness of the proposed techniques.

To achieve the list of goals the structure of the paper is arranged as follows: Section 2 presented the rudiments of different structures of FSs and also explore the deficiency of the existing operational laws of spherical FS. Novel operational laws of spherical FS and their important properties are established in Section 3. Sections 4 and 5 introduced the list novel spherical fuzzy Einstein aggregation operators based on Einstein operational laws. Section 6 presented the two crucial techniques to determined the weight vector of the attributes. The main contribution of this study is three algorithms to tackle the uncertainty in emergency decision‐making problems are executed in Section 7. Section 8 proposes the numerical case study of the outbreak of coronavirus as an emergency decision support problem to demonstrate the applicability and reliability of the proposed techniques. Section 9 presented the comparison of the proposed and existing techniques and the conclusion of this study is drawn in Section 10.

2. PRELIMINARIES

Let us briefly recall in this segment the rudiments of FSs, Pythagorean FSs, and spherical FSs. For the following review, these definitions will be included in the here.

Definition 1

((Zadeh ¹⁰ )) A FS $\tilde{A}$ in fixed nonempty set $\ddot{O}$ is described as follows:

$$\tilde{A}=\left\{〈\varrho ,{\mathit{\text{P}}}_{♭}\left(\varrho \right)〉\right|\varrho \in \ddot{O}\},$$

where ${\mathit{\text{P}}}_{♭}\left(\varrho \right)\in [0,1]$ is said to be the positive membership grade of $\varrho$ in $\widetilde{г}$.

Definition 2

((Yager ¹⁷ )) A Pythagorean FS $\tilde{B}$ in fixed nonempty set $\ddot{O}$ is described as follows:

$$\tilde{B}=\left\{〈\varrho ,{\mathit{\text{P}}}_{♭}\left(\varrho \right),N_{♭}\left(\varrho \right)〉\right|\varrho \in \ddot{O}\},$$

where positive ${\mathit{\text{P}}}_{♭}\left(\varrho \right)$ and negative $N_{♭}\left(\varrho \right)\in [0,1]$ membership grades of $\varrho$ in $\widetilde{г}$. In addition, it is necessary to $0\le {\mathit{\text{P}}}_{♭}^2\left(\varrho \right)+{\mathit{\text{N}}}_{♭}^2\left(\varrho \right)\le 1$, $\forall \varrho \in \ddot{O}$.

Definition 3

((Ashraf and Abdullah ²⁹ )) A spherical FS $\tilde{F}$ in fixed nonempty set $\ddot{O}$ is described as follows:

$$\tilde{F}=\left\{〈\varrho ,{\mathit{\text{P}}}_{♭}\left(\varrho \right),I_{♭}\left(\varrho \right),N_{♭}\left(\varrho \right)〉\right|\varrho \in \stackrel{"}{O}\},$$

where positive ${\mathit{\text{P}}}_{♭}\left(\varrho \right)$, neutral ${\mathit{\text{I}}}_{♭}\left(\varrho \right)$ and negative $N_{♭}\left(\varrho \right)\in [0,1]$ membership grades of $\varrho$ in $\tilde{F}$. In addition, it is necessary to $0\le {\mathit{\text{P}}}_{♭}^2\left(\varrho \right)+{\mathit{\text{I}}}_{♭}^2\left(\varrho \right)+{\mathit{\text{N}}}_{♭}^2\left(\varrho \right)\le 1$, $\forall \varrho \in \ddot{O}$. Also, ${\chi }_{♭}=\sqrt{1-P_{♭}^2\left(\varrho \right)-I_{♭}^2\left(\varrho \right)-N_{♭}^2\left(\varrho \right)}$ called hesitancy of $\varrho$ in $\tilde{F}$.

For convenience, we indicate $\hat{S}F\hat{S}\left(\stackrel{"}{O}\right)$, the list of all spherical FS in $\ddot{O}$. We shall signify the spherical fuzzy number (SFN) by the triplet $\tilde{F}=(P_{♭},I_{♭},N_{♭})$.

Let ${\tilde{F}}_1,{\tilde{F}}_2\in \hat{S}г\hat{S}\left(\stackrel{"}{O}\right).$ Ashraf ²⁹ defined the following notions:

• (1) ${\tilde{F}}_1⊑{\tilde{F}}_2$ if and only if ${\mathit{\text{P}}}_{{♭}_1}\le$ ${\mathit{\text{P}}}_{{♭}_2}$, ${\mathit{\text{I}}}_{{♭}_1}\le$ ${\mathit{\text{I}}}_{{♭}_2}$ and ${\mathit{\text{N}}}_{{♭}_1}\ge$ ${\mathit{\text{N}}}_{{♭}_2}$ for each $\varrho \in \ddot{O}$. Clearly ${\tilde{F}}_1={\tilde{F}}_2$ if ${\tilde{F}}_1⊑{\tilde{F}}_2$ and ${\tilde{F}}_2⊑{\tilde{F}}_1$.
• (2) ${\tilde{F}}_1\sqcap {\tilde{F}}_2=\{\min (P_{{♭}_1},P_{{♭}_2}),\min (I_{{♭}_1},I_{{♭}_2}),\max (N_{{♭}_1},N_{{♭}_2})|\varrho \in \stackrel{"}{O}\}$,
• (3) ${\tilde{F}}_1\bigsqcup {\tilde{F}}_2=\{\max (P_{{♭}_1},P_{{♭}_2}),\min (I_{{♭}_1},I_{{♭}_2}),\min (N_{{♭}_1},N_{{♭}_2})|\varrho \in \stackrel{"}{O}\}$,
• (4) ${\tilde{F}}_1^c=\{N_{{♭}_1},I_{{♭}_1},P_{{♭}_1}\mid \varrho \in \stackrel{"}{O}\}$.

2.1. Existing operations of SFNs

In this segment, we discuss the existing operations for spherical fuzzy numbers.

• (1)Mahmood et al. ³⁹ proposed the basic operation for SFNs, which are described as follows:

Definition 4

((Mahmood et al. ³⁹ )) Let ${\tilde{F}}_1=\{P_{{♭}_1},I_{{♭}_1},N_{{♭}_1}\}$ and ${\tilde{F}}_2=\{P_{{♭}_2},I_{{♭}_2},N_{{♭}_2}\}\in \hat{S}FN\left(\stackrel{"}{O}\right)$ with $\hat{w}>0.$ The operational laws then shall be as follows:

• (1) ${\tilde{F}}_1\otimes {\tilde{F}}_2=\left\{(P_{{♭}_1}+I_{{♭}_1})(P_{{♭}_2}+I_{{♭}_2})-I_{{♭}_1}{I}_{{♭}_2},I_{{♭}_1}{I}_{{♭}_2},\sqrt{1-(1-N_{{♭}_1}^2)(1-N_{{♭}_2}^2)}\right\}$;
• (2) ${\tilde{F}}_1\oplus {\tilde{F}}_2=\left\{\sqrt{1-(1-P_{{♭}_1}^2)(1-P_{{♭}_2}^2)},I_{{♭}_1}{I}_{{♭}_2},(N_{{♭}_1}+I_{{♭}_1})(N_{{♭}_2}+I_{{♭}_2})-I_{{♭}_1}{I}_{{♭}_2}\right\}$;
• (3) ${\tilde{F}}_1^{\hat{w}}=\left\{{(P_{{♭}_1}+I_{{♭}_1})}^{\hat{w}}-I_{{♭}_1}^{\hat{w}},I_{{♭}_1}^{\hat{w}},\sqrt{1-{(1-N_{{♭}_1}^2)}^{\hat{w}}}\right\}$;
• (4) $\hat{w}\cdot {\tilde{F}}_1=\left\{\sqrt{1-{(1-P_{{♭}_1}^2)}^{\hat{w}}},I_{{♭}_1}^{\hat{w}},{(N_{{♭}_1}+I_{{♭}_1})}^{\hat{w}}-I_{{♭}_1}^{\hat{w}}\right\}$.

Operational rules defined in Definition 4 has some deficiency. Multiplication and addition of any two SFNs, violates the basic condition of spherical FS, that is square sum of its membership degrees less or equal to one. For supporting this, let us take ${\tilde{F}}_1=\{1,0,0\}$ and ${\tilde{F}}_2=\{0.7,0.5,0.5\}$.

$$\begin{array}{ccl}{\tilde{F}}_1\otimes {\tilde{F}}_2& =& \{1,0,0\}\otimes \{0.7,0.5,0.5\}\\ & =& \left\{(1+0)(0.7+0.5)-\left(0\right)\left(0.5\right),\left(0\right)\left(0.5\right),\sqrt{1-(1-0^2)(1-0.5^2)}\right\}\\ & =& \{1.2,0.0,0.5\}.\end{array}$$

Now, square sum of its membership degree is ${\left(1.2\right)}^2+{\left(0\right)}^2+{\left(0.5\right)}^2=1.69\nleqq 1$. Hence obtaining results shows the violation of the condition that $0\le {\text{P}}_{♭}^2\left(\varrho \right)+{\text{I}}_{♭}^2\left(\varrho \right)+{\text{N}}_{♭}^2\left(\varrho \right)\le 1$, for each ${\check{r}}_{⋎}\in \ddot{O}$. Similarly,

$$\begin{array}{ccl}{\tilde{F}}_1\oplus {\tilde{F}}_2& =& \{0,0,1\}\otimes \{0.5,0.5,0.7\}\\ & =& \left\{\sqrt{1-(1-0^2)(1-0.5^2)},\left(0\right)\left(0.5\right),(1+0)(0.7+0.5)-\left(0\right)\left(0.5\right)\right\}\\ & =& \{0.5,0.0,1.2\}.\end{array}$$

Now, square sum of its membership degree is ${\left(0.5\right)}^2+{\left(0\right)}^2+{\left(1.2\right)}^2=1.69\nleqq 1.$ Hence obtaining results shows the violation of the condition that $0\le {\text{P}}_{♭}^2\left(\varrho \right)+{\text{I}}_{♭}^2\left(\varrho \right)+{\text{N}}_{♭}^2\left(\varrho \right)\le 1$, for each ${\check{r}}_{⋎}\in \ddot{O}$.

• (2)Liu et al. ⁴⁰ proposed the basic operation for SFNs, which are described as:

Definition 5

((Liu et al. ⁴⁰ )) Suppose ${\tilde{F}}_1=\{P_{{♭}_1},I_{{♭}_1},N_{{♭}_1}\}$ and ${\tilde{F}}_2=\{P_{{♭}_2},I_{{♭}_2},N_{{♭}_2}\}\in \hat{S}FN\left(\stackrel{"}{O}\right)$ with $\hat{w}>0.$ The Algebraic operational laws are described as follows:

• (1) ${\tilde{F}}_1\otimes {\tilde{F}}_2=\left\{P_{{♭}_1}{P}_{{♭}_2},\sqrt{I_{{♭}_1}^2+I_{{♭}_2}^2-I_{{♭}_1}^2{I}_{{♭}_2}^2},\sqrt{N_{{♭}_1}^2+N_{{♭}_2}^2-N_{{♭}_1}^2{N}_{{♭}_2}^2}\right\}$;
• (2) ${\tilde{F}}_1\oplus {\tilde{F}}_2=\left\{\sqrt{P_{{♭}_1}^2+P_{{♭}_2}^2-P_{{♭}_1}^2{P}_{{♭}_2}^2},I_{{♭}_1}{I}_{{♭}_2},N_{{♭}_1}{N}_{{♭}_2}\right\}$;
• (3) ${\tilde{F}}_1^{\hat{w}}=\left\{P_{{♭}_1}^{\hat{w}},\sqrt{1-{(1-I_{{♭}_1}^2)}^{\hat{w}}},\sqrt{1-{(1-N_{{♭}_1}^2)}^{\hat{w}}}\right\}$;
• (4) $\hat{w}\cdot {\tilde{F}}_1=\left\{\sqrt{1-{(1-P_{{♭}_1}^2)}^{\hat{w}}},I_{{♭}_1}^{\hat{w}},N_{{♭}_1}^{\hat{w}}\right\}$.

Operational rules defined in Definition 5 has also some deficiency. Multiplication of any two SFNs, violates the basic condition of spherical FS, that is square sum of its grades are $\le$1. For supporting this, let us take ${\tilde{F}}_1=\{0,0,1\}$ and ${\tilde{F}}_2=\{0,1,0\}$.

$$\begin{array}{ccl}{\tilde{F}}_1\otimes {\tilde{F}}_2& =& \left\{P_{{♭}_1}{P}_{{♭}_2},\sqrt{I_{{♭}_1}^2+I_{{♭}_2}^2-I_{{♭}_1}^2{I}_{{♭}_2}^2},\sqrt{N_{{♭}_1}^2+N_{{♭}_2}^2-N_{{♭}_1}^2{N}_{{♭}_2}^2}\right\}\\ \{0,0,1\}\otimes \{0,1,0\}& =& \left\{\left(0\right)\left(0\right),\sqrt{{\left(0\right)}^2+{\left(1\right)}^2-{\left(0\right)}^2{\left(1\right)}^2},\sqrt{{\left(1\right)}^2+{\left(0\right)}^2-{\left(1\right)}^2{\left(0\right)}^2}\right\}\\ & =& \{0,1,1\}.\end{array}$$

Now, square sum of its membership degree is ${\left(0\right)}^2+{\left(1\right)}^2+{\left(1\right)}^2=2\nleqq 1$. Hence obtaining results shows the violation of the condition that $0\le {\text{P}}_{♭}^2\left(\varrho \right)+{\text{I}}_{♭}^2\left(\varrho \right)+{\text{N}}_{♭}^2\left(\varrho \right)\le 1$, for each ${\check{r}}_{⋎}\in \ddot{O}$.

• (3)Garg et al. ⁴¹ proposed the improved operation for SFNs, which are described as follows.

Definition 6

((Garg et al. ⁴¹ )) Let ${\tilde{F}}_1=\{P_{{♭}_1},I_{{♭}_1},N_{{♭}_1}\}$ and ${\tilde{F}}_2=\{P_{{♭}_2},I_{{♭}_2},N_{{♭}_2}\}\in \hat{S}FN\left(\stackrel{"}{O}\right)$ with $\hat{w}>0$. Then, the proposed operational laws are:

• (1) ${\tilde{F}}_1\otimes {\tilde{F}}_2=\left\{\begin{array}{c}\sqrt[t]{(1-N_{{♭}_1}^t)(1-N_{{♭}_2}^t)-(1-P_{{♭}_1}^t-I_{{♭}_1}^t-N_{{♭}_1}^t)(1-P_{{♭}_2}^t-I_{{♭}_2}^t-N_{{♭}_2}^t)-I_{{♭}_1}^t{I}_{{♭}_2}^t},\\ \sqrt[t]{1-(1-I_{{♭}_1}^t)(1-I_{{♭}_2}^t)},\sqrt[t]{1-(1-N_{{♭}_1}^t)(1-N_{{♭}_2}^t)}\end{array}\right\}$;
• (2)
  ${\tilde{F}}_1^{\hat{w}}=\left\{\begin{array}{c}\sqrt[t]{{(1-N_{{♭}_1}^t)}^{\hat{w}}-{(1-P_{{♭}_1}^t-I_{{♭}_1}^t-N_{{♭}_1}^t)}^{\hat{w}}-{\left(I_{{♭}_1}^t\right)}^{\hat{w}}},\\ \sqrt[t]{1-{(1-I_{{♭}_1}^t)}^{\hat{w}}},\sqrt[t]{1-{(1-N_{{♭}_1}^t)}^{\hat{w}}}\end{array}\right\};$

Operational rules defined in Definition 6 has also some deficiency. Multiplication of any two SFNs, violates the basic condition of spherical FS, that is square sum of its grades are $\le 1$. For supporting this, let us take ${\tilde{F}}_1=\{0,0,1\}$, ${\tilde{F}}_2=\{0,1,0\}$ and $t=2$.

$$\begin{array}{ccc}{\tilde{F}}_1\otimes {\tilde{F}}_2& =& \left\{\begin{array}{c}\sqrt{\left(1-N_{{♭}_1}^2,)\right)\left(1-N_{{♭}_2}^2,)\right)-\left(1-P_{{♭}_1}^2-I_{{♭}_1}^2-N_{{♭}_1}^2,)\right)\left(1-P_{{♭}_2}^2-I_{{♭}_2}^2-N_{{♭}_2}^2,)\right)-I_{{♭}_1}^2{I}_{{♭}_2}^2},\\ \sqrt{1-\left(1-I_{{♭}_1}^2,)\right)\left(1-I_{{♭}_2}^2,)\right)},\sqrt{1-\left(1-N_{{♭}_1}^2,)\right)\left(1-N_{{♭}_2}^2,)\right)}\end{array}\right\}\\ \{1,0,0\}\otimes \{0,1,0\}& =& \left\{\begin{array}{c}\sqrt{(1-0^2)(1-0^2)-(1-1^2-0^2-0^2)(1-0^2-1^2-0^2)-0^2{1}^2},\\ \sqrt{1-(1-0^2)(1-1^2)},\sqrt{1-(1-0^2)(1-0^2)}\end{array}\right\}\\ & =& \{1,1,0\}.\hfill \end{array}$$

Now, square sum of its membership degree is ${\left(1\right)}^2+{\left(1\right)}^2+{\left(0\right)}^2=2\nleqq 1$. Hence obtaining results shows the violation of the condition that $0\le {\text{P}}_{♭}^2\left(\varrho \right)+{\text{I}}_{♭}^2\left(\varrho \right)+{\text{N}}_{♭}^2\left(\varrho \right)\le 1,$ for each ${\check{r}}_{⋎}\in \ddot{O}$.

3. NOVEL OPERATIONS FOR SPHERICAL FUZZY NUMBERS

Ashraf and Abdullah presented the operational laws of SFNs. Here we present three cases to address validity of the algebraic operators to tackle spherical fuzzy settings.

Definition 7

((Ashraf and Abdullah ²⁹ )) Let ${\tilde{F}}_1=\{P_{{♭}_1},I_{{♭}_1},N_{{♭}_1}\}$ and ${\tilde{F}}_2=\{P_{{♭}_2},I_{{♭}_2},N_{{♭}_2}\}\in \hat{S}FN\left(\stackrel{"}{O}\right)$ with $\hat{w}>0$. The operational laws based on algebraic norm are described as follows:

• (1) ${\tilde{F}}_1\otimes {\tilde{F}}_2=\left\{P_{{♭}_1}{P}_{{♭}_2},I_{{♭}_1}{I}_{{♭}_2},\sqrt{N_{{♭}_1}^2+N_{{♭}_2}^2-N_{{♭}_1}^2{N}_{{♭}_2}^2}\right\}$;
• (2) ${\tilde{F}}_1\oplus {\tilde{F}}_2=\left\{\sqrt{P_{{♭}_1}^2+P_{{♭}_2}^2-P_{{♭}_1}^2{P}_{{♭}_2}^2},I_{{♭}_1}{I}_{{♭}_2},N_{{♭}_1}{N}_{{♭}_2}\right\}$;
• (3) ${\tilde{F}}_1^{\hat{w}}=\left\{{\left(P_{{♭}_1}\right)}^{\hat{w}},{\left(I_{{♭}_1}\right)}^{\hat{w}},\sqrt{1-{(1-N_{{♭}_1}^2)}^{\hat{w}}}\right\}$;
• (4) $\hat{w}\cdot {\tilde{F}}_1=\left\{\sqrt{1-{(1-P_{{♭}_1}^2)}^{\hat{w}}},{\left(I_{{♭}_1}\right)}^{\hat{w}},{\left(N_{{♭}_1}\right)}^{\hat{w}}\right\}$.

Now we mentioned three cases to illustrate the validity of the recommended operators, which met the fundamental requirement of spherical FS that is, $0\le {\mathit{\text{P}}}_{♭}^2\left(\varrho \right)+{\mathit{\text{I}}}_{♭}^2\left(\varrho \right)+{\mathit{\text{N}}}_{♭}^2\left(\varrho \right)\le 1$, for each ${\check{r}}_{⋎}\in \ddot{O}$ in all situation. Based on multiplication rules for two spherical numbers, these extreme circumstances are indicated below.

• (1) ${\tilde{F}}_1=(1,0,0)$ and ${\tilde{F}}_2=(0,1,0)$;
• (2) ${\tilde{F}}_1=(0,1,0)$ and ${\tilde{F}}_2=(0,0,1)$;
• (3) ${\tilde{F}}_1=(1,0,0)$ and ${\tilde{F}}_2=(0,0,1)$.

In particular, the three cases highlight the deficiency of the multiply operation in Definitions 4 and 5, The achieved result can no longer be purely determined by an SFN, which is unreasonable to some extent. Using extreme situations, we show the effectiveness and validation of the proposed operators discussed in Definition 7.

Since, we have

$${\tilde{F}}_1\otimes {\tilde{F}}_2=\left\{P_{{♭}_1}{P}_{{♭}_2},I_{{♭}_1}{I}_{{♭}_2},\sqrt{N_{{♭}_1}^2+N_{{♭}_2}^2-N_{{♭}_1}^2{N}_{{♭}_2}^2}\right\}.$$

Case 1.

$$\begin{array}{ccl}\{1,0,0\}\otimes \{0,1,0\}& =& \left\{\left(1\right)\left(0\right),\left(0\right)\left(1\right),\sqrt{{\left(0\right)}^2+{\left(0\right)}^2-{\left(0\right)}^2\left(0\right)2}\right\}\\ & =& \{0,0,0\}\in \hat{S}FN\left(\stackrel{"}{O}\right)\end{array}$$

Case 2.

$$\begin{array}{ccl}\{0,1,0\}\otimes \{0,0,1\}& =& \left\{\left(0\right)\left(0\right),\left(1\right)\left(0\right),\sqrt{{\left(0\right)}^2+{\left(1\right)}^2-{\left(0\right)}^2{\left(1\right)}^2}\right\}\\ & =& \{0,0,1\}\in \hat{S}FN\left(\stackrel{"}{O}\right)\end{array}$$

Case 3.

$$\begin{array}{ccl}\{1,0,0\}\otimes \{0,0,1\}& =& \left\{\left(1\right)\left(0\right),\left(0\right)\left(0\right),\sqrt{{\left(0\right)}^2+{\left(1\right)}^2-{\left(0\right)}^2{\left(1\right)}^2}\right\}\\ & =& \{0,0,1\}\in \hat{S}FN\left(\stackrel{"}{O}\right)\end{array}$$

Hence, Multiplication operation define in Definition 7, satisfied the elementary condition $0\le {\mathit{\text{P}}}_{♭}^2\left(\varrho \right)+{\mathit{\text{I}}}_{♭}^2\left(\varrho \right)+{\mathit{\text{N}}}_{♭}^2\left(\varrho \right)\le 1$, for each ${\check{r}}_{⋎}\in \ddot{O}$ in all situation. The critical circumstances addressed in three cases are also satisfied. Therefore, the existing backdraw in spherical fuzzy operational laws are successfully eliminated. The operation described in this paper shall fulfill the closure property of the multiplication of the SFNs.

4. SPHERICAL FUZZY EINSTEIN OPERATORS

In this segment, we shall familiarized with generalized union and intersection for the spherical fuzzy numbers, which are as follows:

$$\begin{array}{ccc}{\tilde{F}}_1\vee {\tilde{F}}_2& =& \left\{T(P_{{♭}_1}\left(\varrho \right),P_{{♭}_2}\left(\varrho \right)),S(I_{{♭}_1}\left(\varrho \right),I_{{♭}_2}\left(\varrho \right)),S(N_{{♭}_1}\left(\varrho \right),N_{{♭}_2}\left(\varrho \right))\right\}\\ {\tilde{F}}_1\wedge {\tilde{F}}_2& =& \left\{S(P_{{♭}_1}\left(\varrho \right),P_{{♭}_2}\left(\varrho \right)),S(I_{{♭}_1}\left(\varrho \right),I_{{♭}_2}\left(\varrho \right)),T(N_{{♭}_1}\left(\varrho \right),N_{{♭}_2}\left(\varrho \right))\right\}\end{array}$$

We can also write

$$\begin{array}{ccc}{\tilde{F}}_1\vee {\tilde{F}}_2& =& \left\{\max (P_{{♭}_1}\left(\varrho \right),P_{{♭}_2}\left(\varrho \right)),\min (I_{{♭}_1}\left(\varrho \right),I_{{♭}_2}\left(\varrho \right)),\min (N_{{♭}_1}\left(\varrho \right),N_{{♭}_2}\left(\varrho \right))\right\}\\ {\tilde{F}}_1\wedge {\tilde{F}}_2& =& \left\{\min (P_{{♭}_1}\left(\varrho \right),P_{{♭}_2}\left(\varrho \right)),\min (I_{{♭}_1}\left(\varrho \right),I_{{♭}_2}\left(\varrho \right)),\max (N_{{♭}_1}\left(\varrho \right),N_{{♭}_2}\left(\varrho \right))\right\}\end{array}$$

In above equations, $T$ and $S$ represents the t‐norm and s‐norm, respectively. As, we know well that, t‐norm $\left(T\right)$ and s‐norm $\left(S\right)$ are the general terms including all types of operators and also contented the necessitate of conjunction and disjunction operators, respectively. Here, we enlist the some types of t‐norm and s‐norm, respectively.

Name	t‐norm	s‐norm
Algebraic	${\check{T}}_a\left(d,l\right)=dl$	${\widehat{S}}_A\left(d,l\right)=d+l-dl$
Einstein	${\check{T}}_e\left(d,l\right)=\frac{dl}{1+\left(1-d\right)\left(1-l\right)}$	${\widehat{S}}_E\left(d,l\right)=\frac{d+l}{1+dl}$
Hamacher	${\check{T}}_h\left(d,l\right)=\frac{dl}{\gamma +\left(1-\gamma \right)\left(d+l-dl\right)},\gamma >0$	${\widehat{S}}_H\left(d,l\right)=\frac{d+l-dl-\left(1-\gamma \right)dl}{1-\left(1-\gamma \right)dl},\gamma >0$
Frank	${\check{T}}_f\left(d,l\right)={\log }_{\gamma }\left(1+\frac{\left({\gamma }^d-1\right)\left({\gamma }^l-1\right)}{\gamma -1}\right)$	${\widehat{S}}_F\left(d,l\right)=1-{\log }_{\gamma }\left(1+\frac{\left({\gamma }^{1-d}-1\right)\left({\gamma }^{1-l}-1\right)}{\gamma -1}\right)$

However, algebraic sum and algebraic product are obtain using algebraic norm. Algebraic operators are not only which can be use to perform union and intersection. We have many families of norm operators, which can be used to perform corresponding union and intersection. Einstein t‐norm and Einstein s‐norm are one of the effective family member of norm operators. Einstein sum and Einstein product are to be good replacements, that characteristically give the equivalent smooth approximation as algebraic product and algebraic sum, respectively. Einstein t‐norm and Einstein s‐norm for spherical fuzzy environment as follows:

Einstein t‐norm	Einstein s‐norm
${\check{T}}_e\left(d,l\right)=\frac{dl}{\sqrt{1+\left(1-d^2\right)\cdot \left(1-l^2\right)}}$	${\widehat{S}}_E\left(d,l\right)=\frac{\sqrt{d^2+l^2}}{\sqrt{1+d^2\cdot l^2}}$

Where ${\check{T}}_e\left(d,l\right)$ and ${\widehat{S}}_E\left(d,l\right)$ are said to be Einstein t‐norm and Einstein s‐norm, respectively. Also ${\check{T}}_e\left(d,l\right)$ satisfies the basic properties as follows:

For unite interval $\nu =\left[0,1\right],$ the mapping $\text{Ω\hspace{0.05em}}: \nu \times \nu \to \nu$ is said to be t‐norm iff

• (1)Ω is commutative, monotonic, and associative,
• (2)Ω(d,1) = d.

and

For unite interval $\nu =\left[0,1\right],$ the mapping $\text{Ω\hspace{0.05em}}: \nu \times \nu \to \nu$ is said to be s‐norm iff

• (1)Ω is commutative, monotonic, and associative,
• (2) $\mathrm{\Omega }(d,0)=d$.

Definition 8

Let ${\tilde{F}}_1=\{P_{{♭}_1},I_{{♭}_1},N_{{♭}_1}\}$ and ${\tilde{F}}_2=\{P_{{♭}_2},I_{{♭}_2},N_{{♭}_2}\}\in \hat{S}FN\left(\stackrel{"}{O}\right)$ and $\mathrm{\Psi }\ge 0$. Then the Einstein operations for spherical fuzzy numbers are as follows:

• (1) ${\tilde{F}}_1\oplus {\tilde{F}}_2=\left(\frac{\sqrt{P_{{♭}_1}^2+P_{{♭}_2}^2}}{\sqrt{1+P_{{♭}_1}^2\cdot P_{{♭}_2}^2}},\frac{I_{{♭}_1}\cdot I_{{♭}_2}}{\sqrt{1+(1-I_{{♭}_1}^2)\cdot (1-I_{{♭}_2}^2)}},\frac{N_{{♭}_1}\cdot N_{{♭}_2}}{\sqrt{1+(1-N_{{♭}_1}^2)\cdot (1-N_{{♭}_2}^2)}},)\right)$;
• (2) $\mathrm{\Psi }\cdot {\tilde{F}}_1=\left(\frac{\sqrt{{(1+P_{{♭}_1}^2)}^{\mathrm{\Psi }}-{(1-P_{{♭}_1}^2)}^{\mathrm{\Psi }}}}{\sqrt{{(1+P_{{♭}_1}^2)}^{\mathrm{\Psi }}+{(1-P_{{♭}_1}^2)}^{\mathrm{\Psi }}}},\frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{\mathrm{\Psi }}}{\sqrt{{(2-I_{{♭}_1}^2)}^{\mathrm{\Psi }}+{\left(I_{{♭}_1}^2\right)}^{\mathrm{\Psi }}}},\frac{\sqrt{2}{\left(N_{{♭}_1}\right)}^{\mathrm{\Psi }}}{\sqrt{{(2-N_{{♭}_1}^2)}^{\mathrm{\Psi }}+{\left(N_{{♭}_1}^2\right)}^{\mathrm{\Psi }}}},)\right)$;
• (3) ${\tilde{F}}_1\otimes {\tilde{F}}_2=\left(\frac{P_{{♭}_1}\cdot P_{{♭}_2}}{\sqrt{1+(1-P_{{♭}_1}^2)\cdot (1-P_{{♭}_2}^2)}},\frac{I_{{♭}_1}\cdot I_{{♭}_2}}{\sqrt{1+(1-I_{{♭}_1}^2)\cdot (1-I_{{♭}_2}^2)}},\frac{\sqrt{N_{{♭}_1}^2+N_{{♭}_2}^2}}{\sqrt{1+N_{{♭}_1}^2\cdot N_{{♭}_2}^2}},)\right)$;
• (4) ${\tilde{F}}_1^{\mathrm{\Psi }}=\left(\frac{\sqrt{2}{\left(P_{{♭}_1}\right)}^{\mathrm{\Psi }}}{\sqrt{{(2-P_{{♭}_1}^2)}^{\mathrm{\Psi }}+{\left(P_{{♭}_1}^2\right)}^{\mathrm{\Psi }}}},\frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{\mathrm{\Psi }}}{\sqrt{{(2-I_{{♭}_1}^2)}^{\mathrm{\Psi }}+{\left(I_{{\breve{u}}_1}^2\right)}^{\mathrm{\Psi }}}},\frac{\sqrt{{(1+N_{{♭}_1}^2)}^{\mathrm{\Psi }}-{(1-N_{{♭}_1}^2)}^{\mathrm{\Psi }}}}{\sqrt{{(1+N_{{♭}_1}^2)}^{\mathrm{\Psi }}+{(1-N_{{♭}_1}^2)}^{\mathrm{\Psi }}}},)\right)$;
• (5) ${\tilde{F}}_1\ominus {\tilde{F}}_2=\left(\frac{\sqrt{P_{{♭}_1}^2-P_{{♭}_2}^2}}{\sqrt{1-P_{{♭}_1}^2\cdot P_{{♭}_2}^2}},\sqrt{\frac{I_{{♭}_1}^2(2-I_{{♭}_2}^2)}{1-(1-I_{{♭}_1}^2)\cdot (1-I_{{♭}_2}^2)}},\sqrt{\frac{N_{{♭}_1}^2(2-N_{{♭}_2}^2)}{1-(1-N_{{♭}_1}^2)\cdot (1-N_{{♭}_2}^2)}},)\right),$ if $\frac{N_{{♭}_2}^2}{N_{{♭}_1}^2}\ge \frac{1-P_{{♭}_2}^2}{1-P_{{♭}_1}^2}\frac{1+P_{{♭}_1}^2}{1+P_{{♭}_2}^2}\ge 1$;
• (6) ${\tilde{F}}_1\oslash {\tilde{F}}_2=\left(\sqrt{\frac{P_{{♭}_1}^2(2-P_{{♭}_2}^2)}{1-(1-P_{{♭}_1}^2)\cdot (1-P_{{♭}_2}^2)}},\frac{\sqrt{I_{{♭}_1}^2-I_{{♭}_2}^2}}{\sqrt{1-I_{{♭}_1}^2\cdot I_{{♭}_2}^2}},\frac{\sqrt{N_{{♭}_1}^2-N_{{♭}_2}^2}}{\sqrt{1-N_{{♭}_1}^2\cdot N_{{♭}_2}^2}},)\right),$ if $\frac{P_{{♭}_2}^2}{P_{{♭}_1}^2}\ge \frac{1-N_{{♭}_2}^2}{1-N_{{♭}_1}^2}\frac{1+N_{{♭}_1}^2}{1+N_{{♭}_2}^2}\ge 1$.

4.1. Comparison technique for spherical FSs

In this section, we define the score and accuracy values of the spherical FSs. On the basis of score and accuracy values, we can compare that which spherical FS is better than other one.

Definition 9

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$. Then

• (a) $\check{s}\check{c}\left({\tilde{F}}_g\right)=\frac{1}{3}(2+{\text{P}}_{{\breve{u}}_P}-{\text{I}}_{{\breve{u}}_P}-{\text{N}}_{{\breve{u}}_P})\in [0,1]$ is said to be score value of ${\widetilde{г}}_g$.
• (b) $\tilde{a}\check{c}\left({\tilde{F}}_g\right)=(P_{{\breve{u}}_P}-N_{{\breve{u}}_P})\in [0,1]$ is said to be accuracy value of ${\tilde{F}}_g$.

Proposition 1

Let ${\tilde{F}}_1=\{P_{{♭}_1},I_{{♭}_1},N_{{♭}_1}\}$ and ${\tilde{F}}_2=\{P_{{♭}_2},I_{{♭}_2},N_{{♭}_2}\}\in \hat{S}FN\left(\stackrel{"}{O}\right).$ Then

• (1)If $\check{s}\check{c}\left({\tilde{F}}_1\right)<\check{s}\check{c}\left({\tilde{F}}_2\right)$ then ${\tilde{F}}_1<{\tilde{F}}_2$,
• (2)
  If $\check{s}\check{c}\left({\tilde{F}}_1\right)=\check{s}\check{c}\left({\tilde{F}}_2\right)$ then

  • (a)
    $\tilde{a}\check{c}\left({\tilde{F}}_1\right)<\tilde{a}\check{c}\left({\tilde{F}}_2\right)$ then ${\tilde{F}}_1<{\tilde{F}}_2$,
  • (b)
    $\tilde{a}\check{c}\left({\tilde{F}}_1\right)=\tilde{a}\check{c}\left({\tilde{F}}_2\right)$ then ${\tilde{F}}_1={\tilde{F}}_2$.

5. EINSTEIN NORM‐BASED AGGREGATION OPERATORS

In this section, we propose the novel aggregation operators (AgOp) using spherical Einstein t‐norm and spherical Einstein s‐norm under spherical fuzzy environments.

5.1. Einstein norm‐based averaging operators

In this section, we present Einstein norm‐based averaging aggregation operators for spherical fuzzy settings.

Definition 10

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$. The Einstein averaging operator for $\hat{S}гN\left(\ddot{O}\right)$ is characterized as

$$SFEWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\sum _{g=1}^n{\beth }_g{\tilde{F}}_g,$$

and the weight vector is ${\beth }_g\left(g\in \mathbb{N}\right)$ with ${\beth }_g\ge 0$, ${\sum }_{g=1}^n{\beth }_g=1$.

Theorem 1

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hspace{0.17em}\hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and the weight vector is ${\beth }_g\left(g\in \mathbb{N}\right)$ with ${\beth }_g\ge 0$, $\sum _{g=1}^n{\beth }_g=1$. The $SFEWA$ AgOp is a mapping $G^n⟶G$ defined as

$$\begin{array}{ccl}SFEWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)& =& \sum _{g=1}^n{\beth }_g{\tilde{F}}_g\\ & =& \left(\begin{array}{c}\frac{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+P_{{♭}_g}^2,)\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^n{\left(1-P_{{♭}_g}^2,)\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+P_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(1-P_{{♭}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-I_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(I_{{♭}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(N_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-N_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(N_{{♭}_g}^2,)\right)}^{{\beth }_g}}}\end{array},)\right).\end{array}$$ (1)

Mathematical induction is being used on $n$ to prove the Equation (1).

When $n=2,$

$$\begin{array}{ccc}SFEWA({\tilde{F}}_1,{\tilde{F}}_2)& =& \sum _{g=1}^2{\beth }_g{\tilde{F}}_g\\ & =& {\beth }_1{\tilde{F}}_1+{\beth }_2{\tilde{F}}_2\end{array}$$

Utilizing Definition 8, we obtained

$$\begin{array}{ccc}{\beth }_1\hspace{0.17em}\cdot \hspace{0.17em}{\tilde{F}}_1& =& \left(\begin{array}{c}\frac{\sqrt{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}-{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}}}{\sqrt{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}}},\\ \frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}}},\frac{\sqrt{2}{\left(N_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-N_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(N_{{♭}_1}^2,)\right)}^{{\beth }_1}}}\end{array},)\right)\\ {\beth }_2\hspace{0.17em}\cdot \hspace{0.17em}{\tilde{F}}_2& =& \left(\begin{array}{c}\frac{\sqrt{{\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}}{\sqrt{{\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\\ \frac{\sqrt{2}{\left(I_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\frac{\sqrt{2}{\left(N_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}\end{array},)\right)\end{array}$$

Then,

$$\begin{array}{ccl}SFEWA({\tilde{F}}_1,{\tilde{F}}_2)& =& {\beth }_1{\tilde{F}}_1+{\beth }_2{\tilde{F}}_2\\ & =& \left(\begin{array}{c}\frac{\sqrt{\frac{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}-{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}}{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}}+\frac{{\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}{{\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}}}{\sqrt{1+\frac{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}-{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}}{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}}\cdot \frac{{\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}{{\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}}},\\ \frac{\frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}}}\cdot \frac{\sqrt{2}{\left(I_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}}}{\sqrt{1+\left(1-{\left(\frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}}},)\right)}^2,)\right)\cdot \left(1-{\left(\frac{\sqrt{2}{\left(I_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}},)\right)}^2,)\right)}},\\ \frac{\frac{\sqrt{2}{\left(N_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-N_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(N_{{♭}_1}^2,)\right)}^{{\beth }_1}}}\cdot \frac{\sqrt{2}{\left(N_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}}{\sqrt{1+\left(1-{\left(\frac{\sqrt{2}{\left(N_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-N_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(N_{{♭}_1}^2,)\right)}^{{\beth }_1}}},)\right)}^2,)\right)\cdot \left(1-{\left(\frac{\sqrt{2}{\left(N_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(N_{{♭}_2}^2,)\right)}^{{\beth }_2}}},)\right)}^2,)\right)}}\end{array},)\right)\\ & =& \left(\begin{array}{c}\sqrt{\frac{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}{{\left(1+P_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1+P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-P_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1-P_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\\ \frac{\sqrt{2}\left(I_{{♭}_1}^{{\beth }_1}.I_{{♭}_2}^{{\beth }_2},)\right)}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\\ \frac{\sqrt{2}\left(N_{{♭}_1}^{{\beth }_1}.N_{{♭}_2}^{{\beth }_2},)\right)}{\sqrt{{\left(2-N_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(2-N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(N_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}\end{array},)\right)\end{array}$$

Thus, Equation (1), is true for $n=2$.

Suppose that Equation (1), is true for $n=z$, we obtained

$$SFEWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_z)=\left(\begin{array}{c}\frac{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+P_{{♭}_g}^2,)\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^z{\left(1-P_{{♭}_g}^2,)\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+P_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(1-P_{{♭}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-I_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(N_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-N_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(N_{{♭}_g}^2,)\right)}^{{\beth }_g}}}\end{array},)\right)$$

Then, we need to prove the Equation (1) is valid for $n=z+1,$ that is

$$SFEWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_z,{\tilde{F}}_{z+1})=\sum _{g=1}^z{\beth }_g{\tilde{F}}_g+{\beth }_{z+1}{\tilde{F}}_{z+1}$$

$$=\left(\begin{array}{c}\hfill \frac{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+P_{{♭}_g}^2\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^z{\left(1-P_{{♭}_g}^2\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+P_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(1-P_{{♭}_g}^2\right)}^{{\beth }_g}}},\hfill \\ \hfill \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-I_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}^2\right)}^{{\beth }_g}}},\hfill \\ \hfill \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(N_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-N_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(N_{{♭}_g}^2\right)}^{{\beth }_g}}}\hfill \end{array}\right)+\left(\begin{array}{c}\hfill \frac{\sqrt{{\left(1+P_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}-{\left(1-P_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}}{\sqrt{{\left(1+P_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}+{\left(1-P_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}},\hfill \\ \hfill \frac{\sqrt{2}{\left(I_{{♭}_{z+1}}\right)}^{{\beth }_{z+1}}}{\sqrt{{\left(2-I_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}+{\left(I_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}},\hfill \\ \hfill \frac{\sqrt{2}{\left(N_{{♭}_{z+1}}\right)}^{{\beth }_{z+1}}}{\sqrt{{\left(2-N_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}+{\left(N_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}}\hfill \end{array}\right)$$

$$=\left(\begin{array}{c}\hfill \frac{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(1+P_{{♭}_g}^2\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^{z+1}{\left(1-P_{{♭}_g}^2\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(1+P_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^{z+1}{\left(1-P_{{♭}_g}^2\right)}^{{\beth }_g}}},\hfill \\ \hfill \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^{z+1}{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(2-I_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^{z+1}{\left(I_{{♭}_g}^2\right)}^{{\beth }_g}}},\frac{\sqrt{2}{\displaystyle \prod }_{g=1}^{z+1}{\left(N_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(2-N_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^{z+1}{\left(N_{{♭}_g}^2\right)}^{{\beth }_g}}}\hfill \end{array}\right)$$

that is, when $n=z+1$, Equation (1) also holds.

Hence, Equation (1) holds for any $n$.  $\square$

The following properties of SFEWA operator can be simply proved obviously by Definition 8.

• (1)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hspace{0.17em} \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$, if ${\tilde{F}}_1={\tilde{F}}_2=\hspace{0.17em}\text{⋯}\hspace{0.17em}{\tilde{F}}_{n-1}={\tilde{F}}_n=\tilde{F}$, then

  $$SFEWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\tilde{F}.$$
• (2)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and ${\tilde{F}}^{-}=\underset{g}{\min }{\tilde{F}}_g$, ${\tilde{F}}^{+}=\underset{g}{\max }{\tilde{F}}_g$. Then,

  $${\tilde{F}}^{-}\le SFEWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le {\tilde{F}}^{+}.$$
• (3)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ and ${\tilde{F}}_{\tilde{g}}=\{P_{{♭}_{\tilde{g}}},I_{{♭}_{\tilde{g}}},N_{{♭}_{\tilde{g}}}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g,\tilde{g}\in \mathbb{N}\right)$ such that ${\tilde{F}}_g\le {\tilde{F}}_{\tilde{g}}$ for all $g$. Then

  $$SFEWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le SFEWA({\tilde{F}}_{\tilde{1}},{\tilde{F}}_{\tilde{2}},{\tilde{F}}_{\tilde{3}},\text{…},{\tilde{F}}_{\tilde{n}}).$$

Next, we propose the spherical fuzzy Einstein ordered weighted averaging $\left(SFEOWA\right)$ operator as following:

Definition 11

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$. The Einstein ordered weighted averaging operator for $\hat{S}FN\left(\stackrel{"}{O}\right)$ is characterized as

$$SFEOWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\sum _{g=1}^n{\beth }_g{\tilde{F}}_{\mathrm{\Phi }\left(g\right)},$$

where $\mathrm{\Phi }\left(g\right)$ is denoted for ordered and $\left(\mathrm{\Phi }\left(1\right),\mathrm{\Phi }\left(2\right),\mathrm{\Phi }\left(3\right),\text{…},\mathrm{\Phi }\left(n\right)\right)$ is a permutation of $\left(1,2,3,\text{…},n\right)$, subject to ${\tilde{F}}_{\mathrm{\Phi }(g-1)}\ge {\tilde{F}}_{\mathrm{\Phi }\left(g\right)}$ for all $g$. Also ${\beth }_g\left(g\in \mathbb{N}\right)$ is the weight vector with ${\beth }_g\ge 0$, ${\sum }_{g=1}^n{\beth }_g=1$.

Theorem 2

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and the ${\beth }_g\left(g\in \mathbb{N}\right)$ is the weight vector with ${\beth }_g\ge 0$, ${\sum }_{g=1}^n{\beth }_g=1$. The $SFEOWA$ AgOp is a mapping $G^n⟶G$ defined as

$$\begin{array}{ccl}SFEOWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)& =& \sum _{g=1}^n{\beth }_g{\tilde{F}}_{\mathrm{\Phi }\left(g\right)}\\ & =& \left(\begin{array}{c}\frac{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+P_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^n{\left(1-P_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+P_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(1-P_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(I_{{♭}_{\mathrm{\Phi }\left(g\right)}},)\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-I_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(I_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(N_{{♭}_{\mathrm{\Phi }\left(g\right)}},)\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-N_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(N_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}}\end{array},)\right).\end{array}$$

where $\mathrm{\Phi }\left(g\right)$ is denoted for ordered and $\left(\mathrm{\Phi }\left(1\right),\mathrm{\Phi }\left(2\right),\mathrm{\Phi }\left(3\right),\text{…},\mathrm{\Phi }\left(n\right)\right)$ is a permutation of $\left(1,2,3,\text{…},n\right)$, subject to ${\tilde{F}}_{\mathrm{\Phi }(g-1)}\ge {\tilde{F}}_{\mathrm{\Phi }\left(g\right)}$ for all $g$.

This theorem's proof is identical to Theorem 1 and is therefore excluded here.  $\square$

The following properties of SFEOWA operator can be simply proved obviously by Definition 8.

• 1)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$, if ${\tilde{F}}_1={\tilde{F}}_2=\hspace{0.17em}\text{⋯}\hspace{0.17em}{\tilde{F}}_{n-1}={\tilde{F}}_n=\tilde{F}$, then

  $$SFEOWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\tilde{F}.$$
• 2)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and ${\tilde{F}}^{-}=\underset{g}{\min }{\tilde{F}}_g$, ${\tilde{F}}^{+}=\underset{g}{\max }{\tilde{F}}_g$. Then,

  $${\tilde{F}}^{-}\le SFEOWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le {\tilde{F}}^{+}.$$
• 3)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ and ${\tilde{F}}_{\tilde{g}}=\{P_{{♭}_{\tilde{g}}},I_{{♭}_{\tilde{g}}},N_{{♭}_{\tilde{g}}}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g,\tilde{g}\in \mathbb{N}\right)$ such that ${\tilde{F}}_g\le {\tilde{F}}_{\tilde{g}}$ for all $g$. Then

  $$SFEOWA({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le SFEOWA({\tilde{F}}_{\tilde{1}},{\tilde{F}}_{\tilde{2}},{\tilde{F}}_{\tilde{3}},\text{…},{\tilde{F}}_{\tilde{n}}).$$

5.2. Einstein geometric aggregation operators

In this section, we present Einstein norm‐based geometric aggregation operators for spherical fuzzy settings.

Definition 12

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$. The Einstein weighted geometric operator for $\hat{S}FN\left(\stackrel{"}{O}\right)$ is characterized as

$$SFEWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\prod _{g=1}^n{\left({\tilde{F}}_g\right)}^{{\beth }_g},$$

and the weight vector is ${\beth }_g\left(g\in \mathbb{N}\right)$ with ${\beth }_g\ge 0$, ${\sum }_{g=1}^n{\beth }_g=1$.

Theorem 3

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and the weight vector is ${\beth }_g\left(g\in \mathbb{N}\right)$ with ${\beth }_g\ge 0$, ${\sum }_{g=1}^n{\beth }_g=1$. The $SFEWG$ AgOp is a mapping $G^n⟶G$ defined as

$$\begin{array}{ccl}SFEWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)& =& \sum _{g=1}^n{\left({\tilde{F}}_g\right)}^{{\beth }_g}\\ & =& \left(\begin{array}{c}\frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(P_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-P_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(P_{{♭}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-I_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(I_{{\breve{u}}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+N_{{♭}_g}^2,)\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^n{\left(1-N_{{♭}_g}^2,)\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+N_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(1-N_{{♭}_g}^2,)\right)}^{{\beth }_g}}}\end{array},)\right).\end{array}$$ (2)

Mathematical induction is being used on $n$ to prove the Equation (2).

When $n=2,$

$$\begin{array}{ccc}SFEWG({\tilde{F}}_1,{\tilde{F}}_2)& =& \sum _{g=1}^2{\left({\tilde{F}}_g\right)}^{{\beth }_g}\\ & =& {\left({\tilde{F}}_1\right)}^{{\beth }_1}+{\left({\tilde{F}}_2\right)}^{{\beth }_2}\end{array}$$

Utilizing Definition 8, we obtained

$$\begin{array}{ccc}{\left({\tilde{F}}_1\right)}^{{\beth }_1}& =& \left(\begin{array}{c}\frac{\sqrt{2}{\left(P_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-P_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(P_{{♭}_1}^2,)\right)}^{{\beth }_1}}},\\ \frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}}},\frac{\sqrt{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}-{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}}}{\sqrt{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}}}\end{array},)\right)\\ {\left({\tilde{F}}_2\right)}^{{\beth }_2}& =& \left(\begin{array}{c}\frac{\sqrt{2}{\left(P_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(P_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\\ \frac{\sqrt{2}{\left(I_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\frac{\sqrt{{\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}{\sqrt{{\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}\end{array},)\right)\end{array}$$

Then,

$$\begin{array}{ccl}SFEWG({\tilde{F}}_1,{\tilde{F}}_2)& =& {\left({\tilde{F}}_1\right)}^{{\beth }_1}+{\left({\tilde{F}}_2\right)}^{{\beth }_2}\\ & =& \left(\begin{array}{c}\frac{\frac{\sqrt{2}{\left(P_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-P_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(P_{{♭}_1}^2,)\right)}^{{\beth }_1}}}\cdot \frac{\sqrt{2}{\left(P_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(P_{{♭}_2}^2,)\right)}^{{\beth }_2}}}}{\sqrt{1+\left(1-{\left(\frac{\sqrt{2}{\left(P_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-P_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(P_{{♭}_1}^2,)\right)}^{{\beth }_1}}},)\right)}^2,)\right)\cdot \left(1-{\left(\frac{\sqrt{2}{\left(P_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(P_{{♭}_2}^2,)\right)}^{{\beth }_2}}},)\right)}^2,)\right)}},\\ \frac{\frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}}}\cdot \frac{\sqrt{2}{\left(I_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}}}{\sqrt{1+\left(1-{\left(\frac{\sqrt{2}{\left(I_{{♭}_1}\right)}^{{\beth }_1}}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}}},)\right)}^2,)\right)\cdot \left(1-{\left(\frac{\sqrt{2}{\left(I_{{♭}_2}\right)}^{{\beth }_2}}{\sqrt{{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}},)\right)}^2,)\right)}},\\ \frac{\sqrt{\frac{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}-{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}}{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}}+\frac{{\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}{{\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}}{\sqrt{1+\frac{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}-{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}}{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}+{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}}\cdot \frac{{\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}{{\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}}\end{array},)\right)\\ & =& \left(\begin{array}{c}\frac{\sqrt{2}\left(P_{{♭}_1}^{{\beth }_1}.P_{{♭}_2}^{{\beth }_2},)\right)}{\sqrt{{\left(2-P_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(2-P_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(P_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(P_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\\ \frac{\sqrt{2}\left(I_{{♭}_1}^{{\beth }_1}.I_{{♭}_2}^{{\beth }_2},)\right)}{\sqrt{{\left(2-I_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(2-I_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(I_{{♭}_1}^2,)\right)}^{{\beth }_1}.{\left(I_{{♭}_2}^2,)\right)}^{{\beth }_2}}},\\ \sqrt{\frac{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}-{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}{{\left(1+N_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1+N_{{♭}_2}^2,)\right)}^{{\beth }_2}+{\left(1-N_{{♭}_1}^2,)\right)}^{{\beth }_1}\cdot {\left(1-N_{{♭}_2}^2,)\right)}^{{\beth }_2}}}\end{array},)\right)\end{array}$$

Thus, Equation (2), is true for $n=2.$

Suppose that Equation (2), is true for $n=z,$ we obtained

$$SFEWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_z)=\left(\begin{array}{c}\frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(P_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-P_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(P_{{♭}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-I_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+N_{{♭}_g}^2,)\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^z{\left(1-N_{{♭}_g}^2,)\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+N_{{♭}_g}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(1-N_{{♭}_g}^2,)\right)}^{{\beth }_g}}}\end{array},)\right)$$

Then, we need to prove the Equation (2) is valid for $n=z+1,$ that is

$$SFEWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_z,{\tilde{F}}_{z+1})=\prod _{g=1}^z{\left({\tilde{F}}_g\right)}^{{\beth }_g}+{\left({\tilde{F}}_{z+1}\right)}^{{\beth }_{z+1}}$$

$$=\left(\begin{array}{c}\hfill \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(P_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-P_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(P_{{♭}_g}^2\right)}^{{\beth }_g}}},\hfill \\ \hfill \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(2-I_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(I_{{♭}_g}^2\right)}^{{\beth }_g}}},\hfill \\ \hfill \frac{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+N_{{♭}_g}^2\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^z{\left(1-N_{{♭}_g}^2\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^z{\left(1+N_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^z{\left(1-N_{{♭}_g}^2\right)}^{{\beth }_g}}}\hfill \end{array}\right)+\left(\begin{array}{c}\hfill \frac{\sqrt{2}{\left(P_{{♭}_{z+1}}\right)}^{{\beth }_{z+1}}}{\sqrt{{\left(2-P_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}+{\left(P_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}},\hfill \\ \hfill \frac{\sqrt{2}{\left(I_{{♭}_{z+1}}\right)}^{{\beth }_{z+1}}}{\sqrt{{\left(2-I_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}+{\left(I_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}},\hfill \\ \hfill \frac{\sqrt{{\left(1+N_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}-{\left(1-N_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}}{\sqrt{{\left(1+N_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}+{\left(1-N_{{♭}_{z+1}}^2\right)}^{{\beth }_{z+1}}}}\hfill \end{array}\right)$$

$$=\left(\begin{array}{c}\hfill \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^{z+1}{\left(P_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(2-P_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^{z+1}{\left(P_{{♭}_g}^2\right)}^{{\beth }_g}}},\hfill \\ \hfill \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^{z+1}{\left(I_{{♭}_g}\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(2-I_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^{z+1}{\left(I_{{♭}_g}^2\right)}^{{\beth }_g}}},\hfill \\ \hfill \frac{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(1+N_{{♭}_g}^2\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^{z+1}{\left(1-N_{{♭}_g}^2\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^{z+1}{\left(1+N_{{♭}_g}^2\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^{z+1}{\left(1-N_{{♭}_g}^2\right)}^{{\beth }_g}}}\hfill \end{array}\right)$$

that is, when $n=z+1$, Equation (2) also holds.

Hence, Equation (2) holds for any $n$.  $\square$

The following properties of SFEWG operator can be simply proved obviously by Definition 8.

• 1)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$, if ${\tilde{F}}_1={\tilde{F}}_2=\text{…}{\tilde{F}}_{n-1}={\tilde{F}}_n=\tilde{F}$, then

  $$SFEWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\tilde{F}.$$
• 2)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and ${\tilde{F}}^{-}=\underset{g}{\min }{\tilde{F}}_g$, ${\tilde{F}}^{+}=\underset{g}{\max }{\tilde{F}}_g$. Then,

  $${\tilde{F}}^{-}\le SFEWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le {\tilde{F}}^{+}.$$
• 3)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ and ${\tilde{F}}_{\tilde{g}}=\{P_{{♭}_{\tilde{g}}},I_{{♭}_{\tilde{g}}},N_{{♭}_{\tilde{g}}}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g,\tilde{g}\in \mathbb{N}\right)$ such that ${\widetilde{г}}_g\le {\widetilde{г}}_{\tilde{g}}$ for all $g$. Then

  $$SFEWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le SFEWG({\tilde{F}}_{\tilde{1}},{\tilde{F}}_{\tilde{2}},{\tilde{F}}_{\tilde{3}},\text{…},{\tilde{F}}_{\tilde{n}}).$$

Next, we propose the Spherical fuzzy Einstein ordered weighted geometric $\left(SFEOWG\right)$ operator as following:

Definition 13

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$. The Einstein ordered weighted geometric operator for $\hat{S}FN\left(\stackrel{"}{O}\right)$ is characterized as

$$SFEOWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\prod _{g=1}^n{\left({\tilde{F}}_{\mathrm{\Phi }\left(g\right)}\right)}^{{\beth }_g},$$

where $\mathrm{\Phi }\left(g\right)$ is denoted for ordered and $\left(\mathrm{\Phi }\left(1\right),\mathrm{\Phi }\left(2\right),\mathrm{\Phi }\left(3\right),\text{…},\mathrm{\Phi }\left(n\right)\right)$ is a permutation of $\left(1,2,3,\text{…},n\right)$, subject to ${\tilde{F}}_{\mathrm{\Phi }(g-1)}\ge {\tilde{F}}_{\mathrm{\Phi }\left(g\right)}$ for all $g$. Also the weight vector is ${\beth }_g\left(g\in \mathbb{N}\right)$ with ${\beth }_g\ge 0$, ${\sum }_{g=1}^n{\beth }_g=1.$

Theorem 4

Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and the weight vector is ${\beth }_g\left(g\in \mathbb{N}\right)$ with ${\beth }_g\ge 0$, ${\sum }_{g=1}^n{\beth }_g=1.$ The $SFEOWG$ AgOp is a mapping $G^n⟶G$ defined as

$$\begin{array}{ccl}SFEOWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)& =& \sum _{g=1}^n{\left({\tilde{F}}_{\mathrm{\Phi }\left(g\right)}\right)}^{{\beth }_g}\\ & =& \left(\begin{array}{c}\frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(P_{{♭}_{\mathrm{\Phi }\left(g\right)}},)\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-P_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(P_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{2}{\displaystyle \prod }_{g=1}^n{\left(I_{{♭}_{\mathrm{\Phi }\left(g\right)}},)\right)}^{{\beth }_g}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(2-I_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(I_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}},\\ \frac{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+N_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}-{\displaystyle \prod }_{g=1}^n{\left(1-N_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}}{\sqrt{{\displaystyle \prod }_{g=1}^n{\left(1+N_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}+{\displaystyle \prod }_{g=1}^n{\left(1-N_{{♭}_{\mathrm{\Phi }\left(g\right)}}^2,)\right)}^{{\beth }_g}}}\end{array},)\right).\end{array}$$

where $\mathrm{\Phi }\left(g\right)$ is denoted for ordered and $\left(\mathrm{\Phi }\left(1\right),\mathrm{\Phi }\left(2\right),\mathrm{\Phi }\left(3\right),\text{…},\mathrm{\Phi }\left(n\right)\right)$ is a permutation of $\left(1,2,3,\text{…},n\right)$, subject to ${\tilde{F}}_{\mathrm{\Phi }(g-1)}\ge {\tilde{F}}_{\mathrm{\Phi }\left(g\right)}$ for all $g$.

This theorem's proof is identical to Theorem 3 and is therefore excluded here.  $\square$

The following properties of SFEOWG operator can be simply proved obviously by Definition 8.

• 1)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$, if ${\tilde{F}}_1={\tilde{F}}_2=\text{…}{\tilde{F}}_{n-1}={\tilde{F}}_n=\tilde{F}$, then

  $$SFEOWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)=\tilde{F}.$$
• 2)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g\in \mathbb{N}\right)$ and ${\tilde{F}}^{-}=\underset{g}{\min }{\tilde{F}}_g$, ${\tilde{F}}^{+}=\underset{g}{\max }{\tilde{F}}_g$. Then,

  $${\tilde{F}}^{-}\le SFEOWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le {\tilde{F}}^{+}.$$
• 3)
  Let ${\tilde{F}}_g=\{P_{{♭}_g},I_{{♭}_g},N_{{♭}_g}\}$ and ${\tilde{F}}_{\tilde{g}}=\{P_{{♭}_{\tilde{g}}},I_{{♭}_{\tilde{g}}},N_{{♭}_{\tilde{g}}}\}$ $\in \hat{S}FN\left(\stackrel{"}{O}\right)$ $\left(g,\tilde{g}\in \mathbb{N}\right)$ such that ${\tilde{F}}_g\le {\tilde{F}}_{\tilde{g}}$ for all $g$. Then

  $$SFEOWG({\tilde{F}}_1,{\tilde{F}}_2,{\tilde{F}}_3,\text{…},{\tilde{F}}_n)\le SFEOWG({\tilde{F}}_{\tilde{1}},{\tilde{F}}_{\tilde{2}},{\tilde{F}}_{\tilde{3}},\text{…},{\tilde{F}}_{\tilde{n}}).$$

6. ALGORITHMS FOR EMERGENCY DECISION MAKING

The problems of decision making with multiattributes can be displayed in a matrix, The matrix columns and rows are specified by attributes, and alternatives are represented, respectively. Thus, the matrix $D_{n\times m}$, consider a collection of $n$ alternatives $\left\{S_1,S_2,S_3,\text{…},S_n\right\}$ and $m$ criteria/attributes $\left\{f_1,f_2,f_3,\text{…},f_m\right\}$. Attributes weights are described by $W=\left\{{\rho }_1,{\rho }_2,{\rho }_3,\text{…},{\rho }_m\right\}$ with ${\rho }_g\in \left[0,1\right]$, ${\sum }_{g=1}^m{\rho }_g=1$. Consider the matrix $D={\left({\tilde{F}}_{ij}\right)}_{n\times m}={〈{\text{P}}_{ij},{\text{I}}_{ij},{\text{N}}_{ij}〉}_{n\times m},$ represents the spherical fuzzy information. In ordered to construct the algorithm of emergency decision‐making problems for coronavirus (COVID‐19) in the form of spherical fuzzy settings.

$$D_{n\times m}=\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_n\hfill \end{array}\left(\begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \hfill & \hfill f_m\hfill \\ \hfill 〈P_{{♭}_{11}},I_{{♭}_{11}},N_{{♭}_{11}}〉\hfill & \hfill 〈P_{{♭}_{12}},I_{{♭}_{12}},N_{{♭}_{12}}〉\hfill & \hfill \text{⋯}\hfill & \hfill 〈P_{{♭}_{1m}},I_{{♭}_{1m}},N_{{♭}_{1m}}〉\hfill \\ \hfill 〈P_{{♭}_{21}},I_{{♭}_{21}},N_{{♭}_{21}}〉\hfill & \hfill 〈P_{{♭}_{22}},I_{{♭}_{22}},N_{{♭}_{22}}〉\hfill & \hfill \text{⋯}\hfill & \hfill 〈P_{{♭}_{2m}},I_{{♭}_{2m}},N_{{♭}_{2m}}〉\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill 〈P_{{♭}_{n1}},I_{{♭}_{n1}},N_{{♭}_{n1}}〉\hfill & \hfill 〈P_{{♭}_{nm}},I_{{♭}_{nm}},N_{{♭}_{nm}}〉\hfill & \hfill \text{⋯}\hfill & \hfill 〈P_{{♭}_{nm}},I_{{♭}_{nm}},N_{{♭}_{nm}}〉\hfill \end{array}\right)$$

6.1. Analytical hierarchy process

In 1980, Saaty initiated the analytical hierarchy process (AHP), ⁴² a powerful decision‐making mechanism. AHP facilitates decision‐makers in setting goals for various attributes to make the right decision. In pairwise comparisons, the AHP shall determine the weight of each assessment attribute according to the attribute of the decision‐maker.

AHP starts to build a matrix for a pairwise comparisons $г$ to evaluate the weights for the various attributes.

$$F=\left[\begin{array}{ccccc}1& {\varsigma }_{12}& {\varsigma }_{13}& \text{⋯}& {\varsigma }_{1l}\\ {\varsigma }_{21}& 1& {\varsigma }_{23}& \text{⋯}& {\varsigma }_{2l}\\ {\varsigma }_{31}& {\varsigma }_{32}& 1& \text{⋯}& {\varsigma }_{3l}\\ \text{⋮}& \text{⋮}& \text{⋮}& \text{⋱}& \text{⋮}\\ {\varsigma }_{l1}& {\varsigma }_{l2}& {\varsigma }_{l3}& \text{⋯}& 1\end{array}\right]$$

The matrix $F$ is an $l\times l$ real matrix, where $l$ is the list of assessment attributes described. Each element ${\varsigma }_{jg}$ of the matrix $г$ represents the importance of the jth criterion relative to the gth attribute. If ${\varsigma }_{jg}$ $>1$, then the jth attribute is more important than the gth criterion, whereas if ${\varsigma }_{jg}$ $<1$, then the jth attribute is less important than the gth attribute. When two attributes are of the same significance then the component ${\varsigma }_{jg}$ is 1.

Obviously, ${\varsigma }_{jg}=1$ for all $g$. The relative significance of the two attributes is assessed on a scale of 1 to 9, as shown in Table 1.

Table 1.

Scale of importance

Intensity of importance	Definition	Explanation
1	Similar importance (SI)	Both attributes $j$ and $g$ contribute equally
3	Moderate importance (MI)	Experience and judgment slightly favor $j$ over $g$
5	Intense importance (II)	Experience and judgment strongly favor $j$ over $g$
7	Demonstrated importance (DI)	$j$ is favored very strongly over $g$; its dominance is demonstrated in practice
9	Extreme importance (EI)	The evidence favoring $j$ over $g$ is of the highest possible order of affirmation
2,4,6,8 Reciprocal of above	Intermediate values	Reciprocal value

If the matrix $F$ is constructed, the normalized pairwise comparison matrix $\tilde{F}$ can be extracted by keeping sum of the entities in each column equivalent to 1. Elements can be obtained as

$$\overline{{\varsigma }_{jg}}=\frac{{\varsigma }_{jg}}{{\sum }_{j=1}^l{\varsigma }_{jg}}$$

Finally, the attributes weights are computed as

$${\beth }_g=\frac{{\sum }_{g=1}^l\overline{{\varsigma }_{jg}}}{l}$$

6.2. Spherical fuzzy entropy

In 2019, Jin et al., ³² presents the method to determine the weights of the attribute using the fixed spherical fuzzy information presented in Table 2.

Table 2.

Linguistic variables and their corresponding SF‐numbers

Linguistic variables	Corresponding SF‐numbers
Very very bad (VVB)	(0.1, 0.1, 0.9)
Very bad (VB)	(0.2, 0.3, 0.9)
Bad (B)	(0.4, 0.2, 0.8)
Medium (M)	(0.6, 0.2, 0.6)
Good (G)	(0.8, 0.2, 0.5)
Very good (VG)	(0.9, 0.3 ,0.2)
Excellent (E)	(0.9, 0.1, 0.1)

To measure the weights for the various attributes, first, the decision‐maker give the linguistic decision matrix $\Upsilon$ as follows:

$$\Upsilon =\left[\begin{array}{ccccc}\hfill {\varsigma }_{11}\hfill & \hfill {\varsigma }_{12}\hfill & \hfill {\varsigma }_{13}\hfill & \hfill \text{⋯}\hfill & \hfill {\varsigma }_{1l}\hfill \\ \hfill {\varsigma }_{21}\hfill & \hfill {\varsigma }_{22}\hfill & \hfill {\varsigma }_{23}\hfill & \hfill \text{⋯}\hfill & \hfill {\varsigma }_{2l}\hfill \\ \hfill {\varsigma }_{31}\hfill & \hfill {\varsigma }_{32}\hfill & \hfill {\varsigma }_{33}\hfill & \hfill \text{⋯}\hfill & \hfill {\varsigma }_{3l}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill {\varsigma }_{m1}\hfill & \hfill {\varsigma }_{m2}\hfill & \hfill {\varsigma }_{m3}\hfill & \hfill \text{⋯}\hfill & \hfill {\varsigma }_{ml}\hfill \end{array}\right]$$

The matrix $\Upsilon$ is an $m\times l$ rank matrix, where $m$ is the number of evaluation alternative considered and $l$ is the number of evaluation attribute considered. All the linguistic term elements of Matrix $\Upsilon$ convert to spherical fuzzy information according to Table 2. Finally, the weights of the attribute can be calculated as follows:

$${\beth }_j=\frac{1+\frac{1}{m}{\sum }_{i=1}^m{P}_i\log \left(P_i\right)+I_i\log \left(I_i\right)+N_i\log \left(N_i\right)}{{\sum }_{j=1}^l\left(1+\frac{1}{m}{\sum }_{i=1}^m{P}_i\log \left(P_i\right)+I_i\log \left(I_i\right)+N_i\log \left(N_i\right)\right)}\text{such that}i\in m,j\in l$$

where P_i , I_i , and N_i  are the positive, neutral and negative membership degrees, respectively. Measure the closeness coefficient

7. DIFFERENT DECISION MAKING TECHNIQUES

7.1. Technique of aggregating using Einstein aggregation operators

We proposed a method for spherical fuzzy Einstein aggregation operators to resolve MADM difficulties in the context of spherical fuzzy settings. The basic steps contain the algorithm are as follows:

• Step 1.
  The decision maker provide the evaluation of emergency measures to reduced the outbreak of COVID‐19 in linguistic form. After converting the linguistic term to spherical fuzzy number in the decision matrix elements are as follows:

  $$D_{n\times m}=\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_n\hfill \end{array}\left(\begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \hfill & \hfill f_m\hfill \\ \hfill 〈P_{{♭}_{11}},I_{{♭}_{11}},N_{{♭}_{11}}〉\hfill & \hfill 〈P_{{♭}_{12}},I_{{♭}_{12}},N_{{♭}_{12}}〉\hfill & \hfill \text{⋯}\hfill & \hfill 〈P_{{♭}_{1m}},I_{{♭}_{1m}},N_{{♭}_{1m}}〉\hfill \\ \hfill 〈P_{{♭}_{21}},I_{{♭}_{21}},N_{{♭}_{21}}〉\hfill & \hfill 〈P_{{♭}_{22}},I_{{♭}_{22}},N_{{♭}_{22}}〉\hfill & \hfill \text{⋯}\hfill & \hfill 〈P_{{♭}_{2m}},I_{{♭}_{2m}},N_{{♭}_{2m}}〉\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill 〈P_{{♭}_{n1}},I_{{♭}_{n1}},N_{{♭}_{n1}}〉\hfill & \hfill 〈P_{{♭}_{nm}},I_{{♭}_{nm}},N_{{♭}_{nm}}〉\hfill & \hfill \text{⋯}\hfill & \hfill 〈P_{{♭}_{nm}},I_{{♭}_{nm}},N_{{♭}_{nm}}〉\hfill \end{array}\right)$$
• Step 2.

  In this step dealing with application of aggregation operators to decision matrix to aggregate the spherical fuzzy information for alternative. Attributes weights are calculated using AHP and Spherical fuzzy entropy methods.

• Step 2(a).

  Utilization of SFEWA AgOp to accumulate spherical information.

• Step 2(b).

  Utilization of SFEOWA AgOp to accumulate spherical information.

• Step 2(c).

  Utilization of SFEWG AgOp to accumulate spherical information.

• Step 2(d).

  Utilization of SFEOWG AgOp to accumulate spherical information.

• Step 3.

  Determine the scores $\check{s}\check{c}\left({\widetilde{г}}_i\right)$ of aggregated spherical fuzzy numbers and order according to the highest value.

• Step 4.

  Choose the best alternative according to the highest score value.

7.2. Technique for order preference by similarity to ideal solution (TOPSIS) method

We proposed a decision making methodology to solve the MADM problems under spherical fuzzy settings. The TOPSIS method introduced by Hwang and Yoon, ⁴³ it is one of very suitable practical methods of GDM. In practice, the TOPSIS method is based on the idea that the best alternative will be at greatest distance from the negative ideal solution (NIS) and at the shortest distance from the positive ideal solution (PIS). The basic steps contain the algorithm are as follows:

• Step 1.
  The decision maker provide the evaluation of emergency measures to reduced the outbreak of COVID‐19 in linguistic form. After converting the linguistic term to spherical fuzzy number in the decision matrix elements are as follows:

  $$C={\left(c_{ij}\right)}_{m\times l}=\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_m\hfill \end{array}\begin{array}{c}\hfill \begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \text{⋯}\hfill & \hfill f_l\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{cccc}\hfill c_{11}\hfill & \hfill c_{12}\hfill & \hfill \text{⋯}\hfill & \hfill c_{1l}\hfill \\ \hfill c_{21}\hfill & \hfill c_{22}\hfill & \hfill \text{⋯}\hfill & \hfill c_{2l}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill c_{m1}\hfill & \hfill c_{m2}\hfill & \hfill \text{⋯}\hfill & \hfill c_{ml}\hfill \end{array}\right)\hfill \end{array}$$
• Step 2.
  Basically, MADM problems have two types of attributes namely are benefit type and cost type attributes. To facilitate and dimensionless measurements of all the attributes, we proposed the normalize formulas for each attributes value $c_{ij}$ in decision matrix. Normalized decision matrix calculated using following formulas:

  $$D={\left(d_{ij}^N\right)}_{m\times l}=\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_m\hfill \end{array}\begin{array}{c}\hfill \begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \text{⋯}\hfill & \hfill f_l\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{cccc}\hfill d_{11}\hfill & \hfill d_{12}\hfill & \hfill \text{⋯}\hfill & \hfill d_{1l}\hfill \\ \hfill d_{21}\hfill & \hfill d_{22}\hfill & \hfill \text{⋯}\hfill & \hfill d_{2l}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill d_{m1}\hfill & \hfill d_{m2}\hfill & \hfill \text{⋯}\hfill & \hfill d_{ml}\hfill \end{array}\right)\hfill \end{array}$$

  where

  $$d_{ij}=c_{ij},\text{for benefit type attributes}$$

  and

  $$d_{ij}=c{\prime }_{ij}=〈N_{{♭}_{ij}},I_{{♭}_{ij}},P_{{♭}_{ij}}〉,\text{for cost type attributes}.$$
• Step 3.
  Attributes weights are calculated using AHP and spherical fuzzy entropy methods. Suppose that attributes weights $W=\left\{{\rho }_1,{\rho }_2,{\rho }_3,\text{…},{\rho }_l\right\}$ with subject to ${\rho }_j\in \left[0,1\right]$ such that ${\sum }_{j=1}^l{\rho }_j=1$. Weighted normalized decision matrix constructed using following formula:

  $$Z={\left({\rho }_j{d}_{ij}^n\right)}_{m\times l}={\left(z_{ij}\right)}_{m\times l}=\begin{array}{c}\hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_m\hfill \end{array}\begin{array}{c}\hfill \begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \text{⋯}\hfill & \hfill f_l\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{cccc}\hfill z_{11}\hfill & \hfill z_{12}\hfill & \hfill \text{⋯}\hfill & \hfill z_{1l}\hfill \\ \hfill z_{21}\hfill & \hfill z_{22}\hfill & \hfill \text{⋯}\hfill & \hfill z_{2l}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill z_{m1}\hfill & \hfill z_{m2}\hfill & \hfill \text{⋯}\hfill & \hfill z_{ml}\hfill \end{array}\right)\hfill \end{array}$$
• Step 4.
  Identifying the PIS $Z^{+}$ and NIS $Z^{-}$ as follows:

  $$Z^{+}=\left\{z_1^{+},z_2^{+},z_3^{+},\text{…},z_l^{+}\right\},z_j^{+}=\left\{\underset{1\le i\le m}{\max }\left(P_{ij}\right),\underset{1\le i\le m}{\min }\left(I_{ij}\right),\underset{1\le i\le m}{\min }\left(N_{ij}\right)\right\},\left(j\in l\right)$$

  and

  $$Z^{-}=\left\{z_1^{-},z_2^{-},z_3^{-},\text{…},z_l^{-}\right\},z_j^{-}=\left\{\underset{1\le i\le m}{\min }\left(P_{ij}\right),\underset{1\le i\le m}{\min }\left(I_{ij}\right),\underset{1\le i\le m}{\max }\left(N_{ij}\right)\right\},\left(j\in l\right)$$
• Step 5.
  Distance measurement of PIS $Z^{+}$and NIS $Z^{-}$ with each alternative are defined as

  $${\theta }_i^{+}=\sqrt{\sum _{j=1}^m\left({\left(P_{ij}-P_j^{+}\right)}^2+{\left(I_{ij}-I_j^{+}\right)}^2+{\left(N_{ij}-N_j^{+}\right)}^2\right)},i\in l$$

  and

  $${\theta }_i^{-}=\sqrt{\sum _{j=1}^m\left({\left(P_{ij}-P_j^{-}\right)}^2+{\left(I_{ij}-I_j^{-}\right)}^2+{\left(N_{ij}-N_j^{-}\right)}^2\right)},i\in l$$
• Step 6.
  Measure the closeness coefficient to the PIS $Z^{+}$and NIS $Z^{-}$ is defined as

  $${\varrho }_i=\frac{{\theta }_i^{-}}{{\theta }_i^{+}+{\theta }_i^{-}},i\in l.$$

  Rank the ${\varrho }_i$ according to descending order. Choose the larger ${\varrho }_i$ for best alternative.

7.3. GRA method

We provided a decision‐making framework of GRA ⁴⁴ using spherical fuzzy settings to address MADM challenges. The basic steps contain the algorithm are as follows:

• Step 1.
  The decision maker provide the evaluation of emergency measures to reduced the outbreak of COVID‐19 in linguistic form. After converting the linguistic term to spherical fuzzy number in the decision matrix elements are as follows:

  $$C={\left(c_{ij}\right)}_{m\times l}=\begin{array}{c}\hfill \hfill \\ \hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_m\hfill \end{array}\begin{array}{c}\hfill \begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \text{⋯}\hfill & \hfill f_l\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{cccc}\hfill c_{11}\hfill & \hfill c_{12}\hfill & \hfill \text{⋯}\hfill & \hfill c_{1l}\hfill \\ \hfill c_{21}\hfill & \hfill c_{22}\hfill & \hfill \text{⋯}\hfill & \hfill c_{2l}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill c_{m1}\hfill & \hfill c_{m2}\hfill & \hfill \text{⋯}\hfill & \hfill c_{ml}\hfill \end{array}\right)\hfill \end{array}$$
• Step 2.
  Basically, MADM problems have two types of attributes namely are benefit type and cost type attributes. To facilitate and dimensionless measurements of all the attributes, we proposed the normalize formulas for each attributes value $c_{ij}$ in decision matrix. Normalized decision matrix calculated using following formulas:

  $$D={\left(d_{ij}^N\right)}_{m\times l}=\begin{array}{c}\hfill \hfill \\ \hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_m\hfill \end{array}\begin{array}{c}\hfill \begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \text{⋯}\hfill & \hfill f_l\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{cccc}\hfill d_{11}\hfill & \hfill d_{12}\hfill & \hfill \text{⋯}\hfill & \hfill d_{1l}\hfill \\ \hfill d_{21}\hfill & \hfill d_{22}\hfill & \hfill \text{⋯}\hfill & \hfill d_{2l}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill d_{m1}\hfill & \hfill d_{m2}\hfill & \hfill \text{⋯}\hfill & \hfill d_{ml}\hfill \end{array}\right)\hfill \end{array}$$

  where

  $$d_{ij}=c_{ij},\text{for benefit type attributes}$$

  and

  $$d_{ij}=c{\prime }_{ij}=〈N_{{♭}_{ij}},I_{{♭}_{ij}},P_{{♭}_{ij}}〉,\text{for cost type attributes}.$$
• Step 3.
  Identifying the PIS $Z^{+}$and NIS $Z^{-}$as follows:

  $$Z^{+}=\left\{z_1^{+},z_2^{+},z_3^{+},\text{…},z_l^{+}\right\},z_j^{+}=\left\{\underset{1\le i\le m}{\max }\left(P_{ij}\right),\underset{1\le i\le m}{\min }\left(I_{ij}\right),\underset{1\le i\le m}{\min }\left(N_{ij}\right)\right\},\left(j\in l\right)$$

  and

  $$Z^{-}=\left\{z_1^{-},z_2^{-},z_3^{-},\text{…},z_l^{-}\right\},z_j^{-}=\left\{\underset{1\le i\le m}{\min }\left(P_{ij}\right),\underset{1\le i\le m}{\min }\left(I_{ij}\right),\underset{1\le i\le m}{\max }\left(N_{ij}\right)\right\},\left(j\in l\right)$$
• Step 4.
  Distance measurement of PIS $Z^{+}$and NIS $Z^{-}$ with each element of the alternative to determine the spherical fuzzy positive‐ideal separation matrix $H^{+}$ and Spherical fuzzy negative‐ideal separation matrix $H^{-}$ as follows:

  $$H^{+}={\left(h_{ij}^{+}\right)}_{m\times l}=\begin{array}{c}\hfill \hfill \\ \hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_m\hfill \end{array}\begin{array}{c}\hfill \begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \text{⋯}\hfill & \hfill f_l\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{cccc}\hfill h_{11}^{+}\hfill & \hfill h_{12}^{+}\hfill & \hfill \text{⋯}\hfill & \hfill h_{1l}^{+}\hfill \\ \hfill h_{21}^{+}\hfill & \hfill h_{22}^{+}\hfill & \hfill \text{⋯}\hfill & \hfill h_{2l}^{+}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill h_{m1}^{+}\hfill & \hfill h_{m2}^{+}\hfill & \hfill \text{⋯}\hfill & \hfill h_{ml}^{+}\hfill \end{array}\right)\hfill \end{array}$$

  and

  $$H^{-}={\left(h_{ij}^{-}\right)}_{m\times l}=\begin{array}{c}\hfill \hfill \\ \hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill \text{⋮}\hfill \\ \hfill S_m\hfill \end{array}\begin{array}{c}\hfill \begin{array}{cccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill \text{⋯}\hfill & \hfill f_l\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{cccc}\hfill h_{11}^{-}\hfill & \hfill h_{12}^{-}\hfill & \hfill \text{⋯}\hfill & \hfill h_{1l}^{-}\hfill \\ \hfill h_{21}^{-}\hfill & \hfill h_{22}^{-}\hfill & \hfill \text{⋯}\hfill & \hfill h_{2l}^{-}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋱}\hfill & \hfill \text{⋮}\hfill \\ \hfill h_{m1}^{-}\hfill & \hfill h_{m2}^{-}\hfill & \hfill \text{⋯}\hfill & \hfill h_{ml}^{-}\hfill \end{array}\right)\hfill \end{array}$$

  where

  $$h_{ij}^{+}=\sqrt{{\left(d_{ij}-z_j^{-},)\right)}^2} \text{and }{h}_{ij}^{-}=\sqrt{{\left(d_{ij}-z_j^{-},)\right)}^2} \text{with }i\in m,j\in l$$
• Step 5.
  Determine of Grey coefficients matrices using following formulas: 

  $${\mathrm{\Omega }}_{ij}^{+}=\frac{{\min }_{1\le i\le m}{\min }_{1\le j\le l}{h}_{ij}^{+}+\rho \left(\underset{1\le i\le m}{\max }{\max }_{1\le j\le l}{h}_{ij}^{+}\right)}{h_{ij}^{+}+\rho \left({\max }_{1\le i\le m}{\max }_{1\le j\le l}{h}_{ij}^{+}\right)}$$

  and

  $${\mathrm{\Omega }}_{ij}^{-}=\frac{{\min }_{1\le i\le m}{\min }_{1\le j\le l}{h}_{ij}^{-}+\rho \left({\max }_{1\le i\le m}{\max }_{1\le j\le l}{h}_{ij}^{-}\right)}{h_{ij}^{-}+\rho \left({\max }_{1\le i\le m}{\max }_{1\le j\le l}{h}_{ij}^{-}\right)}$$

  where $\mathit{\text{I}}\in m,j\in l$ and $\rho =0.5$ be a fixed coefficient.
• Step 6.
  Attributes weights are calculated using AHP and spherical fuzzy entropy methods. Suppose that attributes weights $W=\left\{{\rho }_1,{\rho }_2,{\rho }_3,\text{…},{\rho }_l\right\}$ with subject to ${\rho }_j\in \left[0,1\right]$ such that ${\sum }_{j=1}^l{\rho }_j=1$. Grey coefficient are obtained as follows:

  $${\theta }_i^{+}=\sum _{j=1}^m{\rho }_j{\mathrm{\Omega }}_{ij}^{+},i\in l$$

  and

  $${\theta }_i^{-}=\sum _{j=1}^m{\rho }_j{\mathrm{\Omega }}_{ij}^{-},i\in l$$
• Step 7.
  Measure the closeness coefficients are obtained as follows:

  $${\varrho }_i=\frac{{\theta }_i^{-}}{{\theta }_i^{+}+{\theta }_i^{-}},i\in l.$$

  Rank the ${\varrho }_i$ according to descending order. Choose the larger ${\varrho }_i$ for best alternative.

8. APPLICATION OF EMERGENCY DECISION MAKING

Under this section, a real case on public health emergency decision‐making for an outbreak of COVID‐19 that occurred in China is presented to demonstrate the application of the proposed techniques.

8.1. Case study

To demonstrate the applicability and validity of the proposed methods, we extant a real case study about an emergency caused by an outbreak of novel coronavirus disease (NCOVID‐19) pandemic that occurred in China.

Actions taken by governments and organizations: The spread was first observed around December 2019 in Wuhan, Hubei, China, and reported by the World Health Organization (WHO) on March 11, 2020 as an epidemic disease. The novel coronavirus pushed the Chinese government to implement the largest lockdown in human history in early 2020, threatening an approximate 45 million population. The WHO has announced the name of the virus “Novel Coronavirus (COVID‐19).” On January 30, 2020 the WHO Director‐General disclosed that the epidemic is causing an international public health emergency.

As of March 25, 2020, more than 436 481 confirmed cases and 19 643 confirmed deaths are reported in 196 countries, areas, or territories. The infected and deaths cases graph are as follows in Figure 1.

Figure 1.

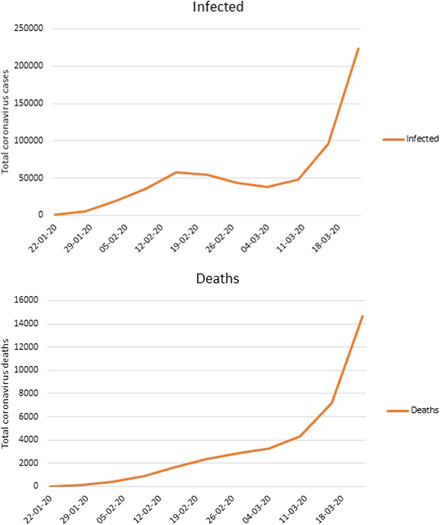
Graph of infected and death case of Coronavirus [Color figure can be viewed at wileyonlinelibrary.com]

Also the statistics of active and closed cases are as follows in Figure 2.

Figure 2.

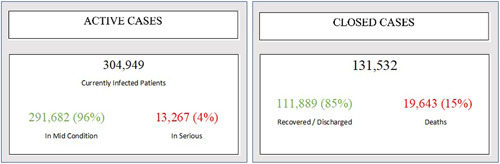
Graph of active and closed case of Coronavirus [Color figure can be viewed at wileyonlinelibrary.com]

The risk of it spreading further is very high. The outbreak has been defined by WHO as a public Health Emergency of international concern. There was no doubt that this disease caused huge economic losses, environmental pollution, insufficient of personal protective equipment (PPE), PPE consists of respiratory/surgical masks, gloves, face protection. The potential for extending the supply of PPE is restricted, and the current requirement for respirators and masks can not be achieved, especially if the widespread, improper use of PPE continues. The WHO collaborates with public health experts and laboratory partnerships, prevention and monitoring of diseases, clinical management and mathematical modeling.

In such situation, it is essential to provide an efficient way in emergency response for avoiding additional losses and to save the lives of the people. Preventive and mitigation measures are key in both health care and community settings. Due to such an emergency decision, the health experts have to make an immediate response, urgently rescue to control the situation efficiently and stop it from more deaths. There are eight basic public health emergency factor to reduce the general risk of this disease. The most effective preventive measure in the community include the following:

Clinical management (${\mathbb{C}}_1$): Vaccination after dispersal of the virus is a massively effective means of reducing these deadly diseases. Vaccines are actually quite effective, and severe side effects are rare. There are currently no clear treatments suitable for COVID‐19. Clinical management requires timely adoption of approved initiatives for disease prevention and control, and support for complication management, providing strategic organ care where necessary.

First‐aid training (${\mathbb{C}}_2$): This disease spread very quickly, so to control on this virus first, trained, or avoid people of this disease symptoms. It is therefore highly recommended that individuals attend a fully supervised practical or online first aid course to learn how to get out of medical emergency.

Increased personal protective equipment (${\mathbb{C}}_3$): The lack of testing kits is another factor, the situation will be improved with increased production of testing kits, the loosing of confirmation criteria and the local governments decision to threat and finally quarantine all suspected cases. Masks, gloves, respirators and gowns to countries in every region. Face masks provide limited protection in preventing some one infected from spreading the virus. Therefore, the easiest way to prevent spread, is by good personal hygiene. However, the world is facing severve disruption in the marked for PPE.

Trained technician (${\mathbb{C}}_4$): It is extremely quick to share the genetic makeup of the virus to enable the rest of the world begin developing specific screening and start working on potential vaccines.

Banned intra‐city transportation (${\mathbb{C}}_5$): The disease caused by the virus is serious. For safety of local people it is necessary for local government that take step or announced to banned intra‐city transportation to force patients to local community clinics. And also suspended all flights and train services from and to Wuhan and cancelled their lunar new year celebrations, and you must also keep a distance of at least 1 m (3 feet) both yourself and somebody who coughs or sneezes.

Global uncertainty (${\mathbb{C}}_6$): The economic fallout from coronavirus: Rapid reduction in the transport and hospitality sectors will damage the economy in the short term and will also harm consumption and trade in the first quarter. It may significantly affect the country's overall economic situation. It has implications, not just for China, but for the entire world. The world depend on Chinese growth. The novel coronavirus has directly affected global oil market. Factory closure delays delivery of goods and parts from China impacting companies worldwide, along with Apple and Nissan.

Country‐level coordination and planning (${\mathbb{C}}_7$): Each government needs the best level of cooperation with its province/states to prepare to overcome the novel uncertainty in the form of COVID‐19.

Monitoring (${\mathbb{C}}_8$): Every government should appoint health and emergency decision‐making experts to assess and track the current situation of every country and provide advice on how to improve the situation.

Suppose that there are five emergency alternatives namely risk communication (RC), lock down the borders and cities (LD), healthcare system (HCS), research needs (RN), and consulted experts (CE), respectively.

Health expert evaluated their information using fuzzy linguistic variable terms (given in Table 2) are shown in the Table 3.

Table 3.

Corresponding linguistic information

	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
$RC$	G	G	VB	VG	B	VB	VG	VB
$LD$	VG	B	M	E	G	VG	M	B
$HCS$	B	E	VB	VG	B	G	M	E
$RN$	VVB	VG	M	G	VG	VB	B	M
$CE$	E	VB	G	B	M	VVB	G	VG

Abbreviations: CE, consulted experts; HCS, healthcare system; LD, lock down the borders and cities; RC, risk communication; RN, research needs.

Based on the Table 2, health expert evaluated fuzzy linguistic information and their corresponding spherical fuzzy numbers are given in Table 4.

Table 4.

Converted spherical fuzzy information

	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$
$RC$	(0.8, 0.2, 0.5)	(0.8, 0.2, 0.5)	(0.2, 0.3, 0.9)	(0.9, 0.3, 0.2)
$LD$	(0.9, 0.3, 0.2)	(0.4, 0.2, 0.8)	(0.6, 0.2, 0.6)	(0.9, 0.1, 0.1)
$HCS$	(0.4, 0.2, 0.8)	(0.9, 0.1, 0.1)	(0.2, 0.3, 0.9)	(0.9, 0.3, 0.2)
$RN$	(0.1, 0.1, 0.9)	(0.9, 0.3, 0.2)	(0.6, 0.2, 0.6)	(0.8, 0.2, 0.5)
$CE$	(0.9, 0.1, 0.1)	(0.2, 0.3, 0.9)	(0.8, 0.2, 0.5)	(0.4, 0.2, 0.8)

	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
$RC$	(0.4, 0.2, 0.8)	(0.2, 0.3, 0.9)	(0.9, 0.3, 0.2)	(0.2, 0.3, 0.9)
$LD$	(0.8, 0.2, 0.5)	(0.9, 0.3, 0.2)	(0.6, 0.2, 0.6)	(0.4, 0.2, 0.8)
$HCS$	(0.4, 0.2, 0.8)	(0.8, 0.2, 0.5)	(0.6, 0.2 ,0.6)	(0.9, 0.1, 0.1)
$RN$	(0.9, 0.3, 0.2)	(0.2, 0.3, 0.9)	(0.4, 0.2, 0.8)	(0.6, 0.2, 0.6)
$CE$	(0.6, 0.2, 0.6)	(0.1, 0.1, 0.9)	(0.8, 0.2, 0.5)	(0.9, 0.3, 0.2)

Abbreviations: CE, consulted experts; HCS, healthcare system; LD, lock down the borders and cities; RC, risk communication; RN, research needs.

8.2. Compute the weight of attributes using AHP

First, we need to compute the pairwise comparison matrix $г.$ In this regarding, the pairwise comparison matrix $г$ is computed using Table 3 as follows:

$$F=\left[\begin{array}{cccccccc}{\mathrm{ℂ}}_1& {\mathrm{ℂ}}_2& {\mathrm{ℂ}}_3& {\mathrm{ℂ}}_4& {\mathrm{ℂ}}_5& {\mathrm{ℂ}}_6& {\mathrm{ℂ}}_7& {\mathrm{ℂ}}_8\\ 1& 1& 7& \frac{1}{3}& 5& 7& \frac{1}{3}& 7\\ 1& 1& 7& \frac{1}{3}& 5& 7& \frac{1}{3}& 7\\ \frac{1}{7}& \frac{1}{7}& 1& \frac{1}{5}& \frac{1}{3}& \frac{1}{3}& \frac{1}{5}& 1\\ 3& 3& 5& 1& 7& 5& 1& 5\\ \frac{1}{5}& \frac{1}{5}& 3& \frac{1}{7}& 1& 3& \frac{1}{7}& 3\\ \frac{1}{7}& \frac{1}{7}& 3& \frac{1}{5}& \frac{1}{3}& 1& \frac{1}{5}& 1\\ 3& 3& 5& 1& 7& 5& 1& 5\\ \frac{1}{7}& \frac{1}{7}& 1& \frac{1}{5}& \frac{1}{3}& 1& \frac{1}{5}& 1\end{array}\right]$$

Normalized matrix is computed by dividing the components of the matrix $г$ to the sum of its corresponding column components. Weights of the attribute are computed by taking the average of the row elements of the normalized pairwise comparison matrix. Weights of the attribute are computed as follows:

$$W^1=\left[\begin{array}{cccccccc}\hfill {\mathbb{C}}_1\hfill & \hfill {\mathbb{C}}_2\hfill & \hfill {\mathbb{C}}_3\hfill & \hfill {\mathbb{C}}_4\hfill & \hfill {\mathbb{C}}_5\hfill & \hfill {\mathbb{C}}_6\hfill & \hfill {\mathbb{C}}_7\hfill & \hfill {\mathbb{C}}_8\hfill \\ \hfill 0.164\hfill & \hfill 0.164\hfill & \hfill 0.030\hfill & \hfill 0.256\hfill & \hfill 0.058\hfill & \hfill 0.041\hfill & \hfill 0.256\hfill & \hfill 0.033\hfill \end{array}\right]$$

Graphical representation is given in Figure 3.

Figure 3.

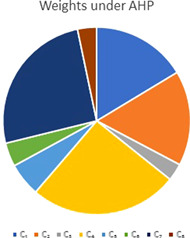
Attributes weights under analytical hierarchy process method [Color figure can be viewed at wileyonlinelibrary.com]

8.3. Compute the weight of attributes using spherical fuzzy entropy

The weights of the attribute can be calculate as following formula and also Tables 2 and 4 are utilized to obtain the spherical fuzzy information

$${\beth }_j=\frac{1+\frac{1}{m}{\sum }_{i=1}^m{P}_i\log \left(P_i\right)+I_i\log \left(I_i\right)+N_i\log \left(N_i\right)}{\sum _{j=1}^l\left(1+\frac{1}{m}{\sum }_{i=1}^m{P}_i\log \left(P_i\right)+I_i\log \left(I_i\right)+N_i\log \left(N_i\right)\right)}\text{such that}i\in m,j\in l$$

where P_i , I_i , and N_i  are the positive, neutral, and negative membership degrees, respectively. Weights of the attribute are computed as

$$W^2=\left[\begin{array}{cccccccc}\hfill {\mathbb{C}}_1\hfill & \hfill {\mathbb{C}}_2\hfill & \hfill {\mathbb{C}}_3\hfill & \hfill {\mathbb{C}}_4\hfill & \hfill {\mathbb{C}}_5\hfill & \hfill {\mathbb{C}}_6\hfill & \hfill {\mathbb{C}}_7\hfill & \hfill {\mathbb{C}}_8\hfill \\ \hfill 0.171\hfill & \hfill 0.144\hfill & \hfill 0.089\hfill & \hfill 0.144\hfill & \hfill 0.086\hfill & \hfill 0.155\hfill & \hfill 0.078\hfill & \hfill 0.133\hfill \end{array}\right]$$

Graphical representation is given in Figure 4.

Figure 4.

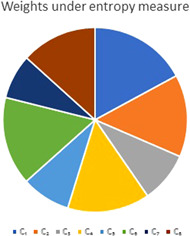
Attributes weights under entropy measure [Color figure can be viewed at wileyonlinelibrary.com]

8.4. Emergency decision making using Einstein aggregation operators

The algorithmic steps are calculated as follows:

• Step 1.

  First, we convert the linguistic information of Table 3 is converted in to the Table 4 as a spherical fuzzy information.

• Step 2.

  The aggregated data is summarized in Table 4 using proposed Einstein aggregation operators.

Using AHP weights

Step 2(a). The aggregated data is summarized in Table 5A using SFEWA AgOp as follows:

Table 5A.

Aggregated SF information (SFEWA)

$RC$	(0.8278, 0.2561, 0.3524)
$LD$	(0.7786, 0.1817, 0.3310)
$HCS$	(0.7670, 0.1956, 0.3572)
$RN$	(0.6870, 0.1982, 0.5489)
$CE$	(0.7612, 0.1876, 0.4430)

Step 2(b) The aggregated data is summarized in Table 5B using SFEWG AgOp as follows.

Table 5B.

Aggregated SF information (SFEWG)

$RC$	(0.7359, 0.2561, 0.5093)
$LD$	(0.6972, 0.1817, 0.5248)
$HCS$	(0.6667, 0.1956, 0.5573)
$RN$	(0.4825, 0.1982, 0.6929)
$CE$	(0.6220, 0.1876, 0.6124)

Step 2(c). The aggregated data is summarized in Table 5C using SFEOWA AgOp as follows.

Table 5C.

Aggregated SF information (SFEOWA)

$RC$	(0.7372, 0.2604, 0.4874)
$LD$	(0.7642, 0.1630, 0.3589)
$HCS$	(0.7697, 0.1927, 0.3914)
$RN$	(0.6918, 0.1937, 0.4984)
$CE$	(0.7418, 0.1617, 0.4282)

Step 2(d). The aggregated data is summarized in Table 5D using SFEOWG AgOp as follows.

Table 5D.

Aggregated SF information (SFEOWG)

$RC$	(0.5400, 0.2604, 0.6809)
$LD$	(0.6839, 0.1927, 0.5653)
$HCS$	(0.6615, 0.1630, 0.5830)
$RN$	(0.4449, 0.1937, 0.6774)
$CE$	(0.4854, 0.1617, 0.6557)

Using spherical fuzzy entropy weights

Step 2(a). The aggregated data is summarized in Table 6 using SFEWA AgOp as follows.

Table 6.

Aggregated SF information (SFEWA)

$RC$	(0.6900, 0.2553, 0.5589)
$LD$	(0.7633, 0.1819, 0.3591)
$HCS$	(0.7784, 0.2070, 0.3615)
$RN$	(0.6635, 0.2082, 0.5567)
$CE$	(0.7415, 0.1790, 0.4320)

Table 7.

Aggregated SF information (SFEWG)

$RC$	(0.4882, 0.2553, 0.7226)
$LD$	(0.6868, 0.2070, 0.5476)
$HCS$	(0.6363, 0.1819, 0.5969)
$RN$	(0.4401, 0.2082, 0.7107)
$CE$	(0.5184, 0.1790, 0.6532)

Step 2(b). The aggregated data is summarized in Table 7 using SFEWG AgOp as follows.

Table 8.

Aggregated SF information (SFEOWA)

$RC$	(0.7128, 0.2639, 0.5134)
$LD$	(0.7515, 0.1763, 0.3630)
$HCS$	(0.7730, 0.1956, 0.3689)
$RN$	(0.7022, 0.2277, 0.5000)
$CE$	(0.7304, 0.1888, 0.4372)

Step 2(c). The aggregated data is summarized in Table 8 using SFEOWA AgOp as follows.

Table 9.

Aggregated SF information (SFEOWG)

$RC$	(0.5032, 0.2639, 0.7073)
$LD$	(0.6949, 0.1956, 0.5385)
$HCS$	(0.6087, 0.1763, 0.6180)
$RN$	(0.5221, 0.2277, 0.6664)
$CE$	(0.5473, 0.1888, 0.6525)

Step 2(d). The aggregated data is summarized in Table 9 using SFEOWG AgOp as follows.

Table 9A.

Score function under AHP weights

	SFEWA	SFEWG	SFEOWA	SFEOWG
$RC$	0.73977	0.65684	0.66308	0.53285
$LD$	0.75530	0.66356	0.74740	0.64193
$HCS$	0.73804	0.63790	0.72851	0.63846
$RN$	0.64660	0.53044	0.66655	0.52457
$CE$	0.71020	0.60734	0.71727	0.55596

Table 9B.

Score function under SF entropy weights

	SFEWA	SFEWG	SFEOWA	SFEOWG
$RC$	0.62526	0.50342	0.64515	0.51064
$LD$	0.74075	0.64405	0.73734	0.65356
$HCS$	0.73661	0.61915	0.73612	0.60474
$RN$	0.63285	0.50705	0.65819	0.54268
$CE$	0.71011	0.56205	0.70148	0.56866

Step 3. Score function calculated using Definition 9 as follows in Table 9A and 9B.

Step 4. Pick the best alternative as described according to the highest score value.

According to score function under AHP weights
	Schemes
SFEWA	$2>1>3>5>4$
SFEWG	$2>1>3>5>4$
SFEOWA	$2>3>5>4>1$
SFEOWG	$2>3>5>1>4$

According to score function under SF entropy weights
	Schemes
SFEWA	$2>3>5>4>1$
SFEWG	$2>3>5>4>1$
SFEOWA	$2>3>5>4>1$
SFEOWG	$2>3>5>4>1$

Hence, $LD$ is the best alternative according to give attributes.

8.5. Emergency decision making using TOPSIS method

The algorithmic steps are calculated as follows:

Step 1. In this step, we convert the linguistic information of Table 3 is converted in to the Table 4 as a spherical fuzzy information.

Step 2. As, the spherical fuzzy information are benefit type. So, the normalized decision matrix computed in Table 10 as follows.

Table 10.

Normalized decision matrix

	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$
$RC$	(0.8, 0.2, 0.5)	(0.8, 0.2, 0.5)	(0.2, 0.3, 0.9)	(0.9, 0.3, 0.2)
$LD$	(0.9, 0.3, 0.2)	(0.4, 0.2, 0.8)	(0.6, 0.2, 0.6)	(0.9, 0.1, 0.1)
$HCS$	(0.4, 0.2, 0.8)	(0.9, 0.1, 0.1)	(0.2, 0.3, 0.9)	(0.9, 0.3, 0.2)
$RN$	(0.1, 0.1, 0.9)	(0.9, 0.3, 0.2)	(0.6, 0.2, 0.6)	(0.8, 0.2, 0.5)
$CE$	(0.9, 0.1, 0.1)	(0.2, 0.3, 0.9)	(0.8, 0.2, 0.5)	(0.4, 0.2, 0.8)

	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
$RC$	(0.4, 0.2, 0.8)	(0.2, 0.3, 0.9)	(0.9, 0.3, 0.2)	(0.2, 0.3, 0.9)
$LD$	(0.8, 0.2, 0.5)	(0.9, 0.3, 0.2)	(0.6, 0.2, 0.6)	(0.4, 0.2, 0.8)
$HCS$	(0.4, 0.2, 0.8)	(0.8, 0.2, 0.5)	(0.6, 0.2, 0.6)	(0.9, 0.1, 0.1)
$RN$	(0.9, 0.3, 0.2)	(0.2, 0.3, 0.9)	(0.4, 0.2, 0.8)	(0.6, 0.2, 0.6)
$CE$	(0.6, 0.2, 0.6)	(0.1, 0.1, 0.9)	(0.8, 0.2, 0.5)	(0.9, 0.3, 0.2)

Step 3. (Case 1. Using AHP weights) Weighted normalized decision matrix computed as follows; Table 11.

Table 11.

Weighted normalized decision matrix

Schemes	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$
1	(0.392, 0.768, 0.892)	(0.392, 0.768, 0.892)	(0.034, 0.964, 0.996)	(0.588, 0.734, 0.662)
2	(0.488, 0.820, 0.768)	(0.167, 0.768, 0.964)	(0.115, 0.952, 0.984)	(0.588, 0.554, 0.554)
3	(0.167, 0.768, 0.964)	(0.488, 0.685, 0.685)	(0.034, 0.964, 0.996)	(0.588, 0.734, 0.662)
4	(0.040, 0.685, 0.982)	(0.488, 0.820, 0.768)	(0.115, 0.952, 0.984)	(0.479, 0.662, 0.837)
5	(0.488, 0.685, 0.685)	(0.081, 0.820, 0.982)	(0.173, 0.952, 0.984)	(0.479, 0.662, 0.837)

Schemes	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
1	(0.100, 0.910, 0.987)	(0.040, 0.951, 0.995)	(0.588, 0.734, 0.662)	(0.036, 0.961, 0.996)
2	(0.239, 0.910, 0.987)	(0.256, 0.951, 0.936)	(0.328, 0.662, 0.877)	(0.075, 0.948, 0.992)
3	(0.100, 0.910, 0.987)	(0.202, 0.936, 0.971)	(0.328, 0.662, 0.877)	(0.230, 0.926, 0.926)
4	(0.303, 0.932, 0.910)	(0.040, 0.951, 0.995)	(0.208, 0.662, 0.944)	(0.120, 0.948, 0.983)
5	(0.159, 0.910, 0.970)	(0.020, 0.909, 0.995)	(0.479, 0.662, 0.837)	(0.230, 0.961, 0.948)

(Case 2: Using spherical fuzzy entropy weights) Table 12.

Table 12.

Weighted normalized decision matrix

Schemes	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$
1	(0.400, 0.759, 0.888)	(0.369, 0.793, 0.905)	(0.060, 0.898, 0.990)	(0.461, 0.840, 0.793)
2	(0.497, 0.813, 0.759)	(0.157, 0.793, 0.968)	(0.197, 0.866, 0.955)	(0.461, 0.717, 0.717)
3	(0.171, 0.759, 0.962)	(0.461, 0.717, 0.717)	(0.060, 0.898, 0.990)	(0.461, 0.840, 0.793)
4	(0.041, 0.674, 0.982)	(0.461, 0.840, 0.793)	(0.197, 0.866, 0.955)	(0.369, 0.793, 0.905)
5	(0.497, 0.674, 0.674)	(0.076, 0.840, 0.984)	(0.294, 0.866, 0.955)	(0.369, 0.793, 0.905)

Schemes	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
1	(0.121, 0.870, 0.980)	(0.079, 0.829, 0.983)	(0.348, 0.910, 0.882)	(0.073, 0.852, 0.986)
2	(0.290, 0.870, 0.980)	(0.476, 0.829, 0.779)	(0.184, 0.882, 0.960)	(0.151, 0.807, 0.970)
3	(0.121, 0.870, 0.980)	(0.382, 0.779, 0.898)	(0.184, 0.882, 0.960)	(0.445, 0.736, 0.736)
4	(0.364, 0.901, 0.870)	(0.079, 0.829, 0.983)	(0.116, 0.882, 0.982)	(0.240, 0.807, 0.934)
5	(0.194, 0.870, 0.957)	(0.039, 0.699, 0.983)	(0.276, 0.882, 0.947)	(0.445, 0.852, 0.807)

Step 4. Identifying the PIS $Z^{+}$and NIS $Z^{-}$as follows:

Case 1.

$$Z^{+}=\left\{\begin{array}{c}\hfill \left(0.488,0.685,0.685\right),\left(0.488,0.685,0.685\right),\left(0.173,0.952,0.984\right),\left(0.588,0.554,0.554\right),\hfill \\ \hfill \left(0.303,0.910,0.910\right),\left(0.256,0.909,0.936\right),\left(0.588,0.662,0.662\right),\left(0.230,0.926,0.926\right)\hfill \end{array}\right\}$$

and

$$Z^{-}=\left\{\begin{array}{c}\hfill \left(0.040,0.685,0.982\right),\left(0.081,0.685,0.982\right),\left(0.034,0.952,0.996\right),\left(0.479,0.554,0.837\right),\hfill \\ \hfill \left(0.100,0.910,0.987\right),\left(0.020,0.909,0.995\right),\left(0.208,0.662,0.944\right),\left(0.075,0.926,0.996\right)\hfill \end{array}\right\}$$

Case 2.

$$Z^{+}=\left\{\begin{array}{l}(0.497,0.674,0.674),(0.461,0.717,0.717),(0.294,0.866,0.955),(0.461,0.717,0.717),\\ (0.364,0.870,0.870),(0.476,0.699,0.779),(0.348,0.882,0.882),(0.445,0.736,0.736)\end{array}\right\}$$

and

$$Z^{-}=\left\{\begin{array}{l}(0.041,0.674,0.982),(0.076,0.717,0.984),(0.060,0.866,0.990),(0.369,0.717,0.905),\\ (0.121,0.870,0.980),(0.039,0.699,0.983),(0.116,0.882,0.982),(0.073,0.736,0.986)\end{array}\right\}$$

Step 5. Distance measurement of PIS $Z^{+}$ with each alternative are computed as follows Table 13A.

Table 13A.

Distance measurement of PIS $Z^{+}$

Case 1: Using AHP weights		Case 2: Spherical fuzzy entropy weights
$RC$	${\theta }_1^{+}=0.754078$	$RC$	${\theta }_1^{+}=0.832059$
$LD$	${\theta }_2^{+}=0.608874$	$LD$	${\theta }_2^{+}=0.641222$
$HCS$	${\theta }_3^{+}=0.645970$	$HCS$	${\theta }_3^{+}=0.638656$
$RN$	${\theta }_4^{+}=0.844492$	$RN$	${\theta }_4^{+}=0.865744$
$CE$	${\theta }_5^{+}=0.709539$	$CE$	${\theta }_5^{+}=0.762356$

Distance measurement of NIS $Z^{-}$ with each alternative are computed as follows Table 13B.

Table 13B.

Distance measurement of PIS $Z^{+}$

Case 1: Using AHP weights		Case 2: Spherical fuzzy entropy weights
$RC$	${\theta }_1^{-}=0.747094$	$RC$	${\theta }_1^{-}=0.613389$
$LD$	${\theta }_2^{-}=0.692229$	$LD$	${\theta }_2^{-}=0.804692$
$HCS$	${\theta }_3^{-}=0.669406$	$HCS$	${\theta }_3^{-}=0.786360$
$RN$	${\theta }_4^{-}=0.552751$	$RN$	${\theta }_4^{-}=0.593169$
$CE$	${\theta }_5^{-}=0.684172$	$CE$	${\theta }_5^{-}=0.771936$

Step 6. Measure the closeness coefficients are computed as follows Table 14.

Table 14.

Closeness coefficients

Case 1: Using AHP weights		Case 2: Spherical fuzzy entropy weights
$RC$	${\varrho }_1=0.497674$	$RC$	${\varrho }_1=0.613389$
$LD$	${\varrho }_2=0.532032$	$LD$	${\varrho }_2=0.804692$
$HCS$	${\varrho }_3=0.508908$	$HCS$	${\varrho }_3=0.786360$
$RN$	${\varrho }_4=0.395601$	$RN$	${\varrho }_4=0.593169$
$CE$	${\varrho }_5=0.490900$	$CE$	${\varrho }_5=0.771936$

Hence,  $LD$ is the best choice according to attributes.

8.6. Emergency decision making using GRA method

The algorithmic steps are calculated as follows:

Step 1. In this step, we convert the linguistic information of Table 3 is converted in to the Table 4 as a spherical fuzzy information.

Step 2. As, the spherical fuzzy information are benefit type. So, the normalized decision matrix is already computed in Table 10.

Step 3. Identifying the PIS $Z^{+}$and NIS $Z^{-}$as follows:

$$Z^{+}=\left\{\begin{array}{c}\hfill \left(0.9,0.1,0.1\right),\left(0.9,0.1,0.1\right),\left(0.8,0.2,0.5\right),\left(0.9,0.1,0.1\right),\hfill \\ \hfill \left(0.9,0.2,0.2\right),\left(0.9,0.1,0.2\right),\left(0.9,0.2,0.2\right),\left(0.9,0.1,0.1\right)\hfill \end{array}\right\}$$

and

$$Z^{-}=\left\{\begin{array}{c}\hfill \left(0.1,0.1,0.9\right),\left(0.2,0.1,0.9\right),\left(0.2,0.2,0.9\right),\left(0.4,0.1,0.8\right),\hfill \\ \hfill \left(0.4,0.2,0.8\right),\left(0.1,0.1,0.9\right),\left(0.4,0.2,0.8\right),\left(0.2,0.1,0.9\right)\hfill \end{array}\right\}$$

Step 4. Distance measurement of PIS $Z^{+}$ with each element of the alternative to determine the spherical fuzzy positive‐ideal separation matrix $H^{+}$ computed in Table 15 as follows.

Table 15.

Positive‐ideal separation matrix $H^{+}$

Schemes	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
1	(0.300)	(0.300)	(0.514)	(0.158)	(0.552)	(0.714)	(0.070)	(0.764)
2	(0.158)	(0.612)	(0.158)	(0.000)	(0.223)	(0.141)	(0.353)	(0.612)
3	(0.612)	(0.000)	(0.514)	(0.158)	(0.552)	(0.234)	(0.353)	(0.000)
4	(0.800)	(0.158)	(0.158)	(0.300)	(0.070)	(0.714)	(0.552)	(0.418)
5	(0.000)	(0.764)	(0.000)	(0.612)	(0.353)	(0.751)	(0.223)	(0.158)

Distance measurement of NIS $Z^{-}$ with each element of the alternative to determine the spherical fuzzy negative‐ideal separation matrix $H^{-}$ computed in Table 16 as follows.

Table 16.

Negative‐ideal separation matrix $H^{-}$

Schemes	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
1	(0.574)	(0.514)	(0.070)	(0.570)	(0.000)	(0.158)	(0.556)	(0.141)
2	(0.764)	(0.173)	(0.353)	(0.608)	(0.353)	(0.764)	(0.200)	(0.173)
3	(0.234)	(0.751)	(0.070)	(0.570)	(0.000)	(0.574)	(0.200)	(0.751)
4	(0.000)	(0.714)	(0.353)	(0.360)	(0.556)	(0.158)	(0.000)	(0.360)
5	(0.800)	(0.141)	(0.509)	(0.070)	(0.200)	(0.000)	(0.353)	(0.714)

Step 5. Determine of Grey coefficient in Tables 17 and 18 as follows.

Table 17.

Grey coefficients for PIS

Schemes	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
1	(0.560)	(0.560)	(0.426)	(0.707)	(0.409)	(0.348)	(0.843)	(0.333)
2	(0.707)	(0.384)	(0.707)	(1.000)	(0.631)	(0.730)	(0.519)	(0.384)
3	(0.384)	(1.000)	(0.426)	(0.707)	(0.409)	(0.619)	(0.519)	(1.000)
4	(0.323)	(0.707)	(0.707)	(0.560)	(0.843)	(0.348)	(0.409)	(0.477)
5	(1.000)	(0.333)	(1.000)	(0.384)	(0.519)	(0.337)	(0.641)	(0.707)

Table 18.

Grey coefficients for NIS

Schemes	${\mathbb{C}}_1$	${\mathbb{C}}_2$	${\mathbb{C}}_3$	${\mathbb{C}}_4$	${\mathbb{C}}_5$	${\mathbb{C}}_6$	${\mathbb{C}}_7$	${\mathbb{C}}_8$
1	(0.399)	(0.426)	(0.843)	(0.401)	(1.000)	(0.707)	(0.407)	(0.730)
2	(0.333)	(0.688)	(0.519)	(0.386)	(0.519)	(0.333)	(0.656)	(0.688)
3	(0.619)	(0.337)	(0.843)	(0.401)	(1.000)	(0.399)	(0.656)	(0.337)
4	(1.000)	(0.348)	(0.519)	(0.514)	(0.407)	(0.707)	(1.000)	(0.514)
5	(0.323)	(0.730)	(0.428)	(0.843)	(0.656)	(1.000)	(0.519)	(0.348)

Step 6. Weighted Grey coefficient are computed in Table 19A as follows Table 19B.

Table 19A.

Weighted Grey coefficients using AHP weights

$RC$	${\theta }_1^{+}=0.668538$	${\theta }_1^{-}=0.516561$
$LD$	${\theta }_2^{+}=0.642794$	${\theta }_2^{-}=0.478885$
$HCS$	${\theta }_3^{+}=0.636117$	${\theta }_3^{-}=0.538667$
$RN$	${\theta }_4^{+}=0.517505$	${\theta }_4^{-}=0.694160$
$CE$	${\theta }_5^{+}=0.578596$	${\theta }_5^{-}=0.625290$

Table 19B.

Weighted Grey coefficients spherical fuzzy entropy weights

$RC$	${\theta }_1^{+}=0.515742$	${\theta }_1^{-}=0.587162$
$LD$	${\theta }_2^{+}=0.642387$	${\theta }_2^{-}=0.497053$
$HCS$	${\theta }_3^{+}=0.654347$	${\theta }_3^{-}=0.531494$
$RN$	${\theta }_4^{+}=0.522915$	${\theta }_4^{-}=0.632721$
$CE$	${\theta }_5^{+}=0.604439$	${\theta }_5^{-}=0.618484$

Step 7. Measure the closeness coefficients are computed in Table 20 as follows.

Table 20.

Closeness coefficients

Using AHP weights		Spherical fuzzy entropy weights
$RC$	${\varrho }_1=0.564120$	$RC$	${\varrho }_1=0.467621$
$LD$	${\varrho }_2=0.573064$	$LD$	${\varrho }_2=0.563774$
$HCS$	${\varrho }_3=0.541476$	$HCS$	${\varrho }_3=0.551800$
$RN$	${\varrho }_4=0.427102$	$RN$	${\varrho }_4=0.452491$
$CE$	${\varrho }_5=0.480607$	$CE$	${\varrho }_5=0.494258$

Hence, $LD$ is the best choice according to attributes.

9. RESULTS AND DISCUSSION

(Ranking using Einstein aggregation operators) In this part of section, computed weight vector is applied to the proposed spherical fuzzy Einstein aggregation operators to find the finest alternative according to give eight attributes.

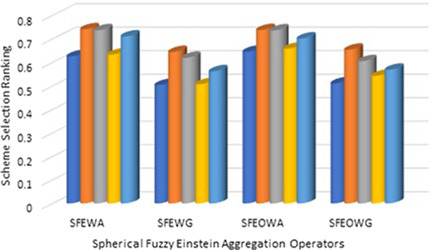
The weight vector is applied to the proposed spherical fuzzy Einstein aggregation operators and the outcomes of decision making methods are shown in Figures 5 and 6. Here, we can seen that $LD$ is the best alternative under given attributes.

Figure 5.

Ranking under AHP weights information [Color figure can be viewed at wileyonlinelibrary.com]

Figure 6.

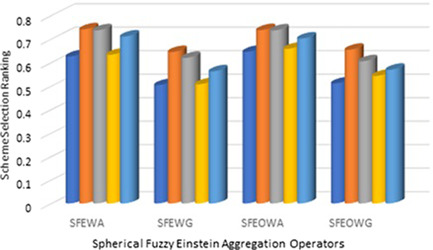
Ranking under entropy weights information [Color figure can be viewed at wileyonlinelibrary.com]

(Ranking using TOPSIS and GRA methods)

According to the proposed TOPSIS and GRA approach using weights under AHP and spherical fuzzy entropy, we computed the finest (best) alternative (scheme) under given eights attributes.

The weight vector is applied to the proposed TOPSIS and GRA approach and the outcomes of decision making methods are shown in Figures 7 and 8. Here, we can seen that $LD$ is the best alternative under given attributes.

Figure 7.

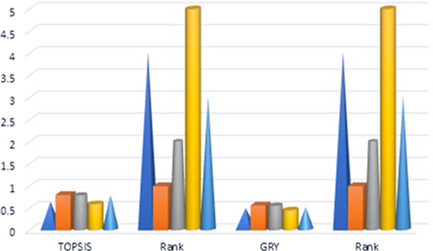
Selection under AHP weights [Color figure can be viewed at wileyonlinelibrary.com]

Figure 8.

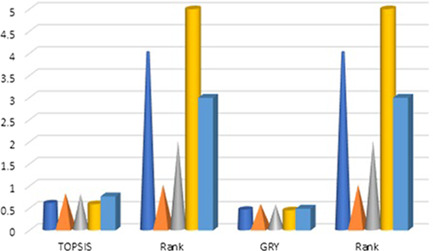
Selection under entropy weights [Color figure can be viewed at wileyonlinelibrary.com]

10. CONCLUSION

COVID‐19, an infectious disease transmissible to the touch, is believed to spread across a population through direct contact between people. Outbreak prevention initiatives intended to decrease the amount of population mixing have the capability to slow down the peak and decrease the final extent of the epidemic. In this situation, an emergency decision makers or disaster response departments should implement strategies or select an appropriate emergency strategy to avoid further escalation of the crisis. For these concerns, the paper focus on emergency decision making to enhance the medical treatment and indorsed the living qualities of peoples. For this purpose, we proposed an emergency decision support techniques under the spherical fuzzy environment. First, give some discussion on the existing operations of spherical FS that's how existing operations have deficiency to fulfill the basic condition of a spherical FS. The novel basic operations are defined with three cases and proved that's the novel operations satisfied the square sum of positive, neutral and negative membership degrees values oscillate between 0 and 1. Next, to aggregate the spherical fuzzy information, proposed the novel Einstein aggregation operators namely, spherical fuzzy Einstein weighted average, spherical fuzzy Einstein weighted geometric, spherical fuzzy Einstein order weighted average, and spherical fuzzy Einstein order weighted geometric aggregation operators. Also, to determine the attributes weights, proposed two techniques first one is AHP method and other on is spherical fuzzy entropy method. Furthermore, to resolve the emergency situation of COVID‐19 as emergency decision making, we introduced two spherical fuzzy decision support techniques namely are TOPSIS and GRA methods for spherical fuzzy information. Based on these three different techniques, we designed three algorithms to tackle emergency situation of COVID‐19 effectively by the physicians or administrators. Validation and effectiveness of the proposed designed algorithms are tested over existing techniques. Results shows that the proposed techniques are reliable and effective to reduce/prevent the outbreak of COVID‐19.

In future research, the other techniques of spherical FSs, like VIKOR, TODAM, Electric‐I, II, and III with real life problems are investigated.

Ashraf S, Abdullah S. Emergency decision support modeling for COVID‐19 based on spherical fuzzy information. Int J Intell Syst. 2020;35:1601–1645. 10.1002/int.22262