Reopening dentistry after COVID-19: Complete suppression of aerosolization in dental procedures by viscoelastic Medusa Gorgo

Abstract

The aerosol transmissibility of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has impacted the delivery of health care and essentially stopped the provision of medical and dental therapies. Dentistry uses rotary, ultrasonic, and laser-based instruments that produce water-based aerosols in the daily, routine treatment of patients. Abundant aerosols are generated, which reach health care workers and other patients. Viruses, including SARS-CoV-2 virus and related coronavirus disease (COVID-19) pandemic, continued expansion throughout the USA and the world. The virus is spread by both droplet (visible drops) and aerosol (practically invisible drops) transmission. The generation of aerosols in dentistry—an unavoidable part of most dental treatments—creates a high-risk situation. The US Centers for Disease Control and The Occupational Safety and Health Administration consider dental procedures to be of “highest risk” in the potential spreading of SARS-CoV-2 and other respiratory viruses. There are several ways to reduce or eliminate the virus: (i) cease or postpone dentistry (public and personal health risk), (ii) screen patients immediately prior to dental treatment (by appropriate testing, if any), (iii) block/remove the virus containing aerosol by engineering controls together with stringent personal protective equipment use. The present work takes a novel, fourth approach. By altering the physical response of water to the rotary or ultrasonic forces that are used in dentistry, the generation of aerosol particles and the distance any aerosol may spread beyond the point of generation can be markedly suppressed or completely eliminated in comparison to water for both the ultrasonic scaler and dental handpiece.

I. INTRODUCTION

The aerosol transmissibility of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has impacted the delivery of health care and essentially stopped the provision of medical and dental therapies. This has traumatized routine provision of the health care industry economically and placed additional barriers in the access to health care by the most vulnerable communities. In dentistry, instruments that commonly produce visible aerosols from the supplied irrigation include dental handpieces, ultrasonic scalers, air polishers, and air abrasion units. The intimate proximity of health care workers to individuals where potential pathogens are aerosolized by interventions using the aforementioned devices places the health care worker at a high risk of disease transmission. Ultrasonic instruments can also aerosolize dilute nascent oral fluid without additional water irrigation. These aerosolized materials incorporate viruses, blood, and supra- and subgingival plaque organisms. While widely overlooked in the past, aerosol generation in medicine and dentistry occasionally gains notoriety when human lives are questioned during infectious outbreaks such as the current COVID-19.¹

The aerosol generation by surgical and dental instrumentation has been largely ignored. In response to the SARS outbreak in 2003, Harrel and Molinari² highlighted the generation of aerosols and droplets during dental procedures. They indicated that the greatest risk to health care workers comes from droplets less than 50 µm in diameter. These aerosols are concentrated within two feet from the patient, thereby exposing the health care worker.³ Contaminated aerosols can remain airborne to possibly be aspirated or ultimately settle as fomites on surfaces in a region surrounding the generating source. It should be noted that this region can potentially be greatly expanded when facilitated by the ventilation system. When considering which dental procedures create the greatest aerosols, ultrasonic scalers and air-driven high-speed handpieces have been recognized as the worst aerosol source.⁴ Based on these earlier studies and highly motivated by the current COVID-19 pandemic at the time of writing, the present work investigates aerosols generated by these two dental instruments and the ways of their complete suppression. As professionals have been encouraged to avoid or minimize aerosol-generating activities, consequently resulting in the widespread cessation of elective dental and medical procedures,⁵ the urgency to create a safe working environment has never been more prevalent.

This pandemic, first attacking the communities of China, Europe, and the USA, continues to expand worldwide and as of June 5, 2020 has infected over 6.5 × 10⁶ people and is associated with nearly 400 000 deaths [https://covid19.who.int/WHO Coronavirus Disease (COVID-19) Dashboard]. These numbers keep growing, and this emergent viral threat to human life presents many challenges to prevention, treatment, and cures. Without vaccination or natural acquisition of herd immunity, prevention requires blocking the transmission of SARS-CoV-2 within populations. The virus may spread by exposure to virus contaminated surfaces or droplets/aerosols emitted by speaking, sneezing, or coughing.^6–9 Importantly, a high percentage of infected individuals may be asymptomatic and there exists evidence of SARS-CoV-2 transmission from asymptomatic individuals. The combined aerosol transmission from asymptomatic infected individuals defines a truly invisible route of transmission that must be defeated to reduce the rapid spread of COVID-19 and other future potential infections.¹⁰ The high risks presented by relatively invisible aerosolized pathogens are further complicated by the retention of aerosols over time. The experimental aerosolization of SARS and SARS-CoV-2 (with the use of a three-jet Collison nebulizer and fed into a Goldberg drum) demonstrated that the half-lives of both aerosolized viruses were ∼1.1 h to 1.2 h,¹¹ indicating that aerosol transmission of SARS-CoV-2 is possible (https://wwwnc.cdc.gov/eid/article/26/8/20-1274_article), problematic, and highly dangerous. The tracing of SARS-CoV-2 transmission in both call center (https://wwwnc.cdc.gov/eid/article/26/8/20-1274_article) and restaurant environments (https://wwwnc.cdc.gov/eid/article/26/7/20-0764_article) strongly implicates an airborne/aerosol route of transmission¹² and presently highlights the importance of this route of disease transmission in public spaces.

Airborne transmission of disease has been classified as obligate (solely aerosol, e.g., tuberculosis), preferential (multiple routes including aerosol, e.g., measles), or opportunistic (facilitated by aerosol-generating procedures).¹³ Respiratory generation and transmission of aerosols occurs by breathing, speaking, sneezing, and coughing, and the potential respiratory generated aerosol transmission of microbial pathogens is well defined for bacterial and viral respiratory diseases. The contemporary acknowledgment that diseases are transmitted by airborne particles generated by physiological/pathological activities (speaking, coughing, and sneezing) is based upon the identification and measurement of aerosols of diverse sizes and characterization of their movement through air and subsequent inspiration or deposition onto surfaces (fomite formation).¹⁴

Opportunistic aerosol transmission is an additional concern that must be addressed to contain pandemic spread of disease, as well as to enable the safe and full return to unrelated medical and dental care in the post-pandemic period. In medicine, endotracheal intubation represents a high risk for aerosol transmission of respiratory disease. In addition, aerosol and droplet generation during surgical procedures is also well-documented. The use of surgical power saws, drills, electric scalpels, cauterization, and lasers produces aerosols of wide particle size-distribution. Measurements in an operating room environment indicated that instrumentation-derived aerosol concentration was dependent on the aerosol source, the room layout, and the transport and diffusion of the aerosol (https://www.cdc.gov/niosh/nioshtic-2/00229128.html).

To return the clinical practices of medicine and dentistry to pre-pandemic levels of activity, aerosol generation must be controlled. Engineering controls such as removal of aerosols and droplets from air, killing of airborne pathogens, or diversion of air flow can reduce the risk of SARS-CoV-2 viral exposure/infection, and all are appearing in clinical practices worldwide. In dentistry, suggested methods of reducing aerosol-related transmission of bacteria, viruses, and blood include pre-operative mouthwashes, rubber dam isolation, the use of high-volume (e.g., 100 ft³/min) evacuation of the direct aerosol field, and the use of distant aerosol elimination by air filtration equipment.² Each of these different approaches can incrementally reduce aerosol generation and transmission of infectious material, yet none of these fully eliminates aerosol production and transmission. The use of personal protective equipment (PPE) is required in these clinical scenarios, and guidelines exist to guide protection of health care workers from aerosol-mediated infection. This approach to protecting individuals is expensive and wholly dependent on human compliance.¹⁵

It should be emphasized that dentistry was in focus of medical researchers from, at least, the year 1857,¹⁶ including the history of dentistry.¹⁷ Dramatic terms were linked to it in several publications in the general medical literature, such as “neglect,”¹⁸ “radical action,”¹⁸ “decay,”¹⁹ “medicine forgets dentistry,”^20,21 and “public health challenge.”²² Dental procedures could lead to a number of different medical conditions,²³ and the COVID-19 pandemia added an enormous threat of viral transmission associated with aerosol generation.

Another approach to controlling the aerosol spread of potential infectious agents is to limit or completely eliminate the generation of aerosols by surgical/dental instrumentation. The avoidance of procedures all together is one approach advocated during pandemic spread of disease. Innovations and controls that reduce procedural times are another means of reducing the total aerosol generated. Direct suppression of aerosol generation by altering the physical creation of water droplets is another approach to limiting or eliminating aerosols. This report aims to demonstrate that the inclusion of high molecular weight FDA-approved polymer additives to irrigation solutions used in surgical/dental instrumentation can completely eliminate aerosols generated by instruments’ physical interaction with liquids. The novelty of this approach is ascertained by the fact that it has never been used in dental procedures. The present work demonstrates that this approach can be revolutionary in reopening post-COVID-19 dentistry.

Section II describes the experimental apparatus used in the present work. Section III contains physical estimates. Section IV discusses the results of the rheological characterization of two FDA-approved non-Newtonian liquids to be used to suppress aerosolization, as well as the results of laboratory experiments with the Cavitron scaler using water and these non-Newtonian liquids in contrast. This section also discusses the experimental results on suppression of aerosolization from the Cavitron scaler and dental drill in dental clinics. Conclusions are also drawn in Sec. V. It should be emphasized that the term aerosolization is typically used in the dental community. It encompasses atomization in the purely fluid mechanical sense, as well as implies that some droplets can become airborne for some time despite gravity and might dry in flight and provide a source of fully airborne pathogens, if the latter have been initially present in the atomized liquid. In the present work, the aim is in complete suppression of atomization (in the fluid mechanical lingo), which becomes identical to the complete suppression of aerosolization (in the dental lingo).

II. EXPERIMENTAL APPARATUSES

A. Aerosolization of water by Cavitron scaler in laboratory experiments

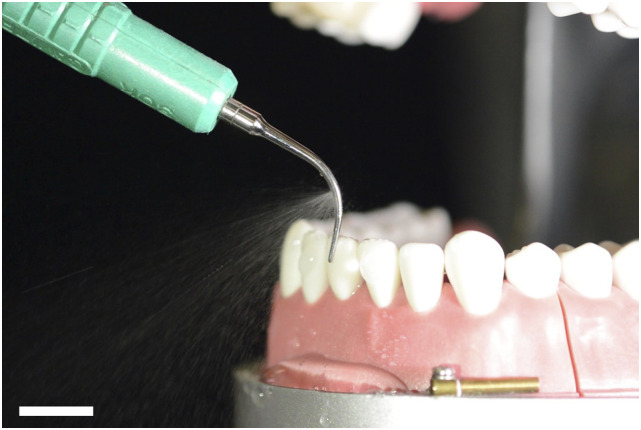
A semi-portable Cavitron scaler (DENTSPLY®, Cavitron® Select^TM SPS^TM Ultrasonic Scaler) requiring 120 V AC and 26.5 psi water supply (with the flow rate of 40.6 ml/min) was used in the laboratory experiments. Three types of tips for the scaler could be used in conjunction with the discrete power options of 10, 100, and 1000. The tips are rated to vibrate at 30 kHz and intended to be cooled and flushed with water delivered as a film released through a small opening in the bend of the scaler. One of the tips is shown in Fig. 1(a), while Fig. 1(b) shows an expanded view of the Cavitron scaler over the machinable ceramic plate. In the present fluid mechanical context, the simulated tooth in the laboratory experiments is just a plane solid surface, on which the Cavitron scaler (and the adjacent liquid blob) leans during its vibrations [cf. Fig. 1(b)]. This situation mimics the one in the dental clinic, in which the Cavitron scaler leans on a tooth of a dental mannequin (cf. Fig. 3) or a patient. Ceramics are frequently used to repair or replace teeth, and in this sense is a material commensurate with teeth from the point of view of stiffness and hardness, as is required in the present experiments. Multiple reviews of material properties of dental ceramics are available, e.g., in Refs. 24 and 25 and references therein.

FIG. 1.

Photos of the Cavitron scaler used for experiments. (a) Magnified image of the tip where the red line spans 567.7 µm. Scale bar: 200 µm. (b) Image of the Cavitron scaler adjacent to the ceramic plate used for the laboratory experiments. Scale bar: 1 cm.

FIG. 3.

Image of the Cavitron scaler adjacent to a dental mannequin installed in a dental chair in the experiments in the dental clinic. Still image taken from video 3, water being the working fluid. Scale bar: 1 cm. Multimedia view: https://doi.org/10.1063/5.0021476.2Download video file ^{(7.1MB, mp4)} DOI: 10.1063/5.0021476.2

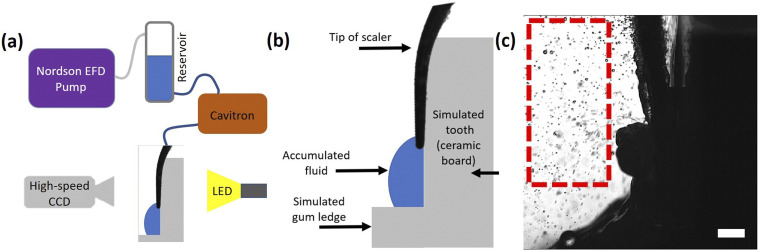
Figure 2(a) presents a global schematic of the model experimental dental setup used in the laboratory experiments including the camera, pump, vessel, and backlight. All the experiments were performed under ambient conditions. Figure 2(b) shows the dental scaler over the simulated tooth [similar configuration as in Fig. 1(b)] used in the model experiments to mimic scaler operation during supra- and subgingival calculus removal. At the scaler tip, fluid forms a blob-like puddle supported by the model gum ledge. This blob is severely aerosolized during the scaler vibrations [Fig. 2(c), taken from video 2(c) (Multimedia view)] due to the Faraday instability discussed in Sec. III. Note that videos were captured using a high-speed CCD camera (Phantom V210) employing backlight [light-emitting diode (LED)] shadowgraphy. An image sequence was chosen and loaded into ImageJ software for image analysis. To sharpen the images, they were inverted and turned binary. To reduce clutter, the program was set to display just one-half of the droplets detected and tracked.

FIG. 2.

Model experimental setup and ImageJ analysis of the results. (a) Global schematic. (b) Local schematic of the setup. (c) The first frame in the sequence of images used for analysis. The red window shows area cropped and analyzed in Figs. 8 and 9. This image is a still from the original cine file used to create video 2(c). Scale bar: 1 mm. Multimedia view: https://doi.org/10.1063/5.0021476.1Download video file ^{(21.9MB, avi)} DOI: 10.1063/5.0021476.1

B. Aerosolization suppression on Cavitron scaler in dental clinic

Complete suppression of aerosolization on the Cavitron scaler was demonstrated at the UIC dental clinic using dilute aqueous solutions of hydrogel (0.8 wt. % xanthan gum) or polymer [2 wt. % polyacrylic acid (PAA)] rather than water. The case of water is shown as a still image in Fig. 3 taken from video 3 (Multimedia view).

C. Aerosolization suppression on rotary drill in dental clinic

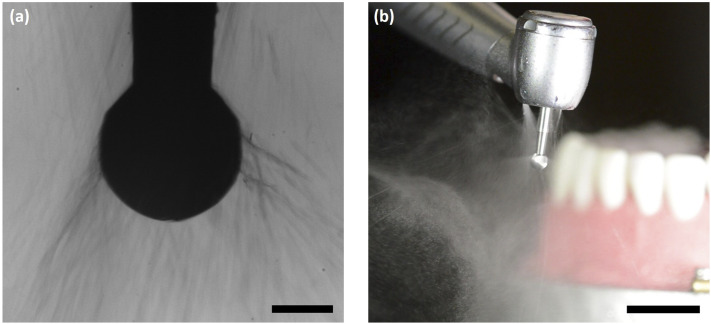
Also incorporated into the dental chair is a pneumatic turbine-powered hand drill used to remove tooth enamel and pulp. On the drill operating with water, aerosolization forms very tiny droplets, barely seen in Fig. 4(a) (Multimedia view), which was recorded at the same magnification as the scaler in Figs. 11–13. Figure 4(b) (Multimedia view) is an expanded color view recorded simultaneously to Fig. 4(a) (Multimedia view). In the present case, the droplets are formed because of the action of the centrifugal force, as discussed in Sec. III.

FIG. 4.

Photographs of the rotary drill loaded with water. The diameter of the spherical part of the drill (the drill head) is 2.3 mm. (a) Magnified image of the drill head loaded with water operating in the experiments. Scale bar: 1 mm. The image is taken from video 4(a). (b) The far-field photo of the drill operating on a dental mannequin installed in a dental chair in the experiments in the dental clinic. This still image is taken from video 4(b). Scale bar: 1 cm. Multimedia views: https://doi.org/10.1063/5.0021476.3Download video file ^{(20.6MB, avi)} DOI: 10.1063/5.0021476.3; https://doi.org/10.1063/5.0021476.4Download video file ^{(4.1MB, mp4)} DOI: 10.1063/5.0021476.4

FIG. 11.

Scaler using water in the dental setting. (a) The initial state as the scaler initiates aerosolization of water blob in which it is submerged. (b) Violent aerosolization with a stream of droplets. (c) Pseudo-steady-state. Scale bar: 1 mm. Images originated from video 11(b). Multimedia view: https://doi.org/10.1063/5.0021476.5Download video file ^{(33.4MB, avi)} DOI: 10.1063/5.0021476.5

FIG. 12.

Scaler using 2 wt. % aqueous PAA solution in the dental setting. (a) The initial state as the scaler initiates sonication of the PAA solution blob in which it is submerged. (b) The most violent moment: the aerosolization is completely eliminated. The corresponding video shows that hair-like protrusions grow and subside similarly to the snake-hairs of Medusa (Gorgo) from the Greek mythology. (c) Pseudo-steady-state. Scale bar: 1 mm. Images originated from video 12(b). Multimedia view: https://doi.org/10.1063/5.0021476.6Download video file ^{(4.6MB, avi)} DOI: 10.1063/5.0021476.6

FIG. 13.

Rotary drill using 2 wt. % aqueous solution of PAA in the dental setting. (a) The initial moment. (b) Tip spooling up. (c) Pseudo-steady-state with no aerosol generated. The drill diameter is 2.3 mm. Images originated from video 13(b). Multimedia view: https://doi.org/10.1063/5.0021476.7Download video file ^{(3.4MB, avi)} DOI: 10.1063/5.0021476.7

D. Rheological characterization of two FDA-approved polymers in shear and elongational flows

Two FDA-approved polymers, polyacrylic acid (PAA, a polymer of M_w = 450 kDa) and xanthan gum (a polysaccharide), were used in the present work. Water-based solution of xanthan gum was prepared at a concentration of 0.8 wt. %, whereas that of PAA was prepared at 2 wt. %. Their flow curves in simple shear flow were measured using the LV-II+ cone and plate Brookfield viscometer.

In the context of the aerosolization, the elongational, rather than shear, behavior is of the utmost importance. It was characterized using the uniaxial elongational flow in a thread undergoing self-thinning driven by capillary forces.^26–28

III. PHYSICAL ESTIMATES FOR WATER DROPLETS

Consider the physical phenomena accompanying the operation of a Cavitron scaler. The appearance of standing waves and instabilities leading to droplet formation at the surface of a liquid layer located on a shaker was discovered in the seminal experiments of Faraday.²⁹ A comprehensive theory of this phenomenon driven by the inertial forces acting on a liquid layer located in the non-inertial frame of reference associated with the shaker surface was proposed by Benjamin and Ursell³⁰ for the case of an inviscid liquid. This is a good approximation for water, which is the only liquid undergoing the aerosolization driven by vibrating the Cavitron tip submerged in a water layer on the surface of a tooth. The theory predicts several bands of unstable waves associated with the three instability islands of Mathieu’s equation for the wave amplitude, to which the linear stability theory reduces. The corresponding wavelength, which, essentially, yields the droplet size, is of the order of d ∼ [σ/(ρω²)]^1/3, where σ and ρ are the surface tension and density of the liquid, respectively, and ω is the angular frequency. For water, σ = 72 g/s² and ρ = 1 g/cm³, and for a Cavitron, ω = 30 kHz, which yields d ∼43 µm, in good agreement with the experimental data discussed below.

The initial velocity of a droplet issued from the free surface is U₀ ∼ hω/(2π), where h is the thickness of the liquid layer. Taking for the estimate h = 1 mm, one obtains U₀ ∼ 4.8 m/s, which is also in good agreement with the experimental data. The corresponding initial Reynolds number Re₀ = U₀d/ν_air, where ν_air is the kinematic viscosity of air; ν_air = 0.15 cm²/s. Then, Re₀ ≈ 14. At this value of the Reynolds number, the Stokes force is still a reasonable approximation of the drag force,³¹ especially given the fact that the Reynolds number rapidly decreases during droplet motion, as well as due to water evaporation. Then, the characteristic time of droplet motion is τ = ρd²/(18μ_air), where μ_air is the air viscosity. Accordingly, the droplet velocity U decays as U = U₀ exp(−t/τ), and the distance x it covers in flight increases as x = τU₀[1 − exp(−t/τ)], t is time. Then, the maximal distance reached by a flying droplet is x_max = τU₀. Taking for the estimate μ_air ∼ 10⁻⁴ g/(cm s), one obtains τ ∼ 10⁻² s, and x_max ∼ 4.8 cm, which is also in good agreement with the experimental data considered below.

The physical phenomena accompanying the operation of a dental drill are different. The swirling drill is covered by a liquid film draining over it. Accordingly, liquid experiences the centrifugal force, accelerating it away from the swirling drill toward air with the acceleration ω²R sin α, where ω is the angular frequency of the drill, R is its radius, and α is the angle reckoned from the rotation axis. Liquid accelerated toward air experiences the Rayleigh–Taylor instability,³¹ and the characteristic droplet size in this case is of the order of d ∼ (ρω²R/3σ)^−1/2. Taking for the estimate ω = 400 000 rpm and R = 0.1 cm, one obtains d = 70 µm, in good agreement with the experimental data considered below.

The danger of formation of droplets resulting in airborne pathogens can be estimated using the so-called d²-law, which is known to be very accurate for spherical droplet evaporation.^32–34 It yields the following expression for the variation of the liquid mass M with time t during the evaporation process: M = M₀[1 − 8ρ_avD ln(1 + B)/(ρd²)t]^3/2, where B = (c_w − c_∞)/(ρ_av − c_w) is the Spalding number, M₀ is the initial liquid mass, D is the diffusion coefficient of the liquid vapor in air, c_w is the saturated liquid vapor concentration over the liquid surface (determined by the surface temperature), c_∞ is the liquid vapor concentration in air determined by humidity in the case of water, and ρ_av is the density of the air–vapor mixture. Accordingly, the evaporation time is t_ev = ρd²/[8ρ_avD ln(1 + B)]. Under the typical conditions, for a 2 µm droplet, t_ev ∼ 1 ms, whereas for a 20 µm droplet, t_ev ∼ 200 ms. Estimate the droplet settling velocity in the absence of entrainment by ventilation as U_settl = ρgd²/(18μ_air), where g is the gravity acceleration. Then, the settling time from height H would be t_settl = 18μ_airH/ρgd². For H = 100 cm and a 2 µm droplet, t_settl ∼ 10⁴ s, whereas for a 20 µm droplet, t_settl ∼100 s. This shows that the 2-20 µm droplets will evaporate before settling. Those droplets that evaporate before settling yield aerosolized airborne pathogens (if the droplets contained them initially). The range of such dangerous small droplets is determined by the inequality t_ev < t_settl, which yields d < [144ρ_avDμ_airH ln(1+B)/(ρ²g)]^1/4. This range could be significantly extended if droplets would be entrained by horizontal or ascending air flow driven by ventilation. All these factors make the droplets generated by the Cavitron scaler and the swirling drill potentially dangerous.

IV. RESULTS AND DISCUSSION

A. Rheological behavior of two FDA-approved polymers in shear and elongational flows

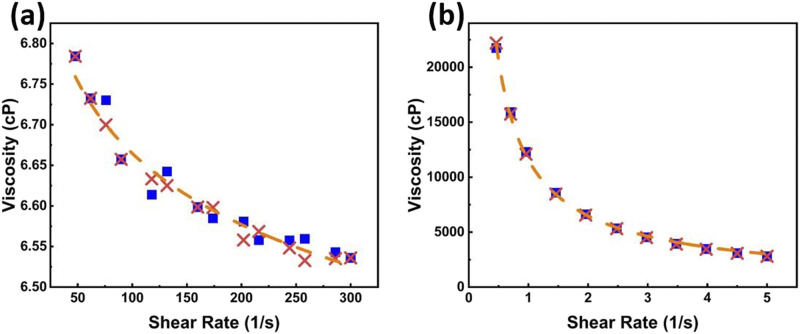
The flow curves measured in simple shear flow are presented in Fig. 5. Both solutions reveal shear-thinning behavior, with the shear viscosity of the 2 wt. % PAA solution being about six times that of water, whereas the shear viscosity of the 0.8 wt. % xanthan gum solution being more than three orders of magnitude higher than that of water. The latter makes the xanthan gum solution less attractive for applications than the PAA solution.

FIG. 5.

(a) The 2 wt. % PAA solution in water. (b) The 0.8 wt. % xanthan gum solution in water. The ramp-up data are shown by blue squares, and the ramp-down data are shown by crosses. The dashed lines trace the experimental data.

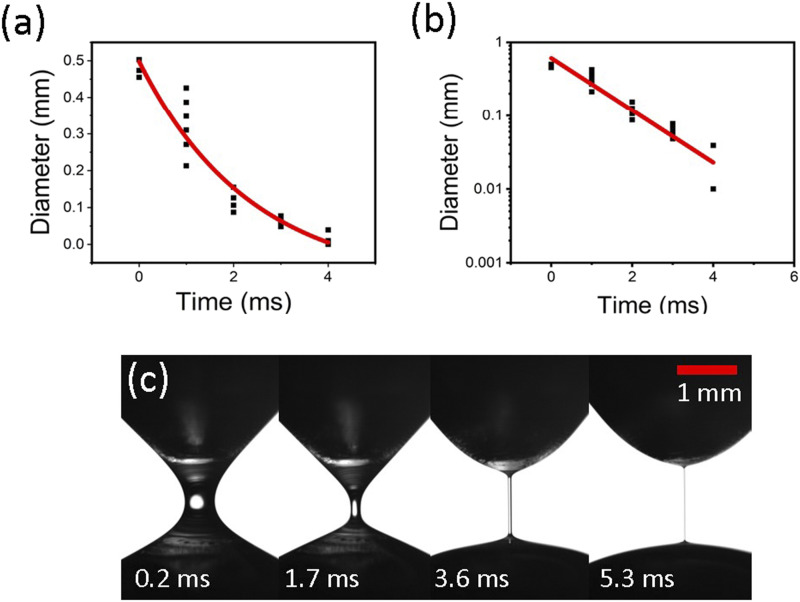
The results obtained with the same two solutions in the uniaxial elongational flow are shown in Fig. 6. The viscoelastic thread diameter decreases in time exponentially [Fig. 6(a)], and the slope in the corresponding semi-logarithmic plot [Fig. 6(b)] is equal to −1/(3θ), where θ is the viscoelastic relaxation time, which is found as 0.5 ms. Viscoelasticity is characteristic of polymer solutions manifesting a tremendous effect of polymer macromolecules on solvent flow even at very low concentrations.^35–38 The physical process of thread thinning [Fig. 6(c)] is an adequate representation of the uniaxial elongational flow accompanying droplet separation from a liquid body.

FIG. 6.

Self-thinning thread of 2 wt. % PAA solution. (a) Thread cross-sectional diameter D vs time and (b) the corresponding semi-logarithmic plot. The experimental data are shown by symbols, while the theoretical result is shown by the red curve D = D₀ exp(−t/3θ), where t is time and D₀ is the diameter value at t = 0. (c) Several snapshots of the self-thinning process.

The self-thinning of a xanthan gum thread depicted in Fig. 7 does not reveal an exponential decay characteristic of viscoelastic polymeric liquids but rather a power-law-like behavior commensurate with that in Fig. 5(b), typical for certain types of gelled liquid-like materials.²⁷

FIG. 7.

Self-thinning thread of 0.8 wt. % solution of xanthan gum. (a) Thread cross-sectional diameter D vs time and (b) the corresponding semi-logarithmic plot. The experimental data are shown by symbols, while the power-law fitting is shown by the red lines. (c) Several snapshots of the self-thinning process.

B. Cavitron scaler aerosolizing water in laboratory experiments

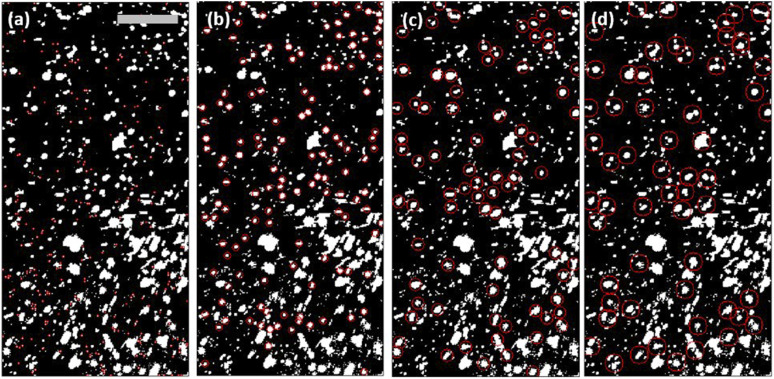
Figure 8 depicts four different examples of the analysis of the same image [the first image in sequence; cf. Fig. 2(c)] with the diameter detection thresholds set to d ∼ 32 µm, 128 µm, 224 µm, and 320 µm in Figs. 6(a)–6(d), respectively. In each of the four panels, red circles are used to visualize one-half of the detected droplets, which are also counted. The detection algorithm can misinterpret the nature of several neighboring droplets, encircling them by a single circle and counting as a single droplet [especially at a larger diameter; cf. Fig. 8(d)]. Therefore, the number of large droplets is inevitably overpredicted.

FIG. 8.

Water droplet analysis using ImageJ (particle counter) with the snapshots ordered according to the droplet diameter threshold. Encircled are droplets with (a) d ∼ 32 µm, (b) d ∼ 128 µm, (c) d ∼ 224 µm, and (d) d ∼ 320 µm. All photographs correspond to the first image in sequence; scale bar: 1 mm. The software was tuned to track one-half of the droplets as to not clutter the photographs, i.e., there would be ∼236 circles in panel (a), rather than 472, as listed in Fig. 10. In this figure, different sized droplets are marked at the same instant in time [i.e., the same image was analyzed ten different times (ten sizes) with four cases being shown]. The point of Fig. 8 is to extract the droplet-size distribution and thus the probability density function shown in Figs. 10(a) and 10(c), respectively. Images for analysis originated from video 2(c) (Multimedia view).

To further explore the aerosolization process in detail, a plugin to ImageJ (Mosaic Particle Tracker) was utilized to analyze 30 frames of the image sequence. The results in Fig. 9 illustrate tracking of several individual water droplets throughout the snapshots where each color represents a specific tracked trajectory over the range of images. The ability of the software to connect a trace or delete the trace if a droplet is not detected for several frames revealed the likelihood of droplet merging on collision with another droplet. If the merger droplet is of a selected diameter, a new trace line would be created starting from that point. Figure 9(a) reveals the absence of directionality of droplets with diameters ∼32 µm that leave only short traces. On the other hand, Figs. 9(b)–9(d) reveal a clear directionality down and away from the scaler.

FIG. 9.

Water droplet tracks found using ImageJ (Mosaic Particle Tracker). Snapshots for droplet diameter threshold: (a) d ∼ 32 µm, (b) d ∼ 128 µm, (c) d ∼ 224 µm, and (d) d ∼ 320 µm. All photographs correspond to the 30th image in the sequence; scale bar: 1 mm. This figure shows one instant in time (the final frame analyzed). The trajectories of four out of ten cases are shown. Colors represent individual trajectories of droplets in the selected range. This figure is meant to show how smaller droplets tend to move in directions misaligned with the overall direction, whereas larger droplets tend to move outward and downward as gravity becomes more of an influence. The white spots in the panels correspond to the Cavitron tip. The software was tuned to track one-half of the droplets to avoid cluttering the images, as in Fig. 8. Images for analysis originated from video 2(c) (Multimedia view).

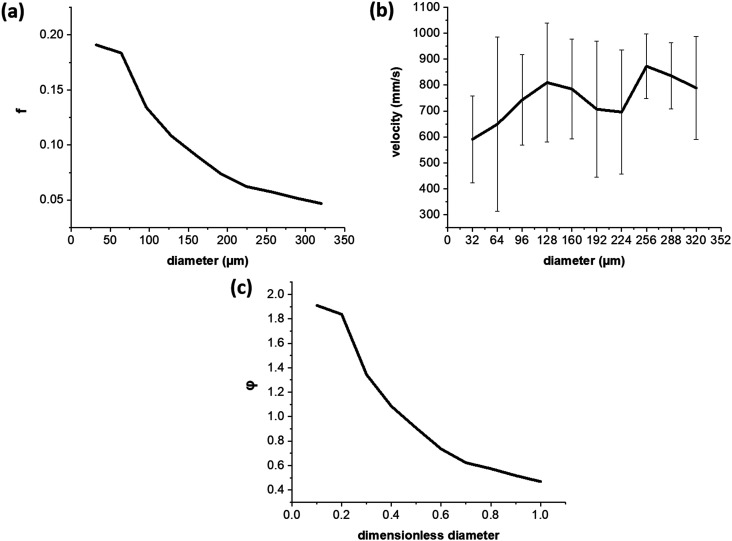
Figure 10 presents the water droplet-size distribution [the frequency f in panel (a) and the probability density function φ in panel (c)] and velocities [Fig. 10(b)], as measured in Figs. 8 and 9. In Fig. 10(a), the steepest slope in the probability density function happens between 60 µm and 100 µm. The most probable droplet size is about 30 µm–40 µm in the remarkable agreement with the theoretical prediction in Sec. III. It should be emphasized that the distribution tail in Fig. 10(a) is probably overestimated by the artificial droplet mergers discussed in relation to Fig. 8(d). Figure 10(b) shows a velocity plateau within the 100 µm–320 µm range with a slight decrease in velocities as droplet diameter decreases below 100 µm. This is likely due to the greater effect the Stokes drag force plays for droplets of smaller diameters. Note that the theoretical estimate of the velocity of 4.8 m/s for 43 µm droplets in Sec. III is an order of magnitude higher than the measured velocity in Fig. 10(b). The reason is that the measurements of velocity in Figs. 9 and 10 are done for droplets at the distances of several millimeters from the free surface of the film of which the droplets originate. At the origin of the droplets at the film surface, the velocities are much higher, as shown below.

FIG. 10.

(a) Frequency f distribution of water droplets. (b) Velocity-size distribution. (c) Probability density function φ; droplet diameter is rendered dimensionless by the maximal diameter, and the integral below the curve is equal to 1.

C. Suppression of aerosolization by Cavitron scaler in dental clinic

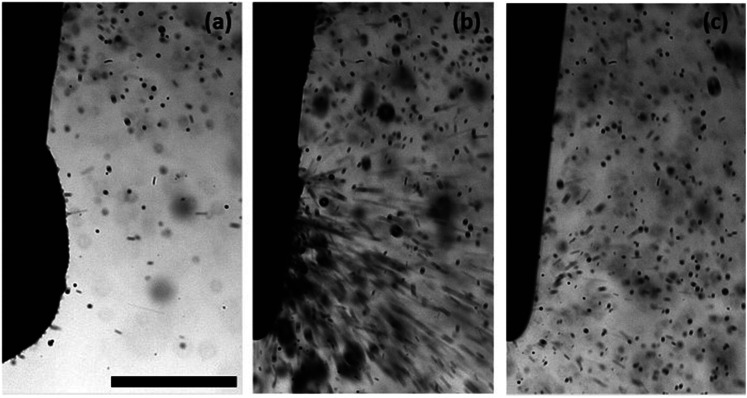
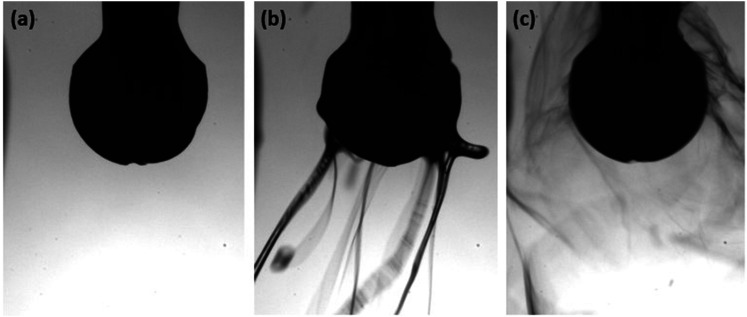
Figure 11 (Multimedia view) shows several snapshots of severe water aerosolization by a scaler integrated in a dental chair (the control case). A mannequin head with false teeth (not seen in the images) was placed in the dental chair. Figure 11(a) corresponds to the initial moment just before the scaler begins to vibrate. Fine droplets are seen in the background as the device issues water slightly before the ultrasonic vibrations begin. Figure 11(b) captures the violent aerosolization moment when a blob of collected water is shattered by the scaler tip, creating a plethora of tiny droplets projected outward. Figure 11(c) shows a pseudo-steady-state in which the scaler has ejected the majority of water blob initially present and the situation has reached a self-sustained equilibrium between the amount of water supplied by the Cavitron and aerosolized by its scaler. This shaky pseudo-equilibrium can be followed by a new imbalance and a violent aerosolization process repeating once again and again.

With the tip vibrating at 30 kHz, the recording speed of 8102 fps is insufficiently fast to capture tip movement and simply blurs the image nearby. The general tip pattern determined by using the scaler is typically either linear or elliptical.

In a clinical dental chair, an integrated fill bottle is available with a selectable switch allowing a dentist to control the fluid being delivered to the instruments. An aqueous 2 wt. % PAA solution was supplied to the same scaler/ mannequin setup just minutes after the experiments with water in Fig. 11. The results for 2 wt. % PAA solution are shown in the snapshots displayed in Fig. 12 (Multimedia view). Figure 12(a) once again shows the scaler as it just begins to vibrate. No background droplets are present in this case because viscoelasticity prevents aerosolization of fluid supplied by the scaler. Figure 12(b) depicts the most violent moment, albeit completely different from that in Fig. 11(b). Note that the “finger” tip velocity here is 3.7 m/s, in good agreement with the theoretical estimate in Sec. III. However, no droplets are formed because the elastic stresses, which develop in the droplet tails [cf. “fingers” in Fig. 12(b)], completely prevent breakup of the tail and droplet detachment. In the pseudo-steady-state, nothing more than tiny ripples are seen at the blob surface despite the scaler vibration because the elastic forces completely suppress aerosolization, as at the previous stages. Not a single droplet could be detected during the entire operation. In addition, it was shown that 0.8 wt. % xanthan gum is also capable of preventing aerosolization at the Cavitron scaler.

D. Suppression of aerosolization on rotary drill in dental clinic

Then, the 2 wt. % aqueous PAA solution was loaded into the selectable bottle attached to the chair, and the drill operation was recorded, as shown in Fig. 13 (Multimedia view). Figure 13(a) illustrates the initial state before the drill swirling and air/water supply have begun. Figure 13(b) shows that during the drill operation with the viscoelastic PAA solution, droplet-like aerosolization characteristic of water is completely suppressed and the drill is spooling viscoelastic threads mostly pulled back to the drill head. Figure 13(c) shows a quasi-steady state (which sets in after the initially accumulated liquid has been ejected) with some fine threads tracing the orbitals surrounding the tip head. The other threads are inevitably moving down because the supply of liquid continues.

Light creates the inverted glimpse points (white circles) seen in Fig. 14. Even though these are not the material points, tracing them using the Mosaic Particle Tracker yields a general pattern of the thread motion (Fig. 14), similar to that of electrospun nanofibers.²⁸

FIG. 14.

Mosaic Particle Tracker analysis of threads originating from the rotary drill loaded with 2 wt. % PAA solution. The drill diameter is 2.3 mm. Image for analysis originated from video 13(b) (Multimedia view).

In addition, it was shown that 0.8 wt. % xanthan gum is also capable of preventing aerosolization at the drill.

It should be emphasized that in the present section, the freely-rotating drill is studied. Unlike the scaler, the rotary drill inflicts “damage” to the substrate. However, that is a mitigating factor because the additional shear forces acting on the liquid layer diminish its azimuthal velocity and thus the propensity to the Rayleigh–Taylor instability and droplet formation. Accordingly, suppression of aerosolization at the drill is achieved here in the worst case.

As previously mentioned, aerosol generation by surgical and dental instrumentation is largely ignored in the absence of pandemic. Two specific cases mentioned, SARS 2003 and COVID-19, highlight the need to understand and suppress the aerosols and droplets produced during dental procedures. The greatest risk to health care workers comes from particles less than 50 µm in diameter suspended in air until aspirated or ultimately settled as fomites on surfaces. It should be emphasized that the affected region surrounding the generating source can be greatly expanded by the building’s ventilation system adding even greater threat. Ultrasonic scalers and air-driven high-speed handpieces have been recognized as the worst aerosol source and focus of the present work.

The formation of droplets by mechanical disruption of water (rotary instrumentation or linear vibration) is a function of device-generated acceleration and the properties of water or other irrigation solution. Based on the fundamental principles of polymer physics, we chose to utilize aqueous solutions of an FDA-approved high-molecular weight polymer possessing viscoelasticity. We predicted and demonstrated complete suppression of aerosolization on the Cavitron scaler and dental drill by elastic forces, preventing droplet detachment.

Detachment of individual droplets from a liquid body, essentially, reduces to an instability of a droplet tail, which is nothing but a thin liquid thread. As was shown in Refs. 28 and 39, such liquid threads undergo a self-thinning process under the action of surface tension. Accordingly, the elongational viscosity of viscoelastic liquids μ_el, which is the ratio of the normal axial stress to the rate of elongation, exponentially increases in time t in such liquid threads, as μ_el = (3θσ/2a₀)exp(t/3θ), where a₀ is the initial cross-sectional radius of the thread. On the scale of several milliseconds, the elongational viscosity could become 10⁴ times that of water,²⁸ which makes the thread practically un-deformable and suppresses droplet detachment. Note that for high-molecular weight polymers with flexible macromolecules, suppression of droplet formation is equivalent to spinnability, i.e., the ability to form fibers under the action of applied forces (the electric ones in electrospinning or the aerodynamic ones in meltblowing and solution blowing).²⁸ This corresponds to the concentration range of a few percent in aqueous solutions,²⁸ which is the concentration range of additives recommended here for suppression of aerosolization when PAA, xanthan gum, as well as oral moisturizers and artificial salivas based on them and similar compounds are used.

It should be emphasized that natural saliva is a viscoelastic liquid by itself²⁶ and, thus, is a mitigating factor in the process of aerosolization. However, as the literature survey in Sec. I shows, natural saliva, especially diluted by the irrigation water, is insufficient to prevent aerosolization, and the present pro-active approach should be taken to enhance viscoelastic properties of liquids involved in dental procedures.

The modification of water to serve as an irrigation solution for dental or surgical instrumentation was achieved using high molecular weight polymers currently used as food additives or agents in dentifrices or artificial salivas. These FDA-approved additives are able to alter the physicochemical properties of the irrigation solution, suppressing droplet formation at the generating source without altering flow behavior in the supply line of standard dental chairs. Three key potential advantages include (i) reduced regulatory hurdles to marketing of a clinical product, (ii) acknowledged biocompatibility as an orally delivered irrigation solution, and (iii) the relatively low cost, availability of reagents to manufacture irrigation solutions with reduced potential for aerosol generation.

This engineering approach to potentially controlling aerosol transmission of viral diseases in clinical dentistry and medicine fundamentally differs from other suggested mitigation methods. Unlike other approaches, here we have demonstrated for the first time the reduction of aerosol generation by ultrasonic or rotary surgical instruments that can reduce the risk of subsequent transmission. The key advantage of targeting the source of aerosol generation is that it limits the inherent risks of human error associated with the implementation of other suggested engineering controls currently advocated in controlling aerosol transmission in dentistry.

V. CONCLUSION

Water used as an irrigation liquid in dental procedures (e.g., Cavitron scaler or dental drill) is aerosolized and presents significant danger to spread viruses to the health care workers and/or nearby patients. The evidence before this study is the following. We searched PubMed, BioRxiv, and MedRxiv for articles published in English from inception to June 15, 2020, with the following keywords: “novel coronavirus,” “COVID-19,” “SARS-CoV-2” AND “aerosol” AND “generation” AND “mitigation.” There is evidence supporting the hypothesis that SARS-CoV-2 is transmitted by aerosols. There was no recent data indicating that any current engineering control is effective in eliminating the risk of aerosol transmission of a viral disease. There has been no report of elimination of aerosol at the point of generation in medicine and dentistry.

Here, we introduce FDA-approved irrigation solutions that reduce or completely eliminate aerosol generation. They are not anti-viral/bacterial nor intended to kill virus/bacteria but rather introduce viscoelastic forces preventing droplet formation. Thus, clinical dentistry will still be required to use PPE to protect workers from natural aerosolization (breathing, speaking, coughing, and sneezing). We demonstrate that such irrigation solutions can be used in ordinary dental office chairs by connection to the water line system. The creation of a two-part irrigation solution including water and a high molecular weight FDA-approved polymer (e.g., PAA) that reduces or completely eliminates droplet formation by rotary and ultrasonic instruments used in medicine and dentistry can be employed to reduce the risks of aerosol transmission of infectious microbes in medicine and dentistry. The cost effectiveness of this technology enables its broad adoption across many communities of interest.

The added value of this study is that we applied fundamental biophysical properties of aqueous solutions of high molecular weight FDA-approved polymers to modify the behavior of irrigation solutions used in the lubrication and cooling of surgical instruments in dentistry. This resulted in the reduction/complete elimination of droplet formation at rotary and ultrasonic dental instruments. Implications of all the available evidence in this research reveal the following: Dental and medical therapies are considered as high risk for transmission of SARS-CoV-2. Given the potential for droplet/aerosol-mediated transmission of infection, the reduction or complete suppression of droplet/aerosol generation at the point of generation offers a broad-based approach to reducing risks of aerosol-transmission of disease during the provision of dental and medical procedures.

The results of this work comprise the provisional patent application related to suppression of aerosolization in dentistry using PAA, xanthan gum, etc., as well as oral moisturizers and artificial salivas based on them and similar compounds.⁴⁰

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.