Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jul 16;124(32):17476–17484. doi: 10.1021/acs.jpcc.0c03414

The Effect of Janus Asymmetry on Thermal Transport in SnSSe

Raveena Gupta †,‡, Bonny Dongre , Chandan Bera †, Jesús Carrete ¶,*
PMCID: PMC7461144  PMID: 32904867

Abstract

graphic file with name jp0c03414_0009.jpg

Several ternary “Janus” metal dichalcogenides such as {Mo,Zr,Pt}-SSe have emerged as candidates with significant potential for optoelectronic, piezoelectric, and thermoelectric applications. SnSSe, a natural option to explore as a thermoelectric given that its “parent” structures are SnS2 and SnSe2 has, however, only recently been shown to be mechanically stable. Here, we calculate the lattice thermal conductivities of the Janus SnSSe monolayer along with those of its parent dicalchogenides. The phonon frequencies of SnSSe are intermediate between those of SnSe2 and SnS2; however, its thermal conductivity is the lowest of the three and even lower than that of a random Sn[S0.5Se0.5]2 alloy. This can be attributed to the breakdown of inversion symmetry and manifests as a subtle effect beyond the reach of the relaxation-time approximation. Together with its low favorable power factor, its thermal conductivity confirms SnSSe as a good candidate for thermoelectric applications.

Introduction

Thermoelectric (TE) materials are reckoned to play a significant role in catering to the present global thrust for green and sustainable energy by enabling the conversion of waste heat into electricity.1,2 Continued research in the field of thermoelectrics over the last decade has led to the discovery of several highly efficient bulk TE materials.3−16 Theory shows that the key to optimizing the performance of TE materials lies in enhancing their TE figure of merit (zT), which is mainly achieved through alloying, doping, or nanostructuring.17zT is defined as S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the the total thermal conductivity [a sum of electronic (κe) and lattice (κl) contributions], and T is the absolute temperature. Here, we use κ as a shorthand for κl since we work with materials and regimes where thermal transport by charge carriers can be neglected as a first approximation. Due to the role of nanostructuring in impeding lattice thermal transport in bulk materials, the potential of low-dimensional materials has drawn a lot of attention in this field. Specifically, several two-dimensional (2D) materials like stanene, silicene, phosphorene, bismuthene, MoS2, MoSe2, WSe2, and SnSe have been reported to show low lattice thermal conductivities at room temperature.18−23

Among the 2D materials mentioned above, transition metal dichalcogenides (2D-TMDs) have attracted considerable interest due to their unique structure and semiconducting characteristics, which can lead to large zT. Shafique et al.24 recently reported on the ultralow lattice thermal conductivity and high carrier mobility in monolayer SnS2 and SnSe2 using first-principles calculations. They showed that high thermoelectric performance could be realized in these simpler compounds that combine chemical stability, low toxicity, and earth abundance. A more complex class of 2D-TMD structures that are being intensely explored in this area are the so-called “Janus” monolayers where the two layers of chalcogen atoms belong to two different elements. The key to their usefulness lies in preserving the desirable characteristics of their “parent” binary structures but using the additional degrees of freedom to tune the material properties further. Applications of Janus monolayers have been proposed in electronics, optoelectronics, and piezoelectronics. Regarding thermal transport specifically, the lattice thermal conductivities of Janus MoSSe/ZrSSe/PtSSe 2D-TMDs have been predicted to be much lower than those of the MoS2/ZrS2/PtS2 monolayers.25−27 This observation is in line with the traditional wisdom that a more complex unit cell leads to increased phonon scattering and lower thermal conductivity.28−30

Guo et al.31 recently reported a new mechanically stable Janus monolayer compound, SnSSe, which can be conceived as derived from SnS2 and SnSe2 and was shown to possess a very high power factor, making it a promising candidate for thermoelectric applications. However, the study focused on the (opto)electronic and piezoelectric properties of the SnSSe monolayer and there is, to our knowledge, no corresponding investigation of its thermal conductivity. Here, we undertake such a study, both as a necessary element to determine the suitability of the Janus SnSSe structure as a thermoelectric material and as a tool to assess the effect of symmetry in the family of monolayers formed by SnS2, SnSe2, and SnSSe. To be able to perform this comparison, we also calculate the phonon contribution to thermal transport in these compounds. We start with ab initio calculations but also employ a simpler predictive model developed by some of us4,32 to enable a more direct comparison of the key ingredients for thermal transport between the three structures.

We find that along with its structure, the Janus SnSSe monolayer also inherits the main features of its phonon dispersion from its parent compounds. Nevertheless, the specific features of the phonon dispersion due to the broken symmetry, together with anharmonicity, make its lattice thermal conductivity lower than those of SnS2 and SnSe2. The effect is not as drastic as in the Janus monolayers investigated in previous reports, and in fact, the order of the conductivities is incorrectly predicted by the commonly employed relaxation-time approximation. To understand it better, we compare the three chalcogenides in detail and also include the case of a Sn[S0.5Se0.5]2 alloy based on a SnS2 structure where S sites are populated by S or Se with the same probability.

Methods

The lattice thermal conductivity tensor is calculated by solving the linearized Boltzmann transport equation (BTE) for phonons as implemented in the almaBTE33 software package. The final result is given by the following:34

graphic file with name jp0c03414_m001.jpg 1

where α, β ∈ {x, y, z} are Cartesian coordinates and λ is the phonon mode comprising both the phonon branch index j and the wave vector q. vλ and Cλ are the group velocity and the mode contribution to the volumetric specific heat, respectively. Fλ is the solution of the linearized BTE written in the form

graphic file with name jp0c03414_m002.jpg 2

In the above equation, τλ is the lifetime of mode λ, and Dλ accounts for the deviation of the population of a specific phonon mode from the prediction of the relaxation-time approximation. The total scattering rate τλ is calculated considering the Taylor series of the potential energy up to the third-order term. It is written as a sum of the contributions from inelastic three-phonon (τ3ph–1) and elastic two-phonon (τ2ph) scattering processes as34

graphic file with name jp0c03414_m003.jpg 3

In this study, two-phonon scattering is enabled by mass disorder at each atomic site, coming from either different isotopes of each element or from alloying. Both are treated in Tamura’s approximation35 where the contribution of a site to the scattering rate of a mode is proportional to the mass variance at that site. In real samples, boundaries33,36 or defects37−39 may have to be taken into consideration as well.

We also approximate the thermal conductivity using a model by Madsen et al.40 that operates within the relaxation-time approximation. The relaxation time is approximated by the contribution from umklapp anharmonic scattering processes parameterized as4,28

graphic file with name jp0c03414_m004.jpg 4

where p is an adjustable parameter given by

graphic file with name jp0c03414_m005.jpg 5

V is the unit cell volume, s is the speed of sound, M is the average atomic mass, and θD~ is the Debye temperature defined as

graphic file with name jp0c03414_m006.jpg 6

In the above equation, n is the number of atoms per unit cell, g(ω) is the vibrational density of states, and γ̃2 is mode-averaged squared Grüneisen parameter given by,29

graphic file with name jp0c03414_m007.jpg 7

The volume derivatives needed to obtain the Grüneisen parameter are calculated for a specific volume range using a finite-difference scheme.

We analyze thermal expansion in SnSSe in the framework of the quasi-harmonic approximation. For each given unit cell volume V, we approximate the free energy of the system by the sum of its potential energy when the atoms are frozen at their equilibrium positions and the free energy contribution from phonons obtained under the usual harmonic approximation for that volume, i.e.,

graphic file with name jp0c03414_m008.jpg
graphic file with name jp0c03414_m009.jpg 8

Here, the sums again run over all phonon modes, ωλ is the angular frequency of each mode, nλ(T) is its Bose–Einstein occupancy factor, and kB is the Boltzmann constant. The dependences on volume of Efrozen, Ephon, Sphon, ωλ, and nλ have been omitted for brevity. Based on F(V, T), the equilibrium volume at each temperature, V(T), is defined as the value of V that minimizes F(V, T) at fixed T. In this context, fixing V is equivalent to fixing the unit cell area A, since the vacuum layer in the simulation box plays no role in contraction and expansion.

For SnSSe, we also obtain finite-temperature phonon spectra. Those are defined and calculated according to the prescription of the Quantum Self-Consistent Ab Initio Lattice Dynamics (QSCAILD) method.41,42 A set of second-order interatomic force constants determines the real-space probability density function for atomic displacements in the canonical ensemble and also the effective harmonic force for each possible displacement. The QSCAILD method looks for the set of force constants that bring the harmonic estimate of the forces as close as possible to the DFT forces (in a least-squares sense) when the atomic displacements are sampled from the aforementioned canonical distribution. In practice, this self-consistency condition is achieved iteratively: from an initial estimate of the force constants, the covariance matrix for the atomic displacements of all atoms in a supercell is obtained as

graphic file with name jp0c03414_m010.jpg 9

where i and j are atom indices, Mi is the mass of atom i, and ϕλ, is is the element of the polarization vector (eigenvector) for mode λ corresponding to atom i and Cartesian direction α. Then, a sample of atomic displacements u is drawn from a Gaussian distribution with a probability density function proportional to Inline graphic, i.e., from the quantum canonical distribution corresponding to the effective harmonic potential built from those constants. Forces on the sampled configurations are calculated from first principles, and then a new set of interatomic force constants is obtained that provides the best fit to those forces in a least-squares sense from which a new covariance matrix is computed, and so on and so forth; the process is iterated until satisfactory convergence is achieved. The QSCAILD approach is able to explain finite-temperature effects like the stability of cubic oxide and fluoride perovskites43 whose regular harmonic spectrum contains imaginary frequencies and can be shown to lead to the same finite-temperature spectrum as other approaches to the same problem that start from different principles,42 like the stochastic self-consistent harmonic approximation (SSCHA).44

Computational Details

All density functional theory (DFT) calculations are performed using the Vienna ab initio simulation package (VASP45,46), the projector augmented wave (PAW) method,47,48 and the Perdew–Burke–Ernzerhof (PBE49) approximation to the exchange and correlation terms of the functional. The plane-wave cutoff is set at 336 eV, corresponding to the highest recommended cutoff among the PAW datasets employed in the calculation plus 30%.

The structures of monolayer SnS2, SnSe2, and SnSSe, oriented perpendicular to the OZ axis, are first relaxed using a 7 × 7 × 1 Monkhorst–Pack grid for integrations over the Brillouin zone (BZ) and a tolerance of 1 × 10–7 eV for the total energy and the band energies, until the absolute value of all components of the force is lower than 1 × 10–4 eV.

We then obtain the phonon spectrum of each structure using the Phonopy package50 by calculating the harmonic force constants in a 7 × 7 × 1 supercell of each of the structures through a finite-difference scheme applying atomic displacements with an amplitude of 0.01 Å. Those force constants are then post-processed to enforce the continuous rotational symmetries of free space,51 which has been shown not only to be necessary to obtain the right behavior of the out-of-plane phonon branches but also to have a large effect on the calculated thermal conductivity. The procedure consists in projecting the interatomic forces onto a space of internal coordinates, all of which are explicitly scalar and, in particular, rotationally invariant, and then transforming them back to the original Cartesian basis. The process separates interactions between pairs of atoms, which were originally aliased on top of one another because of the periodic boundary conditions; therefore, the post-processed constants do not fit in the original supercell, but require a 10 × 10 × 1 one instead. All DFT calculations for supercells are Γ-only and otherwise use all the same parameters as the initial relaxation.

Another set of supercell calculations is required in order to compute the anharmonic force constants leading to the amplitudes of the allowed three-phonon processes and ultimately to the ab initio phonon lifetimes. These are performed using the thirdorder.py script.34 The supercell size is again 7 × 7 × 1, and after careful convergence tests, the cutoff for interactions is set at the 12th nearest neighbors, leading to more than 800 DFT runs for each structure after all symmetries have been harnessed. This is an unusually large cut-off, but related laminar 2D structures like SnSe have been shown52 to require similar attention to this parameter.

In order to solve the phonon BTE and compute the thermal conductivity, phonon properties are sampled with almaBTE33 on a dense 80 × 80 × 1 grid. That choice is again the result of a careful convergence study for all three structures.

We use a version of almaBTE modified so that each three-phonon process allowed by the conservation of energy and momentum is tagged as normal, if all three phonons involved lie in the first Brillouin zone, or umklapp otherwise. This small change enables us to split the anharmonic scattering rates and all other quantities that can be expressed as sums over allowed processes in normal and umklapp contributions. The classification is implemented as part of the existing loop over pairs of phonon modes that the program uses to detect allowed three-phonon processes. An array holds a minimum-norm image of each wave vector in the regular grid used to sample the phonon modes; when a valid process is detected, we check whether the sum (for absorption processes) or difference (for emission processes) of the minimum-norm images of the wave vectors of the two phonons under consideration has a norm compatible with that of its own minimum-norm image.

To obtain the temperature-dependent equilibrium unit cell size of SnSSe in the quasi-harmonic approximation, we again use Phonopy.53 We explore 10 different values of the volume, specifically 96, 97, ..., 105%, of the minimum-energy volume obtained from DFT. Expansions and contractions are isotropic in the in-plane directions, as required by the symmetry of the structure, and do not affect the vacuum layer along the direction perpendicular to the monolayer. For each volume, we fully relax the atomic positions and then obtain the phonon spectrum through a series of calculations completely analogous to those described above, including the supercell size, the DFT parameters, and considerations about rotational symmetry. To obtain a continuous F(V, T) from the discrete samples in V, Phonopy fits the results to the Vinet equation of state.54

As part of the process of finding the self-consistent finite-temperature phonon dispersions of SnSSe in the QSCAILD framework, the hiPhive package55 is used to generate displaced configurations according to the current best estimate of the effective harmonic potential and to fit a new set of second-order force constants to the forces the system experiences in those configurations, as computed by DFT. These calculations also use 7 × 7 × 1 supercells. The QSCAILD iterative process is run for five iterations, in each of which 15 displaced configurations are generated. We choose recursive feature elimination56 as the regularization strategy during the least-squares fits to promote sparsity and avoid overfitting. The cutoff for the second-order force constants is set to 12 Å. Since hiPhive contains its own implementation of the sum rules that preserve the continuous rotational symmetry of the force constants, they do not require any post-processing.

To estimate the properties of a disordered Sn[S0.5Se0.5]2 alloy, we employ the virtual crystal approximation (VCA) functionality implemented in almaBTE, starting from the structures and force constants of the parent compounds. The VCA is very appealing because of its simplicity, but it has been shown57 to not always deliver quantitative predictions because of structural distortions it cannot account for. We consider it suitable for this study because we only use the simplified alloy model as a reference for how much the thermal conductivity is depressed in the Janus monolayer.

Results and Discussion

Structural Properties

The dynamically stable 1T phases of monolayer tin dichalcogenides (SnX2, where X ∈ { S, Se }), belong to the P3̅m1 space group and are shown in Figure 1a,b. The optimized lattice parameters that we obtain are a = b = 3.69 Å for monolayer SnS2 and a = b = 3.86 Å for monolayer SnSe2, in good agreement with the previously reported values.24 This structure provides an octahedrally coordinated environment for Sn(IV), which is surrounded by chalcogen atoms, forming a hexagonal pattern. The vertical distances from the chalcogen atoms to the central plane of the monolayers, where the Sn atoms lie, are ΔS = 1.48 Å and ΔSe = 1.60 Å.

Figure 1.

Figure 1

Open in a new tab

Top and side views of monolayer (a) SnS2, (b) SnSe2, and (c) SnSSe.

The Janus structure of the SnSSe monolayer belongs to the P3m1 space group [Figure 1c] and is less symmetric than the SnS2 and SnSe2 monolayers due to the lack of inversion symmetry with respect to the Sn atoms in the central plane. The optimized lattice constant of the SnSSe monolayer is a = b = 3.78Å, larger than that of SnS2 but smaller than that of SnSe2. In order to be able to provide the thermal conductivities in the usual units, we also need a layer thickness, which we obtain from the interlayer distance (c) in the corresponding layered bulk systems. We use the values 5.92 Å for SnS2, 6.38 Å for SnSe2, and 6.15 Å for SnSSe, which follow the same trend as the lattice constant. In fact, both a = b and c for SnSSe fall remarkably close to the arithmetic mean of their values for the parent structures. The distances from the S and Se atoms to the central Sn plane in the Janus structure are ΔS = 1.46 Å and ΔSe = 1.62 Å. Compared to the symmetric cases, ΔS is slightly shorter and ΔSe is slightly longer, partially compensating for the expanded (with respect to SnS2) or contracted (with respect to SnSe2) unit cell and keeping the Sn–S and Sn–Se bond lengths closer to their values in the symmetric monolayers.

Vibrational and Thermal Properties

Figure 2 shows a comparison of the harmonic properties of the three monolayer compounds, namely SnS2, SnSe2, and Janus SnSSe. No trace of imaginary frequencies is found in any of the dispersions or the density of states, confirming that all the structures are mechanically stable. In contrast, when we run the same calculations for other two possible tin-based Janus monolayers, SnSeTe and SnSTe, using the same DFT parameters and supercell sizes, both turn out to contain clear imaginary frequencies in the phonon spectra, pointing to their being mechanically unstable and making SnSSe singular in this regard.58

Figure 2.

Figure 2

Open in a new tab

Phonon bands and vibrational density of states for Janus SnSSe and its two parent structures, monolayer SnS2 and SnSe2.

A comparison between the phonon dispersions of the SnS2 and SnSe2 monolayers reveals a general trend toward lower frequencies in the latter. This is to be expected, since the atomic mass of Se (78.96) is more than double that of S (32.065). The presence of a common element in both structures (Sn, the heaviest of the three, with an atomic mass of 118.71) leads to different mass ratios in each of these two structures that manifest in another clear difference: a small gap between the acoustic and optical modes in SnS2 that is absent from the spectrum of SnSe2. As another example of the role that the masses play, the highest frequencies computed for SnS2 and SnSe2 are 10.24 and 7.39 THz, respectively. Their ratio is 1.38, close to the value of 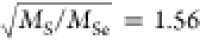Inline graphic. A second-order contribution to the strong softening of the acoustic branches and the large downward shift in the optical branches comes from the unit cell sizes of each monolayer. The larger unit cell of SnSe2 is typically associated with weaker, less stiff bonds.

On the most superficial level, the phonon branches of the Janus SnSSe, as shown in Figure 2, are simply intermediate between those of the parent symmetric monolayers. However, a closer look at points like K quickly shows this not to be the case: the lower symmetry of the SnSSe structure leads to broken degeneracies and large splits between branches that have the same frequency in the parent spectra. This is specifically the case with the two transverse acoustic bands and also with pairs of optical bands. Naturally, this lack of degeneracy at high-symmetry points like K affects the shape of the smooth bands throughout the BZ. The clearest example is perhaps the highest-lying optical band, which is contained in the same range of frequencies as the second highest in the symmetric SnS2 structure but floats well above the rest of the spectrum in the Janus monolayer.

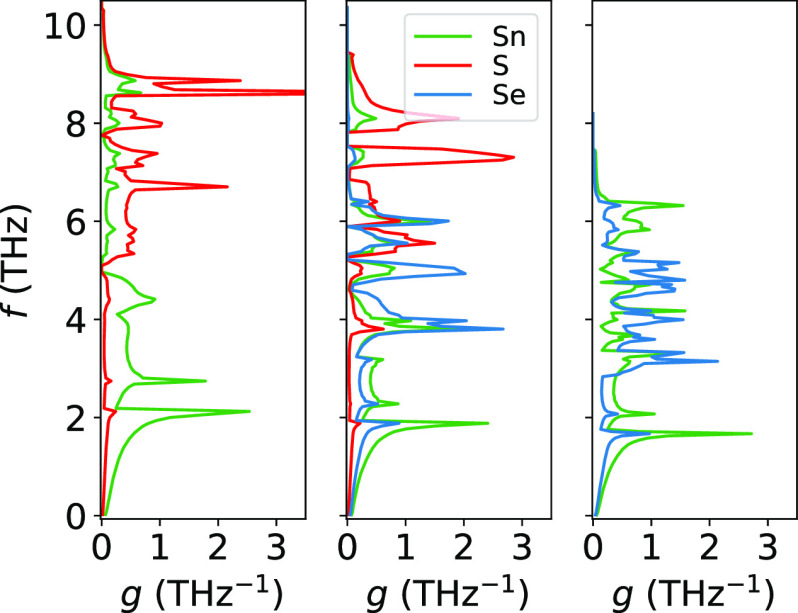
To look deeper into the contribution to the vibrational spectrum from each of the elements of the Janus structure, in Figure 3, we show the projected densities of states (PDOS) for each element in each structure. Note that in the symmetric structures the PDOS corresponds to a single atom of S or Se, to make it more easily comparable with the case of SnSSe.

Figure 3.

Figure 3

Open in a new tab

Projected density of states, colored by respective elements, in each of the three structures studied here: SnS2 (left), SnSSe (center), and SnSe2 (right).

Starting from the low frequencies, the density of states is dominated by the quadratic, non-degenerate ZA branch, as the only one whose contribution does not vanish as f → 0. The protagonists in this region are the more massive Sn atoms, and the differences between all three structures amount to a slight change in the frequencies of each mode, confirming what can be derived directly from the spectra in Figure 2. In fact, the PDOS from each chalcogen atom (S and Se) is very similar in the respective dichalcogenides and the Janus monolayer with a small change in frequency being explainable by the change in unit cell size. In other words, as far as the ZA branch is concerned, each of the sides behaves almost independently. This can be understood based on the fact that the polarization of the ZA branch is largely determined by the symmetry of the underlying structure.

Moving on to higher frequencies, the behavior is far less universal because of the specificities outlined above, especially the overlap between acoustic and optical bands or the lack thereof. A feature can be identified in SnSSe that it inherits from SnS2, namely the very low participation of S in the low-frequency region. A sort of reciprocal phenomenon is observed at the opposite end of the spectrum, i.e., the highest frequencies: there the role of Se is almost negligible, although as discussed above, the shape of the bands in SnSSe and SnS2 is very different in this range.

To advance the discussion beyond the harmonic properties, the panels on the right in Figure 4 show the atom-projected mode Grüneisen parameters for each of the three structures as a descriptor of the contribution of each element to the anharmonicity of the crystal. It can be seen that at higher frequencies, S atoms have larger contributions than Sn atoms in SnS2. In Janus SnSSe, although the atomic contribution of S to the Grüneisen parameter dominates at higher energies, the contribution of Se atoms is larger for lower-energy phonon modes. The ZA branch stands out because of its negative Grüneisen parameter, a sign that its frequencies increase upon expansion of the crystal. The other branches show a similar behavior in all three compounds with respect to their frequency dependency but with the Sn contribution (the dominant one) at low frequencies being typically higher in SnS2 and SnSSe.

Figure 4.

Figure 4

Open in a new tab

Anharmonic scattering rates (left) and atom-projected Grüneisen parameters (right) in each of the three structures studied here: SnSe2 (top), SnSSe (center), and SnS2 (bottom).

Therefore, at this point, most factors point to SnSe2 having a lower thermal conductivity than SnS2, specifically the reduced phonon group velocities caused by the phonon-softening and the increase in phase space for three-phonon processes introduced by the lower-lying optical branches. However, the relatively significant Grüneisen parameters of SnS2 would hint in the other direction. As for SnSSe, with harmonic features sitting between those of its two parent structures, lower band degeneracy and high Grüneisen parameters, it could be suspected to have a lower thermal conductivity than either of the symmetric dichalcogenides.

Surprisingly, when calculated in the relaxation-time approximation, the thermal conductivity of SnSSe is found to be closer to but higher than that of SnSe2 for all temperatures studied. This is shown in the bottom panel of Figure 5, comprising both ab initio results and those from the model explained in the previous section. They highlight how difficult it is to intuitively predict how much each of the factors mentioned above will influence the thermal conductivity. The model and the first-principles calculations agree well, and specifically at T = 300 K, they yield an SnSSe conductivity ∼1.5 times lower than that of SnS2 and only ∼10% higher than that of SnSe2.

Figure 5.

Figure 5

Open in a new tab

Lattice thermal conductivity versus temperature for SnS2, SnSe2, and SnSSe as calculated from the solution of the fully linearized BTE (top) and in the relaxation-time approximation (bottom).

However, the full solution of the BTE (top panel of Figure 5) tells a different story. For the two symmetric 2D-TMDs, the difference between the relaxation-time results and those from the solution of the BTE is roughly a factor of two, but for the Janus monolayer, it is far less drastic. This difference is typically interpreted in terms of the relaxation-time approximation considering all processes as resistive, which is appropriate here in light of the good agreement with the semiempirical method. Hence, the results suggest that the breakdown of inversion symmetry opens up the possibility of more resistive processes and therefore decreases the relevance of normal ones for the final result.

To explore this hypothesis, in Figure 6 we plot the normal and umklapp contributions to the anharmonic scattering rates for all three systems under study with those corresponding to the lowest-lying branch (ZA) represented in a different color. As can be extrapolated from the case of graphene, studied in detail by Lindsay et al.,59 it is the ZA branch that is affected by the lifting of the selection rule arising from inversion symmetry. Comparing the cases of Janus SnSSe (center) and its parent structures (top and bottom) it is clear that both normal and umklapp processes are dramatically affected. However, while the normal contribution to scattering rates stays within the region where it can be considered comparatively modest, in general, the umklapp contribution to the scattering rates of the ZA branch in SnSSe is orders of magnitude higher than most total scattering rates for any of the three compounds. Scattering of phonons from the out-of-plane branch by umklapp processes is so intense in SnSSe that normal processes are comparatively irrelevant. With that branch almost out of the picture, the system behaves much more like a typical three-dimensional low-conductivity material where indeed the RTA and full BTE solutions tend to be closer to one another than in systems like graphene where the ZA branch makes an important contribution.

Figure 6.

Figure 6

Open in a new tab

Scattering rates due to normal (N, left) or umklapp (U, right) processes in SnSe2 (top), SnSSe (center), and SnS2 (bottom) as a function of frequency. Points corresponding to the ZA branch are depicted in a different color because of their relevance for the discussion.

The presence of strong anharmonicity calls into question the assumption, inherent in our treatment, that the phonon dispersions are not affected by temperature. We therefore examine that hypothesis by looking into two specific classes of possible effects in SnSSe: thermal expansion and renormalization of the phonon spectrum for a given unit cell size.

As indicated in the Methods section, we tackle the first category in the framework of the quasi-harmonic approximation, i.e., by calculating the phonon spectrum for a range of possible unit cell sizes, building a free energy F(V, T) that includes the DFT ground state and the vibrational contribution and taking its minimum at each given temperature as the equilibrium V(T). The results are shown in Figure 7, in terms of the volume itself and of the coefficient of thermal expansion 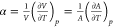Inline graphic where A representes the in-plane unit cell area. Like in other 2D systems,60 the values of α are rather significant in the order of magnitude from 10–5 to 10–4 K–1, larger than those of typical 3D materials.

Figure 7.

Figure 7

Open in a new tab

Equilibrium volume (top) and coefficient of thermal expansion (bottom) of SnSSe as a function of temperature, computed in the quasi-harmonic approximation.

Once the equilibrium unit cell size is known for each temperature of interest, we iteratively calculate the self-consistent finite-temperature phonon spectrum in the QSCAILD framework. Figure 8 shows those spectra for two representative temperatures of 300 and 600 K, compared with the regular harmonic phonon spectrum of SnSSe that we use for all the calculations in this article. There are significant differences between the optical parts of the harmonic and finite-temperature spectra, especially for the higher temperature; in particular, the most energetic branch is softened (i.e., pushed to lower energies) and flattened, as one could expect from an expanded unit cell. However, the acoustic branches, which play a much bigger role in thermal transport, do not change so much, especially when taking into account that in systems where temperature renormalization of the phonon branches is really strong, it can change which phase is stable by pushing the vibrational frequencies from imaginary to real.43 The only noticeable effect detected on closer inspection of Figure 8 is a softening of the ZA branch along the Γ → M line and even then only at 600 K. To put this in more quantitative terms, we calculate the small-grain thermal conductivity tensor κSGαβ, defined as61

graphic file with name jp0c03414_m014.jpg 10

Figure 8.

Figure 8

Open in a new tab

Finite-temperature phonon dispersions of SnSSe in the QSCAILD framework at 300 and 600 K, including thermal expansion, compared with the harmonic result.

Working under the relaxation-time approximation, if all the phonons in a material had the same mean free path Λ, the lattice thermal conductivity computed with eq 1 would be καβ = ΛκSGαβ. The small-grain thermal conductivity, therefore, summarizes the influence of all factors derived from the phonon dispersions (frequencies and group velocities) on the lattice thermal conductivity while leaving scattering aside. Using the regular harmonic phonon spectrum of SnSSe, the in-plane component of the small-grain thermal conductivity is 0.781 W m–1 K–1 nm–1 at T = 300 K and 0.809 W m–1 K–1 nm–1 at T = 600 K; using the temperature-renormalized spectra computed at the volume determined by thermal expansion, the corresponding values are 0.760 W m–1 K–1 nm–1 at T = 300 K and 0.638 W m–1 K–1 nm–1 at T = 600 K. Those values represent decreases of 2.8 and 21% because of finite-temperature effects, respectively. We must therefore conclude that while phonon softening can be neglected at room temperature, the high-temperature κ values reported here are an upper bound, and finite-temperature effects can lead to even higher zT values for SnSSe in that regime.

In light of these results, SnSSe can be considered an ultra-low thermal conductivity material in any context in which SnSe2 can merit that consideration. In fact, the predicted conductivity for Janus SnSSe likely makes it a suitable material for thermoelectric applications. In particular, with the values for the power factor reported earlier,31 namely 65 μW cm–1 K–1 at 800 K, and with κ = 2.9 W m–1 K–1 as calculated in this report at the same temperature, the figure of merit for this monolayer is predicted to be around 1.8 at 800 K.

From the phenomenological model, we can extract that the low value of the thermal conductivity of SnSSe monolayer is due to its strong anharmonicity as evidenced by the high atomistic Grüneisen parameters. However, SnS2 shares this feature and yet displays a significantly higher κ. Part of the explanation is that the Grüneisen parameter is descriptive only of the typical amplitudes of three-phonon processes. It conveys very little information about how easy it is for these processes to be allowed (or, more precisely, how big is the phase space for allowed three-phonon processes). Since SnS2 has higher symmetry than SnSSe, such a phase space is relatively smaller than in the Janus structure, resulting in SnS2 having a higher thermal conductivity. To show that phonon scattering is indeed more intense in the Janus monolayer as compared to SnS2, in the left-hand panels of Figure 4, we plot the total ab initio three-phonon scattering rates for each mode. Note that as discussed above, these scattering rates alone are not enough to explain why the thermal conductivity of SnSSe is also lower than that of SnSe2.

To explore whether a structure based on SnSSe can be built with an even lower thermal conductivity by exploiting disorder (and lead to a higher zT), in Figure 5, we also include an estimate of κ for a random Sn[S0.5Se0.5]2 alloy under the VCA. Given the way this approximation is constructed, such an alloy has the full symmetry of SnS2 or SnSe2 (each S/Se site being equivalent to any other) and the effect of disorder is felt through elastic phonon scattering instead. This is clearly reflected in the temperature dependence of the corresponding curve in the figure. Quite remarkably, the thermal conductivity of the alloy is higher than that of the Janus monolayer throughout the whole temperature range and more drastically at high temperatures. This is because the elastic scattering rates are temperature independent; therefore, the thermal conductivity of the alloy decays more slowly than the T–1 trend of the anharmonic rates. This shows how efficient the effect of removing inversion symmetry is and also that alloying does not appear to be a particularly attractive option for further reduction of the thermal conductivity. That said, other avenues for nanostructuring or doping remain open. In particular, the introduction of carefully chosen point defects can also cause a breakdown of symmetry leading to efficient mixing of phonon modes and to drastic decreases of κ, as has been shown in bulk systems.38

Conclusions

In summary, our detailed study of the thermal conductivity of the Janus SnSSe monolayer points to low values that considered together with its favorable electric transport properties, can make it a promising thermoelectric material. The key to it having a lower thermal conductivity than either of its parent structures is to be found in the lack of inversion symmetry with respect to the central plane of the structure and is captured by the Boltzmann transport equation but only partially by the relaxation-time approximation. The effect is subtler than in Mo- or W-based chalcogenides; however, since the conductivities of Sn-based chalcogenides are lower, SnSSe is a very interesting option. Our results should therefore encourage further experimental work toward the synthesis and thermal transport characterization of Janus SnSSe monolayers.

Acknowledgments

The authors thank DST and OeAD for the bilateral project with nos. INT/AUSTRIA/BMWF/P-02/2018 and IN 03/2018. C.B. and R.G. acknowledge financial support from SERB, DST, India project no. SERB-EMR/2016/003584. B.D. and J.C. acknowledge support from the French (ANR) and Austrian (FWF) Science Funds under project CODIS (ANR-17-CE08-0044-01 and FWF-I-3576-N36).

Author Contributions

§ R.G. and B.D. contributed equally to this work.

The authors declare no competing financial interest.

References

  1. Jana M. K.; Biswas K. Crystalline Solids with Intrinsically Low Lattice Thermal Conductivity for Thermoelectric Energy Conversion. ACS Energy Lett. 2018, 3, 1315–1324. 10.1021/acsenergylett.8b00435. [DOI] [Google Scholar]
  2. Biswas K.; He J.; Blum I. D.; Wu C.-I.; Hogan T. P.; Seidman D. N.; Dravid V. P.; Kanatzidis M. G. High-Performance Bulk Thermoelectrics with All-Scale Hierarchical Architectures. Nature 2012, 489, 414–418. 10.1038/nature11439. [DOI] [PubMed] [Google Scholar]
  3. Zhang J.; Liu X.; Wen Y.; Shi L.; Chen R.; Liu H.; Shan B. Titanium Trisulfide Monolayer as a Potential Thermoelectric Material: A First-Principles-Based Boltzmann Transport Study. ACS Appl. Mater. Interfaces 2017, 9, 2509–2515. 10.1021/acsami.6b14134. [DOI] [PubMed] [Google Scholar]
  4. Gupta R.; Kaur B.; Carrete J.; Bera C. A Theoretical Model of the Thermoelectric Properties of SnSxSe1-x and How to Further Enhance its Thermoelectric Performance. J. Appl. Phys. 2019, 126, 225105. 10.1063/1.5127346. [DOI] [Google Scholar]
  5. Cheng Y.; Yang J.; Jiang Q.; He D.; He J.; Luo Y.; Zhang D.; Zhou Z.; Ren Y.; Xin J. New Insight into InSb-Based Thermoelectric Materials: From a Divorced Eutectic Design to a Remarkably High Thermoelectric Performance. J. Mater. Chem. A 2017, 5, 5163–5170. 10.1039/C6TA10827J. [DOI] [Google Scholar]
  6. Li J.; Shen J.; Ma Z.; Wu K. Thickness-Controlled Electronic Structure and Thermoelectric Performance of Ultrathin SnS2 Nanosheets. Sci. Rep. 2017, 7, 8914. 10.1038/s41598-017-09572-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Zhang X.; Wang D.; Wu H.; Yin M.; Pei Y.; Gong S.; Huang L.; Pennycook S. J.; He J.; Zhao L.-D. Simultaneously Enhancing The Power Factor and Reducing the Thermal Conductivity of SnTe via Introducing its Analogues. Energy Environ. Sci. 2017, 10, 2420–2431. 10.1039/C7EE02530K. [DOI] [Google Scholar]
  8. Zhao L.-D.; Lo S.-H.; Zhang Y.; Sun H.; Tan G.; Uher C.; Wolverton C.; Dravid V. P.; Kanatzidis M. G. Ultralow Thermal Conductivity and High Thermoelectric Figure of Merit in SnSe Crystals. Nature 2014, 508, 373–377. 10.1038/nature13184. [DOI] [PubMed] [Google Scholar]
  9. Yang J.-H.; Yuan Q.; Deng H.; Wei S.-H.; Yakobson B. I. Earth-Abundant and Non-Toxic SiX (X = S, Se) Monolayers as Highly Efficient Thermoelectric Materials. J. Phys. Chem. C 2017, 121, 123–128. 10.1021/acs.jpcc.6b10163. [DOI] [Google Scholar]
  10. Zhu X.-L.; Liu P.-F.; Zhang J.; Zhang P.; Zhou W.-X.; Xie G.; Wang B.-T. Monolayer SnP3: An Excellent p-Type Thermoelectric Material. Nanoscale 2019, 11, 19923–19932. 10.1039/C9NR04726C. [DOI] [PubMed] [Google Scholar]
  11. Wang F. Q.; Guo Y.; Wang Q.; Kawazoe Y.; Jena P. Exceptional Thermoelectric Properties of Layered GeAs2. Chem. Mater. 2017, 29, 9300–9307. 10.1021/acs.chemmater.7b03279. [DOI] [Google Scholar]
  12. Heremans J. P.; Wiendlocha B.; Chamoire A. M. Resonant Levels in Bulk Thermoelectric Semiconductors. Energy Environ. Sci. 2012, 5, 5510–5530. 10.1039/C1EE02612G. [DOI] [Google Scholar]
  13. He W.; et al. High Thermoelectric Performance in Low-Cost SnS0.91Se0.09 Crystals. Science 2019, 365, 1418–1424. 10.1126/science.aax5123. [DOI] [PubMed] [Google Scholar]
  14. Li S.; Yang J.; Xin J.; Jiang Q.; Zhou Z.; Hu H.; Sun B.; Basit A.; Li X. Tailoring the Carrier and Phonon Scattering to Enhanced Thermoelectric Performance of SnTe by Cation–Anion Codoping with Eco-Benign CaI2. ACS Appl. Energy Mater. 2019, 2, 1997–2003. 10.1021/acsaem.8b02096. [DOI] [Google Scholar]
  15. Fu T.; Yue X.; Wu H.; Fu C.; Zhu T.; Liu X.; Hu L.; Ying P.; He J.; Zhao X. Enhanced Thermoelectric Performance of PbTe Bulk Materials with Figure of Merit zT>2 by Multi-Functional Alloying. J. Materiomics 2016, 2, 141–149. 10.1016/j.jmat.2016.05.005. [DOI] [Google Scholar]
  16. Farooq M. U.; Butt S.; Gao K.; Sun X.; Pang X.; Khan S. U.; Xu W.; Mohmed F.; Mahmood A.; Mahmood N. Enhanced Thermoelectric Efficiency of Cu2-xSe–Cu2S Composite by Incorporating Cu2S Nanoparticles. Ceram. Int. 2016, 42, 8395–8401. 10.1016/j.ceramint.2016.02.055. [DOI] [Google Scholar]
  17. Vineis C. J.; Shakouri A.; Majumdar A.; Kanatzidis M. G. Nanostructured Thermoelectrics: Big Efficiency Gains from Small Features. Adv. Mater. 2010, 22, 3970–3980. 10.1002/adma.201000839. [DOI] [PubMed] [Google Scholar]
  18. Peng B.; Zhang H.; Shao H.; Xu Y.; Zhang X.; Zhu H. Low Lattice Thermal Conductivity of Stanene. Sci. Rep. 2016, 6, 20225. 10.1038/srep20225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Shafique A.; Shin Y.-H. Strain Engineering of Phonon Thermal Transport Properties in Monolayer 2H-MoTe2. Phys. Chem. Chem. Phys. 2017, 19, 32072–32078. 10.1039/C7CP06065C. [DOI] [PubMed] [Google Scholar]
  20. Peng B.; Mei H.; Zhang H.; Shao H.; Xu K.; Ni G.; Jin Q.; Soukoulis C. M.; Zhu H. High Thermoelectric Efficiency in Monolayer PbI2 from 300 K to 900 K. Inorg. Chem. Front. 2019, 6, 920–928. 10.1039/C8QI01297K. [DOI] [Google Scholar]
  21. Qin G.; Yan Q.-B.; Qin Z.; Yue S.-Y.; Hu M.; Su G. Anisotropic Intrinsic Lattice Thermal Conductivity of Phosphorene from First Principles. Phys. Chem. Chem. Phys. 2015, 17, 4854–4858. 10.1039/C4CP04858J. [DOI] [PubMed] [Google Scholar]
  22. Cai Y.; Lan J.; Zhang G.; Zhang Y.-W. Lattice Vibrational Modes and Phonon Thermal Conductivity of Monolayer MoS2. Phys. Rev. B 2014, 89, 035438 10.1103/PhysRevB.89.035438. [DOI] [Google Scholar]
  23. Gu X.; Yang R. Phonon Transport in Single-Layer Transition Metal Dichalcogenides: A First-Principles Study. Appl. Phys. Lett. 2014, 105, 131903. 10.1063/1.4896685. [DOI] [Google Scholar]
  24. Shafique A.; Samad A.; Shin Y.-H. Ultra Low Lattice Thermal Conductivity and High Carrier Mobility of Monolayer SnS2 and SnSe2: A First Principles Study. Phys. Chem. Chem. Phys. 2017, 19, 20677–20683. 10.1039/C7CP03748A. [DOI] [PubMed] [Google Scholar]
  25. Guo S.-D. Phonon Transport in Janus Monolayer MoSSe: A First-Principles Study. Phys. Chem. Chem. Phys. 2018, 20, 7236–7242. 10.1039/C8CP00350E. [DOI] [PubMed] [Google Scholar]
  26. Guo S.-D.; Guo X.-S.; Deng Y. Tuning the Electronic Structures and Transport Coefficients of Janus PtSSe Monolayer with Biaxial Strain. J. Appl. Phys. 2019, 126, 154301. 10.1063/1.5124677. [DOI] [Google Scholar]
  27. Cao L.; Ang Y. S.; Wu Q.; Ang L. K. Janus PtSSe and Graphene Heterostructure with Tunable Schottky Barrier. Appl. Phys. Lett. 2019, 115, 241601. 10.1063/1.5130756. [DOI] [Google Scholar]
  28. Kaur P.; Madsen G. K. H.; Bera C. Thermoelectric Figure of Merit and Thermal Conductivity of Type-I Clathrate Alloy Nanowires. MRS Commun. 2019, 9, 370–374. 10.1557/mrc.2018.242. [DOI] [Google Scholar]
  29. Madsen G. K. H.; Katre A.; Bera C. Calculating the Thermal Conductivity of the Silicon Clathrates Using the Quasi-Harmonic Approximation. Phys. Status Solidi A 2016, 213, 802–807. 10.1002/pssa.201532615. [DOI] [Google Scholar]
  30. Madsen G. K. H.; Santi G. Anharmonic Lattice Dynamics in Type-I Clathrates from First-Principles Calculations. Phys. Rev. B 2005, 72, 220301. 10.1103/PhysRevB.72.220301. [DOI] [Google Scholar]
  31. Guo S.-D.; Guo X.-S.; Han R.-Y.; Deng Y. Predicted Janus SnSSe Monolayer: A Comprehensive First-Principles Study. Phys. Chem. Chem. Phys. 2019, 21, 24620–24628. 10.1039/C9CP04590B. [DOI] [PubMed] [Google Scholar]
  32. Kaur P.; Bera C. Effect of Alloying on Thermal Conductivity and Thermoelectric Properties of CoAsS and CoSbS. Phys. Chem. Chem. Phys. 2017, 19, 24928–24933. 10.1039/C7CP05170K. [DOI] [PubMed] [Google Scholar]
  33. Carrete J.; Vermeersch B.; Katre A.; van Roekeghem A.; Wang T.; Madsen G. K. H.; Mingo N. almaBTE : A Solver of the Space–Time Dependent Boltzmann Transport Equation for Phonons in Structured Materials. Comput. Phys. Commun. 2017, 220, 351–362. 10.1016/j.cpc.2017.06.023. [DOI] [Google Scholar]
  34. Li W.; Carrete J.; Katcho N. A.; Mingo N. ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. 10.1016/j.cpc.2014.02.015. [DOI] [Google Scholar]
  35. Tamura S.-i. Isotope Scattering of Dispersive Phonons in Ge. Phys. Rev. B 1983, 27, 858–866. 10.1103/PhysRevB.27.858. [DOI] [Google Scholar]
  36. Dongre B.; Carrete J.; Mingo N.; Madsen G. K. H. Ab Initio Lattice Thermal Conductivity of Bulk and Thin-Film α-Al2O3. MRS Commun. 2018, 8, 1119–1123. 10.1557/mrc.2018.161. [DOI] [Google Scholar]
  37. Katre A.; Carrete J.; Dongre B.; Madsen G. K. H.; Mingo N. Exceptionally Strong Phonon Scattering by B Substitution in Cubic SiC. Phys. Rev. Lett. 2017, 119, 075902 10.1103/PhysRevLett.119.075902. [DOI] [PubMed] [Google Scholar]
  38. Dongre B.; Carrete J.; Katre A.; Mingo N.; Madsen G. K. H. Resonant Phonon Scattering in Semiconductors. J. Mater. Chem. C 2018, 6, 4691–4697. 10.1039/C8TC00820E. [DOI] [Google Scholar]
  39. Wang T.; Carrete J.; Mingo N.; Madsen G. K. H. Phonon Scattering by Dislocations in GaN. ACS Appl. Mater. Interfaces 2019, 11, 8175–8181. 10.1021/acsami.8b17525. [DOI] [PubMed] [Google Scholar]
  40. Bjerg L.; Iversen B. B.; Madsen G. K. H. Modeling the Thermal Conductivities of the Zinc Antimonides ZnSb and Zn4Sb3. Phys. Rev. B 2014, 89, 024304 10.1103/PhysRevB.89.024304. [DOI] [Google Scholar]
  41. van Roekeghem A.; Carrete J.; Mingo N. Anomalous Thermal Conductivity and Suppression of Negative Thermal Expansion in ScF3. Phys. Rev. B 2016, 94, 020303 10.1103/PhysRevB.94.020303. [DOI] [Google Scholar]
  42. van Roekeghem A.; Carrete J.; Mingo N.. Quantum Self-Consistent Ab-Initio Lattice Dynamics. arXiv 2020. [Google Scholar]
  43. van Roekeghem A.; Carrete J.; Oses C.; Curtarolo S.; Mingo N. High-Throughput Computation of Thermal Conductivity of High-Temperature Solid Phases: The Case of Oxide and Fluoride Perovskites. Phys. Rev. X 2016, 6, 041061 10.1103/PhysRevX.6.041061. [DOI] [Google Scholar]
  44. Errea I.; Calandra M.; Mauri F. First-Principles Theory of Anharmonicity and the Inverse Isotope Effect in Superconducting Palladium-Hydride Compounds. Phys. Rev. Lett. 2013, 111, 177002. 10.1103/PhysRevLett.111.177002. [DOI] [PubMed] [Google Scholar]
  45. Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  46. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  47. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  48. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  49. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  50. Togo A.; Tanaka I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  51. Carrete J.; Li W.; Lindsay L.; Broido D. A.; Gallego L. J.; Mingo N. Physically Founded Phonon Dispersions of Few-Layer Materials and the Case of Borophene. Mater. Res. Lett. 2016, 4, 204–211. 10.1080/21663831.2016.1174163. [DOI] [Google Scholar]
  52. Carrete J.; Mingo N.; Curtarolo S. Low Thermal Conductivity and Triaxial Phononic Anisotropy of SnSe. Appl. Phys. Lett. 2014, 105, 101907. 10.1063/1.4895770. [DOI] [Google Scholar]
  53. Togo A.; Chaput L.; Tanaka I.; Hug G. First-Principles Phonon Calculations of Thermal Expansion in Ti3SiC2, Ti3AlC2, and Ti3GeC2. Phys. Rev. B 2010, 81, 174301. 10.1103/PhysRevB.81.174301. [DOI] [Google Scholar]
  54. Vinet P.; Smith J. R.; Ferrante J.; Rose J. H. Temperature Effects on the Universal Equation of State of Solids. Phys. Rev. B 1987, 35, 1945–1953. 10.1103/PhysRevB.35.1945. [DOI] [PubMed] [Google Scholar]
  55. Eriksson F.; Fransson E.; Erhart P. The Hiphive Package for the Extraction of High-Order Force Constants by Machine Learning. Adv. Theory Simul. 2019, 2, 1800184. 10.1002/adts.201800184. [DOI] [Google Scholar]
  56. Guyon I.; Weston J.; Barnhill S.; Vapnik V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. 10.1023/A:1012487302797. [DOI] [Google Scholar]
  57. Arrigoni M.; Carrete J.; Mingo N.; Madsen G. K. H. First-Principles Quantitative Prediction of the Lattice Thermal Conductivity in Random Semiconductor Alloys: The Role of Force-Constant Disorder. Phys. Rev. B 2018, 98, 115205. 10.1103/PhysRevB.98.115205. [DOI] [Google Scholar]
  58. After the energy minimization, for SnSeTe we obtain a = b = 3.95, △Se = 1.56 and △Te = 1.92; for SnSTe the results are a = b = 3.86, △S = 1.42 and △Te = 1.95
  59. Lindsay L.; Broido D. A.; Mingo N. Flexural Phonons and Thermal Transport in Graphene. Phys. Rev. B 2010, 82, 115427. 10.1103/PhysRevB.82.115427. [DOI] [Google Scholar]
  60. Hu X.; Yasaei P.; Jokisaari J.; Öǧüt S.; Salehi-Khojin A.; Klie R. F. Mapping Thermal Expansion Coefficients in Freestanding 2D Materials at the Nanometer Scale. Phys. Rev. Lett. 2018, 120, 055902. 10.1103/PhysRevLett.120.055902. [DOI] [PubMed] [Google Scholar]
  61. Carrete J.; Mingo N.; Wang S.; Curtarolo S. Nanograined Half-Heusler Semiconductors as Advanced Thermoelectrics: An Ab Initio High-Throughput Statistical Study. Adv. Funct. Mater. 2014, 24, 7427–7432. 10.1002/adfm.201401201. [DOI] [Google Scholar]

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES