Mechanics of Pulmonary Airways: Linking Structure to Function Through Constitutive Modeling, Biochemistry, and Histology

Abstract

Breathing involves fluid-solid interactions in the lung; however, the lack of experimental data inhibits combining the mechanics of air flow to airway deformation, making it difficult to understand how biomaterial constituents contribute to tissue response. As such, lung mechanics research is increasingly focused on exploring the relationship between structure and function. To address these needs, we characterize mechanical properties of porcine airways using uniaxial tensile experiments, accounting for bronchial orientation- and location dependency. Structurally-reinforced constitutive models are developed to incorporate the role of collagen and elastin fibers imbedded within the extrafibrillar matrix. The strain-energy function combines a matrix description (evaluating six models: compressible NeoHookean, unconstrained Ogden, uncoupled Mooney-Rivlin, incompressible Ogden, incompressible Demiray and incompressible NeoHookean), superimposed with non-linear fibers (evaluating two models: exponential and polynomial). The best constitutive formulation representative of all bronchial regions is determined based on curve-fit results to experimental data, accounting for uniqueness and sensitivity. Glycosaminoglycan and collagen composition, alongside tissue architecture, indicate fiber form to be primarily responsible for observed airway anisotropy and heterogeneous mechanical behavior. To the authors’ best knowledge, this study is the first to formulate a structurally-motivated constitutive model, augmented with biochemical analysis and microstructural observations, to investigate the mechanical function of proximal and distal bronchi. Our systematic pulmonary tissue characterization provides a necessary foundation for understanding pulmonary mechanics; furthermore, these results enable clinical translation through simulations of airway obstruction in disease, fluid-structure interaction insights during breathing, and potentially, predictive capabilities for medical interventions.

1. Introduction

Billions of dollars are spent annually treating lung disease, which is the leading cause of death worldwide (6; 70; 89). Chronic obstructive pulmonary disease alone claims three million lives each year (24). The lung is a fluid-structure system, but current lung biome chanics research consists predominantly of single-mechanism approaches, where the fluid mechanics community explores fluid flow, particle deposition, and branching algorithms (25; 46; 49; 52; 62; 88; 93; 90), and the solid mechanics community investigates trachea, alveolar, and parenchymal tissue response (39; 58; 59; 67; 83). The lack of experimental data on lung tissue mechanics limits research efforts in modeling airway obstruction behavior due to inflammation or constriction, or tissue remodeling in chronic lung diseases (e.g., asthma or bronchitis). Existing computational studies have been constrained to oversimplification of tissue material properties (19; 20; 42; 45; 55; 87), or restricted to the trachea due to the challenge of acquiring intra-parenchymal bronchi material properties (14; 74; 81; 82). Analogously, unknown pulmonary mechanics cause majority of fluids research to simulate flow through rigid airways (62; 69; 88), despite knowing that accounting for tissue deformations will significantly change airflow patterns, which is even more pronounced in diseased states (53; 85; 94). Experimentally informed mathematical models representative of airway behavior are capable of integrating pulmonary fluid and structure systems to investigate healthy and diseased lung function.

Our recent work experimentally measured uniaxial tensile mechanics of porcine bronchi, demonstrating material region-dependency from proximal to distal airways (23). Circumferentially oriented specimens were nearly twice as stiff in distal airways than proximal airways. Furthermore, stiffness of axially oriented specimens were almost double that of circumferentially oriented specimens; Anisotropy agreed well with fiber orientation, which was primarily aligned in the axial direction. These experimental observations are critical to developing constitutive models of bronchial mechanics.

Research on other fiber-reinforced biological structures, such as cardiovascular tissue or annulus fibrosus of the intervertebral discs, have successfully described bulk tissue mechanics through structural constitutive laws (3; 63; 73; 84; 86). These models have been able to describe the relative stress contribution of each tissue subcomponent, including fibers, extrafibrillar matrix, and their interactions. Moreover, these models have been used to accurately describe the material response under other loading modalities, such as simple shear, which is difficult to measure experimentally due to the lack of fiber engagement (10; 40; 65). However, identifying appropriate constitutive laws without over-constraining or over-parameterizing the model has not been trivial.

The progression of lung research relies on establishing and accurately representing bronchial tissue biomechanical properties (45; 78). Thus, the aim of this study is to develop a structure-based constitutive model describing uniaxial mechanical behavior of proximal and distal airways. Additionally, the biochemical composition for each tissue region is assessed to investigate how individual mechanical constituents impact bulk tissue behavior. Lastly, histology is performed on the trachea, large bronchi, and small bronchi to determine the influence of fiber architecture on mechanical function.

Robust computational models are valuable for understanding three-dimensional deformations in healthy and diseased lungs, and eliciting similarities between porcine and human tissues can facilitate such insights (41; 61; 57). Results from this study provide important information for constructing physiologically relevant models that represent native tissue anisotropy and heterogeneity. Most importantly, the formulated constitutive model in this study enables the connection of air flow forces to deformations, advancing comprehensive fluid-structure analyses, which impeded pulmonary biomechanics research to date.

2. Materials and Methods

2.1. Lung Specimens

Specimen preparation is briefly described here as experimental characterization was the focus of previous work and is used to inform the constitutive model described here. For more details on tissue preparation, protocol development, and mechanical testing, the reader is directed to Eskandari et al. 2018 (23).

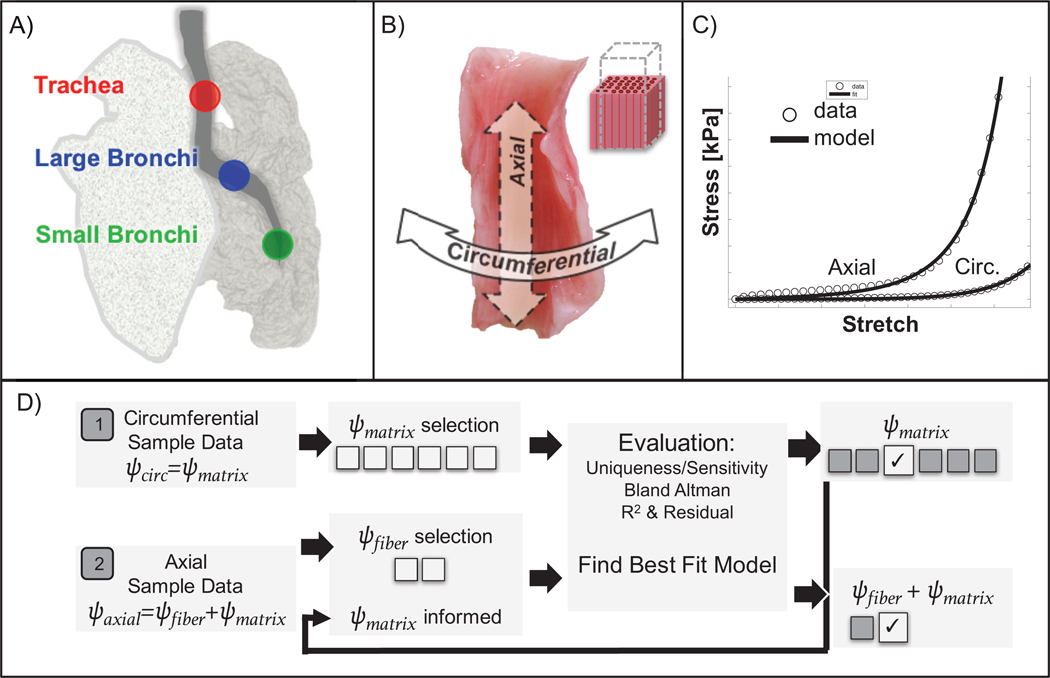
Uniaxial tensile tests were performed on specimens from the trachea, large bronchi, and small bronchi of porcine lungs (n = 27–30 per lung, Figure 1A). Animals were obtained from an abattoir and did not require IACUC approval (n = 5 animal lungs). Bronchi have a cartilaginous layer wrapped around soft tissue, which forms the innermost layers (mucosa and submucosa) (5; 19). Cartilage morphology evolves from a C-ring in the trachea to individual scales distally; samples were consistently collected from proximal and distal regions with disconnected cartilage sections and freely deforming soft tissue to isolate and examine the mucosa and submucosa layers only (18). The specimens were oriented along the airway’s circumferential or axial direction (Figure 1B) (14; 60). Experimental protocol development and consistent tissue handling technique is critical to proper material measurement (23). The biomechanics literature lacks a universal gripping technique or soft tissue tare load (pre-load) procedure to replicate in vivo physiological forces, despite the known impact on measured stress-strain behavior. As a common tare load was inappropriate for samples of varying location and orientation, the unloaded reference state was defined after data collection to consistently locate the initial state on the classical J-shaped curve (using mathematical analysis of curve concavity (23)). Rectangular test specimens (dimensions: 4.4±1.0 mm wide, 6.4±1.9 mm long, and 2.0±0.6 mm thick) were strained to 35% at a rate of 1%/sec for six cycles and the loading stress-strain response from the last cycle was analyzed (Figure 1C) (23; 81).

Figure 1:

Schematic of study design. A) Three regions of porcine airway were evaluated, including trachea, large bronchi, and small bronchi. B) For each region, samples were orientated along the circumferential or axial direction, with fibers aligned along the axial direction. C) The stress-strain response was curve-fit to a structure-based constitutive model that included a description for the fibers and extrafibrillar matrix. D) Methods for model selection, whereby circumferential samples informed the matrix model, which was combined with a fiber model to fit axial samples.

2.2. Continuum Mechanics

Non-linear constitutive equations were used to mathematically describe tissue deformations based on experimental results. The deformation map ϕ(X) related the undeformed state to the deformed state, and the deformation gradient, F(X)=∇ϕ(X), was defined as a diagonal matrix for uniaxial tensile testing (33; 74):

$$F=\left[\begin{array}{lll}{\lambda }_1\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\lambda }_2\hfill & 0\hfill \\ 0\hfill & 0\hfill & {\lambda }_3\hfill \end{array}\right]$$ (1)

λ₁, λ₂ and λ₃ were principle stretches and λ₃ was aligned with the elongation direction of the tissue (Instron 5848 Microtester). λ₃ was described as λ₃ = 1 + d/L, where d was the displacement normalized by the initial length L. λ₁ and λ₂ were assumed to contract equally, according to the Poisson’s ratio ν, which was a free parameter for compressible strain-energy models. The deformation gradient for large deformations was generalized by using Poisson’s ratio to account for transverse direction contractions (Equation 2). F was further reduced to $F=diag\left(\sqrt{{\lambda }_3};\sqrt{{\lambda }_3};{\lambda }_3\right)$ for incompressible models (i.e., ν = 0.5) (34).

$$F=\left[\begin{array}{ccc}{\lambda }_3^{-\nu }& 0& 0\\ 0& {\lambda }_3^{-\nu }& 0\\ 0& 0& {\lambda }_3\end{array}\right]$$ (2)

2.3. Constitutive Models

Observations of anisotropic microstructure and inspection of tissue morphology informed fiber orientation and motivated our use of a structurally defined strain-energy density function (SED) (9; 32; 44). SED functions commonly found in the literature, expressed in terms of material parameters and invariants of the deformation tensor, are listed in Table 1. Six phenomenological hyperelastic constitutive models were assessed as a potential description for the extrafibrillar matrix (11; 13; 71). They differ in representing both compressible and incompressible behaviors, the degree of non-linearity representation (i.e. stretch raised to a power, acting within an exponential, or as an inverse), and number of fitted parameters. Some expressions were originally formulated for rubber-like materials and others for soft biological tissues, and all have precedent for use in formulating new constitutive relationships (10; 29; 51).

Table 1:

Table of strain-energy density functions (SED) used to describe extrafibrillar matrix (circumferentially oriented samples) and fiber (axially oriented samples) mechanics.

Model Name	SED (ψ)	Function of Stretch (λ3)	Parameters [Units] and Definitions
Compressible NeoHookean ψ(I1(λ3), J(λ3))	$\frac{1}{2}\mu \left[I_1-3\right]+\frac{\lambda }{2}\ln {(J)}^2-\mu \ln (J)$	$$\begin{gathered} I_1=\text{tr}(C)=2{\lambda }_3^{-2\nu }+{\lambda }_3^2 \\ J=\det (F)={\lambda }_3^{1-2\nu } \end{gathered}$$ I1 first invariant, J Jacobian	λ [MPa], Lamé constant μ [kPa], Lamé constant ν [ − ], Poisson’s Ratio
Unconstrained Ogden ψ(λ3, aJ(λ3))	$$\begin{gathered} \frac{1}{2}{c}_p{(J-1)}^2 \\ +\frac{c_1}{{\alpha }^2}\left({\lambda }_1^{\alpha }+{\lambda }_2^{\alpha }+{\lambda }_3^{\alpha }-\alpha \ln (J)\right) \end{gathered}$$	$\begin{array}{c}{\lambda }_1={\lambda }_2={\lambda }_3^{-\nu }\\ J=\det (F)={\lambda }_3^{1-2\nu }\end{array}$ J Jacobian	c1 [kPa], coefficient cp [MPa], bulk-like modulus α [ − ], exponent ν [ − ], Poisson’s Ratio
Uncoupled Mooney Rivlin ψ(I1(λ3), I2(λ3)J(λ3))	$\begin{array}{c}{c}_1\left(I_1-3\right)+c_2\left(I_2-3\right)\\ -2\left(c_1+2c_2\right)\ln (J)+\frac{\lambda }{2}\ln {(J)}^2\end{array}$	$\begin{array}{c}J=\det (F)={\lambda }_3^{1-2\nu }\\ I_1=\text{tr}(C)=2{\lambda }_3^{-2\nu }+{\lambda }_3^2\\ I_2=\frac{1}{2}\left[{(\text{tr}(C))}^2+\text{tr}\left(C^2\right)\right]=\\ ={\lambda }_3^{-4\nu }+2{\lambda }_3^{(2-2\nu )}\end{array}$ I1 first invariant, I2 second invariant, J Jacobian	c1 [MPa], coefficient c2 [MPa], coefficient λ [MPa], coefficient ν [ − ], Poisson’s Ratio
Incompressible Ogden ψ(I1λ1(λ3), λ2(λ3))	$\frac{2\mu }{{\alpha }^2}\left({\lambda }_1^{\alpha }+{\lambda }_2^{\alpha }+{\lambda }_3^{\alpha }-3\right)$	$I_1=\text{tr}(C)=2{\lambda }_3^{-2\nu }+{\lambda }_3^2$	α [ − ], exponent μ [kPa], coefficient
Incompressible Demiray ψ(I1(λ3))	$\frac{\mu }{2\beta }\left(\exp \left[\beta \left(I_1-3\right)\right]-1\right)$	$I_1=\text{tr}(C)=2{\lambda }_3^{-2\nu }+{\lambda }_3^2$ I1 first invariant	β [ − ], exponent μ [kPa], coefficient
Incompressible NeoHookean ψ(I1(λ3))	$\frac{\mu }{2}\left(I_1-3\right)$	$I_1=\text{tr}(C)=2{\lambda }_3^{-2\nu }+{\lambda }_3^2$ I1 first invariant	μ [kPa], coefficient
Exponential ψ(I4(λ3))	$\frac{k_1}{k_2}\left({\exp }^{\left[k_2{\left(I_4-1\right)}^2\right]}-1\right)$	$I_4={\lambda }_3^2$	k1 [kPa], coefficient k2 [ − ], exponent
Polynomial ψ(I4(λ3))	k1(I4 − 1)2 + k2(I4 − 1)3	$I_4={\lambda }_3^2$	k1 [kPa], coefficient k2 [kPa], coefficient

Once a constitutive relationship was defined for the matrix, it was augmented with a non-linear stress-stretch description for the fibers, as axial tissues displayed greater strain-stiffening well represented by exponential or polynomial expressions (Figure 2) (29; 79). It was assumed that only the extrafibrillar matrix was engaged for specimens tested along the circumferential direction, and testing along the axial direction engaged fibers embedded within the matrix (Figure 1D, Equations 3–4) (34; 35; 38; 73).

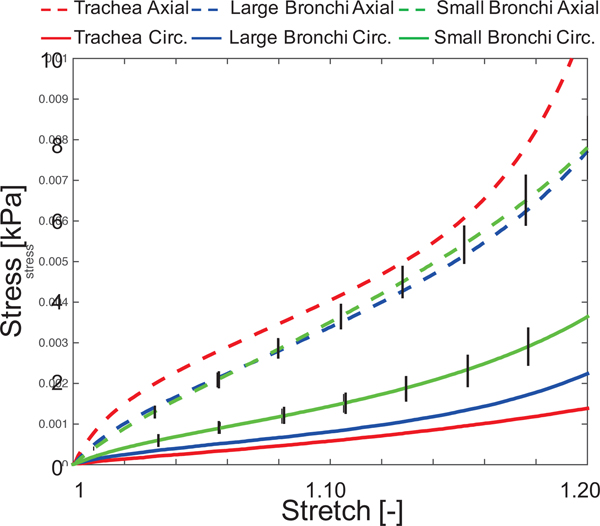
Figure 2:

Average stress-stretch curves for each sample orientation and region. Generally, axial samples displayed greater strain-stiffening than circumferential samples. For clarity, standard error of the mean is shown for the small bronchi.

$${\psi }_{\text{circumferential}}={\psi }_{\text{matrix}}$$ (3)

$${\psi }_{\text{axial}}={\psi }_{\text{matrix}}+{\psi }_{\text{fiber}}$$ (4)

For clarity, only the derivation of the first Piola-Kirchhoff stress, P, for the compressible Neo-Hookean strain-energy is described here (Equations 5–6); the same procedure was followed for all constitutive relationships (21). Briefly, P was found by deriving the strain-energy function with respect to F using chain and product rules. Experimental P, P^exp, was directly measured from uniaxial tensile tests (54), where P^exp = f_z/(WT); f_z was the force measured by the load cell, W represents tissue width, and T represents tissue thickness. J is defined the determinant of F (36).

$$\psi \left(I_1\left({\lambda }_3\right),J\left({\lambda }_3\right)\right)=\frac{1}{2}\mu \left[I_1-3\right]+\frac{\lambda }{2}\ln {(J)}^2-\mu \ln (J)$$ (5)

$$P=\frac{\delta {\psi }_{\text{C}-\text{NH}}}{\delta F}=\frac{\delta {\psi }_{\text{C}-\text{NH}}}{\delta I_1}\frac{\delta I_1}{\delta {\lambda }_3}\frac{{\lambda }_3}{\delta F}+\frac{\delta {\psi }_{\text{C}-\text{NH}}}{\delta J}\frac{\delta J}{\delta {\lambda }_3}\frac{{\lambda }_3}{\delta F}$$ (6)

Partial derivatives terms were (79):

$$\begin{gathered} \frac{\delta {\psi }_{\text{C}-\text{NH}}}{\delta I_1}=\frac{\mu }{2}; \\ \frac{\delta I_1}{\delta {\lambda }_3}=-4\nu {\lambda }_3^{(-2\nu -1)}+2{\lambda }_3; \\ \frac{\delta {\psi }_{C-NH}}{\delta J}=\frac{\mu }{J}+\frac{\lambda }{J}\mathit{ln}(J); \\ \frac{\delta J}{\delta {\lambda }_3}=(1-2\nu ){\lambda }_3^{-2\nu }; \\ \text{and}\frac{{\lambda }_3}{\delta F}=1. \end{gathered}$$

Viscous and porous effects were ignored; however, unlike biological studies where compressibility was commonly assumed a priori, here compressibility was an output of the curve-fitting process (51; 54). Preliminary digital image correlation results substantiated the assumption of homogenous uniaxial tissue deformation (23).

2.4. Material Model Calibration

MATLAB’s non-linear least squares algorithm, lsqnonlin, was used to minimize the difference between model generated P and P^exp. Experimental data was interpolated into 1001 equally spaced points to avoid curve-fit biasing. Upper and lower bounds were set to ±∞ for all parameters, except ν, which was constrained between 0 and 0.5, and c₂ in the uncoupled Mooney-Rivlin model, which was negative for concavity (33). Each parameter’s initial guess was randomized, varied two orders of magnitude, and subject to multiple runs to check for uniqueness in the resulting model parameters.

A Bland Altman analysis was used to provide a measure of agreement between model and experimental data. The coefficient of determination provided goodness of fit and was defined as $R^2=1-S^{\text{residual}}/S^{\text{total}},\text{where}{S}^{\text{residual}}={\mathrm{\Sigma }}_i^{1001}{\left(P_i^{\text{exp}}-P_i\right)}^2,\text{and}{S}^{\text{total}}={\mathrm{\Sigma }}_i^{1001}{\left(P_i^{\text{exp}}-P_{\text{mean}}\right)}^2,$ with P_mean as the mean of observed data (10). The best-fit model was defined as the one with the smallest mean for residual error ${\mathrm{\Sigma }}_i^{1001}\left(P_i^{\exp }-P_i\right)$ in conjunction with an R² value closest to 1.0. The adjusted R² was also considered to account for comparing models with differing number of parameters, but the difference observed was negligible (R² differed by 10⁻⁵).

Once matrix parameters were determined (Equation 3), the stress-stretch data for axial specimens were curve-fit to the matrix and fiber description (Equation 4). Results from circumferential direction specimens were used to determine the upper and lower bound for the matrix parameter curve-fit in the axial direction (bounds = average ± 1 standard deviation; Figure 1D). Thus, the best-fit structurally-reinforced constitutive model representative of all three regions (trachea, large bronchi, and small bronchi) was determined. Matrix and fiber stress contribution was calculated by dividing the stress for each subcomponent by the total stress across the strain range for axial tissues (31).

2.5. Sensitivity Analysis

A sensitivity analysis was conducted to inform how deviations in constitutive model parameter calibrations influenced the stress-stretch response (31; 64). For circumferentially oriented samples fit to the incompressible Demiray model, one parameter, either μ or β, was fixed at the average value, while the other parameter was varied between average ±1 standard deviation. Similarly, for axial samples augmented with an exponential fiber function, μ, β, k₁ or k₂ were varied between average ±1 standard deviation, while the other three parameters were held at their average value.

2.6. Biochemistry

A single porcine lung was used to quantify biochemical composition for the trachea, large bronchi, and small bronchi. A 4 mm diameter biopsy punch was used to prepare three specimens at each location. A scalpel was used to separate the cartilage layer from soft tissue. Samples were weighed to acquire wet weights and then dried overnight in a lyophilizer to measure dry weights before digesting the tissue in 1 mL of 0.5 mg/mL proteinase K (56°C).

Water content was calculated as the difference between wet and dry weights normalized by the wet weight. DNA content was determined using the PicoGreen Kit (Invitrogen). Glycosaminoglycan (GAG) content was determined using 1,9-dimethylmethylene blue (DMMB). A 100μl aliquot of the digested sample was prepared for the hydroxyproline assay through acid hydrolysis (12 M HCl). The ratio of hydroxyproline to collagen was assumed to be 10.0.GAG and collagen contents were normalized by wet weight, dry weight, and DNA content (8).

2.7. Histology

A representative specimen from the trachea, large bronchi, and small bronchi region was prepared for histological staining. Specimens were cut from the airway using a scalpel, fixed in 4% formaldehyde solution (66), and sent to Gladstone Institutes Histology and Light Microscopy Core (University of California, San Francisco) for processing, sectioning, and staining. Dehydrated samples were embedded in paraffin wax blocks and two serial 10 μm thick slices were collected onto glass slides. Sections were axially prepared, as samples displayed axially aligned collagen and elastic fibers (undiscerned between types of collagen or elastic, elaunin, and oxytalan fibers (9)). Samples were stained with Masson’s Trichrome to visualize the tissue architecture (9; 72), where red stained elastin and blue stained collagen (16). Slides were imaged with a digital camera (AmScope FMA037, Irvine CA) attached to an upright microscope (Olympus CKX31).

2.8. Statistics and Correlations

MATLAB was used to identify statistical outliers, which were defined as values exceeding 150% of the interquartile range (Statistics Toolbox, Mathworks Inc.). All values were subject to a Box-Cox transformation to account for non-normal distribution, followed by a one-way analysis of variance (ANOVA) and Bonferroni post-hoc analysis. Spearman’s correlation (ρ) was performed to find potential interparameter dependencies, and dependencies between model parameters and experimentally measured mechanical properties (23). Thresholds for strong, moderate, and weak correlations were defined as ρ≥0.7, 0.7>ρ>0.5, and ρ≤0.5, respectively (15). Significance was set at p<0.05 for all analyses. Bulk tissue stiffness modulus, E, was defined as the slope of stress-strain curve in the toe-region (23), which was found to be significantly correlated to constitutive parameters, and thus, subjected to further relational analyses (31; 64).

3. Results

3.1. Constitutive Model Performance

Specimens tested along the axial direction displayed consistently greater stresses for given strain range than specimens tested along the circumferential direction (Figure 2). Axial-direction stiffness did not depend on spatial location, but the stiffness of circumferential specimens from the small bronchi was greater than the trachea (p<0.01 and large bronchi (p<0.05) (23).

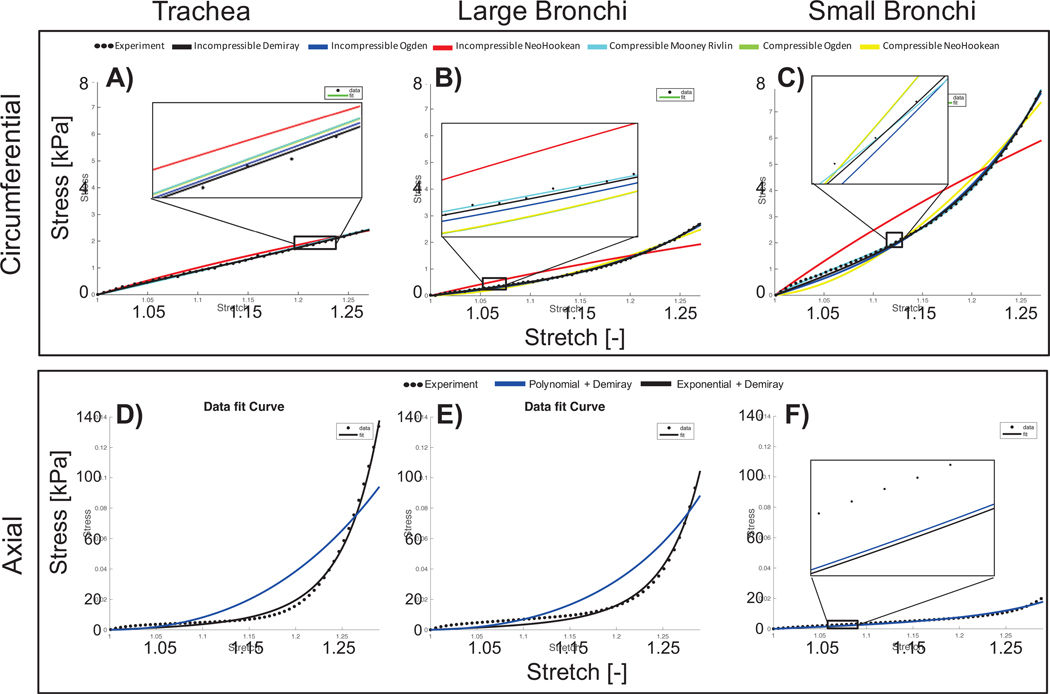
Five of the six matrix models had R² values greater than 0.95. The incompressible Neo-Hookean model did not describe experimental data well (R²=0.82, Table 1; Figure 3B-C), as it was incapable of capturing the non-linear stress-stretch response with a single parameter. Uniqueness evaluations found compressible models were generally over-parameterized, resulting in non-unique curve-fits. Thus, the incompressible Demiray model was determined to be the best matrix model with the highest R² value, minimum residual error (R²=0.997, residual=−0.041 MPa), and to be unique, followed by the incompressible Ogden model (Table 2.6, green highlighted models).

Figure 3:

Representative uniaxial stress-stretch data of circumferential (A-C) and axial (D-F) specimens fit to various constitutive models. Model parameters were fit for each region separately (A and D: trachea, B and E: large bronchi, C and F: small bronchi). Circumferential samples were fit to homogenous compressible and incompressible non-linear matrix models, with incompressible Demiray providing the best fit based on high R², low residual error, and sensitivity analysis (top row, black line). Axial tissues were fit to fiber-reinforced exponential or polynomial function, with incompressible Demiray for the matrix. Fibers were best described with an exponential strain-energy function (bottom row, black line). Incompressible NeoHookean (black line, B-C) and polynomial model (blue line, D-E) poorly represented experimental data. Comparable fit performances are visible in reduced stress-strain range insets.

Table 2:

Model parameters from curve-fitting. All models were evaluated for parameter uniqueness, sensitivity, reproducibility, and agreement between model fit and experimental data (greater R² coefficient and lower residual error). Models highlighted in green satisfied these criteria, while yellow yielded non-unique fits, and orange denoted a poor fit.

Matrix Response (Circumferential Samples)
Compressible Models				Incompressible Models
Neohookean				Ogden
R2=0.964, Residual [Mpa]=−0.131	Trachea	Large Bronchi	Small Bronchi	R2=0.995, Residual [Mpa]=−0.088	Trachea	Large Bronchi	Small Bronchi
ν[−]	0.48 ± 0.07	0.48 ± 0.07	0.48 ± 0.06	μ[kPa]	3.80 ± 2.13	2.58 ± 1.80	5.45 ± 4.55
μ[kPa]	23.7 ± 39.3	147 ± 298	115 ± 166	α[−]	7.64 ± 3.60	13.8 ± 9.34	12.0 ± 5.57
λ[MPa]	−1120 ± 1110	−3760 ± 4920	−3250 ± 3340
Unconstrained Ogden				Demiray
R2=0.964, Residual [Mpa]=−0.131	Trachea	Large Bronchi	Small Bronchi	R2=0.997, Residual [Mpa]=−0.041	Trachea	Large Bronchi	Small Bronchi
ν[−]	0.34 ± 0.09	0.25 ± 0.14	0.24 ± 0.12	μ[kPa]	2.21 ± 1.04	2.02 ± 1.33	3.76 ± 2.95
cp [Mpa]	39.5 ± 245	11.2 ± 49.7	8.86 ± 44.0	β[−]	2.51 ± 1.83	6.19 ± 4.21	5.17 ± 2.89
c1 [kPa]	127 ± 842	−287 ± 932	−322 ± 409
α[−]	−8.68 ± 36.3	2.05 ± 4.12	0.36 ± 7.56
Uncoupled Mooney-Rivlin				Incompressible Neohookean
R2=0.963, Residual [Mpa]=−0.125	Trachea	Large Bronchi	Small Bronchi	R2=0.819, Residual [Mpa]=0.387	Trachea	Large Bronchi	Small Bronchi
ν[−]	0.42 ± 0.06	0.44 ± 0.09	0.44 ± 0.09	μ[kPa]	3.55 ± 2.54	9.35 ± 15.0	10.1 ± 11.1
c1 [Mpa]	23.9 ± 66.7	452 ± 1820	965 ± 4000
c2 [Mpa]	−17.3 ± 90.1	−623 ± 3120	−1560 ± 6940
λ[MPa]	−499 ± 998	−2670 ± 5310	−1910 ± 2980
Fiber + Matrix Response (Axial Samples)
Exponential + Demiray				Polynomial + Demiray
R2=0.991, Residual [Mpa]=−0.175	Trachea	Large Bronchi	Small Bronchi	R2=0.959, Residual [Mpa]=0.607	Trachea	Large Bronchi	Small Bronchi
k1 [kPa]	2.61 ± 2.69	1.94 ± 1.22	1.72 ± 1.26	k1[kPa]	2.07 ± 2.83	3.29 ± 3.05	3.76 ± 2.87
k2 [−]	3.42 ± 2.80	2.01 ± 2.34	0.90 ± 1.85	k2[kPa]	11.5 ± 18.4	2.26 ± 5.00	0.65 ± 1.86
μ[kPa]	2.68 ± 0.91	2.51 ± 1.15	5.06 ± 2.44	μ[kPa]	2.35 ± 1.01	2.65 ± 1.11	4.18 ± 2.51
β[−]	1.20 ± 1.26	3.74 ± 3.12	2.65 ± 1.22	β[−]	3.49 ± 1.43	7.12 ± 3.88	3.73 ± 2.36

After the matrix model was selected, stress-stretch data from axially oriented samples were fit to a 2-term exponential or polynomial strain-energy function to describe fiber mechanics. Residual error was lower and R² values were greater for the exponential description (R² = 0.991, residual=−0.175 MPa; Table 2.6). Therefore, the combined strain-energy function was an incompressible Demiray matrix description with an exponential expression for the fibers, resulting in four model parameters: μ and β for the matrix parameters, and k₁, and k₂ for the fibers (Figure 4), similar to the two-term exponential form introduced by Humphrey and Yin (38).

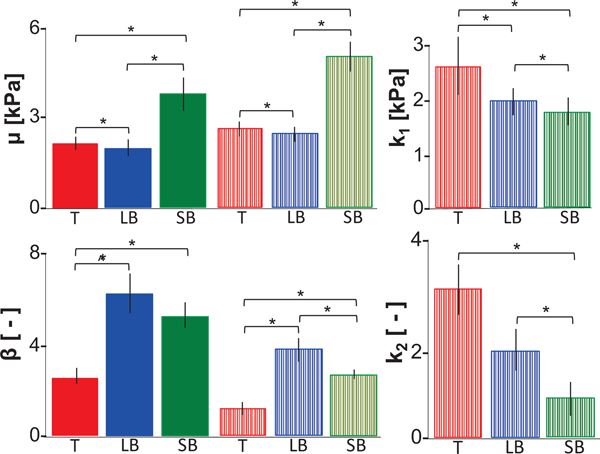
Figure 4:

Average ± standard error of means of incompressible Demiray model parameters (μ, β, k₁ and k₂) determined by fit to circumferentially oriented samples (solid bars) or in combination with a fiber description for axially-oriented samples (striped bars). Regional differences for μ and β were similar for both circumferentially and axially oriented specimens (trachea (T), large bronchi (LB), and small bronchi (SB)). k₁ and k₂ fiber parameters were determined from axially oriented specimens. Regional differences were observed for both fiber parameters. *p<0.001, ^p=0.003.

3.2. Region-Dependent Mechanical Behavior

Matrix parameters were informed by experimental data from both circumferential and axial direction specimens, which led to observed differences in the magnitude of these parameters. However, similar trends were expected and seen with respect to region, where μ was greatest for the small bronchi and β was greatest for the large bronchi (p<0.01). k₁ and k₂ decreased from the trachea to the small bronchi (p<0.01; Figure 4).

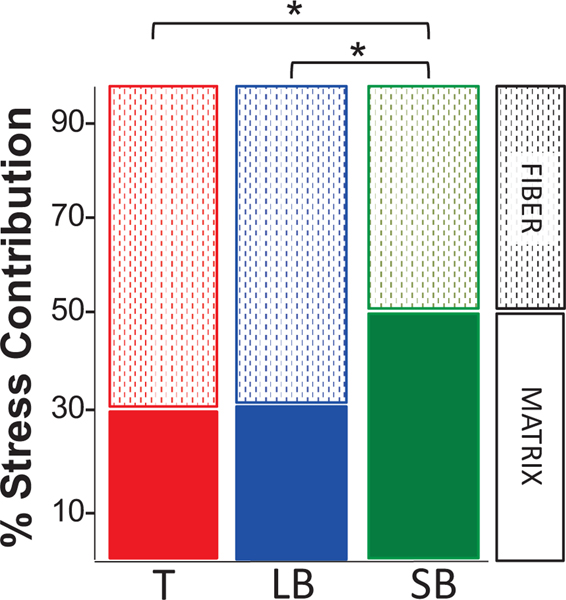
The matrix contribution to uniaxial loading was significantly lower in the trachea and large bronchi (29±19% and 32±16%, respectively) than the small bronchi (50±28%; p<0.002). Stress contribution in the trachea and large bronchi was mostly carried by the fibers (71±19% and (68±16%), while fiber and matrix contribution was nearly equal in the small bronchi (Figure 5).

Figure 5:

Percent stress contribution from fiber (dotted lined bars)and matrix (solid bars) components. Fiber contribution was greater than the matrix contribution in the trachea (T) and large bronchi (LB). Stress contribution was evenly distributed between matrix and fibers in the small bronchi (SB). *p<0.002.

3.3. Correlations to Material Properties

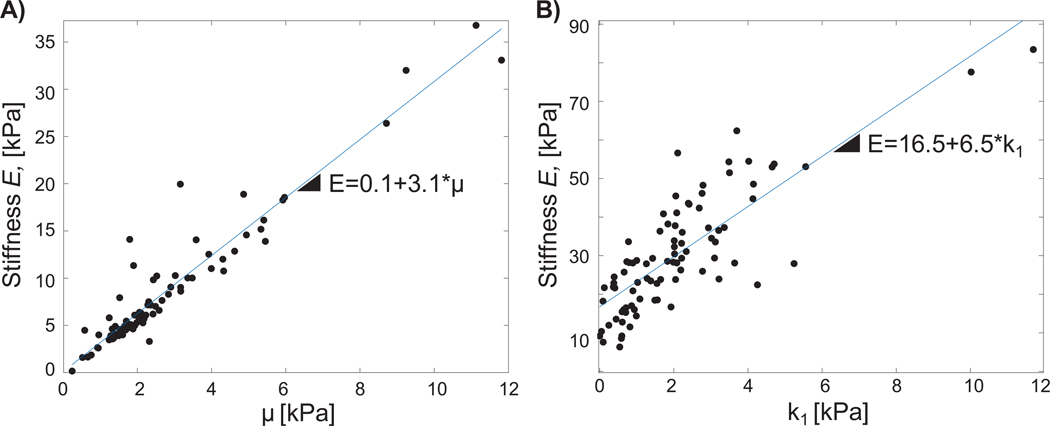
Table 3 reports inter-relationships between model parameters, and correlations between model parameters and measured bulk tissue modulus (E). At the initiation of tissue deformation λ₃=1, μ physically represents the matrix stiffness and k₁ represents the fiber stiffness; β and k₂ define material non-linearity. The only inter-parameter correlation found was between β and k₂ and was very weak (ρ = −0.25, p=0.02); thus, inter-parameter relationships were not further analyzed. In the circumferential direction, E was strongly correlated to μ (ρ>0.9, p=0; Figure 6), with a weak, but significant, correlation to β (ρ=0.26, p=0.02). In the axial direction, there was a weak correlation between E and μ (ρ=0.43, p=0), and a strong correlation between E andk₁ (ρ=0.79, p=0; Figure 6). The slope of E − μ response was observed to be nearly half that of the E − k₁ trend.

Table 3:

Correlations (ρ), between parameters (interparameter), and between model coefficients and measured mechanical properties. No significant interparameter correlations were observed, except for a weak correlation between β and k₂ (ρ=−0.25). E was significantly correlated with mechanical parameters: for circumferential samples, both μ and β had significant relationships to E, but only μ had a strong correlation (ρ=0.91); similarly for axial samples, μ and k₁ were significantly correlated with E, but only k₁ had a strong correlation coefficient (ρ=0.79).

Incompressible Demiray (Circumferential)
		Interparameter Correlation
	ρ	p-value
β, μ	0.01	0.94
		Correlation to Stiffness (E)
	ρ	p-value
E, β	0.26	0.02
E, μ	0.91	0.00
Incompressible Demiray + Exponential Fiber (Axial)
		Interparameter Correlation
	ρ	p-value
β, μ	0.02	0.89
μ, k1	−0.06	0.56
μ, k2	−0.16	0.15
β, k1	0.11	0.30
β, k2	−0.25	0.02
k1, k2	−0.06	0.57
		Correlation to Stiffness (E)
	ρ	p-value
E, μ	0.43	0.00
E, β	0.07	0.52
E, k1	0.79	0.00
E, k2	−0.07	0.50

Figure 6:

A) For circumferential samples, a strong correlation was observed between bulk tissue modulus E and matrix modulus μ. B) For axial samples, a strong correlation was observed between bulk tissue modulus and fiber stiffness k₁. Data for all three regions shown.

3.4. Sensitivity Analysis

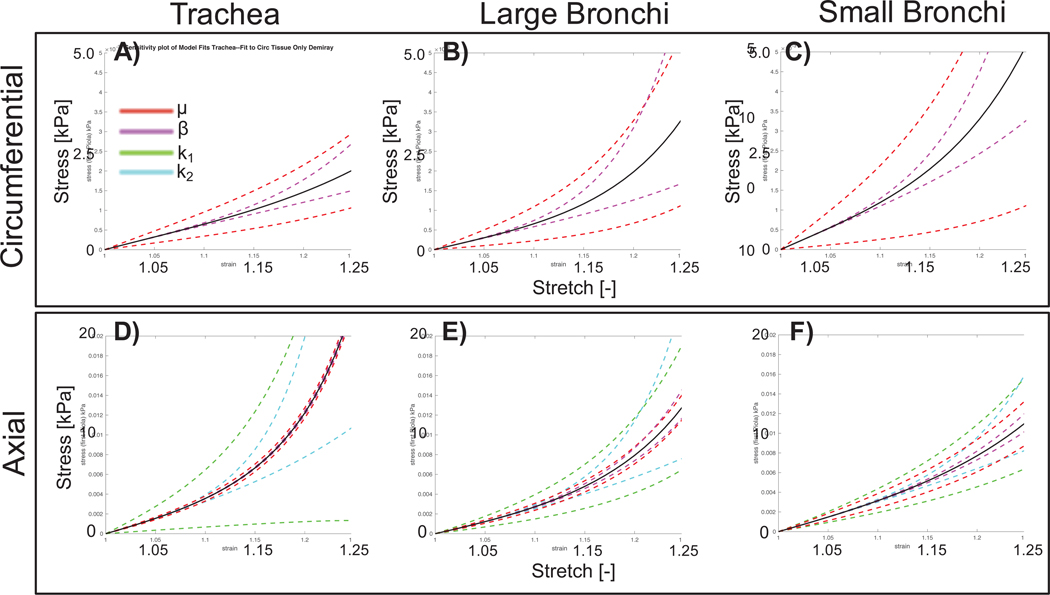
Sensitivity analysis explored how model performance was impacted by variations in determined model parameters (Figure 7). Greater sensitivity was defined as a wider deviation in stress response for a given stretch. Generally more variation from the average response was seen with increased stretch. Stress-stretch behavior for the small bronchi was most sensitive to μ and β. Stress-stretch results for the trachea and large bronchi were more sensitive to fiber parameters k₁ and k₂, than matrix parameters. With respect to regional variations, the small bronchi was almost equally sensitive to matrix and fiber parameters, relating to the equal contribution observed in the overall stress response (Figure 5). k₁ and μ resulted in the most sensitivity for axial and circumferential specimens, respectively.

Figure 7:

Results from sensitivity analysis. A-C) Incompressible Demiray model shown with average model parameters represented by the solid black line. Deviations in model parameters μ, β by ± 1 standard deviation are shown by colored dashed lines. D-F) Combined exponential fiber and incompressible Demiray matrix fit with average model parameters (solid black line) and deviations of μ, β, k₁, k₂ by ± 1 standard deviation. One parameter was varied (colored, dotted lines) while others were held fixed to the average value.

3.5. Tissue Composition and Microstructure

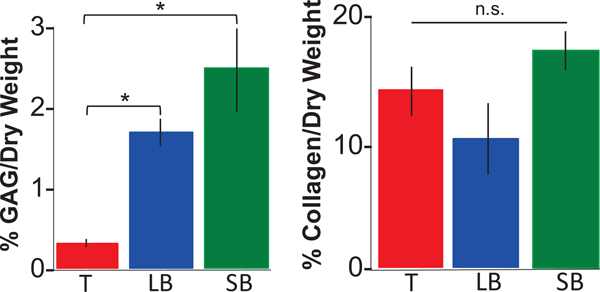
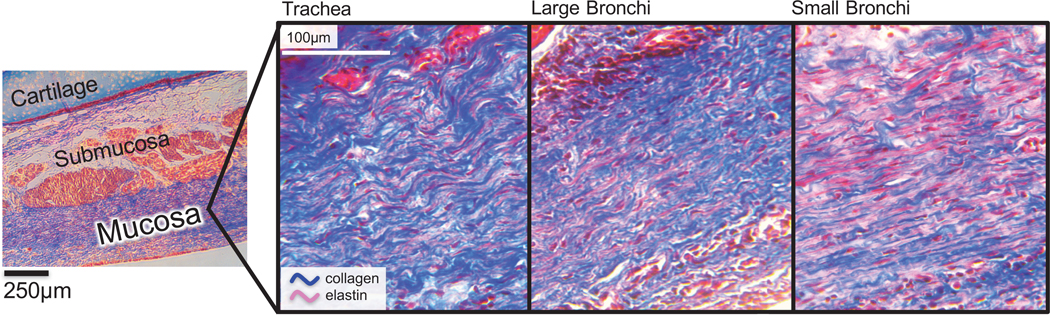
Regional variations in GAG and DNA content normalized by dry weights were observed, where the GAG content in the trachea (0.3± 0.5%) was significantly lower than large; (2±0.1%, p=0.001) and small bronchi (2 ± 0.04%, p<0.001;.Figure 8). There were no significant differences in overall collagen content with respect to airway region (p≥0.07, trachea: 14 ±2%; large bronchi: 10±3%; and small bronchi: 17 ± 2%). However, Masson’s Trichrome staining suggests regional differences between fiber architecture (collagen and elastin; Figure 9). Within the mucosa layer (5), fibers displayed notable crimping for trachea regions and were more taut distally (i.e., small bronchi).

Figure 8:

Glycosaminoglycans (GAG) and collagen content of soft tissue (submucosa and mucosa) normalized by dry weight (average ± standard deviation for all three regions: trachea (T), large bronchi (LB) and small bronchi (SB)). Generally, GAG and DNA content increased from proximal to distal regions (*p<0.001). Conversely, regional differences were not significant (n.s.) for collagen content.

Figure 9:

Representative histological samples stained with Masson’s Trichrome, where collagen fibers are blue and elastin fibers appear red. Fibers in the trachea were crimped, while fibers in the small bronchi appeared to be taut and straightened.

4. Discussion

In this study, we have established the first experimentally informed constitutive model for extra- and intra-parenchymal airways. The structure-based model represents bulk tissue anisotropy by describing non-linear fibers imbedded in the extrafibrillar matrix. Notable bronchial heterogeneity observed in experimental data manifests in the constitutive model as varying parameter values. Good agreement with experimental data and strong correlations between bulk tissue modulus and model parameters for matrix and fiber stiffness demonstrates accurate representation via a non-interacting fiber-matrix description (Figure 6) (31; 65). Describing bronchial tissue as incompressible is also found to be adequate (Table 2.6) (11; 54).

Differences between trachea and small bronchi mechanics are significant across all constitutive model parameter fits (Figure 4). In contrast to experimental observations where significant regional dependency was seen only in circumferential samples, our constitutive model highlights axial tissue heterogeneity. Fiber parameters k₁ and k₂ decreased distally unlike matrix parameters μ and β, which displayed heterogeneity but not unidirectional trends (Figure 4).

Individually calibrated parameters do not directly manifest in bulk tissue response but match the overall stress contribution trends from proximal to distal regions (Figure 5): highest matrix stiffness, as seen in the small bronchi, corresponds with greatest matrix stress contribution; similarly, high fiber stiffness translates to greater fiber stress contribution in the trachea and large bronchi. The increasing role of the matrix contribution distally is important in diseased states, as previous studies have shown the matrix to be responsible for triggering tissue remodeling (17; 30). Our model could be used to study remodeled states through altered matrix and fiber stiffness.

In selecting an appropriate combination of SED functions to describe airway mechanics, sensitivity and uniqueness were evaluated to ensure that the selected model was not over-parameterized or over-sensitive to one particular parameter. Deviation in model fit to experimental data indicates some model parameters to be more sensitive than others (Figure 7). Greater sensitivity corresponds to decreased model fidelity, with more sensitive parameters causing more variability in predicted tissue behavior. Regional sensitivity appears to trend with stress contribution: matrix stress-strain response is increasingly more sensitive to matrix parameters distally (in both axial and circumferential samples), which also corresponds to the tissue region with greatest matrix contribution. Greater sensitivity to fiber parameters is similarly observed in axial trachea and large bronchi specimens, corresponding to regions with greatest fiber contribution.

The datasets for matrix modulus (μ) and fiber modulus (k₁) were from circumferential and axial samples respectively, and their direct positive relationship to E is expected from model construction; however, the differing degree of μ and k₁ correlation with E suggests changes in the matrix modulus less drastically impacts the overall bronchial stiffness, whereas slight changes in fiber modulus would more greatly influence tissue behavior. This indicates that while initial isotropic models helped understand airway obstruction (20; 22; 56; 87), the role of fibers is critical and must be considered in bronchial mechanics.

The association between tissue composition and mechanics is considered. GAGs are coupled to viscoelasticity, resist elongation, and display a stepwise concentration increase from the trachea to the small bronchi (Figure 8) (30). μ is the greatest in the small bronchi but does not continuously increase distally as GAG does. The higher concentration of GAG in small bronchi may resist loading deformations more, resulting in greater stress range and increased matrix contribution distally. Moreover, GAG correlates to energy dissipation: a previous study showed GAG degradation caused increased energy dissipation (1); therefore, one could postulate the increased presence of GAG translates to greater energy efficiency for smaller airways. Our upcoming viscoelastic models better explain the observed heterogeneous stress relaxation (23) and explore the energy efficiency of bronchi.

Contrary to GAG content, collagen is homogenous throughout the airway, unlike fiber parameters k₁ and k₂, which decreased from the trachea to small bronchi (Figure 4 and 8). This difference may be due to limits of measuring hydroxyproline, a molecule that is part of fibrous components that may not directly contribute to tensile mechanics (e.g., elastin or minor collagens) (7). Nonetheless, taken together, these findings provide preliminary support for linking quantitative measures of tissue composition with model parameters, which will be important for understanding tissue remodeling with age and disease (68). Future work will need to assess specific proteins to inform the relationship of fibrous composition to mechanical properties, and how that may evolve in disease.

Collagen and elastin fibers are the major force-bearing pulmonary components (27): collagen fibers are inextensible, stretching 2%, while elastin fibers can stretch 140% (77). The intimate association of these fibers and arrangement throughout the lungs dictates expansion (2). However, the inconclusive correlation of homogenous collagen content to heterogenous constitutive material properties suggests tissue composition alone may not be primarily responsible for mechanical function.

Investigating regional tissue microstructure through histology yields qualitative insights of bronchial fiber evolution, which is unestablished to date (Figure 9) (44). Fibers appear uniformly axially aligned, with dispersion unlikely to influence mechanical function, in contrast to arterial tissue (29; 35). Collagen and elastin fibers evolve from crimped to taut. Curling is more prominent in the trachea and large bronchi, whereas small bronchi fibers have limited curvature. The heterogenous fiber architecture is morphological and is not attributed to ex vivo experimental effects because residual stresses are not observed in pig bronchi (57; 80).

The curve and weave of fibers are key to elastic properties, enabling tissue stretch despite the relative inextensibility of collagen fibers (28; 92). Folded collagen in proximal airways initially undergo straightening and are more compliant when elongated, enabling expansive range of stretch toleration with reduced stress range. Straightened fibers in distal small bronchi reach non-physiological strains sooner, translating to heightened relative levels of stress (Figure 7) (23). The heterogeneity of model parameters and histology confirm conjectures surrounding raised stresses caused by lung inhomogeneity (30), and should be considered in circumstances such as artificial ventilation, where overextension has been identified to induce inflammatory response and trigger remodeling (43).

Collagen-elastin fiber form in differentiating bronchial regions also relates to disease etiology. It is well recognized that environmental exposures such as cigarette smoke, mineral dust exposures, and lung infections alter the extracellular matrix composition and contribute to resulting disease (37; 75; 77). Mechanisms include tissue degradation, superfluous matrix deposition during repair, and immune response activation that leads to further tissue damage. Remodeling of tissue caused by disease has been considered to reorient collagen (91) and degenerate elastin (4; 22; 26; 42; 55). Analogous to computational fluid dynamics models which have already made progress in predicting restricted flow in diseased airways (47), it is prudent to characterize the changing form and architecture of the extracellular matrix throughout the lung in order to better understand how pathologies impacts normative and pathological lung function.

Limitations of this work direct several future studies. While the model formulation replicated experimental data very well, the mathematical construct is still restricted to existing expressions of strain-energies. Physically significant parameters, such as branch generation, inner diameter dimensions, or tissue thickness, can directly inform pulmonary-specific constitutive functions constructed from general continuum theories of strain-energy concavity, similar to formulations of cardiovascular-specific material models (3; 29; 34). Such models can imbed phenomenological representations of fiber crimp with resulting material-force conductance, as seen in worm-like chain models or microstructurally motivated constitutive relations (48; 50). As fiber form is expected to be primarily responsible for mechanical function, image-based constitutive models can yield definitive conclusions by informing the statistical crimp distribution and morphology. We are currently investigating such models.

The role of GAG and elastin should also be explored; a relative increase in elastin fibers between the trachea and smaller bronchi (Figure 7) suggests dynamic testing and pentachrome staining would enable measures of the highly deformable elastin structure and visualization of its regional evolution (72). The unidirectional increasing GAG content distally motivates exploration of viscoelasticity through the incorporation of load-history dependency in constitutive models (12). Exploration of pulmonary viscoelasticity may serve as a potential biomarker for disease, as seen for breast tumors (76).

5. Conclusion

The unknown relationship between pulmonary structure and function imposes significant limitations on medical advancements and clinical translation. Lack of experimentally measured lung material properties disconnects the integral impact of air fluid flow on structural tissue motion, impeding a comprehensive understanding of pulmonary mechanics. We present a combined experimental and computational approach to characterize the mechanical behavior of pulmonary airways. The non-linear anisotropic and heterogeneous nature of porcine bronchi is well-captured by an incompressible strain-energy function with fiber-reinforcement. The resulting material behaviors are substantiated by regional dependency of tissue organization caused by structural form and composition, as illustrated by biochemical analysis and histology. Constitutive material property calibrations establish novel airway behavior and put forth a mathematical model representative of multi-regional bronchi response, implying underlying tissue architecture primarily dictates mechanical function.

Our resulting bronchial constitutive law can be directly imbedded in finite element models to explore airway obstruction patterns, design bronchial stents, and facilitate fluid-structure interaction simulations. This foundational study will facilitate investigation of distal airway injury response and progression of pulmonary disease, and help advance lung biomechanics research translation to the clinic through computational techniques.