Generation and Classification of Activity Sequences for Spatiotemporal Modeling of Human Populations

Abstract

Human activity encompasses a series of complex spatiotemporal processes that are difficult to model but represent an essential component of human exposure assessment. A significant empirical data source, like the American Time Use Survey (ATUS), can be leveraged to model human activity. However, tractable models require a better stratification of activity data to inform about different, but classifiable groups of individuals, that exhibit similar activity sequences and mobility patterns. Using machine learning algorithms, we developed an unsupervised classification and sequence generation method that is capable of generating coherent and stochastic sequences of activity from the ATUS data. This classification, when combined with any spatiotemporal exposure profile, allows the development of stochastic models of exposure patterns and records for groups of individuals exhibiting similar activity behaviors.

Introduction

Estimating human exposure to airborne and other broadly distributed pollutants presents a significant public health challenge. Because humans are mobile and inhabit a variety of microenvironments, it is insufficient to model only the spatiotemporal distribution of pollutants. Even for a geographically homogeneous distribution of pollutants, different individuals experience different levels of total individual exposure depending on their activity patterns [1-3]. Therefore, any successful model of individual human exposure requires an estimation of the sequences of activities human agents perform, along with their locations and context of those activities. Furthermore, a large amount of pollutant emissions in urban environments results directly from human activity. Modeling human activities could, therefore, have potential use in estimating pollution distributions directly from mobile sources, like automobile emissions.

Comprehensive and detailed activity patterns from individuals can be gathered using a variety of tracking devices, including diaries, surveys, and structured observations. But such methods may be cumbersome to implement, prone to privacy concerns, and may fail to capture contextual data [4]. On the other hand, the American Time Use Survey (ATUS) [5] provides a comprehensive picture of human activities in the United States of America (US) and it can be used to infer human behavioral patterns. The ATUS dataset is highly complex, with each annual survey containing over 10,000 activity diaries of recorded temporal sequences detailing daily activities of the survey respondents. Each activity diary can include up to 80 discrete activities with dozens of auxiliary variables and additional demographic variables embedded in the dataset. The composition and timing of activities can have significant overlap, but also present distinct patterns based on demographics. For example, the majority of the respondents report sleeping, eating, and grooming in most activity diaries, but other activities, such as working, recreation, and child care, will have unequal representation across different demographic categories. The ATUS has been described in great detail, including a comprehensive descriptive analysis in a recent publication [6].

The degree of complexity in the ATUS makes expert analysis or the development of a gold standard difficult. Its dimensionality and size are above the threshold for effective manual analysis and visualization. The synthesis of activity sequences has been explored with varying levels of success [7-11], but to the authors' knowledge, no attempts to classify ATUS activities for cohort identification have been reported. Classification of individual activity patterns is a critical step for the development of stochastic models of exposure [12]. To address this need, we developed a method for unsupervised classification of the ATUS data that broadly classifies activity and demographics without relying on human expertise. Identification and classification of activity and demographic classes enable us to construct activity sequences, the latter being artificial constructs used to model behavior in our recently published agent-based model [13] for total exposure. We developed a simple approach to construct activity sequences utilizing the concept of starting windows – which are periods where an activity may start. We then show that our method of generating activities results in sequences that are qualitatively indistinguishable from those collected in the ATUS.

Methods

Classification of the ATUS Activity Diaries

While it can be intuitively conceived that different individuals follow different activity patterns, to our knowledge, there are no studies that have formally organized these activities, recognized common patterns, and classified individuals according to them. The ATUS activity diaries are organized into multiple tables containing demographic properties of the respondents (age, gender, work status, married status, etc.), activities of each of these respondents (a sequence of records containing activity type, start times, length), and some auxiliary information describing their household composition and activity context. The activities are described using the ATUS lexicon [5]. Variables can be categorical or continuous, possibly censored to protect unique respondents, and have hierarchal dependencies based on survey responses. We eliminated variables from the demographic table related to survey questions that had a low response rate and/or low variance, as these would be non-informative and introduce noise in the unsupervised classifiers. Our final selection contains 16 demographic variables listed in Table 1, all of which can also be inferred from the US Census and employment statistics.

Table 1.

List of the 16 demographic variables and activity vectors included in this study. Variable names are given as they appear in the ATUS. The demographic classifier uses only these 16 variables, while the activity classifier used the 16 demographic variables and associated activity vectors as the feature set.

	FEATURE NAME &	DESCRIPTION
DEMOGRAPHIC VARIABLES	TEAGE	Age
	TEHRUSL1	Hours worked at main job
	TELFS	Labor force status (employed, unemployed, not in labor force)
	TESCHENR	Enrolled in high school, college or university
	TESCHFT	Enrolled as full time or part-time student
	TESCHLVL	School enrollment level (high school, college, or university)
	TESEX	Gender
	TESPEMPNOT	Employment status of spouse or unmarried partner
	TESPUHRS	Hours worked by spouse or unmarried partner
	TRCHILDNUM	Number of household children under age 18
	TRDPFTPT	Full time or part-time employment status
	TRHHCHILD	Presence of household children under age 18
	TRSPPRES	Presence of spouse or unmarried partner in household
	TUDIS2	Disability preventing work in the next six months
	TUELNUM	Number of elderly people cared for this month
	TUSPUSFT	Spouse or unmarried partner full time or part-time employment status
ACTIVITY VECTORS	Activity count	The number of times each type of activity is performed in the activity diary. Contains approximately 400 activity counts
	Activity Time	The main activity performed in each five minutes slice in each activity diary. There are 288 five minute slices in a single day.

^& The names of the variables in this table may appear somehow cryptic, but we kept the original ATUS names so anybody interested in reproducing our results know exactly what variables were used. In the second column we give the definition of the variables as described in ATUS.

We transformed the ATUS activity tables into two separate vectors representing the activities reported by each individual participating in the survey. The first vector with approximately 400 dimensions counts the number of instances each unique activity from the ATUS lexicon [5] is found in the activity diary of each individual. The second vector with 288 dimensions discretizes the 24-hour period of each individual's diary into five-minute intervals, assigning the ATUS lexicon code [5] of the primary activity reported in each slice to the corresponding slot. Together, these activity vectors capture both the categorical and temporal patterns of activities for each respondent. We used these vectors along with the 12 demographic variables to create the feature set for activity classification (Table 1).

Our approach to classifying activities and demographics was as follows (Figure 1). First, we generated a random forest with 2,000 truncated trees having a maximum tree depth of five-leaf nodes. We used the Random Trees Embedding method from scikit-learn to generate a random forest-based on random subdivisions of variables in the absence of labels [14]. Next, we generated a proximity matrix according to the method proposed by Breiman [15], by counting the number of times each pair of feature vectors appear on the same leaf node for each tree in the initial random forest. In our third step, we used this proximity matrix as the input for a two-component t-Stochastic Neighbor Embedding (t-SNE) [16], which is used for embedding high-dimensional datasets in low dimensional spaces. We normalized the embedded coordinates from t-SNE to the interval (-1,1) and performed clustering using density-based spatial clustering of applications with noise (DBSCAN) [17]. We manually estimated the maximum cluster distance and sample parameters, since these hyperparameters are dependent on the dataset and features used. We used a maximum cluster distance values of 0.03 for a cluster size of 20, and 0.02 for a cluster size of 10 for the demographic and activity feature sets, respectively. Using these parameters allowed us to select small and dense clusters and the feature vectors to be non-labeled by the algorithm.

Figure 1.

Steps followed in classifying activities and demographics.

The DBSCAN clustering generates a set of labeled and unlabeled feature vectors. In our final step, we used the labeled feature vectors to train a truncated Extra Random Forest [18]. Using the entropy criterion, which is preferred for categorical data [18], we assigned a maximum tree depth of eight for this forest. We then classified all unlabeled feature vectors using this new random forest. We did this because the initial clustering leaves up to 30% of feature vectors unlabeled, and many of the labeled features are similar enough to be classified the same. As we needed our classes to have some level of statistical power, we generated one additional set of random forests, using the same parameters, but this time without truncation (no maximum tree depth). This set of forests was trained on all classes above a size cutoff of 25 feature vectors, with the remaining small classes being classified by this new classifier. This method produces the final classes for the demographic and activity classes and generates a classifier that can be used in conjunction with the US Census as part of our agent-based model [13].

Generation of Activity Sequences using Starting Windows

While the classification by itself is a useful tool for identifying distinct patterns of activity, it is insufficient for predicting or simulating the behavior of an arbitrary agent representing a person in a class. The activity classes generated by our classifier provide a basis for what patterns of activity exist. However, the activity diaries themselves are not suitable for simulation purposes because they are intrinsically tied to the empirical and geographical constraints of the persons interviewed for the ATUS. Instead, we generate synthetic activity sequences from a probabilistic representation of each activity class.

We generated synthetic activity sequences for each activity class according to the following procedure (Figure 2). For each class, we considered each activity present in the cohort separately and collected their starting times. Using Bayesian Gaussian Mixtures [19], we generated a set of one-dimensional clusters of activity starting times to create starting windows, which we define as a period of time when an activity can start. For example, if we were to distinguish daytime naps and nighttime sleeping, we would define two separate starting windows for each type of activity based on starting time, even though both instances are classified as sleeping activities

Figure 2.

A representation of activity window construction and probabilistic window sorting. The top section of this figure, each dot represents an activity with a start time and length, blue and green represent two different types of activities. Although blue represents a single activity type, the circumstances and times of those activities have different contexts. Groups of activities can be broken into windows of time where an activity can start. The same can be done with the lengths of activities. Creating a grid of starting times and lengths can be used to define contextual starting and length windows and, in turn, in defining types of activities. The lower section of the figure shows probabilities calculated based on the starting windows and probabilistic sorting of activities. Trips can be added when activity location change and activity lengths adjusted based on allowed starting times and activity lengths to fill the period of simulation.

Utilizing these starting windows, we calculated four different probabilities. First, we calculated the probability that a member of the activity cohort will perform an activity defined by a starting window. This is the probability of a starting window appearing in an arbitrary sequence drawn from the set of activity diaries that contains the starting window of interest. This probability captures the idea that some activities are repeatedly and consistently performed across the population, such as sleeping, eating, and personal grooming, but also allows for exceptions in ordinary behavior. We expected the members of each activity class to follow a schedule, but with potential variations. The second probability we calculated is the joint probability between start windows and activity lengths. We cluster activity lengths into length windows that are generated the same way as to start windows but using activity lengths instead of start times. The reason for using length windows instead of a more common distribution is that activity lengths can exhibit very different scales depending on the context. For example, a nap could last anywhere from twenty minutes to three hours long, whereas a typical night's sleep might vary from four the twelve hours.

Further, activity lengths can have unusual distributions and cluster in ways that do not approximate to a smooth function. The third probability we calculated is the probability that an activity in one start window is preceded by an activity in another start window. This captures the idea that the order of some activities can be indiscriminate or based on preference, while others have specific causal orders. For example, food preparation always precedes the actual activity of eating. Still, the order of reading a book and watching a movie for evening entertainment largely depends on the preference of the participant. Estimating this probability allows us to effectively sort activities and insert the necessary stochastic components needed to capture variability in activity order. Finally, we calculated the joint probability between the start window and location type. Although the ATUS does not have specific geographic locations in the dataset, it does define the type of location for each activity (e.g., home, workplace, store, etc.). Encoding these location types allows us to utilize contextual information for assigning precise locations to activities in a synthetic activity sequence.

We utilize these four probabilities to generate synthetic activity sequences using Monte Carlo sampling. For this, we selected a set of start windows, assigned activity lengths, sorted those starting windows stochastically, and then assigned locations types. Next, we inserted travel activities between activities that occur at different locations to improve the quality of the sequence. Finally, we adjusted activity lengths within the intervals prescribed by the starting windows and minimum or maximum activity lengths to fill the period of the simulation so that there are no gaps in the synthetic sequence. We performed this adjustment using a weighted coefficient based on the selected length of each activity to preserve the relative lengths of activities. The code developed here is available at: https://github.com/uofu-ccts/prisms-comp-model-stham.

RESULTS AND DISCUSSION

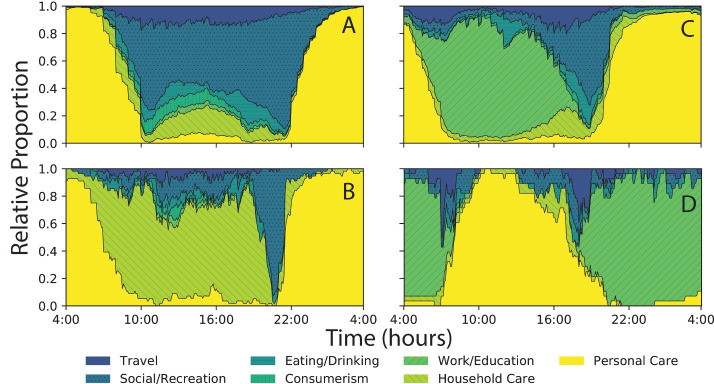
Figure 3 shows an example of activity classes derived from the classification process. Distinctive patterns of activity can be isolated despite the simplicity of the classification algorithm. Significant overlap in activity profiles occurs between some demographic classes, especially in classes where the fundamental activity profiles are essentially the same. Still, the timing of activities can be shifted as in cases where shift work is represented. This suggests that the classification method is effective in making distinctions in both temporal and categorical domains.

Figure 3.

Examples of activity classes generated by the unsupervised classification method. Distinct patterns of activity can be identified from the method. Panel A depicts a cohort that primarily participates in recreation activities (watching TV, reading, attending events). In contrast, panel B depicts a cohort that mostly participates in household activities (cleaning, yard work, child care, etc.). Panels C and D depict two different shifts of working days. The fact that the algorithm can elucidate temporal patterns is especially useful.

For these experiments, the demographic classification produced 95 classes with a median class size of 83 and a maximum of 696 individuals, while the activity classification produced 76 classes with a median class size of 82 and a maximum of 1237 individuals; both classifiers have an artificial minimum of 25 records. The number of classes produced by this approach varies due to stochastic elements in the t-SNE and random forest algorithms. We attempted to broadly classify the activity classes based on the main category of non-sleep activity that dominated each activity record. Roughly 40% of activity classes are dominated by work activities, while recreational activities dominate 25%. The remaining 35% of classes comprise some mixture of household activities, child or elderly care, and school-related activities.

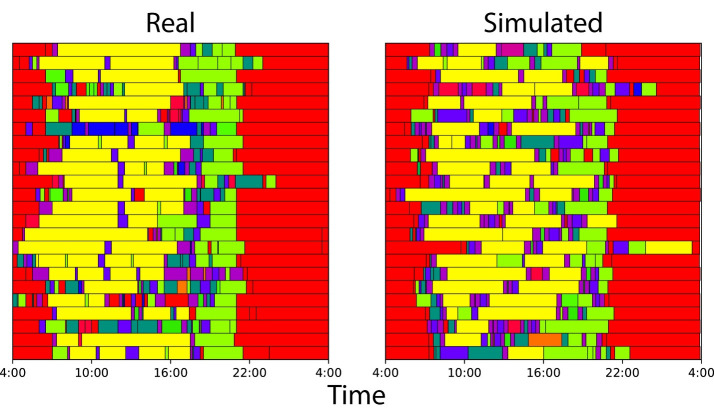
Figure 4 shows sets of real activity sequences from the ATUS and synthetically generated activity sequences for a typical day belonging to a member of the “diurnal working class”. Qualitatively the two sets are difficult to distinguish from each other. Distinctive temporal boundaries are present between some activities in the real sequences, which are an artifact of the classification algorithm, strongly selecting a subset of temporal features. These temporal boundaries disappear in the synthetic activity sequences due to the length adjustment step and the introduction of randomness from the Monte Carlo process. Despite this variation, the overall profile of activity in the synthetic sequence still visually captures the overall prevalence of activities.

Figure 4.

Real and simulated sequences for a single activity class, shown in their sequential form. Each row represents a different sequence, while different colors represent different types of activities. Generally, the simulated sequences conserve the same relative pattern of activity as the real sequences. Deviation from the strict timing of the real sequences is expected since the sequence generation algorithm includes some smearing components.

We performed a quantitative analysis of our synthetic sequences to validate their similarity to the real sequences. Because the temporal sequences are categorical, a detailed temporal analysis of the synthetic sequences is complicated. A realistic way to compare categorical temporal sequences is through a binary comparison at the smallest temporal granularity. Groups of sequences can be compared through their statistical mode, where the mode similarity is the fraction of minutes where the most frequent activity is the same between synthetic and measured sequences and a measure of dispersion. The later can be calculated with a method like the Gini index [20], which is analogous to the mean and standard deviation of a normally distributed continuous variable. We calculated the modes of each activity class by determining the most frequent activity at each minute across all activity sequences in that class. We then made a binary comparison between the modes of the synthetic and the ATUS reported sequences to obtain a percentage similarity between the two. We obtained the Gini index by calculating the frequency of all activities for each minute across all activity probabilities. We compared the synthetic and reported sequences by performing a linear regression of the Gini index.

Figure 5 shows the plot of the r-correlation of the Gini indices and mode similarities for all activity sequences. The majority of activity classes (61%) have both Gini correlation and mode similarities above 0.8, while 95% of classes are above the 0.6 threshold. This presents strong evidence that our sequence generation algorithm correctly reproduces the majority of the activity classes.

Figure 5.

Similarity plot of synthetic and measured activity sequences. For each type of activity sequence, the most frequent activity (the mode) and the Gini index is calculated for each minute across the cohort. The mode similarity is the fraction of minutes where the most frequent activity is the same between synthetic and measured sequences. The Gini R Correlation is from the linear regression of the Gini Indices for each minute. 61% of activity sequences have both similarities and R-values greater than 0.8.

In the development of the sequence generation algorithm, we explored several techniques. Our results using a simple Markov chain ended up being intractable with the generated sequences having little to no resemblance to the ATUS data and incapable of capturing the structured nature of some activities (especially the home-work-home pattern). We also tried to train a recurrent neural network (RNN) against the ATUS activity diaries, but we found that the activity sequences were too short to train the RNN reliably. Specifically, we believe that the RNN needed to be trained on activity sequences spanning multiple days, which are unavailable from the ATUS surveys that only cover 24-hour periods. However, we ultimately found that the method we developed was both simpler and easier to implement than an RNN, and required less computational effort to establish and generate sequences. The method we have developed and presented here is also substantially more explainable than an RNN.

LIMITATIONS

The results presented here represent the classification of the activities reported in the ATUS; therefore, they are subject to any limitation in scope and granularity that may exist in the original ATUS surveys. For instance, the ATUS does not provide data on school-age children, so their activity patterns have to be inferred from their parents. As discussed above, the methodology is quite general. It could be applied to other activity surveys, but as with any classification method, it is subject to the somehow arbitrary selection cut off values to define the size and number of classes. While the parameters selected here are reasonable, it may be necessary to restrict or increase the number of desired classes depending on the intended use of the classification of activities.

CONCLUSIONS

We successfully developed and demonstrated a generalizable method to classify human activity sequences and generate synthetic spatiotemporal activity sequences. While in this study, we derived activity sequences from the ATUS activity classes, our method is not specific to this survey. It can be used for any well-structured activity survey data sets. We believe that the applica

tion of this approach will enable researchers to make significant inroads into simulating human activity patterns at population levels a first step in generating comprehensive personal exposure profiles records for utilization in translational research.

Abbreviations:

American Time Use Survey (ATUS)

t-Stochastic Neighbor Embedding (t-SNE), Density-based Spatial Clustering of Applications with Noise (DBSCAN), Recurrent Neural Network (RNN)