Inflammation Product Effects on Dilatational Mechanics Can Trigger the Laplace Instability and Acute Respiratory Distress Syndrome

Abstract

In the lungs, the Laplace pressure, ΔP = 2γ/R , would be higher in smaller alveoli than larger alveoli unless the surface tension, γ decreases with alveolar interfacial area, A, such that 2ε > γ in which ε = A(dγ/dA) is the dilatational modulus. In Acute Respiratory Distress Syndrome (ARDS), lipase activity due to the immune response to an underlying trauma or disease causes single chain lysolipid concentrations to increase in the alveolar fluids via hydrolysis of double-chain phospholpids in bacterial, viral, and normal cell membranes. Increasing lysolipid concentrations decrease the dilatational modulus dramatically at breathing frequencies if the soluble lysolipid has sufficient time to diffuse off the interface, causing 2ε > γ, thereby potentially inducing the “Laplace Instability”, in which larger alveoli have a lower internal pressure than smaller alveoli. This can lead to uneven lung inflation, alveolar flooding, and poor gas exchange, typical symptoms of ARDS. While the ARDS lung contains a number of lipid and protein species in the alveolar fluid in addition to lysolipids, the surface activity and frequency dependent dilatational modulus of lysolipid suggest how inflammation may lead to the lung instabilities associated with ARDS. At high frequencies, even at high lysolipid concentrations, 2ε - γ > 0, which may explain the benefits ARDS patients receive from high frequency oscillatory ventilation.

Graphical Abstract

Capillary pressure across a 50 μm bubble in a glass capillary is oscillated to measure the dynamic surface tension of lysolipids.

1. Introduction

In healthy lungs, expanding the thoracic cavity via the diaphragm lowers the pressure in the lung pleural sac (P_out) relative to ambient, P_am: (P_am - P_out) by ~ 1000- 1300 Pa. However, surface tension causes the pressure inside the alveolus, P_in, to increase according to Laplace’s equation: (P_in − P_out) = 2γ/R ~ 1500 Pa for the air-saline surface tension, γ = 72 mN/m, and the typical alveolar radius, R ~ 100 μm. For air to flow, (P_am − P_in) > 0; but the capillary pressure generated by the air-water surface tension yields a negative pressure difference and air no longer flows to the lungs. ⁴ In most air-breathing animals, lung surfactant (LS), a mixture of phospholipids and specific proteins, is generated within the cells lining the alveoli to lower the surface tension to make (P_am − P_in) > 0. ⁴

A less appreciated role of lung surfactant may be to insure uniform lung inflation by eliminating the “Laplace Instability” ⁵. The Laplace pressure difference between the inside and outside of the bubble, ΔP = 2γ/R, is inversely proportional to the bubble radius; interconnected bubbles of radius R are at best metastable for a constant surface tension, γ. Smaller bubbles have higher internal pressure than larger bubbles, forcing air to flow to larger, lower pressure bubbles, which causes the pressure inside the small bubbles to increase, further deflating the small bubbles; this dynamic process is known as the “Laplace Instability” ⁵. It is not understood how this Laplace instability translates into the thousands of interconnected alveoli of the lung, which have a significant variation in curvature due to different states of inflation and different inherent sizes. However, if lung surfactants maintained a constant surface tension, smaller alveoli could deflate, while larger alveoli could distend. In the extreme, following deflation, the smallest alveoli could fill with liquid and would be difficult to re-inflate, which is a typical symptom of the lung instabilities in ARDS ^6–10.

Nature has dealt with this issue by having the surface tension of native and clinical lung surfactants decrease with decreasing interfacial area (Fig. 3); if the surface tension changes sufficiently, the Laplace Instability is eliminated. The dilatational modulus, $\epsilon \left(\omega \right)=A\left(\raisebox{1ex}{$\partial \gamma $}\!\left/ \!\raisebox{-1ex}{$\partial A$}\right.\right),$ relates the change in γ to the change in interfacial area, A, at an oscillation frequency ω (6-30 cycles/minute for normal breathing or mechanical ventilation). If $\raisebox{1ex}{$\partial \left(\Delta P\right)$}\!\left/ \!\raisebox{-1ex}{$\partial R$}\right.=\raisebox{1ex}{$\left(2\epsilon -\gamma \right)$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.>0,\mathrm{or}\left(2\epsilon -\gamma \right)>0,$ the Laplace pressure decreases with decreasing radius and increases with increasing radius, which eliminates the Laplace instability, thereby stabilizing the alveoli. While the dilatational modulus of native lung surfactant has not been measured, for the clinical replacement lung surfactant Survanta, ε(ω) ≥ 80 mN/m ^{3, 11}, so (2ε − γ) > 0 for typical breathing frequencies. This means that the Laplace Instability could not occur in a healthy lung as the maximum surface tension is ≤ 72 mN/m. At surface pressures typical in the lung, ε(ω) > 100 mN/m for the double-tailed, insoluble dipalmitoylphosphatidylcholine (DPPC), which is the major lipid component of native and clinical lung surfactants ¹².

However, lung trauma or disease leads to inflammation, increased permeability of the alveolar-capillary barrier and extravasation of lipases and proteases into the alveolar fluids. This is sometimes followed by mechanical instabilities during breathing ^{6, 8, 13–15} which can trigger the onset of Acute Respiratory Distress Syndrome (ARDS). There are ~ 150,000 cases of ARDS per year in the U.S. with a mortality rate of 40% ⁶. How lung injury triggers ARDS is currently unknown, and there is no generally effective therapy, although benefits are obtained by high-frequency mechanical ventilation ^{6, 9–10}. The clinical symptoms of severe respiratory distress due to Covid-19 infection are not unlike ARDS as seen in severe aspiration pneumonia. Surfactant insufficiency/inactivation in ARDS is believed to be induced by extensive inflammation as well as damage to alveolar type 2 cells where lung surfactant is made and stored ¹⁶. The bronchial fluids from ARDS patients contain elevated levels of phospholipase A₂ (PLA₂), a component of the innate immune system that catalyses the hydrolysis of double-chain phospholipids such as DPPC into single-chain lysolipids and fatty acids (Fig. 1) ^{8, 13, 17}. As the PLA₂ hydrolyses the phospholipids in bacterial, fungal and viral membranes to lysolipids, the pathogens are killed by solubilizing the cell membrane, which leads to increased permeability ¹. However, lysolipids in the alveolar fluids are surface active and can compete with lung surfactant for the alveolar air-fluid interface (Figures 1, 3), but are orders of magnitude more soluble in saline than phospholipids such as DPPC ¹⁷. Soluble lysolipids can enter and leave the interface with a characteristic frequency, ω_0; however, phosphatidylcholines (PC) and the other lipids and proteins that make up lung surfactant are insoluble and remain at the interface (Fig. 1). If ω₀ is in the range of breathing frequencies, ω , the surface concentration of lysolipids, Γ, remains roughly constant, which in turn, keeps γ constant, and ε = A dγ/dA → 0 and (2ε − γ) < 0, which could lead to the Laplace instability. However, if ω > ω₀, the soluble lysolipids do not have sufficient time to diffuse off the interface, Γ increases and γ decreases as the surface area decreases, and ε remains large and the lung would remain stable. While the ARDS lung contains a number of lipid and protein species in the alveolar fluid in addition to lysolipids, the surface activity and frequency dependent dilatational modulus of lysolipid may show how inflammation and inflammation products such as lysolipids induce mechanical instabilities in the lung associated with ARDS.

Figure 1.

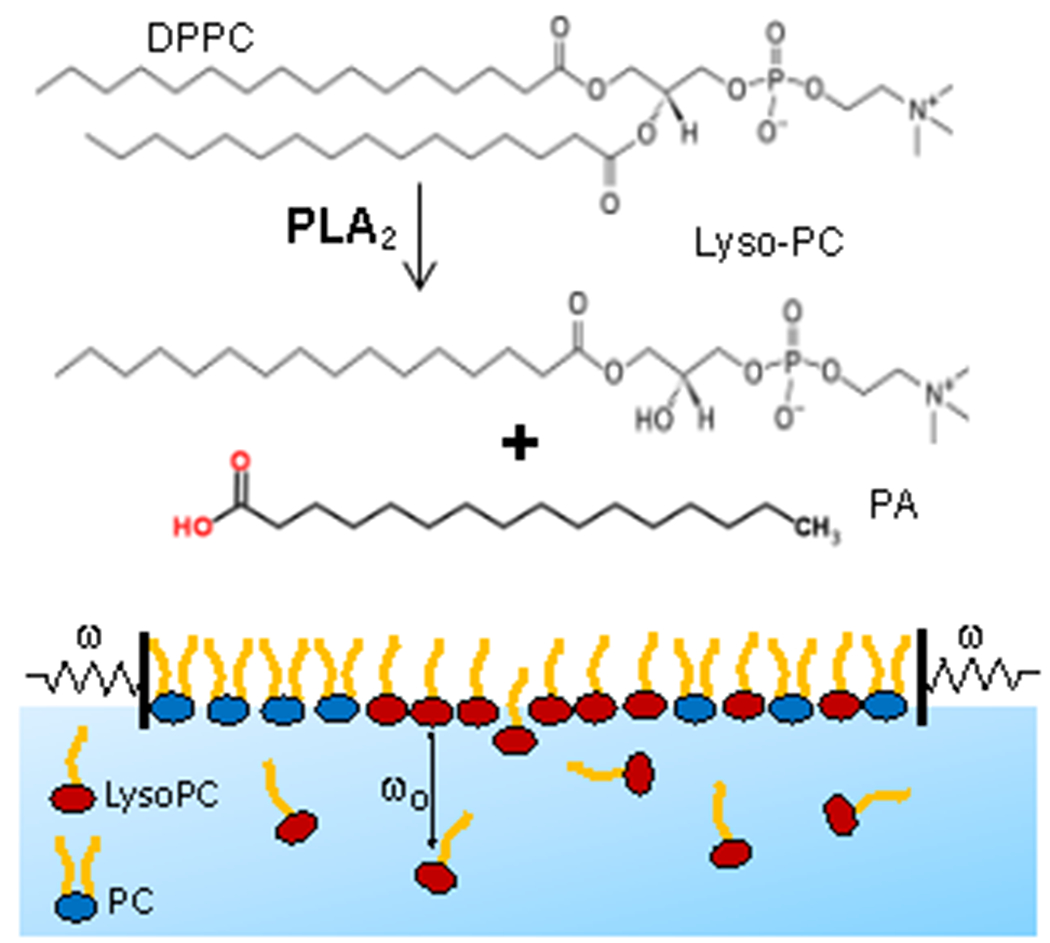
Top) Phospholipase A₂ (PLA₂) catalyses the hydrolysis of phospholipids such as dipalmitoylphosphatidylcholine (DPPC) to form the single chain lysopalmitoylphosphatidylcholine (Lyso-PC) and the associated palmitic acid (PA) ¹. LysoPC is orders of magnitude more soluble in water than DPPC. Bottom) Soluble LysoPC exchanges with the subphase with a characteristic frequency, ω₀; however, phosphatidylcholines such as DPPC (PC) are insoluble and remain at the interface. If the rate of monolayer area change, dA/dt ~ ΔAω, at an oscillation frequency, ω, is such that ω > ω₀, the LysoPC cannot exchange with the subphase solution and is trapped at the interface, and maintains a large dilatational modulus, ε. However, for ω < ω₀, the LysoPC desorbs or adsorbs and maintains a constant γ, causing ε -> 0 as in Figures 3–5.

In ARDS patients, the relevant frequencies are set by normal breathing rates of 10 – 20 breaths/minute and typical mechanical ventilation rates of 6 – 12 breaths/minute. Here we show in a simplified model system that as the lysolipid concentrations increase (consistent with lung inflammation-induced lipase activity) ε (ω) → 0 over normal breathing frequencies making (2ε − γ) < 0, potentially leading to the Laplace Instability and the loss of lung function common to ARDS. At high frequencies, even at high lysolipid concentrations, (2 ε − γ) > 0, which may explain the benefits some ARDS patients receive from high frequency oscillatory ventilation ^1,4,5.

2. Methods

Materials:

Lysopalmitoylphosphatidylcholine (LysoPC) was purchased from Avanti Polar Lipids (Huntsville, AL) and used as received. LysoPC has a critical micelle concentration (CMC) of ~ 6 μM and a minimum surface tension of ~ 36 mN/m ² at the CMC and higher concentrations. Water with a resistivity of 18.2 MΩ·cm at 25 °C was purified with a Millipore Direct Q 3UV-R (Millipore, Billerica, MA) system. Sodium chloride (NaCl), and phosphate buffer were purchased in powder form from Sigma-Aldrich (Saint Louis, MO, USA), and used to prepare phosphate buffered saline (PBS) solutions (150 mM NaCl and pH 7.0). Survanta (AbbVie Inc., IL, USA) was diluted to 2 mg/mL in PBS before use. The lipid dye Texas Red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine triethylammonium salt, (TR-DHPE) was purchased from Life Technologies Corporation, CA, USA and used as received. 1-(dipyrrometheneboron difluoride)undecanoyl-2-hydroxy-sn-glycero-3-phosphocholine, or TopFluor Lyso PC, a green fluorescent derivative of LysoPC with spectral properties similar to Bodipy-FL was purchased from Avanti Polar Lipids and used as received.

Langmuir Trough

A custom-milled Teflon Langmuir trough with continuous steel ribbon barriers was used to measure surface pressure-area isotherms such as those in Fig 3. The surface pressure, π = γ₀ − γ, or reduction in surface tension from the clean saline interface, γ₀, was measured using a filter paper Wilhelmy plate tensiometer (Riegler and Kirstein). Interfacial temperature was measured by an OS36SM miniature infrared thermocouple (Omega Engineering) and controlled to 25°C via a circulating water bath. TR-DHPE lipid dye was dissolved in ethanol and added to the diluted Survanta dispersion (2 mg lipids/ml). The lipid dye quickly partitioned into the Survanta bilayers. In images, disordered phase monolayers appear red, while ordered domains exclude the dye and appear black. ³

About 1 mg of TR-DHPE dyed Survanta was deposited using a glass syringe onto the air-water interface of the trough. A similar procedure was used for the LysoPC subphase, except 6 μM lysopalmitoylphosphatidylcholine was added to the subphase with gentle stirring after the Survanta solution was deposited at the interface. For fluorescence imaging, 1.5 mol% of the TopFluor LysoPC was added to the LysoPC in the subphase. Previous work has shown that the Survanta isotherms and morphology are relatively independent of temperature from 25 – 37° C ^{3, 17}. Surface area vs π isotherms were recorded at a compression rate of 0.2 cm/sec. A C1 confocal scan head fitted on a Nikon Eclipse 80i upright microscope (Nikon Instruments, Melville, NY) was used for imaging. The microscope was controlled with Nikon EZ-C1 software. A Nikon plan apochromatic 20x objective was used for confocal imaging ³.

Capillary Preparation for Microtensiometer

Capillaries of prescribed tip diameters were pulled from 1.5 mm OD, 1.1 mm ID, 10 cm long borosilicate fire-polished glass capillaries in a Sutter Instrument P-1000 micropipette puller (Novato, CA). Capillaries were cleaned with Alnochromix and sulfuric acid (Millipore-Sigma) and rinsed with Millipore water. The capillaries were made hydrophobic by immersion in 5% Xiameter OFS-6124 Silane (Dow Chemical) in ethanol solution, followed by baking under house vacuum at 100°C for one hour (Figure 2B). The hydrophobic coating on the capillary prevents the air/water/glass contact line from slipping during the measurement.

Figure 2.

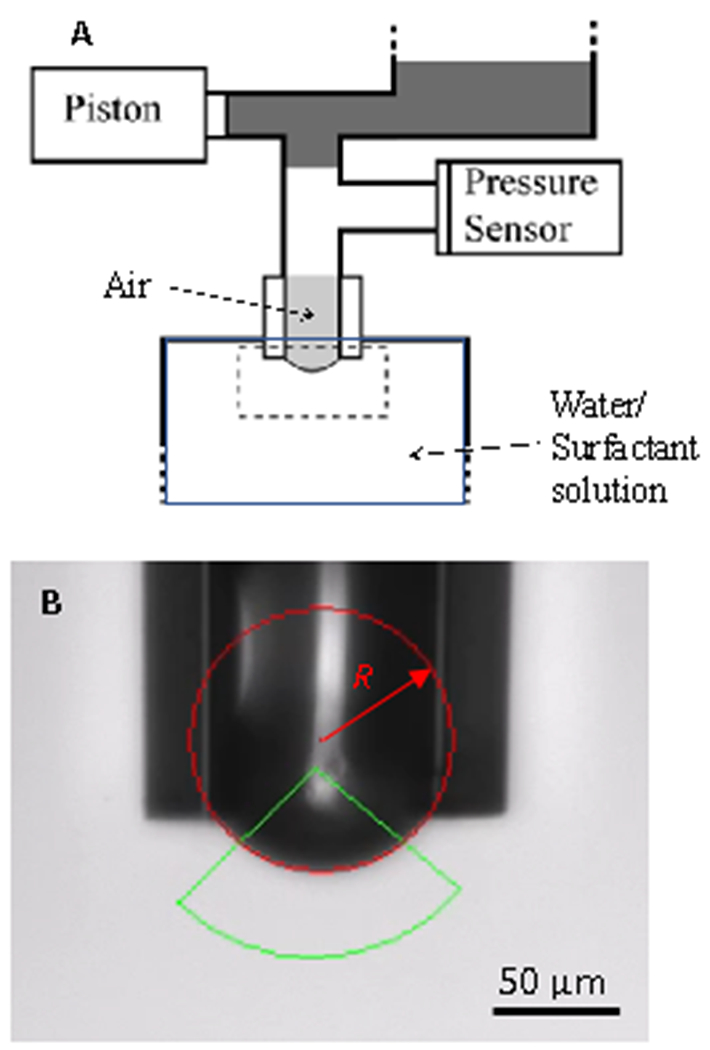
(A) Schematic diagram of the capillary pressure microtensiometer. An air bubble is held at the end of a hydrophobized glass capillary (See B) in a reservoir of surfactant solution in buffer. A pressure transducer measures the pressure within the bubble. Lysolipid in the solution reservoir spontaneously adsorbs to the bubble interface, quickly establishing an equilibrium capillary pressure, ΔP_eq and bubble radius, R_eq. γ_eq is determined by Laplace’s equation ΔP_eq = 2γ_eq / R_eq. Oscillating the capillary pressure via a syringe pump piston induces corresponding radius oscillations, ΔR, with a phase angle ϕ_RP between the pressure and radius oscillation. The dilatational modulus, ε, is calculated from Eqn. 2 using these measured parameters. The apparatus is controlled using LabVIEW.

(B) Bright field microscope image of the capillary containing the air bubble. The radius of the bubble is measured by fitting images of the bubble to a circle (red) over the region defined by the green triangle, to determine, R. Within the image resolution, the bubble is hemispherical up to the pinning line at the capillary tip and remains hemispherical during oscillations.

Microtensiometer Operation

Lysolipid is added to a liquid reservoir (Figure 2A) at the desired concentration and spontaneously absorbs to the air-water interface of a bubble held at the tip of a pulled glass capillary (Figure 2B). The surface tension, γ, is calculated from Laplace’s equation, ΔP = 2γ/R ¹⁸. Bubbles with radii less than the capillary radius (R < R_c) are pushed out of the capillary, which determine the maximum capillary pressure for a given surface tension. To measure ε(ω), small applied changes in the capillary pressure, ΔP, induce changes in the bubble radius and interfacial area, A, which in turn induce changes in the surface tension, γ ^{3, 18–19}. The capillary pressure difference, ΔP, is measured using a pressure transducer and, R, the bubble radius is determined by fitting a circular profile to an image of the bubble (Fig. 2B). The bubble surface area is calculated from the measured radius:

$$A=2\pi R\left(R-\sqrt{R^2-R_c^2}\right)$$ (1)

For $\mathrm{Bo}=\raisebox{1ex}{${{\varrho }_{l}gR}^2$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.\ll 1,$ (Figure 2B), the bubbles are small enough that gravity does not alter the isotropic capillary pressure in the bubble, hence the bubble takes on a hemispherical shape of constant mean curvature ¹⁸. Here, ϱ_l is the liquid density, 1000 kg-m⁻³, g is gravity, 9.8 m-sec⁻², and the minimum surface tension, γ, of LysoPC is 36 mN/m (Fig. 3) giving Bo ~ .006 for R = 150 μm and Bo ~ .0005 for R = 45 μm. Oscillations in the capillary pressure result in a dilatational strain except in the vicinity of the capillary tip at which the bubble is pinned ¹⁸. Away from the capillary tip, the uniform stress imposed by the isotropic capillary pressure produces an equal strain in both principle directions, leading to a purely dilatational strain ²⁰. Anywhere that the surface remains hemispherical during the expansion and contraction of the interface, the principle strains, λ₁ and λ₂, must remain equal and the overall effect is pure dilatation (λ₁ − λ₂ = 0) ²⁰. Any non-dilatational strains would lead to a non-spherical surface, given an initially hemispherical surface ²¹. Fig. 2B shows that by fitting the bubble image to a circle, any deviation from the circle or slip of the bubble in the capillary can be detected; any deviations lead to the data being rejected for that bubble or capillary.

While the stress distribution imposed by the isotropic capillary pressure is uniform and continuous at the pinning line, the strain at the pinning line is not uniform in the radial and transverse directions as the bubble is constrained by the rigid capillary. How far the strain anisotropy imposed by the pinning line propagates into the bubble depends on the magnitude of the surface tension relative to the bending elasticity of the monolayer. Surface tension is the dominant force in our system, and diffusive equilibrium at the interface makes the surface tension uniform across the bubble. The length scale, L_c, for the anisotropy in strain in the vicinity of the pinning line is the ratio of the monolayer bending elasticity, K, to the surface tension, ${\text{L}}_{\text{c}}=\sqrt{\raisebox{1ex}{$\text{K}$}\!\left/ \!\raisebox{-1ex}{${\gamma }^3$}\right.}$. For reasonable estimates of K for monolayer surfactant films, L_c ~ 2 – 30 nm, compared to the bubble radius of 50 – 150 μm ³. This suggests that an area fraction of ~ L_c/R undergoes anisotropic strain, which is < 0.5% of the bubble area. This is confirmed by the images in Figure 2B. Within the image resolution, the bubble is hemispherical up to the pinning line at the capillary tip as shown by the red circle and remains hemispherical during oscillations. While a small fraction of the bubble does undergo shear deformations, Squires and coworkers have shown that the shear modulus of soluble surfactants is effectively zero ²², so the contribution to the total stress of shear deformations near the capillary walls is negligible.

To determine the dilatational modulus, a pressure oscillation is imposed on the bubble that induces a change in the hemispherical bubble area (strain) and the surface tension (stress). The bubble radius and the surface tension both depend on the pressure oscillation through the Laplace equation, γ = ΔPR/2. Hence, the microtensiometer does not impose either a controlled stress or controlled strain rate, but rather the stress and strain rate are coupled via the Laplace equation. Kotula and Anna ¹⁸ derived a regular perturbation analysis to extract the dilatational modulus for a bubble initially at pressure ΔP_eq with radius R_eq undergoing radius oscillations of ΔR with a phase angle ϕ_RP between the pressure and radius oscillations. Eqn. 2a relates the measured tensiometer parameters to the magnitude of the dilatational modulus, ε:

$$\epsilon =\frac{b}{1-b}\left(\frac{R_{eq}}{\Delta R}\right)\left(\frac{\Delta P_{eq}{R}_{eq}}{2}\right)\sqrt{{\left(\frac{\Delta R}{R_{eq}}\right)}^2+2\left(\frac{\Delta R}{R_{eq}}\right)\mathit{cos}{\varphi }_{\mathit{RP}}+1}$$ (2a)

b is a geometric factor that relates the bubble radius to the capillary radius, R_c:

$$b=\sqrt{1-{\left(\frac{R_c}{R_{eq}}\right)}^2}$$ (2b)

The minimum value of ε that can be reliably measured is ~ 1 mN/m due to the resolution of measuring ΔP and ΔR. This is much less than the equilibrium surface tension of LysoPC of ~ 40 mN/m and the range of ε that we have measured. The highest frequency measured is limited to ~ 20 radians/sec (200 breaths/minute) due to the camera frame rate used to measure the bubble radius.

3. Results

During inflammation, the bronchial fluid from ARDS patients contains elevated levels of phospholipase A₂ (PLA₂), a component of the innate immune system that catalyses the hydrolysis of double-chain phospholipids into single-chain lysolipids and fatty acids ^{8, 13, 17}. Lysolipids are surface active and compete with lung surfactant for the alveolar air-fluid interface during dynamic compression and expansion, but are orders of magnitude more soluble in saline than phospholipids ¹⁷. Figure 3A shows the changes in surface pressure, π, (π =γ_o −γ, γ_o =72 mN/m for saline) as a function of Langmuir trough area for the clinical lung surfactant Survanta on a saline subphase (black curve). On compression, Survanta reaches a surface pressure of ~ 66 mN/m, which corresponds to a surface tension of ~ 6 mN/m. Expanding the trough area leads to a rapid decrease in surface pressure to ~ 10 mN/m. Cyclic compression results in a π-A curve with a hysteresis loop characteristic of both native and clinical lung surfactants ^{4, 17, 23}. Fig. 3B shows a representative fluorescence micrograph of the monolayer organization of Survanta on a saline interface. Contrast in the image is provided by the segregation of the Texas Red DHPE dye to the continuous fluid phase regions, while the dye is excluded from the circular solid phase domains, which appear black ³. This phase separated morphology does not change from 25 – 37° C ^{3, 17}. The pink curve in Fig. 3A shows the effects of lysopalmitoylphosphatidylcholine (LysoPC) at its CMC (6 μM ²) in the subphase liquid on the Survanta isotherm. On the initial compression of the interface, the surface pressure does not increase and remains roughly constant at 36 mN/m, which is the equilibrium surface pressure of pure LysoPC at the CMC ². This constant surface pressure equal to the equilibrium surface pressure of LysoPC suggests that LysoPC adsorbs to the surface and likely displaces Survanta from the interface ¹⁷. On expansion of the trough area, the surface pressure decreases, but less than for the Survanta film; the hysteresis is substantially reduced. The isotherm is similar to that of a pure LysoPC monolayer ². This replacement of Survanta by LysoPC at the interface is confirmed by the fluorescence image in Fig. 3C that shows that the green labelled LysoPC is uniformly spread over the fluid phase regions of the monolayer, and is even within the black solid phase domains (arrows). Similar displacement of native and other clinical surfactants including Curosurf and Infasurf by soluble surface-active lysolipids, albumin and serum proteins in the subphase on cyclic compression has been extensively documented ^{8, 14–15, 17, 24–36}, and is reviewed in Refs. 14–17.

Figure 3.

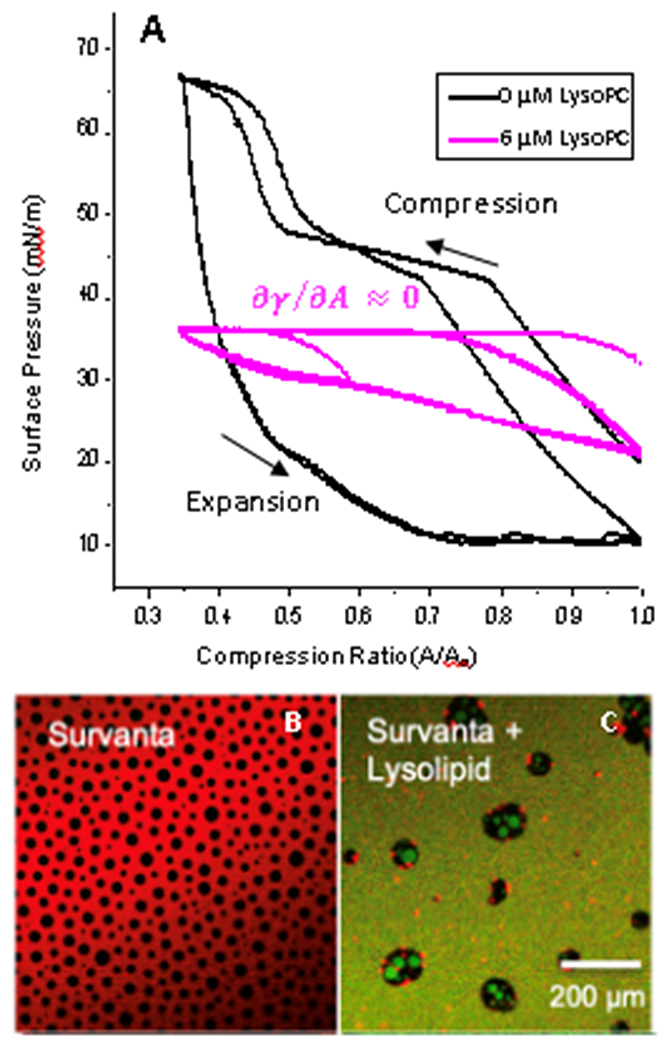
A) The clinical lung surfactant, Survanta on a saline subphase in a Langmuir trough repetitively reaches π_max~66 mN/m on cyclic compression (black). Fluorescence images of this film are shown in B). LysoPC at its CMC of 6 μM in the subphase decreases the maximum surface pressure to 36 mN/m (pink), which is the equilibrium surface pressure of a pure LysoPC monolayer ¹. Fluorescence images of this monolayer are shown in C).

B) Fluorescence image of Survanta labelled with Texas Red DHPE on saline subphase. The dye preferentially locates in fluid regions of the monolayer generating the red contrast. Crystalline domains appear black {Sachan, 2018 #1204}. C) Dynamic compression and expansion of Survanta on the LysoPC containing subphase leads to displacement of the Survanta from the interface in favor of green labelled LysoPC. The green LysoPC is homogeneously distributed in the fluid regions and even appears to displace the solid phase of Survanta. The surface pressure (pink curve in A) is independent of compression, or $\epsilon =A\left(\partial \gamma /\partial A\right)\sim 0$ and $2\epsilon -\gamma <0$ , leading to the Laplace instability.

Simply increasing the surface tension from 6 to 36 mN/m would not completely prevent respiration as (P_am − P_in) remains greater than zero. But on compression, Fig. 3 shows that π becomes independent of interfacial area, making ε = −A(∂π/∂A) ~ 0, meaning (2ε − γ) < 0, resulting in conditions that could lead to the Laplace instability. However, these isotherms are obtained over the course of 10 minutes, which corresponds to a much slower frequency than normal breathing.

To determine if (2ε − γ) < 0 could occur at breathing frequencies, we measure the frequency dependent dilatational modulus, ε(ω), of pure LysoPC monolayers as a limiting model system using a custom-built capillary pressure microtensiometer (CPM) (Figure 2 ^18–19). In the CPM, the hemispherical interface of a 30 – 150 μm radius of curvature bubble pinned at the end of a hydrophobized glass capillary is sinusoidally expanded and compressed by oscillating the bubble pressure (Figure 2B). In addition to being of alveolar dimensions, bubbles of this size are small enough that gravity does not distort their hemispherical shape, resulting in a primarily dilatational deformation ¹⁸ (see red circle in Fig. 2 showing that the bubble is hemispherical within the image resolution up to the capillary tip). The radius of the bubble, R, is fit to images taken with a high-speed camera to determine the surface tension from the Laplace equation, γ_eq = ΔP_eq R_eq/2. For small amplitude pressure oscillations, ε ≈ A_eq (Δγ / ΔA) (See Eqn. 2 for details) in which A_eq is the bubble surface area at the equilibrium surface tension, γ_eq, corresponding to a capillary pressure, ΔP_eq. Δγ is the change in surface tension for an area change of ΔA ¹⁸.

Figure 4 shows the measured dilatational modulus of LysoPC as a function of frequency and concentration for bubbles with equilibrium radii, R_eq ~ 45 μm, corresponding to the smaller alveoli in the lungs (Table 1). At LysoPC concentrations ≤ 0.01 mM that may arise in normal lungs from the chemical hydrolysis of DPPC and other lipids, the dilatational modulus decreases slowly with decreasing frequency and (2ε − γ) > 0 (dotted red line, the surface tension of LysoPC is ~ 38 mN/m from Figure 3A) over the range of normal breathing frequencies (1 radian/sec ~ 10 breaths/minute, yellow box). Hence, the Laplace Instability is arrested and normal lung inflation occurs. For concentrations below 0.1 mM, the modulus decreases at much lower frequencies, which is consistent with the results from the isotherm in Fig. 1, and may lead to difficulties in areas of the lung that are cut off from normal inspiration during ARDS. However, for lysolipid concentrations > 0.1 mM, the dilatational modulus decreases with decreasing frequency such that (2ε − γ) < 0 (dotted red line) at normal breathing/ventilation frequencies (yellow box), which would induce the Laplace Instability. For LysoPC concentrations of 10 mM, (2ε − γ) < 0 over the entire range of breathing frequencies. For frequencies above 10 rad-sec⁻¹, which correspond to high frequency mechanical ventilation (~ 100 breaths/minute, ^{6, 9–10}), the modulus is well above the (2ε − γ) > 0 cut-off for the Laplace Instability.

Figure 4.

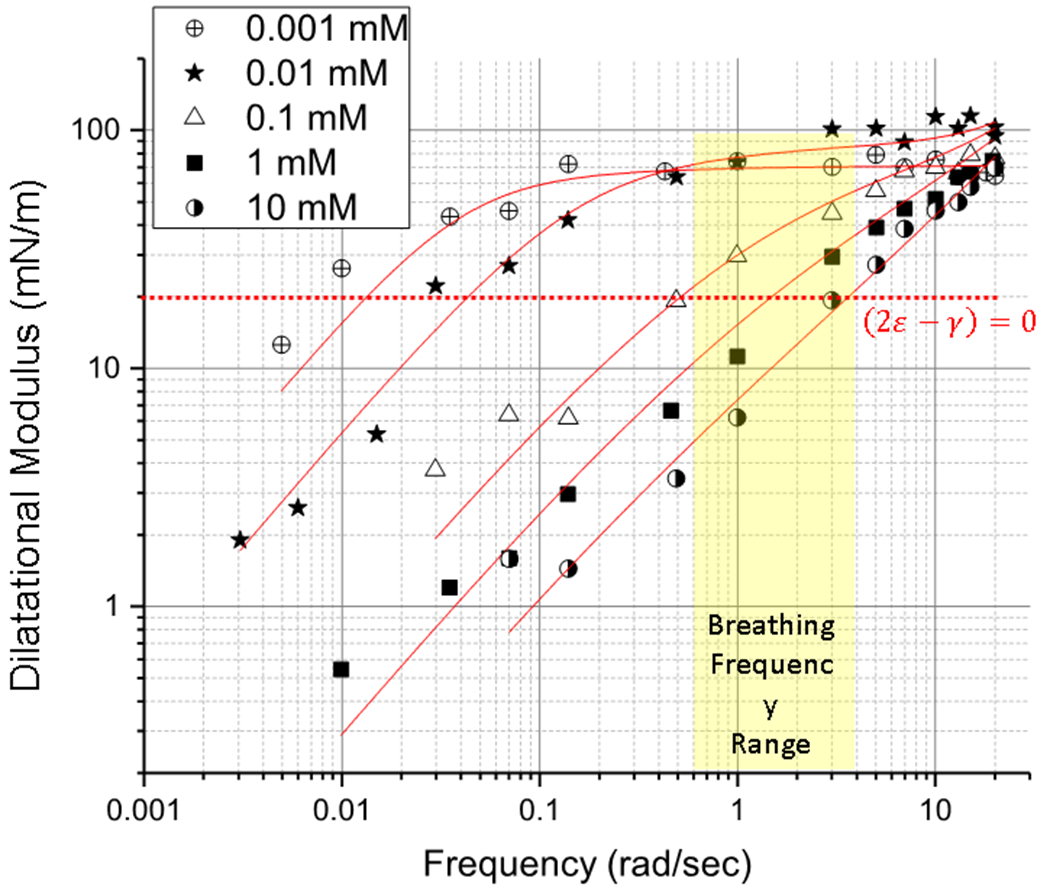
Dilatational Modulus of LysoPC as a function of frequency for increasing concentrations of LysoPC for ~45 μm radius bubbles (Table 1). Concentrations > 0.1 mM of LysoPC that accompany inflammation decrease the dilatational modulus over the range of normal ventilation/breathing rates (yellow) to make 2ε − γ < 0, which is the crossover value for inducing the Laplace instability (dotted red line). Low concentrations of LysoPC ≤ .01 mM, that may occur in normal lungs do not induce the instability. At frequencies > 10 rad/sec, all LysoPC concentrations are above the crossover, and would not be susceptible to the Laplace instability. Solid red lines are fits of Eqn. 22 to the data.

Table 1.

Fitted Parameters to Equation 22. Shaded rows are below the LysoPC CMC concentration of 0.006 mM

LysoPC (mM)	Radius (μm)	ωR (rad/s)	ω0 (rad/s)	ε0 (mN/m)	κ (mN-s/m)
10−5	49	0.080	0.0013	14	0.7
10−4	43	0.11	0.0023	34	0.4
10−3	39	0.13	0.0011	70	0.6
10−2	46	0.095	0.11	110	0
0.1	48	0.085	2.2	96	0
1.0	45	0.099	20	100	1.8
10	50	0.078	140	100	2.1
10−3	147	0.009	0.0006	68	0.7
10−2	144	0.010	0.18	85	0.1
0.1	149	0.009	2.9	105	0
1.0	152	0.009	25	100	2.3
10	142	0.010	120	100	0.8

Figure 5 shows similar effects for R_eq ~ 150 radius bubbles corresponding to the larger alveoli. Again, for LysoPC concentrations ≤ 0.1 mM, the dilatational modulus of LysoPC is well above (2ε − γ) > 0 (dotted red line) over normal ventilation frequencies. For > 0.1 mM LysoPC concentrations, the dilatational modulus decreases with decreasing frequency, but not as rapidly as for the smaller capillary, especially at lower frequencies (Figure 4). Even for the larger bubble, the modulus of 1.0 mM LysoPC drops below the cut-off for the instability, (2ε − γ) < 0, demonstrating that larger alveoli are also at risk of succumbing to the Laplace instability at normal breathing frequencies. For 10 mM LysoPC, (2ε − γ) < 0 over the entire range of breathing frequencies. Increasing the bubble radius decreases the net rate of LysoPC exchange with the subphase, which leads to a lower frequency crossover. Again, at high frequencies, (2ε − γ) > 0 for all concentrations for larger bubbles.

Figure 5.

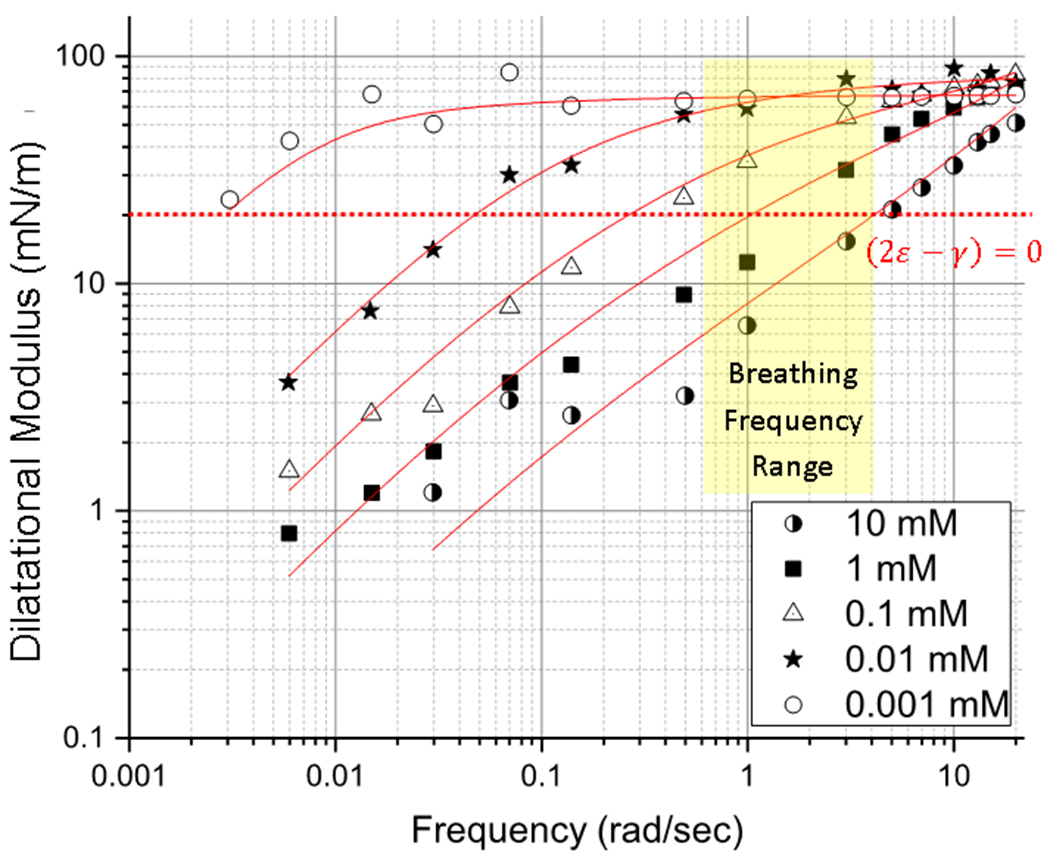
Dilatational modulus of LysoPC as a function of frequency for bubbles of radius ~ 150 μm, corresponding to larger alveoli. As in Fig. 4, for > 0.1 mM LysoPC, (2ε − γ) < 0 (dotted red line) over normal breathing frequencies (yellow). The crossover frequency for the Laplace Instability is slightly lower for the larger bubbles (Compare to Fig. 4), but the main effect of the larger bubble is seen at low frequencies. At high frequencies, (2ε − γ) > 0 for all concentrations and curvatures. Solid red lines are fits to Eqn. 22.

The dilatational modulus for concentrations below the 0.006 mM critical micelle concentration of LysoPC are shown in Figure 6. For these sub-CMC concentrations, the frequency dependence of the different systems is rather similar, with a roughly constant modulus that begins to decrease at 0.1 rad/sec, well below breathing frequencies (Table 1). This suggests that ω₀ is roughly constant below the CMC. However, due to the lower surface concentrations, the plateau value of the modulus decreases from ~ 70 mN/m at 0.001 mM to ~ 14 mN/m at 10⁻⁵ mM. At these low concentrations, the phospholipids in the surfactant monolayer dominate the interface (Figure 1) even though (2ε − γ) < 0 for 10⁻⁵ mM LysoPC.

Figure 6.

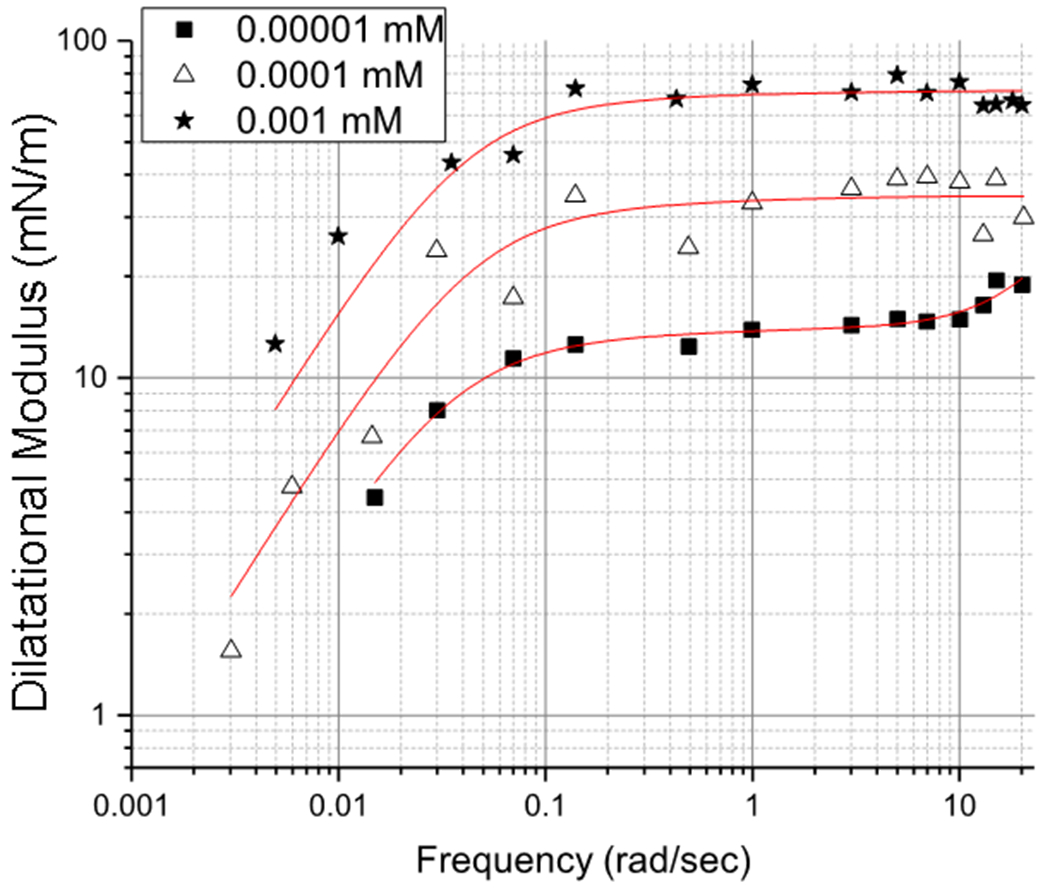
LysoPC dilatational modulus for concentrations below the 0.006 mM critical micelle concentration for 45 μm radius bubbles. Below the CMC, the frequency dependence of ε is similar for all concentrations, suggesting a constant ω₀. However, the plateau value of ε at high frequencies decreases with concentration, unlike at the higher concentrations in Figures 4, 5. The red curves are fits to Eqn. 22.

Theory

To relate the changes in dilatational modulus to the chemical and physical properties of LysoPC, we use a model originally introduced for flat interfaces by Lucassen and Van den Tempel ³⁷ and modified by Joos to included spherical surfaces ³⁸. Kotula and Anna have added terms to include viscous resistance to flow on the bubble surface ¹⁸. For an oscillating surfactant-coated interface, the surface excess normal stress is related to the dilatational strain via a dilatational modulus, ε, and is given by the following expression ^{18, 38}:

$$\epsilon =\frac{d\gamma }{d\left(\ln A\right)}+i\kappa \omega$$ (3)

The first term accounts for the relaxation of dilatational stresses from the thermodynamic limit by diffusive transport of soluble surfactant from the interface to the bulk (Figure 1). The second term is due to the dissipative resistance to interfacial flow described by the Scriven/Boussinesq equations caused by the surface dilatational viscosity, κ ^{18, 39}, with $i=\sqrt{-1}$ . If the initial bubble area is A₀, the area as a function of time is:

$$A=A_0+A^{\prime }{e}^{i\omega t},e^{i\omega t}=\cos \omega t+i\sin \omega t$$ (4)

For small relative area deformations,

$$\ln A=\ln \left(A_0\left(1+\Delta A{e}^{i\omega t}\right)\right)\cong \ln A_0+\Delta A{e}^{i\omega t}$$ (5)

in which ΔA = A′/A₀ ≪ 1 . The area oscillations induce corresponding changes in the surface concentration, Γ, around the equilibrium surface concentration, Γ_e, on a bubble area of A₀:

$$\Gamma ={\Gamma }_e+P{e}^{i\omega t}$$ (6)

The amplitude P can be complex as the surface concentration oscillations may have a phase difference with the area oscillations. We could also write equivalent expressions using:

$$\ln A=\ln A_0+\Delta A\mathit{cos}\omega t$$ (7a)

$$\Gamma ={\Gamma }_e+P\mathit{cos}\left(\omega t+\varphi \right)$$ (7b)

ϕ is the phase difference between changes in area and changes in surface concentration. As with the area oscillations, the initial transient in $\mathrm{\Gamma }$ dies away ¹⁸, resulting in steady oscillations of the surface concentration.

As a result of the surface concentration oscillations, the bulk concentration also changes:

$$\text{C}=C_0+f\left(r\right)e^{i\omega t}$$ (8)

The bulk concentration oscillations decay with distance into the bulk solution as given by f(r), which is governed by the spherical diffusion equation (for small amplitude oscillations, convection is negligible ³⁸):

$$\frac{\partial C}{\partial t}=D\left(\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial C}{\partial r}\right)\right)$$ (9)

D is taken to be the surfactant monomer diffusivity, which is of order 2 × 10⁻¹⁰ m²/sec ¹⁸. Substitution of Eqn. 8 into Eqn. 9 gives

$$\frac{d^{2}f\left(r\right)}{d{r}^2}+\frac{2}{r}\frac{df\left(r\right)}{dr}-n^{2}f\left(r\right)=0,n^2=\frac{i\omega }{D}$$ (10)

The general solution to which is

$$f\left(r\right)=\frac{\alpha }{r}{e}^{-nr},C=C_0+\frac{\alpha }{r}{e}^{-nr}{e}^{-i\omega t}$$ (11)

which fulfills the boundary condition that C → C₀ for large r. α is an unknown constant of integration. The second boundary condition is determined by a mass balance at the interface where the diffusive flux equals the rate of change in the total surface concentration ³⁸:

$$\frac{d\left(\Gamma A\right)}{dt}=AD{\left(\frac{\partial C}{\partial r}\right)}_{R}or\frac{d\Gamma }{dt}+{\Gamma }_e\frac{dlnA}{dt}=D{\left(\frac{\partial C}{\partial r}\right)}_R$$ (12)

Using Eqns. 5, 6 and 11 to evaluate Eqn. 12 gives:

$$i\omega P+i\omega {\Gamma }_e\Delta A=-\frac{\alpha D}{R^2}{e}^{-nR}\left(1+nR\right)$$ (13)

For small oscillation amplitudes, a linearized adsorption isotherm relates $\raisebox{1ex}{$dC$}\!\left/ \!\raisebox{-1ex}{$\text{d}\Gamma $}\right.$ to α:

$$\frac{dC}{d\Gamma }\cong \frac{C\left(r=R\right)-C_0}{\Gamma -{\Gamma }_e}=\frac{\frac{\alpha }{R}{e}^{-nR}{e}^{i\omega t}}{P{e}^{i\omega t}}=\frac{\alpha }{P}\frac{e^{-nR}}{R}$$ (14a)

$$P{R}^{nR}\frac{dC}{d\Gamma }=\alpha$$ (14b)

Inserting (14b) into Eqn. (13) gives P, the amplitude of the surface concentration oscillations:

$$i\omega P+i\omega {\Gamma }_e\Delta A=-\left(P{\mathrm{Re}}^{nR}\frac{dC}{d\Gamma }\right)\frac{D}{R^2}{e}^{-nR}\left(1+nR\right)$$ (15a)

$$P=\frac{-{\Gamma }_e\Delta A}{1+\left(\frac{D}{i\omega R}\right)\frac{dC}{d\Gamma }\left(1+nR\right)}$$ (15b)

The changes in surface tension due to the amplitude of the oscillations in the surface concentration can be approximated as

$$d\gamma =\frac{d\gamma }{d\Gamma }d\Gamma =\frac{d\gamma }{d\Gamma }P=-\frac{d\gamma }{d\Gamma }{\Gamma }_e\frac{\Delta A}{1+\left(\frac{D}{i\omega R}\right)\frac{dC}{d\Gamma }\left(1+nR\right)}$$ (16a)

$$-\frac{d\gamma }{d\Gamma }{\Gamma }_e=-\frac{d\gamma }{d\left(\ln {\Gamma }_e\right)}\equiv {\epsilon }_0$$ (16b)

ε₀ is the limiting interfacial elasticity, also known as the Gibbs elasticity. The first term in the dilatational modulus is obtained from Eqn. 16a:

$$\begin{gathered} \frac{d\gamma }{d\left(\ln A\right)}\approx \frac{\Delta \gamma }{\Delta A}=\frac{{\epsilon }_0}{1+\left(\frac{D}{i\omega R}\right)\frac{dC}{d\Gamma }\left(1+nR\right)} \\ =\frac{{\epsilon }_0}{1+\left(\frac{Dn}{i\omega }\right)\frac{dC}{d\Gamma }\left(1+\frac{1}{nR}\right)} \end{gathered}$$ (17)

We can identify characteristic frequencies as ${\omega }_0=D{\left(\frac{dC}{d\Gamma }\right)}^2$ and ${\omega }_R=\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.$ so that $\left(\frac{Dn}{i\omega }\right)\frac{dC}{d\Gamma }=\sqrt{\frac{D}{i\omega }}\frac{dC}{d\Gamma }={\left(\frac{{\omega }_0}{i\omega }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ and $nR={\left(\frac{i\omega }{\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}={\left(\frac{i\omega }{\omega R}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. This changes Eqn. 17 into:

$$\frac{d\gamma }{d\left(\ln A\right)}=\frac{{\epsilon }_0}{1+{\left(\frac{{\omega }_0}{i\omega }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1+{\left(\frac{\omega R}{i\omega }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}$$ (18)

The concentration dependence of the dilatational modulus is contained in ω₀, while the curvature dependence is contained in ω_R. Clearing the complex numbers from the denominator, and defining $\zeta ={\left(\raisebox{1ex}{${\omega }_0$}\!\left/ \!\raisebox{-1ex}{$2\omega $}\right.\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$:

$$\frac{d\gamma }{d\left(\ln A\right)}=\frac{{\epsilon }_0\left\{1+\zeta +i\zeta \left(1+\sqrt{\frac{2{\omega }_R}{\omega }}\right)\right\}}{1+2\zeta +2{\zeta }^2\left(1+\frac{{\omega }_R}{\omega }+\sqrt{\frac{2{\omega }_R}{\omega }}\right)}$$ (19)

From Eqn. 3, we get:

$$\epsilon =\frac{{\epsilon }_0\left\{1+\zeta +i\zeta \left(1+\sqrt{\frac{2{\omega }_R}{\omega }}\right)\right\}}{1+2\zeta +2{\zeta }^2\left(1+\frac{{\omega }_R}{\omega }+\sqrt{\frac{2{\omega }_R}{\omega }}\right)}+i\kappa \omega$$ (20)

Hence, the elastic (real) and viscous (imaginary) components of the dilatational modulus are:

$${\epsilon }_r=\frac{{\epsilon }_0\left(1+\zeta \right)}{1+2\zeta +2{\zeta }^2\left(1+\frac{{\omega }_R}{\omega }+\sqrt{\frac{2{\omega }_R}{\omega }}\right)}$$ (21a)

$${\epsilon }_i=\frac{{\epsilon }_0\left(\zeta \left(1+\sqrt{\frac{2{\omega }_R}{\omega }}\right)\right)}{1+2\zeta +2{\zeta }^2\left(1+\frac{{\omega }_R}{\omega }+\sqrt{\frac{2{\omega }_R}{\omega }}\right)}+\kappa \omega$$ (21b)

The absolute value of the dilatational modulus is $\left|\epsilon \right|={\left({\epsilon }_r^2+{\epsilon }_i^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ $:$

$$\left|\epsilon \right|=\frac{{\epsilon }_0}{\beta }{\left[\beta +\left(\frac{2\zeta \beta \kappa \omega }{{\epsilon }_0}\left(1+\sqrt{\frac{2{\omega }_R}{\omega }}\right)\right)+\frac{{\kappa }^2{\omega }^2{\beta }^2}{{\epsilon }_0^2}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$ (22)

$$\beta =1+2\zeta +2{\zeta }^2\left(1+\frac{{\omega }_R}{\omega }+\sqrt{\frac{2{\omega }_R}{\omega }}\right)$$ (22a)

and the phase angle is:

$$\tan \delta =\frac{{\epsilon }_i}{{\epsilon }_r}=\frac{\zeta \left(1+\sqrt{\frac{2{\omega }_R}{\omega }}\right)+\beta \kappa \omega }{\left(1+\zeta \right)}$$ (23)

ε_r = |ε| cos δ is the in-phase, elastic or storage component of the dilatational modulus and ε_i = |ε| sin δ is the viscous or dissipative part of the modulus. For 40 μm bubbles, ${\omega }_R=\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.~0.12{\sec }^{-1}$, decreasing to 0.01 sec⁻¹ for 140 μm bubbles for D ~ 2 × 10⁻¹⁰ m²/sec which is typical of monomeric surfactants ¹⁸. The bubble curvature decreases both the real and imaginary parts of the modulus as the interfacial curvature increases the rate of transport to and from the interface ¹⁸. The main effect of curvature is at low frequencies where $\frac{2{\omega }_R}{\omega }>1$.

Figure 7 shows values of ε(ω) calculated from Eqn. 22 for different values of ω₀ for ε₀ = 60 mN/m and ω_R = 0.12 radians/sec, which corresponds to an equilibrium bubble radius of 40 μm for D = 2 × 10⁻¹⁰ m-sec⁻². In Fig. 7A, the dilatational viscosity parameter, κ = 0 and in 7B, κ = 0.3 mN-s-m⁻¹. The horizontal red line corresponds to 2ε − γ = 0, at which the Laplace Instability occurs for LysoPC for which γ ~ 40 mN/m. This crossover frequency increases with increasing ω₀ in both Figs. 7A and 7B, going from ~ 0.05 rad/sec for ω₀= 0.005 rad/sec to ~ 1500 rad/sec for ω₀= 1000 rad/sec when κ = 0. For κ = 0.3 mN-s-m⁻¹, the low frequency crossover remains at ~ 0.05 rad/sec for ω₀= 0.005 rad/sec, but the high frequency crossover for ω₀= 1000 rad/sec decreases to ~ 350 rad/sec. The dilatational viscosity term, κω, in Eqn. 22 is small for low frequencies, but becomes increasingly important for larger frequencies. At sufficiently high frequencies, for which $\zeta ={\left(\raisebox{1ex}{${\omega }_0$}\!\left/ \!\raisebox{-1ex}{$2\omega $}\right.\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\ll 1,{\epsilon }_r\approx {\epsilon }_i\approx \kappa \omega$, and $|\epsilon |={({\epsilon }_0^2+{(\kappa \omega )}^2)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. For ε₀ > κω, ε plateaus at approximately ε₀ as is the case for the smaller values of ω₀ in Figs. 7A and 7B for frequencies below 100 rad/sec, and in Figs. 4,5 below 10 radians/sec at all lysolipid concentrations. However, at sufficiently high frequencies, ${\epsilon }_0^2\ll {(\kappa \omega )}^2$ resulting in $\epsilon \approx \kappa \omega$ so that ε increases linearly with ω as in Fig. 7B for frequencies greater than 10³ rad/sec. Our tensiometer is restricted to frequencies below ~ 20 radians/sec due to limitations in fitting the shape of the bubble at higher frequencies, so we do not see this high frequency response in our data (Fig. 4–6), and it is likely not important to understanding breathing as these frequencies are well above normal breathing rates. The black lines correspond to the resolution limit of our instrument ~ 1 mN/m.

Figure 7.

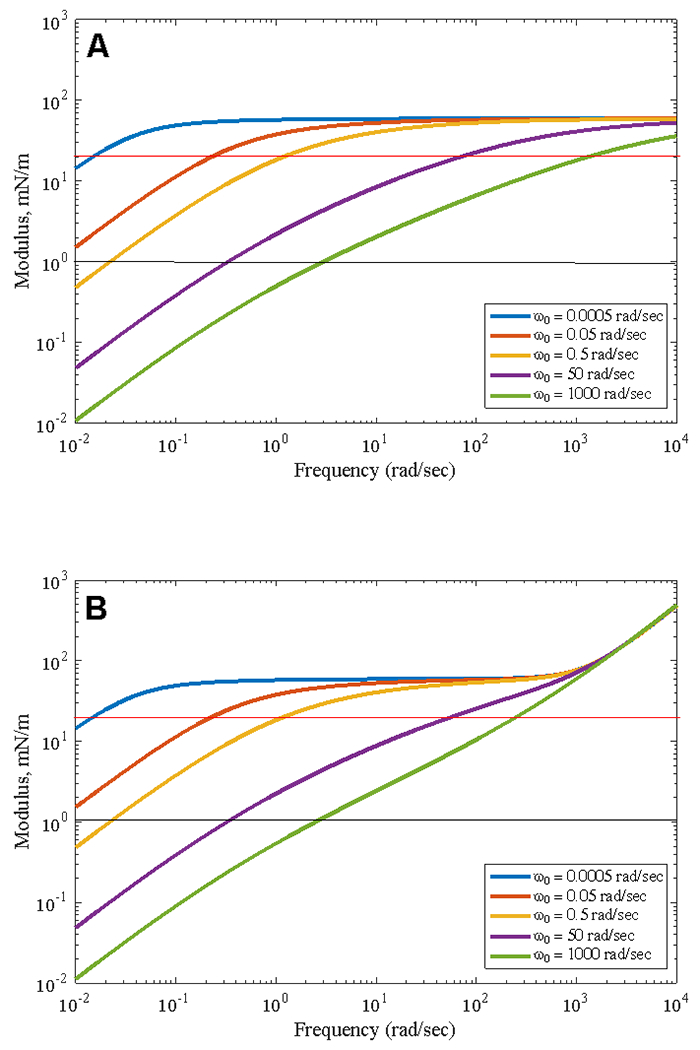
Calculated values of ε(ω) from Eqn. 22 for ε₀ = 60 mN/m for different values of ω₀ for A) κ = 0 and B) κ = 0.3 mN-s-m⁻¹ at a fixed value of ω_R= 0.12 radians/sec. The red line is the crossover defined by 2ε − γ = 0 for LysoPC. The black line is the resolution limit of our instrument, ε ~ 1 mN/m. The maximum operating frequency of our instrument is ~ 20 rad/sec. Increasing ω₀ increases the frequency of the crossover modulus. A finite value of κ increases ε at high frequencies, but has minimal effect at low frequencies relevant to breathing. In A), the maximum value of the modulus is given by ε₀, while in B) the modulus continues to increase linearly at high frequency due to the finite value of κ.

The red curves in Figures 4–6 are fits of Eqn. 22 to the data. For each curve in Figures 4 – 6, the equilibrium radius of curvature of the bubble is fixed (Table 1), which fixes the values of ${\omega }_R=\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.$ for D ~ 2 × 10⁻¹⁰ m²/sec, which is representative of single chain surfactants such as LysoPC (Table 1). ${\epsilon }_0=-\frac{d\gamma }{d\left(\ln {\Gamma }_e\right)}$ is the Gibbs elasticity and in Figures 4–6 is the plateau value of the dilatational modulus for high frequencies. For concentrations above the CMC of LysoPC, ε₀ gradually increases from low to high concentration for both 45 and 150 μm bubbles (Figures 4, 5, Table 1). Below the CMC, surface tension increases and surface concentration decreases, making ε₀ decrease significantly as shown in Figure 6. There is an indication in Figs. 4–6 that the modulus may continue to increase at higher frequencies, suggesting a finite dilatational viscosity contribution (see Figure 7). However, our microtensiometer is limited to frequencies below 20 rad/sec, ε₀ > κω, and there is little effect of κ on the data. However, ω₀ depends strongly on LysoPC concentration above the LysoPC CMC of 0.006 mM, but is roughly independent of concentration below the CMC (shaded rows in Table 1). Hence, ω₀ is the primary influence on the dilatational modulus and determines the crossover frequency at which 2ε − γ = 0. Within experimental variations, ω₀ is independent of the bubble curvature for a given concentration. Table 1 shows the fitted values of the parameters for LysoPC as a function of concentration for the smaller and larger bubbles.

Discussion

Inflammation accompanies ARDS; as the body responds to inflammation, the permeability of the alveolar-capillary barrier increases and phospholipase A₂ (PLA₂) extravasates into the alveolar fluids. PLA₂ catalyses the hydrolysis of double-chain phospholipids in lung surfactant, cell membranes, and bacterial, fungal, and viral membranes into single-chain lysolipids and fatty acids (Figure 1) ^{8, 13, 17}. The orders of magnitude greater solubility of lysolipids leads to facile exchange between the various cell membranes and the surrounding solution, leading to membrane defects and holes, which in turn, lead to bacterial, fungal and viral cell death. These processes of the innate immune system increase the concentration of lysolipids in the alveolar fluids by orders of magnitude ⁸. As shown in Figure 3, lysolipids in the subphase solution can successfully compete with lung surfactants at interface as the alveolar air-fluid interface expands and contracts ¹⁷. As lysolipid replaces lung surfactant (Fig. 3C), the maximum surface pressure decreases from 66 mN/m to 36 mN/m, (the minimum surface tension increases from ~ 6 mN/m to ~ 36 mN/m). However, even this increased surface tension would not completely prevent respiration as the intra-alveolar pressure would still be less than ambient. But Figure 3 shows that for slow expansion and compression cycles, π becomes independent of interfacial area, making ε = −A(∂π/∂A) ~ 0 meaning (2ε − γ) < 0, resulting in conditions that can lead to the Laplace instability. The dilatational modulus of the clinical lung surfactant Survanta is > 120 mN/m, so in the healthy lung, (2ε − γ) > 0 as the maximum surface tension is ~ 70 mN/m.

As shown schematically in Figure 1, the characteristic frequency for LysoPC exchange with the subphase, ${\omega }_0=\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{${\left(\raisebox{1ex}{$d\Gamma $}\!\left/ \!\raisebox{-1ex}{$dC$}\right.\right)}^2$}\right.$, determines the relationship between the frequency and concentration dependence of the dilatational modulus, ε(ω). Figures 4–6 show that the Kotula and Anna model for ε(ω) (Eqn. 22, red curves in Figs. 4–6) fits the measured data over four orders of magnitude of frequency and 3 orders of magnitude in amplitude. ω₀ is roughly the frequency at which the dilatational modulus starts to decrease from ε₀; physically, this is the frequency at which LysoPC begins to exchange with the subphase as shown in Figure 1. Table 1 and Figure 8 show ω₀ increases by orders of magnitude with increasing LysoPC concentration above the CMC and is roughly constant below the CMC of 0.006 mM.

Figure 8.

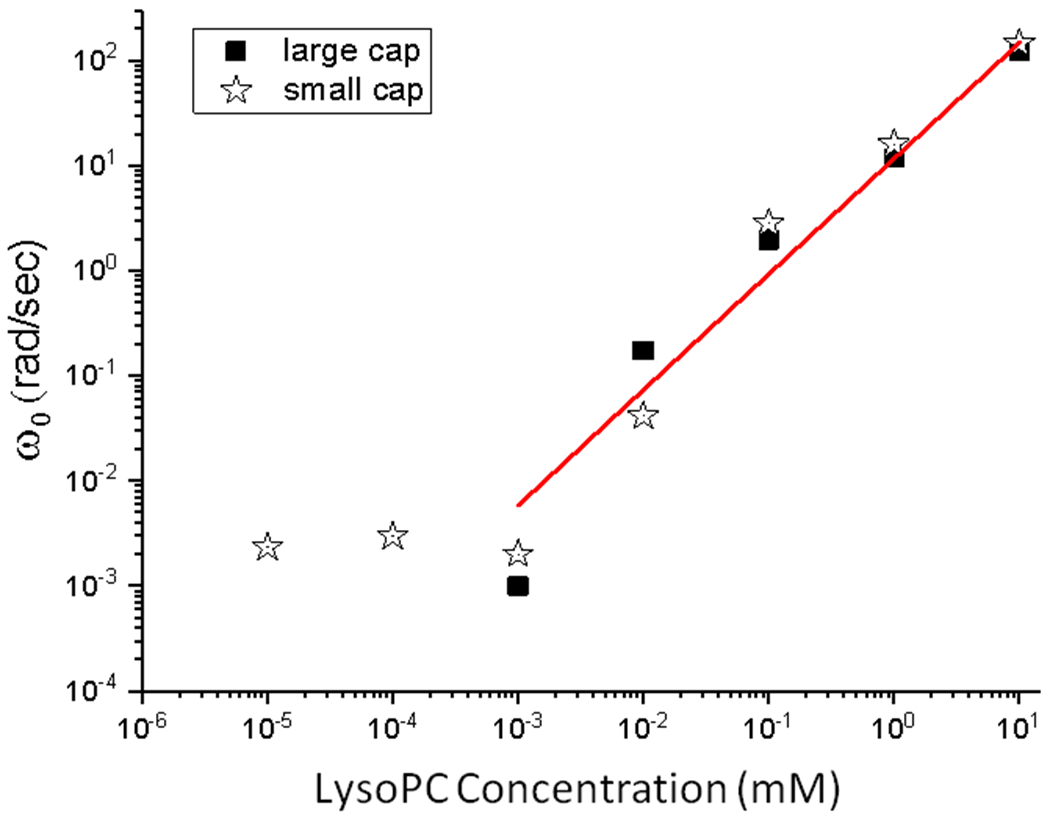
Concentration dependence of ω₀, the characteristic exchange frequency of LysoPC between the subphase and interface for the large (squares, 150 μm radius) and small capillaries (star, 50 μm radius). Below the 0.006 mM CMC of LysoPC, ω₀ is constant. Above the CMC, ω₀ increases as a power law, ω₀ ∝ bC^β with β = 1.1. ω₀ is independent of the bubble size and only depends on LysoPC concentration.

Relating the Model Parameters to LysoPC Concentration

From the model, ${\omega }_0=D/{\left(\frac{d\Gamma }{dC}\right)}^2$ in which D is the lysolipid diffusivity ^{18, 37–38} and $\frac{d\Gamma }{dC}$ is an effective length scale for diffusion given by the change of surface concentration, Γ, with bulk lysolipid concentration, C. Simple thermodynamic models provide a semi-quantitative description that provides physical insight into how surface tension, surface concentration and bulk concentration are related and explain the observed changes in the dilatational modulus. The Gibbs adsorption isotherm relates the change in interfacial tension of a soluble surfactant, γ (mN/m), to the surface concentration, Γ (moles/m²) and the bulk LysoPC concentration, C (mol/m³):

$$\Gamma =\frac{-C}{RT}\left(\frac{\partial \gamma }{\partial C}\right)$$ (24)

For soluble surfactants such as LysoPC, the surface tension, or its equivalent, surface pressure, π (mN/m), can be correlated with the bulk surfactant concentration by the semi-empirical Szyszkowski Equation: ⁴⁰

$${\gamma }_0-\gamma =\pi =RT{\Gamma }_{\infty }\ln \left(1+\raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$a$}\right.\right)$$ (25)

γ₀ is the surface tension of pure water. Γ_∞ (mol/m²), the saturation surface concentration, and a (mol/m³) are material parameters that depend on the individual surfactant ⁴⁰. The Szyszkowski equation provides a good description for soluble surfactants below the CMC concentration, but does not predict the constant limiting value of γ above the CMC. Inserting Eqn. 25 into the Gibbs Adsorption Isotherm (Eqn. 24) gives a Langmuir-type adsorption isotherm model for surfactant adsorption to the interface:

$$\Gamma =\frac{{\Gamma }_{\infty }C}{a+C}$$ (26)

From this model for Γ, the characteristic frequency, ${\omega }_0=\text{D}{\left(\frac{dC}{d\Gamma }\right)}^2$ , which determines the concentration dependence of the diffusive part of the dilatational modulus is:

$$\frac{\text{d}\Gamma }{dC}=\frac{\text{a}{\Gamma }_{\infty }}{{\left(a+C\right)}^2};{\omega }_0=\text{D}\frac{{\left(a+C\right)}^4}{{\left(a{\Gamma }_{\infty }\right)}^2}$$ (27)

At concentrations below the CMC, when C < a, Eqn. 27 predicts that ${\omega }_0\approx \text{D}\left(\raisebox{1ex}{$a^2$}\!\left/ \!\raisebox{-1ex}{${\Gamma }_{\infty }^2$}\right.\right)$ and will be independent of the bulk concentration, while at higher concentrations ω₀ increases strongly with concentration. Figure 8 shows ω₀ plotted against concentration for LysoPC. Consistent with Eqn. 27, below the CMC, ω₀ is roughly constant. Above the CMC, ω₀ increases like a power law in C with increasing concentration: ${\omega }_0\propto b{C}^{\beta }$ , with β ~ 1.1. Since ${\omega }_0=\text{D}{\left(\frac{dC}{d\Gamma }\right)}^2\propto b{C}^{\beta },\frac{d\Gamma }{dc}\propto \varphi C^{-\beta /2}\propto \raisebox{1ex}{$\varphi $}\!\left/ \!\raisebox{-1ex}{$\sqrt{C}$}\right.$ above the CMC, in which ϕ is a constant.

Hence, above the CMC, the characteristic length scale for diffusion decreases with increasing LysoPC concentration, greatly increasing the characteristic frequency of LysoPC exchange with the interface, and the corresponding decrease in the dilatational modulus at a given frequency. For ω < ω₀, lysolipid exchange between subphase and interface is significant. Γ remains roughly constant, which in turn, keeps γ constant, and ε = A dγ / dA → 0 . However, if ω > ω₀, the soluble inhibitors do not have sufficient time to diffuse off the interface, Γ increases and γ decreases as the surface area decreases, and the dilatational modulus, ε, remains large at higher frequencies. In ARDS patients, the relevant frequencies are set by normal breathing rates of 10 – 20 breaths/minute and typical mechanical ventilation rates of 6 – 12 breaths/minute. The crossover frequency at which (2ε − γ) = 0 (dotted red lines in Figures 4,5) increases with increasing ω₀ and hence with increasing LysoPC concentration. For a given bubble or alveolus, the curvature dependence is fixed by ${\omega }_R=\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$R^2$}\right.$; smaller bubbles, and hence smaller alveoli, exchange LysoPC with the subphase more rapidly than larger bubbles, and hence are somewhat more susceptible to the Laplace Instability.

To understand the concentration dependence of ${\epsilon }_0={\Gamma }_e\frac{d\pi }{d{\Gamma }_e}$, we can derive the Frumkin equation that relates the surface pressure, π, to the surface concentration from Eqns. 24 and 25 (17):

$${\gamma }_0-\gamma =\pi =-RT{\Gamma }_{\infty }\ln \left(1+\frac{\Gamma }{{\Gamma }_{\infty }}\right)$$ (28)

Taking the differential of the Frumkin equation (28) shows:

$$d\pi =RT{\Gamma }_{\infty }\frac{\text{d}\Gamma }{{\Gamma }_{\infty }-\Gamma }$$ (29)

Figure 3A shows dπ = 0 for the LysoPC isotherm; from Eqn. 29, dΓ = 0 and a constant surface pressure implies a constant surface concentration. For the Gibbs elasticity, ${\epsilon }_0=-\frac{d\gamma }{d\left(\ln {\Gamma }_e\right)},$ the Frumkin model gives:

$${\epsilon }_0={\Gamma }_e\frac{d\pi }{d{\Gamma }_e}=RT\frac{{\Gamma }_{\infty }{\Gamma }_e}{{\Gamma }_{\infty }-{\Gamma }_e}$$ (30)

ε₀ saturates at higher LysoPC concentrations (Table 1), suggesting that the equilibrium surface concentration, Γ_e, saturates with bulk concentration, which is consistent with the accepted concept of an interface gradually saturating above the CMC ⁵ , and with our results in Table 1. Below the CMC, when Γ_∞ ≫ Γ_e, we expect that ε₀ ≈ RTΓ_e, and there is a larger decrease with decreasing equilibrium surface concentration Γ_e, which in turn decreases with bulk concentration (Eqn. 26), also consistent with Table 1.

Conclusions

Innate immune system responses, including the lipase-catalysed degradation of lung surfactant phospholipids to soluble lysolipids and free fatty acids, have been hypothesized as the origin of many of the lung instabilities resulting from ARDS ^{8, 14–15, 17, 41}. This has led to replacement surfactants based on lipase-resistant diether phosphonolipid analogs ⁴¹, but with modest results. However, the lysolipid concentration in the subphase or alveolar fluids increases due to all lipase activity during inflammation, and as this lysolipid concentration increases, it can compete for the interface even in the presence of a lung surfactant coated interface as shown in Figure 3 for Survanta. Figures 4 and 5 show that the surface activity and diffusivity of lysolipids are such that $\partial \left(\Delta P\right)/\partial R\le 0$ or $\left(2\epsilon -\gamma \right)\le 0$ occurs for LysoPC concentrations > 0.1 mM over the range of normal breathing frequencies due to the concentration dependence of ${\omega }_0=\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{${\left(\raisebox{1ex}{$d\Gamma $}\!\left/ \!\raisebox{-1ex}{$dC$}\right.\right)}^2$}\right.$, the characteristic frequency for exchange between monolayer and subphase. We find that ω₀ increases as a power law in the bulk LysoPC concentration above the CMC concentration of 0.006 mM.

This power law dependence of ω₀ may result from the reservoir of LysoPC micelles in the proximity of the interface, keeping the monomer concentration high and constant, greatly reducing $\frac{d\Gamma }{dc}$, the characteristic length scale for diffusive exchange between the monolayer and the subphase ⁴². Below the CMC, a LysoPC depletion layer may arise near the interface as the monomer surfactant is adsorbed at the interface, greatly increasing $\frac{d\Gamma }{dc}$. Increasing ${\omega }_0$ by increasing the LysoPC concentration moves the crossover frequency at which $\left(2\epsilon -\gamma \right)=0$ into the range of normal breathing frequencies. From our model, we expect soluble surface-active molecules at concentrations well above their CMC will decrease the dilatational modulus such that $\left(2\epsilon -\gamma \right)\le 0$, which, in turn will induce the Laplace Instability.

This suggests that lysolipids may play a previously unsuspected role in the lung instabilities in ARDS. Increasing the lysolipid concentration in the alveolar lining fluids due to lipase activity throughout the lung could displace the lung surfactant film as shown in Figure 3. The higher concentrations in the alveolar fluids could then move the crossover dilatational modulus for the Laplace Instability into the range of normal breathing frequencies. The Laplace instability could in turn, lead to non-uniform lung inflation and alveolar collapse. We find the necessary lysolipid concentration for inducing the Laplace Instability is ~ 20 times the critical micelle concentration of lysopalmitoylphosphatidylcholine (CMC = 6 μM). We speculate that other lysolipids with smaller CMC values, such as lysosteroylphosphatidylcholine (CMC = 0.4 μM) might induce the same effects at lower concentrations. As the chain and head group chemistry that results from PLA₂ degradation in the alveolar fluids is likely quite variable as bacteria, lung cells, and lung surfactant are hydrolysed, the lysolipid concentrations needed to induce the Laplace Instability might also be quite varied. We also do not yet know the effects of lysolipid mixtures or lung surfactant-lysolipid mixtures on the dilatational modulus. The physical properties of the lung surfactant, including surface shear and dilatational rheology may play a role in determining how readily lysolipids, albumin or serum proteins might induce this instability ^{11, 43–50}. Extending our work to more complex lung surfactant-lysolipid and serum protein mixtures should give us a better idea of the importance of the dilatational modulus and the Laplace Instability in the ARDS lung.

Our data also provides a possible explanation for the benefits to ARDS patients obtained by high-frequency oscillatory mechanical ventilation ^{6, 9–10}. For sufficiently high frequencies, $\left(2\epsilon -\gamma \right)>0$, even for the highest concentrations of LysoPC tested. Hence, the lysolipids do not have time to diffuse off the interface, which leaves the dilatational modulus above the threshold for the Laplace Instability. Our work suggests that ARDS patients could benefit by inhibiting lipase activity throughout the lung, thereby decreasing the lysolipid concentration, while maintaining high frequency, > 50 – 60 breaths/min ventilation.