Accounting for Group-Specific Allele Effects and Admixture in Genomic Predictions: Theory and Experimental Evaluation in Maize

Abstract

Populations structured into genetic groups may display group-specific linkage disequilibrium, mutations, and/or interactions between quantitative trait loci and the genetic background. These factors lead to heterogeneous marker effects affecting the efficiency of genomic prediction, especially for admixed individuals. Such individuals have a genome that is a mosaic of chromosome blocks from different origins, and may be of interest to combine favorable group-specific characteristics. We developed two genomic prediction models adapted to the prediction of admixed individuals in presence of heterogeneous marker effects: multigroup admixed genomic best linear unbiased prediction random individual (MAGBLUP-RI), modeling the ancestry of alleles; and multigroup admixed genomic best linear unbiased prediction random allele effect (MAGBLUP-RAE), modeling group-specific distributions of allele effects. MAGBLUP-RI can estimate the segregation variance generated by admixture while MAGBLUP-RAE can disentangle the variability that is due to main allele effects from the variability that is due to group-specific deviation allele effects. Both models were evaluated for their genomic prediction accuracy using a maize panel including lines from the Dent and Flint groups, along with admixed individuals. Based on simulated traits, both models proved their efficiency to improve genomic prediction accuracy compared to standard GBLUP models. For real traits, a clear gain was observed at low marker densities whereas it became limited at high marker densities. The interest of including admixed individuals in multigroup training sets was confirmed using simulated traits, but was variable using real traits. Both MAGBLUP models and admixed individuals are of interest whenever group-specific SNP allele effects exist.

GENOMIC prediction was proposed by Meuwissen et al. (2001) and has since become a central tool in many animal and plant breeding programs. In its simplest application, a set of individuals is evaluated for a given trait and genotyped at a high density using single nucleotide polymorphisms (SNPs). A statistical model is trained on this data set, referred to as the training set (TS), and is used to predict the breeding value of individuals for whom only genomic information is known, referred to as the predicted set (PS). The breeding values of PS individuals are predicted based on their genomic resemblance with TS individuals by taking advantage of the linkage disequilibrium (LD) between the SNPs and the quantitative trait loci (QTL) underlying the trait. Several models have been developed making different assumptions on the distribution of allele effects (Heslot et al. 2012). Most models, including the widely used genomic best linear unbiased prediction (GBLUP) model and the equivalent ridge-regression best linear unbiased prediction (RR-BLUP) model, do not explicitly consider the possible existence of a genetic structure in the population.

When a population is structured into genetic groups, the existence of group-specific allele frequencies and/or effects at QTL may affect genomic prediction accuracy in different manners. First, when the same structure is observed within the TS and the PS, the group mean differences are implicitly taken into account by a standard GBLUP model through the kinship and contribute to the accuracy, as shown by Guo et al. (2014) and Rio et al. (2019). Conversely, when targeting a group-specific PS, training a model on a different group can decrease accuracy dramatically as shown in several species, including dairy and beef cattle (Olson et al. 2012; Chen et al. 2013), and maize (Technow et al. 2013; Lehermeier et al. 2014). The combination of genetic groups in a multigroup TS has been proposed to apply predictions to a wide range of genetic diversity (de Roos et al. 2009). This solution is particularly interesting for genetic groups with a limited population size or to optimize resources for traits that are expensive to evaluate, so that a same TS can be used for different group-specific PSs. Such multigroup TSs showed a good predictive ability in a wide range of species, such as dairy cattle (Brøndum et al. 2011; Pryce et al. 2011; Zhou et al. 2013), maize (Technow et al. 2013; Rio et al. 2019), and soybean (Duhnen et al. 2017). However, the gain in precision is often limited compared to what could be obtained by applying predictions separately within groups (Carillier et al. 2014; Hayes et al. 2018).

Limited accuracy of intergroup predictions may result from differences in genetic information captured by SNPs. An obvious configuration consists in QTL segregating only in a given group, which cannot be accounted for when training the model on other groups. Group differences in genetic information captured by SNPs may also be due to group-specific SNP allele effects. Such heterogeneity may result from differences in LD between SNPs and QTL, as observed in several species including dairy cattle (de Roos et al. 2008) and maize (Technow et al. 2012). They may also be due to group-specific genetic mutations nearby QTL, or to epistatic interactions between QTL and the genetic background. Such heterogeneity in SNP allele effects was shown by Rio et al. (2020) for maize flowering time when studying an inbred maize panel including lines from the Dent and Flint genetic groups, along with admixed individuals. Specifying group-specific SNP allele effects in genomic prediction models thus appears to be an appealing solution to improve genomic prediction accuracy. This was proposed by Karoui et al. (2012) and Lehermeier et al. (2015) by adapting multitrait models to multigroup predictions. In such models, the SNP allele effects are assumed to be different but correlated between groups. This same formalism was also used to derive a priori indicators of accuracy or to find relevant estimators of relatedness in structured populations (Wientjes et al. 2015, 2017). Another possibility to account for the heterogeneity of allele effects is to decompose them as a sum between a main SNP effect and group-specific deviations, as proposed by Schulz-Streeck et al. (2012), de los Campos et al. (2015), Technow and Totir (2015), and Veturi et al. (2019). While proving their efficiency, these models only take into account the existence of distinct genetic groups in the population and cannot be applied directly to account for and/or predict admixed individuals.

Admixture is a common feature in natural and breeding populations. The genome of admixed individuals is a mosaic of chromosome fragments of different group ancestries. In breeding, admixture can be generated by introgressing new favorable alleles into elite germplasm. When predicting the performance of admixed individuals, standard genomic prediction models like GBLUP may poorly account for the possible heterogeneity of allele effects across genetic groups. A heterogeneity observed between pure individuals from different groups should be conserved in admixed individuals, provided that it results from a local genomic difference between groups (group-specific LD and/or group-specific mutations) and not from an interaction with the genetic background. Dedicated genome-wide association study (GWAS) methodologies are available to identify QTL in such configuration in admixed populations (Sillanpää and Bhattacharjee 2006; Skotte et al. 2019; Rio et al. 2020).

Before the advent of genomic data, the animal model, which considers pedigree relationships between individuals, has been adapted to multigroup populations including admixed individuals. The aim was to account for the additional variability observed in an admixed population compared to parental populations, by splitting the genetic variance into group-specific and segregation components using global admixture proportions (i.e., proportions of genome originated from each group for a given individual) (Lo et al. 1993; García-Cortés and Toro 2006). Such methodology was later adapted to genomic prediction by Strandén and Mäntysaari (2013) and Makgahlela et al. (2013) by replacing the pedigree-based kinship matrix with a kinship matrix estimated with SNPs. However, to our knowledge, no model was proposed which accounted both for group-specific allele effects and local admixture (i.e., group origin of each allele for a given individual). Local admixtures are relatively easy to obtain when admixed individuals are generated from a controlled mating design between individuals from different genetic groups, as commonly done in animal and plant breeding. The collection of these data are more difficult to achieve in natural populations because allele ancestry is not directly observable, as opposed to allele genotypes. However, they can be inferred using software such as STRUCTURE (Pritchard et al. 2000), LAMP (Sankararaman et al. 2008), and RFmix (Maples et al. 2013).

Regarding the interest of admixed individuals in multigroup TSs, Toosi et al. (2013) used simulations to show that including them enables high genomic prediction accuracy when predicting either pure or admixed individuals. Such performance can be explained by a good conservation of LD phases between admixed individuals and pure individuals and by a reduction of the LD extent in recombinant admixed individuals that allowed more accurate estimates of QTL allele effects by linked markers.

In this study, we present two genomic prediction models that account both for group-specific allele effects and local admixture. The two models, called multigroup admixed genomic best linear unbiased prediction random individual (MAGBLUP-RI) and multigroup admixed genomic best linear unbiased prediction random allele effect (MAGBLUP-RAE), are easy to implement as a linear mixed model. They were evaluated for their precision in estimating variance components as well as for their genomic prediction accuracy. Both models were applied to a Flint–Dent maize data set including admixed individuals using simulated traits and real traits. In this study, we also evaluated the benefits of using admixed individuals in multigroup TSs. Different scenarios were investigated by leveraging the proportion of pure and admixed individuals within the TS.

Materials and Methods

Modeling the genetic value of admixed individuals

To develop a relevant genomic prediction model for admixed individuals, our general strategy was to (i) propose an infinitesimal model for genetic values, (ii) study the expected genetic value and the covariance between genetic values, and (iii) derive a Gaussian variance component model that can be easily implemented as a linear mixed model. This strategy helps to identify which parameters need to be estimated, and which incidence and covariance matrices are required for their estimation. We considered two statistical formalisms that are classically found in the genomic prediction literature. According to the random individual formalism, the genotypes (both alleles and their ancestry) are assumed to be randomly distributed while allele effects are considered deterministic, as commonly done in the animal model (Henderson 1984; Kruuk 2004). According to the random allele effect formalism, the allele effects are assumed to be randomly distributed, as proposed by Meuwissen et al. (2001), while the genotypes are considered deterministic. The general strategy and the two statistical formalisms are first presented for GBLUP, then applied to admixed populations to derive MAGBLUP-RI and MAGBLUP-RAE. In this section, loci are referred to as QTL but could also be considered as molecular markers in LD or not, with some (unobserved) QTL. In such a case heterogeneity in allele effects may also result from group differences in LD between markers and QTL.

GBLUP

Let us consider a population of homozygous inbred lines without stratification into genetic groups. If we suppose an infinitesimal model with biallelic QTL for a trait of interest and no epistatic interactions among loci, we can model the genetic value of an individual as:

$$G_i={\displaystyle \sum _{m=1}^M\left({\beta }_m^0+W_{im}\left({\beta }_m^1-{\beta }_m^0\right)\right)}$$ (1)

where $G_i$ is the genetic value of individual i, M is the number of QTL controlling the trait, $W_{im}$ is the QTL genotype at locus m, taking the value “1” if individual i has the allele 1 and “0” otherwise, and ${\beta }_m^0$ and ${\beta }_m^1$ refer to the effects of the homozygous genotype for alleles 0 and 1 at locus m, respectively (further referred to as effects of alleles 0 and 1).

GBLUP-RI:

According to the random individual formalism, QTL allele effects are considered deterministic and QTL genotypes are modeled as being drawn from a Bernoulli distribution: $W_{im}\sim \mathrm{ℬ}\left(f_m\right),$ where $f_m$ is the frequency of allele 1 at locus m. An absence of LD is assumed between QTL, which amounts to assuming $\mathrm{cor}\left(W_{im},W_{im\prime }\right)=0$ for all m and $m\prime$.

For a given trait, let $\text{E}\left(G_i\right)$ and $\mathrm{cov}\left(G_i,G_j|{\alpha }_{ij}\right)$ be the expected genetic value and the genetic covariance assuming a kinship coefficient ${\alpha }_{ij}$ [being formally defined as ${\alpha }_{ij}=\mathrm{cor}\left(W_{im},W_{jm}\right)$ for all m] between individuals i and j. One has:

$$\text{E}\left(G_i\right)=\mu$$

where $\mu ={\displaystyle {\sum }_{m=1}^M\left({\beta }_m^0+f_m\left({\beta }_m^1-{\beta }_m^0\right)\right)}$ is the mean of the population, decomposed as the sum of the mean QTL effects over all loci, and:

$$\mathrm{cov}\left(G_i,G_j|{\alpha }_{ij}\right)={\alpha }_{ij}{\sigma }_G^2$$

where ${\sigma }_G^2={\displaystyle {\sum }_{m=1}^M{f}_m\left(1-f_m\right){\left({\beta }_m^1-{\beta }_m^0\right)}^2}$ is the genetic variance, corresponding to the sum of QTL variances over all loci. Note that when $i=j,$ the genetic covariance simplifies to the genetic variance $\text{V}\left(G_i\right)={\sigma }_G^2.$

From this formalism, one can derive an approximate Gaussian variance component model that inherits its mean and variance components from the previous infinitesimal model. The phenotypic values are then modeled as the sum of a fixed intercept and two random components: a genetic component and an error component including environmental effects and other uncontrolled effects, the two components being independent of each other:

$${\displaystyle \mathit{y}}=1\mu +{\displaystyle \mathit{g}}+{\displaystyle \mathit{e}}$$ (2)

where ${\displaystyle \mathbf{y}}$ is the vector of phenotypes of the N individuals, 1 is a vector of 1, ${\displaystyle \mathit{g}}$ is the vector of genetic values with ${\displaystyle \mathit{g}}\sim \mathcal{N}\left(0,{\displaystyle \mathit{K}}{\sigma }_G^2\right),$ ${\displaystyle \mathit{K}}$ is the matrix of kinship coefficients ${\alpha }_{ij}$, ${\displaystyle \mathit{e}}$ is the vector of errors with ${\displaystyle \mathit{e}}\sim \mathcal{N}\left(0,{\displaystyle \mathit{I}}{\sigma }_E^2\right),$ and ${\displaystyle \mathit{I}}$ is the identity matrix.

In practice, the kinship matrix can be computed following VanRaden (2008):

$${\left({\displaystyle \mathit{K}}\right)}_{ij}=\frac{{\displaystyle {\sum }_{m=1}^M\left(W_{im}-{\widehat{f}}_m\right)\left(W_{jm}-{\widehat{f}}_m\right)}}{{\displaystyle {\sum }_{m=1}^M{\widehat{f}}_m\left(1-{\widehat{f}}_m\right)}}$$ (3)

where ${\widehat{f}}_m=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{W}_{im}}$ refers to the estimate of $f_m$.

GBLUP-RAE:

According to the random allele effect statistical formalism in Equation 1, QTL genotypes are now considered deterministic and QTL allele effects are modeled as being drawn from a normal distribution: ${\beta }_m^k\sim \mathcal{N}\left(0,{\sigma }_{\beta }^2\right)$ independent and identically distributed (IID) for all m and k in $\left\{0,1\right\}$, and ${\sigma }_{\beta }^2$ is the variance common to all QTL effects ${\beta }_m^k$.

Let $\text{E}\left(G_i|{\mathit{w}}_i\right)$ and $\mathrm{cov}\left(G_i,G_j|{\mathit{w}}_i,{\mathit{w}}_j\right)$ be the expected genetic value and the covariance between genetic values of individuals i and j over an infinite sampling of allele effects, with ${\mathit{w}}_i$ and ${\mathit{w}}_j$ being the vectors of deterministic QTL genotypes of individuals i and j, respectively. One has:

$$\text{E}\left(G_i|{\mathit{w}}_i\right)=0$$

and

$$\mathrm{cov}\left(G_i,G_j|{\mathit{w}}_i,{\mathit{w}}_j\right)={\phi }_{ij}{\sigma }_U^2$$

where ${\sigma }_U^2=M{\sigma }_{\beta }^2$ is the variance due to QTL effects and ${\phi }_{ij}$ is the identity-by-state (IBS) coefficient between i and j, which has an explicit expression that stems from the derivation of the covariance:

$${\phi }_{ij}=\frac{1}{M}{\displaystyle \sum _{m=1}^M\left(\left(1-w_{im}\right)\left(1-w_{jm}\right)+w_{im}{w}_{jm}\right)}$$ (4)

Note that when $i=j$, the covariance simplifies to the variance $\text{V}\left(G_i|{\mathit{w}}_i\right)={\sigma }_U^2$, as ${\phi }_{ij}=1$ for homozygous inbred lines.

From this formalism, we can also model the phenotypic value of a set of individuals as being a sum between a genetic component and an error component. While not specified by the generative model, a fixed intercept can be assumed:

$${\displaystyle \mathit{y}}=1\mu +{\displaystyle \mathit{u}}+{\displaystyle \mathit{e}}$$ (5)

where $\mathit{u}$ is the vector of genetic values with $\mathit{u}\sim \mathcal{N}\left(0,\mathit{\phi }{\sigma }_U^2\right)$ and $\mathit{\phi }$ is the matrix of IBS coefficients ${\phi }_{ij}$. All other terms are identical to those described in Equation 2.

MAGBLUP:

Let us consider a population of homozygous inbred lines from two pure genetic groups A and B, along with lines admixed between these two groups. If we suppose a polygenic trait with biallelic QTL, whose effects depend both on the allele at the QTL (0/1) and its ancestry or local admixture (A/B), and no epistatic interactions among loci, we can model the genetic value of an individual as:

$$G_i={\displaystyle \sum _{m=1}^M\left(A_{imA}\left({\beta }_{mA}^0+W_{im}\left({\beta }_{mA}^1-{\beta }_{mA}^0\right)\right)+A_{imB}\left({\beta }_{mB}^0+W_{im}\left({\beta }_{mB}^1-{\beta }_{mB}^0\right)\right)\right)}$$ (6)

where $G_i$ is the genetic value of individual i; M is the number of QTL controlling the trait; $A_{imA}$ is the allele ancestry at locus m, taking the value “1” if individual i inherited its allele from group A and “0” otherwise; $A_{imB}=1-A_{imA}$, $W_{im}$ is the QTL genotype at locus m, taking the value “1” if individual i has the allele 1 and “0” otherwise; and ${\beta }_{mA}^0$, ${\beta }_{mA}^1$, ${\beta }_{mB}^0$, and ${\beta }_{mB}^1$ refer to the effects of the homozygous genotype for alleles 0 and 1 in groups A and B at locus m, respectively (further referred to as effects of alleles 0 and 1 in groups A and B).

MAGBLUP-RI:

According to the random individual formalism, QTL allele effects are considered deterministic, local ancestries are modeled as being drawn from a Bernoulli distribution: $A_{imA}\sim \mathrm{ℬ}\left({\pi }_i\right)$ IID where ${\pi }_i$ is the genome proportion that individual i received from group A, QTL genotypes are modeled as being drawn from a Bernoulli distribution conditionally to allele ancestries: $\left(W_{im}|A_{imp}=1\right)\sim \mathrm{ℬ}\left(f_{mp}\right)$, where $p\in \left\{A,B\right\}$ will further refer either to group A or B and $f_{mp}$ is the frequency of allele 1 at locus m in group p. One also assumes that $\mathrm{cor}\left(W_{im},W_{im\prime }|A_{imp}=1,A_{im\prime p\prime }=1\right)=0$ for all $m,m\prime \ne m$ and $p,p\prime$. When $p=p\prime$, this last assumption amounts to assuming an absence of LD between QTL within groups.

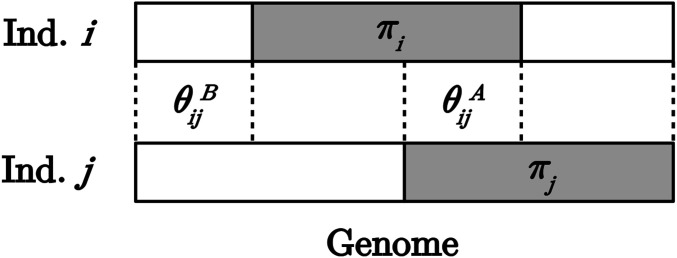
Let us define the following parameters to model the covariance between individuals: ${\alpha }_{ij}^p=\mathrm{cor}\left(W_{im},W_{jm}|A_{imp}=1,A_{jmp}=1\right)$ for all m being the “conditional” kinship between i and j on their shared group p ancestries, and ${\theta }_{ij}^p=\text{E}\left(A_{imp}{A}_{jmp}\right)$ for all m being the proportion of shared group p ancestry (or shared admixture). Note the existence of the following constraint: ${\theta }_{ij}^B=1-{\pi }_i-{\pi }_j+{\theta }_{ij}^A$, as shown in Figure 1.

Figure 1.

Diagram illustrating the genome-wide allele ancestry of two inbred individuals i and j, represented by their haplotypes, with a proportion ${\pi }_i$ of genome A for i and ${\pi }_j$ for j, a proportion of shared group A ancestry ${\theta }_{ij}^A$ between i and j, and a proportion of shared group B ancestry ${\theta }_{ij}^B=1-{\pi }_i-{\pi }_j+{\theta }_{ij}^A$ between i and j.

For a given trait, let $\text{E}\left(G_i|{\pi }_i\right)$ and $\mathrm{cov}\left(G_i,G_j|{\pi }_i,{\pi }_j,{\theta }_{ij}^A,{\theta }_{ij}^B,{\alpha }_{ij}^A,{\alpha }_{ij}^B\right)$ be the expected genetic value and the genetic covariance between i and j. One has:

$$\text{E}\left(G_i|{\pi }_i\right)={\pi }_i{\mu }_A+\left(1-{\pi }_i\right){\mu }_B$$

where ${\mu }_p={\displaystyle {\sum }_{m=1}^M{\mu }_{mp}={\displaystyle {\sum }_{m=1}^M{\beta }_{mp}^0+f_{mp}\left({\beta }_{mp}^1-{\beta }_{mp}^0\right)}}$ is the mean of group p, decomposed as the sum of the mean QTL effects ${\mu }_{mp}$ in group p, and:

$$\mathrm{cov}\left(G_i,G_j|{\pi }_i,{\pi }_j,{\theta }_{ij}^A,{\theta }_{ij}^B,{\alpha }_{ij}^A,{\alpha }_{ij}^B\right)={\text{Δ}}_{ij}{\sigma }_S^2+{\theta }_{ij}^A{\alpha }_{ij}^A{\sigma }_{G_A}^2+{\theta }_{ij}^B{\alpha }_{ij}^B{\sigma }_{G_B}^2$$

where ${\text{Δ}}_{ij}={\theta }_{ij}^A-{\pi }_i{\pi }_j$ is the covariance between the allele ancestries of i and j, ${\sigma }_S^2=\frac{M}{M-1}{\displaystyle {\sum }_{m=1}^M{\left({\mu }_{mA}-{\mu }_{mB}\right)}^2-\frac{1}{M-1}{\left({\mu }_A-{\mu }_B\right)}^2}$ is the segregation variance caused by differences between group-specific mean QTL effects, and ${\sigma }_{G_p}^2={\displaystyle {\sum }_{m=1}^M{f}_{mp}\left(1-f_{mp}\right){\left({\beta }_{mp}^1-{\beta }_{mp}^0\right)}^2}$ is the genetic variance in group p. When $i=j$, the covariance simplifies to the variance $\text{V}\left(G_i|{\pi }_i\right)={\pi }_i\left(1-{\pi }_i\right){\sigma }_S^2+{\pi }_i{\sigma }_{G_A}^2+\left(1-{\pi }_i\right){\sigma }_{G_B}^2$. More details about the derivation of the model are shown in Supplemental Material, File S1. Note that the covariance between the genetic values of two pure individuals of different groups is null here.

From this formalism, we can model the phenotypic value of a set of individuals as the sum of fixed group effects and four random components: an admixture component, two group-specific genetic components, and an error component, with the four components being independent of each other:

$${\displaystyle \mathit{y}}={\displaystyle \mathit{X}\mu }+{{\displaystyle \mathit{g}}}_S+{{\displaystyle \mathit{g}}}_A+{{\displaystyle \mathit{g}}}_B+{\displaystyle \mathit{e}}$$ (7)

where ${\displaystyle \mathit{X}}=\left(\mathit{\pi },\mathbf{1}-\mathit{\pi }\right)$ is the incidence matrix for fixed effects with ${\displaystyle \mathit{\pi }}$ being the vector of group A genome proportions, ${\displaystyle \mathit{\mu }}={\left({\mu }_A,{\mu }_B\right)}^T$ is the vector of group-specific intercepts, ${{\displaystyle \mathit{g}}}_S$ is the vector of the admixture component of the genetic value with ${{\displaystyle \mathit{g}}}_S\sim \mathcal{N}\left(0,{\displaystyle \mathbf{\Delta }}{\sigma }_S^2\right)$, ${\displaystyle \mathbf{\Delta }}$ is the matrix of coefficients ${\text{Δ}}_{ij}$, ${{\displaystyle \mathit{g}}}_p$ is the vector of the group p component of the genetic value with ${{\displaystyle \mathit{g}}}_p\sim \mathcal{N}\left(0,\left({{\displaystyle \mathit{\theta }}}_p○{{\displaystyle \mathit{K}}}_p\right){\sigma }_{G_p}^2\right)$, ${{\displaystyle \mathit{\theta }}}_p$ is the matrix of coefficients $={\theta }_{ij}^p$, and “$○$” refers to the Hadamard product.

In practice, covariance matrices can be estimated as follows:

$${\left({{\displaystyle \mathit{K}}}_p\right)}_{ij}=\frac{{\displaystyle {\sum }_{m=1}^M{A}_{imp}\left(W_{im}-{\widehat{f}}_{mp}\right)A_{jmp}\left(W_{jm}-{\widehat{f}}_{mp}\right)}}{{\displaystyle {\sum }_{m=1}^M{A}_{imp}{A}_{jmp}{\widehat{f}}_{mp}\left(1-{\widehat{f}}_{mp}\right)}}$$ (8)

$${\left({\displaystyle {\mathit{\theta }}_p}\right)}_{ij}=\frac{1}{M}{\displaystyle \sum _M^{m=1}}{A}_{imp}{A}_{jmp}$$ (9)

$${\left({\displaystyle \mathbf{\Delta }}\right)}_{ij}={\left({{\displaystyle \mathit{\theta }}}_A\right)}_{ij}-{\widehat{\pi }}_i{\widehat{\pi }}_j$$ (10)

where ${\widehat{\pi }}_i=\frac{1}{M}{\displaystyle {\sum }_{m=1}^M{A}_{imA}}$ and ${\widehat{f}}_{mp}=\frac{{\displaystyle {\sum }_{i=1}^N{A}_{imp}{W}_{im}}}{{\displaystyle {\sum }_{i=1}^N{A}_{imp}}}$ refer to the estimates of ${\pi }_i$ and $f_{mp}$, respectively. Note that the estimators of kinship matrices were proposed in analogy with Equation 3.

MAGBLUP-RAE:

According to the random allele effect formalism, QTL genotypes are considered deterministic and the allele effects are random. These allele effects can be further decomposed into main effects and group-specific deviations as follows:

$${\beta }_{mp}^0={\gamma }_m^0+{\delta }_{mp}^0,$$

$${\beta }_{mp}^1={\gamma }_m^1+{\delta }_{mp}^1,$$

with ${\gamma }_m^k\sim \mathcal{N}\left(0,{\sigma }_{\gamma }^2\right)$ IID and ${\delta }_{mp}^k\sim \mathcal{N}\left(0,{\sigma }_{{\delta }_p}^2\right)$ IID for all m, p, and $k\in \left\{0,1\right\}$; ${\sigma }_{\gamma }^2$ and ${\sigma }_{{\delta }_p}^2$ are the variance of the QTL effects ${\gamma }_m^k$ and ${\delta }_{mp}^k$, respectively, with all ${\gamma }_m^k$ and ${\delta }_{mp}^k$ being independent.

Combining this decomposition with Equation 6, one obtains:

$$G_i={\displaystyle \sum _M^{m=1}}\left({\gamma }_m^0+W_{im}\left({\gamma }_m^1-{\gamma }_m^0\right)+A_{imA}\left({\delta }_{mA}^0+W_{im}\left({\delta }_{mA}^1-{\delta }_{mA}^0\right)\right)+A_{imB}\left({\delta }_{mB}^0+W_{im}\left({\delta }_{mB}^1-{\delta }_{mB}^0\right)\right)\right).$$ (11)

Let $\text{E}\left(G_i|{{\displaystyle \mathit{a}}}_i,{{\displaystyle \mathit{w}}}_i\right)$ and $\mathrm{cov}\left(G_i,G_j|{{\displaystyle \mathit{a}}}_i,{{\displaystyle \mathit{a}}}_j,{{\displaystyle \mathit{w}}}_i,{{\displaystyle \mathit{w}}}_j\right)$ be the expected genetic value and the covariance between genetic values of individuals i and j over an infinite sampling of allele effects, with ${{\displaystyle \mathit{w}}}_i$ and ${{\displaystyle \mathit{w}}}_j$ being the vector of deterministic QTL genotypes of i and j, respectively, and ${{\displaystyle \mathit{a}}}_i$ and ${{\displaystyle \mathit{a}}}_j$ being the vector of deterministic QTL allele ancestries of i and j, respectively. One has:

$$\text{E}\left(G_i|{{\displaystyle \mathbf{a}}}_i,{{\displaystyle \mathbf{w}}}_i\right)=0$$

and:

$$\mathrm{cov}\left(G_i,G_j|{{\displaystyle \mathit{a}}}_i,{{\displaystyle \mathit{a}}}_j,{{\displaystyle \mathit{w}}}_i,{{\displaystyle \mathit{w}}}_j\right)={\phi }_{ij}{\sigma }_U^2+{\phi }_{ij}^A{\sigma }_{U_A}^2+{\phi }_{ij}^B{\sigma }_{U_B}^2$$

where ${\phi }_{ij}$ is the IBS coefficient between i and j (Equation 4) and ${\phi }_{ij}^p$ is the IBS coefficient between i and j on shared group p ancestries over the total number of loci, ${\sigma }_U^2=M{\sigma }_{\gamma }^2$ is the variance component due to main QTL effects, and ${\sigma }_{U_p}^2=M{\sigma }_{{\delta }_p}^2$ are the variance component due to QTL deviation effects in group p. Note that when $i=j$, the covariance simplifies to the variance $\text{V}\left(G_i|{{\displaystyle \mathit{a}}}_i,{{\displaystyle \mathit{w}}}_i\right)={\sigma }_U^2+{\pi }_i{\sigma }_{U_A}^2+\left(1-{\pi }_i\right){\sigma }_{U_B}^2$. According to this formalism, the genetic covariance between two pure individuals of different groups is nonnull whenever the variance of main QTL effects is nonnull.

Like ${\phi }_{ij}$ in Equation 4, ${\phi }_{ij}^p$ has an explicit expression that stems from the derivation of the covariance:

$${\phi }_{ij}^P=\frac{1}{M}{\displaystyle \sum _{m=1}^M{a}_{imp}{a}_{jmp}}\left(\left(1-w_{im}\right)\left(1-w_{jm}\right)+w_{im}{w}_{jm}\right).$$ (12)

From this formalism, we can model the phenotypic value of a set of individuals as the sum between four components, one genetic component that is due to main QTL effects, two genetic components that are due to group-specific deviation effects, and an error component. Like with GBLUP-RAE, a fixed intercept can be assumed:

$${\displaystyle \mathit{y}}=\mathbf{1}\mu +{\displaystyle \mathit{u}}+{{\displaystyle \mathit{u}}}_A+{{\displaystyle \mathit{u}}}_B+{\displaystyle \mathit{e}}$$ (13)

where ${{\displaystyle \mathit{u}}}_p$ is the vector of the genetic component that is due to QTL deviation effects in group p with ${{\displaystyle \mathit{u}}}_p\sim \mathcal{N}\left(0,{\mathit{\phi }}_p{\sigma }_{U_p}^2\right),$ and ${\mathit{\phi }}_p$ is the matrix of IBS coefficients on shared group p ancestries ${\phi }_{ij}^p$. All other terms are identical to those described in Equations 2 and 5.

Flint–Dent data set

We considered the Flint–Dent panel presented in Rio et al. (2020). It consists of 970 maize inbred lines including 300 pure Dent, 304 pure Flint, and 366 admixed lines, which were genotyped for 482,013 polymorphic SNPs. Missing marker data were imputed and the ancestry (Dent or Flint) of the alleles inherited by admixed individuals were inferred from their marker data and their pedigree, as described in Rio et al. (2020). For all individuals, SNP alleles (coded 0/1) and allele ancestries (Dent or Flint) are considered as known. LD extent was estimated separately for the Dent and Flint lines and suggested the existence of a larger number of effective chromosome segments in the Flint than in the Dent data set, as presented in Figure S1. The panel was evaluated in two trials for five traits: male flowering (MF) and female flowering (FF) in calendar days after sowing, plant height (PH) in centimeters, ear leaf number (ELN), and total number of leaves (TNL). Each trial was a Latinized alpha design where every line was evaluated two times on average, with 98% of lines observed in both trials. The phenotypic analysis was presented by Rio et al. (2020) for flowering traits and applied here for all traits (Table S1). Least-square means were computed over the whole design and are further referred to as phenotypes. No weighted analysis was considered here as the overall design was essentially balanced within and between trials.

Statistical inference and genomic predictions

The genomic prediction models presented in the previous section were applied to the Flint–Dent data set where group A refers to the Dent group (D) and group B refers to the Flint group (F). The four models considered are GBLUP-RI as defined in Equation 2, using a kinship matrix computed following Equation 3; GBLUP-RAE as defined in Equation 5, using the IBS matrix computed following Equation 4; MAGBLUP-RI as defined in Equation 7, using the covariances matrices described in Equations 8–10; and MAGBLUP-RAE as defined in Equation 13, using the three IBS matrices described in Equations 4 and 12. For all models, the inference of parameters was done using the R-package MM4LMM (Laporte et al. 2020). Genomic predictions were computed as BLUPs (Searle et al. 2008) of the genetic values (including fixed effects).

Simulated traits

Phenotypic traits were simulated to study the precision of MAGBLUP-RI and MAGBLUP-RAE in terms of variance estimates and genomic predictions. Genetic values were simulated using the model presented in Equation 11. Three different types of genetic configuration were defined regarding QTL allele effects and are summarized in Table 1: “Main” refers to a trait with only main QTL allele effects, “Dev.” refers to a trait with only group-specific QTL deviation effects, and “Main+Dev.” includes both types of effects. A total of 1000 loci were sampled among all SNPs to be used as QTL. Allele effects were sampled independently from normal distributions with variances defined by the type of genetic configuration. The genetic value of each individual was computed as a sum of QTL effects that depend on both the genotype and the ancestry of the alleles. Residuals were sampled from a normal distribution $\mathcal{N}\left(0,{\sigma }_E^2\right)$, with ${\sigma }_E^2$ chosen to reach a heritability of 0.8, which corresponds to the level of heritability observed for the traits in our real data application case. Genetic configurations complementary to those previously cited were simulated and are briefly presented in the Discussion section.

Table 1. Variances of the main allele effects ${\sigma }_{\gamma }^2$, the Dent-specific deviation effects ${\sigma }_{{\delta }_D}^2$, and the Flint-specific deviation effects ${\sigma }_{{\delta }_F}^2$ for the three types of genetic configuration.

Genetic configuration	${\sigma }_{\gamma }^2$	${\sigma }_{{\delta }_D}^2$	${\sigma }_{{\delta }_F}^2$
Main	2	0	0
Dev.	0	1	3
Main+Dev.	2	1	3

Evaluation of genomic predictions for simulated traits

The precision of genomic prediction of simulated traits was evaluated using two precision criteria: the accuracy and the standardized root-mean-square error of prediction (RMSP). The accuracy was computed by correlating the predicted value of the PS individuals to their simulated genetic value. The standardized RMSP was computed using the square root of the average of the square difference between the predicted value of PS individuals and their simulated genetic value, divided by the SD of the simulated genetic values. MAGBLUP-RI and MAGBLUP-RAE were compared to GBLUP-RI and GBLUP-RAE using two cross-validation (CV) procedures and 50 simulated traits for each type of genetic configuration. The first CV procedure, called averaged holdout (HO), consisted in splitting the data set into proportions $\frac{4}{5}$ and $\frac{1}{5}$ for the TS and the PS, respectively. The second CV procedure, called structured holdout (SHO), allowed us to (i) test the effect of the composition of the TS in terms of genetic background (and more particularly the interest of including admixed individuals), and (ii) evaluate the efficiency of the different genomic prediction models. Because the performance of GBLUP-RI and GBLUP-RAE were identical in the HO procedure, only the GBLUP-RI was considered for the SHO procedure. For the SHO procedure, samples of 90 individuals were predicted using a model trained on 210 other individuals. Those numbers were chosen to fit with all the scenarios described in Table 2. All the scenarios are designated as TS_PS, with TS and PS referring to the genetic backgrounds [Dent (D), Flint (F), admixed (A)] represented in the TS and the PS, respectively. When there is more than one genetic background in the TS or the PS, the composition is always perfectly balanced between them. As an example, DFA_A refers to a TS equally composed of individuals from the three genetic backgrounds and a PS composed of admixed lines only. In scenarios where only a Dent or Flint genetic background is found in the TS (D_D, F_D, D_F, F_F, D_A, and F_A), only GBLUP-RI could be evaluated. In configurations where admixed individuals are absent of the TS (DF_D, DF_F, and DF_A), the admixture term “${{\displaystyle \mathbf{g}}}_S$” of MAGBLUP-RI was removed as its variance component could not be estimated. For both CV procedures, the splitting was done 20 times and the precision criteria were averaged over replicates.

Table 2. Scenarios evaluated with the SHO CV where 90 individuals are predicted by 210 other individuals.

SHO scenario	TS composition	PS composition
DFA_DFA	$\frac{1}{3}$D + $\frac{1}{3}$F + $\frac{1}{3}$A	$\frac{1}{3}$D + $\frac{1}{3}$F + $\frac{1}{3}$A
A_D	A	D
DFA_D	$\frac{1}{3}$D + $\frac{1}{3}$F + $\frac{1}{3}$A	D
DF_D	$\frac{1}{2}$D + $\frac{1}{2}$F	D
D_D	D	D
F_D	F	D
A_F	A	F
DFA_F	$\frac{1}{3}$D + $\frac{1}{3}$F + $\frac{1}{3}$A	F
DF_F	$\frac{1}{2}$D + $\frac{1}{2}$F	F
D_F	D	F
F_F	F	F
A_A	A	A
DFA_A	$\frac{1}{3}$D + $\frac{1}{3}$F + $\frac{1}{3}$A	A
DF_A	$\frac{1}{2}$D + $\frac{1}{2}$F	A
D_A	D	A
F_A	F	A

The TS and the PS were balanced considering their composition in genetic backgrounds [Dent (D), Flint (F) and admixed (A)].

Application to real traits

The variance components of GBLUP-RI, GBLUP-RAE, MAGBLUP-RI, and MAGBLUP-RAE were estimated for the five real traits using the whole data set. The precision of genomic predictions was evaluated using the HO and SHO procedures with a splitting done 100 times. The same precision criteria were used as for simulated traits, but with phenotypes as a reference. Note that the accuracy was then called predictive ability, as it is commonly referred to in the genomic selection (GS) literature. We also investigated the effect of the number of SNPs used to compute the covariance matrices of each GS model on the predictive ability. To this end, different SNP densities were considered (100, 1000, 10,000, and 100,000 SNPs) by resampling among the 482,013 markers initially available. This resampling was performed 100 times per SNP density, and the HO procedure (with 100 splittings) was then applied to compare GS models.

Data availability

The Flint-Dent data set (genotypes and allele ancestries) is available at the Dataverse: Rio Simon, 2020, ”FlintDent GWAS data set”, https://doi.org/10.15454/OQT5CY. Supplemental material includes details on MAGBLUP-RI derivation (File S1), the presentation of an alternative formalism for GBLUP according to which both individuals and allele effects are considered random (File S2), additional results on the estimation of variance components by MAGBLUP-RI and MAGBLUP-RAE (File S3), least-square means of the Flint-Dent data set for the five real traits (File S4), R scripts to run analyses (Files S5 and S6 for main code and functions, respectively), and files with all supplemental figures (File S7) and tables (File S8). Supplemental material available at figshare: https://doi.org/10.25386/genetics.12645833

Results

Precision of genomic prediction for simulated traits

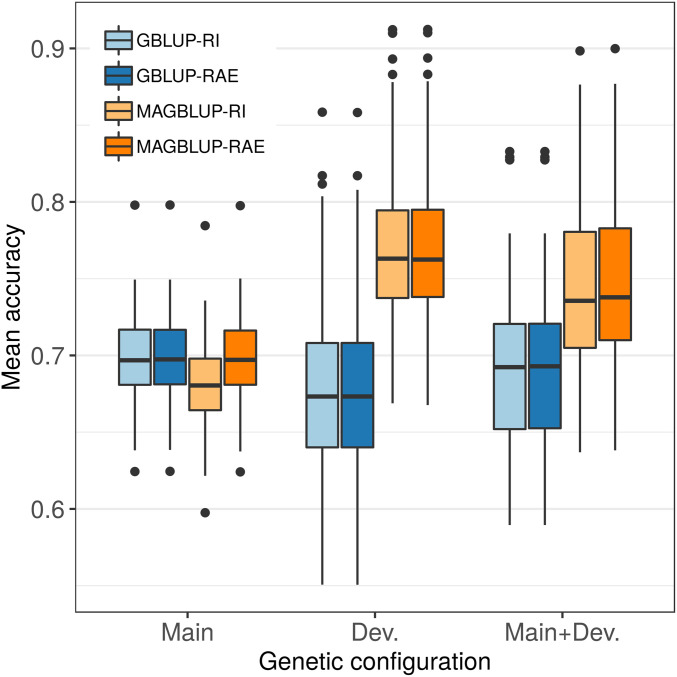
The precision of genomic predictions of the GBLUP-RI, GBLUP-RAE, MAGBLUP-RI, and MAGBLUP-RAE models was first compared using CV (HO method) applied to 150 simulated traits, 50 for each type of genetic configuration. Regarding the accuracy, MAGBLUP-RI and MAGBLUP-RAE outperformed GBLUP-RI and GBLUP-RAE for the genetic configuration Dev. and Main+Dev., for which group-specific QTL deviation effects were simulated (Figure 2). For instance, considering genetic configuration Dev., a mean accuracy of 0.77 was obtained for MAGBLUP-RI and MAGBLUP-RAE compared to 0.68 for GBLUP-RI and GBLUP-RAE. When considering genetic configuration Main, for which only main QTL allele effects were simulated, GBLUP-RI, GBLUP-RAE, and MAGBLUP-RAE slightly outperformed MAGBLUP-RI: a mean accuracy of 0.70 was obtained for GBLUP-RI, GBLUP-RAE, and MAGBLUP-RAE, compared to 0.68 for MAGBLUP-RI. Similar trends were observed using the standardized RMSP: a model with a higher accuracy tended to have a lower standardized RMSP, and vice versa (Figure S2).

Figure 2.

Boxplots of mean accuracies (evaluated by CV over 20 HO replicates) obtained using GBLUP-RI, GBLUP-RAE, MAGBLUP-RI, and MAGBLUP-RAE for 50 traits simulated according to each type of genetic configuration (Main, Dev., and Main+Dev.; see Table 1).

GBLUP-RI, MAGBLUP-RI, and MAGBLUP-RAE were then compared for their genomic prediction accuracy using the SHO CV procedure, which aimed at evaluating the effect of the composition of the TS in terms of genetic backgrounds (D, F, and A) to predict a given PS. This procedure was applied to 50 simulated traits for each genetic configuration. We present the results for genetic configuration Main+Dev. (Table 3); the results for configurations Main and Dev. are reported in Tables S2 and S3, respectively.

Table 3. Mean accuracies over 50 traits simulated according to genetic configuration Main+Dev. (see Table 1) and 20 CV replicates (SHO method), obtained using GBLUP-RI, MAGBLUP-RI, and MAGBLUP-RAE.

	GBLUP-RI	MAGBLUP-RI	MAGBLUP-RAE
DFA_DFA	0.57 (0.11)	0.60 (0.12)	0.60 (0.12)
A_D	0.41 (0.07)	0.41 (0.08)	0.42 (0.08)
DFA_D	0.40 (0.08)	0.42 (0.09)	0.42 (0.09)
DF_D	0.41 (0.08)	0.42 (0.09)	0.42 (0.08)
D_D	0.49 (0.07)	–	–
F_D	0.13 (0.13)	–	–
A_F	0.48 (0.09)	0.49 (0.08)	0.50 (0.08)
DFA_F	0.46 (0.10)	0.48 (0.08)	0.48 (0.09)
DF_F	0.44 (0.11)	0.46 (0.09)	0.47 (0.09)
D_F	0.09 (0.13)	–	–
F_F	0.54 (0.08)	–	–
A_A	0.52 (0.06)	0.59 (0.07)	0.60 (0.06)
DFA_A	0.48 (0.04)	0.54 (0.06)	0.55 (0.05)
DF_A	0.40 (0.05)	0.41 (0.05)	0.41 (0.05)
D_A	0.29 (0.07)	–	–
F_A	0.39 (0.08)	–	–

SD over the 50 mean accuracies (computed over 20 CV replicates) are shown between brackets. “–” indicates that a model could not be applied for the given configuration.

For all models and regardless of the genetic configuration, the highest mean accuracy was obtained for scenario DFA_DFA, for which the PS and TS composition are balanced between the three genetic backgrounds. To predict a specific pure genetic background (D or F), the highest accuracies were achieved when the TS was trained on individuals from the same genetic background. The lowest accuracies were obtained for across-group scenarios (F_D or D_F), while across-genetic backgrounds scenarios involving admixed lines led to intermediate accuracies (A_D or A_F). When considering multigroup TSs, with an equal contribution of both Dent and Flint genetic groups (DF_D, DAF_D, and A_D or DF_F, DAF_F, and A_F), including admixed individuals either improved or led to similar accuracies compared to including only pure individuals. Note that any TS including only admixed individuals can be considered as a multigroup TS, since admixed individuals represent both groups. When predicting admixed lines, using an admixed TS (A_A) led to higher accuracies than using all genetic background in the TS (DFA_A), or pure individuals only (D_A, F_A, or DF_A).

MAGBLUP-RI and MAGBLUP-RAE were considered as an alternative to GBLUP-RI for multigroup TSs. When group-specific allele effects were simulated, as in genetic configuration Main+Dev., MAGBLUP-RAE generally outperformed MAGBLUP-RI, itself outperforming GBLUP-RI. For instance, in scenario A_F, the average accuracy was 0.48 for GBLUP-RI, 0.49 for MAGBLUP-RI, and 0.50 for MAGBLUP-RAE. As expected, the gain in accuracy was higher when MAGBLUP-RI and MAGBLUP-RAE were used to predict admixed lines. For instance, in scenario A_A, the average accuracy was 0.52 for GBLUP-RI, 0.59 for MAGBLUP-RI, and 0.60 for MAGBLUP-RAE.

Application to real traits

Variance components were estimated using the four models for five traits and are summarized in Table 4. Residual variance estimates were comparable between models for all traits. The genetic variance ${\sigma }_G^2$ estimated using GBLUP-RI can be compared to the group-specific genetic variances ${\sigma }_{G_D}^2$ and ${\sigma }_{G_F}^2$ estimated using MAGBLUP-RI. For all traits but MF, ${\sigma }_G^2$ was larger than ${\sigma }_{G_D}^2$ and ${\sigma }_{G_F}^2$. For instance, ${\sigma }_G^2$ was estimated at 19.51 for FF while ${\sigma }_{G_D}^2$ and ${\sigma }_{G_F}^2$ were estimated at 17.69 and 15.99, respectively. The segregation variance estimates ${\sigma }_S^2$ were always smaller than group-specific genetic variances for all traits, but were substantial, especially for PH. For MAGBLUP-RAE, ${\sigma }_U^2$ was always larger than ${\sigma }_{U_D}^2$ and ${\sigma }_{U_F}^2$, which suggests a minor contribution of group-specific deviation effects within this data set. For instance, ${\sigma }_U^2$ was estimated as being equal to 37.90 for MF using MAGBLUP-RAE, while ${\sigma }_{U_D}^2$ and ${\sigma }_{U_F}^2$ were estimated as being equal to 2.64 and 0.00, respectively. The variance component due to Flint deviation effects was lower than the component due to Dent deviation effects for all traits but TNL. The sum of the genetic components estimated by MAGBLUP-RAE (i.e., ${\sigma }_U^2+{\sigma }_{U_D}^2+{\sigma }_{U_F}^2$) was always approximately equal to the genetic component estimated by GBLUP-RAE (i.e., ${\sigma }_U^2$).

Table 4. Variance components of real traits estimated by GBLUP-RI, GBLUP-RAE, MAGBLUP-RI, and MAGBLUP-RAE using all 970 lines.

Model	Variance	MF	FF	PH	ELN	TNL
GBLUP-RI	${\sigma }_G^2$	13.95 (1.26)	19.51 (1.86)	640.35 (58.72)	1.22 (0.11)	1.74 (0.16)
	${\sigma }_E^2$	3.77 (0.51)	2.89 (0.51)	114.97 (19.69)	0.32 (0.05)	0.46 (0.06)
MAGBLUP-RI	${\sigma }_S^2$	3.56 (1.93)	4.60 (2.25)	312.28 (139.21)	0.49 (0.24)	0.43 (0.26)
	${\sigma }_{G_D}^2$	14.36 (1.66)	17.69 (1.96)	583.61 (69.43)	1.16 (0.14)	1.52 (0.19)
	${\sigma }_{G_F}^2$	12.10 (1.46)	15.99 (1.82)	487.25 (60.39)	1.11 (0.14)	1.71 (0.20)
	${\sigma }_E^2$	3.63 (0.52)	3.46 (0.58)	131.00 (21.51)	0.32 (0.05)	0.46 (0.07)
GBLUP-RAE	${\sigma }_U^2$	40.53 (3.66)	51.53 (4.41)	1779.59 (158.51)	3.53 (0.33)	5.03 (0.46)
	${\sigma }_E^2$	3.77 (0.51)	3.59 (0.56)	126.40 (20.44)	0.33 (0.05)	0.47 (0.06)
MAGBLUP-RAE	${\sigma }_U^2$	37.90 (3.91)	48.89 (4.64)	1567.70 (183.04)	3.29 (0.35)	4.60 (0.49)
	${\sigma }_{U_D}^2$	2.64 (3.13)	2.38 (3.66)	246.96 (152.00)	0.27 (0.29)	0.12 (0.40)
	${\sigma }_{U_F}^2$	0.00 (3.33)	0.01 (3.90)	0.07 (155.90)	0.02 (0.30)	0.33 (0.42)
	${\sigma }_E^2$	3.81 (0.51)	3.65 (0.56)	127.53 (20.53)	0.32 (0.05)	0.47 (0.06)

SE are shown between brackets.

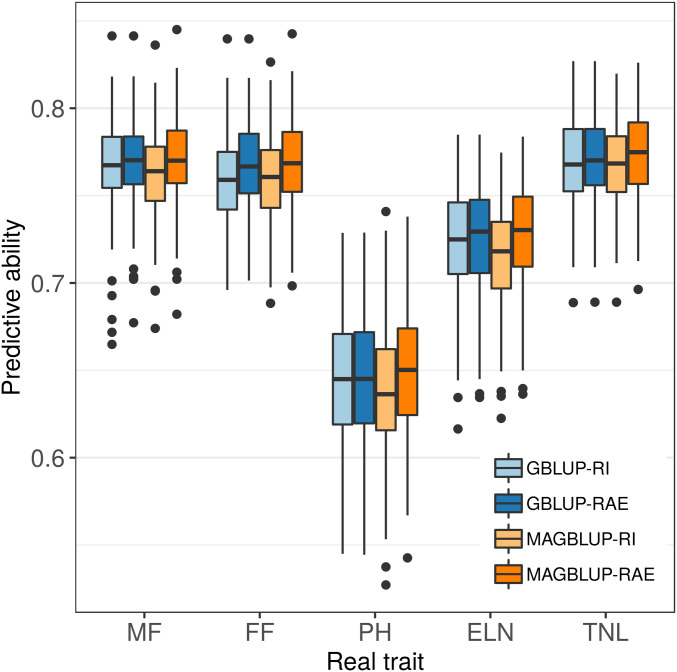
The four models were compared for their predictive ability using the HO CV procedure applied to the five real traits (Figure 3). Lower predictive abilities were obtained for PH compared to the four other traits. The four models led to very similar predictive abilities no matter the trait and the population sample evaluated, but the following ranking was generally observed (best to worst): MAGBLUP-RAE, GBLUP-RAE, GBLUP-RI, and MAGBLUP-RI. For instance, with MF, the average predictive ability was equal to 0.768 for MAGBLUP-RAE, 0.767 for GBLUP-RAE, 0.764 for GBLUP-RI, and 0.761 for MAGBLUP-RI. Like for simulated traits, similar trends were observed using the standardized RMSP: a model with a higher predictive ability tended to have a lower standardized RMSP, and vice versa (Figure S3).

Figure 3.

Boxplots of predictive abilities obtained by CV (HO method with 100 replicates) for GBLUP-RI, GBLUP-RAE, MAGBLUP-RI, and MAGBLUP-RAE on real traits.

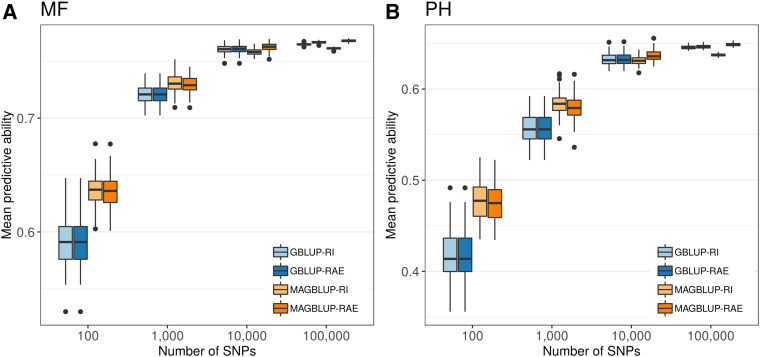
The effect of the number of SNPs used to compute the covariance matrices of each GS model was investigated by applying the HO CV procedure to GBLUP-RI, GBLUP-RAE, MAGBLUP-RI, and MAGBLUP-RAE, with covariance matrices computed using SNP samples of various densities. Boxplots of mean predictive abilities are presented in Figure 4 for MF and PH, and in Figure S4 for FF, ELN, and TNL. With small SNP sample sizes, MAGBLUP-RI and MAGBLUP-RAE outperformed GBLUP-RI and GBLUP-RAE (e.g., for MF, the predictive ability was of 0.59 for GBLUP-RI and GBLUP-RAE, and 0.64 for MAGBLUP-RI and MAGBLUP-RAE), and this advantage tended to decrease with larger SNP sample sizes.

Figure 4.

Boxplots of mean predictive abilities (evaluated by CV over 100 HO replicates) obtained using GBLUP-RI, GBLUP-RAE, MAGBLUP-RI, and MAGBLUP-RAE for (A) MF and (B) PH, with covariance matrices computed using SNP samples (100 replicates) of various densities: 100, 1000, 10,000, and 100,000 SNPs.

The effect of genetic structure on the predictive ability was then evaluated using the SHO CV procedure applied to the five real traits. The predictive abilities obtained are summarized in Table 5 for MF and PH, and in Tables S4–S6 for FF, ELN, and TNL, respectively. Some results were consistent with the SHO results on simulated traits: the highest predictive abilities were obtained for scenario DFA_DFA, while the across-group scenarios (F_D and D_F) led to the lowest predictive abilities when predicting a given group-specific PS. Contrary to what was observed on simulated traits, applying genomic predictions within a given genetic background did not always lead to the highest predictive abilities. For instance, when a Flint PS was predicted using Flint lines for PH (F_F), the average GBLUP-RI predictive ability was lower (0.37) than when using admixed lines (A_F, with 0.41). Compared to simulated traits, a larger asymmetry was observed between across-group scenarios, as Flint lines were better predicted by Dent lines than the opposite (e.g., GBLUP-RI predictive ability of 0.60 and 0.33 for MF with scenarios D_F and F_D, respectively). When considering multigroup TSs with an equal contribution of both Dent and Flint genetic groups (DF_D, DFA_D, and A_D or DF_F, DFA_F, and A_F), including admixed individuals sometimes depreciated predictive abilities compared to including only pure individuals, unlike with simulated traits. When predicting an admixed PS, using admixed lines (A_A) was not necessarily the best option as a higher GBLUP-RI predictive ability was observed when using a TS including both Dent and Flint lines (DF_A with 0.57) compared to using A_A (0.55) for MF. When comparing genomic prediction models, GBLUP-RI and MAGBLUP-RAE reached very similar levels of predictive ability and were generally superior to those obtained using MAGBLUP-RI, as observed in genetic configuration Main for simulated traits.

Table 5. Mean predictive abilities over 100 CV replicates (SHO method) for MF and PH using GBLUP-RI, MAGBLUP-RI, and MAGBLUP-RAE.

	MF			PH
	GBLUP-RI	MAGBLUP-RI	MAGBLUP-RAE	GBLUP-RI	MAGBLUP-RI	MAGBLUP-RAE
DFA_DFA	0.76 (0.04)	0.75 (0.04)	0.76 (0.04)	0.57 (0.06)	0.57 (0.06)	0.57 (0.06)
A_D	0.60 (0.06)	0.59 (0.06)	0.60 (0.06)	0.34 (0.09)	0.32 (0.09)	0.34 (0.09)
DFA_D	0.63 (0.06)	0.62 (0.05)	0.64 (0.05)	0.41 (0.08)	0.40 (0.08)	0.41 (0.08)
DF_D	0.66 (0.05)	0.65 (0.05)	0.67 (0.05)	0.44 (0.08)	0.43 (0.08)	0.43 (0.08)
D_D	0.70 (0.04)	–	–	0.52 (0.06)	–	–
F_D	0.33 (0.11)	–	–	0.07 (0.10)	–	–
A_F	0.67 (0.05)	0.65 (0.05)	0.67 (0.05)	0.41 (0.08)	0.39 (0.09)	0.41 (0.08)
DFA_F	0.71 (0.05)	0.69 (0.05)	0.71 (0.05)	0.37 (0.08)	0.33 (0.09)	0.35 (0.09)
DF_F	0.70 (0.05)	0.68 (0.05)	0.69 (0.05)	0.35 (0.08)	0.33 (0.09)	0.34 (0.09)
D_F	0.60 (0.07)	–	–	0.15 (0.11)	–	–
F_F	0.69 (0.05)	–	–	0.37 (0.07)	–	–
A_A	0.55 (0.06)	0.53 (0.07)	0.55 (0.07)	0.39 (0.08)	0.37 (0.08)	0.38 (0.08)
DFA_A	0.56 (0.08)	0.53 (0.09)	0.55 (0.08)	0.37 (0.08)	0.35 (0.08)	0.36 (0.08)
DF_A	0.57 (0.08)	0.55 (0.08)	0.56 (0.08)	0.39 (0.08)	0.38 (0.09)	0.38 (0.08)
D_A	0.53 (0.07)	–	–	0.36 (0.08)	–	–
F_A	0.52 (0.08)	–	–	0.38 (0.06)	–	–

SD over the predictive abilities of the 100 CV replicates are shown between brackets. “–” indicates that a model could not be applied for the given configuration.

Discussion

Modeling group-specific allele effects in admixed populations

We developed two genomic prediction models adapted to the prediction of admixed individuals.

MAGBLUP-RI was derived using a formalism in which the genotypic information at QTL is random, and is thus in line with the animal model (Henderson 1984) and the decomposition of variance in admixed populations proposed by Lo et al. (1993) and García-Cortés and Toro (2006). We proposed estimators of the covariance matrices that take advantage of both genotypic information and local admixtures, unlike Strandén and Mäntysaari (2013) and Makgahlela et al. (2013), who adapted these models using global admixture proportions and a standard kinship matrix estimated with SNPs. For given genetic groups A and B, the model is expressed as a variance component model including a segregation variance ${\sigma }_S^2$ and two group-specific genetic variances ${\sigma }_{G_A}^2$ and ${\sigma }_{G_B}^2$. The segregation variance ${\sigma }_S^2$ was presented by Lande (1981), Lo et al. (1993), and Lynch and Walsh (1998), and corresponds to a part of the additional variance observed in an admixed population that is due to contrasted mean QTL effects between groups. It depends on two factors: the differentiation of allele frequencies between groups and the existence of group-specific allele effects. Note that the additional variance observed in admixed populations also results from the variability in admixture proportions of individuals, which is accounted for in the fixed part of the model.

MAGBLUP-RAE was derived using a formalism in which SNP allele effects are random, and is thus is line with a Bayesian conception of genomic prediction models (Meuwissen et al. 2001; Gianola et al. 2009). Using this formalism, it is possible to allow for genetic covariances between individuals from different groups, assuming that SNP allele effects are at least partly conserved between groups (Karoui et al. 2012; Lehermeier et al. 2015). Rather than modeling directly covariances between effects across groups, we re-parametrized QTL allele effects into a main effect and group-specific deviations, as proposed by Schulz-Streeck et al. (2012), de los Campos et al. (2015), Technow and Totir (2015), and Veturi et al. (2019). Here, also, the main innovation of our model lies in the valorization of genomic data and local admixtures, whereas other methods based on the second formalism only accounted for distinct genetic groups. MAGBLUP-RAE could be expressed as a variance component model including a component that is due to main SNP allele effects ${\sigma }_U^2$ and two components that are due to group-specific deviation effects ${\sigma }_{U_A}^2$ and ${\sigma }_{U_B}^2$. These components can be used to better understand the genetic architecture of a given trait as they provide insights concerning the conservation of SNP allele effects across genetic groups. This information is tightly linked to the concept of genetic correlation between genetic groups, which is an important parameter to consider when applying GS in a structured population (Porto-Neto et al. 2015; Wientjes et al. 2017).

Genomic prediction models MAGBLUP-RI and MAGBLUP-RAE differed in terms of the origin of genetic covariance between individuals. According to MAGBLUP-RI, the genetic value of a pure individual from a given group A is correlated with those of other group A individuals and with those of admixed individuals. However, no information can be shared with a pure individual of the alternative group B (i.e., an individual from group A cannot contribute to the prediction of an individual from group B, and conversely), as a null kinship is assumed between individuals coming from different groups. The genetic value of an admixed individual is correlated with those of all types of individuals, including other admixed individuals that do not share any allele ancestry, through the segregation covariance of ${{\displaystyle \mathit{g}}}_S$. According to MAGBLUP-RAE, the genetic value of a pure individual from group A is correlated with those of admixed and group A individuals, but also to individuals belonging to group B as soon as the SNP effects are at least partially conserved between groups (i.e., ${\sigma }_U^2>0$). In such a case an individual from group A can contribute to the prediction of an individual from group B. In conclusion, these two models underline the main sources of genetic covariance between individuals: their kinship, the conservation of QTL alleles effects between groups, and the segregation of allele ancestries within admixed individuals. The extension to more than two groups is straightforward for MAGBLUP-RAE but not for MAGBLUP-RI, as it would require to divide the segregation variance into pairwise components, as shown by Lo et al. (1993) and (García-Cortés and Toro 2006).

The random individual and random allele effect formalisms lead to genomic prediction models with different variance components that are not directly comparable. However, an equivalence between the genomic prediction models obtained from both formalisms can be shown for GBLUP provided that adjustments of the random allele effect formalism are made, as presented by Schreck et al. (2019): the substitution effect ${\beta }_m^1-{\beta }_m^0$ must be directly modeled rather than the effect of each allele, and the genotypes $W_{im}$ must be standardized as $W_{im}^{\text{*}}=\frac{W_{im}-{\widehat{f}}_m}{\sqrt{{\displaystyle {\sum }_{m=1}^M{\widehat{f}}_m\left(1-{\widehat{f}}_m\right)}}}$. In such a case, the matrix that stems from the derivation of the covariance in the random allele effect formalism is the one presented in Equation 3, rather than the IBS matrix presented in Equation 4. Note that this equivalence only holds if the kinship between individuals (an unknown parameter) is estimated following Equation 3, as proposed by VanRaden (2008). Other kinship estimators exist and allow for a similar equivalence provided that another standardization of $W_{im}$ is used in the random allele effect formalism (Astle and Balding 2009; Yang et al. 2010; Speed et al. 2012; Weir and Goudet 2017). Note that kinship can also be estimated by maximum likelihood (Choi et al. 2009; Laporte et al. 2017) in which case no equivalence is possible with the random allele effect formalism. Regarding MAGBLUP, adapting the random allele effect formalism to develop a model equivalent to our MAGBLUP-RI model would require (i) the consistency between the effects modeled in the random allele effect formalism and those observed in the variance components of MAGBLUP-RI (e.g., group-specific substitution effects ${\beta }_{mp}^1-{\beta }_{mp}^0$), (ii) the possibility of defining standardized variables in the random allele effect formalism leading to the estimators proposed in Equations 8–10, and (iii) the definition of group-specific fixed effects. While the first and third conditions are easy to satisfy, the second is problematic for resemblance parameters of the form ${\alpha }_{ij}^p$, as the denominator of Equation 8 is specific of each pair of individuals. Alternatively, one may consider a new formalism in which both individuals and allele effects are considered random. However, for GBLUP, this formalism is not helpful to define a new genomic prediction model (File S2).

Variance components and genomic predictions

Using simulations, MAGBLUP-RI and MAGBLUP-RAE were evaluated for their precision in estimating their respective variance components, as presented in File S3. Both models estimated their variance components accurately.

Regarding genomic prediction, the two MAGBLUP models were compared to the two GBLUP models for the same three genetic configurations using standard CV procedures. Both MAGBLUP-RI and MAGBLUP-RAE led to higher accuracies than GBLUP-RI and GBLUP-RAE when group-specific QTL allele effects were simulated, and the gain was the highest for the genetic configuration with QTL allele effects drawn independently within each group. To quantify the minimum relative size of the deviation effects (compared to the main effects) required to observe a gain in precision between the two MAGBLUP models and the two GBLUP models, additional genetic configurations with increasing magnitude of deviation effects were tested. Deviation effects that were of the order of half the size of the main effects allowed for a substantial gain in accuracy (Figure S5). When evaluated for the genetic configuration with conserved QTL allele effects between groups, MAGBLUP-RAE led to accuracies similar to GBLUP-RI and GBLUP-RAE, while MAGBLUP-RI resulted in slightly lower accuracies. These results indicated that MAGBLUP-RAE is more robust than MAGBLUP-RI over a wide variety of genetic configurations. This may be explained by the possibility for genetic information to be shared between groups, which gives a substantial advantage when QTL allele effects are conserved between groups, as discussed by Lehermeier et al. (2015). These simulations also show evidence of the robustness of GBLUP-RI and GBLUP-RAE with respect to the heterogeneity of SNP allele effects across groups, as the gain in accuracy did not exceed 0.15 in the genetic configuration Dev., where allele effects are drawn independently between groups. The robustness of all genomic prediction models to a nonnormal distribution of allele effects was also investigated by comparing the accuracy of the models for two alternative genetic configurations based on the Main+Dev. genetic configuration, as presented in Figure S6. The first genetic configuration included a QTL with a large substitution effect, partially conserved between the Dent and Flint genetic groups. Here, the gains of MAGBLUP models over GBLUP models were slightly reduced. The second genetic configuration included 10% of the QTL with an effect that depends solely on allele ancestry. Such effects may result from QTL differentially fixed between groups whose information is captured by polymorphic linked SNPs. Here, the gains of MAGBLUP models over GBLUP models were largely increased.

Using five real traits, MAGBLUP-RI and MAGBLUP-RAE were compared to GBLUP-RI for variance component estimates and genomic prediction accuracy. The genetic variance ${\sigma }_G^2$ estimated with GBLUP was comparable and generally higher than the group-specific variances ${\sigma }_{G_D}^2$ and ${\sigma }_{G_F}^2$ estimated with MAGBLUP-RI. The segregation variance estimates were relatively low for flowering traits compared to group-specific genetic variances, but was substantial for PH. These results suggest a substantial additional variance generated by admixture for PH, which is consistent with the high genotypic variance estimated in the phenotypic analyses for admixed individuals compared to pure genetic groups (Table S1). Using MAGBLUP-RAE, the proportion of variance estimated to be due to main SNP allele effects was much higher than those due to group-specific deviation effects for all traits. These results suggested that the genetic architecture of these five traits consisted of a polygenic background whose QTL allele effects are mainly conserved between the Dent and Flint groups. As expected on the basis of these results, the two MAGBLUP models did not lead to a substantial gain in accuracy, even though MAGBLUP-RAE allowed the highest predictive abilities for all traits.

Previous QTL mapping and GWAS studies had shown differences in terms of genetic architecture between Dent and Flint groups for flowering traits (Giraud et al. 2014, 2017; Rincent et al. 2014). In a previous study based on the same data set, Rio et al. (2020) identified QTL showing a group heterogeneity of allele effects for flowering traits. Based on these results, we could have expected that the proportion of variance due to group-specific deviation effects would be higher for MF and FF. One possible explanation for the discrepancy between expected and observed results is that part the heterogeneity of allele effects results from interactions between QTL and the genetic background. In presence of such interactions, SNP alleles effects would not be conserved between pure groups (due to a different allele ancestry and genetic background), nor between pure and admixed individuals with the same allele ancestry. The two MAGBLUP models will improve GS accuracy if group-specific deviation effects are mainly caused by local genomic differences, as shown in the simulation study, but will be of limited interest if the deviation effects are caused by interactions between QTL and the genetic background. Several results support this hypothesis for the present experimental data: (i) QTL interacting with the genetic background were detected by Rio et al. (2020) for MF and FF using this data set; (ii) epistatic interactions contributed significantly to the variability, as tested using a likelihood-ratio test on a model adapted from Vitezica et al. (2017) for MF, FF, and PH (Table S7); and (iii) variance components estimated using MAGBLUP-RAE, trained only on pure Dent and Flint individuals (i.e., without admixed individuals), suggested a higher contribution of group-specific deviation effects than that suggested by the variance estimates obtained when including admixed individuals (Table S6 and Table 4). In such data, epistatic interactions with the genetic background may contribute to group-specific deviation effects, while the presence of admixed individuals is likely to minimize their contribution. In such a situation, it could be more appropriate to perform genomic predictions using models that account directly for epistatic interactions between QTL (Vitezica et al. 2017), or other methods accounting for various types of heterogeneity between genetic groups, such as computing an alternative covariance matrix based on specific kernel functions (Heslot and Jannink 2015; Ramstein and Casler 2019). A simple modeling of epistatic interactions between QTL pairs according to Vitezica et al. (2017) led to limited gains in terms of predictive ability for flowering traits using this data set (Figure S7). It suggests the need for a more complex modeling of epistatic interactions between QTL that also account for allele ancestry.

As discussed by Ibánez-Escriche et al. (2009) and Technow et al. (2012), the modeling of group-specific allele effects would probably be more beneficial compared to standard GBLUP for data sets genotyped at low to medium density. This hypothesis is based on the idea that LD between SNPs and QTL is more likely to differ between groups at low densities, leading to a heterogeneity of group-specific allele effects estimated at SNPs, even when the true QTL allele effects are conserved between groups. This hypothesis was confirmed using this data set, showing a substantial advantage of MAGBLUP-RI and MAGBLUP-RAE compared to GBLUP when subsets of 100 and 1000 SNP were used. Alternatively, in presence of true different QTL allele effects between groups, a high SNP density is likely to enhance the robustness of GBLUP, as SNPs showing a high differentiation in terms of allele frequencies may be used to adjust the group specificity of QTL effects.

Benefits from admixed individuals in multigroup TSs

The effect of the composition of the TS was evaluated using both simulated and real traits, based on the SHO CV procedure that leverages the contribution of each genetic background (Dent, Flint, or admixed) to the TS and the PS. Several observations were in accordance with the results of Rio et al. (2019): (i) the best accuracies were obtained in scenarios for which all genetic backgrounds were represented in the TS and the PS, (ii) a given group-specific PS was generally best predicted using a TS including only individuals from the same genetic group, (iii) applying across-group predictions could highly depreciate genomic prediction accuracy, and (iv) multigroup TSs showed a relatively high accuracy no matter the target PS. Interestingly, Flint lines were better predicted by Dent lines than the other way round for all real traits. This asymmetry may result from the higher contribution of Dent-specific compared to Flint-specific deviation effects as quantified through the estimates of ${\sigma }_{U_D}^2$ and ${\sigma }_{U_F}^2$ (see Table S8 and Table 4), making Dent lines more difficult to predict by the Flint lines than the other way round. These results suggest that MAGBLUP-RAE can be useful to forecast the accuracy of across-group predictions.

One could question whether including admixed individuals in multigroup TSs, instead of assembling pure individuals, would improve genomic prediction accuracy when predicting both admixed and pure individuals. Based on simulated traits, applying MAGBLUP-RI or MAGBLUP-RAE instead of using GBLUP-RI led to limited gains when predicting Dent or Flint lines, but greatly improved the accuracy when predicting admixed lines. For real traits, the predictive ability was little affected by the GS model or the constitution of the TS when predicting admixed individuals, even though a TS including only Dent or Flint lines generally led to the lowest accuracies. The inclusion of admixed lines in multigroup TSs, rather than assembling pure individuals, was not always beneficial for real traits, unlike previous results based on simulations presented by Toosi et al. (2013) and on simulated traits in this study. Here, also, the existence of epistatic interactions between QTL and the genetic background may explain the discrepancy between the results on simulated and real traits. Such interactions would be shuffled within admixed individuals and would limit the amount of genetic information to be shared between an admixed and a pure individual. In such context, the main source of genetic information to predict a given pure individual would consist in other individuals from the same genetic group.

In conclusion, MAGBLUP-RI and MAGBLUP-RAE showed their complementarity as genomic prediction models in the context of admixed populations and traits with QTL showing group-specific allele effects. While MAGBLUP-RI can be used to evaluate the segregation variance generated by admixture, MAGBLUP-RAE can be used to disentangle the variance that is due to main allele effects from the variability that is due to group-specific deviation allele effects. In breeding, admixed individuals are generated on many occasions by breeders when (i) exotic genetic pools are crossed to elite germplasm to sustain long-term genetic gain, (ii) progenitors are derived from commercial hybrids to assemble group-specific favorable alleles, or (iii) when breeding company mergers go along with genetic resources mergers. Beyond breeding, the growing interest of the quantitative genetics community in admixture should be accompanied by an increasing availability of genomic data for which information on allele ancestry will be available.