Skip to main content
PMC home page
Microorganisms logoLink to Microorganisms
. 2020 Jul 30;8(8):1158. doi: 10.3390/microorganisms8081158

Forecasting the Spreading of COVID-19 across Nine Countries from Europe, Asia, and the American Continents Using the ARIMA Models

Ovidiu-Dumitru Ilie 1,*, Roxana-Oana Cojocariu 1, Alin Ciobica 1,*, Sergiu-Ioan Timofte 2, Ioannis Mavroudis 3,4, Bogdan Doroftei 5
PMCID: PMC7463904  PMID: 32751609

Abstract

Since mid-November 2019, when the first SARS-CoV-2-infected patient was officially reported, the new coronavirus has affected over 10 million people from which half a million died during this short period. There is an urgent need to monitor, predict, and restrict COVID-19 in a more efficient manner. This is why Auto-Regressive Integrated Moving Average (ARIMA) models have been developed and used to predict the epidemiological trend of COVID-19 in Ukraine, Romania, the Republic of Moldova, Serbia, Bulgaria, Hungary, USA, Brazil, and India, these last three countries being otherwise the most affected presently. To increase accuracy, the daily prevalence data of COVID-19 from 10 March 2020 to 10 July 2020 were collected from the official website of the Romanian Government GOV.RO, World Health Organization (WHO), and European Centre for Disease Prevention and Control (ECDC) websites. Several ARIMA models were formulated with different ARIMA parameters. ARIMA (1, 1, 0), ARIMA (3, 2, 2), ARIMA (3, 2, 2), ARIMA (3, 1, 1), ARIMA (1, 0, 3), ARIMA (1, 2, 0), ARIMA (1, 1, 0), ARIMA (0, 2, 1), and ARIMA (0, 2, 0) models were chosen as the best models, depending on their lowest Mean Absolute Percentage Error (MAPE) values for Ukraine, Romania, the Republic of Moldova, Serbia, Bulgaria, Hungary, USA, Brazil, and India (4.70244, 1.40016, 2.76751, 2.16733, 2.98154, 2.11239, 3.21569, 4.10596, 2.78051). This study demonstrates that ARIMA models are suitable for making predictions during the current crisis and offers an idea of the epidemiological stage of these regions.

Keywords: prevalence, incidence, Europe, Asia, the American continents, COVID-19, SARS-CoV-2, epidemiological

1. Introduction

The outbreak with the new coronavirus (COVID-19) caused by severe acute respiratory syndrome (SARS-CoV-2) has led to a ‘global pandemic’ due to its unprecedented speed of spreading worldwide. Since patient zero that was reported back in mid-November, over ten million people from two hundred and sixteen territories were identified as SARS-CoV-2-infected patients [1].

Significant discoveries have been made in this context during these last nine months. During this period, the clinical panel has been established [2,3,4,5,6,7,8,9]. However, the early studies have also revealed a low [3,4,5,10], up to medium [6,7,8,9] incidence of gastrointestinal deficiencies. The most common symptom was diarrhea [11,12,13,14], which suggests a potential route of action of COVID-19 at the level of the digestive tract.

Unfortunately, until the 10th of July 2020, more than half a million people have died, predisposition being higher in people suffering from chronic diseases and, especially elderly [15]. However, the number of people confirmed positive varies due to finite capacities in epidemiological surveillance between countries.

It can be said without a shadow of a doubt, that this member of the zoonotic coronavirus family has spread over the entire world until the present day. Given that scientists are in a fight against the clock, the need for a sustainable and reliable strategy for planning health infrastructure to control the spread is crucial. This need is all the more imperative as there is no SARS-CoV-2 treatment/vaccine [15].

Modeling daily cases are pivotal for management and future directions. Estimating COVID-19 possible evolution or regression through mathematical and statistical models is groundbreaking to determine short and long-term case estimates. Such approaches are viable not only to predict the COVID-19 spreading course, but also to allocate the resources necessary to restrict the virus spreading [15].

Distinct approaches have been applied with relatively high accuracy for different prediction purposes. Some examples are represented by statistical methods aiming to predict epidemic cases. These include time series [16], or simulation models [17,18], multivariate linear regression [19], backpropagation neural network [20,21,22], and gray forecasting [23,24].

Any epidemiology evolution is defined and influenced by different factors, more precisely by a tendency of randomness. Retrospectively, the usage of the statistics tools above-mentioned are insufficient for analysis and are difficult to generalize. This is why the Automatic Regressive Integrated Moving Average (ARIMA) model has been successfully applied at a much larger scale in various fields, mainly due to its easy-to-use concept and utility algorithm [25].

Therefore, the present study aims to estimate the prevalence trend in Ukraine, Romania, the Republic of Moldova, Serbia, Bulgaria, and Hungary as Central European countries. Moreover, we will also consider the most affected countries presently, such as USA, Brazil, and India.

2. Materials and Methods

2.1. Data

The daily prevalence data of COVID-19 was taken from The Ministry of Internal Affairs of Romania (https://www.mai.gov.ro/informare-covid-19-grupul-de-comunicare-strategica), World Health Organization (WHO) (https://covid19.who.int/?gclid=CjwKCAjwi_b3BRAGEiwAemPNUYzgrAMkQXN5Z848tjCmGZLJecod03yWxqW_bN248wjgdezXeYg0RoCeFcQAvD_BwE), and European Centre for Disease Prevention and Control (ECDC) (https://www.ecdc.europa.eu/en). MS Excel was used to build a time-series database. Descriptive statistics of the COVID-19 data for the established intervals (10 March and 10 July) are given in Table 1. In order to create an optimum ARIMA model, at least 30 observations are needed [26].

Table 1.

Descriptive statistics on the prevalence and incidence of coronavirus (COVID-19) in the established countries.

(a) Prevalence
Continents Country Mean SE Mean St. Dev Minimum Maximum Skewness Kurtosis
Central and Eastern Europe Ukraine 17,545.34 1424.02 15793.16 1 52,043 0.5836 −0.8257
Romania 13,958.65 837.07 9283.60 25 31,381 −0.0447 −1.1718
Republic of Moldova 6341.02 516.67 5730.20 3 18,666 0.6936 −0.7263
Serbia 8159.77 468.22 5192.87 5 17,342 −0.3619 −1.1779
Bulgaria 2063.34 151.29 1677.90 4 6672 0.7943 −0.0721
Hungary 2618.48 138.75 1538.90 12 4220 −0.5892 −1.2725
South and North America, and South Asia USA 1,242,336.35 80,297.41 890,541.35 696 3,038,325 0.1309 −1.1182
Brazil 405,199.86 45,415.32 503,680.30 25 1,713,160 1.1576 0.0707
India 168,929.42 19,430.70 215,496.91 50 793,802 1.3365 0.7176
(b) Incidence
Continents Country Mean SE Mean St. Dev Minimum Maximum Skewness Kurtosis
Central and Eastern Europe Ukraine 423.10 25.90 287.33 0 1366 0.3931 −0.0052
Romania 255.00 11.65 129.25 6 614 0.2298 −0.0560
Republic of Moldova 151.74 10.03 111.27 0 478 0.7573 0.1075
Serbia 140.98 10.22 113.38 0 445 0.8188 −0.4346
Bulgaria 54.21 5.08 56.44 0 330 1.9756 4.8870
Hungary 34.23 3.09 34.36 0 210 1.6979 4.7398
South and North America, and South Asia USA 24,697.99 1152.30 12,779.70 0 64,630 0.1378 0.8261
Brazil 13,927.92 1307.41 14,499.97 0 54,771 0.8961 −0.3030
India 6453.31 644.93 7152.72 0 26,506 1.1402 0.2809
Open in a new tab

Data analyzed corresponds to the period between 10 March and 10 July. The data set was used to perform and analyze a case estimation model by applying ARIMA that could help us to predict the SARS-CoV-2 evolution in the future.

Therefore, for this study, a time series containing at least 45 data was used to predict COVID-19 prevalence in six Central and Eastern European countries (Romania, Bulgaria, Serbia, Ukraine, Republic of Moldova, and Hungary) was conducted. Furthermore, the same concept was applied for one country from South America (Brazil) and North America (United States of America), and one from South Asia (India) over the next fourteen days with 95% relative confidence intervals (CI).

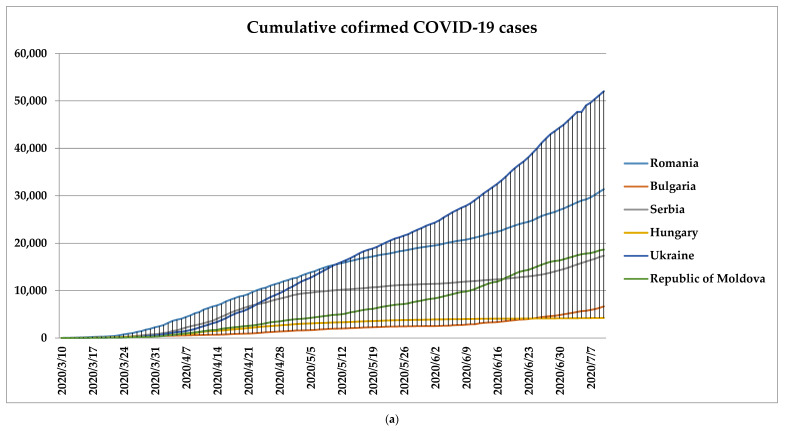
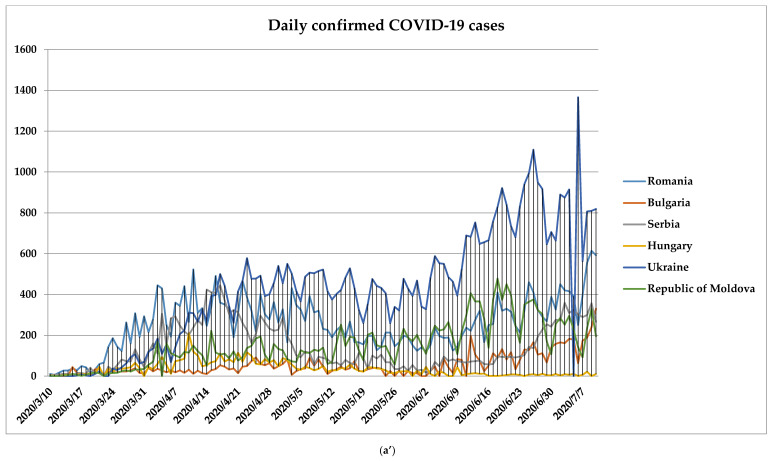
As seen from Figure 1, the COVID-19 outbreak hit Ukraine harder than the other five countries between the established period. The first case in Ukraine was reported on 3 March 2020. In contrast with the related regions, the COVID-19 pandemic had started earlier in Romania (26 February) and later in the other four (4 March in Hungary, 6 March in Serbia, 7 March in the Republic of Moldova, and 8 March in Bulgaria). In Ukraine, the total number of confirmed cases of COVID-19 reported during the period is 52,043, the highest number of new cases reported being 1366 registered on 6 July.

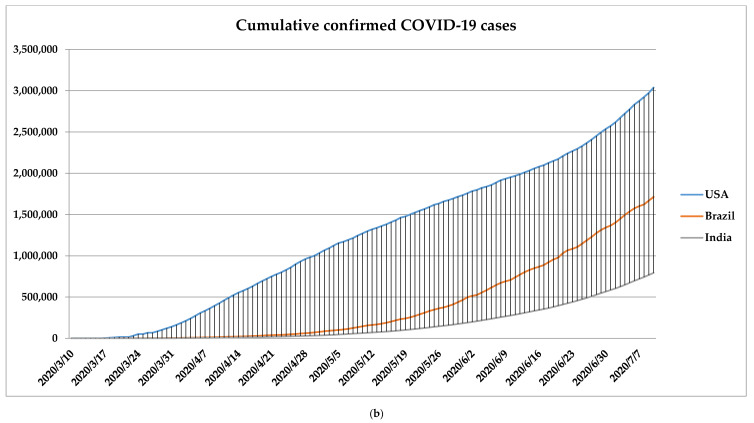
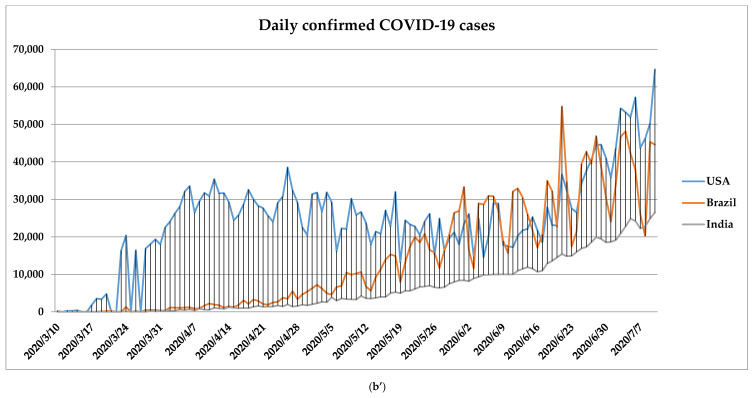
Figure 1.

Figure 1

Figure 1

Figure 1

Figure 1

Open in a new tab

The (a,b) prevalence and (a’,b’) incidence of the COVID-19 within the established countries.

The overall prevalence for Romania was 31,381, the second hardest-hit region, followed by the Republic of Moldova with 18,666, Serbia with 17,342, Bulgaria with 6672, and Hungary with 4220 cases. Analogous, the second highest incidence between the remaining five regions was in Romania with 614 new cases in 9 July, followed by the Republic of Moldova with 478 on 18 June, 445 in Serbia on 17 April, 330 in Bulgaria on 10 July, and 210 in Hungary on 10 April.

On the other hand, the first case reported in the USA took place on 20 January, almost one week later compared with Romania. The second hardest-hit region was Brazil, where the first case was reported on 26 February, while in India on 30 January. The overall prevalence for these three countries is as follows: USA with 3,038,325, Brazil with 1,713,160, and India with 793,892 cases. Concerning the incidence, the highest was as expected in USA with 64,630 on 10 July, followed by Brazil with 54,771 on 21 June, and last, India with 26,506 on 10 July.

2.2. ARIMA Models

A time series is simply a series of time-dependent data points [27] used for analyses dedicated to revealing reliable and meaningful statistical data for the subsequent prediction of values of a series [28]. Since it was introduced by Box and Jenkins approximately half a century ago, ARIMA began to be used at a much larger scale [26].

In most cases, ARIMA is used since it takes into account all trends and periodic changes, even random disturbances. Thus, ARIMA is suitable for a large spectrum of data, from seasonality to cyclicity. In this context can be modeled a temporal dependency in a flexible manner.

Non-seasonal ARIMA models are defined by three parameters (p, d, q) where p is the order of autoregression, d is the degree of differencing, and q the order of moving average [29]. ARIMA offers the possibility to be modified so that can be conducted different and simple AR, I, or MA models.

AR (p) usually explains the present value Yt, unidirectionally it terms of its previous values Yt−1, Yt−2, ..., Yt−p, and the current residuals εt. MA (q) refers to the current value of the time series Yt in terms of its current and previous residuals εt−1, εt−2,…, εt−𝑞. The general formula of AR (p) and MA (q) can be expressed in Equations (1) and (2).

Yt = Φ1Yt−1 + Φ2Yt−2 + … + ΦpYt−p + εt (1)
Yt = θ1 εt−1−θ2 εt−2−… θp εt−p + εt (2)

where:

p—past value;

Φ and θ—parameters that indicate the autoregression, and moving average, respectively;

t—time;

Yt—observed value at a time t;

εt—value of the random shock dependent by t;

p—past value.

In other words, ARMA (p, q) model expresses the current values, as well as its previous ones and residuals linearly. The corresponding formula is given in the below equation:

Yt = α + Φ1Yt−1 + Φ2Yt−2 + … + ΦpYt−p + εt − θ1 εt−1 − θ2 εt−2 − …θp εt − q (3)

where:

α—constant;

εt−1—value of the previous random shock.

2.3. Model Selection

In the present study, three performance criteria entitled Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE) were applied to test the predictive accuracy of the current ARIMA model. Mathematically, the equations for these three criteria are presented above:

RMSE=1n∑t=1net2 (4)
MAE=1n∑t=1n|et| (5)
MAPE=100%n∑i=1n|etyt| (6)

where:

yt—value observed at a time t;

et—difference between values;

n—number of time points;

For a better fit of the data, RMSE, MAE, and MAPE must have low values. All analyses were performed using STATGRAPHICS Centurion (v.18.1.13) software with a statistically significant level of p < 0.005.

3. Results and Discussion

Forecasting the Prevalence of COVID-19 Pandemic Using the ARIMA Model

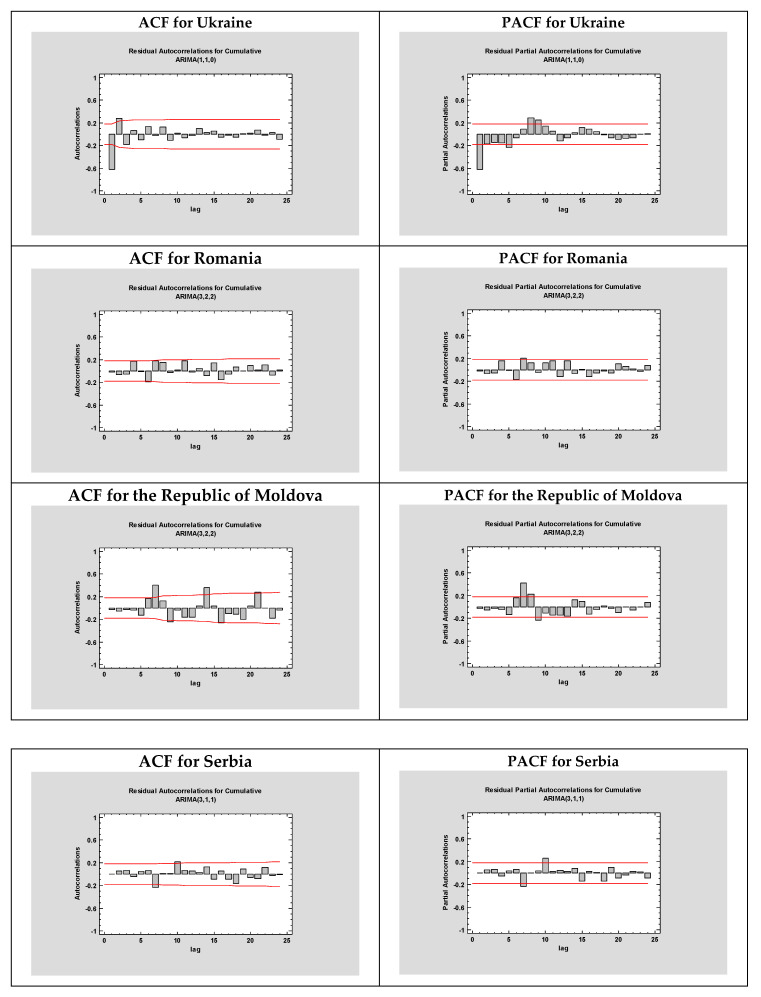
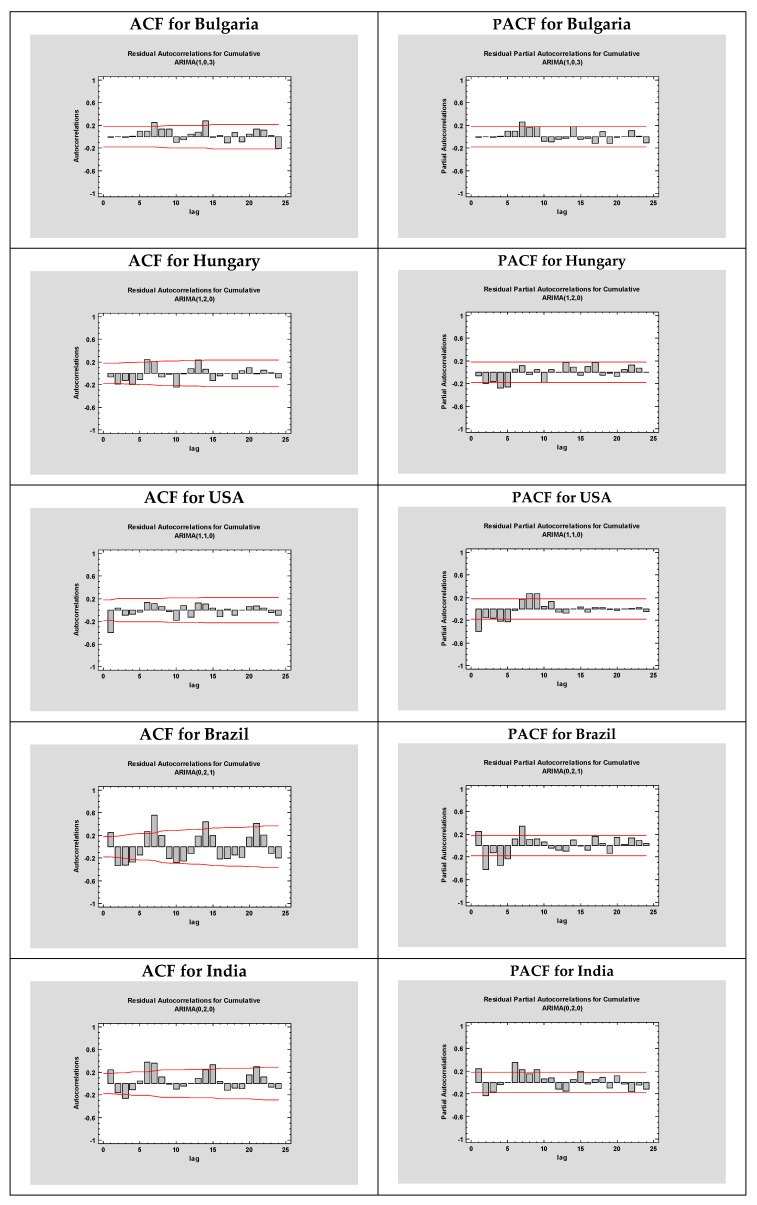
The ARIMA modeling is composed of four repetitive steps: assessment of the model, estimation of parameters, diagnostic checking, and prediction. The first step is to control whether the time series’ mean, variance, and autocorrelation constancy over time are stationary and seasonal for a better accuracy [30]. In this context, Time Series plot, Autocorrelation Function (ACF), and Partial Autocorrelation Function (PACF) (Figure 2) graphs were constructed to verify the seasonality and stationarity. On one hand, ACF can determine whether the previous values from the series are related to the following one, while PACF highlights the degree of correlation between a variable and a lag of the said variable [31]. Estimated autocorrelations for the time series of the established countries are shown in Figure 3. Straight lines represent two standard deviations limits, while bars that extend beyond the lines indicate statistically significant autocorrelations.

Figure 2.

Figure 2

Figure 2

Open in a new tab

The estimated Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) graphs to predict the epidemiological trend of COVID-19 prevalence for Ukraine, Romania, the Republic of Moldova, Serbia, Bulgaria, Hungary, USA, Brazil, and India.

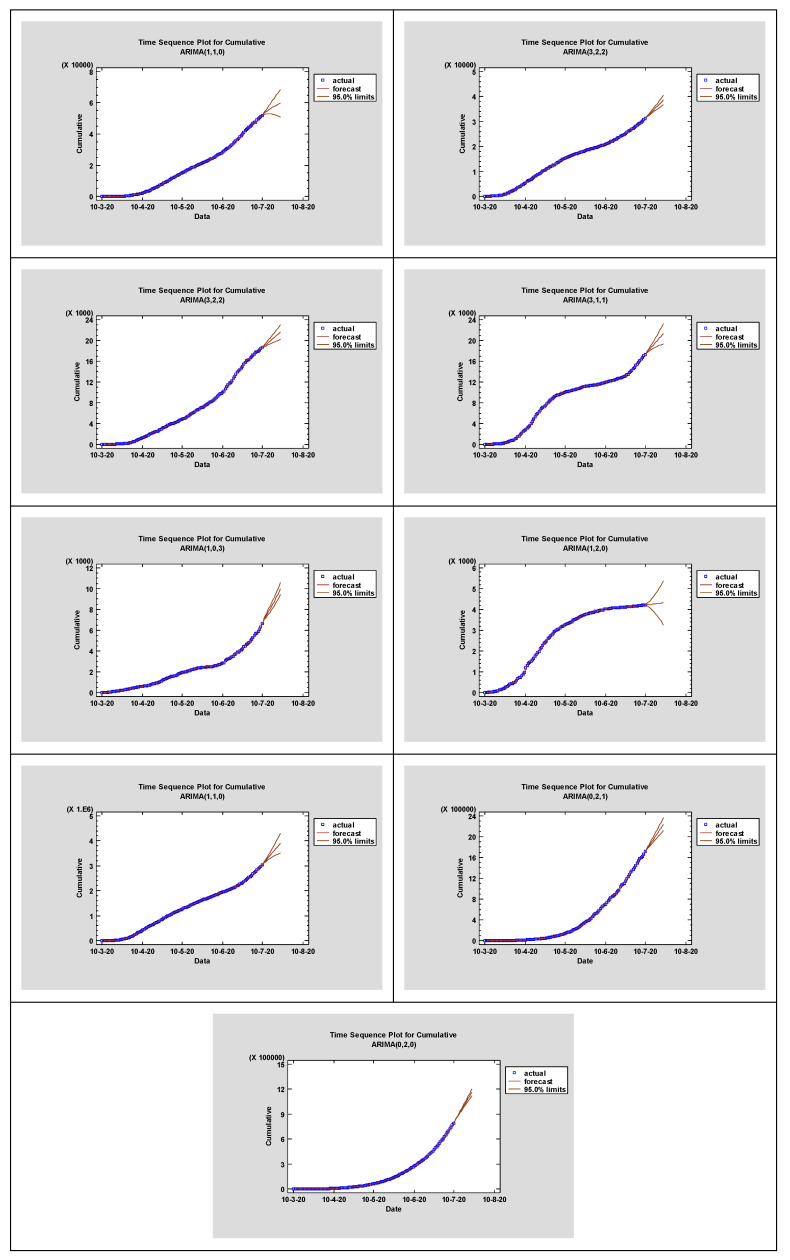
Figure 3.

Figure 3

Open in a new tab

Time-series plots for the best ARIMA models.

Additionally, a series of ARIMA models have been also created, and their performances were compared using various statistical tools. All statistical procedures were performed on the transformed COVID-19 data. ARIMA models with the minimum MAPE values were selected as the best model. Among the tested models, the ARIMA (1, 1, 0), ARIMA (3, 2, 2), ARIMA (3, 2, 2), ARIMA (3, 1, 1), ARIMA (1, 0, 3), ARIMA (1, 2, 0), ARIMA (1, 1, 0), ARIMA (0, 2, 1), and ARIMA (0, 2, 0) models were chosen as the best models for Ukraine, Romania, the Republic of Moldova, Serbia, Bulgaria, Hungary, USA, Brazil, and India. The models fitted the COVID-19 data are presented in Figure 2 and Table 2 and Table 3 with a minimum MAPEUkraine = 4.70244, MAPERomania = 1.40016, MAPERepublic of Moldova = 2.76751, MAPESerbia = 2.16733, MAPEBulgaria = 2.98154, MAPEHungary = 2.11239, MAPEUSA = 3.21569, MAPEBrazil = 4.10596, MAPEIndia = 2.78051.

Table 2.

Comparison of tested Auto-Regressive Integrated Moving Average (ARIMA) models.

Country Model RMSE MAE MAPE
Ukraine (1, 1, 0) 182.403 86.857 4.70244
(0, 2, 0) 184.534 84.6694 4.75145
(3, 2, 0) 140.184 87.0874 4.86564
(3, 0, 0) 140.834 83.9104 5.02043
(2, 2, 0) 141.809 86.6818 5.08194
Romania (3, 2, 2) 72.2811 54.8283 1.40016
(1, 2, 3) 77.4246 57.1017 1.45906
(2, 2, 3) 74.5154 55.2809 1.48125
(3, 2, 3) 76.4564 56.4977 1.52647
(2, 2, 2) 78.7986 58.4657 1.53212
Republic of Moldova (3, 2, 2) 61.1658 43.5817 2.76751
(3, 2, 1) 60.7849 43.5131 2.77257
(2, 2, 1) 60.6597 43.5749 2.77809
(3, 2, 3) 61.6063 43.8593 2.84718
(2, 2, 3) 61.341 43.8542 2.85937
Serbia (3, 1, 1) 43.0079 28.8086 2.16733
(2, 1, 3) 43.0409 29.127 2.17147
(1, 1, 3) 42.8633 29.1174 2.17271
(3, 1, 0) 42.8659 28.847 2.17729
(2, 1, 2) 42.8686 29.1841 2.17814
Bulgaria (1, 0, 3) 33.4732 23.1431 2.98154
(2, 0, 2) 33.7635 23.0537 3.04647
(3, 0, 0) 33.5995 22.8279 3.08918
(3, 2, 0) 35.4064 23.7486 3.08997
(2, 2, 2) 78.7986 58.4657 1.53212
Hungary (1, 2, 0) 23.0452 15.101 2.11239
(0, 2, 3) 21.7985 13.6316 2.15973
(3, 2, 0) 22.6729 14.2714 2.16096
(3, 0, 0) 22.6563 14.488 2.16571
(2, 2, 3) 21.9873 13.6272 2.16876
USA (1, 1, 0) 6539.46 4673.82 3.21569
(0, 2, 0) 6541.2 4710.64 3.2431
(3, 2, 1) 5818.42 4379.88 3.29508
(1, 2, 3) 5868.51 4434.36 3.29553
(2, 2, 3) 5888.31 4430.09 3.29999
Brazil (0, 2, 1) 6134.91 3838.17 4.10596
(2, 1, 0) 6493.37 3521.69 4.14127
(2, 2, 1) 5454.19 3118.73 4.15452
(1, 2, 0) 6515.51 3598.89 4.16568
(3, 2, 1) 5457.52 3082.2 4.1698
India (0, 2, 0) 642.607 416.132 2.78051
(1, 1, 0) 574.812 376.235 2.7951
(2, 1, 0) 570.378 373.247 3.06874
(1, 1, 2) 524.071 358.294 3.19978
(3, 0, 1) 543.562 358.125 3.29689
Open in a new tab

Table 3.

Parameters of ARIMA models.

Country and Best Model Parameters Estimate Standard Error t-Statistic p-Value
Ukraine (1, 1, 0) AR(1) 0.943844 0.0325404 29.0053 0.000000
Romania (3, 2, 2) AR(3) −0.410628 0.103264 −3.97648 0.000122
MA(2) −0.758911 0.0916899 −8.27702 0.000000
Republic of Moldova (3, 2, 2) AR(3) −0.162489 10.6563 −0.0152482 0.987860
MA(2) 0.341459 26.5106 0.0128801 0.989746
Serbia (3, 1, 1) AR(3) 0.241924 1.06252 0.227689 0.820282
MA(1) −0.572339 2.98064 −0.192018 0.848058
Bulgaria (1, 0, 3) AR(1) 1.02769 0.00227845 451.048 0.000000
MA(3) −0.267346 0.0937488 −2.85172 0.005128
Hungary AR(1) −0.401032 0.0836831 −4.79227 0.000005
USA (1, 1, 0) AR(1) 0.99441 0.0217047 45.8154 0.000000
Brazil (0, 2, 1) MA(1) 0.758422 0.0565645 13.4081 0.000000
India (0, 2, 0) no parameter (s)
Open in a new tab

Table 3 shows the parameter estimates for the best models. The p-values of the associated with the parameters are less than 0.005, so the terms are considerably different from zero at the 95.0% CI. The fitted and predicted values are presented in Figure 3. As seen in Table 4, the next 14-day estimate of confirmed cases may be between 52,816–59,679 in Ukraine, 31,838–38,650 in Romania, and 18,836–21,601 in the Republic of Moldova, 17,639–21,313 in Serbia, 6931–10,000 in Bulgaria, 4225–4319 in Hungary, 3.10259 × 106–3.90611 × 106 in USA, 1.75087 × 106–2.24113 × 106 in Brazil, and 8.20308 × 105–116,489 × 106 in India, respectively.

Table 4.

Prediction of total confirmed cases of COVID-19 for the next fourteen days according to ARIMA models with 95% confidence interval.

Ukraine ARIMA (1,1,0) Romania ARIMA (3,2,2) Republic of Moldova ARIMA (3,2,2)
Lower 95% Upper 95% Lower 95% Upper 95% Lower 95% Upper 95%
Period Forecast Limit Limit Period Forecast Limit Limit Period Forecast Limit Limit
11-7-20 52,816.0 52,454.9 53,177.1 11-7-20 31,838.2 31,694.9 31,981.5 11-7-20 18,836.6 18,715.5 18,957.8
12-7-20 53,545.6 52,756.2 54,335.0 12-7-20 32,261.6 32,023.7 32,499.5 12-7-20 19,037.2 18,806.5 19,268.0
13-7-20 54,234.2 52,941.6 55,526.9 13-7-20 32,719.8 32,386.2 33,053.5 13-7-20 19,259.3 18,940.0 19,578.5
14-7-20 54,884.2 53,031.4 56,736.9 14-7-20 33,267.3 32,849.6 33,685.1 14-7-20 19,478.9 19,081.4 19,876.5
15-7-20 55,497.6 53,040.6 57,954.7 15-7-20 33,872.9 33,362.9 34,383.0 15-7-20 19,691.4 19,211.9 20,170.8
16-7-20 56,076.7 52,980.2 59,173.1 16-7-20 34,469.6 33,845.7 35,093.5 16-7-20 19,901.5 19,332.3 20,470.6
17-7-20 56,623.2 52,859.4 60,386.9 17-7-20 35,003.7 34,237.5 35,769.8 17-7-20 20,113.1 19,448.2 20,778.0
18-7-20 57,139.0 52,685.5 61,592.4 18-7-20 35,477.4 34,549.7 36,405.1 18-7-20 20,326.1 19,561.3 21,090.8
19-7-20 57,625.8 52,464.9 62,786.7 19-7-20 35,938.6 34,844.5 37,032.8 19-7-20 20,539.0 19,670.8 21,407.3
20-7-20 58,085.3 52,202.9 63,967.7 20-7-20 36,438.8 35,182.0 37,695.7 20-7-20 20,751.6 19,775.9 21,727.3
21-7-20 58,519.0 51,904.2 65,133.8 21-7-20 36,992.8 35,575.4 38,410.2 21-7-20 20,964.0 19,876.7 22,051.2
22-7-20 58,928.3 51,573.0 66,283.7 22-7-20 37,572.2 35,988.4 39,156.0 22-7-20 21,176.4 19,973.7 22,379.1
23-7-20 59,314.7 51,212.8 67,416.6 23-7-20 38,132.9 36,369.6 39,896.1 23-7-20 21,389.0 20,067.1 22,710.8
24-7-20 59,679.3 50,826.8 68,531.9 24-7-20 38,650.7 36,693.2 40,608.1 24-7-20 21,601.5 20,156.8 23,046.2
Serbia ARIMA (3,1,1) Bulgaria ARIMA (1,0,3) Hungary ARIMA (1,2,0)
Lower 95% Upper 95% Lower 95% Upper 95% Lower 95% Upper 95%
Period Forecast Limit Limit Period Forecast Limit Limit Period Forecast Limit Limit
11-7-20 17,639.6 17,554.5 17,724.8 11-7-20 6931.5 6865.22 6997.79 11-7-20 4225.99 4180.36 4271.62
12-7-20 17,927.0 17,765.1 18,088.8 12-7-20 7179.18 7065.11 7293.25 12-7-20 4233.59 4147.54 4319.64
13-7-20 18,214.2 17,956.8 18,471.6 13-7-20 7405.16 7239.7 7570.63 13-7-20 4240.54 4102.74 4378.34
14-7-20 18,501.8 18,135.5 18,868.0 14-7-20 7610.22 7392.89 7827.55 14-7-20 4247.75 4051.78 4443.73
15-7-20 18,786.8 18,300.4 19,273.2 15-7-20 7820.95 7559.81 8082.1 15-7-20 4254.86 3993.94 4515.78
16-7-20 19,072.0 18,454.5 19,689.5 16-7-20 8037.53 7736.95 8338.1 16-7-20 4262.01 3930.38 4593.64
17-7-20 19,355.4 18,597.4 20,113.5 17-7-20 8260.09 7922.85 8597.34 17-7-20 4269.14 3861.35 4676.93
18-7-20 19,638.3 18,730.5 20,546.1 18-7-20 8488.83 8116.76 8860.89 18-7-20 4276.28 3787.29 4765.27
19-7-20 19,919.9 18,854.1 20,985.8 19-7-20 8723.89 8318.28 9129.5 19-7-20 4283.42 3708.46 4858.38
20-7-20 20,200.7 18,968.8 21,432.6 20-7-20 8965.47 8527.2 9403.73 20-7-20 4290.56 3625.12 4955.99
21-7-20 20,480.4 19,075.0 21,885.8 21-7-20 9213.73 8743.44 9684.02 21-7-20 4297.69 3537.49 5057.89
22-7-20 20,759.2 19,173.2 22,345.2 22-7-20 9468.87 8966.96 9970.78 22-7-20 4304.83 3445.76 5163.91
23-7-20 21,036.9 19,263.5 22,810.3 23-7-20 9731.07 9197.81 10,264.3 23-7-20 4311.97 3350.08 5273.86
24-7-20 21,313.7 19,346.4 23,281.0 24-7-20 10,000.5 9436.04 10,565.0 24-7-20 4319.11 3250.6 5387.62
USA ARIMA (1,1,0) Brazil ARIMA (0,2,1) India ARIMA (0,2,0)
Lower 95% Upper 95% Lower 95% Upper 95% Lower 95% Upper 95%
Period Forecast Limit Limit Period Forecast Limit Limit Period Forecast Limit Limit
11-7-20 3.10259 × 106 3.08965 × 106 3.11554 × 106 11-7-20 1.75087 × 106 1.73873 × 106 1.76302 × 106 11-7-20 820,308 819,036 821,580
12-7-20 3.1665 × 106 3.13762 × 106 3.19539 × 106 12-7-20 1.78858 × 106 1.76922 × 106 1.80795 × 106 12-7-20 846,814 843,969 849,659
13-7-20 3.23006 × 106 3.18183 × 106 3.27828 × 106 13-7-20 1.8263 × 106 1.79985 × 106 1.85275 × 106 13-7-20 873,320 868,560 878,080
14-7-20 3.29325 × 106 3.2228 × 106 3.3637 × 106 14-7-20 1.86401 × 106 1.83027 × 106 1.89775 × 106 14-7-20 899,826 892,858 906,794
15-7-20 3.3561 × 106 3.26091 × 106 3.45129 × 106 15-7-20 1.90172 × 106 1.86038 × 106 1.94306 × 106 15-7-20 926,332 916,897 935,767
16-7-20 3.41859 × 106 3.2964 × 106 3.54077 × 106 16-7-20 1.93943 × 106 1.89016 × 106 1.98871 × 106 16-7-20 952,838 940,702 964,974
17-7-20 3.48073 × 106 3.3295 × 106 3.63196 × 106 17-7-20 1.97714 × 106 1.91958 × 106 2.03471 × 106 17-7-20 979,344 964,291 994,397
18-7-20 3.54253 × 106 3.36035 × 106 3.7247 × 106 18-7-20 2.01486 × 106 1.94866 × 106 2.08105 × 106 18-7-20 1.00585 × 106 987,679 1.02402 × 106
19-7-20 3.60398 × 106 3.3891 × 106 3.81885 × 106 19-7-20 2.05257 × 106 1.9774 × 106 2.12774 × 106 19-7-20 1.03236 × 106 1.01088 × 106 1.05383 × 106
20-7-20 3.66508 × 106 3.41586 × 106 3.91431 × 106 20-7-20 2.09028 × 106 2.0058 × 106 2.17476 × 106 20-7-20 1.05886 × 106 1.0339 × 106 1.08382 × 106
21-7-20 3.72585 × 106 3.44073 × 106 4.01097 × 106 21-7-20 2.12799 × 106 2.03387 × 106 2.22211 × 106 21-7-20 1.08537 × 106 1.05675 × 106 1.11399 × 106
22-7-20 3.78627 × 106 3.46379 × 106 4.10876 × 106 22-7-20 2.16571 × 106 2.06163 × 106 2.26978 × 106 22-7-20 1.11187 × 106 1.07944 × 106 1.14431 × 106
23-7-20 3.84636 × 106 3.48513 × 106 4.2076 × 106 23-7-20 2.20342 × 106 2.08907 × 106 2.31776 × 106 23-7-20 1.13838 × 106 1.10197 × 106 1.17479 × 106
24-7-20 3.90611 × 106 3.5048 × 106 4.30743 × 106 24-7-20 2.24113 × 106 2.11621 × 106 2.36605 × 106 24-7-20 1.16489 × 106 1.12435 × 106 1.20542 × 106
Open in a new tab

In the present study, an ARIMA model has been selected, in which the best model forecast for future data is given by a parametric model relating the most recent data value to previous data values and previous noise, or residuals in this context. The output summarizes the statistical significance of the terms in the forecasting model. Terms with p-values less than 0.05 are statistically significantly different from zero at the 95.0% confidence level. The p-value for the AR(x) or term is less than 0.05, so it is significantly different from 0. The p-value for the MA(x) term is less than 0.05, so it is significantly different from 0. When the trend is increasing, in order to obtain a linearity or central trend, the model also chooses q. The estimated standard deviation of the input white noise depends on the best model that was selected during the simulations performed.

According to the current literature, this would be the first study of such a manner. Therefore, the idea of a cluster of nations, and the rate of the spread between them is novel. This adds to the fact that this is the first study to address the situation of the most affected nations globally. In the present study the current situation of the COVID-19 pandemic in Ukraine, Romania, the Republic of Moldova, Serbia, Bulgaria, Hungary, USA, Brazil, and India was presented, and the ongoing trend and extent of the outbreak were estimated by the ARIMA model. According to our best of knowledge, this study is the first of its kind to implement ARIMA models to predict the prevalence of COVID-19 in such a manner.

In the current literature can be found limited data regarding the usage of ARIMA for the prediction of the COVID-19 course. Most reports evaluated the situation from western and southern Asia. Reports regarding the status of Europe are elusive for an unknown reason, and as a consequence, Europe gradually become the second mainland (Table 5). It should be also mentioned that papers that have been subjected to the peer-review process were excluded.

Table 5.

Studies conducted to predict COVID-19 spreading in which were used distinct statistical approaches.

Disease Method(s) Reference
COVID-19 Hybrid ARIMA-WBF [32] $
SutteARIMA [33] *
Seasonal ARIMA [34] *
ARIMA [35] *
NARNN
LSTM
ARIMA [36] *
ARIMA [37] $
ARIMA [38] $
ARIMA [39] $
ARIMA [40] $
HWAAS
TBAT
Facebook’s Prophet
DeepAR
N-Beats
Open in a new tab

$ European and non-European countries are included; * strictly European countries included.

Effective strategies are now all more imperative to control the spreading of COVID-19. Thus, estimating epidemiological trends is crucial for the allocations of medical resources and production activities.

Among the most effective alternatives that proved their efficacity is quarantine. Chintalapudi et al. [34] have discussed the beneficial impact lockdown had within the Italian population in terms of transmissibility. A data-driven model analysis demonstrated a decrement up to 35% of total registered cases, concomitantly with an increase up to 66% of recovered cases after lockdown and self-isolation. The accuracy of these two parameters was 93.75 and 84.4%, respectively.

This tendency of regression proved to be true according to the results obtained by another group of authors. The accuracy of six performance metric models has been tested. Long short-term memory (LSTM) was found to be the most accurate during the study, perspective predictions within the next two weeks being made. Thus, is expected a slight decrease in the number of the total cumulative cases [35].

These observations are strengthened by the results of Papastefanopoulos et al. [40]. Six different time series approaches were also utilized to test the accuracy concerning the COVID-19 outbreak for the top ten most affected countries. Machine learning time series methods were efficiently used to estimate the percentage of the population that will be affected.

By using a stochastic modified SEIR model (susceptible–exposed–infectious–recovered) and due to lack of effective pharmaceutical interventions against SARS-CoV-2, López et al. [41] concluded that social confinement should remain in place for the next two months. Behavior, awareness, and immunity decay is attributed to 99% of the current wave. The gradual incorporation of up to 50% of daily working proportion should be also considered.

It has been recently shown that Black and South Asian people are more prone to infection and subsequently death than the rest. Among the risk factors is age, being male, deprivation, diabetes, asthma, and numerous other medical conditions following the analysis of a cohort consisting of 17,278,392 UK individuals [42].

If all these restrictions are not respected, humanity will face a second wave of infections much more severe than the previous one [37] according to the latest statistics reported by WHO. Most certainly, governments’ internal politics and capability in managing the current situation would be definitory during this temporary crisis [33,36,37,38].

Assuming that 20% of the population of each country in the US will be infected, age-specific mortality pattern shown that counties will be probably heavily affected. These findings suggest the adequate allocation of the medical care resources per capita needed to outside communities to restrain the spread [43].

Chakraborty et al. [32] revealed that to people over the age of 65 should be paid more attention, which is why for them it is recommended intensive care and isolation. In addition, they suggests that the locktime period must be extended, in parallel with the arranging medical centers by increasing the number of beds.

Furthermore, Demongeot et al. [39] have brought a new perspective regarding the important role temperature has on COVID-19 spreading, reflected by the total number of active cases. It seems that high temperature directly reduces contagion rates, but this does not mean seasonal temperature could not support the later reappearance following the usage of time series methods.

4. Conclusions

Forecasting the prevalence of a disease is crucial for health departments to create an optimum environment and conditions for patients. As has been presented throughout this manuscript, time series models play an important role in disease prediction. In this study, ARIMA time series models were successfully applied to estimate the overall prevalence of COVID-19 in nine countries, six of them being neighbors, while the other three are the most affected today.

Acknowledgments

Not applicable, with the exception of the research grant mentioned above.

Author Contributions

Writing—original draft, O.-D.I., R.-O.C., S.-I.T.; Software, S.-I.T.; Conceptualization, Visualization, Writing—review and editing, O.-D.I., A.C., I.M.; Methodology and Validation, B.D. All authors have read and agreed to the published version of the manuscript.

Funding

A.C. is supported by a research grant for Young Teams offered by UEFISCDI Romania, No. PN-III-P1-1.1-TE-2016-1210, contract No. 58 from 02/05/2018, called “Complex study regarding the interactions between oxidative stress, inflammation and neurological manifestations in the pathophysiology of irritable 278 bowel syndrome (animal models and human patients)”.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

  • 1.Rothan H.A., Byrareddy S.N. The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. J. Autoimmun. 2020;109:102433. doi: 10.1016/j.jaut.2020.102433. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Zhu N., Zhang D., Wang W., Li X., Yang B., Song J., Zhao X., Huang B., Shi W., Lu R., et al. A Novel Coronavirus from Patients with Pneumonia in China, 2019. N. Engl. J. Med. 2020;382:727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Guan W., Ni Z., Hu Y., Liang W., Ou C., He J., Liu L., Shan H., Lei C., Hui D.S.C., et al. Clinical Characteristics of Coronavirus Disease 2019 in China. N. Engl. J. Med. 2020;382:1708–1720. doi: 10.1056/NEJMoa2002032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y., Zhang L., Fan G., Xu J., Gu X., et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395:497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Chen N., Zhou M., Dong X., Qu J., Gong F., Han Y., Qiu Y., Wang J., Liu Y., Wei Y., et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. Lancet. 2020;395:507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Jin X., Lian J.-S., Hu J.-H., Gao J., Zheng L., Zhang Y.-M., Hao S.-R., Jia H.-Y., Cai H., Zhang X.-L., et al. Epidemiological, clinical and virological characteristics of 74 cases of coronavirus-infected disease 2019 (COVID-19) with gastrointestinal symptoms. Gut. 2020;69:1002. doi: 10.1136/gutjnl-2020-320926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Xiang J., Wang Y., Song B., Gu X., et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet. 2020;395:1054–1062. doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Wang D., Hu B., Hu C., Zhu F., Liu X., Zhang J., Wang B., Xiang H., Cheng Z., Xiong Y., et al. Clinical Characteristics of 138 Hospitalized Patients With 2019 Novel Coronavirus–Infected Pneumonia in Wuhan, China. JAMA. 2020;323:1061–1069. doi: 10.1001/jama.2020.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Lin L., Jiang X., Zhang Z., Huang S., Zhang Z., Fang Z., Gu Z., Gao L., Shi H., Mai L., et al. Gastrointestinal symptoms of 95 cases with SARS-CoV-2 infection. Gut. 2020;69:997. doi: 10.1136/gutjnl-2020-321013. [DOI] [PubMed] [Google Scholar]
  • 10.Xu X.-W., Wu X.-X., Jiang X.-G., Xu K.-J., Ying L.-J., Ma C.-L., Li S.-B., Wang H.-Y., Zhang S., Gao H.-N., et al. Clinical findings in a group of patients infected with the 2019 novel coronavirus (SARS-Cov-2) outside of Wuhan, China: Retrospective case series. BMJ. 2020;368:m606. doi: 10.1136/bmj.m606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Zhang H., Kang Z., Gong H., Xu D., Wang J., Li Z., Li Z., Cui X., Xiao J., Zhan J., et al. Digestive system is a potential route of COVID-19: An analysis of single-cell coexpression pattern of key proteins in viral entry process. Gut. 2020;69:1010. doi: 10.1136/gutjnl-2020-320953. [DOI] [Google Scholar]
  • 12.Ong J., Young B.E., Ong S. COVID-19 in gastroenterology: A clinical perspective. Gut. 2020;69:1144. doi: 10.1136/gutjnl-2020-321051. [DOI] [PubMed] [Google Scholar]
  • 13.Song Y., Liu P., Shi X.L., Chu Y.L., Zhang J., Xia J., Gao X.Z., Qu T., Wang M.Y. SARS-CoV-2 induced diarrhoea as onset symptom in patient with COVID-19. Gut. 2020;69:1143. doi: 10.1136/gutjnl-2020-320891. [DOI] [PubMed] [Google Scholar]
  • 14.Liang W., Feng Z., Rao S., Xiao C., Xue X., Lin Z., Zhang Q., Qi W. Diarrhoea may be underestimated: A missing link in 2019 novel coronavirus. Gut. 2020;69:1141. doi: 10.1136/gutjnl-2020-320832. [DOI] [PubMed] [Google Scholar]
  • 15.Wang L., Li J., Guo S., Xie N., Yao L., Cao Y., Day S.W., Howard S.C., Graff J.C., Gu T., et al. Real-time estimation and prediction of mortality caused by COVID-19 with patient information based algorithm. Sci. Total Environ. 2020;727:138394. doi: 10.1016/j.scitotenv.2020.138394. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Kurbalija V., Radovanović M., Ivanović M., Schmidt D., von Trzebiatowski G.L., Burkhard H.-D., Hinrichs C. Time-series analysis in the medical domain: A study of Tacrolimus administration and influence on kidney graft function. Comput. Biol. Med. 2014;50:19–31. doi: 10.1016/j.compbiomed.2014.04.007. [DOI] [PubMed] [Google Scholar]
  • 17.Nsoesie E., Beckman R., Shashaani S., Nagaraj K., Marathe M. A Simulation Optimization Approach to Epidemic Forecasting. PLoS ONE. 2013;8:e67164. doi: 10.1371/journal.pone.0067164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Orbann C., Sattenspiel L., Miller E., Dimka J. Defining epidemics in computer simulation models: How do definitions influence conclusions? Epidemics. 2017;19:24–32. doi: 10.1016/j.epidem.2016.12.001. [DOI] [PubMed] [Google Scholar]
  • 19.Thomson M.C., Molesworth A.M., Djingarey M.H., Yameogo K.R., Belanger F., Cuevas L.E. Potential of environmental models to predict meningitis epidemics in Africa. Trop. Med. Int. Health. 2006;11:781–788. doi: 10.1111/j.1365-3156.2006.01630.x. [DOI] [PubMed] [Google Scholar]
  • 20.Liu Q., Li Z., Ji Y., Martinez L., Zia U.H., Javaid A., Lu W., Wang J. Forecasting the seasonality and trend of pulmonary tuberculosis in Jiangsu Province of China using advanced statistical time-series analyses. Infect. Drug Resist. 2019;12:2311–2322. doi: 10.2147/IDR.S207809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Ren H., Li J., Yuan Z.-A., Hu J.-Y., Yu Y., Lu Y.-H. The development of a combined mathematical model to forecast the incidence of hepatitis E in Shanghai, China. BMC Infect. Dis. 2013;13:421. doi: 10.1186/1471-2334-13-421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Zhang X., Liu Y., Yang M., Zhang T., Young A., Li X. Comparative Study of Four Time Series Methods in Forecasting Typhoid Fever Incidence in China. PLoS ONE. 2013;8:e63116. doi: 10.1371/journal.pone.0063116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Wang Y., Shen Z., Jiang Y. Comparison of ARIMA and GM(1,1) models for prediction of hepatitis B in China. PLoS ONE. 2018;13:e0201987. doi: 10.1371/journal.pone.0201987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Zhang L., Wang L., Zheng Y., Wang K., Zhang X., Zheng Y. Time Prediction Models for Echinococcosis Based on Gray System Theory and Epidemic Dynamics. Int. J. Environ. Res. Public Health. 2017;14:262. doi: 10.3390/ijerph14030262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Cao L., Liu H., Li J., Yin X., Duan Y., Wang J. Relationship of meteorological factors and human brucellosis in Hebei province, China. Sci. Total Environ. 2020;703:135491. doi: 10.1016/j.scitotenv.2019.135491. [DOI] [PubMed] [Google Scholar]
  • 26.Wilson T.G. Time Series Analysis: Forecasting and Control, 5th Edition, by George E. P. Box, Gwilym M. Jenkins, Gregory C. Reinsel and Greta M. Ljung, 2015. Published by John Wiley and Sons Inc., Hoboken, NJ USA, pp. 712, ISBN: 978-1-118-67502-1. J. Time Ser. Anal. 2016;37 doi: 10.1111/jtsa.12194. [DOI] [Google Scholar]
  • 27.Fanoodi B., Malmir B., Jahantigh F.F. Reducing demand uncertainty in the platelet supply chain through artificial neural networks and ARIMA models. Comput. Biol. Med. 2019;113:103415. doi: 10.1016/j.compbiomed.2019.103415. [DOI] [PubMed] [Google Scholar]
  • 28.Benvenuto D., Giovanetti M., Vassallo L., Angeletti S., Ciccozzi M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Br. 2020;29:105340. doi: 10.1016/j.dib.2020.105340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Li X., Zhang C., Zhang B., Liu K. A comparative time series analysis and modeling of aerosols in the contiguous United States and China. Sci. Total Environ. 2019;690:799–811. doi: 10.1016/j.scitotenv.2019.07.072. [DOI] [PubMed] [Google Scholar]
  • 30.Elevli S., Uzgören N., Bingöl D., Elevli B. Drinking water quality control: Control charts for turbidity and pH. J. Water Sanit. Hyg. Dev. 2016;6:511–518. doi: 10.2166/washdev.2016.016. [DOI] [Google Scholar]
  • 31.He Z., Tao H. Epidemiology and ARIMA model of positive-rate of influenza viruses among children in Wuhan, China: A nine-year retrospective study. Int. J. Infect. Dis. 2018;74:61–70. doi: 10.1016/j.ijid.2018.07.003. [DOI] [PubMed] [Google Scholar]
  • 32.Chakraborty T., Ghosh I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis. Chaos Solitons Fractals. 2020;135:109850. doi: 10.1016/j.chaos.2020.109850. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Ahmar A.S., del Val E.B. SutteARIMA: Short-term forecasting method, a case: Covid-19 and stock market in Spain. Sci. Total Environ. 2020;729:138883. doi: 10.1016/j.scitotenv.2020.138883. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Chintalapudi N., Battineni G., Amenta F. COVID-19 virus outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: A data driven model approach. J. Microbiol. Immunol. Infect. 2020;53:396–403. doi: 10.1016/j.jmii.2020.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Kırbaş İ., Sözen A., Tuncer A.D., Kazancıoğlu F. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos Solitons Fractals. 2020:110015. doi: 10.1016/j.chaos.2020.110015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci. Total Environ. 2020;729:138817. doi: 10.1016/j.scitotenv.2020.138817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Singh R.K., Rani M., Bhagavathula A.S., Sah R., Rodriguez-Morales A.J., Kalita H., Nanda C., Sharma S., Sharma Y.D., Rabaan A.A., et al. Prediction of the COVID-19 Pandemic for the Top 15 Affected Countries: Advanced Autoregressive Integrated Moving Average (ARIMA) Model. JMIR Public Health Surveill. 2020;6:e19115. doi: 10.2196/19115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Modeling and Forecasting for the number of cases of the COVID-19 pandemic with the Curve Estimation Models, the Box-Jenkins and Exponential Smoothing Methods. Eurasian J. Med. Oncol. 2020;4:160–165. [Google Scholar]
  • 39.Demongeot J., Flet-Berliac Y., Seligmann H. Temperature Decreases Spread Parameters of the New Covid-19 Case Dynamics. Biology. 2020;9:94. doi: 10.3390/biology9050094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Papastefanopoulos V., Linardatos P., Kotsiantis S. COVID-19: A Comparison of Time Series Methods to Forecast Percentage of Active Cases per Population. Appl. Sci. 2020;10:3880. doi: 10.3390/app10113880. [DOI] [Google Scholar]
  • 41.López L., Rodó X. The end of social confinement and COVID-19 re-emergence risk. Nat. Hum. Behav. 2020;4:746–755. doi: 10.1038/s41562-020-0908-8. [DOI] [PubMed] [Google Scholar]
  • 42.Williamson E.J., Walker A.J., Bhaskaran K., Bacon S., Bates C., Morton C.E., Curtis H.J., Mehrkar A., Evans D., Inglesby P., et al. OpenSAFELY: Factors associated with COVID-19 death in 17 million patients. Nature. 2020 doi: 10.1038/s41586-020-2521-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Miller I.F., Becker A.D., Grenfell B.T., Metcalf C.J.E. Disease and healthcare burden of COVID-19 in the United States. Nat. Med. 2020 doi: 10.1038/s41591-020-0952-y. [DOI] [PubMed] [Google Scholar]

Articles from Microorganisms are provided here courtesy of Multidisciplinary Digital Publishing Institute (MDPI)

RESOURCES