Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 25;12(27):30731–30739. doi: 10.1021/acsami.0c09451

Flexible C6BN Monolayers As Promising Anode Materials for High-Performance K-Ion Batteries

Pan Xiang †,‡, Sitansh Sharma ‡,*, Zhiming M Wang †, Jiang Wu †,*, Udo Schwingenschlögl ‡,*
PMCID: PMC7467560  PMID: 32584015

Abstract

graphic file with name am0c09451_0006.jpg

K-ion batteries attract extensive attention and research efforts because of the high energy density, low cost, and high abundance of K. Although they are considered suitable alternatives to Li-ion batteries, the absence of high-performance electrode materials is a major obstacle to implementation. On the basis of density functional theory, we systematically study the feasibility of a recently synthesized C6BN monolayer as anode material for K-ion batteries. The specific capacity is calculated to be 553 mAh/g (K2C6BN), i.e., about twice that of graphite. The C6BN monolayer is characterized by high strength (in-plane stiffness of 309 N/m), excellent flexibility (bending strength of 1.30 eV), low output voltage (average open circuit voltage of 0.16 V), and excellent rate performance (diffusion barrier of 0.09 eV). We also propose two new C6BN monolayers. One has a slightly higher total energy (0.10 eV) than the synthesized C6BN monolayer, exhibiting enhanced electronic properties and affinity to K. The other is even energetically favorable due to B–N bonding. All three C6BN monolayers show good dynamical, thermal, and mechanical stabilities. We demonstrate excellent cyclability and improved conductivity by K adsorption, suggesting great potential in flexible energy-storage devices.

Keywords: energy storage, K-ion battery, flexible anode, C6BN monolayer, first-principles calculation

Introduction

The limited reserves of traditional energy sources and the environmental issues caused by them make the development of clean sustainable energy sources an urgent task.1,2 However, these sources, such as solar energy and wind energy, are greatly affected by environmental and weather conditions, resulting in fluctuating output.3 Therefore, large scale energy storage systems are required that combine safety, stability, and low cost.4,5 In addition, emerging electric vehicles and wearable electronics need high performance (high capacity, fast charging) batteries as power source.6−9 Regrettably, the current commercial Li-ion batteries are not able to fulfill these demands because of a shortage of Li sources and their uneven global distribution.10,11 On the other hand, K-ion batteries can rely on abundant K sources. In combination with fast ion transport in the electrolyte this makes them to promising alternatives for large scale energy storage systems and electric vehicles.12,13 In this context, it is essential to develop for K-ion batteries suitable low cost and high performance electrode materials, as they determine their electrochemical properties.

Interestingly, graphite, the most mature anode material applied in Li-ion batteries, is not suitable for Na-ion batteries but can be used to store K.14 However, because of the larger atomic radius of K as compared to Li, only one K atom can be stored per eight C atoms, corresponding to a specific capacity of 279 mAh/g.15 On the basis of first-principles calculations, the binding energy of a single K atom on graphene was found to be 1.05 eV, which is only slightly larger than the cohesive energy of K (0.93 eV), indicating potential risk of dendrite formation.16 While the electrochemical performance of C-only anode materials is unsatisfactory for K-ion batteries, improvement is found for two-dimensional C3B.17 Two-dimensional C3N provides a high specific capacity of 1072 mAh/g, however, only through multilayer adsorption.18 For Li-ion batteries the electrochemical performance of ternary B–C–N anode materials (borocarbonitrides) was studied systematically, proposing that C-rich B0.15C0.73N0.12 provides the highest surface area and specific capacity.19 Recently, a C-rich borocarbonitride monolayer, C6BN, could be synthesized using a low cost two-step borylation reaction.20 The material combines valley-selective circular dichroism with high carrier mobility,21 consistent with the conclusion that higher C content in borocarbonitrides improves the conductivity.22,23 This development together with the low mass density and possibility of low-cost fabrication motivates us to explore C6BN monolayers as anode materials for K-ion batteries.

We determine the basic properties and electrochemical performance of the synthesized C6BN monolayer and put forward two other C6BN monolayers based on first-principles calculations. For each of the three C6BN monolayers we first optimize the structure and examine the stability. Then, the band structure, density of states, Young’s modulus, Poisson’s ratio, and out-of-plane bending stiffness are studied to obtain insights into the electronic structure, in-plane strength, and flexibility. We also evaluate the adsorption and diffusion of K on the C6BN monolayers. The specific capacity and open circuit voltage (OCV) are calculated by obtaining the energetically favorable structures of potassiated C6BN monolayers. Finally, the effect of K adsorption in the conductivity of the C6BN monolayers is investigated.

Computational Details

First-principles calculations are performed by the DMol324,25 program using a double-numerical polarized basis, the all electron relativistic method, and the Perdew–Burke–Ernzerhof generalized gradient approximation of the exchange-correlation functional. The Grimme dispersion correction is adopted to describe the long-range van der Waals interaction.26 The convergence thresholds of the energy, maximum force, and displacement in the structure optimization are set to 1.0 × 10–6 Ha, 0.001 Ha/Å, and 0.002 Å, respectively. Convergence tests (Figure S1) show that a Monkhorst–Pack 7 × 7 × 1 k-mesh for sampling the Brillouin zone provides reliable results. A small smearing of 5 × 10–4 Ha and a large global orbital cutoff of 5.6 Å are employed in all calculations. To avoid artificial interaction between periodic images in the out-of-plane direction, a large vacuum thickness of 25 Å is used. To evaluate the thermal stability of the C6BN monolayers, we use ab initio molecular dynamics simulations at 300 and 1200 K (NVT ensemble) for 10 ps with a time step of 1 fs. Still adopting the Perdew–Burke–Ernzerhof and Grimme schemes, the dynamic stability is investigated by calculating the phonon spectrum by the Phonopy27 and VASP28 (projector augmented-wave potentials, 1 × 10–6 eV energy convergence threshold, Monkhorst–Pack 12 × 12 × 1 k-mesh) programs, and charge densities and electron localization functions are obtained by means of the CASTEP29 program (norm-conserving pseudopotentials, 5 × 10–7 eV/atom energy convergence threshold, Monkhorst–Pack 7 × 7 × 1 k-mesh).

Results and Discussion

Structure, Stability, and Material Properties

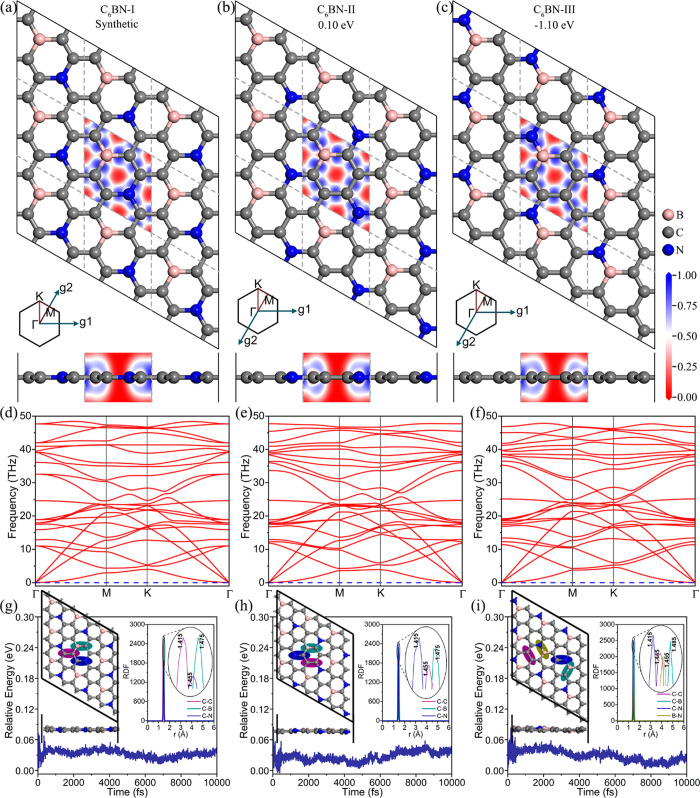
The synthesized C6BN monolayer has a hexagonal unit cell with space group P6̅m2 and point group D3h, containing pure and B–N para-doped C rings, as shown in Figure 1a. We obtain a lattice constant of 4.982 Å and equilibrium C–C, C–B, and C–N bond lengths of 1.412, 1.473, and 1.456 Å, respectively, in agreement with previously reported results.21 Because of the bond energy order B–N (4.00 eV) > C–C (3.71 eV) > N–C (2.83 eV) > B–C (2.59 eV) > B–B (2.32 eV) > N–N (2.11 eV) in borocarbonitrides,30 B–N bonds are most favorable. However, as shown in Figure 1a, there exists no B–N bond in the synthesized C6BN monolayer (named C6BN-I in the following), probably because the synthesis is based on pyrolysis of specific precursors. By adjusting the sites of the B and N atoms in the hexagonal C network, we obtain two new monolayers, named C6BN-II and C6BN-III. Unlike C6BN-I, the unit and primitive cells of C6BN-II and C6BN-III are different because of reduced symmetry, the unit cell being orthogonal (Figure S2), and the primitive cell being almost hexagonal (angle very close to 120°; Figure 1b, c). To enable better comparison with C6BN-I, we used the primitive cells in further study. As shown in Figure 1b, c, C6BN-II (B–N meta-doped) and C6BN-III (B–N ortho-doped) stay perfectly planar. According to Table 1, the lattice constants and bond lengths of the C6BN monolayers are similar due to the identical elemental compositions and similarity of the crystal structures. Expectedly, introduction of strong B–N bonds in C6BN-III lowers the total energy by 1.10 eV per formula unit with respect to synthesized C6BN-I. The total energy of C6BN-II turns out to be only 0.10 eV higher than that of synthesized C6BN-I. Therefore, synthesis of C6BN-II and C6BN -III should be possible by the same method employed successfully in the case of C6BN-I. The insets in Figure 1a–c show the electron localization function for the C6BN monolayers to analyze the electron distribution and bonding features. Because of the comparable electronegativities of B, C, and N, high values (blue) between atoms indicate a covalent bond character as in the case of graphene.31

Figure 1.

Figure 1

Open in a new tab

C6BN monolayers: (a–c) Top and side views of the optimized structure with Brillouin zone and electron localization function. (d–f) Phonon dispersion relation. (g–i) Total potential energy during the ab initio molecular dynamics simulation with final structure and radial distribution functions.

Table 1. Structural Details, Relative Energy, and Material Properties.

                  Young’s modulus (N/m)
 Poisson’s ratio
  lattice constant (Å) C–B bond length (Å) C–C bond length (Å) C–N bond length (Å) B–N bond length (Å) relative energy (eV) band gap (eV) bending stiffness (eV) AC ZZ AC ZZ
C6BN-I 4.982 1.473 1.412 1.456   0 1.28 1.30 310 311 0.176 0.177
C6BN-II 4.983 1.477 1.430 1.421   0.10 0.13 1.36 317 312 0.175 0.173
C6BN-III 4.975 1.485 1.428 1.411 1.455 –1.10 1.16 1.38 314 317 0.180 0.182
Open in a new tab

To examine the dynamical stability of the C6BN monolayers, we study the phonon spectra. The absence of imaginary frequencies in the entire first Brillouin zone demonstrates dynamical stability, as shown in Figure 1d–f. The maximal frequencies of 1616, 1599, and 1591 cm–1 obtained for C6BN-I, C6BN-II, and C6BN-III, respectively, are comparable to those of C3N (1638 cm–1) and C3B (1510 cm–1)32 and indicate strong bonding. Ab initio molecular dynamics simulations are executed for each C6BN monolayer using a 3 × 3 supercell. As shown in Figure 1g–i, the fluctuations of the total energy are of the order of 0.01 eV at 300 K. The C6BN monolayers maintain their structure without relevant distortions, which is confirmed by peaks in the radial distribution functions at the equilibrium lengths of the C–B, C–C, and C–N bonds (insets of Figure 1g–i). Similar results are observed up to 1200 K (Figure S3), indicating excellent thermal stability to endure elevated temperatures during device operation. 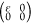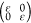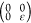The mechanical stability of the C6BN monolayers is examined by determining the linear elastic constants, Cij, by fitting the energy of the orthogonal unit cell under armchair axial Inline graphic, hydrostatic planar Inline graphic, zigzag axial Inline graphic, and shear 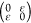Inline graphic deformations for external strain ε from −2% to 2% (steps of 0.5%). We obtain for C11, C12, C22, and C44 values of 320, 56, 321, and 131 N/m for C6BN-I; 327, 56, 322, and 132 N/m for C6BN-II; and 325, 59, 328, and 132 N/m for C6BN-III; i.e., in each case the Born criteria (C11 > 0, C22 > 0, C11C22 – C122 > 0, C44 > 0)33 imply mechanical stability.

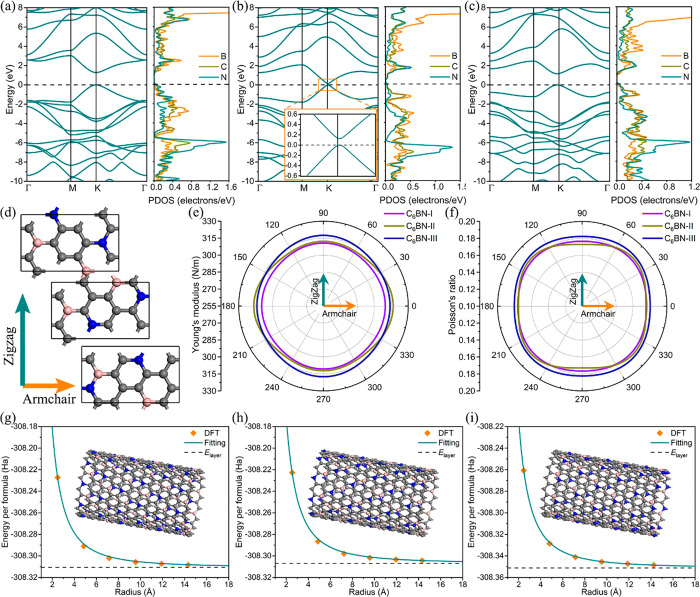
Having confirmed the structural stability of the C6BN monolayers, the band structure and partial densities of states are addressed in Figure 2a–c to examine the electronic properties. C6BN-I and C6BN-III show similar band structures with both the valence band maximum and conduction band minimum at the K point (band gaps of 1.28 and 1.16 eV, respectively). The partial densities of states indicate that the valence band edge is mainly due to the C and N atoms, whereas the conduction band edge is mainly due to the B and C atoms. C6BN-II is characterized by a very small direct band gap of only 0.13 eV at the K point with the bands resembling a Dirac cone, pointing to excellent charge transport.

Figure 2.

Figure 2

Open in a new tab

C6BN monolayers: (a–c) Band structure and partial densities of states. (d) Armchair and zigzag directions. (e, f) Young’s modulus and Poisson’s ratio. (g–i) Energy per formula unit for C6BN-I, C6BN-II, and C6BN-III nanotubes of different radius with insets showing the typical structure.

As the mechanical properties are correlated with the battery cyclability, we estimate the in-plane stiffness by deriving the direction-dependent (θ, angle to the armchair direction) Young’s modulus

graphic file with name am0c09451_m005.jpg 1

and Poisson’s ratio

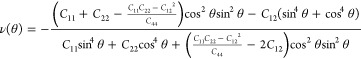graphic file with name am0c09451_m006.jpg 2

from the linear elastic constants.34 The polar diagrams of E(θ) and ν(θ) in Figure 2e,f show that Young’s modulus and Poisson’s ratio are almost isotropic in each case. Unlike the electronic properties, the mechanical properties of the C6BN monolayers are very similar. The average Young’s modulus and Poisson’s ratio are 309 N/m and 0.178 for C6BN-I, 313 N/m and 0.178 for C6BN-II, and 315 N/m and 0.183 for C6BN-II, which is comparable to graphene (342 N/m and 0.173) and reflects strong bonding and high in-plane stiffness.

To evaluate the usability of C6BN-based anodes in wearable electronics, we calculate the out-of-plane bending strength (BM) by fitting to the formula35

graphic file with name am0c09451_m007.jpg 3

where Etube and Elayer are the total energies per formula unit of a C6BN nanotube and a corresponding C6BN monolayer, respectively, Slayer is the area per formula unit of the C6BN monolayer, and r is the radius of the C6BN nanotube. For each of the C6BN monolayers, nanotubes with six different radii are constructed. The fitting curves are shown in Figure 2g–i and the structural details of the optimized nanotubes are summarized in Table S1. We obtain BM values of 1.30, 1.36, and 1.38 eV for C6BN-I, C6BN-II, and C6BN-III, respectively, which are lower than those reported for the well-known flexible 2D materials graphene (1.44 eV35) and MoS2 (9.33 eV36). This indicates enhanced flexibility of the C6BN monolayers and, therefore, great potential in wearable electronics.

Adsorption and Diffusion of K

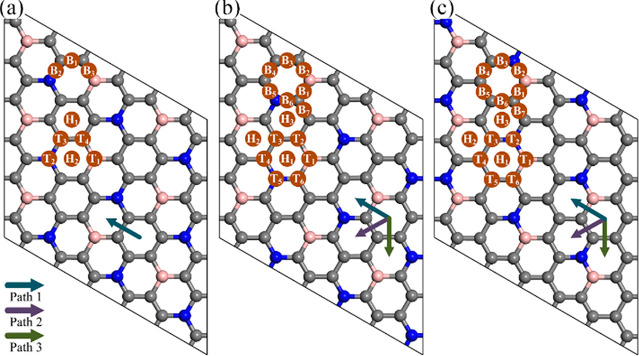
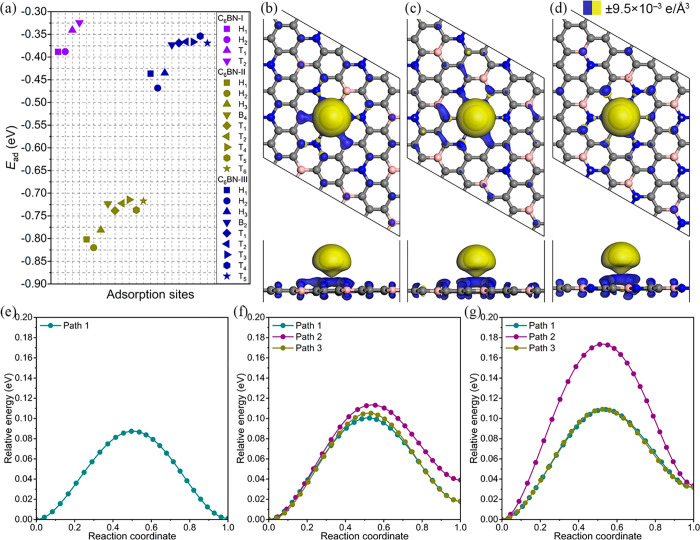
Although the C6BN monolayers are promising anode materials in terms of their low mass density, high stability, and excellent mechanical properties, spontaneous adsorption of metal atoms is an essential prerequisite. For this reason, we determine the energetically favorable adsorption site of K, i.e., the most likely position of a K atom on the anode material. Based on the different symmetries, nine possible adsorption sites are considered for C6BN-I and 16 for C6BN-II and C6BN-III as shown in Figure 3 (Tn, site on top of an atom; Bn, site on top of a bond; Hn, site on top of the center of a C ring). Unstable adsorption sites show up in the structure optimization by spontaneous diffusion of the K atom to another adsorption site. To determine the affinity of K to a C6BN monolayer, we calculate the adsorption energy Ead = EKC6BN – EC6BN – μK, where EKC6BN and EC6BN are the total energies of a C6BN monolayer after and before K adsorption, respectively, and μK is the chemical potential of a K atom from the bcc bulk. The obtained values are summarized in Figure 4a. The negative values indicate spontaneous adsorption of K. It turns out that the Hn sites are more attractive to K than the Tn and Bn sites, which can be attributed to interaction with delocalized electrons of the C rings, see the results of the electron localization function in Figure 1a–c. Concretely, the favorable adsorption sites are H1 for C6BN-I and H2 for both C6BN-II and C6BN-III with adsorption energies of −0.39, – 0.82, and −0.47 eV and adsorption heights of 2.61, 2.59, and 2.60 Å, respectively.

Figure 3.

Figure 3

Open in a new tab

K adsorption sites and diffusion paths for (a) C6BN-I, (b) C6BN-II, and (c) C6BN-III.

Figure 4.

Figure 4

Open in a new tab

C6BN monolayers: (a) Adsorption energy of a K atom. (b–d) Charge density difference due to adsorption of a K atom at the energetically favorable site. (e, f) Energy profiles for K diffusion.

To gain further insights into the interaction between K and a C6BN monolayer, we calculate for the energetically favorable adsorption site the electron density difference ρ = ρKC6BN – ρC6BN – ρK, where ρKC6BN and ρC6BN are the electron densities of a C6BN monolayer after and before K adsorption, respectively, and ρK is the electron density of an isolated K atom. The results are shown in Figure 4b–d with blue and yellow isosurfaces representing electron accumulation and depletion, respectively. We observe a pronounced transfer of electrons from the K atom to the C6BN monolayer, consistent with the much smaller electronegativity of K as compared to B, C, and N. Using the Hirshfeld partitioning method, we derive transfers of 0.69, 0.68, and 0.69 electrons to C6BN-I, C6BN-II, and C6BN-III, respectively. Despite the strong interaction, the adsorption of K has virtually no effect on the structure of the C6BN monolayers (no corrugations or other deformations).

Because the diffusion barrier (Ebar) determines the battery charge/discharge rate, we next study the migration of K on the C6BN monolayers. As adsorption of K is strongly favorable at the Hn sites as compared to the Tn and Bn sites, we focus on diffusion from the energetically favorable adsorption site to the neighboring Hn site. There is only one such diffusion path for C6BN-I, whereas there are three possible paths for C6BN-II and C6BN-III, as shown in Figure 3. Employing the linear and quadratic synchronous transit methods as well as the transition-state confirmation tool of DMol3, we obtain the diffusion energy profiles shown in Figure 4e–g. The saddle points of all the considered diffusion paths appear in the middle of a bond connecting two C rings. Because of the high symmetry of C6BN-I, the K diffusion in this case is isotropic with Ebar = 0.087 eV. In the case of C6BN-II, the diffusion barriers of the three paths are very similar (0.100, 0.113, and 0.105 eV), resulting in almost isotropic diffusion. On the other hand, in the case of C6BN-III, the diffusion is anisotropic with Ebar = 0.173 eV for path 2 and Ebar = 0.109 eV for both paths 1 and 3. Using the Arrhenius equation, D ∝ exp(−Ebar/kBT), where D, kB, and T are the diffusion coefficient, Boltzmann constant, and operating temperature, respectively, we estimate for T = 300 K that the diffusion is 12 times faster along paths 1 and 3 than along path 2. The fact that Ebar is much smaller than for commercial Li-graphite batteries (0.45–1.20 eV)37,38 indicates that C6BN monolayers can provide excellent rate performance.

Specific Capacity and OCV

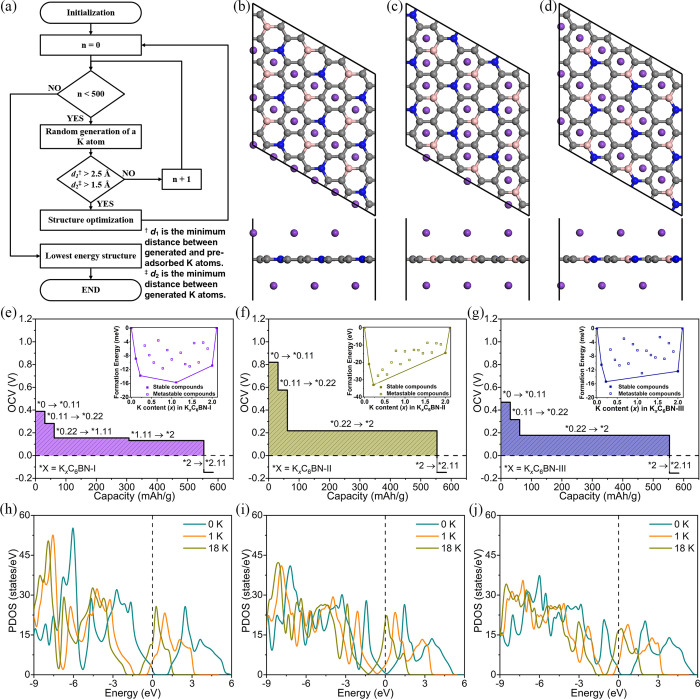
The specific capacity and OCV are two key electrochemical parameters of an anode material. For this reason, we study the concentration-dependent adsorption behavior of K on the C6BN monolayers. To accurately simulate the potassiation process during charging, we add K atoms one after the other to a 3 × 3 supercell. The lowest energy structure is obtained for each K concentration (1 to 19 K atoms) and C6BN monolayer by the method presented in Figure 5a, considering a total of 3660 structures. The relative stabilities of the intermediate KxC6BN structures are then determined relative to the pristine (C6BN) and maximally potassiated (K2.11C6BN) monolayers in terms of the formation energy39

graphic file with name am0c09451_m008.jpg 4

based on total energy calculations. The obtained convex hulls are shown as insets in Figure 5e–g. We find for K adsorption on C6BN-I four points (x = 0.11, 0.22, 1.11, and 2) on the convex hull, i.e., only these four intermediated KxC6BN structures are thermodynamically stable. For C6BN-II and C6BN-III there are only three thermodynamically stable intermediate KxC6BN structures (as x = 1.11 here is metastable). The intermediate structures during potassiation are shown in Figure S4.

Figure 5.

Figure 5

Open in a new tab

KxC6BN monolayers: (a) Flowchart of the script used to obtain the lowest energy structure when adding a K atom. No additional sites are found when the number of attempts n approaches 500. (b–d) Maximally potassiated C6BN monolayer. (e–g) OCV as a function of the specific capacity with insets showing the formation energy as a function of x. (h–j) Variation of the density of states during K adsorption.

The voltage associated with the potassiation KxC6BN + (y – x)K+ + (y – x)e– → KyC6BN is

graphic file with name am0c09451_m009.jpg 5

which yields the OCV curves shown in Figure 5e–g. For increasing K concentration, the OCV decreases in each case monotonically from an initial positive value. Once a negative value is reached, the K adsorption must stop to prevent dendrite formation. The voltage profile of C6BN-I in Figure 5e shows at the beginning a rapid drop to less than half of the initial value (0.39 V at x = 0; 0.15 V at x = 0.22) and afterward a wide K concentration range with almost constant value (0.13 V at x = 2) in that the battery can provide stable output voltage during discharge. At the K2C6BN to K2.11C6BN transition the voltage switches from positive to negative, suggesting that the maximal K concentration is reached at x = 2 (fully potassiated K2C6BN). The potential profiles of C6BN-II and C6BN-III in Figure 5f, g are very similar to that of C6BN-I. Therefore, all C6BN monolayers can store 2 K atoms per C6BN formula unit, which is almost twice the storage capacity of a graphite anode (1 K atom per 8 C atoms).15 We obtain average OCVs for the whole potassiation of 0.16, 0.27, and 0.20 V for C6BN-I, C6BN-II, and C6BN-III, respectively. These low values ensure that there is no risk of dendrite growth (K is stored homogeneously on the C6BN monolayers, see Figure S5) and that the assembled battery can provide high voltage.40

After determining the maximal K concentration, the specific capacity of the half-cell is obtained as C = nF/3.6MC6BN, where n, F, and MC6BN are the number of transferred electrons, Faraday constant, and mass of the C6BN monolayer, respectively. We find that fully potassiated K2C6BN provides a specific capacity of 553 mAh/g, outperforming graphite (279 mAh/g for KC8),15 Ti3C2 (192 mAh/g),41 MoN2 (432 mAh/g),42 and phosphorene (433 mAh/g for K0.5P).43 The maximal in-plane expansion due to K adsorption is found to be less than 1% for all C6BN monolayers. Together with the absence of structural deformations (Figure 4b–d), this points to robustness of anodes based on C6BN monolayers and, therefore, to excellent cyclability and long service life of the battery.

The conductivity of the anode material determines the Ohmic heating during battery operation. As mentioned previously, K adsorption comes along with electron transfer to the C6BN monolayers. For further evaluation of the consequences, we compare in Figure 5h–j the (partial) density of states of a C6BN monolayer before K adsorption with those after adsorption of 1 and 18 K atoms. All pristine C6BN monolayers show a band gap, consistent with our previous discussion. After adsorption of K they turn metallic, because the electrons transferred from K partially occupy the conduction band (higher occupation when more K is adsorbed). Therefore, adsorption of K significantly improves the conductivity of the C6BN monolayers.

Conclusion

Motivated by recent synthesis of a C6BN monolayer, we predict two new C6BN monolayers. They likely can be synthesized by the same experimental method because of structural and energetic similarity combined with good dynamical, thermal, and mechanical stabilities. The C6BN monolayers exhibit in-plane stiffnesses comparable to that of graphene while providing enhanced flexibility, which makes them interesting for flexible devices. An investigation of K adsorption demonstrates high specific capacities and low average OCVs for K-ion battery anodes based on C6BN monolayers. Also, low K diffusion barriers point to excellent rate performance. The conductivity of the C6BN monolayers is significantly improved when K is adsorbed. Overall, our results indicate that C6BN monolayers are excellent candidate materials for anodes of K-ion batteries, combining high specific capacity with low cost, high strength, excellent flexibility, low output voltage, excellent rate performance, and improved conductivity. This set of properties calls for experimental efforts to verify the predicted electrochemical performance of C6BN monolayers.

Acknowledgments

The research reported in this publication was supported by funding from King Abdullah University of Science and Technology (KAUST). Computational resources were provided by the Supercomputing Laboratory of KAUST. We also acknowledge support by the National Key Research and Development Program of China (2019YFB2203400), the 111 Project (B20030), and the UESTC Shared Research Facilities of Electromagnetic Wave and Matter Interaction (Y0301901290100201)

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.0c09451.

  • Structural details of the optimized C6BN nanotubes; total energy of C6BN-I for different k-meshes; top and side views of the unit cells of C6BN-II and C6BN-III; thermal stability of the C6BN monolayers at 1200 K; intermediate structures during potassiation; maximally potassiated C6BN monolayers at 300 K (PDF)

The authors declare no competing financial interest.

Supplementary Material

am0c09451_si_001.pdf (1MB, pdf)

References

  1. Meier P. J.; Wilson P. P. H.; Kulcinski G. L.; Denholm P. L. US Electric Industry Response to Carbon Constraint: A Life-Sycle Assessment of Supply Side Alternatives. Energy Policy 2005, 33, 1099–1108. 10.1016/j.enpol.2003.11.009. [DOI] [Google Scholar]
  2. Larcher D.; Tarascon J. M. Towards Greener and More Sustainable Batteries for Electrical Energy Storage. Nat. Chem. 2015, 7, 19–29. 10.1038/nchem.2085. [DOI] [PubMed] [Google Scholar]
  3. Kousksou T.; Bruel P.; Jamil A.; El Rhafiki T.; Zeraouli Y. Energy Storage: Applications and Challenges. Sol. Energy Mater. Sol. Cells 2014, 120, 59–80. 10.1016/j.solmat.2013.08.015. [DOI] [Google Scholar]
  4. Dunn B.; Kamath H.; Tarascon J.-M. Electrical Energy Storage for the Grid: A Battery of Choices. Science 2011, 334, 928–935. 10.1126/science.1212741. [DOI] [PubMed] [Google Scholar]
  5. Yang Z.; Zhang J.; Kintner-Meyer M. C. W.; Lu X.; Choi D.; Lemmon J. P.; Liu J. Electrochemical Energy Storage for Green Grid. Chem. Rev. 2011, 111, 3577–3613. 10.1021/cr100290v. [DOI] [PubMed] [Google Scholar]
  6. Mo R.; Rooney D.; Sun K.; Yang H. Y. 3D Nitrogen-Doped Graphene Foam with Encapsulated Germanium/Nitrogen-Doped Graphene Yolk-Shell Nanoarchitecture for High-Performance Flexible Li-Ion Battery. Nat. Commun. 2017, 8, 13949. 10.1038/ncomms13949. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cano Z. P.; Banham D.; Ye S.; Hintennach A.; Lu J.; Fowler M.; Chen Z. Batteries and Fuel Cells for Emerging Electric Vehicle Markets. Nature Energy 2018, 3, 279–289. 10.1038/s41560-018-0108-1. [DOI] [Google Scholar]
  8. Jia J.; Li B.; Duan S.; Cui Z.; Gao H. Monolayer MBenes: Prediction of Anode Materials for High-Performance Lithium/Sodium Ion Batteries. Nanoscale 2019, 11, 20307–20314. 10.1039/C9NR05708K. [DOI] [PubMed] [Google Scholar]
  9. Cui H.; Guo Y.; Ma W.; Zhou Z. 2 D Materials for Electrochemical Energy Storage: Design, Preparation, and Application. ChemSusChem 2020, 13, 1155–1171. 10.1002/cssc.201903095. [DOI] [PubMed] [Google Scholar]
  10. Gruber P. W.; Medina P. A.; Keoleian G. A.; Kesler S. E.; Everson M. P.; Wallington T. J. Global Lithium Availability. J. Ind. Ecol. 2011, 15, 760–775. 10.1111/j.1530-9290.2011.00359.x. [DOI] [Google Scholar]
  11. Yabuuchi N.; Kubota K.; Dahbi M.; Komaba S. Research Development on Sodium-Ion Batteries. Chem. Rev. 2014, 114, 11636–11682. 10.1021/cr500192f. [DOI] [PubMed] [Google Scholar]
  12. Kim H.; Kim J. C.; Bianchini M.; Seo D.-H.; Rodriguez-Garcia J.; Ceder G. Recent Progress and Perspective in Electrode Materials for K-Ion Batteries. Adv. Energy Mater. 2018, 8, 1702384. 10.1002/aenm.201702384. [DOI] [Google Scholar]
  13. Zhang W.; Liu Y.; Guo Z. Approaching High-Performance Potassium-Ion Batteries Via Advanced Design Strategies and Engineering. Science Advances 2019, 5, eaav7412. 10.1126/sciadv.aav7412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jian Z.; Xing Z.; Bommier C.; Li Z.; Ji X. Hard Carbon Microspheres: Potassium-Ion Anode Versus Sodium-Ion Anode. Adv. Energy Mater. 2016, 6, 1501874. 10.1002/aenm.201501874. [DOI] [Google Scholar]
  15. Luo W.; Wan J.; Ozdemir B.; Bao W.; Chen Y.; Dai J.; Lin H.; Xu Y.; Gu F.; Barone V.; Hu L. Potassium Ion Batteries with Graphitic Materials. Nano Lett. 2015, 15, 7671–7677. 10.1021/acs.nanolett.5b03667. [DOI] [PubMed] [Google Scholar]
  16. Yang J.; Yuan Y.; Chen G. First-Principles Study of Potassium Adsorption and Diffusion on Graphene. Mol. Phys. 2020, 118, e1581291 10.1080/00268976.2019.1581291. [DOI] [Google Scholar]
  17. Joshi R. P.; Ozdemir B.; Barone V.; Peralta J. E. Hexagonal BC3: A Robust Electrode Material for Li, Na, and K Ion Batteries. J. Phys. Chem. Lett. 2015, 6, 2728–2732. 10.1021/acs.jpclett.5b01110. [DOI] [PubMed] [Google Scholar]
  18. Bhauriyal P.; Mahata A.; Pathak B. Graphene-Like Carbon-Nitride Monolayer: A Potential Anode Material for Na- and K-Ion Batteries. J. Phys. Chem. C 2018, 122, 2481–2489. 10.1021/acs.jpcc.7b09433. [DOI] [Google Scholar]
  19. Sen S.; Moses K.; Bhattacharyya A. J.; Rao C. N. R. Excellent Performance of Few-Layer Borocarbonitrides as Anode Materials in Lithium-Ion Batteries. Chem. - Asian J. 2014, 9, 100–103. 10.1002/asia.201301037. [DOI] [PubMed] [Google Scholar]
  20. Matsui K.; Oda S.; Yoshiura K.; Nakajima K.; Yasuda N.; Hatakeyama T. One-Shot Multiple Borylation toward BN-Doped Nanographenes. J. Am. Chem. Soc. 2018, 140, 1195–1198. 10.1021/jacs.7b10578. [DOI] [PubMed] [Google Scholar]
  21. Liu X.; Ma X.; Gao H.; Zhang X.; Ai H.; Li W.; Zhao M. Valley-Selective Circular Dichroism and High Carrier Mobility of Graphene-Like BC6N. Nanoscale 2018, 10, 13179–13186. 10.1039/C8NR03080D. [DOI] [PubMed] [Google Scholar]
  22. Rao C. N. R.; Gopalakrishnan K. Borocarbonitrides, BxCyNz: Synthesis, Characterization, and Properties with Potential Applications. ACS Appl. Mater. Interfaces 2017, 9, 19478–19494. 10.1021/acsami.6b08401. [DOI] [PubMed] [Google Scholar]
  23. Rao C. N. R.; Pramoda K. Borocarbonitrides, BxCyNz, 2D Nanocomposites with Novel Properties. Bull. Chem. Soc. Jpn. 2019, 92, 441–468. 10.1246/bcsj.20180335. [DOI] [Google Scholar]
  24. Delley B. An All-Electron Numerical-Method for Solving the Local Density Functional for Polyatomic-Molecules. J. Chem. Phys. 1990, 92, 508–517. 10.1063/1.458452. [DOI] [Google Scholar]
  25. Delley B. From Molecules to Solids with the DMol3 Approach. J. Chem. Phys. 2000, 113, 7756–7764. 10.1063/1.1316015. [DOI] [Google Scholar]
  26. Grimme S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  27. Togo A.; Tanaka I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  28. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  29. Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. J.; Refson K.; Payne M. C. First Principles Methods Using CASTEP. Z. Kristallogr. - Cryst. Mater. 2005, 220, 567–570. 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
  30. Nozaki H.; Itoh S. Structural Stability of BC2N. J. Phys. Chem. Solids 1996, 57, 41–49. 10.1016/0022-3697(95)00088-7. [DOI] [Google Scholar]
  31. Qin Z.; Qin G.; Hu M. Origin of Anisotropic Negative Poisson’s Ratio in Graphene. Nanoscale 2018, 10, 10365–10370. 10.1039/C8NR00696B. [DOI] [PubMed] [Google Scholar]
  32. Wang H.; Li Q.; Pan H.; Gao Y.; Sun M. Comparative Investigation of the Mechanical, Electrical and Thermal Transport Properties in Graphene-Like C3B and C3N. J. Appl. Phys. 2019, 126, 234302. 10.1063/1.5122678. [DOI] [Google Scholar]
  33. Mouhat F.; Coudert F.-X. Necessary and Sufficient Elastic Stability Conditions in Various Crystal Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 224104. 10.1103/PhysRevB.90.224104. [DOI] [Google Scholar]
  34. Cadelano E.; Palla P. L.; Giordano S.; Colombo L. Elastic Properties of Hydrogenated Graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 235414. 10.1103/PhysRevB.82.235414. [DOI] [Google Scholar]
  35. Wei Y.; Wang B.; Wu J.; Yang R.; Dunn M. L. Bending Rigidity and Gaussian Bending Stiffness of Single-Layered Graphene. Nano Lett. 2013, 13, 26–30. 10.1021/nl303168w. [DOI] [PubMed] [Google Scholar]
  36. Zou X.; Liu Y.; Yakobson B. I. Predicting Dislocations and Grain Boundaries in Two-Dimensional Metal-Disulfides from the First Principles. Nano Lett. 2013, 13, 253–258. 10.1021/nl3040042. [DOI] [PubMed] [Google Scholar]
  37. Toyoura K.; Koyama Y.; Kuwabara A.; Oba F.; Tanaka I. First-Principles Approach to Chemical Diffusion of Lithium Atoms in a Graphite Intercalation Compound. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 214303. 10.1103/PhysRevB.78.214303. [DOI] [Google Scholar]
  38. Ganesh P.; Kim J.; Park C.; Yoon M.; Reboredo F. A.; Kent P. R. C. Binding and Diffusion of Lithium in Graphite: Quantum Monte Carlo Benchmarks and Validation of Van Der Waals Density Functional Methods. J. Chem. Theory Comput. 2014, 10, 5318–5323. 10.1021/ct500617z. [DOI] [PubMed] [Google Scholar]
  39. Jena N. K.; Araujo R. B.; Shukla V.; Ahuja R. Borophane as a Benchmate of Graphene: A Potential 2D Material for Anode of Li and Na-Ion Batteries. ACS Appl. Mater. Interfaces 2017, 9, 16148–16158. 10.1021/acsami.7b01421. [DOI] [PubMed] [Google Scholar]
  40. Eftekhari A. Low Voltage Anode Materials for Lithium-Ion Batteries. Energy Storage Materials 2017, 7, 157–180. 10.1016/j.ensm.2017.01.009. [DOI] [Google Scholar]
  41. Er D.; Li J.; Naguib M.; Gogotsi Y.; Shenoy V. B. Ti3C2 MXene as a High Capacity Electrode Material for Metal (Li, Na, K, Ca) Ion Batteries. ACS Appl. Mater. Interfaces 2014, 6, 11173–11179. 10.1021/am501144q. [DOI] [PubMed] [Google Scholar]
  42. Zhang X.; Yu Z.; Wang S.-S.; Guan S.; Yang H. Y.; Yao Y.; Yang S. A. Theoretical Prediction of MoN2 Monolayer as a High Capacity Electrode Material for Metal Ion Batteries. J. Mater. Chem. A 2016, 4, 15224–15231. 10.1039/C6TA07065E. [DOI] [Google Scholar]
  43. Sibari A.; Kerrami Z.; Kara A.; Hamedoun M.; Benyoussef A.; Mounkachi O.; Benaissa M. Adsorption and Diffusion on a Phosphorene Monolayer: A DFT Study. J. Solid State Electrochem. 2018, 22, 11–16. 10.1007/s10008-017-3703-3. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am0c09451_si_001.pdf (1MB, pdf)

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES