Abstract
Background
The Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) creatinine equation is routinely used to assess renal function but exhibits varying accuracy depending on patient characteristics and clinical presentation. The overall aim of the present study was to assess if and to what extent glomerular filtration rate (GFR) estimation based on creatinine can be improved.
Methods
In a cross-sectional analysis covering the years 2003–17, CKD-EPI was validated against measured GFR (mGFR; using various tracer methods) in patients with high likelihood of chronic kidney disease (CKD; five CKD cohorts, n = 8365) and in patients with low likelihood of CKD (six community cohorts, n = 6759). Comparisons were made with the Lund–Malmö revised equation (LMR) and the Full Age Spectrum equation.
Results
7In patients aged 18–39 years old, CKD-EPI overestimated GFR with 5.0–16 mL/min/1.73 m2 in median in both cohort types at mGFR levels <120 mL/min/1.73 m2. LMR had greater accuracy than CKD-EPI in the CKD cohorts (P30, the percentage of estimated GFR within 30% of mGFR, 83.5% versus 76.6%). CKD-EPI was generally the most accurate equation in the community cohorts, but all three equations reached P30 above the Kidney Disease Outcomes Quality Initiative benchmark of 90%.
Conclusions
None of the evaluated equations made optimal use of available data. Prospects for improved GFR estimation procedures based on creatinine exist, particularly in young adults and in settings where patients with suspected or manifest CKD are investigated.
Keywords: chronic kidney disease, creatinine, glomerular filtration rate, kidney function tests, renal failure
INTRODUCTION
In 2013, the Kidney Disease: Improving Global Outcomes work group recommended clinical laboratories to report estimated glomerular filtration rate (eGFR) in adults using the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) creatinine equation [1], unless an alternative equation improves accuracy of glomerular filtration rate (GFR) estimates [2]. This recommendation has made the use of CKD-EPI common practice in many hospitals. However, there is evidence suggesting that GFR estimations based on creatinine can be improved in patients with known or suspected chronic kidney disease (CKD) [3–9]. Moreover, the CKD-EPI equation is not intended for the entire life span, as the present formulation of the equation severely overestimates GFR in children [10, 11]. This restricted scope of the CKD-EPI equation also most likely explains its substantial overestimation and low accuracy among young adults [6, 11, 12], and the implausible changes in eGFR when switching from the recommended creatinine-based Chronic Kidney Disease in Children equation (‘Schwartz bedside') in paediatric care to CKD-EPI in adults [13]. Thus, although GFR estimation based on creatinine has a long history [14], it seems to still be an area where improvements can be made. Guidance in future refinement of GFR equations and estimation approaches are warranted from more solid empirical evidence from external validation studies.
It is essential to distinguish between ‘diagnostic correctness’ and ‘diagnostic predictiveness’ when investigating GFR estimation accuracy [15]. Diagnostic correctness represents GFR estimation accuracy stratified by measured GFR (clearance of external tracers, mGFR) and is analogous to sensitivity and specificity of a binary test. For binary tests, there is a trade-off between sensitivity and specificity, which for GFR equations corresponds to a trade-off between accuracy of eGFR among patients with and without renal impairment [15, 16]. However, when a diagnostic test is used in clinical practice typically, the index test (eGFR) but not the reference method (mGFR) is available. Diagnostic predictiveness represents GFR estimation accuracy stratified by eGFR, analogous to presenting predictive values of a binary test for use in the clinical situation [15]. Diagnostic predictiveness is dependent not only on sensitivity (accuracy at low mGFR) and specificity (accuracy at normal mGFR), but also on the clinical setting, e.g. primary versus specialized healthcare and the resulting distribution of patient characteristics, symptomatology and severity of renal disease [15, 17]. Most validation studies of GFR equations have focused on diagnostic correctness [15, 18] and have often pooled data from different populations. However, overall validation in pooled data adds little insight into diagnostic predictiveness, as the pooling makes the study population and underlying clinical setting poorly defined [19]. Additionally, few studies have studied diagnostic accuracy at two or more dimensions simultaneously, e.g. mGFR and age [9, 13, 20].
The overall aim of the present cross-sectional multicentre study was to assess if and to what extent diagnostic predictiveness of GFR estimation based on creatinine can be improved in two distinct clinical settings: (i) patients with high prior likelihood of CKD and (ii) patients with low prior likelihood of CKD. We compared CKD-EPI with one GFR equation developed specifically for use in patients with suspected or confirmed CKD [the Lund–Malmö revised equation (LMR)] [21] and one primarily intended for use in patients with no prior suspicion of CKD [the Full Age Spectrum (FAS) equation] [7, 22].
MATERIALS AND METHODS
Patient data
The European Kidney Function Consortium (EKFC), a new working group under the umbrella of the ERA-EDTA, has taken the initiative to pool and structure data on mGFR, plasma/serum creatinine, age, sex, height and weight of Europeans and non-black North Americans aged ≥18 years. Data were obtained from 11 cohorts (Supplementary data, Table S1) used in ongoing or published cross-sectional and longitudinal studies in France [7, 8, 23, 24], the UK [7–9, 25], Germany [7–9, 26], Norway [7, 8, 27], Sweden [4, 6, 9, 28, 29] and the USA [7, 8, 30, 31]. We classified the individual cohorts according to the clinical setting: (i) patients with high prior likelihood of CKD (labelled ‘CKD cohorts’; n = 5) and (ii) patients with low prior likelihood of CKD (labelled ‘community cohorts’; n = 6). Common causes for referral in the CKD cohorts were manifest or suspected diabetic nephropathy, interstitial nephritis, glomerulonephritis, nephrotic syndrome, haematuria, proteinuria, reflux nephropathy, myeloma, vasculitis, consideration of initiation of haemodialysis, control after organ transplantation and to dose drugs cleared by the kidneys. The community cohorts included studies of general populations, healthy older people and potential kidney donors.
Patient data were pooled in an anonymous database for the present study at Lund University, Sweden. All procedures involving subjects and data followed the ethical principles for medical research involving human subjects established in the World Medical Association Declaration of Helsinki. For this type of retrospective study, all extracted data were fully anonymous without any personal information, therefore informed consent was not required according to the Regional Ethical Board approval in Lund, Sweden, which approved the study (Dnr 2018/220). The present study was limited to the first measurement of GFR in each patient, resulting in 8365 patients in the CKD cohorts (median age 60 years, 45% females, median mGFR 58 mL/min/1.73 m2) and 6759 patients in the community cohorts (median age 59 years, 55% females, median mGFR 88 mL/min/1.73 m2; Table 1).
Table 1.
Patient characteristics in the CKD and community cohorts
| Variables | CKD cohorts (n = 8365) | Community cohorts (n = 6759) |
|---|---|---|
| Age, years | 60 (18–84) | 59 (30–84) |
| Females, n (%) | 3758 (45) | 3722 (55) |
| Weight, kg | 75 (45–118) | 75 (50–112) |
| Height, cm | 170 (151–188) | 168 (152–186) |
| Body surface area, m2 | 1.86 (1.42–2.34) | 1.85 (1.49–2.30) |
| BMI, kg/m2 | 25 (17–40) | 26 (19–38) |
| Plasma/serum creatinine, μmol/L | 102 (46–377) | 70 (47–122) |
| mGFR, mL/min/1.73 m2 | 58 (12–123) | 88 (41–128) |
| mGFR, n (%), mL/min/1.73 m2 | ||
| <30 | 1752 (21) | 30 (0.4) |
| 30–44 | 1310 (16) | 206 (3.0) |
| 45–59 | 1279 (15) | 452 (6.7) |
| 60–89 | 2306 (28) | 2891 (43) |
| 90–119 | 1426 (17) | 2824 (42) |
| ≥120 | 292 (3.5) | 356 (5.3) |
Descriptive measures given as median values (2.5 and 97.5 percentiles) if not stated otherwise
Laboratory methods
Details of laboratory methods used are summarized in Supplementary data, Table S2. Clearance methods for determination of GFR (mGFR) included renal clearance of inulin, chromium-51 labelled ethylene-diamine-tetra-acetic-acid (51Cr-EDTA) and iothalamate, and plasma clearance of iohexol, all considered acceptable as reference tests [32]. Samples of creatinine were obtained on the day of GFR measurement in all cohorts but Stockholm, where samples within 48 h of mGFR were accepted. All centres used creatinine assays traceable to isotope dilution mass spectrometry (IDMS) and standardized against primary reference material (National Institute of Standards and Technology Standard Reference Material 967), except for Kent, where it was measured directly with IDMS [25].
GFR equations
The CKD-EPI, FAS and LMR creatinine equations are presented in the Supplementary material. None of the included cohorts has been used for the development of any of the equations.
Statistical evaluation
Statistical evaluations were conducted using SPSS Statistics (version 25; IBM Corp.), STATA (version 14; StataCorp) and R (version 3.5.2), focussing on bias, precision and accuracy [33]. ‘Bias’ was defined as the median of the individual differences between eGFR and mGFR in mL/min/1.73 m2. ‘Precision’ was assessed as the interquartile range (IQR) of the differences eGFR – mGFR. ‘Accuracy’ was assessed from the absolute error |eGFR – mGFR|/mGFR and summarized as the median absolute percentage difference (absolute accuracy) and as the percentage of estimates within ±10% and ±30% of mGFR (P10 and P30). The complementary value 1 – P30 reflects the proportion of ‘large’ estimation errors [34]. The Kidney Disease Outcome Quality Initiative (K/DOQI) 2002 benchmark is to reach P30 accuracy of ≥90% [35, 36]. Equation performance was evaluated against this benchmark. We also assessed equation performance using pairwise comparisons with CKD-EPI equation as benchmark.
Non-parametric and asymptotic 95% confidence intervals (CIs) were calculated as measures of the statistical uncertainty in medians and proportions (P10/P30) of the overall results, respectively. CIs for IQR were estimated from the 2.5 to 97.5 percentiles of a simulated distribution obtained using a bootstrap method with 10 000 replications [37].
Diagnostic correctness—stratification by mGFR
Evaluation of diagnostic correctness implies analysis of equation performance (bias, precision and accuracy) stratified by mGFR, analogous to reporting sensitivity and specificity of a binary test [15]. We collapsed the two cohort types to improve statistical precision and presented diagnostic correctness in a simultaneous stratification by mGFR (<30, 30–59, 60–89, 90–119 and ≥120 mL/min/1.73 m2) and age (18–39, 40–59, 60–69 and ≥70 years). We also added sex (female and male) as a third dimension to this stratification.
Diagnostic predictiveness—stratification by estimated GFR
Evaluation of diagnostic predictiveness implies analysis of equation performance (bias, precision and accuracy) stratified by estimated GFR, analogous to presenting predictive values of a binary test for use in the clinical situation [15]. ‘Accuracy diagrams’ were constructed using quantile regression with fractional polynomials (linear, logarithm and square) as input to illustrate how the estimation errors varied across eGFR for each equation in the two population types [15, 16]. In the diagrams, we expressed estimation errors in mL/min/1.73 m2 using the quantiles (percentiles) Q10, Q50 (median bias) and Q90, where the accuracy interval (AI, Q10–Q90), reflects the largest estimation error with 80% certainty. The presentation was limited to the range between 1% and 99% percentile of the estimated GFR values for each equation to limit the statistical uncertainty in the tails of the quantile curves. The constancy of bias stratified by eGFR in the accuracy diagrams is an indicator of how similarly an equation behaves in the validation compared with the original development cohort [16, 18].
Performance in a given eGFR range of each equation cannot be directly compared because it is unlikely that all evaluated equations produce GFR estimates within that range for the same set of patients [15]. Results in tables were therefore stratified by eGFR values calculated from the CKD-EPI equation (eGFRCKD-EPI: <30, 30–59, 60–89, 90–119 and ≥120 mL/min/1.73 m2) to permit direct comparison of diagnostic predictiveness between the equations in the same patients. Since diagnostic predictiveness is dependent on pretest likelihood of disease [17], performance was evaluated for each population type (CKD and community) separately. Quantile regression was used in multivariable models to investigate how the median bias was dependent not only on eGFRCKD-EPI in the intervals defined above, but also on age, sex and body mass index (BMI; <18.5, 18.5–24.9, 25.0–29.9 and ≥30.0 kg/m2).
RESULTS
Overall results by cohort type
All three equations showed no major bias overall but substantial imprecision in both the CKD and community cohorts. In the CKD cohorts, none of them reached the K/DOQI 2002 benchmark of a P30 accuracy ≥90%, while they all reached this benchmark in the community cohorts (Table 2). LMR had better bias, higher precision and greater accuracy than both CKD-EPI and FAS in the CKD cohorts. The P30 difference was seven percentage points (P30 = 83.5% for LMR versus 76.6% for CKD-EPI and 76.5% for FAS), which corresponds to seven fewer estimation errors exceeding 30% per 100 tested CKD patients if LMR is used. Differences between the equations in the P10–P50 accuracy range were larger in the CKD than in the community cohorts (Figure 1). CKD-EPI was generally the most accurate equation in the community cohorts, as reflected by lower absolute percentage error and higher P10 than the two other equations, but the difference versus FAS was smaller than versus LMR (Table 2). Statistical evaluations of the pairwise comparisons in performance with CKD-EPI as benchmark are presented stratified by cohort type in Supplementary data, Table S3. All comparisons had narrow CIs as a result of the large cohort sizes. Results for the 11 individual cohorts are presented in Supplementary data, Table S4.
Table 2.
Bias, precision, accuracy (95% CIs) of CKD-EPI, FAS and LMR in the CKD and community cohorts
| Equations | Bias | Precision | Absolute error (%) | P10 (%) | P30 (%) |
|---|---|---|---|---|---|
| (mL/min/1.73 m2) | (mL/min/1.73 m2) | ||||
| CKD cohorts (n = 8365) | |||||
| CKD-EPI | 3.8 (3.5–4.1) | 16.6 (16.1–17.0) | 16.0 (15.6–16.4) | 33.4 (32.3–34.4) | 76.6 (75.7–77.5) |
| FAS | 3.3 (3.0–3.6) | 15.5 (15.0–16.0) | 15.3 (14.9–15.7) | 34.3 (33.3–35.3) | 76.5 (75.6–77.4) |
| LMR | −1.4 (−1.7, −1.1) | 14.4 (14.0–14.8) | 14.1 (13.8–14.5) | 35.9 (34.9–37.0) | 83.5 (82.7–84.3) |
| Community cohorts (n = 6759) | |||||
| CKD-EPI | 2.1 (1.8–2.6) | 17.2 (16.7–17.7) | 10.4 (10.1–10.7) | 48.6 (47.4–49.8) | 91.0 (90.4–91.7) |
| FAS | −1.4 (−1.8, −1.0) | 17.8 (17.3–18.3) | 10.8 (10.5–11.0) | 46.9 (45.7–48.0) | 91.9 (91.3–92.6) |
| LMR | −6.7 (−7.0, −6.4) | 16.7 (16.2–17.1) | 11.5 (11.2–11.8) | 43.7 (42.5–44.9) | 92.8 (92.1–93.4) |
Median bias (eGFR − mGFR) and precision (IQR) expressed in mL/min/1.73 m2, absolute error expressed as median absolute percentage error |eGFR − mGFR|/mGFR and P10 and P30 accuracy (percentage of GFR estimates within 10% and 30% of mGFR).
FIGURE 1.
The proportion of patients with sufficiently accurate estimated GFR (y-axis) at different requirements on highest percentage absolute error (x-axis), that is, from 10% to 50% (P10–P50) in relation to mGFR. (A) CKD cohorts and (B) community-based cohorts. In the example indicated by the arrows, P20 ranged between about 60% (CKD-EPI and FAS) and 66% (LMR) in (A) and was about 78% for all three equations in (B).
Diagnostic correctness—results stratified by mGFR, age and sex
LMR was generally the least biased equation at all ages in patients with known GFR (mGFR) <90 mL/min/1.73 m2 (Table 3). It was generally also more precise than CKD-EPI and generally more accurate than both CKD-EPI and FAS at all mGFR levels <90 mL/min/1.73 m2 (Supplementary data, Table S5A–C). CKD-EPI and FAS showed marked overestimations at younger ages at all mGFR levels <90 or 120 mL/min/1.73 m2, respectively (Table 3). As an example, CKD-EPI overestimated GFR by 13 mL/min/1.73 m2 (95% CI 11.5–15.5 mL/min/1.73 m2) on average in individuals <40 years of age with mGFR 30–59 mL/min/1.73 m2.
Table 3.
Diagnostic correctness (bias stratified by mGFR) in the two cohort types combined (CKD and community; n = 15 124)
| Age intervals (years) |
||||
|---|---|---|---|---|
| mGFR | 18–39 | 40–59 | 60–69 | ≥70 |
| <30, number | 101 | 270 | 338 | 1073 |
| CKD-EPI | 5.0 (3.6–7.0) | 1.4 (0.7–2.8) | 2.9 (2.1–3.9) | 2.0 (1.5–2.5) |
| FAS | 9.7 (7.8–12.7) | 6.6 (5.5–7.6) | 5.6 (4.8–6.4) | 2.9 (2.5–3.3) |
| LMR | 2.8 (1.6–3.8) | 1.2 (0.4–1.9) | 1.8 (1.1–2.5) | 0.2 (−0.2, 0.7) |
| 30–59, number | 381 | 656 | 767 | 1443 |
| CKD-EPI | 13.4 (11.5–15.5) | 3.7 (2.6–5.0) | 3.4 (2.0–4.4) | 4.0 (3.4–4.6) |
| FAS | 14.5 (13.0–16.4) | 7.1 (6.0–8.3) | 2.7 (1.8–3.8) | −0.2 (−0.8, 0.2) |
| LMR | 6.3 (4.1–8.6) | 1.3 (0.3–2.6) | 0.6 (−0.9, 1.9) | −0.3 (−0.8, 0.5) |
| 60–89, number | 736 | 1772 | 1556 | 1133 |
| CKD-EPI | 15.6 (13.6–17.3) | 8.0 (7.3–8.9) | 7.0 (6.2–7.6) | 5.9 (5.1–5.6) |
| FAS | 10.9 (9.5–12.2) | 4.4 (3.8–5.1) | −0.4 (−1.0, 0.3) | −4.5 (−5.5, −3.8) |
| LMR | 2.6 (1.4–3.8) | −0.1 (−0.7, 0.5) | −2.2 (−2.7, −1.6) | −4.4 (−5.2, −3.9) |
| 90–119, number | 1278 | 2088 | 798a | 147a |
| CKD-EPI | 10.4 (9.2–11.5) | −1.9 (−2.5, −1.4) | −5.3 (−6.1, −4.5) | −9.5 (−12.2, −7.0) |
| FAS | 4.4 (3.4–6.0) | −2.8 (−3.4, −2.2) | −9.5 (−10.8, −8.5) | −14.2 (−16.8, −12.7) |
| LMR | −9.0 (−9.8, −8.3) | −12.0 (−12.5, −11.5) | −15.1 (−16.0, −14.1) | −20.0 (−22.3, −18.1) |
| ≥120, number | 338 | 249 | –a | –a |
| CKD-EPI | −5.2 (−7.3, −2.8) | −23.9 (−26.4, −21.2) | ||
| FAS | −5.8 (−9.3, −3.3) | −17.9 (−21.4, −15.1) | ||
| LMR | −25.7 (−27.0, −24.2) | −32.4 (−35.7, −31.0) | ||
Median bias (eGFR – mGFR in mL/min/1.73 m2; 95% CIs) of CKD-EPI, FAS and LMR stratified by mGFR and age (years). The lowest bias is marked with bold and italic in each stratum.
mGFR intervals ≥120 were collapsed with 90–119 due to small numbers (n < 100).
LMR exhibited noticeable underestimation in patients with mGFR >90 mL/min/1.73 m2 (Table 3). CKD-EPI and FAS also yielded underestimations in patients with high mGFR but mostly to a lesser degree than LMR. LMR and CKD-EPI were both more precise than FAS at mGFR >90 mL/min/1.73 m2 (Supplementary data, Table S5A), but CKD-EPI was more accurate due to its lower bias (Supplementary data, Tables S5B and S5C). None of the three equations showed any consistent differences in bias among females and males (Supplementary data, Table S6).
Diagnostic predictiveness—results stratified by estimated GFR and cohort type
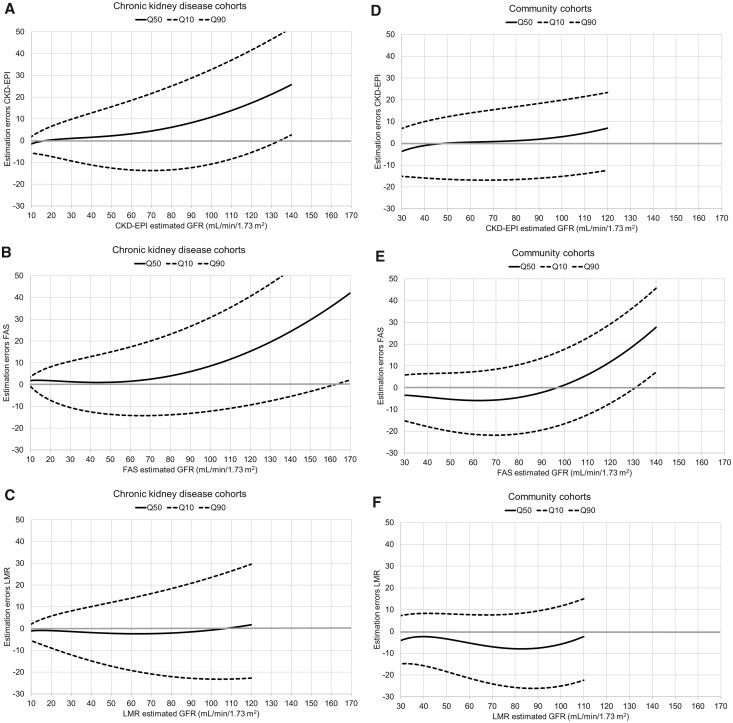
The accuracy diagrams further illustrate the substantial imprecision across eGFR for all three equations and in both two population types (Figure 2). Low and constant bias were seen both for LMR in the CKD cohorts and for CKD-EPI in the community cohorts at eGFR <120 mL/min/1.73 m2.
FIGURE 2.
Estimation errors (eGFR – mGFR in mL/min/1.73 m2 on the Y-axis) at different levels of eGFR on the X-axis (diagnostic predictiveness) in the CKD cohorts for (A) CKD-EPI, (B) FAS and (C) LMR and in the community cohorts for (D) CKD-EPI, (E) FAS and (F) LMR. The quantile regression curves for the estimation errors reflect bias (Q50; solid line) and estimation error with 80% certainty (accuracy interval Q10–Q90; dashed lines). Note that the curves are of different length as they are truncated at the 1 and 99% percentile of the estimated GFR values for each equation.
In the CKD cohorts, LMR had lower bias and higher accuracy than CKD-EPI in patients with eGFR >60 mL/min/1.73 m2 according to the CKD-EPI equation (eGFRCKD-EPI; Table 4). Estimates of the CKD-EPI equation >120 mL/min/1.73 m2 occurred among 9% of all patients in the CKD cohorts, most of them young (median age 21 years). The overestimation exceeded 20 mL/min/1.73 m2 on average for these patients when CKD-EPI or FAS was used, whereas the estimates from LMR were virtually unbiased for the same patients. In particular, FAS exhibited imprecision at eGFRCKD-EPI >120 mL/min/1.73 m2 (Table 4).
Table 4.
Diagnostic predictiveness (bias, precision and accuracy stratified by eGFR) in CKD cohorts
| eGFRCKD-EPI | Number | Age (years) | BMI (kg/m2) | Equation | Bias (mL/min/1.73 m2) | Precision (mL/min/1.73 m2) | Absolute error (%) | P30 (%) |
|---|---|---|---|---|---|---|---|---|
| <30 | 1504 | 72 | 27 | CKD-EPI | −0.3 (−0.7, 0.0) | 6.8 (6.4–7.2) | 18.1 (16.8–18.9) | 74.5 (72.3–76.7) |
| FAS | 2.0 (1.6–2.2) | 7.0 (6.7–7.4) | 19.6 (18.2–20.8) | 68.4 (66.1–70.8) | ||||
| LMR | −1.1 (−1.4, −0.8) | 6.7 (6.4, 7.2) | 17.8 (17.0–18.6) | 77.1 (75.0–79.3) | ||||
| 30–59 | 2419 | 65 | 27 | CKD-EPI | 1.6 (1.2–2.1) | 12.5 (11.9–13.3) | 15.3 (14.7–16.0) | 78.6 (77.0–80.3) |
| FAS | 1.9 (1.5–2.4) | 13.5 (13.0–14.2) | 15.8 (15.2–16.6) | 76.6 (74.9–78.3) | ||||
| LMR | −1.8 (−2.4, −1.4) | 12.6 (11.9–13.1) | 15.7 (14.9–16.4) | 81.1 (79.5–82.7) | ||||
| 60–89 | 2130 | 58 | 25 | CKD-EPI | 6.5 (5.6–7.2) | 19.7 (18.9–20.8) | 15.8 (14.8–16.6) | 76.3 (74.5–78.1) |
| FAS | 1.8 (1.0–2.7) | 19.7 (18.7–20.7) | 14.0 (13.3–14.5) | 82.1 (80.5–83.7) | ||||
| LMR | −0.7 (−1.4, 0.0) | 18.8 (18.0–19.9) | 13.8 (13.2–14.3) | 84.0 (82.4–85.5) | ||||
| 90–119 | 1578 | 46 | 24 | CKD-EPI | 10.1 (9.2–11.2) | 21.2 (20.2–22.4) | 13.6 (12.7–14.6) | 80.4 (78.5–82.4) |
| FAS | 7.3 (6.4–8.0) | 21.8 (20.5–23.2) | 12.6 (12.1–13.4) | 81.6 (79.6–83.5) | ||||
| LMR | −2.8 (−3.7, −1.8) | 20.8 (19.7–22.0) | 11.7 (11.1–12.3) | 90.1 (88.6–91.6) | ||||
| ≥120 | 734 | 21 | 21 | CKD-EPI | 22.5 (20.6–23.8) | 24.3 (22.3–25.8) | 21.1 (19.2–22.5) | 67.0 (63.6–70.4) |
| FAS | 20.4 (17.9–22.3) | 33.7 (30.7–37.1) | 19.6 (17.7–21.9) | 65.8 (62.4–69.2) | ||||
| LMR | −0.6 (−2.9, 1.1) | 25.2 (22.9–27.4) | 11.2 (10.6–12.4) | 88.7 (86.4–91.0) |
Estimation results for CKD-EPI, FAS and LMR (95% CI) stratified by eGFR (mL/min/1.73 m2) based on the CKD-EPI equation (eGFRCKD-EPI). The best result for each performance marker is marked with bold and italic in each stratum. Number of patients, median age (years) and BMI (kg/m2) are given in each stratum Median bias (eGFR − mGFR) and precision (IQR) expressed in mL/min/1.73 m2. Absolute error expressed as median absolute percentage error |eGFR − mGFR|/mGFR, and P10 and P30 accuracy (percentage of GFR estimates within 10% and 30% of mGFR).
In the community cohorts, changing equation from CKD-EPI to either FAS or LMR would not consistently improve accuracy in patients with eGFRCKD-EPI <120 mL/min/1.73 m2 (98% of all patients; Table 5). FAS exhibited increasing overestimations at high eGFRCKD-EPI in the community cohorts. The underestimation of LMR varied between 4 and 7 mL/min/1.73 m2 across all levels of eGFRCKD-EPI. None of the three equations was consistently more precise than the others across all levels of eGFRCKD-EPI.
Table 5.
Diagnostic predictiveness (bias, precision and accuracy stratified by eGFR) in community cohorts
| eGFRCKD-EPI | Number | Age (years) | BMI (kg/m2) | Equations | Bias (mL/min/1.73 m2) | Precision (mL/min/1.73 m2) | Absolute error (%) | P30 (%) |
|---|---|---|---|---|---|---|---|---|
| <60a | 473 | 78 | 27 | CKD-EPI | −0.2 (−1.2, 0.6) | 12.8 (12.2–14.5) | 13.7 (12.2–15.5) | 83.7 (80.4–87.1) |
| FAS | −4.3 (−5.0, −3.4) | 12.2 (10.7–13.9) | 13.9 (12.8–15.5) | 85.4 (82.2–88.6) | ||||
| LMR | −4.5 (−5.2, −3.3) | 11.9 (10.9–13.8) | 15.1 (13.8–16.1) | 82.5 (79.0–85.9) | ||||
| 60–89 | 2479 | 63 | 27 | CKD-EPI | 1.0 (0.4–1.7) | 18.2 (17.3–19.0) | 11.6 (11.1–12.2) | 85.7 (82.4–89.0) |
| FAS | −5.8 (−6.2, −5.2) | 15.5 (14.8–16.3) | 11.7 (11.2–12.2) | 92.7 (91.6–93.7) | ||||
| LMR | −7.1 (−7.6, −6.5) | 16.3 (15.5–17.1) | 12.4 (12.0–12.9) | 91.4 (90.3–92.5) | ||||
| 90–119 | 3687 | 55 | 26 | CKD-EPI | 3.0 (2.6–3.6) | 17.0 (16.4–17.7) | 9.2 (8.9–9.7) | 88.9 (87.6–90.1) |
| FAS | 2.2 (1.7–2.7) | 18.4 (17.7–19.2) | 9.6 (9.2–10.0) | 92.9 (92.1–93.7) | ||||
| LMR | −7.0 (−7.6, −6.5) | 17.2 (16.6–17.8) | 10.7 (10.3–11.0) | 94.8 (94.0–95.5) | ||||
| ≥120 | 120 | 29 | 23 | CKD-EPI | 12.9 (6.9–15.6) | 18.7 (15.4–22.5) | 12.8 (10.7–15.6) | 92.5 (87.7–97.3) |
| FAS | 19.3 (15.5–23.2) | 26.8 (20.5–29.7) | 16.3 (14.0–21.9) | 73.3 (65.3–81.4) | ||||
| LMR | −4.5 (−7.9, −1.8) | 19.1 (16.0–23.9) | 9.6 (8.6–10.6) | 98.3 (94.1–99.8) |
Estimation results for CKD-EPI, FAS and LMR (95% CI) stratified by eGFR (mL/min/1.73 m2) based on the CKD-EPI equation (eGFRCKD-EPI). The best result for each performance marker is marked with bold and italic in each stratum. Number of patients, median age (years) and BMI (kg/m2) are given in each stratum Median bias (eGFR − mGFR) and precision (IQR) expressed in mL/min/1.73 m2. Absolute error expressed as median absolute percentage error |eGFR − mGFR|/mGFR, and P10 and P30 accuracy (percentage of GFR estimates within 10% and 30% of mGFR). amGFR intervals <44 were collapsed with 45–59 due to small numbers (<100).
Multivariable quantile regression based on eGFRCKD-EPI, age, sex and BMI confirmed the substantial overestimations for CKD-EPI and FAS at high levels of eGFRCKD-EPI in the CKD cohorts (Table 6). Additionally, overestimation due to underweight was noted for all three equations and with similar magnitude. Age and sex did not have strong independent effects on bias for any of the three equations in the CKD cohorts. Bias varied more noticeably with eGFRCKD-EPI for CKD-EPI and FAS than for LMR also in the multivariable quantile regression models for the community cohorts (Table 6). In addition, bias varied according to age for CKD-EPI and LMR. Being male increased the underestimation of the LMR equation. BMI at any level was not related to bias for any of the three equations in the community cohorts.
Table 6.
Diagnostic predictiveness (bias stratified for eGFR) in CKD and community cohorts
| CKD cohorts |
Community cohorts |
|||||
|---|---|---|---|---|---|---|
| CKD-EPI | FAS | LMR | CKD-EPI | FAS | LMR | |
| Constanta | 1.9 (0.6 – 3.2) | 5.8 (4.6 – 7.1) | −2.3 (−3.5, −1.1) | −10.4 (−12.5, −8.3) | −7.7 (−9.9, −5.4) | −16.7 (−18.8, −14.7) |
| eGFRCKD-EPI | ||||||
| <30 | Reference | Reference | Reference | −b | −b | −b |
| 30 – 59 | 2.0 (1.0 – 3.0) | −0.8 (−1.8, 0.2) | −0.8 (−1.7, 0.2) | Reference (<60) | Reference (<60) | Reference (<60) |
| 60 – 89 | 6.7 (5.6 – 7.7) | −1.3 (−2.4, −0.3) | 0.2 (−0.8, 1.3) | 6.1 (4.6 – 7.7) | 0.7 (−0.9, 2.4) | 0.7 (−0.8, 2.2) |
| 90 – 119 | 10.1 (8.9 – 11.3) | 3.2 (2.0 – 4.4) | −1.4 (−2.6, −0.3) | 11.8 (10.1 – 13.4) | 9.9 (8.1 – 11.7) | 3.6 (2.0 – 5.2) |
| ≥120 | 19.5 (17.9 – 21.1) | 14.4 (12.8 – 16.0) | 0.2 (−1.3, 1.8) | 22.4 (19.2 – 25.7) | 26.3 (22.8 – 29.8) | 10.1 (6.9 – 13.3) |
| Age | ||||||
| <40 | Reference | Reference | Reference | Reference | Reference | Reference |
| 40 – 59 | −2.8 (−3.8, −1.7) | 0.2 (−0.9, 1.2) | 1.9 (0.9 – 2.9) | −0.7 (−2.0, 0.7) | −0.4 (−1.8, 1.0) | 3.4 (2.1 – 4.7) |
| 60 – 69 | −1.1 (−2.2, 0.1) | −1.9 (−3.1, −0.8) | 2.6 (1.6 – 3.7) | 2.5 (1.0 – 3.9) | −1.1 (−2.7, 0.4) | 5.7 (4.3 – 7.2) |
| ≥70 | 0.1 (−1.0, 1.2) | −3.0 (−4.0, −1.9) | 2.6 (1.5 – 3.6) | 10.0 (8.3 – 11.7) | 3.3 (1.5 – 5.1) | 11.0 (9.4 – 12.7) |
| Female | −0.3 (−1.0, 0.3) | −1.3 (−1.9, −0.6) | 0.2 (−0.4, 0.8) | 2.6 (1.9 – 3.3) | 1.0 (0.3 – 1.8) | 4.2 (3.5 – 4.8) |
| BMI | ||||||
| <18.5 | 6.9 (5.4 – 8.4) | 6.8 (5.3 – 8.3) | 6.8 (5.4 – 8.2) | −1.6 (−3.6, 0.3) | −0.9 (−3.0, 1.2) | −1.5 (−3.4, 0.4) |
| 18.5 – 24.9 | Reference | Reference | Reference | Reference | Reference | Reference |
| 25.0 – 29.9 | −2.2 (−3.0, −1.4) | −1.9 (−2.7, −1.1) | −1.9 (−2.7, −1.2) | 0.0 (−0.9, 0.8) | −0.2 (−1.1, 0.7) | −0.0 (−0.8, 0.8) |
| ≥30.0 | −2.5 (−3.4, −1.6) | −2.0 (−2.9, −1.1) | −2.1 (−2.9, −1.2) | −0.1 (−1.0, 0.9) | −0.1 (−1.1, 0.9) | 0.2 (−0.8, 1.1) |
Multivariable quantile regression estimates of median bias (mL/min/1.73 m2; 95% CI) by cohort type and subgroups of eGFR (mL/min/1.73 m2) according to the CKD-EPI equation (eGFRCKD-EPI), age (years), sex and BMI (kg/m2). The following example illustrates how to interpret the table by using CKD-EPI in the CKD cohort: a female (bias 1.9 − 0.3) aged 45 (bias −2.8) with a BMI of 17 (bias 6.9) and an eGFR of 125 (bias 19.5) results in an estimated eGFR with a bias of 1.9 – 0.3 – 2.8 + 6.9 + 19.5 = 25.2 mL/min/1.73 m2.
The constant reflects the estimated bias for an individual that belong to the reference group in all four dimensions (eGFR, age, sex and BMI).
mGFR intervals <30 were collapsed with 30 – 59 due to small numbers.
DISCUSSION
The salient finding of our comprehensive validation study is that prospects for improved GFR estimation based on creatinine still exist. The widely used CKD-EPI equation was generally sufficiently accurate with P30 exceeding 90% only in patients with low likelihood of CKD, but it was neither the most accurate equation in patients with known or suspected renal impairment nor the most accurate in young adults irrespective of their renal status. The FAS equation shared similar weaknesses as CKD-EPI when applied in the CKD cohorts and in young adults. LMR, on the other hand, was the most accurate equation among patients with high likelihood of CKD but did not perform as well in the community cohorts.
The explanation for the superior accuracy of LMR in patients with known or suspected renal impairment may be that the equation was formulated with the explicit goal to improve sensitivity (estimations in CKD patients) [21], whereas the goal of developing CKD-EPI was to improve specificity (estimations in patients with normal mGFR) [1]. The development of FAS was established from a mathematical construction based on age-average GFR and population-normalized serum creatinine valid for a healthy population [7, 22], which may explain its poor performance in patients with severe CKD.
The noticeable differences in performance depending on cohort type suggest that incorporation of prior information about the patient’s disease history (e.g. pre-test probability of CKD) could improve estimation accuracy. More complex GFR estimation procedures, either rule-based choice of equation depending on clinical setting or machine learning algorithms [38], would open up the possibility of fine-grained estimations depending on, for example, age or pre-test probability of CKD. Such estimation procedures should ideally be applicable for the full age span of children, adults and older people, and use of cystatin C when available, and could also incorporate other patient characteristics such as height and weight to avoid overestimation of GFR in underweight patients. However, complex algorithms are often less transparent than explicitly formulated estimating equations, which means that a thorough assessment of algorithm fairness and accountability is warranted before implementation [39].
A major strength of the present study was the large sample size, which allowed for evaluation of diagnostic accuracy with sufficient statistical precision in three dimensions simultaneously (mGFR, age and sex). Another strength was the consistent stratification on cohort type in the evaluation of diagnostic predictiveness, as clinical presentation and related prevalence of CKD is fundamental for the interpretation of eGFR. This stratification, for example, highlighted how the expected error in eGFR as well as the influence of low BMI may differ importantly depending on clinical setting. Yet, another strength was that measurement of plasma/serum creatinine was based on enzymatic assays or directly measured with IDMS in all but two cohorts that only partly used Jaffe. A major limitation was that available data did not allow for separate validation in additional subgroups such as patients with diabetes, malignant disease or with organ transplantation, or other ethnicities than Europeans and non-black North Americans. The initial CKD-EPI study suggested that eGFR based on creatinine must be multiplied by a correction factor (1.159) to yield valid results for African Americans [1]. It seems logical to use the same correction factor for other creatinine-based equations such as LMR (or FAS) to extend their applicability to African Americans. However, we believe that differences in creatinine generation should be corrected at the creatinine level rather than at the GFR level to avoid misleading interpretations that GFR differs between ethnicities. This may be achieved using the approach implemented in the FAS equations [7, 40].
A potential limitation of the generalizability of the results is that the Swedish data constituted two-thirds of patients in the CKD cohorts. However, none of these cohorts has been used for the development of LMR. The results of the Swedish cohorts were consistent with those from another European centre, Lyon (France), insofar as LMR performed better than CKD-EPI, while the latter was more accurate in the North American Chronic Renal Insufficiency Cohort Study (CRIC) cohort (Supplementary data, Table S3). One possible explanation for these divergent results may be differences in creatinine calibration. The CRIC study used Siemens creatinine enzymatic assay recalculated to the Roche Creatinine Plus assay, while the European cohorts all used enzymatic assays traceable to primary reference materials with values assigned by IDMS. Indirect creatinine calibration was also used in the development and initial validation of the CKD-EPI equation [1, 41], which may explain why this equation performs less well in CKD cohorts where creatinine assays directly traceable to IDMS are used [42]. Another explanation for diverging results across studies may be the use of different methods when measuring GFR. However, apart from renal clearance of inulin, considered the ‘gold standard’ for measuring GFR, renal clearance of iothalamate and 51Cr-EDTA as well as plasma clearance of iohexol have all been considered sufficiently accurate methods to measure GFR [32]. In addition, the single plasma sample method is highly concordant with a multiple sample strategy [43–45] providing that sampling time is adjusted according to estimated renal function [46] as used in the present cohorts.
In conclusion, the present study provides evidence that the widespread CKD-EPI equation is generally sufficiently accurate according to K/DOQI benchmark only in patients with low likelihood of CKD. Accuracy of GFR estimation based on creatinine can be improved in patients with known or suspected renal impairment and in young adults. Caution is necessary when using any of the three evaluated equations in clinical practice, as all exhibited considerable imprecision. Incorporation of the pre-test probability of CKD in the GFR estimation procedure can be an important step towards improved accuracy of eGFR across the full spectrum of age and renal function.
DATA SHARING
The EKFC dataset used in the present study is hosted by the Lund University Population Research Platform. Legal and ethical restrictions prevent public sharing of the dataset. Data can be made available for collaborations upon request to interested researchers but would generally require a new ethical permission and the permission of each of the data-owners. You can find contact information for the data host at https://www.lupop.lu.se/
SUPPLEMENTARY DATA
Supplementary data are available at ckj online.
Supplementary Material
ACKNOWLEDGEMENTS
The Chronic Renal Insufficiency Cohort Study (CRIC) was conducted by the CRIC Investigators and supported by the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK). The data from the CRIC Study reported here were supplied by the NIDDK Central Repositories. This manuscript was not prepared in collaboration with investigators of the CRIC study and does not necessarily reflect the opinions or views of the CRIC study, the NIDDK Central Repositories or the NIDDK. We also thank Physiologist Dr Marion Vallet and Physiologist Dr Renaud de la Faille for measuring glomerular filtration rate at Toulouse and Bordeaux University Hospital, respectively. J.B., U.N., M.C., L.D., N.E., B.O.E., F.G., A.G., E.J.L., T.M., A.D.R., E.S., P.D. and H.P. are members of the European Kidney Function Consortium.
FUNDING
Swedish Research Council (Vetenskapsrådet; grant no. 2019-00198).
AUTHORS’ CONTRIBUTIONS
J.B. and U.N. contributed to analysis and interpretation of data, drafting the article, provided intellectual content of critical importance to the work described and finally approved the version to be published. All other authors contributed with analysis and interpretation of data, revising the article, provided intellectual content of critical importance to the work described and finally approved the version to be published.
CONFLICT OF INTEREST STATEMENT
The results presented in this article have not been published previously in whole or part. U.N., J.B. and A.G. have developed the Lund–Malmö revised equation that was validated in the present study. H.P. has developed the Full Age Spectrum equation equation that was validated in the present study. U.N. and J.B. have received reimbursement for letting GE Healthcare AB distribute the computer programme OmniVis in radiology departments for estimation of glomerular filtration rate based on the creatinine equations presented in the current article, with no special preference of any of the included equations. U.N. has received lecture fees from GE Healthcare AB. M.C. has received grant support from BIOPAL, USA. R.N.D. is a Director of and minority shareholder in a University/NHS spin-out company, SpOtOn Clinical Diagnostics and has grant supports from NHS Health Technology Assessment and Juvenile Diabetes Research Foundation. N.E. has received lecture fees from Siemens Healthineers. B.O.E. has received lecture fees from Sanofi-Aventis. N.K. has received consulting fees or paid advisory boards, lecture fees and travel support from the following companies: Abbvie, Amgen, Astellas, Chiesi, Fresenius Medical Care, Gilead, Merck Sharp and Dohme, Neovii, Novartis, Roche, Sanofi and Shire. C.L. received consulting fees or paid advisory boards from CSL Behring and Novartis and lecture fees from Sandoz. E.S. has received lecture fees from Siemens Healthineers and Fresenius Kabi. All remaining authors declared no competing interests.
REFERENCES
- 1. Levey AS, Stevens LA, Schmid CH. et al; for the CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration). A new equation to estimate glomerular filtration rate. Ann Intern Med 2009; 150: 604–612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.KDIGO. Kidney Disease: Improving Global Outcomes (KDIGO) CKD Work Group. KDIGO 2012 clinical practice guideline for the evaluation and management of chronic kidney disease. Kidney Int Suppl 2013; 3: 1–150 [Google Scholar]
- 3. Murata K, Baumann NA, Saenger AK. et al. Relative performance of the MDRD and CKD-EPI equations for estimating glomerular filtration rate among patients with varied clinical presentations. Clin J Am Soc Nephrol 2011; 6: 1963–1972 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Björk J, Jones I, Nyman U, Sjöström P.. Validation of the Lund-Malmö, Chronic Kidney Disease Epidemiology (CKD-EPI) and Modification of Diet in Renal Disease (MDRD) equations to estimate glomerular filtration rate in a large Swedish clinical population. Scand J Urol Nephrol 2012; 46: 212–222 [DOI] [PubMed] [Google Scholar]
- 5. Evans M, van Stralen KJ, Schon S. et al. ; On the behalf of the ERA-EDTA Registry and the Swedish Renal Registry oration. Glomerular filtration rate-estimating equations for patients with advanced chronic kidney disease. Nephrol Dial Transplant 2013; 28: 2518–2526 [DOI] [PubMed] [Google Scholar]
- 6. Nyman U, Grubb A, Larsson A. et al. The revised Lund-Malmo GFR estimating equation outperforms MDRD and CKD-EPI across GFR, age and BMI intervals in a large Swedish population. Clin Chem Lab Med 2014; 52: 815–824 [DOI] [PubMed] [Google Scholar]
- 7. Pottel H, Hoste L, Dubourg L. et al. An estimated glomerular filtration rate equation for the full age spectrum. Nephrol Dial Transplant 2016; 31: 798–806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Pottel H, Delanaye P, Schaeffner E. et al. Estimating glomerular filtration rate for the full age spectrum from serum creatinine and cystatin C. Nephrol Dial Transplant 2017; 32: 497–507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Björk J, Bäck SE, Ebert N. et al. GFR estimation based on standardized creatinine and cystatin C: a European multicenter analysis in older adults. Clin Chem Lab Med 2018; 56: 422–435 [DOI] [PubMed] [Google Scholar]
- 10. Leion F, Hegbrant J, den Bakker E. et al. Estimating glomerular filtration rate (GFR) in children. The average between a cystatin C- and a creatinine-based equation improves estimation of GFR in both children and adults and enables diagnosing Shrunken Pore Syndrome. Scand J Clin Lab Invest 2017; 77: 338–344 [DOI] [PubMed] [Google Scholar]
- 11. Selistre L, Rabilloud M, Cochat P. et al. Comparison of the Schwartz and CKD-EPI equations for estimating glomerular filtration rate in children, adolescents, and adults: a retrospective cross-sectional study. PLoS Med 2016; 13: e1001979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Selistre L, De Souza V, Cochat P. et al. GFR estimation in adolescents and young adults. J Am Soc Nephrol 2012; 23: 989–996 [DOI] [PubMed] [Google Scholar]
- 13. Pottel H, Björk J, Bökenkamp A. et al. Estimating glomerular filtration rate at the transition from pediatric to adult care. Kidney Int 2019; 95: 1234–1243 [DOI] [PubMed] [Google Scholar]
- 14. Kemperman FA, Krediet RT, Arisz L.. Formula-derived prediction of the glomerular filtration rate from plasma creatinine concentration. Nephron 2002; 91: 547–558 [DOI] [PubMed] [Google Scholar]
- 15. Björk J, Grubb A, Sterner G. et al. Performance of GFR estimating equations stratified by measured or estimated GFR: implications for interpretation. Am J Kidney Dis 2015; 66: 1107–1108 [DOI] [PubMed] [Google Scholar]
- 16. Björk J, Grubb A, Sterner G. et al. Accuracy diagrams: a novel way to illustrate uncertainty of estimated GFR. Scand J Clin Lab Invest 2017; 77: 199–204 [DOI] [PubMed] [Google Scholar]
- 17. Björk J, Grubb A, Nyman U.. Variability in diagnostic accuracy can be estimated using simple population weighting. J Clin Epidemiol 2009; 62: 54–57 [DOI] [PubMed] [Google Scholar]
- 18. Rule AD, Kremers WK.. What is the correct approach for comparing GFR by different methods across levels of GFR? Clin J Am Soc Nephrol 2016; 11: 1518–1521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Rule AD. The CKD-EPI equation for estimating GFR from serum creatinine: real improvement or more of the same? Clin J Am Soc Nephrol 2010; 5: 951–953 [DOI] [PubMed] [Google Scholar]
- 20. Björk J, Nyman U, Berg U. et al. Validation of standardized creatinine and cystatin C GFR estimating equations in a large multicentre European cohort of children. Pediatr Nephrol 2019; 34: 1087–1098 [DOI] [PubMed] [Google Scholar]
- 21. Björk J, Grubb A, Sterner G. et al. Revised equations for estimating glomerular filtration rate based on the Lund-Malmö Study cohort. Scand J Clin Lab Invest 2011; 71: 232–239 [DOI] [PubMed] [Google Scholar]
- 22. Pottel H, Hoste L, Yayo E. et al. Glomerular filtration rate in healthy living potential kidney donors: a meta-analysis supporting the construction of the full age spectrum equation. Nephron 2017; 135: 105–119 [DOI] [PubMed] [Google Scholar]
- 23. Gagneux-Brunon A, Delanaye P, Maillard N. et al. Performance of creatinine and cystatin C-based glomerular filtration rate estimating equations in a European HIV-positive cohort. AIDS 2013; 27: 1573–1581 [DOI] [PubMed] [Google Scholar]
- 24. Gaillard F, Courbebaisse M, Kamar N. et al. Impact of estimation versus direct measurement of predonation glomerular filtration rate on the eligibility of potential living kidney donors. Kidney Int 2019; 95: 896–904 [DOI] [PubMed] [Google Scholar]
- 25. Kilbride HS, Stevens PE, Eaglestone G. et al. Accuracy of the MDRD (Modification of Diet in Renal Disease) study and CKD-EPI (CKD Epidemiology Collaboration) equations for estimation of GFR in the elderly. Am J Kidney Dis 2013; 61: 57–66 [DOI] [PubMed] [Google Scholar]
- 26. Schaeffner ES, Ebert N, Delanaye P. et al. Two novel equations to estimate kidney function in persons aged 70 years or older. Ann Intern Med 2012; 157: 471–481 [DOI] [PubMed] [Google Scholar]
- 27. Melsom T, Mathisen UD, Eilertsen BA. et al. Physical exercise, fasting glucose, and renal hyperfiltration in the general population: the Renal Iohexol Clearance Survey in Tromso 6 (RENIS-T6). Clin J Am Soc Nephrol 2012; 7: 1801–1810 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Grubb A, Horio M, Hansson LO. et al. Generation of a new cystatin C-based estimating equation for glomerular filtration rate by use of 7 assays standardized to the international calibrator. Clin Chem 2014; 60: 974–986 [DOI] [PubMed] [Google Scholar]
- 29. Björk J, Grubb A, Larsson A. et al. Accuracy of GFR estimating equations combining standardized cystatin C and creatinine assays: a cross-sectional study in Sweden. Clin Chem Lab Med 2015; 53: 403–414 [DOI] [PubMed] [Google Scholar]
- 30. Feldman HI, Appel LJ, Chertow GM. et al. ; Chronic Renal Insufficiency Cohort (CRIC) Study Investigators. The Chronic Renal Insufficiency Cohort (CRIC) study: design and methods. J Am Soc Nephrol 2003; 14: S148–S153 [DOI] [PubMed] [Google Scholar]
- 31. Rule AD, Bailey KR, Lieske JC. et al. Estimating the glomerular filtration rate from serum creatinine is better than from cystatin C for evaluating risk factors associated with chronic kidney disease. Kidney Int 2013; 83: 1169–1176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Soveri I, Berg UB, Björk J. et al. Measuring GFR: a systematic review. Am J Kidney Dis 2014; 64: 411–424 [DOI] [PubMed] [Google Scholar]
- 33. Stevens LA, Zhang Y, Schmid CH.. Evaluating the performance of equations for estimating glomerular filtration rate. J Nephrol 2008; 21: 797–807 [PMC free article] [PubMed] [Google Scholar]
- 34. Inker LA, Schmid CH, Tighiouart H. et al. Estimating glomerular filtration rate from serum creatinine and cystatin C. N Engl J Med 2012; 367: 20–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.NKF5. K/DOQI clinical practice guidelines for chronic kidney disease: evaluation, classification, and stratification. Part 5. Evaluation of laboratory measurements for clinical assessment of kidney disease. Guideline 4. Estimation of GFR. Am J Kidney Dis 2002; 39: S76–S92 [PubMed] [Google Scholar]
- 36. Earley A, Miskulin D, Lamb EJ. et al. Estimating equations for glomerular filtration rate in the era of creatinine standardization: a systematic review. Ann Intern Med 2012; 156: 785–795 [DOI] [PubMed] [Google Scholar]
- 37. Efron B, Tibshirani RJ.. An Introduction to the Bootstrap. New York, NY: Chapman and Hall; 1993 [Google Scholar]
- 38. Obermeyer Z, Emanuel EJ.. Predicting the future - big data, machine learning, and clinical medicine. N Engl J Med 2016; 375: 1216–1219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Lepri B, Oliver N, Letouzé E. et al. Fair, transparent, and accountable algorithmic decision-making processes. Philos Technol 2018; 31: 611–627 [Google Scholar]
- 40. Hoste L, Dubourg L, Selistre L. et al. A new equation to estimate the glomerular filtration rate in children, adolescents and young adults. Nephrol Dial Transplant 2014; 29: 1082–1091 [DOI] [PubMed] [Google Scholar]
- 41. Levey AS, Coresh J, Tighiouart H. et al. Measured and estimated glomerular filtration rate: current status and future directions. Nat Rev Nephrol 2020; 16: 51–64 [DOI] [PubMed] [Google Scholar]
- 42. Björk J, Bäck SE, Nordin G. et al. How valid are GFR estimation results from the CKD-EPI databases? Am J Kidney Dis 2018; 71: 446. [DOI] [PubMed] [Google Scholar]
- 43. Bird NJ, Peters C, Michell AR. et al. Comparison of GFR measurements assessed from single versus multiple samples. Am J Kidney Dis 2009; 54: 278–288 [DOI] [PubMed] [Google Scholar]
- 44. Delanaye P, Flamant M, Dubourg L. et al. Single- versus multiple-sample method to measure glomerular filtration rate. Nephrol Dial Transplant 2018; 33: 1778–1785 [DOI] [PubMed] [Google Scholar]
- 45. Eriksen BO, Schaeffner E, Melsom T. et al. Comparability of plasma iohexol clearance across population-based cohorts. Am J Kidney Dis 2019. pii: S0272-6386(19)31122-9, doi: 10.1053/j.ajkd.2019.10.008 (Epub ahead of print) [DOI] [PubMed] [Google Scholar]
- 46. Sterner G, Frennby B, Hultberg B. et al. Iohexol clearance for GFR-determination in renal failure–single or multiple plasma sampling? Nephrol Dial Transplant 1996; 11: 521–525 [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.