A New Benchmark Set for Excitation Energy of Charge Transfer States: Systematic Investigation of Coupled Cluster Type Methods

Abstract

The numerous existing publications on benchmarking quantum chemistry methods for excited states rarely include Charge Transfer (CT) states, although many interesting phenomena in, e.g., biochemistry and material physics involve the transfer of electrons between fragments of the system. Therefore, it is timely to test the accuracy of quantum chemical methods for CT states, as well. In this study we first propose a new benchmark set consisting of dimers having low-energy CT states. On this set, the vertical excitation energy has been calculated with Coupled Cluster methods including triple excitations (CC3, CCSDT-3, CCSD(T)(a)*), as well as with methods including full or approximate doubles (CCSD, STEOM-CCSD, CC2, ADC(2), EOM-CCSD(2)). The results show that the popular CC2 and ADC(2) methods are much less accurate for CT states than for valence states. On the other hand, EOM-CCSD seems to have similar systematic overestimation of the excitation energies for both types of states. Among the triples methods the novel EOM-CCSD(T)(a)* method including noniterative triple excitations is found to stand out with its consistently good performance for all types of states, delivering essentially EOM-CCSDT quality results.

1. Introduction

Charge transfer (CT) states are special types of electronically excited states that play a key role in processes related to molecular conductance and electron transfer properties. As these states tend to show up in larger molecules and complexes, approximate theoretical methods need to be invoked for their description.

Popular approaches based on time-dependent density functional theory (TDDFT) are known to underestimate considerably the excitation energies of CT states, at least when standard functionals are employed.¹ It was shown, e.g., in refs (1−4) that most functionals do not perform well for valence and CT type states at the same time, and only hybrid functionals which include a substantial amount of Hartree–Fock exchange (often close to 100%) are capable of giving reasonable results for CT states.⁴ Better performance is observed with long-range corrected (LRC) hybrid models.^1,3,5,6 Although these functionals were designed to provide the correct long-distance charge transfer behavior,³ this is essentially achieved via the inclusion of exact exchange.⁷ At the same time, LRCs introduce instability issues for triplet states,⁸ and the range separation parameter also turns out to be system dependent. The latter problem can be solved by the various optimally tuned range separated hybrid functionals,^7,9 and while this does yield improved results, it also leads to an escalation of the computational cost. The same conclusion holds for double hybrids in the context of CT states.¹⁰ Recent studies also found the restricted open-shell Kohn–Sham approach a promising way of obtaining CT states by DFT methods.^11,12 For more recent developments in the treatment of charge transfer states within TDDFT, the reader is referred to two excellent reviews on the subject.^13,14 Due to these uncertainties, there is still a demand for wave function methods which are economic enough to treat large systems of chemical interest or at least can provide reliable benchmark results to test and calibrate lower level methods.

Yet, the performance of quantum chemical methods has never been systematically examined for CT states. Typically, earlier studies included only one or two systems with only one state per system.^2−4,15 In these works the investigated methods included several DFT functionals, CIS, and SAC-CI. The most systematic study has been published by Dutta et al.¹⁶ which includes six states of two systems, and results for various Coupled Cluster (CC) ansätze are presented. The importance of a wider systematic study is emphasized by the observation that certain popular methods show a severe inconsistency in the description of Rydberg type electronic states,^17,18 which poses a warning that not all techniques may be well suited for CT states, either.

Over the past few years, a large number of test calculations have been presented on excited state methods. Most of them used the benchmark set established by Thiel and co-workers¹⁹ (often referred as the Mülheim set) and concentrated on vertical¹⁷⁻³⁰ or 0–0 excitation energies.³¹⁻³⁴ See a recent review for further details.³⁵ More recently, the scope of the benchmark studies has been extended to potential energy surfaces^36,37 as well.

Realizing that the information on the performance of different methods on charge transfer states is rather sparse,^29,35 in this paper we aim at establishing a benchmark set from local and CT type states of two-component molecular complexes by providing high level (CCSDT and CCSDT-3) benchmark vertical excitation energies. This set is then used to characterize the reliability of various methods of the Coupled Cluster hierarchy.

2. Computational Details

2.1. Excitation Energy Calculations

In this study, Coupled Cluster type methods are used to calculate the excitation energies corresponding to CT states. In this respect, the CCSD level approximation termed either EOM-CCSD³⁸⁻⁴⁰ (Equation of Motion Coupled Cluster with Singles and Doubles) or CCSD-LR^41,42 (CCSD Linear Response; no distinction between EOM and LR will be made here since these two give the same excitation energy, so for our purpose they are equivalent) represents a standard starting point which may be too expensive for larger applications, while not accurate enough for certain high accuracy demands. Therefore, on one hand, we include lower cost methods, such as the second-order approximations to CCSD, like the popular CC2⁴³ and ADC(2)^44,45 (second order Algebraic Diagrammatic Construction) methods, as well as EOM-CCSD(2)⁴⁶ (second order approximation to Equation-of-Motion Coupled Cluster Singles and Doubles, also known as EOM-MBPT(2)⁴⁷) and STEOM-CCSD (Similarity Transformed Equation-of-Motion Singles and Doubles).⁴⁸⁻⁵⁰ The latter, though cheaper than EOM-CCSD, cannot be considered as an approximation thereof:³⁵ STEOM-CCSD aims at eliminating the doubles–singles (DS) block of the Hamiltonian matrix, thereby making it possible to obtain excitation energies solely in the space of single excitations. This is done by a similarity transformation of the untruncated Hamiltonian matrix which changes also the SS block and makes certain blocks (e.g., ST) smaller, in this respect including some contributions of connected triple excitations.

On the other hand, we also go beyond the CCSD approximation by including the effect of connected triple excitations as the next step of hierarchical improvement. For some of the systems under inspection, calculations even at the EOM-CCSDT level^51,73 were possible. Several approximate triples methods (iterative and noniterative) have been included in the present study, e.g., the iterative EOM-CCSDT-3⁵² and the closely related CC3-LR⁵³ variant, as well as the recent, noniterative EOM-CCSD(T)(a)* method of Matthews and Stanton.⁵⁴ EOM-CCSD(T)(a)*, while economic since noniterative, gives results very close to EOM-CCSDT, its error being similar to that of EOM-CCSDT-3.¹⁷

As a reference, we use EOM-CCSDT for the smaller systems, while EOM-CCSDT-3 results are used for this purpose when treating all complexes. The justification for this choice will be apparent from the discussions below, as EOM-CCSDT-3 is found to perform better than CC3-LR in the case of CT type states. (In the following the designation EOM or LR will be skipped for brevity, which should not cause any misunderstanding since only excitation energies are reported in this paper.)

Several program systems have been used in this study. CC2, CCSD, CCSD, CCSDT, CCSDT-3, CC3, and CCSD(T)(a)* calculations have been performed using CFOUR,⁵⁵ while for ADC(2) calculations TURBOMOLE⁵⁶ has been used with the resolution of identity (RI) approximation. By evaluating CC2 results also obtained this way, it was found that the RI approximation does not influence the excitation energies by more than 0.01 eV. STEOM-CCSD calculations were done with Orca.⁵⁷ The STEOM-CCSD calculations require an active space within both the occupied and the virtual spaces. The process of selecting this active space has already been made automatic using a procedure based on configuration interaction singles averaged densities.⁵⁸ In the present study, the default value (0.01) is used for both the occupied (OTHRESH) and virtual (VTHRESH) active space selection thresholds, in all but one case: for the system containing a tetrafluoroethylene and an ethylene molecule separated by 3.5 Å, both values are set to 0.001 to reach convergence with respect to the size of the active space.

2.2. Basis Set Issues

In all excitation energy calculations the cc-pVDZ basis set of Dunning and co-workers⁵⁹ was used with the core electrons uncorrelated. This relatively small basis set was chosen to ensure that a statistically significant number of states can be calculated with the various triples corrections included. Normally, the use of diffuse functions is also warranted for studying molecular complexes, as they might be important for the accurate description of intermolecular interaction energies. However, the presence of diffuse functions in the calculation will result in the appearance of Rydberg states, some of them close in energy to the CT ones: at the equilibrium geometry of the complexes used in this study, we have experienced a large density of states with a strong mixing of several dominant contributions of different nature, which often renders the assignment of CT states impossible. (The problem of assignment near surface crossings will be discussed below.) Since the aim of this study is to understand the performance of different methods for CT states and not to seek the best absolute accuracy for the interaction energy, we decided not to include the diffuse functions in the basis set and allow the investigation of “clean” CT states instead. While this procedure should answer the scientific question we raised, it leaves one important question open, namely, the role and magnitude of the mixing of Rydberg and CT type states, which needs to be investigated in the future. This, however, cannot be done at isolated points; rather, it necessitates the investigation of potential energy surfaces (curves) of excited states, which is a more involved procedure than what we follow in the present study.

The other question concerns whether the conclusions reached with a double-ζ basis hold in larger basis sets. For this reason calculations with the cc-pVTZ basis set⁵⁹ have also been performed for certain CT states, and the comparison to cc-pVDZ results is presented in Table 1. The excitation energies of the CT states decrease significantly when using the larger basis set; however, the change in relative accuracy is less pronounced: CCSDT-3 still gives very close results to CCSDT, and neither the accuracy of the triples methods nor that of STEOM-CCSD does change significantly. The overestimation by CCSD increases slightly, while the underestimation of CC2 decreases by the same amount. This latter finding is related to the fact that, compared to triples methods, both CC2 and CCSD underestimate the decrease of the excitation energy upon the extension of the basis set. As these differences do not alter the conclusions of this paper, we refrain from the use of the cc-pVTZ basis set in order to allow high level triples calculations for a significant number of states but keep these differences in mind while making final conclusions.

Table 1. Comparison of the Excitation Energies (in eV) of Some Complexes Calculated with cc-pVDZ (DZ) and cc-pVTZ (TZ) Basis Sets with Various CC Methods^a.

	state
	CT1		CT5		CT2		CT14		ΔEexcb
	DZ	TZ	DZ	TZ	DZ	TZ	DZ	TZ	DZ	TZ
CC2	5.97	5.73	6.33	6.23	5.18	4.83	10.16	9.84	–0.63	–0.52
CCSD(2)	6.72	6.66	7.14	7.09	6.10	6.02	10.74	10.46	0.13	0.38
CCSD	6.90	6.66	7.33	7.08	6.28	5.97	10.87	10.54	0.30	0.39
STEOM-CCSD	6.43	6.13	7.06	6.81	5.85	5.45	10.62	10.26	–0.05	–0.02
CCSD(T)(a)*	6.63	6.34	7.03	6.90	5.83	5.38	10.52	10.15	–0.04	0.01
CC3	6.53	6.15	6.83	6.67	5.75	5.23	10.46	10.08	–0.15	–0.15
CCSDT-3	6.62	6.28	7.09	6.82	5.90	5.43	10.56	10.19	-	-
CCSDT	6.64	6.28	7.04	6.76

^aCT states can be identified in Table 2.

^bMean error of the four CT states with respect to CCSDT-3.

2.3. Characterization of CT States

The identification and characterization of electronic states was performed by inspecting the natural orbitals of the difference density of the ground and excited states,⁶⁰ as well as by examining the numerical descriptors defined by Plasser and co-workers.^61,62

The natural orbitals of the difference density can conveniently be used to graphically illustrate in the one-electron picture the dominant orbitals where the excited electron comes from (“from” orbital) and where it goes (“to” orbital). The corresponding “occupation numbers”, which are negative for “from” orbitals and positive for the “to” orbitals, also inform about the weight of these orbitals in the wave function. In most cases there is only one orbital with a substantial occupation number for both types, presenting a nice simple description of the excitation corresponding to chemical intuition. For the criteria of the simple orbital picture to hold see the recent paper by Kimber and Plasser.⁶³ However, when dealing with a large number of excited states, the inspection of these orbitals can be tedious; therefore, in an automated procedure well-defined numerical descriptors are more useful.

The CT or local nature of excited states can be evaluated using the Ω-descriptors introduced by Plasser and co-workers,^61,62 based on the one-particle transition density. In this formalism, the CT character (ω_CT) is defined as the weight of configurations with charges separated on different fragments. An excitation is more local if ω_CT is closer to 0, while it has a stronger charge transfer character if it is closer to 1.

The average exciton position (ω_POS) is given by the mean of ω_POSi and ω_POSf, which represent the average position of the initial and the final orbitals, respectively. In a system consisting of just two fragments, ω_POS ranges from 1 to 2, with ω_POS ≈ 1 corresponding to a local excitation on the first fragment and ω_POS ≈ 2 to one on the second fragment, while ω_POS ≈ 1.5 values are typical for CT and completely delocalized (one-to-one mixed) Frenkel-type excitations.

Similarly to ω_POS, ω_PR is the arithmetic mean of ω_PRi and ω_PRf, which gives the participation ratio of the fragments in the initial and final orbitals, respectively. Thus, ω_PR ≈ 1 holds for both clear CT and local excitations, while in a two-component system, ω_PR ≈ 2 is seen for completely delocalized Frenkel-type, as well as charge resonance states.⁶¹

This analysis tool depends on the definition of the fragments corresponding to the chromophores. In the present case, since the systems are molecular complexes, this definition is trivial.

The characters have been calculated with the TheoDORE program and libwfa library developed by Plasser et al.⁶⁴⁻⁶⁷ at the CC2 and CCSD levels, utilizing the CFOUR⁵⁵/libwfa interface developed by us. It has to be noted that, unlike the TheoDORE interface to the TURBOMOLE⁵⁶ program that approximates the one-particle transition density matrix with the single excitation part of the solution vector in the CC2 case, this analysis utilizes the entire one-particle transition density to obtain the descriptors.

Since the Ω descriptors are available only for CCSD and CC2, for the other methods the dominant character of the states was obtained by first classifying the states using the ω_CT characters calculated at the CCSD level (see Table 2), followed by the comparison of the dominant singles contributions of the eigenvectors obtained with the given method to their CCSD counterparts.

Table 2. Excitation Energy, Assignment of the States, ω_CT, ω_PR, and ω_POS Characters, and AEL Values of All Considered States Calculated at the CCSD Level.

system (1–2)	assignment	state	Eexc, / eV	ωPOS	ωPR	ωCT	AEL	CT state no.
ammonia–fluorine	2 → 2	11E	4.08	1.99	1.02	0.02	1.10
	1 → 2(1)	21A1	6.90	1.41	1.29	0.76	1.10	CT1
	1 → 1(2)	31A1	8.04	1.09	1.20	0.17	1.07
acetone–fluorine	2 → 2	21A′	4.27	2.00	1.00	0.00	1.09
	2 → 2	11A″	4.27	2.00	1.00	0.00	1.09
	1 → 1	21A″	4.44	1.00	1.00	0.00	1.08
	1 → 2	31A″	6.28	1.48	1.04	0.96	1.11	CT2
pyrazine–fluorine	2 → 2	21A1	4.25	2.00	1.01	0.01	1.09
	2 → 2	11B1	4.28	2.00	1.00	0.00	1.09
	1 → 1	31A1	4.44	1.00	1.00	0.00	1.10
	1 → 1	21B1	5.14	1.00	1.00	0.00	1.12
	1 → 1	11A2	5.25	1.00	1.00	0.00	1.11
	1 → 1	11B2	6.10	1.00	1.00	0.00	1.11
	1 → 2	21B2	6.77	1.51	1.02	0.98	1.12	CT3
	1,2 → 2	21A2	6.73	1.68	1.42	0.64	1.12	CT4
ammonia–oxygendifluoride	2 → 2	21A′	4.33	2.00	1.00	0.00	1.09
	2 → 2	11A″	5.04	2.00	1.00	0.00	1.08
	2 → 2	21A″	6.78	2.00	1.00	0.00	1.10
	2 → 2	31A′	7.01	1.96	1.09	0.08	1.10
	1 → 2	41A′	7.33	1.52	1.15	0.86	1.11	CT5
	2 → 2	31A″	7.51	2.00	1.01	0.01	1.13
	1 → 1	51A′	7.98	1.02	1.05	0.04	1.06
acetone–nitromethane	2 → 2	21A	4.08	2.00	1.01	0.01	1.09
	1 → 1	31A	4.44	1.01	1.01	0.01	1.08
	2 → 2	41A	4.50	1.99	1.02	0.02	1.09
	1(2) → 2	51A	6.75	1.55	1.23	0.80	1.11	CT6
	2(1) → 2	61A	6.62	1.89	1.26	0.20	1.10
ammonia–pyrazine	2 → 2	21A′	4.51	2.00	1.00	0.00	1.10
	2 → 2	11A″	5.14	2.00	1.00	0.00	1.12
	2 → 2	21A″	5.30	2.00	1.00	0.00	1.11
	2 → 2	31A′	6.17	2.00	1.00	0.00	1.11
	2 → 2	31A″	7.20	2.00	1.00	0.00	1.14
	2 → 2	41A′	7.13	2.00	1.00	0.00	1.06
	1 → 2,1	51A′	7.93	1.38	1.45	0.63	1.10	CT7
	1 → 1,2	61A′	7.59	1.15	1.37	0.27	1.08
pyrrole–pyrazine (H-bonded)	2 → 2	11B2	4.49	1.99	1.02	0.02	1.10
	2 → 2	11B1	5.11	2.00	1.00	0.00	1.12
	2 → 2	11A2	5.36	1.99	1.02	0.02	1.11
	1 → 2	21B1	5.60	1.50	1.00	1.00	1.12	CT8
	1 → 2	21A1	6.32	1.49	1.04	0.97	1.13	CT9
	2 → 2	21B2	6.20	1.98	1.03	0.03	1.11
	1 → 2	31A1	6.47	1.50	1.01	0.99	1.11	CT10
	1 → 1	41A1	6.65	1.02	1.04	0.04	1.13
pyrrole–pyrazine (stacked)	2 → 2	21A′	4.44	2.00	1.01	0.01	1.10
	2 → 2	31A′	5.08	1.95	1.11	0.08	1.12
	2 → 2	11A″	5.22	2.00	1.01	0.01	1.11
	1 → 2	21A″	5.68	1.50	1.18	0.84	1.10	CT11
	2 → 2	31A″	6.10	1.97	1.06	0.05	1.11
	1 → 2,1	41A′	6.22	1.39	1.41	0.66	1.11	CT12
	1 → 2,1	51A′	6.52	1.38	1.47	0.61	1.11	CT13
tetrafluoroethylene–ethylene (5 Å)	1 → 1	11B2	7.52	1.00	1.00	0.00	1.06
	2 → 2	11B1	8.73	1.96	1.08	0.00	1.04
	2 → 2	21B2	8.83	2.00	1.00	0.00	1.08
	1 → 1	21B1	9.14	1.03	1.07	0.00	1.06
	1 → 2	51B1	10.87	1.50	1.01	0.99	1.09	CT14
tetrafluoroethylene–ethylene (3.5 Å)	1 → 1	11B2	7.47	1.00	1.01	0.01	1.06
	1,2 → 2(1)	11B1	8.24	1.68	1.75	0.24	1.05
	2 → 2	21B2	8.76	1.99	1.01	0.01	1.08
	1(2) → 1,2	21B1	9.05	1.34	1.72	0.34	1.08
	1(2) → 1,2	31B1	9.19	1.26	1.64	0.05	1.06

2.4. Structures

With one exception, the structures used in the calculations have been obtained by a full-dimensional optimization for the ground states of the complexes, thereby all totally symmetric coordinates were allowed to change. These optimizations were performed at the CC2/cc-pVDZ level.

The pyrrole–pyrazine stacked structure was, for technical reasons, obtained as follows. The structures of the monomers were taken from the Mülheim set¹⁹ and placed above each other in such a way that their planes are parallel and their main axes perpendicular to their planes coincide. Moreover, the N–H bond of pyrrole was set to be perpendicular to the line defined by the two nitrogen atoms of pyrazine. Then, only the distance of the two planes was optimized at the MP2/aug-cc-pVDZ level, resulting in a minimum-energy distance of 3.41 Å. The reason for this constrained optimization is that all attempts of fully optimizing the complex resulted in a structure where the two molecules end up in a single plane.

The structures are presented in the Supporting Information.

3. New Charge Transfer Benchmark Set for Two-Component Molecular Complexes

The new benchmark set we propose here consists of molecular complexes with low-lying charge transfer states. This time we do not consider well-known examples of intramolecular CT states since in such cases the chromophores need to be well separated, resulting in quite large molecules which would prevent high level reference calculations.

To test quantum chemical methods on CT states, only a few systems had been suggested and used in the literature. The tetrafluoroethylene–ethylene (C₂F₄–C₂H₄) and ammonia–fluorine (NH₃–F₂) complexes appear as test systems in several applications.^1,2,4,16 Using the former system, Dreuw and Head-Gordon^1,2 tested different TDDFT methods and compared the results to those obtained with the CIS method. Zhao and Truhlar⁴ used the ammonia–fluorine system in their investigation of various TDDFT approaches. In these studies only one CT state per system was considered; thus only limited information on the performance of the methods could be obtained. Dutta et al.¹⁶ also used these two systems to test STEOM-CCSD and its variants with respect to CCSDR(3)⁶⁸ reference values but included no more than six states altogether. This set is clearly insufficient, in particular, since most of the states considered were higher lying ones involving nonvalence orbitals. Recently, Mester and Kállay⁶⁹ tested approximate local CC approaches including also the CT state of the tetrafluoroethylene–ethylene system.

When finding additional systems, we had two guiding principles: the molecules are required to have π bonds and lone pairs and the CT states should be energetically low lying. While the second requirement is trivial, the first one is related to the fact that these types of chromophores are present in, e.g., biomolecules with CT states of high interest. Starting with the traditional ammonia–fluorine complex, the ammonia and the fluorine molecules were replaced with other molecules showing lower ionization potential (IP) and electron affinity (EA) values, respectively. The resulting complexes include acetone–fluorine (C₃H₆O–F₂), pyrazine–fluorine (C₄H₄N₂–F₂), ammonia–oxygendifluoride (NH₃–OF₂), ammonia–pyrazine (NH₃–C₄H₄N₂), and acetone–nitromethane (C₃H₆O–CH₃NO₂). Finally, the pyrrole–pyrazine pair, both in the stacked and the H-bonded forms, has also been considered to include ring systems.

As we will discuss in more detail, for these systems 41 local and 14 CT states could be identified and included in the test sets.

4. Results and discussion

4.1. Selection of the CT States

Table 2 shows the CCSD results on all states considered in this study. Beside the excitation energy and the assignment of the states, the table shows the different characters (ω_CT, ω_PR, and ω_POS), as well as the AEL (approximate excitation level) values.³⁹ Examining the table, local and CT states can be classified. In most cases local states can easily be identified by ω_PR being close to 1 and ω_CT being close to 0, with ω_POS pointing to the appropriate fragment. On the other hand, about one-third of the CT states are mixed with local states giving eventually CT characters as low as 0.6. As expected, for the clean CT states the ω_POS value is near 1.5, while ω_PR is close to 1 and increases to 1.5 for mixed type ones. The only exception is the tetrafluoroethylene–ethylene complex, which will be discussed below.

The mixing of states of different character complicates the classification of the individual states to either local or CT. To have a clear definition, we decided that in the analysis below states showing ω_CT > 0.5 (with ω_CT evaluated at the CCSD level) are considered as charge transfer, while all others as local. As there is a certain degree of arbitrariness in this choice, further below we will also examine the accuracy of different methods as a function of ω_CT.

An unfortunate consequence of the above definition is that none of the states of the tetrafluoroethylene–ethylene system are included in the CT set, although this complex is one of the most often used test examples for CT type states. We investigate this system more closely in the next subsection, revealing that, instead of the optimized complex, a structure represented by an interfragmental distance of 5 Å should be included in the statistical analysis. In this case, corresponding to the intuition, one finds among the low-lying states two local π–π* excitations on the fragments and a clear CT state with ω_CT = 0.99. This particular distance was used by Mester and Kállay⁶⁹ in their test calculation on approximate local CC approaches.

4.2. Mixing of Different Characters

In spite of the fact that local (valence) and CT excitations are very different in nature, we often find strong mixing between these types of states. The presence of such mixings is due to the rapid, decrease of the energy of the CT state with the fragments approaching each other, causing the potential curve of a CT state to often “cross” with that of several local states. In the vicinity of these (avoided) crossings CT and local states might interact strongly, resulting in mixed states with a character changing rapidly with the intermolecular distance. The mixing is particularly intense if the local and CT states share either the dominant “from” or “to” orbitals. Several models to describe these couplings can be found in the literature, see, e.g., refs (70 and 71) and references therein.

The investigation of the ability of different methods to describe this coupling is beyond the scope of this study. Here the focus is on the “vertical excitation energy”; therefore, we discuss only one aspect of this problem, namely, that close to the “crossing” the assignment of the CT and local states is not trivial, which hampers the definition of the two classes to be used in the statistical analysis.

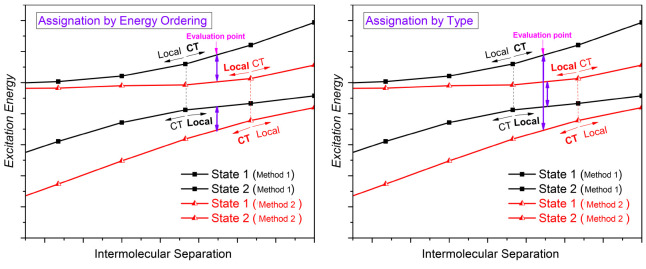
Figure 1 demonstrates this problem: on the figure black and red curves are the pairs of curves obtained by two different methods. In the case of the black curves, the exchange of characters happens at a smaller distance than with the red ones. If the evaluation point (where the vertical excitation energy is calculated) happens to be between these two points, there are two possibilities to assign the states, which leads to quite distinct energy differences. On the left panel, the lowest lying state of one calculation is matched to the lowest state of the other calculations, and the states with the higher energy are paired analogously. On the right panel, the states with the same dominant character are paired. The figure clearly shows that the errors are substantially larger in the latter case. Aiming to establish distinguished benchmark sets for CT states, in this study we compare the energy of those states which show the same dominant configurations, i.e., according to the right panel. One should keep in mind, however, that this procedure will result in an overestimated error for the CT state if the evaluation point is between the two “crossings”, compared to a measurement when it is on the same side of the “crossing” for both methods.

Figure 1.

Demonstration of the assignment problem around a crossing point. Right panel: assignation by energy ordering. Right panel: assignation by state character.

One possibility to avoid the assignment problem is to diabatize the potentials, thereby obtaining cleaner local and CT states.⁷¹ However, the result of the diabatization might be highly dependent on the employed model, which eventually could, again, bias the comparison. Therefore, we prefer to compare directly obtained ab initio quantities. Another possibility is to perform the calculations at distances long enough so that such a strong coupling does not occur. However, with the exception of one case, we refrain from this solution, since we believe that from the point of view of practical applications the vicinity of the equilibrium structure of these complexes is more relevant than large intermolecular distances are.

It was for the tetrafluoroethylene–ethylene complex in which we, too, decided to include in the statistics a more distant pair of fragments instead of the equilibrium geometry. Here, the lowest-energy (valence) excitations of ethylene and tetrafluoroethylene are the respective π–π* transitions, in the latter case the involved orbitals also containing significant contribution on the fluorine atoms. Accordingly, the lowest CT state is expected to be the one dominated by an excitation from the π orbital of tetrafluoroethylene to the π* orbital of ethylene. As Table 3 shows, at an interfragment separation of 5 Å the corresponding three states can be identified by almost perfect Ω characters: the two lowest ¹B₁ excitations are the two local π–π* transitions, while the one at 10.87 eV (CCSD) is the CT excitation.

Table 3. Excitation Energies and the Characters of the States of the Tetrafluoroethylene–Ethylene Complex Calculated at 3.5 and 5 Å Separations with Different Methods.

	excitation energy (eV)						character (CCSD)
state	CC2	CCSD	CCSD(T)(a)*	CC3	CCSDT-3	CCSDT	ωPOS	ωPR	ωCT
R = 3.5 Å
11B1	7.99	8.24	8.08	8.05	8.09	8.08	1.68	1.75	0.24
21B1	8.77	9.05	8.81	8.78	8.84	8.81	1.34	1.72	0.34
31B1	8.93	9.19	9.00	8.98	9.02	9.00	1.26	1.64	0.05
R = 5 Å
ethylene π–π*	8.62	8.73	8.59	8.60	8.61	8.61	1.96	1.08	0.00
tetrafluoroethylene π–π*	8.86	9.14	8.98	8.95	8.99	8.96	1.03	1.07	0.00
CT	10.16	10.87	10.52	10.46	10.56	10.57	1.50	1.01	0.99

Figure 2 shows the “from” and “to” (difference density natural) orbitals of the corresponding three states of the complex at the equilibrium distance of about 3.5 Å. While the third state is essentially still a local π–π* excitation on tetrafluoroethylene with an excitation energy differing by just a few hundredths of an eV from the corresponding state at 5 Å at all levels of theory, the other two states are strong mixtures of local and CT character, sharing the “to” orbital as that of the π* orbital of ethylene. In Table 3 we observe ω_CT characters of 0.24 and 0.39 for these two states, also reflecting this strong mixing, while the CT character of the third state is practically zero. Since the splitting of the energy of these two states is about 0.8 eV for all methods, we can conclude that there is no typical CT state at 3.5 Å, and thus, none of the states of this complex at the equilibrium could be included in the test set. Since the terafluoroethylene–ethylene complex was used in earlier studies, we decided to use this complex with an intermolecular separation of 5 Å, where a typical CT state can be identified.

Figure 2.

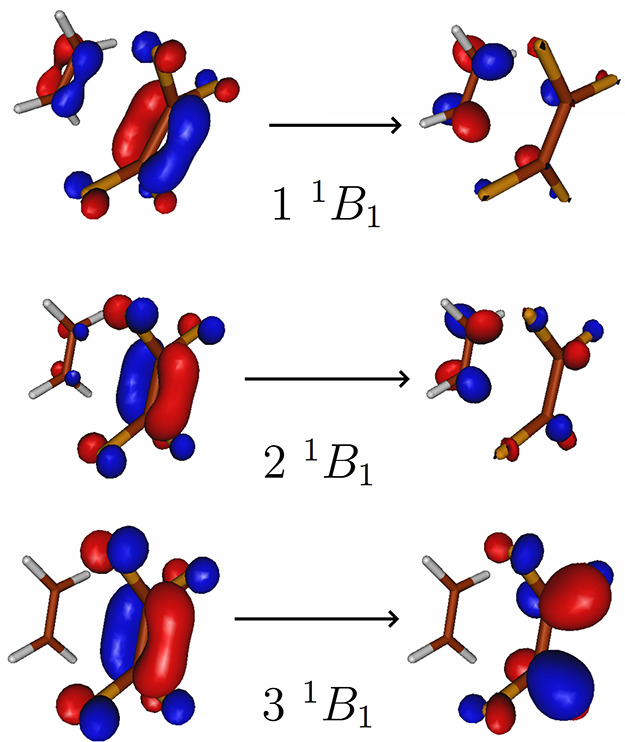
Orbitals of different states of the tetrafluoroethylene–ethylene complex at the equilibrium distance. Natural orbitals of the CCSD difference densities are depicted.

4.3. Vertical Excitation Energies

Vertical excitation energies of the complexes obtained with the various methods are given in Table 5 of the Supporting Information.

Although not the main objective of this paper, let us first shortly discuss local states. In Table 4 statistics are presented for these local states using CCSDT-3 results as reference values. A similar conclusion is expected as in the case of valence excitations of single molecules, although the interaction with the other fragment might slightly influence the results. Indeed, both the mean error and its standard deviation (SD) resemble the statistical values seen in ref (17) for the valence states obtained in the cc-pVDZ basis. It is only CC2 that shows now a slightly larger standard deviation which can be explained by the mixing of some local states with CT type ones. Nevertheless, one can safely conclude that the accuracies of local excitations are the same as for single molecules for all the methods investigated here. Note that for those states where CCSDT results are available, a very similar conclusion can be drawn.

Table 4. Statistics on the Error of Excitation Energies (in eV) for Local States (CT Character below 0.5) Relative to CCSDT-3 Reference Values^a.

	meanb	SDc	min	max
ADC(2)	0.01	0.16	–0.29	0.26
CC2	0.05	0.14	–0.19	0.33
CCSD(2)	0.14	0.19	–0.33	0.36
CCSD	0.10	0.08	–0.24	0.30
STEOM-CCSD	–0.12	0.11	–0.38	0.10
CCSD(T)(a)*	−0.01	0.05	–0.24	0.05
CC3	–0.04	0.04	–0.13	0.12

^aThe number of states included is 41 for all methods.

^bMean error with respect to CCSDT-3.

^cStandard deviation of the error to CCSDT-3.

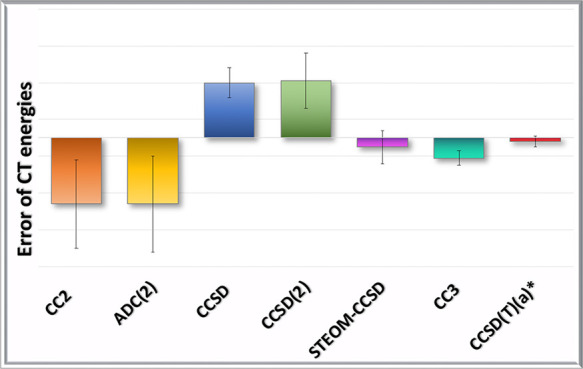
Turning to the CT states, one must realize that CCSDT results are available for no more than seven states only; thus, we have to select the best approximate triples method to use as a reference for the entire set. The errors of the excitation energies calculated with the triples methods are presented in Table 5. All triples methods are seen to have very small errors compared to CCSDT, which indicates strongly that results at the CCSDT level are practically converged. It is the CCSDT-3 method which shows the smallest mean error, as well as the smallest standard deviation. The error is typically no larger than +0.05 eV, and the oppositely signed error can only be observed for the ammonia–fluorine (−0.03 eV) and terafluoroethylene–ethylene (−0.01 eV) complexes. The errors of CCSD(T)(a)* are spread around 0, resulting in a small mean error. A large error of 0.24 eV can be observed in the case of the ammonia–pyrazine system (CT7) which is due to the assignment uncertainty of close-lying states as discussed above. This error essentially means that the “crossing” at the CCSD(T)(a)* level is on the other side of the sampling point than in the case of the reference CCSDT calculation. If this state is not considered, CCSD(T)(a)* seems to give statistical values very similar to those of CCSDT-3, but even with this state included the method performs very well on average. Contrary to CCSDT-3, CC3 systematically underestimates the vertical excitation energy. The largest error is observed for the ammonia–oxygendifluoride complex (CT5), but here, too, the strong coupling of a local and a CT state makes the assignment ambiguous. If we disregard this state, the typical error of CC3 is around −0.10 eV. The final conclusion from this table is that CCSDT-3 performs slightly better than other triples methods do, so it will be used for reference in the remainder of this study.

Table 5. Vertical Excitation Energies (E_exc , in eV) of the CT States Obtained with CCSDT and the Relative Error of the Excitation Energies (ΔE_exc , in eV) Calculated with Triples Methods as well as Statistics (Mean Error and Standard Deviation (SD)).

		Eexc	ΔEexc
system	state no.	CCSDT	CCSD(T)(a)*	CC3	CCSDT-3
ammonia–fluorine	CT1	6.64	–0.01	–0.12	–0.03
acetone–fluorine	CT2	5.85	–0.03	–0.10	0.05
pyrazine–fluorine	CT3	6.28	0.02	–0.13	0.05
	CT4	6.45	0.03	–0.05	0.00
ammonia–oxygendifluoride	CT5	7.04	–0.01	–0.21	0.05
ammonia–pyrazine	CT7	7.49	0.24	–0.03	0.04
tetrafluorethylene–ethylene (5 Å)	CT14	10.57	–0.05	–0.11	–0.01
mean			0.03a	–0.11b	0.02
SD			0.10a	0.06b	0.03

^aIf CT7 is not included, the mean error (standard deviation) is −0.01 eV (0.03 eV). See text for explanation.

^bIf CT5 is not included, the mean error (standard deviation) is −0.09 eV (0.04 eV). See text for explanation.

The accuracy of the methods for all CT states can be examined in Table 6 where the relative energies with respect to CCSDT-3 are shown. CCSD(T)(a)* gives results very close to CCSDT-3; the deviation is usually no more than a couple of hundredths of an eV. The only exception is the ammonia–pyrazine system (CT7) with an error of 0.20 eV, the cause of which has been discussed above. Inclusion or exclusion of this state does not influence the statistics significantly. In the case of CC3 we continue observing a regular underestimation, as it was the case for the smaller set with respect to CCSDT. The largest error found is again for ammonia–oxygendifluoride complex (CT5) which, as discussed above, is due to the assignment uncertainty, since CC3 gives a different order of local and CT states not only with respect to CCSDT but also with respect to CCSDT-3. Irrespective of this, the average error in the case of CC3 is about −0.1 eV with a small SD.

Table 6. Relative Error of the Calculated Excitation Energies (ΔE_exc , in eV) with Respect to CCSDT-3 Results for CT States.

		ΔEexc
system	state no.	ADC(2)	CC2	CCSD(2)	CCSD	STEOM	CCSD(T)(a)*	CC3
ammonia–fluorine	CT1	–0.63	–0.65	0.11	0.28	–0.19	0.01	–0.09
acetone–fluorine	CT2	–0.77	–0.72	0.20	0.38	–0.05	–0.07	–0.15
pyrazine–fluorine	CT3	–0.58	–0.70	0.49	0.44	0.01	–0.03	–0.18
	CT4	–0.09	–0.18	0.30	0.27	0.10	0.03	–0.06
ammonia–oxygendifluoride	CT5	–0.80	–0.76	0.03	0.24	–0.03	–0.06	–0.27
acetone–nitromethane	CT6	–0.67	–0.36	0.36	0.33	–0.08	0.00	–0.14
ammonia–pyrazine	CT7	–0.25	–0.22	0.37	0.40	–0.15	0.20	–0.06
pyrazine–pyrrole (H-bonded)	CT8	–0.15	–0.21	0.53	0.32	0.03	–0.02	–0.12
	CT9	–0.24	–0.25	0.52	0.33	0.00	–0.01	–0.14
	CT10	–0.22	–0.24	0.38	0.30	0.02	–0.03	–0.12
pyrazine–pyrrole (stacked)	CT11	–0.15	–0.15	0.37	0.20	–0.08	–0.01	–0.08
	CT12	–0.15	–0.14	0.24	0.16	–0.11	–0.02	–0.07
	CT13	–0.12	–0.10	0.32	0.18	–0.16	–0.01	–0.08
ethylene-tetrafluoroethylene	CT14	–0.28	–0.40	0.18	0.31	0.05	–0.04	–0.10
mean		–0.36	–0.36	0.31	0.30	–0.05	0.00a	–0.12b
SD		0.26	0.24	0.15	0.08	0.09	0.06a	0.05b

^aIf CT7 is not included, the mean error (standard deviation) is −0.02 eV (0.03 eV). See text for explanation.

^bIf CT5 is not included, the mean error (standard deviation) is −0.11 eV (0.04 eV). See text for explanation.

Continuing with the doubles methods, CCSD is found to always overestimate the excitation energy of CT states, the mean error being less than 0.3 eV with an SD of 0.1 eV. This shows that the errors of CCSD are quite systematic, although somewhat larger than those for valence states.¹⁷ The CCSD(2) results are very close to those of CCSD with a slightly larger standard deviation. CC2, on the other hand, systematically underestimates; the error can be as large as −0.7 eV (for the acetone–fluorine, pyrazine–fluorine, and ammonia–oxygendifluoride complexes). For larger systems there is a tendency for somewhat smaller errors, but in most cases the inaccuracy is not less than 0.2 eV in absolute value. ADC(2) also underestimates the CT excitation energies systematically; even the individual excitation energies are almost indistinguishable from CC2, with only one exception (the acetone–nitromethane complex (CT6)), where the error is almost twice as large as that of CC2. Looking for the cause of this unexpected discrepancy, we have observed that even for the local states of acetone–nitromethane the differences between CC2 and ADC(2) excitation energies are considerably larger (see the Supporting Information). The analysis of the wave function reveals that the norm of the T₁ amplitudes in CC2 is about 0.15 in this case, compared to 0.09 or smaller for the other systems investigated in this paper. The reasonable explanation is therefore that, contrary to the general situation,¹⁸ the T₁ transformation included in CC2 but not in ADC(2) makes a difference for this complex. STEOM-CCSD is found to be significantly more accurate than the other singles-doubles methods; in fact the statistical values resemble more those of the triples methods. This can be regarded as an indication that STEOM-CCSD indeed includes some important triples effects.⁵⁰

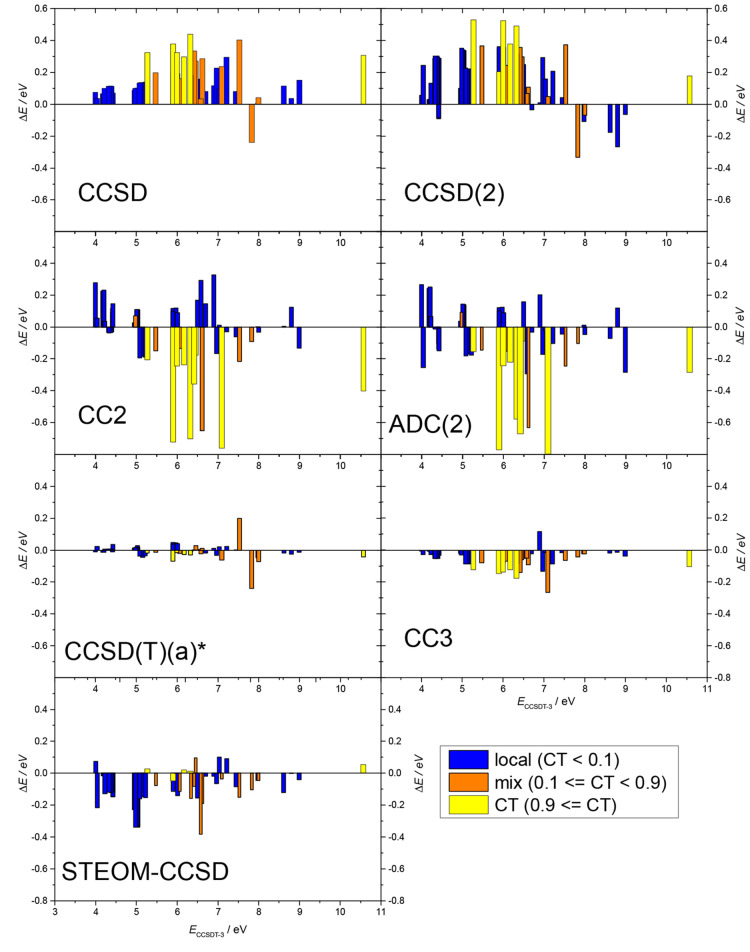
In Figure 3 the errors of the calculated excitation energies of all states obtained with different methods are shown with respect to CCSDT-3, as a function of the excitation energy. It is apparent at first glance that for none of the methods is there an observable correlation between the size of the error and the magnitude of the excitation energy, i.e., all methods perform independently of the excitation energy. Indeed, the correlation coefficient between the two quantities is in no case larger than 0.3 in absolute value. The negative errors observed for CCSD(2) above 7.5 eV represent an exception in this regard; i.e., CCSD(2) seems to perform somewhat differently for larger excitation energies than for smaller ones.

Figure 3.

Error of the calculated excitation energy (ΔE) with respect to CCSDT-3 as the function of the CCSDT-3 excitation energy (E_CCSDT–3). The colors of the bar show the character of the respective excited state: blue for local states (ω_CT < 0.1), yellow for CT states (ω_CT ≥ 0.9), and orange for states of mixed character (0.1 ≤ ω_CT < 0.9).

The doubles methods give substantially larger error than the triples methods, and it appears that triple excitations are needed to get the error down to 0.1 eV. CCSD, CCSD(2), and STEOM-CCSD are clearly more systematic than CC2, showing errors of the same sign in most cases. Note that systematic behavior is rather important to get the relative position of the bands in the spectrum correctly or to perform reliable nonadiabatic dynamics.

An even more detailed picture can be obtained when considering the colors of Figure 3. Here the states are assigned to three categories: “clean” local states (ω_CT < 0.1, marked with blue) and “clean” CT states (ω_CT ≥ 0.9, marked with yellow), while all other states are in the “mixed” category (0.1 ≤ ω_CT < 0.9, marked with orange). This is a more detailed classification than the one we used for the statistics above where the local and CT states have been divided by the rather arbitrary value of ω_CT = 0.5.

As mentioned before, CCSD appears to be quite systematic, but CT and mixed states clearly show a slightly larger error than local ones. There is only one state with a substantial negative error, which is the highest considered state of the ammonia–pyrazine complex with ω_CT = 0.27. Note that by 0.4 eV below this state there is another state of the same system (CT7, ω_CT = 0.63) with a rather large positive error. These two states mix strongly, and the discrepancy can again be explained by the assignment uncertainty caused by a close-lying crossing: the geometry used for the calculation is between the CCSD and the CCSDT-3 crossings. The CCSD(2) figure is very similar to the CCSD one, but the systematically larger error is apparent. In the case of the ammonia–pyrazine complex the pair of orange colored bars with oppositely signed errors shows up again, i.e., CCSD(2) reproduces even the discrepancy observed for CCSD. The blue bars with negative sign have been mentioned already and warn that CCSD(2) might perform worse for higher excitation energies.

In contrast to the systematic behavior of the errors of CCSD and in most part also CCSD(2), eye-catching is the discrepancy in the case of the CC2 method: blue bars are small and positive, while yellow ones are negative and substantially larger. This demonstrates again the systematic underestimation of CT excitation energies by CC2. Since almost all orange bars are also on the negative side, one can conclude that even a partial CT contribution is enough to spoil the accuracy of CC2. A similar behavior has been observed for Rydberg states¹⁷ and might have the same cause: in both Rydberg and CT states long-range interaction of the active electrons needs to be described. It is apparent that CC2 is not balanced enough in this regard, which is most probably due to the missing off-diagonal elements in the double–double block of the Jacobian. Note, however, that CC2, contrary to CCSD and CCSD(T)(a)*, gives the right order of the CT and local states for the ammonia–pyrazine system but, similarly to CC3, gives the wrong order for the ammonia–oxygendifluoride complex. The graph of ADC(2) is very similar to that of CC2; thus, all conclusions for CC2 also apply to ADC(2).

As for STEOM-CCSD, the yellow bars are very short on the respective panel of Figure 3, indicating that STEOM-CCSD is very accurate for CT states. On the other hand, the blue bars of the local states are more sizable, in most cases showing underestimation. This is also true for the orange bars which are smaller than the blue ones but larger than the yellow ones. This shows that the size of the error depends on the ratio of the local and CT characters in the given state. The largest negative orange bar belongs to one of two close-lying states of the acetone–nitromethane complex with the known uncertainty of its assignment. Thus, the cause for this outlier is again the relative position of the geometry used in the calculation with respect to the “crossing”. (Note that, contrary to the triples methods, CCSD and CCSD(2) also give the same order of the respective two states as STEOM-CCSD but the error of their energy is smaller, therefore not resulting in outliers.)

CCSD(T)(a)* performs well; its error is usually below 0.05 eV and scattered around 0. The pair of orange outliers belongs to the ammonia–pyrazine case discussed earlier: the noniterative triples correction cannot completely correct the wrong relative position of the “crossing” obtained at the CCSD level.

CC3 produces clearly larger differences with respect to CCSDT-3 than CCSD(T)(a)*. Yellow and orange bars are more negative than blue ones, indicating that CC3 also shows the misbalance of CC2, although at a much smaller absolute value. Note that here CCSDT-3 is used as a reference, but a similar trend has been observed for cases where CCSDT results are also available (see above). The large orange bar at 7 eV, together with the positive blue one at 6.8 eV, correspond to the ammonia–oxygendifluoride complex, the pair of states for which CC3 (and CC2) gives the opposite energy ordering than all other methods (see the discussion above).

It has to be noted that no significant correlation between the error of the excitation energies and the AEL value of the states could be observed for any of the methods. This finding is in agreement with the fact that all states included in this study are clean, singly excited states with AEL ≤ 1.14; thus, the results are not biased by non-negligible double excitation characters.

5. Conclusions

The main goal of this study was to set up a benchmark set for charge transfer type excited states. Our proposal includes 14 CT states of nine bimolecular complexes and reference values obtained at the CCSDT-3 level with the cc-pVDZ basis set. For the half of these states also CCSDT results are available, which show that CCSDT-3 is very accurate, and the approximate treatment of connected triple excitations does not change the quality of the benchmark values.

This benchmark set with high level reference data has been used to test the accuracy of various CC-type methods. We emphasize here that the goal was not to find the most accurate technique relative to experiment but rather to test the intrinsic errors in the Coupled Cluster hierarchy for CT states.

Considering CCSD as the standard method of choice, we have studied approximate techniques which are more cost-effective, as well as more advanced ones which include connected triple excitations. CCSD itself seems to be quite systematic by overestimating CT excitation energies as it does for local (valence) states. This overestimation is, however, somewhat larger and slightly increases when extending the basis to triple-ζ quality. The results show that the second-order approximations to CCSD deteriorate the results for CT states: while CCSD(2) gives less systematic results with slightly larger mean error and standard deviation, CC2 and ADC(2) substantially underestimate the excitation energy of these states. This is particularly problematic since these methods are otherwise quite accurate for local (valence) states; therefore, the wrong ordering of excited states with different character may be observed. The failure of CC2 and ADC(2) for CT states shows some parallelity to the case of Rydberg states¹⁷ and can likely be attributed to the inappropriate description of the electron moved far from its ground state position. Note that extending the basis to cc-pVTZ reduces the underestimation of the CT excitation energy by CC2, but this is more likely an error compensation since it is related to the smaller decrease of CT excitation energies compared to triples methods.

STEOM-CCSD, which is, though cost-effective, not an approximation to CCSD, shows some improvement and clearly gives the best statistics among singles-doubles methods for CT states. This superior performance can be understood as follows: to describe CT states, the simultaneous description of IP and EA states is necessary. For these states relaxation effects are important, which require 2-holes/1-particle (2h/1p) and 2-particles/1-hole (2p/1h) excitations, respectively. Consequently, the simultaneous description necessitates (3h/3p), i.e., triple excitations which are absent in most SD approaches. The STEOM-CCSD method is an exception as such combined relaxation effects are included due to the exponential e^S form of the correlation operator.⁴⁸ As a result, STEOM-CCSD incorporates relaxation effects (simultaneously) for both particles and holes; thus, it is charge-transfer separable⁵⁰ and implicitly includes (some) triple excitation effects. This also explains its general accuracy for valence excited states and in particular the general lowering of valence excitation energies compared to EOM-CC. Since the improvement for local (valence) states is somewhat smaller, here, too, some misbalance between different types of states can be observed.

Adding connected triple excitations to the wave function improves the results considerably. The least accurate among the investigated methods is CC3 which systematically underestimates the excitation energy of CT states with respect to both CCSDT and CCSDT-3 benchmark values. The underestimation, though significantly smaller, resembles the behavior of the CC2 method. As found earlier for non-CT type excitations,^17,36 the noniterative CCSD(T)(a)* of Matthews and Stanton⁵⁴ is very promising: the error with respect to CCSDT-3 is just a few hundredths of an eV for those states where the assignment is obvious (see below), with no significant difference between the accuracy of the CT and the local states. This method can be applied to all systems for which ground state CCSD(T) calculations are feasible.

In this paper we have calculated vertical excitation energies, and therefore (with one exception), the equilibrium structures of the complexes were used; i.e., the fragments were relatively close to each other. At these geometries the energies of the CT states are often close to those of the local (valence) states, and in many cases we observed strong couplings between the different types of states. The resulting strong mixing often hampers the classification of the states as either CT or local. In particular, uncertainties of the assignment and consequently large errors have been observed when the used geometry was between the “crossing” points predicted by the methods in comparison. We have found examples where CCSD, CCSD(2), and even CCSD(T)(a)* suffered from this, while in other cases CC2 and CC3, as well as STEOM-CCSD, also show this problem. Although the position of the “crossing” point is an important quantity to reproduce by approximate methods, the single point calculations presented in this work do not allow us to draw a conclusion about the ability of the methods to describe the geometry dependence of the coupling between CT and local states. In a subsequent study⁷² we will investigate this problem in detail by comparing the potential energy surfaces obtained by different methods.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00154.

• Structures of the studied systems and all excitation energies calculated for the benchmark systems (PDF)

This work has been supported by the National Research, Innovation and Development Fund (NKFIA) Grant Nos. 124293 and 124018. B.D. and R.I. thank the Max Planck Society for financial support. M.N. acknowledges support from an NSERC discovery grant.

The authors declare no competing financial interest.