Combining Machine Learning and Enhanced Sampling Techniques for Efficient and Accurate Calculation of Absolute Binding Free Energies

Abstract

Calculating absolute binding free energies is challenging and important. In this paper, we test some recently developed metadynamics-based methods and develop a new combination with a Hamiltonian replica-exchange approach. The methods were tested on 18 chemically diverse ligands with a wide range of different binding affinities to a complex target; namely, human soluble epoxide hydrolase. The results suggest that metadynamics with a funnel-shaped restraint can be used to calculate, in a computationally affordable and relatively accurate way, the absolute binding free energy for small fragments. When used in combination with an optimal pathlike variable obtained using machine learning or with the Hamiltonian replica-exchange algorithm SWISH, this method can achieve reasonably accurate results for increasingly complex ligands, with a good balance of computational cost and speed. An additional benefit of using the combination of metadynamics and SWISH is that it also provides useful information about the role of water in the binding mechanism.

Introduction

Reliably estimating target-ligand binding free energies (BFEs) is a challenging and important task in computer-aided drug discovery (CADD). In recent years, thanks to significant improvements in protein and ligand force fields,¹⁻⁴ parallel molecular dynamics (MD) codes,⁵ and enhanced sampling algorithms,^6,7 the calculation of relative and absolute binding free energies has become more accurate and more accessible.^8,9 In particular, recent advances in free energy perturbation (FEP) methodologies have made them amenable for routine and successful use in drug discovery pipelines.¹⁰⁻¹³ Although this mainly applies to the determination of relative BFEs, which can be used in the hit-to-lead optimization phase, significant progress¹⁴⁻¹⁶ has been made in the calculation of absolute binding free energies (ABFEs) using alchemical approaches, such as double decoupling methods.¹⁷⁻²³ However, the routine use of alchemical methods for the calculation of ABFEs still faces a number of challenges, especially with targets that undergo significant conformational changes, as well as with charged or noncongeneric ligands.²⁴⁻²⁶ A valid alternative for performing ABFE calculations is found in collective-variable-based free energy methods. Umbrella sampling^27,28 and metadynamics^6,9,29 have repeatedly been used to compute the ABFE along physical binding trajectories associated with both simple and complex systems.^18,30−33 In contrast to alchemical ones, these methods can be used to directly enhance the exploration of target conformational changes. Moreover, they also explore metastable minima and transition states that determine binding kinetics while, due to their nature, alchemical methods only sample the bound and unbound states. However, their suitability for drug discovery pipelines is reduced by two main factors: the need to define an optimal set of collective variables (CVs) and their computational cost. With respect to optimal coordinates that approximate the association path, pathlike variables such as PathCVs have been successful^34,35 but require knowledge of end states that is not always available. Alternatively, smart boundaries (e.g., funnel shaped) as in funnel metadynamics have been proposed.⁹ In spite of all this progress, however, designing optimal CVs for many systems is complicated and time-consuming. In these cases, metadynamics and umbrella sampling have been combined with multiple replica approaches such as parallel tempering to improve their convergence with nonoptimal CVs.³⁶⁻³⁸ These approaches allow one to converge the free energy associated with ligands binding to very flexible systems, such as GPCRs, with remarkable accuracy.³⁹ However, the computational cost of multiple replica methods such as PT-metaD or ITS-umbrella sampling,⁴⁰ compounded by the long sampling times needed to converge the BFE profiles, is prohibitive for most CADD tasks.

Recently a number of strategies have been developed to overcome the historic limitations of CV-based methods, increasing their potential to be routinely included in drug discovery pipelines. Here we combine the strengths of some of these more promising methods, including a new implementation of funnel metadynamics,⁴¹ optimal machine-learning-based collective variables,⁴² and a Hamiltonian replica-exchange algorithm.^43,44 Our aim is to estimate the performance and accuracy of these methods in calculating ABFE in a complex and realistic target, establishing the areas in which each one excels. We also report on the relative balance between accuracy, computational cost, and speed of each of them, providing some guidelines on their application in different settings.

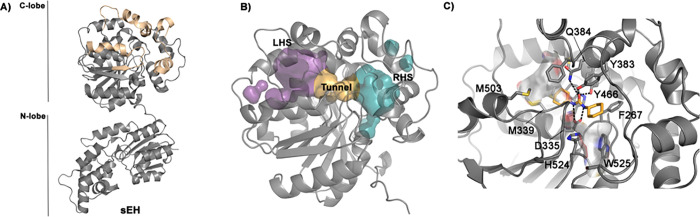
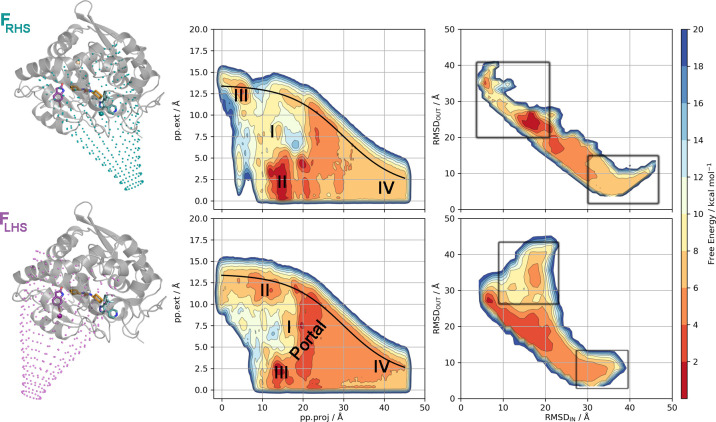
To test the chosen methods, we have selected a complex and realistic target, the human soluble epoxide hydrolase (sEH) and a number of noncongeneric ligands spanning a wide range of affinities and sizes. This enzyme has enduring pharmaceutical⁴⁵ and computational^46,47 significance, and a proof of that is the number of inhibitors that have been synthesized.⁴⁸ The first generation of compounds mostly contained urea-like motifs that participate in H-bonding interactions with the active-site residues. More recently, inhibitors with a greater diversity of structural features have been developed.⁴⁹ From a structural point of view, human sEH is interesting due to its flexibility and the large binding site (see Figure 1). The binding site is located in the C-lobe with two pockets, the right-hand side (RHS) and the left-hand side (LHS), connected by a narrow channel, giving the appearance of a dumbbell shape accessible from two different directions (Figure 1B).

Figure 1.

A) Cartoon representation of human soluble epoxide hydrolase (sEH). This protein is formed by an N- and a C-lobe connected through a long linker. In the C-lobe the regions directly related to the large binding pocket are highlighted in yellow. B) The volume of the binding cavity is shown colored in cyan for the right-hand side (RHS), orange for the narrow tunnel, and purple for the left-hand side (LHS) pockets. C) C-lobe of sEH is shown in gray cartoon interacting with a fragment that contains a urea-like motif in yellow sticks (Protein Data Bank (PDB) code: 5ai5). The residues surrounding the binding cavity are shown as sticks. The main interactions between the protein and the ligand are indicated with dashed lines.

High-resolution structures for a large variety of ligand–complexes are available. In particular, Öster and co-workers⁵⁰ have published a useful database, that provides more than 50 structures of human sEH-ligand complexes together with thermodynamic data and therefore offers a comprehensive view of the active site in terms of protein–ligand interactions.⁴⁹ The variety of the inhibitors resides in the groups selected to cover the space in the RHS and LHS, respectively.

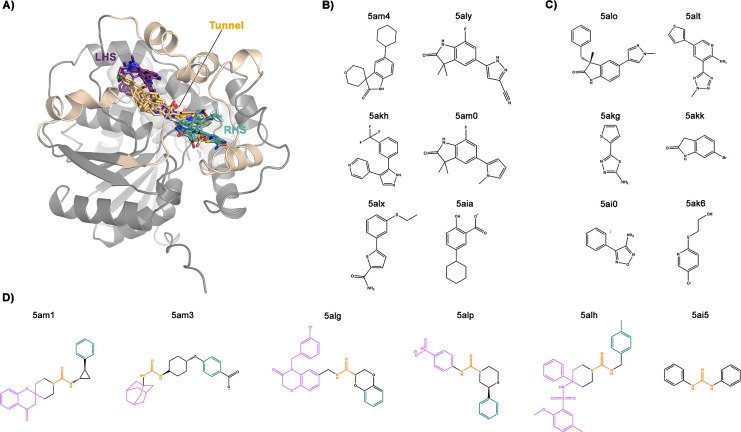
To investigate the performance of the free energy methods, we have selected 18 different ligands, from the Öster database,^49,50 binding to the narrow tunnel (6 systems), the RHS (6 systems) and the LHS pockets (6 systems, see Figure 2). Our results show that metadynamics with funnel-shaped restraints (fun-metaD) yields reasonably accurate results for the smallest fragments with a relatively low computational cost. For more complex ligands, COMet-Path and the combination of metadynamics with Hamiltonian replica-exchange (fun-SWISH) achieve better results, increasing the success rate of ABFE prediction from 50% to 80–90% with respect to fun-metaD (see Tables 1 and 2). The results were obtained with an aim to keep the computational costs low (see Figure S1) and work equally well with ligands that have larger dimensions and that are noncongeneric (see the Results and Discussion section and Figure S2 for details). An added bonus of the fun-SWISH approach is that it also provides detailed information about the role of the solvent in the binding.

Figure 2.

A) Cartoon representation of the C-lobe of sEH. The ligands selected for our simulations are shown as sticks in their initial positions taken from their respective X-ray structures. The PDB code of crystallized and selected complexes for our study will be used throughout the manuscript to refer to the crystallized ligands in complexes mentioned. B) Chemical structure of RHS ligands, colored in cyan in (A), crystallized together with the target could be found under PDB IDs 5am4, 5aly, 5akh, 5am0, 5alx, and 5aia. C) Chemical structure of LHS ligands, colored in purple in (A), crystallized together with the target could be found under PDB IDs 5alo, 5alt, 5akg, 5akk, 5ai0, and 5ak6. D) Chemical structure of narrow-tunnel ligands, colored in yellow in (A), could be found under PDB IDs 5am1, 5am3, 5alg, 5alp, 5alh, and 5ai5. The latter ligands contain the urea-like motif colored in orange, which sits in the tunnel position.

Table 1. Systems Used for the Enhanced Sampling Simulations with Experimental and Calculated Absolute Binding Free Energies with the Combined Error in Parentheses (in kcal mol^–1)^a.

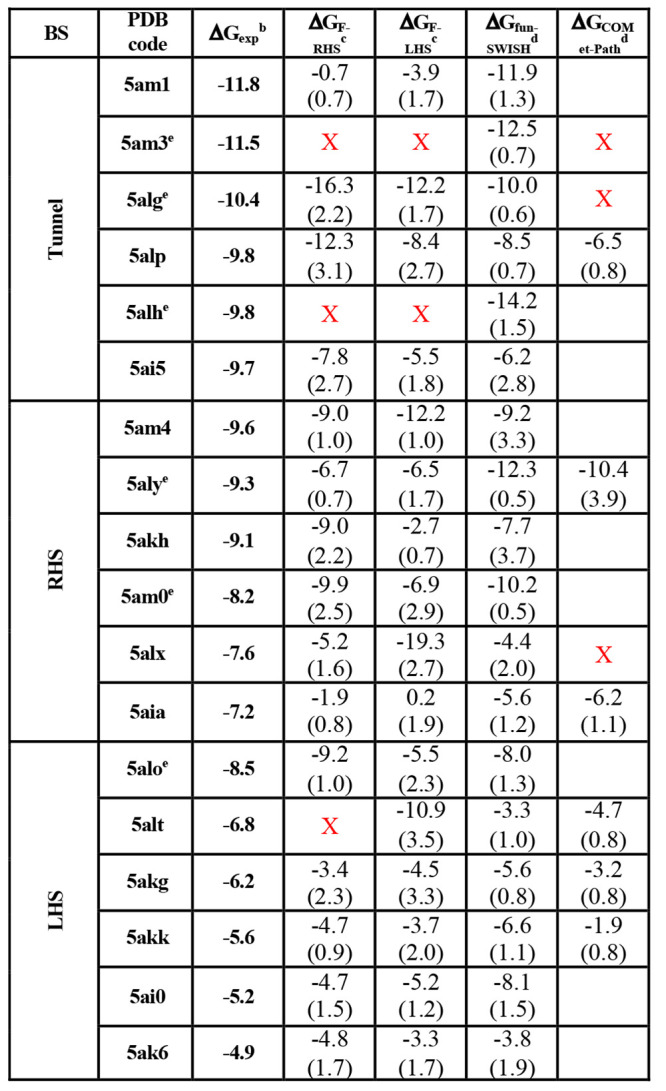
^aAll of the values have been corrected for the standard volume and funnel potential used, as described in refs (20 and 18).

^bExperimental free energies were obtained from the relation ΔG = −RT ln(K_i) at T = 298 K.^49,50

^cResults of fun-metaD for the funnel located over the RHS (F_RHS) and the LHS (F_LHS) of the binding cavity for the whole simulation time (500 ns).

^dResults of fun-SWISH and COMet-Path methodologies applied at the funnel located over the left-hand side (F_LHS), for the whole simulation time (300 ns for fun-SWISH and 350 ns for COMet-Path).

^eResults up to 1000 ns of fun-SWISH simulations.

Table 2. Percentage Difference between Experimental and Calculated Absolute Binding Free Energies^a.

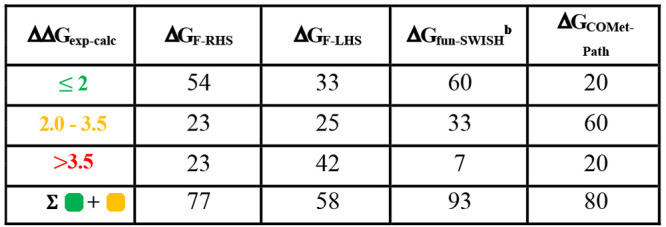
^aThe color code shows the difference between the experimental and the calculated binding free energies (ΔG_calc – ΔG_exp) for each methodology. If the difference is equal to and/or lower than 2 kcal mol^–1, then it is colored in green; if it is between 2 and 3.5 kcal mol^–1, then it is colored in orange; and if the difference is larger than 3.5 kcal mol^–1, it is colored in red. Only systems satisfying both convergence criteria, i.e., a minimum number of recrossing events of 1 and a combined error ≤2.5 kcal mol^–1, are considered for these statistics.

^b% when considering the 1 μs fun-SWISH simulations for 5am3, 5alg, 5alh, 5aly, 5am0, and 5alo.

Overall, with generic CVs that can be used for a range of systems and by lowering the computational cost, we address the most pressing challenges hindering the adoption of CV-based free energy methods for ABFE evaluation in routine computer-aided drug discovery pipelines.

Results and Discussion

Selection of the Model

We performed an extensive set of MD simulations (18) with the whole protein (Figure 1A) to check whether or not the long linker and the N-lobe play a role in the binding (e.g., by obstructing the access to the pocket). As discussed in the SI (Figures S3–S6), the two lobes are, as expected, dynamically independent, and there is no obstruction of the pocket by the N-lobe.

Thus, having shown that simulating the full system does not provide any specific advantage when it comes to modeling the binding of ligands to the C-lobe cavity, we chose to focus on simulating only those residues that comprise the C-lobe (aa 224–548). In order to confirm that this choice does not affect the stability or shape of the binding site, we carried out 300 ns of unbiased MD simulations for all the C-lobe–fragment complexes and compared the results to those of the full system (see Figures S7–S9).

As mentioned above, the selection of the ligands was made by considering the resolution of the X-ray structure, the chemical diversity, the sizes (which range from very small fragments to long and flexible ligands), and the binding affinity. A table reporting the most important features is in the SI (Table S1). It is worth noting the different chemical and physical properties of the ligands based on the location in the X-ray structures.

For instance, the ligands located at the narrow tunnel contain a urea-like moiety with different bulky and aromatic groups that are able to form hot-spot interactions with both sides of the tunnel. In Figure 2D, the ligands are colored in accordance with the part of the target they bind to, i.e., the parts bind to the tunnel, colored in orange, to the RHS, in cyan, and to the LHS, in purple. These ligands tend to contain more than 20 heavy atoms, with a high molecular weight and a number of rotatable bonds. Due to the presence of the urea-like motif that yields strong hydrogen bond interactions with the residues in the tunnel, these ligands are very stable for the duration of the simulations (see Tables S1 and S2). The ligands initially located in the RHS pocket are characterized by the presence of aromatic rings, with lower flexibility and with a “U” shape. Their number of heavy atoms and molecular weight, as well as their number of rotatable bonds, are all characteristic of fragments (Table S1). The ligands selected for the LHS are small fragments, that are highly stiff and linear. The root mean squared deviations (RMSDs) of ligands crystallized in the LHS show large fluctuations, most likely because these small ligands are located in a big flexible cavity and because no important hot spots are formed (see Figures S10 and S11 and Table S2).

To assess the ABFE of the binding and unbinding processes of the different ligands to sEH we have used a combination of different enhanced sampling techniques and machine learning algorithms that have been developed in our group. For the methods tested we have used the equilibrated C-lobe systems obtained from the unbiased simulations.

Testing Metadynamics with Funnel-Shaped Boundaries

The first enhanced sampling technique tested was funnel-shaped restraint metadynamics (fun-metaD).^9,41 The advantage of funnel-shaped restraints is related to the gain in speed of the convergence. The restraints limit the exploration of the ligand in the bulk water once it is unbound, and recrossing between bound and unbound states is thus favored. Here we use a novel translationally and rotationally invariant implementation of the funnel-shaped restraints. This implementation is based on a vector that passes between centers of mass of two groups of protein atoms (see the Computational Methods section). Defining the orientation of the funnel in this way ensures that a realignment of the structure to a fixed orientation for the funnel-shaped restraint is no longer required. Its computational cost is thus lower than that of the original “funnel metadynamics”⁹ and the resulting free energy reconstruction is less noisy.

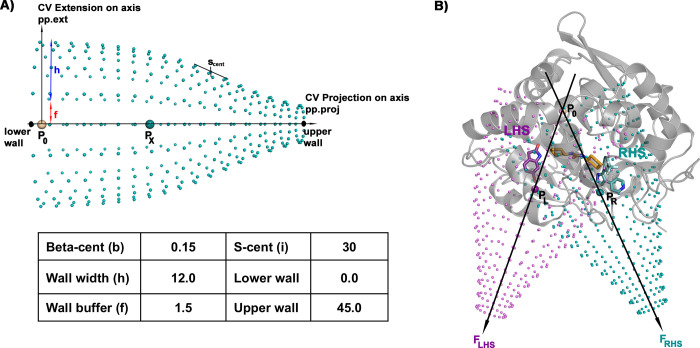
An important consideration when using these sorts of boundaries is the location and the direction of the funnel. Sometimes, e.g., for targets with small cavities, the choice is evident. However, in more complex cases (as for sEH) the parameters that define the funnel shape (see Figure 3) need to be adapted to the cavity. This might make the efficiency of this approach dependent on the structural complexity of the protein cavity. In the specific case of human sEH, and due to the especially elongated binding cavity, the definition of the funnel axis is particularly challenging. Taking into consideration the previous ligand exploration in the unbiased MD simulations, we tested two different sets of funnel-shaped restraints. The first of these was oriented over the right-hand side (RHS), while the second was oriented over the left-hand side (LHS) pocket of the large binding cavity. The ligand could, therefore, explore all the pockets (RHS, tunnel, and LHS) of the cavity and we could differentiate between them, avoiding the possibility that the funnel could negatively affect the convergence or the results. This allows an in-depth analysis of the dependence on the choice of the funnel orientation and shape (see Figure 3B and Computational Methods for parameters and reference points selected).

Figure 3.

A) Funnel-shaped restraints applied to the metadynamics. The values of the parameters used to define the funnel are indicated in the table in Å. B) Representation of human sEH protein with one fragment molecule in the left-hand side (LHS, purple), tunnel (yellow), and right-hand side (RHS, cyan) binding sites, respectively. The points P₀, P_L, and P_R that define the vector direction for each funnel (LHS and RHS) are indicated. See Computational Methods for details.

Figure 4 shows the free energy surfaces (FES) reconstructed for a single complex (PDB code 5ak6) with both funnel-shaped restraints, F_RHS and F_LHS, respectively, after 500 ns of sampling. It is evident from the FESs shown (see also Figures S12–S14 for the rest of the complexes), that the ligands can explore all the pockets of the large sEH binding site during the fun-metaD simulations. Additionally, any experimental results used for comparison will make no distinction between the pockets, nor will the crystallized binding pocket be guaranteed to be the optimal binding pose for each ligand. Therefore, it was proposed that the free energies could be reprojected onto the RMSD space between bound and unbound reference structures to provide a pocket-independent measurement of the BFE. For the details of how the reference structures were selected, refer to Computational Methods: Reprojection of the Free Energy Surfaces. Table 1 compiles the calculated absolute BFEs for the 18 holo complexes (the results for the reweighted BFEs are gathered in Table S1), while Figure 7 (top) shows the correlation between the calculated and experimental BFEs. An important question with well-tempered metadynamics-based methods is when to stop the simulation. This is particularly important for ABFE calculations as their computational cost is an important concern. Here, after analyzing the data with an eye on the balance of computational cost vs accuracy, we have observed that the following general convergence criteria yield good results: (i) at least one recrossing (rebinding) event has to be observed, and (ii) the combined error in the ABFE should be equal to or lower than 2.5 kcal mol^–1. Of these two points, we would like to stress the importance of the number of recrossing events. Without a proper recrossing the relative height of the bound and unbound free energy states might be incorrect. For this reason, the systems with no recrossings in the simulation have not been considered in Table 1 (systems indicated with red X’s). Regarding the calculation of errors of predicted ABFE, we have calculated them in two different ways: (i) the average standard error and (ii) the oscillation along the time. However, none of them were individually able to distinguish between the systems or methodologies used. Consequently, a combination of these two errors has been applied to define the second criterion (see Computational Methods for details). Table 1 shows the combined error for all the systems and methods. Based on these established criteria, we would recommend systems with a combined error larger than 2.5 kcal mol^–1 to be extended to satisfy the convergence criteria.

Figure 4.

Free energy surface (FES) for the binding/unbinding of the sEH-ligand complex (PDB code 5ak6) through the funnel-shaped restraint metadynamics simulations F_RHS (top) and F_LHS (bottom). The central plots show the raw metadynamics FES, from which the BFE is measured between the bound state, encompassing the tunnel (I), RHS (II), and LHS pockets (III), and the unbound state (IV). The funnel boundary is shown in black. The right-most plots show the reweighted free energy surfaces, with RMSD_OUT from a system-specific unbound reference structure plotted against the RMSD_IN from a system-specific bound reference structure. The regions that are taken as delimiting the bound (independent of the pocket location) and unbound states are shown with the labeled squares. Contour lines are drawn every 2 kcal mol^–1.

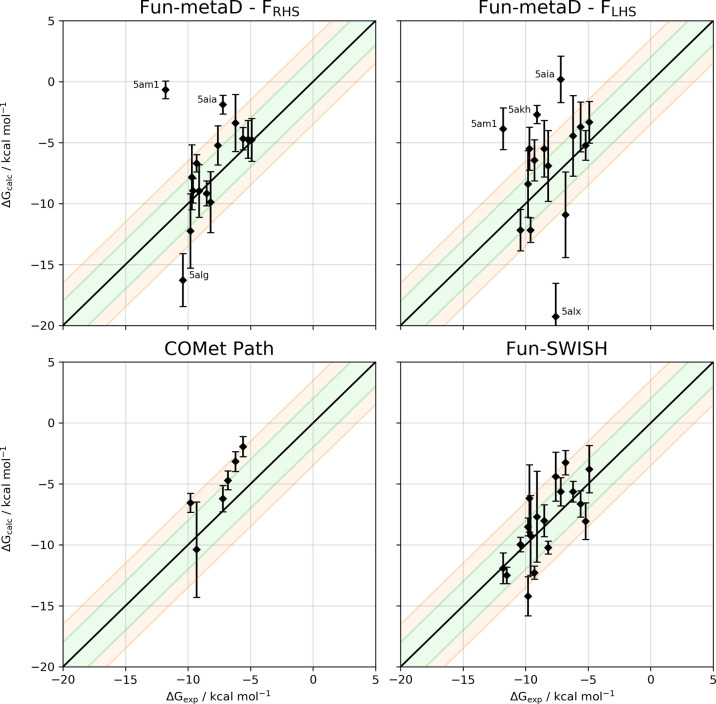
Figure 7.

Correlation between the experimental and calculated binding free energies of all complexes selected for (top) fun-metaD at F_RHS and F_LHS, (bottom-left) COMet-Path methodology, and (bottom-right) fun-SWISH. For the six outliers of fun-SWISH (see the main text) we show the results of the extended simulations. For the methodologies at the bottom, only F_LHS was applied. The black line indicates the ideal behavior, while the green and orange shadows show the ±2 and 3.5 kcal·mol^–1 tolerance, respectively, around the ideal behavior. Error bars are shown for the calculated ABFE using the values shown in Table 1.

For fun-metaD we have removed the data for 5am3 and 5alh for both funnels, due to the lack of recrossings. Also, the projection CV (pp.proj) obtained for 5alt with F_RHS shows the same behavior. Regarding the combined error, only two systems with F_RHS have an error larger than 2.5 kcal mol^–1, while for F_LHS, five systems present an error greater than 2.5 kcal mol^–1, demonstrating that these systems should be extended to satisfy the convergence criteria. For the correlation with experimental values, only the systems satisfying both criteria have been considered in Table 2, which show the success on the prediction of ABFE and how it compares with the experimental value. For F_RHS the number of ligands with a ΔG within 3.5 kcal·mol^–1 of the experimental value is larger than for F_LHS amounting to 77% and 58%, respectively (Table 2).

These results suggest that the direction of the funnel and the different natures of the RHS and LHS pockets have a significant influence on the ligand-binding process. For the F_RHS the binding/unbinding processes are governed by the same protein environment, and better convergence is observed in most of the cases. Meanwhile, for the F_LHS the convergence is more complicated, as evidenced by the success rate with the new criteria, due to the larger space available to the ligands and the lack of clear hot spots that could drive the binding/unbinding processes (see Figures S11, S15–S18).

The dependence of the convergence of the free energy on the size of the ligands is even more pronounced. For small fragments, such as 5akk, the calculated BFE converges with four or five recrossing events (Figure S18) and with small error values throughout the simulation. Moreover, it reaches the experimental BFE value after 200 ns of simulation, independently of the direction of the funnel (Figure S21). For the large ligands that bind in the tunnel or the RHS pocket, however, the calculated BFE only starts to converge at the end of the simulation, even when only considering the systems that satisfied both criteria mentioned above (Figures S19 and S20). It is thus not only the funnel orientation that has an effect on the results but also the size of the ligands has a clear influence on the BFE accuracy. This can be observed in the correlation between the calculated and the experimental BFEs when divided per site of crystallization (Figures S23 and S24). In this case, there is a slight increase in the correlation for small and less flexible fragments (R² of 0.50 and 0.41 for ligands that crystallized in the RHS and LHS pocket at F_RHS). Altogether, this result shows that the large and highly flexible ligands are not converged, and in most of these cases, the simulations should be extended to reach the convergence criteria of minimum number of recrossing events and decrease the error values in the estimated ABFEs (Figure S22). These features are generally more remarkable for F_LHS, which shows poorer results than F_RHS.

We can thus conclude that fun-metaD seems to be an efficient tool for the determination of ABFEs for small and rigid fragments with a good trade-off in terms of accuracy, computational cost, and speed of calculation. However, it struggles in the presence of (i) large and flexible ligands and (ii) large and open cavities. Clearly, for large and flexible ligands single replica metadynamics with a funnel-shaped boundary takes a long time to converge and thus it is not an optimal tool for the calculation of ABFEs.

We therefore tested our recently developed COMet-Path, which provides an optimal association coordinate, and a combination of metadynamics with SWISH, a Hamiltonian replica-exchange based approach. As the results from fun-metaD show that the funnel over the LHS pocket presents the greatest challenge to convergence, we henceforth use only this funnel (F_LHS), as it represents the worst-case scenario for the choice of the funnel.

COMet-Path (Coefficients Optimization of a Metric for Path Collective Variables)⁴² was designed to define the metric of pathlike collective variables as a linear combination of collective variables (CVs) selected from a pool of possible variables and thus extend the usefulness of Path Collective Variables (PCVs).^34,51,52

First, we selected nine of the 18 protein–ligand complexes, three systems per pocket (tunnel, RHS, and LHS) from the previous fun-metaD simulations using F_LHS. From this starting point, the coefficients defining the metrics were first optimized. We performed several iterations in order to find the best parameters: in terms of the combinations of CVs and the optimization of coefficients for the chosen CVs, as well as a refinement of how the path was built (see Supporting Information Scheme S1). After trying a number of combinations, we found the optimized settings that we finally used to run the COMet-Path simulations (see Computational Methods for details). With these settings, the parameters needed to run COMet-Path simulations could be obtained within 1 day of the postprocessing of data from fun-metaD.

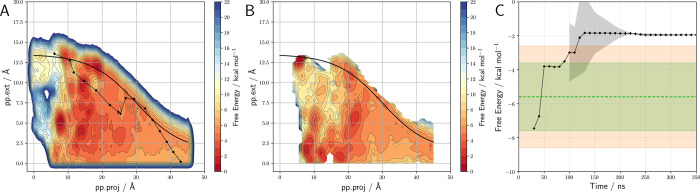
Using these optimal CVs and applying the convergence criteria, after 350 ns there are three systems showing zero recrossing events. Additionally, for one of the remaining systems, the combined error is larger than 2.5 kcal mol^–1, demonstrating that the simulations for most complicated ligands should be extended (Table 1, Figure 5 and Figures S25 and S26). The remaining systems show an ABFE very close to the experimentally determined ones (see Figure 7).

Figure 5.

A) Free energy surface for the binding/unbinding of the sEH-ligand complex (PDB code 5akk) through the fun-metaD simulations F_LHS. Contour lines are drawn every 2 kcal mol^–1. B) Reconstruction of the free energy surface obtained by COMet-Path simulation. C) Evolution of calculated ABFE through simulation time obtained for COMet-Path simulation.

The optimized coefficients of the chosen CVs suggest that the water coordination of the ligand is an important factor in the binding/unbinding processes. Indeed protein–ligand solvation and desolvation effects have been repeatedly shown to be of the utmost importance.⁵³⁻⁶⁰ However, the use of bridging waters as a component of COMet-Path shows mixed results. The convergence of the free energies is not particularly improved, while the time to compute the CV is significantly longer. Upon closer inspection, we found that while water solvation/desolvation plays a very important role in specific parts of the path, it is irrelevant elsewhere. Thus, in the current form of COMet-Path, this variable is not very advantageous (and has not been included in the final round). In a reformulation with position-specific coefficients, it could prove very effective.

Overall, this approach might be particularly useful for large congeneric series of ligands, where the initial optimization would be run only once. The advantage of COMet-Path over fun-metaD is that, by providing an optimal association CV, it is able to converge the free energy profile faster, in an exposed and large cavity, with less extra computational cost. Although it is necessary to optimize the coefficients on at least one converged free energy landscape, with another set of variables, it can also provide a satisfactorily accurate estimation of the ABFE for noncongeneric ligands.

The final approach we tested was a combination of fun-metaD with SWISH (Sampling Water Interfaces through Scaled Hamiltonians) a method recently developed by our group.^43,44 SWISH is a Hamiltonian replica-exchange method that improves the sampling of hydrophobic cavities by scaling the interactions between water molecules and protein atoms. It has been shown to be very effective in sampling the opening of hidden (cryptic) cavities.⁴⁴ Here, for the first time, we also scaled the interactions between the water and the ligand, which have been revealed to be important by COMet-Path. Therefore, this implementation of fun-SWISH can also help us to understand the hydration/dehydration process during the dynamics itself. Additionally, fun-SWISH is able to overcome the main fun-metaD convergence problem, specifically related to the hindrance during the rebinding process. Due to the entropic penalty of being bound in a pocket rather than in bulk water, the rebinding events are always harder to sample, as well as any steric factors that hinder the ligand returning to a bound pose. While the funnel-shaped restraints attempt to account for this by constraining the number of unbound states available to the ligand, this effect is difficult to overcome with metadynamics alone.

We scaled the ligand–water and protein–water interactions to favor binding events in four of the six replicas, as the unbinding events are more easily achieved with the metadynamics bias, specifically that along the projection CV. After a few trials, we selected the scaling (λ) of the protein–water interactions to range from 0.95 to 1.20, while the ligand–water goes from 1.05 to 0.80 to favor the binding process (see SI Figure S27). We ran fun-SWISH with six replicas for 300 ns on each of the 18 systems, using the F_LHS, as mentioned above.

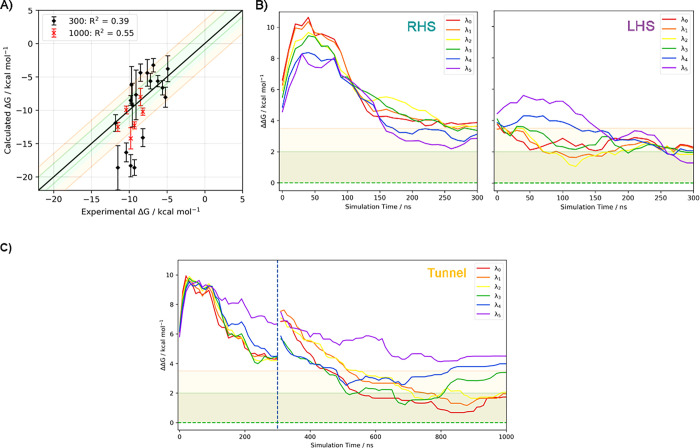
For all the fun-SWISH systems, the first criterion is satisfied, as the number of recrossing events is larger than 1000 in all cases. It is clear, that using replica exchange improves the conformational sampling and increases the number of transitions between the bound and unbound states (see Figures S28–S30). Regarding the combined errors, three systems show an error greater than 2.5 kcal·mol^–1 and thus were not included in Table 2 for experimental comparison purposes. However, for these simulations six outliers were identified with a difference between the experimental and estimated BFE larger than 3.5 kcal·mol^–1 (Figure 6A). These cases are particularly complicated, and the convergence is problematic due to the rebinding as shown by the faster convergence at higher λ where the rebinding is favored (see Table S3). Extending the simulations for these six outliers (5am3, 5alg, 5alh, 5aly, 5am0, and 5alo) up to 1 μs provides a much-improved agreement with experiment, with a success rate of 93% and with a correlation coefficient (R²) of 0.55, with only one outlier (see Figures 6 and 7and Table S4 and Figure S31 in the Supporting Information). For fun-SWISH the accuracy increased significantly −60% of the computed free energies were now within 2 kcal·mol^–1 of the experiment, in comparison to the 33% obtained using fun-metaD (F_LHS, see Table 2).

Figure 6.

A) Correlation between the experimental and calculated BFEs of fun-SWISH (F_LHS) simulations for all the ligands after 300 ns and for the six outliers after 1000 ns (data shown with black and red markers, respectively.) The black line indicates the ideal behavior, while the green and orange shaded regions show the ±2 and 3.5 kcal·mol^–1 tolerance, respectively, around the ideal behavior. The correlation coefficient is indicated for each case. Evolution of the difference between the experimental and estimated data along the six replicas of fun-SWISH considering the results for the six systems initially crystallized at B) RHS and LHS pockets and C) the tunnel pocket. For three systems located in the tunnel pocket, where the simulation was extended up to 1000 ns, the extended evolution is also shown. The dashed green line indicates the ideal behavior, while the green and orange shaded regions show the ±2 and 3.5 kcal·mol^–1 tolerance, respectively, around the ideal behavior.

These results compare favorably with ABFE obtained with alchemical transformations,⁶¹⁻⁶⁴ such as in the case of a bromodomain, for which Aldeghi et al. achieved a success rate of 91% and a correlation coefficient of 0.6. Moreover, in the case of fun-SWISH, although the size and physicochemical properties of the ligands have a significant effect on the convergence of the simulations, its performance is less adversely affected than alchemical methods by large and flexible binding cavities and noncongeneric ligands. While the free energy profiles for the ligands binding in the LHS converged, according to the chosen convergence criteria, between 150 and 200 ns, the ligands initially bound in the RHS need at least 300 ns of sampling to converge, and at least 1000 ns are required for the largest and most flexible ligands (Figure 6B and Table S4).

Finally, we were able to relate the calculated BFE obtained from fun-SWISH with the log P of the ligands studied (see details in SI Figure S32). We found that lower log P values correspond to ligands that are more comfortable in the unbound state, while the ligands with higher log P values correspond to those that prefer the bound state. This relationship could also help in the drug design of new ligands for which no experimental data is available.

Fun-SWISH emerges as a very promising technique to compute ABFE, as it has achieved estimates with good accuracy in almost 90% of the cases, even for noncongeneric ligands, with very different physicochemical properties, and in an exposed and open cavity, factors which would usually add considerable difficulty to BFE prediction. It is a replica-exchange method, which involves six replicas per system and therefore more computational resources, but the better sampling and the considerably improved convergence make this a suitable trade-off. On a relatively affordable setup with one GPU per λ this technique enables an acceptably accurate prediction of ABFEs in difficult cases, in less than 1 week.

Conclusions

We tested the ability of three different metadynamics-based methods to predict ABFEs in a complex and realistic system. The target selected presents an elongated binding cavity which could be divided into three different pockets of different structural complexity. Likewise, the ligands selected present very different physicochemical properties, mostly classified depending on their initial crystallization position. In many cases, the simulations with enhanced sampling techniques demonstrate that these ligands can bind in any of the pockets of the large binding site.

The first approach, fun-metaD, was adapted to avoid any alignment steps during the simulation and thus became a more efficient method. It provides an adequate estimation of ABFEs for small fragments in the RHS pocket, which could be described as a typical binding cavity in terms of concavity, number of available hot-spot interactions, or solvent exposure. However, this technique also highlights some of the most challenging aspects of ABFE prediction, such as the difficulty of properly assessing the binding in open and exposed pockets and with large and flexible ligands.

Based on our results, we believe that the second methodology used, COMet-Path, might prove useful in drug development pipelines with large sets of congeneric ligands where the initial optimization needs to be performed only once. It also has the capacity to provide rapid ABFE prediction for noncongeneric ligands but requires a nontrivial optimization procedure.

Finally, we developed a new combination, fun-SWISH, which easily fulfills the convergence criteria established in this paper, providing a promising agreement with experimental BFEs with a reasonable balance of computational cost and speed. This method not only works for small fragments but also works for large and flexible ligands, bound in pockets where the BFE is more difficult to estimate due to solvent exposure. This technique can be easily deployed for the determination of accurate ABFEs in pre-existing computational pipelines for Drug Discovery and could impact the field as much as FEP methods have done for relative binding free energies.

Computational Methods

General Setup of Molecular Dynamics (MD) Simulations

MD simulations were performed starting from the X-ray structure of the human sEH in the apo form (PDB entry 5AHX, resolution 2 Å). For the selected holo complexes the positions of the ligand in the binding pocket, obtained from the respective X-ray structures, were considered as the starting point. We have run MD simulations for the full system (N- and C-lobes, residues 1–548) and the C-lobe (residues 224–548) considering the 18 different complexes. The 18 fragments were parametrized using the generalized AMBER force field (GAFF2) in conjunction with RESP charges calculated at the B3LYP/6-31G(d) level.⁶⁵ Each complex was immersed in a pre-equilibrated octahedral box using the four-point water model from the a99SB-disp force field,¹ which is a modified version of TIP4P-D.⁶⁶ The standard protonation state at physiological pH was assigned to ionizable residues. The final systems considering the full-size enzyme contain the model protein, around 57,500 water molecules, and 0.15 M of NaCl, forcing the system to be neutral, leading to simulation systems comprising of around 240,000 atoms. For the systems considering only the C-lobe of sEH, we retained only the protein residues 224–548, approximately 17,200 water molecules, adding the appropriate numbers of neutralizing sodium and chloride ions to give C-lobe systems containing around 74,000 atoms. All the simulations were performed using the a99SB-disp force field, which is a modified form of the a99SB force field that improves the modeling of intrinsically disordered peptides while retaining the accurate description of folded proteins,¹ using Gromacs 2018.3.⁵

The initial system was minimized using 50,000 cycles of energy minimization. The equilibration process was performed in three steps. The first step involved the heating of the system from 0 to 300 K in 1 ns (NVT ensemble) and was followed by two steps of equilibration under NPT conditions using the velocity-rescale thermostat.⁶⁷ In the first step, a Berendsen barostat was used, restraining the position of the protein–ligand complex for 10 ns. Finally, a full relaxation of the system using Parrinello–Rahman pressure coupling was performed for a further 10 ns. The final structure from the equilibration process was used as a starting point for the MD simulations. All systems were simulated with periodic boundary conditions using an NVT ensemble. The Particle Mesh Ewald (PME) method was used for treating long-range electrostatics using a cutoff of 12 Å.⁶⁸ A time step of 2 fs was used for all simulations after imposing constraints on the hydrogen stretching modes. Each complex was simulated considering the full-size and the C-lobe systems in order to check the convergence of the dynamical behavior. Each replica was run for 300 ns, leading to a total simulation time of approximately 11 μs.

Funnel-Shaped Restraint Metadynamics (fun-metaD)

Metadynamics simulations were performed in order to obtain estimates of the binding free energy profiles using GROMACS 2018.3⁵ with PLUMED 2.4.⁶⁹ We used a combination of the well-tempered metadynamics (WT)^70,71 and funnel-shaped walls in the spirit of path collective variables (PCVs) and funnel metadynamics (fun-metaD).^9,41 The last snapshot of the MD simulations was used as the starting point for the fun-metaD simulations (in the NVT ensemble) to explore the binding/unbinding processes of each fragment in the C-lobe complexes.

A metadynamics history-dependent bias was applied along the two collective variables that define the funnel-shaped restraints (see Figure 3A), that is projection (pp.proj, CV1) and extension (pp.ext, CV2) on the funnel-shaped potential. However, the most critical decision pertains to the location of the funnel-shaped restraints used to perform the metadynamics simulations. Due to the particularly large size of the binding pocket, we have implemented the funnel-shaped restraints following two different vectors, being centered over the LHS and RHS pockets, respectively. In such a way, the origin of both vectors (P₀) is the same for both funnel-shaped restraints and defined on the Cα of Trp464 of the full-size system. The difference emerges from the definition of the second point (P_X), as it defines the orientation of the funnel to be above the LHS or RHS pockets of the binding cavity. Thus, for the funnel orientated over RHS, the P_R is defined by the center of mass of the Cα of residues Ser417, Val 497, and His523, while for the funnel orientated over the LHS pocket, the P_L is calculated as being the center of mass of the Cα of residues Ile362, Ser373, Val379, and Met520 (see Figure 3B). Finally, we ran 36 simulations (18 holo systems × 2 funnel-shaped restraint orientations) of 500 ns each, with an accumulated time of 18 μs

1

For the fun-metaD, Gaussians hills with an initial height of 1.5 kJ·mol^–1 were applied every 1000 MD steps. The hill width chosen for the projection and extension CVs are 0.25 and 0.3 Å, respectively. The Gaussian functions were rescaled in the WT scheme using a bias factor of 10 for all the systems. The resulting free energies were calculated using the sum_hills function of the PLUMED plugin⁶⁹ and corrected for the loss of translational and rotational freedom of the unbound ligand due to the funnel-like boundaries using the following equations

2

3

where C_f/sv is the funnel/standard volume correction. The bound states were defined by the position of the global minimum, and the unbound states were defined by values of the distance CV greater than 30 Å. An upper limit for the CV was set at 45 Å on the basis of the box size and available solvent phase. The correction for the standard volume and funnel restraint, C_f/sv, was computed as described in refs (20) and (18) according to the formula

4

where ξ_bulk^metaD is the fraction of the total possible orientations explored by the ligand in the unbound state, V₀ is the standard volume accessible to a ligand at 1 mol·dm^–3 concentration, and V_bulk is the bulk volume (i.e., V_box – V_{protein+membrane}). The correction was found to be 1.54 kcal·mol^–1 for the C-lobe complexes. To assess the convergence of the simulations, we compared the usual reconstruction of the free energy surfaces obtained by integrating the bias at various time points with a time-independent estimate of the free energy.⁷²

Reprojection of the Free Energy Surfaces

Reweighting of the free energy surfaces as a function of RMSD from reference bound and unbound structures was performed using the Tiwary et al. algorithm.⁷² This resulted in a clearer separation between bound and unbound states. The reference structures selected for the bound state were those where the ligand is bound in the initial binding pose after the equilibration simulations. For the unbound states we have selected a snapshot of the simulation where the ligand is in an optimal position away from the pocket as defined by a combination of the two funnel CVs (>32 Å in pp.proj and <5 Å in pp.ext), and the distance from the ligand to any protein atoms is greater than the PME cutoff of 12 Å.

New Convergence Criteria

We have established new convergence criteria in order to assess the reliability of the estimated ABFE without comparison with experimental values. These criteria are based on two important statements, i.e., (i) the minimum number of recrossings and (ii) the estimation of ABFE error.

Recrossing

Recrossings relate to the number of unbinding/rebinding events indicating whether the ligand has explored the relevant conformational space, and how many times it has done so within each simulation. In this case, a recrossing is defined as one unbinding/rebinding event, where the ligand explores bounds conformations, exits the pocket to the bulk water, and then returns to the pocket. To measure this motion, we use the projection CV (pp.proj), as shown in the Supporting Information Figures S16–18, S26, and S28–30. Due to the differing geometries of the funnel, and with the two orientations placing the three initial binding pockets (tunnel, LHS, and RHS) at different positions relative to the funnel, it was necessary to define different “bound” states for each combination. As such, the bound state thresholds were calculated using the average projection value at the beginning of the simulations, per funnel, per initial binding site. This led to six new bound-state definitions, which were used to identify the recrossings.

Estimation of the Error

The error in our ABFE estimate was calculated in two ways. First, we performed block averaging on 50 ns blocks of simulations to obtain the standard error for every grid point. We then averaged this error over the entire grid and doubled it, since the ABFE is a difference of free energy between two states.

The second way of estimating the error was to observe the variation of our ABFE estimate over time, as calculated through the reweighting procedure described above. We have defined this error as the average of the unsigned differences between the final estimate and the previous ten estimates, which cover the previous 100 ns of the simulation.

The oscillation over time will eventually reach zero in a fully converged simulation that also contains recrossing events. The observed variations within the standard error are minimal, and so the oscillation over time is much more useful when deciding when to stop a simulation. However, even when converged, the actual error on the free energy will still be nonzero. The final error we present is therefore a sum of the standard error and the oscillation over time. The two component errors can be considered independent of each other to a good extent. We have chosen 2.5 kcal/mol as the limiting value for the convergence of the simulation and our ABFE estimate, to exclude simulations with significant recent variation to the ABFE estimate.

COMet-Path (Coefficients Optimization of a Metric for Path Collective Variables) Simulations

This technique allows the definition of a metric as a linear combination of CVs selected from a pool of possible variables.⁴²

Preliminary Simulations

For the systems under consideration, the data from fun-metaD simulations obtained for F_LHS was used as a basis for reweighting. The r_bias (metadynamics bias corrected for the c(t) factor) has been computed throughout the simulation as described in ref (72), which is more accurate than estimating it during postprocessing. Another simulation was performed to pull the systems out of the binding site to get an initial estimate for the unbinding path. This was done using 50 ns of steered MD that pulled the ligand from its initial binding site along a previously used path, where appropriate, or from the initial funnel projection to a final value of 43 Å for systems where no initial path existed. The snapshots from this pulling sampled every 200 ps formed the basis of the estimated path. Once the ligand stopped interacting with the protein, the following snapshots were replaced by a linear motion toward funnel projection of 43 Å and extension of 0 Å. This replacement procedure did not include water, since at that point the value for the bridging water CV (see below) is already zero. However, all other CVs defined above/below were calculated for the trial path snapshots.

Collective Variables

The collective variables considered include the funnel projection and extension over the left-hand side of the binding cavity (see fun-metaD section, Figure 3B). Likewise, due to the importance of the water molecules in the binding and unbinding processes, we have also considered the bridging water variable.⁷³ Within this CV are defined the polar atoms for the ligands, as well as the neighboring ones in the binding site. The resulting value of the CV is computed as the sum of the product of contact maps between these two groups and the oxygen atoms of all water molecules and is demonstrative of the number of water molecules bridging the polar sites of the protein and the ligand. The switching value used was 3 Å, and the cutoff was 10 Å. However, despite using neighbor lists and some optimizations within the custom PLUMED code, this CV requires considerable computational resources and in complex systems can be detrimental to the performance (see the Results and Discussion section). Finally, four additional CVs are defined considering the distances between the two funnel sites and two defined points on the ligand (Figure 8). These were chosen differently for every ligand but always represent opposite sides of the ligand. Taken together, the four distances represent the orientation of the ligand with respect to the important sites within the protein and help to constrain the rotational degrees of freedom of the ligand.

Figure 8.

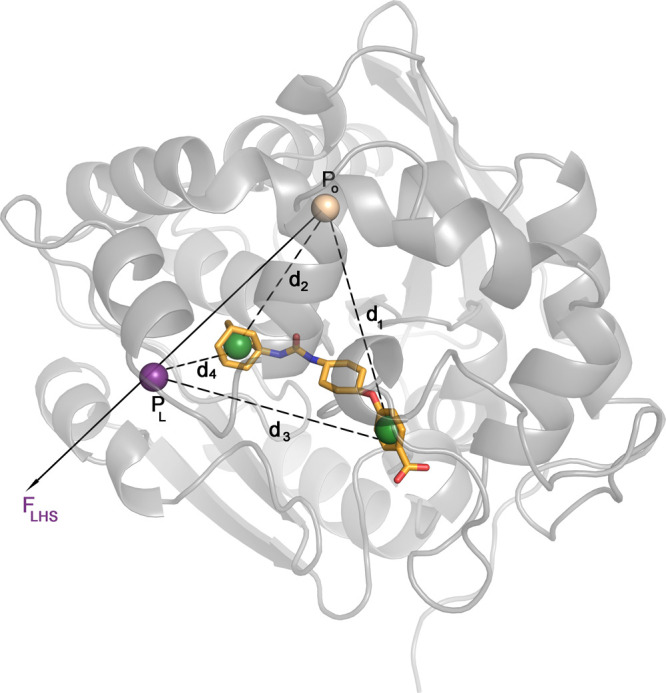
Definition of distance CVs tested for the COMet-Path method. All calculations were done considering the CVs that define the funnel (F_LHS) and the distances that connect the center of masses of the opposite sides of the ligands with P₀ (d1 and d2) and P_L (d3 and d4), the points that define the funnel orientation (see Figure 3). The ligand shown corresponds to PDB code 5am3.

COMet Settings

The coefficient space for the defined CVs was explored using 1 million steps of a simulated annealing procedure with a geometric cooling coefficient of 0.99. The CVs were normalized (over 1) to ensure the importance of the assigned coefficients. The values of the coefficients were optimized between 0 and 0.5. The maximum value would correspond to a 25% contribution. The minimum value for the funnel projection was fixed to 0.25 (see Scheme S1 in the Supporting Information). Combinations of coefficients that would result in no barriers were dismissed as artifacts.

Path Metadynamics Settings

For metadynamics simulations, we have used the same funnel-shaped restraints defined above (see Figure 3). Gaussians with a height of 2 kJ·mol^–1 are deposited every 1000 steps, using the bias factor of 12. The sigma values were 0.15 for the (s) variable, which describe the progression along the coordinate, and 0.0004 for the (z) variable, which is defined as the distance from an initial (guess) path in the free energy space. These two variables are mathematically defined as

5

6

where X represents the atomic coordinates at the current simulation time-step, and X_i denotes the same of the i-th snapshot. The function R represents a chosen metric, which in our case is a combination of CVs with coefficients as optimized by the COMet algorithm. The λ parameter serves to smooth the variation of the s variable.

We ran 350 ns simulations of the selected systems, and additional simulations were run for three systems considering the bridging water CV, leading to a total time of almost 5 μs.

Funnel SWISH Simulations (fun-SWISH)

Finally, we have also combined the SWISH (Sampling Water Interfaces through Scaled Hamiltonians) methodology, which has been recently developed by our group,^43,44 with funnel-shaped restraint metadynamics (fun-SWISH). SWISH is a Hamiltonian replica-exchange method that improves the sampling of hydrophobic cavities by scaling the interactions between water molecules and protein atoms. Due to the crucial role of water molecules in binding and unbinding processes, we intend to join both the fun-metaD and SWISH together in order to assess the ABFEs. We have implemented this methodology on the 18 systems analyzed and have created six replicas for each system, with a different scaling factor (λ) applied not only for the protein but also for the ligands, which is also a novel application of SWISH. We have run every simulation up to 300 ns for all the systems. For the six identified outliers (complexes with PDB code 5am3, 5alg, 5alh, 5aly, 5am0, and 5alo), we have extended the simulation time scale up to 1 μs leading to a total accumulated time of 60 μs. Exchanges among replicas were attempted every 1000 MD steps. The average exchange probability between replicas was approximately 30–40% for all systems considered.

Restraints were applied to the C-lobe of sEH protein, to prevent any general unfolding at higher λ values. A contact map was applied to monitor the distances between pairs of key representative atoms belonging to secondary structures of the protein according to the Timescapes⁷⁴ definition. The pairs were chosen looking at the most consistent contacts between equilibrated apo and holo structures, to exclude any region that underwent natural conformational changes and were limited to ∼100–200 in number to ease the computational burden. The movements of these atoms were restrained to abide by average fluctuations observed during a simple MD simulation with a spring constant of 3000 kJ·mol^–1·nm^–1.

Reproducing the Simulations

The files required to reproduce our simulations have been uploaded to the Plumed-Nest repository (plumedID 20.012). The source code for the new CV we have introduced, namely the projection on axis and the general path collective variables, is now part of the development branch of the Plumed package and will be made available in the next release.

Glossary

Abbreviations

BFE

binding free energy

FES

free energy surface

MD

molecular dynamics

PDB

Protein Data Bank

RMSD

root mean squared deviation

RMSF

root mean squared fluctuation

PME

particle mesh Ewald

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00075.

• Additional results for the structural, dynamical, and energetic analysis of sEH complexes and convergence analysis of fun-metaD, COMet-Path, and fun-SWISH methodologies (PDF)

The authors declare no competing financial interest.