Harnessing Conformational Plasticity to Generate Designer Enzymes

Abstract

Recent years have witnessed an explosion of interest in understanding the role of conformational dynamics both in the evolution of new enzymatic activities from existing enzymes and in facilitating the emergence of enzymatic activity de novo on scaffolds that were previously non-catalytic. There are also an increasing number of examples in the literature of targeted engineering of conformational dynamics being successfully used to alter enzyme selectivity and activity. Despite the obvious importance of conformational dynamics to both enzyme function and evolvability, many (although not all) computational design approaches still focus either on pure sequence-based approaches or on using structures with limited flexibility to guide the design. However, there exist a wide variety of computational approaches that can be (re)purposed to introduce conformational dynamics as a key consideration in the design process. Coupled with laboratory evolution and more conventional existing sequence- and structure-based approaches, these techniques provide powerful tools for greatly expanding the protein engineering toolkit. This Perspective provides an overview of evolutionary studies that have dissected the role of conformational dynamics in facilitating the emergence of novel enzymes, as well as advances in computational approaches that allow one to target conformational dynamics as part of enzyme design. Harnessing conformational dynamics in engineering studies is a powerful paradigm with which to engineer the next generation of designer biocatalysts.

Introduction

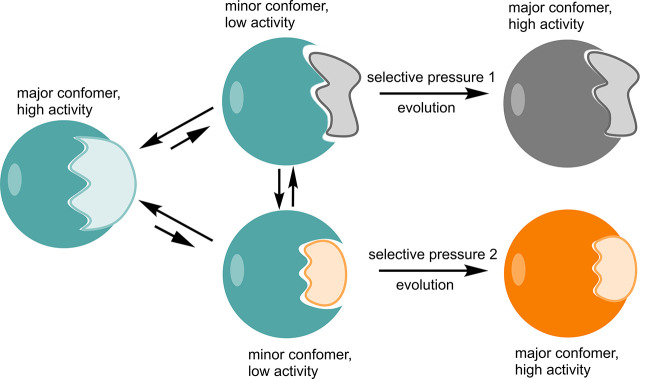
Enzymes are conformationally dynamic, and there has been significant debate in the literature about the extent to which their flexibility corresponds to their catalytic activity.¹⁻⁶ However, in recent years, the focus has shifted toward trying to understand the extent to which conformational dynamics contributes to enzyme evolvability, and the acquisition of new enzyme functions.⁷⁻¹³ This so-called “New View” of enzyme catalysis⁷ describes proteins as existing on an energy landscape with multiple local minima, corresponding to discrete conformations with different energy levels. These different conformations can potentially bind different substrates and facilitate different chemistry, allowing for enzyme promiscuity (the ability to catalyze multiple, distinct chemical reactions).^7,8 One would expect the landscape for the wild-type enzyme to be dominated by one of these minima, which binds the native substrate and corresponds to the native activity of the enzyme. However, mutations introduced over the course of an evolutionary trajectory can shift the equilibrium between conformational states, such that previously minor conformations increase in population, leading to the emergence of new activities (Figure 1).

Figure 1.

Schematic illustration of the relationship between ligand binding, conformational dynamics, and protein evolution.^7,8 The major conformation adopted by the enzyme is responsible for its native activity, however the existence of minor conformations (that may or may not also be able to interconvert directly) can give rise to promiscuous activities for non-natural substrates. Mutations accumulated over the course of evolutionary trajectories (through either natural or directed evolution) with the appropriate selective pressure(s) can ultimately lead to population shifts, with these minor conformations now becoming the major conformers and the promiscuous activity becoming the new “native” activity. For further discussion, see e.g. refs (7, 8, and 31).

It is by now well established that enzyme promiscuity plays an important role in enzyme evolvability.^{7,8,10,12,14−16} This has generated great interest in trying to use Nature’s tricks to harness promiscuity in enzyme design.¹⁶⁻¹⁹ But what about conformational dynamics? Many enzymes harbor decorating loops on their scaffolds (this is very common for example in the case of TIM barrel proteins^20,21) that theoretically could be manipulated to alter activity. Or, activity could be altered by the controlled introduction of mutations to fine-tune enzymes’ conformational ensembles (as has been observed in a number of directed evolution studies²²⁻²⁷). This can even be coupled with the incorporation of non-canonical amino acids, thus expanding the genetic code and either facilitating completely novel chemistry in existing active sites or allowing for the emergence of catalytic activity on previously non-catalytic scaffolds.²⁸⁻³⁰

While harnessing conformational diversity has tremendous potential in enzyme engineering, several technical challenges remain that make laboratory engineering of conformational dynamics far from routine.^31,32 However, recent advances in computational approaches targeting conformational dynamics may allow for further progress in this area, opening up a highly powerful new avenue for targeted enzyme design. This is particularly important, as many computational enzyme design studies still focus on either exclusively sequence-based approaches, or, where structure-based approaches are used, they are limited in scope as they frequently focus on static structures and disregard dynamical properties of the system (e.g., refs (23, 33−42)).

This Perspective will discuss the role of conformational dynamics in enzyme evolution, as well as providing examples where manipulation of conformational dynamics has been successfully harnessed as a tool for enzyme engineering. We will particularly discuss recent work from both our own as well as the Tawfik laboratories, while also showcasing important contributions to the field from other research teams. We will also discuss recent developments and advances in computational methodologies that incorporate conformational dynamics as part of the design process, providing a promising avenue for the generation of novel enzymes with tailored catalytic and dynamical profiles.

Repeating Structural Motifs Facilitate the Emergence of Novel Proteins

There has been substantial interest in understanding the evolution of enzymatic activity on existing enzymatic scaffolds, either through specialization toward one of a set of generalist functionalities, or through emergence of completely new activities in existing active sites (see e.g. refs (16, 43−49)). This focus on existing enzymes makes sense considering that at least 87% of all existing enzyme functions have been estimated to have either evolved from another pre-existing catalytic function, or evolved through specialization of a generalist enzyme.⁵⁰ What then about the remaining enzymes—what is their origin? Clearly, these enzymes must have, in some format, evolved on scaffolds that were previously non-catalytic. In addition, even if one assumes that all modern enzymes have evolved from pre-existing enzymes, still, the first enzymes must have somehow evolved at some point in our evolutionary history. This is likely to have occurred at a very early stage in the evolution of life on Earth, as it has been estimated that a wide array of enzymes already existed in the last universal common ancestor (LUCA).^51,52 So how then are non-enzymatic scaffolds repurposed for enzymatic function, and how do new proteins emerge to provide these scaffolds in the first place?

In this context, Tawfik and co-workers have explored the evolutionary constraints and driving forces that underlie the emergence of β-propeller proteins.⁵³ Specifically, by combining ancestral reconstruction with biochemical and structural analysis, the authors were able to trace the emergence of functional 5-bladed lectin β-propeller via tandem duplication from short (<50 amino acids) motifs that are present in known genomes. This is in perfect agreement with Dayhoff’s hypothesis that the first folded functional protein domains arose through the fusion, duplication, and diversification of short polypeptide sequences,⁵⁴ as discussed in detail in ref (55). In a related study, Voet and co-workers were recently able to exploit the modular structure of WD40 proteins to design a symmetrical 8-bladed β-propeller protein through pure computational design.⁵⁶

Following from this, Tawfik and co-workers have traced an “ancient fingerprint” in Rossman-fold enzymes, comprised of an interaction between a carboxylate (Asp or Glu) sitting at the tip of the second β-strand of these enzymes and bound ribose (ribose- β2-Asp/Glu).⁵⁷ This interaction appears to both have unique geometrical features and also be exclusively present in Rossman-fold enzymes that bind cofactors. In addition, the authors demonstrated that ribose–carboxylate interactions found in other protein folds are both rare and topologically different from those observed in the Rossman-fold enzymes. This led to the suggestion that the presence of this fingerprint indicates the divergence of Rossman-fold enzyme from a common pre-LUCA ancestor that possessed the same binding motif.⁵⁷ In subsequent analysis, Grishin and co-workers⁵⁸ defined a minimal Rossman-like structure motif (RLM) involved in ligand binding, comprised of a “doubly-wound” α/β/α sandwich structure, and used this as a baseline for analysis of RLM domains in the Protein Data Bank (PDB).⁵⁹ This structural analysis was coupled with evolutionary analysis, using the Evolutionary Classification of Protein Structure Domains (ECOD) database,^60,61 and indicated that the RLM binding motif likely arose several times during the evolution of these proteins; it was likely used already by the LUCA.

How then do these motifs get translated into function? Phosphate binding proteins are an excellent model system to address this question, as phosphate binding is ubiquitous in biology, and phosphate esters are the building blocks of life itself, being involved in essentially all cellular processes.⁶² We recently performed detailed sequence and structural analysis of all phosphate binding motifs in the PDB, combined with evolutionary analysis using ECOD.⁶³ Curiously, across 4 billion years of evolutionary time, the dominant mode of phosphate binding appears to be mediated through side-chain interactions, with no involvement at all from the protein backbone. However, in the earliest proteins (particularly αβα sandwich enzyme domains), the dominant binding mode (to any of mono-, di-, or triphosphate binding) involves interactions with the N-terminus of an α-helix, primarily through interactions with the backbones and/or side chains of the Prebiotic amino acids Gly, Ser, and Thr⁶⁴⁻⁶⁶ (Figure 2). This provides a putative snapshot of the first phosphate binding interactions in proteins and a baseline for further engineering of binding or catalytic activity. As an example of this, Tawfik and co-workers have used phylogenetic analysis to identify the ancestral “sequence logo” of the Walker-A P-loop element, which is absolutely critical for facilitating binding and phosphoryl transfer in modern P-loop NTPases.⁶⁷ They then used computational design to incorporate this sequence logo into de novo designed scaffolds, obtaining soluble and stable proteins with an expanded binding repertoire. In addition to polynucleotides and both RNA and single-stranded DNA, they were also able to bind adenosine triphosphate (ATP) without the involvement of metal cofactors. In addition, phosphate binding was apparently facilitated by complex cooperative conformational changes that were likely only feasible due to the structural plasticity of these designed proteins.⁶⁷ This highlights the engineering potential of transferring minimal motifs capable of conferring binding ability to conformationally diverse scaffolds to generate new functionality.

Figure 2.

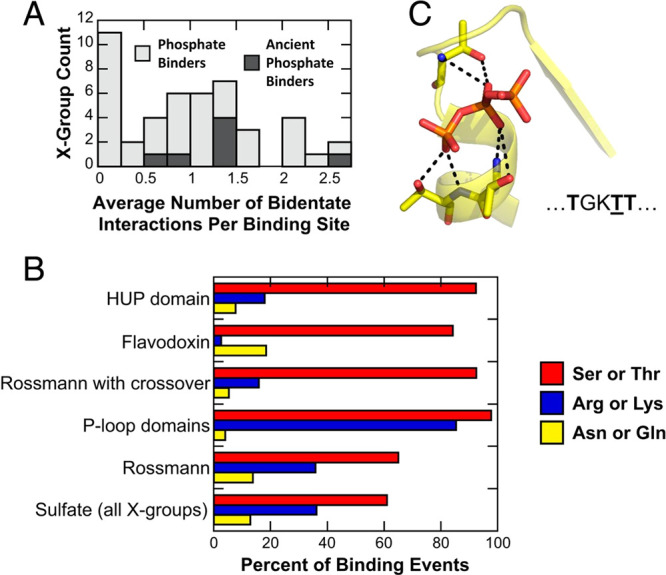
Observed prevalence of bidentate interactions in phosphate binding (where “phosphate” in this case refers broadly to mono-, di-, and triphosphates), based on combined analysis of structural data in the Protein Data Bank⁵⁹ and evolutionary information in the ECOD database.^60,61 X-groups provide the broadest level of classification in ECOD, corresponding to discrete events of evolutionary emergence with no detectable sequence homology or fold identity. Shown here are (A) the frequency of bidentate phosphate binding interactions across all X-groups, including also ancient phosphate binders, and (B) the amino acids involved in forming these bidentate interactions across X-groups and in specific protein folds. Here, it can be seen that Thr and Ser (both prebiotic amino acids) are essential for the formation of bidentate interactions in the N-helix binding mode at the tip N-terminus of an α-helix, an illustrative example of which is shown in the case of the binding of a triphosphate in panel (C). For more details, see ref (63). Reproduced with permission from ref (63). Copyright 2020 National Academy of Sciences.

Conformational Dynamics and the Emergence of Novel Enzymes

It is clear that the modular nature of protein structure can act as a driving force to facilitate the evolution of novel scaffolds with novel functionalities, and the modular structure of proteins has been frequently used also in protein engineering studies to control protein structure and function.⁶⁸⁻⁷⁴ But it is one thing to simply assemble a stable, folded scaffold, and another to confer enzymatic activity to that scaffold. One of the easiest ways to confer enzymatic activity to a non-catalytic scaffold is simply by repurposing existing functionality, in particular a binding site, as ligand binding is an important first step toward efficient catalysis. There exist several examples in the literature of the emergence of novel enzymatic activity on previously non-catalytic scaffolds,^25,75−80 for example through the functionalization of binding sites. The evolutionary trajectories that can lead to the emergence of enzymatic activity can be characterized by ancestral sequence reconstruction,^47,81 alongside any combination of structural, biochemical, and computational characterization, and it appears that conformational dynamics can play an important role in the emergence of enzymatic activity. Here, we showcase two systems where conformational dynamics appears to play a role in the transition from a solute binding protein to an enzyme.

The first of these is the enzyme cyclohexadienyl dehydratase (CDT), which catalyzes the cofactor-independent Grob-type fragmentation of prephenate and l-arogenate respectively to yield phenylpyruvate and l-phenylalanine.⁸² Sequence and structural analysis of this enzyme has suggested that CDT has evolved from solute-binding proteins.^75,79 Jackson and co-workers have recently harnessed the power of ancestral sequence reconstruction^47,81 coupled with biochemical characterization in order to explore the physiochemical parameters that allowed for the evolutionary transition of CDT from a solute-binding protein to an enzyme.⁷⁹ The key feature leading to the emergence of CDT activity appeared to be the incorporation of a desolvated general base into the ancestral active site, conferring catalytic activity to this scaffold. Directed evolution indicated the presence of multiple independent mutational pathways leading to higher catalytic activity once the key catalytic residues were introduced, as well as separate mutational pathways from the historic mutational pathway observed in the ancestral proteins, suggesting that the enhancement of CDT activity on this scaffold occurred non-deterministically. Other mutations reshaped the active site and introduced hydrogen-bonding networks that improved enzyme–substrate complementarity as well as placement of the reacting fragments in the active site. Finally, remote mutations refined the conformational ensemble of the enzyme, by dampening the sampling of catalytically non-productive conformations.⁷⁹ More recent experimental work performing double electron–electron resonance (DEER)⁸³ on putative evolutionary intermediates along the trajectory toward a modern catalytically efficient CDT has further illustrated the role of remote mutations in reducing the sampling of catalytically non-productive conformations of the enzyme.

In parallel work, we have studied the evolution of chalcone isomerases (CHI) from solute binding proteins.^25,84 Chalcone isomerases catalyze the enantioselective intramolecular Michael addition of chalconaringenin, to yield the plant flavonoid (2S)-naringenin, making it a key enzyme in plant flavonoid biosynthesis.⁸⁵ Ancestral sequence inference suggests that both modern CHIs and a related group of CHI-like proteins (CHILs) that lack enzymatic activity^86,87 have evolved from fatty acid binding proteins (FAPs, which are enzymes that are important for plant fatty acid biosynthesis⁸⁸) via a common ancestor lacking isomerase activity.^25,88 By combining ancestral sequence reconstruction,^47,81 X-ray crystallography, NMR, and simulations, we were able to identify four founder mutations that each, individually, are able to confer chalcone isomerase activity.²⁵

One important factor in examining the effect of these founder mutations is whether the effect of these mutations is additive or not. In epistasis, the effect of the mutations is not additive (i.e., the order in which the mutations are introduced becomes important). As discussed in ref (25), epistasis is significant from an evolutionary point of view, because where present, epistasis will limit the number of accessible evolutionary pathways, as mutations need to be introduced in a specific sequence in order to reach the desired effect. There is evidence in the literature for epistasis, including sign epistasis (where new mutations can change the effect of previous mutations from beneficial to deleterious, or vice versa), playing an important role in protein evolution.⁸⁹⁻⁹⁶ Curiously, however, a laboratory reconstructed mutational trajectory of CHI showed only weak functional epistasis between key founder mutations, with multiple subsequent trajectories that each could confer isomerase activity. This suggests that the order in which these founder mutations are introduced is not important, which is indicative of a smooth evolutionary landscape underlying the emergence of CHI activity. This suggests that the gain of enzymatic activity is relatively facile despite the evolutionary origin of this enzyme from a non-catalytic ancestor.

Our combined analysis also indicated a combined role for reshaping of the active site by mutations toward a productive substrate-binding mode, as well as repositioning of a key catalytic arginine inherited from the ancestral FAPs (Figure 3) as major driving forces for the emergence of isomerase activity.²⁵ We later demonstrated that the side chain of this arginine acts as a combined Brønsted and Lewis acid in bifunctional substrate activation during the Michael addition catalyzed by CHI.⁸⁴ Such bifunctional activation is also observed when employing the guanidine- and urea-based chemical reagents that are frequently used for asymmetric organocatalysis.^97,98 This highlights the potential application of the CHI scaffold in the design of biocatalysts for guanidine-based asymmetric catalysis. A critical observation here, however, is the fact that even the inactive CHI ancestor possessed all key catalytic residues in the correct position in the active site,²⁵ demonstrating that simply having the correct catalytic residues in the correct position is not alone sufficient for catalysis to actually occur.

Figure 3.

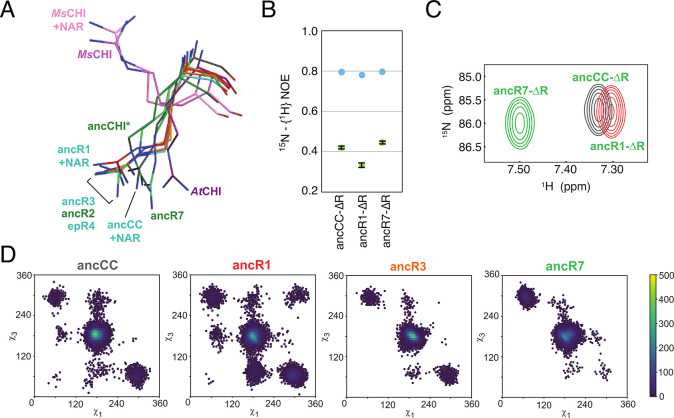
Changes in the conformational ensemble of the catalytic arginine, R34, during the evolution of chalcone isomerases (CHIs) from binders to catalysts. (A) Structural alignment of crystal structures of different CHIs, showing how widely the conformation of R34 varies. This is in agreement with (B) NMR steady-state heteronuclear NOE values for the catalytic arginine, and the corresponding (C) HSQC signals of the arginine side chain. These indicate both the changes in the mobility of this residue during the evolution of CHI from ancCC to ancR1 to ancR7, as well as the corresponding changes in the electrostatic environment of this side chain. Finally, this is corroborated by long-time-scale molecular dynamics simulations, where the corresponding χ₁ and χ₃ dihedral angles of R34 during simulation of the different variants once again show the changes in the conformational space of this residue. Reproduced with permission from ref (25). Copyright 2018 Springer Nature.

Conformational Dynamics Modulates the Activity of Extant Enzymes

Functionally important conformational dynamics in enzymes can manifest themselves in different ways, and on different time scales, spanning several orders of magnitude. Such conformational dynamics can range from simple side chain fluctuations through to larger-scale conformational changes such as loop dynamics, domain movements, or large allosteric motions.⁹⁹ From a catalytic perspective, these may or may not be ligand-gated, in that substrate binding energy can be used to drive an otherwise catalytically unfavorable conformational change.^100,101 The relevance of conformational dynamics and enzyme evolution has been reviewed in great detail elsewhere,^{7,8,10−13,32} and therefore we will only touch briefly upon selected relevant systems in this section. We note that in this section, we focus in particular on evolutionary fine-tuning of enzyme loop dynamics, as this can be targeted for protein engineering;¹⁰² however, clearly, other forms of conformational dynamics can also be evolutionarily important.

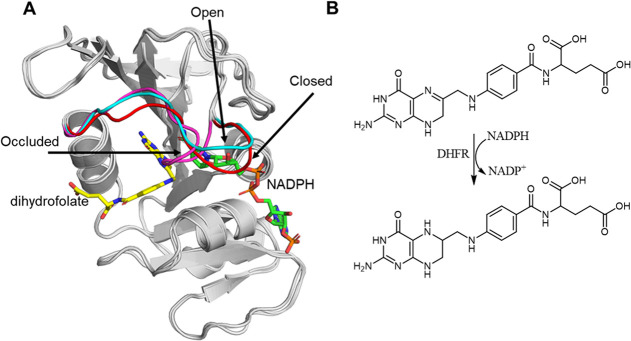
One of the classical examples of an important enzyme for understanding the role of conformational dynamics in enzyme function and evolution has been dihydrofolate reductase (DHFR).^{3,4,6,9,103−106} DHFR uses NADPH as a cofactor to catalyze the reduction of dihydrofolate (DHF), through a two-step mechanism (Figure 4). In E. coli DHFR (EcDHFR), the catalytic mechanism is aided by the movement of multiple loops close to the binding pocket, including the catalytically important “Met20 loop”. This is a highly flexible loop that acts as a lid to hold the cofactor tightly in the binding pocket. It can occupy three distinct conformations: open, closed, and occluded (Figure 4).¹⁰⁴ Upon cofactor binding, it undergoes a conformational transition from an open to a closed conformation, thus placing the reacting fragments in a catalytically competent conformation and increasing the probability of productive binding.¹⁰⁷ In between the first and second mechanistic steps, another conformational change occurs from the closed to the occluded state, where the cofactor binding pocket is obstructed by the Met20 loop, thus forcing the nicotinamide ring out of its bound position and facilitating the rate-limiting product release step.^108,109 The conformational dynamics of DHFR’s Met20 loop has been probed by using NMR, with loop rearrangements occurring on the millisecond time scale having been demonstrated to be responsible for the required changes in the active-site configuration throughout the catalytic cycle.¹⁰⁸

Figure 4.

(A) Overlay of three X-ray crystal structures of E. coli DHFR with the Met20 loop crystallized in different conformations. Shown here are structures of DHFR with the Met20 loop in the closed (red, PDB: 1RX2), occluded (magenta, PDB: 1RX4), and open (cyan, PDB: 1RE7) conformations, based on data provided in conjunction with ref (107). (B) Schematic overview of the hydride transfer reaction catalyzed by DHFR, in which dihydrofolate is reduced to tetrahydrofolate, and NADPH is oxidized to NADP⁺.

DHFR has historically been an important model system for probing the role of conformational dynamics in enzyme catalysis.^{4,6,103,104,106} More recently, there has also been increasing interest in understanding the role of conformational dynamics in DHFR evolution.^{9,105,110−113} In particular, despite high structural similarity, human DHFR (hDHFR) exhibits very different conformational movements throughout the catalytic cycle compared to EcDHFR.¹¹⁰ That is, the loop analogous to the Met20 loop in EcDHFR remains in a closed position throughout the catalytic cycle of hDHFR. In addition, millisecond time scale fluctuations facilitate flux through the catalytic cycle in EcDHFR.^114−117 Such millisecond fluctuations are not observed in hDHFR which instead exhibits pervasive fluctuations on the microsecond time scale, including in regions which border the binding pocket, suggesting that these fluctuations may be productive for product release.¹¹⁰ Other studies have explored how DHFR dynamics has changed over the course of evolution, focusing in particular on whether the conformational fluctuations of the wild-type enzyme are conserved, or whether they are dampened or amplified during evolution (see e.g. refs (105 and 112)), as well as exploring the coupling of fast dynamics to the reaction coordinate.¹¹¹

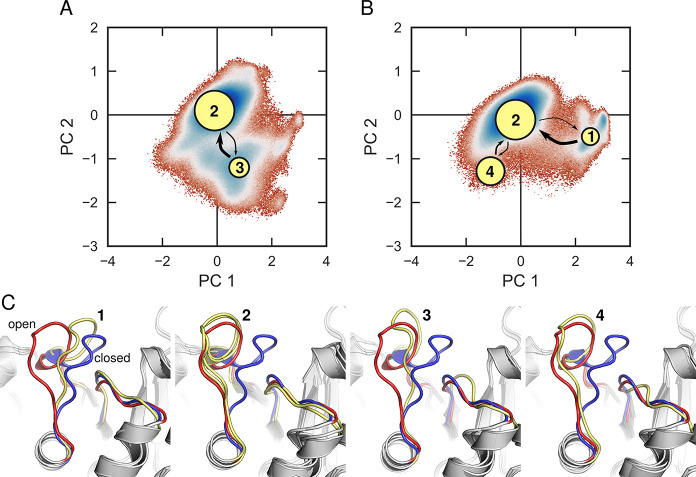
Another example of systems where evolution appears to have focused on fine-tuning loop dynamics are TIM barrel proteins. The TIM barrel is highly evolvable^20,118,119 and one of the most common protein folds observed in the PDB.^20,59,120 The name giving enzyme, triosephosphate isomerase, possesses several decorating loops that are active within the catalytic cycle.^100,121,122 Of these, loop 6, undergoes a large ligand-gated conformational change upon substrate binding, moving up to 7 Å from the open to closed position, thus creating a catalytic cage that sequesters the active site from solvent.¹⁰⁰ Despite the persistent image of this loop as a classical example of a two-state rigid-body motion,^123−128 simulation studies have shown that this loop is highly flexible and can take on multiple conformations, thus yielding multiple different potential trajectories that can lead from the inactive open conformation of the enzyme to the catalytically competent closed conformation of the enzyme (Figure 5).¹²⁹

Figure 5.

Superimposition of Markov state models (MSMs)^130,131 of (A) unliganded triosephosphate isomerase (TIM) and (B) TIM in complex with substrate dihydroxyacetone phosphate (DHAP), onto the corresponding free energy surfaces (T = 300 K) obtained from performing principal component analysis (PCA) on conventional MD simulations of each system. The free energy surfaces are defined in terms of the first two principal components, PC1 and PC2. The area of the nodes representing each of the metastable states in panels (A) and (B), and the thickness of the arrows connecting them, correspond to the populations of each node and the transition probabilities between them, respectively (note that areas and thicknesses do not scale linearly with transition probabilities). Shown here also are (C) overlays of representative structures from each of the metastable states sampled in these simulations, with the crystallographic “open” and “closed” conformations of the loop shown in red and blue, respectively, and the loop conformation at each state shown in yellow. Note that the metastable state 2 is virtually identical for simulations of both the liganded and unliganded forms of the enzyme. For details, see ref (129). Reprinted with permission from ref (129). Copyright 2018 American Chemical Society.

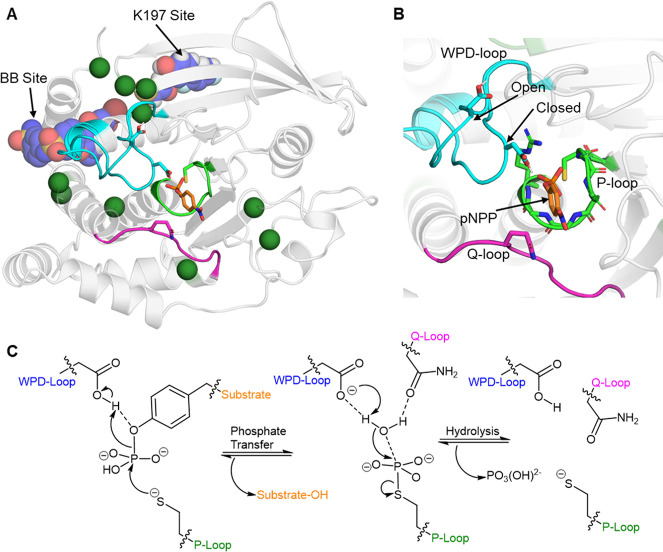
Another family of enzymes where loop dynamics appears to be evolutionarily important are protein tyrosine phosphatases (PTPs).¹³² PTPs catalyze the dephosphorylation of phospho-tyrosine residues through a two-step “ping-pong” mechanism, in an active site composed of three highly conserved loops (Figure 6).¹³³ Of these, the “P-loop” is responsible for coordinating the reacting phosphate group and providing a nucleophilic cysteine to dephosphorylate the phospho-tyrosine residue in the first step. Furthermore, this reaction is promoted by the closure of a highly flexible “WPD-loop”, which contains an active-site aspartic acid that acts as a general acid to stabilize the leaving group. In the second step, the thiol-phosphate group is subjected to nucleophilic attack by an active-site water molecule, which is again promoted by the aspartic acid on the WPD-loop, in this case acting as a general base, deprotonating the active-site water to enhance its nucleophilicity. Finally, vital to the second step is the coordination of a glutamine on the “Q-loop” to the nucleophilic water molecule. An NMR study on two different PTPs demonstrated the rate of WPD-loop closure to be highly correlated with the rate of the first chemical step.¹³² Given that PTPs are responsible for regulating many cellular signaling processes (meaning their catalytic rates will have been subjected to strict evolutionary pressure), and that throughout nature the rate of PTP catalysis can vary by several orders of magnitude,¹⁴⁰ this data may suggest that evolution has fine-tuned individual PTP loop dynamics to regulate their catalytic rates. Further, numerous PTPs have known allosteric sites (Figure 6),^{134,135,141,142} and a recent combined bioinformatics and biomolecular simulation study has identified evolutionarily conserved allosteric communication within PTPs, suggesting that PTPs have been subjected to both local and distal mutagenesis in order to regulate the conformational dynamics of its active-site loops.¹⁴³

Figure 6.

(A, B) Aligned crystal structures of PTP1B with the WPD-loop in its closed and open conformations, respectively (PDB: 6B90,¹³⁴ this structure contains both conformations of the loop). Panel (A) depicts the overall structure of PTP1B, highlighting the three major loops which make up the active site (WPD-loop: cyan, P-loop: green, and Q-loop: purple) indicated. The two known allosteric drug binding sites on PTP1B are labeled and depicted with a representative drug bound to each site (BB site, PDB ID: 1T49,¹³⁵ and K197 site, PDB ID: 6B95(134)). Dark green spheres are residues not located within the active site, but where single-point substitutions have been shown to alter PTP1B’s k_cat or K_m by |>50%| (data collated from refs (134, 136−139)). (B) A close-up of the PTP1B active site, with a model substrate p-nitrophenyl phosphate (pNPP) bound. The backbone nitrogen atoms and the arginine side chain on the P-loop that are harnessed to coordinate the phosphate group are also shown. (C) Conserved two-step reaction mechanism utilized by PTPs.¹³³

Fructose-1,6-bisphosphate (FBP) is another enzyme with an active site primarily composed of loops, with these loops used to catalyze a two-step reaction in which FBP first acts as an aldolase before undergoing a large-scale conformational change in order to act as a phosphatase in its second catalytic step.^144,145 This dual aldolase/phosphatase activity likely emerged in FBP to prevent degradation of the reaction intermediates if they were released back into the high temperature environment that FBP is natively found in. In many other cases in which an unstable intermediate is formed, modular catalytic systems are directly connected to one another, allowing for a cascade of chemical reactions to occur before releasing the reactant back into the environment (see e.g. refs (146 and 147)). The solution adopted by FBP in which the active site is able to (re)organize itself in order to allow for a different form of catalysis is striking, and it could be argued that this approach is notably more accessible due to the large amount of conformational plasticity available to the active site. That is, an active site composed primarily of loops (as opposed to more defined secondary structure) is likely to have a wider range of accessible conformational substates from which dual aldolase and phosphatase activity could emerge. While FBP represents a remarkable instance of evolutionary ingenuity, the competing interests associated with using one active site to engineer multiple different reactivities is likely to be particularly challenging. Indeed, several identified single point mutations that enhanced aldolase activity came at the cost of reduced phosphatase activity and vice versa.¹⁴⁴

We note that there exist many other systems where conformational dynamics appears to be evolutionarily important, including organophosphate hydrolases,^148−150 β-lactamases,^151−155 tryptophan synthase,¹⁵⁶Pseudomonas aeruginosa arylsulfatase,¹⁵⁷ thioredoxins,¹⁵⁸ cold-adapted enzymes,^159,160 and guanylate kinase¹⁶¹ as just some examples. For economy of space we have not discussed these systems in detail here, but instead refer readers to the cited references for more details on each of these systems.

Enzyme Engineering by Fine-Tuning Protein Conformational Dynamics

It is becoming clear that fine-tuning of conformational dynamics plays a crucial role in enzyme evolution. Being able to enhance enzyme activity through manipulating conformational dynamics requires either being able to increase the population of catalytically productive conformations and/or being able to dampen the population of catalytically unproductive conformations of an enzyme. This is challenging, but not impossible, to achieve in silico or in the laboratory. There are a number of examples, both where the conformational ensemble has been serendipitously optimized through directed evolution, and where the conformational ensemble has been successfully targeted for enhancing an enzyme’s activity, indicating that there is great potential for doing this more systematically. In particular, it appears that maintaining conformational dynamics similar to that of the native enzyme is not critical for the engineering of functional proteins,¹⁶² suggesting that there is significant scope for the manipulation of conformational dynamics while at the same time maintaining catalytic activity. We discuss here some examples of the engineering of enzyme conformational dynamics (for detailed reviews see e.g. refs (12, 31, and 102)), with a particular focus on the engineering of enzyme specificity and activity.

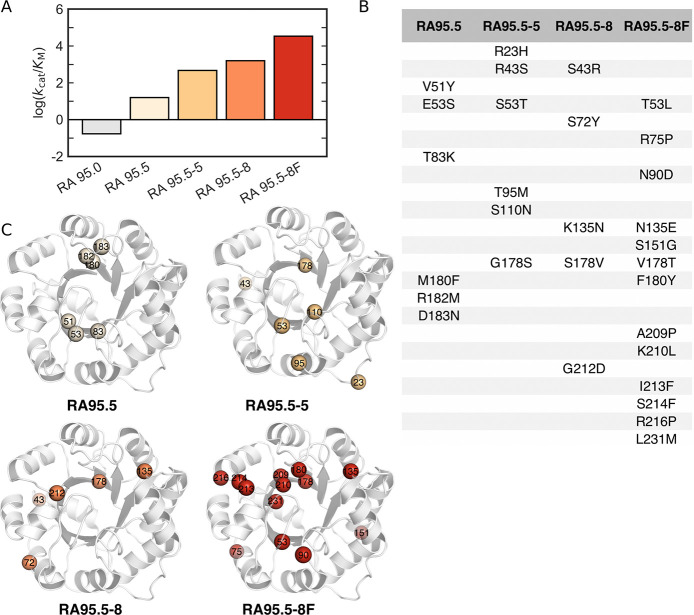
Retro-aldolases (RAs) are among the most complex computationally designed enzymes to date.^163−165 They catalyze the amine-assisted cleavage of a methodol substrate through a multi-step mechanism involving an enzyme-bound Schiff base intermediate. In 2012, Baker and co-workers performed an expansive study introducing a catalytic motif likely to be capable of Kemp elimination onto a variety of scaffolds, including TIM barrel and Jelly Roll folds.¹⁶⁴ The resulting de novo designs only exhibited modest catalytic activity, but were enhanced substantially through directed evolution (from initial k_cat/K_M values of <1 M^–1 s^–1 for all designed variants with subsequent improvements between 7-fold and 88-fold). Following from this, Hilvert and co-workers used directed evolution to increase the catalytic efficiency of a de novo RA, and were able to successfully reach catalytic efficiencies comparable to those of natural enzymes (Figure 7).^165,166 During the evolutionary pathway, the binding site underwent a complete remodeling event, with the catalytic lysine being abandoned in favor of another lysine in the binding pocket. In addition, mutations were observed both in the binding site and at distal positions. With the introduction of distal mutations, both significant changes to loop conformations and more extensive conformational changes were observed.

Figure 7.

Overview of directed evolution experiments of the in silico designed retro-aldolase RA95, showing the increase in activity toward that of natural enzymes. Shown here are (A) the catalytic efficiencies of various evolved RA95 variants toward (R)-methodol, (B) the mutations introduced in each variant, and (C) the corresponding position of the different mutations on the structure, based on kinetic and structural data presented in refs (165 and 166). Reproduced with permission from ref (10). Copyright 2018 the authors, published by the Royal Society. All rights reserved.

Biochemical analysis indicated a shift in rate-limiting step from C–C bond scission to product release for the evolved variants, with a catalytic tetrad that emerges in the later rounds of evolution playing an important role in facilitating the tremendous rate acceleration (>9000 fold increase in k_cat/K_M for the most evolved variants) observed in these enzymes.¹⁶⁷ In addition, computational modeling indicated that the conformational space sampled by the highly efficient enzyme contains a high percentage of catalytically competent conformations, in contrast to variants from earlier rounds of evolution which sample only small populations of catalytically competent substates.²³ Finally, further computational modeling identified fast time scale motions that were present only in the most catalytically efficient evolved variant of the de novo RA.¹⁶⁸ The change in conformational ensemble during directed evolution thus occurs as an unintentional but essential consequence of the mutations introduced during laboratory evolution.

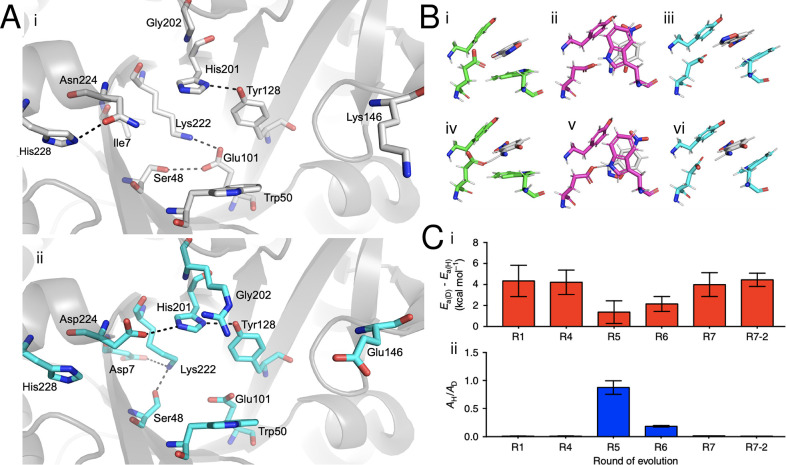
Optimization of conformational dynamics has played an unforeseen but important role in several other successful de novo enzyme design studies.^{10−12,31,169} In a series of studies, Baker and co-workers first generated a de novo Kemp eliminase (KE07) catalyzing proton elimination from 5-nitrobenzisoxazole with modest catalytic activity, which was then further optimized by directed evolution to increase k_cat/K_M by 200-fold.¹⁷⁰ This led to a further study to improve KE07 through (1) optimizing the electrostatic environment of the active site by removal of a catalytically unfavorable “quenching” interaction between an active-site lysine and the catalytic base as well as fine-tuning the pK_a of the catalytic base, and (2) stabilizing the active site in a conformation optimal for catalysis.¹⁷¹ There have subsequently been several experimental and computational studies of KE07,^171−175 which have provided significant insight into catalysis by the original design and the evolved variants. However, accounting for the effect of mutations that emerge in later rounds of evolution has been challenging. In this context, we have performed detailed crystallographic and computational analysis of the evolutionary trajectory of KE07,²⁴ where we showed that across the trajectory, the instability of the original designed active site leads to the emergence of two additional active-site configurations, involving significant active-site reorganization (Figure 8). The most efficient of these is then gradually stabilized by evolutionary conformational selection. Our computational analysis indicates that the new active-site configurations are not only catalytically active, they are, in fact, catalytically preferred over the original design. In particular, our work demonstrated that substitution of residues remote from the active site appeared to play an important role in allowing for the emergence of these new active-site configurations, and thus in controlling and shaping the active site for efficient catalysis.²⁴

Figure 8.

Directed evolution (DE) of Kemp eliminase KE07 involves binding pocket restructuring and conformational diversification of a key catalytic residue. (A) Binding pocket restructuring from the first round of directed evolution (R1, gray) to the fourth round of directed evolution (R4, cyan). (B) Conformational plasticity in Trp50 introduces three distinct conformations, conformation A (green) is present prior to DE, conformation B (magenta) is present in intermediate DE steps, and conformation C (cyan) is present in later DE steps. Representative structures for Michaelis complexes (i–iii) and transition states (iv–vi) obtained from simulations of the reaction mechanism are shown. (C) Kinetic isotope effects (KIEs) on (i) activation energies and (ii) pre-exponential factors. Conformational mixing of different Trp50 conformations leads to anomalous KIEs in R5-R6, while the values at the end points of the evolutionary trajectory remain similar. Adapted from ref (24). Copyright 2018 Springer Nature. Published under a CC-BY license (http://creativecommons.org/licenses/by/4.0/).

Following this, in 2013, Hilvert and co-workers were able to obtain a de novo Kemp eliminase (KE), HG3, which was further optimized by directed evolution, with the most efficient evolved variant after 17 rounds of evolution (HG3.17) being able to cleave 5-nitrobenzisoxazole with k_cat = 700 ± 60 s^–1 and k_cat/K_M = 230 000 ± 20 000 M^–1 s^–1.¹⁷⁶ Structural analysis suggested three potential origins for this tremendous enhancement of catalytic activity: (1) improved shape complementarity of the evolved active site toward the substrate, which includes the elimination of a non-productive substrate binding mode, (2) improved alignment of the catalytic base, and (3) the introduction of a new catalytic group contributing to the stabilization of negative charge developed during the reaction.¹⁷⁶ More recently, Chica and co-workers used room-temperature crystallography to study changes in the conformational ensemble of the HG3 series of Kemp eliminases during directed evolution.²⁷ They observed a number of key changes across the evolutionary trajectory, specifically, rigidification of key catalytic residues, improved active-site preorganization, and enlargement of the entrance to the active site, which in turn facilitates substrate entry and product release. They then created a construct, HG4, which contained the minimal subset of mutations observed in the HG3 series, all of which are in or close to the active site, in order to establish the conformational changes necessary to enhance the activity of HG3. The designed variant (HG4, k_cat/K_M = 120 000 M^–1 s^–1) is >700-fold more effective than HG3 itself (k_cat/K_M = 160 M^–1 s^–1), but not as efficient as HG3.17 (k_cat/K_M = 230 000 M^–1 s^–1), since only a minimal subset of mutations was introduced.²⁷ Significantly, these key changes in the conformational ensemble could be predicted using computational design, indicating again the importance of including conformational flexibility as part of the design procedure.

In another example of using conformational flexibility to design efficient Kemp eliminases, we harnessed the conformational flexibility of Precambrian β-lactamases, identified through ancestral inference,^47,81 and used these enzymes as a scaffold to insert a de novo active site capable of Kemp elimination.¹⁷⁷ This was achieved through a single hydrophobic-to-ionizable substitution of a tryptophan to an aspartic acid side chain (due to both shape congruity with the substrate for Kemp elimination, as well as introduction of a general base to the active site). Our most proficient Kemp eliminase, an ancestral eliminase at the GNCA node, showed catalytic parameters of k_cat ≈ 10 s^–1 and k_cat/K_M ≈ 5 × 10³ M^–1 s^–1, only 2 orders of magnitude below that of HG3.17.¹⁷⁶ Curiously, while our design strategy was highly effective in the ancestral lactamases, it was unsuccessful in modern lactamases. Combined structural and computational analysis suggested that this was due to the increased rigidity of the evolved active sites, which could not adapt to bind the substrate and catalyze Kemp elimination with optimal electrostatic preorganization. Subsequently, we performed computationally focused ultra-low-throughput screening of variants of our most efficient lactamase predicted by FuncLib,⁴⁰ and were able to further enhance our most proficient lactamase from our earlier study¹⁷⁷ to k_cat ≈ 10² s^–1 and k_cat/K_M ≈ 2 × 10⁴ M^–1 s^–1,⁴⁹ bringing it to the range of the catalytic activities of naturally occurring enzymes.¹⁷⁸ We note that the catalytic base (D229) introduced into the de novo active site lies on the end of a flexible loop. Therefore, subsequent studies could potentially target the flexibility of this loop, in order to optimize its placement in the active site.¹⁰²

As more is discovered about the connection between loop dynamics and enzyme catalysis, directed evolution of loops and conformational dynamics is being harnessed to produce more efficient enzymes. For example, Kim and co-workers performed concerted insertion and deletion of dynamic loops using SIAFE (Simultaneous Incorporation and Adjustment of Functional Elements) and directed evolution, in order to successfully confer β-lactamase activity onto a glyoxalase II αβ/βα hydrolase scaffold.¹⁷⁹ More recently, Zhu and co-workers focused on mutations in the active-site decorating loops of PpADI (Pseudomonas plecoglossicida arginine deaminase).¹⁸⁰ Through targeted mutations, they determined that loop flexibility appears to be a critical basis for efficient substrate affinity, not only by reducing the amount the loop blocks access to the active site, but that synergy between the motions of the two decorating loops plays a role in determining the binding efficiency. As another example, Fraser and co-workers performed directed evolution on a catalytically impaired variant of cyclophilin A (CypA), and were able to partially restore the catalytic activity of the enzyme through the introduction of two second-shell mutations that “rescued” activity through modulation of conformational dynamics.¹⁸¹ For several more examples, we refer the readers to refs (26, 181, and 182). Taken together, these successful examples of modulating enzyme activity through targeting conformational dynamics, either deliberately or serendipitously, indicate their importance and further highlight the vast opportunity still present in the field.

Computational Approaches to Engineer Conformational Dynamics

Experimental approaches for the laboratory evolution of functional enzyme conformational dynamics has been discussed in detail in refs (31 and 183). A wide array of techniques exist that can be used to probe conformational dynamics on a variety of time scales, including NMR,¹⁸⁴ single-molecule FRET,¹⁸⁵ fluorescence anisotropy,¹⁸⁶ time-resolved¹⁸⁷ or multi-temperature¹⁸⁸ X-ray crystallography, and mass spectrometry.¹⁸⁹ As these techniques have also been reviewed in detail elsewhere, we refer the reader to e.g. refs (106, 184, 187, and 190) for further discussion of relevant techniques and the contributions they have made to our understanding of the role of conformational dynamics in enzyme function (not just enzyme evolvability). In parallel, molecular simulation has also played an important part in dissecting the physico-chemical parameters that lead to the emergence of new enzyme functions.^10,11,191 Simulation is also playing an increasingly important role in enzyme design, combining both sequence- and structural-based approaches, including approaches that take into account conformational dynamics as part of the design process,^23,33−42 with increasing contributions from machine-learning approaches.^192−195 Clearly, both conventional and even enhanced molecular dynamics-based approaches are far too computationally expensive for the extensive screening necessary for efficient design of conformational dynamics, and are more suited to characterization of a select number of variants from a pool of different designs. However, coupling structural bioinformatics/loop engineering with experimental design strategies has tremendous potential for the targeted engineering of enzyme–substrate selectivity and catalytic activity. In this section we will present some relevant techniques that are likely to play an important role in protein engineering efforts in the coming years.

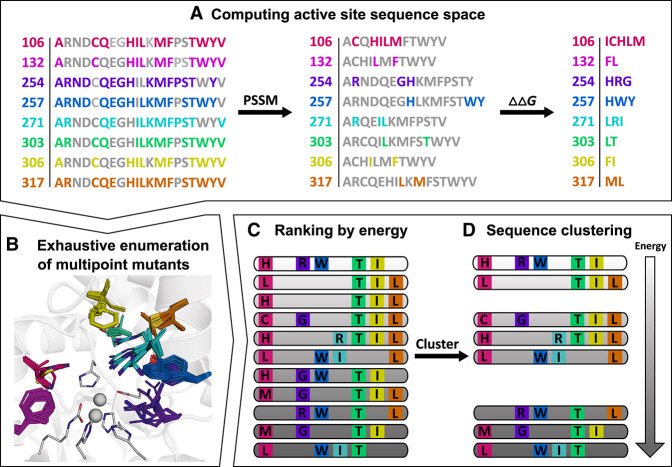
The information obtained from studying the conservation and co-evolution patterns of residues in a protein/enzyme family has been used to great benefit in homology modeling,¹⁹⁶ protein–protein docking,^197,198 and protein/enzyme engineering.^38,40,199 In enzyme engineering, these methods can be used to massively reduce the sequence search space, under the principle that deleterious mutations will largely not be preserved by natural selection.¹⁶⁹ PROSS³⁸ combines the above-described phylogenetic analysis with Rosetta design calculations and has been successfully used to improve the stability and/or expression of several proteins.^38,200,201 Building on the successes of PROSS, FuncLib⁴⁰ (Figure 9) was designed specifically for enzyme engineering, with the aim to generate large increases in activity with a minimal set of mutations. Further, FuncLib can be performed with or without a model of the substrate or transition state, and a repertoire of enzymes with different actives, specificities, and enantioselectivities can be obtained.⁴⁰ While, strictly, techniques such as PROSS³⁸ and FuncLib⁴⁰ focus on optimizing stability rather than conformational dynamics, they hold great potential as tools that can move a significant part of in vitro screening approaches in silico, and techniques such as these will likely become the “go-to” starting point in future enzyme engineering studies; therefore we have included these techniques in this section. In addition, while these methods do not directly target conformational dynamics (they focus on optimizing stability), they do so indirectly by preferentially optimizing one conformation of the enzyme over all others. In doing so, they induce a population shift toward the desired state, thus reducing unproductive “floppiness”.

Figure 9.

Overview of the FuncLib workflow,⁴⁰ using the steps involved in generating a repertoire of phosphotriesterase enzymes starting from a bacterial phosphotriesterase as an illustrative example. (A) First, the active-site positions to be modified for design are selected, and, at each position, the sequence space is constrained through a combination of evolutionarily-conservation analysis (PCCM) and mutational-scanning calculations (based on calculated folding–free energy differences, ΔΔG). Following from this, (B) the resulting multipoint mutants are exhaustively enumerated with the aid of Rosetta atomistic design calculations. This allows for (C) ranking of the resulting constructs by energy, followed by (D) sequence clustering to obtain a final repertoire of diverse designs, ranked by energy, which can be subjected to experimental testing. For further details, see ref (40). Reproduced with permission from ref (40). Copyright 2018 Elsevier.

Molecular dynamics (MD) simulations have been used extensively to provide insight into the conformational dynamics of enzymes and its relationship with catalysis.^{23,24,129,156,202−206} MD simulations can also be coupled with QM/MM calculations, to explicitly link conformational dynamics to chemistry.^207,208 The insights gained from MD simulations can be directly applied toward the (semi-)rational design of variants with altered conformational dynamics.^182,203,209 Dodani et al. utilized extensive MD simulations to identify a single residue that was responsible for controlling the conformational dynamics of the F/G loop of a nitrating cytochrome P450 TxtE, with point variants ultimately able to switch substrate regioselectivity.²⁰³ Extensive MD simulations can be used to construct MSMs, which can provide thermodynamic and kinetic characterization of conformational substates.^130,131 While MSMs are information rich, they often require at least many μs of aggregate sampling in order to be produced. Unbiased enhanced sampling techniques such as accelerated or Gaussian accelerated MD (aMD or GaMD),^210,211 scaled MD,²¹² and temperature or Hamiltonian replica exchange (TREX or HREX)^213,214 offer a means to much more efficiently sample available conformational space. For example, a 500 ns long aMD simulation of bovine pancreatic trypsin inhibitor was able to sample equivalent phase space as compared to a 1 ms long conventional MD simulation.²¹⁰ The identification of rarely sampled conformational states from MD simulations of a WT enzyme could be used as the starting point for computational design efforts. For example, HREX-MD simulations of a promiscuous P450 enzyme identified numerous conformational states available to the WT enzyme’s active site that would ultimately lead to different products.²⁰⁶ Semi-rational design using information from the HREX-MD simulations and MMPBSA calculations was then used to generate distal variants with altered preferences for the available conformational states, ultimately leading to different product distributions for the enzyme variants.²⁰⁶

In cases such as the above where one wishes to stabilize a specific conformational state(s) over others, enhanced sampling techniques that bias along user specified reaction coordinate(s) may be beneficial for low-to-medium throughput screening of variants, with methods such as metadynamics,²¹⁵ steered MD,²¹⁶ umbrella sampling (US),²¹⁷ and adaptive biasing force²¹⁸ all falling into this category. Michielssens et al. performed US MD simulations to screen 15 distal variants that tune the binding selectivity of ubiquitin through altering the relative populations of the two major ubiquitin binding-site conformations, ultimately taking forward six variants for experimental validation.²¹⁹ As another example, MD simulations can be used to identify correlated motions and allosteric networks in enzymes, providing a means to identify the impact of distal mutations on enzyme catalysis.^12,220−222 Numerous methodologies based on analysis of correlated motions allow one to probe allostery, including: WISP,²²³ CNA²²⁴ and CARDS.²²⁵ The “shortest path map” (SPM) method²³ allows one to identify the key residues distributed throughout the entire enzyme that play a significant role in regulating the overall conformational dynamics. The potential of this approach toward enzyme engineering was demonstrated by evaluating several intermediates along a multi-step evolutionary trajectory of a retro-aldolase enzyme, in which distal residues mutated throughout the directed evolution trajectory were repeatedly found on or very close to the SPM.²³ SPM could thus be applied to guide further design efforts, by targeting a specific set of residues, allowing for a more exhaustive search at these positions. Another potentially valuable tool is the “dynamic flexibility index”, which can be used to calculate the contribution of each residue to the enzyme’s functionally important dynamics.²²⁶

Machine learning (ML) is finding increasing applicability in the field of biomolecular simulation and more specifically enzyme engineering.^195,227 ML has been shown to improve the efficiency of directed evolution experiments,¹⁹³ as well as predict allosteric mutations that increase the activity of beta-lactamases toward antibiotics.²²⁸ In addition, databases such as ProtMiscuity may provide valuable insight into selecting an optimal starting enzyme for further optimization.²²⁹ Furthermore, there are many enzyme design approaches that focus more directly on the active site, such as CASCO,³⁷ CADEE,²³⁰ multi-state design approaches,²³¹ the “inside/out” approach from Rosetta²³² and also Rosetta-based de novo design approaches as in ref (170). While these approaches do not specifically focus on targeting conformational dynamics (similarly to PROSS³⁸ and FuncLib⁴⁰), they provide nevertheless a powerful complementary tool to drive the engineering of designer enzymes with tailored physico-chemical properties.

Conclusions and Future Perspectives

Almost two decades since James and Tawfik presented their “New View” of enzyme catalysis,⁷ it is becoming increasingly clear that conformational dynamics are critical to enzyme evolvability.⁷⁻¹³ This manifests itself in all contexts: from the emergence of novel enzymes, through to the natural evolution of existing enzymes, and even to the fine-tuning of dynamical properties of designed enzymes during laboratory evolution, whether incidentally or intentionally. As has been discussed elsewhere,³¹ and as we show in this Perspective, the role of conformational dynamics in evolution is two-fold: on the one hand, an expanded repertoire of conformational states being available to an enzyme allows for a greater diversity of catalytically competent conformations, that can facilitate the emergence of new activities (Figure 1).^7,8 However, with this also comes an expanded repertoire of catalytically non-productive conformations, and once an initial activity has been established, the subsequent focus of evolution appears to be dampening of catalytically non-productive conformations.³¹

Here, it is possible to learn from the tricks Nature uses in natural evolution for enzyme design. Engineering of conformational dynamics has already been effectively applied to, for instance, improve binding^219,233,234 or stability.^{200,201,234,235} Clearly, this suggests that conformational dynamics is therefore also a feature that can be manipulated in protein engineering, to generate new designer enzymes with targeted substrate specificities or improved catalytic activity, and there are a number of such success stories in the literature.^11,31,49 Computational approaches have played a big role in protein engineering, in particular in the context of designing de novo enzymes.^164,170,236 As an illustration, the topic of de novo enzyme design has been recently reviewed extensively by Korendovcyh and DeGrado,²³⁷ who describe three key stages of de novo design: (1) manual protein design (based on work from the 1970s and 1980s), (2) computational design guided by fundamental physico-chemical principles (from the mid 1980s to the early 2000s), and (3) fragment-based and bioinformatically informed computational design (starting in the early 2000s). Only the first of these three stages (manual protein design) is arguably non-computational. Historically, however, the computational approaches harnessed for protein design either have been purely sequence based or have focused mainly on design based on static structures,²³⁸ with the major enhancements in activity coming from subsequent laboratory evolution.^{164−166,171,176} This is changing, as greater awareness of the importance of conformational dynamics, as well as the role of remote mutations in modulating activity,^239−245 means that both conformational dynamics and mutations of outer shell residues are starting to be incorporated into design approaches.^11,31,49

There exist already a large number of computational approaches that can be used to incorporate dynamical properties into the design process, for example those presented in refs (40, 206, and 219). However, their use in computational design is at present far from routine, in part due to the not insubstantial computational cost involved. However, approaches such as PROSS³⁸ and FuncLib⁴⁰ enable large-scale in silico screening of potential enzyme variants, allowing for the design of novel enzymes. Further, coupling structural bioinformatic approaches with machine learning could be used to help predict enzyme variants that are optimized for a given physico-chemical property. Analysis using structural bioinformatics approaches will further help guide the design process, and it is not inconceivable that computational protein design will become a pipeline of multiple different approaches with varying levels of complexity, a portion of which will be focused on targeting conformational dynamics.

One of the biggest challenges that we currently face in incorporating conformational dynamics in either computational or laboratory engineering of protein function is simply that not enough is known about the precise way in which the dynamical properties of a given system affect its activity, and alterations to dynamical properties of an enzyme can just as easily be catalytically detrimental as beneficial. For example, it would be tremendously useful if one could define a list of requirements that should be satisfied in order to determine that conformational dynamics is important for evolution for a given case study. However, the problem is that creating such a list would be non-trivial, because the role of conformational dynamics can be important in different ways for different systems. To take just a few of the examples discussed in this work, in the case of chalcone isomerases (CHI),²⁵ the role of conformational dynamics is easy to assign, as all the key catalytic residues are already in place in the non-catalytic ancestor, and evolution appears to be primarily fine-tuning both side-chain conformational dynamics (through optimizing the position of the catalytic arginine, Figure 3) and substrate positioning (through elimination of non-productive substrate binding conformations in the evolved enzyme). In the case of the β-lactamases we have repurposed as Kemp eliminases,^49,177 once again, scaffold flexibility appears to play an important role both in the process of specialization from a generalist to a specialist β-lactamase,¹⁵¹ and for whether the Precambrian vs modern enzymes are capable of accommodating our de novo active site for catalyzing Kemp elimination.^49,177 In the case of the designed Kemp eliminase, KE07, we observed that the introduction of remote mutations facilitates the stabilization of completely new active-site conformations through evolutionary conformational selection.²⁴ However, the question remains of whether the changes in conformational dynamics drive the changes in function, or the selection pressure on the changes in function drives the changes in conformational dynamics.

Following from this, and as pointed out by a reviewer, it is unclear whether it will be necessary to “dial-in” or “dial-out” conformational dynamics for a given system, as one needs to balance sampling catalytically competent (productive) conformations with dampening the sampling of catalytically non-productive conformations. This can potentially be achieved in targeted way through engineering, provided that the behavior of the system is sufficiently well understood. Ultimately, however, this will be a system-specific balancing act, driven by the intrinsic physico-chemical properties of a given system, and will therefore need to be determined on a case-by-case basis. However, clearly, considering dynamical properties in the design process is critical, as simply having the catalytic residues in the correct place is not always enough to impart efficient catalytic activity.²⁵ Shifting this paradigm is essential for overcoming one of the next big barriers on the path to designing green biocatalysts for a sustainable future.

The authors declare no competing financial interest.