PdTe2-based photodetectors reveal anisotropic and highly efficient intraband photocurrents at long wavelength.
Abstract
Emergent topological Dirac semimetals afford fresh pathways for optoelectronics, although device implementation has been elusive to date. Specifically, palladium ditelluride (PdTe2) combines the capabilities provided by its peculiar band structure, with topologically protected electronic states, with advantages related to the occurrence of high-mobility charge carriers and ambient stability. Here, we demonstrate large photogalvanic effects with high anisotropy at terahertz frequency in PdTe2-based devices. A responsivity of 10 A/W and a noise-equivalent power lower than 2 pW/Hz0.5 are achieved at room temperature, validating the suitability of PdTe2-based devices for applications in photosensing, polarization-sensitive detection, and large-area fast imaging. Our findings open opportunities for exploring uncooled and sensitive photoelectronic devices based on topological semimetals, especially in the highly pursuit terahertz band.
INTRODUCTION
The discovery of condensed-matter systems, such as topological insulators and topological semimetals (TSMs) (1–5), has stimulated the exploration of elementary excitations and nontrivial topological features in crystalline solids. In particular, Weyl (6) and Dirac semimetals (7, 8) (WSMs/DSMs) have attracted considerable interest as a platform for exploring emergent quasiparticles in condensed matter, due to their versatile operation of inversion symmetry breaking. The low-energy excitations in these TSMs can be regarded as overlap of paired fermions with opposite chirality in three-dimensional momentum space (6, 9). Materials such as Na3Bi, TaAs, NbAs, and Cd3As2 belong to the class of type I TSMs. To separate definite chirality of a single Weyl node, either inversion or time-reversal symmetry breaking represents a prerequisite to identify phenomena driven by the singularities (monopole and antimonopole) of Berry curvature (10). The concept of broken Lorenz invariance also results in a new system named type II TSMs (11, 12), featuring a strongly tilted Weyl/Dirac cone appearing at the crossing boundary between electron and hole pockets, as demonstrated to occur for some transition metal dichalcogenides (TMDs), such as MoTe2, WTe2, PtSe2, PtTe2, and PdTe2 (13). Materials belonging to the class of type II TSMs are predicted to enable new quantum phenomena, such as field-selective anomaly (14) and chiral mode reversal (15), as well as a novel mechanism for entropy transport (16). Therefore, the exploration of nonlinear optical properties in TSMs combines fundamental and technological interest. To date, most theoretical and experimental efforts have been focused on type I TSMs, especially concerning multiple excitations in the vicinity of Weyl nodes (17) and the properties of injection photocurrents at low frequencies in WSMs (18). Under light excitation at infrared frequency, a nonzero photocurrent caused by each tilted Weyl cone of different chiralities (19) and a large second-order nonlinear optical response has been observed as a hallmark of the diverging Berry’s curvature near the Weyl nodes (20). The nonlinear optical response studied so far on type II TSMs mainly concerns the WSMs in visible and infrared wavelength (21) under large pumping power. Very recently, theoretical predictions on the intraband second-order response in time-reversal invariant noncentrosymmetric materials have indicated TSMs as promising candidates for high-frequency rectifier (22). Photon absorption of type II TSMs is enhanced at terahertz wavelength (23), owing to the gapless nature, along with broad absorption enabled by the anisotropic dispersion and unprecedented enhancement of transport, related to their Bloch wave functions (24).
Notably, photocurrent in the terahertz range is strongly enhanced by the density of fermion states, with a subsequent superior photoresponse in type II TSMs, due to the 1/ω term diverging in the low-energy limit (25). Thus, as a key priority toward new-generation photoelectric technology, it is desirable to determine whether centrosymmetric type II TSMs can enable efficient energy harvesting of electromagnetic field in the terahertz frequency, which remains one of the most important technological challenges nowadays with wide applications in homeland security, quality testing, biology, medicine, spectroscopy, data communication, and imaging (26). In this work, a previously unknown photodetector based on type II TSM PdTe2 is developed and elucidated experimentally with large nonlinear generation of shift photocurrent at the millimeter and terahertz wavelength regime (from 0.04 to 0.3 THz) at room temperature. In addition, we demonstrate that polarization-dependent photogalvanic effect (PGE) produces directional photocurrent with high anisotropy. The superb responsivity (10 A/W), fast response (1 μs), and low noise-equivalent power (NEP) (2 pW/Hz0.5) for room-temperature operation pave the way for the realistic exploitation of TSMs for large-area and fast imaging of macroscopic objects.
RESULTS
Our experiment is based on the TMD PdTe2, which hosts type II Dirac fermions and high-mobility charge carriers. PdTe2 has a CdI2-type structure and belongs to the space group (Fig. 1A). Three mirror planes on the (001) surface exist in the absence of any electric field (Fig. 1B). The high-resolution transmission electron microscope (HR-TEM) image and the corresponding fast Fourier transform shown in Fig. 1C indicate crystalline interplanar spacing of 1.99 Å (110), consistent with a previous report (27). The band structure of PdTe2 (12) (fig. S1) displays electron pockets near the Fermi surface in the kx-ky plane, as shown in Fig. 1D. The high-symmetry contours of these pockets also indicate the C3 rotational symmetry around the c axis and the inversion symmetry of PdTe2. The projection of the Dirac cone, protected by the crystal symmetry, onto the kx-kz plane is reported in Fig. 1E. These two bands show linear dispersions in the vicinity of the Dirac point, with strong tilting along the kz direction, which is the distinctiveness of the type II Dirac band topology (11, 13). To investigate the behavior of PdTe2 under the action of radiant field, a PdTe2-based planar device was fabricated through different nanofabrication routes. The normally incident millimeter/terahertz wave is first converted into a localized electric field along a 6-μm channel by the patterned electrodes (Fig. 1G), which ensures strong in-plane interaction between the PdTe2 layer and electromagnetic wave, and drives the imbalanced distribution of charge carriers. Technically, the introduction of built-in field breaking inversion symmetry either internally or externally is a straightforward strategy for separating the photoexcited carriers to generate a photocurrent. At zero bias, the photocurrent in gapless materials could come from the interaction of different mechanisms, such as (i) PGE, (ii) photon drag effect (PDE), and (iii) photothermal effect (PTE). Nevertheless, PTE can be achieved by nonsymmetric Seebeck coefficient or photon flux density, which can be eliminated by our device implementation. The prerequisite for a selective excitation of photocurrent generated by specific properties of PGE is a lack of inversion center, whereas it is not strictly obeyed by PDE ones. Therefore, it is worthwhile to distinguish both photocurrent schemes by considering the microscopic circumstances.
Fig. 1. Characterization and interface behavior of type II DSM PdTe2.
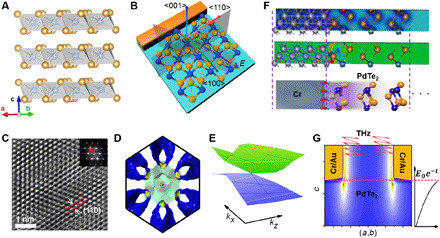
(A) Crystallographic structure of PdTe2. Orange and blue balls denote Te and Pd atoms, respectively. (B) Microscopic view of the metal-PdTe2 contact along with the atomic chains. The shaded area represents the mirror planes on the (001) surface. (C) HR-TEM images of PdTe2 single crystal. (D) The coexistence of hole and electron pockets in the Fermi surface along the kx-ky plane as a result of the type II Dirac cone. The hole pocket was marked by the red dotted circle, whereas the electron pocket, corresponding to the translucent aqua-like pocket, forms an apple pit–shaped pocket in the reciprocal space. (E) The projection of the Dirac cone along the kx-kz plane. The tilted Dirac cone is evident along the kz direction. (F) The charge density (top) and charge density difference (middle) near the metal (Cr/Au)–PdTe2 interface. The bottom panel represents a schematic diagram of the corresponding range of atomic structures. (G) The cross-sectional view of localized-field distribution along the c axis near the metal-PdTe2 interface under terahertz illumination.
The PdTe2 bulk crystal has a C3v symmetry point group, including a center of inversion. Specifically, in this point group, the anisotropy of carrier elastic scattering can be equivalent to scattering by a double triangular pyramid. In realistic settings, such a symmetry is nonconserved at the PdTe2-metal interface, since the electron transfer and chemical interaction strongly makes the electronic states distributed asymmetrically across several atomic layers along the c-axis direction. Our density functional theory (DFT) calculations of the charge density (n) and charge density difference (∆n = n − nmetal − nPdTe2) in Fig. 1F clearly reveal the interfacial charge localization. Besides, the localized field (fig. S2) plotted in Fig. 1G shows exponential decay along the c direction.
The device structure is shown in Fig. 2A, in which the as-exfoliated PdTe2 flake symmetrically adheres to the two sleeves of log-corrugated electrodes. Here, under our experimental configuration, carrier scatterings from the top and bottom pyramids are endowed with different probabilities when they are driven back and forth by the terahertz field. In the framework of photocurrent generated by means of planar motion of free carriers, the scatters can be regarded as randomly distributed wedges but identically oriented along the channel. In the absence of radiation, the flow of anisotropic scattered electrons cancels out exactly (Fig. 2B, i). Under illumination, the excessive number of carriers driven by the terahertz field breaks the flow balance and generates a net shift current. The direction of the induced current depends on the relative orientation of the terahertz field and wedges. A field parallel to the base of wedges yields the current flow in the x direction, while rotation of the electric field by 90° reverses the current direction (see Fig. 2B, ii and iii). Aside from the PGE, one should also consider the contribution of PDE, which is caused by the transfer of the photon momentum to the charge carriers. PDE describes photocurrents resulting from the transfer of linear momentum from incident photons to excited carriers, thus permitting a photocurrent even if states are symmetrically distributed in k-space. Taking into account the microscopic mechanisms (section S3), the photocurrent density jx caused by the PGE and PDE is given by jx ∝ Ex2 − Ey2 and jx ∝ EyEz, respectively. To unveil these two mechanisms for photocurrent generation, the finite difference time domain (FDTD) method was devoted to simulate the field profile of our structure, and here, TM (Transverse magnetic wave)–polarized electromagnetic wave at photon energy hυ ~ 0.48 meV (0.12 THz) irradiates our device. As shown in Fig. 2 (C and D), the intensities (Ex2 − Ey2)/E02 and EyEz/E02 are the highest at two electrode-material interfaces. It can be retrieved that the photocurrent distribution related to the PGE is symmetrically arranged with respect to the two interfaces and the nonzero photocurrent is expected. However, the photocurrent density associated with the PDE is antisymmetrically distributed, resulting in a sum of zero photocurrent. Therefore, in our proposed structure, the net photocurrent can be induced by the PGE, notable exceeding PDE contribution.
Fig. 2. The photoresponse of unbiased PdTe2-based devices at 300 K.
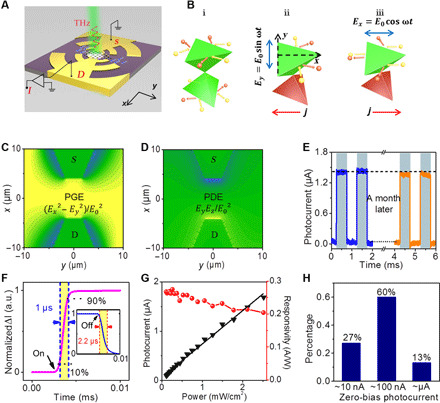
(A) Schematic diagram of the PdTe2-based photodetector. (B) The process of the PGE and its dependence on the polarized terahertz field. (i) Carrier scattering from scatters without terahertz field. (ii and iii) Ratchet scatterings under action of terahertz field with y and x polarizations. (C and D) The contributions of PGE and PDE in a single device under 0.48-meV terahertz excitation. (E) The impulse photocurrent response of the PdTe2-based device after exposure to ambient atmosphere for 1 month (hυ ~ 0.48 meV and power density ~ 2.5 mW/cm2). (F) Display of rising and falling edges of the time-resolved response in a single period, exhibiting the video-rate time response at around 1 and 2.2 μs. a.u., arbitrary units. (G) Dependence of the photocurrent (black solid symbols, left axis) and the responsivity (red symbols, right axis) on the radiation power intensity. (H) The counts of unbiased devices with different magnitudes of photocurrent.
To probe the nonlinear response, the photocurrent is measured from all the unbiased PdTe2-based devices under ambient environment at 300 K. It approaches 1.5 μA when the device is subjected to 0.12-THz plane-wave illumination uniformly within the incident power of 2.5 mW/cm2 (see the “Photocurrent measurements” section). In addition, the signal is well preserved and exhibits good reproducibility under the fast on/off modulation of terahertz radiation, and it remains stable even after storage in air for 1 month. The response speed defined as time required for the increase from 10 to 90% (or, analogously, decrease from 90 to 10%) is determined to be about 1 μs (or 2.2 μs) from Fig. 2D. Other critical factors affecting the performance of photodetectors, such as the power dependence and the responsivity, are also explored in our devices. As expected for the second-order nonlinear process, the behavior of the photocurrent as a function of the incident power in Fig. 2G displays excellent linearity (28), so that the responsivity of 0.2 A/W exhibits no obvious reduction. Such a zero-bias responsivity outperforms that of all two-dimensional materials or topological materials, which also required more complicated nanofabrication processes with appropriate encapsulation of the active channel, with outstanding cost-effectiveness (29–31). Repeatability was validated by repeating tests under the same conditions on dozens of devices fabricated with the same structure (Fig. 2H and fig. S3). For the sake of completeness, we point out that the fluctuation of the photocurrent response is naturally related to flake thickness and to the orientation of the crystallographic axis. Nevertheless, most devices displayed photocurrent larger than 100 nA, thus outperforming state-of-the-art terahertz devices (30, 31).
Anisotropic photocurrent in PdTe2 TSMs
The difference in the magnitude of photocurrent from the above statistical results (Fig. 2H) could be associated to the strongly tilted Dirac cone formed by electron and hole pockets, which makes the transport highly anisotropic. To rule out the accidental asymmetric PTE that may contribute to this phenomenon, we fabricated a crossly aligned four-electrode device to reveal the anisotropic shift photocurrent. Measurements were taken under the terahertz light propagation along the c axis, and its polarization is changed by a wire grid polarizer (Fig. 3A). Ideally, it is expected that the generated photocurrent, symmetry-allowed, follows the polarization of freely incident light field (Fig. 3B). It is noteworthy here to highlight that the incident field directly interacts with the electrodes, causing the redistribution of electric vector due to the subwavelength (the active-channel scale is actually about λ/L ~ 103 shorter than the wavelength) near-field effect in realistic microscaled device. When the incident light polarization is 45°, the electric field amplitude distributed symmetrically across the four electrodes as shown in Fig. 3C. In this regard, the photocurrent depends on the interplay between the near-field and anisotropic ratchet scattering and can also be tuned by the incident field polarization. Figure 3D shows the change of photocurrent along the x and y directions as a function of the polarization angle θ. The anisotropy ratio is defined as the ratio of the photocurrent response in the x direction to that in the y direction. Although the material (and the corresponding Fermi level) is the same, a notable difference of the photocurrent, with an anisotropic ratio >6, is achieved. Meanwhile, the resistances along the x and y directions are almost overlapped (fig. S4). Thus, the potential mechanism should be connected to interaction between carrier scattering and terahertz field. Note that no substantial phase difference between the x and y photocurrent is evident in our experimental results. To explain this phenomenon and to rule out the possible polarization-dependent PTE (only depending on power intensity |E|2), we numerically simulated the relationship of photocurrents along the x and y directions of devices under different polarization angles (Fig. 3E). The photocurrent generated by PTE exhibits a phase difference of 90° between the x and y photocurrents, while no phase difference exists according to the PGE model, due to the near-field effect. This phenomenon is consistent with our experimental results, further supporting the occurrence of polarization-dependent PGE photocurrents in our experiments. All fabricated devices rigorously envision the uniqueness of anisotropy, regardless of the variation in resistance from one sample to another.
Fig. 3. The anisotropic photocurrent of the PdTe2-based device at zero-bias voltage.
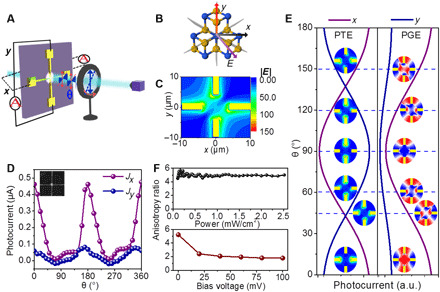
(A) Schematic diagram of the polarization-resolved photocurrent measurement setup. (B) Ideal microscopic diagram of polarization field and relative direction of material. (C) Simulated electric field distribution at specific polarization angle (45°). (D) Dependence of the photocurrents (Jx, Jy) along two orthogonal axes on the polarization angle θ (inset: scanning electron microscope image of the four-terminal PdTe2-based device). (E) Comparison of theoretical results of PGE and PTE in x and y directions. (F) Relationship between anisotropic ratio (Jx/Jy) and incident power (top) and bias (bottom).
The in-plane anisotropy is found to be notable near the Dirac node, following the asymmetric band structures. Using DFT calculations within the framework of the nonequilibrium Green’s function formalism (32), we can qualitatively enumerate the PGE photocurrent when the PdTe2-based devices are irradiated by linear polarized light. It reveals the essential involvement of the anisotropy harnessed by the PGE photocurrent during the experimental processes (in fig. S4). Nevertheless, the anisotropic ratio remains basically unchanged with the power, contrarily to recent observations for type II WSMs (21). Explicitly, differently from the mechanism here presented for the terahertz range, the Berry curvature divergence at Weyl point causes a large nonlinearity of shift current response at the low power of the infrared frequency. The anisotropic ratio decreased under applied voltage, probably due to the elimination of PGE with the involvement of other photocurrent mechanisms related to the inversion symmetry breaking by electric field. Such anisotropic features are expected to be applied to polarization detection without the need for additional optical components.
Modulation of PGE in PdTe2 through field polarization
By means of circularly contacted devices, we would like to further verify the rectified photocurrent, as well as the anisotropy. Here, the photocurrent was collected between the nearest electrode pairs around the sample in a counterclockwise sequence, as described in Fig. 4A. Similarly, the actual local electric field of the device will be redistributed because of the interplay between the oscillating ac current among the electrode pattern and the incident polarization. It suggests that a phase difference between different electric components (Ex and Ey) is introduced, so that the photocurrent changing versus incident polarization will not only have a 2θ term of linear polarization but also have a 4θ term. The variations of photocurrent extracted from different adjacent electrode pairs at different angles θ are shown in Fig. 4 (D to I). The observed photocurrents obey the rule of
| (1) |
where LPGE refers to the polarization-dependent nonlinear PGE current with a phase shift φ and D0 is the polarization-independent component. The 4θ term is probably derived from the interference between material and electrodes impinged by the terahertz wave, and MPGE is the magnitude of the polarization-dependent mixing photocurrent. The angle-independent photocurrent D0 can arise from PTE, i.e., the thermal gradient caused by accidental asymmetry. Another possibility is related to the photo-Dember (33) effect, arising from the asymmetric diffusivity of photoexcited electrons and holes, which creates a transient spatial charge distribution and, hence, the buildup of a voltage. Such an asymmetry is extraordinarily prominent in type II DSMs, as a result of unbounded electron and hole pockets at the node. Last, PDE could also contribute, owing to photocurrents resulting from the transfer of linear momentum from incident photons to excited carriers (34).
Fig. 4. Polarization-resolved photocurrent in a circularly arranged contact device.
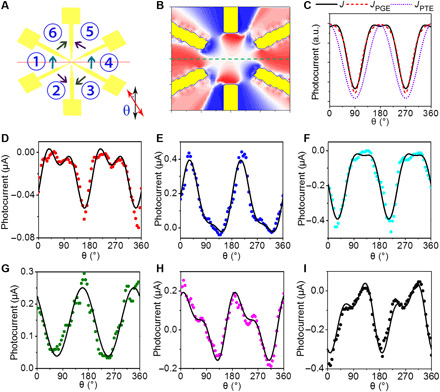
(A) Schematic diagram of the experimental setup for polarization-resolved photocurrent measurement. The photocurrent was collected between nearest electrode pairs around the sample in the sequence of anticlockwise. θ is the angle of incident light polarization. (B) Simulated distribution of PGE photocurrent at θ = 45° (see fig. S5 for additional angular configurations). (C) Dependence of the photocurrent on polarization angle θ. JPGE derives from PGE, and JPTE is related to PTE. J = Asin(4θ + a) + Bcos(2θ + b) + C. (D to I) Dependence of the photocurrent on different electrode pairs (① to ⑥) on polarization angle θ.
To confirm the polarization nature of the photocurrents, we focus on the terms depending on the polarization LPGE and MPGE (Table 1). Depending on the relative orientation of localized ac electric field and wedges, the photocurrent can have different values, as well as orientations. Typically, following the nonlinear rectification of the localized electric field from PGE, we obtain the distribution of photocurrent theoretically in Fig. 4B, where the polarity of the photocurrent exhibits mirror symmetry with respect to the dashed green line, and the photocurrent collected between nearest electrode pairs (② and ⑤ and ③ and ⑥) reverses its sign, even though it could be the same order of magnitude. As a consequence, the photocurrent components LPGE and MPGE of electrode pairs change their signs alternatively from ① to ③ and show the mirror symmetry across the red line marked in Fig. 4A and Table 1. Such a variation of polarization-controlled photocurrent is unlikely to originate from the scattering of impurities and/or spatial disorder, since the photocurrent can flow along random directions, depending on the local symmetry breaking (32). Moreover, the polarization-dependent photocurrents LPGE and MPGE from different electrode pairs, e.g., ① and ④, ② and ⑤, and ③ and ⑥, exhibit similar value across the mirror plane (Table 1). This result is unambiguously a joint effect by the near-field distribution and anisotropic ratchet scattering (the electric field redistribution is simulated by FDTD method; fig. S5). Similar polarization-dependent photocurrent can also be found in other devices of the same structure (fig. S7).
Table 1. The results of different contributions are summarized.
LPGE and MPGE are expressed in nanoamperes.
| ① | ② | ③ | ④ | ⑤ | ⑥ | |
| LPGE | −70 | 160 | −160 | 85 | 160 | −160 |
| MPGE | −14 | 65 | −65 | 14 | 65 | −65 |
In addition to the PGE, local nonequilibrium can also be ushered by the PTE depending on the asymmetry of power intensity distribution between adjacent electrodes (|E|2). However, the PTE is naturally distinguishable from the PGE based on the polarization-controlled photocurrent. Note here that the PGE is only related to the orientation of the electric field, while the PTE depends on the square of electric field. To elucidate such a large difference, the photocurrents from PGE and PTE are simulated simultaneously by following the field profile of the FDTD method and shown in Fig. 4C. It can be inferred that the photocurrent JPTE is not consistent with the formula [J = Asin(4θ + a) + Bcos(2θ + b) + C], and it does not match the experimental results. In addition, |E|2 dependence of PTE photocurrent does not obey the measured polarization-dependent results for the adjacent electrodes, that is, without mirror symmetry, as well as sign change of photocurrent measured among electrode pairs. Instead, the polarization dependence exhibits a phase shift between two adjacent electrode pairs, and the photocurrent in every electrode pair will change its sign when the polarization changes (see fig. S6).
Terahertz detection and imaging applications under electrical bias
On the basis of the giant shift current response, exploring the nonlinearity under DC electric field allows better understanding the optical properties of PdTe2-based devices. It is found that the in-plane photocurrent can be enlarged by more than an order of magnitude under finite DC field. As shown in Fig. 5A, the dc electric field EDC introduced by bias voltage can break the symmetrical plane, making the nonequilibrium carriers move laterally along the electric field and the photocurrent generate a linear growth behavior similar to the photoconductive process (35). In addition, applying in-plane EDC has recently been found to provide additional control means for giant shift current, as a result of the production of imbalanced allowed momentum space for optical excitations (21). In this regard, the nonequilibrium carriers localized near the metal-material interface could produce a net nonlinear component of photocurrent proportional to the EDC, in addition to the bias-independent components. Under a finite bias voltage, the signal-to-noise ratio of the device is still improved without bringing any deterioration in response time (Fig. 5B). The fast response can be attributed to the absence of trapping and recombination processes governed by the intraband process at such low-energy photon band. Meanwhile, the response of the device is notably linear across a large power dynamic range in Fig. 5C. This finding can be explained considering that the second-order nonlinearity carrier injection process of PGE is expected to have a linear dependence on the input power. Correspondingly, the responsivity RA grows from 0.2 up to 10 A/W under a bias voltage of 100 mV (Fig. 5D and see Materials and Methods, where the choice of a diffractive-limited area rather than the device area is argumented). The fast response time, the large dynamic range, and the high responsivity under bias voltage reveal the potential of this class of TSMs for terahertz technology. Furthermore, fast and stable optical response can be preserved across the range from 0.04 to 0.3 THz in our PdTe2-based device (Fig. 5E), certifying the prospect of broadband operation. To facilitate the applications, we also evaluated the NEP, that is, the figure of merit used to evaluate the performance of a detector. The NEP is estimated to be ~1 pW/Hz0.5 at 0.12 THz and 53 pW/Hz0.5 at 0.3 THz at 100 mV (NEP = vn/RA; see Materials and Methods). These results are slightly lower than the NEP obtained by the noise spectra of device measured experimentally (NEP = 1.3 pW/Hz0.5 at 0.12 THz and 57 pW/Hz0.5 at 0.3 THz can be obtained; see fig. S8). Both experimental and theoretical results consistently demonstrate that our detector is competitive with other commercially available ones [such as Golay cells (36) and Schottky diodes (37)], in terms of performance, compactness, and speed.
Fig. 5. The photoresponse of the biased PdTe2-based device and its noninvasive imaging applications.
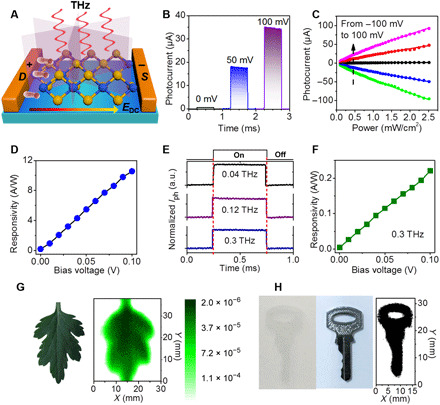
(A) Schematic diagram of the measurement of the bias-mode photocurrent mechanism. (B) The time-resolved photocurrent response of the device in a single period (1 ms) at different bias voltages with a light source at 0.12 THz and a power density of 0.525 mW/cm2. (C) Dependence of the photocurrent on the radiation power intensity at different bias voltages. (D) Dependence of the responsivity on the bias voltage. (E) The time-resolved photoresponse at different photon frequencies. (F) Dependence of the responsivity on the bias voltage at 0.3 THz. (G and H) The terahertz imaging of a fresh leaf (0.12 THz) and the hidden key (0.3 THz) at 300 K. Photo credit: Cheng Guo, State Key Laboratory for Infrared Physics, Shanghai Institute of Technical Physics, Chinese Academy of Sciences.
In addition, note that the performance of the studied device is mainly limited by the structure of antenna, with substantial potential improvements possible by the exploration of wavelength-matched structures. In addition, it is particularly attractive to substantiate the topological nature of Bloch wave functions at Weyl nodes through inversion symmetry breaking, with the involvement of divergent Berry curvature dipole or skew scattering for high-frequency rectifier (38). Even so, our device is already exploitable for high-resolution terahertz transmission imaging benefiting from the fast response, high stability, and broadband nature. As test objects, a fresh leaf and a key behind a paperboard are used. High-contrast image of a fresh leaf was obtained at 0.12 THz, reflecting the water-level distribution (Fig. 5G). In the 0.3-THz range, the hidden key and its jagged edges are revealed in the image, with a reasonable spatial resolution (Fig. 5H).
DISCUSSION
In summary, we show that PdTe2 could be an ideal platform for terahertz technology, due to their high anisotropy and strong PGE in the terahertz band, enabling unique opportunities for studying exotic transport for next-generation optoelectronic devices. The PdTe2-based device exhibits superior performance, with sensitivity over 10 A/W and NEP lower than 2 pW/Hz0.5 at room temperature. Such a large responsivity is originated from finely tuned symmetry breaking, and it is anisotropic depending on the crystallographic direction. Polarization-controlled huge photocurrent is extremely powerful for identifying the lattice symmetry, as well as for polarization-sensitive detection, for which anisotropic properties are desired. Future devices optimized for operation might require geometry with more elaborated signal coupling schemes interplayed with the electric field. Our findings are expected to boost the exploration of extraordinary photoelectric phenomena, such as nonlinear anomalous photocurrent, colossal bulk photovoltaic, helical magnetic effect, and Weyl orbit transport led by Dirac/Weyl physics.
MATERIALS AND METHODS
PdTe2 crystal growth
PdTe2 single crystal was grown by the melt growth method. A certain amount of Pd and Te powder (from Alfa Aesar) with an atomic ratio of 1:2.2 was sealed in an evacuated ampoule. The ampoule was heated up and maintained at 790°C for 48 hours. The melt then was slowly cooled down to 500°C for 7 days and then annealed at this temperature for seven more days before natural cooling to room temperature. Centimeter-scale single crystals were obtained, which easily could be exfoliated to small flakes by micromechanical cleavage.
First-principles simulation
The transport properties of PdTe2 were calculated by the first-principles simulation package nanodcal (39), which is based on the DFT combined with the nonequilibrium Green’s function. A double-zeta double-polarization linear combination of atomic orbital basis is used to expand physical quantities. Standard norm-conserving pseudo-potentials are used to define the atomic cores. The generalized gradient approximation [PBE (Perdew-Burke-Ernzerhof) (40)] is used for the exchange-correlation potential in all the calculations. Spin-orbit interacting effect is considered in all calculations.
Device fabrication
PdTe2-based photodetectors are fabricated by starting from mechanically exfoliated flakes of PdTe2 on top of low-conductivity silicon wafer capped with a thin oxide layer SiO2 (300 nm). The resulting log shape antenna was patterned using ultraviolet lithography to define contact regions. Then, metal contacts to PdTe2 were made by evaporating 10 nm of Cr and 90 nm of Au. Last, we obtained source and drain terminals by reactive ion etching to selectively remove the areas unprotected by a lithographic mask.
Photocurrent measurements
Our photocurrent measurements were performed by a terahertz light source propagating along the PdTe2 crystal growth direction (c axis). The terahertz radiation is generated from a 40-GHz microwave oscillator, which is connected with a VDI-WR 9.0 Tripler to generate radiation at 0.12 THz. Similarly, the 0.3-THz radiation is generated from a 0.1-THz IMPATT diode, which is connected with a VDI-WR 2.8 Tripler. The power densities of terahertz radiations at different frequencies were calibrated by a Golay cell.
The photoresponse was recorded by a lock-in amplifier (LIA) and an oscilloscope after a low-noise voltage preamplifier. The value of photocurrent Δi can be estimated from the voltage signal Δu on the LIA via the relation Δi = 2.2·Δu/Gn, where the factor 2.2 accounts for the square-wave modulation Fourier component and Gn is the gain factor of preamplifier. The detector responsivity (RA) was then extracted from Δi through the relation RA = Δi/(PTHz·Sa), where Sa is the effective area and PTHz is the power density (1 mW/cm2 at 0.3 THz). Considering that the effective area of our device Sd = 500 μm × 250 μm is much smaller than the diffraction-limited area Sλ = λ2/4π at 0.12 THz (at 0.3 THz, Sd is greater than Sλ, so Sa = Sd), here the effective area Sa = Sλ rather than Sd is used for the calculation of incident power and responsivity.
The figure of merit used to evaluate the performance of the device is NEP = vn/RA, corresponding to the minimum detectable power with a 1-Hz bandwidth, where vn is the root mean square of the noise current. For terahertz detection, the thermal Johnson-Nyquist noise (νt) associated with the nonzero resistance of the device channel and the noise (νb) owing to the bias current must be included, described as vn = (vt2 + vb2)1/2 = (4kBT/r + 2qId)1/2, where kB is Boltzmann constant, T is the temperature, r is the resistance, q is the elementary charge, and Id is the bias current of the device. All measurements were carried out at room temperature.
Supplementary Material
Acknowledgments
Funding: The work is supported by the State Key Program for Basic Research of China (nos. 2018YFA0306200 and 2017YFA0305500), the National Natural Science Foundation of China (nos. 61521005, 61675222, 61875217, 91850208, and 51773041), and the STCSM Grants (nos. 1859078100 and 19590780100). Author contributions: C.G. prepared and measured devices, wrote the manuscript, and analyzed the data. L.W. and X.C. designed the research and discussed the experimental results. W.L. conceived and supervised the project. A.P. made part of the theoretical results and improved the English of the manuscript. Y.H., X.W., and X.B. performed the first-principles calculation. L.Z. and Z.C. simulated the FDTD method. C.-N.K., C.S.L., and A.P. contributed to single-crystal growth and surface science characterization. W.G., H.X., and D.W. contributed to material characterization. All authors commented on the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the corresponding author.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/36/eabb6500/DC1
REFERENCES AND NOTES
- 1.Tang F., Po H. C., Vishwanath A., Wan X., Comprehensive search for topological materials using symmetry indicators. Nature 566, 486–489 (2019). [DOI] [PubMed] [Google Scholar]
- 2.Liu D. F., Liang A. J., Liu E. K., Xu Q. N., Li Y. W., Chen C., Pei D., Shi W. J., Mo S. K., Dudin P., Kim T., Cacho C., Li G., Sun Y., Yang L. X., Liu Z. K., Parkin S. S. P., Felser C., Chen Y. L., Magnetic Weyl semimetal phase in a Kagome crystal. Science 365, 1282–1285 (2019). [DOI] [PubMed] [Google Scholar]
- 3.Clark O. J., Neat M. J., Okawa K., Bawden L., Marković I., Mazzola F., Feng J., Sunko V., Riley J. M., Meevasana W., Fujii J., Vobornik I., Kim T. K., Hoesch M., Sasagawa T., Wahl P., Bahramy M. S., King P. D. C., Fermiology and superconductivity of topological surface states in PdTe2. Phys. Rev. Lett. 120, 156401 (2018). [DOI] [PubMed] [Google Scholar]
- 4.Sajadi E., Palomaki T., Fei Z., Zhao W., Bement P., Olsen C., Luescher S., Xu X., Folk J. A., Cobden D. H., Gate-induced superconductivity in a monolayer topological insulator. Science 362, 922–925 (2018). [DOI] [PubMed] [Google Scholar]
- 5.Li J. H., Li Y., Du S. Q., Wang Z., Gu B. L., Zhang S. C., He K., Duan W. H., Xu Y., Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci. Adv. 5, eaaw5685 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Weng H., Fang C., Fang Z., Bernevig B. A., Dai X., Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phy. Rev. X 5, 011029 (2015). [Google Scholar]
- 7.Bahramy M. S., Clark O. J., Yang B.-J., Feng J., Bawden L., Riley J. M., Marković I., Mazzola F., Sunko V., Biswas D., Cooil S. P., Jorge M., Wells J. W., Leandersson M., Balasubramanian T., Fujii J., Vobornik I., Rault J. E., Kim T. K., Hoesch M., Okawa K., Asakawa M., Sasagawa T., Eknapakul T., Meevasana W., King P. D. C., Ubiquitous formation of bulk Dirac cones and topological surface states from a single orbital manifold in transition-metal dichalcogenides. Nat. Mater. 17, 21–28 (2018). [DOI] [PubMed] [Google Scholar]
- 8.Xu S.-Y., Alidoust N., Chang G., Lu H., Singh B., Belopolski I., Sanchez D. S., Zhang X., Bian G., Zheng H., Husanu M.-A., Bian Y., Huang S.-M., Hsu C.-H., Chang T.-R., Jeng H.-T., Bansil A., Neupert T., Strocov V. N., Lin H., Jia S., Hasan M. Z., Discovery of Lorentz-violating type II Weyl fermions in LaAlGe. Sci. Adv. 3, e1603266 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Xu S.-Y., Belopolski I., Alidoust N., Neupane M., Bian G., Zhang C., Sankar R., Chang G., Yuan Z., Lee C.-C., Huang S.-M., Zheng H., Ma J., Sanchez D. S., Wang B. K., Bansil A., Chou F., Shibayev P. P., Lin H., Jia S., Hasan M. Z., Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Sodemann I., Fu L., Quantum nonlinear Hall effect induced by Berry curvature dipole in time-reversal invariant materials. Phys. Rev. Lett. 115, 216806 (2015). [DOI] [PubMed] [Google Scholar]
- 11.Yan M., Huang H., Zhang K., Wang E., Yao W., Deng K., Wan G., Zhang H., Arita M., Yang H., Sun Z., Yao H., Wu Y., Fan S., Duan W., Zhou S., Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2. Nat. Commun. 8, 257 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fei F., Bo X., Wang R., Wu B., Jiang J., Fu D., Gao M., Zheng H., Chen Y., Wang X., Bu H., Song F., Wan X., Wang B., Wang G., Nontrivial Berry phase and type-II Dirac transport in the layered material PdTe2. Phys. Rev. B 96, 041201 (2017). [Google Scholar]
- 13.Huang H., Zhou S., Duan W., Type-II Dirac fermions in the PtSe2 class of transition metal dichalcogenides. Phys. Rev. B 94, 121117 (2016). [Google Scholar]
- 14.Udagawa M., Bergholtz E. J., Field-selective anomaly and chiral mode reversal in type-II Weyl materials. Phys. Rev. Lett. 117, 086401 (2016). [DOI] [PubMed] [Google Scholar]
- 15.Pikulin D., Chen A., Franz M., Chiral anomaly from strain-induced gauge fields in Dirac and Weyl semimetals. Phys. Rev. X 6, 041021 (2016). [Google Scholar]
- 16.McCormick T. M., Watzman S. J., Heremans J. P., Trivedi N., Fermi arc mediated entropy transport in topological semimetals. Phys. Rev. B 97, 195152 (2018). [Google Scholar]
- 17.Ma Q., Xu S.-Y., Chan C.-K., Zhang C.-L., Chang G., Lin Y., Xie W., Palacios T., Lin H., Jia S., Lee P. A., Jarillo-Herrero P., Gedik N., Direct optical detection of Weyl fermion chirality in a topological semimetal. Nat. Phys. 13, 842–847 (2017). [Google Scholar]
- 18.de Juan F., Grushin A. G., Morimoto T., Moore J. E., Quantized circular photogalvanic effect in Weyl semimetals. Nat. Commun. 8, 15995 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chan C.-K., Lindner N. H., Refael G., Lee P. A., Photocurrents in Weyl semimetals. Phys. Rev. B 95, 041104 (2017). [Google Scholar]
- 20.Osterhoudt G. B., Diebel L. K., Gray M. J., Yang X., Stanco J., Huang X., Shen B., Ni N., Moll P. J. W., Ran Y., Burch K. S., Colossal mid-infrared bulk photovoltaic effect in a type-I Weyl semimetal. Nat. Mater. 18, 471–475 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Ma J., Gu Q., Liu Y., Lai J., Yu P., Zhuo X., Liu Z., Chen J.-H., Feng J., Sun D., Nonlinear photoresponse of type-II Weyl semimetals. Nat. Mater. 18, 476–481 (2019). [DOI] [PubMed] [Google Scholar]
- 22.Isobe H., Xu S.-Y., Fu L., High-frequency rectification via chiral Bloch electrons. Sci. Adv. 6, eaay2497 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Matsuda T., Kanda N., Higo T., Armitage N. P., Nakatsuji S., Matsunaga R., Room-temperature terahertz anomalous Hall effect in Weyl antiferromagnet Mn3Sn thin films. Nat. Commun. 11, 909 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sadhukhan K., Politano A., Agarwal A., Novel undamped gapless plasmon mode in a tilted type-II Dirac semimetal. Phys. Rev. Lett. 124, 046803 (2020). [DOI] [PubMed] [Google Scholar]
- 25.X. Yang, K. Burch, Y. Ran, Divergent bulk photovoltaic effect in Weyl semimetals. arXiv:1712.09363 [cond-mat.mes-hall] (26 December 2017).
- 26.Chan W. L., Deibel J., Mittleman D. M., Imaging with terahertz radiation. Rep. Prog. Phys. 70, 1325–1379 (2007). [Google Scholar]
- 27.Ryan G. W., Sheils W. L., Electronic states and surface structure of PdTe2 as probed by scanning tunneling microscopy and photoemission spectroscopy. Phys. Rev. B 61, 8526–8530 (2000). [Google Scholar]
- 28.Glazov M., Ganichev S., High frequency electric field induced nonlinear effects in graphene. Phys. Rep. 535, 101–138 (2014). [Google Scholar]
- 29.Auton G., But D. B., Zhang J., Hill E., Coquillat D., Consejo C., Nouvel P., Knap W., Varani L., Teppe F., Torres J., Song A., Terahertz detection and imaging using graphene ballistic rectifiers. Nano Lett. 17, 7015–7020 (2017). [DOI] [PubMed] [Google Scholar]
- 30.Viti L., Coquillat D., Politano A., Kokh K. A., Aliev Z. S., Babanly M. B., Tereshchenko O. E., Knap W., Chulkov E. V., Vitiello M. S., Plasma-wave terahertz detection mediated by topological insulators surface states. Nano Lett. 16, 80–87 (2016). [DOI] [PubMed] [Google Scholar]
- 31.Viti L., Hu J., Coquillat D., Knap W., Tredicucci A., Politano A., Vitiello M. S., Black phosphorus terahertz photodetectors. Adv. Mater. 27, 5567–5572 (2015). [DOI] [PubMed] [Google Scholar]
- 32.Xie Y., Zhang L., Zhu Y., Liu L., Guo H., Photogalvanic effect in monolayer black phosphorus. Nanotechnology 26, 455202 (2015). [DOI] [PubMed] [Google Scholar]
- 33.Liu C.-H., Chang Y.-C., Lee S., Zhang Y., Zhang Y., Norris T. B., Zhong Z., Ultrafast lateral photo-Dember effect in graphene induced by nonequilibrium hot carrier dynamics. Nano Lett. 15, 4234–4239 (2015). [DOI] [PubMed] [Google Scholar]
- 34.Mciver J. W., Hsieh D., Steinberg H., Jarillo-Herrero P., Gedik N., Control over topological insulator photocurrents with light polarization. Nat. Nanotechnol. 7, 96–100 (2012). [DOI] [PubMed] [Google Scholar]
- 35.Dhara S., Mele E. J., Agarwal R., Voltage-tunable circular photogalvanic effect in silicon nanowires. Science 349, 726–729 (2015). [DOI] [PubMed] [Google Scholar]
- 36.Tydex, Golay cells terahertz detectors (2018); www.tydexoptics.com/products.
- 37.Virginia Diodes, Schottky diodes terahertz detectors (2018); www.vadiodes.com/en/products/detectors.
- 38.Ji Z., Liu G., Addison Z., Liu W., Yu P., Gao H., Liu Z., Rappe A. M., Kane C. L., Mele E. J., Agarwal R., Spatially dispersive circular photogalvanic effect in a Weyl semimetal. Nat. Mater. 18, 955–962 (2019). [DOI] [PubMed] [Google Scholar]
- 39.Taylor J., Guo H., Wang J., Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 63, 245407 (2001). [Google Scholar]
- 40.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 78, 1396–1396 (1997). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/36/eabb6500/DC1


