Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 14;53(8):3021–3029. doi: 10.1021/acs.macromol.0c00278

Interplay between Viscoelasticity and Force Rate Affects Sequential Unfolding in Polyproteins Pulled at Constant Velocity

Moran Elias-Mordechai †, Einat Chetrit †, Ronen Berkovich †,‡,*
PMCID: PMC7467765  PMID: 32905266

Abstract

graphic file with name ma0c00278_0007.jpg

Polyproteins are unique constructs, comprised of folded protein domains in tandem and polymeric linkers. These macromolecules perform under biological stresses by modulating their response through partial unfolding and extending. Although these unfolding events are considered independent, a history dependence of forced unfolding within polyproteins was reported. Here we measure the unfolding of single poly(I91) octamers, complemented with Brownian dynamics simulations, displaying increasing hierarchy in unfolding-foces, accompanied by a decrease in the effective stiffness. This counters the existing understanding that relates stiffness with variations in domain size and probe stiffness, which is expected to reduce the unfolding forces with every consecutive unfolding event. We utilize a simple mechanistic viscoelastic model to show that two effects are combined within a sequential forced unfolding process: the viscoelastic properties of the growing linker chain lead to a hierarchy of the unfolding events, and force-rate application governs the unfolding kinetics.

Introduction

Polyproteins are biological constructs made of proteins repeats tethered in tandem, often related to physiological activity that involves mechanical stresses, such as muscle contractions,1,2 mechano-transduction,3,4 etc. Their unique structure enables them to respond to the applied load by unfolding some of their folded domains and extend them in order to regulate stresses and energy,1,2 adjust cell adhesion,5,6 reveal hidden sites,3,7 and enable actin cross-linking.8 The mechanical response of polyproteins to external forces has been extensively studied using single-molecule force spectroscopy (SMFS) through conformational changes, such as unfolding, folding and collapse, in response to various forms of direct load application protocols.9−20 In force extension (FX) measurements, direct load is applied to a single polyprotein molecule, which is tethered at both termini, by pulling it at constant velocity. As a result, the polyprotein displays a series unfolding events in a characteristic “sawtooth” pattern, where each unfolding event occurs at a specific maximal force. Each unfolding event is followed by rapid relaxation due to the exposed length of the unfolded domain, which then is extended due to the continuous application of external load until the next domain unfold and vice versa.

SMFS approach relays on a device to which the molecule of interest (RNA hairpins/proteins/polyproteins) under investigation is tethered (cantilevers tips/beads), and a polymeric linker (connecting amino acid sequences/unfolded domains polypeptides/folded domains). Thereby, a growing body of literature studies the effects introduced by the application of force to the recorded unfolding/rupture probabilities and rates.11,18,20−40 Specifically to polyprotein constructs, sequential hierarchy in the measured unfolding forces was reported using FX SMFS studies of I91 polyproteins.11,37,41,42 This unfolding history dependency was explained as a biphasic behavior, resulting from two competing effects: (a) increase of domain unfolding probability with each unfolding event along the polyprotein chain (N-effect), and (b) decrease of domain unfolding rates resulting from an increase in the cantilever-polymeric (linker) component of the polyprotein after each unfolding event (compliance effect). According to the latter, with the consecutive unfolding of each domain, the overall compliance (inverse of the chain effective stiffness) grows. It is claimed that while the first (N) effect tends to increase the force required to unfold domains with the reduction of the number of folded domains, the second (stiffness) effect inclines to reduce the unfolding forces along the elongating unfolded chain with the increase of the cantilever spring constants. Numerical Monte Carlo simulations exemplified the biphasic behavior for considerably large domains, and increasing number of domains and cantilever spring constants.11 Other works also demonstrated that the unfolding forces depend not only on the pulling velocity but also on the stiffness of the pulling device.32,38 A recent study on the history of mechanical unfolding of I91 polyprotein showed a monotonous increase of the unfolding forces in time (with no biphasic behavior),18 which was explained by the use of long linkers that eliminate possible nonspecific interaction of the first unfolding domain with the surface.

Here we suggest that sequential unfolding in a polyprotein results from an interplay between the viscoelastic properties of its elongating polymeric linker after each unfolding event12,43 and the direct effect of the applied force-rate, dF/dt on the unfolding probabilities.44−46 This interplay eventually encapsulates the two effects mentioned above (compliance and event probability11,37) as a manifestation of the same phenomenon. The application of higher loading rates, with the increase in the pulling velocity, is associated with the reduction of the unfolded chain internal friction, which propagates the tension faster through the stretched elongating linker. Accordingly, the effect of the applied mechanical work on the polyprotein domains becomes more direct. While previous works focused on the stiffness of the pulling device and the nonlinear elasticity of the polymeric linkers on the unfolding probabilities, this work investigates the relation between the variations in the local stiffness of the polyprotein (linker and folded/unfolded domains) and internal friction of the elongating linker at high extensions and their relation to hierarchical unfolding forces within a polyprotein under tension. To this end we performed FX SMFS measurements using atomic force microscopy (AFM) on octameric repeats of I91 domain, denoted as poly(I91), pulled at a constant velocity, V [nm/s]. We use a simple mechanistic viscoelastic model to describe the dynamical response of the molecule–-probe system in order to explain the observed behavior. The experiments were complemented with Brownian dynamics (BD) simulations that reproduced the experimentally observed trend, where the mean unfolding forces corresponds to domain number, in concert with the changes in the chain viscoelastic properties and local unfolding rates.

Experimental Section

Materials

Poly(I91) octamers were expressed and purified in the laboratory of Dr. Neta Sal-Man at Ben-Gurion University of the Negev, using plasmids that were kindly provided by Prof. J. M. Fernandez from Columbia University. The proteins were purified using HEPES buffer (1.0 mM EDTA, 150 mM NaCl, 20 mM HEPES, pH 7.5) as described elsewhere.47

Atomic Force Spectroscopy Measurements

Pulling experiments were carried out with a Luigs & Neumann LTD AFM. The polyprotein solution was centrifuged at 14 000 rpm at 4 °C for 4 min. Next, 20 μL of polyprotein solution was deposited on gold-coated glass coverslides. The glass coverslides were rinsed with 99.9% ethanol (Romical) followed by deionized water (Ultra 370 series, Aqua Max, 18.2 MΩ·cm), then coated with Ni layer and topped with an Au layer by thermal evaporation (Quorum K975X) at 14 mA and 3 min for each layer. All the measurements were carried out in ambient conditions at room temperature. The force-extension (FX) measurements were performed on piezo movement velocities ranging between 50 and 1000 nm/s. The traces were fitted with the Worm-Like-Chain model48,49 to properly identify the I91 domains, resulting with a mean persistence length ⟨lp⟩ = 0.4 ± 0.1 nm and mean contour length increment ⟨ΔLC⟩ = 27.6 ± 0.5 nm. Since the polyprotein attach to the cantilever at random position, traces that were collected had 6–8 unfolding events in the measurements. The cantilevers used (gold-coated Si-Ni Biolevers, BL-TR400PB Asylum Research, Oxford Instruments) were calibrated prior to each experiment using the equipartition theorem,50 measuring spring constants, KS, ranging between 24 and 26 pN/nm. The measurements were carried out in HEPES buffer. Data analysis was performed using IGOR Pro 6.3.7.2 software (WaveMetrics) and Matlab (R2013b).

Brownian Dynamics Simulations

The dynamics of a polyprotein unfolding under constant velocity were numerically reproduced by integrating a set of nine conjugated overdamped Langevin equations29 using Matlab (R2013b). Full details are provided in the Supporting Information (SI).

Results and Discussion

We measured the unfolding dynamics by pulling on an eight domain poly(I91) at several velocities varying from 50 to 1000 nm/s. Accordingly, N (= 1–8) unfolding events were observed in the sawtooth curve.9,15 Since no specific attachment technique was implemented (to avoid the effect of an additional long linker), each polyprotein molecule can be arbitrary picked up by the cantilever tip at any domain between the first one to the eighth. Consequently, we excluded unfolding traces that displayed less than five events, which provided the following average number of data points for the analysis of the unfolding events: n = 65 for the first through fifth events, 50 for the sixth, 31 for the seventh, and 8 for the eighth. Since the recorded number of traces with eight unfolded events were too low to estimate reliable statistics (ranging from 1 to 12, with an average of 8), we relate in the analyses to the unfolding events in the polyprotein up to the seventh event.

Figure 1A shows three representative FX traces with eight unfolding events, measured at V = 50, 100, and 1000 nm/s (red, blue, and green, respectively). For simplicity, in the following we will present the analysis for these three velocities with their color coding, and compare the observed trends to the ones obtained via BD simulations at three representative velocities of 40, 400, and 4000 nm/s. It can be clearly seen that the unfolding forces generally grow with the pulling velocity.9,10,16,51 We examined the behavior of the unfolding forces (Fmax) and stiffness for the each event at the various pulling velocities. The mean unfolding forces, calculated from the distributions of the maximal values collected from every unfolding peak, show a hierarchical increase with event number for all velocities, with no evidence of biphasic behavior. The same trend was observed in the forces obtained from the BD simulations at all velocities (see SI).

Figure 1.

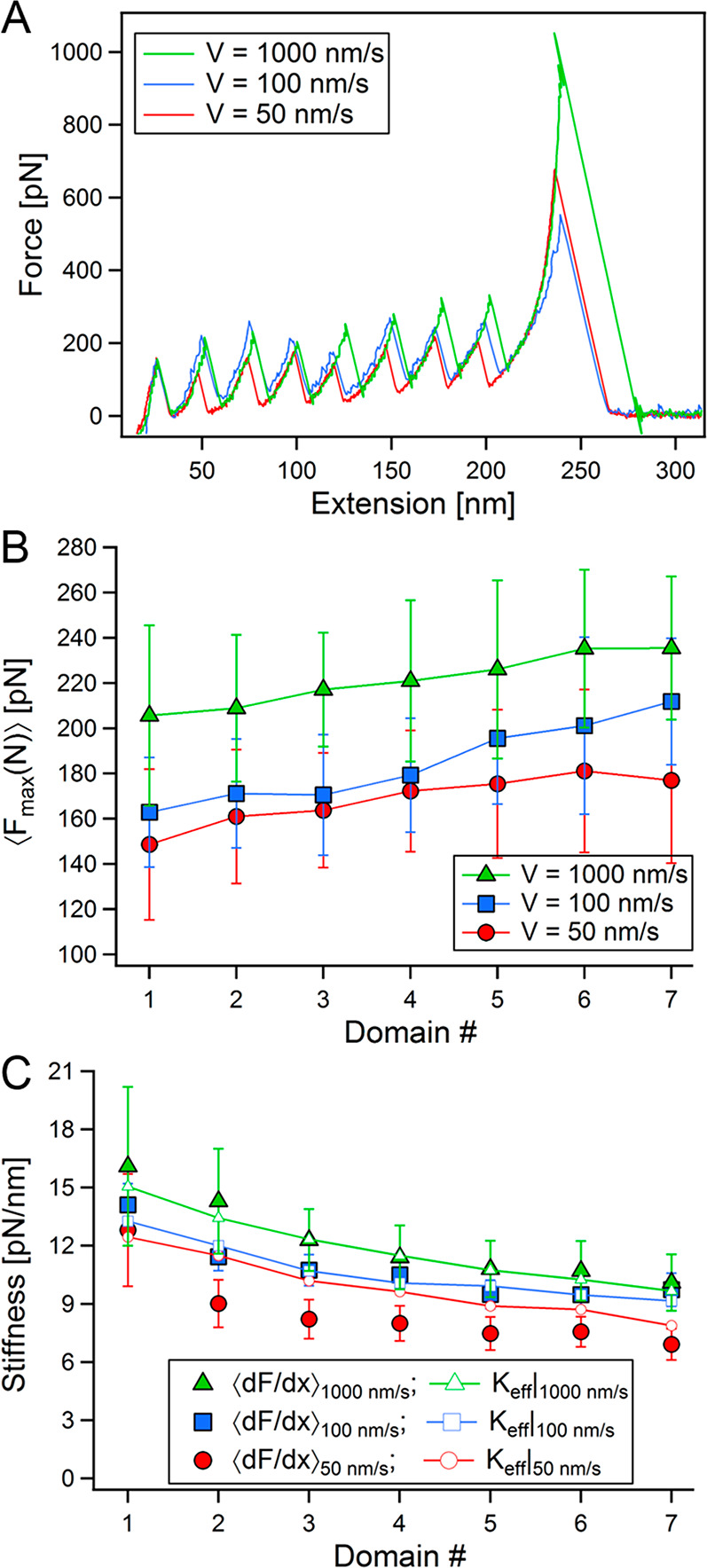
Figure 1

Open in a new tab

FX measurements of poly(I91) unfolding at three representative pulling velocities, V = 50 (red), 100 (blue), and 1000 (green) nm/s. (A) Three exemplary FX unfolding traces. (B) Mean unfolding forces (obtained from the maximal forces at each unfolding event) as a function of unfolding event (domain) number, N. (C) Mean chain stiffness, measured by the slope of the linear regime prior to each unfolding event (dF/dx), at each unfolding event (filled symbols), and the effective stiffness (Keff), estimated with eq 2 and eq 3 (open symbols), showing a softening of the chain with the increase of its polymeric (linker) element after each unfolding event.

The overall effective stiffness can be estimated by taking the slope of the force with respect to its extension at the linear regime at high stretches, before the unfolding event. This effective stiffness encompasses contributions from the polyprotein components and the stiffness of the cantilever to which it is tethered according to

graphic file with name ma0c00278_m001.jpg 1

where KS is the spring constant of the cantilever, Kl (N) is the stiffness of the polymeric linker after each unfolding event, and KP( N) = ∑KP,i, i = 1–N, are the stiffnesses of the remaining folded protein domains. The stiffness of the polymeric linkers can be approximated with an asymptotic phenomenological expression, based on the Worm-Like-Chain (WLC) model at high stretches:43

graphic file with name ma0c00278_m002.jpg 2

where the overall contour length is estimated at high stretch x/LC ≈ 0.85 by LC(N) ≙ (8 – N + 1).LC,folded + 0.85.(LC,0 + N.LC,unfolded), with LC,0 being the contour length of the initial extension of the chain. The stiffness of a folded domain can be approximated by the second derivative of a Morse potential representing a one-dimensional projection of a protein energy landscape, KP = ∇2UP ≈ 6(b/RC) 2U0,52 with b being the curvature of the potential, RC the size of an unfolded domain, and U0 the unfolding barrier amplitude. Based on the characteristic values used for the BD simulations (see SI), the characteristic stiffness of a folded domain can be estimated as KP ≈ 6210 pN/nm, while the stiffness of the linker (unfolded domains) varies from Kl,n=1| F≈200 pN ≈ 101 pN/nm to Kl,n=8|F≈200 pN ≈ 17 pN/nm, which is in the same order of magnitude as KS. Since a folded protein domain is much stiffer than the linker,36 its contribution can thus be neglected compared to those of the considerably more compliant linkers, and the overall effective stiffness can be written as (effective stiffness approximation53)

graphic file with name ma0c00278_m003.jpg 3

Figure 1C plots the variation of stiffness of the system with domain number, comparing the mean of the measured slopes, ⟨dF/dx⟩, with Keff calculated with eqs 3 and 2, using the corresponding experimental parameters. The stiffness shows a decrease with the progression of unfolding events. This result is not surprising, and was shown for a five repeat I91 polyprotein.12 Additionally, stretched polymers were also shown to be effectively more flexible (reduce) under tension.54eq 3 predicts this behavior, as can be seen in Figure 1C, since according to it the stiffness of the linker is proportional to the inverse of its contour length, i.e., Keff ∼ 1/LC. On the other hand, the stiffness is also expected to grow with the unfolding force (Keff ∼ F3/2), which grows with N; however the observed increase in the unfolding forces (Figures 1B and S1B) is considerably milder compared to the increase in the extension of the polyprotein after each unfolding event, meaning that the increase in LC has more prominent effect of the stiffness.

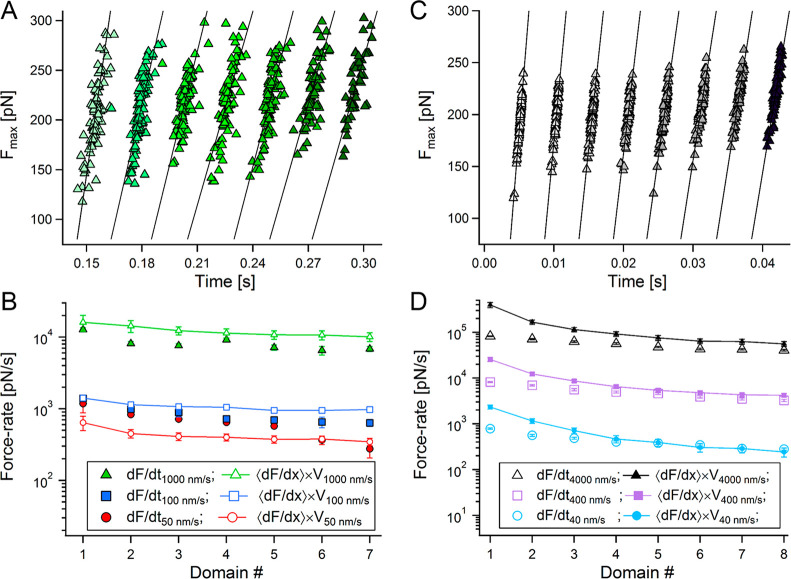
Within the distribution range, Keff deviates from the measured ⟨dF/dx⟩, while still following the same general decreasing trend with N. This deviation is also apparent in the BD simulations (see SI). At low pulling velocities, Keff overestimates ⟨dF/dx⟩, while at the other extreme (at high velocity) it lags behind it. Since the force vary nonlinearly as the chain elongates at constant pulling velocity, we estimated the local unfolding force-rates, dF/dt, at each unfolding event. The force-rate is typically estimated as the product of the velocity with the stiffness of the last unfolding event, i.e., dF/dx|last event × V. In addition to this approach, we evaluated force-rates by taking the slope of the maximal unfolding forces with respect to the times in which they occurred. Figure 2A shows the unfolding forces vs their event time measured at V = 1000 nm/s (triangles in green shades), with linear fittings (straight lines). Similar estimations were performed for the forces measured at the other lower pulling velocities, all displaying a similar decreasing of the force rates experienced by the polyproteins with unfolding progression.

Figure 2.

Figure 2

Open in a new tab

Force-rate variations with the domain number. (A) Unfolding forces (maximal forces, Fmax, collected from the FX unfolding traces measured at V = 1000 nm/s) plotted against the time they took place on (green triangles, with increasing shade for each consecutive unfolding event). The slopes of the linear fits (solid black lines) estimate the local, event dependent, unfolding rate, dF/dt. (B) Force-rates from experimental data measured at V = 50 (red), 100 (blue), and 1000 (green) nm/s. dF/dt obtained from the slopes of the maximal unfolding forces with time (as in A) are marked by solid symbols, while rates estimated by ⟨dF/dx⟩N × V are marked by blank, line connected small symbols. (C) Estimation of dF/dt from the maximal unfolding forces from BD simulations at V = 4000 nm/s. (D) Force-rates calculated from BD simulations at V = 40 (light blue), 400 (purple), and 4000 (black) nm/s.

Figure 2B plots the mean unfolding rates per sequential unfolding events at V = 50, 100, and 1000 nm/s (filled symbols), together with the local rates, estimated by ⟨dF/dx⟩N × V (small open symbols). Both unfolding rates, estimated by the two approaches, decrease with the elongation of the linker, as N increases. Two important observables should be pointed. First, since the various domains along the polyprotein chain unfold at different rates, their mean would better describe the unfolding rate at a given pulling velocity than the one estimated by the final unfolding events, which have the lowest value (i.e., with ⟨dF/dx⟩N × V, rather than dF/dx|last event × V). Second, estimation of the unfolding rate with ⟨dF/dx⟩ × V (or Keff × V) appear to considerably deviate from the direct dF/dt approach (the rates in Figure 2B are plotted on a logarithmic scale). The BD simulations resulted with similar behavior. Figure 2C shows the evaluation of dF/dt from the simulated data obtained at V = 4000 nm/s (triangles in gray shades), with linear fits (straight lines), and Figure 4D plots the measured unfolding rates (colored empty symbols) and the rates estimated by ⟨dF/dx⟩N × V (solid symbols, line connected small symbols) as a function of the increments in chain length (at the sequential unfolding of each domain).

Figure 4.

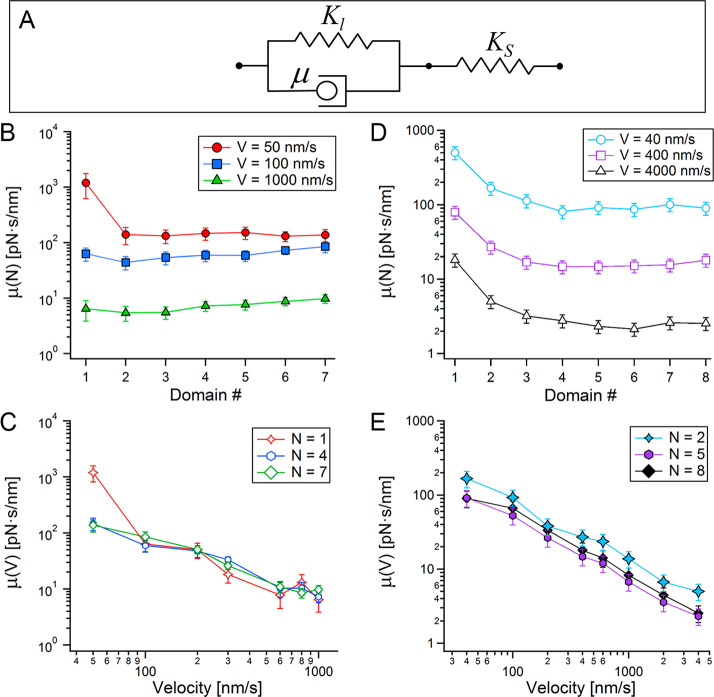
Figure 4

Open in a new tab

Viscoelastic response of the extending linker with unfolding events and pulling velocity. (A) Adaptation of the constitutive Zener model to a linker (characterized with a stiffness Kl and internal friction μ), in series with the stiffness of the probe (KS). μ calculated with eq 5, with the experimental parameters as a function of chain length (B) and pulling velocity for three extensions (C), and with the BD parameters (D, E) respectively.

The experimental data is naturally more scattered compared to the simulated data; however, both show similar trends. Due to the fact that the simulations benefit from larger statistics (100 data points per each events), without being subjected to experimental limitations (as it is only based on phenomenological models), it is consequently less noisy, and assists in providing a distilled picture of the experiments. Figure 2B shows that apart from V = 50 nm/s, at the other (higher) velocities the rate assessed by the stiffness (⟨dF/dx⟩N × V) overestimates the values evaluated by dF/dt. This behavior is not observed in the simulated data (Figure 2D), where ⟨dF/dx⟩N × V > (dF/dt)N. Figure 3A,B plots the N-averaged force-rates as a function of the applied pulling velocity for the experimental and the simulated data. As can be seen for both cases, apart from the experimental data at V = 50 nm/s, ⟨⟨dF/dx⟩⟩ × V > ⟨dF/dt⟩. This exception probably results from the relatively large drift encountered when measuring at low velocities.

Figure 3.

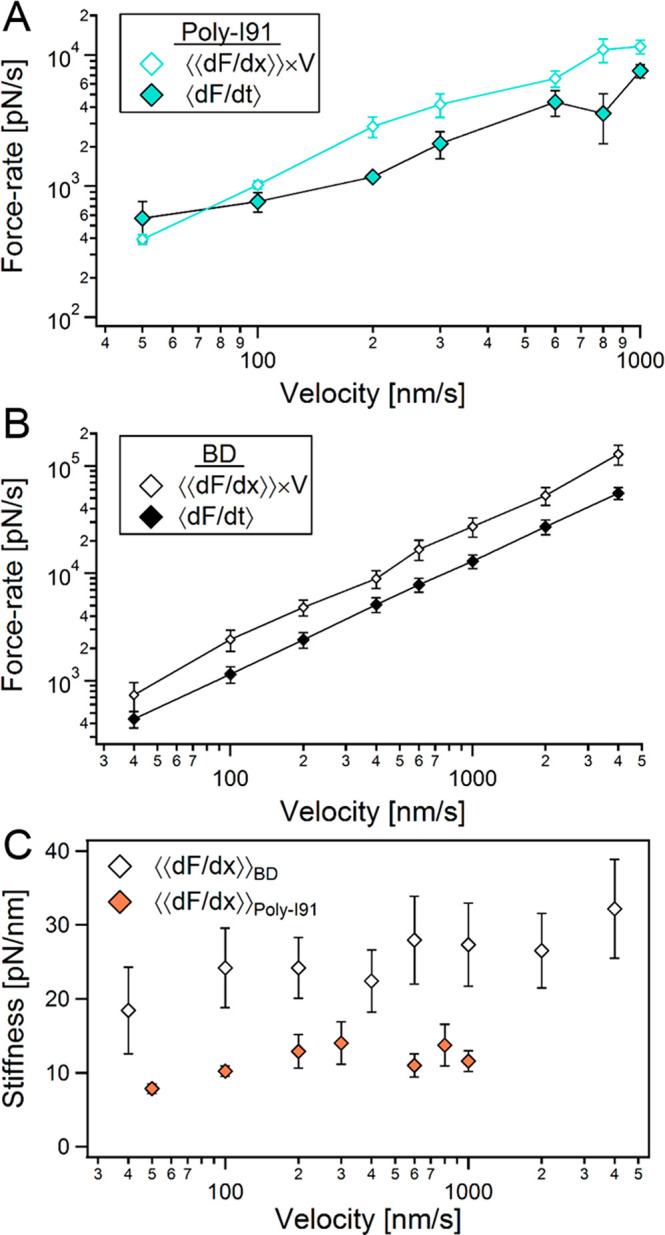
Figure 3

Open in a new tab

Effect of the pulling velocity on force-rates and chain stiffness. (A) Poly(I91) N-averaged force-rates ⟨dF/dt⟩ (solid turquoise diamonds) and ⟨⟨dF/dx⟩⟩ × V (small open turquoise diamonds) as a function of the pulling velocity. (B) BD N-averaged force-rates ⟨dF/dt⟩ (solid black diamonds) and ⟨⟨dF/dx⟩⟩ × V (small open diamonds) as a function of the pulling velocity. (C) N-averaged stiffness, ⟨⟨dF/dx⟩⟩, as a function of the pulling velocity for poly(I91) (solid tangerine diamonds), and BD simulations (open diamonds).

The varying polyprotein stiffness was observed (and predicted) to decrease with chain increase after every unfolding event; however, as can be seen in Figure 1C, it grows with the pulling velocity on average for each event. Figure 3C plots the N-averaged stiffness obtained from both experiments (tangerine triangles) and simulations (open triangles). The experimentally measured stiffness slightly increase, and shortly reaches a plateau, while the simulated stiffness seems to grow with the applied pulling velocity. This indicates that the response of the polyprotein during unfolding under force is not purely elastic.

The modulation of the stiffness with the applied pulling velocity, raises questions regarding the nature and role of the polymeric linker that grows after every unfolding event along the polyprotein. The change of the stiffness with the velocity cannot be explained by eq 3, which disregards the viscoelastic nature of the extended linker, reflected through its internal friction, μ12,43 We therefore utilize the Zener model,55 a constitutive model also known as the standard linear solid, which provides a useful idealized description of a viscoelastic material. It is described by a spring added in series to a Kelvin–Voigt model (spring and a dashpot in parallel), as depicted in Figure 4A. Equilibrium requires that the stress be the same in both elements, which can be indicated by estimating a critical velocity, VC ≈ LC(N)/τZimm, below which, the extension of the chain can considered to be in equilibrium.56τZimm ≈ 23(LClp)3/2η/[kBT(3π)1/2],57 is the Zimm relaxation time for polymer chain (taking into account hydrodynamic interactions between its monomers58), where η ≈ 1 × 10–3 Pa·s is the solvent viscosity. For the parameters obtained from our measurements ⟨VC⟩|n ≈ 1 × 109 nm/s, which are 8–6 orders of magnitude larger than the pulling velocities applied in our measurements, and therefore linker extension can be considered as an equilibrium process (unlike domain unfolding). In the context of this work, the linker is described by a stiffness Kl, given by eq 2, and a viscous term, μ, accounting for its internal friction in series with the spring constant of the probe, KS:

graphic file with name ma0c00278_m004.jpg 4

where the extension x can be approximated as LC under the high stretch assumption.43 Notice that the first term in the right-hand-side is Keff, given by eq 3. When dF/dt = KS·V (which is not the case here, as can be seen in Figures 2 and 3), then eq 4 reduces to the simple harmonic description, F = Keff·x, which means that the force dependency is purely elastic, and thus should not vary with the pulling velocity. Substituting eq 2 into this model and taking the derivative with respect to x, a connection can be established between dF/dx and μ (see SI for details):

graphic file with name ma0c00278_m005.jpg 5

where Kl = Kl(N, F) is given by eq 2, and ∂F/∂x ≈ ⟨dF/dx⟩. For a situation in which dF/dt ≪ KS·V, μ diminishes, while at the opposite limit, where dF/dt → KS·V, it becomes more dominant. Using the experimental parameters, we used eq 5 to calculate μ. Figure 4B,C shows that μ decreases with the extension of the chain length and with the applied velocity, respectively. Figure 4D,E shows the equivalent behavior of μ calculated from BD simulations. The decrease of μ with the increase in chain length is not so obvious from the experimental data, showing almost no change, and even a slight increase. μ calculated from the simulated data with eq 5, however, displays an explicit decrease with the increase in chain length, in agreement with previous works.12,43 The decrease of μ with the length of the linker can be understood in terms of its proximity to the surface, which can be represented with Faxén correction for the hydrodynamic drag parallel to the direction of the force application (up to the second order) by59 μ(x) ≈ μ0/[1 – 9/16(aeff/x)], with μ0 = 6πηaeff, where η is the solution viscosity and aeff is an effective size of the cantilever tip.25 According to this description, the friction decrease to a characteristic μ0 at sufficient distance from the surface.

The observed decrease of μ with V can also be expected (as the decrease of the stiffness with the extension). The force acting on the linker, represented here by a Kelvin–Voigt circuit is F = Kl·x + μ·V. This expression states that μ is proportional to the inverse of V (and the stiffness is proportional to the inverse of x). Remarkably, Lee and Thirumalai introduced an expression for velocity dependent force, with a general form analogues to the Kelvin–Voigt circuit for long DNA molecules, where Kl ≡ kBT/(LC·lp) is the stiffness of a Gaussian chain, and μ ≡ μ0·g(x), with μ0 = kBT/D0, where D0 is the monomeric diffusion constant and g(x) = (1/8)·(x/LC)2/[1 – (x/LC)2]} is a geometric factor on which the effective friction depends.56

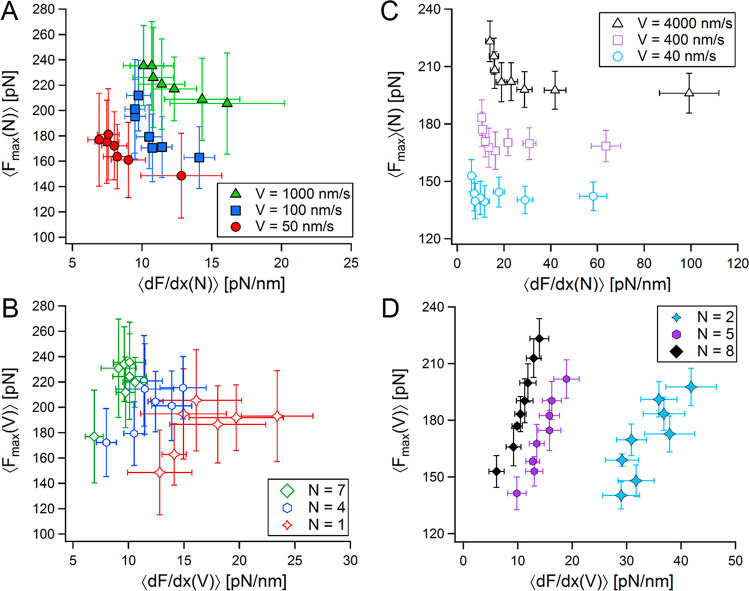
According to the viscoelastic description of the linker, it is possible to understand the stiffening of the linker with the applied velocity, as μ decreases with the overall stiffness. This occurs with the increase of the pulling velocity, resulting in high force-rates (see SI). This behavior coexists with the increase in the internal friction with the chain stiffness as the chain becomes shorter; i.e., for a chain with increasing length, both stiffness and internal friction decrease under similar loads. We therefore turn to examine these effects on the recorded unfolding forces during the sequential unfolding within a polyprotein. As unfolding progresses, the elongating polymeric linker becomes more compliant as its stiffness decreases (Figure 1C) for a given pulling velocity (V = const.); however, an increase in the unfolding forces is observed (Figure 1B). This observable is shown in Figure 5A, where unfolding forces lessen with the increase of the overall stiffness of the system. Since the poly(I91) used here are homopolyproteins, it is a reasonable assumption that their protein domains are nearly similar, and can therefore be characterized by a relatively narrow distribution of unfolding barriers. The measured restoring forces during unfolding, ⟨Fmax⟩ are proportional to the stress required to overcome a characteristic energy activation barrier, ⟨U0⟩ (with a variance that results from thermal fluctuations and possible structural variations). In the absence of an extending linker, a series of domains with a similar ⟨U0⟩ is expected to result with a proportionally similar force distributions around a mean value of ⟨Fmax⟩. However, here, ⟨Fmax⟩ increases as the linker chain becomes longer and softer. For this to happen, a substantial amount of the invested mechanical work (∼F2/Keff) is required to achieve high stretching of the linker chain to transduce the tension on the folded molecule until it reaches the amount of stress required to overcome its ⟨U0⟩. A similar behavior is obtained with the BD simulations (Figure 5C).

Figure 5.

Figure 5

Open in a new tab

Measured unfolding forces as a function of their corresponding local stiffness. (A) Maximal unfolding forces vs mean chain stiffness from poly(I91) FX measurements, both as a function of domain number (chain length), at V = const. (B) Maximal unfolding forces vs mean chain stiffness from poly(I91) FX measurements, both as a function of pulling velocity, at N = const. Respectively corresponding to (A) and (B), maximal unfolding forces vs mean chain stiffness from BD simulations for V = const. (C), and N = const. (D).

An opposite trend, where the ⟨Fmax⟩ grows with system stiffness, is observed for the unfolding events with similar linker length (N = const.) under increasing pulling velocities. In this situation, the faster a linker (at a given length) will be stretched, the faster the tension will propagate through it. Accordingly, the effect emerging from the presence of the linker diminishes, and the force is communicated directly to the folded domain along the polyprotein chain. The direct effect of the applied stress on folded domains (or bond rupture) is well understood within the framework of reaction-rate theory, predicting an increase of the unfolding (or rupture) forces will the applied force-rate.44−46 This trend can be seen more explicitly in Figure 5D that presents the same properties obtained with the BD simulations. In all, the interplay of between these two mechanisms is unraveled by showing that increasing the length of the polymeric (polypeptide) linker component with each successive unfolding event (at a constant pulling velocity) has an opposing effect to the one of increasing the pulling velocity (at constant length).

Conclusions

In this work we measured the unfolding of poly(I91) using AFM at constant pulling velocities, and performed corresponding BD simulations. By analyzing the unfolding forces, we observed a hierarchical increase of the unfolding events with the length increase of the linker with the progression of unfolding, accompanied by a decrease in the mean chain stiffness. The force-rates estimated at each pulling velocity displayed a decease with each consecutive unfolding event. Moreover, comparison of these force-rates with the conventional estimation of the force-rates as the product of the mean stiffness and pulling velocity shows that ⟨dF/dt⟩ < ⟨⟨dF/dx⟩⟩ × V (or equivalently Keff × V). An explanation for this difference, manifested through the increase of the mean stiffness with the pulling velocity, is offered through the viscoelastic behavior of the growing linker. Finally, an interpretation of sequential unfolding in experiments performed under constant pulling velocity conditions is offered as an interplay between two underlying mechanisms: N-effect and V-effect (or dF/dt-effect).

The N-effect is an outcome of the variation in the viscoelastic properties of the linker that increases in size. The WLC phenomenological stiffness of the linker at high stretches, Kl(LC, F),43 given by eq 2, refers to the polymeric nature of an extending chain, at which the force serves as a cutoff value. However, here we measure a more complicated system, whose stiffness is related to the ratio between the folded and unfolded domains. If we consider the folded domains to be similar, all characterized by roughly the same ⟨U0⟩, then all domains should unfold at proportional ⟨Fmax⟩, with no specific hierarchy (or N-effect). Nevertheless, in practice this is not the case. For homogeneous polyproteins (comprised from the same repeating domain), the unfolding of the domains occurs randomly,51 where the probability of the first domain to unfold should be similar to the probability of the fifth or eighth domain to unfold. With the consecutive unfolding of every protein in the polyprotein chain, the overall length of the polymeric linker component increases with ΔLC increments. This softens the polyprotein with every event (or alternatively, increases its compliance, as the longer linker chain is “looser” under the same load). As the overall stiffness decreases with event number, the force required for unfolding is increased, since a larger amount of work is required to further extend the longer linker, such that the tension through it will be sufficient to overcome the protein unfolding mechanical stability (the mean unfolding forces reduce with the increase of the mean stiffness). Conversely, the V-effect (or force-rate effect) causes the mean unfolding forces to increase with the increase in the force-rate application. Increasing the pulling velocity propagates the tension faster through the various components of the polyprotein chain. This communicates the perturbation faster (the chain becomes stiffer and less viscous), and thus it is directly applied to the protein. Additional measurements and simulations performed under the application of constant force-rate, i.e., force-ramp experiments,45 can assist in the understanding of sequential unfolding in polyproteins, particularly since the models used to interpret forced unfolding use the force-rate as the independent variable.44,46 To conclude, stiffness lowering with domain unfolding can provide an additional mechanism to understand mechanical viscoelasticity regulation in physiological systems wherein polyproteins are involved, as in Titin, where this property is involved in tuning its performance as a complex molecular spring.1,2

Acknowledgments

The authors are grateful to the financial support by the I-CORE Program of the Planning and Budgeting Committee and The Israel Science Foundation (Grant No. 152/11).

Glossary

ABBREVIATIONS

SMFS

single molecule force spectroscopy

FX

force extension

BD

Brownian-Dynamics

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.0c00278.

  • Details on the BD simulations, unfolding forces and stiffness from BD simulations, variations of mean unfolding forces, stiffness and force rates with pulling velocity at constant length, and Zener (standard linear solid) model for the viscoelastic description of the linker (PDF)

Author Contributions

R.B. conceived and planned the study. M.E.-M. and E.C. performed the measurements. M.E.-M. and R.B. and analyzed the data and wrote the paper. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ma0c00278_si_001.pdf (1.5MB, pdf)

References

  1. Rivas-Pardo J. A.; Eckels E. C.; Popa I.; Kosuri P.; Linke W. A.; Fernandez J. M. Work Done by Titin Protein Folding Assists Muscle Contraction. Cell Rep. 2016, 14 (6), 1339–1347. 10.1016/j.celrep.2016.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Freundt J. K.; Linke W. A. Titin as a Force-Generating Muscle Protein under Regulatory Control. J. Appl. Physiol. 2019, 126 (5), 1474–1482. 10.1152/japplphysiol.00865.2018. [DOI] [PubMed] [Google Scholar]
  3. del Rio A.; Perez-Jimenez R.; Liu R.; Roca-Cusachs P.; Fernandez J. M.; Sheetz M. P. Stretching Single Talin Rod Molecules Activates Vinculin Binding. Science 2009, 323 (5914), 638–641. 10.1126/science.1162912. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Haining A. W. M.; Lieberthal T. J.; Hernández A. d. R. Talin: A Mechanosensitive Molecule in Health and Disease. FASEB J. 2016, 30 (6), 2073–2085. 10.1096/fj.201500080R. [DOI] [PubMed] [Google Scholar]
  5. Chothia C.; Jones E. Y. The Molecular Structure of Cell Adhesion Molecules. Annu. Rev. Biochem. 1997, 66 (1), 823–862. 10.1146/annurev.biochem.66.1.823. [DOI] [PubMed] [Google Scholar]
  6. Boggon T. J.; Murray J.; Chappuis-Flament S.; Wong E.; Gumbiner B. M.; Shapiro L. C-Cadherin Ectodomain Structure and Implications for Cell Adhesion Mechanisms. Science 2002, 296 (5571), 1308–1313. 10.1126/science.1071559. [DOI] [PubMed] [Google Scholar]
  7. Le S.; Yu M.; Yan J. Direct Single-Molecule Quantification Reveals Unexpectedly High Mechanical Stability of Vinculin—Talin/Α-Catenin Linkages. Sci. Adv. 2019, 5 (12), eaav2720 10.1126/sciadv.aav2720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Schwaiger I.; Schleicher M.; Noegel A. A.; Rief M. The Folding Pathway of a Fast-Folding Immunoglobulin Domain Revealed by Single-Molecule Mechanical Experiments. EMBO Rep. 2005, 6 (1), 46–51. 10.1038/sj.embor.7400317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Rief M.; Gautel M.; Oesterhelt F.; Fernandez J. M.; Gaub H. E. Reversible Unfolding of Individual Titin Immunoglobulin Domains by Afm. Science 1997, 276 (5315), 1109–1112. 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
  10. Carrion-Vazquez M.; Oberhauser A. F.; Fowler S. B.; Marszalek P. E.; Broedel S. E.; Clarke J.; Fernandez J. M. Mechanical and Chemical Unfolding of a Single Protein: A Comparison. Proc. Natl. Acad. Sci. U. S. A. 1999, 96 (7), 3694–3699. 10.1073/pnas.96.7.3694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Zinober R. C.; Brockwell D. J.; Beddard G. S.; Blake A. W.; Olmsted P. D.; Radford S. E.; Smith D. A. Mechanically Unfolding Proteins: The Effect of Unfolding History and the Supramolecular Scaffold. Protein Sci. 2002, 11 (12), 2759–2765. 10.1110/ps.0224602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kawakami M.; Byrne K.; Brockwell D. J.; Radford S. E.; Smith D. A. Viscoelastic Study of the Mechanical Unfolding of a Protein by Afm. Biophys. J. 2006, 91 (2), L16–L18. 10.1529/biophysj.106.085019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Borgia A.; Williams P. M.; Clarke J. Single-Molecule Studies of Protein Folding. Annu. Rev. Biochem. 2008, 77 (1), 101–125. 10.1146/annurev.biochem.77.060706.093102. [DOI] [PubMed] [Google Scholar]
  14. Chen H.; Yuan G.; Winardhi R. S.; Yao M.; Popa I.; Fernandez J. M.; Yan J. Dynamics of Equilibrium Folding and Unfolding Transitions of Titin Immunoglobulin Domain under Constant Forces. J. Am. Chem. Soc. 2015, 137 (10), 3540–3546. 10.1021/ja5119368. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hughes M. L.; Dougan L. The Physics of Pulling Polyproteins: A Review of Single Molecule Force Spectroscopy Using the Afm to Study Protein Unfolding. Rep. Prog. Phys. 2016, 79 (7), 076601. 10.1088/0034-4885/79/7/076601. [DOI] [PubMed] [Google Scholar]
  16. Rico F.; Gonzalez L.; Casuso I.; Puig-Vidal M.; Scheuring S. High-Speed Force Spectroscopy Unfolds Titin at the Velocity of Molecular Dynamics Simulations. Science 2013, 342 (6159), 741–743. 10.1126/science.1239764. [DOI] [PubMed] [Google Scholar]
  17. Lei H.; He C.; Hu C.; Li J.; Hu X.; Hu X.; Li H. Single-Molecule Force Spectroscopy Trajectories of a Single Protein and Its Polyproteins Are Equivalent: A Direct Experimental Validation Based on a Small Protein Nug2. Angew. Chem., Int. Ed. 2017, 56 (22), 6117–6121. 10.1002/anie.201610648. [DOI] [PubMed] [Google Scholar]
  18. Sumbul F.; Marchesi A.; Rico F. History, Rare, and Multiple Events of Mechanical Unfolding of Repeat Proteins. J. Chem. Phys. 2018, 148 (12), 123335. 10.1063/1.5013259. [DOI] [PubMed] [Google Scholar]
  19. Tapia-Rojo R.; Eckels E. C.; Fernández J. M. Ephemeral States in Protein Folding under Force Captured with a Magnetic Tweezers Design. Proc. Natl. Acad. Sci. U. S. A. 2019, 116 (16), 7873–7878. 10.1073/pnas.1821284116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Pyo A. G. T.; Woodside M. T. Memory Effects in Single-Molecule Force Spectroscopy Measurements of Biomolecular Folding. Phys. Chem. Chem. Phys. 2019, 21 (44), 24527–24534. 10.1039/C9CP04197D. [DOI] [PubMed] [Google Scholar]
  21. Evans E.; Ritchie K. Strength of a Weak Bond Connecting Flexible Polymer Chains. Biophys. J. 1999, 76 (5), 2439–2447. 10.1016/S0006-3495(99)77399-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hummer G.; Szabo A. Kinetics from Nonequilibrium Single-Molecule Pulling Experiments. Biophys. J. 2003, 85 (1), 5–15. 10.1016/S0006-3495(03)74449-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Friedsam C.; Wehle A. K.; K hner F.; Gaub H. E. Dynamic Single-Molecule Force Spectroscopy: Bond Rupture Analysis with Variable Spacer Length. J. Phys.: Condens. Matter 2003, 15 (18), S1709–S1723. 10.1088/0953-8984/15/18/305. [DOI] [Google Scholar]
  24. Ratto T. V.; Langry K. C.; Rudd R. E.; Balhorn R. L.; Allen M. J.; McElfresh M. W. Force Spectroscopy of the Double-Tethered Concanavalin-a Mannose Bond. Biophys. J. 2004, 86 (4), 2430–2437. 10.1016/S0006-3495(04)74299-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Janovjak H.; Struckmeier J.; Muller D. J. Hydrodynamic Effects in Fast Afm Single-Molecule Force Measurements. Eur. Biophys. J. 2005, 34 (1), 91–96. 10.1007/s00249-004-0430-3. [DOI] [PubMed] [Google Scholar]
  26. Ray C.; Brown J. R.; Akhremitchev B. B. Correction of Systematic Errors in Single-Molecule Force Spectroscopy with Polymeric Tethers by Atomic Force Microscopy. J. Phys. Chem. B 2007, 111 (8), 1963–1974. 10.1021/jp065530h. [DOI] [PubMed] [Google Scholar]
  27. Bura E.; Klimov D. K.; Barsegov V. Analyzing Forced Unfolding of Protein Tandems by Ordered Variates, 1: Independent Unfolding Times. Biophys. J. 2007, 93 (4), 1100–1115. 10.1529/biophysj.107.105866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hyeon C.; Thirumalai D. Forced-Unfolding and Force-Quench Refolding of Rna Hairpins. Biophys. J. 2006, 90 (10), 3410–3427. 10.1529/biophysj.105.078030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Berkovich R.; Garcia-Manyes S.; Klafter J.; Urbakh M.; Fernández J. M. Hopping around an Entropic Barrier Created by Force. Biochem. Biophys. Res. Commun. 2010, 403 (1), 133–137. 10.1016/j.bbrc.2010.10.133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Maitra A.; Arya G. Model Accounting for the Effects of Pulling-Device Stiffness in the Analyses of Single-Molecule Force Measurements. Phys. Rev. Lett. 2010, 104 (10), 108301. 10.1103/PhysRevLett.104.108301. [DOI] [PubMed] [Google Scholar]
  31. Maitra A.; Arya G. Influence of Pulling Handles and Device Stiffness in Single-Molecule Force Spectroscopy. Phys. Chem. Chem. Phys. 2011, 13 (5), 1836–1842. 10.1039/C0CP01528H. [DOI] [PubMed] [Google Scholar]
  32. Yoon G.; Na S.; Eom K. Loading Device Effect on Protein Unfolding Mechanics. J. Chem. Phys. 2012, 137 (2), 025102. 10.1063/1.4732798. [DOI] [PubMed] [Google Scholar]
  33. Berkovich R.; Hermans R. I.; Popa I.; Stirnemann G.; Garcia-Manyes S.; Berne B. J.; Fernandez J. M. Rate Limit of Protein Elastic Response Is Tether Dependent. Proc. Natl. Acad. Sci. U. S. A. 2012, 109 (36), 14416–14421. 10.1073/pnas.1212167109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hinczewski M.; Gebhardt J. C. M.; Rief M.; Thirumalai D. From Mechanical Folding Trajectories to Intrinsic Energy Landscapes of Biopolymers. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (12), 4500–4505. 10.1073/pnas.1214051110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Makarov D. E. Communication: Does Force Spectroscopy of Biomolecules Probe Their Intrinsic Dynamic Properties?. J. Chem. Phys. 2014, 141 (24), 241103. 10.1063/1.4904895. [DOI] [PubMed] [Google Scholar]
  36. Cossio P.; Hummer G.; Szabo A. On Artifacts in Single-Molecule Force Spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2015, 112 (46), 14248–14253. 10.1073/pnas.1519633112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tych K. M.; Hughes M. L.; Bourke J.; Taniguchi Y.; Kawakami M.; Brockwell D. J.; Dougan L. Optimizing the Calculation of Energy Landscape Parameters from Single-Molecule Protein Unfolding Experiments. Phys. Rev. E 2015, 91 (1), 012710. 10.1103/PhysRevE.91.012710. [DOI] [PubMed] [Google Scholar]
  38. Arya G. Models for Recovering the Energy Landscape of Conformational Transitions from Single-Molecule Pulling Experiments. Mol. Simul. 2016, 42 (13), 1102–1115. 10.1080/08927022.2015.1123257. [DOI] [Google Scholar]
  39. De Sancho D.; Schönfelder J.; Best R. B.; Perez-Jimenez R.; Muñoz V. Instrumental Effects in the Dynamics of an Ultrafast Folding Protein under Mechanical Force. J. Phys. Chem. B 2018, 122 (49), 11147–11154. 10.1021/acs.jpcb.8b05975. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Chetrit E.; Meroz Y.; Klausner Z.; Berkovich R. Correlations within Polyprotein Forced Unfolding Dwell-Times Introduce Sequential Dependency. J. Struct. Biol. 2020, 107495. 10.1016/j.jsb.2020.107495. [DOI] [PubMed] [Google Scholar]
  41. Brockwell D. J.; Beddard G. S.; Clarkson J.; Zinober R. C.; Blake A. W.; Trinick J.; Olmsted P. D.; Smith D. A.; Radford S. E. The Effect of Core Destabilization on the Mechanical Resistance of I27. Biophys. J. 2002, 83 (1), 458–472. 10.1016/S0006-3495(02)75182-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Best R. B.; Brockwell D. J.; Toca-Herrera J. L.; Blake A. W.; Smith D. A.; Radford S. E.; Clarke J. Force Mode Atomic Force Microscopy as a Tool for Protein Folding Studies. Anal. Chim. Acta 2003, 479 (1), 87–105. 10.1016/S0003-2670(02)01572-6. [DOI] [Google Scholar]
  43. Khatri B. S.; Byrne K.; Kawakami M.; Brockwell D. J.; Smith D. A.; Radford S. E.; McLeish T. C. B. Internal Friction of Single Polypeptide Chains at High Stretch. Faraday Discuss. 2008, 139 (0), 35–51. 10.1039/b716418c. [DOI] [PubMed] [Google Scholar]
  44. Evans E.; Ritchie K. Dynamic Strength of Molecular Adhesion Bonds. Biophys. J. 1997, 72 (4), 1541–1555. 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Schlierf M.; Li H.; Fernandez J. M. The Unfolding Kinetics of Ubiquitin Captured with Single-Molecule Force-Clamp Techniques. Proc. Natl. Acad. Sci. U. S. A. 2004, 101 (19), 7299–7304. 10.1073/pnas.0400033101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Dudko O. K.; Hummer G.; Szabo A. Intrinsic Rates and Activation Free Energies from Single-Molecule Pulling Experiments. Phys. Rev. Lett. 2006, 96 (10), 108101. 10.1103/PhysRevLett.96.108101. [DOI] [PubMed] [Google Scholar]
  47. Nadler H.; Shaulov L.; Blitsman Y.; Mordechai M.; Jopp J.; Sal-Man N.; Berkovich R. Deciphering the Mechanical Properties of Type Iii Secretion System Espa Protein by Single Molecule Force Spectroscopy. Langmuir 2018, 34 (21), 6261–6270. 10.1021/acs.langmuir.8b01198. [DOI] [PubMed] [Google Scholar]
  48. Bustamante C.; Marko J.; Siggia E.; Smith S. Entropic Elasticity of Lambda-Phage DNA. Science 1994, 265 (5178), 1599–1600. 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
  49. Marko J. F.; Siggia E. D. Stretching DNA. Macromolecules 1995, 28 (26), 8759–8770. 10.1021/ma00130a008. [DOI] [Google Scholar]
  50. Hutter J. L.; Bechhoefer J. Calibration of Atomic-Force Microscope Tips. Rev. Sci. Instrum. 1993, 64 (7), 1868–1873. 10.1063/1.1143970. [DOI] [Google Scholar]
  51. Hoffmann T.; Dougan L. Single Molecule Force Spectroscopy Using Polyproteins. Chem. Soc. Rev. 2012, 41 (14), 4781–4796. 10.1039/c2cs35033e. [DOI] [PubMed] [Google Scholar]
  52. Fugmann S.; Sokolov I. M. Scaling of the Rupture Dynamics of Polymer Chains Pulled at One End at a Constant Rate. Phys. Rev. E 2009, 79 (2), 021803. 10.1103/PhysRevE.79.021803. [DOI] [PubMed] [Google Scholar]
  53. Severino A.; Monge A. M.; Rissone P.; Ritort F. Efficient Methods for Determining Folding Free Energies in Single-Molecule Pulling Experiments. J. Stat. Mech.: Theory Exp. 2019, 2019 (12), 124001. 10.1088/1742-5468/ab4e91. [DOI] [Google Scholar]
  54. Dobrynin A. V.; Carrillo J.-M. Y.; Rubinstein M. Chains Are More Flexible under Tension. Macromolecules 2010, 43 (21), 9181–9190. 10.1021/ma101860t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Zener C.Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, 1948. [Google Scholar]
  56. Lee N.-K.; Thirumalai D. Pulling-Speed-Dependent Force-Extension Profiles for Semiflexible Chains. Biophys. J. 2004, 86 (5), 2641–2649. 10.1016/S0006-3495(04)74320-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Doi M.; Edwards S. F.. The Theory of Polymer Dynamics; Oxford University Press, 1988; Vol. 73. [Google Scholar]
  58. Zimm B. H. Dynamics of Polymer Molecules in Dilute Solution: Viscoelasticity, Flow Birefringence and Dielectric Loss. J. Chem. Phys. 1956, 24 (2), 269–278. 10.1063/1.1742462. [DOI] [Google Scholar]
  59. Happel J.; Brenner H.. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media; Springer: The Netherlands, 1983; p 553. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ma0c00278_si_001.pdf (1.5MB, pdf)

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES