Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 24;20(8):5792–5798. doi: 10.1021/acs.nanolett.0c01659

Single Nanoparticle Chiroptics in a Liquid: Optical Activity in Hyper-Rayleigh Scattering from Au Helicoids

Lukas Ohnoutek †,‡, Nam Heon Cho §, Alexander William Allen Murphy †,‡, Hyeohn Kim §, Dora Maria Răsădean ∥, Gheorghe Dan Pantoş ∥, Ki Tae Nam §, Ventsislav Kolev Valev †,‡,*
PMCID: PMC7467767  PMID: 32579377

Abstract

graphic file with name nl0c01659_0005.jpg

Linear optical methods of determining the chirality of organic and inorganic materials have relied on weak chiral optical (chiroptical) effects. Nonlinear chiroptical characterization holds the potential of much greater sensitivity and smaller interaction volumes. However, suitable materials on which to perform measurements have been lacking for decades. Here, we present the first nonlinear chiroptical characterization of crystallographic chirality in gold helicoids (≈150 nm size) and core/shell helicoids with the newly discovered hyper-Rayleigh scattering optical activity (HRS OA) technique. The observed chiroptical signal is, on average, originating from between ≈0.05 and ≈0.13 helicoids, i.e., less than a single nanoparticle. The measured HRS OA ellipticities reach ≈3°, for a concentration ≈109 times smaller than that of chiral molecules with similar nonlinear chiroptical response. These huge values indicate that the helicoids are excellent candidates for future nonlinear chiroptical materials and applications.

Keywords: chirality, nanophotonics, hyper-Rayleigh scattering, optical activity, spectroscopy, plasmonics

Due to their lack of mirror symmetry, chiral inorganic nano/meta-materials have recently enabled research into fascinating physical phenomena,1,2 such as negative refractive index and superchiral light. In turn, these phenomena have heralded promising technological applications in ultrasensitive chiral molecular sensing,3−5 super-resolution imaging,6 nanorobotics,7,8 and ultrathin broadband optical components for circularly polarized light.9,10

Many earlier studies have focused on the properties of well-defined quasi-planar chiral nano/meta-arrays, whose 3D chirality is attributable to the presence of substrate11 or to imperfections of the fabrication process.12 However, because chirality is intrinsically a 3D property, more explicit 3D geometries are highly desirable, for instance, multilayers,13 3D networks,14 helices,15 and 3D chiral assemblies.16 Moreover, in all chiral nano/meta-materials, the regular order in arrays/networks can introduce anisotropy and/or extrinsic chirality, thereby greatly complicating the true characterization of chirality. Hence, explicitly 3D chiral nanomaterials dispersed in an isotropic liquid medium are extremely desirable.

Within this context, a new type of 3D chiral nanomaterials has emerged, namely, chiral metal nanocrystals (also known as helicoids),17−19 where the chirality of the nanoparticles has purely crystallographic (high Miller index) origin and is obtained by chirality transfer from molecules.19 Although high Miller index surfaces are well-known for exhibiting chirality, the uniqueness of the helicoids is that this “surface chirality” develops into a morphological/crystallographic chirality in the full three-dimensional (3D) nanoparticle. The solution-based, bottom-up fabrication process is inherently scalable and compatible with liquid phase applications in chemical and biological processes.

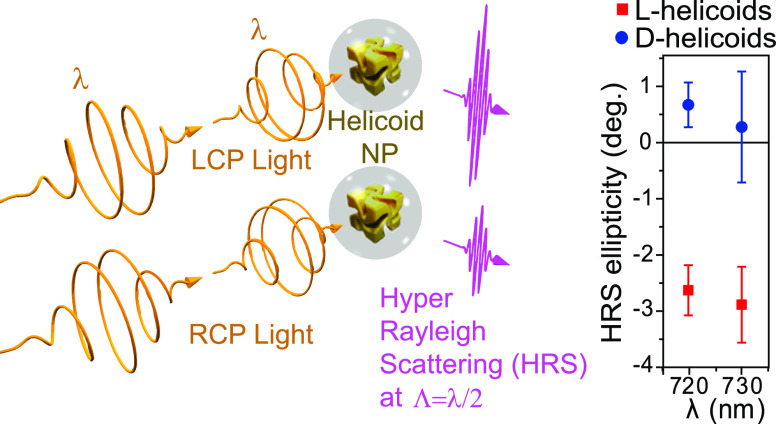
Here, we present the first and unambiguous measurements of the nonlinear chiroptical response of gold helicoids and of core/shell helicoids with an approximately 20 nm thick SiO2 shell. For these purposes, we made use of the recently discovered hyper-Rayleigh scattering (HRS) optical activity effect, which was first observed in inorganic chiral materials, namely, silver nanohelices.20 This effect had been predicted 40 years ago,21 and its general significance was recently confirmed by a reported occurrence in molecules.22 It should be noted that the molecular concentration reported was ≈109 times higher than that of our gold helicoids. The effect is illustrated in Figure 1 (a). The measurements took place in an illumination volume 1011 times smaller than that typically used for circular dichroism (CD) spectroscopy in the linear optical regime, corresponding to an average illumination of <1 nanoparticle. From this tiny volume, we report a remarkable HRS ellipticity of up to 3°, for illumination at 730 nm. To avoid any confusion, here, “optical activity” is used as a general term, designating any and all effects on the polarization of light originating from chirality. Examples of optical activity are the linear and nonlinear optical “circular dichroism” (sometimes referred to as “circular difference” in the nonlinear optical regime), the linear and nonlinear optical “optical rotation”, nonlinear optical “linear dichroism”, etc.

Figure 1.

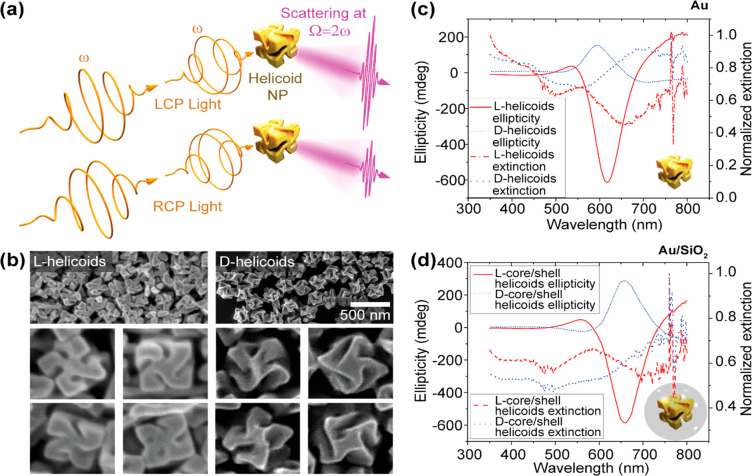
Figure 1

Open in a new tab

Well-defined crystallographic chirality in Au chiral nanocubes (helicoids) results in pronounced chiral optical response. (a) A schematic illustration of optical activity in hyper-Rayleigh scattering from helicoid nanoparticles (NPs), illuminated with left and right circularly polarized light (LCP and RCP, respectively), with frequency ω. (b) Scanning electron microscopy (SEM) images of the chiral forms (enantiomorphs) of the l- and d-helicoids. The average edge length of the helicoids is approximately 150 nm. (c) Ellipticity (in the linear optical regime) and extinction spectra of the two helicoid enantiomorphs, suspended in 1 mM aqueous cetrimonium bromide (CTAB) solution. The extinction spectra were normalized to the maximum value. (d) Ellipticity (in the linear optical regime) and normalized extinction spectra of silica coated l- and d-helicoids suspended in a 9:1 solution of 1 mM CTAB and ethanol. The thickness of the silica shell was approximately 20 nm.

Figure 1(b) shows the scanning electron microscopy (SEM) images of the gold helicoids. The helicoids exhibit a cube-like shape with a chiral center in the middle of each of the sides. The average length of the edges of the cubes is 150 nm. There is little variation among the l- and d-helicoids. Despite the expected morphological differences between l- and d-helicoids, both helicoids present a clearly defined, opposite chiral shape. Their chiroptical properties in the linear optical regime (once dispersed in a liquid, see the Methods section) were characterized with a commercial CD spectrometer. Figure 1(c) and 1(d) show the obtained ellipticity (in the linear optical regime) spectra for both enantiomorphs of the helicoids, in (c), and of the core/shell helicoids, in (d). Clearly, the ellipticities of the two enantiomorphs have an opposite sign, as expected for a chiral structure. The extinction spectra present similar features that have been emphasized by plotting the data with a normalization to the maximum intensity (the raw data are available in the Supporting Information). The l-handed particles exhibit a clear peak around 550 nm (quadrupole mode) and another that extends above 800 nm (dipole mode). For the d-particle, there is a small spectral feature at 525 nm (quadrupole mode) and another at 700 nm (dipole mode). For both the CD and the extinction spectra, the differences in peak value and spectral position are attributable to variations in shape and size between the l- and d-helicoids, which is common for inorganic samples. Also as expected, the spectra in Figure 1(d) are red-shifted with respect to those in Figure 1(c), due to the refractive index of the SiO2 shells.

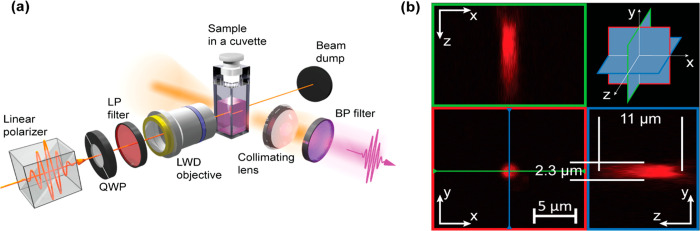
The schematic diagram of the HRS setup is presented in Figure 2 (a); for details see the Methods section. In this setup, left and right circularly polarized (LCP and RCP) ultrafast laser pulses were focused into a cuvette filled with a suspension of l- or d-helicoids using a microscope objective. Scattered light was collected at a right angle to the incident beam. Spectral information about the measured light was obtained by placing various band-pass filters in front of the light detector. In order to estimate the illumination volume within the cell, the objective was mounted onto a commercial multiphoton microscope and a Z-stack scan was performed of a calibration fluorescent nanosphere with a diameter of ≈200 nm. The measurements are presented in Figure 2(b), and the illuminated volume was found to be ≈30 μm3 (i.e., 3 × 10–17 m3). By comparison, as a rough estimate, the illumination volume in a typical CD spectrometer with 10 mm optical cell path length yields an illumination volume of approximately 10–6 m3 (see the Supporting Information). This value is 11 orders of magnitude larger compared to the HRS case. Given the concentration of helicoids in the suspension, which was between ≈1.5 × 1015 nanoparticles (NPs)/m3 and ≈4.5 × 1015 NPs/m3 (see the Supporting Information), there is, on average, between ≈0.05 and ≈0.13 nanoparticles in the illumination volume, which is well below 1. Yet, a clear HRS signal is observed.

Figure 2.

Figure 2

Open in a new tab

Hyper-Rayleigh scattering optical activity is observed from a volume of ≈30 μm3. (a) A schematic of the hyper-Rayleigh scattering experimental setup. The setup comprises a quarter-wave plate (QWP), a low-pass (LP) filter, a long working distance (LWD) microscope objective with 50× magnification, and a band-pass (BP) filter. (b) Estimate of the illumination volume with our objective. The images correspond to a multiphoton microscope Z-stack scan of a fluorescent nanosphere (≈ 200 nm in diameter), situated in the XY plane, with an illumination wavelength of 730 nm.

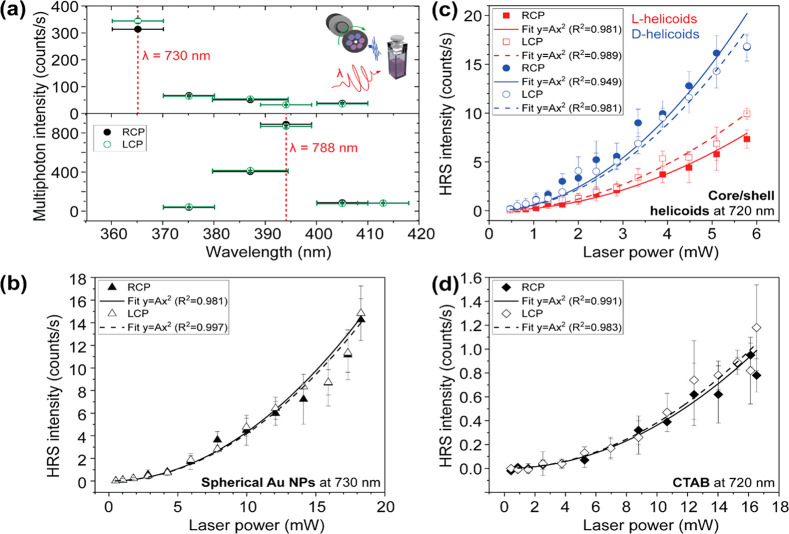
A clear HRS signal means that the HRS emission should be well distinguishable above other multiphoton emission and that the HRS intensity should scale quadratically with incident power. Figure 3(a) shows the emission spectra of l-helicoids. In these experiments, the incident wavelength was kept constant and measurements were done with different spectral filters in front of the detector to spectrally distinguish the multiphoton emissions. For illuminations within our lab’s currently available laser/detector spectral range (here, at 730 and 788 nm), the maximum emission clearly is at the HRS wavelengths (375 and 394 nm, respectively). Moreover, the HRS emission is well above any other multiphoton emission, such as two- and three-photon luminescence. It should be noted that in these experiments, illumination was performed with LCP and RCP and that there is already a good indication of HRS OA in the emission spectrum, upon illumination at 730 nm. This indication is necessary but not sufficient.

Figure 3.

Figure 3

Open in a new tab

Emission wavelengths and the quadratic power-law dependence demonstrate unambiguous hyper-Rayleigh scattering (HRS) from the helicoids. (a) Emission spectrum of the l-helicoids dispersed in 1 mM aqueous cetrimonium bromide (CTAB) solution. Illumination was performed with left and right circularly polarized light (LCP and RCP, respectively) at the wavelengths (λ) of 730 and 788 nm. The dashed vertical lines indicate the HRS wavelengths corresponding to each λ. The wavelength error bars indicate the full-width at half-maximum (fwhm) of the transmission peak of the filters used. The detected signal at the HRS wavelengths is clearly above the multiphoton luminescence background. (b) Power dependence of the HRS intensity in spherical Au nanoparticles (NPs) (80 nm in diameter) suspended in water for LCP and RCP illumination at 730 nm. (c) Power dependence of the HRS intensity from core/shell helicoids with SiO2 shell dispersed in 9:1 solution of 1 mM aqueous CTAB and ethanol, for LCP and RCP illumination with 720 nm light. (d) Power dependence of HRS from the solvent in which the helicoids were dispersed (1 mM aqueous CTAB), for LCP and RCP illumination at 720 nm. For figures (b), (c), and (d), the lines correspond to quadratic power-law fits.

To rule out any systematic error in the setup, we performed control measurements with achiral nanostructures. Figure 3(b) shows the HRS intensity as a function of incident power, from a suspension of spherical Au nanoparticles (80 nm in diameter), for LCP and RCP illumination. The lines correspond to fits with a quadratic power-law. As expected, the data from these achiral nanoparticles show no OA. Moreover, the data points follow the expected quadratic power dependence. This quadratic power dependence can also be observed in the chiral samples.

Figure 3(c) presents the power dependence of HRS intensity from the l- and d-core/shell helicoids for the two circular polarizations of light. Just like Figure 3(a), these results indicate HRS OA; the HRS intensity depends on the circular polarization of the light, and this dependence reverses with reversing chirality. Could this OA originate from the solvent?

To answer this question, we repeated the experiment with only the solvent (no helicoids); the results are shown in Figure 3(d). The detected HRS intensity is tiny (≈ 100 times smaller) compared to the response from the helicoids. These data demonstrate both that the solvent contribution is negligible in the HRS signal from helicoids and that our experimental setup is highly sensitive. Clearly, there is no appreciable HRS OA from the solvent.

The hyper-Rayleigh scattering intensity can be written as the sum of the contributions from individual helicoids:21

graphic file with name nl0c01659_m001.jpg 1

where M indicates the hyper-Rayleigh energy transitions, k = ω/c, V is the volume, and the angular brackets represent rotational averaging. The full expression for M can be found in eq 2.5 of ref (23), where the expression for hyper-Raman can be easily adapted to hyper-Rayleigh by setting the initial and final energy states to be identical. M can be approximated as

graphic file with name nl0c01659_m002.jpg 2

where the first term involves electric dipole interactions only, whereas the second and third terms also involve magnetic dipole interactions and electric quadrupole interactions. Substituting eq 2 into eq 1, the scattering intensities become:

graphic file with name nl0c01659_m003.jpg 3

where N is the number of nanoparticle scatterers, I(β2) is the contribution from |M(β)|2, and the intensity terms I(βJ) and I(βK) are associated with the βJ and βK cross terms, respectively. For the full expressions of these terms, see eqs 10 to 12 in ref (21). The purely electric dipole interactions I(β2) do not contribute to the chiroptical response; this term is associated with the HRS hyperpolarizability. The chiroptical response we observe can therefore be attributed to I(βJ), to I(βK), or to a combination of both. In other words, it arises due to the presence of magnetic dipole and electric quadrupole interactions.

To quantify HRS OA, the HRS polarization ellipticity θHRS can be calculated from the measured HRS intensities IRCPHRS and ILCP for incident light with RCP and LCP, respectively, using the equation20

graphic file with name nl0c01659_m004.jpg 4

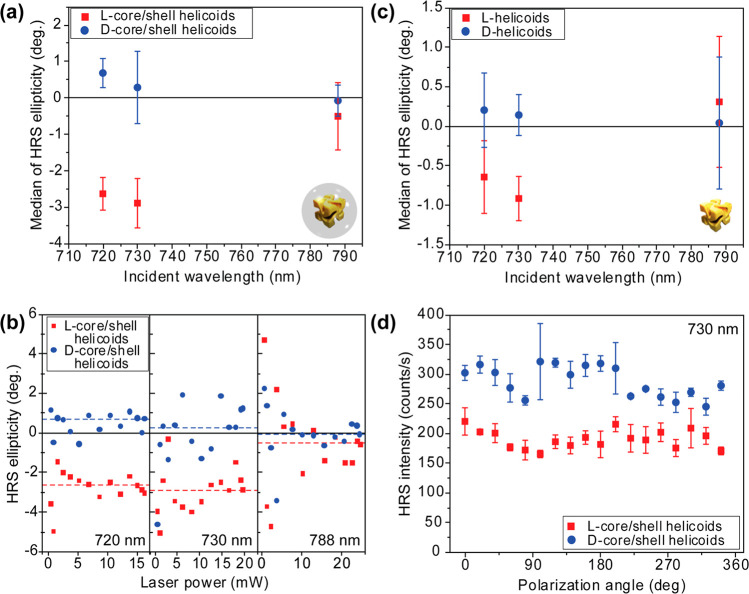
In Figure 4 (a), HRS ellipticity is shown as a function of wavelength for the core/shell helicoids. At 720 and 730 nm, there is a clear HRS OA, illustrated by the well-distinguishable data points and opposite ellipticity depending on the chirality of the core/shell helicoids. At 788 nm, the HRS OA is close to zero. Each one of the data points in Figure 4(a) corresponds to a calculated average (using the median) of >10 HRS ellipticity measurements at various laser powers. These measurements as a function of laser power are shown in Figure 4(b), where the HRS ellipticities of l- and d-core/shell helicoids are clearly separated at 720 nm and at 730 nm, but not at 788 nm. A very similar spectral response is observed in the HRS OA of the helicoids (no shell), as demonstrated in Figure 4(c). However, the HRS ellipticity of the core/shell helicoids is clearly much larger (≈3 times) than that of the helicoids with no shell. This difference could be attributable to the role of the shell, which preserves individual nanocrystals from aggregating and contributes a SiO2/Au interface with its own hyper-polarizability. The exact origin of the difference exceeds the scope of this Letter and will be the subject of further investigations. The spectral range of these experiments was determined by the tuning range of our equipment.

Figure 4.

Figure 4

Open in a new tab

Clear hyper-Rayleigh scattering (HRS) optical activity from suspensions of Au helicoids at multiple wavelengths and independent of incident power. (a) HRS ellipticity spectra from suspensions of core/shell helicoids dispersed in 9:1 solution of 1 mM aqueous cetrimonium bromide (CTAB) and ethanol. Each data point corresponds to the median average of >10 individual HRS ellipticity measurements, at different illumination powers; error bars are the interquartile range. All these individual measurements are shown in (b). (c) The corresponding HRS CD spectra for helicoids with no shell dispersed in 1 mM aqueous CTAB solvent. (d) HRS intensity of core/shell helicoids dispersed in 9:1 solution of 1 mM aqueous CTAB and ethanol, as a function of the angle of linearly polarized illumination, at the wavelength of 730 nm.

So far, we have assumed that the liquid constitutes an isotropic environment. To verify this hypothesis, we have measured the HRS response of the helicoids as a function of the angle of linear polarization. The results are shown in Figure 4(d), where no anisotropy is observed.

In summary, we have presented the first nonlinear chiroptical characterization of gold helicoids (≈150 nm size) and core/shell helicoids, where the chirality is of crystallographic origin and the shell is made of SiO2. In a volume of illumination 11 orders of magnitude smaller than that of commercial CD spectrometers, corresponding to average illumination well below the single helicoid, we observed HRS ellipticities of up to ≈3°. For comparison, similar HRS chiroptical values have been recently reported from molecules, whose concentration is ≈109 times higher.22 These results indicate that the helicoids have an extremely large nonlinear chiroptical response, which could be even larger at wavelengths beyond those investigated here. As such, the helicoids could be an excellent model system, comparable to Pendry’s “chiral spheres”,24 to precisely evidence the roles of chirality parameters, such as geometric chirality and optical chirality,25,26 in the nonlinear optical regime. Nonlinear chiroptical effects at the second harmonic frequency have so far been often limited by the unwanted role of sample anisotropy.27,28 In combination with these helicoids, HRS OA could enable hyper-sensitive nonlinear chiroptical molecular characterization with superchiral light.3−5 Such technology would be highly valuable in the pharmaceutical, agrochemical, perfume, and food industries.

Methods

Synthesis of Helicoid NPs

The synthesis of the nanoparticles follows a two-step seed mediated method. Presynthesized octahedral nanoparticles were dispersed in 1 mM aqueous (CTAB) solution. In a typical synthesis, 0.8 mL of 100 mM CTAB and 0.2 mL of 10 mM gold chloride trihydrate was added into 3.95 mL of deionized water to form a [AuBr4]− complex. Au3+ was then reduced to Au+ by the rapid injection of 0.475 mL of 100 mM l-ascorbic acid (AA) solution. The chiral growth of nanoparticles was initiated by adding 5 μL of 5 mM L- and d-glutathione solution and 50 μL of octahedral seed nanoparticle solution into the growth solution. The temperature of the growth solution was maintained at 30 °C in a water bath for 2 h, where the pink solution gradually became blue and highly scattering. After the reaction, the particle solution was centrifuged twice (1.677 g, 60 s) to be dispersed in a 1 mM aqueous CTAB solution for further characterization.

Synthesis of Helicoid@SiO2 Core–Shell NPs

Before silica coating, 0.3 mL of 0.25 mM mPEG-SH aqueous solution was added dropwise under vigorous stirring to 10 mL of as-synthesized helicoid solution, and their reaction was continued for 30 min. The mixture was centrifuged twice at 6000 rpm for 5 min and redispersed in ethanol. For silica coating, 1.2 mL of mPEG-SH capped helicoid solution was added to 1 mL of DI water followed by addition of 2.3 mL of ethanol and 0.42 mL of 2 M NH4OH solution. The reaction was started by the addition of 90 μL of TEOS solution (40 vol % in IPA) under vigorous stirring and continued for 2 h. After the reaction was completed, the particle solution was centrifuged three times (1.677 g, 5 min) to be dispersed in ethanol for further characterization.

Sample Concentration

A detailed description of the sample concentration estimates is provided in the Supporting Information.

Optical Characterization in the Linear Optical Regime

An Applied Photophysics Chirascan CD spectrometer was used for optical characterization of nanoparticle suspensions in the linear optical regime. Measurements were performed with a 1 nm step and 2 nm bandwidth. Time-per-point was set to 2 s. A measurement of a fused quartz cuvette filled with 1 mM CTAB was taken as a background reading and was automatically subtracted from the measurements of the nanoparticle suspensions by the appliance software.

Estimation of Illumination Volume

The estimation of the illumination volume was performed by mounting the microscope objective used in the HRS experiments onto a Zeiss LSM 880 microscope. A slide with 200 nm fluorescent beads (Invitrogen TetraSpeck Fluorescent Microspheres) was illuminated with 730 nm light, and fluorescence was collected. A Z-stack (set of images at multiple heights of the objective) was taken.

HRS Experiments

A Spectra-Physics Mai Tai Ti:sapphire tunable laser with an 80 MHz repetition rate and 100 fs pulses was used as the laser source for the HRS experiments. An optical chopper with a duty cycle of 1.7% reduced the average power of the laser beam while maintaining the peak power. The beam was passed through a calcite Glan-Laser linear polarizer with 650–1050 nm antireflection coating and then either through an achromatic half-wave plate or a superachromatic quarter-wave plate. Subsequently, the beam was passed through a pair of 665 nm long-pass filters. A Zeiss 50× LD EC Epiplan-Neofluar focused the beam into a quartz cuvette filled with nanoparticle suspensions. A plano-convex lens was used to collect and collimate the scattered light. Another plano-convex lens focused the scattered light into a photomultiplier tube. Hard-coated bandpass filters were placed in front of the detector. The pulses from the photomultiplier tube were preamplified 5× before entering the photon counter. Gated counting was used with A gate measuring the signal when light was incident on the sample and B gate measuring dark/ambient counts. Discrimination levels were set to −7 mV on both of the gates. The number of dark/ambient counts was typically less than 0.2 counts/s. Error bars in plots of HRS intensity were calculated as the standard deviation of six measurements. The results presented in Figures 3(a) and 3(d) were obtained with 12 mW incident laser power.

Acknowledgments

V.K.V. acknowledges support from the Royal Society through the University Research Fellowships. The authors acknowledge Royal Society grants PEF1\170015 and RGF\EA\180228, as well as STFC grant ST/R005842/1 and EPSRC grant EP/L015544/1. Part of this research was supported by the Creative Materials Discovery Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (NRF-2017M3D1A1039377) and the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2017R1A2B3012003). D.M.R. and G.D.P. acknowledge support from the EPSRC through grant EPSRC DTP EB-BB1250.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c01659.

  • Chemical information; estimating the illumination volume; determining the concentration of nanoparticles; comparison of concentration of scattering centres with the work of Verreault et al.; and additional figures (PDF)

Note: Data created during this research is openly available from the University of Bath Research Data Archive at 10.15125/BATH-00862.29

The authors declare no competing financial interest.

Supplementary Material

nl0c01659_si_001.pdf (367.5KB, pdf)

References

  1. Valev V. K.; Baumberg J. J.; Sibilia C.; Verbiest T. Chirality and Chiroptical Effects in Plasmonic Nanostructures: Fundamentals, Recent Progress, and Outlook. Adv. Mater. 2013, 25 (18), 2517–2534. 10.1002/adma.201205178. [DOI] [PubMed] [Google Scholar]
  2. Collins J. T.; Kuppe C.; Hooper D. C.; Sibilia C.; Centini M.; Valev V. K. Chirality and Chiroptical Effects in Metal Nanostructures: Fundamentals and Current Trends. Adv. Opt. Mater. 2017, 5 (16), 1700182. 10.1002/adom.201700182. [DOI] [Google Scholar]
  3. Hendry E.; Carpy T.; Johnston J.; Popland M.; Mikhaylovskiy R. V.; Lapthorn A. J.; Kelly S. M.; Barron L. D.; Gadegaard N.; Kadodwala M. Ultrasensitive Detection and Characterization of Biomolecules Using Superchiral Fields. Nat. Nanotechnol. 2010, 5 (11), 783–787. 10.1038/nnano.2010.209. [DOI] [PubMed] [Google Scholar]
  4. Tullius R.; Karimullah A. S.; Rodier M.; Fitzpatrick B.; Gadegaard N.; Barron L. D.; Rotello V. M.; Cooke G.; Lapthorn A.; Kadodwala M. Superchiral” Spectroscopy: Detection of Protein Higher Order Hierarchical Structure with Chiral Plasmonic Nanostructures. J. Am. Chem. Soc. 2015, 137 (26), 8380–8383. 10.1021/jacs.5b04806. [DOI] [PubMed] [Google Scholar]
  5. Zhao Y.; Askarpour A. N.; Sun L.; Shi J.; Li X.; Alù A. Chirality Detection of Enantiomers Using Twisted Optical Metamaterials. Nat. Commun. 2017, 8 (1), 14180. 10.1038/ncomms14180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Khorasaninejad M.; Chen W. T.; Zhu A. Y.; Oh J.; Devlin R. C.; Rousso D.; Capasso F. Multispectral Chiral Imaging with a Metalens. Nano Lett. 2016, 16 (7), 4595–4600. 10.1021/acs.nanolett.6b01897. [DOI] [PubMed] [Google Scholar]
  7. Urban M. J.; Zhou C.; Duan X.; Liu N. Optically Resolving the Dynamic Walking of a Plasmonic Walker Couple. Nano Lett. 2015, 15 (12), 8392–8396. 10.1021/acs.nanolett.5b04270. [DOI] [PubMed] [Google Scholar]
  8. Schamel D.; Pfeifer M.; Gibbs J. G.; Miksch B.; Mark A. G.; Fischer P. Chiral Colloidal Molecules And Observation of The Propeller Effect. J. Am. Chem. Soc. 2013, 135 (33), 12353–12359. 10.1021/ja405705x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gansel J. K.; Wegener M.; Burger S.; Linden S. Gold Helix Photonic Metamaterials: A Numerical Parameter Study. Opt. Express 2010, 18 (2), 1059. 10.1364/OE.18.001059. [DOI] [PubMed] [Google Scholar]
  10. Li W.; Coppens Z. J.; Besteiro L. V.; Wang W.; Govorov A. O.; Valentine J. Circularly Polarized Light Detection with Hot Electrons in Chiral Plasmonic Metamaterials. Nat. Commun. 2015, 6 (1), 8379. 10.1038/ncomms9379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Kuwata-Gonokami M.; Saito N.; Ino Y.; Kauranen M.; Jefimovs K.; Vallius T.; Turunen J.; Svirko Y. Giant Optical Activity in Quasi-Two-Dimensional Planar Nanostructures. Phys. Rev. Lett. 2005, 95 (22), 1–4. 10.1103/PhysRevLett.95.227401. [DOI] [PubMed] [Google Scholar]
  12. Arteaga O.; Sancho-Parramon J.; Nichols S.; Maoz B. M.; Canillas A.; Bosch S.; Markovich G.; Kahr B. Relation between 2D/3D Chirality and the Appearance of Chiroptical Effects in Real Nanostructures. Opt. Express 2016, 24 (3), 2242. 10.1364/OE.24.002242. [DOI] [PubMed] [Google Scholar]
  13. Jack C.; Karimullah A. S.; Leyman R.; Tullius R.; Rotello V. M.; Cooke G.; Gadegaard N.; Barron L. D.; Kadodwala M. Biomacromolecular Stereostructure Mediates Mode Hybridization in Chiral Plasmonic Nanostructures. Nano Lett. 2016, 16 (9), 5806–5814. 10.1021/acs.nanolett.6b02549. [DOI] [PubMed] [Google Scholar]
  14. Radke A.; Gissibl T.; Klotzbücher T.; Braun P. V.; Giessen H. Three-Dimensional Bichiral Plasmonic Crystals Fabricated by Direct Laser Writing and Electroless Silver Plating. Adv. Mater. 2011, 23 (27), 3018–3021. 10.1002/adma.201100543. [DOI] [PubMed] [Google Scholar]
  15. Gibbs J. G.; Mark A. G.; Lee T.-C.; Eslami S.; Schamel D.; Fischer P. Nanohelices by Shadow Growth. Nanoscale 2014, 6 (16), 9457–9466. 10.1039/C4NR00403E. [DOI] [PubMed] [Google Scholar]
  16. Kuzyk A.; Schreiber R.; Fan Z.; Pardatscher G.; Roller E.-M.; Högele A.; Simmel F. C.; Govorov A. O.; Liedl T. DNA-Based Self-Assembly of Chiral Plasmonic Nanostructures with Tailored Optical Response. Nature 2012, 483 (7389), 311–314. 10.1038/nature10889. [DOI] [PubMed] [Google Scholar]
  17. Lee H.-E.; Ahn H.-Y.; Mun J.; Lee Y. Y.; Kim M.; Cho N. H.; Chang K.; Kim W. S.; Rho J.; Nam K. T. Amino-Acid- and Peptide-Directed Synthesis of Chiral Plasmonic Gold Nanoparticles. Nature 2018, 556 (7701), 360–365. 10.1038/s41586-018-0034-1. [DOI] [PubMed] [Google Scholar]
  18. Cho N. H.; Lee H.; Ahn H.; Lee Y. Y.; Im S. W.; Kim H.; Nam K. T. Cysteine Induced Chiral Morphology in Palladium Nanoparticle. Part. Part. Syst. Charact. 2019, 36 (5), 1900062. 10.1002/ppsc.201900062. [DOI] [Google Scholar]
  19. Im S. W.; Ahn H.; Kim R. M.; Cho N. H.; Kim H.; Lim Y.; Lee H.; Nam K. T. Chiral Surface and Geometry of Metal Nanocrystals. Adv. Mater. 2019, 1905758, 1905758. 10.1002/adma.201905758. [DOI] [PubMed] [Google Scholar]
  20. Collins J. T.; Rusimova K. R.; Hooper D. C.; Jeong H.-H.; Ohnoutek L.; Pradaux-Caggiano F.; Verbiest T.; Carbery D. R.; Fischer P.; Valev V. K. First Observation of Optical Activity in Hyper-Rayleigh Scattering. Phys. Rev. X 2019, 9 (1), 011024. 10.1103/PhysRevX.9.011024. [DOI] [Google Scholar]
  21. Andrews D. L.; Thirunamachandran T. Hyper-Raman Scattering by Chiral Molecules. J. Chem. Phys. 1979, 70 (2), 1027. 10.1063/1.437535. [DOI] [Google Scholar]
  22. Verreault D.; Moreno K.; Merlet É.; Adamietz F.; Kauffmann B.; Ferrand Y.; Olivier C.; Rodriguez V. Hyper-Rayleigh Scattering as a New Chiroptical Method: Uncovering the Nonlinear Optical Activity of Aromatic Oligoamide Foldamers. J. Am. Chem. Soc. 2020, 142 (1), 257–263. 10.1021/jacs.9b09890. [DOI] [PubMed] [Google Scholar]
  23. Andrews D. L.; Thirunamachandran T. The Hyper-Raman Effect: A New Approach to Vibrational Mode Classification and Assignment of Spectral Lines. J. Chem. Phys. 1978, 68 (6), 2941. 10.1063/1.436047. [DOI] [Google Scholar]
  24. Pendry J. B. A Chiral Route to Negative Refraction. Science (Washington, DC, U. S.) 2004, 306 (5700), 1353–1355. 10.1126/science.1104467. [DOI] [PubMed] [Google Scholar]
  25. Tang Y.; Cohen A. E. Optical Chirality and Its Interaction with Matter. Phys. Rev. Lett. 2010, 104 (16), 163901. 10.1103/PhysRevLett.104.163901. [DOI] [PubMed] [Google Scholar]
  26. Tang Y.; Cohen A. E. Enhanced Enantioselectivity in Excitation of Chiral Molecules by Superchiral Light. Science (Washington, DC, U. S.) 2011, 332 (6027), 333–336. 10.1126/science.1202817. [DOI] [PubMed] [Google Scholar]
  27. Hooper D. C.; Mark A. G.; Kuppe C.; Collins J. T.; Fischer P.; Valev V. K. Strong Rotational Anisotropies Affect Nonlinear Chiral Metamaterials. Adv. Mater. 2017, 29 (13), 1605110. 10.1002/adma.201605110. [DOI] [PubMed] [Google Scholar]
  28. Collins J. T.; Hooper D. C.; Mark A. G.; Kuppe C.; Valev V. K. Second-Harmonic Generation Optical Rotation Solely Attributable to Chirality in Plasmonic Metasurfaces. ACS Nano 2018, 12 (6), 5445–5451. 10.1021/acsnano.8b00601. [DOI] [PubMed] [Google Scholar]
  29. Ohnoutek L.; Murphy A.; Rasadean D.; Pantos D.; Valev V. Dataset for “Single Nanoparticle Chiroptics in a Liquid: Optical Activity in Hyper-Rayleigh Scattering from Au Helicoids". University of Bath Datasets 2020, 1. 10.15125/BATH-00862. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c01659_si_001.pdf (367.5KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES