Abstract
SARS-CoV-2 (COVID-19) virus is a havoc pandemic that infects millions of people over the world and thousands of infected cases dead. So, it is vital to propose new intelligent data analysis tools and enhance the existed ones to aid scientists in analyzing the COVID-19 virus. Fragmented Local Aligner Technique (FLAT) is a data analysis tool that is used for detecting the longest common consecutive subsequence (LCCS) between a pair of biological data sequences. FLAT is an aligner tool that can be used to find the LCCS between COVID-19 virus and other viruses to help in other biochemistry and biological operations. In this study, the enhancement of FLAT based on modified Ions Motion Optimization (IMO) is developed to produce acceptable LCCS with efficient performance in a reasonable time. The proposed method was tested to find the LCCS between Orflab poly-protein and surface glycoprotein of COVID-19 and other viruses. The experimental results demonstrate that the proposed model succeeded in producing the best LCCS against other algorithms using real LCCS measured by the SW algorithm as a reference.
Keywords: COVID-19 virus, Ions motion optimization, Smith–Waterman alignment algorithm, Pairwise local alignment, Longest common consecutive substrings
1. Introduction
Coronavirus (COVID-19) is a novel havoc pandemic flare-up through most of the countries in the world since December 2019 and leading to huge infections of up to 10.5 million people through the world until July 2020 and deaths reach up to 500 thousand people as reported by World Health Organization (WHO). COVID-19 is a severe human pathogen, which affects the respiratory system, liver, digestive and nervous systems is distributed among birds, humans, mice, bats, and other wildlife [1], [2]. Two previous coronavirus (SARS-CoV was discovered in the year of 2003 and MERS-CoV in 2012) outbreaks and had the ability of transmission from human to human or animal to animal [3]. The transmission of viruses can be occurred between humans to humans through the air, close personal contact, touching surfaces containing viral particles, and rare stool contamination, which was confirmed by the Centers for Disease Control and Prevention (CDC). One of the serious problems with COVID-19 its incubation period, which ranges from 3 to 14 days, and the average age of the diseases is 47.0 years [4].
Now, it is the rule of sciences to analyze and control the spreading of the COVID-19 virus, such as biochemistry sciences trying to design a drug for it with co-operating with biological analyses of the biological protein of the virus by analyzing and medicine for clinical trials. Some studies were performed in this direction, such as [5], [6], [7], [8]. Therefore, computational tools in bioinformatics can be used for the analysis of the genetic data and protein of COVID-19, such as docking peptides, antibodies against the potential ligands of COVID-19 [9], [10]. Therefore, the intelligent data analysis tools are vital to helping scientists for modeling the behavior of the pandemic, detecting the infected cases, and designing a drug for COVID-19 [11], [12].
Aligning genomic sequences (DNA, Protein, and RNA) is a vital operation in bioinformatics that measures the functional and evolutionary relationships between the genomic sequences [13]. Besides, other operations in biology use alignment operation such as prediction of protein secondary structure [14], construction of phylogenetic trees [15], and DNA fragment assembly [16]. Local pairwise sequence alignment is one of two common kinds of alignment algorithms that finds the LCCS between pairs of biological sequences, and the standard algorithm to perform the local alignment is the SW algorithm [17], which depends on the dynamic programming approach. Therefore, it produces the accurate LCCS between a pair of sequences; however, it engrosses powerful execution time, especially for sequences with huge lengths.
Fragmented Local Aligner Technique (FLAT) [18] is an intelligent biological data analysis tool is used for detecting the LCCS between a pair of sequences. FLAT is a developed version of the Smith–Waterman (SW) algorithm [17], which finds the accurate real LCCS between a pair of sequences but consumes huge execution of time. FLAT speeds up the execution time of the SW algorithm to produce reasonable LCCS in a reasonable time to produce primary results instead of wasting time with no benefit results. Therefore, it allows scanning huge databases to filter the sequences that have acceptable results and then aligning it using SW algorithm which produce the most accurate alignment.
COVID-19 virus is a novel virus, so FLAT can be used to align it against other viruses to find the common features that will aid in understanding the behaviors of pandemic and construct the phylogenetic tree of the virus, especially for aligning the virus against the huge biological database. Hence, the motivation of this work to enhance the performance of FLAT to find LCCS of COVID-19 against other viruses in a reasonable time.
FLAT was proposed to speed up the execution time of the SW algorithm with acceptable alignment results [18] to speed up the process of aligning sequences with huge length and search databases. The idea is fragmenting the two sequences into many fragments with short lengths and perform the SW algorithm on these fragments where SW will consume a short time due to the short length of sequences. Due to there are many possibilities of positions to cut the fragments, Meta-Heuristic Algorithms (MA) are used to point the search toward the locations in the sequences that have LCCS found. MA are stochastic algorithms based on search methodology inspired by nature, animals, and physics phenomena to find the optimal solution. Common and recent released MA, for example, Sine–Cosine Optimization Algorithm [19], Particle Swarm Optimization [20], Volleyball premier league algorithm [21], Lightning Attachment Procedure Optimization [22], Lightning search algorithm [23] Electron radar search algorithm [24], The Whirlpool Algorithm [25] and Squirrel Search Algorithm for optimization [26].
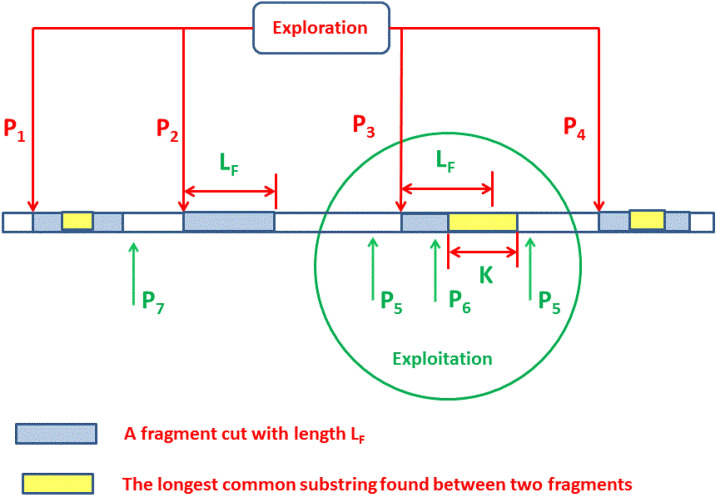
FLAT was implemented using the Sine–Cosine Optimization (SCA) algorithm [19] and the improved algorithm of SCA using PSO (ASCA-PSO) [18]. The two algorithms are succeeded in finding reasonable alignment results with a high percentage of real LCCS in a reasonable time. The percentage of the length of LCCS founded relative to real LCCS founded by the SW algorithm is the criteria for evaluating the performance of FLAT. FLAT based on ASCA-PSO produces the highest average percentage of 83% real LCCS can be founded over sequences with a product of lengths in the range from 250,000 to 9,000,000 while it produces 40% of real LCCS when using SCA. Therefore, the quality of the founded solution still causes a flaw that motivates the development of FLAT for enhancing the founded solutions. The poor performance of the FLAT version, which is based on SCA due to SCA, has good exploration capability but poor exploitation capability. The positions of sequence lengths represent the search space that was explored using FLAT, and the LCCS between the two aligned sequences is the desired output that was located at certain positions in each sequence. As seen in Fig. 1, there are 4 positions (P1 to P4) explore the search space by visiting most positions over the entire length of the sequence, and two fragments are cut (one in each sequence) to be aligned to find the length of the common subsequence.
Fig. 1.
Synergy of exploration and exploitation over the sequence length for FLAT.
The algorithms try to find the positions in each sequence to cut a fragment, and the fragments that have the longest common subsequence founded all other search agents moved toward its position to diverse the solutions and may found better LCCS. As shown, the search agent P3 found part of real LCCS that have a length (K), and this part is the longest founded part; hence all other solutions will move toward it according to the updating mechanism of metaheuristic algorithm. The search agents intensify around the best search agent (P3) and improve the search around the region marked by a green circle.
For enhancement of FLAT, a modified version of the metaheuristic algorithm named Ions Motion Optimization (IMO) algorithm [27] is developed. Since no one optimization algorithm can handle all problems efficiently, as stated by No Free Lunch (NFL) theorem [28]. IMO is inspired by the attraction and repulsion law of ions for performing the search process.
Ions Motion Optimization (IMO) algorithm has two groups of search agents; each group has global best solutions and the movement of these agents based on the attraction and repulsion force law. Two global best solutions will increase the diversity of released solutions due to the updating movement of search agents; hence it has efficient exploration capability, and this the main advantage of IMO. Another main advantage IMO, its few parameters to be tuned and efficient exploration for the feasible search space. However, the exploitation of IMO is weak, which is performed if a certain condition is satisfied hence it cannot execute on all iterations for all search agents; hence it produces poor performance, which needs to be enhanced.
The performance of IMO was tested for implementing FLAT, which produces poor results, which represented as finding LCCS far from real one measured by the SW algorithm or very small percentage of real LCCS. The reason for these poor results is the huge length of sequences that represent the search space, and IMO succeeded in locating the region of LCCS due to its good exploration capability. However, poor exploitation makes it fail to intensify the region to increase the common part is found.
According to the huge length of aligned sequences in the FLAT, so efficient exploration of the search space needed to visit most regions of the sequences. Therefore, IMO is predicted to propose an enhancement performance better than that of SCA. However, It has poor exploitation capability, so it is merged with PSO to enhance its exploitation phase. IMO has been successful in optimizing many engineering applications such as load economic dispatch (Wang, Pan, et al. 2020), short-term hydrothermal scheduling [29], breast cancer prediction [30], AGC investigation in [31], protein folding prediction [32], robotics [33] and cloud job scheduling [34].
Some trials were performed to enhance the exploitation of IMO, such as [35] proposed enhancement of IMO based on adding random perturbations to the update equations of ions during solid states. The enhanced version was called diversity IMO (DIMO) due to it based on the diversity of solutions. The proposed version was tested on mathematical benchmark function and the engineering problem of localization in a wireless sensor network. They claimed that the convergence speed of IMO and localization accuracy in wireless sensor network was enhanced. Another trial for enhancing IMO by combining the greedy algorithm and was tested on the problem of the protein folding prediction of the HP model [32]. The proposed enhanced version of IMO (IMOG) proposed an efficient ability to produce high accuracy of prediction with high stability, especially for longer sequences.
In this work, DIMO and IMOG were used for implementing FLAT to test their performance, and they produced poor results, which prove that the enhancement of exploitation of IMO using the two versions is not efficient for FLAT according to No Free Launch theorem [28].
In this paper, an improved IMO algorithm for FLAT is proposed based on enhancing the exploitation phase of IMO by combining the PSO algorithm with has efficient exploitation process. In general, the PSO algorithm [20], which inspired its search methodology from bird flocking, is the best choice since it has efficient exploitation of the search space. So, there is motivation to use it due to its success to optimize the exploitation phase in a lot of metaheuristics such as SCA [18], Grey Wolf Optimization (GWO) [36], Differential Evolution [37], Tabu Search [38], Gravitational Search Algorithm (GSA) [39], Swallow Optimization Algorithm (SOA) [40], Bacterial Foraging Algorithm (BFA) [41], Ant Colony Algorithm [42], [43], Genetic algorithms [44]. There are other trials of optimization of different algorithms.
The proposed model starting by accepting the protein sequences of COVID-19 and the against protein virus, and the LCCS between the two protein sequences is the required output. Then FLAT explores the search space using IMO, and then the founded solutions are assigned as initial solutions to be exploited by PSO then return to IMO. These operations are performed for some iterations. Therefore, each algorithm is self-contained with no influence of one of them on the search methodology of the other and are executed in a relay execution manner. The way of assigning solutions between search agents of each algorithm during the transition between the two algorithms (from IMO to PSO or the reverse) will affect the enhancement of IMO. So, in the improved IMO, and there are some rules for assigning these solutions. The required LCCS between COVID-19 and the other virus is the one founded by the best global solution of PSO.
In this paper, the main achievements can be concluded as follow:
-
1-
Propose an alternative method to improve the analysis of COVID-19 using modified FLAT.
-
2-
Enhance the performance of FLAT based on the improved IMO.
-
3-
Propose an improved IMO algorithm based on merging with PSO.
The following sections of this article are organized as follows: Section 2 presents the basic information for the Fragmented Local Aligner Technique, IMO, and PSO. Section 3 presents the Proposed IMO-PSO for FLAT. In Section 4, the experimental results and discussion are given. Section 5 introduces the conclusion and future works.
2. Preliminaries
The following subsections propose a brief description of Ions Motion Optimization (IMO) and Particle Swarm Optimization (PSO) algorithms also presented.
2.1. Fragmented Local Aligner Technique (FLAT)
Aligning genomic sequences (DNA, Protein, and RNA) is a vital operation in bioinformatics that measures the functional and evolutionary relationships between the genomic sequences (Cohen 2004). Besides, other operations in biology use alignment operation such as prediction of protein secondary structure (Di Francesco, Garnier et al. 1996), construction of phylogenetic trees (Feng and Doolittle 1990), and DNA fragment assembly (Li and Khuri 2004). Local pairwise sequence alignment is one of two common kinds of alignment algorithms that finds the LCCS between pairs of biological sequences, and the standard algorithm to perform the local alignment is the SW algorithm (Smith and Waterman 1981), which depends on the dynamic programming approach. Therefore, it produces the accurate LCCS between a pair of sequences; however, it engrosses powerful execution time, especially for sequences with huge lengths.
Fragmented Local Aligner Technique (FLAT) was proposed to speed up the execution time of the SW algorithm with acceptable alignment results (Issa, Hassanien, et al. 2018) to speed up the process of aligning sequences with huge length and search databases. The idea is fragmenting the two sequences into many fragments with short lengths and perform the SW algorithm on these fragments where SW will consume a short time due to the short length of sequences.
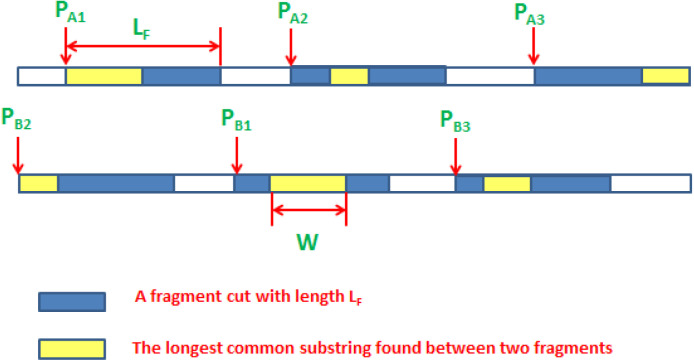
As shown in Fig. 2, there are three fragments with length and the yellow parts are the common between each corresponding fragments. As shown, fragments are cut at positions and are aligned using the SW algorithm, and it contains the LCCS founded with length W. Hence, other positions must be moved toward this position to enhance the search operation. This is the rule of using MA, which aid in traversing the huge length of sequences and point the search toward the location has LCCS founded.
Fig. 2.
A representation of the fragmentation of sequences into short fragments.
Eq. (1) is used as an objective function (The fitness function that is used to evaluate the solutions) that is used to control the movement of search agents and assess the finding alignments.
| (1) |
where and are the aligned sequences with length . The procedure of FLAT is presented in the algorithm (1).
FLAT has a complexity of time , where , , and are the number of search agents, the length of cutting fragments, and the number of iteration respectively.
2.2. Ions Motion Optimization (IMO) algorithm
IMO algorithm is a stochastic optimization algorithm which inspired its search methodology from the properties of ions in physics. The population (candidate solutions) of the IMO algorithm is divided into two sets of anions and cations. Updating the movement of these ions (solutions) according to the theory of attraction and repulsion of the ions that states, “ions with the same charges repel each other, but with opposite charges attract each other” [45]. The algorithm consists of two states: liquid state and solid state wherein liquid state, the ions are moved freely more than in the solid-state that give possibilities for exploration search space and produce more diversification of the solutions, which is an advantage of IMO. While in solid-state (exploitation phase), the stabilized attraction forces between ions make it not free enough to search around in narrow regions; hence the exploitation phase is poor. In the following liquid and solid phase are described :
- Liquid phase (exploration phase)
In the liquid state, each population of anions and cations update its movement such that each anion move toward the best cation and each cation move toward the best anion found. Eq. (2) and Eq. (3) are used for update anions and cations in order.
| (2) |
| (3) |
where i is the ion index, j is the dimension, A is anion candidate solution, C is the cation candidate solution. A is the best anion solution, and C is the best cation solution found, A and C is the mathematical model that represents the distance between ions and cations as in Eq. (4) and Eq. (5).
| (4) |
| (5) |
Exploration can be guaranteed due to ions are attracted to the opposite charges ions, and during the next iterations, more interaction between ions leads to converging toward the best opposite charge ions until reaching balance attraction force between ions leads to stabilization of the ions form.
For a certain condition where the best fitness found becomes more than half of the worse fitness of anion and cations, the solid-state was entered where the ions become approximately fixed due to the stability of attraction forces. This condition may not be satisfied in some cases (for certain runs or certain engineering problems), and the exploitation phase cannot be occurred or not clear hence it needs to be enhanced.
- Solid-state (exploitation phase)
In the solid-state, ions are difficult to be moved and form the stabilization phase, so there is a need for an external force to move the ions around the search space to escape from local minima. Eq. (6) and Eq. (7) are used for this purpose, and also there is a random initialization of some ions around search space to increase the diversity of ions around search space. Hence, the important condition to apply external force is the value of the best ion of anions (and cations) is bigger than or equal half of the worst value of anions (and cations), which means the ions are in the stable case.
| (6) |
| (7) |
and are random variables in the range [−1, 1]. After updating ions based on Eq. (7) and Eq. (8) if a probability lower than 0.05 hence re-initialize the ions in the search space to guarantee to escape from freezing and enhance exploration.
IMO has a time complexity is where T and n are the number of iterations and the number of search agents in order. and C are the costs time for updating equations of one search agent in the liquid and solid phase iteratively.
2.3. Particle Swarm Optimization (PSO)
PSO is a swarm optimization algorithm that mimics the attitude of birds flocking for flying. It has a stochastic search strategy that depends mainly on the global communications between the search agents, where all search agents modify their movement pointed to the global search agents that finds the global solution. Besides, it memorizes the best solutions each search agent pass through, which influences the new update of it as stated in Eq. (8), and this memorization of location enhances the exploitation phase of PSO.
The updating equations of PSO are represented as Eq. (8) and Eq. (9), where the particle (P) has the global best position (solution) among all search agents and the best personal position (P) that each search agents found during the previous iterations.
| (8) |
| (9) |
Where represents the velocity of the th particle, and are the local the global best position coefficient in order. w is the inertia coefficient that estimates the influence of the prior velocity on the new estimated velocity. rand () is a uniformly distributed random variable in the range [0–1].
PSO has a complexity of time where T, n, and express the number of iterations, the number of search agents, and the cost time of modifying the position of one search agent, respectively. PSO has a main advantage is the interchanging of information between search agents, which gives it more reliability to achieve an approximate optimal solution with acceptable convergence speed besides robustness.
PSO was used in many optimization problems such as solar cell design [46], [47], electrical motor design [48], and surgical robot applications [49].
3. Proposed IMO-PSO for FLAT
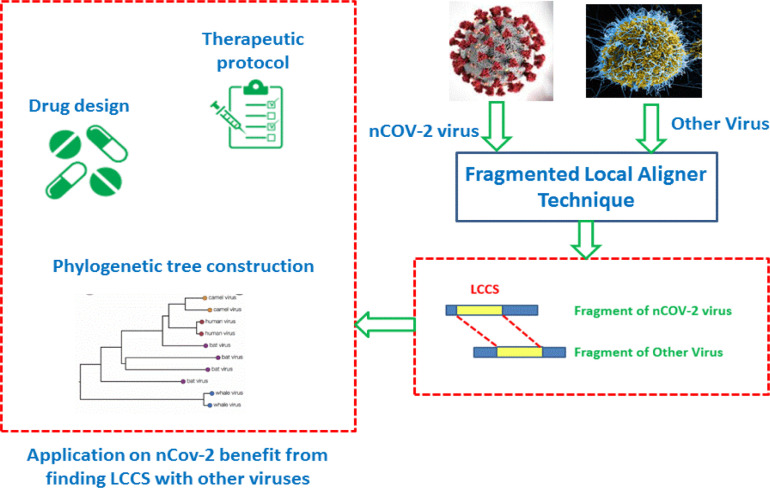
This section proposes the details of the proposed IMO-PSO algorithm for FLAT, which is described as a framework in Fig. 3, which describes the rule of using FLAT for aligning the COVID-19 virus against another virus to find LCCS between them. LCCS will be input for another biochemistry and biological operations on COVID-19 to aid in drug design of it, constructing its phylogenetic tree or updating therapeutic protocols.
Fig. 3.
A framework explaining the rule of using FLAT and the relation with other applications on COVID-19.
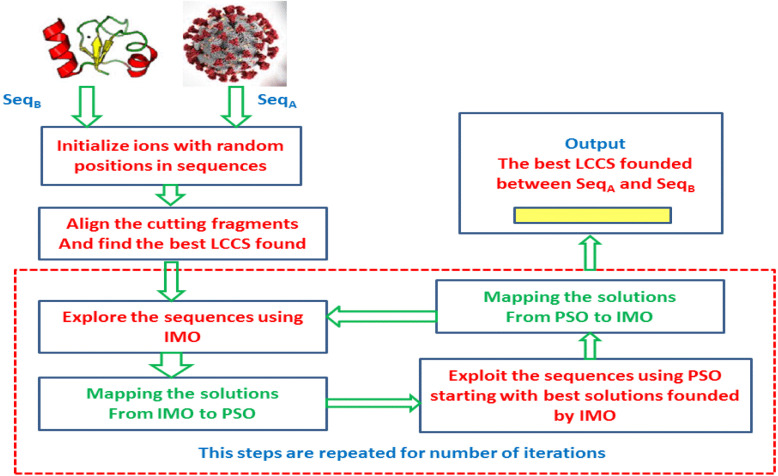
Fig. 4 shows the detailed procedure of the enhanced FLAT based on IMO-PSO. It accepts a pair of biological sequences (Proteins, DNA or RNA) as COVID-19 protein sequence (or any sequence) and any other virus sequence to be compared with where the output is the longest common consecutive subsequence (LCCS) between the two input sequences. The search agents of the improved IMO (IMO-PSO) represent the positions in the pair of sequences to cut fragments (a position in each sequence), and the cutting fragments by ions (search agents of IMO) are aligned using SW algorithm [17]. To determine the best anion and best cation, which represents the position of sequences at which the cutting fragments have the LCCS found. The fitness function that is used to measure the objective of solutions of search agents as expressed in Eq. (1), where it used to count the number of similar residues (character of sequences which represents amino acids).
Fig. 4.
Description of FLAT based on the improved IMO algorithm for aligning COVID-19 with other viruses.
FLAT processing finding the LCCS starting from the third step in a framework where the ions will be attracted to opposite best ion to move the positions toward the best positions founded in each sequence, and this step represents exploring the sequences by producing more diversifications of positions. The founded solutions (positions) due to exploration by IMO are mapped to the search agents of PSO to be intensified and find better LCCS around the founded one.
Since IMO can find part of the LCCS but PSO can enhance it by finding the remainder by searching around the founded one. The solutions founded by PSO mapped back to IMO to resume exploration, and the transition between IMO and PSO is executed for some iterations. Still, the main rule during the mapping is mapping the solutions if it provides better fitness.
The best LCCS that will be output is that of the best global search agent of PSO, which has the best global solutions over all iterations and overall search agents.
3.1. Implementation of the proposed model
In this section, the steps of the proposed COVID-19 model are discussed as in algorithm (2) that describes the details of FLAT based on the improved IMO (IMO-PSO) algorithm. The proposed model starts by accepting the pair of sequences to be aligned. Then initialize (n) ions of IMO (two groups of ions anion and cation, so the total number of ions is 2*n) with two positions (one position in each sequence) and the lower limit of solutions is 1 (the first residue of the sequence) while the upper limit is the end position of the sequence subtracted by the width of the fragment (L). These two positions represent the start of cutting fragments (one fragment in each sequence) to be aligned using the SW algorithm (in step 3). The next step is to align the two cutting fragments by anion or cation ions using the SW algorithm, and the similarity measurements of the LCCS founded are measured using Eq. (1) (In step 4).
Thereafter, the best cation and anion ions are updated from the cation and anion ions that produce the highest fitness (the longest common consecutive subsequence) (as in step 5). Next, updating the ions based on exploring the search space for some iteration (T). The cation and anion ions are updated based on the movement equations of IMO during liquid and solid-state if the condition satisfied (Step 6). The fragments in the two sequences are cut according to the updated positions toward the fragments have LCCS founded until this step, and the new LCCS are founded using the SW algorithm in step 7. The best cation and anion ions are updated in step 8.
Steps (9–10) represents the mapping of solutions for transition from IMO to PSO where solutions found by IMO are assigned to the search agents of PSO (y), the best personal solutions for each search agents (y) and the global best solutions among all search agents (y).
The global best solutions (y) are updated from the best anion (A) or best cation (C) if they provide better fitness (In step 10). As shown, IMO explore the search space and move the ions toward two best solutions, which lead to more diversity of solutions and exploring large search space hence the global best solutions (y) each iteration may locate the regions of best fitness. In step 11, the best personal solutions of each search agent (y) are updated from the corresponding anion ion (A) or cation ion (C) if they provide better fitness and the corresponding search agent (y) is assigned with the left choice.
Steps (11–14) are the procedure of updating equations of PSO for some iterations T. In step 11, the fragments are cut and aligned using the SW algorithm for each particle, and the fitness is evaluated based on Eq. (1). Steps 12–14 update the particle positions and best particle of PSO.
The exploited results found by PSO will return back to be assigned to the ions of IMO if they provide better fitness to resume exploring and exploitation of the search space for some iterations T. In steps (15–20), the mapping between PSO to IMO is performed as the anions search agents are assigned by the corresponding best personal solutions of each search agent (y). The cations are assigned with the solutions (y) of PSO, but these assignments are done if it provides better fitness. The best anion is assigned the global best solution (y), while cation is chosen from the cation ions that provide the minimum fitness. Note that, the solutions of PSO are assigned to cation ions since it will attract to the best anion (A) while anions which are assigned by corresponding (y) will be attracted to the best cation that is determined from the solutions of cations. The assignment mechanism will lead to more diversity of solutions to explore the search space.
The final output (best LCCS founded) is produced in step 19 where the positions stored in the best particle of PSO (y) represent the positions of the fragments that have the best LCCS founded in the overall length of aligned sequences. Therefore, the fragments are cut and aligned to find LCCS and calculate its width, which represents the output.
3.2. Complexity of IMO-PSO
IMO-PSO has a complexity of time is O (T * (T * N * (C + C))) where T and T are the number of iterations for each algorithm and the number of a total round of execution in order. N is the number of search agents, and C is the cost time of modifying the position of one ion of IMO, and C is the cost time of modifying the position of one search agent of PSO.
4. Experimental results and discussion
The experimental results of measuring the performance of FLAT based on the improved IMO algorithm against other algorithms in the literature work will be presented in this section. Two experimental tests are performed to evaluate the performance of FLAT based on the improved (IMO-PSO). The first test measure different metrics for the performance of FLAT, such as the quality of solutions represented as average LCCS founded, the success rate of finding 75% of real LCCS, and statistical analysis using the Wilcoxon test [50]. The second test for finding the LCCS for COVID-19 virus against the protein of other viruses using FLAT based on the improved IMO (IMO-PSO) relative to the real LCCS founded by the SW algorithm.
The performance of the IMO-PSO algorithm in the two tests is compared with standard IMO [27], SCA [19], ASCA-PSO [18], IMOG [32], and DIMO [35]. All the settings of parameters of algorithms as listed in Table 1. In this study, ASCA-PSO [18], SCA [19], IMOG [32], and [35] are used in our comparison.
The number of iterations was 30 iterations for all algorithms except IMO-PSO; the number of iteration for each algorithm was 10, and the two algorithms repeated 5 times. The fragment length was 30. The number of individual runs is 20; the number of search agents was assigned to the length of each sequence as listed in Table 2.
Table 2.
The percentage of LCCS founded by IMO-PSO versus other algorithms.
| m X n | Search Agent # |
SCA | ASCA-PSO | IMO | Improved IMO |
IMOG | DIMO |
|---|---|---|---|---|---|---|---|
| 250000 | 40 | 45 | 89 | 34 | 95 | 78 | 44 |
| 350000 | 40 | 45 | 78 | 34 | 95 | 75 | 28 |
| 550000 | 100 | 56 | 89 | 50 | 93 | 78 | 45 |
| 750000 | 120 | 50 | 84 | 50 | 94 | 73 | 23 |
| 1000000 | 150 | 50 | 89 | 60 | 95 | 79 | 23 |
| 1400000 | 180 | 56 | 89 | 56 | 92 | 77 | 56 |
| 1800000 | 200 | 50 | 78 | 50 | 93 | 63 | 28 |
| 2200000 | 240 | 56 | 80 | 45 | 91 | 67 | 39 |
| 2600000 | 400 | 56 | 78 | 39 | 93 | 62 | 28 |
| 3000000 | 400 | 56 | 84 | 39 | 92 | 60 | 67 |
| 4000000 | 450 | 56 | 89 | 50 | 95 | 62 | 50 |
| 5000000 | 450 | 56 | 78 | 45 | 94 | 62 | 45 |
| 6000000 | 450 | 47 | 73 | 56 | 93 | 50 | 34 |
| 7000000 | 500 | 39 | 78 | 28 | 92 | 45 | 39 |
| 8000000 | 700 | 45 | 84 | 39 | 94 | 45 | 34 |
| 9000000 | 700 | 42 | 84 | 28 | 94 | 30 | 34 |
Table 1.
The setting values for the parameters of MA used to implement FLAT.
| Algorithm | Parameter | Value |
|---|---|---|
| SW alignment | Match | +1.0 |
| −0.5 | ||
| −1.0 | ||
| SCA | a | 2.0 |
| IMO – PSO | Inertia Coefficient | 0.2 |
| Local coefficient (C1) | 0.5 | |
| Global coefficient (C2) | 0.5 | |
| ASCA-PSO | Inertia Coefficient | 0.2 |
| Local coefficient (C1) | 0.5 | |
| Global coefficient (C2) | 0.5 | |
| a | 2.0 | |
4.1. Measurement criteria
Various measurement criteria are used to evaluate the performance of FLAT are described in the following:
-
•
The average of LCCS: the average of the length of the common substring that is found for all runs of the algorithm and for each range of sequence product lengths.
-
•
The success of rate: It is the number of runs that found 75% of the real length of common subsequence (LCCS founded by the SW algorithm) divided by the total number of runs.
-
•
The execution time: it is the execution time of FLAT using different algorithms for each range of products of sequence lengths.
4.2. Experimental series 1: Evaluation performance of FLAT using the IMO-PSO algorithm on biological sequences datasets
4.2.1. Dataset description
For testing the performance of FLAT for measuring the percentage of LCCS founded relative to one founded by the SW algorithm, real biological protein sequences datasets that are used are gathered from GenBank of NCBI (https://www.ncbi.nlm.nih.gov/). FLAT has a pair of sequences as input, so each pair of gathered sequences have approximately equal lengths and have common consecutive subsequences founded by SW alignment algorithm. The sequences are divided at 16 ranges based on the product of pair sequence lengths, and the levels range from 250,000 to 9,000,000 to measure the performance over different lengths of sequences.
4.2.2. Results and discussion
Table 2 proposes the results of testing the average percentage of LCCS founded by FLAT based on the improved IMO (IMO-PSO) algorithm versus other algorithms relative to the real LCCS founded by the SW algorithm. In this test, each pair of sequences of the datasets are aligned using to measure the length of LCCS between it using the SW algorithm. Then the FLAT based on different metaheuristic algorithms is executed to measure the LCCS founded, and the percentage of it relative to the ones founded by the SW algorithm is presented in Table 2. Then the quality of solution criteria for FLAT is represented by what is the percentage of the length of real LCCS founded by any metaheuristic algorithm. In the first and second columns of Table 2 are the length of sequences product and the corresponding search agents (population) of each metaheuristic algorithm that was used. As the length of sequences increasing, the search space increasing hence the search of agents increasing to substitute the increasing of the span of search space.
IMO, SCA and DIMO have the same results approximately, and the lowest percentages LCCS founded in comparison with other algorithms. DIMO cannot produce an enhancement of IMO in FLAT that guarantee the theorem of NFL [28] where no algorithm cannot solve all engineering problem with the same efficiency. IMOG produces little enhancement of IMO for analyzing FLAT on biological sequences. ASCA-PSO algorithm was produced the highest percentage of LCCS using FLAT with an average percentage of 83% overall lengths; however, IMO-PSO has a percentage of 93.5%, which proves the superiority of IMO-PSO overall algorithms.
The efficiency of IMO-PSO is due to the balancing of exploration of IMO over the huge length of sequences and the exploitation of PSO to enhance the best results found in narrow regions, and the repetition of this process ensures the enhancement of best results founded.
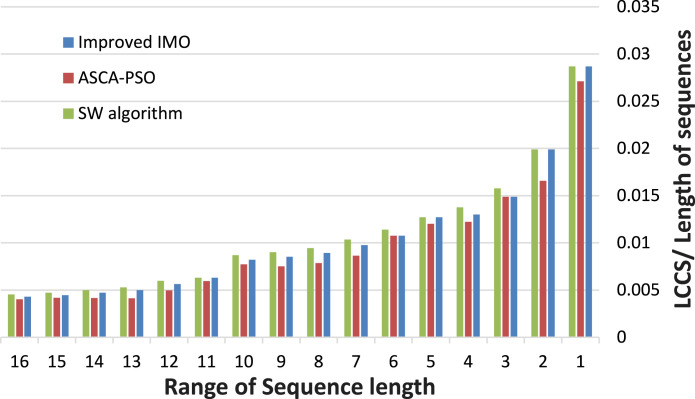
In Fig. 5, the quality of the solution is represented as the length of LCCS founded divided by the maximum length of the two aligned sequences. As shown, the results are produced by the improved IMO are better than those delivered by ASCA-PSO, which makes it clear the enhancement of performance of FLAT using the improved IMO.
Fig. 5.
Measuring of length of LCCS relative to the maximum length of the pair of sequences.
The second criterion was measured to guarantee the performance of IMO-PSO versus other algorithms is the success rate of finding LCCS but with at least 75% of the real LCCS founded by the SW algorithm. As shown in Table 3, SCA, IMO, and DIMO produced the lowest poor success rate with DIMO has zero values in some test which mean no one result of the 20 independent runs achieve 75% of the real length founded by SW algorithm. IMOG produces a success rate better than IMO but not efficient like ASCA-PSO. IMO-PSO produced the highest success rate versus all other algorithms, which implies the superiority of it.
Table 3.
The success rate of founding 75% of real LCCS by FLAT based on the improved IMO and the development versions of it.
| m X n | Search Agent # |
SCA | ASCA-PSO | IMO | Improved IMO |
IMOG | DIMO |
|---|---|---|---|---|---|---|---|
| 250000 | 40 | 14 | 90 | 20 | 100 | 70 | 10 |
| 350000 | 40 | 20 | 60 | 14 | 100 | 70 | 10 |
| 550000 | 100 | 27 | 87 | 34 | 100 | 50 | 30 |
| 750000 | 120 | 27 | 80 | 34 | 96 | 60 | 0 |
| 1000000 | 150 | 27 | 87 | 67 | 97 | 70 | 0 |
| 1400000 | 180 | 20 | 94 | 34 | 93 | 70 | 30 |
| 1800000 | 200 | 14 | 60 | 34 | 95 | 60 | 10 |
| 2200000 | 240 | 34 | 87 | 20 | 96 | 50 | 20 |
| 2600000 | 400 | 20 | 74 | 14 | 97 | 50 | 0 |
| 3000000 | 400 | 34 | 80 | 20 | 95 | 40 | 40 |
| 4000000 | 450 | 27 | 87 | 40 | 97 | 35 | 30 |
| 5000000 | 450 | 20 | 54 | 27 | 97 | 50 | 20 |
| 6000000 | 450 | 74 | 54 | 34 | 96 | 50 | 10 |
| 7000000 | 500 | 0 | 67 | 14 | 96 | 20 | 20 |
| 8000000 | 700 | 20 | 80 | 14 | 94 | 20 | 10 |
| 9000000 | 700 | 27 | 80 | 7 | 94 | 25 | 10 |
For the statistical analysis of the results, the Wilcoxon rank-sum test [50], (a non-parametric test detailing of t-test for two independent groups) was performed on the 20 independent runs of algorithms. Table 4 shows the results of the statistical analysis between standard IMO and each other algorithm. As shown, the -value of comparing IMO with IMO-PSO and ASCA-PSO has the best results over other algorithms (SCA, IMOG, and DIMO). Table 5 shows the execution time of FLAT based on the IMO-PSO algorithm versus IMO and other algorithms in the literature besides time executed by the SW algorithm. All experiments were performed on MATLAB software tool, and a computer machine has the following specifications: RAM with 4 GB and Intel Core I3 processor with 3.1 GHz each. Due to the huge time complexity of SW algorithms, the execution time has a huge increase with increasing the length of sequences. Hence, if there is a biological database that needs to be scanned, it will consume a huge time, especially if the databases contain thousands of biological sequences.
Table 4.
Wilcoxon test results (P-value < 0.05) for comparing IMO with other algorithms.
| m X n | SCA | ASCA-PSO | Improved IMO | IMOG | DIMO |
|---|---|---|---|---|---|
| 250000 | 0.043 | 5.25E−05 | 3.35E−05 | 0.580 | 0.531 |
| 350000 | 0.031 | 0.001 | 0.001 | 0.127 | 0.211 |
| 550000 | 0.464 | 0.006 | 0.005 | 0.027 | 0.736 |
| 750000 | 0.643 | 0.023 | 0.003 | 0.620 | 0.801 |
| 1000000 | 0.014 | 0.833 | 0.004 | 1 | 0.001 |
| 1400000 | 0.602 | 0.001 | 0.001 | 0.001 | 0.476 |
| 1800000 | 0.498 | 0.094 | 0.004 | 0.828 | 0.410 |
| 2200000 | 0.134 | 6.163E−05 | 3.97E−05 | 0.271 | 0.011 |
| 2600000 | 0.017 | 0.006 | 3.89e−05 | 0.354 | 0.789 |
| 3000000 | 0.009 | 5.48E−06 | 4.27E−06 | 0.792 | 0.080 |
| 4000000 | 0.316 | 0.015 | 0.001 | 0.118 | 0.202 |
| 5000000 | 0.031 | 0.006 | 0.006 | 0.629 | 0.434 |
| 6000000 | 0.119 | 0.193 | 0.005 | 0.096 | 0.267 |
| 7000000 | 0.002 | 8.64E−05 | 1.13E−05 | 6.95E−05 | 0.005 |
| 8000000 | 0.032 | 7.34E−05 | 3.82E−06 | 0.357 | 0.328 |
| 9000000 | 0.001 | 2.58E−05 | 1.62E−05 | 0.036 | 0.454 |
Table 5.
The execution time of SW local alignment algorithm versus FLAT using IMO-PSO and other algorithms.
| m X n | Search agent # |
SCA | ASCA-PSO | IMO | Improved IMO |
IMOG | DIMO |
|---|---|---|---|---|---|---|---|
| 250000 | 40 | 4.70 | 6.04 | 5 | 14 | 5 | 5 |
| 350000 | 40 | 4.70 | 6.04 | 5 | 13 | 5 | 5 |
| 550000 | 100 | 12.0 | 12.7 | 12 | 32 | 12 | 12 |
| 750000 | 120 | 14.3 | 14.9 | 15 | 32 | 14 | 14 |
| 1000000 | 150 | 18.8 | 18.9 | 22 | 48 | 21 | 23 |
| 1400000 | 180 | 21.7 | 21.7 | 22 | 54 | 21 | 22 |
| 1800000 | 200 | 25.0 | 26.0 | 24 | 59 | 23 | 26 |
| 2200000 | 240 | 29.0 | 30.2 | 48 | 113 | 49 | 55 |
| 2600000 | 400 | 49.2 | 51.2 | 48 | 112 | 47 | 46 |
| 3000000 | 400 | 49.2 | 51.2 | 53 | 139 | 52 | 51 |
| 4000000 | 450 | 53.9 | 55.9 | 53 | 141 | 52 | 50 |
| 5000000 | 450 | 53.9 | 55.9 | 54 | 139 | 52 | 51 |
| 6000000 | 450 | 53.9 | 55.9 | 54 | 139 | 52 | 51 |
| 7000000 | 500 | 67.0 | 69.8 | 59 | 140 | 64 | 57 |
| 8000000 | 700 | 78.9 | 83.7 | 77 | 208 | 75 | 88 |
| 9000000 | 700 | 78.9 | 83.7 | 77 | 202 | 75 | 107 |
Fig. 6 presents a comparison of the execution time of the SW algorithm, improved IMO, and ASCA-PSO for performing the alignment over various length products of pair of sequences and FLAT based on. As shown in the figure, FLAT save huge execution time in comparison with others but improved IMO consumes little time more ASCA-PSO for long sequences. The incensement comes from serial execution of IMO and PSO but provides better performance for finding LCCS approximately 93.5% of the real one, and this is the main advantage of improved IMO.
Fig. 6.
Comparison of time performance of the SW algorithm and FLAT based on improved optimization algorithms.
4.3. Experimental series 2: Finding LCCS between COVID-19 poly-protein and other viruses
FLAT was tested for finding the LCCS between the orf1ab poly-protein of COVID-19 and other viruses protein sequences such as Alveolar Proteinosis, Human Immunodeficiency, Hepatitis C, Influenza A, Influenza B, and Trachea Infections. The real LCCS that was founded by the SW algorithm is used as the reference to measure the FLAT performance.
4.3.1. Datasets description
The protein data of viruses were gathered from GenBank of NCBI (https://www.ncbi.nlm.nih.gov/). The protein ID of the virus was used in the test as follows: the orf1ab poly-protein of COVID-19 (Protein ID: YP_009724389.1), the surface glycoprotein of COVID-19 (ID: QJX59884.1), Alveolar Proteinosis (ID: Q8IWL2.2), Human Immunodeficiency (ID: AAB50262.1), Hepatitis C (ID: SLM22236.1), Influenza A (ID: YP_009118631.1), Influenza B (ID: BAA00002.1) and Trachea Infections (ID: Q460N5.3)
4.3.2. Results and discussion
Table 6 shows the result of finding LCCS between COVID-19 and other diseases using FLAT based on the improved IMO algorithm versus standard IMO, standard SCA, DIMO, IMOG, and ASCA-PSO algorithm besides, SW algorithm was used to find the real LCCS. The score column in the table represents the length of LCCS founded and also denotes the number of similar residues. As shown in Table 6, the IMO-PSO algorithm succeeded in locating the real LCCS but part of it in all tests; however, the ASCA-PSO algorithm locates it three times only. However, other algorithms cannot determine the real LCCS located by the SW algorithm; it finds common subsequences with small length.
Table 6.
Testing the Local aligner based Improved IMO for finding LCCS of COVID-19 orf1ab polyprotein against other diseases.
| Virus Protein Name | Method | Score | The obtained LCCS | |
|---|---|---|---|---|
| 1 | Alveolar Proteinosis | Smith–Waterman | 22 | IDAMMFTSDLATNNLVVMAYIT |
| SCA | 4 | LMAA | ||
| ASCA-PSO | 5 | MAYIT | ||
| IMO | 4 | GAVC | ||
| Improved IMO | 8 | IDAMMFTS | ||
| IMOG | 5 | VGGSC | ||
| DIMO | 3 | MLR | ||
| 2 | Human Immunodeficiency | Smith–Waterman | 24 | TYPSLETIQITSSFKWDLTAFGLV |
| SCA | 3 | PAG | ||
| ASCA-PSO | 5 | TYPSL | ||
| IMO | 3 | GAC | ||
| Improved IMO | 11 | TYPSLETIQIT | ||
| IMOG | 4 | FGLV | ||
| DIMO | 3 | LLS | ||
| 3 | Hepatitis C | Smith–Waterman | 10 | TSSGDATTAY |
| SCA | 4 | CARA | ||
| ASCA-PSO | 4 | VDIL | ||
| IMO | 3 | SLL | ||
| Improved IMO | 5 | TSSGD | ||
| IMOG | 4 | NGSI | ||
| DIMO | 3 | SLL | ||
| 4 | Influenza A | Smith–Waterman | 16 | TGSSKCVCSVIDLLLD |
| SCA | 4 | EELQ | ||
| ASCA-PSO | 4 | LLEM | ||
| IMO | 4 | SLVP | ||
| Improved IMO | 6 | TGSSKC | ||
| IMOG | 3 | LEM | ||
| DIMO | 3 | VLV | ||
| 5 | Influenza B | Smith–Waterman | 24 | FSTVFPPTSFGPLVRKIFVDGVPF |
| SCA | 5 | GRDGL | ||
| ASCA-PSO | 7 | FVDGVPF | ||
| IMO | 4 | KGRL | ||
| Improved IMO | 9 | FSTVFPPTS | ||
| IMOG | 5 | LSTFI | ||
| DIMO | 3 | LSL | ||
| 6 | Trachea Infections | Smith–Waterman | 19 | QQLRVESSSKLWAQCVQLH |
| SCA | 5 | VQLSL | ||
| ASCA-PSO | 5 | VQLSL | ||
| IMO | 3 | VPG | ||
| Improved IMO | 8 | QQLRVESS | ||
| IMOG | 4 | SFPL | ||
| DIMO | 4 | CYLA | ||
Table 7 shows the test results of using FLAT to analyze the surface glycoprotein of COVID-19 with other different surface glycoproteins with ID as in the table. Here, the pair of sequences have many common consecutive subsequences, and the LCCS has a length no more than 5 residues, so the challenge is finding the real LCCS from many ones common but with lower length. IMO-PSO algorithm succeeded in enhancing the performance of FLAT to locate the real LCCS as produced by the SW algorithm, and the ASCA-PSO algorithm locates it in most test cases.
Table 7.
Testing the Local aligner based Improved IMO for finding LCCS of the surface glycoprotein of COVID-19.
| Protein ID | Method | Score | The obtained LCCS | |
|---|---|---|---|---|
| 1 | A0A329S877 | Smith–Waterman | 5 | VIRGD |
| SCA | 3 | IAN | ||
| ASCA-PSO | 5 | KLIAN | ||
| IMO | 2 | IA | ||
| Improved IMO | 5 | VIRGD | ||
| IMOG | 2 | LL | ||
| DIMO | 2 | FLV | ||
| 2 | A0A178ALB2 | Smith–Waterman | 4 | EPLV |
| SCA | 3 | SSG | ||
| ASCA-PSO | 4 | GAGA | ||
| IMO | 3 | KGV | ||
| Improved IMO | 4 | GAGA | ||
| IMOG | 3 | PGQT | ||
| DIMO | 3 | KGV | ||
| 3 | A0A1B8CCB5 | Smith–Waterman | 4 | SANN |
| SCA | 3 | CCS | ||
| ASCA-PSO | 4 | SANN | ||
| IMO | 2 | SA | ||
| Improved IMO | 4 | SANN | ||
| IMOG | 4 | CCSA | ||
| DIMO | 4 | LS | ||
| 4 | ATZ77013.1 | Smith–Waterman | 4 | KIAD |
| SCA | 3 | AYT | ||
| ASCA-PSO | 4 | KIAD | ||
| IMO | 2 | NL | ||
| Improved IMO | 4 | AYTL | ||
| IMOG | 3 | LYR | ||
| DIMO | 2 | SQ | ||
| 5 | 2H2Z_A | Smith–Waterman | 5 | DLEGK |
| SCA | 3 | DLL | ||
| ASCA-PSO | 5 | DLEGK | ||
| IMO | 3 | NGL | ||
| Improved IMO | 5 | DLEGK | ||
| IMOG | 2 | ED | ||
| DIMO | 3 | FLV | ||
These tests show the superiority of the improved IMO algorithm to enhance FLAT and its ability in a biological application where COVID-19 was tested as a case study, and the application can be developed to not locate only one feature (LCCS) but more than ones. However, the idea is proposing the application of FLAT with efficient results in an acceptable time.
4.3.3. Advantages and limitation of FLAT based IMO-PSO algorithm
The main advantages of implementing FLAT based on the improved IMO (IMO-PSO) algorithm are listed as in the following
-
1.
The synergy between exploration of IMO and exploitation of PSO aids efficiently for solving the problems with huge search space such as FLAT.
-
2.
It produces a better quality of solutions by finding real LCCS with a percentage of 93.5% over various sequences lengths with the highest success of rate for finding 75% of the length of real LCCS in comparisons with other algorithms.
However, the limitation of FLAT based on the IMO-PSO algorithm is consuming more execution time more than that of other algorithms for aligning sequences with huge length since the serial execution of IMO and PSO algorithms. However, its execution time still reasonable in comparison with the time of the SW algorithm.
5. Conclusion and future work
This paper proposed enhancement for FLAT based on novel hybrid optimization of IMO and PSO algorithms. The key to hybridization is using the exploration of the IMO and then mapping solutions to PSO to exploit it and then mapping solutions to IMO, and this process is repeated for some iterations. To guarantee the efficiency of FLAT based on the IMO-PSO algorithm, it was tested to measure the LCCS between biological sequences gathered at various levels of lengths. The performance criteria are the average of LCCS found for 15 independent runs and the success rate for finding 75% of the real LCCS founded by the SW alignment algorithm. IMO-PSO algorithm has the superiority to find the average of LCCS with percent 93.5% on average of various lengths, and the following is the ASCA-PSO algorithm produces average LCCS with percent 83%. IMOG algorithm proposes little enhanced IMO but poor than the IMO-PSO algorithm. SCA, IMO, and DIMO produces a poor percentage of LCCS found. However, IMOG and DIMO succeeded in optimizing another engineering problem efficiently but cannot succeed in optimizing FLAT, which guarantees No Free Launch theorem. Besides, the IMO-PSO algorithm has the superiority with the highest success of rate for finding 75% of the length of LCCS founded by the SW algorithm overall lengths of sequences. For measuring the performance of IMO-PSO algorithm efficiency versus other algorithms for FLAT, it was used to analyze orflab polyprotein and surface glycoprotein of COVID-19 versus other diseases to finds the common features. IMO-PSO proves its superiority to locate the LCCS found by the SW algorithm in all cases of the test; however, ASCA-PSO algorithm success in most cases but not all, especially in sequences that have many common features with the same lengths. Therefore, this paper presents an enhanced version of FLAT based on a novel hybrid technique of IMO and PSO that produces alignment results with percent 93.5% of that one produced by SW alignment. But in a reasonable time that motivates biological researchers to use FLAT for primary scanning of the biological database to finds common features of COVID-19.
As future work, the percentage of LCCS founded by FLAT using IMO-PSO algorithm LCCS can be enhanced. Besides, the limitation of the execution time of it must be overcome, especially for sequences with more lengths, and a parallelized model of the IMO-PSO algorithm on GPU can be proposed.
CRediT authorship contribution statement
Mohamed Issa: Data curation, Software, Validation, Writing - original draft. Mohamed Abd Elaziz: Conceptualization, Software, Writing, Validation, Methodology, Software.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This work is supported by the China Postdoctoral Science Foundation under Grant No. 2019M652647.
References
- 1.Chen Y., Liu Q., Guo D. Emerging coronaviruses: genome structure, replication, and pathogenesis. J. Med. Virol. 2020;92(4):418–423. doi: 10.1002/jmv.25681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ge X.-Y. Isolation and characterization of a bat SARS-like coronavirus that uses the ACE2 receptor. Nature. 2013;503(7477):535–538. doi: 10.1038/nature12711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cauchemez S. Transmission scenarios for Middle East Respiratory Syndrome Coronavirus (MERS-CoV) and how to tell them apart. Euro Surveillance: Bull. Eur. Maladies Trans. Eur. commun. Dis. Bull. 2013;18(24) [PMC free article] [PubMed] [Google Scholar]
- 4.Guan W.-j. 2020. Clinical characteristics of 2019 novel coronavirus infection in China. MedRxiv. [Google Scholar]
- 5.Pendyala B., Patras A. 2020. In silico screening of food bioactive compounds to predict potential inhibitors of COVID-19 main protease (Mpro) and RNA-dependent RNA polymerase (RdRp) [Google Scholar]
- 6.F. Stancioiu, et al. A dissection of SARS-CoV2 with clinical implications, Int. J. Mol. Med. [DOI] [PMC free article] [PubMed]
- 7.Roda-Serrat M.C. Optimization of the recovery of anthocyanins from chokeberry juice pomace by homogenization in acidified water. Waste Biomass Valoriz. 2020:1–13. doi: 10.1007/s12649-020-01127-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sen Gupta P.S. Binding insight of clinically oriented drug famotidine with the identified potential target of SARS-CoV-2. J. Biomol. Struct. Dyn. 2020:1–7. doi: 10.1080/07391102.2020.1784795. [DOI] [PubMed] [Google Scholar]
- 9.Kong R. 2020. COVID-19 docking server: An interactive server for docking small molecules, peptides and antibodies against potential targets of COVID-19. arXiv preprint arXiv:2003.00163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.P.S.S. Gupta, et al. Binding Mechanism and Structural Insights into the Identified Protein Target of Covid-19 with In-Vitro Effective Drug Ivermectin. [DOI] [PMC free article] [PubMed]
- 11.Hamzah F.B. CoronaTracker: worldwide COVID-19 outbreak data analysis and prediction. Bull. World Health Organ. 2020;1:32. [Google Scholar]
- 12.Rahmatizadeh S., Valizadeh-Haghi S., Dabbagh A. The role of artificial intelligence in management of critical COVID-19 patients. J. Cell. Mol. Anesthesia. 2020;5(1):16–22. [Google Scholar]
- 13.Cohen J. Bioinformatics—an introduction for computer scientists. ACM Comput. Surv. 2004;36(2):122–158. [Google Scholar]
- 14.Di Francesco V., Garnier J., Munson P. Improving protein secondary structure prediction with aligned homologous sequences. Prot. Sci. 1996;5(1):106–113. doi: 10.1002/pro.5560050113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Feng D.-F., Doolittle R.F. [23] progressive alignment and phylogenetic tree construction of protein sequences. Methods Enzymol. 1990;183:375–387. doi: 10.1016/0076-6879(90)83025-5. [DOI] [PubMed] [Google Scholar]
- 16.L. Li, S. Khuri, A comparison of DNA fragment assembly algorithms, in: METMBS, 2004.
- 17.Smith T.F., Waterman M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981;147(1):195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- 18.Issa M. ASCA-PSO: Adaptive sine cosine optimization algorithm integrated with particle swarm for pairwise local sequence alignment. Expert Syst. Appl. 2018;99:56–70. [Google Scholar]
- 19.Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016;96:120–133. [Google Scholar]
- 20.Kennedy Particle swarm optimization. Neural Netw. 1995 [Google Scholar]
- 21.Moghdani R., Salimifard K. Volleyball premier league algorithm. Appl. Soft Comput. 2018;64:161–185. [Google Scholar]
- 22.Nematollahi A.F., Rahiminejad A., Vahidi B. A novel physical based meta-heuristic optimization method known as lightning attachment procedure optimization. Appl. Soft Comput. 2017;59:596–621. [Google Scholar]
- 23.Shareef H., Ibrahim A.A., Mutlag A.H. Lightning search algorithm. Appl. Soft Comput. 2015;36:315–333. [Google Scholar]
- 24.Rahmanzadeh S., Pishvaee M.S. Electron radar search algorithm: a novel developed meta-heuristic algorithm. Soft Comput. 2019:1–23. [Google Scholar]
- 25.Zou Y. The whirlpool algorithm based on physical phenomenon for solving optimization problems. Eng. Comput. 2019 [Google Scholar]
- 26.Jain M., Singh V., Rani A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019;44:148–175. [Google Scholar]
- 27.Javidy B., Hatamlou A., Mirjalili S. Ions motion algorithm for solving optimization problems. Appl. Soft Comput. 2015;32:72–79. [Google Scholar]
- 28.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1(1):67–82. [Google Scholar]
- 29.Das S., Bhattacharya A., Chakraborty A.K. Quasi-reflected ions motion optimization algorithm for short-term hydrothermal scheduling. Neural Comput. Appl. 2018;29(6):123–149. [Google Scholar]
- 30.Yang C.-H., Wu K.-C., Chuang L.-Y. Breast cancer risk prediction using ions motion optimization algorithm. J. Life Sci. Technol. 2016;4(2):49–55. [Google Scholar]
- 31.Mohapatra G., Debnath M.K., Mohapatra K.K. IMO Based novel adaptive dual-mode controller design for AGC investigation in different types of systems. Cogent Eng. 2020;7(1) [Google Scholar]
- 32.Yang C.-H. Protein folding prediction in the HP model using ions motion optimization with a greedy algorithm. BioData Min. 2018;11(1):17. doi: 10.1186/s13040-018-0176-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pan J.-S. International Conference on Engineering Research and Applications. Springer; 2018. A multi-objective ions motion optimization for robot path planning. [Google Scholar]
- 34.Hassan M., Yousif A. Cloud job scheduling with ions motion optimization algorithm. Eng. Technol. Appl. Sci. Res. 2020;10(2):5459–5465. [Google Scholar]
- 35.Pan J. Diversity enhanced ion motion optimization for localization in wireless sensor network. J. Inf. Hiding Multimedia Signal Process. 2019;10:221–229. [Google Scholar]
- 36.Kamboj V.K. A novel hybrid PSO–GWO approach for unit commitment problem. Neural Comput. Appl. 2016;27(6):1643–1655. [Google Scholar]
- 37.Zhang W.-J., Xie X.-F. SMC’03 Conference Proceedings. 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme-System Security and Assurance (Cat. No. 03CH37483) IEEE; 2003. DEPSO: hybrid particle swarm with differential evolution operator. [Google Scholar]
- 38.Shen Q., Shi W.-M., Kong W. Hybrid particle swarm optimization and tabu search approach for selecting genes for tumor classification using gene expression data. Comput. Biol. Chem. 2008;32(1):53–60. doi: 10.1016/j.compbiolchem.2007.10.001. [DOI] [PubMed] [Google Scholar]
- 39.Jiang S., Ji Z., Shen Y. A novel hybrid particle swarm optimization and gravitational search algorithm for solving economic emission load dispatch problems with various practical constraints. Int. J. Electr. Power Energy Syst. 2014;55:628–644. [Google Scholar]
- 40.Kaveh A., Bakhshpoori T., Afshari E. An efficient hybrid particle swarm and swallow swarm optimization algorithm. Comput. Struct. 2014;143:40–59. [Google Scholar]
- 41.Abd-Elazim S., Ali E. A hybrid particle swarm optimization and bacterial foraging for optimal power system stabilizers design. Int. J. Electr. Power Energy Syst. 2013;46:334–341. [Google Scholar]
- 42.Holden N., Freitas A.A. Proceedings 2005 IEEE Swarm Intelligence Symposium, 2005. SIS 2005. IEEE; 2005. A hybrid particle swarm/ant colony algorithm for the classification of hierarchical biological data. [Google Scholar]
- 43.Pan T.-S., Dao T.-K., Chu S.-C. Genetic and Evolutionary Computing. Springer; 2015. Hybrid particle swarm optimization with bat algorithm; pp. 37–47. [Google Scholar]
- 44.Garg H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016;274:292–305. [Google Scholar]
- 45.Silberberg M. McGraw-Hill Higher Education; 2012. Principles of General Chemistry. [Google Scholar]
- 46.Khanna V. Physics of Semiconductor Devices. Springer; 2014. Estimation of photovoltaic cells model parameters using particle swarm optimization; pp. 391–394. [Google Scholar]
- 47.Harrag A., Daili Y. Three-diodes PV model parameters extraction using PSO algorithm. Rev. Energies Renouvelables. 2019;22(1):85–91. [Google Scholar]
- 48.Hannan M. Optimization techniques to enhance the performance of induction motor drives: A review. Renew. Sustain. Energy Rev. 2017 [Google Scholar]
- 49.Wang W. A universal index and an improved PSO algorithm for optimal pose selection in kinematic calibration of a novel surgical robot. Robot. Comput.-Integr. Manuf. 2018;50:90–101. [Google Scholar]
- 50.Higgins J.J. 2003. Introduction to Modern Nonparametric Statistics. [Google Scholar]