The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018

Abstract

Global aviation operations contribute to anthropogenic climate change via a complex set of processes that lead to a net surface warming. Of importance are aviation emissions of carbon dioxide (CO₂), nitrogen oxides (NO_x), water vapor, soot and sulfate aerosols, and increased cloudiness due to contrail formation. Aviation grew strongly over the past decades (1960–2018) in terms of activity, with revenue passenger kilometers increasing from 109 to 8269 billion km yr⁻¹, and in terms of climate change impacts, with CO₂ emissions increasing by a factor of 6.8 to 1034 Tg CO₂ yr⁻¹. Over the period 2013–2018, the growth rates in both terms show a marked increase. Here, we present a new comprehensive and quantitative approach for evaluating aviation climate forcing terms. Both radiative forcing (RF) and effective radiative forcing (ERF) terms and their sums are calculated for the years 2000–2018. Contrail cirrus, consisting of linear contrails and the cirrus cloudiness arising from them, yields the largest positive net (warming) ERF term followed by CO₂ and NO_x emissions. The formation and emission of sulfate aerosol yields a negative (cooling) term. The mean contrail cirrus ERF/RF ratio of 0.42 indicates that contrail cirrus is less effective in surface warming than other terms. For 2018 the net aviation ERF is +100.9 milliwatts (mW) m⁻² (5–95% likelihood range of (55, 145)) with major contributions from contrail cirrus (57.4 mW m⁻²), CO₂ (34.3 mW m⁻²), and NO_x (17.5 mW m⁻²). Non-CO₂ terms sum to yield a net positive (warming) ERF that accounts for more than half (66%) of the aviation net ERF in 2018. Using normalization to aviation fuel use, the contribution of global aviation in 2011 was calculated to be 3.5 (4.0, 3.4) % of the net anthropogenic ERF of 2290 (1130, 3330) mW m⁻². Uncertainty distributions (5%, 95%) show that non-CO₂ forcing terms contribute about 8 times more than CO₂ to the uncertainty in the aviation net ERF in 2018. The best estimates of the ERFs from aviation aerosol-cloud interactions for soot and sulfate remain undetermined. CO₂-warming-equivalent emissions based on global warming potentials (GWP* method) indicate that aviation emissions are currently warming the climate at approximately three times the rate of that associated with aviation CO₂ emissions alone. CO₂ and NO_x aviation emissions and cloud effects remain a continued focus of anthropogenic climate change research and policy discussions.

Graphical abstract

Highlights

• •Global aviation warms Earth's surface through both CO₂ and net non-CO₂ contributions.
• •Global aviation contributes a few percent to anthropogenic radiative forcing.
• •Non-CO₂ impacts comprise about 2/3 of the net radiative forcing.
• •Comprehensive and quantitative calculations of aviation effects are presented.
• •Data are made available to analyze past, present and future aviation climate forcing.

1. Introduction

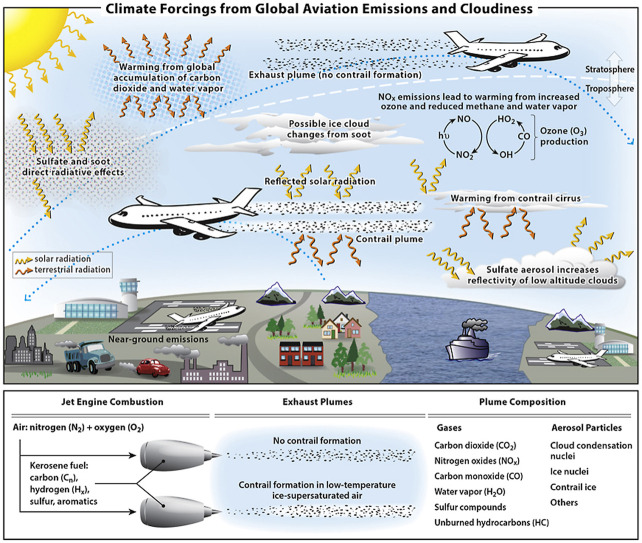
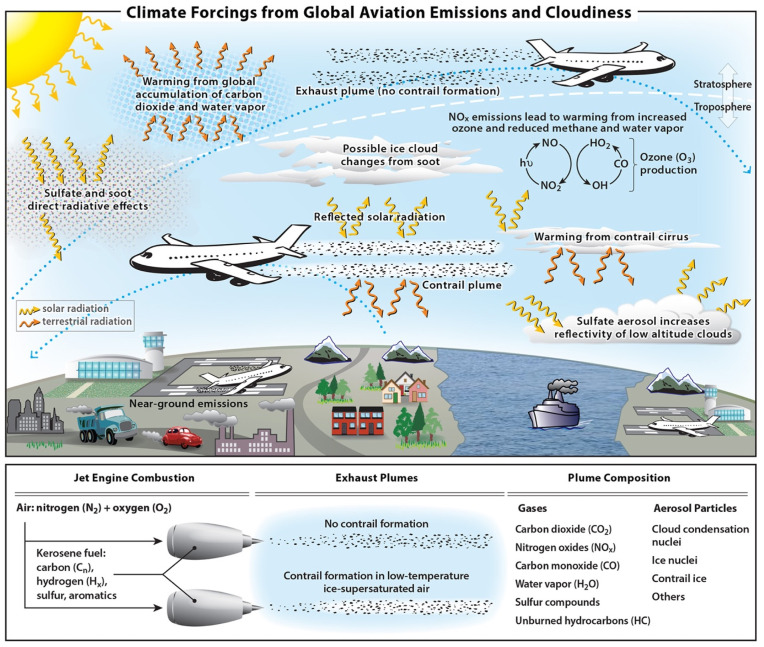
Aviation is one of the most important global economic activities in the modern world. Aviation emissions of CO₂ and non-CO₂ aviation effects result in changes to the climate system (Fig. 1 ). Both aviation CO₂ and the sum of quantified non-CO₂ contributions lead to surface warming. The largest contribution to anthropogenic climate change across all economic sectors comes from the increase in CO₂ concentration, which is the primary cause of observed global warming in recent decades (IPCC, 2013, 2018). Aviation contributions involve a range of atmospheric physical processes, including plume dynamics, chemical transformations, microphysics, radiation, and transport. Aggregating these processes to calculate changes in a greenhouse gas component or a cloud radiative effect is a complex challenge for contemporary atmospheric modeling systems. Given the dependence of aviation on burning fossil fuel, its significant CO₂ and non-CO₂ effects, and the projected fleet growth, it is vital to understand the scale of aviation's impact on present-day climate forcing.

Fig. 1.

Schematic overview of the processes by which aviation emissions and increased cirrus cloudiness affect the climate system. Net positive RF (warming) contributions arise from CO₂, water vapor, NO_x, and soot emissions, and from contrail cirrus (consisting of linear contrails and the cirrus cloudiness arising from them). Negative RF (cooling) contributions arise from sulfate aerosol production. Net warming from NO_x emissions is a sum over warming (short-term ozone increase) and cooling (decreases in methane and stratospheric water vapor, and a long-term decrease in ozone) terms. Net warming from contrail cirrus is a sum over the day/night cycle. These contributions involve a large number of chemical, microphysical, transport and, radiative processes in the global atmosphere. The quantitative ERF values associated with these processes are shown in Fig. 3 for 2018.

Historically, estimating aviation non-CO₂ effects has been particularly challenging. The primary (quantified) non-CO₂ effects result from the emissions of NO_x, along with water vapor and soot that can result in contrail formation. Aviation aerosols are small particles composed of soot (black and organic carbon (BC/OC)) and sulfur (S) and nitrogen (N) compounds. The largest positive (warming) climate forcings adding to that of CO₂ are those from contrail cirrus and from NO_x-driven changes in the chemical composition of the atmosphere (Lee et al., 2009). Lee et al. (2009) estimated that in 2005, aviation CO₂ radiative forcing (RF (Wm⁻²)) was 1.59% of total anthropogenic CO₂ RF and that the sum of aviation CO₂ and non-CO₂ effects contributed about 5% of the overall net anthropogenic forcing.

Understanding of aviation's impacts on the climate system has improved over the decade since the last comprehensive evaluation (Lee et al., 2009), but remains incomplete. Published studies of aviation contributions to climate change generally focus on one or a few ERF terms. For example, about 20 studies are cited here that quantify the contribution from global NO_x emissions. In contrast, only a few studies have addressed the net RF from global aviation (IPCC, 1999; Sausen et al., 2005; Lee et al., 2009). A more recent study updated some aviation terms without providing a net RF (Brasseur et al., 2016). Here, a comprehensive analysis of individual aviation ERFs is undertaken in order to provide an overall ERF for global aviation, along with the associated uncertainties, which is an analysis unavailable elsewhere. This step updates and improves the analysis of Lee et al. (2009). Best estimates of individual aviation ERF terms are derived here for the first time and combined to provide a net ERF for global aviation. Quantifying the terms required new analyses of CO₂ and NO_x ERFs and recalibration of other individual ERFs accounting for factors not previously applied in a common framework.

In Lee et al. (2009), the net RF was calculated with and without the full contrail cirrus term but including an estimate for linear contrails. The exclusion was based on the lack of a best estimate derived from existing studies. At that time radiative forcing estimates were limited to linear or line-shaped contrails since the modelling approaches required scaling contrail formation frequency to observed coverage and only satellite observations of linear contrails existed (Burkhardt et al., 2010). The contrail cirrus term requires the simulation of the whole contrail cirrus life cycle, starting from persistent linear contrails which spread and often become later indistinguishable from natural cirrus. Persistent contrail formation requires ice-supersaturated conditions along a flight track, which are variable in space and time in the troposphere and tropopause region (Irvine et al., 2013). Estimating the RF from contrail cirrus requires knowledge of complex microphysical processes, radiative transfer, and the interaction with background cloudiness (Burkhardt et al., 2010). Contrail cirrus forcing dominates that of persistent linear contrails with the latter on the order of 10% of the combined forcing (Burkhardt and Kärcher, 2011). In the present study, we present a best estimate and uncertainty based on the results from global climate models employing process-based contrail cirrus parameterizations.

Emissions of NO_x from aviation lead to photochemical changes that increase global ozone (O₃) formation while decreasing the lifetime and abundance of methane (CH₄). The changes result in positive and negative (cooling) RF contributions, respectively. Since Lee et al. (2009), improved understanding and modeling capabilities have emerged, as well as additional RF terms in response to NO_x emissions, namely a longer-term decrease in background O₃ and a reduction in H₂O in the stratosphere in response to decreased CH₄. Here, model results are used to calculate the additional RF terms, and to incorporate the updated CH₄ forcing as assessed by Etminan et al. (2016) and the equilibrium-to-transient corrections for the CH₄ term (see Appendix D). Finally, aviation-specific efficacies (Appendix C) of the individual NO_x components are used to estimate a net NO_x ERF for the first time.

Lee et al. (2009) includes best estimates for the RFs resulting from the aerosol-radiation interactions (previously called direct effects) of soot and sulfate aerosols from aviation. However, no best estimates of RFs from aerosol-cloud interactions (previously called indirect effects) were available in 2009. Subsequent studies discussed here have yet to provide a basis for best estimates of ERFs from aviation aerosol-cloud interactions that may be significant.

The primary motivations for the present study are to provide an updated, comprehensive evaluation of aviation climate forcings in terms of RF and ERF based on new calculations and the normalization of values from published modeling studies, and to combine the resulting best estimates via a Monte-Carlo analysis to yield a best estimate for the net ERF for global aviation for the years 2000–2018. The three years 2018, 2011, and 2005 are notable because the year 2018 is the latest year for which air traffic and fuel use datasets are available, 2011 is the most recent year evaluated for net anthropogenic climate forcing by the IPCC (IPCC, 2013), and 2005 is the year evaluated in the latest comprehensive aviation and climate evaluation (Lee et al., 2009). By normalizing the calculations across these years, more specific and self-consistent comparisons can be made of the changes in aviation contributions over time. The normalization step requires addressing in each study, for example, the choice of air traffic inventory, the integration of emissions along flight tracks, and the assumed jet-engine emission indices. The new best estimates of aviation ERF, for example, show that the 2018 value is about 48% larger than the updated 2005 value.

In general, previous global aviation climate assessments have made different assumptions concerning emissions, cloudiness effects, and aviation operations (e.g., IPCC, 1999). Here, our self-consistent set of component and net aviation ERFs for 2000 to 2018 allows historical and scenario projections of aviation climate impacts to be assessed in context with other sectors, such as maritime shipping, ground transportation and energy generation. This updated understanding is especially important given the potential role of international aviation in meeting the goals of the Paris Agreement (Section 2) on limiting future temperature increases.

The remaining sections address global aviation growth statistics (Section 2); a brief summary of methods used in the analysis (Section 3); results for the ERF estimates of CO₂, NO_x, water vapor, contrail cirrus, and aerosol-radiation and aerosol-cloud interactions with soot and sulfate (Section 4); results for the net ERF of global aviation (Section 5); emission metrics (Section 6); and aviation CO₂ vs non-CO₂ forcings (Section 7). The appendices contain additional detailed information on trends in aviation emissions (App. A); aviation CO₂ radiative forcing calculations (App. B); radiative forcing, efficacy and ERF definitions (App. C); aviation NO_x RF calculations (App. D); contrail cirrus RF scaling factors and uncertainty (App. E); and emission equivalency metric calculations (App. F). A Supplemental Data (SD) file is provided containing the interactive spreadsheet used to calculate RFs and ERFs for each aviation term.

2. Global aviation growth

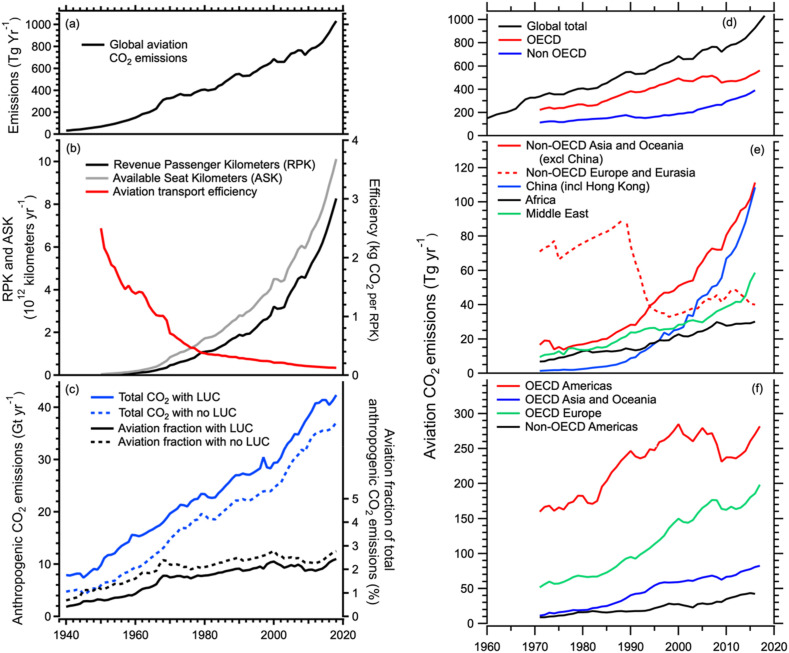
Global aviation fuel use and CO₂ emissions have increased in the last four decades with large growth occurring in Asia and other developing regions due to the rapid expansion of civil aviation (Fig. 2 and Appendix A). Looking forward, this pattern of growth is expected to be maintained—for example, of the 1229 orders of Airbus and 1031 orders of Boeing in 2017, 20.3% and 37.5%, respectively, are for airlines in the Asia region (Airbus, 2017; Boeing, 2018). Airbus projects 41% of orders over the next two decades to be from the Asia-Pacific region (Airbus, 2017). The uncertainty in this expectation has increased due to the slowdown in aviation operations in the early months of 2020 due to the COVID-19 pandemic (Le Quéré et al., 2020). Annual aviation emissions in 2020 are now expected to be below recent projections that are based on historical growth.

Fig. 2.

Data related to the growth of aviation traffic and CO₂ emissions from 1940 to 2018. Panel (a): Global aviation CO₂ emissions. Underlying fuel usage data for 1940 to 1970 are derived from Sausen and Schumann (2000) and for 1970–2016 from International Energy Agency (UKDS, 2016) data, which include international bunker fuels. For 2017/18, the values are scaled from information from the International Air Transport Association (see Appendix A). The average annual increase of global emissions from 1960 to 2018 is 15 Tg CO₂ yr⁻¹ and the corresponding decadal average growth rates are 8.0, 2.2, 3.0, 2.3 and 1.1% yr⁻¹, yielding an overall average of 3.3% yr⁻¹. Panel (b): Global aviation traffic in RPK and ASK from airlines.org (http://airlines.org/dataset/world-airlines-traffic-and-capacity/), and the transport efficiency of global aviation in kg CO₂ per RPK. The passenger load factor defined as RPK/ASK increased from about 60% in 1960 to 82% in 2018. Panel (c): Total anthropogenic CO₂ emissions and the aviation fractions of this total with and without the inclusion of CO₂ emissions from land use change (LUC) from the Global Carbon Budget 2018 (Le Quéré, 2018). Panel (d)–(f): Additional aviation emissions data by region and year. The yearly sums of OECD and non-OECD values in (d) equal the respective global total values. The regional values in (e) and (f) also sum to equal the yearly global total values. Note different vertical scales (http://www.oecd.org/about/membersandpartners/) (UKDS, 2016) (Country listings in SD Spreadsheet).

A striking feature of Fig. 2a is the sustained multi-decade growth in CO₂ emissions; the average rate for the period 1960–2018 is 15 Tg CO₂ yr⁻¹. The growth rate for 2013 through 2018 is much larger (44 Tg CO₂ yr⁻¹). The annually averaged growth rate over the period 1970 to 2012 is 2.2% yr⁻¹and for 2013 to 2018 is 5% yr⁻¹(increase of 27%). In 2018, global aviation CO₂ emissions exceeded 1000 million tonnes per year for the first time (see methodology for scaling 2016 IEA data in Appendix A). The cumulative emissions of global aviation (1940–2018) are 32.6 billion (10⁹) tonnes of CO₂, of which approximately 50% were emitted in the last 20 years. Current (2018) CO₂ emissions from aviation represent approximately 2.4% of anthropogenic emissions of CO₂ (including land use change) (Fig. 2c).

Aviation has grown strongly over time (Fig. 2b) in terms of available seat kilometers (ASK, a measure of capacity) and revenue passenger kilometers (RPK, a measure of transport work). Fuel usage and hence CO₂ emissions have grown at a lesser rate than RPK, reflecting increases in aircraft efficiency derived from changes in technology, larger average aircraft sizes and increased passenger load factor. Aviation transport efficiency has improved by approximately eightfold since 1960, to 125 gCO₂ (RPK)⁻¹.

At present and for some considerable time into the future, aviation growth is likely to be largely dependent upon the combustion of kerosene fossil fuel (Jet A-1/A) (OECD, 2012), resulting in emission of CO₂. Renewable biofuels partially offset fossil fuel emissions but these have yet to be produced in sufficient quantities to offset growth of fossil fuel use. Furthermore, considerable uncertainties remain regarding the life-cycle emissions of biofuels, which determine the reductions in net CO₂ emissions (e.g., Hari et al., 2015). There are current regulations regarding aviation emissions of CO₂, NO_x, and soot mass and number based on decisions by the International Civil Aviation Organization (ICAO). Under the 2016 Paris climate agreement, nations are committing to limiting future increases in global temperatures with Nationally Determined Contributions (NDCs) (UNFCCC). Whereas domestic aviation CO₂ emissions are included in the NDCs, CO₂ emissions from international aviation are not mentioned in the agreement. It remains open as to whether emissions from international aviation or global emissions beyond greenhouse gases (e.g., short-lived (non-CO₂) climate forcers) will be included in future international agreements.

3. Methods

The methodologies used to calculate ERF and RF for individual aviation terms are described in this section, and results of these calculations are given in Section 4. Common to the methodologies is a comprehensive multi-page spreadsheet (see SD) that begins with a user's guide. The spreadsheet pages include those for contrail cirrus, CO₂, NOx, H₂O, and sulfate and soot aerosol, along with CO₂-equivalent metrics, ERF probability distributions, ERF time series, and estimates of forcings from aerosol-cloud effects. The spreadsheet displays the results of aviation forcings provided by individual published studies. ERF and RF values were calculated for 2018 and other years based on the normalized values of ERF or RF per unit emission or distance, choice of appropriate emission indices, and times series data on fuel use and distance travelled. In the case of the contrail cirrus forcing, the flight-track distance was chosen as the proxy over fuel usage. Annual global emissions are derived from fuel burn by multiplying by the average emission indices (Table 1 ). The combined and normalized results are used to create sets of RF and ERF aviation terms for the years 2000–2018. In addition to facilitating the present study, the spreadsheet also provides a quantitative framework for follow-on analyses.

Table 1.

Emission indices used in ERF and RF calculations.

Emission	Emission index	Reference	Notes
CO2	3.16 kg/kg fuel	ICAO (2018)
NOx	15.14 g/kg fuel 14.12 g/kg fuel	Fleming and Ziegler (2016) Barrett et al. (2010)	2018, 2011 2005
Water vapor	1.231 kg/kg fuel	Barrett et al. (2010)
Soot	0.03 g/kg fuel 2 × 1014 particles/kg fuela	Barrett et al. (2010)
Sulfur (SO2)	1.2 g/kg fuel	Miller et al. (2010)	Assumed S content of 600 ppm

^aAssumes mean particle size in the range of 11–79 nm diameter.

Calculations of radiative forcing are expanded here beyond the approach in Lee et al. (2009) to include ERF values in addition to the traditional RF values (Table 2, Table 3 and Fig. 3 ). The distinction between ERF and RF is presented in Appendix C. ERF is the preferred metric for comparing the expected impacts of climate forcing terms (Myhre et al., 2013). Its use derives from the stronger correlation between ERF and the change in the equilibrium global-mean surface temperature for some forcing agents than for the corresponding RF. ERF is calculated as the change in net top-of-the-atmosphere (TOA) downward radiative flux after allowing for rapid adjustments in atmospheric temperatures, water vapor and clouds with globally-averaged sea surface and/or land surface temperatures unchanged. ERF is preferred over RF estimates because the imposed forcing and rapid responses to the forcing cannot always be separately evaluated, especially for aerosols. In general, the largest differences between ERF and RF are expected for aerosol-cloud interactions and contrail cirrus (Myhre et al., 2013; Boucher et al., 2013). In calculating ERF values for 2000–2018, the ERF/RF ratio is assumed to be constant with time.

Table 2.

Best estimates and high/low limits of the 90% likelihood ranges for aviation ERF components derived in this study.

ERF (mW m−2)	2018a	2011a	2005a	Sensitivity to emissions	ERF/RF
Contrail cirrus	57.4 (17, 98)	44.1 (13, 75)	34.8 (10, 59)	9.36 × 10−10 mW m−2 km−1	0.42
CO2	34.3 (28, 40)	29.0 (24, 34)	25.0 (21, 29)		1.0
Short-term O3 increase	49.3 (32, 76)	37.3 (24, 58)	33.0 (21, 51)	34.4 ± 9.9 mW m−2 (Tg (N) yr−1)−1	1.37
Long-term O3 decrease	−10.6 (−20, −7.4)	−7.9 (−15, −5.5)	−6.7 (−13, −4.7)	−9.3 ± 3.4 mW m−2 (Tg (N) yr−1)−1	1.18
CH4 decrease	−21.2 (−40, −15)	−15.8 (−30, −11)	−13.4 (−25, −9.4)	−18.7 ± 6.9 mW m−2 (Tg (N) yr−1)−1	1.18
Stratospheric water vapor decrease	−3.2 (−6.0, –2.2)	−2.4 (−4.4, −1.7)	−2.0 (−3.8, −1.4)	−2.8 ± 1.0 mW m−2 (Tg (N) yr−1)−1	1.18
Net NOx	17.5 (0.6, 29)	13.6 (0.9, 22)	12.9 (1.9, 20)	5.5 ± 8.1 mW m−2 (Tg (N) yr−1)−1
Stratospheric H2O increase	2.0 (0.8, 3.2)	1.5 (0.6, 2.4)	1.4 (0.6, 2.3)	0.0052 ± 0.0026 mW m−2 (Tg (H2O) yr−1)−1	–
Soot (aerosol-radiation)	0.94 (0.1, 4.0)	0.71 (0.1, 3.0)	0.67 (0.1, 2.8)	100.7 ± 165.5 mW m−2 (Tg (BC) yr−1)−1	–
Sulfate (aerosol-radiation)	−7.4 (−19, −2.6)	−5.6 (−14, −1.9)	−5.3 (−13, −1.8)	−19.9 ± 16.0 mW m−2 (Tg (SO2) yr−1)−1	–
Sulfate and soot (aerosol-cloud)	–	–	–	–	–
Net ERF (only non-CO2 terms)	66.6 (21, 111)	51.4 (16, 85)	41.9 (14, 69)	–	–
Net aviation ERF	100.9 (55, 145)	80.4 (45, 114)	66.9 (38, 95)	–	–
Net anthropogenic ERF in 2011	–	2290 (1130, 3330)b	–	–	–

^aThe uncertainty distributions for all forcing terms are lognormal except for CO₂ and contrail cirrus (normal) and Net NO_x (discrete pdf).

^bBoucher et al., 2013. IPCC also separately estimated the contrail cirrus term for 2011 as 50 (20, 150) mW m⁻².

Table 3.

Best estimates and low/high limits of the 95% likelihood ranges for aviation RF components derived in this study^a.

RF (mW m−2)	2018b	2011b	2005b	Lee et al. (2009) 2005 values	Sensitivity to emissions (this work)
Contrail cirrus	111.4 (33, 189)	85.6 (25, 146)	67.5 (20, 115)	(11.8c)	1.82 × 10−9 mW m−2 km−1
CO2	34.3 (31, 38)	29.0 (26, 32)	25.0 (23, 27)	28.0
Short-term O3 increase	36.0 (23, 56)	27.3 (17, 42)	24.0 (15, 37)	26.3	25.1 ± 7.3 mW m−2 (Tg (N) yr−1)−1
Long-term O3 decrease	−9.0 (−17, −6.3)	−6.7 (−13, −4.7)	−5.7 (−11, −4.0)	–	−7.9 ± 2.9 mW m−2 (Tg (N) yr−1)−1
CH4 decrease	−17.9 (−34, −13)	−13.4 (−25, −9.3)	−11.4 (−21, −7.9)	−12.5	−15.8 ± 5.9 mW m−2 (Tg (N) yr−1)−1
Stratospheric water vapor decrease	−2.7 (−5.0–1.9)	−2.0 (−3.8, −1.4)	−1.7 (−3.2, −1.2)	–	−2.4 ± 0.9 mW m−2 (Tg (N) yr−1)−1
Net NOx	8.2 (−4.8, 16)	6.5 (−3.3, 12)	6.6 (1.9, 12)	13.8d	1.0 ± 6.6 mW m−2 (Tg (N) yr−1)−1
Stratospheric H2O increase	2.0 (0.8, 3.2)	1.5 (0.6, 2.4)	1.4 (0.6, 2.3)	2.8	0.0052 ± 0.0026 mW m−2 (Tg (H2O) yr−1)−1
Soot (aerosol-radiation)	0.94 (0.1, 4.0)	0.71 (0.1, 3.0)	0.67 (0.1, 2.8)	3.4	100.7 ± 165.5 mW m−2 (Tg (BC) yr−1)−1
Sulfate (aerosol-radiation)	−7.4 (−19, −2.6)	−5.6 (−14, −1.9)	−5.3 (−13, −1.8)	−4.8	−19.9 ± 16.0 mW m−2 (Tg (SO2) yr−1)−1
Sulfate and soot (aerosol-cloud)	–	–	–	–	–
Net RF (only non-CO2 terms)	114.8 (35, 194)	88.4 (27, 149)	70.3 (22, 119)	–	–
Net aviation RF	149.1 (70, 229)	117.4 (56, 179)	95.2 (47, 144)	78.0	–

^aERF values are shown in Table 2.

^bThe uncertainty distributions for all forcing terms are lognormal except for CO₂ and contrail cirrus (normal) and Net NO_x (discrete pdf).

^cLinear contrails only; excludes the increase in cirrus cloudiness due to aged spreading contrails.

^dExcludes updated CH₄ RF evaluation of Etminan et al. (2016) and equilibrium-to-transient correction.

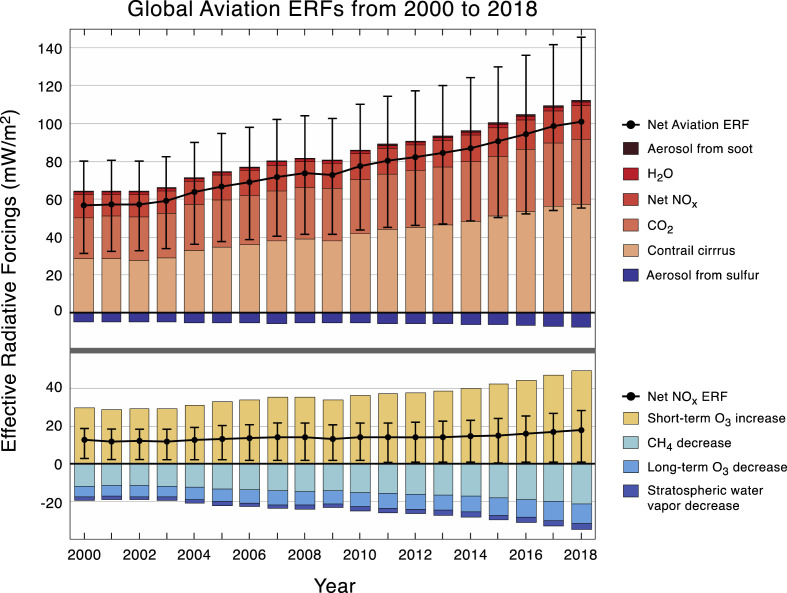
Fig. 3.

Best-estimates for climate forcing terms from global aviation from 1940 to 2018. The bars and whiskers show ERF best estimates and the 5–95% confidence intervals, respectively. Red bars indicate warming terms and blue bars indicate cooling terms. Numerical ERF and RF values are given in the columns with 5–95% confidence intervals along with ERF/RF ratios and confidence levels. ERF and RF values are shown for other years in Table 2, Table 3, Fig. 6 and the SD spreadsheet. RF values are multiplied by the respective ERF/RF ratio to yield ERF values. ERF/RF values designated as [1] indicate that no estimate is available yet. The basis for confidence levels is presented in Table 4b, Table 4a.

Most of the results for the non-CO₂ terms have associated statistics from which the median was chosen as the best estimate, including the net aviation ERF and RF, and the net non-CO₂ ERF and RF. For CO₂ and contrail cirrus, for which the sample sizes are small (3, in both cases), the mean was used as the best estimate. The best estimates of the non-CO₂ terms except contrail cirrus have associated uncertainties expressed as 5% and 95% confidence intervals calculated from 5, 95% percentile statistics. The uncertainty distributions for all forcing terms other than CO₂ and contrail cirrus are lognormal and that for net NO_x has a discrete probability distribution function (PDF). The uncertainties for the ERF and RF of CO₂ were taken from IPCC (2013) and fitted with a Monte Carlo analysis with a normal distribution (see Section 5). The uncertainties for contrail cirrus were estimated partly from expert judgement of the underlying processes, as described in Appendix E, again fitted with a Monte Carlo analysis with a normal distribution.

4. Calculations of ERFs for aviation terms

4.1. CO₂

The time series of aviation CO₂ emissions is shown in Fig. 2 as derived from combined kerosene and avgas usage (UKDS, 2016). Calculating CO₂ concentrations from emissions requires use of a global carbon-cycle model, which has a range of complexity from a comprehensive Earth system model (ESM) to a simple climate model (SCM), with the latter being based on a box model or impulse response function (IRF) model. Three SCMs were used here: LinClim, an IRF model based on Sausen and Schumann (2000) (Appendix B); the Finite-amplitude Impulse Response (FaIR) model (Millar et al., 2017); and the CICERO-SCM (Fuglestvedt and Berntsen, 1999; Skeie et al., 2017). The performance of LinClim and CICERO-SCM with respect to aviation emissions is documented in the multi-model comparison of Khodayari et al. (2013). The CO₂ concentrations attributable to aviation in 2018 based on LinClim, CICERO-SCM and FaIR are 2.9, 2.4 and 2.4 ppm, respectively, with concentrations nearly doubling in the last 20 years (see SD spreadsheet). The ERF/RF ratio for CO₂ is assumed to be unity. The resulting CO₂ ERFs, as derived from global concentrations using standard IPCC expressions (IPCC, 2001), are 38.6, 32.0 and 32.4 mW m⁻², respectively. With only three model estimates, the average of 34.3 mW m⁻² (5 and 95% percentiles of 29 and 40 mW m⁻²), is chosen be the CO₂ RF best estimate.

4.2. NO_x

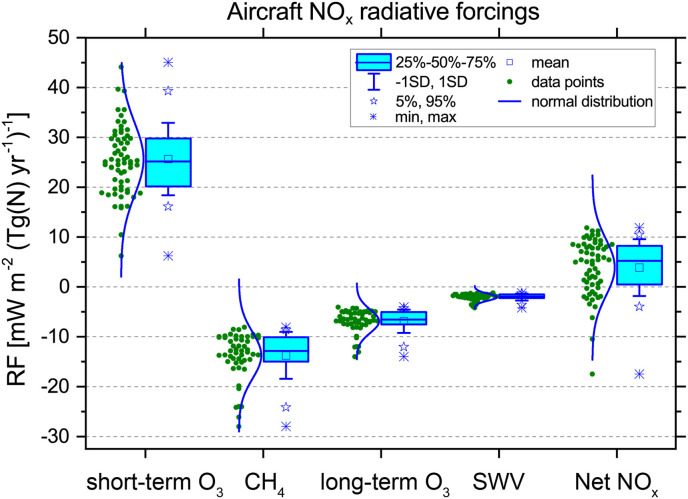
The photochemical effects of aviation NO_x emissions on the atmospheric abundances of O₃, CH₄, carbon monoxide (CO) and reactive hydrogen (HO_x) are well established (Fuglestvedt et al., 1999). Earlier studies assessed the short-term increase of O₃ and the longer-term reduction in CH₄ lifetime and abundance, which yield positive and negative RFs, respectively (IPCC, 1999; Sausen et al., 2005). Lee et al. (2009) introduced the concept of the ‘net NO_x’ effect by combining the two components, extending and updating the study of Sausen et al. (2005). Later studies expanded the analysis of NO_x effects to include the long-term decreases in both O₃ and stratospheric water vapor (SWV) resulting from the CH₄ reduction. Both effects yield negative RFs (Holmes et al., 2011; Myhre et al., 2011). In the present study, an ensemble of 20 NO_x studies is assessed to provide NO_x forcing best estimates based on a wide range of global atmospheric chemistry/climate models and a broad range of present-day aviation emission inventories (details in Appendix D and SD spreadsheet). Results from 6 of the studies were adopted from Holmes et al. (2011).

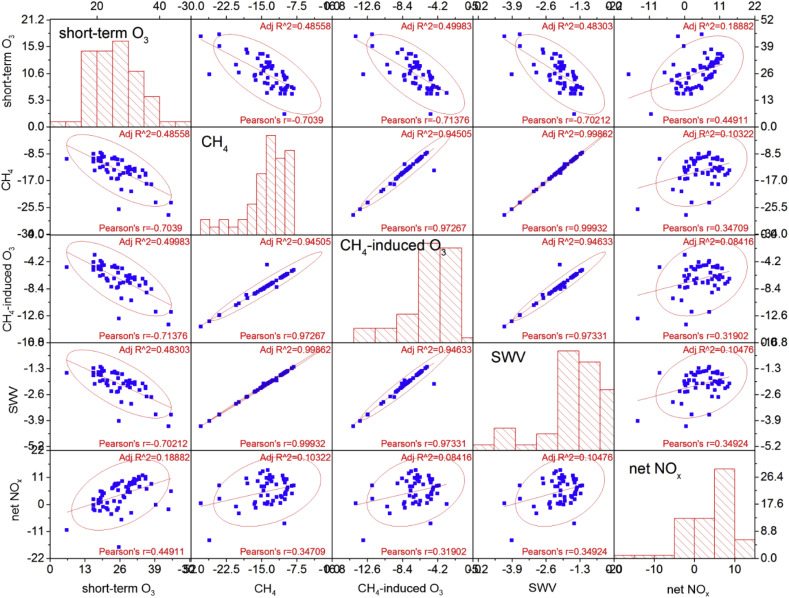
The study ensemble represents various model methodologies in calculating and treating both the short-term and the long-term NO_x components. In order to avoid gaps and additional uncertainties, standardized ERFs were developed that estimated disparate elements (e.g., CH₄ mediated decreases in SWV and long-term O₃). Moreover, most of the studies were based upon a parameterization of the CH₄ response that assumed a full equilibrium response. In order to calculate the transient response for a specific year more accurately, a correction factor is needed (Myhre et al., 2011). Here, the CH₄ responses for individual years were calculated (see Appendix D) using the difference between two simulations with differing aviation NO_x emissions. A number of transient and equilibrium simulations were conducted with a 2D chemical-transport model to find that the requirement for a correction factor is well supported and that the 2018 value is 0.79 (see Transient vs. equilibrium in Appendix D and Appendix Table D.2). In addition, a scaling factor (1.23) is applied to derived CH₄ ERF numbers to account for the effect of shortwave CH₄ forcing, following Etminan et al. (2016) (see Appendix D). The existence and nature of correlations between the NO_x RF components were also explored (see Correlations in Appendix D and Appendix Fig. D.1) since the degree of correlation between short-term O₃ and CH₄ terms was a source of uncertainty in the calculation of the net-NO_x forcing in Lee et al. (2009). The work of Holmes et al. (2011) supports the prior assumption of correlation, which is greatly expanded here. Regardless of inter-model differences, significant correlations are observed; for example, a significant negative correlation (p = −0.7) exists between the short-term and the long-term NO_x RF components.

The normalized sensitivity results for net NO_x in units of mW m⁻² (Tg (N) yr⁻¹)⁻¹ for the individual modeling studies are shown in Fig. 4 along with statistical parameters (see Ensemble values in Appendix D). Given the diversity of studies conducted over nearly two decades, the standard deviations of the distributions are reasonably small. In contrast, the sign of the net-NO_x RF obtained from summing over the 4 component values varies from positive to negative. The spread in NO_x RF values is caused by various factors (e.g., emissions inventories, experimental design or inter-model differences) and is particularly sensitive to the NO_x distribution in the model background troposphere (Holmes et al., 2011). The NO_x efficacies are 1.37 for the short-term ozone increases and 1.18 for methane decreases (Ponater et al., 2006). The efficacies do not equal the ERF/RF ratios, in general (Ponater et al., 2020; Appendix C); nonetheless, in the present study, we assume the efficacies and the ERF/RF ratios are equal, in the absence of better information. The factor of 1.18 was similarly adopted for the CH₄-mediated decreases in long-term ozone and SWV. It is noted that these ratios are from one study and that, in general, the ratio of ERF to RF for CH₄ and tropospheric O₃ are currently the subject of some debate (Smith et al., 2018; Xie et al., 2016; Richardson et al., 2019). Given the strength of the net effect of the ERF adjustment on the net NO_x forcing (more than doubling over its stratosphere-adjusted RF), these ratios warrant further study.

Fig. 4.

Results from an ensemble of 18 models from 20 studies for aviation NO_x impacts: short-term O₃ increases; CH₄ reductions, CH₄-induced long-term reductions of O₃, CH₄-induced reductions of stratospheric water vapor (SWV) and Net NO_x. Each data point represents a value of RF per unit emission (mW m⁻² (Tg N yr⁻¹)⁻¹) as normalized from a published study (see SD). CH₄-induced O₃ and SWV are calculated using standardized methodology (see text for details). Note that the displayed values do not include correction factors to account for the non-steady-state CH₄ responses to NO_x emissions and the new CH₄ RF parameterization. These adjustments are applied in forming the best estimates as discussed in Appendix D.

The net-NO_x ERF sensitivity of 5.5 ± 8.1 mW m⁻² (Tg (N) yr⁻¹) ⁻¹ yields a 2018 best estimate of 17.5 (0.6, 28.5) mW m⁻². This best estimate includes the correction factor for non-steady state conditions as well as the revised formulation of CH₄ RF (Appendix D).

Other potential short-term effects from NO_x emissions involve the direct formation of nitrate aerosol and indirect enhancement of sulfate aerosol. These effects, addressed in a few modelling studies, are associated with large uncertainties (Righi et al., 2013; Pitari et al., 2017; Unger, 2011). The effects of NO_x on aerosol abundances are not further considered here owing to the limited number of studies and the large associated uncertainties.

4.3. Water vapor emissions

A large fraction of annual aircraft emissions from the global fleet occurs in the stratosphere, primarily in the northern hemisphere (Forster et al., 2003). The accumulation of water vapor emissions perturbs the low background humidity in the lower stratosphere and changes the water vapor radiative balance. Calculating the water vapor RF is complicated by the sensitivity to the vertical and horizontal distribution of emissions, seasonal changes in tropopause heights, and short stratospheric residence times. Some earlier studies do not include the water vapor effect.

The water vapor effects were explored in detail (see SD) using results from nine studies: IPCC (1999), Marquart et al., (2001), Gauss et al. (2003), Ponater et al. (2006), Frömming et al. (2012), Wilcox et al. (2012), Lim et al. (2015), Pitari et al. (2015) and Brasseur et al. (2016). The reported RFs from these studies vary from 0.4 mW m⁻² (Wilcox et al., 2012) through 1.5 mW m⁻² (Frömming et al., 2012; Lim et al., 2015) to 3.0 mW m⁻² (IPCC, 1999). The differences are attributed to the different transport models used, with some contribution from the different meteorologies in different studies. Normalizing to the same emissions and averaging these reported estimates yields a water vapor sensitivity of 0.0052 ± 0.0026 mW m⁻² (Tg (H₂O) yr⁻¹)⁻¹. Scaling this value linearly to emissions of 382 Tg H₂O yields an ERF best estimate of 2.0 (0.8, 3.2) mW m⁻² for 2018, which is well within the uncertainty range of the 2005 Lee et al. (2009) value of 2.8 (0.39, 20.3) mW m⁻². The ERF/RF ratio for stratospheric water increases is assumed to be unity. We have greater confidence in the new estimate and its smaller uncertainty since it is based on detailed physical studies, rather than a scaling of the earlier IPCC (1999) estimate. The new best estimate is also in good agreement with the earlier results of Gauss et al. (2003) and Ponater et al. (2006), after scaling their results to account for emissions differences.

4.4. Contrail cirrus

The aviation fleet increases global cloudiness through the formation of persistent contrails when the ambient atmosphere is supersaturated with respect to ice (IPCC, 1999). Contrail cirrus, consisting of linear contrails and the cirrus cloudiness arising from them, have cooling (short-wave) and warming (long-wave) effects, with the effect at night being exclusively warming. In past assessments (e.g., IPCC, 1999; Lee et al., 2009), a best estimate was only available for the RF of linear persistent contrails, in part because of the difficulty of quantifying the cloudiness contribution of aging and spreading contrails (Minnis et al., 2013). The ERF of contrail cirrus was estimated for 2011 as 50 (20, 150) mW m⁻² by Boucher et al. (2013). Results of a recent assessment of contrail cirrus and other aviation effects are included here, although the study did not propose new best estimates (Brasseur et al., 2016).

A persistent contrail requires ice-supersaturated conditions along the flight track. Contrail cirrus life cycles are dependent on the temporal and spatial scales of the ice supersaturated areas, which are highly variable in the troposphere and tropopause region (e.g., Lamquin et al., 2012; Irvine et al., 2013; Bier et al., 2017). Estimating the impact of contrail cirrus on upper tropospheric cloudiness requires the simulation of complex microphysical processes, contrail spreading, overlap with natural clouds, radiative transfer, and the interaction with background cloudiness (Burkhardt et al., 2010). We present new best estimates based on the results of global climate models employing process-based contrail cirrus parameterizations (Appendix E). Due to the small number of independent estimates the uncertainty must be estimated from the sensitivities of the respective processes and the uncertainty in the underlying parameters and fields.

Here, we consider RF and ERF estimates from global climate models (Burkhardt and Kärcher, 2011; Bock and Burkhardt, 2016; Chen and Gettelman, 2013; Schumann et al., 2015; Bickel et al., 2020) to ultimately produce an ERF best estimate. For the present study, the Chen and Gettelman study was repeated with lower prescribed initial ice-crystal diameters, thereby bringing assumptions in line with measurements e.g., Schumann et al. (2017). Since the RF estimates differ regarding the air traffic inventory, the measure of air traffic distance (i.e., taking only surface-projected or overall flight distances into account) and the temporal resolution of the air traffic data, the estimates were homogenized using known sensitivities (Bock and Burkhardt, 2016) (see Appendix E). Furthermore, the estimates were corrected to account for the underestimation of the contrail cirrus RF, as calculated by climate models that use frequency bands, relative to more detailed line-by-line radiative transfer calculations (Myhre et al., 2009). The Chen and Gettelman (2013) study is closer to a calculation of an ERF, since it accounts for fast feedbacks on natural clouds, which Bickel et al. (2020) show in their model explains most of the differences between an ERF and an RF calculation. Bickel et al. (2020) presents an explicit calculation of the contrail cirrus ERF and uses the same basic model formulation of Bock and Burkhardt, so the ERF calculation was not used here directly but rather the estimation of the ERF/RF ratio was used.

The RF best estimate for 2011 was calculated here for comparison to the most recent IPCC estimate (Boucher et al., 2013). With each study weighted equally, the resulting 2011 RF best estimate for contrail cirrus (excluding any adjustments) is approximately 86 (25, 146) mW m⁻² (see Table 3). The IPCC best estimate of 50 (20, 150) mW m⁻² (including the natural cloud feedback) was derived from scaling and averaging two studies. IPCC assigned a large uncertainty and low confidence to reflect important aspects with incomplete knowledge (e.g., spreading rate, optical depth, and radiative transfer). The RF best estimate derived here for 2018 is 111 (33, 189) mW m⁻². The uncertainties in the present study are reduced due to the development of process-based approaches simulating contrail cirrus in recent years. The uncertainty in the new RF estimate, excluding the uncertainty in the ERF/RF scaling of individual RF values, is ±70%, a value substantially lower than the factor of three stated in IPCC.

The ±70% uncertainty was derived differently than for the NO_x forcing due to the smaller number of available studies. Instead, the uncertainty was derived from the combined uncertainties associated with the processes involved (see Appendix E). The processes fall into two groups: those connected with the upper tropospheric water budget and the contrail cirrus scheme itself, and those associated with the change in radiative transfer due to the presence of contrail cirrus. We considered uncertainty in upper tropospheric ice-supersaturation frequencies and their simulation in global models and the uncertainty of ice-crystal numbers due to uncertainty in soot-number emissions, ice nucleation within the plume, and loss processes in the contrail's vortex phase. Finally, an important uncertainty comes from the adjustment of natural clouds (Burkhardt and Kärcher, 2011). There is also a small uncertainty associated with the contrail cirrus life cycle, which affects the difference in nighttime and daytime contrail cirrus cover (Stuber et al., 2006) based on work analyzing the diurnal cycle (Chen and Gettelman, 2013; Newinger and Burkhardt, 2012).

Uncertainty connected with the radiative response to contrail cirrus is largely due to the differences in the radiation schemes across climate models and the approximations made therein (Myhre et al., 2009; Gounou and Hogan, 2007); the background cloud field and its vertical overlap with contrail cirrus; and assumptions about the homogeneity of the contrail cirrus field. Furthermore, the presence of very small ice crystals (<5 μm) (Bock and Burkhardt, 2016) and unknown ice-crystal habits (Markowicz and Witek, 2011) add to the uncertainty.

Our best estimate of the contrail cirrus uncertainty does not include the impact of contrails forming within natural clouds, which was recently shown to be observable from space (Tesche et al., 2016), or the change in radiative transfer due to soot cores in contrail cirrus ice crystals (Liou et al., 2013), which decreases the albedo at solar wavelengths and increases the top of atmosphere net RF. Both effects are very likely to lead on average to an increase in contrail cirrus RF, causing our best estimate to be conservative. The estimated uncertainty relates to the average contrail cirrus RF. In specific synoptic situations, uncertainties may be much larger and correlated with each other.

In contrast to other aviation forcing terms, the average ERF/RF ratio for contrail cirrus is estimated to be 0.42, much less than unity. The associated uncertainty is thought to be very large and dependent on prevailing aviation traffic and its geographic distribution. The low ERF/RF value is largely due to the reduction in natural cloudiness caused by increased contrail cirrus similar to the reduction in natural cirrus cloudiness as reported by Burkhardt and Kärcher (2011). The ERF/RF value is the average of three global climate model studies: two that estimated climate efficacies of 31% and 59% (Ponater et al., 2005; Rap et al., 2010) and a third that gave a direct estimate of the ERF of contrail cirrus that is 35% of the corresponding RF (Bickel et al., 2020). These studies conclude that efficacies equal to that of CO₂ overstate the role of cirrus changes due to aviation on global mean surface temperatures. The average ERF/RF ratio was applied to the homogenized estimates of RF, while the RF of Chen and Gettelman (2013) was interpreted as an ERF (see above). Weighting each study equally, the resulting ERF for contrail cirrus is 57 (17, 98) mW m⁻² for 2018. It is important to note that the uncertainty does not include any contribution coming from the ERF/RF estimate. Despite the large ERF/RF adjustment, this ERF term is the largest for global aviation in 2018 and is comparable in magnitude to the CO₂ term in the normalized results for 2000 to 2018 (Fig. 6 ). While comparable in magnitude, these ERFs have different implications for future climate change (Section 6).

Fig. 6.

Timeseries of calculated ERF values and confidence intervals for annual aviation forcing terms from 2000 to 2018. The top panel shows all ERF terms and the bottom panel shows only the NO_x terms and net NO_x ERF. All values are available in the SD spreadsheet, in Table 2, Table 3, and in Fig. 3 for 2018 values. The net values are not arithmetic sums of the annual values because the net ERF, as shown in Fig. 3 for 2018, requires a Monte Carlo analysis that properly includes uncertainty distributions and correlations (see text).

4.5. Aerosol-radiation interaction

Aircraft engines directly emit soot, defined as mixture of BC and OC, and precursors for sulfate ($\text{S}{\text{O}}_4^{2-}$) and nitrate ($\text{N}{\text{O}}_3^{-}$) aerosol along flight tracks. Soot aerosol is formed from the condensation of unburnt aromatic compounds in the combustor (e.g. Ebbinghaus and Wiesen, 2001) and sulfate aerosol from the oxidation of sulfur in the fuel (Dstan 91-91, 2015). Most of the sulfur is emitted as SO₂, whilst a small fraction (~3%) is emitted as oxidized H₂SO₄ (Petzold et al., 2005). Most of the sulfate aerosol is produced after emission from sulfur precursor compounds by oxidation in the ambient atmosphere. Both aerosol types create RFs from aerosol-radiation interactions: soot absorbs short-wave radiation leading to net warming and sulfate aerosol scatters incoming short-wave radiation leading to net cooling (IPCC, 1999). As figures of merit, year 2000 global aviation emissions increase aerosol mass for both soot and sulfate by a few percent and aerosol number by 10–30% near air traffic flight corridors in the northern extratropics (Righi et al., 2013).

Past calculations of aerosol-radiation RF values using a variety of global aerosol models have yielded values of a few mW m⁻² and with large uncertainties (e.g., Righi et al., 2013; Gettelman and Chen, 2013; Lee et al., 2009). In the present study, 10 estimates across 8 models were used to evaluate soot and sulfate aerosol normalized RFs (IPCC, 1999; Sausen et al., 2005; Fuglestvedt et al., 2008; Balkanski et al., 2010; Gettelmann and Chen, 2013; Unger et al., 2013; Pitari et al., 2015; Brasseur et al., 2016) (see SD spreadsheet). Averaging the normalized values yields a 2018 best estimate of the soot aerosol-radiation RF of 0.9 (0.1, 4.0) mW m⁻² for 0.0093 Tg soot emitted. The corresponding best estimate for sulfate aerosol is −7.4 (−19, −3) mW m⁻² for 0.37 Tg SO₂ emitted. The uncertainties are derived from the standard deviation of the model values. The ERF/RF ratios for soot and sulfate are assumed to be unity in the absence of any estimates of this ratio.

4.6. Aerosol-cloud interaction

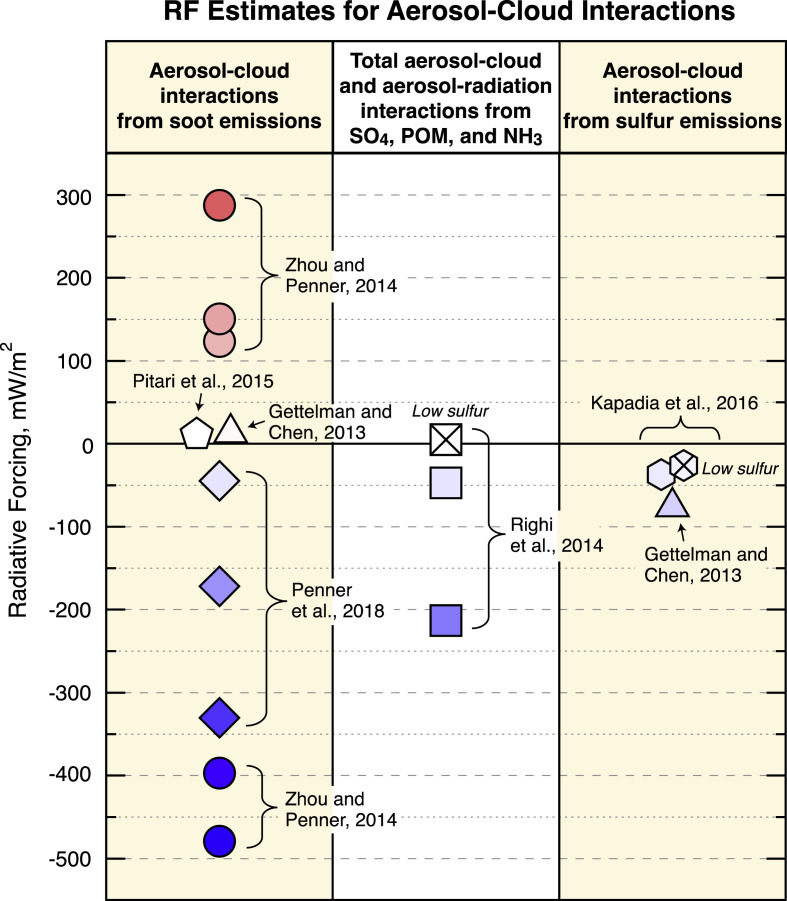
Aerosol-cloud interactions are those processes by which aerosols influence cloud formation. For example, cloud droplets and ice crystals nucleate on aerosol particles. Thus, aerosol-cloud interactions involving aviation aerosol potentially result in an ERF. Aviation soot and sulfate particles are the predominant primary and secondary aerosol from aircraft. The uncertainties in evaluating the aerosol-cloud interactions of aviation soot and sulfate preclude best estimates of ERF contributions. Given the potential importance of these ERF terms, placeholders are included in Fig. 3. Furthermore, to promote progress towards future best estimates, the results of relevant modeling studies were compiled and normalized to global aviation fuel usages in 2005, 2011, 2018, to a soot emission index, and to a fuel S content of 600 pm (except in the cases of low fuel-S content tests) (see Fig. 5 and spreadsheet). As noted in the caption of Fig. 5, some earlier wide-ranging values for the soot aerosol-cloud interaction have been superseded by a more recent study (Penner et al., 2018).

Fig. 5.

Summary of RF estimates for aerosol-cloud interactions for aviation aerosol as calculated in the SD spreadsheet for a variety of published results normalized to 2018 air traffic and 600 ppm fuel sulfur. The results are shown for soot; total particulate organic matter (POM), sulfate and ammonia (NH₃); and sulfate aerosol from the indicated studies. The color shading gradient in the symbols indicates increasing positive or negative magnitudes. No best estimate was derived in the present study for any aerosol-cloud effect due to the large uncertainties. In previous studies, the estimates for the soot aerosol-cloud effect are associated with particularly large uncertainty in magnitude and uncertainty in the sign of the effect (Penner et al., 2009, 2018; Zhou and Penner, 2014). As part of the present study, an author (JEP) re-evaluated these earlier studies and concluded that the Penner et al. (2018) results supersede the earlier Penner et al. (2009) and Zhou and Penner (2014) results because of assumptions regarding updraft velocities during cloud formation. In addition, a bounding sensitivity case in which all aviation soot acts as an IN in Penner et al. (2018) is not included here.

4.6.1. Sulfate aerosol

Aviation sulfate aerosol primarily affects liquid clouds in the background atmosphere. Sulfate aerosol is very efficient as a cloud condensation nuclei (CCN) for liquid clouds, and for promoting homogeneous freezing of solution particles at cold temperatures, thus nucleating ice clouds. Two integrated model simulations (Kapadia et al., 2016; Gettelman and Chen, 2013) found large impacts on liquid clouds from aviation sulfate aerosol that is transported to liquid clouds at lower altitudes over oceans, which have low albedo. The reported RF values in these studies, when scaled appropriately, are −37 to −76 mW m⁻² in 2018, excluding a low fuel-sulfur case. Note that the study of Righi et al. (2013) that yields an RF of −213 mW m² in 2018 includes sulfate aerosol-cloud interactions but cannot be directly compared with Kapadia et al. (2016) and Gettelman and Chen (2013), since the former treats the combined effects of sulfate, nitrate and particulate organic matter (POM) rather than isolating the effects of sulfate as done in the latter studies. While these RF estimates do not support a best estimate at present, they do suggest that the sign of the sulfate aerosol-cloud effect on low-level clouds is likely to be negative (i.e., a cooling), similar to the ERF for the aerosol-cloud interactions of other anthropogenic sources of sulfate aerosol (IPCC, 2013).

Sulfate aerosol-cloud interaction forcing estimates are highly dependent on the sensitivity (or susceptibility) of the cloud radiative field to aerosol perturbations, which is dependent on uncertain model processes and the model background aerosol state. Clouds that form with small CCN number concentrations in the background atmosphere are more sensitive to CCN perturbations. Forcing by these cloud effects are largely concentrated near flight corridors over oceans because the high albedo contrast between the ocean surface and clouds increases forcing sensitivity to CCN perturbations.

A large uncertainty was also reported for the magnitude of the aerosol-cloud ERF from all anthropogenic activities, estimated for 2011 to be −450 (−1200, 0.0) mW m⁻² (Myhre et al., 2013). A more recent estimate of the aerosol-cloud RF from all anthropogenic activities has a 68% confidence interval of −650 to −1600 mW m⁻² (Bellouin et al., 2019). In general, aerosol-cloud interactions contribute the largest uncertainty in calculations of anthropogenic ERF (IPCC, 2013).

4.6.2. Soot

The magnitude and the sign of the global RF from aviation soot effects on background cloudiness remain highly uncertain. The uncertainties center on the difficulties in accurately simulating homogeneous and heterogeneous ice nucleation in the background atmosphere, variations in the treatment of updraft velocities during cirrus formation, and the lack of knowledge of the ice nucleating (IN) ability of aviation soot particles during their atmospheric lifetime (Zhou and Penner, 2014; Penner et al., 2018).

Two studies find moderate effects of soot aerosol on ice clouds, depending on the ice nucleating efficiency and the size distribution. RF values of about 11–13 mW m⁻² (normalized to 2018 emissions) are calculated in some studies for moderate ice-nucleating efficiencies (Pitari et al., 2015; Gettelman and Chen, 2013).

In sensitivity tests, if soot processed within contrails is assumed to be an efficient IN particle, then the RF may be negative by up to −330 mW m⁻² due to reductions in ice crystal number in regions dominated by homogeneous freezing (Penner et al., 2018; see Fig. 5). The RF could be significantly smaller (less negative) if additional ice-forming particles, such as secondary organic aerosol (SOA), are already present in the background atmosphere (Penner et al., 2018; Gettelman and Chen, 2013). In addition, increases in ice crystal numbers occur when the background atmosphere has much lower sulfate or haze-forming aerosol number concentrations and is dominated by heterogeneous freezing, causing forcings near zero or even positive (Zhou and Penner, 2014). Other studies predict decreases in cirrus number for smaller numbers of larger soot particles (Hendricks et al., 2011), resulting in a slight warming (Gettelman and Chen, 2013).

A dominant uncertainty for the aerosol-cloud effect from soot is the IN properties of aviation soot aerosol. Some laboratory studies indicate soot particles are not efficient ice nuclei (DeMott et al., 1999), while other studies indicate higher efficiencies (Möhler et al., 2005; Hoose and Möhler, 2012). The possibility that contrail-processed soot particles would show enhanced IN activity after sublimation in the background atmosphere was addressed in the laboratory (Mahrt et al., 2020). The effect was limited to large soot particles, suggesting that the impact of aviation soot on cloudiness may be overestimated in previous studies that assume soot processed through contrails and not covered by a sulfate coating is an efficient IN (Penner et al., 2018).

Another source of uncertainty is soot number concentrations. For individual engines, the soot number can vary by two orders of magnitude (Agarwal et al., 2019). Soot number concentrations from aviation vary with the assumed size of the particles emitted as well as the mass emissions. Soot emissions from aircraft are set as a regulatory parameter for the landing/take-off (LTO) cycle by ICAO and are measured in terms of mass. Robust conversion factors from mass to number have recently been developed for the ICAO-LTO cycle (Agarwal et al., 2019) but have not yet been made for cruise, although other methodologies exist (Teoh et al., 2019).

5. Calculated net aviation ERF and RF values

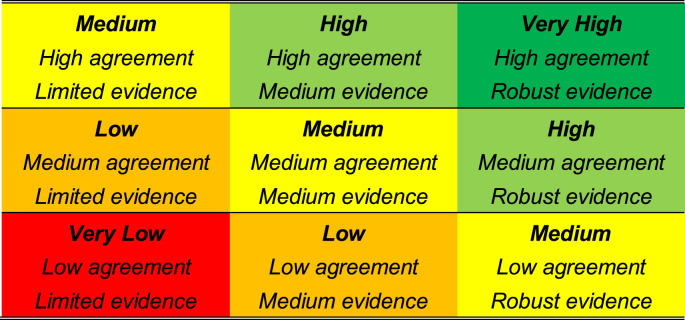
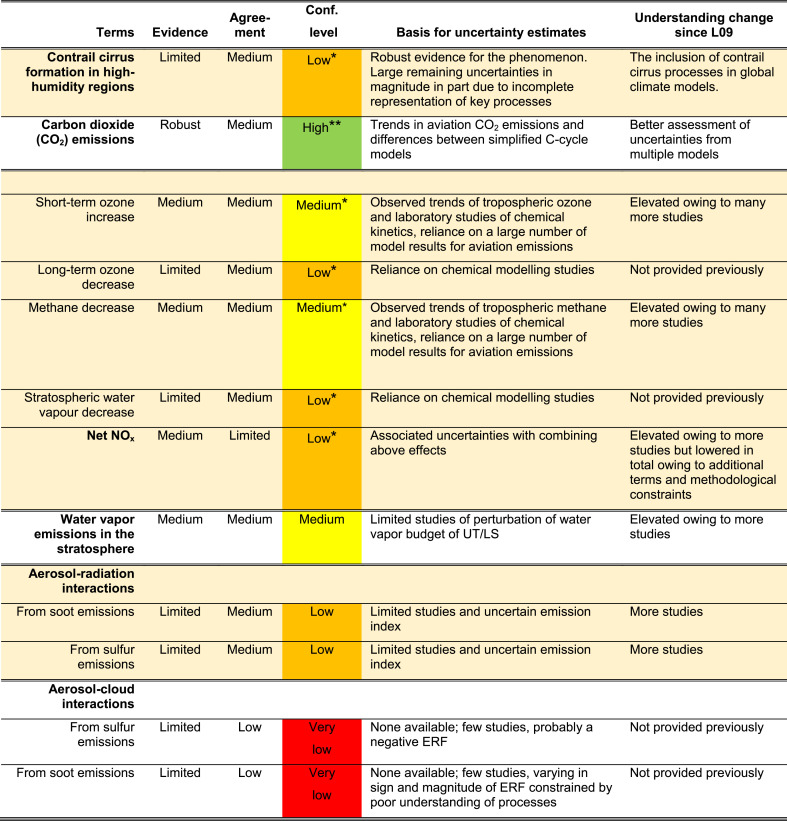
ERF and RF values for the terms associated with global aviation emissions and cloudiness are given in Table 2, Table 3, respectively, for the years 2018, 2011, and 2005, along with uncertainties, sensitivities to emissions and the ERF/RF ratio for selected terms. ERF values are shown for all years in Fig. 6. All ERF and RF values are available in the analysis spreadsheet (SD). Through normalization and scaling, all 2000 to 2018 values are self-consistent. The sensitivity of each term to emission magnitudes or flight track distances is derived in the normalization process. ERF best estimates and uncertainties (95% confidence limits) are highlighted for year 2018 in Fig. 3 along with their assessed confidence levels. No best estimates are included for sulfate and soot aerosol-cloud interactions because of the substantial uncertainties noted above. However, placeholder spaces are included in both Table 2, Table 3 and Fig. 3 to indicate the potential importance of these terms and to flag the associated knowledge gaps for consideration in future research and assessment activities. The confidence levels and their justifications shown in Fig. 3 are obtained by employing the methodology of Mastrandrea et al. (2011), which is based on evidence and agreement in accordance with IPCC guidance (Table 4b, Table 4a ).

Table 4b.

Basis for confidence levels in Table 4a.^a

^aThe basis for the confidence level is given as a combination of evidence (limited, medium, robust) and agreement (low, medium and high) based on guidance given by Mastrandrea et al. (2011).

Table 4a.

Confidence levels for the ERF estimates in Fig. 3.

*This term has the additional uncertainty of the derivation of an effective radiative forcing from a radiative forcing.

**This term differs from ‘Very High’ level in IPCC (2013) because additional uncertainties are introduced by the assessment of marginal aviation CO₂ emissions and their resultant concentrations in the atmosphere from simplified carbon cycle models.

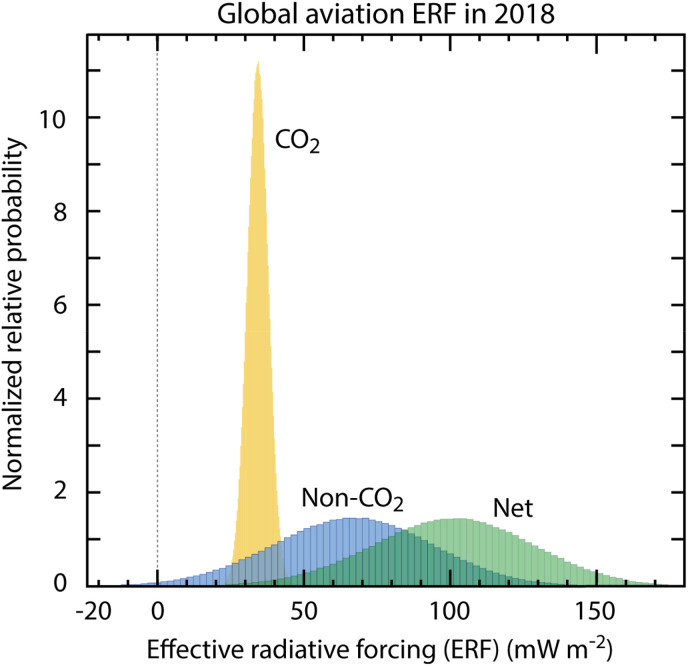
In Fig. 3, contrail cirrus formation yields the largest positive (warming) ERF term, followed by CO₂ and NO_x emissions. For the 1940 to 2018 period, the net aviation ERF is +100.9 mW m⁻² (5–95% likelihood range of (55, 145)) with major contributions from contrail cirrus (57.4 mW m⁻²), CO₂ (34.3 mW m⁻²), and NO_x (17.5 mW m⁻²). The aerosol and water vapor terms represent minor contributions. The formation and emission of sulfate aerosol yields the only significant negative (cooling) term. Non-CO₂ terms sum to yield a positive (warming) ERF that accounts for 66% of the aviation net ERF in 2018 (66.6 (21, 111) mW m⁻²). The application of ERF/RF ratios more than halves the RF value of contrail cirrus while approximately doubling the NO_x value. ERF/RF ratios were not included in the Lee et al. (2009) analysis. Uncertainty distributions (5%, 95%) show that non-CO₂ forcing terms contribute about 8 times more than CO₂ to the uncertainty in the aviation net ERF in 2018. The best estimates of the ERFs from aviation aerosol-cloud interactions remain undetermined.

The time series of ERF values for individual terms is shown in Fig. 6 for the 2000–2018 period. Through normalization and scaling the terms are self-consistent over this period. The increase in all of the terms with time is consistent with the growth of aviation fuel burn and CO₂ emissions over the same period (Fig. 2). Note that net ERF values shown for each year are not linear sums over the component terms due to the separate probability distributions associated with each component term in the sum, and instead are calculated with a Monte Carlo sampling method described below.

A comparison of updated RF estimates with Lee et al. (2009) values for 2005 is given in Table 3. The large increase in the contrail cirrus RF between 2005 and 2018 results in part because the 2005 value only includes linear contrails. In Lee et al. (2009), only an estimate of 2005 contrail cirrus was provided rather than a best estimate. The present study now includes a process-based model estimate of the contrail cirrus term (Section 4.4). The NO_x treatment in Lee et al. (2009) did not include the negative forcing contributions of the long-term O₃ decrease or the SWV decrease, the updated treatment of CH₄ of Etminan et al. (2016), nor an equilibrium-to-transient correction. As a result, the updated RF values for NO_x are approximately a factor of 2 smaller. Incorporating all the updated information in the RF calculations of the NO_x and contrail cirrus terms yields an approximately 30% increase in the net aviation RF for 2005, from 78.0 to 95.2 mW m⁻². In the ERF evaluation for 2005 the net aviation forcing is reduced from 95.2 to 66.9 mW m⁻² because the ERF/RF ratios for NO_x and contrail cirrus are different than unity.

In seeking comparison of net aviation ERF with net anthropogenic ERF, we note that IPCC (Myhre et al., 2013) provides a value for 1750–2011 of 2290 (1130, 3330) mW m⁻². The percentage contributions of aviation to the net ERF in 2011 are 3.5% (4.0, 3.4%) and 1.59% (1.65, 1.56%) for the sum of all terms and the CO₂ term alone, respectively. The 2005 and 2018 percentages are likely the same because the fraction of aviation CO₂ emissions of total anthropogenic CO₂ emissions has averaged 2.1% (±0.15) for the last two decades (see Fig. 2). Normalized relative probabilities of CO₂ and non-CO₂ ERFs for 2018 as derived from the Monte Carlo simulations show that non-CO₂ uncertainties are the predominant contribution to the uncertainty in the aviation net ERF (Fig. 7 ). IPCC also separately estimated the contrail cirrus term for 2011 as 50 (20, 150) mW m⁻² as discussed above, which compares well with the updated value of 44.1 (13, 75) mW m⁻².

Fig. 7.

Probability distribution functions (PDFs) for aviation ERFs in 2018 based on the results in Fig. 3 and Table 2. PDFs are shown for separately for CO₂, the sum of non-CO₂ terms, and the net aviation ERF. Since the area of each distribution is normalized to the same value, relative probabilities can be intercompared. Uncertainties are expressed by a distribution about the best-estimate value that is normal for CO₂ and contrail cirrus, and lognormal for all other components. A one-million-point Monte Carlo simulation run was used to calculate all PDFs.

The determination of net aviation ERFs and their uncertainties shown in Fig. 3 and accompanying tables required a Monte Carlo approach to summing over terms with discrete probability distributions. A similar method was employed in Lee et al. (2009). PDFs of each term were constructed from the respective individual studies as normal, lognormal or discrete distributions (see SD spreadsheet). Monte Carlo samplings (one million random points) of the individual forcing PDFs were then used to combine terms to yield net ERFs and the uncertainties (95% likelihood range) for the sum of all terms and for only non-CO₂ terms (Fig. 7). The forcing terms are generally assumed to be independent (uncorrelated) with the notable exception of the NO_x component terms which have strong paired correlations as shown in Appendix Fig. D.1. Only the short-term O₃ and CH₄ terms were included in Lee et al. (2009) and a 100% correlation was assumed, in part, because the assumption of uncorrelated effects was deemed less acceptable. A subsequent study showed that these terms are indeed strongly correlated (R² = 0.79) (Holmes et al., 2011), similar to the present results in Appendix Fig. D.1. The Holmes et al. (2011) study further concluded that the assumption of 100% correlation in this case would lead to an underestimate of uncertainty in the NO_x RF. Another correlation of forcing terms not considered here may be the dependence of the soot direct effect and contrail properties on the soot number index since ice nucleation at the time of contrail formation depends on the soot number index (e.g., Kärcher, 2018).

6. Emission equivalency metrics

Using the best estimate ERFs, we calculate updated aviation-specific Global Warming Potential (GWP) and Global Temperature change Potential (GTP) values, presented for 20-, 50-, and 100-year time horizons in Table 5 . These metrics assign so-called ‘CO₂-emission equivalences’ for non-CO₂ emissions via ratios of time-integrated ERF and changes in future temperatures, respectively. The choice of metric depends upon the particular underlying application (Fuglestvedt et al., 2010) such that there is no uniquely ‘correct’ metric or time horizon, and alternative metrics are available. GWP and GTP are the most commonly applied metrics and the values calculated here allow a comparison with previous estimations (e.g., Lee et al., 2010; Lund et al., 2017). In calculating the GWPs and GTPs, the CO₂ IRF from Joos et al. (2013) is used and the climate response IRF from Boucher and Reddy (2008) for the GTPs (see Appendix F for futher details about the metrics calculations).

Table 5.

Emission metrics and corresponding CO₂-equivalent emissions for the ERF components of 2018 aviation emissions and cloudiness.

Metrics
ERF term	GWP20	GWP50	GWP100	GTP20	GTP50	GTP100
CO2	1	1	1	1	1	1
Contrail cirrus (Tg CO2 basis)	2.32	1.09	0.63	0.67	0.11	0.09
Contrail cirrus (km basis)	39	18	11	11	1.8	1.5
Net NOx	619	205	114	−222	−69	13
Aerosol-radiation
Soot emissions	4288	2018	1166	1245	195	161
SO2 emissions	−832	−392	−226	−241	−38	−31
Water vapor emissions	0.22	0.10	0.06	0.07	0.01	0.008

CO2-eq emissions (Tg CO2 yr−1) for 2018
ERF term	GWP20	GWP50	GWP100	GTP20	GTP50	GTP100	GWP*100 (E*CO2e)
CO2	1034	1034	1034	1034	1034	1034	1034
Contrail cirrus (Tg CO2 basis)	2399	1129	652	695	109	90	1834
Contrail cirrus (km basis)	2395	1127	651	694	109	90	1834
Net NOx	887	293	163	−318	−99	19	339
Aerosol-radiation
Soot emissions	40	19	11	12	2	2	20
SO2 emissions	−310	−146	−84	−90	−14	−12	−158
Water vapor emissions	83	39	23	27	4	3	42
Total CO2-eq (using km basis)	4128	2366	1797	1358	1035	1135	3111
Total CO2-eq/CO2	4.0	2.3	1.7	1.3	1.0	1.1	3.0

GWPs and GTPs for contrail cirrus and for water vapor reported here are similar to, albeit slightly smaller than, corresponding results previously reported, while soot and sulfate numbers are larger in magnitude (positive and negative) than previous estimates (Fuglestvedt et al., 2010; Lund et al., 2017). The Fuglestvedt et al. (2010) estimates for soot are based on RF due to soot emissions from all sources, not just aviation, which yields a lower radiative efficiency (i.e., forcing per unit emission) than in the present study. Also given in Table 5 are CO₂-equivalent aviation emissions, along with ratios of total CO₂-equivalent emissions to CO₂ emissions. Such ratios are sometimes used as ‘multipliers’ to illustrate the additional climate impact from aviation non-CO₂ terms over those from CO₂ emissions alone. Here, estimated multipliers for 2018 range from 1.0 to 4.0 depending on the choice of time horizon and emission metric. This is broadly consistent with what has been reported and used previously (Lee et al., 2010). The broad range emphasizes the challenges associated with developing comparisons of emission equivalences for short- and long-lived climate forcers within a common framework and how such considerations strongly depend on the chosen perspective.

One of the significant uncertainties in calculating GWPs and GTPs is the treatment of climate-carbon (C-cycle) feedbacks in the modeling framework. The efficiency of carbon sinks reduces with increasing warming (Ciais et al., 2013) and this climate feedback is implicitly included in the Absolute GWP of CO₂ through the IRF used (Joos et al., 2013). However, Myhre et al. (2013) highlighted that this introduces an inconsistency since the numerators for the GWP and GTP do not include such a climate carbon feedback. One of the studies that have proposed ways of addressing this inconsistency is Gasser et al. (2017). They show that when the C-cycle feedback is consistently accounted for, the non-CO₂ emission metrics increase, but less so than initially suggested by Myhre et al. (2013). They also find that removing the C-cycle feedback from both numerator and denominator give similar metric values as including it in both places. Using the CO₂ IRF without the C-cycle feedback provided by Gasser et al., 2017, we calculate a second set of aviation emission metrics (Table F.1a and Table F.1b), showing that the changes to the GWP100 and GTP100 values from those given in Table 5 are rather small.

In response to the challenges related to comparing short-lived and long-lived forcing components, a number of new ‘flow-based’ methods have been introduced representing both short-lived and long-lived climate forcers explicitly as ‘warming-equivalent’ emissions that have approximately the same impact on the global average surface temperature over multi-decade to century timescales (Lauder et al., 2012; Allen et al., 2016, 2018; Cain et al., 2019; Collins et al., 2019). A simple version of these methods, known as GWP*, defines the average annual rate of CO₂-warming-equivalent emissions (E* _CO2e) over a period of $\Delta t$ years arising from a particular component of RF or ERF by (Cain et al., 2019):

$$E_{CO2e}^{\ast }=\left[\left(1-\alpha \right)H/AGW{P}_H\right]\Delta F/\Delta t+\left[\alpha /AGW{P}_H\right]\bar{F},$$ (1)

where $\Delta F$ is the ERF change and $\bar{F}$ the average ERF arising from that component over that period, $AGW{P}_H$ is the Absolute GWP of CO₂ (Wm⁻² kg⁻¹ year) over time-horizon $H$ and $\alpha$ is a small coefficient depending on the previous history of that RF component. Eqn (1) gives the rate of CO₂ emission that would, alone, create the same rate of global temperature increase as the combined effect of aviation climate forcings. For historically small and/or rapidly changing RF components, $\alpha$ may be neglected, and hence to a good approximation, total CO₂-warming-equivalent emissions over this period ($\Delta t{E}_{CO2e}^{\ast }$) are approximated by an increase in forcing, $\Delta F$, multiplied by $H/AGW{P}_H$ (see Appendix F ), which is about 1000 GtCO₂ per W/m² for $H$ in the range 20–100 years (Myhre et al., 2013; IPCC, 2018, Figure SPM.1, caption). This result follows from the definition of AGWP: since all GWP calculations assume a linearization, the $AGW{P}_H$ is equivalent to the forcing change resulting from the emission of $H$ tonnes of CO₂ spread over $H$ years (Shine et al., 2005), so $AGW{P}_H/H$ is the forcing change per tonne of CO₂. Under the historical profile of increasing global annual aviation-related emissions and associated ERFs, CO₂-warming-equivalent emissions based on GWP* indicate that aviation emissions are currently warming the climate around three times faster than that associated with aviation CO₂ emissions alone (Table 5).

It is important to note that, unlike the conventional GWP and GTP metrics given in Table 5, the ratio between total CO₂-warming-equivalent emissions from all forcing agents and those from CO₂ alone will change substantially if future aviation emissions deviate from their current growth trajectory (calculated here over the period 2000–2018). If annual global aviation emissions were to stabilize, this ratio declines towards unity, as $\Delta F/\Delta t$ would decline to zero. This does not indicate, however, that the non-CO₂ effects do not have a warming affect. This human-induced warming still represents a mitigation potential. Warming-equivalent emissions capture the fact that constant emission of short-lived climate forcers maintain an approximately constant level of warming, whilst constant emissions of long-lived climate forcers, such as CO₂, continue to accumulate in the atmosphere resulting in a constantly increasing level of associated warming. Hence warming-equivalent emissions show that the widely-used assumption of a constant ‘multiplier’, assuming that net warming due to aviation is a constant ratio of warming due to aviation CO₂ emissions alone, only applies in a situation in which aviation emissions are rising exponentially such that the rate of change of non-CO₂ RF is approximately proportional to the rate of CO₂ emissions (assuming non-CO₂ RF is proportional to CO₂ emissions, and noting that the rate of change any quantity is proportional to that quantity only when both are growing exponentially). In contrast, under a future hypothetical trajectory of decreasing aviation emissions, this GWP* based multiplier could fall below unity, as a steadily falling rate of emission of (positive) short-lived climate forcers has the same effect on global temperature as active removal of CO₂ from the atmosphere. The GWP* based ‘multiplier’ calculated here (which depends on the ratio of the increase in net aviation warming to the increase in warming due to aviation CO₂ emissions alone over the recent past), should not be applied to future scenarios that deviate substantially from the current trend of increasing aviation-related emissions. The broad range of values for a ‘multiplier' presented here is an illustration of the limitations of using a constant multiplier in the assessment of climate impacts of aviation, and a reminder that the choice of metric for such a multipler involves subjective choices.

7. Aviation CO₂ vs non-CO₂ forcings

Since IPCC (1999), the comparison of aviation CO₂ RF with the non-CO₂ RFs has been a major scientific topic, as well as a discussion point amongst policy makers and civil society (ICAO, 2019). Aviation as a sector is not unique in having significant non-CO₂ forcings; the same is true of agriculture with significant CH₄ and N₂O emissions, or maritime shipping with net-negative current-day RF despite CO₂ emissions of a similar magnitude to those from aviation (Fuglesvedt et al., 2009). However, unlike direct emissions of the greenhouse gases N₂O and CH₄ from the agricultural sector, aviation non-CO₂ forcings are not covered by the former Kyoto Protocol. It is unclear whether future developments of the Paris Agreement or ICAO negotiations to mitigate climate change, in general, will include short-lived indirect greenhouse gases like NO_x and CO, aerosol-cloud effects, or other aviation non-CO₂ effects. Aviation is not mentioned explicitly in the text of the Paris Agreement, but according to its Article 4, total global greenhouse-gas emissions need to be reduced rapidly to achieve a balance between anthropogenic emissions by sources and removals by sinks of greenhouse gases in the second half of this century.

The IPCC concludes: “Reaching and sustaining net-zero global anthropogenic CO ₂ emissions and declining net non-CO ₂ radiative forcing would halt anthropogenic global warming on multi-decadal time scales.” (IPCC, 2018, bullet A2.2, SPM). Crucially, both conditions would need to be met to halt global warming. Hence, to halt aviation's contribution to global warming, the aviation sector would need to achieve net-zero CO₂ emissions and declining non-CO₂ radiative forcing (unless balanced by net negative emissions from another sector): neither condition is sufficient alone. Some combination of reductions in CO₂ emissions and non-CO₂ forcings might halt further warming temporarily, but only for a few years: it would not be possible to offset continued warming from CO₂ by varying non-CO₂ radiative forcing, or vice versa, over multi-decade timescales.

That aviation's non-CO₂ forcings are not included in global climate policy has resulted in studies as to whether they could be incorporated into existing policies, such as the European Emissions Trading Scheme, using an appropriate overall emissions ‘multiplier’; however, scientific uncertainty has so far precluded this (Faber et al., 2008). In addition, as noted above, the multiplier is highly dependent on the future emissions scenario (Section 6). Alternatively, proposals have been made to reduce aviation's non-CO₂ forcings by, for example, avoiding contrail formation by re-routing aircraft (Matthes et al., 2017), or optimizing flight times to avoid the more positive (warming) fractional forcings (e.g., by avoiding night flights, Stuber et al., 2006). There is a developing body of literature on this topic (e.g., Newinger and Burkhardt, 2012; Yin et al., 2018). Similarly, studies have assessed whether changes in cruise altitudes could mitigate NO_x impacts (e.g. Frömming et al., 2012). The potential impacts of changes in technology have also been examined to reduce the non-CO₂ forcings such as lowering the emission index for NO_x (Freeman et al., 2018) or soot particle number emissions (Moore et al., 2017) to reduce net NO_x and contrail cirrus forcings, respectively (Burkhardt et al., 2018).

Avoidance of contrail formation through re-routing can incur a fuel penalty and therefore additional CO₂ emissions during a flight, and changes in combustor technology to minimize NO_x generally increases marginal fuel burn and CO₂ emission. Both methods invoke the usage of climate metrics such as those calculated and presented in Section 6 to evaluate whether there is a net climate benefit or disbenefit over a defined period. In examining such mitigation scenarios involving tradeoffs (e.g. Teoh et al., 2020), the perceived success or otherwise of the outcome will be a function of the user's choice of metric and time horizon. A limitation noted for the GWP is that it has an ‘artificial memory’ over longer time horizons, since the integrated-RF nature of the metric accumulates ‘signal’ over time that the climate system has ‘forgotten’ (Fuglestvedt et al., 2010). The GTP, being an ‘end point’ metric that captures the temperature response, overcomes this limitation of the GWP but is not yet in usage within current climate policy.

Changes to aviation operations or technology that result in a reduction of a non-CO₂ forcing with the added consequence of increased CO₂ emissions can result in net reductions of forcing on short timescales while increasing the net forcing on longer timescales (e.g., Freeman et al., 2018). In a case study of contrail avoidance through routing changes, Teoh et al. (2019) found that the resultant small increase in CO₂ emissions still reduces the net forcing over a timescale of 100 years. In such ‘tradeoff cases’ the balance between non-CO₂ and CO₂ forcings have to be weighted carefully, since CO₂ accumulates in the atmosphere and a fraction has millennial timescales (Archer and Brovkin, 2008; IPCC, 2007). Prior to the COVID-19 pandemic, global aviation traffic and emissions were projected to grow to 2050 (Fleming and de Lepinay, 2019). As the COVID-19 pandemic diminishes, aviation traffic is likely to recover to meet projected rates on varying timescales (IATA, 2020), with continued growth further increasing CO₂ emissions. Thus, reducing CO₂ aviation emissions will remain a continued focus in reducing future anthropogenic climate change, along with aviation non-CO₂ forcings. The latter increase the current-day impact on global average temperatures by a factor of around 3 (using GWP*) above that due to CO₂ alone.

Funding

DSL, AS, RRdL, LL, BO acknowledge support from the UK Department for Transport. PMF acknowledges support of the European Union’s Horizon 2020 Research and Innovation Programme under grant agreement number 820829 (CONSTRAIN) by the UK National Environment Research Council (NERC) SMURPHS project (NE/N006038/1). MRA acknowledges support from the EU H2020 grant agreement number 821205 (FORCeS) and the Oxford Martin Programme on Climate Pollutants. MTL and JSF acknowledges support from the Norwegian Research Council (RCN) grant number 300718 (AVIATE), for which DSL and RS have a collaboration agreement. JEP acknowledges support from the National Science Foundation (NSF 1540954).

CRediT authorship contribution statement

D.S. Lee: Investigation, Methodology, Writing - review & editing, Data curation, Formal analysis, Project administration, Supervision. D.W. Fahey: Investigation, Methodology, Writing - review & editing, Data curation, Formal analysis, Project administration, Supervision. A. Skowron: Investigation, Methodology, Writing - review & editing, Data curation, Formal analysis, Software. M.R. Allen: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. U. Burkhardt: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. Q. Chen: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. S.J. Doherty: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. S. Freeman: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. P.M. Forster: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. J. Fuglestvedt: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. A. Gettelman: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. R.R. De León: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. L.L. Lim: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. M.T. Lund: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. R.J. Millar: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. B. Owen: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. J.E. Penner: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. G. Pitari: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. M.J. Prather: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. R. Sausen: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis. L.J. Wilcox: Writing - review & editing, Investigation, Methodology, Writing - original draft, Data curation, Formal analysis.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendices.

A. Trends in aviation CO₂ emissions

Global aviation CO₂ emissions for 1940–1970 were taken from Sausen and Schumann (2000) and for the years 1971–2016 were calculated from International Energy Agency (IEA) data on usage of JET-A and aviation gasoline, largely from annual ‘Oil Information’ digests (e.g., https://webstore.iea.org/oil-information-2019). The regional data are from the same source but accessed online from the IEA Oil Information (1960–2017) held at the UK Data Service (IEA, 2019). Note that these data are proprietary and must be purchased from IEA. Data were unavailable for 2017 and 2018, so incremental annual percentage increases in global aviation fuel usage and, therefore CO₂ emissions, for those years were taken from reports of the International Air Transport Association (IATA, 2019). Some uncertainties exist from the annual fuel estimations and to a much smaller extent, the emission factors. The IEA does not give uncertainties for annual kerosene fuel sales or usage. Sausen and Schumann (2000), from which the 1940 to 1970 data are based here, estimated that the uncertainty in cumulative fuel consumption from 1940 to 1995 (their dataset) is 20%. There is a known discrepancy of IEA estimates of aviation fuel usage being greater by about 10% than that derived from bottom-up global civil aviation inventories. Actual fuel usage is likely to be somewhere between the two estimates: aviation emissions inventories are known to be incomplete, with only scheduled traffic being available from some air traffic regions, and fuel usage potentially being underestimated from flight routing and cruise altitudes; IEA data on the other hand includes military aviation fuel (not included in civil aviation inventories) and a small fraction of kerosene not used in aviation, but sold for that purpose (Lee et al., 2009). The CO₂ emission factors for aviation fuel on the other hand are well determined, and the uncertainty is likely within 1%.

B. Aviation CO₂ radiative forcings

Calculation of CO₂ concentrations from emissions—LinClim SCM

The response of CO₂ concentrations, C(t), to a CO₂ aviation emissions rate, E(t), is modelled using the method described in Hasselmann et al. (1997) and is expressed as:

$$\Delta C\left(t\right)={\int }_{t_0}^t{G}_C(t-t^{\prime })E\left(t^{\prime }\right)d{t}^{\prime }$$ (B.1)

where in Eqn (B.1)

$$G_C\left(t\right)=\sum _{j=0}^5{\alpha }_j{e}^{-t/{\tau }_j}$$ (B.2)

and τ _j in Eqn( B.2) is the e-folding time of mode j and the equilibrium response of mode j to a unit emissions of α _j τ _j.

The mode parameters used in this study are presented in Sausen and Schumann (2000) and approximate the carbon-cycle model in Maier-Reimer and Hasselmann (1987). The applicability of these parameters in the context of aviation response was tested in a model intercomparison exercise (Khodayari et al., 2013). For the time horizon of 50–60 years into the future, these were found to compare well with other more sophisticated carbon-cycle models such as MAGICC 6.0, which is widely used in the IPCC Fourth Assessment Report (IPCC, 2007). Beyond this horizon, aviation CO₂ concentrations begin to have an impact on the ocean and biosphere uptake of CO₂ and the non-linearities of the system must be accounted for.

Calculation of CO₂ concentrations from emissions—CICERO-2 SCM

The CICERO-2 SCM (Fuglestvedt and Berntsen, 1999; Skeie et al., 2017) uses interconnected process-specific IRFs with explicit treatment of air-sea and air-biosphere exchange of CO₂ (Joos et al., 1996; Alfsen and Berntsen, 1999) that forms a nonlinear carbon cycle. The ocean and biosphere IRFs in CICERO-2 express how the CO₂ impulse decays within each reservoir. The CO₂ partial pressure in each reservoir is calculated as a function of the carbon in that reservoir, and the CO₂ partial pressure in each reservoir is related to the CO₂ partial pressure in the atmosphere by explicitly solving for the atmosphere/ocean/biosphere CO₂ mass transfer. Therefore, the CICERO-2 carbon cycle takes into account the nonlinearity in ocean chemistry and biosphere uptake at high CO₂ partial pressures since it represents the atmospheric change in CO₂ as a function of total background.

Calculation of CO₂ concentrations from emissions—FaIR SCM

The FaIR SCM is described by Millar et al. (2017) and summarized as follows. FaIR is a modified version of the IPCC AR5 four time-constant impulse response function (IRF) model, which represents the evolution of atmospheric CO₂ by partitioning emissions of anthropogenic CO₂ between four reservoirs of an atmospheric CO₂ concentrations change, following a pulse emission (see Myhre et al., 2013 for more details). In more comprehensive models, ocean uptake efficiency declines with accumulated CO₂ in ocean sinks (Revelle and Suess, 1957) and uptake of carbon into both terrestrial and marine sinks are reduced by warming (Friedlingstein et al., 2006). FAIR captures some of these dynamics within the simple IRF structure, mimicking the behaviour of Earth System Models/Earth System Models of Intermediate Complexity in response to finite-amplitude CO₂ injections; this is achieved by introducing a state-dependent carbon uptake with a single scaling factor, α, to all four of the time constants in the carbon cycle of the IPCC AR5 impulse response model used for the calculation of CO₂-equivalence metrics. This approach is described in more detail by Millar et al. (2017).

C. Radiative forcing, efficacy and effective radiative forcing (ERF)

Radiative forcing (RF) has been introduced as a predictor for the expected equilibrium global mean of the (near) surface temperature change ΔT_s that results from the introduction of climate forcers, such as additional atmospheric CO₂ or a change in the solar irradiation (e.g., IPCC, 2007):

ΔT_s = λ RF (C.1)

where λ is the climate sensitivity parameter (K (W m⁻²)⁻¹). Several definitions of RF exist. According to the simplest one, the instantaneous RF is the change in the total irradiation (incoming short-wave solar radiation minus the outgoing long-wave terrestrial radiation) at the top of the atmosphere over the industrial era. However, for most of the climate forcers a better definition (with respect to the linearity of Eq. (C.1)) is the stratosphere-adjusted RF at the tropopause. Here, after the introduction of the new climate forcer, the temperature of the stratosphere is allowed to reach a new radiative equilibrium, while all other atmospheric state variables are kept constant. The stratosphere-adjusted RF at the tropopause was used in many of the earlier IPCC reports (IPCC, 1999) and in earlier assessments of aviation climate impacts (Sausen et al., 2005; Lee et al., 2009).

While Eq. (C.1) is a fairly good approximation for many nearly spatially homogeneously distributed climate forcers, such as global increases of CO₂ or CH₄, Eq. (C.1) fails to some extent for many forcers that are heterogeneously distributed either horizontally or vertically; such is the case for aviation-induced ozone perturbations and contrail cirrus (e.g., Hansen et al., 1997, 2005; Forster and Shine, 1997; Stuber et al., 2005). To overcome this problem Hansen and Nazarenko (2004) introduced the efficacy, r_i, into Eqn (C.1):

ΔT_s = r_i λ_CO2 RF = λ_i RF with λ_i = r_i λ_CO2 (C.2)

Here λ_CO2 is the climate sensitivity parameter for a CO₂ perturbation. While λ in (C.1) is considered a universal constant, which can only be determined by climate models and hence is model dependent, λ_i depends on the type of forcing, as does r_i. (While r_CO2 is 1 by definition, r_{linear contrails} is < 1 (Ponater et al., 2005; Rap et al., 2010)). Eqn (C.2) can also be expressed differently:

T_s = λ_CO2 RF_i* with RF_i* = r_i RF (C.3)

In Eqn (C.3) RF_i* is the forcing modified by the efficacy, which yields a better approximation for the surface temperature change than RF. However, the calculation of the RF_i* is computationally much more expensive than the calculation of RF, as it requires the determination of the equilibrium temperature change, ΔT_s, with a comprehensive climate model.

As an alternative, the effective radiative forcing (ERF) has been introduced as a more practical indicator of the eventual global mean temperature response (IPCC, 2013). While RF_i* assumes equilibrium climate change, ERF only includes all 'fast' atmospheric responses to a given climate forcer. For example, rapid adjustments in cloud cover, such as from aerosols, or in properties that respond to changes in water vapor, can either increase or decrease the initial RF. In contrast, the instantaneous, stratosphere-adjusted, and effective RFs for well-mixed greenhouse gases are nearly equal. In practice, ERF is determined with a comprehensive climate model, which calculates a new equilibrium radiative imbalance, while the sea surface temperature and/or the global surface temperature is kept constant. As a consequence, an ERF value is expected to be somewhere between RF and RF_i* values and closer to RF_i* values.

D. Aviation NO_x radiative forcings

Impacts of NO_x emissions on ozone, methane and stratospheric water vapor

Model studies. In this ensemble analysis of the climate forcing from aviation NO_x emissions, the results of 20 studies published since the IPCC (1999) aviation report were considered: IPCC (1999), Sausen et al. (2005), Stordal et al. (2006), Köhler et al. (2008), Hoor et al. (2009), Myhre et al. (2011), Frömming et al. (2012), Olivié et al. (2012), Gottschaldt et al. (2013), Köhler et al. (2013), Olsen et al. (2013), Skowron et al. (2013), Khodayari et al., 2014a, Khodayari et al., 2014b, Khodayari et al., 2014, Søvde et al. (2014), Skowron et al. (2015), Pitari et al. (2015), Kapadia et al. (2016), Pitari et al. (2017), Lund et al. (2017). Three studies that reported results from a 100-year integration of a pulse NO_x emission (Wild et al., 2001; Derwent et al., 2001; Stevenson et al., 2004) were not included in this analysis, nor has as Unger et al. (2010) which uses a different methodology to the aforementioned.

This model ensemble represents various methodologies in calculating and treating the long-term effects; in order to avoid gaps and additional uncertainties, standardized RFs for reductions in CH₄-induced O₃ and SWV were adopted, except for one study that calculates the ‘real’ long-term effects from their 5$0$-yr integrations (Pitari et al., 2017):

• •All analyzed short-term O₃ RFs account for a stratospheric adjustment: Assuming that it reduces the instantaneous RF by ~20% (Myhre et al., 2013; Stevenson et al., 1998), a factor of 0.8 was applied to any O₃ RF that is an instantaneous RF (e.g., in the cases of Khodayari et al., 2014a, Khodayari et al., 2014b and Olsen et al. (2013)).
• •Reductions in CH₄-induced O₃ and SWV are defined as 50% (Myhre et al., 2013) and 15% (Myhre et al., 2007) of reported CH₄ RFs, respectively. This is applicable for studies that either originally did not provide CH₄-induced O₃ and SWV estimates (e.g., IPCC, 1999; Sausen et al., 2005; Olsen et al., 2013) or derived these RFs using another assumptions (e.g., Stordal et al., 2006; Köhler et al., 2008; Hoor et al., 2009; Gottschaldt et al., 2013; Köhler et al., 2013; Skowron et al., 2013; Khodayari et al., 2014a).

Further assumptions regarding data treatment are:

• • Frömming et al. (2012), Olivié et al. (2012), Khodayari et al. (2014b) and Kapadia et al. (2016) provide the short-term O₃ RFs only and p-TOMCAT in Stordal et al. (2006) calculates just the long-term effects; thus, these numbers are included in the respective NO_x variable analysis but do not contribute to the net NO_x estimate.
• •Whenever the same estimate appears repetitively in subsequent studies, it is treated as a single entry: this is the case for CAM4 short-term O₃ RF that appears in Khodayari et al., 2014a, Khodayari et al., 2014b and Olsen et al. (2013), CAM5 short-term O₃ RF that can be found in Khodayari et al., 2014a, Khodayari et al., 2014b and NASA ModelE2 short-term O₃ and CH₄ RFs presented by Unger et al. (2013) and Olsen et al. (2013).

In addition, the ERF estimates for the CH₄ term include shortwave RF (Etminan et al., 2016). The inclusion of shortwave forcing in the simplified expression increases CH₄ RF from aviation NO_x emissions by 23% (based on MOZART-3 CTM runs driven for all the aircraft emission inventories represented in the model ensemble) (Table D.1).

Ensemble values. This ensemble analysis covers a period of almost two decades; however, none of the RF per unit of emitted N estimates show any trends over time of publication and the spread in RF per unit of emitted N values has not changed. The short-term O₃ RF varies from 6.2 to 45.1 mW m⁻² (Tg (N) yr⁻¹)⁻¹, where these values come from the NASA ModelE2 (Olsen et al., 2013) and p-TOMCAT (Hoor et al., 2009) models, respectively. The long-term CH₄ RF varies from −27.9 to −8.1 mW m⁻² (Tg (N) yr⁻¹)⁻¹, from the p-TOMCAT (Köhler et al., 2008) and MOZART3 (Skowron et al., 2015) models, respectively. The spread of other CH₄-induced long-term effects follows that of CH₄. The net-NO_x RF varies from −17.5 to 11.9 mW m⁻² (Tg (N) yr⁻¹)⁻¹ from ECHAM/MESSy (Gottschaldt et al., 2013) and CAM4 (Khodayari et al., 2014a), respectively. The Results from the mid-1990s CTMs are within the envelope of RFs generated more recently (Fig. 3). The numbers from IPCC (1999) and related studies, Sausen et al. (2005) and Lee et al. (2009), where the non-CO₂ effects were originally calibrated to the results from IPCC (1999), do not alter the best NO_x RF values and their uncertainties (Table D.2).

Correlations. The correlations between the NO_x RF components are shown in Fig. D.1. In addition to the significant negative correlations between the short-term and the long-term aviation RF components, correlations between the net-NO_x effect and its components are also apparent, especially for the short-term O₃ and net-NO_x components; however, their strength is around half. The high correlations (p = 1, R² = 1) across the long-term effects is expected since CH₄-induced O₃ and SWV are all derived based on CH₄ RFs. In units of mW m⁻² (Tg(N yr⁻¹)⁻¹, 49% of this ensemble short-term O₃ RF is concentrated between 20 and 35, 43% of CH₄ RFs is found between −14 and −10, 41% of CH₄-induced O₃ RFs is between −7 and −5 and 45% of SWV RFs vary from −2.5 to −1.5. Of the normalized net-NO_x RFs resulting from this ensemble, 44% are observed between 5 and 10 mW m⁻² (Tg(N) yr⁻¹)⁻¹.

Transient vs. equilibrium. In calculating the CH₄ RF response to aviation NO_x emissions, the lack of steady-state conditions is an important consideration. Since methane (CH₄) has a lifetime of the order 8–12 years (largely model-dependent) any NO_x perturbation takes on the order ~40 years to come within 2% of the steady state solution. Moreover, the timescale of removal of CH₄ from the atmosphere is made longer through a positive chemical feedback (Prather, 1994). In order to overcome the necessity to run a global chemical transport model (CTM) with full chemistry for such long integrations, a parameterization to account for this perturbation was originally developed by Fuglestvedt et al. (1999) and has been widely adopted since then. However, with the significant annual increases in aviation NO_x emissions over the last several decades (Fig. D.2a) the CH₄ response does not reach its steady-state value in any given year of emissions, so the steady-state solution generally overstates the CH₄ response in a particular year from historical time-evolving emissions. Similar considerations apply to other sectors with substantial NO_x emissions such as shipping (Myhre et al., 2011). If steady-state conditions are utilized, there is a conceptual and quantitative mismatch when comparing the NO_x RF from aviation with other RF terms, since RF represents a particular condition at a point in time, not the steady-state conditions. To remedy this mismatch, Myhre et al. (2011) suggested that a factor accounting for the non-steady-state condition of CH₄ be introduced, thereby modifying the CH₄ impact for a given year of interest, and further suggested that for the aviation RF in the year 2000 the CH₄ term be reduced by approximately 35% for aircraft emissions using a simplified estimation derived from Grewe and Stenke (2008).

Here, we present an updated methodology to calculate the non-steady-state aviation-NO_x-induced CH₄ perturbation for the specific year of 2018. The method relies on transient and steady-state runs of the TROPOS 2D CTM. The results of the steady-state runs using constant emissions for a given year are compared with those of transient runs using background historical surface emissions from anthropogenic activities and the corresponding aviation NO_x emissions. The latter requires full implementation of time-varying CH₄ emissions into the model simulation, a requirement that is not a standard set-up for many of the CTM/GCMs currently in use where CH₄ conditions are defined from observations as fixed concentrations with relaxation terms introduced to accommodate perturbations to these concentrations. The use of CTM runs explicitly accounts for changing background atmospheric conditions over the integration period as well as the change in emission rate dependence of the O₃ and CH₄ responses.

Method. In order to compare these two methods, two types of experiments were performed:

• •Transient experiment: a long-term simulation with anthropogenic (surface and aviation) emissions evolving over time covering the period 1950–2050, using historical data up to 2000 and the RCP-4.5 scenario after 2000 (Fig. D.2a),
• •Steady-state experiment: a 100-year simulation with constant anthropogenic (surface and aviation) emissions representing the year 2000, 2018 or 2050 (Fig. D.2a); the steady-state CH₄ response starts to be observed 60–70 years into the run.

Each of these experiments was run twice, with and without aviation emissions, and the difference between these two Results defined as the aircraft response (e.g., Fig. D.2d-f). The initial concentrations of CH₄ were set using the observations from NOAA surface stations (Montzka et al., 2000) for 1950 and 2000; for the year 2050 the CH₄ concentrations are taken from projections of the MAGICC model (Meinshausen et al., 2011). The background anthropogenic emissions of CO, CH₄, NO_x, N₂O, and non-methane volatile organic carbon (NMVOC) compounds, as well as aircraft NO_x emissions, evolve during the period 1950–2050 (Lamarque et al., 2010; Clarke et al., 2007) (Fig. D.2a). The natural emissions from soils and oceans were kept constant and represent the year 2000 (Prather et al., 2001).

The TROPOS CTM is a latitudinally-averaged, two-dimensional Eulerian global tropospheric chemistry model extensively evaluated by Hough (1989, 1991). The model's domain extends from pole-to-pole (24 latitudinal grid cells) and from the surface to an altitude of 24 km (12 vertical layers). TROPOS is driven by chemistry, emissions, transport, removal processes and upper boundary conditions. There are 56 chemical species in the chemical mechanism of the model, which consists of 91 thermal reactions, 27 photolytic reactions and 7 more reactions, which include night-time NO₃ chemistry. The reaction rates and cross sections were updated to the evaluation of Sander et al. (2006) (see Skowron et al., 2009). There are no fixed concentrations within the model domain other than the upper boundary conditions, which are specified for long-lived species and for gases that have stratospheric sources. This 2D CTM has the disadvantage of zonal symmetry but has the advantage of an adequate chemical scheme and computational efficiency, such that long-term integrations can be reasonably performed. Owing to the aforementioned reasons, the O₃ response in TROPOS is overestimated by a factor of ~2 by comparison with a range of up-to-date 3D models. As a consequence, the CH₄ results in Fig. D.2d-f were reduced accordingly. This modification of the original TROPOS responses does not affect the core result of this study, which is the relative difference of CH₄ responses between transient and equilibrium methods.

Results. Fig. D.2b shows the evolution of the global CH₄ burden over the period 1950–2050 in the transient TROPOS simulation. There is a steady growth in the atmospheric CH₄ burden, with a small decline over the period 1997–2007 in response to the decrease in CH₄ emissions over the period 1990–2000. The steady-state simulations for the year 2000 and 2050 agree well (within 1%) with transient CH₄ responses for the respective years. A similar agreement is observed for modelled transient and steady-state CH₄ lifetimes in Fig. D.2c. Most of the CH₄ loss in the atmosphere is driven by OH and the oxidative capacity of the atmosphere changes over time (thus CH₄ lifetime as well), influenced by emissions of CO, NO_x, NMVOC or CH₄.

Fig. D.2c shows the evolution of global CH₄ lifetime (LT) over the period 1950–2050: there is a decrease in the CH₄ lifetime between 1950 and 2000 (until around 2007), whilst under the RCP-4.5 scenario the opposite is observed, with the CH₄ lifetime increasing by 3.5% by the end of 2050 compared with 2000. The TROPOS CH₄ lifetimes agree relatively well with other studies (e.g., Holmes et al., 2013; Voulgarakis et al., 2013; Dalsøren et al., 2016) not only in terms of absolute numbers but also the rate of changes; a detailed comparison is presented in Table D.3. The perturbation lifetime of CH₄ in TROPOS is 37% longer than its global lifetime and the sensitivity coefficient s = ∂ln(LT)/∂ln(CH₄) is 0.27, placing these estimates in the middle of model ranges (e.g., Prather et al., 2001; Holmes et al., 2011). These terms were calculated using a 5% increase of CH₄ global levels for the year 2000. There is no need to apply the feedback factor (1.37) to the TROPOS CH₄ estimates as it is already included in the observed responses; TROPOS does not have a fixed boundary conditions, so CH₄ and OH can freely interact.

Aircraft NO_x emissions, via the chemical coupling to OH and HO₂, enhance OH, which reduces the global CH₄ lifetime. Fig. D.2d shows the evolution of the CH₄ lifetime reduction in the transient 1950–2050 simulation and in steady-state runs for conditions representing the years 2000 and 2050. In the transient run, there is a steady decrease of global CH₄ lifetime as a consequence of a constant increase of aviation NO_x emissions during the period 1950–2050. The agreement in 2000 and 2050 between the transient and steady-state CH₄ lifetime reductions is within 6% (on a global scale) (see Table D.3). These relatively small differences in CH₄ lifetime lead to much more pronounced differences in the associated global CH₄ burdens as shown in Fig. D.2e. In contrast to the lifetime results, the CH₄ burden response in the transient run lags behind the steady-state CH₄ response with differences of 27% in the year 2000 and 20% in the year 2050. Similarly, the calculations for 2018 emissions yield a multiplicative correction factor of 0.79 (Fig. D.2f), which has been incorporated into the ERF values of CH₄, long-term O₃ and SWV shown in Fig. 5.

The CH₄ results contrast with O₃ changes from aircraft NO_x emissions, which agree within 3% between transient and steady-state experiments with aircraft O₃ burdens of 10.3 and 10.6 Tg (O₃), respectively, in the year 2000. These TROPOS O₃ magnitudes are at the upper limit of model ranges, as present-day aircraft O₃ perturbations found in the literature vary from 3 to 11 Tg (O₃) (e.g., Hoor et al., 2009; Holmes et al., 2011; Khodayari et al., 2014a). The aircraft O₃ burden increases by 41% in 2050, reaching 17.2 and 18.0 Tg(O₃) for transient and steady-state experiments, respectively. This agrees with other studies (e.g., Olsen et al., 2013) that report a multi-model average increase of 44% in O₃ burden from future aircraft NO_x emissions under the RCP-4.5 scenario.

The present approach is in general agreement with that presented by Grewe and Stenke (2008), which accounts for CH₄ concentrations not being in steady-state with OH changes in the year of simulation. The present CTM Results further demonstrate the importance of explicitly calculating CH₄ changes in response to time-dependent aviation NO_x emissions rather than assuming constant emissions. The difference between transient and steady-state CH₄ for the year 2000 found with TROPOS is smaller than that resulting from the Grewe and Stenke (2008) approach (Myhre et al., 2011) (27% and 35%, respectively). Table D.4presents a further comparison of CH₄ correction factors derived in this study. The systematic differences are likely due to the Grewe and Stenke (2008) values being based on a simplified chemistry/climate model (AirClim) and the present TROPOS simulations having a different experimental setup (all our emissions (surface + aircraft) are time-varying) and a full chemical reaction scheme with explicit calculations performed on time-varying emissions. Indeed, if TROPOS is run with constant background emissions representing the year 2000 in a similar manner using Grewe and Stenke (2008) methodology, the difference between transient and steady-state CH₄ for the year 2000 increases from 27% to 31%. This change shows that background emissions modify the CH₄ correction factor and further emphasizes the need to have surface and aircraft emissions that simultaneously follow historical pathways. In other studies using the Grewe and Stenke (2008) methodology, CH₄ correction factors vary from 0.74 to 1.15 depending on the investigated year (2025 or 2050) and aircraft emission scenario (SRES A1B, B1 and B1 ACARE) (the factor can be larger than 1 if the aircraft emissions are assumed to decrease in the preceding years) (Hodnebrog et al., 2011, 2012).

Uncertainties in the CH₄ correction factor are associated mainly with inter-model differences and the applied emission scenarios; the correction factor is sensitive, within ~10%, to inter-model differences (based on two models, TROPOS and AirClim) and it can vary by another ± 10% depending on emission scenario (based on a range of RCP projections up to 2050). Given that the uncertainties of the CH₄ correction factor on the net-NO_x RF are rather small, especially when compared with overall uncertainties, we do not include in the estimated uncertainty of the net-NO_x RF value a separate uncertainty due to the correction factor.

E. Contrail cirrus

The global contrail cirrus RF is calculated by homogenizing existing estimates through the use of specific scaling factors. The factors relate to the choice of air traffic inventory and its basis year; the use of the full 3D flight distance; the use of hourly air traffic data; the feedback of natural clouds; and correcting for weaknesses in the radiative transfer calculations. The corrections and scaling actions are:

• •The estimate of Chen and Gettelman (2013) was corrected by redoing the CAM simulation using a lower ice crystal radius of 7 μm and a larger contrail cross-sectional area of 0.09 km² for the initialization of contrails at an age of about 15–20 min, in agreement with observations (Schumann et al., 2017). The resulting change in cirrus cloudiness including the adjustment in cloudiness due to the presence of contrail cirrus leads to a radiative forcing of 57 mW m⁻².
• •A scaling S₁ of 1.4 is applied for estimates based on the AERO2k inventory for the year 2002 instead of the AEDT inventory for the year 2006 (Bock and Burkhardt, 2016);
• •A scaling S₂ of 1.14 is applied to estimates that are based on track distance instead of slant distance (Bock and Burkhardt, 2016). The ‘slant’ air traffic distance is the full flight distance and not the ground projected ‘track’ distance.
• •A scaling S₃ of 0.87 is applied to estimates that used monthly instead of hourly resolved air traffic data. This scaling is based on an estimate for the impact of the temporal resolution of the air traffic data of −25% to −30% within CAM (Chen et al., 2012) and one of no significant change in ECHAM4-CCMod.
• •A scaling S₄ of 1.15 is applied to account for the underestimation of RF in radiative transfer calculations that use frequency bands instead of line by line calculations (Myhre et al., 2009).

The study details and scaling results are shown in Table E.1. Weighting each estimate equally, the best estimate of global contrail cirrus RF is approximately 66 mW m⁻². As noted in the main text, the Chen and Gettelman (2013) calculation is interpreted as being closer to an ERF than an RF, so was excluded from this averaging. This mean RF estimate does not include the RF due to contrails forming within natural cirrus. Uncertainty due to scalings S₃–S₄ is included in the uncertainty discussion below, whereas uncertainty in scalings S₁–S₂, namely updating the ECHAM4-CCMod estimates using sensitivities from ECHAM5-CCMod, is neglected.

The statistical uncertainty of global contrail cirrus RF cannot be estimated from the small number of available studies. Uncertainties affecting our contrail cirrus estimates are, on the one hand, due to (A) uncertainties in the radiative response to the presence of contrail cirrus and, on the other hand, (B) uncertainties in the upper tropospheric water budget and the contrail cirrus scheme. In most cases, we can only infer very rough estimates for the uncertainties related to specific processes.

(A) Uncertainties associated with the radiative response to contrail cirrus are:

• A1Uncertainty related to the model's radiative transfer scheme of approximately 35% (Myhre et al., 2009).
• A2Uncertainty in the inhomogeneity of ice clouds within a grid box of a climate model (Carlin et al., 2002; Pomroy and Illingworth, 2000), the vertical cloud overlap, and the use of plane parallel geometry as compared to full 3D radiative transfer (Gounou and Hogan, 2007), which together amount to approximately 35%.
• A3Uncertainty estimating radiative transfer in a global climate model in the presence of very small ice crystals within young contrails, which may amount to about 10% (Bock and Burkhardt, 2016). The uncertainty is dependent on the contrail cirrus ice water content.
• A4Uncertainty due to the ice crystal habit is approximately 20% according to Markowicz and Witek (2011).
• A5Uncertainty in the radiative transfer due to soot cores within the contrail cirrus ice crystals is thought to be large, as the change in the shortwave (SW) albedo is large (Liou et al., 2013). The soot impact on contrail cirrus RF has not yet been quantified.

Overall, uncertainty in the radiative response to contrail cirrus (excluding A3) is estimated to be about 55%, assuming independence of different uncertainties and excluding the impact of ice crystal soot cores. The uncertainty A3 is included in the uncertainty estimate under (B) because A3 and B2 are dependent uncertainties.

(B) Uncertainty in contrail cirrus RF associated with the upper-tropospheric water budget and the contrail cirrus scheme are:

• B1Uncertainty in contrail cirrus RF associated with the uncertainty in upper-tropospheric ice supersaturation. This results from a lack of knowledge in ambient conditions due to the low vertical resolution of satellite instruments (Lamquin et al., 2012) and to the ability of models to reproduce the observed statistics of ice supersaturation. This contributes about 20% to uncertainty.
• B2There is uncertainty related to ice crystal number densities within young contrails. Ice nucleation within the plume can vary drastically depending on the water supersaturation reached within the plume and on the soot emissions (Kärcher et al., 2015, 2018). This dependency on the atmospheric state leads to a reduction in the number of nucleated ice crystals in particular in the tropics and at lower flight levels (Bier and Burkhardt, 2019) leading to a large uncertainty in the impact of tropical and subtropical air traffic. Depending on the atmospheric state and ice crystal numbers, a varying fraction of ice crystals can be lost in the contrail vortex phase (Unterstrasser, 2014). We assume an uncertainty in average contrail ice crystal numbers after the vortex phase of about 50% leading to an uncertainty in contrail cirrus RF of about 20%. This estimate of the sensitivity of contrail cirrus RF to ice crystal numbers in newly formed contrails is based on simulations with ECHAM5-CCMod (Burkhardt et al., 2018).
• B3The uncertainty in the lifetime of contrail cirrus, affecting the day-/night-time contrail cover, has only a small impact on the estimated contrail cirrus RF (Chen and Gettelman, 2013; Newinger and Burkhardt, 2012). We estimate the associated uncertainty to be 5–10%.
• B4From the sensitivity of the contrail cirrus RF to the temporal resolution in the air traffic dataset in ECHAM5 and CAM, we deduce an uncertainty of about 10%.
• B5The estimate of the feedback of natural clouds, due to contrail cirrus changing the water and heat budget of the upper troposphere, is very uncertain and has not been properly quantified yet (Burkhardt and Kärcher, 2011; Schumann et al., 2015). We assume here the uncertainty related to this estimate to be only slightly smaller than the estimate itself, or about 15%.
• B6Uncertainty in the RF estimate of Chen and Gettelman (2013) to assumptions in the initial ice-crystal radii and contrail cross-sectional areas is about 33%.

We assume independence of the uncertainties except for the dependence of A3 and B3 on the uncertainty in B2. The overall uncertainty due to the water budget and the contrail cirrus scheme (including uncertainty A3) is about 40% and more than 50% in the case of the Chen and Gettelman (2013). From the two different sources of uncertainty (list A, radiative, and list B, contrail cirrus properties, above) we calculate an overall contrail cirrus RF uncertainty of about 70%, assuming independence of the overall uncertainties described in A and B.

Note that we do not attempt to infer an estimate for the uncertainty of the factor ERF/RF. When calculating the contrail cirrus ERF, the error range given refers to the error range of contrail cirrus RF and not ERF.

F. Emission metrics calculations

We calculate the AGWP and AGTP, and corresponding GWPs and GTPs, for aviation CO₂, NO_x (which encompasses the ERF of short-term O₃, CH₄, CH₄-induced O₃ and SWV), soot, SO₂, and contrail cirrus. The methodology and analytical expressions for the emissions metrics are described in detail in previous literature (e.g., Fuglestvedt et al., 2010; Myhre et al., 2013). The impulse response function (IRF) that describes the atmospheric decay of CO₂ upon emission is taken from Joos et al. (2013). For the other species, the atmospheric decay is given by a constant e-folding time taken as the ‘perturbation lifetime’. The lifetimes used here are broadly consistent with Fuglestvedt et al. (2010). The radiative efficiency (RE) for CO₂ is calculated using year 2018 background concentrations of 407 ppm (annual mean, from monthly mean observed concentrations from NOAA GMD - ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_mm_gl.txt). This yields a RE of 1.68 × 10⁻¹⁵ W m⁻² kg⁻¹), 4% lower than used in the IPCC Fifth Assessment report (AR5) (Myhre et al., 2013). The climate response IRF is taken from Boucher and Reddy (2008). The latter has an inherent equilibrium climate sensitivity (ECS) of 1.06K (W m⁻²)⁻¹, equivalent to a 3.9K equilibrium response to a doubling of CO₂.

For the calculation of the average rate of CO₂-warming-equivalent emissions for aviation non-CO₂ forcings (E_CO2e*) under the GWP* metric in Table 5, we use the relationship between recent changes in effective RF and CO₂-equivalent emissions from Allen et al. (2018) (or Equation (1) with $\alpha =0)$,

E_CO2e* = [ΔF / Δt] × [H / AGWP_H(CO2)] (F.1)

where ΔF in Eqn (F.1) is the change in ERF over the recent period, Δt, and AGWP_H(CO2) is the absolute global warming potential of CO₂ at time horizon H. We use updated AGWP_H(CO2) values incorporating the updated radiative efficiency of CO₂ as described in the previous paragraph. Allen et al. (2018) used a backward-looking period of 20 years as Δt, whereas here we use a backward-looking 18-yr period as our time series of ERF components only extends back to 2000.

G. List of Acronyms and abbreviations used in tables and figures of the Appendices

ACARE

Advisory Council for Aeronautical Research in Europe

ACCMIP

Atmospheric Chemistry and Climate Model Intercomparison Project

AEDT

Aviation Environmental Design Tool

AEM

Advanced Emission Model

AERO2K

Global aircraft emissions data project for climate impacts evaluation

AGAGE

Advanced Global Atmospheric Gases Experiment

CAM

Community Atmosphere Model

CCMod

Contrail Cirrus Module

CH₃CCl₃

Methyl chloroform

COCIP

Contrail Cirrus Prediction Tool

CTM

Chemical Transport Model

ECHAM

European Centre/Hamburg Model

IPCC

Intergovernmental Panel on Climate Change

MAGICC

Model for the Assessment of Greenhouse Gas Induced Climate Change

MOZART

Model for OZone And Related chemical Tracers

NOAA

National Oceanic and Atmospheric Administration

QUANTIFY

Quantifying the Climate Impact of Global and European Transport System

REACT4C

Reducing Emissions from Aviation by Changing Trajectories for the benefit of Climate

RCP

Representative Concentration Pathway

SRES

Special Report on Emission Scenarios

TAR

Third Assessment Report

TRADEOFF

Aircraft emissions: contribution of different climate components to changes in radiative forcing–tradeoff to reduce atmospheric impact

TROPOS

2D global TROPOSpheric model

WDCGG

World Data Centre for Greenhouse Gases

Table D.1.

The CH₄ RFs derived for all the aircraft emission inventories that are present in the model ensemble.^a

Inventories	CH4 RF, mW m−2
	Old	New
AEDT	−6.67	−8.22
AEM	−6.82	−8.41
AERO2K	−7.09	−8.74
REACT4C	−6.97	−8.59
QUANTIFY	−6.96	−8.58
TRADEOFF	−7.11	−8.76

^a Values are those represented in the model ensemble based on MOZART-3 CTM simulations (Old) and recalculated values using a revised simplified expression for the CH₄ RF (New) as presented by Etminan et al. (2016). The NO_x emissions of each inventory are normalized so that all RFs are scaled to the same global total emissions (0.71 Tg(N) yr⁻¹) as in the REACT4C model.

Table D.2.

The best NO_x RFs per unit emission derived for datasets that include and exclude late 1990s numbers and related estimates, see text for details.

Components	Value	Uncertainty*	Value	Uncertainty*
	(mW m−2 (Tg (N) yr−1)−1
	with IPCC (1999)		without IPCC (1999)
Short-term O3	25.6	$\pm$7.3	25.1	$\pm$7.2
CH4	−13.8	$\pm$4.7	−13.4	$\pm$4.5
CH4-induced O3	−6.9	$\pm$2.3	−6.7	$\pm$2.3
SWV	−2.1	$\pm$0.7	−2.0	$\pm$0.7
Net NOx	3.9	$\pm$5.7	4.0	$\pm$5.8

*Stated uncertainties are one standard deviation (68% confidence interval).

Table D.3.

Methane response in TROPOS and other studies

Variable	Year	2D CTM, TROPOS		Literature
		Transient	Steady-statea	Study	Ref	Model/Years	Variable estimate/change
CH4 burden, Tg	2000	4770.8	4785.1
				IPCC TAR		1998	4850 Tg
				Voulgarakis et al. (2013)		ACCMIP	4750d Tg
				Dalsøren et al. (2016)		Oslo CTM3	4560d Tg
				Dalsøren et al. (2016)		1970–2012	+15%
				This studyc			+13%
	2050	5051.6	5081.4	Voulgarakis et al. (2013) Voulgarakis et al. (2013) This studyc		ACCMIP	5000d Tg +5.3d % +5.9%
						2000–2050
CH4 abundance, ppb	2000	1784.2	1787.5	Observations		NOAA AGAGE WDCGG	1773 ppb 1774 ppb 1783 ppb
	2050	1886.2	1897.6	Meinshausen et al. (2011)		MAGICC	1833 ppb
CH4 lifetime (τCH4+OH)b, yr	2000	10.6	10.5	Prather et al. (2012) Voulgarakis et al. (2013) Holmes et al. (2013) This studyc Voulgarakis et al. (2013) This studyc		CH3CCl3-based	11.2 ± 1.3 yr 9.8 ± 1.6 yr −2.2 ± 1.8% −2.06% −4% −2%
						ACCMIP
						1980/85–2000/05
						1980–2000
	2050	11.0	11.0	Voulgarakis et al. (2013) This studyc		2000–2050	+1.0d % +3.5%
aircraft CH4 lifetime (τCH4+OH), yr	2000	−0.137	−0.145	Hoor et al. (2009) Myhre et al. (2011) Holmes et al. (2011) Søvde et al. (2014) This studyc		AERO2K QUANTIFY Model ensemble REACT4C dENOx = QUANTIFY	−1.55% Tg(N)−1
							−1.46% Tg(N)−1
							−1.77% Tg(N)−1
							−1.36% Tg(N)−1
							−1.48% Tg(N)−1
	2050	−0.293	−0.311	Hodnebrog et al. (2011)		SRES B1	−1.61% Tg(N)−1
						B1 ACARE	−1.48% Tg(N)−1
				Hodnebrog et al. (2012)		SRES A1B	−1.22% Tg(N)−1
				Khodayari et al. (2014a)		AEDT Scenario1	−1.88% Tg(N)−1
						AEDT Baseline	−1.59% Tg(N)−1
				This studyc		RCP45	−1.36% Tg(N)−1

^athis is an average of the last 10 years of simulations

^bthe chemcial (τ_CH4+OH) lifetime is around 7% greater than the total CH₄ lifetime, as modelled by TROPOS

^cnumbers are based on transient simulation

^dnumbers might not be very accurate as they are read directly from the graphs found in the respecitve papers

Table D.4.

Calculated CH₄ correction factors

Aviation emissions year	CH4 correction factors
	This study	Grewe and Stenke (2008) methodology
2000	0.73	0.65
2005	0.75	0.73
2011	0.78	0.81
2018	0.79	0.86

Table E.1.

Scaling of contrail cirrus RF and ERF Results ^a

Model	Inventory	Representation of flight distance	RF (mW/m2)	Scalings	Scaled RF (mW/m2)b	Reference
ECHAM4-CCMod	AERO2K 2002	track	38	S1, S2, S4	70	Burkhardt and Kärcher (2011)
ECHAM5-CCMod	AEDT 2006	slant	56	S3, S4	56	Bock and Burkhardt (2016)
COCIP	AEDT 2006	flight vectors	63	S4	72	Schumann et al. (2015)
CAM5	AEDT 2006	slant	13 [57]c	S3, S4	57	Chen and Gettelman (2013)
Best estimate					66d

^aAdapted from Table 1 of Bock and Burkhardt (2016).

^bRF that would be expected in 2006 when using slant distance from the AEDT inventory with hourly resolution.

^cAn updated simulation (see text) yielded 57 mW m⁻².

^dThe best estimate is of RFs, and excludes the Chen and Gettelman (2013) results since this is closer to an ERF (see main text).

Table F.1a.

Emission metrics and corresponding CO₂-equivalent emissions for the ERF components of 2018 aviation emissions and cloudiness using CO₂ IRF without C-cycle feedbacks from Gasser et al., 2017, and climate IRF from Boucher and Reddy (2008).

Metrics
ERF term	GWP20	GWP50	GWP100	GTP20	GTP50	GTP100
CO2	1	1	1	1	1	1
Contrail cirrus (Tg CO2 basis)	2.39	1.15	0.68	0.70	0.11	0.10
Contrail cirrus (km basis)	40	19	11	12	1.9	1.6
Net NOx	637	216	122	−231	−75	14
Aerosol-radiation
Soot emissions	4409	2125	1252	1295	210	177
SO2 emissions	−856	−412	−243	−251	−41	−34
Water vapor emissions	0.22	0.11	0.06	0.07	0.01	0.009

Table F.1b.

Emission metrics and corresponding CO₂-equivalent emissions for the ERF components of 2018 aviation emissions and cloudiness using CO₂ IRF without C-cycle feedbacks, and climate IRF from Gasser et al. (2017).

Metrics
ERF term	GWP20	GWP50	GWP100	GTP20	GTP50	GTP100
CO2	1	1	1	1	1	1
Contrail cirrus (Tg CO2 basis)	2.39	1.15	0.68	0.3	0.19	0.15
Contrail cirrus (km basis)	40	19	11	4	3.3	2.6
Net NOx	637	216	122	−420	−18	22
Aerosol-radiation
Soot emissions	4409	2125	1252	466	360	284
SO2 emissions	−856	−412	−243	−90	−70	−55
Water vapor emissions	0.22	0.11	0.06	0.03	0.018	0.014

Fig. D.1.

Matrix of pair-wise scatter plots of RF values from NO_x terms: short-term O₃, CH₄, CH₄-induced O₃, SWV and net NO_x (i.e., the sum of all 4 components), all represented as normalized RFs (mW m⁻² (Tg(N)yr⁻¹)⁻¹) from the ensemble studies (see details in text). The red line is the linear fit, the ellipse shows the 95% confidence level and histograms present frequencies.

Fig. D.2.

(a) Past and future anthropogenic emissions of CO, CH₄, NO_x, NMVOC, N₂O and aircraft NO_x (IIASA RCP Database: http://www.iiasa.ac.at/web-apps/tnt/RcpDb/). Dots represent conditions for ‘constant 2000’ and ‘constant 2050’ simulations. (b) Evolution of the global CH₄ burden in TROPOS for transient aircraft NO_x emissions combining historical emissions (1950–2000) and RCP-4.5 emissions (2000–2050); and constant emissions for the years 2000 and 2050. (c) Global CH₄ lifetime due to aircraft NO_x emissions in TROPOS for transient emissions combining historical emissions (1950–2000) and RCP-4.5 emissions (2000–2050); and constant emissions for the years 2000 and 2050. (d) Global CH₄ lifetime reduction due to aircraft NO_x emissions in TROPOS for transient emissions combining historical emissions (1950–2000) and RCP-4.5 emissions (2000–2050); and constant emissions for the years 2000 and 2050. The dashed lines represent 2000 and 2050 equilibrium values (light and dark blue) and 2000 and 2050 transient values (red). (e) Global CH₄ burden reduction due to aircraft NO_x emissions in TROPOS for transient emissions combining historical emissions (1950–2000) and RCP-4.5 emissions (2000–2050); and constant emissions for the years 2000 and 2050. The dashed lines represent 2000 and 2050 equilibrium values (light and dark blue) and 2000 and 2050 transient values (red). (f) Global CH₄ burden reduction due to aircraft NO_x emissions in TROPOS for transient emissions combining historical emissions (1950–2000) and RCP-4.5 emissions (2000–2050); and constant emissions for the year 2018. The dashed lines represent 2018 equilibrium (green) and transient values (red).

Supplementary data

The following is the Supplementary data to this article: