Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Aug 19;5(34):21824–21835. doi: 10.1021/acsomega.0c02887

Unconventional Type III Halogen···Halogen Interactions: A Quantum Mechanical Elucidation of σ-Hole···σ-Hole and Di-σ-Hole Interactions

Mahmoud A A Ibrahim 1,*, Nayra A M Moussa 1
PMCID: PMC7469378  PMID: 32905309

Abstract

graphic file with name ao0c02887_0009.jpg

Herein, two unconventional type III halogen···halogen interactions, namely, σ-hole···σ-hole and di-σ-hole interactions, were reported in a series of halogenated complexes. In type III, the A-halogen···halogen angles are typically equal to 180°, and the occurrence of σ-hole on halogen atoms is mandatory. Using diverse quantum mechanical calculations, it was demonstrated that the occurrence of such interactions with binding energies varied from −0.35 to −1.30 kcal/mol. Symmetry-adapted perturbation theory-based energy decomposition analysis (SAPT-EDA) revealed that type III interactions are dominated by dispersion forces, while electrostatic forces are unfavorable. Cambridge Structure Database (CSD) survey unveiled the experimental evidence for the manifestation of σ-hole···σ-hole interactions in crystal structures. This work might be deemed as a foundation for a vast number of forthcoming crystal engineering and materials science studies.

1. Introduction

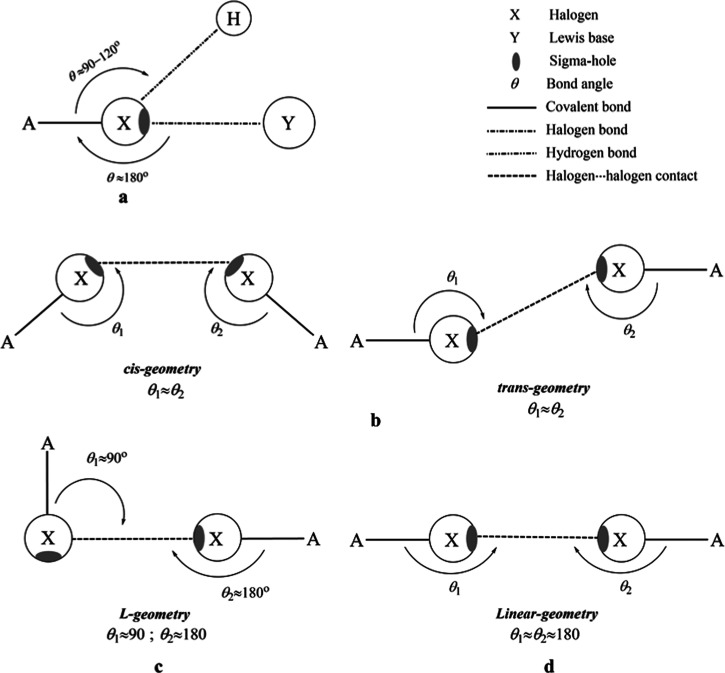
Halogens are widely utilized to stabilize drug–protein1 and supramolecular systems.2,3 This is due to the ability of halogens to participate as Lewis bases and acids in noncovalent interactions with Lewis acids and bases, forming hydrogen4 and halogen bonds,5,6 respectively (Figure 1a). This dual behavior of halogens is mainly attributed to the anisotropic distribution of electron density around the halogen atom, forming a positive (or less negative) electrostatic potential along the A–X covalent bond (called σ-hole).7−12 The ability of halogen-containing molecules to interact with Lewis acid/base at a halogen···Lewis acid/base angle of 180° has been reported.13 In addition to hydrogen and halogen bonds, halogens participate in halogen···halogen inter- and intramolecular interactions, playing an important role in determining crystal packing and cohesion.11,14,15 Characterization of halogen···halogen contacts has been a subject of a variety of theoretical and crystallographic studies.9,16,17 According to the literature, halogen···halogen contacts can be classified into two main types: type I, in which the A-halogen···halogen angle (θ1) is nearly equal to the halogen···halogen-A angle (θ2) (Figure 1b), and type II, in which the θ1 angle is about 180° and θ2 is about 90° (Figure 1c).16,18,19 Two different geometries could be taken for type I halogen···halogen contact, the cis- and trans-geometrical structures, as illustrated in Figure 1b. The interpretation of type I and II interactions can be given as a donor–acceptor interaction between an σ-hole on one halogen atom and a negative belt on the second halogen atom.20 As mentioned earlier, the main force behind type I is van der Waals interaction, while the electrostatic force is the dominant factor in type II.21,22

Figure 1.

Figure 1

Open in a new tab

Schematic representation for (a) the dual behavior of the A–X molecule in noncovalent interactions, (b) cis- and trans-geometries of type I halogen···halogen interactions, (c) type II halogen···halogen interactions, and (d) type III halogen···halogen interactions.

Very recently, σ–σ-centered type II terminology has been proposed to describe fluorine-centered noncovalent interactions of atomic sites with positive or negative electrostatic potential.23−25 So far, however, the ability of halogen-containing molecules to form type III halogen···halogen interaction, in which the θ1 and θ2 angles are typically equal to 180°, has not been yet well characterized. Consequently, the current study was designed to assess the versatility of halogen-containing molecules to form type III halogen···halogen interactions. The occurrence of positive σ-hole on both halogen atoms (i.e., A–X and A–X′) is a mandatory condition to characterize the halogen···halogen interaction with θ1 and θ2 angles of 180° as type III interaction. Based on the involved halogen-containing molecules, type III can be classified into (i) σ-hole···σ-hole (A–X···X–A) interaction, in which the halogen···halogen interaction occurs between two identically charged halogens, and (ii) di-σ-hole (A–X···X′–A) interaction, in which two different or not identically charged halogens are utilized.

In this study, geometrical optimization, molecular electrostatic potential (MEP), and maximum positive electrostatic potential (Vs,max) calculations will be carried out on halogen-containing molecules, namely, hydrogen halide (HX), halobenzene (C6H5X), and halomethane (CH3X). With the help of the point-of-charge (PoC) approach, ±σ-hole tests will be executed to reveal the ability of investigated halomolecules to interact with both the Lewis base and acid from the electrostatic perspective. Moreover, potential energy surface (PES) scans will be performed for A–X···X/X′–A (where A = H, C6H5, and CH3, and X/X′ = F, Cl, Br, and I) complexes. At the most favorable halogen···halogen distance, binding energies will be benchmarked at the CCSD(T)/CBS level of theory. Quantum theory of atoms in molecules (QTAIM), noncovalent interaction (NCI) index, and symmetry-adapted perturbation theory-based energy decomposition analysis (SAPT-EDA) will be established to explore the nature of the type III halogen···halogen interactions. Furthermore, a survey of the Cambridge Structure Database (CSD) will be conducted to explore the occurrence of such unconventional interactions in crystal structures. This study provides a solid characterization of the features and nature of type III halogen···halogen interactions, which will lead in turn to the enhancement of research in supramolecular chemistry and materials science.

2. Results and Discussion

2.1. MEP, Vs,max, and ±σ-Hole Test

Molecular electrostatic potential (MEP) is a reliable method to conceive the electron-deficient and electron-rich regions on molecular systems, indicating the electrophilic and nucleophilic sites.26,27 In this study, MEPs were generated for all of the optimized monomers at the MP2/aug-cc-pVTZ (with PP functions for Br and I atoms) level of theory and then mapped on 0.002 au electron density contours. MEP maps for all of the studied monomers are depicted in Figure 2.

Figure 2.

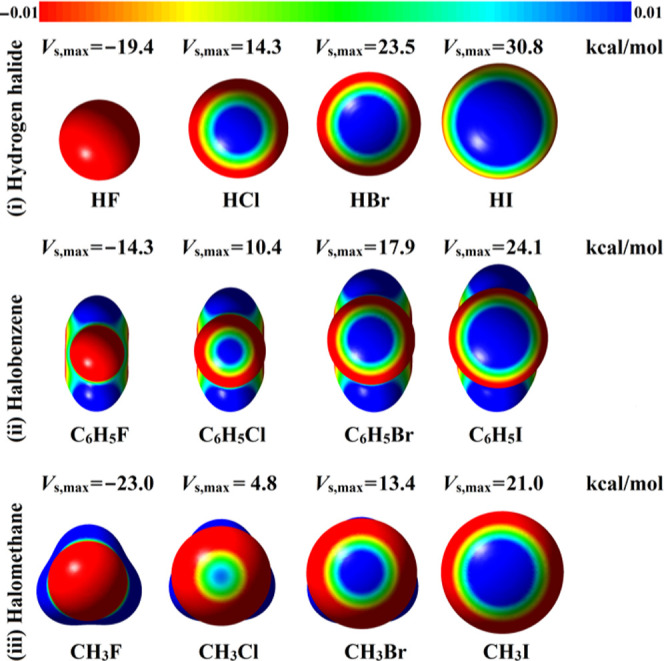
Figure 2

Open in a new tab

Molecular electrostatic potential (MEP) maps of hydrogen halide (HX), halobenzene (C6H5X), and halomethane (CH3X) molecules plotted on to 0.002 au electron density contours. The electrostatic potential varies from −0.01 (red) to +0.01 (blue) au. The calculated maximum positive electrostatic potentials (Vs,max) of the studied molecules are given in kcal/mol.

According to MEP maps, σ-hole was observed along the extension of the A–X covalent bond on the molecular surface of halogen atoms in all studied halomolecules except in the fluorine-containing molecules. This exception might be attributed to the small size of the fluorine atom and its high electronegativity. Furthermore, the size of σ-hole increased with increasing atomic size of the halogen atom in the order Cl < Br < I.28,29

For computing the numerical value of σ-hole, the maximum positive electrostatic potential (Vs,max) calculations were carried out on the optimized monomers. The values of Vs,max for all halomolecules are given in Figure 2. According to the Vs,max results, the magnitude of σ-hole decreased as the electronegativity of the halogen atom increased to become negative in the case of fluorine-containing molecules. For the studied halomolecules, Vs,max increased in the order halomethane < halobenzene < hydrogen halide. For instance, Vs,max values of 21.0, 24.1, and 30.8 kcal/mol were obtained for iodomethane, iodobenzene, and hydrogen iodide, respectively.

It is worth noting that the absence of positive σ-hole on the investigated fluorine-containing molecules indicates their inability to form type III interactions, as discussed in the Section 1. As a result, all fluorine-centered interactions will be characterized as traditional halogen bonds between the negative fluorine atom and the positive σ-hole on the other halogen atom.

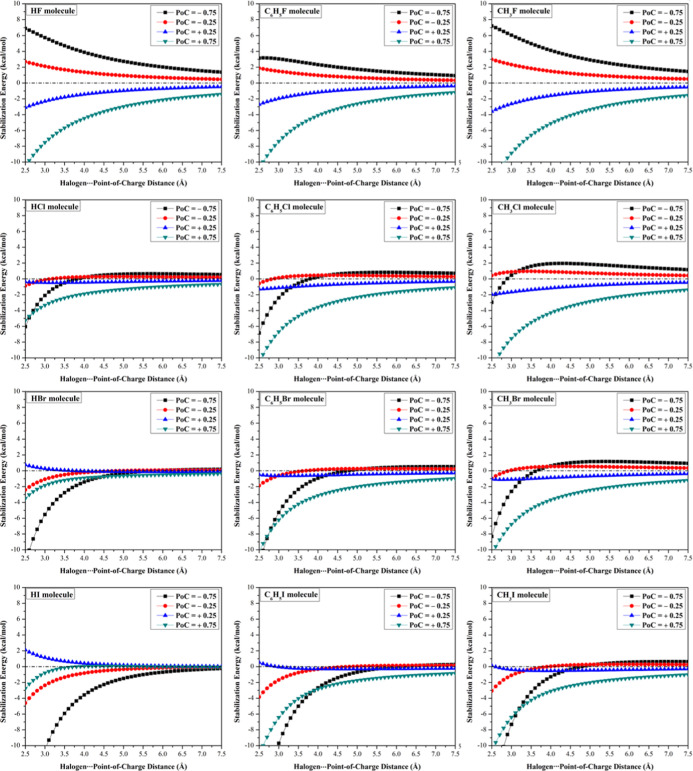
To assess the electrostatic potentiality of all studied halomolecules to participate in noncovalent interactions with Lewis base and acid at an A–X···base/acid angle of 180°, –σ-hole and +σ-hole tests were performed, respectively. The correlation between molecular stabilization energy and X···PoC distance was studied in the range from 2.5 to 7.5 Å along the x-axis with a step size of 0.1 Å (Figure 3). Molecular stabilization energies of the A–X···PoC systems calculated in the presence of ±0.25 and ±0.75 au PoCs at an X···PoC distance of 2.5 Å with an A–X···PoC angle (θ) of 180° are compiled in Table 1.

Figure 3.

Figure 3

Open in a new tab

Molecular stabilization energies of the HX···, C6H5X···, and CH3X···PoC systems in the presence of PoC with values of ±0.25 and ±0.75 au at the X···PoC distance ranging from 2.5 to 7.5 Å and the A–X···PoC angle (θ) of 180°.

Table 1. Molecular Stabilization Energies of the A–X···PoC (Where A = H, C6H5, and CH3X) Systems in the Presence of PoC with Values of ±0.25 and ±0.75 au at an X···PoC Distance of 2.5 Å and an A–X···PoC Angle of 180°.

  molecular stabilization energy (Estabilization, kcal/mol)
PoC = −0.25 au
 PoC = −0.75 au
molecule F Cl Br I F Cl Br I
HX 2.69 –0.87 –2.42 –4.61 6.90 –6.05 –11.78 –20.44
C6H5X 1.86 –0.58 –1.88 –3.85 3.15 –6.85 –11.93 –20.03
CH3X 2.98 0.42 –0.97 –3.07 7.22 –2.97 –8.31 –16.76
  molecular stabilization energy (Estabilization, kcal/mol)
PoC = +0.25 au
 PoC = +0.75 au
molecule F Cl Br I F Cl Br I
HX –3.09 –0.37 0.76 2.11 –10.54 –5.24 –3.49 –2.76
C6H5X –2.71 –1.30 –0.49 0.53 –10.83 –10.60 –10.25 –11.24
CH3X –3.58 –1.97 –1.06 0.13 –12.66 –11.29 –10.57 –10.69
Open in a new tab

According to the results of the –σ-hole test, molecular stabilization energies were observed for all studied halomolecules in the presence of negative PoC with an exception for fluorine-containing molecules due to the absence of σ-hole (see the MEP maps in Figure 2). Furthermore, the molecular stabilization energy decreased as the X···PoC distance increased and the electronegativity of the halogen atom increased. For instance, molecular stabilization energies of HI···, HBr···, and HCl···PoC systems with a PoC value of −0.25 au at the X···PoC distance of 2.5 Å were found to be −4.61, −2.42, and −0.87 kcal/mol, respectively. Moreover, increasing the negativity of PoC value (i.e., Lewis basicity) enhanced the molecular stabilization energies of the A–X···PoC systems. For instance, the presence of PoC with values of −0.25 and −0.75 au for the CH3I···PoC system at a distance of 2.5 Å led to molecular energies of −3.07 and −16.76 kcal/mol, respectively.

In the case of +σ-hole test, almost all of the studied halomolecules were observed with substantial molecular stabilization energies, especially in the presence of +0.75 au PoC at short A–X···PoC distances (Figure 3). It is worth pointing out that molecular destabilization and stabilization energies for A–I···PoC systems were recorded in the presence of +0.25 and +0.75 au PoC values, respectively. For the CH3I···PoC system, for instance, the molecular energies were 0.13 and −10.69 kcal/mol for +0.25 and +0.75 au PoC values, respectively. This informative result ensured the prominent role of polarization in the case of large PoC, which is in great accordance with our previous work.13 Overall, molecular stabilization energies for the studied halomolecules in the presence of positive PoC were found to be inversely correlated with Vs,max values. For instance, molecular energies of HX···PoC systems with Vs,max values of −19.4, 14.3, 23.5, and 30.8 kcal/mol (for X = F, Cl, Br, and I, respectively) were found to be −10.54, −5.24, −3.49, and −2.76 kcal/mol, respectively, in the presence of PoC of +0.75 au at an X···PoC distance of 2.5 Å.

2.2. Potential Energy Surface (PES) Scan

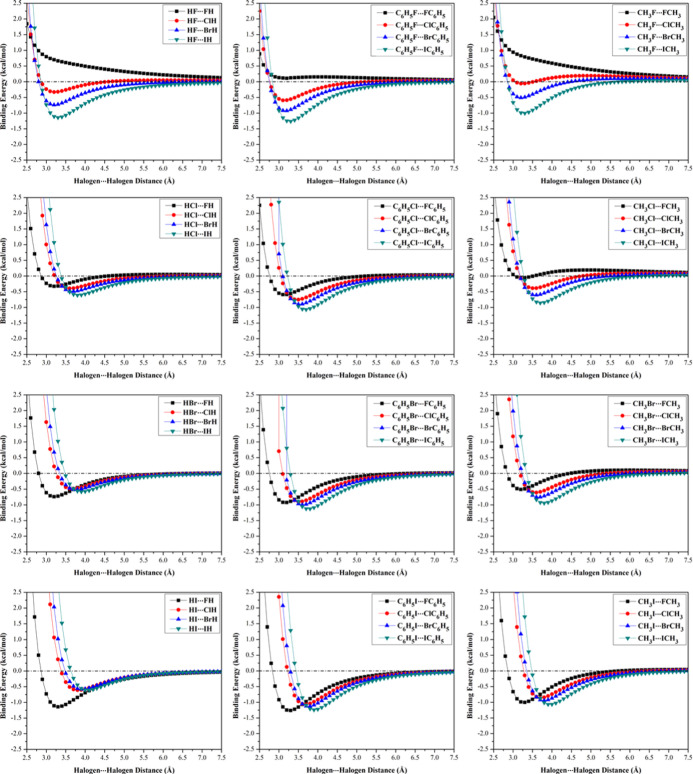
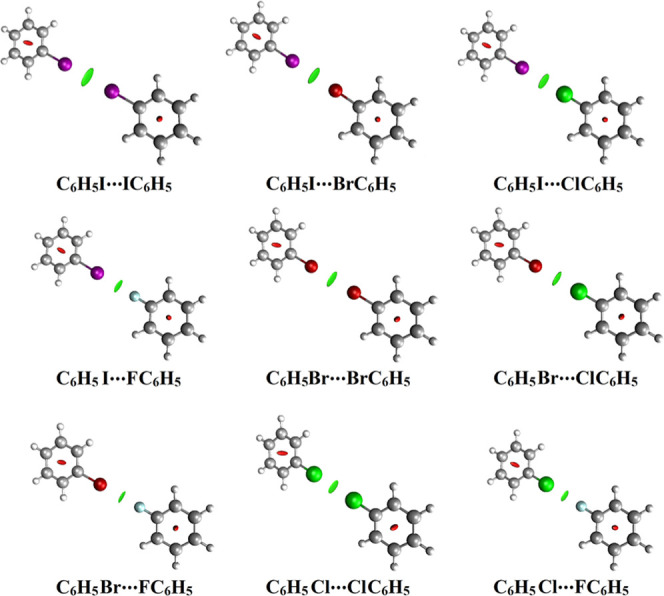
Potential energy surface (PES) scan was invoked to reveal the ability of halogen-containing molecules to participate in σ-hole···σ-hole and di-σ-hole interactions. PES scan was performed for HX···XH, C6H5X···XC6H5, and CH3X···XCH3 (where X = F, Cl, Br, and I) complexes at an X···X/X′ distance ranging from 2.5 to 7.5 Å in the x-direction with a step size of 0.1 Å. Binding energy curves were generated at the MP2/aug-cc-pVTZ(PP) level of theory and are depicted in Figure 4. Moreover, CCSD(T)/CBS binding energies were also computed for type III complexes at the most favorable X···X/X′ distances and are listed in Table 2.

Figure 4.

Figure 4

Open in a new tab

Potential energy surface (PES) curves for HX···XH, C6H5X···XC6H5, and CH3X···XCH3 (where X = F, Cl, Br, and I) complexes calculated (in kcal/mol) at the MP2/aug-cc-pVTZ(PP) level of theory at an X···X/X′ distance ranging from 2.5 to 7.5 Å and with an A–X···X/X′ angle (θ) of 180°.

Table 2. Binding Energies Calculated (in kcal/mol) at the MP2/aug-cc-pVTZ(PP) and CCSD(T)/CBS Levels of Theories for HX···XH, C6H5X···XC6H5, and CH3X···XCH3 (Where X = F, Cl, Br, and I) Complexes at the Most Favorable X···X/X′ Distances.

 
 σ-hole binding features
complexes interaction type distance (Å) EMP2/aug-cc-pVTZ(PP) (kcal/mol) ECCSD(T)/CBS (kcal/mol)
hydrogen halide HI···IH σ-hole···σ-hole 4.06 –0.61 –0.65
HI···BrH di-σ-hole 3.91 –0.58 –0.56
HI···ClH di-σ-hole 3.82 –0.61 –0.56
HI···FH halogen bond 3.30 –1.14 –1.20
HBr···BrH σ-hole···σ-hole 3.76 –0.51 –0.46
HBr···ClH di-σ-hole 3.69 –0.49 –0.44
HBr···FH halogen bond 3.20 –0.74 –0.77
HCl···ClH σ-hole···σ-hole 3.61 –0.39 –0.35
HCl···FH halogen bond 3.21 –0.33 –0.37
HF···FH repulsive a a a
halobenzene C6H5I···IC6H5 σ-hole···σ-hole 3.90 –1.23 –1.30
C6H5I···BrC6H5 di-σ-hole 3.75 –1.13 –1.13
C6H5I···ClC6H5 di-σ-hole 3.68 –1.07 –1.06
C6H5I···FC6H5 halogen bond 3.27 –1.26 –1.21
C6H5Br···BrC6H5 σ-hole···σ-hole 3.61 –1.00 –0.95
C6H5Br···ClC6H5 di-σ-hole 3.53 –0.90 –0.85
C6H5Br···FC6H5 halogen bond 3.16 –0.93 –0.93
C6H5Cl···ClC6H5 σ-hole···σ-hole 3.47 –0.75 –0.71
C6H5Cl···FC6H5 halogen bond 3.14 –0.60 –0.59
C6H5F···FC6H5 repulsive a a a
halomethane CH3I···ICH3 σ-hole···σ-hole 3.94 –1.07 –1.07
CH3I···BrCH3 di-σ-hole 3.79 –0.94 –0.90
CH3I···ClCH3 di-σ-hole 3.71 –0.86 –0.81
CH3I···FCH3 halogen bond 3.28 –1.01 –1.00
CH3Br···BrCH3 σ-hole···σ-hole 3.65 –0.76 –0.68
CH3Br···ClCH3 di-σ-hole 3.58 –0.61 –0.55
CH3Br···FCH3 halogen bond 3.20 –0.51 –0.52
CH3Cl···ClCH3 σ-hole···σ-hole 3.54 –0.39 –0.35
CH3Cl···FCH3 halogen bond 3.23 –0.06 –0.08
CH3F···FCH3 repulsive a a a
Open in a new tab
a

No local minimum was observed in the corresponding potential energy surface (PES) curves for A–F···F–A complexes (Figure 4).

It can be concluded from the data presented in Figure 4 that all investigated halomolecules (except fluorine-containing molecules) can favorably interact with “like” halomolecules via σ-hole···σ-hole type III interactions. The binding energies of σ-hole···σ-hole interactions decreased with decreasing atomic size of the halogen atom in the order A–I···I–A > A–Br···Br–A > A–Cl···Cl–A complexes and faded in the case of A–F···F–A complexes. For instance, the CCSD(T)/CBS binding energies of CH3I···ICH3, CH3Br···BrCH3, and CH3Cl···ClCH3 complexes were obtained to be −1.07, −0.68, and −0.35 kcal/mol, respectively. The inability of fluorine-containing molecules to participate in σ-hole···σ-hole type III interactions might be related to the absence of σ-hole on the fluorine atom and the large repulsive electrostatic interaction between the two isotropic negative fluorine atoms. Furthermore, halobenzene complexes were obviously observed with maximum binding energies followed by halomethane, then hydrogen halide complexes. For instance, CCSD(T)/CBS binding energies of C6H5I···IC6H5, CH3I···ICH3, and HI···IH complexes were found to be −1.30, −1.07, and −0.65 kcal/mol, respectively. Based on the inspection of the aforementioned results, the σ-hole···σ-hole interactions might be explained as a sum of (i) attractive electrostatic forces between the positive σ-hole of one halogen atom and the negative belt of the other halogen atom, (ii) repulsive electrostatic forces between the positive σ-holes of the two halogen atoms, (iii) repulsive electrostatic forces between the negative belts of the two halogen atoms, (iv) the van der Waals interactions between the two halogen atoms, and (v) polarization contribution of one halogen atom by the other halogen atom.

Turning to “unlike” complexes, all investigated halomolecules showed solid potentiality to favorably interact with “unlike” halomolecules with A–X···X′ and A–X′···X angles of 180°. According to the data summarized in Table 2, the most favorable binding energies were denoted in the case of HF···XH complexes. The interpretation of the binding energies of “unlike” fluorine-containing complexes might be relevant to the highly attractive forces between the isotropic negative fluorine atom in one monomer and positive σ-hole on the “unlike” monomer. Consequently, the binding energy of the latter interaction increased as the σ-hole size of the “unlike” monomer increased in the order HF···ClH < HF···BrH < HF···IH with values of −0.37, −0.77, and −1.20 kcal/mol, respectively. Due to the lack of the σ-hole on the fluorine atom, the A–F···X′-A interaction might be characterized as a traditional halogen bond rather than di-σ-hole interaction.

For di-σ-hole interactions, the binding energies of the studied “unlike” complexes decreased in the order A–X···I–A > A–X···Br–A > A–X···Cl–A. For instance, the CCSD(T)/CBS binding energies were found to be −0.90, −0.68, and −0.55 kcal/mol for the CH3Br···XCH3 complexes, where X = I, Br, and Cl, respectively. This might reflect the favorable halogens’ van der Waals contribution to the di-σ-hole binding energies.

To sum up, the aforesaid results endeavor to demonstrate the potentiality of the studied halomolecules (except fluorine-containing molecules) to participate in σ-hole···σ-hole and di-σ-hole interactions.

2.3. QTAIM Analysis

Quantum theory of atoms in molecules (QTAIM) furnishes reliable information for the occurrence of noncovalent interactions through generating bond critical points (BCPs) and bond paths (BPs) between two interacting monomers.30 In the present study, QTAIM calculations were accomplished for type III halogen···halogen complexes at the most favorable X···X/X′ distance at the MP2/aug-cc-pVTZ(PP) level of theory. Figure S1 presents the generated BCPs and BPs for all studied type III halogen···halogen complexes. The BCPs and BPs of halobenzene complexes, as an example, are displayed in Figure 5. Electron density (ρb), Laplacian (∇2ρb), and total energy density (Hb) were also computed and are summarized in Table 3.

Figure 5.

Figure 5

Open in a new tab

Quantum theory of atoms in molecules (QTAIM) diagrams for C6H5X···XC6H5 (where X = F, Cl, Br, and I) complexes at the most favorable X···X/X′ distances. The red dots indicate the locations of bond critical points (BCP) at bond paths (BP) between two interacting monomers.

Table 3. Topological Parameters Including Electron Density (ρb, au), Laplacian (∇2ρb, au), and Total Energy Density (Hb, au) at Bond Critical Points (BCPs) of HX···XH, C6H5X···XC6H5, and CH3X···XCH3 (Where X = F, Cl, Br, and I) Complexes at the Most Favorable X···X/X′ Distances.

complexes interaction type ρb (au) ∇2ρb (au) Hb (au)
hydrogen halide HI···IH σ-hole···σ-hole 0.00076 0.01383 0.00404
HI···BrH di-σ-hole 0.00086 0.01484 0.00389
HI···ClH di-σ-hole 0.00093 0.01531 0.00381
HI···FH halogen bond 0.00130 0.02619 0.00578
HBr···BrH σ-hole···σ-hole 0.00097 0.01593 0.00376
HBr···ClH di-σ-hole 0.00101 0.01577 0.00354
HBr···FH halogen bond 0.00138 0.02582 0.00517
HCl···ClH σ-hole···σ-hole 0.00107 0.01593 0.00341
HCl···FH halogen bond 0.00128 0.02154 0.00408
HF···FH repulsive a a a
halobenzene C6H5I···IC6H5 σ-hole···σ-hole 0.00078 0.01818 0.00592
C6H5I···BrC6H5 di-σ-hole 0.00093 0.01991 0.00578
C6H5I···ClC6H5 di-σ-hole 0.00105 0.02011 0.00542
C6H5I···FC6H5 halogen bond 0.00129 0.0279 0.00643
C6H5Br···BrC6H5 σ-hole···σ-hole 0.00107 0.02135 0.00556
C6H5Br···ClC6H5 di-σ-hole 0.00128 0.02225 0.00530
C6H5Br···FC6H5 halogen bond 0.00140 0.02827 0.00593
C6H5Cl···ClC6H5 σ-hole···σ-hole 0.00144 0.02217 0.00482
C6H5Cl···FC6H5 halogen bond 0.00145 0.02564 0.00501
C6H5F···FC6H5 repulsive a a a
halomethane CH3I···ICH3 σ-hole···σ-hole 0.00074 0.01686 0.00549
CH3I···BrCH3 di-σ-hole 0.00087 0.01838 0.00534
CH3I···ClCH3 di-σ-hole 0.00102 0.01903 0.00509
CH3I···FCH3 halogen bond 0.00129 0.02762 0.00631
CH3Br···BrCH3 σ-hole···σ-hole 0.00100 0.01959 0.00513
CH3Br···ClCH3 di-σ-hole 0.00113 0.01986 0.00480
CH3Br···FCH3 halogen bond 0.00133 0.02615 0.00544
CH3Cl···ClCH3 σ-hole···σ-hole 0.00117 0.01870 0.00422
CH3Cl···FCH3 halogen bond 0.00121 0.02084 0.00412
CH3F···FCH3 repulsive a a a
Open in a new tab
a

No local minimum was observed in the corresponding potential energy surface (PES) curves for A–F···F–A complexes (Figure 4).

As shown in Figure 5, halobenzene complexes had one BCP and one BP between the two interacting monomers, which consistently emphasized the existence of σ-hole···σ-hole and di-σ-hole interactions. The same observation was denoted for all of the studied complexes depicted in Figure S1.

From Table 3, relatively low values of ρb and positive values of ∇2ρb and Hb were observed, indicating the closed-shell nature of type III halogen···halogen interactions. In accordance with PES scan results (Table 2), there was a direct correlation between the Hb values at the BCP and the calculated binding energies of the considered complexes. For instance, the Hb values in C6H5X···XC6H5 complexes were found to be 0.00592, 0.00556, and 0.00482 au with binding energies of −1.30, −0.95, and −0.71 kcal/mol for X = I, Br, and Cl, respectively.

2.4. NCI Analysis

Toward a deeper understanding of the nature of σ-hole···σ-hole and di-σ-hole interactions, the noncovalent interaction (NCI) index was executed for type III halogen···halogen complexes at the most favorable X···X/X′ distances. Through NCI analysis, the two-dimensional (2D) reduced density gradient (RDG) and the three-dimensional (3D) color-mapped plots of noncovalent interaction regions were generated and are depicted in Figures S2 and S3, respectively. Figure 6 shows the 3D color-mapped plots of the iodobenzene complexes as an example.

Figure 6.

Figure 6

Open in a new tab

3D NCI plots of C6H5I···XC6H5 (where X = F, Cl, Br, and I) complexes at the most favorable X···X/X′ distance. The isosurfaces are plotted with a reduced density gradient value of 0.50 au and colored from blue to red according to sign(λ2)ρ ranging from −0.035 (blue) to 0.020 (red) au.

Subject to 2D plots of the studied halogen···halogen complexes, all of the spikes denoted with negative values of sign(λ2)ρ confirm the attractive interactions between two interacting halogen-containing monomers. Also, a low gradient was apparently discriminated in the case of HX···XH interactions and then peaked in CH3X···XCH3 and C6H5X···XC6H5 interactions, reflecting the trend of the calculated binding energies (Figure S2).

Moreover, the expanded green regions between the two interacting monomers in Figure S3 were obviously denoted, indicating the occurrence of weak attractive interactions between the interacting monomers. From the inspection of QTAIM and NCI results, we can affirm the potentiality of the studied halomolecules to participate in σ-hole···σ-hole and di-σ-hole interactions that are in line with molecular stabilization and binding energies of similar patterns.

2.5. SAPT-EDA Calculation

Symmetry-adapted perturbation theory-based energy decomposition analysis (SAPT-EDA) is an adequate tool to scrutinize the nature of noncovalent interactions in molecular systems.31 For the investigated type III halogen···halogen complexes, energy decomposition analysis was executed using the SAPT0 level of truncation. Table 4 gathers the total SAPT-based binding energy (ESAPT0) and its basic contributing factors calculated in kcal/mol.

Table 4. Symmetry-Adapted Perturbation Theory-Based Energy Decomposition Analysis (SAPT-EDA) for HX···XH, C6H5X···XC6H5, and CH3X···XCH3 (Where X = F, Cl, Br, and I) Complexes Calculated (in kcal/mol) at the MP2/aug-cc-pVTZ(PP) Level of Theory and the Most Favorable X···X/X′ Distances.

complexes interaction type Eelst(10) Eexch(10) Edisp Eind ESAPT0a ΔΔEb
hydrogen halide HI···IH σ-hole···σ-hole 0.66 1.02 –1.91 –0.29 –0.52 –0.09
HI···BrH di-σ-hole 0.44 0.86 –1.62 –0.20 –0.53 –0.05
HI···ClH di-σ-hole 0.16 0.80 –1.41 –0.15 –0.61 0.00
HI···FH halogen bond –1.32 1.22 –1.10 –0.31 –1.50 0.36
HBr···BrH σ-hole···σ-hole 0.33 0.72 –1.40 –0.14 –0.48 –0.03
HBr···ClH di-σ-hole 0.18 0.62 –1.18 –0.10 –0.48 –0.01
HBr···FH halogen bond –0.70 0.86 –0.90 –0.20 –0.94 0.20
HCl···ClH σ-hole···σ-hole 0.15 0.54 –1.02 –0.07 –0.39 0.00
HCl···FH halogen bond –0.15 0.53 –0.67 –0.11 –0.41 0.08
HF···FH repulsive c c c c c c
halobenzene C6H5I···IC6H5 σ-hole···σ-hole 0.40 1.92 –2.98 –0.47 –1.12 –0.11
C6H5I···BrC6H5 di-σ-hole 0.25 1.66 –2.64 –0.35 –1.08 –0.05
C6H5I···ClC6H5 di-σ-hole 0.03 1.46 –2.30 –0.28 –1.08 0.01
C6H5I···FC6H5 halogen bond –0.99 1.51 –1.80 –0.33 –1.62 0.36
C6H5Br···BrC6H5 σ-hole···σ-hole 0.21 1.39 –2.31 –0.25 –0.96 –0.04
C6H5Br···ClC6H5 di-σ-hole 0.11 1.25 –2.05 -0.20 –0.89 –0.01
C6H5Br···FC6H5 halogen bond –0.46 1.12 –1.53 –0.22 –1.09 0.16
C6H5Cl···ClC6H5 σ-hole···σ-hole 0.13 1.03 –1.76 –0.15 –0.75 0.00
C6H5Cl···FC6H5 halogen bond –0.04 0.77 –1.24 –0.15 –0.65 0.05
C6H5F···FC6H5 repulsive c c c c c c
halomethane CH3I···ICH3 σ-hole···σ-hole 0.25 1.82 –2.69 –0.39 –1.02 –0.05
CH3I···BrCH3 di-σ-hole 0.18 1.57 –2.36 –0.31 –0.91 –0.03
CH3I···ClCH3 di-σ-hole 0.01 1.43 –2.04 –0.26 –0.85 –0.01
CH3I···FCH3 halogen bond –0.92 1.57 –1.48 –0.41 –1.24 0.23
CH3Br···BrCH3 σ-hole···σ-hole 0.24 1.31 –2.04 –0.22 –0.70 –0.06
CH3Br···ClCH3 di-σ-hole 0.22 1.14 –1.74 –0.18 –0.56 –0.05
CH3Br···FCH3 halogen bond –0.14 1.05 –1.19 –0.27 –0.54 0.03
CH3Cl···ClCH3 σ-hole···σ-hole 0.34 0.87 –1.41 –0.13 –0.33 –0.06
CH3Cl···FCH3 halogen bond 0.44 0.59 –0.86 –0.17 0.01 –0.07
CH3F···FCH3 repulsive c c c c c c
Open in a new tab
a

ESAPT0 = Eelst(10) + Eexch + Edisp + Eind.

b

ΔΔE = EMP2/aug-cc-pVTZ(PP) – ESAPT0.

c

No SAPT-EDA was performed since no local minimum was observed in the corresponding potential energy surface (PES) curves for A–F···F–A complexes (Figure 4).

The total SAPT-based binding energy (ESAPT0) for the studied complexes were similar to the BSSE-corrected MP2/aug-cc-PVTZ(PP) binding energies (ΔΔE was close to 0 kcal/mol, Table 4), demonstrating the reliability of the implemented SAPT level of theory.

The SAPT-EDA results given in Table 4 revealed that type III halogen···halogen interactions were dominated by dispersion forces (Edisp). These results demonstrated that the nature of type III halogen···halogen interactions is similar to that of type I halogen···halogen interactions. In contrast to type II halogen···halogen interactions, the electrostatic forces (Eelst) were repulsive in the case of σ-hole···σ-hole and di-σ-hole interactions and attractive in the case of traditional halogen bond (i.e., in fluorine-containing complexes). The positive Eelst values were expected as a result of repulsion between the interacting sites of similar electrostatic potential (i.e., the two positive σ-holes and the two negative belts of halogen atoms). The larger the σ-hole size, the more unfavorable the Eelst contribution, becoming attractive when σ-hole is absent. For example, the Eelst of the CH3I···ICH3, CH3I···BrCH3, CH3I···ClCH3, and CH3I···FCH3 complexes were observed with values of 0.25, 0.18, 0.01, and −0.92 kcal/mol, respectively, where σ-hole size decreased in the same order: I > Br > Cl and disappeared in F. The exchange repulsion (Eexch) and induction (Eind) components were positive and negative for all studied complexes, respectively.

Overall, the SAPT-EDA results of type III halogen···halogen interactions exhibited a prominent similarity in dispersive nature with the analogues of type I interactions. Unlike type I interactions, electrostatic forces in type III halogen···halogen interactions were unfavorable.

2.6. CSD Survey

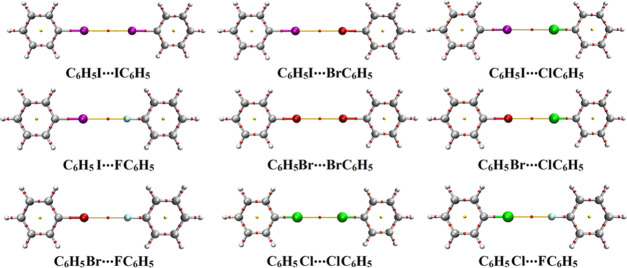
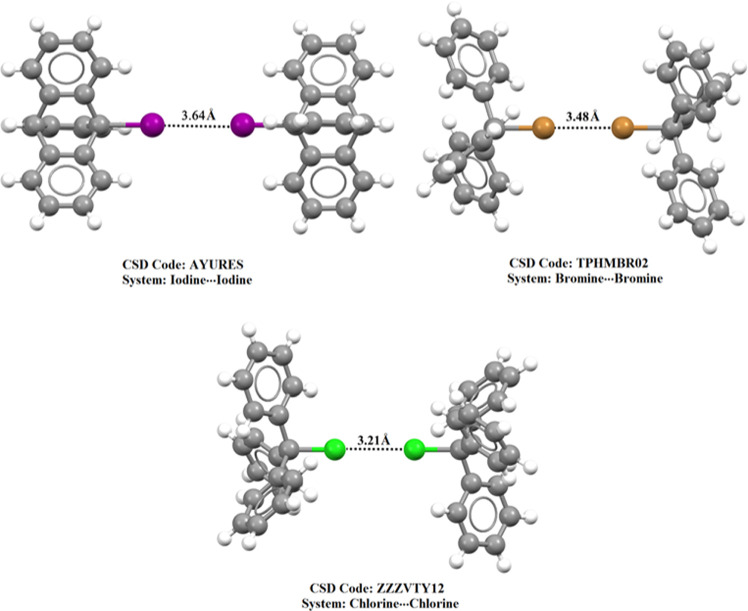
To pinpoint the reliability of type III halogen···halogen interactions, the CSD database was explored to investigate the existence of such interactions in the solid state. The CSD survey unveiled 24 crystal structures with the standard geometric requirements for desired type III interactions (see the Section 4 for details). The CSD codes, halogen···halogen distances, and A-halogen···halogen angles (θ) of the identified hits are collected in Table S1. It can be seen from the data in Table S1 that the halogen···halogen distances in identified crystal structures are smaller than the sum of van der Waals radii of the contacted halogen atoms. Interestingly, investigation of the hits revealed that all observed type III interactions are σ-hole···σ-hole (see Table S1). The absence of di-σ-hole interactions in the explored hits emphasized the relatively low strength of such interactions compared to those of σ-hole···σ-hole interactions. These results are in line with the calculated binding energies, which showed the favorability of the inspected halomolecules to participate in σ-hole···σ-hole interactions rather than di-σ-hole interactions (see Table 2). Three crystal structures demonstrating σ-hole···σ-hole interactions are given in Figure 7.

Figure 7.

Figure 7

Open in a new tab

Type III halogen···halogen interactions in crystal structures.

As shown in Figure 7, I···I interactions are established in AYURES between two directional and identical iodine-containing molecules, which emphasizes the occurrence of σ-hole···σ-hole interaction. Such interaction was also denoted between identical bromine- and chlorine-containing molecules in TPHMBR02 and ZZZVTY12, respectively. Overall, it is appealing to affirm the versatility of halomolecules to engage in type III halogen···halogen interactions.

3. Conclusions

This study has proved the occurrence of σ-hole···σ-hole and di-σ-hole interactions in a series of halogenated complexes in which the halogen···halogen interaction observed between two identically charged halogens and two different ones, respectively. Substantial binding energies were denoted for all of the studied halomolecules, interpreted as the sum of (i) attractive electrostatic forces between the positive σ-hole of one halogen atom and the negative belt of the other halogen atom, (ii) repulsive electrostatic forces between the positive σ-holes of the two halogen atoms, (iii) repulsive electrostatic forces between the negative belts of the two halogen atoms, (iv) the van der Waal interactions between the two halogen atoms, and (v) polarization contribution of one halogen atom by the other halogen atom. Fluorine-based interactions were recognized as traditional halogen bonds, due to the absence of σ-hole on the fluorine atom. The closed-shell nature of type III halogen···halogen interactions was elucidated through the incorporation of the quantum theory of atoms in molecules (QTAIM) and noncovalent interaction (NCI) index calculations. Symmetry-adapted perturbation theory-based energy decomposition analysis (SAPT-EDA) revealed that dispersion energy plays a crucial role in the σ-hole···σ-hole and di-σ-hole interactions. However, the traditional halogen bond in the studied fluorine-containing complexes was stabilized by electrostatic forces. Through exploring the Cambridge Structure Database (CSD), several crystal structures were identified to reveal the experimental reliability of σ-hole···σ-hole interactions. Overall, these findings will enrich the role of halogen···halogen contacts in crystal engineering and materials design.

4. Computational Methodology

In the current study, the ability of hydrogen halide (HX), halobenzene (C6H5X), and halomethane (CH3X) (where X = F, Cl, Br, and I) to participate in type III halogen···halogen interactions was investigated. Initially, geometrical structures of the monomers were fully optimized by the second-order Møller–Plesset (MP2) method32 with the aug-cc-pVTZ-PP basis set33−35 for the Br and I atoms and the aug-cc-pVTZ basis set33,34 for all other atoms. On the optimized structures, molecular electrostatic potentials (MEPs) were generated and mapped on 0.002 au electron density contours as previously recommended, where the 0.001 au isodensity envelope may provide incorrect information about the complete nature of the surface reactive sites.23,36

Moreover, maximum positive electrostatic potential (Vs,max) values were also computed using Multiwfn 3.5 software.37 To reveal the halogens’ interactions from the electrostatic perspective, ±σ-hole tests were carried out for the studied monomers with the point-of-charge (PoC) approach.13,38−43 In the PoC approach, negative and positive PoCs were used to mimic Lewis bases and acids in –σ-hole and +σ-hole tests, respectively. Through ±σ-hole tests, the effect of the X···PoC distance on the molecular stabilization energy was examined in the range 2.5–7.5 Å along the x-axis with a step size of 0.1 Å and A–X···PoC angle (θ) of 180°. The molecular stabilization energies (Estabilization) were computed in the presence of PoC with values of ±0.25 and ±0.75 au, and are estimated as follows

4.

The PoC values of ±0.25 and ±0.75 au were selected to represent moderate Lewis basicity and acidity. In the current study, the optimized structures of the monomers were kept frozen and placed relatively in one plane to form type III halogen···halogen interactions (i.e., with A–X···X/X′ angle of 180°, see Figure 1d). Potential energy surface (PES) scan was then performed at X···X/X′ distances from 2.5 to 7.5 Å in the x-direction with a step size of 0.1 Å, and the corresponding binding energy curves were generated. Binding energy was estimated as the difference between the energy of the complex and the sum of energies of the monomers. The basis set superposition error (BSSE) was taken into account using the counterpoise correction method.44 Also, CCSD(T)/CBS binding energies were estimated for the studied complexes at the most favorable X···X/X′ distances using the following equations45

4.

where

4.
4.

Moreover, the occurrence of type III halogen···halogen interaction in the studied complexes was unveiled through the incorporation of the quantum theory of atoms in molecules (QTAIM).30 For type III complexes at the most favorable X···X/X′ distances, bond critical points (BCPs) and bond paths (PBs) were generated and visualized. The topological features including electron density (ρb), Laplacian density (∇2ρb), and total energy density (Hb) were investigated. The noncovalent interaction (NCI) index was also established and NCI plots were depicted.46

To set forth the physical nature of the type III halogen···halogen interactions, symmetry-adapted perturbation theory-based energy decomposition analysis (SAPT-EDA) was performed at the SAPT0 level of truncation47,48 using PSI4 code.49 In the context of SAPT-EDA, total binding energy was estimated as the sum of its basic physical components, namely, electrostatic (Eelst(10)), exchange (Eexch), dispersion (Edisp), and induction (Eind), as follows

4.

where

4.
4.

All quantum mechanical calculations were performed using Gaussian09 software50 at the same level of the theory of geometrical optimization. Besides, QTAIM and NCI analyses were implemented using Multiwfn 3.5 software.37 QTAIM and NCI plots were visualized using Visual Molecular Dynamics (VMD) software.51

Finally, the Cambridge Structure Database (CSD version 5.41,52,53 updated in November 2019) survey was executed to explore the occurrence of σ-hole···σ-hole and di-σ-hole type III interactions in crystal structures. The survey was limited to consider only chlorlo-, bromo-, and iodo-hydrocarbons (i.e., C–X···X–C and C–X···X′–C, where X = Cl, Br, and I). Fluorine-containing molecules were excluded from the survey to avoid contamination of the results by the traditional halogen-bonded complexes. The halogen···halogen angles (i.e., C–X···X′ and C–X′···X) were explored in the range of 179–180°. The halogen···halogen contact parameters and angles were defined using the “3D” function of Conquest.

Acknowledgments

The computational work was completed with resources supported by the Science and Technology Development Fund, STDF, Egypt, grant nos. 5480 and 7972.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c02887.

  • Quantum theory of atoms in molecules (QTAIM) diagrams, 2D noncovalent interaction (NCI) reduced density gradient (RDG) plots, 3D noncovalent interaction (NCI) plots for the studied halogen···halogen complexes; and a list of hits resulted from CSD survey (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c02887_si_001.pdf (647.9KB, pdf)

References

  1. Sirimulla S.; Bailey J. B.; Vegesna R.; Narayan M. Halogen interactions in protein-ligand complexes: implications of halogen bonding for rational drug design. J. Chem. Inf. Model. 2013, 53, 2781–2791. 10.1021/ci400257k. [DOI] [PubMed] [Google Scholar]
  2. Priimagi A.; Cavallo G.; Metrangolo P.; Resnati G. The halogen bond in the design of functional supramolecular materials: recent advances. Acc. Chem. Res. 2013, 46, 2686–2695. 10.1021/ar400103r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Metrangolo P.; Meyer F.; Pilati T.; Resnati G.; Terraneo G. Halogen bonding in supramolecular chemistry. Angew. Chem., Int. Ed. 2008, 47, 6114–6127. 10.1002/anie.200800128. [DOI] [PubMed] [Google Scholar]
  4. Brammer L.; Bruton E. A.; Sherwood P. Understanding the behavior of halogens as hydrogen bond acceptors. Cryst. Growth Des. 2001, 1, 277–290. 10.1021/cg015522k. [DOI] [Google Scholar]
  5. Cavallo G.; Metrangolo P.; Milani R.; Pilati T.; Priimagi A.; Resnati G.; Terraneo G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. 10.1021/acs.chemrev.5b00484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Feng G.; Evangelisti L.; Gasparini N.; Caminati W. On the Cl...N halogen bond: a rotational study of CF3Cl···NH3. Chem. – Eur. J. 2012, 18, 1364–1368. 10.1002/chem.201101582. [DOI] [PubMed] [Google Scholar]
  7. Clark T.; Hennemann M.; Murray J. S.; Politzer P. Halogen bonding: the σ-hole. J. Mol. Model. 2007, 13, 291–296. 10.1007/s00894-006-0130-2. [DOI] [PubMed] [Google Scholar]
  8. Varadwaj A.; Varadwaj P. R.; Jin B. Y. Can an entirely negative fluorine in a molecule, viz. perfluorobenzene, interact attractively with the entirely negative site(s) on another molecule(s)? Like liking like!. RSC Adv. 2016, 6, 19098–19110. 10.1039/C5RA27039A. [DOI] [Google Scholar]
  9. Varadwaj P.; Varadwaj A.; Marques H.; Yamashita K. Can Combined Electrostatic and Polarization Effects Alone Explain the F···F Negative-Negative Bonding in Simple Fluoro-Substituted Benzene Derivatives? A First-Principles Perspective. Computation 2018, 6, 51–84. 10.3390/computation6040051. [DOI] [Google Scholar]
  10. Metrangolo P.; Murray J. S.; Pilati T.; Politzer P.; Resnati G.; Terraneo G. The fluorine atom as a halogen bond donor, viz. a positive site. CrystEngComm 2011, 13, 6593–6596. 10.1039/c1ce05554b. [DOI] [Google Scholar]
  11. Politzer P.; Murray J. S.; Clark T. Halogen bonding and other sigma-hole interactions: a perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. 10.1039/c3cp00054k. [DOI] [PubMed] [Google Scholar]
  12. Politzer P.; Murray J. S. Halogen bonding: an interim discussion. ChemPhysChem 2013, 14, 278–294. 10.1002/cphc.201200799. [DOI] [PubMed] [Google Scholar]
  13. Ibrahim M. A. A.; Hasb A. A. M. Polarization plays the key role in halogen bonding: a point-of-charge-based quantum mechanical study. Theor. Chem. Acc. 2019, 138, 2 10.1007/s00214-018-2388-8. [DOI] [Google Scholar]
  14. Johansson M. P.; Swart M. Intramolecular halogen-halogen bonds?. Phys. Chem. Chem. Phys. 2013, 15, 11543–11553. 10.1039/c3cp50962a. [DOI] [PubMed] [Google Scholar]
  15. Varadwaj P. R.; Varadwaj A.; Jin B.-Y. Unusual bonding modes of perfluorobenzene in its polymeric (dimeric, trimeric and tetrameric) forms: entirely negative fluorine interacting cooperatively with entirely negative fluorine. Phys. Chem. Chem. Phys. 2015, 17, 31624–31645. 10.1039/C5CP03209A. [DOI] [PubMed] [Google Scholar]
  16. Pedireddi V. R.; Reddy D. S.; Goud B. S.; Craig D. C.; Rae A. D.; Desiraju G. R. The Nature of Halogen-Center-Dot-Center-Dot-Center-Dot-Halogen Interactions and the Crystal-Structure of 1,3,5,7-Tetraiodoadamantane. J. Chem. Soc. Perkin Trans. 2 1994, 11, 2353–2360. 10.1039/p29940002353. [DOI] [Google Scholar]
  17. Awwadi F. F.; Willett R. D.; Peterson K. A.; Twamley B. The Nature of Halogen···Halogen Synthons: Crystallographic and Theoretical Studies. Chem. – Eur. J. 2006, 12, 8952–8960. 10.1002/chem.200600523. [DOI] [PubMed] [Google Scholar]
  18. Desiraju G. R.; Parthasarathy R. The nature of halogen.cntdot..cntdot..cntdot.halogen interactions: are short halogen contacts due to specific attractive forces or due to close packing of nonspherical atoms?. J. Am. Chem. Soc. 1989, 111, 8725–8726. 10.1021/ja00205a027. [DOI] [Google Scholar]
  19. Sarma J. A. R. P.; Desiraju G. R. The role of Cl.cntdot..cntdot..cntdot.Cl and C-H.cntdot..cntdot..cntdot.O interactions in the crystal engineering of 4-.ANG. short-axis structures. Acc. Chem. Res. 1986, 19, 222–228. 10.1021/ar00127a005. [DOI] [Google Scholar]
  20. Bent H. A. Structural Chemistry of Donor-Acceptor Interactions. Chem. Rev. 1968, 68, 587–648. 10.1021/cr60255a003. [DOI] [Google Scholar]
  21. Saha A.; Rather S. A.; Sharada D.; Saha B. K. C–X···X–C vs C–H···X–C, Which One Is the More Dominant Interaction in Crystal Packing (X = Halogen)?. Cryst. Growth Des. 2018, 18, 6084–6090. 10.1021/acs.cgd.8b00955. [DOI] [Google Scholar]
  22. Bui T. T. T.; Dahaoui S.; Lecomte C.; Desiraju G. R.; Espinosa E. The Nature of Halogen···Halogen Interactions: A Model Derived from Experimental Charge-Density Analysis. Angew. Chem., Int. Ed. 2009, 48, 3838–3841. 10.1002/anie.200805739. [DOI] [PubMed] [Google Scholar]
  23. Varadwaj A.; Marques H. M.; Varadwaj P. R. Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions?. Molecules 2019, 24, 379–407. 10.3390/molecules24030379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Varadwaj P. R.; Varadwaj A.; Marques H. M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics 2019, 7, 40–102. 10.3390/inorganics7030040. [DOI] [Google Scholar]
  25. Varadwaj A.; Varadwaj P. R.; Yamashita K. Do surfaces of positive electrostatic potential on different halogen derivatives in molecules attract? like attracting like!. J. Comput. Chem. 2018, 39, 343–350. 10.1002/jcc.25125. [DOI] [PubMed] [Google Scholar]
  26. Bundhun A.; Ramasami P.; Murray J. S.; Politzer P. Trends in σ-hole strengths and interactions of F3MX molecules (M = C, Si, Ge and X = F, Cl, Br, I). J. Mol. Model. 2013, 19, 2739–2746. 10.1007/s00894-012-1571-4. [DOI] [PubMed] [Google Scholar]
  27. Weiner P. K.; Langridge R.; Blaney J. M.; Schaefer R.; Kollman P. A. Electrostatic potential molecular surfaces. Proc. Natl. Acad. Sci. U.S.A. 1982, 79, 3754–3758. 10.1073/pnas.79.12.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Brinck T.; Murray J. S.; Politzer P. Surface Electrostatic Potentials of Halogenated Methanes as Indicators of Directional Intermolecular Interactions. Int. J. Quantum Chem. 1992, 44, 57–64. 10.1002/qua.560440709. [DOI] [Google Scholar]
  29. Auffinger P.; Hays F. A.; Westhof E.; Ho P. S. Halogen bonds in biological molecules. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 16789–16794. 10.1073/pnas.0407607101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Bader R. F. W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. 10.1021/ar00109a003. [DOI] [Google Scholar]
  31. Lao K. U.; Herbert J. M. Energy Decomposition Analysis with a Stable Charge-Transfer Term for Interpreting Intermolecular Interactions. J. Chem. Theory Comput. 2016, 12, 2569–2582. 10.1021/acs.jctc.6b00155. [DOI] [PubMed] [Google Scholar]
  32. Møller C.; Plesset M. S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
  33. Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. IV. Calculation of static electrical response properties. J. Chem. Phys. 1994, 100, 2975–2988. 10.1063/1.466439. [DOI] [Google Scholar]
  34. Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. 10.1063/1.464303. [DOI] [Google Scholar]
  35. Feller D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. . [DOI] [Google Scholar]
  36. Ibrahim M. A. A. Molecular mechanical perspective on halogen bonding. J. Mol. Model. 2012, 18, 4625–4638. 10.1007/s00894-012-1454-8. [DOI] [PubMed] [Google Scholar]
  37. Lu T.; Chen F. Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
  38. Ibrahim M. A. A.; Moussa N. A. M.; Safy M. E. A. Quantum-mechanical investigation of tetrel bond characteristics based on the point-of-charge (PoC) approach. J. Mol. Model. 2018, 24, 219 10.1007/s00894-018-3752-2. [DOI] [PubMed] [Google Scholar]
  39. Ibrahim M. A. A.; Safy M. E. A. A new insight for chalcogen bonding based on Point-of-Charge approach. Phosphorus, Sulfur Silicon Relat. Elem. 2019, 194, 444–454. 10.1080/10426507.2018.1528255. [DOI] [Google Scholar]
  40. Ibrahim M. A. A.; Telb E. M. Z. A Computational Investigation of Unconventional Lone-Pair Hole Interactions of Group V–VIII Elements. ChemistrySelect 2019, 4, 5489–5495. 10.1002/slct.201900603. [DOI] [Google Scholar]
  41. Ibrahim M. A. A.; Mahmoud A. H. M.; Moussa N. A. M. Comparative investigation of ±σ–hole interactions of carbon-containing molecules with Lewis bases, acids and di-halogens. Chem. Pap. 2020, 74, 3569–3580. 10.1007/s11696-020-01187-1. [DOI] [Google Scholar]
  42. Ibrahim M. A. A.; Hasb A. A. M.; Mekhemer G. A. H. Role and nature of halogen bonding in inhibitor···receptor complexes for drug discovery: casein kinase-2 (CK2) inhibition as a case study. Theor. Chem. Acc. 2018, 137, 38 10.1007/s00214-018-2207-2. [DOI] [Google Scholar]
  43. Ibrahim M. A. A.; Ahmed O. A. M.; Moussa N. A. M.; El-Taher S.; Moustafa H. Comparative investigation of interactions of hydrogen, halogen and tetrel bond donors with electron-rich and electron-deficient π-systems. RSC Adv. 2019, 9, 32811–32820. 10.1039/C9RA08007D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Boys S. F.; Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. 10.1080/00268977000101561. [DOI] [Google Scholar]
  45. Mishra B. K.; Karthikeyan S.; Ramanathan V. Tuning the C-H...pi Interaction by Different Substitutions in Benzene-Acetylene Complexes. J. Chem. Theory Comput. 2012, 8, 1935–1942. 10.1021/ct300100h. [DOI] [PubMed] [Google Scholar]
  46. Johnson E. R.; Keinan S.; Mori-Sánchez P.; Contreras-García J.; Cohen A. J.; Yang W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. 10.1021/ja100936w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Hohenstein E. G.; Parrish R. M.; Sherrill C. D.; Turney J. M.; Schaefer H. F. 3rd Large-scale symmetry-adapted perturbation theory computations via density fitting and Laplace transformation techniques: investigating the fundamental forces of DNA-intercalator interactions. J. Chem. Phys. 2011, 135, 174107–174119. 10.1063/1.3656681. [DOI] [PubMed] [Google Scholar]
  48. Hohenstein E. G.; Sherrill C. D. Density fitting and Cholesky decomposition approximations in symmetry-adapted perturbation theory: Implementation and application to probe the nature of pi-pi interactions in linear acenes. J. Chem. Phys. 2010, 132, 184111–184120. 10.1063/1.3426316. [DOI] [Google Scholar]
  49. Turney J. M.; Simmonett A. C.; Parrish R. M.; Hohenstein E. G.; Evangelista F. A.; Fermann J. T.; Mintz B. J.; Burns L. A.; Wilke J. J.; Abrams M. L.; Russ N. J.; Leininger M. L.; Janssen C. L.; Seidl E. T.; Allen W. D.; Schaefer H. F.; King R. A.; Valeev E. F.; Sherrill C. D.; Crawford T. D. PSI4: an open-source ab initio electronic structure program. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 556–565. 10.1002/wcms.93. [DOI] [Google Scholar]
  50. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, revision E01; Gaussian Inc.: Wallingford, CT, USA, 2009.
  51. Humphrey W.; Dalke A.; Schulten K. VMD: visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  52. Groom C. R.; Bruno I. J.; Lightfoot M. P.; Ward S. C. The Cambridge Structural Database. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016, 72, 171–179. 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Allen F. H. The Cambridge Structural Database: a quarter of a million crystal structures and rising. Acta Crystallogr., Sect. B: Struct. Sci. 2002, 58, 380–388. 10.1107/S0108768102003890. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c02887_si_001.pdf (647.9KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES