Abstract
Purpose
To quantify the effects of operator head posture and different types of protective eyewear on the eye lens dose to operators in interventional radiology (IR).
Methods
A deformable computational human phantom, Rensselaer Polytechnic Institute (RPI) Adult Male, consisting of a high‐resolution eye model, was used to simulate a radiologist who is performing an interventional radiology procedure. The radiologist phantom was deformed to a set of different head postures. Three different protective eyewear models were incorporated into the posture‐deformed radiologist phantom. The eye lens dose of the radiologist was calculated using the Monte Carlo code, MCNP. Effects of the radiologist's head posture and different types of protective eyewear on eye lens doses were studied. The relationship between efficacy of protective eyewear and the radiologist's head posture was investigated. Effects of other parameters on efficacy of protective eyewear were also studied, including the angular position of the radiologist, the gap between the eyewear and the face of the radiologist, and the lead equivalent thickness.
Results
The dose to both lenses decreased by 80% as the head posture moved from looking downward to looking upward. Sports wrap glasses were found to reduce doses further than the other two studied models. The efficacy of eyewear was found to be related to radiologist's head posture as well. When the radiologist was looking up, the protective eyewear almost provided no protection to both lenses. Other factors such as the face‐to‐eyewear distance and the lead equivalent thickness were also found to have an impact on the efficacy of protective eyewear. The dose reduction factor (DRF), defined as the ratio of the dose to the lens without protection to that with protection, decreased from 4.25 to 1.07 as the face‐to‐eyewear distance increased. The DRF almost doubled when the lead equivalent thickness increased from 0.07 to 0.35 mm. However, further increase in lead equivalent thickness showed little improvement in dose reduction.
Conclusion
The radiologist's head posture has a significant influence on the eye lens dose in IR. Sports wrap protective eyewear which conforms to the curve of the face is essential for the radiation protection of the eye lens. However, the radiologist's head posture and other exposure parameters should be considered when evaluating the protection of the radiologist's eyes.
Keywords: eye lens dose to radiologists, interventional radiology, Monte Carlo, phantom
1. Introduction
The lens of the human eye is an optically clear, curved tissue that focuses light on the retina at the back of the eye. The International Commission on Radiological Protection (ICRP) publication 118 provides a detailed illustration of the structure of the eye lens and emphasizes that proper division and differentiation of epithelial cells are vital to the formation of fiber cells in the lens.1 When the integrity of the epithelial cell layer is disrupted — such as through ionizing radiation interactions — cataracts may form as the lens loses its transparency. Although radiation‐induced cataracts are a well‐known effect of exposure to radiation, recent debates focus on whether they are formed deterministically or stochastically.1, 2, 3 In previous studies,4, 5, 6 it was believed that radiation‐induced cataracts develop deterministically and a threshold dose was required for detectable lens opacities. Recent data reveal that radiation‐induced cataracts may occur stochastically; they may develop at a lower dose level or potentially with no dose threshold. In response to growing evidence, ICRP recently recommended to lower the equivalent dose limit to the eye lens for occupational exposure from 150 to 20 mSv/yr over five consecutive years, with no single year exceeding 50 mSv/yr.1 The National Council on Radiation Protection and Measurements (NCRP) also released new guidelines recommending that the annual absorbed dose limit to eye lens for occupational exposure be reduced to 50 mGy.7
According to United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR), among all medical professionals who are exposed to x rays, interventional radiologists involved in x‐ray fluoroscopic procedures receive the greatest occupational radiation exposure due to scattered photons from the patient.8 Many studies have been conducted to measure radiation exposure to radiologists’ eye lenses in various interventional procedures.9, 10, 11, 12 Those studies indicated that without proper protection, the dose to the lens of the eye could exceed limits recommended by the ICRP and NCRP.
Protective eyewear such as leaded glasses is an effective means of dose reduction to the eye lens in IR. This has been shown by other studies involving either experimental measurements or Monte Carlo (MC) calculations. Findings in these studies indicated that the efficacy of the protective eyewear was influenced by many geometric factors as well as parameters of fluoroscopic x‐ray equipment. Based on the MIRD phantom, the project Optimization of Radiation Protection for Medical Staff (ORAMED) conducted a simulation campaign to investigate various parameters that contribute to eye lens dose in IR.13, 14, 15 Koukorava and Principi also examined similar parameters using the MIRD phantom.16, 17 However, phantoms used in these studies are not able to accurately represent the anatomical structure of the human body, especially small features such as the eye lens. The commonly used MIRD phantom is a stylized phantom based on quadratic equations.18, 19 Representation of organs in this phantom is crude and only general description of the geometry of each organ is given. In addition, the effects of some factors such as the posture of the radiologist's head are not well‐investigated, partially due to the fact that the head in the MIRD phantom is rigidly defined.
This paper describes a systematic study of the effects of operator head posture and different types of protective eyewear on the eye lens dose to operators in IR. The work is based on an innovative computational phantom consisting of ultra‐fine eye model embedded in a whole‐body voxel phantom which is deformed to simulate the radiologist's head posture.20 Different protective eyewear models are incorporated into the posture‐deformed radiologist phantom. Other parameters and their effects on the efficacy of protective eyewear are also studied, including the angular position of the radiologist, the distance between protective eyewear and the face of the wearer, and the lead equivalent thickness.
2. Materials and methods
This study uses anatomically realistic and deformable phantoms and MC simulations to analyze the effect of operator head posture on the eye lens dose and performance of protective eyewear in terms of eye lens dose reduction, as well as its relationship with various parameters in IR. In this section, the geometry of the IR suite, the human phantoms, and the protective eyewear models are presented in detail. A brief introduction to the MC code, MCNP, is given.
2.A. Geometry of the IR suite
The modeling of the IR suite is based on a realistic clinical setup of transcatheter arterial chemoembolization (TACE) procedure, which is representative of many typical IR procedures. Figure 1(a) illustrates the IR suite on which the modeling and simulation in this study were based. Two computational human phantoms are used to simulate the radiologist and patient. An aluminum table underneath the patient and three protective lead shields which attenuate scattered x ray are modeled. The three lead shields, including two ceiling‐suspended shields and one table shield, are illustrated in Fig. 1(a). The two ceiling‐suspended lead shields above the patient are placed 3 cm from the right edge of the beam area, parallel to the transverse plane of the patient. The gap between the shields and patient is minimized by placing the lower edge of the lead shields against the top surface of the patient. The table shield is fixed on one side of the table close to the radiologist. In the clinical setup, the ceiling‐suspended shield is typically one piece but in our study the ceiling‐suspended shields are modeled as two pieces for convenience. All lead shields are made of lead with a thickness of 2 mm. The table is 105 cm above the ground, with an equivalent Al thickness of 0.215 mm. The thickness and width of the patient at the location of exposure volume is 26 and 32 cm approximately. The location of the x‐ray source with a PA projection is illustrated in Fig. 1(b). The source‐to‐skin distance (SSD) and source‐to‐image receptor distance (SID) are 57 and 105 cm, respectively. The image receptor is 22 cm above the top surface of the patient. The x‐ray tube voltage is 90 kVp and the additional filtration is 0.1 mm Cu. It should be noted that the C‐arm depicted in Fig. 1(a) is not explicitly modeled, so the minor contribution from x‐ray tube leakage or collimator scatter is ignored in this study. The x‐ray spectrum is generated using a widely accepted software called Xcomp5r.21 Figure 1(b) also shows the location of the radiologist's eye lens relative to the patient. The eye lens of the radiologist is 34 cm away from the top skin surface of the patient. The location of the radiologist and patient relative to the beam area is specified in Fig. 1(c). A 40 cm field of view is used to cover a major part of the patient's abdomen. The beam center is located 60.5 cm away from the head of the patient along the X direction and 6 cm to the right of the patient sagittal plane. The distance between the radiologist and the beam center is 43 cm along the X direction and 62 cm along the Y direction.
Figure 1.
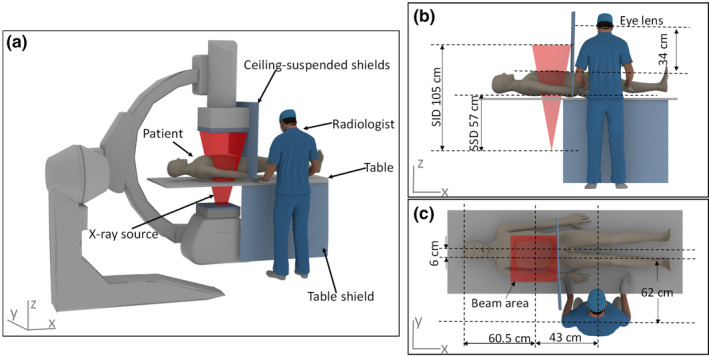
Geometric information for the simulation. (a) The interventional radiology suite consisting of two phantoms; (b) The side view showing the geometry of the x‐ray source and the height of the eye lens relative to the top surface of the patient; (c) The top view showing the location of the radiologist and patient relative to the beam area. [Color figure can be viewed at wileyonlinelibrary.com]
2.B. Human phantoms
The RPI Adult Male (RPI‐AM) phantom is adopted in this study to simulate the radiologist and the patient, respectively.22 RPI‐AM is a three‐dimensional computational human phantom that provides an anatomically realistic representation of the whole human body, including 122 organs and tissues and 27 different materials in total.22 It represents male individuals in the 50th percentile using parameters from ICRP 89.23 The original RPI‐AM phantom does not include extremely small features such as the lens of the eye — a focus in our research. In a previous study, Caracappa et al.20 addressed this problem by designing and integrating a high‐resolution eye model into the whole‐body RPI‐AM phantom.20 The voxel size of the eye model is 0.1 mm and the whole eye model consists of 1.9 million voxels. The mass and volume of the lens of the eye match the ICRP 89 reference data. This multiresolution phantom, as depicted in Fig. 2, is ideally suited for this study to calculate lens doses to the radiologist accurately. The whole phantom is depicted on the left of Fig. 2. A cross‐sectional view of the head of the phantom is shown in the middle of Fig. 2 and a more detailed view of the lens is given on the right of Fig. 2. To expedite MC simulations, the patient which scatters the primary x ray toward the radiologist is modeled using the RPI‐AM phantom without the ultra‐fine eye model.
Figure 2.
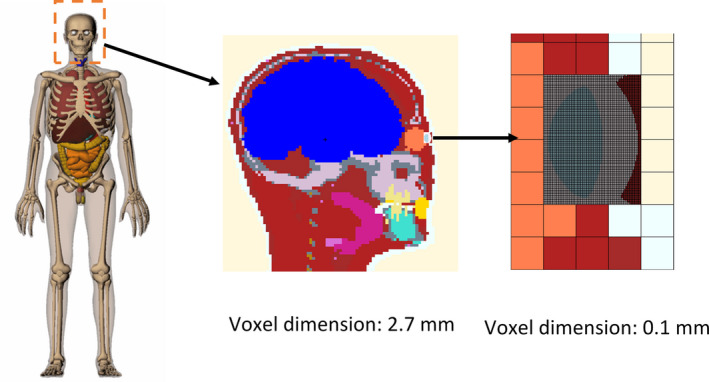
The multiresolution phantom for simulation of the radiologist in this study. The whole phantom is shown on the left; a cross‐sectional view of the head of the phantom is shown in the middle; a detailed cross‐sectional view of the lens is shown on the right. [Color figure can be viewed at wileyonlinelibrary.com]
In order to investigate the effect of the radiologist's head posture to the eye lens dose and the efficacy of protective eyewear, the head of the radiologist phantom is modified to look up or down at different angles, ranging from −30° to 30°, in intervals of 15°. Since head tilting with large angle is rarely encountered in clinical practice, head tilts outside this range are not studied. Figure 3 depicts the deformed radiologist phantom in different head postures: looking down at −30°, looking straight forward and looking up at 30°. The phantom deformation was based on the RPI‐AM — a triangular mesh‐based phantom. The commercial software Rhinoceros was used to perform the deformation. Area and volume checking tools were used to preserve the volume of skin surface and other organs involved in the deformation. The deformed mesh‐based phantom was then processed by an in‐house voxelization software to generate the head posture specific voxel‐based phantom for MCNP simulations.
Figure 3.
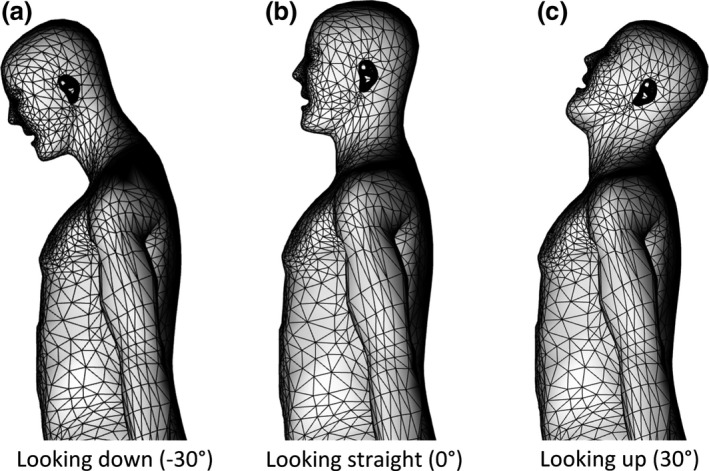
Radiologist in different head postures. (a) Looking down at −30°; (b) Looking straight forward; (c) Looking up at 30°.
2.C. Protective eyewear models
Three common designs of protective eyewear are modeled in constructive solid geometry (CSG). Images of these three types of commercially available eyewear (INFAB Corporation, CA, USA) are shown in Figs. 4(a)–4(c). Model 1 is classic eyeglasses without any side shield. Model 2 has similar shape of lens as model 1, but with lead glass side shields. Model 3 is a pair of sports wrap glasses with a curvature conforming to the face of the radiologist. All models of eyewear are made of lead glass with a lead equivalent thickness of 0.5 mm. In this study, the frame of each type of eyewear is not modeled, and lead glass is modeled as pure lead with corresponding Pb equivalence. Fig. 4(d)–4(f) display the three CSG models representing eyewear model 1, 2, and 3, respectively. The CSG models have similar shape and size to that of corresponding glasses models. The lens cross‐sectional area is 44.05 cm2 for CSG model 1. The frontal cross‐sectional area of CSG model 2 is the same as model 1, and the side shields cross‐sectional area of CSG model 2 is 27.03 cm2. The approximate eyeglass cross‐section of CSG model 3 is 48.14 cm2. The three models of protective eyewear are integrated into the radiologist phantom in each respective simulation. The cross‐sectional views of the head of the phantom wearing different protective eyewear models are shown in Fig. 4(g)–4(i), respectively.
Figure 4.
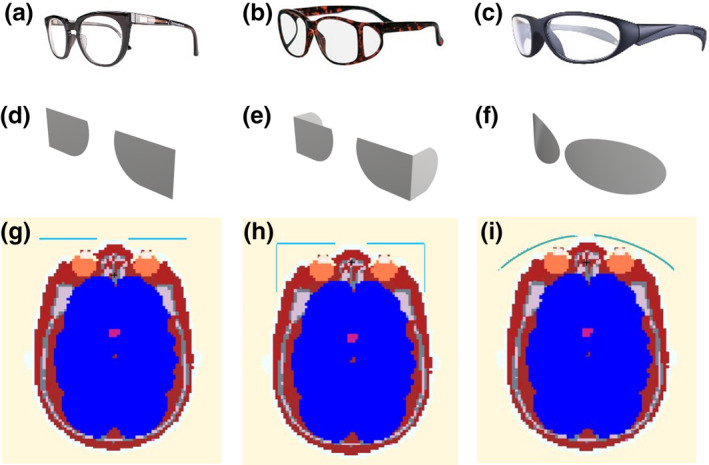
Images of protective eyewear and cross‐sectional views of the head of the phantom wearing different protective eyewear. (a) Eyewear model 1, classic, without side shield; (b) Eyewear model 2, classic, with side shield; (c) Eyewear model 3, sports wrap; (d)–(f) constructive solid geometry models of eyewear model 1, 2, and 3, respectively; (g)–(i) Cross‐sectional view of the head with eyewear model 1, 2, and 3, respectively. [Color figure can be viewed at wileyonlinelibrary.com]
To investigate the effect of angle of the radiologist relative to the patient axis on the efficacy of protective eyewear, the angular position was changed from −45° to 45°, with an interval of 15°. As illustrated in Fig. 5, the position of 0° is defined as the radiologist standing in front of the table, facing the patient. The position of −45° means that the radiologist is rotated counterclockwise by 45° from the position of 0°, facing the beam area of the patient. Accordingly, the position of 45° means the radiologist is rotated clockwise by 45° from the position of 0°, facing the feet of the patient, away from the beam area.
Figure 5.
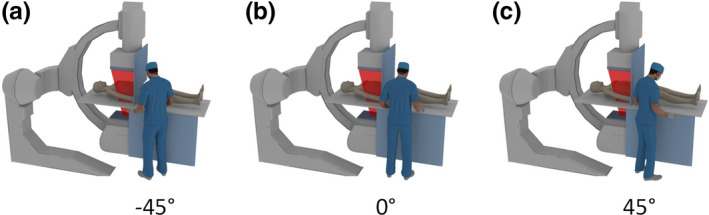
Different angular positions of the radiologist. (a) The radiologist is rotated by 45° to the left, denoted as position −45°; (b) The radiologist is facing the patient, denoted as position 0°; (c) The radiologist is rotated by 45° to the right, denoted as position 45°. [Color figure can be viewed at wileyonlinelibrary.com]
In addition, the effect of distance between protective eyewear and the face of the radiologist is studied for eyewear model 1 by placing the eyewear at different distances from the face of the radiologist. Figure 6 shows the location of the eyewear relative to the operator's face in a sagittal plane. The face‐to‐eyewear distance is defined as the gap between the lens and the operator's face below the eye. The vertex distance is defined as the distance between the back surface of the eyewear lens and the front of the cornea. The smallest face‐to‐eyewear distance (0.5 cm) is determined by placing the bridge of the eyewear onto the nose of the radiologist phantom. Considering the nose shape and size difference among radiologists and different thickness of eyewear nose pads, the investigated face‐to‐eyewear distance ranges from 0.5 to 2.5 cm, and the vertex distance ranges from 1.16 to 3.16 cm. The influence of lead equivalent thickness is also studied. We investigated the most common and commercially available lead equivalent thickness, including 0.07, 0.35, 0.5, and 0.75 mm.
Figure 6.
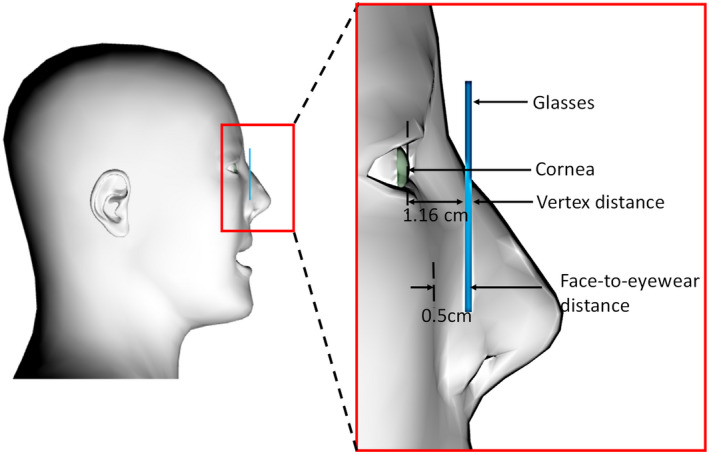
Illustration of the face‐to‐eyewear distance and vertex distance. [Color figure can be viewed at wileyonlinelibrary.com]
2.D. Monte Carlo calculations
All simulations are performed using the MCNP (Version 6.1) code.24 MCNP is a general‐purpose Monte Carlo N‐Particle code providing ample capabilities for geometry modeling including CSG, repeated structure, and unstructured mesh. For low‐energy x rays, the type 6 (F6:P) tally of MCNP is used to calculate the absorbed dose in the eye lens accurately. The photon heating function takes into account the energy deposited by electrons generated during photon collisions with the reasonable assumption that secondary electrons deposit their energies locally. This assumption is justified because the maximum range of electrons produced by the 90 kVp x ray in tissue is about 0.12 mm,25 while the depth of the eye lens in the phantom used in this study is about 3 mm. Additionally, the radiative energy loss of charged particles can be ignored since the diagnostic x‐ray beam energy is low and the human tissue mainly consists of low Z materials. Therefore, it is valid to estimate the dose to the lens by calculating kerma in the volume using F6:P tally. For the same reason, the time‐consuming electron transport is turned off without compromising accuracy. Variance reduction methods such as Geometry Splitting with Russian Roulette24 are also implemented to increase the number of particles as they migrate in an important direction (to the lens of the eye). All simulations are run on an Intel E5 v3 2697 CPU using 28 threads in parallel. The CPU has 14 cores, each supporting two hyper threads. In each calculation, about 1 billion particles are simulated, taking 6–7 hr to achieve a relative statistical error of <5% for dose in the eye lens which is extremely small.
3. Results
The base‐case parameters used in this study are as follows, with specific parameters adjusted as specified in the following sections:
Head posture: 0°;
Angular position: 0°;
Distance between protective eyewear and the face of the radiologist: 0.5 cm;
Lead equivalent thickness of protective eyewear: 0.5 mm;
Protective eyewear: Model 1.
3.A. Effect of operator head posture on eye lens dose
Figure 7 illustrates the relationship between the dose to the lens of the eye and the radiologist's head posture. Doses to both lenses are calculated without the use of lead glasses. All doses are normalized to left lens dose at the head posture of −30°, which is the highest dose case. The dose to the lens of the eye is found to vary greatly with the posture of the head. As shown in Fig. 7, doses to both lenses almost decrease by ~80% when the angle of the head tilting increases from −30° to 30°. This is mostly because the eye lens of the radiologist is closer to the patient and almost facing directly to the scattered radiation from the patient when the radiologist is looking down. When the radiologist is looking up, the eye lens of the radiologist is further from the patient who scatters the x ray. The face of the radiologist also provides some protection to the lens of the eye in this head posture.
Figure 7.
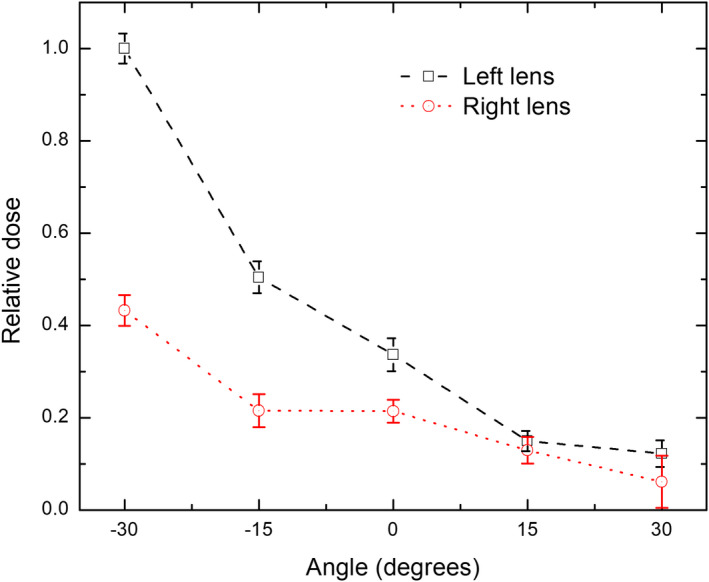
Relationship between the lens dose and head posture of the radiologist [Color figure can be viewed at wileyonlinelibrary.com]
3.B. Effect of protective eyewear on eye lens dose in different head postures
Table 1 shows the relationship between the efficacy of eyewear and the radiologist's head posture. Efficacy of eyewear is expressed as the dose reduction factor (DRF), which is the ratio of the dose to the lens without the use of protective eyewear to that with eyewear. As shown in Table 1, the overall performance of eyewear model 3 is better than the other two models. The difference in DRFs of the three models of eyewear may come from the gap size between the protective eyewear and the face of the phantom. The shape of eyewear model 3 fits the face of the radiologist phantom more closely, resulting a smaller gap between the face and eyewear.
Table 1.
Dose reduction factors of three models of protective eyewear in different head postures
| Head posture (°) | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|
| Left lens | Right lens | Left lens | Right lens | Left lens | Right lens | |
| −30 | 4.66 | 3.83 | 5.32 | 4.06 | 5.27 | 5.02 |
| −15 | 5.48 | 2.68 | 5.95 | 2.97 | 6.59 | 4.52 |
| 0 | 4.25 | 1.44 | 4.82 | 1.44 | 5.14 | 2.97 |
| 15 | 1.14 | 1.05 | 1.17 | 1.06 | 2.08 | 1.20 |
| 30 | 1.10 | 0.97 | 1.10 | 1.00 | 1.14 | 0.98 |
As shown in Table 1, the DRF of each eyewear model varies greatly with the posture of the head. It is found that the lead glasses provide good protection to both lenses when the radiologist is looking down or looking forward. However, the efficacy of the glasses decreases dramatically when the radiologist is looking up. This is mainly because when the radiologist is looking up, the scattered x ray from the patient can easily reach the eye of the radiologist through the gap between the glasses and radiologist's face. The results indicate the importance of reducing exposure from below the eyewear. Close‐fitting glasses that have a smaller gap between the glasses and the radiologist's face would be helpful to reduce exposures from the below.
3.C. Effects of other parameters on the efficacy of protective eyewear
Table 2 shows the effect of angular positions on efficacy of protective eyewear model 1. The DRF is found to be very sensitive to the angular position of the radiologist, especially for the left lens which is closer to the irradiated area of the patient. In general, protective eyewear provides better protection when the radiologist is facing left. When the radiologist is at the position of 45°, the studied eyewear almost provides no protection to either lens, since the opening of the side gap between the face and eyewear is facing the direction of the irradiated area and more scattered photons can reach the eye through this gap. This indicates that a sufficient side shield is very important to protect the lens of the eye. Our findings are consistent with those reported in other studies.26, 27
Table 2.
Dose reduction factor of protective eyewear model 1 in different angular positions
| Angular position (°) | Left lens | Right lens |
|---|---|---|
| −45 | 1.48 | 5.37 |
| −30 | 3.58 | 4.03 |
| −15 | 5.67 | 2.32 |
| 0 | 4.25 | 1.44 |
| 15 | 4.41 | 1.04 |
| 30 | 1.84 | 1.15 |
| 45 | 1.04 | 0.97 |
To verify that the gap between the protective eyewear and the face of the radiologist is an important source of scattered radiation that reaches the eyes, eyewear model 1 is placed at different distances from the face of phantom. The DRF at each face‐to‐eyewear distance is calculated and shown in Table 3. The DRF decreases dramatically from 4.25 to 1.07 with the increase of the face‐to‐eyewear distance for the left lens. The DRF for right lens also decreases, though slowly, with the increase of the face‐to‐eyewear distance. When the face‐to‐eyewear distance is 2.5 cm, the eyewear almost provides no protection to the lens of the eye. Our findings are consistent with that reported in other literature.16
Table 3.
Dose reduction factor of protective eyewear model 1 at different face‐to‐eyewear distances
| Face‐to‐eyewear distance (cm) | Left lens | Right lens |
|---|---|---|
| 0.5 | 4.25 | 1.44 |
| 1.0 | 1.46 | 1.16 |
| 1.5 | 1.36 | 1.12 |
| 2.0 | 1.11 | 1.05 |
| 2.5 | 1.07 | 1.03 |
The DRF of eyewear model 1 with different lead equivalent thicknesses, ranging from 0.07 to 0.75 mm, is shown in Table 4. Due to radiation that enters the eye from the side and below, the DRF of the eyewear is much less than that expected from the attenuation of the lead equivalent thickness. For left lens, the DRF with 0.35 mm Pb equivalence is almost double that with 0.07 mm Pb equivalence. Further increase in the lead equivalent thickness only leads to a very small increase in DRF. Similar results were also reported by other studies.15, 16
Table 4.
Dose reduction factor of protective eyewear model 1 with different lead equivalent thicknesses
| Lead equivalent thickness (mm) | Left lens | Right lens |
|---|---|---|
| 0.07 | 2.13 | 1.24 |
| 0.35 | 4.10 | 1.39 |
| 0.5 | 4.25 | 1.44 |
| 0.75 | 4.58 | 1.40 |
Another finding worth mentioning is that higher DRF can be achieved for the left lens under most exposure scenarios in this study. This is mainly because the irradiated area is at the left side of the radiologist, except when the radiologist is facing left. As illustrated in Fig. 8, due to difference in the x‐ray scattering angle relative to the protective eye glasses, the left lens is well protected by the eyewear, while for the right lens, the protected area (the shaded area in Fig. 8) by the eyewear is shifted a little bit to the right, thus the right eye is exposed to scattered photons through the gap between the two lenses of the glasses. As a result, the leaded glasses are more effective in protecting the left eye than the right eye.
Figure 8.
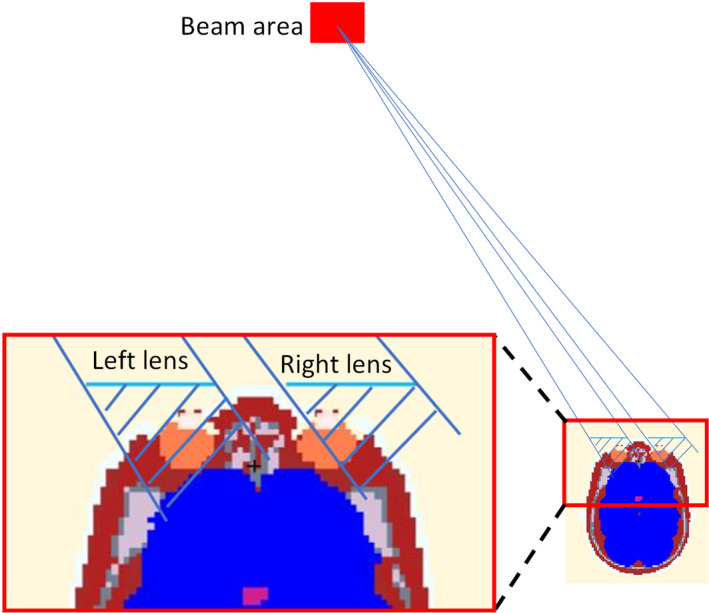
Illustration of difference in protected area provided by glasses for left lens and right lens. [Color figure can be viewed at wileyonlinelibrary.com]
4. Discussion
In an attempt to further improve the accuracy in eye lens dose assessment and efficacy of protective eyewear, we evaluated the effects of operator head posture and different types of protective eyewear on dose to the lens of the eye in IR. Our results indicate that the lens dose decreases by almost 80% as the radiologist's head posture is changed from looking down to looking up when no protective eyewear is worn. Since the radiologist should be always looking at the display monitor when fluoroscopy is on, a properly located monitor is essential to reduce the dose to the lens of the eye. The location of the monitor is recommended to be adjustable to accommodate the height of the radiologist. Our results suggest that to reduce the dose to the operator's eye lens, the monitor should be placed at the same level or slightly higher than the operator's eye level. To estimate the lens dose from a realistic interventional procedure in which the head is not always in a single fixed position, techniques such as motion capture can be used to track the real‐time head posture of the operator. It is worth noting that if the monitor is placed below or above the eye level, radiologists might tilt their eyes instead of heads. Another limitation of this work is that the radiologist's height is not modified in this study. To some extent, this effect is minimized by adjusting the table position to match the height of the radiologist, but the magnitude of this effect could be investigated in future work.
The protective eyewear is essential for reducing the eye lens dose. However, the efficacy of protective eyewear depends on the shape of the protective eyewear. The DRF of sports wrap protective eyewear is generally higher than the other two eyewear models. Close‐fitting eyewear that properly fits the face of the wearer is recommended for eye lens protection. It is important to note that other aspects such as comfort and convenience should be considered as well. It is reported that because of discomfort, <30% of operators wear protective eyewear.3 There is a tradeoff between efficacy and comfort when choosing appropriate eyewear. Radiologist's head posture also has an influence on the efficacy of protective eyewear. Higher dose reduction can be achieved when the radiologist is looking down. The efficacy of protective eyewear is also found to be very sensitive to other factors such as the angular position of the radiologist. Research by Challa28 speculated that the overall dose reduction during a procedure could be much lower than expected, since the parameters involved in practical use are much more complicated than that in calibration. It is found in our study that due to the gap between the two lenses of the glasses, the DRF is much higher for the left lens than that for the right lens when the irradiated area is on the left side of the radiologist. Glasses with a lead bridge or goggles with a one‐piece lens would be better for right eye lens protection. The gap between the protective eyewear and the face of the radiologist plays an important role in dose reduction as well. Our results also suggest that increasing the lead equivalent thickness above 0.35 mm has little impact on the efficacy of eyewear because of the backscattered radiations from the head of the operator, as well as radiation though the gap between eyewear and the face of the wearer, which is unable to be blocked by the glasses.
One underlying issue of our work is the lengthy computation time, of the order of 6–7 hr per run with 28 threads on a high‐end CPU, or even longer if the absorbed dose is to be calculated by the *f8 tally using the MCNP code. In addition, it would be a fairly computationally intensive problem to investigate a wide range of parameters. Further work would include adding the support for multiresolution phantoms to the next‐generation MC code ARCHER,29 which is capable of calculating both absorbed dose and kerma on graphics processing units (GPUs) with high speed and accuracy.
5. Conclusion
The results of this work have demonstrated the need to consider the potential impact of radiologist's head posture on the eye lens dose in IR. Data suggest that dose to the lens of the eye decreases as the head posture of the radiologist is changed from looking down to looking up. It is also clear that protective eyewear is essential for radiation protection of the eye lens. Compared with other eyewear models, sports wrap glasses that more closely fit the face are found to yield higher dose reduction. However, the efficacy of protective eyewear is affected by the radiologist's head posture and other exposure parameters. Particular attention should be paid to possible radiation exposures through the side and below, as well as the gap between the two lenses of the eyewear. The efficacy of protective eyewear has a twofold increase when the lead equivalent thickness increases from 0.07 to 0.35 mm. Further increase in lead equivalent thickness has negligible effect on eye lens dose reduction.
Conflict of interest
Dr. Xu and Dr. Caracappa are co‐founders of Virtual Phantoms, Inc (Albany, New York) that commercializes software technologies—VirtualDose for medical dose reporting and ARCHER for real‐time Monte Carlo dose engine through STTR grants from the National Institute of Biomedical Imaging and Bioengineering (R42EB010404 and R42EB019265‐01A1).
References
- 1. ICRP . ICRP statement on tissue reactions and early and late effects of radiation in normal tissues and organs–threshold doses for tissue reactions in a radiation protection context; 2012. [DOI] [PubMed]
- 2. NCRP . Guidance on radiation dose limits for the lens of the eye; 2016.
- 3. Seals KF, Lee EW, Cagnon CH, Al‐Hakim RA, Kee ST. Radiation‐induced cataractogenesis: a critical literature review for the interventional radiologist. Cardiovasc Inter Rad. 2016;39:151–160. [DOI] [PubMed] [Google Scholar]
- 4. Chmelevsky D, Mays C, Spiess H, Stefani F, Kellerer AM. An epidemiological assessment of lens opacifications that impaired vision in patients injected with radium‐224. Radiat Res. 1988;115:238–257. [PubMed] [Google Scholar]
- 5. Gus'kova A. Fifty years of the nuclear industry in Russia—through the eyes of a physician. At Energ. 1999;87:903–908. [Google Scholar]
- 6. Hourihan F, Mitchell P, Cumming RG. Possible associations between computed tomography scan and cataract: the Blue Mountains Eye Study. Am J Public Health. 1999;89:1864–1866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Dauer LT, Ainsbury EA, Dynlacht J, et al. Guidance on radiation dose limits for the lens of the eye: overview of the recommendations in NCRP Commentary No. 26. Int J Radiat Biol. 2017;93:1015–1023. [DOI] [PubMed] [Google Scholar]
- 8. Vano E, Gonzalez L, Fernandez J, Prieto C, Guibelalde E. Influence of patient thickness and operation modes on occupational and patient radiation doses in interventional cardiology. Radiat Prot Dosim. 2011;118:325–330. [DOI] [PubMed] [Google Scholar]
- 9. Vano E, Gonzalez L, Fernández JM, Haskal ZJ. Eye lens exposure to radiation in interventional suites: caution is warranted. Radiology. 2008;248:945–953. [DOI] [PubMed] [Google Scholar]
- 10. Vanhavere F, Carinou E, Domienik J, et al. Measurements of eye lens doses in interventional radiology and cardiology: final results of the ORAMED project. Radiat Meas. 2011;46:1243–1247. [DOI] [PubMed] [Google Scholar]
- 11. Domienik‐Andrzejewska JK, Ciraj‐Bjelac O, Askounis P, et al. Past and present work practices of European interventional cardiologists in the context of radiation protection of the eye lens‐results of the EURALOC study. J Radiol Prot. 2018;38:934–950. [DOI] [PubMed] [Google Scholar]
- 12. Omar A, Kadesjö N, Palmgren C, Marteinsdottir M, Segerdahl T, Fransson A. Assessment of the occupational eye lens dose for clinical staff in interventional radiology, cardiology and neuroradiology. J Radiol Protect. 2017;37:145. [DOI] [PubMed] [Google Scholar]
- 13. Carinou E, Ferrari P, Koukorava C, Krim S, Struelens L. Monte Carlo calculations on extremity and eye lens dosimetry for medical staff at interventional radiology procedures. Radiat Prot Dosimetry. 2011;144:492–496. [DOI] [PubMed] [Google Scholar]
- 14. Koukorava C, Carinou E, Ferrari P, Krim S, Struelens L. Study of the parameters affecting operator doses in interventional radiology using Monte Carlo simulations. Radiat Meas. 2011a;46:1216–1222. [Google Scholar]
- 15. Vanhavere F, Carinou E, Gualdrini G, et al. ORAMED: optimization of radiation protection of medical staff. EURADOS Rep. 2012;2:2012. [Google Scholar]
- 16. Koukorava C, Farah J, Struelens L, et al. Efficiency of radiation protection equipment in interventional radiology: a systematic Monte Carlo study of eye lens and whole body doses. J Radiol Protect. 2014;34:509–528. [DOI] [PubMed] [Google Scholar]
- 17. Principi S, Farah J, Ferrari P, Carinou E, Clairand I, Ginjaume M. The influence of operator position, height and body orientation on eye lens dose in interventional radiology and cardiology: Monte Carlo simulations versus realistic clinical measurements. Phys Med. 2016;32:1111–1117. [DOI] [PubMed] [Google Scholar]
- 18. Snyder WS, Ford MR, Warner GG. Estimates of specific absorbed fractions for monoenergetic photon sources uniformly distributed in various organs of a heterogeneous phantom MIRD Pamphlet 5, revised. Oak Ridge, TN: Oak Ridge National Laboratory; 1978. [Google Scholar]
- 19. Xu XG. An exponential growth of computational phantom research in radiation protection, imaging, and radiotherapy: a review of the fifty‐year history. Phys Med Biol. 2014;59:R233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Caracappa PF, Rhodes A, Fiedler D. Multi‐resolution voxel phantom modeling: a high‐resolution eye model for computational dosimetry. Phys Med Biol. 2014;59:5261–5275. [DOI] [PubMed] [Google Scholar]
- 21. Nowotny R. XCOMP5R: Calculation of Diagnostic X–Ray Spectra. Austria: Inst Biomed Technik & Physik, University of Vienna; 1996. [Google Scholar]
- 22. Zhang J, Na YH, Caracappa PF, Xu XG. RPI‐AM and RPI‐AF, a pair of mesh‐based, size‐adjustable adult male and female computational phantoms using ICRP‐89 parameters and their calculations for organ doses from monoenergetic photon beams. Phys Med Biol. 2009;54:5885–5908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. ICRP . Basic anatomical and physiological data for use in radiological protection reference values. ICRP Publication 89. Ann ICRP. 2002;32:571–574. [PubMed] [Google Scholar]
- 24. Goorley T. MCNP6. 1.1‐beta release notes. Los Alamos National Laboratory Technical Report; 2014.
- 25. Ziegler JF, Ziegler MD, Biersack JP. SRIM–the stopping and range of ions in matter (2010). Nucl Instrum Methods Phys Res, Sect B. 2010;268:1818–1823. [Google Scholar]
- 26. Wang Y, Huo W, Xiong Z, Gao Y, Xu X, Chen Z. Monte Carlo‐based comparison of radiation protection efficiency of lead glasses vs. lead mask for eye lens of doctor in different standing postures during transcatheter arterial chemoembolization. Chin J Med Phys. 2016;33:554–558. [Google Scholar]
- 27. van Rooijen BD, de Haan MW, Das M, et al. Efficacy of radiation safety glasses in interventional radiology. Cardiovasc Inter Rad. 2014;37:1149–1155. [DOI] [PubMed] [Google Scholar]
- 28. Challa K, Warren SG, Danak S, Bates MC. Redundant protective barriers: minimizing operator occupational risk. J Intervent Cardiol. 2009;22:299–307. [DOI] [PubMed] [Google Scholar]
- 29. Xu XG, Liu T, Su L, et al. ARCHER, a new Monte Carlo software tool for emerging heterogeneous computing environments. Ann Nucl Energy. 2015;82:2–9. [Google Scholar]


