A unified framework for association and prediction from vertex‐wise grey‐matter structure

Abstract

The recent availability of large‐scale neuroimaging cohorts facilitates deeper characterisation of the relationship between phenotypic and brain architecture variation in humans. Here, we investigate the association (previously coined morphometricity) of a phenotype with all 652,283 vertex‐wise measures of cortical and subcortical morphology in a large data set from the UK Biobank (UKB; N = 9,497 for discovery, N = 4,323 for replication) and the Human Connectome Project (N = 1,110). We used a linear mixed model with the brain measures of individuals fitted as random effects with covariance relationships estimated from the imaging data. We tested 167 behavioural, cognitive, psychiatric or lifestyle phenotypes and found significant morphometricity for 58 phenotypes (spanning substance use, blood assay results, education or income level, diet, depression, and cognition domains), 23 of which replicated in the UKB replication set or the HCP. We then extended the model for a bivariate analysis to estimate grey‐matter correlation between phenotypes, which revealed that body size (i.e., height, weight, BMI, waist and hip circumference, body fat percentage) could account for a substantial proportion of the morphometricity (confirmed using a conditional analysis), providing possible insight into previous MRI case–control results for psychiatric disorders where case status is associated with body mass index. Our LMM framework also allowed to predict some of the associated phenotypes from the vertex‐wise measures, in two independent samples. Finally, we demonstrated additional new applications of our approach (a) region of interest (ROI) analysis that retain the vertex‐wise complexity; (b) comparison of the information retained by different MRI processings.

This manuscript introduces a set of analyses, that rely on linear mixed models to perform association and prediction, while being suited to tackle the challenges of big‐data in neuroimaging. Our framework allows estimating new sample characteristics such as the total association (morphometricity) between a phenotype and vertex‐wise brain data or grey‐matter correlations that quantify how much phenotypes may be similarly associated with grey‐matter. In addition, it offers to build performant brain‐based predictors that do not require hyper‐parameter estimation.

1. INTRODUCTION

The field of MRI studies is at a turning point owing to the recent availability of large data sets to researchers, including the UKB (Miller et al., 2016) and HCP (Van Essen et al., 2012; Van Essen et al., 2013) samples. These data sets promote the replication of previous findings, but also the identification of small(er) associations and the expansion of the range of phenotypes available for study (e.g., psychiatric symptoms and lifestyle factors). Furthermore, the boost in statistical power may allow the simultaneous use of all the brain complexity data of current MRI acquisitions rather than relying on data reduction techniques (e.g., the region‐of‐interest [ROI] approach). In addition, these community samples can complement the typical case–control paradigm by identifying confounders of MRI analyses or by studying related traits (e.g., cognition domains relevant in Alzheimer's disease). However, “big‐data” neuroimaging offers a number of statistical challenges (on top of the obvious computing ones)(Smith & Nichols, 2018): (a) the curse of dimensionality (the number of tests may increase faster than the sample size) which requires efficient methods and appropriate control of multiple testing; (b) the possibility that (small) associations result from confounding (via another variable, or acquisition noise); (c) the difficulty to generate prediction from complex data sets.

Here, we propose a linear mixed model (LMM), efficiently implemented to tackle several of these big‐data neuroimaging challenges. Our approach allows performing association and prediction analyses on tens of thousands of participants with more than 650,000 vertex‐wise morphological measurements of grey‐matter structure per individual. Specifically, we overcame the curse of dimensionality by estimating the total correlation of all cortical and subcortical measurement at vertices with a phenotype of interest (previously coined morphometricity [Sabuncu et al., 2016], here we prefer the more specific brain‐morphometricity). Using the same framework, we also estimate the total association of a trait with differently processed MRI images as well with subset of the vertex‐wise data corresponding to specific brain features, hemispheres or regions of interest (ROI). We further introduce multi‐trait LMMs that can quantify shared morphometricity between traits (grey‐matter correlation). Grey‐matter correlation can help generate hypotheses about putative confounders (that may be regressed out in a conditional analysis) or about the origin of brain‐morphometricity. Finally, we show how the same LMMs can be used to construct grey‐matter scores that achieve brain MRI‐based prediction in independent samples. As such, our approach unifies association and prediction analyses, in order to unravel the brain‐phenome relationships (Rosenberg, Casey, & Holmes, 2018) in big‐data neuroimaging.

To demonstrate the applicability and usefulness of our methods, we analysed two of the largest MRI data sets available (UKB [split into discovery N = 9,888 and replication N = 4,561] and HCP [N = 1,110]) and considered a wide range of phenotypes spanning demographics, blood cell composition, diet, psychiatric and traumatic history, physical capacities and substance use. We discuss our results in the context of the recent commentary article of Smith & Nichols (Smith & Nichols, 2018). We have released our image processing and analysis software/scripts as well as all summary statistics to facilitate replication and re‐use of the results.

2. MATERIALS AND METHODS

2.1. UK biobank sample(s)

The UK biobank (UKB) participants were unselected volunteers from the United Kingdom (Sudlow et al., 2015) living near the imaging centres (Manchester for 96.5% of our sample, Newcastle for the remaining 3.5%). Exclusion criteria included: presence of metal implant, recent surgery and health conditions problematic for MRI imaging (e.g., hearing, breathing problems or extreme claustrophobia) (Miller et al., 2016). MRI acquisition parameters have been reported previously (Miller et al., 2016) and are summarised in Appendix S1.

We split the available UKB data into a discovery and replication sample based on their imaging date. The discovery sample consisted of 9,497 adults aged 62.5 on average (SD = 7.5, range 44.6–79.6) and comprised 52.4% of female participants (see Appendix S2 for details of processing and QC; Data set S1 for description of excluded participants). The UKB replication sample (N = 4,323) was on average 63.1 years old (SD = 7.46, range 46.1–80.3) with 52.1% of females (see Data set S1, Appendix S2).

We included 168 variables grouped in several categories: demographics, cognition, physical test, psychiatry, recent feelings, stress and traumas, substance use, miscellaneous, brain measurements, blood assay and diet (see Data set S2 for details). When longitudinal observations were available for a participant, we used the one collected as part of the imaging assessment or the closest in time to that.

2.2. UKB image processing

We processed the T1w and T2w images using FreeSurfer 6.0 (Fischl, 2012) to extract cortical surface area and thickness, and we used the ENIGMA‐shape protocols to measure the structure of seven subcortical volumes (hippocampus, putamen, amygdala, thalamus, caudate, pallidum and accumbens) (Boris A. Gutman, Madsen, Toga, & Thompson, 2013; B. A. Gutman, Wang, Rajagopalan, Toga, & Thompson, 2012). In FreeSurfer, we processed T1w and T2w together to enhance the tissue segmentation, hence a more precise skull stripping and pial surfaces definition. When the T2w was not acquired or not usable, we processed the T1w image by itself.

We retained the full cortical information by using the (“fsaverage”) cortical mesh for cortical thickness and surface area. This corresponded to about ~149,900 cortical vertices for each hemisphere and modality. In addition, we extracted subcortical radial thickness and log Jacobian determinant (surface deformation, somewhat analogous to a relative surface area [Roshchupkin et al., 2016]) for 13,560 vertices across the seven subcortical volumes (Boris A. Gutman et al., 2013). Overall, the imaging data used in the analyses comprised 652,283 vertex measurements per individual: 299,009 for cortical thickness, 299,034 for cortical surface area, 27,120 for subcortical thickness and 27,120 for subcortical curvature.

For comparison with ROI based processing, we extracted cortical thickness and surface area of 34 cortical regions (Desikan et al., 2006; Fischl et al., 2004) and volumes of the subcortical structures (ENIGMA processing). To further the comparison of processing options, we extracted cortical measurements from smoothed fsaverage meshes (fwhm 5, 10, 15, 20 and 25 mm) as well as (unsmoothed) coarser meshes provided by FreeSurfer: fsaverage6 (149,091 vertices across all hemispheres and modalities), fsaverage5 (37,455 vertices), fsaverage4 (9,457 vertices) and fsaverage3 (2,414 vertices).

2.3. Human connectome project sample

Human connectome project (HCP) participants were recruited from ongoing longitudinal studies of the Missouri Family Study and had to be between 22 and 35 years of age. Inclusion and exclusion criteria have been described previously (Van Essen, Ugurbil, et al., 2012) (see Appendix S1 for the MRI acquisition parameters, Appendix S2 for QC). As per the HCP “1200 Subjects data release” (first of March 2017), 1,113 participants were scanned on the 3T MRI and underwent extensive behavioural testing. Participants were mostly (54.4%) females and were 28.8 years old on average (SD = 3.7, range 22–37). The sample comprised 286 monozygotic twins (138 complete pairs) and 169 dizygotic twins (78 complete pairs). In addition, siblings and half siblings of twins were also recruited which resulted in 445 distinct families in the sample.

For the HCP sample, we included 161 variables, some of which were also available in the UKB (e.g., demographics, cognition, physical assessment, blood assay or psychiatry). We also included: personality, emotion, mental health assessment (Semi‐Structured Assessment for the Genetics of Alcoholism [SSAGA] and Adult Self Report [ASR] [Thomas M Achenbach, 2009; T. M. Achenbach, Dumenci, & Rescorla, 2003]), detailed cognition, Pittsburgh sleep index (PSQI) (Buysse, Reynolds 3rd, Monk, Berman, & Kupfer, 1989), or results from the urine drug tests (see Data set S2).

2.4. Image processing in the HCP

The FreeSurfer processing was performed by the HCP team (Glasser et al., 2013; Marcus et al., 2013; Van Essen, Glasser, Dierker, Harwell, & Coalson, 2012) using an optimal combination of automated and manual steps (Appendix S3). We downloaded the segmented images (Marcus et al., 2011) and performed the ENIGMA‐shape analysis (Boris A. Gutman et al., 2013; B. A. Gutman et al., 2012) to extract vertex‐wise measurements of the subcortical volumes. As with the UKB sample, a total of 652,283 vertex measurements were extracted for each individual.

2.5. Covariates used

Our baseline model included commonly used covariates in MRI analyses: acquisition variables (UKB imaging wave, processing with T1w or with combined T1w + T2w), age, sex, and head size (intra‐cranial volume [ICV] as well as left and right total cortical surface area and cortical thickness that correspond to the measurements used here). In a follow‐up analysis, we included other covariates such as height, weight and BMI to evaluate their confounding effect on the reported associations. As some of the covariates are correlated we report the adjusted R ² (from linear regression in R3.3.3 (R Development Core Team, 2012)) calculated by adding progressively the covariates (same order as above). The associations with covariates was highly concordant between the two UKB samples (Figure S1).

2.6. LMM for association and prediction

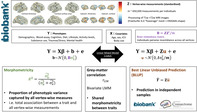
We aimed to estimate the proportion of variance of a trait captured by brain features, which Sabuncu et al., called “morphometricity” (Sabuncu et al., 2016). To do so we consider the following LMM (Figure 1) that allows estimating the association between a phenotype and M vertices even when M is greater than the sample size (N):

$$\mathbf{Y}=\mathbf{X\beta }+\mathbf{b}+\mathbf{e}$$ (1)

FIGURE 1.

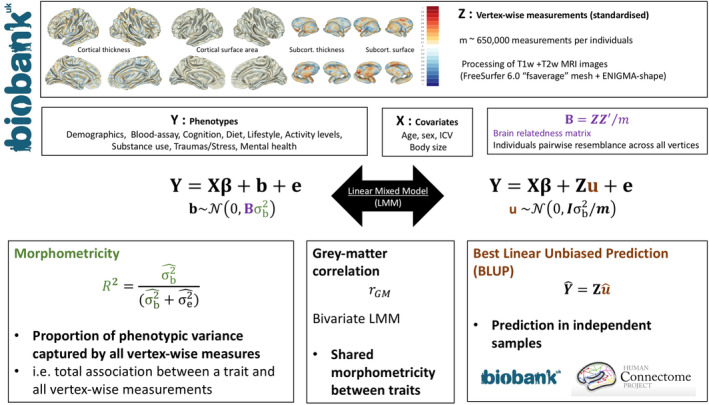
Summary of the analyses and methods. The data used in the analyses are detailed at the top, and include phenotypes, covariates and vertex‐wise measurements. Calculation of the brain relatedness matrix from the vertex‐wise data are also described. The two LMM formulations are equivalent, though the first one emphasises how morphometricity relates to the brain relatedness matrix and the second emphasises the joint effects of all vertex‐wise measurements. The boxes at the bottom provide brief interpretations of the new methods and concepts. Morphometricity estimate may be restricted to vertex‐wise measurements within a ROI, to estimate the phenotype‐ROI association that takes into account all local variations within the ROI. Morphometricity may also be used to compare the information retained by different MRI image processing (“Best processing”). Grey‐matter correlation measures the shared morphometricity between traits, or in other words the correlation between the vertex‐phenotypes associations for each phenotype. BLUP scores are predictors of the random effect, and make the hypothesis that the vertex‐phenotypes marginal joint associations weights are normally distributed. BLUP prediction, expressed in proportion of phenotypic variance, is capped by the morphometricity

where Y_N,1 is the phenotype considered with N the number of observations, X_N,c is a matrix of c covariates (as such does not include any vertex variable), β _c,1 is a vector of fixed effects, b is a vector of random effects with $\mathbf{b}~N\left(0,\mathbf{B}{\mathrm{\sigma }}_{\mathrm{b}}^2\right)$ and e is a vector of error terms with $\mathbf{e}~N\left(0,\mathbf{I}{\mathrm{\sigma }}_{\mathrm{e}}^2\right)$. In this formulation I_{N, N} is the identity matrix as we assume the error terms to be independent and identically distributed. B_{N, N} is a matrix of variance–covariance between individuals calculated from all vertex measurements, which we will refer to as the brain relatedness matrix (BRM, Figure 1). Off‐diagonal elements of the BRM reflect the grey‐matter similarity between two individuals (see Appendix SA). Finally, ${\mathrm{\sigma }}_{\mathrm{e}}^2$ and ${\mathrm{\sigma }}_{\mathrm{b}}^2$ are the variance components for the random effects e and b. For context, this model is analogous to that used in complex trait genetics to estimate SNP‐based heritability, where a Genetic Relatedness Matrix (GRM) replaces the BRM (Yang et al., 2010; Yang, Lee, Goddard, & Visscher, 2011), or that used to estimate the proportion variance in a phenotype captured by all DNA methylation or gene expression measures of the genome (Zhang et al., 2019). The element i,j of the BRM can be calculated as the inner product of brain measurements of individuals i and j: ${\mathrm{b}}_{\mathrm{i},\mathrm{j}}=\frac{\sum _1^{\mathrm{M}}{\mathrm{z}}_{\mathrm{i},\mathrm{m}}{\mathrm{z}}_{\mathrm{j},\mathrm{m}}}{\mathrm{M}}$. Here, z_{i, m} represents the value of vertex m for individual i centred and standardised over all individuals, z_{j, m}represents the value of vertex m for individual j centred and standardised over all individuals, M is the total number of vertices or brain features included. In matrix notation,$\mathbf{B}=\frac{\mathbf{ZZ}\prime }{\mathrm{M}}$ with Z_N,M being a matrix of the centred and standardised brain observations. We estimated the proportion of the trait variance captured by the grey‐matter measurements as: ${\mathrm{R}}^2=\frac{{\mathrm{\sigma }}_{\mathrm{b}}^2}{{\mathrm{\sigma }}_{\mathrm{b}}^2+{\mathrm{\sigma }}_{\mathrm{e}}^2}$ (Figure 1) using the REstricted Maximum Likelihood (REML)(Patterson & Thompson, 1971) implemented in OSCA (OmicS‐data‐based Complex trait Analysis) (Zhang et al., 2019). We tested whether the morphometricity was different from 0 using a likelihood ratio test (see Appendix S5 for details).

We extended the LMM above to jointly estimate the variance accounted for by the different modalities (cortical thickness, cortical area, subcortical thickness, subcortical area).

$$\mathbf{Y}=\mathbf{X\beta }+{\mathbf{b}}_{\mathbf{1}}+{\mathbf{b}}_{\mathbf{2}}+{\mathbf{b}}_{\mathbf{3}}+{\mathbf{b}}_{\mathbf{4}}+\mathbf{e}$$

with ${\mathbf{b}}_{\mathbf{i}}~\mathcal{N}\left(0,{\mathbf{B}}_{\mathbf{i}}{\mathrm{\sigma }}_{\mathrm{bi}}^2\right),\mathrm{i}\in \left.⟦1;\left(4\right.⟧\right)$, and all other parameters left unchanged. Each B_i is constructed from the vertex‐wise measurements of a single modality, with ${\mathrm{\sigma }}_{\mathrm{bi}}^2$ the corresponding association and $\frac{{\mathrm{\sigma }}_{\mathrm{b}1}^2+{\mathrm{\sigma }}_{\mathrm{b}2}^2+{\mathrm{\sigma }}_{\mathrm{b}3}^2+{\mathrm{\sigma }}_{\mathrm{b}4}^2}{{\mathrm{\sigma }}_{\mathrm{b}1}^2+{\mathrm{\sigma }}_{\mathrm{b}2}^2+{\mathrm{\sigma }}_{\mathrm{b}3}^2+{\mathrm{\sigma }}_{\mathrm{b}4}^2+{\mathrm{\sigma }}_{\mathrm{e}}^2}$ the brain‐morphometricity.

Next, we sought to estimate the correlation between two traits that is attributable to the same grey‐matter variation, which we call grey‐matter correlation r_GM (Figure 1 ). This can be achieved by fitting a bivariate LMM, a direct extension of the models presented above (Thompson, 1973). We restricted our bivariate analysis to variables that were significantly associated with grey‐matter structure. We derived the residual correlations (r_E) from the phenotypic (r) and grey‐matter correlations estimated by GCTA (Genome‐wide Complex Trait Analysis) (Yang et al., 2011) (option not yet included in OSCA). We calculated its SE using the delta method (Appendix S6 and [Bijma & Bastiaansen, 2014; Lee, Yang, Goddard, Visscher, & Wray, 2012; Visscher, 1998]).

We detailed power calculations for the LMMs (Appendix S7, Visscher et al., 2014), which showed that in the UKB discovery sample we had good power to detect a small morphometricity (R ² > 2.2%) but only a moderate grey‐matter correlation (r_GM > 0.35). Statistical power was a lot reduced in the HCP due to the smaller sample size.

We demonstrated two further utilities of LMMs for neuroimaging data analyses. First, we conducted post hoc analyses to test the associations with each modality and each cortical (Desikan et al., 2006) or subcortical structure. We used BRMs specific to each region and brain measurement (Figure 1), which bridges the gap between ROI and vertex‐wise analyses. Second, we define as “best” processing the MRI cortical processing that maximises the association with a trait of interest, from the minimal number of features (vertices). Thus, we evaluated which of our FreeSurfer processing (fsaverage—no smoothing; fsaverage—smoothing fwhm5, 10, 15, 20, 25; fsaverage6, 5, 4, 3—no smoothing; ENIGMA ROI processing) maximised the brain‐morphometricity for all the UKB traits (See Appendix S2 for details about QC). As the ENIGMA processing only consists of 150 measurements, we used linear models (multiple regression and adjusted R²) to estimate the brain‐morphomometricity.

Finally, we derived brain prediction scores using the Best Linear Unbiased Predictors (BLUP, Figure 1) (Henderson, 1950, 1975; G. K. Robinson, 1991) and evaluated them in the UKB discovery sample using a 10‐fold cross‐validation design. In addition, we derived BLUP brain prediction scores constructed from the UKB discovery sample, and applied them to the UKB replication and HCP participants to evaluate the “out of sample” predictive performance. BLUP estimates the predicted values of the random effects (b or Zu, see [1] and Figure 1) (Goddard, Wray, Verbyla, & Visscher, 2009; G. K. Robinson, 1991). In short, BLUP scores integrate the correlations between vertices to derive weights that correspond to the joint effects of all the vertices (Figure 1). BLUP have desirable statistical properties: they are unbiased and are best predictors in the sense that they minimise the mean square error in the class of linear unbiased predictors (Henderson, 1975; G. K. Robinson, 1991), leading to more accurate prediction than other linear predictors (M. R. Robinson et al., 2017; Vilhjalmsson et al., 2015).

2.7. Prediction accuracy of BLUP versus LASSO

We compared prediction accuracy achieved by BLUP scores to that of LASSO (least absolute shrinkage and selection operator) (Tibshirani, 1996) for phenotypes with significant brain‐morphometricity (baseline covariates). LASSO penalises vertices coefficients of the linear regression, leading to select a subset of vertices (and their weights) that maximise prediction accuracy. We used the LASSO function implemented in the bigstatsr R package (Privé et al., 2018) and estimated the hyper‐parameter using cross‐model selection and averaging on fivefolds within the UKB discovery sample. For each grey‐matter score, we reported the prediction R ² on the UKB replication sample and tested the difference in prediction using a Wilcoxon test on the absolute errors of the BLUP and LASSO predictors.

2.8. Data and code availability statement

Data used in this manuscript are held and distributed by the HCP and UKB teams. We have released the scripts used in image processing and LMM analyses to facilitate replication and dissemination of the results (see URLs). We have also released BLUP weights to allow meta‐analyses or application of the grey‐matter scores in independent cohorts.

3. RESULTS

3.1. Associations between phenotypes and all grey‐matter structure vertices

For the phenotypes of interest, we summarised in circular barplots (Figure 2) the proportion of phenotypic variance associated with all 652,283 vertex‐wise grey‐matter measures (brain‐morphometricity, R ²) as well as with baseline covariates (see Methods). Figure 2 shows only the results that were significant after Bonferroni correction (p_{UKB_discovery} < 2.8e−4 and p_HCP < 2.9e−4). The full results are available in Data set S3, S4 (see Figure S2 for positive control associations with global measures of the brain).

FIGURE 2.

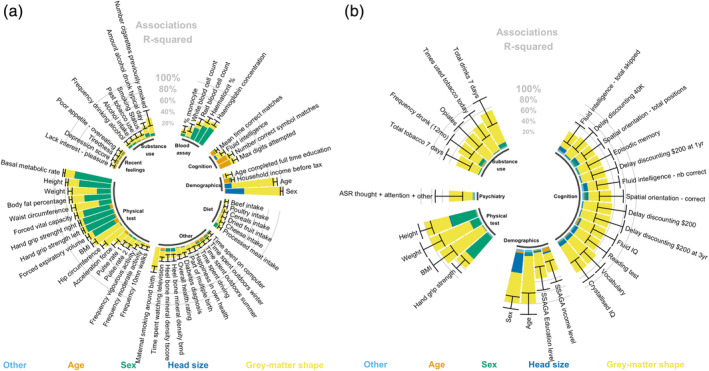
Circular barplot of the associations (R²) between phenotypes and grey‐matter structure vertices (morphometricity). For clarity, we only plotted the significant associations in the UKB discovery (Panel a) and HCP sample (Panel b). We applied Bonferroni correcting to account for multiple testing in each sample. The black bars represent the 95% confidence intervals of the morphometricity estimates. For context, we also present the association R ² between phenotypes and covariates of the baseline model, as per the legend under the barplot. As some covariates may be correlated, the R ² was calculated by adding progressively the covariates in that order: acquisition and processing variables (labelled “other”), age, sex and head size (ICV, total cortical thickness and surface area). Age and sex were not included as covariates when studying them as phenotypes. See Data set S3, S4 for full results. See Figure S1 for positive control associations

Grey‐matter structure was strongly associated (R ² > 0.40) with age, sex, as well as weight, BMI waist and hip circumference but also with maternal smoking around birth (R² = 0.39) and number of cigarettes previously smoked (R ² = 0.27) (Figure 2). We identified many other phenotypes significantly associated with grey‐matter structure (Figure 2, Data set S3) including other measures of build (e.g., height, body fat percentage, basal metabolic rate), substance use (e.g., amount of alcohol drank each day), household income level and education level, strength (e.g., hand grip, acceleration), cognition (e.g., fluid IQ), blood assay (e.g., white blood cell count), diet (cheese intake), but also perhaps more surprisingly with being a twin or overall health rating. We also found associations with clinical phenotypes such as diabetes, depression score and depression symptoms. We replicated 23 of the 58 associations listed above in the UKB replication sample (p < .05/58; Figure S3, Data set S4). We did not detect any significant association between grey‐matter structure and other psychiatric variables (diagnoses and symptoms), self‐reported stresses and traumas, or neuroticism (Data set S3). The interested readers may also find the morphometricity estimates for the full UKB sample (inverse‐variance weighted meta‐analysis) in Data set S3.

In the UKB (discovery), results and conclusions did not change regardless of fitting a single random effect or several random effects each corresponding to one of the grey‐matter modalities (Figure S4). In the HCP, we observed three extra significant associations between grey‐matter structure and cocaine (urine test), self‐reported number of times used cocaine or hallucinogens. Similar to the association found with opiate (urine test), these results warrant replication due to the small number of positive participants. Finally, the HCP results did not change when excluding related individuals (Appendix S8).

3.2. Adjustment for possible confounders

The large associations between grey‐matter structure and height, weight, BMI, waist and hip circumference (Figure 2) led us to perform a sensitivity analysis to evaluate their contribution to the brain‐morphometricity of the traits studied. We repeated the analysis further controlling for height, weight and BMI, which yielded lower R ² estimates (Figure S5) and fewer significant associations with grey‐matter structure. Thus, when correcting for height in the UKB, 4 of the 58 associations with grey‐matter structure did not remain significant: household income, monocyte percentage, beef intake, and time spent using computer, Data set S3). Such finding is consistent with the reported association between body size and income or socioeconomic status in the UKB (Tyrrell et al., 2016). When further correcting for weight and BMI another 14 associations did not remain significant including educational attainment, frequency drinking alcohol, most diet items (cereal, dried fruits, poultry, processed meat), time spent driving, red blood cell count, frequency of walks and small exercise. Notably, the brain‐morphometricity of the depression score could be completely explained by differences in weight and BMI (R ² _baseline = 0.050, SE = 0.018; R ² _{baseline + height} = 0.048, SE = 0.017, R² _{baseline + height + BMI + weight} < 0.001, SE = 0.007), and none of the associations between grey‐matter structure and depression symptoms remained significant conditioning on weight and BMI (Tiredness, Anhedonia, Poor appetite‐overeating, R² _{baseline + height + BMI + weight} < 0.014). Yet, even after controlling for body size, we still detected a significant morphometricity for cheese intake as well as time watching TV (Data set S3), suggesting that these behaviours are associated with brain structure irrespective of body size. The morphometricity estimates in the UKB replication sample aligned with those from the discovery sample (cor = 0.90), except for age and sex that showed larger associations with grey‐matter structure in the replication analysis (Figure S6). In the HCP data set, after controlling for body size, four of the 27 associations did not remain significant (Data set S4) though we had limited power to detect associations smaller than R ² of 0.2 in this sample (see Appendix S7).

In light of these results, we chose a conservative approach to control for body size variables in the main text, though the analyses using baseline covariates can be found in the supplementary. We acknowledge (see discussion) that this may be overly conservative, by implicitly making strong assumptions about body size acting as a confounding factor. On the other hand, it avoids reporting associations that may be fully or in part caused by differences in body shape.

3.3. Grey‐matter correlations

We estimated grey‐matter correlation (r_GM) between the phenotypes that showed significant brain‐morphometricity in the univariate analyses (Figure 2). r_GM can be interpreted as the correlation between the grey‐matter vertices associations with each trait. We controlled for height, weight and BMI on top of the baseline covariates, leaving a conservative set of 35 UKB (18 HCP) phenotypes (Figure 3; Data set S5 [UKB], Data set S6 [HCP]). In the UKB, we observed significant positive grey‐matter correlations between cognition domains, substance use phenotypes or between measures of physical activity (Figure 3). In addition, we found unexpected large grey‐matter correlations. For example, cheese intake and forced expiratory volume were both correlated (r_GM = 1.0, SE = 0.11) with fluid intelligence, and waist circumference was correlated with overall health rating and pulse rate (r_GM > 0.67). Overall, 9 out of the 26 significant correlations replicated in the UKB replication sample (p < .05/26 that is, p < 1.9e−3, Table S1). In the HCP, we also observed positive grey‐matter correlations between cognition domains or between the two tobacco related phenotypes. Though, unlike in the UKB, we found a significant r_GM between IQ dimensions and education level (Figure 3, Data set S6).

FIGURE 3.

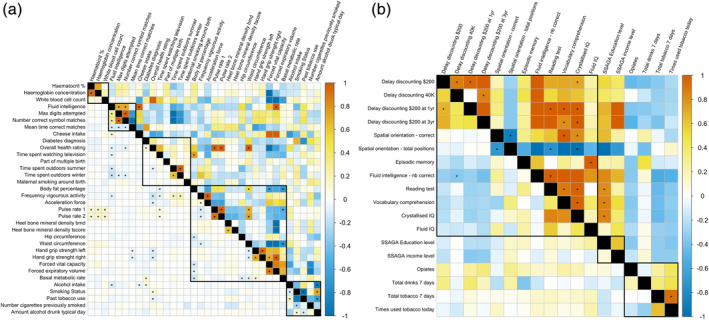
Matrices of grey‐matter correlations (upper diagonals) and residual correlations (lower diagonals) between all the variables showing significant morphometricity after controlling for baseline covariates, as well as height, weight and BMI. Panel (a) shows the results for the UKB and Panel (b) the HCP results. We excluded phenotypes used as covariates (age, sex, head and body size) as regressing them out makes them orthogonal (i.e., not associated) with the remaining traits. We used conservative significance thresholds of 0.05/(35*34) = 4.2e−5 for UKB and 0.05/(18*17) = 1.6e−4 for HCP that account for the total number of correlations performed in each sample. Correlations significant after multiple testing correction are indicated by a star. Blocks circled in black indicate the different phenotype categories used previously (see Figure 2). r_GM is a measure of the shared brain‐morphometricity between 2 traits. Contrasting r_GM and residual correlation (r_E) indicate how much of the phenotypic co‐variance is attributable to individual's resemblance in term of grey‐matter structure vs. other factors (brain or nonbrain resemblances)

For completeness, we estimated grey‐matter correlations under the baseline model (Figure S7), which reveals many large grey‐matter correlations between measures of body size and diet, blood assay, activity levels and depression symptoms and score. These results further highlight that in the phenome, the brain‐morphometricity of some traits may be accounted for by the covariation between these phenotypes and body size measurements. In particular, depression score was correlated (r_GM = 1) with weight, BMI waist or hip circumference, consistent with its brain‐morphometricity lowered to 0 when controlling for body size (Figure S7).

3.4. Associations with grey‐matter structure of specific cortical and subcortical regions

We investigated the brain‐morphometricity of traits by estimating the association with grey‐matter structure of specific cortical (Desikan et al., 2006) and subcortical regions, correcting for multiple testing (Bonferroni significance threshold of 0.05/[164*39] = 7.2e−6 in the UKB, 1.2e−5 in the HCP). We found many significant ROIs associations with UKB phenotypes, including age, sex, maternal smoking around birth, fluid intelligence, diabetes or substance use (Figure S8 and Data set S7). In particular, the associations between grey‐matter structure and body size were pervasive (72/164 significant ROIs associations with height, 109 with waist circumference, 105 with BMI) (Figure S9, Data set S8), suggesting that when acting as confounders height, weight or BMI could lead to false positives in many brain regions. We replicated 633 of the 975 significant ROI‐trait associations (p < .05/975, see Data set S9 for results on UKB replication sample). Most replicated associations were found with age, sex and body size variables, though we also replicated associations between subcortical volumes and hand grip strength or time spent watching TV (Data set S7–S9). Overall, some of the trait‐ROIs associations were partially redundant as indicated by a sum of R ² (over ROIs) greater than the morphometricity (see Appendix S9 for detailed results and discussion, Data set S10 for results in HCP).

3.5. Better cortical processing

We compared the brain‐morphometricity estimates obtained by varying the cortical processing options: smoothing of the cortical meshes and applying coarser FreeSurfer meshes. We found that applying smoothing (5–25 mm) or reducing the cortical mesh complexity always led to a lower point estimate of brain morphometricity in the UKB discovery (Figure 5) and replication (Figure S10, Data sets S11,12 for full tables) samples. These differences were significant for a handful of variables (incl. age, sex, maternal smoking or body size) using a stringent definition of significance based on overlapping confidence intervals (Table S3). Thus, the fsaverage cortical mesh with no smoothing may be deemed a better processing approach for at least some of the phenotypes considered. Similarly, we found that the vertex‐wise approach always yielded greater association R ², thus retained more information than a ROI based dimension reduction (Figure S11).

FIGURE 5.

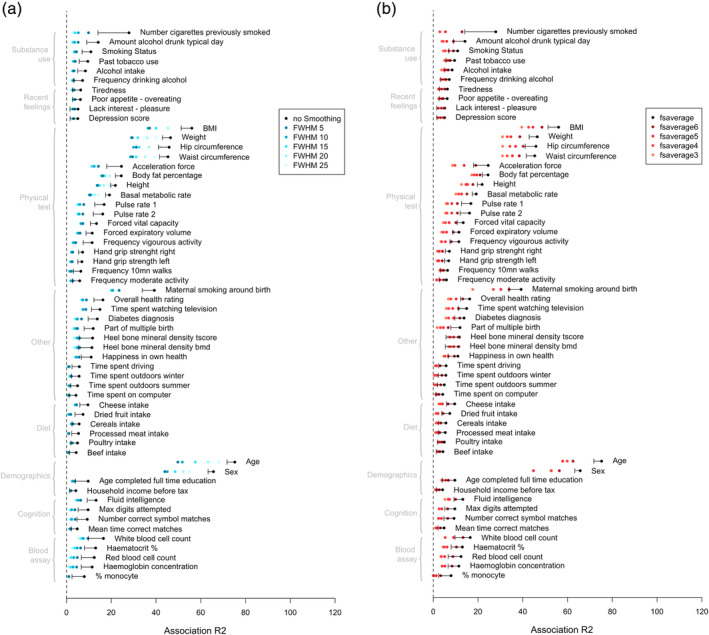
Comparison of brain‐morphometricity estimates varying cortical processing options in FreeSurfer. The reduction of brain‐morphometricity as a function of mesh smoothing is presented on the left panel (a), while the right panel (b) shows the effect of reducing the cortical mesh complexity. The black bar indicates the lower bound of the 95% confidence interval of the fsaverage‐no smoothing estimate (identical to results presented in Figure 2, except that covariates R ² are not plotted here to simplify the figure). Brain‐morphometricity estimates below the 95%CI lower bound cannot be deemed significantly lower. Rather the 95%CI are presented for context and to remind that all estimate from Figure 2 do not have the same SE. See Table S3 for a conservative list of phenotypes with significantly reduced morphometricity compared with fsaverage—no smoothing

3.6. Ten‐fold cross‐validation in the UKB and prediction into the UKB replication sample

For each UKB participant, we calculated (BLUP) grey‐matter scores relative to phenotypes showing significant brain‐morphometricity. As in sections above, for height, weight and BMI we controlled for baseline covariates and further regressed out body size for all other phenotypes.

In the 10‐fold cross‐validation analysis, most grey‐matter scores significantly correlated (positively) with their corresponding phenotypes (significance threshold of 0.05/39 = 1.2e−3, Table 1, S3, Figure 4). Albeit significant, prediction accuracy was overall low (typically r < 0.10, including r = 0.11 for sex, r < 0.09 with cognition, r = 0.08 for alcohol intake, r = 0.06 with smoking status) except for age (r = 0.60) and maternal smoking around birth (r = 0.26). We found similar prediction results in the UKB replication sample, with 29 associations reaching significance at p < 1.2e−3 (Table 1, S3). Prediction accuracy into the UKB replication sample was on par for most traits, though slightly greater for age and sex compared with the cross‐validation results (Figure 4, Table 1, S3). This is consistent with a larger training sample being used and larger morphomometricity observed in the replication set (Figure S6).

TABLE 1.

Summary of the prediction accuracy (R²) of the BLUP grey‐matter scores

	In sample prediction (UKB)				Prediction into UKB replication				Out of sample prediction (HCP)
	r	p‐value	R2	AUC (SE)	r	p‐value	R2	AUC (SE)	HCP variable predicted	r	p‐value	R2	AUC (SE)
Age	0.64	0.0e+00	0.41		0.68	0.0e+00	0.46		Age	0.15	3.1e−08	0.024
Sex	0.26	0.0e+00	0.067	0.58 (0.0059)	0.33	9.8e−305	0.11	0.8 (0.0064)	Sex	−0.25	8.0e−42	0.061	0.68 (0.016)
Part of multiple birth	0.078	4.1e−14	0.0061	0.66 (0.022)	0.13	1.5e−03	0.016	0.72 (0.065)	Being a twin	0.31	1.1e−28	0.098	0.69 (0.016)
Body fat percentage#	0.29	0.0e+00	0.085		0.31	7.7e−190	0.095		BMI	0.21	5.6e−13	0.045
Waist circumference#	0.39	0.0e+00	0.16		0.38	2.0e−205	0.14		BMI	0.21	3.5e−13	0.046
BMI#	0.45	0.0e+00	0.2		0.45	7.4e−235	0.20		BMI	0.21	2.4e−12	0.042
Hip circumference#	0.38	0.0e+00	0.15		0.36	7.3e−143	0.13		BMI	0.21	5.2e−13	0.045
Height#	0.25	6.5e−318	0.062		0.23	2.6e−132	0.054		Height	0.17	1.8e−17	0.03
Weight#	0.39	0.0e+00	0.15		0.39	5.8e−231	0.15		Weight	0.19	1.2e−12	0.036
Maternal smoking around birth	0.26	9.8e−132	0.069	0.66 (0.0067)	0.25	1.7e−08	0.063	0.65 (0.027)	FTND score	0.19	8.9e−04	0.037

Note: We constructed BLUP scores for the 39 UKB variables showing significant morphometricity and evaluated their predictive power in the UKB (10‐fold‐cross validation) and HCP sample. When the phenotype corresponding to the grey‐matter score was not available in the HCP, we chose the closest available (e.g., waist circumference grey‐matter score evaluated against BMI). We evaluate the prediction accuracy by fitting GLM controlling for height, weight and BMI as well as for the baseline covariates (acquisition, age, sex and head size); except for (#) denoting associations not controlling for height, weight and BMI. Rows in bold indicate significant association after correcting for multiple testing (p < .05/39 = 1.3e−3) both in and out of sample. This reduced table only shows prediction results significant in all three scenarios, see Table S2 for full table of results. We reported the AUC (for discrete variables) as it is independent of the proportion of twins and males, thus differences in AUC likely reflect differences in morphometricity between the UKB and HCP samples.

FIGURE 4.

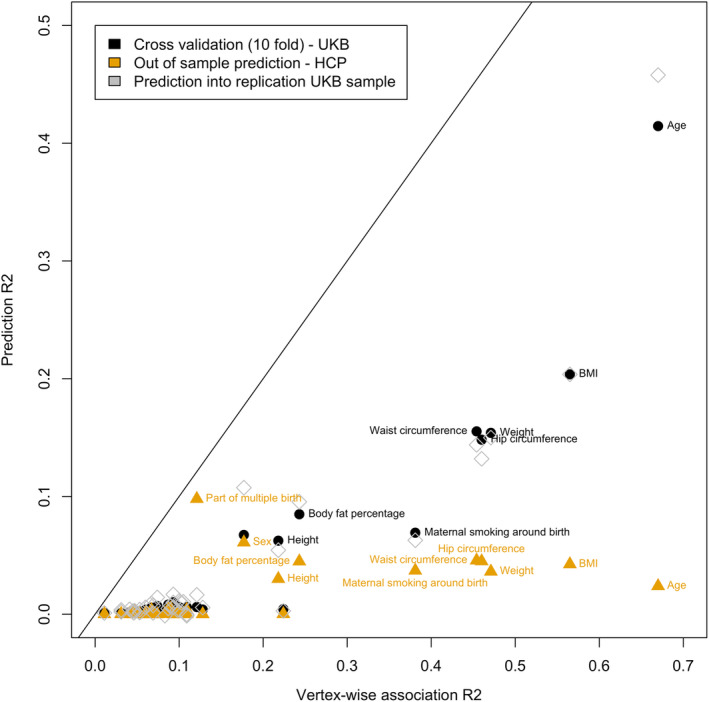
In sample and out of sample prediction accuracy as a function of the total association R ². Labels highlight some of the significant prediction having the greatest accuracy. As predicted by the theory, the prediction accuracy is capped by the total association R ² (points below the diagonal). We limited the prediction analysis to phenotypes showing a significant brain‐morphometricity in the UKB discovery sample

When not correcting for body size, 56/58 BLUP scores significantly correlated with the observed values in the 10‐fold cross validation and 42 associations replicated using the UKB replication sample (p < .05/58, See Figure S12 and Data set S13). Predicted age correlated with chronological age (r = 0.72 in the discovery, r = 0.70 in the replication), while predicted sex also strongly associated with the observed value (AUC of 0.90 and 0.89). Grey‐matter scores of body shape (under the baseline covariates) were also significantly correlated with the observed values (r = 0.25 for height, r = 0.29 for body fat percentage, r = 0.39 for weight and hip or waist circumference, r = 0.45 for BMI). Finally, grey‐matter scores of BMI correlated positively with depression symptom count (r = 0.10, p‐value<1e−14), as expected from the brain‐morphometricity of depression being limited by the covariation with body size. It even outperformed the grey‐matter score built from the depression score itself (r = 0.05, p‐value<1e.5).

BLUP achieved similar to superior prediction accuracy (R ²) compared to LASSO brain scores across the 58 phenotypes (Figure S13, Data set S13). BLUP significantly outperformed LASSO (Wilcoxon test on absolute errors, p < .05/58) in predicting hip circumference, alcohol intake and number of correct symbol matches (cognition).

3.7. Out of sample prediction—Application in the HCP sample

Of sample prediction validates that the morphometric associations are generalizable to independent brain images, beyond population and scanner differences. For traits only available in the UKB (e.g., waist circumference) we used a proxy in the HCP (e.g., BMI). Grey matter scores for age, sex, and being a twin significantly correlated with the observed values (r _age = 0.15, r _sex = 0.25, r _{twin‐status} = 0.31, Table 1, Table S3 and Figure 4). Grey‐matter score for maternal smoking around birth correlated with smoking status (r = 0.19). None of the other grey‐matter scores significantly correlated with a similar HCP variable.

Without correcting for body size, 19 BLUP scores correlated to corresponding variables (Data set S13, Figure S12). For example, scores for BMI, body fat percentage, hip or waist circumference also correlated positively with BMI (r = 0.21, p‐value<1.2e−3), while scores for height and weight also correlated with the observed phenotypes (r _Height = 0.17, r _Weight = 0.19). Finally, scores build from diet items or quantifying activity levels significantly predicted BMI in the HCP.

4. DISCUSSION

We have introduced a set of analyses, that rely on LMM (Figure 1) to perform association and prediction, while being suited to tackle the challenges of big‐data in neuroimaging (Smith & Nichols, 2018). We have demonstrated their applications in two of the largest MRI cohorts available for research (UKB (Miller et al., 2016) and HCP (Van Essen et al., 2013)) using a fine‐grained processing of anatomical MRI that consisted in >650,000 grey‐matter measurements per individual. In LMMs, the overall effect of the high dimensional vertex‐wise measures is modelled by a single random effect, with a variance–covariance structure calculated from the vertex‐wise data: the brain relatedness matrix (BRM, Figure 1). BRM off‐diagonal elements represent the relative global similarity between grey‐matter structure of two people. The model is equivalent to fitting all vertices as a set of random effects, constraining the association effect sizes to be normally distributed (Figure 1), which can be seen as an extension of multiple regression when the number of variables exceeds the number of participants. This framework allows estimating new sample characteristics such as the total association (morphometricity Sabuncu et al., 2016) between a phenotype and vertex‐wise brain data or grey‐matter correlations that quantify how much phenotypes may be similarly associated with grey‐matter. In addition, it offers to build performant brain‐based predictors that do not require hyper‐parameter estimation.

Our analyses replicated and extended previous morphometricity reports (Sabuncu et al., 2016) (Figure 2, Data set S3, S4). We have demonstrated that our methods produce robust, replicable results (Figure S3, S6, S10, Table S1, S3) that were partly transferrable on a completely independent sample (the HCP) despite large differences between the samples (Table S2, Data set S13). We have shown additional utilities of this LMM framework such as the ROI based association test that retained the vertex‐wise complexity of a brain region (Figure S8–S8, Appendix S9, Data set S7–S10), rather than summarising them by a single average measure, effectively bridging the gap between ROI/atlas based and vertex‐wise analyses. Our results aligned with previously published associations with sex (Ritchie et al., 2018), BMI (Cole et al., 2013; Gupta et al., 2015; Kurth et al., 2013; Masouleh et al., 2016; Medic et al., 2016; Opel et al., 2017) or substance use (Cardenas, Studholme, Gazdzinski, Durazzo, & Meyerhoff, 2007; Gallinat et al., 2006; Gillespie et al., 2018; Hanlon et al., 2016; Pitel, Segobin, Ritz, Eustache, & Beaunieux, 2015) (see details in Appendix S9). We showed another application of LMMs for big‐data neuroimaging: to compare the amount of information retained by different MRI image processing. We found that using the most complex cortical mesh (“fsaverage”) with no smoothing maximised the brain‐morphometricity across all phenotypes studied, though further statistical testing of the difference is required (Table S3). This suggests there is meaningful information in fine grained grey‐matter data that is lost when performing local averages (via smoothing, coarser mesh or average over a ROI). More work is needed to compare our surface‐based approach (Fischl, 2012) to volume based processing (Flandin & Friston, 2008), or evaluating the putative added value of including the T2w image (on top of the T1w). To finish on processing, in the UKB we combined vertex‐wise data estimated from T1w and T1w + T2w which is meant to improve grey‐matter segmentation, though few studies quantified it (Lindroth et al., 2019). Here, we confirmed a difference in cortical thickness between processing groups (Lindroth et al., 2019)(Figure S2), though our data driven QC (Appendix S2) excluded 80% of the 400‐odd participants processed using T1w only (flagged as outliers). We corrected for processing type in the analyses and the good replication of the UKB associations (Figure S3, S6, Table S1) in addition to the out of sample prediction (Figure 4) suggest that our results are robust.

Beyond the large morphometricity estimates found for age and sex, BMI, weight, waist and hip circumference, and both passive and active smoking (Figure 2, Data set S3), we found many small(er) associations, with a wide array of phenotypes, including some more unexpected ones [e.g., self‐reported diet, being a twin, happiness with one's health, blood assay results (Figure 2, Data set S3)]. Such findings may echo the concerns raised by Smith and Nichols about the presence of many (small) confounded associations in big‐data neuroimaging (Smith & Nichols, 2018). The fact that we replicated the morphometricity in another UKB sample, does not completely rule out a confounding effect, as the same bias [e.g., healthy bias in recruitment (Fry et al., 2017)] may be present.

We illustrated this concern using the example of body size (BMI, weight, height), which showed large, replicated morphometricity and was available in both cohorts. We evaluated its contribution to the reported morphometricity by performing conditional analyses and bivariate LMMs. Both approaches yielded the same conclusions: a large fraction of the morphometricity detected was attributable to body size (Figure S7, Data set S3). However, co‐variation does not necessarily imply confounding (which requires establishing direction of effects) but may instead point to intermediate phenotypes or arise from the pervasive pleiotropy across the human phenome (Solovieff, Cotsapas, Lee, Purcell, & Smoller, 2013). In addition, we are dealing with associations, meaning that (except for exposures such as age or sex) the trait‐vertex associations responsible for the morphometricity may be a cause and/or a consequence of the phenotypes. For example, there is a known association between BMI and depression, with evidence of pleiotropy, but also of a causal effect of BMI on depression (Wray et al., 2018), though we do not know which of BMI and grey‐matter structure cause the other and cannot label body size a confounder. Thus, a conservative interpretation is that morphometricity of the depression score is limited to the shared variation with body size in the UKB (Data set S3, Figure S7). However, our findings shed a new light on previously published results, as even the largest case–control international initiatives [e.g., ENIGMA‐MDD (Schmaal et al., 2016; Schmaal et al., 2016)] may reflect, at least in part, variance shared between depression and BMI (Cole et al., 2013). More work is needed to understand body size contribution to published results linking grey‐matter anatomy to psychiatric disorders (MDD, bipolar, schizophrenia and substance use are all associated with BMI [Luppino et al., 2010; McElroy & Keck, 2012; Rajan & Menon, 2017; Saarni et al., 2009; Wray et al., 2018]) or sexually dimorphic traits (likely associated with height and weight). In addition, body size may be differently associated with the phenome across countries or age groups, which may limit the replication of findings and predictive abilities of body size dependent scores. Finally, the possible confounding effects of body size are exacerbated in small case–control samples, leading to increased chances of false positive associations (Button et al., 2013; Ioannidis, 2005). Note that body size being associated to many brain regions (Figure S9), its confounding effect could lead to widespread cortical or subcortical false positives.

A different example may be that of cheese intake, previously given as an absurd example of putative association likely confounded by socioeconomic status (Smith & Nichols, 2018), and for which we found a significant (replicated) morphometricity, even after correcting for body size (Figure 2, Data set S3). Consistent with the hypothesis of a confounded association, our bivariate analysis identified large r_GM (r_GM = 1) between cheese intake and household income level, or fluid intelligence (Figure S7), though the latter was significant only when controlling for body‐size (Figure 3). Thus, grey‐matter correlation may allow hypothesis‐generation about the origin of the morphometricity signal and could help better identifying putative confounders. If confirmed, such confounded morphometricity would not translate into significant prediction into the general population (where IQ may not be associated with cheese intake) or into another sample/country with different dietary habits.

Beyond the confounding/mediating effect between phenotypes one should also be wary of known MRI acquisition artefacts and confounds (Smith & Nichols, 2018). Here, we focused on well‐studied MRI modalities (T1w and T2w) which may be among the least sensitive to artefacts, especially that acquisition was performed on a single MRI machine and processed using standard image processing pipelines (Fischl, 2012). However, we detected significant morphometricity for pulse rate, bone mineral density and indirect measures of breathing rate/depth (Smith & Nichols, 2018), even after controlling for body size (Data set S3). In addition, the large grey‐matter correlations between pulse rate and overall health rating, and between forced expiratory volume and fluid intelligence (Figure 3), suggest they might indeed act as confounders. More work is needed to extend the list of acquisition confounders studied (e.g., head motion), and more power is needed to detect finer grained r_GM with the phenotypes of interest (Appendix S7). Finally, note that r_GM would also capture correlated measurement errors between traits (e.g., when two traits are associated with head motion).

Next, we constructed BLUP scores that estimate the random effects of the LMM and demonstrated their predictive abilities in independent samples [UKB replication and to a lower extend in the HCP, (Figure 4, S12, Table 1, S2, Data set S11), which differs in term of scanner and sample composition]. In addition to its statistical properties (unbiased, best predictor in the class of linear predictors), we demonstrated that BLUP achieved similar (to greater) prediction accuracy compared with LASSO based prediction, while being more computationally efficient than most traditional machine learning approaches as it does not require hyper‐parameter estimation. Note that prediction relates naturally to association which is apparent from our model formulation (Figure 1). Thus, the morphometricity value represents the upper asymptote achievable in linear prediction [Figure 4, (Dudbridge, 2013)]; in addition, grey‐matter correlation indicates when transfer learning is possible between the two variables. The limited prediction accuracy currently prevents BLUP scores being used in the clinical settings. However, they open the way to new analyses on samples already collected, for which information was not or could not be collected. Further application of our BLUP grey‐matter scores include studying correlates of brain age or predicted age difference (difference between predicted and chronological age) (Cole, 2017; Cole et al., 2017; Liem et al., 2017).

Despite good statistical power in theory (Appendix S7), the low numbers for some of the binary variables may explain the lack of associations found with psychiatry (e.g., schizophrenia, ADHD), stresses, traumas (Data set S3), which would have to be confirmed using a larger UKB sample or case–control samples [see results in (Sabuncu et al., 2016)]. Similarly, a lot of the trait variance remains unaccounted for by the grey‐matter structure variation (Figure 2) which calls to study brain regions not extracted here (e.g., brain stem, cerebellum), other processing options (e.g., volume based processing), or MRI images (diffusion weighted, fMRI) to further characterise the phenotypes.

Our approach is suited to studying other MRI contrasts and even multiple MRI modalities at once by fitting several random effect components (Figure S4). In addition, the efficient implementation in the OSCA software (Zhang et al., 2019) means the analyses are scalable to the future full UKB sample of 100,000 participants, which should improve power and BLUP prediction accuracy (Dudbridge, 2013). Beyond the global or regional associations reported here, future analyses should aim at identifying the vertices that contribute to the morphometricity. An existing method is mass‐univariate vertex‐wise analysis, though this comes as a huge increase of multiple testing burden and may still be underpowered with the current sample sizes (Smith & Nichols, 2018).

URLs

Summary‐level data (BLUP weights): https://cnsgenomics.com/content/data and https://cloudstor.aarnet.edu.au/plus/s/T1gyJyQsF6wTMjF; Code used for the analyses and plots is downloadable at https://github.com/baptisteCD/Brain-LMM and viewable at https://baptistecd.github.io/Brain-LMM/index.html; OSCA: http://cnsgenomics.com/software/osca/; ENIGMA processing protocols: http://enigma.ini.usc.edu/protocols/imaging-protocols/;

CONFLICT OF INTERESTS

The authors declare no conflict of interests.

AUTHOR CONTRIBUTIONS

Peter M. Visscher, Naomi R. Wray, Jian Yang and Baptiste Couvy‐Duchesne designed the analyses. Futao Zhang and Jian Yang developed the OSCA software. Yan Holtz and Baptiste Couvy‐Duchesne created the plots. Kathryn E. Kemper, Loic Yengo and Zhili Zheng assisted Baptiste Couvy‐Duchesne with the UKB phenotypic and genetic data, including download, formatting and curation. Lachlan T. Strike downloaded and processed the HCP MRI images under Margaret J. Wright supervision. Baptiste Couvy‐Duchesne downloaded and processed the UKB MRI images. Baptiste Couvy‐Duchesne performed the analyses and wrote the manuscript. All the authors reviewed the manuscript.

Supporting information

Appendix S1: Supporting Information

Couvy‐Duchesne B, Strike LT, Zhang F, et al. A unified framework for association and prediction from vertex‐wise grey‐matter structure. Hum Brain Mapp. 2020;41:4062–4076. 10.1002/hbm.25109

DATA AVAILABILITY STATEMENT

Data used in this manuscript are held and distributed by the HCP and UKB teams. We have released the scripts used in image processing and LMM analyses to facilitate replication and dissemination of the results (see URLs). We have also released BLUP weights to allow meta‐analyses or application of the grey‐matter scores in independent cohorts.