Monitoring Dynamic Binding of Chromatin Proteins In Vivo by Fluorescence Recovery After Photobleaching

Abstract

Fluorescence recovery after photobleaching (FRAP) has now become widely used to investigate nuclear protein binding to chromatin in live cells. FRAP can be applied qualitatively to assess if chromatin binding interactions are altered by various biological perturbations. It can also be applied semi-quantitatively to allow numerical comparisons between FRAP curves, and even fully quantitatively to yield estimates of in vivo diffusion constants and nuclear protein binding rates to chromatin. Here we describe how FRAP data should be collected and processed for these qualitative, semi-quantitative, and quantitative analyses.

1. Introduction

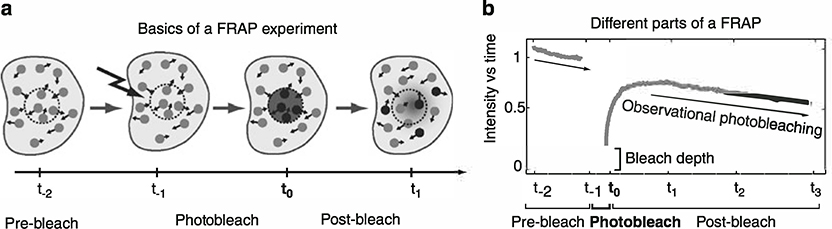
In fluorescence recovery after photobleaching (FRAP), a region of a cell is selectively photobleached and then the rate at which fluorescence enters the bleached region is measured (Fig. 1a). The fluorescence recovery contains information about both the protein’s diffusion rate plus any binding interactions with large, relatively immobile substrates that may be present in the bleached region (1, 2). Chromatin is a good example of such a substrate, as nuclear proteins that bind to it will be retarded as they enter a bleached region of the nucleus. The amount of retardation in the FRAP recovery rate depends on the residence time of the protein on chromatin. In this way, FRAP has been increasingly used as a tool to detect and quantify nuclear protein interactions with chromatin (3).

Fig. 1.

Basics of FRAP, (a) Shown is a nucleus (solid black outline) containing fluorescently tagged proteins (solid gray circles). Small arrows indicate protein motion. FRAP is performed by photobleaching a region (dashed circle) of the nucleus. During the recovery phase, bleached molecules (black circles) move out of the bleach zone and unbleached molecules move in. The rate of fluorescence recovery can be measured by estimating the average fluorescent intensity inside the measurement area (dashed circle) as a function of time, generating a FRAP curve. (b) The FRAP curve shows observational photobleaching, i.e., the fluorescence intensity decreases over time due to unintentional photobleaching during all periods of observation. The bleach depth is defined here as the initial measured value of the FRAP curve immediately after the photobleach.

A typical FRAP experiment is composed of three parts (Fig. 1a, b): (1) the pre-bleach, which is the first part of the FRAP measurement to establish that the fluorescence concentration is at equilibrium; (2) the photobleach, which is the next part of the FRAP measurement where a specific region in the cell is intentionally photobleached; (3) the post-bleach, which is the last part of the FRAP measurement where the recovery of fluorescence in the bleached region is recorded. During all phases of image acquisition (pre-bleach and post-bleach), unintentional, low-level bleaching occurs. This is called observational photobleaching. It must be minimized when designing the FRAP protocol, and corrected for when computing the FRAP curve.

Here we describe procedures for three different types of FRAP experiment: qualitative FRAP, semi-quantitative FRAP, and quantitative FRAP, where the latter two procedures include additional processing steps to extract quantitative information.

In qualitative FRAP, the FRAP curve is generated and then conclusions are drawn about whether a protein is very stably bound (recoveries on a time scale of hours) or very transiently bound (recoveries on a time scale of seconds). Often, qualitative FRAP is used to compare two different biological conditions. For example, FRAP might be performed on the wild-type and on a mutant version of a nuclear protein to see if the FRAP curve changes (4). A different FRAP curve often indicates that chromatin binding interactions have been disrupted in the mutant.

Semi-quantitative FRAP extends qualitative FRAP by enabling a quantitative comparison of two FRAP curves (4, 5). Different metrics can be employed for this comparison, including the time it takes the FRAP recovery to reach 50% of its final value (the half time) or the fraction of fluorescent molecules that are permanently bound (the immobile fraction).

Quantitative FRAP goes beyond a semi-quantitative analysis by enabling estimates of the protein’s diffusion constant and its association and dissociation rates with chromatin (1, 2, 6). These numbers can in turn be used to calculate the fraction of free and bound molecules in the nucleus, plus the time to diffuse from one binding site to the next and the dwell time on a chromatin target site. The quantitative estimates are obtained by fitting mathematical models for diffusion and binding to the FRAP data.

2. Materials

2.1. GFP-Tagged Proteins

To perform FRAP the molecule of interest must be fluorescently tagged. Fluorescent proteins are typically used for this purpose, with eGFP being the most common.

The fusion protein gene can be transiently transfected or stably incorporated into the cell of interest. Low expression levels are preferable to avoid over-expression artifacts, but expression must be high enough to provide a sufficient signal above background.

2.2. Microscope

The protocols below are for a specific microscope, the Zeiss LSM 5 Live confocal microscope. FRAP can be performed on most confocal microscopes, and also on two-photon microscopes or wide-field microscopes equipped with a photobleaching laser. The principles (although not all the details) described in the protocols below are applicable to these other systems. For more detailed information on the operation of a confocal microscope, consult the excellent Web site http://www.microscopyu.com/articles/confocal/.

2.3. Imaging Chamber

Temperature and CO₂ content during imaging should be regulated by an environmental chamber, such as the one from Precision Plastics Inc. (Beltsville, MD, USA).

2.4. Software

The microscope is typically equipped with software to collect the data and to do some of the early processing steps. If necessary, further image analysis can be done with other image processing software, such as ImageJ. A spreadsheet program such as Excel is required to tabulate and manipulate the initial measurements of the FRAP. For quantitative FRAP, we can provide Matlab software that performs the analysis. Alternatively, the equations described in the Notes can be implemented in any software program that permits data fitting.

3. Methods

Three FRAP protocols are described: qualitative, semi-quantitative, and quantitative FRAP. General guidelines are provided. Specific examples are also included at many points in the protocol and accompanying figures. These are all derived from FRAP experiments using an eGFP-tagged glucocorticoid receptor (GR) in the nuclei of mouse fibroblast cells.

3.1. Protocol for Qualitative FRAP

Use qualitative FRAP to compare FRAP curves. For example, compare wild-type and mutant versions of the same protein (7), or compare the same protein in the presence and absence of a specific cofactor (removed for example by siRNA knockdown) (4), or compare wild-type and drug-treated cells (8), or compare FRAPs of different proteins belonging to the same regulatory complex (4).

3.1.1. Set Up Time-Lapse Imaging

These conditions should be optimized in preliminary tests and then used without modification such that different FRAP curves can be compared (see Note 1).

1. Objective lens. For imaging of most nuclei, choose a 63× or l00× objective lens with high numerical aperture (NA = 1.2–1.4) (see Note 2).

2. Pixel size and zoom. For imaging of mammalian nuclei set the zoom such that the pixel-size is 0.1–0.2 μm (see Note 3).

3. Size of the imaged area. Typically the whole nucleus or a sub-region of the nucleus is sufficient (see Note 4).

   Example: The entire nucleus is imaged using a region of 160×160 pix² = 17×17 μm² (Fig. 2a).

4. Confocal pinhole. For bleaching an arbitrary region of the nucleus in which the protein is homogenously distributed, set the pinhole to a value that gives an optical slice, which is somewhat less than the thickness of the nucleus in that region (see Note 5). In this way, the maximum amount of nuclear fluorescence is collected without any contribution of cytoplasmic fluorescence. For bleaching a specific nuclear structure, such as a nuclear organelle, adjust the pinhole such that the optical slice corresponds to the dimensions of the structure.

   Example. GR distribution is relatively homogeneous throughout the nucleus (with the exception of nucleoli) (Fig. 2a), so the photobleach is not designed for a specific structure. The pinhole is set to 2.5 Airy units, which yields an optical slice thickness of 2.0 μm. Note that the nucleus in these cells is an ellipsoid with a maximum height of about 4 μm.

5. Gain and offset. Determine first the range of cell intensities that are of interest (e.g., an intermediate intensity range might be of interest, thereby avoiding very bright cells, which might yield over-expression artifacts and very dim cells which might yield insufficient signal). Then set the gain (see Note 6) such that all cells within the desired intensity range can be recorded without further gain adjustments. Specifically, the brightest cells within the selected intensity range should not cause saturation of the detector. The offset should be set such that the dimmest cells within the selected intensity range should be above zero. Practically speaking, this means that a background measurement outside of the cell should yield intensities that are 5–10% of the total dynamic range of the detector.

   Example: For an 8-bit image the dynamic range of the detector is from 0 to 255. To avoid saturation, the gain is then set such that cell intensities do not exceed 255. The offset is set such that background levels range from 12 to 25.

6. Acousto-optical tunable filter (AOTF) setting for imaging. The laser power used for imaging is modulated by the AOTF. It should be set as low as possible to minimize observational photobleaching, but high enough such that cell signals are well above background.

   Example: FRAP on the Zeiss LSM 5 Live is performed with a 488-nm/100-mW diode laser in the DuoScan mode. In this mode 80% of the laser power is used for the photobleach and 20% is used for imaging. The AOTF is set to use 6% of the imaging laser. Thus the final fraction of the 100 mW laser that is used for imaging is 6% of 20% or 1.2%.

7. Scan speed for imaging. Set the scan speed as fast as possible in order to record the first post-bleach frame as quickly as possible. We recommend the fastest possible setting regardless of how fast or slow the FRAP recovery is.

   Example: Imaging scan speed of 40 fps (frames per second).

8. Number of frames to collect before the photobleach. Optimally, collect pre-bleach images for at least 2–5 s before the photobleach. For fast scanning this can be up to 100 frames. Reduce this number to as low as five frames if fluorescent signal is rapidly lost due to observational photobleaching. This is often necessary for small nuclei, which have limited reservoirs of fluorescence and so lose signal rapidly during the imaging process.

   Example: 100 pre-bleach frames for the large 10 μm diameter mouse fibroblast nucleus (Fig. 2c).

9. Number of frames to collect after the photobleach. Optimally, collect around 1,000 frames after the photobleach. Reduce this number if the fluorescent signal has decayed close to background levels by the end of the FRAP measurement. Depending on the time scale of the recovery, it may be necessary to add delay times between images (step 10 below), particularly if the number of post-bleach frames has been reduced to avoid excessive observational photobleaching (see Note 7).

   Example: 1,100 post-bleach frames at 0 fps for a FRAP recovery that requires ~20 s to equilibrate (Fig. 2c).

10. Delay time between images. The delay time should be the same for both pre-bleach and post-bleach imaging. Use a delay time of 0 s for FRAPs that recover within a few seconds, but for slower FRAPs, introduce delay times to limit observational photobleaching.

Fig. 2.

Processing steps in qualitative FRAP. (a) Image of cells before and after the photobleach. Circles indicate the different measurement regions: solid gray – bleached region, solid black – correction region, dashed gray – background region. (b) Averaged fluorescence intensity from each of the regions in (a). Note that the bleached and correction regions have comparable brightness and that the background region does not show observational photobleaching. (c) The corrected FRAP curve is obtained by first correcting for the loss of fluorescence due to both intentional photobleaching and observational photobleaching, and then renormalizing the resulting curve by its pre-bleach intensity. (d) Application of qualitative FRAP to the glucocorticoid receptor (GR). Treatment of the cells with a proteasome inhibitor leads to a slowdown of the FRAP (8).

Example: 0 s delay time. The settings in steps 7–10 yield a pre-bleach imaging duration of 2.5 s and a post-bleach imaging duration of 28 s (Fig. 2b).

3.1.2. Set Up the Intentional Photobleach

The first three steps below (steps 1–3) are designed to provide a deep bleach in a short time. This minimizes movement of proteins during the photobleach (see Note 8). The bleach depth, which is the initial value of the normalized FRAP recovery (computed in step 5, Subheading 3.1.4 below), should be from 0.3 to 0.5 (i.e., 30–50% of the initial fluorescence before the bleach). If this bleach depth is not achieved, longer intentional bleaching and/or more bleach iterations should be used.

1. AOTF setting for bleaching. Set the AOTF to 100% for the intentional photobleach. This maximizes the number of fluorescent molecules that can be photobleached with one bleach pulse.

   Example: 100% AOTF of a 488 nm/100 mW diode laser used in DuoScan mode. In this setting, 80% of the total laser power is used for bleaching. Thus the final fraction of the 100 mW laser that is used for bleaching is 100% of 80% or 80%.

2. Scan speed of the intentional bleach. Bleach as fast as possible. If the bleaching scan speed can be set independently, then set it to as high a rate as possible. If the bleaching scan speed is determined by the imaging scan speed, then set the imaging scan speed as high as possible (step 7, Subheading 3.1.1). This usually results in a photobleach of 15–50 ms.

   Example: Bleaching scan speed of 63 fps. Note that this bleaching scan speed is faster than the imaging scan speed of 40 fps (step 7, Subheading 3.1.1). Since the Zeiss LSM 5 Live permits setting these scan speeds independently, we chose an even faster scan rate for the bleach.

3. Number of iterations for the intentional photobleach. Perform one iteration of the photobleach.

   Example: With one iteration of the bleach and the settings in steps 1–2, the bleach depth is ~0.3 (Fig. 2c).

4. Bleach geometry. For homogeneously distributed proteins, use a circular bleach spot whose area does not exceed 10% of the total nuclear area. This will leave a sufficient reservoir of fluorescence to allow for recovery and for the loss of fluorescence from observational photobleaching. Alternate bleach geometries, such as a square, rectangular or strip bleaches, are also possible (see Note 9). For bleaching a specific structure, the bleached region should be drawn to match the shape of the structure. The goal is to bleach the entire structure without bleaching any of its surroundings.

   Example: GR fluorescence is relatively homogeneous. A circular bleach region is selected with a diameter of 2.5 μm (Fig. 2a). (The diameter of the nucleus is about 15 μm). Using the scan speed setting in step 2 above, the bleach time is 16 ms.

5. Positioning of the photobleached region. For FRAP at a specific structure, the photobleach region should overlay it. Otherwise, for FRAP of a generic region in the nucleus, place the bleach region far away from the nuclear membrane and also try to avoid nucleoli.

   Example. GR is relatively homogeneous in its distribution, so the bleach is set up for a generic region of the nucleus. The bleach region is positioned with sufficient nuclear fluorescence surrounding it (as far away as possible from the nuclear membrane and nucleoli) to allow for influx of fluorescence from all sides (Fig. 2a).

3.1.3. Collect the FRAP Data

Configure the microscope as described above in Subheadings 3.1.1 and 3.1.2, and then run the FRAP macro in the confocal software.

3.1.4. Process the FRAP Data

Typically the processing is done either with software available on the confocal microscope or with freely available software such as ImageJ or Fiji. The numbers extracted from this software can be transferred to a spreadsheet program such as Excel, and then the calculations described below can be performed. If the FRAP recovery is slow, cell movement may become a problem and this must be corrected before performing the following measurements (see Note 10).

1. Extraction of time-stamps. The time at which the bleach occurs and at which the images are recorded can usually be extracted from the software that is used to operate the confocal microscope. These times are transferred to a spreadsheet file, and then corrected by subtracting the time value at the first post bleach frame from all the time points. This sets the time at the first post-bleach frame to zero, which is the convention in displaying FRAP data.

2. Measurement of background intensity. Background intensity is produced by the detection system. It corresponds to the fluorescence signal recorded with no fluorescent molecules in the field of view. This is best measured in a region outside of the cell, since even for a nuclear localized protein there may be some residual fluorescence in the cytoplasm.

   The averaged intensity value in the background region can then be calculated by the software at each time point. These values should be copied to the spreadsheet program and averaged. This averaged background value, designated here as BGD, will then be used for background correction in step 5 below. There are several quality checks that should be performed to determine if background is correctly measured (see Note 11).

   Example: Background is measured in the dotted gray circle in Fig. 2a.

3. Measurement of fluorescence loss due to photobleaching. To correct for the losses of fluorescence due to the intentional photobleach and observational photobleaching, measure the fluorescence loss in a control region far away from the region that was photobleached. This can be done with a region of interest comparable in size to the region used for photobleaching. For consideration of how best to position this region in the nucleus, see Note 12. The region’s averaged intensities designated here as CORR will then be used to generate the corrected FRAP curve in step 5 below.

   Example: The correction curve is measured in the black circle in Fig. 2a.

4. Measurement of fluorescence recovery. Generally, use a region of interest that is the same shape and size of the region that was photobleached, but other sizes are possible. Position this measurement region over the region that was photobleached. Use the image processing software to compute the average intensity within the measurement region at all pre and post bleach time points. Copy the averaged intensities at each time point to the spreadsheet file. These numbers designated here as BLEACH will then be used to generate the corrected FRAP curve in step 5.

   Example: Recovery is measured in the gray circle in Fig. 2a.

5. Calculation of the FRAP curve. The spreadsheet file should now contain the following data: (1) the time points (t) for each frame, where t = 0 s corresponds to the first post-bleach frame; (2) the averaged background intensity BGD; (3) the fluorescence intensity at each time point in the control region CORR(t); (4) the fluorescence intensity at each time point in the bleached zone BLEACH(t).

   Use the spreadsheet program to calculate the corrected FRAP curve using the following formula:

   $$\text{FRAP}(t)=(\text{BLEACH}(t)-\text{BGD})/(\text{CORR}(t)-\text{BGD}).$$ (1)

   Then normalize the preceding curve such that the pre-bleach intensity is 1. This is done by first calculating the averaged pre-bleach intensity. Then each time point of the FRAP(t) curve from above is divided by this value, yielding a renormalized FRAP curve.

   Example: Fig. 2b shows BLEACH(t), CORR(t), BGD, and Fig. 2c shows the final corrected curve for the GR FRAP data

3.1.5. Compare FRAP Curves Under Different Biological Conditions

1. Replicating the FRAP experiment. Repeat the procedures in Subheadings 3.1.3 and 3.1.4 on at least ten different cells of comparable brightness and then average these FRAP curves. For dimmer cells or smaller nuclei, up to 50 curves may be required to get a smooth, averaged curve. Calculate standard errors at each time point, and then plot the FRAP curve with these error bars.

2. Comparison with FRAP under different biological conditions. Repeat step 1 above on the mutant, or whatever alternate biological condition is being studied. Plot the two averaged FRAP curves on the same plot.

3. Repeating experiments on different days. Often there are only small differences between FRAP curves, with one curve being slightly faster or slightly slower than the other. These differences could be biologically significant (8). To test for this, repeat steps 1 and 2 above on different days. If the differences between curves are reproducible, then they are probably biologically significant.

   Example: Small differences in FRAP curves are found for the transcription factor GR in the presence and absence of the proteasome inhibitor (Fig. 2d). These are reproducibly seen and also correlate with different transcription levels with and without the proteasome inhibitor (8).

3.2. Protocol for Semi-quantitative FRAP

Use semi-quantitative FRAP for simple numerical comparisons between FRAP curves.

3.2.1. Microscope Set-Up, Data Collection, and Processing

Perform as described above for qualitative FRAP (Subheadings 3.1.1–3.1.5).

3.2.2. Semi-quantitative Measurements

Measure either the mobile and immobile fractions (step 1 below) or a FRAP recovery half-time (step 2 below) or both.

1. Measuring mobile and immobile fractions. Some FRAP curves recover on two very different timescales. The first phase may be complete within a few seconds while the second phase may require tens of minutes or hours or even longer. Data for such FRAP curves are often collected for only a few minutes yielding a second phase of the curve that appears to be flat because the timescale of recovery is very slow. The first fast phase is referred to as the mobile fraction M, while the second slow phase is referred to as the immobile fraction IM. The magnitude of the two fractions can be calculated with the following simple equation:

   $$M=\frac{\eta -F_0}{1-F_0},\text{IM}=1-M,$$ (2)

   where η is the final, plateaued value of the FRAP and F₀ is the value of the FRAP at the first post-bleach frame. η can be easily estimated from the FRAP curve by averaging the intensity values once the curve reaches a final plateau.

   When applying this measurement, be certain that the destruction of fluorescence caused by the intentional photobleach is accounted for in the correction for observational photobleaching. This is the case for the qualitative FRAP protocol described above, but not for the quantitative FRAP protocol described below (see Note 13)

   Example: GR exhibits a larger immobile fraction in the presence of the proteasome inhibitor (Fig. 3a, b).

2. Measuring the recovery half-time. The recovery half-time is the time required for the FRAP curve to reach 50% of its final value minus its starting value. It can be measured either by eye, or by fitting a sum of exponentials to the FRAP data. We recommend using the exponential fit since it allows describing a large number of FRAP curves automatically, and it works more reliably for curves with fast recoveries. Furthermore, this method can also be easily adapted to measure other times for recovery to different final fractions (e.g., 75% instead of 50%), which can be useful to describe FRAP curves with recoveries on different timescales.

   Use the following bi-exponential function to fit the FRAP data (which should already be normalized to one):

   $$\mathrm{FRAP}(t)=\eta -A\exp \left(-t/k_1\right)-B\exp \left(-t/k_2\right),$$ (3)

   where η is the measured final recovery level from step 1 above, and A, B, and k₁ and k₂ are parameters to be estimated from the fit. Once the four free parameters are estimated, then t_1/2 is obtained by solving the equation:

   $$0.5\times (A+B)=\eta -A\exp \left(-t_{1/2}/k_1\right)-B\exp \left(-t_{1/2}/k_2\right)$$ (4)

   This can be done numerically with the Matlab function fzero.

   Note that the estimated half-times are useful numbers for semi-quantitative comparison, but they do not directly reflect the diffusion rate or the binding rate or the residence time of the protein under study.

   Example: The GR half-time increases from t_1/2 = 1 s to t_1/2 = 2 s after proteasome inhibition (Fig. 3c, d).

Fig. 3.

Semi-quantitative FRAP. (a, c) FRAP of GR under control conditions (gray circles). The mobile fraction of M = 96% is determined from the starting point of the FRAP curve and the averaged intensity once the FRAP shows a plateau. For estimation of t_1/2, the FRAP is first fit with an exponential function (black line). Then t_1/2 is estimated from this model fit (see inset, t_1/2 = 1 s). (b, d) FRAP of GR after treating cells with a proteasome inhibitor. Treatment leads to an increased immobilization (only 90% mobile fraction) and a slowdown of the FRAP (t_1/2 = 2 s). This has been interpreted as an increased GR residence time on the DNA after proteasome treatment (8).

3.3. Protocol for Quantitative FRAP

Quantitative FRAP allows estimation of a protein’s diffusion rate (D_prot) and its association $\left(k_{\text{on}}^{*}\right)$ and dissociation (k_off) rates of binding. The binding estimates can be used to calculate several biologically relevant parameters, namely the time to diffuse from one binding site to the next $\left(1/k_{\text{on}}^{*}\right)$, the residence time at a binding site (1/k_off), the bound fraction $\left(k_{\text{on}}^{*}/\left(k_{\text{on}}^{*}+k_{\text{off}}\right)\right)$ and the free fraction $\left(k_{\text{off}}/\left(k_{\text{on}}^{*}+k_{\text{off}}\right)\right)$.

Binding estimates are obtained by fitting the experimental data with a kinetic model that describes the FRAP recovery (1, 2). In recent years several different kinetic FRAP models have been developed for a variety of different proteins and experimental situations. For a comprehensive list of different modeling approaches see ref. 9.

This section will focus on a description of the approach developed in our group, which is suitable for analyzing FRAP data from nuclear proteins that are binding to chromatin (10). The nuclear protein distribution should be relatively homogeneous and the nucleus should be at least 5 μm in diameter such that a 1–2 μm diameter bleach spot can be used. (With smaller bleach spots, it is difficult to accurately measure the photobleaching profile, which is a critical for performing the quantitative analysis).

It is important to recognize that uncertainties remain about the accuracy of in vivo binding estimates obtained from FRAP kinetic modeling (9). Thus, cross validation with other approaches is important, including by fluorescence correlation spectroscopy (see Chapter 12).

3.3.1. Microscope Set-up and Data Collection

Perform as described above in Subheadings 3.1.1–3.1.3 for qualitative FRAP. However, in Subheading 3.1.1, step 3, it is critical for quantitative FRAP that images of the entire nucleus be recorded, since the entire nuclear fluorescence intensity is used to correct for observational photobleaching, rather than just a sub-region as in qualitative FRAP. It is also critical for the mathematical model described here that the bleach geometry in step 4, Subheading 3.1.2 is circular.

3.3.2. Process and Fit the FRAP Data

The entire workflow below (steps 1–7, 9, 11, 12) has been implemented in Matlab and the scripts are available on request. The basic processing steps (steps 1–6) could also be performed in ImageJ, and the model equations in Subheading 4. could be implemented in other software packages, such as Mathematica, which allow parameter estimation.

1. Extraction of time-stamps. Perform as described m Subheading 3.1.4, step 1 in qualitative FRAP.

2. Measurement and subtraction of background intensity. Measure background as described in Subheading 3.1.4, step 2 in qualitative FRAP. Then for quantitative FRAP, subtract the averaged background value from all recorded images. This is necessary because the intensity profile across the circular bleach spot must be measured in quantitative FRAP.

3. Measurement and correction for observational photobleaching. Measure the total nuclear fluorescence F at each time point before and after the photobleach. To correct in the pre-bleach phase, multiply the image at each time point t in the pre-bleach phase by the scaling factor F(t) / F(t₋₁), where F(t₋₁) is the total nuclear fluorescence in the last pre-bleach image. To correct in the post-bleach phase, multiply the image at each time point t in the post-bleach phase by the scaling factor F(t) / F(t₀), where F(t₀) is the total nuclear fluorescence in the first image after the photobleach.

4. Measurement of fluorescence recovery. Perform as described in Subheading 3.1.4, step 4 in qualitative FRAP. However, a circular region must be used for the measurement and the radius of the circle R_M should be recorded since it is one of the parameters needed for the kinetic model.

5. Generate the FRAP curve for fitting. The measurement of fluorescence recovery in step 4 produces a FRAP curve that has already been corrected for background (step 2) and observational photobleaching (step 3). Normalize this curve to one by following the same normalization procedure described in step 5, Subheading 3.1.4. Note that the final curve will not recover to one since the correction method only accounts for loss of fluorescence due to imaging, but does not account for the fluorescence destroyed by the intentional photobleach (see Note 13).

   Finally, resample the FRAP data such that the slower part of the FRAP recovery will not be overrepresented in the fitting procedure (11). To do so, identify a time point at which the FRAP curve begins to flatten out. For explanatory purposes here, we will assume that this turning point in the FRAP curve occurs at the 25th time point, but in general the turning point depends on the particular protein under study and the temporal sampling selected for the FRAP. Resample the FRAP curve beyond this time point by first computing the difference between the first two resampled time points on a logarithmic time scale: Δ = ln(t₂₇)−ln(t₂₆). Then define a new set of time points: t_i = t₁,t₂,t₃,…,t₂₅,t₂₅ + 10^Δ, t₂₅ + 10^2Δ,…. Use these time points to generate a new FRAP data set (t_i, FRAP(t_i)), where the value of FRAP(t_i) is unchanged for t₁–t₂₅, while the value of FRAP(t_i) at the subsequent time points is given by the average of the original FRAP data that lie within the new time point interval. This data set will be used for fitting.

6. Determine the initial conditions. The FRAP model requires the intensity profile of the circular photobleach. This is the average intensity as a function of distance from the center of the photobleach, i.e., the radial intensity profile I₀(r) (Fig. 4a). Use the images obtained in step 3 above. Measure the radial intensity profile from the center of the photobleach using the first image after the photobleach and divide this profile by the radial intensity profile centered at the same location but measured from the last image right before the photobleach. (This division normalizes out any variation in the intensity profile due to cellular structures). Note that these measurements are typically performed over a circle with a larger diameter than the bleach circle such that the fluorescence at the edge of the circle reaches the equilibrium value in the rest of the cell (Fig. 4a). The resultant profile should be fit with Eq. 6 (see Note 14) to yield a functional form for I₀(r) (Fig. 4b). Although Eq. 6 provides a good fit for our circular photobleaches, any functional form can be used to fit I₀(r).

7. Determine the effective size of the nucleus. The effective nuclear size is based on the requirement that the photobleach in the model nucleus destroys the same proportion of fluorescence as in the real nucleus. The effective size can be estimated by using the function I₀(r) determined in step 6 above combined with the final recovery level η of the FRAP curve estimated as described in step 1 of Subheading 3.2.2. The values of η and I₀(r) are substituted into Eq. 7 and then solved for the effective size of the model nucleus R_Nuc (see Note 15).

8. Test for the role of diffusion during the recovery. The FRAP data will be fit with different quantitative models depending on whether or not diffusion plays a role during the recovery. Two different tests for diffusion can be used, the bleach-spot size test (12) or the gradient-smoothing test (13), but we recommend the latter because it is more sensitive (unpublished data).

   To perform the gradient smoothing test, determine intensity profiles across the bleach spot at all time points using the same procedure as described in step 6 above. Then renormalize the intensity profiles from 0 to 1 at each time point, and plot them on the same graph. If the profiles systematically change their shape over time, then diffusion plays a role during the FRAP recovery.

   Example: The changing profile shapes for a GR FRAP show that diffusion plays a role in this FRAP recovery (Fig. 4c).

   If the test for diffusion shows that diffusion does not play a role during the FRAP recovery, then proceed to step 9, otherwise proceed to step 10.

9. If the preceding test in step 8 showed that diffusion does not play a role during the FRAP recovery, then the FRAP curve obtained in step 5 should be fit with Eq. 8 with N = 1, which is a model for binding to a single type of binding site (see Note 16). If this yields a good fit, then an estimate of the binding off rate is given by the value of k_off obtained in the fit.

   If Eq. 8 with N = 1 does not yield a good fit, then fit with N = 2, which is a model for binding to two distinct types of binding sites. If this gives a good fit, then the values of k_off,1 and k_off,2 obtained from the fit provide estimates of the two distinct binding off rates. If this two-binding state model also fails to fit, then it is possible that there are three binding states present, and a fit with N = 3 could be tried. However, caution is advised as a three-binding state model uses six free parameters, and so the predictive power of such a fit becomes questionable.

   In any event, the fitting procedure is now complete and the subsequent steps can be ignored since they apply only to curves where diffusion plays a role in the recovery.

10. Test for an immobile fraction. If the test in step 8 showed that diffusion plays a role in the FRAP recovery, then before applying the kinetic models that account for diffusion, it is also necessary to test if the FRAP recovery has an immobile fraction. This can be done by performing two consecutive FRAP experiments in the same region of the nucleus (14). The first bleach affects both mobile and – if present – immobile proteins, whereas the second bleach affects only mobile proteins. By comparing the final recovery levels of the two FRAP curves, the immobile fraction β can be calculated by

    $$\beta =1-F_1^2/F_2,$$ (5)

    where F₁ and F₂ are the final, plateaued recovery values reached after the first and second photobleach, respectively. If there is an immobile fraction, then β will be greater than zero, and the kinetic models described below should not be used.

    To perform the immobile fraction test follow the same protocol as for quantitative FRAP with the following changes. (a) Use multiple bleach iterations to achieve a complete photobleach (five iterations are usually sufficient). (b) Repeat the same FRAP at the same location immediately after the first FRAP experiment is completed.

    Example. This test shows that GR has no immobile fraction (Fig. 4d).

11. Fit with a model for diffusion. If there is no immobile fraction (step 10) and diffusion plays a role in the FRAP recovery (step 8), then the FRAP data should be fit with Eq. 9, which is a model that accounts only for diffusion (see Note 17).

    The fit with Eq. 9 requires the initial profile I₀(r) measured in step 6, the effective size of the nucleus R_Nuc determined in step 7, the radius of the measurement region R_M noted in step 4, and the FRAP data generated in step 5. If the FRAP data are well fit with Eq. 9, then the fit yields an estimate of the fusion protein’s diffusion constant ( D_prot ).

    If this diffusion constant is slow enough, then it likely contains information about binding, allowing an estimate of the ratio of the protein’s association and dissociation rates $\left(k_{\text{on}}^{*}/k_{\text{off}}\right)$. To determine if this is possible, compare the fusion protein’s diffusion constant with a freely diffusing protein, such as unconjugated GFP. This can be done by performing a quantitative FRAP of unconjugated GFP and fitting with the same diffusion model to estimate the GFP diffusion constant ( D_gfp ) (Fig. 5a). Then use this to estimate the mass of the fusion protein in kD ( M_prot ) according to the following formula: (12) which assumes roughly spherical proteins, and uses 27 kD as the mass of GFP

    $$M_{\text{prot}}=27{\left(D_{\text{GFP}}/D_{\text{prot}}\right)}^3,$$

    If the estimated mass M_prot is much larger than would be expected for the fusion protein (or a molecular complex containing the protein), then the diffusion constant for the fusion protein contains information about DNA binding, which retards the free diffusion of the fusion protein. This process is called effective diffusion (2, 12), and the diffusion constant measured for the fusion protein is called the effective diffusion constant. The following formula can then be used to estimate the ratio of the association to the dissociation rate of binding of the fusion protein: $\left(k_{\text{on}}^{*}/k_{\text{off}}\right)=\left(D_{\text{GFP}}/D_{\text{prot}}\right)-1$. Please note that when effective diffusion occurs, it is impossible to obtain independent estimates of the association and dissociation rates from the FRAP data. Such independent estimates might be obtained by using FRAP with a smaller bleach-spot size (12) or by using fluorescence correlation spectroscopy (15) or temporal image correlation spectroscopy (16) (see also Chapter 12).

12. Fit with a reaction-diffusion model. If the fit in step 11 is not good, then the FRAP data should be fit with a model that explicitly incorporates the binding terms, namely Eq. 10 (see Note 18). As in step 11, the initial profile I₀(r) from step 6 above, the measurement radius R_M, and the effective size of the nucleus R_Nuc from step 7 above must also be input into Eq. 10. If this equation yields a good fit to the FRAP data (Fig. 5b), then independent estimates for the association $k_{\text{on}}^{*}$ and dissociation rates k_off can be obtained. If this fit fails, it is possible that the FRAP data reflect two distinct binding states. It is a straightforward mathematical problem to extend the one-binding state model described in Mueller et al. (10) to account for two distinct binding sites, but this has not been done.

Fig. 4.

Quantitative FRAP, (a) A plot of the radial profile of the photobleach is shown. The inset shows how the profile is measured by calculating the average intensity in annuli centered on the photobleach. (b) The profile is used to supply the initial conditions for the model equations. Shown is the profile from (a) normalized to the measured pre-bleach profile, and then fit using the function in Eq. 6. (c) To determine which version of the quantitative model to use, it is necessary to assess if diffusion plays a role in the recovery. This is done by comparing radial intensity profiles as a function of time, as shown here for GR. The inset shows the same profiles normalized between 0 and 1. The normalized profiles change their shape, indicating that diffusion should be incorporated into the FRAP model. (d) Before applying the quantitative model, it is necessary to test for an immobile fraction. The final recovery levels after the first and second bleach are F₁ = 0.96 and F₁ = 0.92. This yields an immobile fraction of $\mathrm{\beta }=1-F_1^2/F_2=0\%$, i.e., GR is fully mobile on the timescale of the FRAP experiment, and so the model in this protocol is applicable.

Fig. 5.

Fits of FRAP models to unconjugated GFP and GR. (a) Quantitative FRAP of unconjugated GFP fused to a nuclear localization signal. The data are well fit by a diffusion model (Eq. 9) yielding an estimate for the diffusion constant of GFP in the nucleus (D_GFP = 18.8 μm²/s). When the same data are fit with a full reaction diffusion model (Eq. 10), the fit is only slightly better (compare the squared sum of residual curves below) and the estimates are very similar (D_GFP = 20.0 μm²/s with negligible bound fraction). (b) Quantitative FRAP of GR. In this case, the diffusion model (Eq. 9) is a poor fit to the data, while the full reaction diffusion model yields a good fit (D_prot = 6.3 μm²/s, k_on^*; = 0.44 s⁻¹, k_off = 0.38 s⁻¹).

4. Notes

1. Different experiments may require their own set of optimized time-lapse imaging parameters tuned to the protein under study and the microscope in use.

2. The parameters of the objective lens that are relevant for FRAP are the magnification and the NA. Higher magnification corresponds to a smaller field of view. Higher NA provides better light collection efficiency and better bleaching efficiency, but the bleach profile along the optical (z) axis becomes more conical. This could lead to inaccurate estimates in quantitative FRAP where a cylindrical photobleach is presumed (17).

3. The pixel size is the number of microns per pixel in the image. It is affected by the NA of the objective and the zoom factor set in the confocal software. The smallest pixel size necessary is 0.1 μm, which is half of the best resolution that can be achieved by conventional light microscopy (~0.2 μm using a 1.4 NA objective). The confocal zoom can be adjusted to achieve the 0.1-μm pixel size. Larger pixel sizes can be used if the structure or region of interest is larger.

4. The whole nucleus should be imaged whenever possible because this simplifies the correction procedures. However, if the protein recovers quickly, only a sub-region of the nucleus should be imaged to enable faster data collection. The sub-region should be large enough to include a non-bleached region that can be used for correction of observational photobleaching. On the other hand, if the FRAP recovery is slow and cells move during the recovery process, then a larger imaged area should be used. This allows for correction for cell movement before processing the data (see Note 10).

5. The confocal pinhole sets the thickness of the optical section from which the recovery data are collected. Thicker optical sections (more open pinholes) are desirable for FRAP measurements, since they include more signals and thus improve the signal-to-noise ratio. Note, however, that the confocal pinhole affects only the detection process, but not the pattern of the photobleach, which always extends along the optical (z) axis in a conical profile.

6. On most confocals, the settings for gain and offset can be checked by changing the color palette to a “range indicator.” Pixels with intensity of 0 are displayed as one color (blue in the Zeiss LSM 5 Live software) and pixels with intensity of 255 (for 8 bit images) are displayed as another color (red in the Zeiss LSM 5 Live software). Optimal settings are obtained when very few pixels are either red or blue.

7. In selecting the number of frames to collect after the bleach, the goal is to achieve frequent sampling of the FRAP recovery, but at the same time limit observational photobleaching. If a FRAP has a very fast initial phase followed by a very slow second phase, two separate FRAP experiments can be performed: one optimized for the fast initial part and one optimized for the slow second part. However, do not change the temporal sampling rate during the recovery measurement as this introduces artifactual reversible photobleaching (18).

8. Proteins move during the photobleach (19). To minimize this effect, bleach as fast as possible (use the highest scan speed) with as few iterations of the bleach as possible. Increase the number of bleach iterations only if the initial value of the normalized FRAP recovery (the bleach depth) is larger than 0.5 (see Fig. 1b for an illustration of the bleach depth).

9. There are advantages and disadvantages to different bleach geometries. Circles can be more easily positioned to avoid inhomogeneous distributions of fluorescence, but the noise levels may be higher because of the small circular area (10, 20). Strips increase the measurement area and so reduce noise levels, but are more difficult to position and still avoid inhomogeneous distributions of fluorescence (1, 14, 21). Half-nuclear FRAP reduces the signal-to-noise ratio but takes longer and cannot be used for smaller structures (13, 22). In quantitative FRAP protocols, the bleach geometry is usually predefined. The protocol described here requires a circular bleach, whereas other quantitative FRAP protocols make use of strip bleaches (1, 14, 21) or half-nuclear bleaches (13).

10. Movement of the bleached region due to cell migration will produce an artifactual fluorescence recovery if measurements are made in a fixed location. To track the bleached region, use image registration methods such as the stackreg plugin with rigid body registration in ImageJ.

11. There are two quality checks to determine if background has been correctly measured. First, check if background intensities are constant over time. A background signal that decays over time indicates that some residual fluorescence has been measured (e.g., from the cytoplasm). Second, check if background intensities remain constant on a given day for the same imaging conditions. A background intensity that is much higher than other background intensities measured on the same day indicates again that some residual fluorescence has been measured.

12. Proper correction for observational photobleaching requires correct placement of the correction region. The fluorescence intensity in the correction region should be comparable to the pre-bleach intensity of the bleached region. Further, the correction region should not be positioned too close to the bleached region, i.e., the correction measurement should not show any FRAP.

13. Fluorescence is lost in a FRAP experiment due to both intentional photobleaching and observational photobleaching. When a FRAP curve is corrected for both of these effects, then it will recover to one (provided the protein has no immobile fraction). When a FRAP curve is corrected only for observational photobleaching, then it will never recover to one even if the protein has no immobile fraction. This is because the destruction of fluorescence produced by the intentional photobleach is not accounted for, so the final recovery level is automatically reduced by the fraction of fluorescence destroyed by the intentional photobleach.

    The qualitative FRAP protocol incorporates a correction procedure that corrects for the loss of fluorescence from both intentional photobleaching and observational photobleaching, whereas the quantitative protocol incorporates a correction procedure that accounts only for the loss of fluorescence due to observational photobleaching. In qualitative FRAP the correction is measured in a separate control region away from the FRAP. The loss of fluorescence in this region is due both to observational photobleaching and the influx of bleached fluorophores from the bleached region. Thus, this correction curve accounts for both sources of fluorescence loss, and so the corrected FRAP curve will recover to one for fully mobile proteins. In quantitative FRAP, the correction procedure for the post-bleach phase is designed to keep the total nuclear fluorescence constant relative to the first image after the photobleach. Since the fluorescence loss from the photobleach has already occurred in this first image after the photobleach, this procedure does not account for this loss and so the FRAP curve will not recover to one even for fully mobile proteins.

14. The initial conditions for a circular photobleach are typically well fit by the following equation, which describes a constant function with Gaussian flanks (10). The values for θ, r_C, and σ can be estimated by fitting Eq. 6 to the measured intensity profile I₀(r)

    $$I_0(r)=\{\begin{array}{cc}\mathrm{\theta }& \text{for}r\le r_c\\ 1-(1-\theta )\exp (-\frac{{\left(r-r_c\right)}^2}{2{\sigma }^2})& \text{for}r>r_c\end{array}.$$ (6)

15. The kinetic model assumes that the nucleus is circular and that its fluorescence is conserved. The real nucleus is a three dimensional ellipsoid and often contains large regions (nucleoli) that are mostly devoid of fluorescence. Nevertheless, the model nucleus can be a reasonable approximation to the real nucleus if its size is set such that the photobleach destroys the same proportion of fluorescence as in the real nucleus.

    The size of the model nucleus can be estimated from two measurable parameters: the profile of the photobleach, I₀(r) (step 6. Subheading 3.3.2) and the final recovery level of the FRAP, η (step 1, Subheading 3.2.2) (10). Since intensities are normalized to one, the amount of fluorescence before the photobleach, F_b, equals the area of the nucleus, whereas the amount of fluorescence after the photobleach, F_A, equals the integral of I₀(r) over the nuclear area. These parameters are therefore related by

    $$\frac{F_A}{F_B}=\eta =\frac{2\pi \underset{0}{\overset{R_{\mathrm{Nuc}}}{\int }}{I}_0(r)rdr}{\pi R_{\text{Nuc}}^2},$$ (7)

    where R_Nuc is the radius of the model nucleus. Substituting the measured values for η and I₀(r) allows solving the equation for R_Nuc. If I₀(r) is given by Eq. 6, then Eq. 7 can be solved analytically for R_Nuc. For more complex forms of I₀(r), Eq. 7 can be solved numerically for R_nuc.
16. When diffusion is very fast compared both to the time to associate with a binding site and to the timescale of the FRAP recovery, then the FRAP behavior is termed reaction dominant (12). The gradient smoothing test will show no change in the shape of the recovery profiles. In this case, diffusion can be neglected in the model and the recovery is solely determined by the binding rates, more specifically by the off-rate(s). The FRAP can be described by a simple equation

    $$\mathrm{FRAP}(t)=\eta -\sum _{i=1}^N{A}_i\exp \left(-t/k_{\text{off},i}\right),$$ (8)

    where η is set to the final recovery level of the FRAP (step 1, Subheading 3.2.2) and N, which denotes the number of different binding sites, is set to one or two. The fit yields estimates for the dissociation rates k_off,i,; and the A_i’s. The A_i’s yield the relative fraction sizes of the two bound fractions, but they do not provide estimates of absolute bound fraction sizes. This requires knowledge of the size of the freely diffusible fraction, which is difficult to estimate because it recovers so rapidly (10).
17. The equation describing the FRAP recovery for a molecule that diffuses with a diffusion constant D_prot is (10):

    $$\begin{gathered} \mathrm{FRAP}(t)=U_0\exp \left(-D_{\text{prot}}{\alpha }_0^{2}t\right)+\sum _{k=1}^{\infty }{U}_k\exp \left(-D_{\text{prot}}{\alpha }_k^{2}t\right) \\ \left[2J_1\left({\alpha }_k{R}_M\right)/\left({\alpha }_k{R}_M\right)\right] \end{gathered}$$ (9)

    where J₁ is a Bessel function α_k = χ_k / R_Nuc with χ_k the k^th zero of the Bessel function of the first kind, and the constants U_k are given by:

    $$U_k=\frac{2}{R_{\text{Nuc}}^2{J}_0^2\left({\chi }_k\right)}\underset{0}{\overset{R_{\text{Nuc}}}{\int }}{I}_0(r)J_0\left({\alpha }_{k}r\right)rdr,$$

    R_Nuc is the radius of the nucleus (see Note 15), R_M is the radius of the measurement region of the FRAP curve (noted in step 4, Subheading 3.3.2), and I₀(r) is the initial profile of the photobleach (step 6 in Subheading 3.3.2).

18. The full reaction diffusion solution, incorporating terms for both diffusion and binding, is given by (10):

    $$\begin{gathered} \mathrm{frap}(t)=\left[\left(U_0+W_0\right)\exp \left(-\left(w_0+v_0\right)t\right)+\left(V_0+X_0\right)\exp \left(-\left(w_0-v_0\right)t\right)\right]+ \\ \sum _{k=1}^{\infty }\left[\left(U_k+W_k\right)\exp \left(-\left(w_k+v_k\right)t\right)+\left(V_k+X_k\right)\exp \left(-\left(w_k-v_k\right)t\right)\right] \\ \left[2J_1\left({\alpha }_k{R}_M\right)/\left({\alpha }_k{R}_M\right)\right] \end{gathered}$$ (10)

    with the constants given by:

    $$w_k=\frac{1}{2}\left(D_{\text{prot}}{\alpha }_k^2+k_{\text{on}}^{*}+k_{\text{off}}\right)\text{and}$$

    $$v_k=\sqrt{\frac{1}{4}{\left(D_{\text{prot}}{\alpha }_k^2+k_{\text{on}}^{*}+k_{\text{off}}\right)}^2-k_{\text{off}}{D}_{\text{prot}}{\alpha }_k^2}$$

    $$\begin{gathered} U_k=\frac{1}{-2k_{\text{off}}{v}_k}\left[\left(-w_k-v_k+k_{\text{off}}\right)\left(w_k-v_k\right)\right] \\ \frac{2\left(\frac{k_{\text{off}}}{k_{\text{off}}+k_{\text{on}}^{*}}\right)}{R_{\text{Nuc}}^2{J}_0^2\left({\chi }_k\right)}\underset{0}{\overset{R_{\mathrm{Nuc}}}{\int }}{I}_0(r)J_0\left({\alpha }_{k}r\right)rdr \end{gathered}$$

    $$\begin{gathered} V_k=\frac{1}{2k_{\text{off}}{v}_k}\left[\left(-w_k+v_k+k_{\text{off}}\right)\left(w_k+v_k\right)\right] \\ \frac{2\left(\frac{k_{\text{off}}}{k_{\text{off}}+k_{\text{on}}^{*}}\right)}{R_{\text{Nuc}}^2{J}_0^2\left({\chi }_k\right)}\underset{0}{\overset{R_{\text{Nuc}}}{\int }}{I}_0(r)J_0\left({\alpha }_{k}r\right)rdr \end{gathered}$$

    $$W_k=U_k\frac{k_{\text{on}}^{*}}{-\left(w_k+v_k\right)+k_{\text{off}}},X_k=V_k\frac{k_{\text{on}}^{*}}{-\left(w_k-v_k\right)+k_{\text{off}}},$$

    The J’s are Bessel functions, and α_k = χ_x/R_N with χ_k the k^th zero of the Bessel function of the first kind. R_Nuc is the radius of the model nucleus (see Note 15), R_M is the radius of the measurement region of the FRAP curve (step 4, Subheading 3.3.2), and I₀(r) is the photobleach profile (step 6, Subheading 3.3.2). The series expansion can typically be truncated at 500 terms for fitting of most FRAP curves. The fit yields estimates for the unknown parameters, namely the protein’s diffusion constant D_prot and the association $k_{on}^{*}$ and dissociation rates k_off of binding.