Two-photon fluorescence-assisted laser ablation of non-planar metal surfaces: fabrication of optical apertures on tapered fibers for optical neural interfaces

Abstract

We propose a feedback-assisted direct laser writing method to perform laser ablation of fiber optic devices in which their light-collection signal is used to optimize their properties. A femtosecond-pulsed laser beam is used to ablate a metal coating deposited around a tapered optical fiber, employed to show the suitability of the approach to pattern devices with a small radius of curvature. During processing, the same pulses generate two-photon fluorescence in the surrounding environment and the signal is monitored to identify different patterning regimes over time through spectral analysis. The employed fs beam mostly interacts with the metal coating, leaving almost intact the underlying silica and enabling fluorescence to couple with a specific subset of guided modes, as verified by far-field analysis. Although the method is described here for tapered optical fibers used to obtain efficient light collection in the field of optical neural interfaces, it can be easily extended to other waveguide-based devices and represents a general approach to support the implementation of a closed-loop laser ablation system of fiber optics.

1. Introduction

Ultrafast lasers opened new paradigms to material processing thanks to the high peak intensity achievable with focused pulses at relative low energies [1]. Femtosecond laser ablation and micromachining has been applied both on dielectric and on metallic samples [2–4], and it has been used for the realization of laser-inscribed metallic surface structures such as micro-holes [4], micro-grooves [5], and micro-pillars [6]. Laser ablation has been also applied to optical fibers to obtain side emission of light by drilling micro discontinuities inside the fiber’s core [7,8]. Although this process enables multi-site emission of light, it compromises the light propagation and collection properties of the waveguide itself, hence affecting its performances in sensing applications. This is a particularly relevant factor in applications where modal properties of the waveguide should be preserved while maximizing the light collection efficiency of the fiber.

Sensors based on Tapered Fibers (TFs) are an example [9] that has found a range of applications over the years, including sensing of biomolecules [10,11], and, very recently, implantable systems to optically monitor neural activity [12]. In this latter case, the taper does not shrink at its central portion, as in canonical tapered fibers sensors based on transmission measurements, but it interrupts at its narrower section, creating a tip that enables for a smooth implantation in the brain and functional fluorescence collection [12]. The tip is then coated with reflective metal and a set of optical windows are opened along the narrowing waveguide, enabling guided modes of different order to interact with different regions of the brain. This approach enables micro-structured TFs (µTFs) to deliver and collect light with depth resolution along a single probe, a unique feature for optical neural interfaces [12–16]. Accordingly, tailoring the shape and size of the optical windows enables to engineer light delivery and collection volumes in order to collect functional fluorescence signal from groups of few neural cells [12]. However, it is important that the structuring of the narrowing region preserves the effect of the waveguide on propagating modes, not to compromise the optical interaction between the environment and the modal content [17].

The fabrication of µTFs with optical windows can be carried out with high-resolution fabrication techniques including Focused Ion Beam (FIB) Milling [18,19], as well as fast-writing methods such as Ultraviolet Direct Laser Writing (UV-DLW) [20]. This latter approach allows for high-speed patterning of the metal coating at the cost of limited resolution and higher roughness of the window profile. However, both FIB and UV-DLW unavoidably undermine the underlying dielectric surface. Although this does not compromise the multi-site light delivery capability of the TFs, light collection efficiency would greatly benefit from an intact surface interacting with incoming fluorescence signal.

In this work, we propose a Two-Photon Fluorescence Assisted Direct Laser Writing (2PFA-DLW) method to pattern the edge of a TF to optimize light collection properties for applications in the field of optical neural interfaces. The method takes advantage of laser ablation of the metal layer on the highly non-planar surface of the taper while it is submerged in a fluorescent bath. A scanning Near Infra-Red (NIR) femtosecond pulsed laser ablates the region of interest and simultaneously generates a two-photon fluorescent signal in the bath. Continuously monitoring this signal provides a spectral fingerprint that identifies when the metal is totally removed. The laser pulses interact mostly with the metal coating, leading to its ablation, while leaving the underlying glass surface intact. This enabled the production of optical windows that couple light in defined subset of guided modes, as verified by far-field analysis on the distal facet. The result is a fabrication approach that preserves the waveguides modal properties while optimizing the collection efficiency of the device.

2. Two-photon fluorescence assisted fabrication of micro-structured TFs

2.1. 2PFA-DLW setup

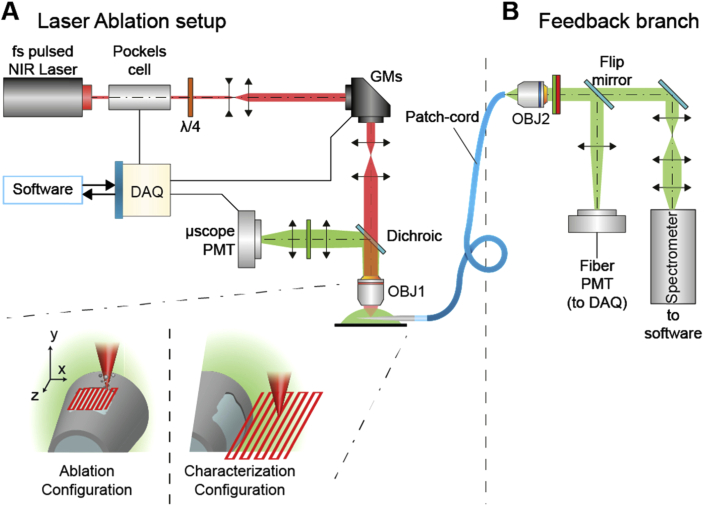
The particular advantage of the proposed method is the ability to monitor the ablation progress in real-time. In order to record the collection properties of the optical apertures during the fabrication, we designed a Two-Photon Fluorescence (2PF) assisted ablation system, which takes advantage of a feedback spectral signal (Fig. 1(a)). A fs pulsed NIR Laser (Coherent Chameleon Discovery, 100 fs pulse, 80 MHz repetition rate, wavelength tunable in the range 680-1300 nm, with average output power at λ = 800 nm of P_avg ≈ 1800 mW) was modulated by a Pockels Cell. A quarter wavelength plate was used to obtain circular polarization, and the beam was expanded to fit the size of a 6 mm galvanometric mirrors pair (GMs) employed to deflect the beam over the (x,y) plane. The beam was then expanded and collimated by a scan-tube lens assembly and sent on the back aperture of a 4x 0.28 numerical aperture NA objective lens (OBJ1). The setup was controlled by a DAQ system interfaced with the open source software Vidrio ScanImage.

Fig. 1.

(a) Custom Two-Photon Microscope for spatially restricted Laser Ablation of Aluminum deposited on TFs and for the optical characterization of the resulting devices. The zooms show sketched details on the raster scanning trajectories of the Laser spot in two different configurations: the Ablation Configuration on the left and the Characterization Configuration on the right. (b) Fluorescence Collection optical setup that allows for real-time Feedback of the Ablation process and the related optical characterization.

The laser spot was raster scanned in the field of view of OBJ1 (2085 × 2085 µm²) (Fig. 1(a)) generating a fluorescence spot into a fluorescent bath (30µM C20H12O5 (Fluorescein) in Phosphate buffered saline (PBS)), in which the aluminum-coated tapered fiber was submerged.

PBS:Fluorescein solution is a standard choice in the framework of optical neural interfaces, thanks to its spectral features similarity with Green Fluorescent Protein (GFP) [21]. GFP is one of the most widely employed fluorescent compound in indicators of neural activity, for monitoring either membrane potentials [22], for calcium concentration [23] or neurotransmitters concentration [24].

The fluorescence collected by OBJ1 was reflected by a dichroic mirror (D1) and detected by a Photo-Multiplier Tube (µscope-PMT). The TF is mounted on a Scientifica PatchStar stepper motor micromanipulator (step size ∼0.1 µm), employed for the positioning over the (x,z) plane allowing for a first, coarse positioning in the field of view thanks to its high speed mode (v = 4 mm/s). Then, live 2P fluorescence imaging, provided by the µscope-PMT allows for the fine positioning in the (x,z) plane using the high precision mode of the micromanipulator (v = 0.1 µm/s). Finally, OBJ1 is mounted on a Physik Instrumente P-725 PIFOC Piezoelectric Objective Scanner, allowing for focusing the laser on the (x,z) plane tangent to the TF surface.

A second collection path through the TF was employed to monitor ablation, exploiting light entering the waveguide across the ablated pattern (referred to as Feedback Branch in Fig. 1(b)). Light guided by the taper propagated in the patch-cord and entered the feedback branch by an objective lens (OBJ2). The signal was filtered by a band-pass (central wavelength 525 nm, bandwidth 39 nm) and a NIR block filters (cutoff wavelength 770nm, short pass), and was directed toward two different optical detectors. A Spectrometer offered a real time feedback during fabrication, while a second PMT (Fiber-PMT) allowed for measuring a collection intensity map from the window just after the ablation.

2.2. Optical windows fabrication

TFs were obtained from OptogeniX (www.optogenix.com), and were produced from NA=0.39 fibers (Thorlabs FT200UMT) with core/cladding diameter of 200µm/225µm through a heat and pull procedure, described in detail by Sileo et al. [19]. Thermal evaporation was then employed to conformally deposit a 400 nm thick Aluminum layer around the taper, setting the deposition rate at about 1.5 Å/sec while the TF was continuously rotated with a stepper motor.

The size of the windows was set by restricting the scanning region of the GMs to a 40 × 40 µm² area in correspondence of a taper diameter of 60 µm. Fabrication parameters were chosen considering two factors. (i) The laser fluence has to be higher than the ∼100 fs pulse ablation threshold of Aluminum, found to be F_t,Al ∼ 0.1 J/cm², [25,26] but lower than both the damage threshold and the ablation threshold for fused silica, found to be, respectively, F_damage,SiO2 > 2 J/cm² and F_t,SiO2 > 3 J/cm² [27]. Hence, we set the laser fluence at F ∼ 0.2 J/cm². Working close to the threshold enables an ablation rate of ∼2-6 nm/shot in air [26], with the liquid environment further reducing this rate. [28] (ii) The employed laser system allows for selecting the wavelength of the laser beam in the range between 680 nm and 1300 nm. We set λ = 800 nm for a compromise between the output power of the laser source, maximized at this wavelength, and the two photon absorption cross section of the used dye (Fluorescein) with ∼100 fs laser pulses, reported to be σ_2PA(λ = 800nm) = 36 ± 5 GM, very close to the maximum of σ_2PA(λ = 782nm) = 46 ± 6 GM, in Makarov et al. and Song et al. [29,30]. We configured a dwell time on each raster pattern’s point of t_dwell= 3.2 µs (about one frame per second with 512×512 pixels).

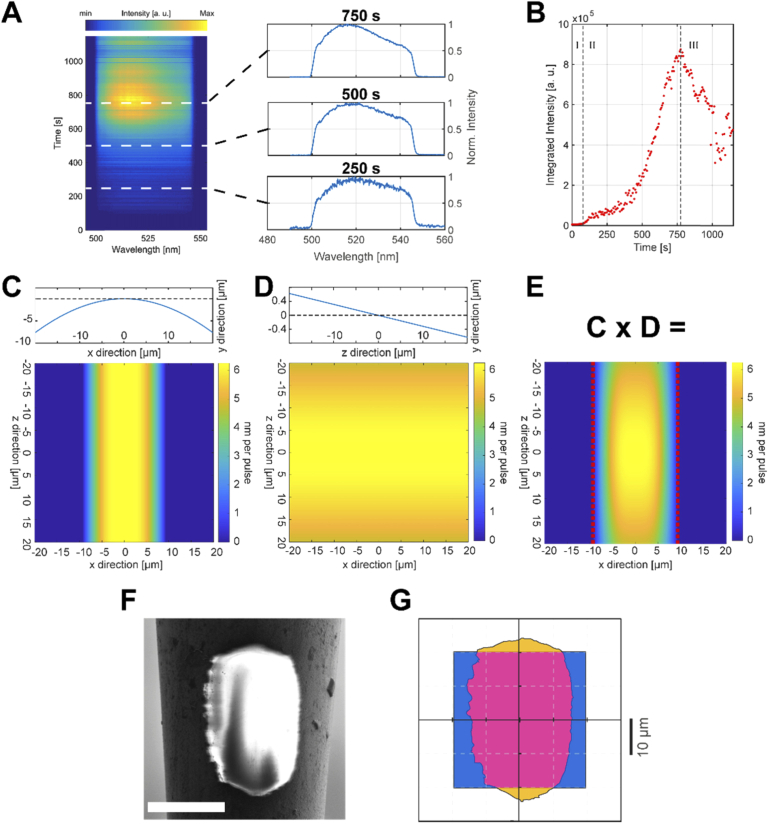
Representative spectral map recorded during the process is reported in Fig. 2(a) as a function of time. Although the processing of a 40 × 40 µm² optical window can be obtained in about 90 seconds, the spectra reported in Fig. 2(a) were recorded with a laser fluence near to F_t,Al, in order to slow down the fabrication and to better display the evolution of the process through the collected fluorescence signal. From the beginning of the fabrication, the spectra grow in intensity from an initial near-to-zero flat shape to eventually unfold into the typical fluorescein emission spectrum, [31] with no additional spectral features clearly recognizable, as shown in the inset of Fig. 2(a), in which three spectra are extracted at different timestamps. The integrated intensity values versus time, displayed in Fig. 2(b), show three different regimes (defined here as ‘regime I’ for 0 < t < 75 s, ‘regime II’ for 75 s < t < 750 s, and ‘regime III’ for t > 750 s).

Fig. 2.

(a) Real-time time-resolved fluorescence collection map used as feedback of the ablation process. Inset: three spectra are extracted at different timestamps from the map to better show the spectral shape of the collected signal. Spectra are normalized to the respective maximum value. (b) Scatter plot of the spectra integrated intensity versus time, with the beginning of the process being at t = 0). The dashed lines divide the plot into three different regimes, described in the main text. (c) Ablation depth per pulse dependence from the TF curvature, determined through Eq. (1). (d) Ablation depth per pulse dependence from the axial inclination of the TF, determined throug Eq. (1). (e) Resulting effect on the ablation depth per pulse. Red dashed lines enclose the non-zero ablation depth per pulse region. (f) Scanning Electron Micrograph of a 2PFA-DLW window at a diameter of ∼60 µm. Scale bar is 25 µm. (g) Difference between the Field of View and the final 2PFA-DLW window surface.

During ‘regime I’, no light is coupled inside the waveguide because the aluminum layer has not been sufficiently ablated yet. This is followed by ‘regime II’ in which the integrated intensity progressively increases. This corresponds to progressing metal ablation from the region of interest. During ‘regime III’ the integrated intensity starts decreasing and oscillating, although a constant fluorescence signal could have been expected after the complete ablation of the metal. After metal ablation ends, we observe the presence of cavitation bubbles over the ablated region, which likely induce a decrease of collected fluorescence signal. Indeed, the high repetition rate of the laser (80 MHz) produces consecutive pulses separated by Δt ∼ 12 ns, which interacts only with the dielectric glass surface of the fiber once the aluminum has been removed. This interaction could bring to local heating [32–34], due to energy accumulation [35]. In fact, the thermal conductivity of dielectrics is lower than the one of metals, with thermal diffusivity η typically ranging in the order of magnitude of 10⁻³ cm²/s for the former (η_SiO2 = 0.0083 cm²/s [36]) and in the units of cm²/s for the latter (η_Al = 0.97 cm²/s [36]). From these considerations, a dielectric region irradiated by a laser beam over an area of l² ≃ 10 µm² will cool in a time t ≃ l²/η ≃ 10 µs > Δt. Therefore, the temporal distance between two consecutive laser pulses is much faster than the thermal relaxation time [37]. In the case of Al instead t ≃ l²/η ≃ 10 ns < Δt.

However, we could not exclude that small bubbles are generated also during ‘regime II’, but our experiments suggest that the increasing in the collected fluorescence is faster than the cavitation-related decrease, in particular because of the smaller dielectric region exposed during ‘regime II’.

Since the ablation takes place on a curved surface while the laser scans in a plane, the local effective fluence depends on the cosine of the incidence angle [38]. Thus, the radius of curvature of the taper imposes a variation of the ablation depth per pulse as a function of the surface profile versus the planar scan plane, following [38]:

$$\mathrm{\Delta }y(x)={\alpha }^{-1}\log \left\{\frac{F}{F_t}\cos \left[{\tan }^{-1}\left(\frac{dy}{dx}\right)\right]\right\},$$ (1)

where α=4πκ/λ is the effective absorption index of Aluminum, and κ = 7.05 is its extinction index at λ = 800 nm taken from Ref. [39]. We calculated these variations considering the TF profile in the x-direction (Fig. 2(c)) and the taper angle along the z axis (Fig. 2(d)). Ablation could take place only for positions at which the ablation depth per pulse is positive (Fig. 2(e)). From these calculations we expect that the window size is minimally affected by variations in the z-direction (expected z-size 40 μm) but that it changes considerably along the x-direction (expected x-size ~20 μm). A representative Scanning Electron Micrograph (SEM) of a 2PFA-DLW window is shown in Fig. 2(f). From the SEM image it is clear that the shape of the window is similar to the expected one outlined by the iso-depth lines in Fig. 2(e), with the final size differing by about 5 μm in each direction. This is because Eq. (1) does not consider the actual size of the laser spot, especially along the y direction, while our system has a PSF with lateral FWHM of 3 μm and axial FWHM of ~30 μm [40]. Following Vorobyev et al. [41,42], a minor possible contribution could arise from thermal energy deposition, which is present also in fs-pulse irradiation and it could induce surface modifications. The software MATLAB Image Segmentation tool was employed to calculate the effective area of the window and to compare it with the size of the ablation Field of View (Fig. 2(g)). The actual size was estimated in 1375 μm², resulting in the 85% of the target 1600 μm².

3. Collection properties characterization

The possibility to collect light with µTF is enabled by the dielectric openings, e.g. the optical windows, on the surface. Let us consider a dielectric TF (Fig. 3(a)) and a description of propagating energy based on linearly polarized (LP) modes. The transversal propagation constant of the l,m-th guided mode at the section of radius r(z) is given by the following relation [43]:

$$k_{t-l,m}(z)\simeq \frac{r(z=0)}{r(z)}{k}_{t-l,m}(z=0),$$ (2)

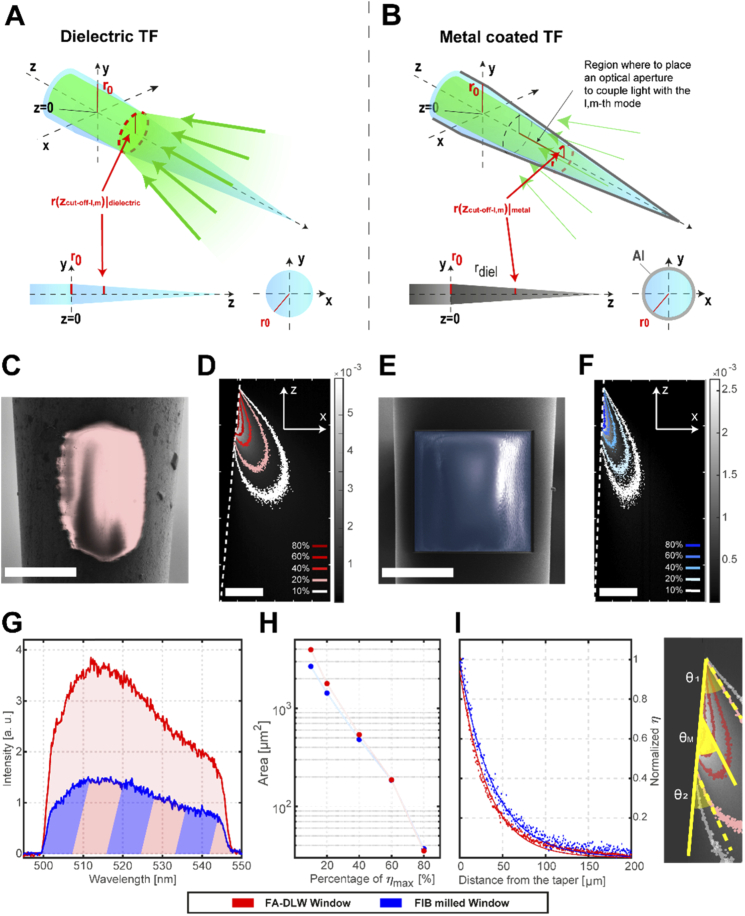
where k_t-l,m(z = 0) is the transversal propagation constant of the l,m-th guided mode at the widest taper section. In this dielectric confinement regime, the l,m-th mode is propagative only if its transversal propagation constant fulfill the condition k_t-l,m(z) < k₀NA. Therefore, since smaller r(z) implies higher k_t-l,m(z), a cutoff radius for the l,m-th mode can be defined (r(z_c-l,m)|_dielectric), and for r(z) < r(z_c-l,m)|_dielectric the mode can couple with light in the environment (Fig. 3(a)).

Fig. 3.

(a) Schematic representation of a dielectric TF. (b) Schematic representation of a metal coated TF. (c) Scanning Electron Micrograph of a 2PFA-DLW window. Scale bar is 25 µm. (d) Collection efficiency map for 2PFA-DLW window (red). Scale bar is 20 µm. White dashed line represents the edge of the fiber. (e) Scanning Electron Micrograph of a 40 × 40 µm² FIB milled window. Scale bar is 25 µm. (f) Collection efficiency map for FIB milled window (blue). Scale bar is 20 µm. White dashed line represents the edge of the fiber. (g) Spectra registered for the two type of windows. (h) Collection areas at different percentages of the maximum collection efficiency value. (i) Decay profile for normalized collection efficiencies. The decay is measured along a straight line which starts from the center of the window and forms with the taper edge (white dashed lines in Figs. 3(d) and (f)) an angle equal to θ_M, that is the mean between the angles formed by the taper edge and the two edges of the 20% iso-surface profile (θ₁ and θ₂, example on a detail from Fig. 3(d)).

In metal coated TFs, equation Eq. (2) holds true, but the l,m-th mode is guided under the evanescence condition k_t-l,m < k₀n, where k₀ is the free-space wavenumber, defined as k₀= 2π/λ for a given wavelength λ, and n is the refractive index of the waveguide. This sets a different cutoff section for metal-coated TFs r(z_c-l,m)|_metal < r(z_c-l,m)|_dielectric since n > NA (Fig. 3(b)) [15,44]. As a consequence, light entering an optical window realized at a section with radius r along the taper will couple with guided modes having a k_t-l,m(z = 0) such that they can propagate in a metallic waveguide.

Because of this mechanism, two different characterizations are required to fully describe the light collection properties of the window: (i) to estimate the efficiency of photons collection through the aperture and (ii) to determine how photons are coupled to guided modes. Thus, we characterized the near-field properties in terms of collection efficiency maps (η) [12,40], as well as the far-field pattern of light emerging from the distal facet, obtaining direct access to the transversal propagation constant of modal content back-propagating into the fiber [12,15]. The two approaches are described in following paragraphs 3.1 and 3.2, respectively.

3.1. Collection efficiency maps

Collection efficiency maps (η(x,z)) represent the percentage of photons collected by the window when an omnidirectional point source emits in the generic point of the space (x,z). To obtain a direct measurement of η for the 2PFA-DLW windows (Fig. 3(c)), we placed the fiber inside a drop of PBS:Fluorescein solution making sure that the normal to the window’s surface lied perpendicularly to the optical axis of the Objective Lens (Characterization Configuration in Fig. 1(a)).

A λ = 920 nm fs-pulsed NIR laser beam was focused and scanned in a ∼ 260 × 260 µm² area, in order to obtain the scan of a point-like fluorescence source in close proximity to the window. The fluorescence signal collected by the window was recorder by the Fiber-PMT in terms of number of photons per pixel (N_f(x,z)), while the µscope-PMT builds an image of the same area, also in this case in terms of number of photons per pixel (N_s(x,z)) [40]. Considering the detection loss of the system, η was therefore determined by the following relation:

$$\eta (x,z)=\frac{N_f(x,z)}{Q\cdot N_s(x,z)},$$ (3)

where Q is a factor that takes into account the detection loss of the epifluorescence collection path and the term Q·N_s(x,z) represents the number of photons emitted by the excited fluorescence spot.

A representative collection efficiency map is displayed in Fig. 3(d), showing iso-intensity lines in the (x,z) plane for different values of η.

In order to minimize the contribution of artifacts or outliers in the estimation of the maximum collection efficiency value attributable to the 2PFA-DLW window, we defined the quantity <η>_90% as the sum of all the pixel values with η > 90% of the maximum pixel value divided by the corresponding number of pixels, obtaining <η>_90%= (5.50 ± 0.13) × 10⁻³ (mean ± standard deviation, n=3 fibers). We carried out a quantitative comparison between the 2PFA-DLW window and a Focused Ion Beam milled window realized at the same diameter on a different metal coated TF (Fig. 3(e)) [18], milling an area equal to the ablation FOV (1600 µm²). This resulted in the η maps displayed in Fig. 3(f) and a <η>_90% = (2.30 ± 0.06) × 10⁻³ (mean ± std, n=3 fibers). The integrated intensity detected by 2PFA-DLW spectrum (red) resulted to be ∼2.6 times higher than the FIB spectrum (blue), as confirmed by the spectra in Fig. 3(g).

To better compare the properties of the 2PFA-DLW and FIB windows, we measured the surface area defined by the iso-lines at different percentages of <η>_90% (Fig. 3(h)). While the high relative efficiency areas (60% and 80% of <η>_90%) are similar, the low relative efficiency area (10% of <η>_90%) is 1.5 times wider for the 2PFA-DLW one (3956 µm² versus 2676 µm²). If the decay profiles of the normalized η are considered (Fig. 3(i)), two similar trends can be observed, with the efficiency that drops below the 20% of the maximum after the first 50 µm after the window.

This lets us suggest that 2PFA-DLW windows are better suited to detect optical signals than FIB-milled windows, as the higher collection efficiency of the formers allows gathering a stronger signal from larger sample volumes.

3.2. Angle-selective light coupling setup and far-field imaging

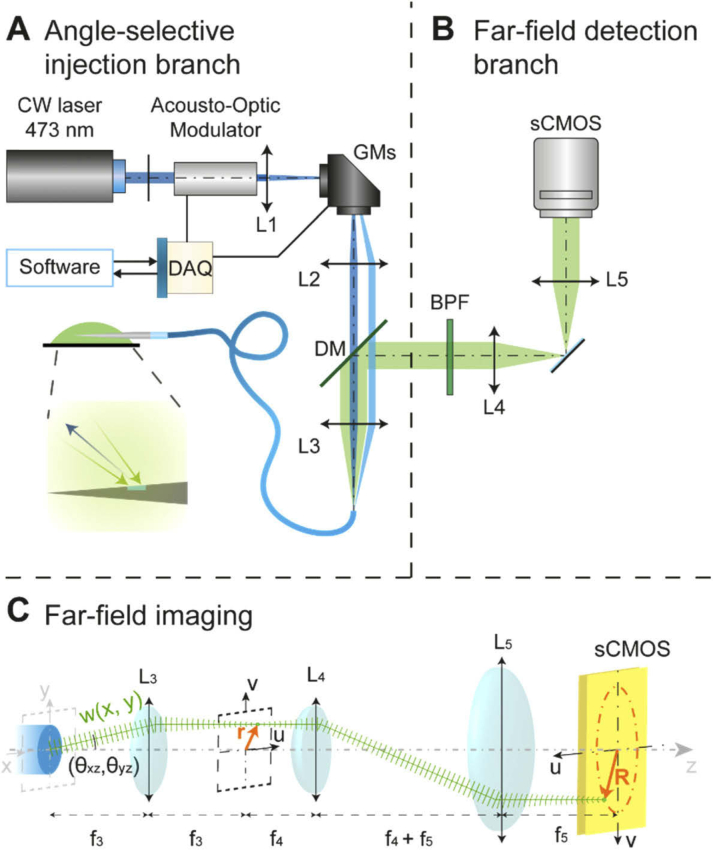
To identify the transversal propagation constant of modal content excited by light coupled through the window, we have implemented the optical path in Figs. 4(a) and (b). The patterned TF was placed in a PBS:Fluorescein bath, and a Continuous Wave laser at 473 nm was injected into the fiber with a specific angle to maximize output power from the window. Generated fluorescence was collected by the same window and it was directed through a far-field imaging path by a dichroic mirror.

Fig. 4.

(a) Sketch of the light emitted by the fiber and the correlation between the emission angle and the coordinates on the focal plane. (b) Scheme of the optical setup employed for angle selective light coupling inside the fiber and (B) far-field imaging of the collected signal. (c) Sketch of the light emitted by the fiber and the correlation between the emission angle and the coordinates on the detection plane (Band Pass Filter BPF is omitted).

Light emitted by the fiber facet can be expressed as a weighted sum of plane wave components w(x,y) which propagate at manifold (θ_xz, θ_yz) angles (in the scheme in Fig. 4(c), only one plane wave is shown). Passing through lens L₃, those components are separated and focused at different points r(u,v) = (f₃tan(θ_xz)·û, f₃tan(θ_yz)·v^) on the focal plane, hence being directly correlated with the angular distribution of light, which is intrinsically related to the transversal wave-vector k_t emitted from the fiber [12,45].

An additional relay with lenses L4 and L5 matches the size of the far-field image in the (u,v) plane with the size of the imaging sensor, with the image being related to k_t values by Eq. (4):

$$k_t=\frac{2\pi }{\lambda }\sin \left[{\tan }^{-1}\left(\frac{f_4}{f_3{f}_5}|\mathbf{R}(u,v)|\right)\right],$$ (4)

where R(u,v) is the magnitude of the distance vector of the pixel from the center of the resized (u,v) plane, f₃, f₄ and f₅ are respectively the focal lengths of L₃, L₄ and L₅ in Fig. 3(b). Because of the cylindrical symmetry of the modes’ propagation into the waveguide, we observed a ring-shaped intensity distribution pattern on the detection sensor.

In order to correctly analyze the recorded pattern, the auto-fluorescence background signal, induced by the fiber patch has also been measured, repeating the measurement in a non-fluorescent bath (PBS) [46]. This signal could arise by the interaction of the excitation laser with photoactive compounds in the optical fiber and associated elements, and even by interaction with the glue used for the patch-cord and taper connectorization, and it spectrally overlaps the fluorescein spectrum, making spectral filtering unusable to remove this background.

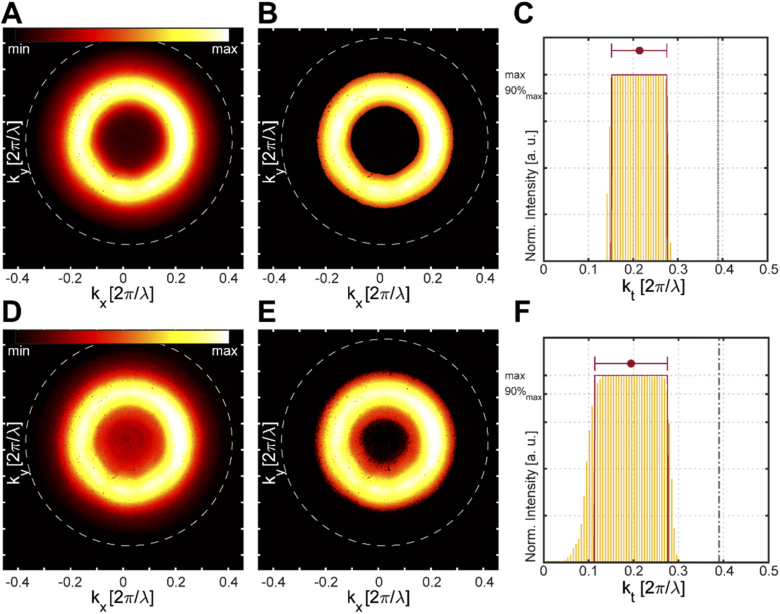
Representative far-field patterns of light detected from a window placed at a diameter d = 55 µm is displayed in Fig. 5(a), after background subtraction. The image was numerically segmented by: (i) a low-pass intensity threshold to remove the residual excitation laser and outliers, and (ii) a high-pass intensity filter to remove residual noise (placed at two times the mean value of the background pixels).

Fig. 5.

(a) “Raw” Far-Field pattern obtained from the subtraction between the signal collected while the fiber is submerged in a PBS:Fluorescein solution drop and the signal collected while the TF is submerged in non-fluorescent PBS. (b) Ring-shaped pattern obtained from the algorithm. (c) (Yellow) Histogram of the distance in units of 2π/λ between the non-zero pixels of the image corrected as described in the main text and the centroid of the image (only a bar each 4 is shown for visibility). Red lines indicate the interval of histogram values greater than the 90% of the maximum. This interval corresponds to the extracted modal subpopulation. The dot-dashed line corresponds to the maximum k_t that could be emitted by the fiber (0.39 2π/λ). (d-f) As in A-C for a FIB milled window. White dashed circles the maximum k_t that could be emitted by the fiber (0.39 2π/λ).

A representative segmented image is shown in Fig. 5(b). Subsequently we plot the histogram of the k_t values related to non-zero pixels from the centroid of the segmented image (Fig. 5(c)). The k_t interval of the modal subpopulation outcoupled from the patch cord is then extracted from the histogram as the values greater than the 90% of the maximum (red dot in Fig. 5(c)). From this analysis we obtained k_t = 0.21 ± 0.06 [2π/λ] for 2PFA-DLW windows. We repeated the experiment for the FIB milled window (Figs. 5(d) and (e)), and we extracted the outcoupled k_t distribution from the histogram (Fig. 5(f)), obtaining k_t = 0.19 ± 0.08 [2π/λ].

As expected, the collection diameter determines the modal subset at which the collected light propagates in the fiber. From the comparison of far field images, we observed that FIB-milled and 2PFA-DLW milled windows collect modal subsets with compatible k_t. Therefore, the 2PFA-DLW window shows higher collection efficiency, while preserving unchanged the modal coupling properties of the waveguide, an important feature for depth-selective fluorescence collection [12].

4. Discussion and conclusions

We propose an ultrafast Direct Laser Writing setup that takes advantage of real-time spectral feedback to optimize light collection properties of microstructures realized on the edge of a fiber optic-based device. The system was applied to ablate a conformal metal coating on the edge of a tapered fiber, while monitoring the two-photon fluorescence signal simultaneously generated in the environment by the same fs laser pulses. In this work, the two-photon fluorescence feedback signal has been monitored by the user during the process, but the same protocol can be automatized. For example, an algorithm could analyze the progress of the integrated signal also in terms of first-order derivative or higher-order momenta, to better identify when ‘regime III’ is reached.

When compared with canonical FIB-milled patterns, a quantitative analysis of the optical properties of collected light in both near-field (collection efficiency maps) and in far-field (out-coupled modes dispersion analysis) show ∼60% improvement in the collected signal, while the uncoupled modal subset is comparable between the fabrication processes. We attributed these findings to the lower alteration of glass induced from the laser ablation process, in terms of both roughness and dielectric properties. From the SEM micrographs (Figs. 3(c) and (e)), we observe no notable texture in the active area of the 2PFA-DLW window. The maximum achievable laser fluorescence at the window plane was indeed measured to be F_max ∼ 0.34 J/cm², well below both the damage threshold and the ablation threshold of glass reported in literature to be, respectively, F_damage,SiO2 ∼ 2 J/cm² and F_t,SiO2 ∼ 3 J/cm² [27], above which one would expect a decrease in collection efficiency similar to the one we measured for the FIB-milled windows.

On the other hand, FIB processing shows no textures in the central part, for an extension of ∼20 µm in the transversal direction with respect to the TF axis, but a rough surface in the lateral part, where the curvature of the fiber is higher. In addition, the FIB milling on glass is known to induce a variation of its optical properties, with a refractive index rise from n = 1.46 to n ∼ 1.75 in the visible range, and therefore a transmissivity decreases from T = 90% to T = 80-85%, due to Ga⁺ ions implantation [47]. Moreover, the feedback offered by the developed system, as well as the possibility to characterize optical apertures’ properties using a single setup, sensibly reduce the overall fabrication time with respect to FIB.

As FIB processed µTFs have proven their potential in depth-resolved photometry experiments in brain tissue [12], we envision that the presented 2PFA-DLW fabrication of optical apertures on the edge of the TF surface could be employed to engineer the collection sites along the TF itself. Indeed, the measured collection volumes (Figs. 3(h) and (i)) are comparable with the mean free path µ of photons in the brain, reported to be µ ∼ 49 µm [48]. Moreover, the angular properties (Figs. 3(d) and (f)), decay profiles (Fig. 3(i)) and the far-field patterns (Fig. 5) obtained with the two fabrication methods are very similar, letting us expect that FIB-milled and laser-ablated windows behave similarly from a near-field geometrical perspective as well as in terms of photons coupling with guided modes. Although here we showed 2PFA-DLW in the field of optical neural interfaces, the same concepts can be extended to a range of fiber-based biosensors, which would greatly benefit of optimized and selective interactions of guided modes with the environment.

Funding

H2020 European Research Council10.13039/100010663 (677683, 692943); National Institutes of Health10.13039/100000002 (1UF1NS108177-01, U01NS094190); Horizon 2020 Framework Programme10.13039/100010661 (828972).

Disclosures

LS, MDV, BLS and F. Pisanello are founders and hold private equity in Optogenix, a company that develops, produces and sells technologies to deliver light into the brain. Tapered fibers commercially available from Optogenix were used as tools in the research.