Accounting for Global COVID-19 Diffusion Patterns, January–April 2020

Abstract

Key factors in modeling a pandemic and guiding policy-making include mortality rates associated with infections; the ability of government policies, medical systems, and society to adapt to the changing dynamics of a pandemic; and institutional and demographic characteristics affecting citizens’ perceptions and behavioral responses to stringent policies. This paper traces the cross-country associations between COVID-19 mortality, policy interventions aimed at limiting social contact, and their interactions with institutional and demographic characteristics. We document that, with a lag, more stringent pandemic policies were associated with lower mortality growth rates. The association between stricter pandemic policies and lower future mortality growth is more pronounced in countries with a greater proportion of the elderly population and urban population, greater democratic freedoms, and larger international travel flows. Countries with greater policy stringency in place prior to the first death realized lower peak mortality rates and exhibited lower durations to the first mortality peak. In contrast, countries with higher initial mobility saw higher peak mortality rates in the first phase of the pandemic, and countries with a larger elderly population, a greater share of employees in vulnerable occupations, and a higher level of democracy took longer to reach their peak mortalities. Our results suggest that policy interventions are effective at slowing the geometric pattern of mortality growth, reducing the peak mortality, and shortening the duration to the first peak. We also shed light on the importance of institutional and demographic characteristics in guiding policy-making for future waves of the pandemic.

Introduction and Overview

This paper takes stock of the data gathered during the first three months of the COVID-19 pandemic, tracing the associations between COVID-19 mortality and pandemic policy interventions, accounting for global pandemic diffusion patterns. Pandemic policy interventions in our consideration refer to containment and closure policies that aim to limit social contact. Anecdotal evidence and policy dynamics suggest that accelerated COVID-19 mortality induces a tighter pandemic policy response aimed at slowing the otherwise geometric patterns of the pandemic. With a lag of several weeks, these policies ought to reduce the mortality rate, with reductions varying systematically across countries. Specifically, as COVID-19 mortality affects disproportionally the older population and people with pre-existing conditions, a given increase in policy intensity may have a greater proportionate impact on future mortality in older societies, and in countries with higher average exposure to pre-existing medical conditions. In the same vein, higher urbanization rates, higher population density, and mobility, other things being equal, ought to magnify the decline in future mortality rates associated with a more aggressive pandemic policy stance.

Key factors in modeling a pandemic and in guiding policy-making include the infection rates; the mortality rates associated with infections; the ability and effectiveness of the policies, medical system, and society to adapt to the changing dynamics of a pandemic; and other structural factors [Verity et al. 2020]. In the absence of vaccines, policies which limit social contact are a key strategy adopted by most countries amid the COVID-19 pandemic to flatten the curve. However, the strictness and timing of such policy interventions vary substantially across countries. Additionally, institutional and demographic characteristics such as the proportion of elderly and urban populations, the nation’s level of democracy, etc., may influence mortality dynamics both directly through the size of vulnerable populations, and indirectly through citizens’ perceptions and behavioral responses to stringent policies (Van Bavel et al. 2020). Our empirical specification controls for these considerations, subject to the limited data available on key factors. Specifically, the scarcity of COVID-19 testing, and the limited information on the precision of available tests, implies a vast underestimation of the infection rates per capita, possibly by a factor of two digits.1 The undercount of COVID-19 population mortality rates is also prevalent, but by an order of magnitude below the errors associated with infection rates.2 Therefore, we focus mostly on accounting for the COVID-19 population mortality rates per capita during the first phase of the pandemic, controlling for policy and structural factors subject to data availability and quality. We plan to revisit these issues with better quality and longer-term data in the coming quarters.

A fair share of the countries reached a local peak of the COVID-19 population daily new mortality rate curve during the sample period [see Figs. 1, 2 and 3].3 Applying various techniques, we study the factors accounting for the empirical shape of the mortality curve from the onset of the pandemic to the local peak, with a focus on the impact of policy intensity interacting with structural variables. Like similar studies, one should use healthy skepticism in reading the results. First, data quality and availability are a major limitation, as each country has its challenges with data collection, aggregation, and reporting. Second, ‘better performance’ in the first mitigation phase of a pandemic does not guarantee superior future performance, as the dynamics of a new viral pandemic are yet unknown. By design, flattening the pandemic curve shifts some mortality incidence forward. The susceptibility to secondary waves of infection remains a looming threat.4 Policies adopted in the second quarter of 2020, and the realized pandemic infections, containment, and treatment will explain the future performance of each country. Furthermore, only time and much more medical research will tell the degree to which infected persons that recovered gained immunity for a long enough period to allow smooth convergence to ‘herd immunity.’

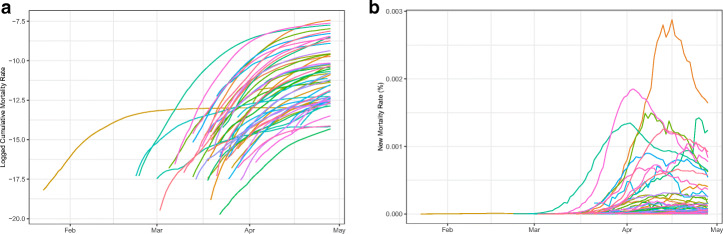
Fig. 1.

COVID-19 mortality rate curves, by country. LHS (a): Cumulative logged mortality rate. RHS (b): New Mortality Rate. 7-day rolling averages. Series starts from the 5th COVID-assigned death

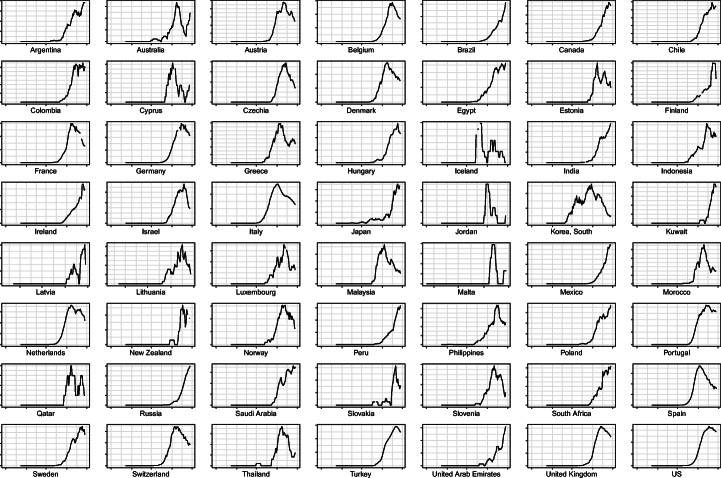
Fig. 2.

Sample Countries and New Mortality Curves, 1/23/20–4/28/20. Note: 7-Day rolling average new mortality rate by country. Y-axis normalized to have all countries fit the same scale. Period: January 23 – April 28, 2020. Special case countries we omit from the above plots: China (a discrete large spike in mortality in mid-April to account for past reporting delays and omissions), Singapore (highly fluctuating case curves associated to immigrant workers), and Vietnam (a flat line)

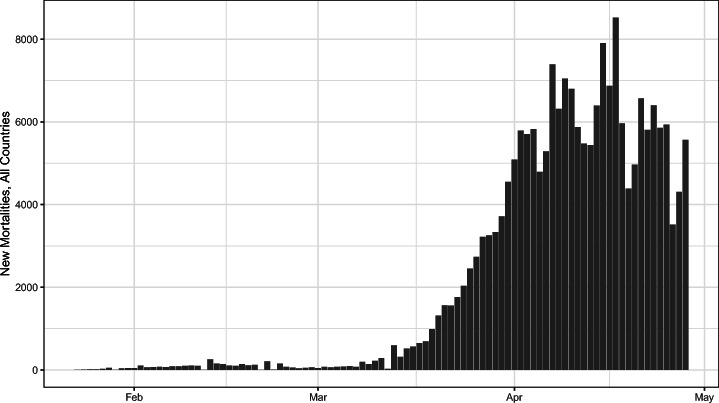
Fig. 3.

Daily New COVID-19 Global Mortalities. Note: Cumulated daily deaths across all countries in the sample

Our study relies on daily COVID-19 policy and case data reported by Oxford and John Hopkins University, as well as Apple mobility data and various controls. Our baseline estimation study examines OECD and Emerging Market (EM) sub-samples based on data from 1/23/2020–4/28/2020; or the first 97 days of the pandemic. Below, we summarize the main results.

First, we investigate the evolution of weekly mortality growth rates over time and across countries. Applying dynamic panel analysis, local projections (Jordà 2005) suggest that administering more stringent pandemic policies were associated with significantly lower mortality growth rates, with a lag of 2 to 4 weeks, during the first pandemic phase (i.e., during the time from the first death through the end of the sample period). Countries with a Stringency Index (SI) 10 units higher than average had, two weeks later, mortality growth rates that were on average 22 percentage points lower (Oxford’s SI is normalized between 0 to 100; where 100 = strictest response). The reductions in mortality growth rate are smaller after three and four weeks, roughly 17 and 13 percentage points respectively. While the reduction in growth rates seem quite large, it is important to put these numbers in perspective. Given the geometric nature of disease spread, oftentimes, week-over-week mortality growth rates can be anywhere from +50% to +100% or greater.

Taking slow-moving country fundamentals from the period pre-COVID-19 as exogeneous, we find that countries in the 75th percentile in terms of proportion elderly (65 or older) saw a much stronger reduction in mortality growth rates from the same 10 unit rise in SI, compared to countries with relatively low proportions of elderly (25th percentile). Countries in the 75th (25th) percentile saw mortality growth rates of about −25% (−10%) after two weeks. Countries with a greater proportion of the elderly are unconditionally more susceptible to the pandemic, but for this same reason, they are likely to benefit more under stringent policies. In countries with a higher proportion of urban population, SI measures had a stronger impact on mortality growth than in countries with a lower proportion of urban population. This heterogeneity is consistent with the fact that urban populations may face greater exposure due to their high population densities. Greater policy stringency is also more strongly associated with lower mortality growth during the first phase of the pandemic in countries with greater inbound travel, greater GNI per capita, higher health expenditures and a greater level of democracy (measured with the EIU Democracy Index).5 While international travel flows are quite intuitive risk factors for a pandemic like COVID-19, the role of democratic freedom is an ongoing topic of debate (Ang 2020). Our results are consistent with the view that greater individual rights may be detrimental in this situation, making it more difficult for the government to administer strict quarantines and have citizens abide by them.

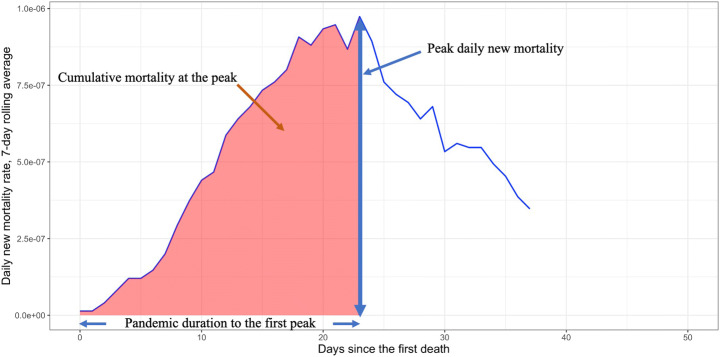
Next, we turn to cross-country regression results, where the dependent variables include the logged peak new mortality rate (calculated as the new deaths out of the population at the peak of daily new mortality, by country), and the ratio of ‘peak new mortality rate’-to-‘pandemic duration to first peak’ measured in days (a proxy for flatness/steepness of the mortality rate curve). Definitions of these peak-related dependent variables are illustrated in Fig. 4 using the daily new mortality curve of Czechia. Countries with more aggressive policy interventions in place prior to the first death tend to exhibit a lower new mortality rate at the peak (“Early SI” or “proactive stringency policy”).6 We find that a one unit increase in Early SI (average SI level prior to the first COVID mortality) is associated with peak new mortality rates on average − 12% lower. Quantitatively, early SI was also associated with flatter mortality curves, but the estimate is statistically insignificant. Unsurprisingly, higher early mortality growth rates (growth rate of new mortality rate in the first week following the first death) are significantly associated with higher peak mortalities and steeper mortality curves, while higher levels of the mortality rate early on (cumulative mortality rate within the first week following the first death) were associated with flatter overall mortality curves.7 Greater early mobility was also significantly associated with higher mortality peaks. Higher population density is, somewhat surprisingly, associated with flatter mortality curves (column [2]). However, this association may be driven by the fact that many of the high-density countries are in Asia. Overall, the evidence suggests (but does not necessarily assert) that policy stringency directly reduced the peak mortality rates, and that other forces were also at play (e.g., early mobility, initial pandemic conditions, institutional features).

Fig. 4.

Peak-related dependent variables in country case of Czechia

Not only do mortality rates during the first pandemic phase differ across countries, there is also considerable variation in how long new deaths continued to climb in terms of days. We term this as the ‘pandemic duration to the first peak’ (PD). One should be careful when interpreting the effects of covariates on the PD in terms of altering the shapes of mortality curves, as a longer PD could be accompanied by a higher peak mortality rate and thus a steeper curve, or a lower peak mortality rate and thus a flatter curve. Fitting a Kaplan-Meyer curve for the PD over all countries in the sample, in number of days, suggests that countries with stronger Early SI measures (above the average) had significantly lower PDs on the way to the first local peak of the mortality/day curve, compared to countries which did not. The probability of peaking after 40 days is close to 0% for above-average Early SI countries (virtually all of these countries experienced their first local peak by day 40). For below-average Early SI countries, it took approximately 80 days, twice the amount of time, until the first peak was reached. To better understand the cross-country variation in PD, we estimate a Cox proportional hazards model. Higher mortality rates early on are associated with shorter pandemic durations to the peak, while countries realizing higher mortality peaks tend to have, unsurprisingly, longer pandemic durations to the peak. Although the negative association between the strictness of early policy interventions and the pandemic duration to the peak is not significant under the Cox model, more aggressive policy interventions early on could still be associated with a shorter pandemic duration to the peak through reducing mortality peaks as evidenced by the cross-country analysis. Countries that responded faster prior to the first death had shorter pandemic duration to the peak. Additionally, countries with greater proportions of elderly populations, greater proportions of urban population, greater shares of vulnerable employment tend to exhibit shorter pandemic durations to the peak.8 Moreover, under certain specifications, the level of democratic freedom appears to be a highly significant determinant in pandemic duration to the peak. That is, countries that have a higher level of democracy saw longer pandemic durations to the peak. Countries further away from the equator also tended to experience longer PD. While at this stage we are reporting suggestive statistical associations, more data and research are needed to get fuller identifications of all these factors.

Empirical Specification

We focus on two aspects of COVID-19 mortality over the first three months of the pandemic spanning from January 23rd, 2020 to April 28th, 2020, which we refer to as the first pandemic phase: first, the dynamic of COVID-19 mortality rates out of the total population, examining the weekly growth rate of the new mortality rate per capita; and second, the empirical shape of the mortality rate curve from the onset to the local peak of the first pandemic phase, examining three dependent variables discussed below. To filter out noise in the daily mortality data, we construct a 7-day rolling average of the daily mortality rate per capita and use these series of averages in our estimations and peak identifications. For simplicity, the mortality rate mentioned hereafter is referred to as the 7-day rolling average of the mortality rate.

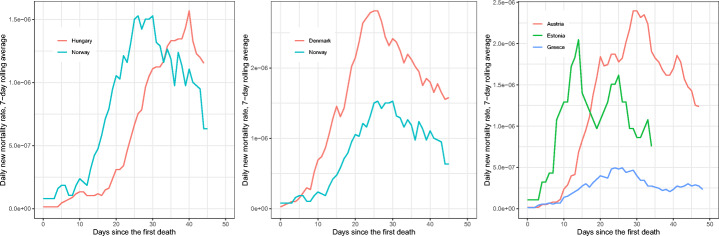
Although examining the growth rate of the new mortality rate per capita provides evidence on how mortality rates evolve over time, it is not trivial to conclude which variables can characterize the cross-country difference in the empirical shape of the mortality curve from the onset to the local peak of the first pandemic phase. We argue that three outcome variables related to the local peak matter: first, the new mortality rate at the peak; second, the pandemic duration to the peak; third, the ratio of the new mortality rate at the peak to the pandemic duration to the peak. We illustrate this idea by comparing country cases. Figure 5 shows the daily new mortality rate curves for several countries: the left one comparing that of Hungary and Norway, the middle one comparing to that of Denmark and Norway, and the last one comparing that of Austria, Estonia, and Greece. The left figure shows that although the peak mortality rates of Hungary and Norway are around the same, their durations to the peak are different: Norway reached the peak faster, and thus had a steeper mortality curve. The middle figure shows that although the durations to the peak of Denmark and Norway are around the same (i.e., both around 25 days), their peak mortality rates are different: Denmark’s mortality rate climbed to a higher level before going down, and thus had a steeper mortality curve. Hence, a lower peak mortality rate or a longer duration to the peak implies a flatter mortality curve; however, only on the condition that all other things are held equal. Once both the peak mortality rate and the duration to the peak change in the same direction, it may be ambiguous whether the mortality curve is flattened or not, as demonstrated in the right figure of Fig. 5. Both Estonia and Greece realized a lower peak mortality rate and a shorter duration to the peak than Austria; however, it is obvious that Estonia has a much steeper mortality curve while Greece has a much flatter mortality curve compared with Austria. This implies that the ratio of the peak mortality rate to the duration to the peak also plays a key role in understanding the empirical mortality curve. Hence, it follows that all three outcome variables related to the peak (including the daily new mortality rate at the peak, the duration to the peak, and the ratio of the peak rate to the duration) together characterize the empirical shape of the mortality curve from the onset to the local peak of the first pandemic phase. By knowing how these three outcome variables are impacted by government pandemic policies or country-specific structural variables can we uncover to what extent these factors account for the pattern of mortality’s climb to the local peak of the first pandemic phase.

Fig. 5.

Daily new mortality curves of selected countries

Policy Stringency and Mortality Dynamics

We start with a panel study of mortality growth rate dynamics, using the week-over-week growth rate of the new mortality rate per capita, accounting for containment and closure policy interventions (see Oxford’s COVID-19 Government Response Tracker).9 Specifically, our dependent variable y_{i, t} in country i on date t is defined as

$$y_{i,t}=log\left({\mathit{\text{MortalityRate}}}_{i,t}\right)-log\left({\mathit{\text{MortalityRate}}}_{i,t-7}\right),$$ 1

where MortalityRate_{i, t} is the new mortality rate in country i on date t. A lower growth rate of the new mortality rate implies a flattening of the mortality curve.

Our first benchmark estimation uses the method of local projections (Jordà 2005), examining future (or current) mortality growth rate as a function of current (or past) mortality growth rate and degree of policy stringency. We aim to understand to what degree policy interventions are associated with future mortality growth, and therefore, the evolution of the pandemic. Local projections do not only simplify our problem but also produce robust estimates under misspecification.10 Specifically, our model is

$$y_{i,t+h}={\alpha }_i\left(h\right)+{\delta }_t\left(h\right)+\gamma \left(h\right){\mathit{SI}}_{i,t}+\beta \left(h\right)y_{i,t-1}+{\epsilon }_{i,t}\left(h\right),$$ 2

where y_{i, t + h} is the week-on-week growth rate of the new mortality rate in country i at date t + h for h = {14, 21, 28}. SI_{i, t} is the Stringency Index constructed in the Oxford COVID-19 Government Response Tracker, an aggregate measure of the overall stringency of containment and closure policies,11 at date t and y_{i, t − 1} is the one-day lagged mortality growth rate. Fixed effects are denoted as a_i and δ_t, representing the country and time fixed effects, respectively. We choose to examine the response of new mortality growth with respect to SI at horizons no shorter than two weeks, with reference to studies on the incubation and death periods: The incubation period is 6 days on average (McAloon et al. 2020), and the death period (number of days from symptom onset to death) ranges from 12 to 15 days for different age groups on average according to CDC estimates.12 The collection of estimates $\widehat{\gamma }\left(h\right)$ for h = {14, 21, 28} trace out the dynamic impact of stringency policies on mortality growth at the weekly frequency.13

Additionally, we study the heterogeneity in the association between policy interventions and mortality growth by estimating the model with interaction terms between the Stringency Index and country-specific social and economic variables

$$y_{i,t+h}={\alpha }_i\left(h\right)+{\delta }_t\left(h\right)+\gamma \left(h\right){\mathit{SI}}_{i,t}+\beta \left(h\right)y_{i,t-1}+\theta \left(h\right){\mathit{SI}}_{i,t}\ast x_i+{\epsilon }_{i,t}\left(h\right),$$ 3

where x_i is the country-specific variable of interest. We consider: the proportion of the elderly population (people aged 65 and over), the proportion of the urban population, proportion of employment in vulnerable sectors, population density, the logarithm of GNI per capita, health expenditure (% of GDP), population-weighted exposure to ambient PM2.5 pollution, the logarithm of tourist arrivals and departures, level of democracy, and country location measured with latitude and longitude.14

Cross-Country Differences in Peak Mortality

We follow with a cross-country analysis examining the mortality rate at the peak, a key moment in the first quasi-bell curve, which puts hospitals’ capacity to their most severe test. The quasi-bell shapes are normalized by the day of the first significant death. As discussed before, we consider three outcome variables related to the peak: first, the logged peak mortality rate, second, the pandemic duration to the first peak (PD), and third, the ratio of the logged peak mortality rate to the PD. We opt to use linear regression analysis to examine the cross-country difference in the logged peak mortality rate and the ratio of the logged peak mortality rate to the PD and use survival analysis to examine the cross-country difference in the PD. Our cross-country peak mortality data is calculated from the sample from January 23rd, 2020 to April 28th, 2020, during which many OECD countries and emerging market economies finished their ride up to the first peak of the first quasi-bell in terms of contagion per capita and fatality per capita.

Our cross-sectional linear regression model is

$$y_i={\beta }_0+Z_i\gamma +X_i\beta +{\epsilon }_i,$$ 4

where y_i is the logged peak mortality rate or the ratio of the logged peak mortality rate to the PD in country i. A higher peak mortality rate implies a larger inflow of patients, stretching hospitals’ capacity. Accounting for the pandemic duration to the first peak, a higher ratio of the logged peak mortality rate to the PD implies a steeper mortality curve, characterized by either a larger or a faster patient inflow that could potentially overwhelm the healthcare system. We include a set of potential endogenous variables Z_i. First, one may be interested in whether the cross-country difference in the intensity of the COVID-19 outbreak explains the cross-country difference in the empirical shape of the mortality curve. We include log(Early Mortality_i), the logged cumulative mortality rate in the first week after the first death, and Early Mortality Growth_i, the growth rate of daily mortality rate in the first week after the first death, to control for the cross-country difference in the initial level and growth of the mortality rate. Second, one may be interested in whether proactive stringency (i.e., stringency policies in place before the first reported death) policy interventions influence the cross-country difference in the empirical shape of the mortality curve. We also include Early SI_i, the average of the Stringency Index (SI) from its first non-zero value to the first death, accounting for how strict government interventions were before the first confirmed death, and Days from First SI to First Death_i, the number of days from the first non-zero SI to the first death, accounting for how early government interventions are implemented. Additionally, to account for cross-country differences in how aggressively countries respond to the pandemic and increase their policy intensities, we include a variable which we refer to as the SI Delta_i (or Stringency Delta), calculated as the difference between a country’s maximum level of SI and its initial level of SI (SI_{i, 0}), normalized by the number of days (T_i) between them:

$$\mathit{SI}\mathit{\text{Delt}}{a}_i=\frac{\left[max\left(S{I}_i\right)-S{I}_{i,0}\right]}{T_i}.$$ 5

A higher maximum SI and/or a shorter time to the maximum SI will yield a higher SI Delta. Third, we include Early Mobility_i, the weekly average mobility index in terms of walking (reported by Apple) in the week before the first death. We emphasize that while these variables are important to investigate, all of them are endogenous, as they are calculated over part of the first wave period of COVID-19. We also include a set of country-specific control variables X_i that we take as exogenous, including the proportion of the elderly population (people aged 65 and over), the proportion of the urban population, proportion of employment in vulnerable sectors, population density, GNI per capita, health expenditure (% of GDP), level of democracy, and country location measured with latitude and longitude.

Cross-Country Differences in Time-to-Peak

We then proceed with a survival analysis studying the association between the pandemic duration to the first peak (PD) and a set of explanatory variables. We focus on the survival function of the mortality peaking.

$$S\left(t\right)=Pr\left(\mathrm{T}>\mathrm{t}\right),$$ 6

which is defined as the probability that the PD is later than date t, which is the probability that the mortality peaks after date t. A higher probability that the PD is later than a certain date implies a longer PD, which could have ambiguous implications. On the one hand, it suggests a slower surge in hospitalization that could ease the burden on the healthcare system. On the other hand, a longer time-to-peak may imply a longer-lived, poorly managed pandemic.15 Our benchmark specification is the Cox proportional hazards model (Cox 1972), which examines the relationship between the hazard function and a set of explanatory variables.16 The hazard function is defined as the probability that the peak is on date t conditional on that the peak is reached until date t or later,

$$\lambda \left(t\right)=\underset{\mathit{dt}\to 0}{lim}\frac{Pr\left(t\le T<t+\mathit{dt}\right)}{\mathit{dt}·S\left(t\right)}=-\frac{S^{\prime }\left(t\right)}{S\left(t\right)}.$$ 7

Our benchmark Cox proportional hazards model is

$$\lambda \left(t|Z_i,X_i\right)={\lambda }_0\left(t\right)exp\left({\beta }_0+Z_i\gamma +X_i\beta \right),$$ 8

where λ(t| X_i) is the hazard function for country i on date t, conditioning on a set of endogenous variables Z_i and exogenous variables X_i, and λ₀(t) is the baseline hazard function. In addition to the same set of endogenous and exogenous variables as in the cross-country regression analysis, we also include the endogenous logged peak new mortality rate, log(Peak Mortality_i), to control for the cross-country difference in the peak level of mortality rates. The specification of the Cox Model implies that the effect on the hazard function of a one-unit increase in one covariate w ∈ {Z, X} with coefficient δ is to multiply the hazard function by e^δ, and that the effect on the survival function is to raise it to a power given by the effect on the hazard function

$$S_1\left(t\right)=S_0{\left(t\right)}^{e^{\delta }},$$ 9

where S₁(t) is the survival function on date t for a group with a one-unit higher value of the covariate w, all other variables held constant.

Limitations

We wish to briefly call out the limitations of our research design. First, our estimates cannot (and should not) be interpreted as causal. What we are reporting, across all models, are associations. Some of our variables are endogenous, which may bias our estimates. Moreover, given our choice to investigate country factors one-by-one, our regression estimates may also be biased from omitted variables. To overcome these challenges, we are in the process of collecting additional data at varying levels of detail to help deal with these issues, with the aim of achieving cleaner identification going forward. Nonetheless, under such data constraints, we believe our approach strikes a balance between parsimony, robustness, and informativeness.

Data

Our data relate prudential and reactionary government interventions to COVID-19 mortality rates per capita, controlling for country-specific characteristics. We construct the mortality rates using the John Hopkins Center for Systems Science and Engineering (CSSE) COVID-19 data repository, which details confirmed cases and deaths across our sample period. The seven-day rolling average of the new mortality rate per capita is calculated as the ratio of the cumulative total of country deaths by population, while the seven-day rolling average of the cumulative mortality rate is the ratio of new daily deaths by population.17 This data, which is provided as a global panel at the provincial level, was aggregated to the country-level for the purposes of our estimation. Our full sample considers 59 Advanced Economy (AE) and Emerging Market (EM) countries.18 We choose to exclude developing nations from this first sample for two reasons. First, data quality and availability in these nations is poor over our sample period. Additionally, many of these developing nations experienced lags in the contagion of the virus, thus hitting their peaks later than global hubs like Europe and the United States.19

The central covariates of interest were pulled from Oxford’s COVID-19 Government Response Tracker. As of April 29th, 2020, Oxford provides country-level indicators on containment and closure, economic responses; the quality of health systems; and unorthodox responses to the COVID-19 pandemic.20 Of the 59 countries in our sample, government response data is reported for 55. We focus our estimation on the Stringency Index (SI), which mainly captures variation in government policies related to containment and closure. Each nation is scaled with a composite score from 0 to 100, with higher scores indicating more stringent policy interventions. In our dynamic panel estimation, we lag these interventions by between 2 and 5 weeks to account for delayed implementation or latent effects.

In addition to the Oxford data, we control for various country-specific features using a wide range of publicly available data. We pull country coordinates from Google and integrate data on recent mobility trends from Apple.21 From the World Bank, we gather World Development Indicators for the proportion of the population above age 65; the proportion of the population which is urban; total population density (people per 100 sq. km. of land area); tourist arrivals and departures; the proportion of vulnerable employment; gross national income per capita (calculated in current USD using the Atlas method); the number of cellular subscriptions; current health expenditures; and micrograms of PM2.5 air pollution per capita.22 We also include cross-country indicators of the strength of democracy, from the Economist and Freedom House (2020).23 From the Correlates of War Project, we aggregate data on military expenditures and personnel, iron and steel production, and energy consumption.24 Lastly, we collect data on prior infections and deaths by the disease through the World Health Organization’s International Classifications of Diseases.25 This data is collapsed by country, across the years 2015–2018. The analysis is restricted to deaths by respiratory, endocrine, or high blood pressure conditions. We choose not to incorporate testing covariates, given discrepancies, and measurement error in currently available data.26 Depending on the quality of future data, we may choose to integrate these covariates in our future analyses.

Estimation and Results

We take a multi-faceted approach to understand the cross-country dynamics of pandemic diffusion. As mentioned, the dynamic panel enables us to study to what degree stringency policies are associated with weekly mortality growth rates, and whether such policies start taking effect with a lag. We include the Stringency Index at date t and one-day lagged mortality growth (date t − 1), and then estimate a set of specifications with the independent variable being weekly mortality growth two to four weeks from date t via LSDV.27 Given that residuals within countries are likely correlated, we employ robust standard errors clustered by country.

Then, moving to cross-country analysis we focus on explaining differences in mortality outcomes at the peak of the first quasi-bell curve. For this, we rely on OLS estimation, adjusting the standard errors for heteroscedasticity. Finally, we conduct a cross-country survival analysis to better understand what drives variation in pandemic duration to the first peak (PD) across countries. Initially, we employ a cross-country Kaplan-Meyer analysis on the number of days to the first new mortality peak, subsequently extending it under a Cox proportional hazard model to introduce additional controls, estimated via maximum (partial) likelihood. For robustness, we also test and report whether the proportional hazards assumption is satisfied.

Stringency Policy and Mortality Dynamics

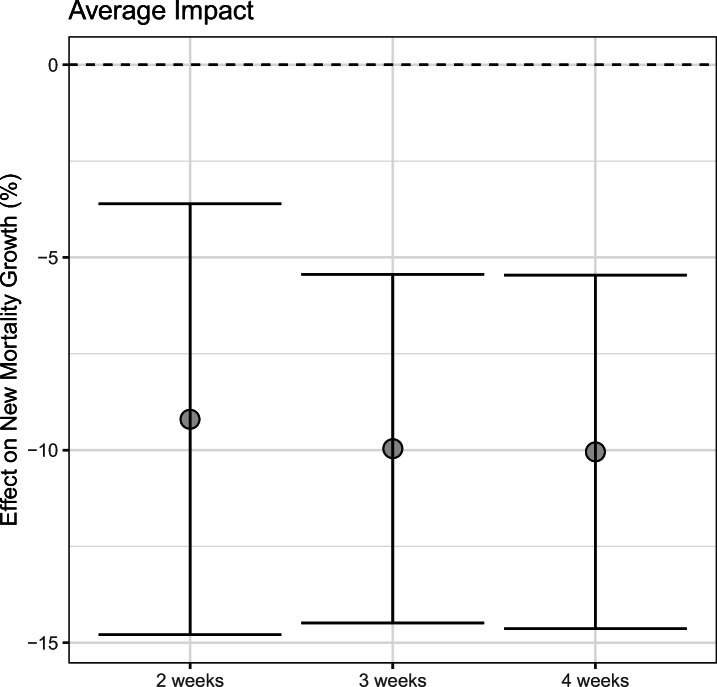
Table 1 reports the baseline results from the local projection regressions (dynamic panel analysis). Notice that across local projection regressions at horizons two to four weeks, Stringency is statistically significant and negative.28 These cursory results suggest that countries administering more stringent pandemic policies realized, on average, significantly lower mortality growth rates, with a lag of two to four weeks (Fig. 6). The estimated effect sizes are also economically significant: countries with a Stringency Index (SI) 10 units higher than average in week W realized mortality growth rates that were on average 22, 17, and 13 percentage points lower in weeks W + 2, W + 3 and W + 4, respectively. While the reductions in growth rates seem quite large (and certainly should not be ignored), it is important to put these numbers in perspective. Given the exponential nature of disease spread, weekly mortality growth rates are highly volatile, potentially reaching anywhere from +50% to +100% (or greater).

Table 1.

Mortality projection – average impact

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.021984***	−0.016790***	−0.012890***
	(0.007866)	(0.004940)	(0.004888)
New Mortality Growth (t-1)	0.103532	0.031686	−0.001775
	(0.074386)	(0.033875)	(0.041413)
Fixed effects?	Y	Y	Y
Observations	1266	929	590
R2	0.086550	0.048007	0.026846
F Statistic	53.818610***	20.372910***	6.648424***

*,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Fig. 6.

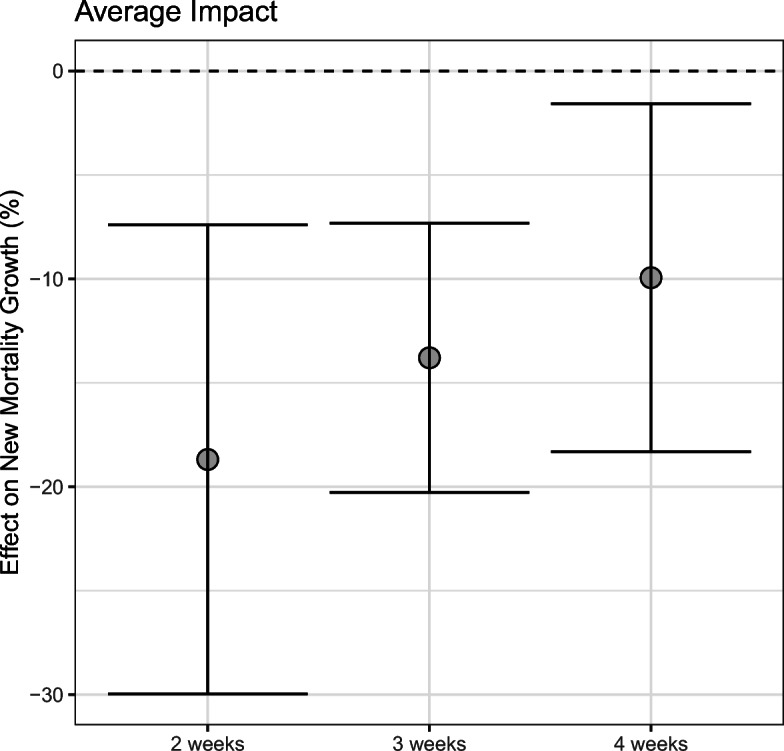
The mortality rate is negatively associated with the intensity of government response. Note: Pooled estimates from local projections are represented as gray circles. Error bars reflect 95% confidence intervals based on HAC-robust standard errors clustered by country

In the baseline analysis (Table 1) we do not explore cross-country heterogeneity in mortality dynamics. However, it is of great interest to understand whether and to what degree stringency policies were more effective in some countries than others in slowing down mortality growth. In the Appendix, we report local projection regression results which allow for the impact of SI to depend on each of our country fundamentals following Eq. 3. We take these country fundamentals as exogenous, as they are from the period pre-COVID-19 and are highly persistent (e.g., population, democracy). Due to the number of country fundamentals we are interested in exploring, we estimate regressions one-by-one. While this yields parsimonious interpretations and preserves degrees of freedom, a key drawback of this approach is that it may suffer from omitted variables. That the estimates of policy stringency became statistically insignificant when its interaction with some of the country fundamentals may suggest that the level of stringency applied was correlated with several pre-conditioning variables in the first-wave of COVID-19.

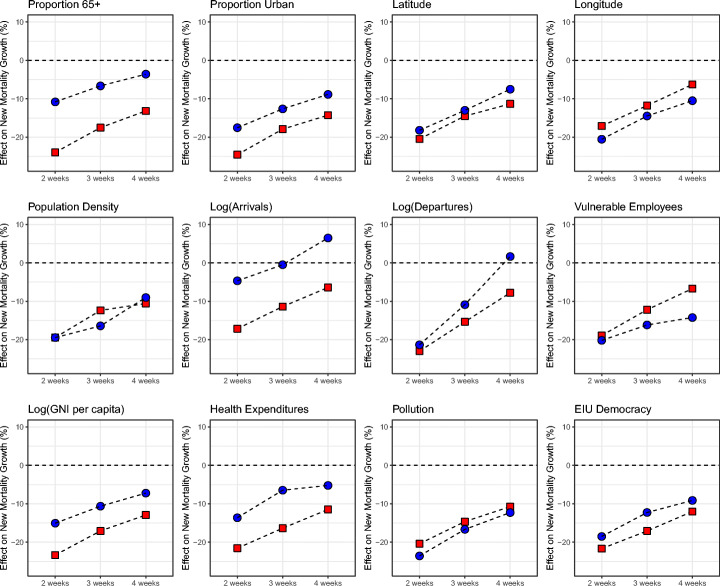
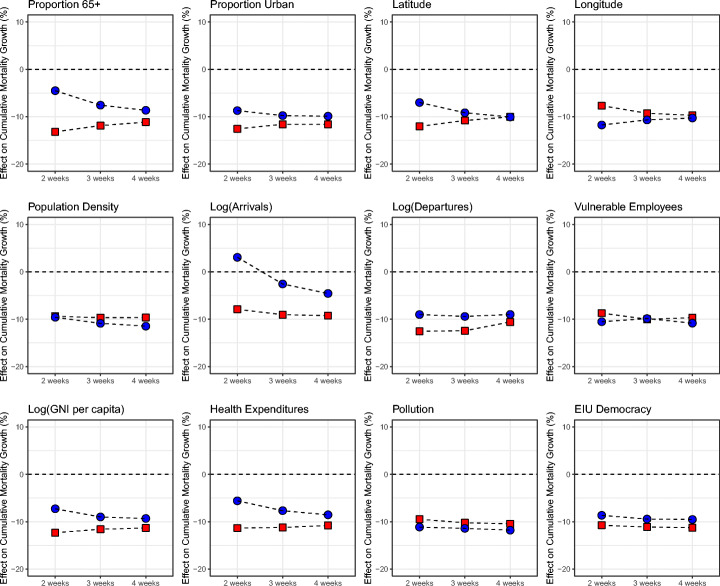
Figure 7 characterizes the results into impulse response plots, highlighting the impact of a 10 unit rise in SI for countries in the 25th percentile of a given characteristic against those in the 75th percentile of the same characteristic. For example, notice that countries in the 75th percentile in terms of proportion elderly (65 or older) saw a much stronger reduction in mortality growth rates from the same 10 unit rise in SI, compared to countries with relatively low proportions of elderly (25th percentile): Countries in the 75th (25th) percentile saw mortality growth rates fall about −25% (−10%) two weeks later. These results are consistent with the proportion of the elderly being a risk factor for the pandemic. Countries may be more susceptible to the pandemic conditional on a greater proportion of the elderly, and for this same reason, stringency policies may be more beneficial in these countries.

Fig. 7.

Mortality impacts: government response, demographics, geography, and development level. Note: Red squares (blue circles) represent the local projection impact from a 10-unit higher stringency index on mortality growth for countries in the 75th percentile (25th percentile) of the country characteristic

We also find that in countries with a higher proportion of urban population, SI measures had a stronger impact on mortality growth than in countries with a lower proportion of urban population. This heterogeneity is be consistent with the proportion of urban population being a risk factor for the pandemic as urban population may face greater exposure possibility. SI policies are also more strongly associated with lower mortality growth in countries with greater international travel arrivals, greater GNI per capita, higher health expenditures, and greater EIU Democracy. While greater international flow is quite an intuitive risk factor for a pandemic like COVID-19, the role of democratic freedom is an ongoing topic of debate. Our results may support the view that greater ex ante individual liberties may be detrimental in the present situation in the sense that they increase the risk of pandemic severity (thereby leading to a stronger effect of mandated SI policies).29 While our results suggest that stringency policies were more impactful among countries that are considered more democratically free, the effectiveness of governments at responding to Covid-19 also depends on other complementary factors, notably leadership and administrative capacity (Ang 2020). The specific channel the association captures is not clear at this point, but it’s possible that countries with higher EIU Democracy scores also exhibit greater ex-ante mobility. Alternatively, it’s possible that there is greater variance in publicly available information among high EIU countries, inducing differential beliefs related to the seriousness of the pandemic. Both scenarios can potentially lead to greater pandemic risk, and therefore greater stringency policy effectiveness.

Kaplan-Meyer Curves of Pandemic Duration-to-Peak across Countries

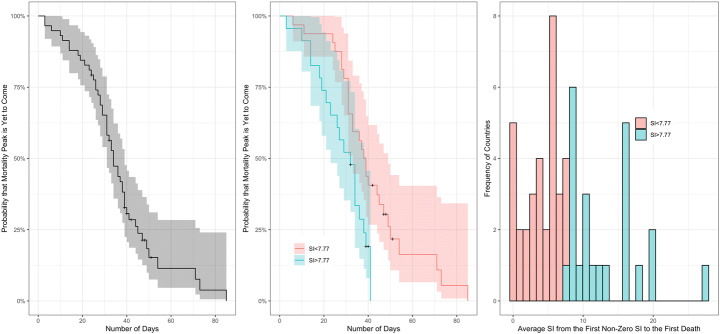
Figure 8 reports Kaplan-Meyer (KP) curves on PD (pandemic duration to the first peak). The Y-axis can be interpreted as the ‘probability of peaking later than day (t)’ or equivalently, as the ‘probability the first peak is yet to come by day (t).’ The LHS plots the unconditional duration probability and shows how the probability the peak is yet to come is decreasing with the number of days since the first death increases (X-axis). About 35 days into the pandemic, the probability of peaking reaches 50%; 45 days into the pandemic, the probability rises to 75%. The center chart plots the KP curves of countries stratified by early SI policy (above versus below average). According to the KP curve, pandemic durations were significantly shorter in countries which proactively issued more stringent policies. That is, for high Early SI countries, the probability of peaking reached 25% by about 35 days while it took close to 50 days for countries with low Early SI policies. The probability of peaking after 40 days is close to 0% for high Early SI countries (virtually all of these countries experienced their first local peak by day 40). For low Early SI countries, it took approximately 80 days, twice the amount of time, until the first peak was reached.

Fig. 8.

Time-to-peak duration analysis of mortality rates. Note: Y-axis indicates the probability the peak mortality/case is ‘yet to come’. The higher y-axis implies a lower probability of peaking. X-axis reflects the number of days since the first mortality/case was realized. Shaded areas represent 95% confidence intervals

Cross-Country Differences in COVID-19 Mortality

Not only is there wide variation in mortality dynamics, but we also observe significant heterogeneity in mortality peaks and curvatures across countries. Cross-section regression results, where the dependent variable is the logged peak new mortality rate (calculated as the deaths/population at the first peak of daily new deaths) are reported in Table 2, column [1]. In addition, we include results for the outcome logged peak new mortality rate to PD (column [2]), and results from the survival analysis via Cox regression on PD itself (column [3]). Several broad patterns emerge.

Table 2.

Explaining cross-country differences in the empirical shape of mortality rate curve from the onset to the local peak of the first pandemic phase

Dependent variable:
	Log(Peak New Mortality Rate)	Log(Peak New Moratlity Rate)-to-PD Ratio	Survival Probability of Mortality Peaking at Time (t)
	OLS	OLS	Cox prop. hazards
	(1)	(2)	(3)
Intercept	−17.751***	−3.487***
	(5.398)	(1.316)
Log(Peak Mortality)			−0.389**
			(0.198)
Log(Early Mortality)	0.231	−0.133**	1.588***
	(0.208)	(0.067)	(0.320)
Early Mortality Growth	0.428***	0.123*	−0.331
	(0.143)	(0.070)	(0.258)
Early SI	−0.120*	−0.009	0.097
	(0.073)	(0.012)	(0.081)
Days between First SI and First Death	0.016	0.001	−0.033*
	(0.015)	(0.003)	(0.019)
Stringency Delta	0.150	0.070	−0.244
	(0.160)	(0.054)	(0.239)
Early Mobility	0.017**	0.001	−0.012
	(0.007)	(0.001)	(0.008)
Prop. 65+	0.036	0.002	0.124**
	(0.045)	(0.009)	(0.050)
Prop. Urban	0.002	−0.002	−0.008
	(0.014)	(0.003)	(0.018)
Pop. Density	−0.0001	−0.00004*	0.0003*
	(0.0001)	(0.00003)	(0.0002)
Vulnerable Emp.	−0.014	−0.003	0.109***
	(0.017)	(0.003)	(0.033)
Log(GNI)	0.519*	0.089	1.008*
	(0.299)	(0.064)	(0.585)
EIU Democracy	−0.011	−0.013	−0.441**
	(0.123)	(0.026)	(0.222)
Latitude:Longitude	−0.0001	0.00001	−0.0005***
	(0.0001)	(0.00001)	(0.0001)
Observations	49	49	49
R2	0.763	0.496	0.788
Adjusted R2	0.674	0.309
Log Likelihood			−89.867
Residual Std. Error	1.018	0.254
F Statistic	8.647***	2.653**
Wald Test			46.790***
LR Test			75.978***
PH Test p value			0.05

*,**,*** correspond to 10%, 5% and 1% significance, respectively

PH Test refers to testing the proportional hazards assumption (Grambsch and Therneau (1994))

Null hypothesis is the assumption is not violated

Standard errors in linear models are Heteroscedastic-Robust standard errors

First, early stringency measures are significantly negatively associated with mortality peaks: Greater early stringency is associated with lower peak mortality rates (column [1], an estimate of −0.12), implying that countries with Early SI 1 unit higher than average realized first mortality peaks that were about −12% lower. Quantitatively, greater policy stringency early on was also associated with flatter mortality curves (column [2]), but the estimate is statistically insignificant. However, there is a significant negative association between logged peak mortality rates and the PD, which implies that more aggressive policy interventions early on may still be associated with a shorter PD through its negative impacts on mortality peaks. Additionally, we find no evidence suggesting that the timing of initial policy interventions is correlated with the peak or slope of mortality curves (columns [1] and [2]). Unsurprisingly, higher early mortality growth rates are significantly associated with higher peak mortalities and steeper mortality curves (columns [1] and [2]), while higher levels of the mortality rate early on were associated with flatter overall mortality curves, but longer pandemic durations to the first peak (columns [2] and [3]). Greater early mobility was significantly associated with higher mortality peaks (columns [1]) and faster response, that is a larger number of days between the first non-zero SI and the first death, was significantly associated with shorter pandemic duration (column [3]). Countries with greater elderly populations, greater population density, and/or greater shares employed in vulnerable sectors saw, on average, significantly longer PDs (column [3]). At the same time, countries scoring higher in EIU Democracy and those further from the equator realized shorter PDs. Higher population density is, somewhat surprisingly, associated with flatter mortality curves (column [2]). However, this association may be driven by the fact that many of the high-density countries are in Asia. These countries contained the spread of COVID-19 relatively effectively, given their preparedness in light of battling SARS in 2003. We find no cross-sectional evidence of increasing SI policies during the pandemic (Stringency Delta) affecting peak mortalities or PD.

The cross-sectional regression and survival analysis results, taken together with the evidence from local projections in our dynamic panel analysis, indicate (but do not assert) that 1) aggressive policy responses may have helped slow down the growth rate of new mortalities with a lag, 2) having stringent policies in place early may have helped to lower peak mortality rates and PD (through reducing peak mortality rates). In contrast, evidence on the effectiveness of increasing the SI after the fact (via Stringency Delta) on peak mortality is much weaker.

Discussion and Robustness

To summarize, we investigate the impact of stringency policies on mortality growth dynamics, along with cross-country patterns in the empirical shape of the mortality curve. First, we find that higher SI levels were significantly associated with lower mortality growth rates with a lag of 2, 3, and 4 weeks. The effect of a 10-unit rise in the SI levels on future mortality growth was stronger in countries that appear to be more vulnerable ex-ante to COVID-19 type breakouts: countries with greater elderly populations, cooler temperatures, more international travel flow, and higher levels of the EIU Democracy index. In terms of peak mortality rates across countries, we find that proactive stringency policies (Early SI) – those already in place prior to the first reported mortality - were significantly associated with lower mortality peaks, while higher mobility levels were significantly associated with higher mortality peaks. As for pandemic duration-to-first peak, higher mobility levels were associated with shorter average pandemic durations (despite higher mortality peaks), while greater elderly population and greater shares of employment in vulnerable sectors were associated with longer average pandemic durations. Estimates from a Kaplan-Meyer analysis indicate that proactive stringency policies early on were associated with significantly shorter PD.

We have conducted several robustness checks. First, to explore the potential nonlinear effect of SI on weekly new mortality growth, we replace the level variable of SI in the local projection method by the logarithm transformation of SI. Results are similar to our main findings: there were significantly negative associations between weekly new mortality growth and the log(SI) at horizons two to four weeks. Specifically, a 10 % increase in SI was associated with 7.1, 5.8, and 4.7 percentage points decrease in weekly new mortality growth rates, at horizon two, three and four weeks, respectively. These results suggest nonlinearity in the effects of SI on weekly new mortality growth rates: an increase in SI when the SI level is low is likely to have a greater effect on reducing mortality growth rates. Such nonlinearity is also consistent with the finding in the cross-sectional analysis that countries had a greater average SI before the first death saw a lower new mortality rate at the peak. Second, in addition to closure and containment measures, the SI constructed by Oxford COVID-19 Government Response Tracker considers public information campaigns, which may be argued as different from closure and containment measures. Hence, we check this by constructing an alternative SI excluding the public information campaigns. Additionally, we construct a second alternative SI which only consists of domestic closure and containment measures,30 as many countries implemented international travel restrictions early and aggressively while not carrying out domestic closure and containment policies. Results using these alternative SIs are similar to our main findings: alternative measures of stringency were significantly and negatively associated with weekly new mortality growth, at horizons two to four weeks. Third, we experiment with including lagged SI as controls and find similar results.31

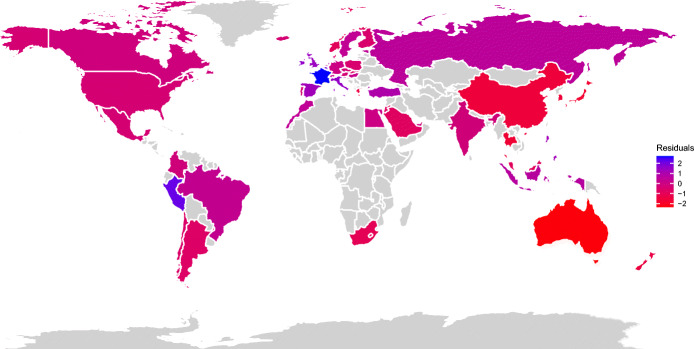
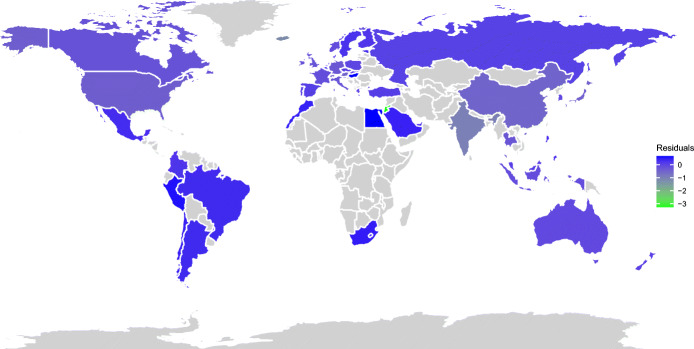
In the Appendix, we also report a robustness check using growth in cumulative mortalities (as opposed to growth in new mortalities) and a first pass at a residual analysis based on our benchmark estimation, identifying countries which appear to be statistical outliers.32 There are countries oft-cited in the public discussion as exceptionally better or worse than predicted in terms of their infection and mortality rates, several of which are consistent with the residuals in our estimation. The contributing factors are likely to be many, including that several of these countries previously experienced recent outbreaks, including SARS-CoV-1 (2002–2004). These include: (i) mortality rates worse than expected: Brazil, Ecuador, Iran, Italy, Peru, United States; (ii) mortality rates better than expected: Cambodia, Greece, India, Indonesia, Iraq, Japan, Lebanon, Myanmar, South Korea, Sub-Saharan Africa (including Ebola-affected areas), Thailand, Venezuela, Vietnam. Japan, for example, offers an interesting case study with its proximity to the initial hotspots (China and South Korea), but is currently cited as successfully managing the infection and mortality rates without lockdown or mass testing (Bloomberg 2020). Additionally, the degree of enforcement of policy intervention rules may be of great importance in explaining the cross-country difference in the empirical shape of the mortality curve, which, however, lacks data to measure. As the pandemic continues to unfold and as new data comes in, we’ll continue the process of analyzing these exceptional cases for country-specific factors underlying their mortality rates from COVID-19.

Related Studies

Avery et al. (2020) provide an overview of the modeling of the spread of COVID-19. By and large, the ongoing challenges surround data on the infection rates. As noted by Manski and Molinari (2020), because of missing data on tests for infection and imperfect accuracy of tests, reported rates of population infection by the SARS CoV-2 virus are lower than actual rates of infection, resulting in infection fatality rates that are lower than reported. In addition, as argued by Atkeson (2020), in the presence of effective mitigation measures, the model with a high initial number of active cases and a low fatality rate gives the same predictions for the evolution of the number of deaths in the early stages of the pandemic as the same model with a low initial number of active cases and a high fatality rate. Modeling the COVID-19 infection also face with uncertainty about the evolution of infection rates, due to parameter uncertainty and the realization of future shocks (Liu et al. 2020). To ameliorate these empirical challenges, our study uses the mortality rate per capita as the main variable of interest. In this section, we synthesize our estimates with findings from related studies in the field. Notwithstanding different empirical specifications across studies, we find our main results are consistent and communicable with the literature and offer valuable new evidence.

Mortality Rates

Closely related to our study are The Economist (2020), Stojkoski et al. (2020) and Castex et al. (2020). The Economist’s review uses a sample of U.S. states focusing on the case-fatality rate. It finds the following associations between the case-fatality rate and the listed variables, ordered by their significance (one standard deviation increase): median age (pos.), ICU beds per 100,000 people (neg.), population density (pos.), and median income (neg.), the prevalence of heart disease, diabetes and smoking (pos.), the share of the population that is African-American (pos.), and amount of social distancing three weeks prior (neg.). Stojkoski et al.’s study finds that greater government intervention, measured by a slight variant of the stringency index used in our research, is associated lower mortality per capita. Our results are consistent with this. Given our most comprehensive specification in the cross-country estimates, we find a significant association between the stringency index and the mortality rate peak levels (Table 2, column [1]). An increase of 1 unit of the stringency index is statistically associated with −12% decrease in the first peak mortality rate (Table 2, column [1]). Our cross-country results revealing heterogeneity effects of government interventions on COVID-19 mortality growth rates also relate to those findings of Castex et al. (2020) on the COVID-19 transmission rates; that the effectiveness of non-pharmaceutical interventions (such as school and workplace closures) is increasing with lower air pollution and higher health expenditure. They also find that the effectiveness of such interventions is declining with higher proportion of elderly population, which seems to contradict with our results. One potential reason could be the dependent variables are different, with us focusing on mortality rates and them focusing on transmission rates.33

Demographics and Culture

Our study finds supportive evidence for the role of the aging population, urbanization, pre-existing conditions, mortality from high-blood pressure, obesity, diabetes, and trust. The findings are consistent with case studies on the association between social networks and COVID-19 infection. Kuchler et al. (2020) find in Facebook data that areas with stronger social ties to two early COVID-19 “hotspots” (Westchester County, NY, in the U.S. and Lodi province in Italy) generally have more confirmed COVID-19 cases, after controlling for geographic distance to the hotspots as well as for the income and population density of the regions. Allcott et al. (2020) find in location data from a large sample of smartphones to show that areas with more Republicans engage in less social distancing (controlling for other factors including state policies, population density, and local COVID cases and deaths, pointing to significant gaps between Republicans and Democrats in beliefs about personal risk and the future path of the pandemic. Fetzer et al. (2020) find that the perception of a weak government and public response is associated with higher levels of worries and depression, and those strong government reactions correct misperceptions and reduce worries and depression. Our findings on the association between trust, the stringency index, and mortality from COVID-19 yield consistent messages along this line.

Geography

We find that the mortality growth rates are associated with the impact of stringency policies interacted with distance from the equator: countries in higher latitude appear to benefit more from stringency policies, as they are associated with lower mortality growth from an equivalent rise in stringency relative to countries which lie closer to the equator. This evidence suggests that geographic location may be a potential COVID-related risk factor such that stringency measures are more effective in higher risk, high latitude countries. The finding is consistent with evidence linking temperatures to the spread of influenza. Slusky and Zeckhauser (2019) find that sunlight strongly protects against influenza, a relationship driven by sunlight in late summer, and early fall (when there are sufficient quantities of both sunlight and influenza activity).

Government Policies

Across countries, our estimates suggest that government policy, institutions, and the intensity of government response to COVID-19 are negatively associated with the mortality per capita. This evidence reflects in the coefficient estimates of stringency index, government effectiveness, democracy, health expenditures, vulnerable employees, capita GNI, and level pollution. These cross-country findings are consistent with several case studies of COVID-19. Dave et al. (2020) find in the data of U.S. states that approximately three weeks following the adoption of a Shelter-in-Place Orders (SIPO), cumulative COVID-19 cases fell by 44% and, in an event-study analysis, that SIPO-induced case reductions grew larger over time, with the early adopters and high population density states appear to reap larger benefits from their SIPOs, though the estimated mortality reduction effects were imprecisely estimated. This finding is consistent with our estimates of the stringency index under the local projection approach.

Our finding in the cross-country data on the importance of the extent of vulnerable employees is largely consistent with the evidence from influenza. Markowitz et al. (2019) find in the U.S. data that a one percentage point increase in the employment rate increases the number of influenza-related doctor visits by about 16%; these effects are highly pronounced in the retail sector and healthcare sector, the sectors with the highest levels of interpersonal contact. Clay et al. (2018) find evidence on the link between air pollution and influenza infection and suggest that poor air quality was an important cause of mortality during the pandemic.

The empirical issues remain on the endogeneity of mobility and in-bound/out-bound travels to government response in the estimation. For instance, Gupta et al. (2020) find that mobility fell substantially in all the U.S. states, even ones that have not adopted major distancing mandates. They find that there is little evidence, for example, that stay-at-home mandates induced distancing; in contrast, early and information-focused actions have had bigger effects. Their event studies show that first case announcements, emergency declarations, and school closures reduced mobility by 1–5% after 5 days and 7–45% after 20 days. We are in the process of addressing endogenous regressors in our estimation (policy stringency, lagged mortality, and mobility) with more updated data.

Future Research and Closing Remarks

We conclude by cautioning that our results are subject to data limitations, including undercounts of COVID-19 infections and mortality. ‘Better or worse performance’ of a country in the first phase of the pandemic does not guarantee similar future outcomes. The levels of COVID-19 policy stringency applied in the first wave were correlated with several pre-conditions [aging population, urbanization, travels, income, health spending, and democracy], the correlations that might influence the policy efficiency in the following wave(s) if any (Table 3). Flattening the mortality and infection curves may shift mortality and painful adjustment forwards. Premature opening of the economy without proper testing, contact-tracing, and selective quarantines of vulnerable or impacted segments of the population may induce future acceleration of the pandemic (Acemoglu et al. 2020). More medical research and advances towards better treatment and possible vaccinations, the quality of local and global public policies, and adjustment capabilities of countries will determine future dynamics of the pandemic (Lipsitch et al. 2020).

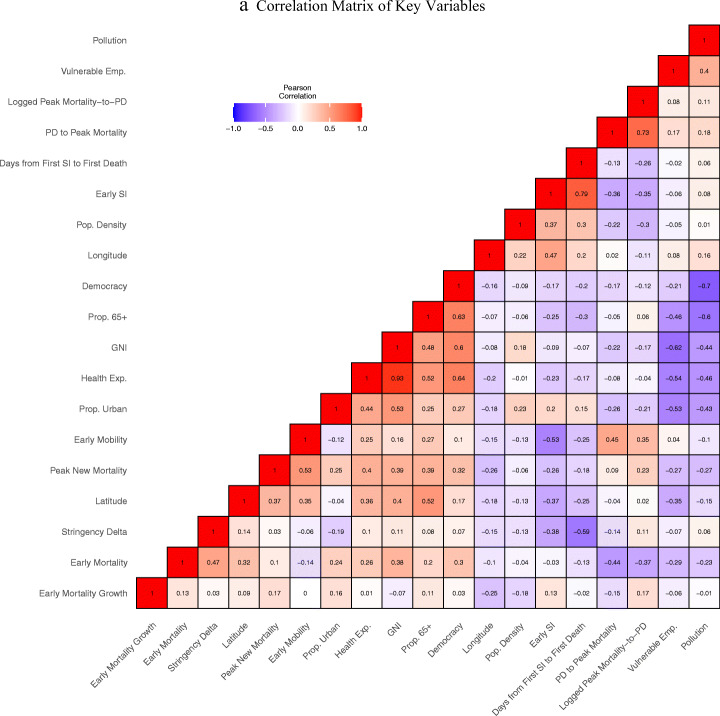
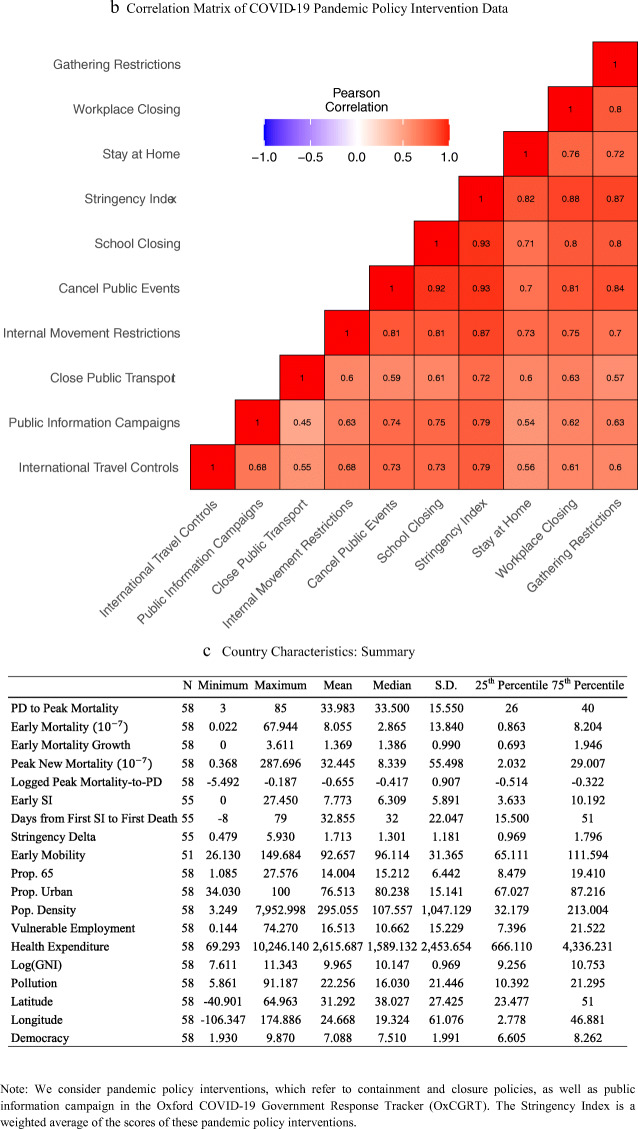
Table 3.

Correlations of mortality rates, government responses, and country characteristics

Appendix

Supplemental Results of Baseline Panel Analysis on New Mortality Growth Rate

Table 4.

Variable definitions and sources

Variable	Definition	Source
New Mortality Rate	7-day rolling average of daily new mortality rate out ot the total population	Authors’ calculation based on JHU COVID-19 Data
Early Mortality	Cumulative mortality rate in the week following the first death	Authors’ calculation based on JHU COVID-19 Data
Early Mortality Growth	Growth rate of new mortality rate in the week following the first death	Authors’ calculation based on JHU COVID-19 Data
Peak New Mortality	New mortality rate at the peak of new mortality rate in the first quasi-bell curve	Authors’ calculation based on JHU COVID-19 Data
PD to Peak Mortality	Day-to-peak of new mortality rate in the first quasi-bell curve	Authors’ calculation based on JHU COVID-19 Data
Logged Peak Mortality-to-PD	The ratio of the logged peak new mortality rate to the PD to peak mortality	Authors’ calculation based on JHU COVID-19 Data
Early SI	Average of SI from its first non-zero value to the first death	Authors’ calculation based on OxCGRT Data
Days from First SI to First Death	Number of days from first non-zero SI to the first death	Authors’ calculation based on OxCGRT Data
Stringency Delta	Growth rate of SI from its first non-zero value to its maximum level	Authors’ calculation based on OxCGRT Data
Early Mobility	Weekly average level of mobility in terms of walking in the week prior to the first death, reported by Apple	Authors’ calculation based on Apple COVID-19 Mobility Trends Reports
Prop. 65+	Elderly population (people aged 65 and over) as a percentage of the total population	World Development Indicators
Prop. Urban	Urban population as a percentage of the total population	World Development Indicators
Pop. Density	Midyear population divided by land area in square kilometers	World Development Indicators
Vulnerable Employment	Employment in vulnerable sectors (i.e., family workers and own-account workers) as a percentage of the total employment	World Development Indicators
Health Expenditure	Level of current health expenditure (including healthcare goods and services) as a percentage of GDP	World Development Indicators
Log(GNI)	The logged gross national income per capita	World Development Indicators
Pollution	Population-weighted exposure to ambient PM2.5 pollution	World Development Indicators
Tourist Arrivals	International inbound tourists to the country	World Development Indicators
Tourist Departures	International outbound tourists from the country	World Development Indicators
Latitude	Latitude coordinate of the country	Country-level coordinates from Google
Longitude	Longitude coordinate of the country	Country-level coordinates from Google
Democracy	The Democracy index calculated by The Economist Intelligence Unit (2019)	The EIU Democracy Index 2019 Database

Table 5.

Mortality Projection – Proportion of Age above 65 Population

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.001006	0.001458	0.003538
	(0.011664)	(0.005207)	(0.007936)
New Mortality Growth (t-1)	0.070344	−0.011277	−0.042271
	(0.062111)	(0.047846)	(0.050568)
Stringency (t) X Proportion 65+	−0.001184**	−0.000978**	−0.000861
	(0.000575)	(0.000414)	(0.000576)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.072771	0.037506	0.020423
F Statistic	29.954000***	10.534230***	3.363587**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 6.

Mortality Projection – Proportion of Urban Population

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.005617	0.004818	0.009061
	(0.016953)	(0.008169)	(0.011368)
New Mortality Growth (t-1)	0.085230	0.001939	−0.029877
	(0.062211)	(0.044643)	(0.046623)
Stringency (t) X Proportion Urban	−0.000349*	−0.000262**	−0.000270
	(0.000211)	(0.000127)	(0.000188)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.070766	0.034867	0.019492
F Statistic	29.065970***	9.766239***	3.207170**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 7.

Mortality Projection – Latitude

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.016482**	−0.011871***	−0.004601
	(0.008083)	(0.004488)	(0.005173)
New Mortality Growth (t-1)	0.083068	0.000937	−0.034184
	(0.062968)	(0.045434)	(0.053642)
Stringency (t) X Latitude	−0.000078	−0.000052	−0.000132
	(0.000090)	(0.000069)	(0.000103)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.063921	0.030954	0.017270
F Statistic	26.062620***	8.635236***	2.835236**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 8.

Mortality Projection – Longitude

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.020795***	−0.014686***	−0.010800***
	(0.006198)	(0.003615)	(0.003809)
New Mortality Growth (t-1)	0.083229	0.001601	−0.024742
	(0.064252)	(0.042077)	(0.050609)
Stringency (t) X Longitude	0.000075*	0.000059	0.000092**
	(0.000040)	(0.000052)	(0.000046)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.067552	0.033238	0.020290
F Statistic	27.650070***	9.294305***	3.341238**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 9.

Mortality Projection – Population Density

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.019453***	−0.017125***	−0.008746
	(0.006640)	(0.004184)	(0.006033)
New Mortality Growth (t-1)	0.088915	0.008777	−0.027667
	(0.060622)	(0.041849)	(0.048828)
Stringency (t) X Population Density	0.000000	0.000021**	−0.000008
	(0.000001)	(0.000010)	(0.000023)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.062949	0.035617	0.015586
F Statistic	25.639490***	9.984036***	2.554293*

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 10.

Mortality Projection – Travel Arrivals

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.111648**	0.101309**	0.126787***
	(0.054341)	(0.042350)	(0.044481)
New Mortality Growth (t-1)	0.058664	−0.019535	−0.051550
	(0.061179)	(0.044369)	(0.049817)
Stringency (t) X Log(Arrivals)	−0.007603**	−0.006653***	−0.007863***
	(0.003025)	(0.002429)	(0.002605)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.074203	0.038917	0.025531
F Statistic	30.590740***	10.946500***	4.226886***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 11.

Mortality Projection – Travel Departures

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.007286	0.026951	0.081786*
	(0.068928)	(0.054669)	(0.046774)
New Mortality Growth (t-1)	0.094169	−0.003565	−0.040745
	(0.060496)	(0.043595)	(0.044961)
Stringency (t) X Log(Departures)	−0.000935	−0.002519	−0.005335**
	(0.004070)	(0.003104)	(0.002669)
Fixed effects?	Y	Y	Y
Observations	1145	850	546
R2	0.082130	0.039163	0.018646
F Statistic	30.482630***	9.986145***	2.799441**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 12.

Mortality Projection – Vulnerable Employees

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.020826***	−0.018219***	−0.018106**
	(0.005034)	(0.006186)	(0.007128)
New Mortality Growth (t-1)	0.088387	0.002826	−0.031370
	(0.062288)	(0.044618)	(0.046253)
Stringency (t) X Vulnerable Employees	0.000088	0.000276	0.000523*
	(0.000208)	(0.000292)	(0.000316)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.063244	0.033579	0.025218
F Statistic	25.767680***	9.392848***	4.173833***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 13.

Mortality Projection – Income Level

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.035894	0.028850	0.027754
	(0.031427)	(0.018368)	(0.024123)
New Mortality Growth (t-1)	0.085178	0.002606	−0.028715
	(0.061755)	(0.046563)	(0.047679)
Stringency (t) X Log(GNI per capita)	−0.005514*	−0.004273**	−0.003785
	(0.003015)	(0.001985)	(0.002624)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.071900	0.036131	0.019462
F Statistic	29.567720***	10.133590***	3.202166**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 14.

Mortality Projection – Health Expenditures

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.012473	−0.005034**	−0.004308
	(0.008092)	(0.002565)	(0.003159)
New Mortality Growth (t-1)	0.090457	0.009770	−0.021132
	(0.062357)	(0.044787)	(0.045583)
Stringency (t) X Health Expenditures	−0.000002	−0.000003***	−0.000002
	(0.000001)	(0.000001)	(0.000001)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.070173	0.042075	0.019817
F Statistic	28.804070***	11.873970***	3.261793**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 15.

Mortality Projection – Pollution

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.026185***	−0.018337***	−0.013563**
	(0.006261)	(0.004334)	(0.005423)
New Mortality Growth (t-1)	0.086254	0.004577	−0.026531
	(0.061609)	(0.044548)	(0.048239)
Stringency (t) X Pollution	0.000251***	0.000160**	0.000122
	(0.000090)	(0.000067)	(0.000084)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.075104	0.035749	0.018264
F Statistic	30.992370***	10.022320***	3.001416**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 16.

Mortality Projection – Level of Democracy

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.005800	0.007013	0.002435
	(0.018837)	(0.008324)	(0.009397)
New Mortality Growth (t-1)	0.090181	0.006915	−0.025264
	(0.062633)	(0.045217)	(0.047252)
Stringency (t) X EIU Democracy	−0.001934	−0.002936**	−0.001761
	(0.002256)	(0.001468)	(0.001598)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.066536	0.038840	0.018083
F Statistic	27.204670***	10.924170***	2.971115**

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Robustness Results of Panel Analysis on New Mortality Growth Rate

Table 17.

Mortality Projection – Average Impact (Logged SI)

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Logged Stringency (t)	−0.710909**	−0.577075***	−0.470731***
	(0.335622)	(0.187711)	(0.161767)
New Mortality Growth (t-1)	0.087405	0.008859	−0.013496
	(0.067062)	(0.041834)	(0.042783)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.044177	0.028483	0.018888
F Statistic	26.483640***	11.903000***	4.668460***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Note: Specification is same as the benchmark, except that the level measure of SI is replaced by the logarithm transformation of SI. Results are similar to those in the benchmark

Table 18.

Mortality Projection – Average Impact (Alternative SI [1])

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.018912***	−0.014804***	−0.012165***
	(0.006718)	(0.004319)	(0.004504)
New Mortality Growth (t-1)	0.093227	0.029326	−0.006721
	(0.074240)	(0.037322)	(0.040538)
Fixed effects?	Y	Y	Y
Observations	1297	938	592
R2	0.079926	0.044409	0.028367
F Statistic	50.601290***	18.960860***	7.050716***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Note: Specification is same as the benchmark, except that the SI is replaced by an alternative excluding the public information campaigns. Results are similar to those in the benchmark

Table 19.

Mortality Projection Average Impact (Alternative SI [2])

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.017395***	−0.013944***	−0.010151***
	(0.006038)	(0.004169)	(0.003723)
New Mortality Growth (t-1)	0.092050	0.029785	−0.010423
	(0.071946)	(0.037462)	(0.040227)
Fixed effects?	Y	Y	Y
Observations	1297	938	592
R2	0.085334	0.048988	0.024230
F Statistic	54.344330***	21.016790***	5.996885***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Note: Specification is same as the benchmark, except that the SI is replaced by an alternative excluding the public information campaigns and international travel restrictions. Results are similar to those in the benchmark

Table 20.

Mortality Projection – Average Impact (Lagged SI)

Dependent variable:
	Weekly New Mortality Growth (t + 14)	Weekly New Mortality Growth (t + 21)	Weekly New Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.013319**	−0.010201***	−0.007504*
	(0.005999)	(0.003345)	(0.004347)
Stringency (t-1)	−0.006240**	−0.003815	−0.002709
	(0.002865)	(0.002528)	(0.003899)
New Mortality Growth (t-1)	0.087064	0.004278	−0.024800
	(0.060272)	(0.043168)	(0.046638)
Fixed effects?	Y	Y	Y
Observations	1276	933	593
R2	0.065489	0.031600	0.015925
F Statistic	26.746620***	8.821250***	2.610737*

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Note: Specification is same as the benchmark, except that a one-day lagged SI is added. Results are similar to those in the benchmark

Table 21.

Mortality Projection – Average Impact

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.009200***	−0.009962***	−0.010049***
	(0.002854)	(0.002310)	(0.002342)
Cum. Mortality Growth (t-1)	0.055148	0.017638	−0.027729
	(0.046278)	(0.031291)	(0.024830)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.122776	0.214357	0.300179
F Statistic	88.734250***	125.235100***	124.391700***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 22.

Mortality Projection – Proportion of Age above 65 Population

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.001965	−0.004367	−0.006794*
	(0.002812)	(0.003560)	(0.003727)
Cum. Mortality Growth (t-1)	0.022421	0.000552	−0.039041
	(0.046730)	(0.029896)	(0.030053)
Stringency (t) X Proportion 65+	−0.000781***	−0.000387*	−0.000224
	(0.000153)	(0.000227)	(0.000208)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.189555	0.239247	0.310549
F Statistic	98.779660***	96.128210***	86.933060***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 23.

Mortality Projection – Proportion of Urban Population

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.004059	−0.003662	−0.004190
	(0.006513)	(0.006154)	(0.005651)
Cum. Mortality Growth (t-1)	0.038079	0.008961	−0.036625
	(0.048777)	(0.030359)	(0.027817)
Stringency (t) X Proportion Urban	−0.000192**	−0.000092	−0.000086
	(0.000095)	(0.000088)	(0.000080)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.153645	0.224490	0.310667
F Statistic	76.669000***	88.482590***	86.980680***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 24.

Mortality Projection – Latitude

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.003163	−0.007922***	−0.010059***
	(0.003043)	(0.002473)	(0.002792)
Cum. Mortality Growth (t-1)	0.030825	0.010153	−0.027692
	(0.047107)	(0.031320)	(0.028863)
Stringency (t) X Latitude	−0.000175***	−0.000057*	0.0000003
	(0.000052)	(0.000030)	(0.000056)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.168633	0.221070	0.300179
F Statistic	85.665170***	86.751910***	82.784910***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 25.

Mortality Projection – Longitude

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.012039***	−0.010779***	−0.010322***
	(0.003002)	(0.002483)	(0.002485)
Cum. Mortality Growth (t-1)	0.021155	0.005929	−0.032775
	(0.050295)	(0.030332)	(0.028980)
Stringency (t) X Longitude	0.000089***	0.000030*	0.000012
	(0.000015)	(0.000018)	(0.000022)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.207271	0.228580	0.302867
F Statistic	110.425100***	90.572260***	83.848020***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 26.

Mortality Projection Population Density

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.009641***	−0.011080***	−0.011782***
	(0.002961)	(0.002783)	(0.003231)
Cum. Mortality Growth (t-1)	0.054927	0.016861	−0.029213
	(0.046076)	(0.029851)	(0.023432)
Stringency (t) X Population Density	0.000001*	0.000006	0.000010
	(0.000001)	(0.000004)	(0.000010)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.126515	0.220220	0.306982
F Statistic	61.170710***	86.324130***	85.492120***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 27.

Mortality Projection Travel Arrivals

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.105422***	0.057881**	0.038960*
	(0.021222)	(0.025567)	(0.019903)
Cum. Mortality Growth (t-1)	0.014701	−0.005585	−0.046564*
	(0.042305)	(0.025237)	(0.025268)
Stringency (t) X Log(Arrivals)	−0.006690***	−0.003951***	−0.002845**
	(0.001261)	(0.001513)	(0.001119)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.241832	0.276938	0.339263
F Statistic	134.711500***	117.072500***	99.097950***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 28.

Mortality Projection – Travel Departures

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.020893	0.016164	0.004469
	(0.046732)	(0.033627)	(0.026610)
Cum. Mortality Growth (t-1)	0.043333	−0.021901	−0.041557
	(0.041034)	(0.026964)	(0.028191)
Stringency (t) X Log(Departures)	−0.001991	−0.001703	−0.000896
	(0.002733)	(0.001955)	(0.001594)
Fixed effects?	Y	Y	Y
Observations	1230	922	606
R2	0.288212	0.446255	0.450532
F Statistic	149.278200***	216.246000***	136.656900***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 29.

Mortality Projection – Vulnerable Employees

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.011462***	−0.009805***	−0.011427***
	(0.003532)	(0.003203)	(0.003021)
Cum. Mortality Growth (t-1)	0.045639	0.018350	−0.034410
	(0.049659)	(0.029842)	(0.027895)
Stringency (t) X Vulnerable Employees	0.000126	−0.000009	0.000080
	(0.000125)	(0.000102)	(0.000090)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.131440	0.214422	0.306190
F Statistic	63.912280***	83.430920***	85.174300***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 30.

Mortality Projection – Income Level

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	0.023814**	0.006932	0.003056
	(0.011607)	(0.011471)	(0.010972)
Cum. Mortality Growth (t-1)	0.035574	0.007080	−0.037246
	(0.047994)	(0.030226)	(0.028383)
Stringency (t) X Log(GNI per capita)	−0.003363***	−0.001723	−0.001339
	(0.001248)	(0.001194)	(0.001133)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.166610	0.231623	0.312807
F Statistic	84.431930***	92.141630***	87.852690***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 31.

Mortality Projection – Health Expenditures

	Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.004753*	−0.007166***	−0.008221***
	(0.002802)	(0.002495)	(0.002472)
Cum. Mortality Growth (t-1)	0.040067	0.008104	−0.034544
	(0.050194)	(0.030674)	(0.026221)
Stringency (t) X Health Expenditures	−0.000002**	−0.000001	−0.000001
	(0.000001)	(0.000001)	(0.0000004)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.166622	0.239285	0.312900
F Statistic	84.439430***	96.148390***	87.890620***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 32.

Mortality Projection – Pollution

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.012509***	−0.012391***	−0.012884***
	(0.002950)	(0.002463)	(0.002850)
Cum. Mortality Growth (t-1)	0.055933	0.019301	−0.025354
	(0.047249)	(0.032324)	(0.026997)
Stringency (t) X Pollution	0.000131***	0.000094**	0.000105***
	(0.000050)	(0.000046)	(0.000032)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.147707	0.234290	0.331865
F Statistic	73.192440***	93.527020***	95.863660***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 33.

Mortality Projection Level of Democracy

Dependent variable:
	Cum. Mortality Growth (t + 14)	Cum. Mortality Growth (t + 21)	Cum. Mortality Growth (t + 28)
	(1)	(2)	(3)
Stringency (t)	−0.000268	−0.002780	−0.002562
	(0.008155)	(0.005876)	(0.004129)
Cum. Mortality Growth (t-1)	0.053390	0.015681	−0.030187
	(0.048881)	(0.032354)	(0.026039)
Stringency (t) X EIU Democracy	−0.001277	−0.001015	−0.001059
	(0.001078)	(0.000792)	(0.000665)
Fixed effects?	Y	Y	Y
Observations	1399	1040	689
R2	0.135608	0.226321	0.315627
F Statistic	66.256860***	89.415500***	89.009980***

Note: *,**,*** correspond to 10%, 5% and 1% significance, respectively

HAC robust standard errors, clustered by country. Time and Country FEs

Table 34.

List of Countries that are the Most Over-Predicted and Under-Predicted

(a) Top Five Over-Predicted Countries		(b) Top Five Under-Predicted Countries
Country	Residual	Country	Residual
Australia	−2.343	France	2.715
Japan	−1.670	Peru	2.207
Thailand	−1.580	Belgium	2.140
Korea, South	−1.542	Kuwait	1.862
China	−1.479	Ireland	1.589

Note: Residuals are calculated from cross-country regression specified in Column [1] of Table 2, with the omission of the “Early Mobility” for a greater country coverage

Table 35.

List of Countries that are the Most Over-Predicted and Under-Predicted

(a) Top Five Over-Predicted Countries		(b) Top Five Under-Predicted Countries
Country	Country	Residual
Jordan	Egypt	0.682
Iceland	Hungary	0.667
India	Kuwait	0.633
China	Peru	0.601
Austria	Belgium	0.546

Note: Residuals are calculated from cross-country regression specified in Column [1] of Table 2, with the omission of the “Early Mobility” for a greater country coverage

Robustness Results of Panel Analysis on Cumulative Mortality Growth Rate

Fig. 9.

The cumulative mortality growth rate is negatively associated with the intensity of government response. Note: Results of panel analysis on cumulative mortality growth rates. Pooled estimates from local projections are represented as gray circles. Error bars reflect 95% confidence intervals based on HAC-robust standard errors clustered by country

Fig. 10.

Cumulative mortality growth impacts: government response, demographics, geography, and development level. Note: Results of panel analysis on cumulative mortality growth rates. Red squares (blue circles) represent the local projection impact from a 10-unit higher stringency index on mortality growth for countries in the 75th percentile (25th percentile) of the country characteristic

Results of Residual Analysis

Fig. 11.

Global Distribution of Residuals of Cross-Country Analysis - Peak Mortality Rate. Note: Residuals are calculated from cross-country regression specified in Column [1] of Table 2, with the omission of the “Early Mobility” for a greater country coverage

Fig. 12.

Global Distribution of Residuals of Cross-Country Analysis - Peak Mortality Rate-to-PD Ratio. Note: Residuals are calculated from cross-country regression specified in Column [1] of Table 2, with the omission of the “Early Mobility” for a greater country coverage

Data Availability and Code Availability

Data and codes available at Github Repository: https://github.com/snairdesai/COVID-19.