Abstract
The thickness of the cerebral cortical sheet and its surface area are highly heritable traits thought to have largely distinct polygenic architectures. Despite large-scale efforts, the majority of their genetic determinants remain unknown. Our ability to identify causal genetic variants can be improved by employing brain measures that better map onto the biology we seek to understand. Such measures may have fewer variants but with larger effects, that is, lower polygenicity and higher discoverability. Using Gaussian mixture modeling, we estimated the number of causal variants shared between mean cortical thickness and total surface area, as well as the polygenicity and discoverability of regional measures. We made use of UK Biobank data from 30 880 healthy White European individuals (mean age 64.3, standard deviation 7.5, 52.1% female). We found large genetic overlap between total surface area and mean thickness, sharing 4016 out of 7941 causal variants. Regional surface area was more discoverable (P = 2.6 × 10−6) and less polygenic (P = 0.004) than regional thickness measures. These findings may serve as a roadmap for improved future GWAS studies; knowledge of which measures are most discoverable may be used to boost identification of genetic predictors and thereby gain a better understanding of brain morphology.
Keywords: cortical thickness, parcellation, pleiotropy, polygenicity, surface area
Introduction
The morphology of the human cerebral cortex is highly heritable, and identifying the genetic variants involved will have a big impact on our understanding of brain development. Despite large-scale efforts, the majority of these genetic variants remain unknown (Grasby et al. 2020). This is in part due to the genetic signal of cortical morphology being distributed across many causal variants, each having a small effect (Fan et al. 2018; Holland et al. 2019). Our ability to identify causal SNPs can be improved not only by increasing sample sizes to boost statistical power but also by employing better delineated, less noisy brain measures that better map onto the biology we seek to understand. Such measures might have fewer causal variants but with larger effects, that is, lower polygenicity and higher discoverability. Quantifying these characteristics of the polygenic architecture across often-used cortical measures may therefore optimize the selection of the most informative measures, enhancing gene discovery.
The thickness of the cerebral cortical sheet and its surface area are two separable morphological measures which have been reported to follow differing trajectories over the lifespan (Hogstrom et al. 2012) and to be differentially associated with cognitive ability (Schnack et al. 2015) and psychiatric disorders (Rimol et al. 2012). The radial unit hypothesis of cortical expansion posits that the extent and timing of developmental cellular processes, particularly neurogenesis and neuronal migration from the embryonic proliferative zone, differentially impact cortical thickness and surface area (Rakic 1988). In line with this, the largest genome-wide association study (GWAS) of the cortex to date found that surface area is influenced by genetic variants regulating neural progenitor cells during fetal development, while thickness is influenced by active regulatory elements in adult brain samples, which may reflect processes later in life, such as myelination, branching, or pruning (Grasby et al. 2020). This study found a small negative genetic correlation between area and thickness through linkage disequilibrium score regression (LDSC), a genome-wide measure of the correlation of additive genetic effects on two traits. Further, twin- and family-based studies have reported that there is no genetic correlation between these two measures, suggesting their genetic underpinnings should be assessed separately (Panizzon et al. 2009; Winkler et al. 2010). However, this claim does not take into account that complex traits such as brain measures may have a substantial number of shared genetic loci (Smeland et al. 2019) even in the absence of genetic correlation, due to mixed directions of effects (Smeland et al. n.d.; Frei et al. 2019). Identification of the fraction of shared causal variants between two brain phenotypes (Frei et al. 2019), beyond genetic correlation, is valuable for an understanding of their biological relation. This overlap may further be exploited to boost identification of genetic factors for these traits (Andreassen et al. 2013; van der Meer et al. 2019).
Here, we sought to quantify important characteristics of the polygenic architecture of the cerebral cortex through MiXeR, a Gaussian mixture modeling tool (Frei et al. 2019; Holland et al. 2019). We estimated the genetic overlap between mean cortical thickness and total surface area, as well as the polygenicity, discoverability, and heritability of regional measures.
Materials and Methods
Participants
For this study, we made use of data from White European participants of the UK Biobank that had undergone the neuroimaging protocol, obtained from the data repository under accession number 27412. The composition, set-up, and data gathering protocols of the UKB have been extensively described elsewhere (Sudlow et al. 2015; Miller et al. 2016). After data preprocessing, described below, our final sample consisted of 30 880 individuals with a mean age of 64.3 (standard deviation [SD] 7.5). 52.1% was female.
Image Acquisition and Processing
T1 scans were collected from three scanning sites throughout the United Kingdom, all on identical Siemens Skyra 3 T scanners with a 32-channel receive head coil. T1 images with 1-mm isotropic voxel size were acquired through a 3D MPRAGE sequence in sagittal plane (208 × 256 × 256), with a TI/TR of 880/2000 ms. The UKB core neuroimaging team has published more extensive information on the applied scanning protocols and procedures, which we refer to for more details (Miller et al. 2016). The T1 scans were obtained from the UKB data repositories and stored locally at the secure computing cluster of the University of Oslo. We applied the standard “recon-all” processing pipeline of Freesurfer v5.3, performing automated surface-based morphometry segmentation (Desikan et al. 2006). From the output, we extracted global and regional estimates of cortical thickness and surface area.
Parcellation
For the primary analyses, we made use of the Desikan–Killiany atlas, dividing each hemisphere into 34 regions, based on gyral and sulcal patterns (Desikan et al. 2006). We additionally extracted regional estimates of cortical thickness and surface area using three other parcellation approaches: 1) the Chen et al. surface area atlas, which divides each hemisphere into 12 clusters, based on genetic correlations derived from cortical surface area data from 406 monozygotic and dizygotic twins (Chen et al. 2012). For this, we made use of the GCLUST phenotype extraction protocol, 2) the Yeo et al. atlas, which provides a 7- and a 17-cluster solution of dividing each hemisphere, based on functional connectivity patterns in resting-state fMRI data of a 1000 subjects (Yeo et al. 2011), and 3) the Glasser et al. atlas, dividing the hemispheres into 180 regions, based on multimodal MRI data from the Human Connectome Project (HCP) and an objective semi-automated neuroanatomical approach (Glasser et al. 2016).
Data Preprocessing
We first selected all White European individuals that had undergone the UK Biobank neuroimaging protocol up to February 2020 with good-quality genetic data (N = 35 660). We then excluded anyone with a primary or secondary ICD10 diagnosis of a mental or neurological disorder (ICD10 codes, as indicated by data fields 41 202 and 41 204, starting with and “F” or “G,” n = 3095). Following that, we removed all T1 scans with an Euler number (a measure of scan quality, Rosen et al. 2018), pre-residualized for age and sex, 3 SD below the scanner mean (n = 764), or with a global brain measure more than 5 SD from the sample mean (n = 10). We then removed one of each genetically related pair of individuals, as defined by a threshold of 0.0625 determined by genome-wide complex trait analysis (GCTA, n = 911). For all processed brain measures, in the remaining sample (N = 30 880), we regressed out age, sex, scanning site, Euler number, genetic batch, and the first 20 genetic principal components. For the regional measures of thickness and area, we also regressed out the corresponding hemisphere-specific global measure, in accordance with previous work (van der Meer et al. 2019). This was done to obtain region-specific information. Subsequently, we applied a rank-based inverse normal transformation to the residuals of each measure, ensuring normally distributed input into the GWAS.
We conducted several supplementary analyses of the Desikan–Killiany atlas: 1) leaving out the correction for the global cortical measures; 2) constructing an overview of the phenotypic and genetic correlations between all the regions and calculating the number of independent measures through spectral decomposition of the correlation matrices; 3) analyzing cortical volume, that is, the composite measure (product) of cortical thickness and surface area; and 4) rerunning the primary analyses while additionally pre-residualizing for scan bore coordinates (X, Y, and Z), age2, age*sex, and age2*sex. Please see Supplementary material for more details and the results.
GWAS Procedure
We made use of the UKB v3 imputed data, which has undergone extensive quality control procedures as described by the UKB genetics team (Bycroft et al. 2017). We additionally carried out standard quality check procedures, including filtering out individuals with more than 10% missingness, as well as removal of SNPs with low imputation quality scores (INFO < 0.8), with more than 5% missingness, or failing the Hardy–Weinberg equilibrium test at P = 1*10−9. We further set a minor allele frequency threshold of 0.001 leaving 12 245 112 SNPs. The GWAS on each pre-residualized and normalized brain morphology measures was carried out using the standard additive model of linear association between genotype vector, 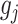 , and phenotype vector,
, and phenotype vector, 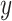 , using PLINK2 (Chang et al. 2015).
, using PLINK2 (Chang et al. 2015).
Causal Mixture Models (MiXeR) Procedure
We applied causal mixture models to the GWAS summary statistics, using the MiXeR tool (Frei et al. 2019; Holland et al. 2019). MiXeR estimates the likely total number of the underlying causal variants, without identifying their specific location. This is implemented by fitting a causal mixture model that allows us to estimate the proportion of such variants and then multiply that proportion with the total number of genetic variants in a reference panel. This procedure includes detailed information of linkage disequilibrium (LD) structure in the reference panel, thus estimating how many causal variants are underlying SNP associations across SNPs that are in strong LD with each other. As an example, schizophrenia and Crohn’s disease are both highly heritable diseases, with SNP heritability from GWAS estimated to be around 45%. At the same time, schizophrenia is estimated to have nearly 20 times higher polygenicity (Frei et al. 2019). As heritability is the product of polygenicity and discoverability, the discoverability of schizophrenia is 20 times lower. Thus, the size of the GWAS sample needed for discoveries in Crohn’s disease is much smaller than needed to obtain genome-wide significant findings in schizophrenia. In the current study, we aim to provide similar insights with respect to differences in discoverability and polygenicity across brain regions. For more details on the MiXeR procedure, please see Supplementary material.
Through univariate MiXeR, we estimated polygenicity (estimated number of causal variants, NC), discoverability (proportion of phenotypic variance explained on average by a causal variant, 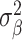 ), and narrow-sense heritability (the product of polygenicity and discoverability, that is, proportion of phenotypic variance explained, h2). Standard errors on the MiXeR estimates are calculated via the observed information matrix (the hessian of the log-likelihood function). We excluded from our analyses regions where the ratio between the estimated heritability and its standard error (SE) was less than 3, as this suggests there may be insufficient signal in the data to reliably estimate MiXeR parameters (Frei et al. 2019). We used bivariate MiXeR to calculate genetic overlap, as the estimated number of causal variants with an effect on both traits.
), and narrow-sense heritability (the product of polygenicity and discoverability, that is, proportion of phenotypic variance explained, h2). Standard errors on the MiXeR estimates are calculated via the observed information matrix (the hessian of the log-likelihood function). We excluded from our analyses regions where the ratio between the estimated heritability and its standard error (SE) was less than 3, as this suggests there may be insufficient signal in the data to reliably estimate MiXeR parameters (Frei et al. 2019). We used bivariate MiXeR to calculate genetic overlap, as the estimated number of causal variants with an effect on both traits.
We contrast the MiXeR parameter estimates with genetic correlations estimated through linkage disequilibrium score regression (Bulik-Sullivan et al. 2015).
Statistical Analyses
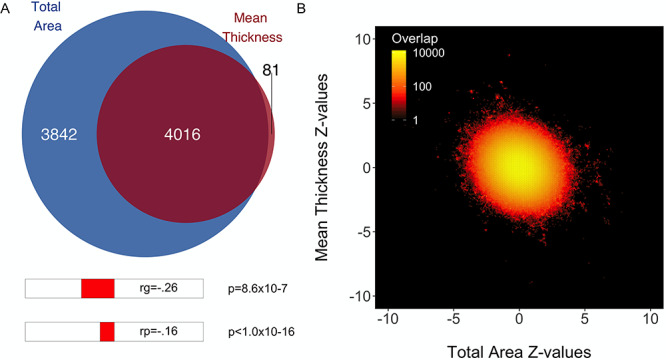
All downstream analyses were carried out in R v3.5.1 (Team 2015). We applied Bonferroni corrections for the multiple comparisons: given we compared polygenicity, discoverability, and heritability (i.e., three measures) of surface area and thickness, we set a significance threshold of 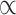 = 0.05/3 = 0.017; for the 10 pairwise comparisons of parcellation schemes, we consider the
= 0.05/3 = 0.017; for the 10 pairwise comparisons of parcellation schemes, we consider the 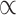 = 0.05/30 = 0.0017. Data was visualized through the R package ggplot2 (Wickham 2009). The code for running the MiXeR analyses, together with a tutorial and example data, is available at https://github.com/precimed/mixer. The GWAS summary statistics are available upon request.
= 0.05/30 = 0.0017. Data was visualized through the R package ggplot2 (Wickham 2009). The code for running the MiXeR analyses, together with a tutorial and example data, is available at https://github.com/precimed/mixer. The GWAS summary statistics are available upon request.
Results
Genetic Overlap between Global Measures
We identified a large degree of genetic overlap between total surface area and mean thickness, with a Dice coefficient of 0.67 (see Fig. 1A). This is in contrast to the negative phenotypic and genetic correlations displayed below the Venn diagram, which suggest a smaller degree of overlap. The bivariate density plot, Figure 1B, illustrates mixed directions of effects for many SNPs, which explains these apparent conflicting findings; some SNPs have the same direction of effect on both traits, while others have a positive effect on area and a negative effect on thickness or vice versa, with the net result being a smaller negative correlation.
Figure 1.
Genetic overlap of total surface area and mean thickness. (A) Venn diagram depicting the estimated number of causal variants shared between total surface area and mean thickness and unique to either of them. Below the diagram, we show the estimated genetic (“rg”) and phenotypic (Pearson’s, “rp”) correlation. (B) Bivariate density plot, illustrating the relationship between the observed GWAS Z-values for total area (on the x-axis) and mean thickness (on the y-axis).
Our analysis revealed that the total surface area is more heritable (h2 = 0.32, SE = 0.02) than mean thickness (h2 = 0.23, SE = 0.02), in accordance with previous findings (Grasby et al. 2020). We show that surface area has a marginally higher polygenicity (NC = 7858, SE = 1449) than mean thickness (NC = 4097, SE = 1032), at similar levels of discoverability (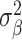 =4.0 × 10−5, SE = 5.9 × 10−6 vs.
=4.0 × 10−5, SE = 5.9 × 10−6 vs. 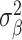 =5.5 × 10−5, SE = 1.0 × 10−5).
=5.5 × 10−5, SE = 1.0 × 10−5).
Regional Estimates
Using the Desikan–Killiany regional estimates, we observed a strong trade-off between the polygenicity and discoverability (Spearman’s rs = −0.88, P < 1 × 10−16), as shown in Figure 2A. The heritability of regional measures was positively correlated with discoverability (rs = 0.41, P = 4.9 × 10−6) but not with polygenicity (rs = 0.03, P = 0.76). Regional area was significantly less polygenic and more discoverable and heritable than regional thickness, as shown in Figure 2B–D. Further, we found that the size of the brain regions was significantly positively correlated with their discoverability (rs = 0.53, P = 1.9 × 10−5) and negatively related to their polygenicity (rs = −0.40, P = 0.002), for the area-specific estimates only. For the full results, and an overview of parameter estimates per region, see Supplementary material.
Figure 2.
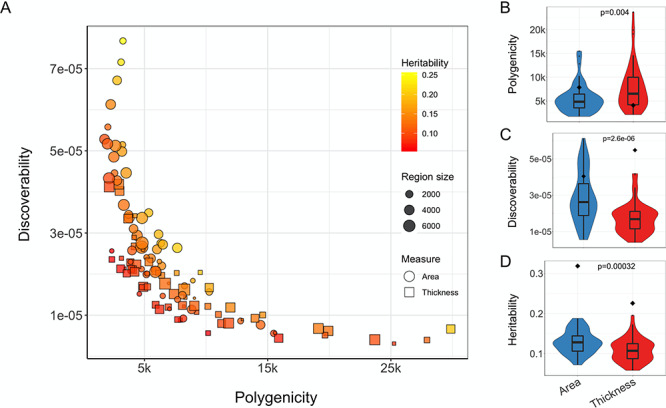
Polygenicity, discoverability, and heritability of regional cortical surface area and thickness. (A) Scatter plot depicting the relationship between estimates of polygenicity (x-axis) and discoverability (y-axis) for regional cortical measures. The shape of the data points distinguishes between surface area and thickness estimates, the point size reflects the size of the region, and the color relates to the estimated heritability. (B–D) Violin plots comparing the polygenicity, discoverability, and heritability (on the y-axis) of regional area and thickness estimates (x-axis). Significance, indicated at the top of each graph, is calculated through the Wilcoxon signed-rank test. For comparison, the diamonds indicate the estimate for the corresponding global measure.
Comparison of Parcellation Schemes
Given that the definition of regions likely plays an important role in imaging genetics studies, we additionally compared the Desikan–Killiany atlas with other often-used parcellation schemes that differ both in the biological basis of their parcellation and the number of regions they divide the brain in, that is, their granularity (see Materials and Methods section). Of the five schemes, for the area measures, the Chen et al. parcellation was both the most discoverable and the most heritable. Further, generally, the less granular schemes were more discoverable and heritable. There were no significant differences in polygenicity between the parcellation schemes. These results are summarized in Figure 3. There were no differences in discoverability of regional thickness estimates between the parcellations (see Supplementary material).
Figure 3.
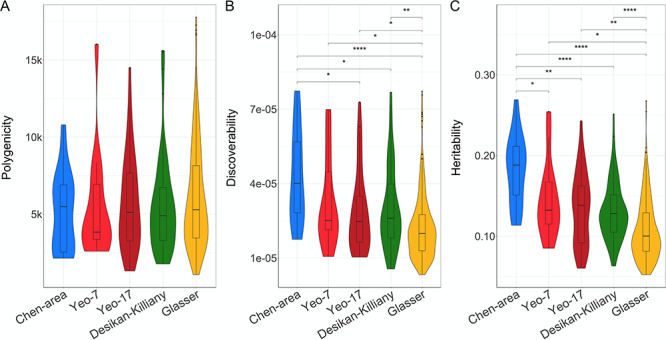
Comparisons of discoverability and polygenicity of regional surface area across parcellation schemes. Violin plots comparing the polygenicity (A), discoverability (B), and heritability (C) (on the y-axis) of the five different parcellation schemes (x-axis). Significance of each paired comparison, indicated at the top of each graph, is calculated through the Wilcoxon signed-rank test with *P < 0.05, **P < 0.0017, ***P < 0.00017, and ****P < 0.000017.
Discussion
These findings provide new insights into the polygenic architecture of the cerebral cortex, with three main take-home messages. First, there is large genetic overlap between mean cortical thickness and total surface area. Second, regional surface area measures are more discoverable and less polygenic than regional thickness measures. And third, the genetically informed and less granular parcellation schemes had highest discoverability.
We provide evidence of strong genetic overlap between mean cortical thickness and total surface area, contrary to previous reports based on genetic correlations (Panizzon et al. 2009; Winkler et al. 2010; Grasby et al. 2020). The previously reported weak negative, or even absent, genetic correlation therefore appears not to be the result of a small amount of shared genetic variants with opposing direction of effects, but rather a large amount of shared genetic variants with a mixture of opposite and same direction of effects. This is a likely scenario for brain morphology, as numerous neurobiological processes are to a large degree overlapping between brain regions, while at the same time, there are important differences in tuning and activity levels of these processes between regions. This further adds to recent literature revealing high levels of pleiotropy between brain-related behavioral traits and disorders (Watanabe et al. 2019). For instance, nearly all causal variants for schizophrenia are shared with educational attainment despite a negligible genetic correlation (Frei et al. 2019), in accordance with research identifying many shared genetic loci between the two traits without a clear pattern of sign concordance (Le Hellard et al. 2016; Bansal et al. 2018). This is critical for our understanding of the biological relationships between brain-related traits and disorders and how to study them, as knowledge of loci shared by two traits should provide clues to the underlying mechanisms. In the case of cortical thickness and surface area, identification of these loci may improve our understanding of the developmental processes of cell number regulation and neuronal migration that together determine the thickness and size of the cortical sheet (Rakic 1988). The genetic overlap may particularly inform us on (the extent of) the interactions between these processes, for example, how a balance between cortical thickness and area may be determined through genetically regulated temporal shifts in neurogenesis and migration. This, in turn, is essential for greater insight into the pathogenesis of neurodevelopmental disorders (Geschwind and Rakic 2013).
We further found that regional area is more heritable than regional thickness, in line with previous reports (Eyler et al. 2012), and we show that this is driven by higher discoverability. This matches findings from a recent GWAS study, with 187 genome-wide significant hits for regional area versus only 84 for regional thickness (Grasby et al. 2020). There appears to be more variation in the distribution of the estimates for regional surface area compared to regional cortical thickness, suggesting the latter has a more homogeneous polygenic architecture across regions. Larger differences between the polygenic architectures of regional surface area measures may also underlie the somewhat higher polygenicity for total surface area compared to mean thickness. It may further explain why most genome-wide significant variants are found for surface area, as only those regions with high discoverability have effects that may be identified with current sample sizes.
Our comparison of different parcellation schemes indicates that the choice of scheme makes a significant difference on the outcome of imaging genetics studies. While all schemes had similar levels of polygenicity, the Chen et al. parcellation performed best in terms of discoverability. Besides the fact that this parcellation was based on twin data, that is, genetically informed, granularity may play an important role in the performance of the schemes we compared; measurement noise due to inaccuracy of boundary placement will disproportionally affect smaller regions, thereby lowering heritability (Eyler et al. 2012; Patel et al. 2018) and discoverability, compounding the multiple comparisons problem faced by studying more granular schemes. This is also in line with the global measures having higher heritability and discoverability than the vast majority of regional measures. Boundary placement accuracy at the individual level is of less importance for thickness estimates (Eyler et al. 2012), likely contributing to why we only saw differences between the schemes for the area estimates.
To conclude, we revealed that surface area and thickness share a considerable number of genetic variants, and provide the first estimates of discoverability and polygenicity of regional cortical measures across parcellation schemes. These findings may serve as a roadmap for improving future studies. Knowledge of which measures or parcellations are most discoverable, and why, as well as the genetic overlap between these measures, can be exploited to boost identification of genetic predictors (Andreassen et al. 2013; van der Meer et al. 2019) and thereby gain a better understanding of brain morphology and associated disorders.
Funding
Research Council of Norway (276082, 213837, 223273, 204966/F20, 229129, 249795/F20, 225989, 248778, 249795); South-Eastern Norway Regional Health Authority (2013-123, 2014-097, 2015-073, 2016-064, 2017-004); Stiftelsen Kristian Gerhard Jebsen (SKGJ-Med-008); European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (ERC Starting Grant, Grant agreement No. 802998); National Institutes of Health (R01MH118281, R01GM104400).
Notes
This work was partly performed on the TSD (Tjeneste for Sensitive Data) facilities, owned by the University of Oslo, operated and developed by the TSD service group at the University of Oslo, IT-Department (USIT) (tsd-drift@usit.uio.no). Computations were also performed on resources provided by UNINETT Sigma2—the National Infrastructure for High Performance Computing and Data Storage in Norway.
Dr Andreassen has received the speaker’s honorarium from Lundbeck and is a consultant to HealthLytix. Dr Dale is a Founder of and holds equity in CorTechs Labs, Inc., and serves on its Scientific Advisory Board. He is a member of the Scientific Advisory Board of Human Longevity, Inc., and receives funding through research agreements with General Electric Healthcare and Medtronic, Inc. The terms of these arrangements have been reviewed and approved by the UCSD in accordance with its conflict of interest policies. The other authors declare no competing financial interests.
A version of this article was published as a preprint on bioRxiv (doi: https://doi.org/10.1101/868307).
The data incorporated in this work were gathered from public resources. The code is available via https://github.com/precimed/mixer (GPLv3 license). Correspondence and requests for materials should be addressed to d.v.d.meer@medisin.uio.no.
Supplementary Material
References
- Andreassen OA, Thompson WK, Dale AM. 2013. Boosting the power of schizophrenia genetics by leveraging new statistical tools. Schizophr Bull. 40:13–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bansal V, Mitjans M, Burik CAP, Karlsson Linner R, Okbay A, Rietveld CA, Begemann M, Bonn S, Ripke S, Vlaming R et al. . 2018. Genome-wide association study results for educational attainment aid in identifying genetic heterogeneity of schizophrenia. Nat Commun. 9:3078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulik-Sullivan B, Finucane HK, Anttila V, Gusev A, Day FR, Loh P-R, Duncan L, Perry JRB, Patterson N, Robinson EB. 2015. An atlas of genetic correlations across human diseases and traits. Nat Genet. 47:1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bycroft C, Freeman C, Petkova D, Band G, Elliott LT, Sharp K, Motyer A, Vukcevic D, Delaneau O, O’Connell J. 2017. Genome-wide genetic data on ~500,000 UK biobank participants. Nature. 562:203–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Chow CC, Tellier LCAM, Vattikuti S, Purcell SM, Lee JJ. 2015. Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience. 4:7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C-H, Gutierrez ED, Thompson W, Panizzon MS, Jernigan TL, Eyler LT, Fennema-Notestine C, Jak AJ, Neale MC, Franz CE et al. . 2012. Hierarchical genetic organization of human cortical surface area. Science. 335:1634–1636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT et al. . 2006. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 31:968–980. [DOI] [PubMed] [Google Scholar]
- Eyler LT, Chen C-H, Panizzon MS, Fennema-Notestine C, Neale MC, Jak A, Jernigan TL, Fischl B, Franz CE, Lyons MJ et al. . 2012. A comparison of heritability maps of cortical surface area and thickness and the influence of adjustment for whole brain measures: a magnetic resonance imaging twin study. Twin Res Hum Genet. 15:304–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan CC, Smeland OB, Schork AJ, Chen C-H, Holland D, Lo M-T, Velkur S, Frei O, Jernigan TL, Andreassen OA et al. . 2018. Beyond heritability: improving discoverability in imaging genetics. Hum Mol Genet. 27:R22–R28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frei O, Holland D, Smeland OB, Shadrin AA, Fan CC, Maeland S, O’Connell KS, Wang Y, Djurovic S, Thompson WK. 2019. Bivariate causal mixture model quantifies polygenic overlap between complex traits beyond genetic correlation. Nat Commun. 10:2417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geschwind DH, Rakic P. 2013. Cortical evolution: judge the brain by its cover. Neuron. 80:633–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M. 2016. A multi-modal parcellation of human cerebral cortex. Nature. 536:171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grasby KL, Jahanshad N, Painter JN, Colodro-Conde L, Bralten J, Hibar DP, Lind PA, Pizzagalli F, Ching CRK, McMahon MAB et al. . 2020. The genetic architecture of the human cerebral cortex. Science (80-). 367:eaay6690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogstrom LJ, Westlye LT, Walhovd KB, Fjell AM. 2012. The structure of the cerebral cortex across adult life: age-related patterns of surface area, thickness, and gyrification. Cereb Cortex. 23:2521–2530. [DOI] [PubMed] [Google Scholar]
- Holland D, Frei O, Desikan R, Fan CC, Shadrin A, Smeland O, Sundar VS, Thompson P, Andreassen OA, Dale AM. 2019. Beyond SNP heritability: polygenicity and discoverability of phenotypes estimated with a univariate Gaussian mixture model. PLOS Genet. 16:e1008612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Hellard S, Wang Y, Witoelar A, Zuber V, Bettella F, Hugdahl K, Espeseth T, Steen VM, Melle I, Desikan R. 2016. Identification of gene loci that overlap between schizophrenia and educational attainment. Schizophr Bull. 43:654–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KL, Alfaro-Almagro F, Bangerter NK, Thomas DL, Yacoub E, Xu J, Bartsch AJ, Jbabdi S, Sotiropoulos SN, Andersson JLR. 2016. Multimodal population brain imaging in the UK biobank prospective epidemiological study. Nat Neurosci. 19:1523–1536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panizzon MS, Fennema-Notestine C, Eyler LT, Jernigan TL, Prom-Wormley E, Neale M, Jacobson K, Lyons MJ, Grant MD, Franz CE. 2009. Distinct genetic influences on cortical surface area and cortical thickness. Cereb Cortex. 19:2728–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel S, Patel R, Park MTM, Masellis M, Knight J, Chakravarty MM. 2018. Heritability estimates of cortical anatomy: the influence and reliability of different estimation strategies. Neuroimage. 178:78–91. [DOI] [PubMed] [Google Scholar]
- Rakic P. 1988. Specification of cerebral cortical areas. Science (80-). 241:170–176. [DOI] [PubMed] [Google Scholar]
- Rimol LM, Nesvåg R, Hagler DJ, Bergmann Ø, Fennema-Notestine C, Hartberg CB, Haukvik UK, Lange E, Pung CJ, Server A et al. . 2012. Cortical volume, surface area, and thickness in schizophrenia and bipolar disorder. Biol Psychiatry. 71:552–560. [DOI] [PubMed] [Google Scholar]
- Rosen AFG, Roalf DR, Ruparel K, Blake J, Seelaus K, Villa LP, Ciric R, Cook PA, Davatzikos C, Elliott MA. 2018. Quantitative assessment of structural image quality. Neuroimage. 169:407–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnack HG, Haren NEM, Brouwer RM, Evans A, Durston S, Boomsma DI, Kahn RS, Hulshoff Pol HE. 2015. Changes in thickness and surface area of the human cortex and their relationship with intelligence. Cereb Cortex. 25:1608–1617. [DOI] [PubMed] [Google Scholar]
- Smeland O, Frei O, Dale A, Andreassen OA. n.d.The polygenic architecture of schizophrenia – rethinking pathogenesis and nosology. Nat Rev Neurol. [DOI] [PubMed] [Google Scholar]
- Smeland OB, Frei O, Shadrin A, O’Connell K, Fan C-C, Bahrami S, Holland D, Djurovic S, Thompson WK, Dale AM. 2019. Discovery of shared genomic loci using the conditional false discovery rate approach. Hum Genet. 139:85–94. [DOI] [PubMed] [Google Scholar]
- Sudlow C, Gallacher J, Allen N, Beral V, Burton P, Danesh J, Downey P, Elliott P, Green J, Landray M. 2015. UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 12:e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Team RC 2015. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; http://www. R-project. org/food webs, and the structure of phytophagous insect communities, 25 June 2015, last accessed). [Google Scholar]
- Meer D, Frei O, Kaufmann T, Shadrin AA, Devor A, Smeland OB, Thompson W, Fan CC, Holland D, Westlye LT. 2019. Making the MOSTest of imaging genetics. bioRxiv. 51:1339–1348. [Google Scholar]
- Watanabe K, Stringer S, Frei O, Mirkov MU, Leeuw C, Polderman TJC, Sluis S, Andreassen OA, Neale BM, Posthuma D. 2019. A global overview of pleiotropy and genetic architecture in complex traits. Nat Genet. 1–10. [DOI] [PubMed] [Google Scholar]
- Wickham H. 2009. Ggplot2: elegant graphics for data analysis. New York: Springer. http//hadconz/ggplot2/book.
- Winkler AM, Kochunov P, Blangero J, Almasy L, Zilles K, Fox PT, Duggirala R, Glahn DC. 2010. Cortical thickness or grey matter volume? The importance of selecting the phenotype for imaging genetics studies. Neuroimage. 53:1135–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BTT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zollei L, Polimeni JR et al. . 2011. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol. 106:1125–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


