Computational Study on the Boundary Between the Concerted and Stepwise Mechanism of Bimolecular S_NAr Reactions

Abstract

The text-book mechanism of bimolecular nucleophilic aromatic substitutions (S_NAr) reactions is a stepwise process that proceeds via a so-called Meisenheimer intermediate. Only recently the alternative, concerted version of this mechanism has gained acceptance as more and more examples thereof have been reported. But so far only isolated examples of concerted S_NAr reactions have been described and a coherent picture of when a S_NAr reaction proceeds via a stepwise and when via a concerted mechanism has not yet been established. Here key factors are identified that influence the mechanistic choice of S_NAr reactions. Moreover, the electron affinity is used as a simple descriptor to make a prediction on whether a given aryl fluoride substrate favors a concerted or stepwise mechanism.

Introduction

Nucleophilic substitutions on aromatic systems can proceed via several different reaction mechanisms.¹ Of these, the most fundamental is the bimolecular nucleophilic aromatic substitution (S_NAr) as described in the landmark review by Bunnett et al.² As detailed more recently,³ the widely accepted stepwise energy profile of the S_NAr reaction appears not to be the only possible route. In fact, over the last decades, more and more reports accumulated in the literature that suggested certain S_NAr reactions to follow a concerted pathway. In particular the recent study by Jacobsen et al. was important in raising the general awareness of the two mechanistic domains accessible to S_NAr reactions.⁴ The combined impact of these investigations has now reached a critical momentum. It seems appropriate to fundamentally question the long-established mechanistic picture of the S_NAr reaction.

Probing the mechanism of the S_NAr reaction is challenging, however. Experimentally, complex structure–activity relationship studies need to be performed. This approach has been followed by Williams et al. in several thorough studies.⁵⁻¹⁰ Although the concept behind these studies is elegant and intuitive, the approach is limited to certain suitable model systems. With computational tools, in contrast, it is straightforward to determine the energy profile of any imaginable S_NAr reaction. Consequently, it is not surprising that most claims for concerted S_NAr reactions are based on computational models, including the above-mentioned study by Jacobsen. However, the question arises whether the computational methods used are reliable. Only rarely was a thorough validity of the method established and if so, only for selected examples.¹¹ Importantly, it has never been thoroughly established that a computational model is able to predict correctly the mechanism of both concerted and stepwise S_NAr reactions.

Because of these challenges, the exact nature of the S_NAr mechanism has only been investigated for isolated examples. Besides some general trends and rough guidelines, there is no coherent picture of when bimolecular S_NAr reactions follow a stepwise and when a concerted mechanism. The aim of this work was to first establish the validity of a DFT method to predict the reaction mechanism and then to use this method to investigate the trends of what types of S_NAr reactions follow which mechanistic pathway.

For this work to be as beneficial as possible for the community of chemists, it was important to choose appropriate descriptors to parametrize S_NAr reactions. Broadly speaking, one expects an S_NAr reaction to depend on several components: the nucleophile (and a countercation in case of charged nucleophiles), the leaving group, the aromatic system, and the solvent. There are numerous parameters that would allow any of these three aspects to be described. For the description of the aromatic system, a particularly convenient measure is the Hammett substituent constants. In fact, Hammett correlations have been applied to S_NAr reactions in many instances and, usually, a good linear regression was observed for the σ_p^– substituent constant.^12,13 More recently, the slope of Hammett correlations has also been interpreted as an indication of the mechanistic nature of S_NAr reactions.¹⁴⁻¹⁶ However, while intuitive, this approach lacks a sound theoretical foundation, as with the exception of particular classes of reactions such as proton-coupled electron transfers,^17,18 the relationship between the reaction free energy and the mechanism is not explicit—indeed, in the current work there is no observed relationship (see Supporting Information, SI, Figures S15–S18). Moreover, there are no well-established reference values for typical concerted and typical stepwise reactions and often the fact that the Hammett slope is temperature-dependent is ignored. Therefore, instead of analyzing the slope of the linear regression, in this study it was examined whether there is a sharp turning point from a stepwise to a concerted mechanism as the aromatic systems become more electron-rich (i.e., the ring substituents become less electron-withdrawing—this corresponds to a less positive value of the σ_p^– substituent constant). Encouragingly, one isolated example of such a mechanistic turning point on the σ_p^– scale has previously been reported.¹⁹ The values of the σ_p^– constants used here were taken from the review by Hansch et al.²⁰

Due to the historic importance of Hammett correlations to characterize S_NAr reactions and given the fact that generally good correlations have been found, we sought to describe the mechanistic turning point based on the σ_p^– substituent constants. To do so, one can think of a hypothetical para-substituent for which the energy profile of the S_NAr reaction passes through a saddle point (i.e., the curvature and the slope along the reaction coordinate are zero). This substituent would mark the mechanistic turning point; thus, we will refer to its Hammett constant as τ_p^–. Any substituent that was more electron-withdrawing would cause the reaction to proceed via a stepwise energy-profile with a local minimum (and a general inflection point—with slope ≠ zero—instead of the saddle point), whereas the reaction would proceed via a concerted mechanism for substrates with a less electron-withdrawing substituent.

Since the Hammett σ_p^– scale consists of discrete values, a way to approximate τ_p^– based on the chemically existing and viable para-substituents was needed. This can be achieved by taking the least electron-withdrawing substituent for which the reaction still follows a stepwise energy profile (σ_{p,min–stepwise}) and the most electron-withdrawing substituent for which the reaction still follows a concerted energy profile (σ_{p,max–concerted}^–). Then the average of the two substituent constants is calculated (eq 1). This value gives a measure for how sharply the mechanistic turning point is projected onto the Hammett σ_p^– scale. In other words, Δσ_p shows how precisely the mechanistic turning point can be possibly known based on the available σ_p^– values.

1

The turning point itself can then be expressed according to eq 2.

2

Results and Discussion

A thorough benchmarking study showed that the M11 functional is well suited to predict the mechanism of S_NAr reactions. (Full details of the functional evaluation study and further validation studies for the M11 functional can be found in the SI).

To gain a broad overview of the two mechanistic domains—stepwise vs concerted S_NAr—three classes of S_NAr reactions were investigated. These are the halide displacement with potassium methoxide (Figure 1), halide–halide exchange reactions (Tables S2–4) and the analogous chalcogen-chalcogen exchange reactions (Tables S2–5).

Figure 1.

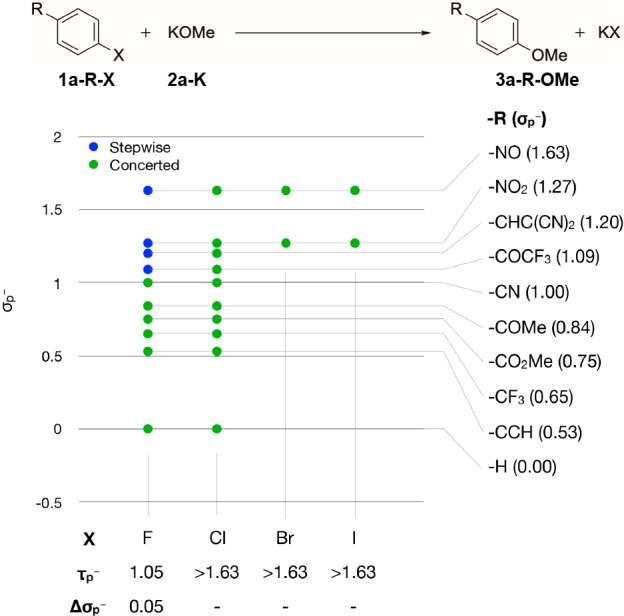
Mechanistic turning point for the halide displacement by potassium methoxide and benzene derivatives. A stepwise mechanism was only observed for examples with fluoride as a leaving group and strongly electron-withdrawing substituents.

Only for the fluoride series was the mechanistic turning point identified, with τ_p^– = 1.05 (Figure 1). For the displacement of chloride, bromide, and iodide the mechanistic turning point does not fall into the chemically plausible range of the σ_p^– scale. In fact, these reactions all showed a concerted energy profile even with the most electron-withdrawing para-nitroso substituent that was considered in this study.

A similar picture was obtained for the halide exchange reactions (Tables S2–S4). The mechanistic turning point for most of the chalcogen exchange reactions, in contrast, actually fell mainly onto the applied σ_p^– scale (Tables S2–S5). In general, a concerted mechanism is favored for the chalcogen exchange reaction by the participation of larger (i.e., softer) chalcogens. The analogous statement holds true for the halide exchange reaction. Overall, the halides chloride, bromide and iodide all strongly favor a concerted mechanism, either in the halide exchange reaction or in an exchange reaction with potassium methoxide (Figure 1). Only for the S_NAr reactions involving fluoride a stepwise energy profile was found to have significant importance. Because of this finding and because fluoride is the prototype leaving group for S_NAr reactions, further discussion will focus on S_NAr displacements of fluoride.

So far, only the potassium cation has been considered as a countercation in the examined model systems. The effect of the countercation on the S_NAr mechanism was studied, based on the displacement of fluoride from 1a-R-F with different alkali metal methoxide salts 2a-M (Figure 2). As a general trend, the stepwise mechanism becomes more dominant with increasing size of the countercation, i.e., the value for τ_p^– decreases as the countercation becomes larger. This trend culminates in the extreme case where no countercation is present at all. Closer inspection of the data shows that there is no or only a small difference between the reactions with the cations sodium, potassium, rubidium, and cesium. Only the boundary cases with lithium as a countercation on the one hand and without a countercation at all on the other hand show a pronounced change of the τ_p^– value.

Figure 2.

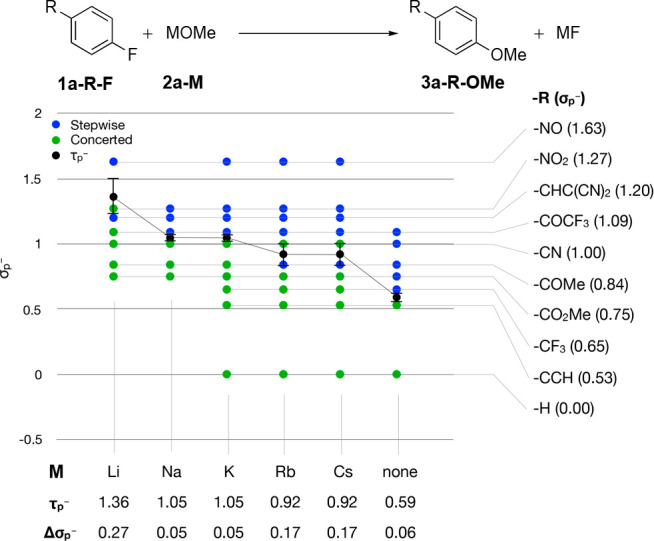
As the countercation gets larger, the reaction tends to favor a stepwise mechanism.

The observed trend suggests that the better the countercation can stabilize the negative charge on the fluoride leaving group, the more strongly a concerted reaction mechanism is favored. This is in agreement with the trend of decreasing lattice energy of alkali fluoride salts with increasing atomic number of the alkali cation (i.e., weaker bonding between the fluoride anion and the alkali metal cation).²¹ The observed trend is also in line with observations made on the computational investigation²⁰ of the amide α-arylation by Clayden et al.¹⁴ (Including explicit solvent molecules in the model only had a minor effect on the τ_p^– value, see the SI).

Keeping the fluoride leaving group, the potassium cation and the aromatic core constant, the mechanistic turning point was investigated for different nucleophiles (Figure 3). It was found that potassium methanethiolate 2b-K, potassium azide 2c-K, and the two carbon nucleophiles 2d-K and 2f-K all have the same mechanistic turning point τ_p^– as potassium methoxide. The S_NAr reaction of the nucleophile 2e-K is the only exception.

Figure 3.

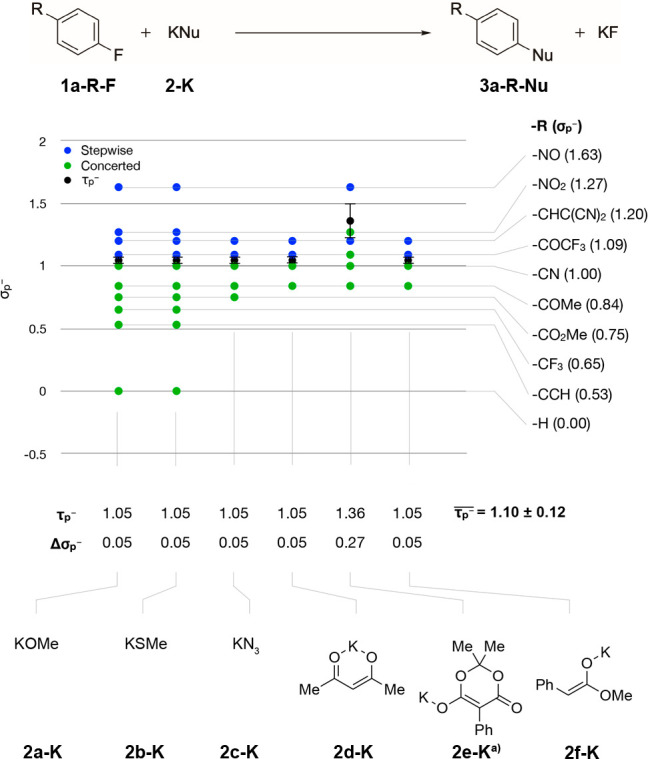
A similar mechanistic turning point was found for a number of very different nucleophiles. With R = NO the reaction likely follows a S_N(ET)Ar pathway (see Supporting Information).

This series of reactions favors a concerted mechanism more (τ_p^– = 1.36) than the other investigated reaction series (τ_p^– = 1.05). Closer inspection of the geometries of the rate limiting transition states with nucleophile 2e-K showed that steric repulsion (i.e., dispersion interactions) may be at the heart of this pronounced tendency to follow a concerted mechanism (see Figure S5, see Figure S8 further discussion of such effects). The average 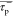over all six nucleophiles was 1.10 ± 0.12 for the substrate series 1a-R-F.

The observation that a number of very different nucleophiles showed the same mechanistic turning point was somewhat surprising. The same investigation for an additional two aromatic systems–pyridine and naphthalene–led to a similar conclusion (see the SI).

Since there is relatively little variation between different nucleophiles attacking the same aromatic substrate, (i.e., the value τ_p^– is mainly characteristic for the aromatic system and the fluoride leaving group), it is, in principle, sufficient to examine the mechanistic turning point with one nucleophile only in order to characterize the mechanistic preference of a given aryl fluoride electrophile. Hence, potassium methoxide was selected as the probe nucleophile and the aromatic systems 1a-R-F to 1e-R-F (Figure 4) were investigated. It can be seen that a stepwise reaction profile became more favored as either the aromatic system was extended (going from 1a-R-F to 1b-R-F to 1c-R-F) or nitrogen atoms were introduced (going from 1a-R-F to 1d-R-F to 1e-R-F). The effect of one additional fused benzene ring equaled approximately the effect of one additional nitrogen atom. The observed trends have an intuitive explanation. An additional fused ring, or a nitrogen atom in the ring, help to stabilize the negative charge that accumulates on the aromatic system during the addition of the nucleophile. The better the aromatic core is able to accommodate this negative charge, the less the stabilization of a (potential) Meisenheimer intermediate depends on the electron-withdrawing nature of the para-substituent.

Figure 4.

The better the aromatic core can accommodate the accumulating negative charge in the transition state, the more strongly a stepwise mechanism is favored.

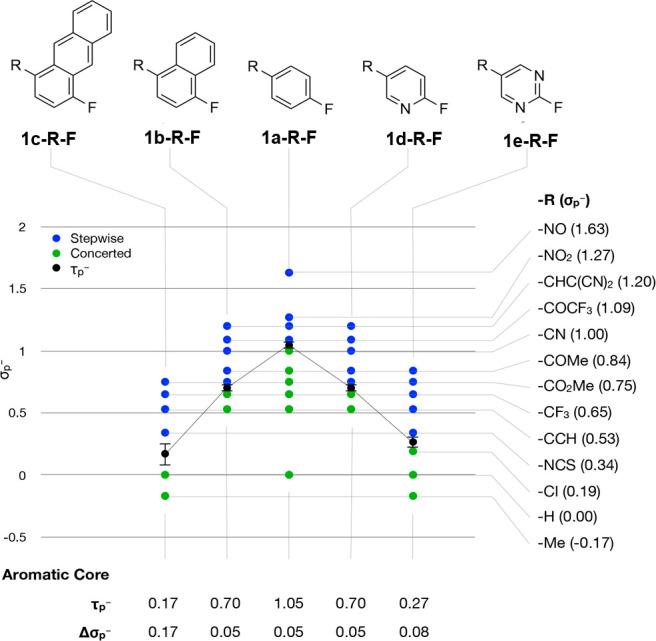
Obviously, the mechanistic turning point is highly sensitive to the nature of the aromatic system beyond the para-substituent. Hence, the next question is whether a readily accessible descriptor can be identified that allows to classify aryl fluorides according to what S_NAr mechanism they are likely to follow. The calculated gas-phase electron affinity was found to be a suitable measure to do this (Figure 5). (Other descriptors have been considered as well but were found inferior, see SI). Analogous to τ_p^–, we calculated the turning point electron affinity EA_T according to eq 3 where EA_{max_stepwise} is the largest electron affinity for which the reaction proceeds stepwise, whereas EA_{min_concerted} is the smallest electron affinity for which the reaction proceeds in a concerted manner.

Figure 5.

Electron affinity of an aryl fluoride compound allows for a quick classification of what S_NAr mechanism the substrate in question is likely to follow. The dashed (---) line indicates the average over all τ_p^– and the dotted lines (···) mark the standard deviation.

Note that the sign of the electron affinity axis is opposite to the sign of the Hammett substitution constant axis.

3

In Figure 5, the mechanistic pathway and the electron affinity of the substrate is shown for 14 series of aromatic system. The average EA_T over these 14 examples was found to be (−18.3 ± 6.7) kcal/mol. Thus, if an aryl fluoride substrate shows an electron affinity of smaller than −25.0 kcal/mol, it is likely to undergo a stepwise S_NAr reaction, whereas an electron affinity of greater than −11.6 kcal/mol indicates the preference for a concerted pathway. We note the exception of the 1h-R-F series from the general trend. This is due to the localization of the frontier orbitals in the S_NAr transition state for this series, whereas the SOMO of the corresponding radical anion (used to calculate the EA) is delocalized across the ring system.

As mentioned at the outset, the slope of the Hammett correlation for series of S_NAr reactions was often used in the literature as an indicator for the nature of the mechanism. In this work, a different angle is taken on the Hammett correlation, instead. It builds on the fact that the mechanism of the S_NAr reaction changes as the para-substituent is varied. This indicates already that the slope of the Hammett correlation is an unsuitable measure for the mechanistic nature of S_NAr mechanism. Also, a more detailed analysis of the Hammett correlation showed that there is no signature for the mechanistic turning point in the Hammett correlation (Figure 6). For example, the two nucleophiles 2a-K and 2b-K have the same mechanistic turning point but a different slope in the Hammett correlation when reacting with the electrophile 1a-R-F. Alternatively, the electrophiles 1a-R-F and 1a-R-Cl have a similar slope but different turning point when reacting with the nucleophile 2a-K. Further, no kink can be found in the correlation. (Additionally, key geometric properties of the rate-limiting transition state were investigated in an analogous correlation. Again, the correlation did not harbor any information about the mechanistic turning point—see the SI).

Figure 6.

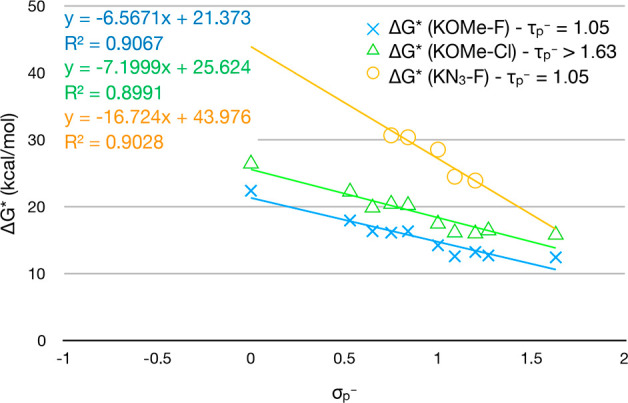
Activation energy of the rate limiting step of a series of S_NAr reactions does not contain information about the overall mechanism.

It becomes evident that in general the rate limiting step does not contain information about the nature of the S_NAr mechanism. The mechanistic choice depends on the features of the bond that is more easily broken (or formed). In light of this conclusion it becomes obvious why the reaction series of different nucleophiles with the same aromatic system have roughly the same value of τ_p^– (Figure 3). In all these apparently different reactions, the key step where the nature of the mechanism is decided is the same—the expulsion of the fluoride leaving group.

Conclusions

On the basis of a thoroughly bench-marked computational model, an in-depth analysis of factors influencing the choice of the reaction mechanism—concerted or stepwise—has been performed for the S_NAr reaction. Besides obvious trends such as a preference for the stepwise mechanism in systems that can accommodate the buildup of negative charge better (e.g., larger aromatic cores or the presence of nitrogen heteroatoms), it was found that the nature of the incoming nucleophile has only a minimal influence on the mechanistic choice. The electron affinity was found to be a readily available descriptor to judge the mechanistic preference of a particular aryl fluoride acting as the electrophile in a S_NAr reaction. Finally, it was demonstrated that the slope of the Hammett correlation is a potentially misleading indicator of the S_NAr mechanism of a reaction class. Consequently, it should no longer be considered when discussing the mechanism of S_NAr reactions. Instead, the electron affinity offers a better alternative indicator.

Glossary

Abbreviations Used

S_NAr

nucleophilic aromatic substitution

DFT

density functional theory

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c01975.

• Description and validation of the method, additional examples, and descriptions for every computational output file (PDF)

• Data set underlying this research, 10.15129/254ecae8-9c72-4bb9-9319-b16eada94f9c

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.