Mathematical Models for Hantavirus Infection in Rodents

Abstract

Hantavirus pulmonary syndrome is an emerging disease of humans that is carried by wild rodents. Humans are usually exposed to the virus through geographically isolated outbreaks. The driving forces behind these outbreaks is poorly understood. Certainly, one key driver of the emergence of these viruses is the virus population dynamics within the rodent population. Two new mathematical models for hantavirus infection in rodents are formulated and studied. The new models include the dynamics of susceptible, exposed, infective, and recovered male and female rodents. The first model is a system of ordinary differential equations while the second model is a system of stochastic differential equations. These new models capture some of the realistic dynamics of the male/female rodent hantavirus interaction: higher seroprevalence in males and variability in seroprevalence levels.

1. Introduction

Hantaviruses are rodent-borne zoonotic agents that, in humans, result in hemorrhagic fever with renal syndrome—HFRS (Europe and Asia) or hantavirus pulmonary syndrome—HPS (Americas) (Schmaljohn and Hjelle, 1997). HFRS was first recognized in 1951 when an outbreak occurred in military personnel involved in the Korean War (Lee and van der Groen, 1989). HPS, identified in 1993 from an outbreak in New Mexico, is recognized as an emerging disease (Schmaljohn and Hjelle, 1997), and more recently, a biodefense agent. The case fatality rate for HPS in the United States is 37%, which stands as the highest mortality rate for any pathogen in the US (CDC MMWR, 2002). Human infection occurs primarily through the inhalation of aerosolized saliva and/or excreta of infected rodents (CDC MMWR, 2002). However, HFRS or HPS may also occur after individuals have been bitten by infected rodents (CDC MMWR, 2002). Thirty different hantavirus strains are recognized throughout the world; some of which are associated with HPS or HFRS (Mills et al., 1997; Schmaljohn and Hjelle, 1997). Each hantavirus is generally associated with a primary rodent host within which substantial coevolutionary adaptations have probably occurred (Monroe et al., 1999; Plyusnin and Morzunov, 2001). Hantaviruses pathogenic to humans in the United States include Sin Nombre virus hosted by the deer mouse (Peromyscus maniculatus) (Mills et al., 1997), New York virus hosted by the white-footed mouse (Peromyscus leucopus) (Song et al., 1994), Black Creek Canal virus hosted by the cotton rat (Sigmodon hispidus) (Glass et al., 1998), and Bayou virus hosted by the rice rat (Oryzomys palustris) (Ksiazek et al., 1997; McIntyre, et al., 2005). There are many other hantaviruses associated with human disease. For example, Laguna Negra virus hosted by the vesper mouse (Calomys laucha) is present in western Paraguay (Yahnke et al., 2001; Chu et al., 2003). To increase our understanding of the spread of the disease in humans, it is necessary to understand the disease dynamics within the rodent population.

In this investigation, two new mathematical models for hantavirus infection in rodents are formulated. The models include the dynamics of susceptible, exposed, infective, and recovered male and female rodents. These new models extend some recent epidemic models that have been applied to hantavirus infection in rodents (Abramson and Kenkre, 2002; Abramson et al., 2003; Allen et al., 2003; Sauvage et al., 2003). The models of Abramson and Kenkre (2002) and Abramson et al., (2003) were applied to Sin Nombre virus in deer mice. Their models are reaction–diffusion systems of partial differential equations for susceptible and infected mice. Mice move randomly within a one-dimensional spatial habitat. Logistic growth is assumed with carrying capacity K. The carrying capacity is the driving force for the model dynamics. Traveling wave solutions and variability in population densities are studied as a function of the carrying capacity K. The model of Sauvage et al. (2003) was applied to Puumala virus infection in bank voles (Clethrionomys glareolus). Their model is a system of ordinary differential equations for rodents infected with hantavirus in two different habitats: optimal and suboptimal. The population is subdivided into susceptible and infected juveniles and adults. Logistic growth is assumed but the population dynamics are driven by an annual periodic birth function and a 3-year periodic carrying capacity. The model of Allen et al. (2003) was applied to an hantavirus infection (Black Creek Canal virus) and an arenavirus infection (Tamiami virus) in cotton rats (Sigmodontine hispidus). Their model is a system of differential equations with two states for infection with the two viruses. The two viruses differ in their modes of infection; the first virus is horizontally transmitted, whereas the second is primarily vertically transmitted. Conditions are determined for the two strains to coexist in the population.

The infection and persistence of hantavirus in its rodent host has little or no effect on survival (Glass et al., 1998). However, several studies, including our own, suggest there are distinct differences in males and females in the duration of shedding and viremia (Klein et al., 2001; Yahnke et al., 2001; Chu et al., 2003; McIntyre, et al., 2005). Further, males because of their biting and other aggressive behavior, generally have a higher prevalence of antibody to hantavirus in a rodent community (Childs, et al., 1994; Mills et al., 1997; Glass et al., 1998; Bernshtein, et al., 1999; Klein et al., 2001; Yahnke et al., 2001; McIntyre, et al., 2005). The presence of antibody does not give insight into the levels of virus that are shed nor into the duration of the shedding (Klein et al., 2001). Unfortunately, these types of analyses are difficult in nature, although recently, McIntyre et al. (2005) have looked at the RNA levels in male and female rodents infected with Bayou virus. It is clear that males are viremic but females are not. This suggests that the infectious period is longer for males than for females. As in most infectious diseases, there is a lag between exposure and infectivity, referred to as the incubation period. Because the life expectancy of rodents is relatively short, the incubation period cannot be neglected. Furthermore, infected rodents do not shed virus for their entire life. Once their infectious period ends, animals can be classified as recovered.

Our two new models are based in part on these recent models, however, they account for the differences in male and female seroprevalence and length of infectivity. The new features in our models are the inclusion of (i) males and females, (ii) an incubation or exposed class of individuals, (iii) and a recovered class of individuals (positive seroprevalence but not shedding the virus). The first model is a system of ordinary differential equations. The second model extends the first model to a system of stochastic differential equations (SDEs). Epidemic models that include an exposed class and a recovered class, in addition to susceptible and infective classes, are referred to as SEIR epidemic models. Unlike some of these recent models, we do not include spatial variation nor stages based on juveniles and adults.

In the next section, the male/female SEIR deterministic model is described. The basic reproduction number is computed for this model. For a special case of this model, the endemic equilibrium is computed. Then, in Section 3, a male/female SEIR stochastic model is formulated. Several numerical examples are presented in Section 4. The last section concludes with a summary.

2. SEIR deterministic model

The population is subdivided into males and females and further subdivided according to disease status: susceptible (S), exposed (E), infective (I), and recovered (R). Male rodents are denoted with a subscript m and females with a subscript f. For male rodents, the SEIR model takes the form

$$\frac{\text{d}{S}_{\text{m}}}{\text{d}t}=\frac{B\left(N_{\text{m}},N_{\text{f}}\right)}{2}-S_{\text{m}}\text{d}(N)-S_{\text{m}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right),$$ (1)

$$\frac{\text{d}{E}_{\text{m}}}{\text{d}t}=-E_{\text{m}}\text{d}(N)+S_{\text{m}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right)-\delta E_{\text{m}},$$ (2)

$$\frac{\text{d}{I}_{\text{m}}}{\text{d}t}=\delta E_{\text{m}}-I_{\text{m}}\text{d}(N)-{\gamma }_{\text{m}}{I}_{\text{m}},$$ (3)

$$\frac{\text{d}{R}_{\text{m}}}{\text{d}t}={\gamma }_{\text{m}}{I}_{\text{m}}-R_{\text{m}}\text{d}(N),$$ (4)

and for female rodents,

$$\frac{\text{d}{S}_{\text{f}}}{\text{d}t}=\frac{B\left(N_{\text{m}},N_{\text{f}}\right)}{2}-S_{\text{f}}\text{d}(N)-S_{\text{f}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{mf}}{I}_{\text{m}}\right),$$ (5)

$$\frac{\text{d}{E}_{\text{f}}}{\text{d}t}=-E_{\text{f}}\text{d}(N)+S_{\text{f}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{mf}}{I}_{\text{m}}\right)-\delta E_{\text{f}},$$ (6)

$$\frac{\text{d}{I}_{\text{f}}}{\text{d}t}=\delta E_{\text{f}}-I_{\text{f}}\text{d}(N)-{\gamma }_{\text{f}}{I}_{\text{f}},$$ (7)

$$\frac{\text{d}{R}_{\text{f}}}{\text{d}t}={\gamma }_{\text{f}}{I}_{\text{f}}-R_{\text{f}}\text{d}(N),$$ (8)

where density of males is $N_{\text{m}}=S_{\text{m}}+E_{\text{m}}+I_{\text{m}}+R_{\text{m}}$, density of females is $N_{\text{f}}=S_{\text{f}}+E_{\text{f}}+I_{\text{f}}+R_{\text{f}}$, and total population density is $N=N_{\text{m}}+N_{\text{f}}$. The function $B\left(N_{\text{m}},N_{\text{f}}\right)$ is the birth function. A harmonic birth function is assumed, one of the most commonly used birth functions,

$$B\left(N_{\text{m}},N_{\text{f}}\right)=\frac{2b{N}_{\text{m}}{N}_{\text{f}}}{N_{\text{m}}+N_{\text{f}}},$$

where b is the average litter size (Caswell, 2001; Iannelli et al., 2005). The maximal per capita birth rate occurs when the number of males equals the number of females.

In model (1)–(8), ${\beta }_{\text{f}},{\beta }_{\text{m}}$, and ${\beta }_{\text{mf}}$ are the contact rates, which differ depending on whether contact is with an infective male. In particular, ${\beta }_{\text{f}}$ is the contact rate of an infective female with either a susceptible female or a susceptible male. The contact rate β_m,f is an infective male with a susceptible female and the contact rate β_m is an infective male with a susceptible male. These contact rates generally differ because of the males’ aggressive behavior. The quantity 1/δ is the average length of the incubation period which is the same for males and females. The quantities 1/γ_m and 1/γ_f are the average lengths of the infectious periods for males and females, respectively.

The parameters ${\gamma }_{\text{m}},{\gamma }_{\text{f}},{\beta }_{\text{f}},{\beta }_{\text{m}}$, and ${\beta }_{\text{mf}}$ account for the differences in the epizoology between males and females. Fighting between males results in greater contacts and spread of hantavirus. Also, the infectious period in females is thought to be shorter than in males. Therefore, we make the following assumptions regarding the contact rates and the infectious periods,

$$\begin{array}{l}{\beta }_{\text{m}}\ge {\beta }_{\text{mf}}\ge {\beta }_{\text{f}},\\ \text{and}1/{\gamma }_{\text{m}}>1/{\gamma }_{\text{f}},\text{that}\text{is,}\\ {\gamma }_{\text{f}}>{\gamma }_{\text{m}}.\end{array}$$

The incubation period is the same for males and females (1/δ) as well as the density-dependent death rate $\text{d}(N)=a+cN,0<a<b/2$, and $0<c.$ A more general form for the density-dependent death rate can be assumed (e.g., Allen and Cormier, 1996; Mena-Lorca and Hethcote, 1992), but here we assume a simple linear form which leads to logistic growth of the population.

Differential equations for the densities of males, females, and total population can be found by summing the individual differential equations for the states. The male, female, and total population densities satisfy the following differential equations:

$$\begin{array}{l}\frac{\text{d}{N}_{\text{m}}}{\text{d}t}=\frac{B\left(N_{\text{m}},N_{\text{f}}\right)}{2}-N_{\text{m}}\text{d}(N),\\ \frac{\text{d}{N}_{\text{f}}}{\text{d}t}=\frac{B\left(N_{\text{m}},N_{\text{f}}\right)}{2}-N_{\text{f}}\text{d}(N),\\ \frac{\text{d}N}{\text{d}t}=B\left(N_{\text{m}},N_{\text{f}}\right)-N\text{d}(N),\end{array}$$

respectively. It can be shown that there exists a globally stable positive equilibrium for the total population densities (see the appendix). At this equilibrium, the number of males equals the number of females, $N_{\text{m}}=K/2=N_{\text{f}}$, and the total population density is N = K, where K is referred to as the carrying capacity. The carrying capacity K is the solution of $\text{d}(K)=b/2\text{or}K=(b/(2-a))/c$. Therefore, every equilibrium for the full model (1)–(8), must have the property that

$$S_{\text{m}}+E_{\text{m}}+I_{\text{m}}+R_{\text{m}}=K/2=S_{\text{f}}+E_{\text{f}}+I_{\text{f}}+R_{\text{f}}.$$

One particular equilibrium with this property is the disease-free equilibrium (DFE), where $S_{\text{m}}=K/2=S_{\text{f}}$ and $E_j=I_j=R_j=0,j=\text{m},\text{f}$. Whether the DFE is stable in the full model (1)–(8) is important for the control of the disease in the rodent population.

The stability of the DFE depends on the magnitude of the basic reproduction number. The basic reproduction number, ${\mathcal{R}}_0$, is an important parameter in epidemiology. This parameter represents the number of secondary infections caused by one infective individual in an entirely susceptible population (Diekmann et al., 1990; Hethcote, 2000). When ${\mathcal{R}}_0>1$, then the DFE is locally asymptotically stable and when ${\mathcal{R}}_0>1$, the DFE is unstable and a disease outbreak is possible (van den Driessche and Watmough, 2002).

The method of Diekmann et al. (1990) and van den Driessche and Watmough (2002) can be used to calculate the basic reproduction number. First, the next generation matrix $F{V}^{-1}$ is formed. Then, the spectral radius of the next generation matrix is calculated, ${\mathcal{R}}_0$ = ρ(FV⁻¹).

To form the next generation matrix, states are divided into infectious, (E_m, E_f, I_m, I_f), and noninfectious (S_m, S_f, R_m, R_f). Then, on the basis of the infectious states at the DFE, entries in the matrix F represent the rate at which new infections are created and the entries in matrix V−¹ represent the average length of time spent in a particular state. For our model, F and V−¹ are 4 × 4 matrices,

$$F=\left(\begin{array}{cccc}0& 0& {\beta }_{\text{m}}K/2& {\beta }_{\text{f}}K/2\\ 0& 0& {\beta }_{\text{mf}}K/2& {\beta }_{\text{f}}K/2\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right),$$

and

$$V^{-1}=\left(\begin{array}{cccc}\frac{1}{b/2+\delta }& 0& 0& 0\\ 0& \frac{1}{b/2+\delta }& 0& 0\\ \frac{\delta }{\left(b/2+{\gamma }_{\text{m}}\right)(b/2+\delta )}& 0& \frac{1}{b/2+{\gamma }_{\text{m}}}& 0\\ 0& \frac{\delta }{\left(b/2+{\gamma }_{\text{f}}\right)(b/2+\delta )}& 0& \frac{1}{b/2+{\gamma }_{\text{f}}}\end{array}\right).$$

The spectral radius ρ(FV−¹) can be calculated,

$$\begin{gathered} {\mathcal{R}}_0=\frac{{\beta }_{\text{m}}\delta K/4}{\left(b/2+{\gamma }_{\text{m}}\right)(b/2+\delta )}+\frac{{\beta }_{\text{f}}\delta K/4}{\left(b/2+{\gamma }_{\text{f}}\right)(b/2+\delta )} \\ +\frac{\delta K/4\sqrt{{\left[{\beta }_{\text{m}}\left(b/2+{\gamma }_{\text{f}}\right)+{\beta }_{\text{f}}\left(b/2+{\gamma }_{\text{m}}\right)\right]}^2-4{\beta }_{\text{f}}\left({\beta }_{\text{m}}-{\beta }_{\text{mf}}\right)\left(b/2+{\gamma }_{\text{f}}\right)\left(b/2+{\gamma }_{\text{m}}\right)}}{\left(b/2+{\gamma }_{\text{m}}\right)\left(b/2+{\gamma }_{\text{f}}\right)(b/2+\delta )}. \end{gathered}$$ (9)

It is important to note that the basic reproduction number, defined in (9), is proportional to the carrying capacity K. As K increases ${\mathcal{R}}_0$ also increases and so does ${\mathcal{R}}_0$ and K is a consequence of the assumption of mass action transmission rate, a reasonable assumption for rodent populations.

In the special case, β_mf = β_m, males and females have similar dynamics. The basic reproduction number in this special case simplifies to

$${\mathcal{R}}_0=\frac{{\beta }_{\text{m}}\delta K/2}{\left(b/2+{\gamma }_{\text{m}}\right)(b/2+\delta )}+\frac{{\beta }_{\text{f}}\delta K/2}{\left(b/2+{\gamma }_{\text{f}}\right)(b/2+\delta )}.$$

Notice that this latter expression for the basic reproduction number is the sum of two basic reproduction numbers, one for males and one for females. The endemic equilibrium is straightforward to calculate in this special case (Hethcote, 2000),

$$\begin{array}{l}{\overline{S}}_j=\frac{K}{2{\mathcal{R}}_0},\\ {\overline{E}}_j=\frac{(b/2)(K/2)}{b/2+\delta }\left(1-\frac{1}{{\mathcal{R}}_0}\right),\\ {\overline{I}}_j=\left(\frac{\delta }{b/2+{\gamma }_j}\right){\overline{E}}_j,\\ {\overline{R}}_j=\left(\frac{{\gamma }_j}{b/2}\right){\overline{I}}_j,\end{array}$$

for j = m, f. Thus, at the endemic equilibrium, the fraction of rodents that are antibody positive (seroprevalence) equals the proportion of rodents that are either infective or recovered.

$$\frac{{\overline{I}}_{\text{m}}+{\overline{I}}_{\text{f}}+{\overline{R}}_{\text{m}}+{\overline{R}}_{\text{f}}}{K}=\frac{\delta }{b/2+\delta }\left(1-\frac{1}{{\mathcal{R}}_0}\right).$$ (10)

An estimate for the magnitude of ${\mathcal{R}}_0$ can be obtained from formula (10). As an example, we consider the rice rat (O. palustris), the rodent host for Bayou virus. Let the time unit be 2 months which is the approximate gestation period (25 days) plus the time to reach sexual maturity (40–45 days) (Davis and Schmidley, 1994). The incubation period for Bayou virus in O. palustris is approximately 2–3 weeks, 1/δ ≈ 1/4 − 3/8 (Chu, personal communication). The litter size for O. palustris ranges from two to seven with an average litter size of four (with five to six litters per year), b ≈ 4 (Davis and Schmidley, 1994). Studies conducted in eastern Texas on the prevalence of Bayou virus in O. palustris indicate that the overall seroprevalence is about 16% of the population (McIntyre et al., 2005). Applying formula (10), the value of ${\mathcal{R}}_0$ is approximately 1.32–1.39, very close to the thresh-old value of 1. When β_m > β_mf the value of ${\mathcal{R}}_0$ is even smaller, as can be seen from formula (9).

When δ is large relative to b/2, the incubation period 1/δ is short and the exposed class E may be ignored. The model in this case simplifies to an SIR model. The equilibrium fraction in the SIR model corresponding to (10) satisfies

$$\frac{{\overline{I}}_{\text{m}}+{\overline{I}}_{\text{f}}+{\overline{R}}_{\text{m}}+{\overline{R}}_{\text{f}}}{K}=\left(1-\frac{1}{{\mathcal{R}}_0}\right).$$

In this case, the factor δ/(b/2 + δ) in formula (10) is equal to 1.

The estimate for ${\mathcal{R}}_0$ based on formula (10) assumes the proportion of seropositive males and females are equal. Our data suggest that this is not the case for New World hantaviruses. Thus, this estimate obtained from (10) provides only an upper bound for the ${\mathcal{R}}_0$ given in (9). In the numerical simulations, we make the more realistic assumptions that β_m > max{β_mf,β_f} and β_mf = β_f. Contacts between two males are generally aggressive encounters to defend territory and result in greater transmission of the disease than contacts between two males or a male and a female.

3. SEIR stochastic model

We formulate a stochastic differential equation (SDE) model based on the deterministic formulation (1)–(8). The stochastic model assumes there is variability due to births, deaths, and transitions between the states (a susceptible individual becomes exposed, then infective and recovered). We apply a method developed by Allen (1999) to derive a system of Ito SDEs. The variables for the males, S_m,..., R_m and the females, S_f,..., R_f, are continuous random variables whose values lie in [0,∞]. The DFE, where the exposed, infective, and recovered states are zero, E_m = 0 = E_f, I_m = 0 = I_f, and R_m = 0 = R_f, is an absorbing state for the stochastic model. When this state is reached the epidemic ends. However, depending on the parameters, the time to reach this state may be extremely long.

The derivation of the SDEs is based on the continuous-time Markov (chain formulation. The expected rate of change in the state variables, $\mathrm{\Delta }X={\left(\mathrm{\Delta }{S}_{\text{m}},\mathrm{\Delta }{E}_{\text{m}},\dots ,\mathrm{\Delta }{R}_{\text{f}}\right)}^{\text{T}}$, where $\mathrm{\Delta }{S}_{\text{m}}=S_{\text{m}}(t+\mathrm{\Delta }t)-S(t)$, etc., is given by the right-hand side of the SEIR deterministic model (1)–(8). However, the covariance for the rate of change in the state variables leads to a system of Itô SDEs (Allen, 1999; Allen, 2003; Kirupaharan and Allen, 2004). The Itô SDEs for the males take the form

$$\frac{\text{d}{S}_m}{dt}=\frac{B\left(N_m,N_f\right)}{2}-S_m\text{d}(N)-S_m\left({\beta }_f{I}_f+{\beta }_m{I}_m\right)+\sum _{j=1}^8{a}_{1j}\frac{\text{d}{W}_j}{dt}$$

$$\frac{\text{d}{E}_m}{dt}=-E_m\text{d}(N)+S_m\left({\beta }_f{I}_f+{\beta }_m{I}_m\right)-\delta E_m+\sum _{j=1}^8{a}_{2j}\frac{\text{d}{W}_j}{dt},$$

$$\frac{\text{d}{I}_m}{dt}=\delta E_m-I_m\text{d}(N)-{\gamma }_m{I}_m+\sum _{j=1}^8{a}_{3j}\frac{\text{d}{W}_j}{dt},$$

$$\frac{\text{d}{R}_m}{dt}={\gamma }_m{I}_m-R_m\text{d}(N)+\sum _{j=1}^8{a}_{4j}\frac{\text{d}{W}_j}{dt},$$

where W_j, j = 1,2,...,8, are eight independent Wiener processes. A similar set of SDEs apply to the female population.

The coefficients a_ij of the Wiener processes in the male/female SDE model are elements of the matrix A= (a_ij). Matrix A is an 8 × 8 matrix satisfying A = $\sqrt{CV}$, the unique square root of the positive definite symmetric matrix CV_. Matrix CV Δt is the approximate covariance matrix for the change in the states ΔX in time Δt.

To order Δt, CV

$$\begin{gathered} CV\mathrm{\Delta }t=\mathbf{E}\left(\mathrm{\Delta }X{[\mathrm{\Delta }X]}^{\text{T}}\right)-\mathbf{E}(\mathrm{\Delta }X)\left[\mathbf{E}{(\mathrm{\Delta }X)}^{\text{T}}\right] \\ \approx \mathbf{E}\left(\mathrm{\Delta }X{[\mathrm{\Delta }X]}^{\text{T}}\right) \\ =\mathbf{E}\left(\begin{array}{cccc}\mathrm{\Delta }{S}_{\text{m}}\mathrm{\Delta }{S}_{\text{m}}& \mathrm{\Delta }{S}_{\text{m}}\mathrm{\Delta }{E}_{\text{m}}& \cdots & \mathrm{\Delta }{S}_{\text{m}}\mathrm{\Delta }{R}_{\text{f}}\\ \mathrm{\Delta }{S}_{\text{m}}\mathrm{\Delta }{E}_{\text{m}}& \mathrm{\Delta }{E}_{\text{m}}\mathrm{\Delta }{E}_{\text{m}}& \cdots & \mathrm{\Delta }{E}_{\text{m}}\mathrm{\Delta }{R}_{\text{f}}\\ ⋮& ⋮& ⋮& ⋮\\ \mathrm{\Delta }{S}_{\text{m}}\mathrm{\Delta }{R}_{\text{f}}& \mathrm{\Delta }{E}_{\text{m}}\mathrm{\Delta }{R}_{\text{f}}& \cdots & \mathrm{\Delta }{R}_{\text{f}}\mathrm{\Delta }{R}_{\text{f}}\end{array}\right) \end{gathered}$$

where E is the expectation (see, e.g., Allen, 1999; Allen, 2003; Kirupaharan and Allen, 2004). The preceding approximation holds because E(ΔX)[E(ΔX)^T] is order (Δt)². In particular, for our model, matrix CV is the positive definite symmetric matrix which takes the form,

$$CV=\left(\begin{array}{cc}{C}_{\text{m}}& 0\\ 0& C_{\text{f}}\end{array}\right).$$

Submatrices C_m and C_f are 4 × 4 tridiagonal matrices and 0 is a 4 × 4 zero matrix. Submatrix C_m is

$$\left(\begin{array}{cccc}\frac{B}{2}+S_{\text{m}}\left(\text{d}+{\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right)& -S_{\text{m}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right)& 0& 0\\ -S_{\text{m}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right)& E_{\text{m}}(\delta +\text{d})+S_{\text{m}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right)& -\delta E_{\text{m}}& 0\\ 0& -\delta E_{\text{m}}& \delta E_{\text{m}}+I_{\text{m}}\left({\gamma }_{\text{m}}+\text{d}\right)& -{\gamma }_{\text{m}}{I}_{\text{m}}\\ 0& 0& -{\gamma }_{\text{m}}{I}_{\text{m}}& {\gamma }_{\text{m}}{I}_{\text{m}}+R_{\text{m}}\text{d}\end{array}\right)$$

and submatrix C_f is

$$\left(\begin{array}{cccc}\frac{B}{2}+S_{\text{f}}\left(\text{d}+{\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{mf}}{I}_{\text{m}}\right)& -S_{\text{f}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right)& 0& 0\\ -S_{\text{f}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{m}}{I}_{\text{m}}\right)& E_{\text{f}}(\delta +\text{d})+S_{\text{f}}\left({\beta }_{\text{f}}{I}_{\text{f}}+{\beta }_{\text{mf}}{I}_{\text{m}}\right)& -\delta E_{\text{f}}& 0\\ 0& -\delta E_{\text{f}}& \delta E_{\text{f}}+I_{\text{f}}\left({\gamma }_{\text{f}}+\text{d}\right)& -{\gamma }_{\text{f}}{I}_{\text{f}}\\ 0& 0& -{\gamma }_{\text{f}}{I}_{\text{f}}& {\gamma }_{\text{f}}{I}_{\text{f}}+R_{\text{f}}\text{d}\end{array}\right),$$

where d ≡ d(N).

The system of Itô SDEs can be easily seen to be consistent with the ordinary differential equation model (1)–(8). Numerical methods applied to the Ito SDEs are generally more efficient than, for example, a continuous-time Markov chain model (Kloeden and Platen, 1992; Kloeden et al., 1997; Allen and Allen, 2003). Stochastic sample paths of the system of Ito SDEs are presented in the next section and compared to the solution of the deterministic model.

4. Numerical examples

Three sets of figures illustrate the dynamics of the deterministic and the stochastic SEIR epidemic models. Parameter values are chosen in accordance with the epizoology of the rice rat (O. palustris) and Bayou virus. The basic time unit is chosen as 2 months, a time period approximately equal to the gestation period plus the time for rodents to become sexually mature. For a bimonthly time period, we choose δ = 4(1/δ = 2 weeks) and b = 4 (average litter size). Other parameter values are chosen in a realistic range, but estimates for them are not known. We assume that the contact rate for males is five times that for females ${\beta }_{\text{m}}=5{\beta }_{\text{f}}\text{and}{\beta }_{\text{mf}}={\beta }_{\text{f}}$; the infectious period for males is twice that for, females, $1/{\gamma }_{\text{m}}=2\left(1/{\gamma }_{\text{f}}\right)$; and the carrying capacity is K = 1000 animals. The remaining parameter values are chosen so that a reasonable estimate is obtained for ${\mathcal{R}}_0$.

$${\beta }_{\text{m}}=0.01,{\gamma }_{\text{m}}=0.5,a=0.01,\text{and}c=1.99\times {10}^{-3}.$$

With these parameter values, the basic reproduction number is ${\mathcal{R}}_0$ = 1.38 (based on formula (9)). In the numerical simulations, the initial conditions are S_m(0) = 450 = S_f(0), E_m(0) = 10 = I_m(0) = R_m(0), and E_f(0) = 5 = I_f(0) = R_f(0).

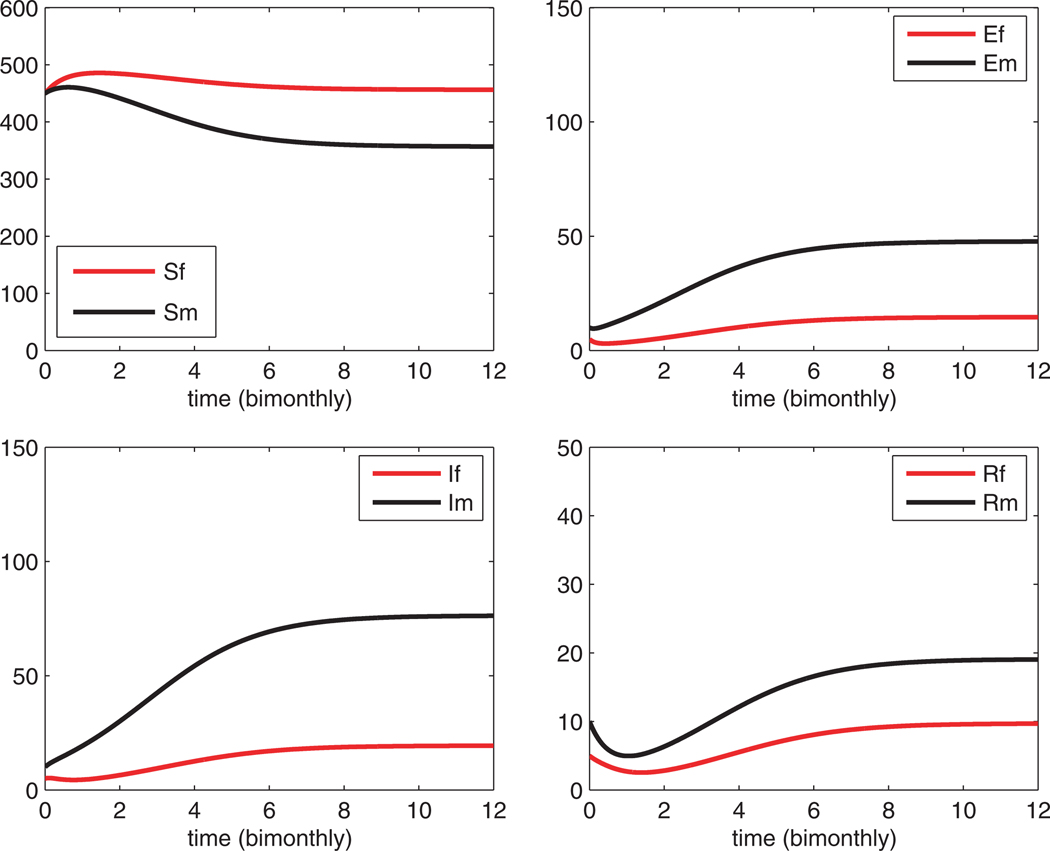
Because ${\mathcal{R}}_0$ > 1, the DFE with ${\overline{S}}_{\text{m}}=500={\overline{S}}_{\text{f}}$ is not stable. However, there is a stable endemic equilibrium, as illustrated in the numerical simulations in Fig. 1. Solutions eventually level off at the endemic SEIR equilibrium, males: 357.1, 47.7, 76.2, 19.1, and females: 456.4, 14.5, 19.4, 9.7. It is clear that male seroprevalence is much greater than female seroprevalence. Seroprevalence at the endemic equilibrium is approximately 12.5%. Male seroprevalence is approximately 3.3 times greater than female seroprevalence.

Fig. 1.

Solution to the deterministic SEIR epidemic as a function of time. An endemic equilibrium for males: 357.1, 47.7, 76.2, 19.1, and females: 456.4, 14.5, 19.4. 9.7, is reached. The total population size at equilibrium equals the carrying capacity K = 1000. Seroprevalence is 12.5% at the endemic equilibrium.

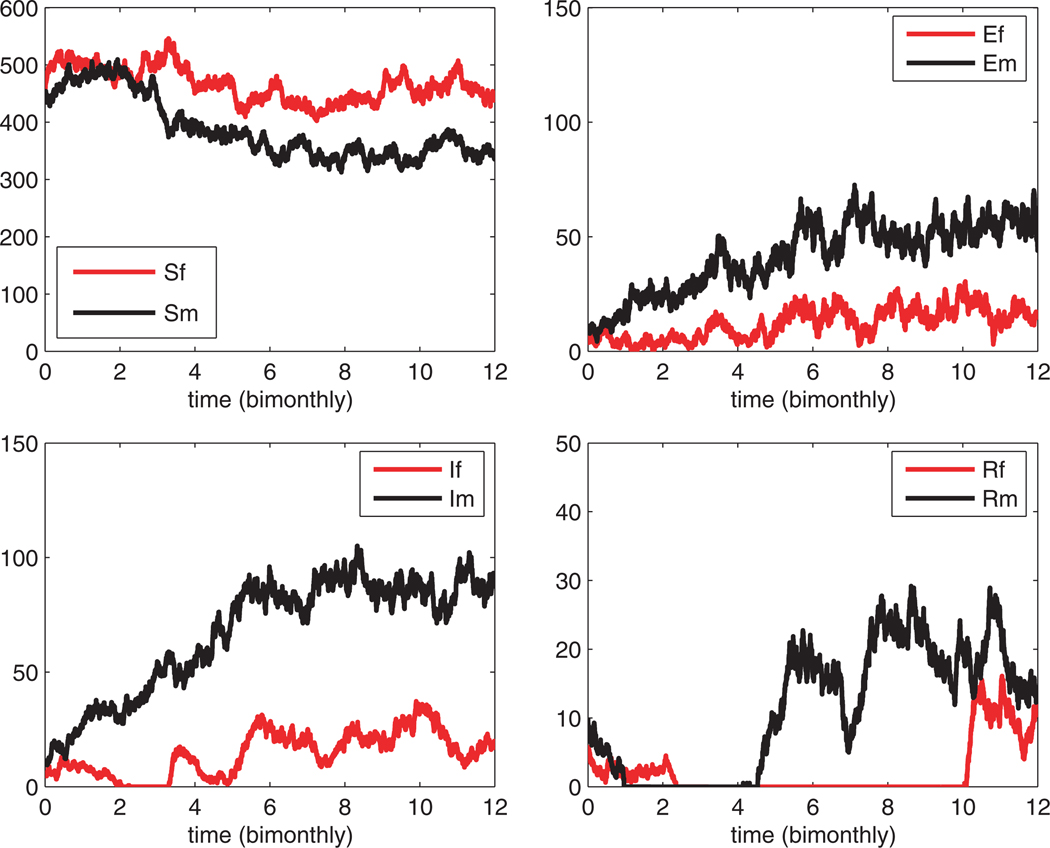
One sample path of the stochastic SEIR epidemic model is graphed in Fig. 2. The parameter values are the same as in Fig. 1. Note that the stochastic variability allows for certain disease stages to reach very low levels but, because infection is maintained in the male population, the disease persists in the population.

Fig. 2.

One sample path of the stochastic SEIR epidemic model. The parameter values and initial conditions are the same as in Fig. 1.

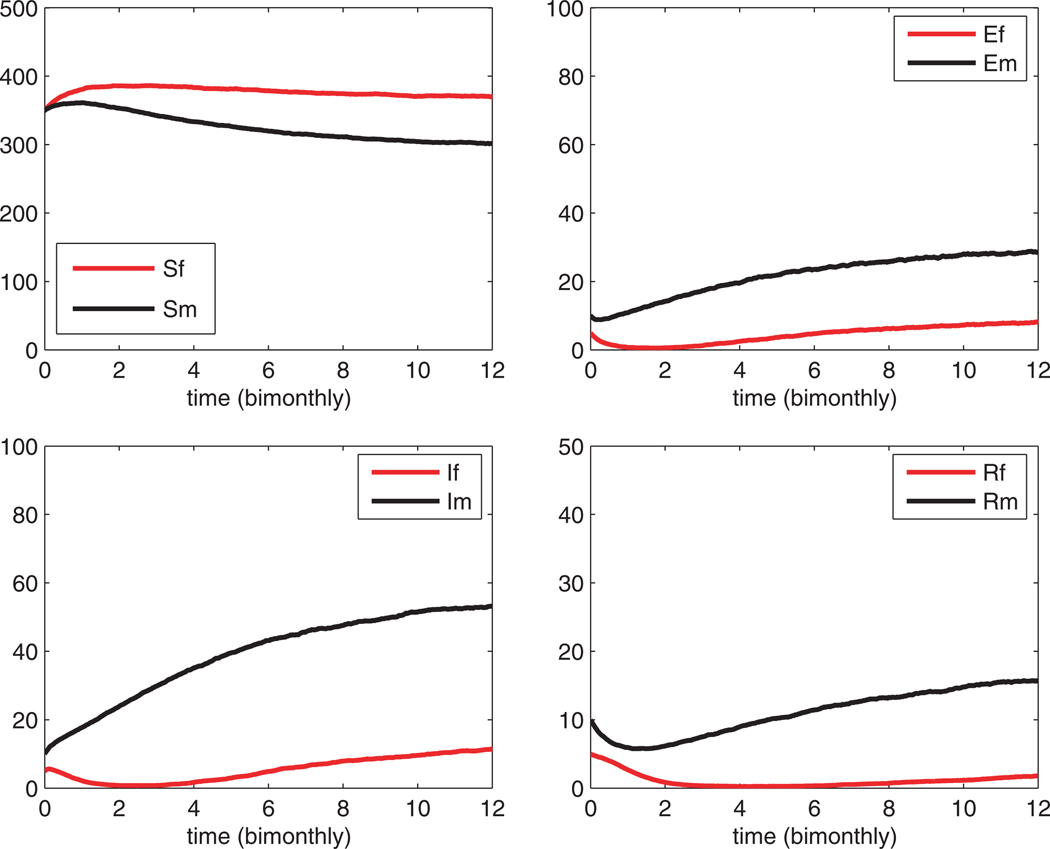
In Fig. 3. 1000 sample paths are averaged. The average seroprevalence in the second year is 10.4%. This level is lower than the deterministic model. The reason for this difference in the two models is that in the stochastic model, absorption may occur (the DFE is reached) or some of the random variables may be zero for a period of time in some of the sample paths (as in Fig. 2).

Fig. 3.

An average of 1000 sample paths for the stochastic SEIR model. Compare this figure with Fig. 1. The average seroprevalence in year 2 is 10.4%.

5. Conclusion

Hantavirus seroprevalence in wild rodent populations is relatively low, ranging from 5 to 12% in C. laucha in Paraguay (Yahnke et al., 2001; Chu et al., 2003) and 16% in O. palustris in eastern Texas (McIntyre et al., 2005). Seroprevalence is generally much higher in males than in females, four times greater in male O. palustris in eastern Texas (McIntyre et al., 2005) and approximately three times greater in male C. laucha in Paraguay (Chu et al., 2003). Two new SEIR epidemic models have been developed to capture these realistic features of rodent–hantavirus dynamics. Their dynamics are illustrated in the numerical examples. In addition, the stochastic models capture the large variability in male and female seroprevalence that is seen in field data (Yahnke et al., 2001; Chu et al., 2003; McIntyre, et al., 2005).

It is clear from calculation of the basic reproduction number (9) that the carrying capacity K is an important parameter that affects disease outbreaks in rodent populations. The importance of the carrying capacity was also shown in the hantavirus models studied by Abramson and Kenkre (2002) Abramson et al. (2003) and Sauvage et al. (2003). The outbreak of Sin Nombre virus in 1993 that occurred in New Mexico was associated with increased densities of deer mice (CDC NCID, 2004). Densities increased from less than one deer mouse per hectare prior to 1991 to 20–30 per hectare during the spring of 1993 (CDC NCID, 2004). Environmental variations in space and time impact the carrying capacity and ultimately rodent densities (Langlois et al., 2001). In future work, we plan to extend our male/female SEIR epidemic models to spatially explicit patch models.

Appendix

The dynamics of the male/female system without infection can be completely analyzed. The male/female system satisfies

$$\begin{array}{l}\frac{\text{d}{N}_{\text{m}}}{\text{d}t}=\frac{B\left(N_{\text{m}},N_{\text{f}}\right)}{2}-N_{\text{m}}\text{d}(N)=N_{\text{m}}\left(\frac{b{N}_{\text{f}}}{N_{\text{m}}+N_{\text{f}}}-a-c\left(N_{\text{m}}+N_{\text{f}}\right)\right),\\ \frac{\text{d}{N}_{\text{f}}}{\text{d}t}=\frac{B\left(N_{\text{m}},N_{\text{f}}\right)}{2}-N_{\text{f}}\text{d}(N)=N_{\text{f}}\left(\frac{b{N}_{\text{m}}}{N_{\text{m}}+N_{\text{f}}}-a-c\left(N_{\text{m}}+N_{\text{f}}\right)\right),\end{array}$$

where $N=N_{\text{m}}+N_{\text{f}},N_{\text{m}}(0)>0\text{and}{N}_{\text{f}}(0)>0$. Solutions $N_{\text{m}}(t)\text{and}{N}_{\text{f}}(t)$ are positive for all time. This system has a unique positive equilibrium given by $N_{\text{m}}=K/2=N_{\text{f}}$, where $K=(b/2-a)/c>0$. We show that this equilibrium is globally symptotically stable.

Let $u=N_{\text{m}}-N_{\text{f}}$. Then

$$\frac{\text{d}u}{\text{d}t}=-u(a-cN).$$

It follows that ${\lim }_{t\to \infty }u(t)=0={\lim }_{t\to \infty }[N_{\text{m}}(t)-N_{\text{f}}(t)]$. In addition, if u(0) ≥ 0(≤ 0), then $u(t)\ge 0(\le 0)$ for all time. Without loss of generality, assume u (0) ≥ 0. Let $ϵ>0$ such that $b/2>cϵ+a$. Choose T sufficiently large such that $0\le u(t)<ϵ$ for $t\text{>}T$. Then for t > T,

$$\frac{\text{d}{N}_{\text{m}}}{\text{d}t}\le N_{\text{m}}\left(\frac{b}{2}+cϵ-a-2c{N}_{\text{m}}\right),$$

and

$$\frac{\text{d}{N}_{\text{f}}}{\text{d}t}\le N_{\text{f}}\left(\frac{b}{2}-cϵ-a-2c{N}_{\text{f}}\right).$$

Thus,

$$\frac{b/2-cϵ-a}{2c}\le \underset{t\to \infty }{\lim \inf }{N}_{\text{f}}(t)\le \underset{t\to \infty }{\lim \sup }{N}_{\text{m}}(t)\le \frac{b/2-cϵ-a}{2c}.$$

Because ϵ is arbitrary, solutions N_m(t) and N_f(t) approach the unique positive equilibrium K/2.