Strategic design of precautionary measures for airport passengers in times of global health crisis Covid 19: Parametric modelling and processing algorithms

Abstract

Presently, the negative results of a pandemic loom in a threatening manner on an international scale. Facilities such as airports have contributed significantly to the global spread of the COVID-19 virus. Therefore, in order to address this challenge, studies on sanitary risk management and the proper application of countermeasures should be carried out. To measure the consequences over passenger flow, simulation modelling has been set up at Casablanca Mohammed V International Airport. Several scenarios using daily traffic data were run in different circumstances. This allowed the development of some assumptions regarding the overall capacity of the airport. The proposed simulations make it possible to calculate the number of passengers to be processed in accordance with the available check-in counters based on the proposed sanitary measures.

Highlights (for review)

• ●The aviation sector has been experiencing an unprecedented crisis since March 2020 due to the Covid-19 pandemic and a solution need to be found for the gradually reopening and the risk minimisation.
• ●This article proposes simulations and discussions on the possible effects of the social distanciation measures and to test their applicability in an international airport.
• ●A bibliographic study of recent work in the same field of the article.
• ●Distribution of passengers according to various scenarios.
• ●Mathematical modelling of the problem.

1. Introduction

The aviation sector has been experiencing an unprecedented crisis since March 2020. Indeed, almost all airports have been paralyzed following the outbreak of the Covid-19 pandemic. Euro control had announced a significant 88% reduction in the number of flights by May 1, 2020 (Eurocontrol, 2020a, 2020b). The flow of international traffic contributed significantly to the spread of the virus worldwide (Kraemer et al., 2020). In Europe, for example, it seems that the areas least affected by the virus are those where no international airport is located. One of the main characteristics of COVID-19 is its long incubation period, which currently averages 5.2 days (Guan et al., 2020). Contagiousness during the incubation period is one of the reasons why COVID19 spreads so widely compared to other viruses, making it extremely difficult to exclude the possibility of asymptomatic passengers passing through the airport (Postorino et al., 2020; Pullano et al., 2020). According to the International Civil Aviation Organization (ICAO) (ICAO, 2020), international air traffic will experience a significant decline in the order of 44%–80% in the number of international passengers in 2020 compared to 2019. The Airports Council International (ACI) (ACI, 2012) estimates that airports will lose two fifths of their passenger traffic or more than $76 billion in revenues in 2020 compared to the status quo. The International Air Transport Association (IATA) (IATA, 2020), which represents the airlines, estimates that revenue passenger-kilometers will decrease by 48% in 2020 compared to 2019. Over time, economic activity will resume as governments strive to restore economic growth and recover, which will require a resumption of airport activity. However, airports need to be reopened gradually while being aware of the potential risk generated by the hyper mobility experienced so far in order to avoid a second wave of the pandemic. To date, there is no published solution for a passenger flow management system within the framework of the new health constraints. Nevertheless, certain rules and standards are defined by IATA to guarantee the quality requirements of the passenger assistance service in the terminal area, on which we have based our proposals for additional measures in line with sanitary requirements for such a pandemic. Social distancing is one of the main measures agreed, which will affect the capacity of the airport, although the distances recently adopted by some airports make this issue a subject for debate. Accordingly, this study seeks to determine the necessary parameters for passengers distancing in order to minimize the potential spread of the virus without compromising the airport's ability to manage the flow of passengers. Therefore, this study proposes simulations and discussions on the possible effects of these measures and test their applicability.

The proposed solution differs from other passenger flow management systems in that it introduces preventive measures mandated by the World Health Organization (WHO), as well as health precautionary measures at airports. This has led us to study the movement of passengers in this context in order to develop a parametric model capable of adjusting the health measures to the expected flow of passengers and also of verifying its usefulness.

It has been decided to carry out the study in the country's busiest and best-equipped terminal, based on statistical data relative to the time of congestion. This is intended to evaluate the actions taken so that it is possible to determine if they have had viable results.

This document proposes a simulation tool to better manage the flow of passengers, as part of an approach that integrates quality of service standards and the new requirements of health regulations within airports. This paper is divided into eight sections: The first section highlights the immediate and lasting impact on the aviation sector in the wake of the Covid-19 pandemic crisis. The second section outlines context information for the simulation process. In the third section, the conception is presented. The fourth section is about the mathematical modelling of the variables parameters. Then in section five the simulation is exposed. The validation model and the simulation analysis are discussed. In the sixth section Results and discussion are presented in the seventh section. In the last section, some conclusions are drawn.

2. Context

2.1. Context of the simulation process

Casablanca Mohammed V International Airport has three terminals with a total capacity of 14 million passengers per year and is the hub of the Moroccan airport network. The surface area of each terminal is respectively 76,000 $m^2$ for T1, 66,000 $m^2$ for T2 and 4000 $m^2$ for T3. It is connected to more than 96 international destinations by 840 weekly frequencies operated by 24 airlines. The T1 terminal will be used in this study because of its capacity, state-of-the-art infrastructure and equipment that meets current international standards for safety, security and quality of service (ONDA, 2019).

2.2. Precautionary measures required at the airport

Under the International Health Regulations (IHR), airport authorities are required to establish effective contingency plans and arrangements to deal with events that may constitute a public health emergency of international concern. The current outbreak of a new coronavirus disease (COVID-19) has spread across several borders, resulting in demands for detection and management of suspicious cases. In order to implement the sanitary passenger flow management model proposed in this article, it is assumed that the guidelines for the detection and management of sick travelers suspected of being infected are applied in accordance with the Interim Guidelines for the Management of Ill Travelers published on February 16, 2020 (World Health Organization, Apr. 2020), and that the prevention rules defined by the World Health Organization (WHO) are implemented within airport facilities (World Health organization, Feb. 2020). In addition, we have proposed additional precautionary measures, such as physical separators between passengers and users, barriers between boarding gates, and signage indicating itineraries, so that departing and arriving passengers do not cross each other.

2.3. IATA terminal standards

Attention to the LOS here is essential, especially in times of crisis. Indeed, it is an indicator that allows to observe the fluidity in the treatment of the flow of passengers. In times of crisis, it is easy to observe overflows, passengers who get angry because of the conditions, etc. Compliance with the LOS partly makes it possible to avoid having to manage overflows due for example to a long waiting time. This is why it remains an indicator which, even in times of crisis, must be watched. International standards have been established for terminals. The study's approach advocates that measures relating to waiting time, queue size and passenger handling rates should follow the IATA quality of service standards (Bezerra and Gomes, 2020) illustrated in the section. Table 1 present the quality of service scale represented by IATA (IATA, 1989; Guilhem and FuSo, 2010).

Table 1.

Level of Service (LOS) as transcribed by IATA in the form of a quality of service scale.

Level	Level of Service	Flow	Delay	Confort
A	Excellent	Free	None	Excellent
B	High	Stable	Very Few	High
C	Good	Stable	Acceptable	Good
D	Adequate	Unstable	Passable	Adequate
E	Inadequate	Unstable	Unacceptable	Inadequate

The occupancy of a waiting area varies considerably according to the time spent by a passenger in that area. Waiting time at the various modules is a key factor in the quality of service and an essential parameter in the sizing and study of a terminal's capacity. It is extremely difficult to establish a precise relationship between waiting time, level of service and available space per passenger. A first indicator of the quality of service is the space available per passenger in waiting and traffic areas, translated on the level of service scale by space allocation ratio expressed in $m^2$ per passenger. Table 2 presents the ratios recommended by IATA for each passenger as a function of quality of service. A simplified way to approach the problem is to set maximum acceptable wait times. Table 3 shows the maximum waiting times, in minutes, recommended by IATA for each processing module based on quality of service (IATA, 1989), (Baumann et al., 2017). These maximum acceptable waiting times are to be adapted according to the context, the airport's service quality objectives and the type of traffic (Guilhem and FuSo, 2010). Generally speaking, for a passenger, a waiting time is unacceptable as soon as it exceeds 20 min (Chang et al., 2008).

Table 2.

Level of Service (LOS) as transcribed by IATA in the form of a quality of service scale.

	$M^2$ /PAX
Wait at check-in	A	B	C	D	E
	1,7	1,4	1,2	1,1	0,9
	1,8	1,5	1,3	1,2	1,1
	2,3	1,9	1,7	1,6	1,5
	2,6	2,3	2	1,9	1,8

Table 3.

The maximum waiting time for passengers.

Level of Service	A	B	C	D	E
Time (min)	0–12		12–30

3. Conception

3.1. Passenger flow conception

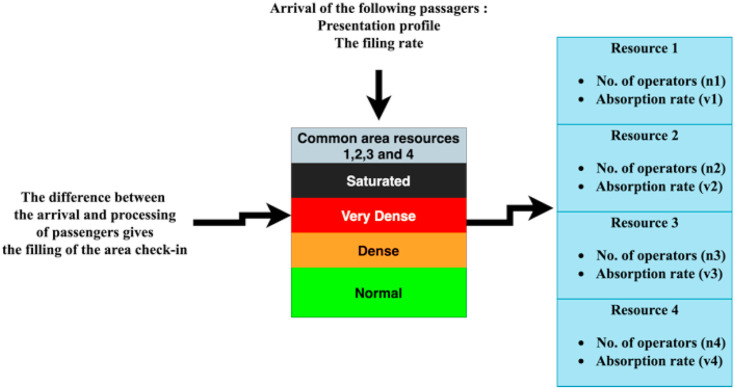
Regarding passenger flow management, it is based on the concept of the faucet filling a leaking bucket, as shown in Fig. 1 , where the faucet represents the flow of passengers, and the leakage represents the flow of processed passengers, while the filling of the bucket results from the difference between incoming and processed passengers (Park and Se-Yeon; KağanAlbayrak et al., 2020) Passengers are required to proceed to the check-in area in accordance with the rules in force and to follow the process laid down for departing passengers (Bezerra and Gomes, 2020), as illustrated in Fig. 2 .

Fig. 1.

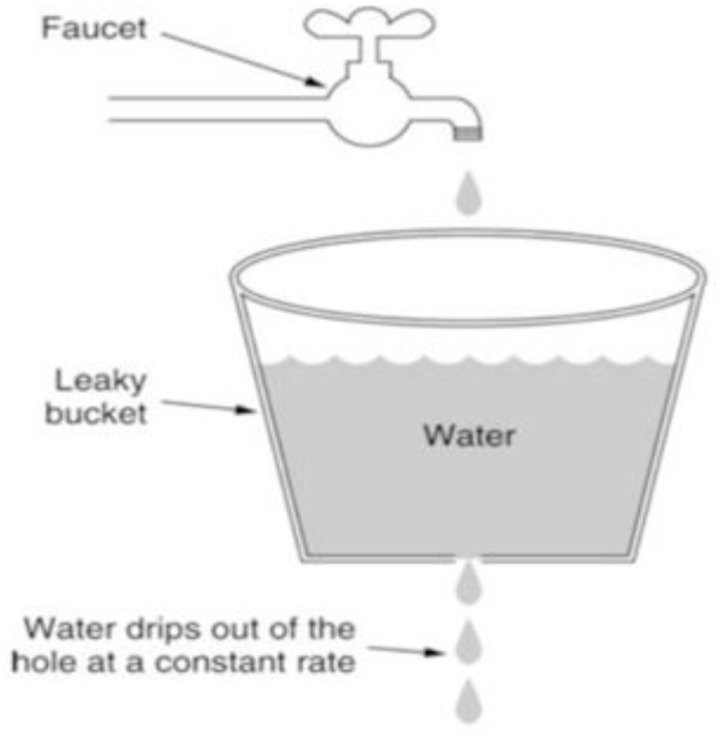
Principle of Filling a Leaking bucket.

Fig. 2.

Presentation of the passengers in the check-in area.

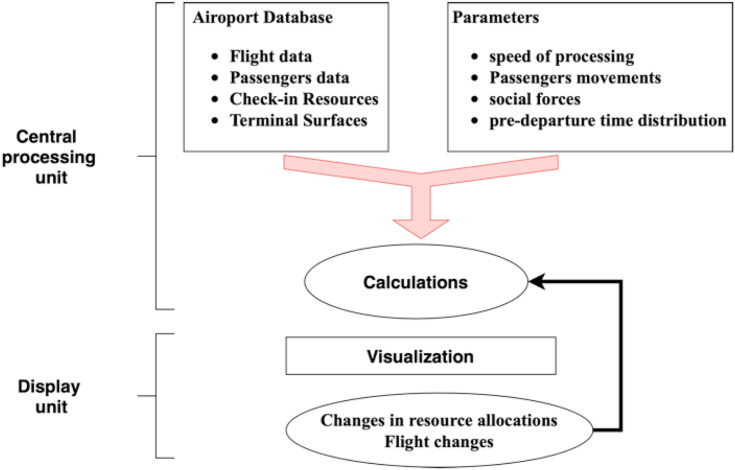
3.2. DATA input

The simulation model contains a central processing unit and a display unit. The input data is divided into two groups as shown in Fig. 3 . The first part in blue corresponds to flight data, passenger data, check-in surface and resources. The second part in green represents the variable parameters, which include the speed of processing, passengers’ movement models, social force and deviations, and the distribution of pre-departure time (Yeh and Kuo, 2003).

Fig. 3.

Presentation of the passengers in the check-in area.

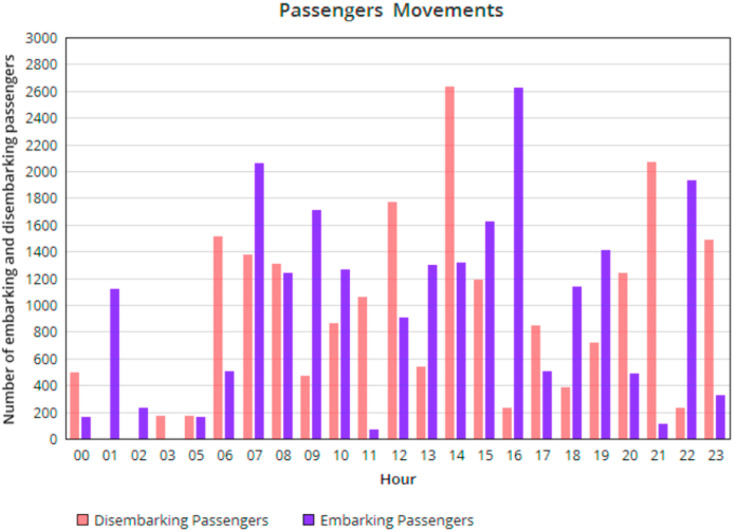
The input flight data are retrieved from the open data provided by the Air Navigation Service Provider. A distinction is made between national and international passengers as they do not share the same process within the airport structure. In order to have the most realistic and accurate simulation possible in the management of passenger flows, the data used are based on the airport's 2019 summer period. This makes it possible to check its applicability. On the basis of the number of movements per hour, taken from the actual timetables. The passenger flow can be obtained as illustrated in Fig. 4 .

Fig. 4.

Number of passengers embarking and disembarking movements at Casablanca Mohammed V International Airport.

Fig. 4. present the evolution of passenger flows over one day during disembarking and boarding. The flight slots are such that the largest number of departing passengers are between 7.00 a.m. and 9.00 a.m. as well as 2:00 p.m. and 5:00 p.m. Casablanca Mohammed V International Airport handles an average of 43,000 passengers a day. The number of embarking and disembarking passengers is roughly balanced with a ratio of 22,000 passengers embarking for 21,400 passengers disembarking. The peak hour counts 2059 passengers boarding from 7:00 a.m. to 8:00 a.m. in the morning, while 2626 passengers board between 4:00 p.m. and 5:00 p.m.

4. Mathematical modelling of variable parameters

The random, non-directional motion model is a unidirectional motion with the option of changing position forward or remaining stationary. The steps are assumed to be independent. Therefore, the subsequent steps only depend on their current position x. x is a random variable. The probability $P^{\text{'}}\left(x,t\right)$ that x is occupied at time t (probability of stay) is the result of the transition possibilities to leave the position x $P^{\text{'}}(x\to x^{\text{'}})$ or to enter it from the outside $P^{\text{'}}(x^{\text{'}}\to x)$. As expressed below, a forward transition is defined by equation (1). Immobility is defined by equation (2).

$$F=P^{\text{′}}(x\to x+1)=P^{\text{′}}(x-1\to x)$$ (1)

$$S=P^{\text{′}}(x\to x)=P^{\text{′}}(x+1\to x+1)$$ (2)

Residence probabilities $P\left(x,t-1\right)$ and $P\left(x^{\text{'}},t-1\right)$ indicate the probability with which the respective positions are filled at the previous point in time. If the transition probabilities are weighted by the residence probabilities, then the probability of occupation $P\left(x,t\right)$ from position x to time point t results according to equation (3).

$$P\left(x,t\right)=F\left[P\left(x-1,t-1\right)-P\left(x,t-1\right)]+S[\left(x,t-1\right)\right]$$ (3)

For the spatial mapping of the random walk, a fixed position is assumed $x_{t=0}$ and the following position $x_{t+1}$ is determined by the addition of a random variable ${\lambda }_x$ in equation (4).

$$x_{t+1}=x_t+{\lambda }_x$$ (4)

In order not to induce a preferred direction of movement, the probability of the random walk according to the following model is assumed by the following equation (5)

$$F+S=1$$ (5)

Since for each time step t the same decision has to be made, it is therefore possible to obtain the probability of arriving at a point k with a number n of steps by a binomial distribution (equation (6)).

$$P(x=k)=\left(\begin{array}{c}n\\ k\end{array}\right)F^k{\left(S\right)}^{n-k}$$ (6)

In general, the standard deviation increases with the number n of measurements taken according to equations (7), (8)) below:

$$\sigma \left(x\right)=\sqrt{n\ast F\ast S}$$ (7)

$$\mu \left(x\right)=n\ast F$$ (8)

According to the Limit Plant Theorem, in the case of $n\to \infty$ the binomial distribution b (n,F) opposes a normal distribution $N\left(n\ast F,n\ast F\ast S\right)$. Departing passengers are distributed according to their arrival time at the airport. All departing passengers are generated according to a flight number. This generation is based on the probability density function of a horizontally shifted normal distribution (equation (9)), given by the time in minutes prior to arrival (t), average arrival time (μ) before departure and standard deviation (σ). The normal distribution has been demonstrated to be well suited to passenger arrivals at airports (Schultz, 2010; Helbing and Molnár, 1995) detected a rightward asymmetry and therefore used Johnson's $S_U$ distribution to get a better fit as with a normal distribution.

$$P\left(t|\mu ,\sigma \right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}\left(-\frac{{\left(t-\mu \right)}^2}{2{\sigma }^2}\right)$$ (9)

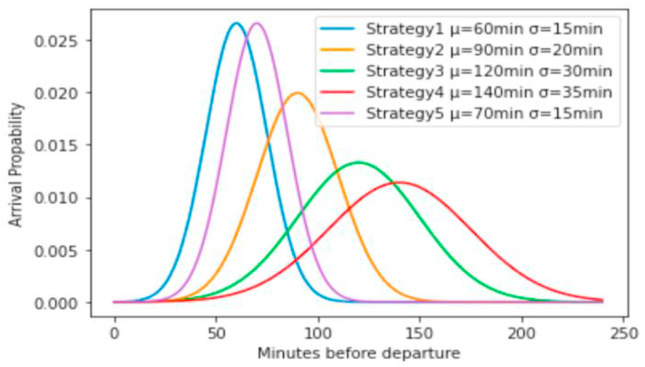
As passenger arrival time is a critical point in determining the percentage of travelers missing their flight due to sanitary barriers as well as determining the level of quality of service, five strategies with different arrival distributions are studied, which are presented in Fig. 5 . The abscissa values represent the time remaining until the departure of the aircraft. Thus, the origin represents the departure of the aircraft. In the horizontal offset of the distribution function, a buffer time (tp)is included. This guarantees that all passengers are generated in the airport's boarding lounge at least 45 min before it is time for departure. The buffer time assumption is based on information provided by airlines. Possible waiting times at security checks are not taken into account in the first instance.

Fig. 5.

Arrival time of departing passengers distribution for five strategies.

Table 4 gives an overview of the strategies studied with varying average arrival times (μ), of standard deviations (σ) and buffer times ( $t_p$).

Table 4.

The maximum waiting time for passengers.

	Mean Time of Arrival (μ)	Standard deviation (σ)	buffer time (minutes) $t_p$
Strategy 1	60	15	10
Strategy 2	90	20	10
Strategy 3	120	30	10
Strategy 4	140	35	10
Strategy 5	70	15	10

From strategy 1 to strategy 4, the mean time of arrival and standard deviation were gradually increased by 10 min or 5 min, respectively, which means that the time range within which passengers arrive at the station was extended. Strategy 5 is a variant of strategy 1 with a 5-min delay from the departure time. The processing times for security checks are based on IATA recommended measures with an average processing time of 35 s. The processing delays during the various operations in the check-in area are based on the operators’ speed of processing passengers. The accumulation of passengers in the check-in zone is done by the arrival of passengers according to their presentation profile and the occupancy rate of the check-in zone. The difference between the arrival at the airport and the processing of passengers gives the fill rate of the check-in zone. The speed of the passenger processing (equation (10)) depends on resources and increases by the number of operators (n) with the rate of absorption (v).

$$V=\sum n_i\text{*}{v}_i$$ (10)

Given the possible differences that exist according to the age and gender of the different passengers, an average obstacle-free walking speed was suggested by (Young, 1999). The mean value is 4.9 km/h with a standard deviation of 0.918 km/h, which corresponds to approximately 1.36 m/s and 0.255 m/s. Based on this distribution of values, this value distribution was accepted as an input to generate the preferred walking speed for the simulation. A similar data on preferred walking speeds has already been successfully used by (Helbing and Molnár, 1995) Furthermore, both minimum (2.47 km/h) and maximum (6.18 km/h) walking speeds were established, approaching the transition speed of running (Raynor et al., 2002; Daamen and Hoogendoorn, 2003) During the simulation, actual walking speeds are influenced by the presence of social forces (Helbing, 2010). As a result, obstacles can slow down the speed within a certain period of time. On the other hand, thrust forces coming from behind can increase speed or even cause walking to deviate (Helbing, 2010). Mathematically, the basis of the social forces model is now formulated (Helbing, 2010; Helbing et al., 2000a; Klingsch, 2010) and have recently given an interpretation in terms of optimal control and differential play (Helbing et al., 2005). The position of a passenger can be represented by a point $r_{\alpha }\left(t\right)$ in space, which changes continuously over time t, so the speed $v_{\alpha }\left(t\right)$ is given by the following equation (11):

$$\frac{d{r}_{\alpha }\left(t\right)}{dt}=v_{\alpha }\left(t\right)$$ (11)

Indeed, if the global social force $f_{\alpha }\left(t\right)$ represents the sum of the different systematic influences of different environmental factors on a passenger's behavior α, and the fluctuation term ${\epsilon }_{\alpha }\left(t\right)$ reflects random behavioural variations resulting from voluntary or involuntary deviations from optimal behavior, the following equation for passenger acceleration or deceleration and change of direction is obtained by equation (12):

$$\frac{d{v}_{\alpha }\left(t\right)}{dt}=f_{\alpha }\left(t\right)+{\epsilon }_{\alpha }\left(t\right)$$ (12)

According to the description of $f_{\alpha }\left(t\right)$ (equation (13)), an acceleration force is taken into account $f_{\alpha }^0\left(v_{\alpha }\right)$ repulsive effects, $f_{\alpha \beta }\left(r_{\alpha }\right)$ due to boundaries, repulsive interactions $f_{\alpha \beta }\left(r_{\alpha },v_{\alpha },r_{\beta },v_{\beta }\right)$ with other passengers β, and attraction effects $f_{\alpha i}\left(r_{\alpha },r_i,t\right)$.

$$\begin{array}{l}{f}_{\alpha }\left(t\right)=f_{\alpha }^0\left(v_{\alpha }\right)+f_{\alpha \beta }\left(r_{\alpha }\right)+\sum _{\beta \ne \alpha }{f}_{\alpha \beta }\left(r_{\alpha },v_{\alpha },r_{\beta },v_{\beta }\right)+\\ \sum _i{f}_{\alpha i}\left(r_{\alpha },r_i,t\right)\end{array}$$ (13)

In equation (14), the single-force terms are discussed. Each passenger has his own speed of travel $v_{\alpha }^0$ into the direction $e_{\alpha }$ of his/her next destination. Deviations of the actual velocity $v_{\alpha }$ from the desired velocity $v_{\alpha }^0=v_{\alpha }^0\text{*}{e}_{\alpha }$ due to disturbances (by obstacles or avoidance maneuvers) are corrected within the so-called “relaxation time" ${\tau }_{\alpha }\simeq 1s$ :

$$f_{\alpha }^0\left(v_{\alpha }\right)=\frac{1}{{\tau }_{\alpha }}\left(v_{\alpha }^0{e}_{\alpha }^0-v_{\alpha }\right)$$ (14)

Under normal circumstances, the desired speed $v_{\alpha }^0$ (equation (15)) is approximately Gaussian distributed with a mean value of 1.3 m/s, possibly smaller, and a standard deviation of around 0.3 m/s. In order to make up delays, the desired speed $v_{\alpha }^0\left(t\right)$ is often increased over time. It can be described, for instance, by the following formula $v_{\alpha }^{max}$ which is the maximum desired velocity and $v_{\alpha }^0\left(0\right)$ the initial one, which corresponds to the planned departure speed (equation (16)) (Helbing et al., 2005). This parameter, which is time-dependent, reflects nervousness or impatience of passengers.

$$v_{\alpha }^0\left(t\right)=[1-n_{\alpha }\left(t\right)]v_{\alpha }^0\left(0\right)+n_{\alpha }\left(t\right)v_{\alpha }^{max}$$ (15)

$$n_{\alpha }\left(t\right)=1-\frac{v_{\alpha }\left(t\right)}{v_{\alpha }^0\left(0\right)}$$ (16)

According to our description of $f_{\alpha }\left(t\right)$, an acceleration force is taken into account $f_{\alpha }^0\left(v_{\alpha }\right)$ repulsive effects, where $v_{\alpha }\left(t\right)$ indicates the average speed over the desired motion direction. Basically, long waiting times decrease the actual speed while desired speed increases. Tragically, at high pressures, crowding effects can occur and people may find themselves at risk to lose the social distance separating them (Helbing et al., 2000a). To avoid this type of situation, passengers must keep a certain distance from the barriers at all times. The closer the barrier is, the more (Klingsch et al., 2010) uncomfortable a passenger feels (Helbing et al., 2000b). This effect can be described (equation 17) by a repulsive force $f_{\beta }^{\alpha }$ , which decreases monotonically with the distance $\left||r_{\alpha }-r_{\beta }^{\alpha }|\right|$ between the place $r_{\alpha }\left(t\right)$ of passengers and the nearest point $r_{\beta }^{\alpha }$ of the barrier In the simplest case, this force can be expressed in terms of a repulsive potential $V_{\beta }$ :

$$f_{\alpha \beta }\left(r_{\alpha }\right)=-{\text{Δ}}_{r_{\alpha }}{V}_{\beta }\left(\left||r_{\alpha }-r_{\beta }^{\alpha }|\right|\right)$$ (17)

Similar repulsive force terms $f_{\alpha \beta }\left(r_{\alpha },v_{\alpha },r_{\beta },v_{\beta }\right)$ can describe that each passenger keeps a distance from other passengers according to the situation of β. Simulations performed in this paper have defined the repulsive interaction force according to the following formula (18):

$$f_{\alpha \beta }\left(t\right)=A_{\alpha }^1\text{exp}\left[\frac{r_{\alpha \beta }-d_{\alpha \beta }}{B_{\alpha }^1}\right]n_{\alpha \beta }(=(1-{\lambda }_{\alpha })\frac{1+\cos \left({\varphi }_{\alpha \beta }\right)}{2})+A_{\alpha }^2\exp \left[\frac{r_{\alpha \beta }-d_{\alpha \beta }}{B_{\alpha }^2}\right]n_{\alpha \beta }$$ (18)

5. Simulation of the distribution for arrival earliness

5.1. Distribution of earliness on arrival per day

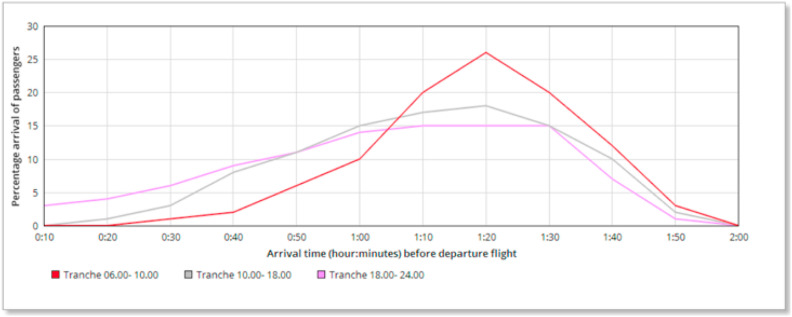
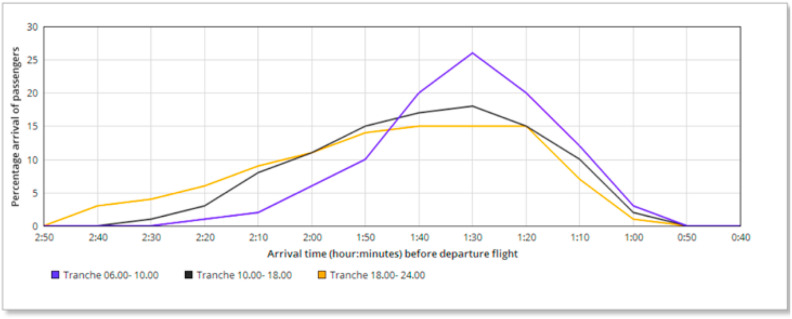
Using the distribution Equation (9) and within the IATA Airport Terminal Manual (Pullano et al., 2020), we have come to present the pattern of arrival earliness at the check-in area of terminal 1 of Casablanca Mohammed V International Airport for domestic (Fig. 6 and international flights (Fig. 7 ). The program is aimed to obtain the appropriate passenger distribution. The program is developed by utilizing Python functions, the program consists of 5 worksheets: Arrival distribution, input data, daily distribution, and chart.

Fig. 6.

IATA arrival earliness distribution domestic.

Fig. 7.

IATA arrival earliness distribution international.

Figs. 6 and 7 showing the passenger flow rate at check-in are provided at intervals of 10 min before departure time. They both also show that the pattern will be different depending on the time of day. There are three different periods applied, from 06:00 to 10:00, 10:00 to 18:00, and 18:00 to 24:00. The time slot between 00.00 and 06.00 is not taken into account as it is a low-traffic period.

5.2. Correlation between the Passenger's time of arrival and boarding time

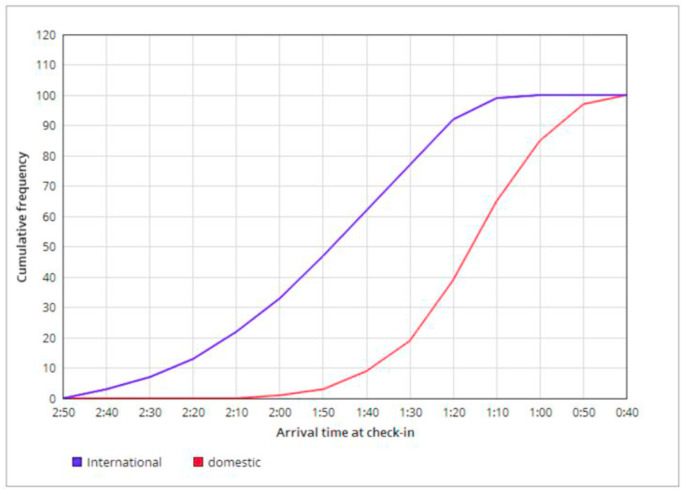
The comparison of passenger arrival earliness is shown in Fig. 8 These show the difference of passenger arrival earliness for international and domestic flights (IATA, 1989). For international flights, the last passengers should arrive 70 min before departure time. For domestic flights, the passengers may arrive much later. However, passengers on international and domestic flights now have to arrive earlier, as they have to undergo additional formalities and respect sanitary measures, described in the next section. There may also be mandatory quarantine and testing.

Fig. 8.

Relationship of arrival time for planning passengers.

6. Model validation and simulation analysis

The flight and passenger data displayed in the simulations correspond to a typical summer peak departure time (7:00 am) per day. Around this hour, there are about 14 flights for a total of 2050 passengers, with 62.5% travelling in Boeing B-737s, 18.75% in Embraer E−190s, 12.5% in B-787s and 6.25% in B-767s. The flights operate out of terminal T1, reserved essentially for the national airline Royal Air Maroc. As the terminal complies with IATA standards, according to the design standards (IATA, 1989; Guilhem and FuSo, 2010) the check-in area measures no more than 1462 $m^2$ for a total of 52 check-in counters.

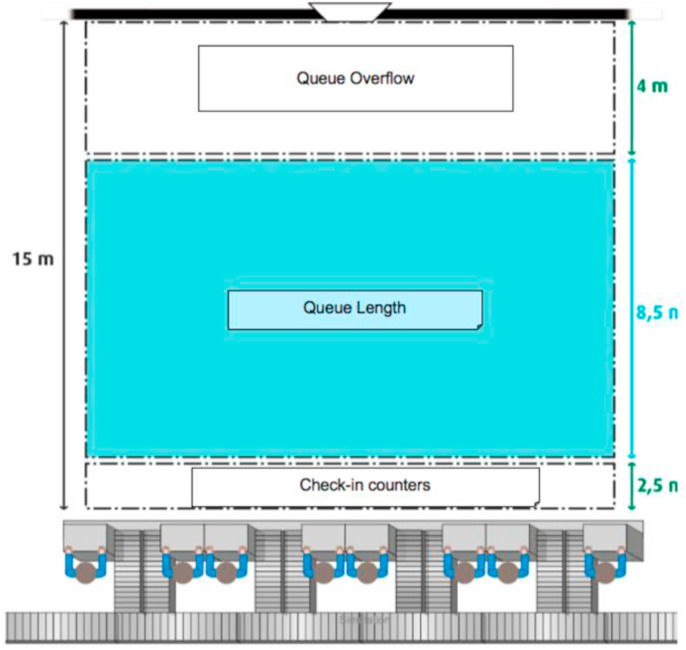
6.1. Scenario development

Check-in counters as they are organised today (Fig. 9 ) do not provide any physical separation between check-in operators and passengers. Therefore it is necessary to establish a procedure for managing passengers when carrying out check-in formalities in compliance with the sanitary rules required (Guilhem and FuSo, 2010). The simulations support two possible scenarios. The first scenario considers the closure of one out of every two counters in the absence of Plexiglass separation panels. The second scenario assumes the installation of separation panels between the queues and the operators as well as side-by-side counters, thus bringing all the counters into operation. Each scenario runs three simulations in order to adjust the social distancing between passengers. For instance, the first simulation operates a distance of 2 m, the second a distance of 1.50 m and the third a distance of 1 m.

Fig. 9.

Checking counter organization (source: French Civil Aviation Technical Service/DGAC).

6.2. Simulation program interface

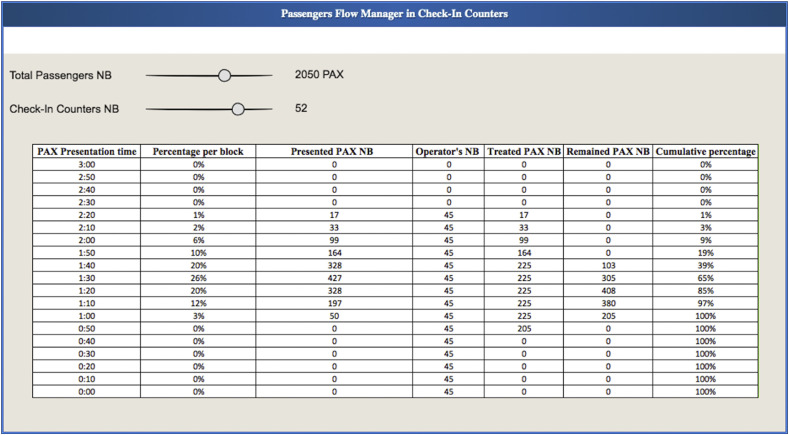
Normally, passengers must be present at the airport 3 h before departure for international flights. The simulation program is developed to manage the flow of passengers in the check-in areas considering the new sanitary measures. Some display screen of the simulator is shown in Fig. 10 and Fig. 11 . According to the parameters input (distance between two passengers, the capacity of the check-in area, the average processing time) illustrated in Fig. 11 The simulation program will estimate in steps of 10 min according to the open check-in counters, the cumulative percentage and number of passengers present in the check-in area, the passages registered and those in the process of being checked in as illustrated in Fig. 10.

Fig. 10.

Passengers flow manager check-in counters.

Fig. 11.

Sanitary measure parameters.

7. Results analysis and discussion

In order to validate the proposed model, a Turing test (Spring 1993; Knauf et al., 1997) was carried out to observe the behavior of the system in extreme conditions, allowing data to be collected in order to compare them with real data from Terminal 1 of Casablanca Mohamed V International Airport.

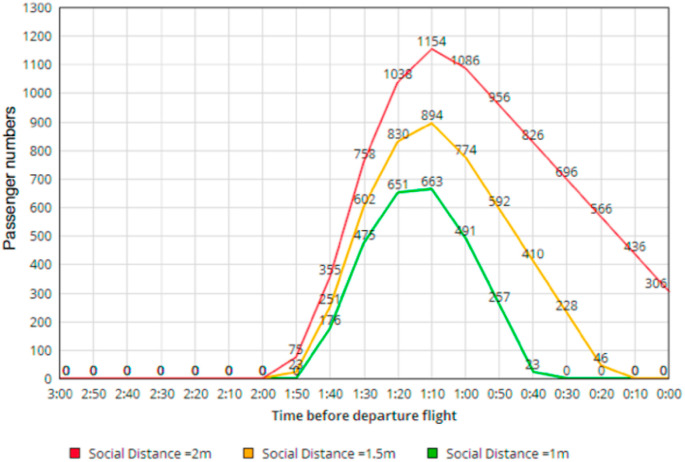
Fig. 12 represents, for each of the three simulations performed in the first scenario, the queue length observed in units of people before the aircraft departure. With a social distance of 2 m (red curve), the accumulation of passengers is very fast. A high point is observed 1h10 before departure with 1154 people still waiting. Overall, at the departure of the aircraft, there are still 306 passengers that have not yet been treated. Based on the closing time for check-in, which usually occurs 40 min before departure, 826 passengers will not have been processed. With a social distance of 1.50 m (orange curve), the accumulation of passengers is fast. A high point is also observed 1h10 before departure with 894 passengers still waiting. At the end, 20 min before departure, there are still 46 people left in the queue. Knowing that 40 min before the departure of the aircraft the check-in is closed, it is then 410 people who, at that time, will not have been processed yet. With a social distance of 1 m (green curve), the accumulation of passengers is slower. The processing of passengers is smoother. As in the other two scenarios, there is a high point in the waiting time, as in the other two scenarios, 1 h 10 min before departure, with 663 people still waiting. 40 min before departure, there are still 23 passengers in the queue and the check-in is about to close.

Fig. 12.

Distribution of passengers as a function of time and distance - case of scenario 1.

In all three scenarios here, the number of departing passengers, despite a fluctuation in the social distance measure, is not processed in the time available. Indeed, even with a distance of 1 m, 40 min before the check-in counter close for departure there are still passengers in the queue. The solution of opening only one check-in counter in two to ensure the application of health measures is therefore not an optimal solution in terms of passenger flow management.

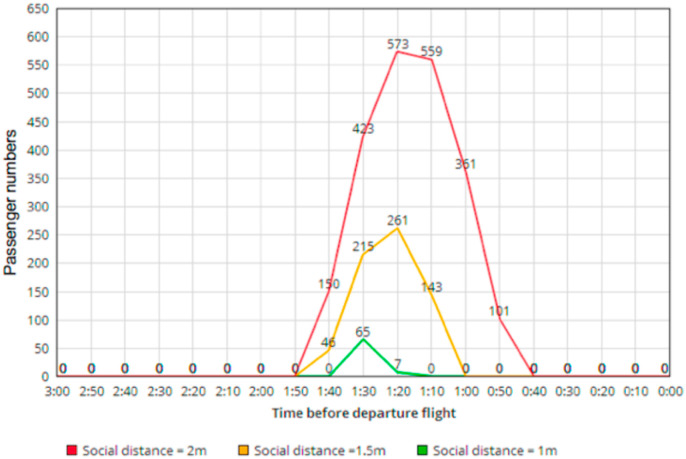
Fig. 13 represents, for each of the three simulations in the second scenario, the observed queue length in units of people before the aircraft's departure. With a social distance of 2 m (red curve), the observed accumulation of passengers is rapid. A peak is observed 1h20 before departure with 573 people still waiting. However, contrary to what could be observed previously, 40 min before departure, all the passengers could be processed. With a social distance of 1.50 m (orange curve), the accumulation of passengers is slower. A peak is also observed 1h20 before departure with 261 people still waiting. However, contrary to what was observed previously, 60 min before departure, all passengers were processed. With a social distance of 1 m (green curve), the total number of passengers is almost non-existent. The processing of passengers is done in a fluid manner. A slight high point is observed as in the two other scenarios 1h30 before departure with 65 people waiting. However, contrary to what could be observed previously, 1h10 before departure, all passengers could be processed. With more check-in counters open, it is easier to comply with social distancing measures while at the same time ensuring an efficient passenger processing flow. Indeed, in all simulations of the first scenario, there are still passengers who are unable to board the aircraft because they are still in the queue, whereas in all simulations of the second scenario all passengers manage to finish checking in.

Fig. 13.

Distribution of passengers as a function of time and distance - case of scenario 2.

It should therefore be said that an effective measure to maintain the proper management of the flow of passengers processing would be to have a system for separating the check-in counters and the associated queues in order to be able to open as many counters as possible and thus be able to contain the flow of passengers arriving at the departure point.

In the case of a large influx of passengers, the requested capacity may exceed the possible processing capacity. This creates queue hoarding.

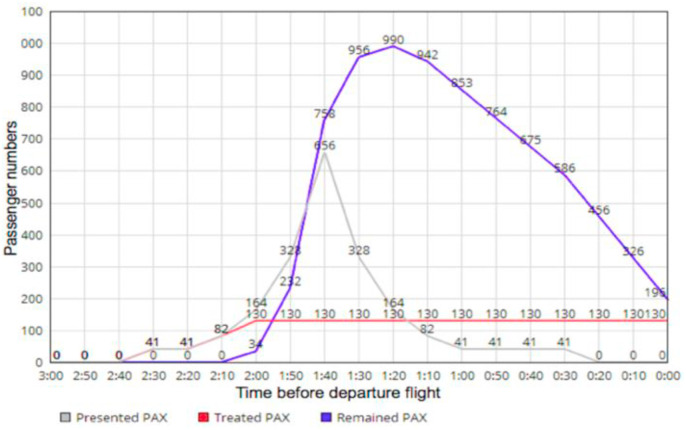
Fig. 14 shows the waiting-time variation for a distance measurement of 2 m, in the case of the first scenario.

Fig. 14.

Representation of cumulative passengers in case of peak according to scenario 1.

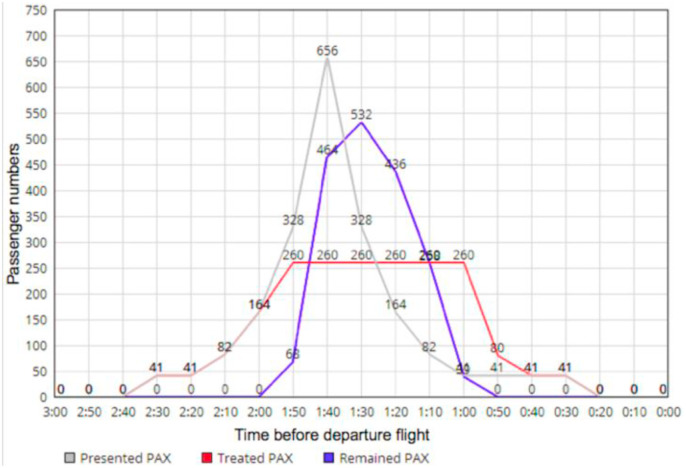
The grey line represents the number of passengers arriving at the check-in counter. The high point of passenger presentation occurs 1h40 before departure with 656 people.

The red line represents the number of passengers that are processed in time. With only 26 check-in counters open, it is not possible to exceed a maximum of 130 passengers processed in a 10 min interval. This limits capacity and creates a wait as passengers arrive.

The blue line represents the passengers remaining in the queue. A high point in the total number of remaining passengers can be observed 1 h 20 min before the flight departure with 990 passengers waiting.

Here it can be observed that the cumulated number of passengers cannot be absorbed, because even after the departure there is still passengers waiting. The capacity to handle the flow of departing passengers was therefore exceeded. The limited number of check-in counters opened due to the diversion measures did not allow the flow to be processed.

Fig. 15 shows the total for a distance measurement of 2 m in the case of the second scenario. The grey line represents the number of passengers arriving at the check-in counter. The high point of passenger presentation occurs 1h40 before departure with 656 people. The red line represents the number of passengers that are processed in time. With only 52 check-in counters open, it is not possible to exceed a maximum of 260 passengers processed in a 10 min interval. This limits capacity and creates a wait as passengers arrive. The blue line represents the passengers remaining in the queue. A high point in the total number of remaining passengers can be observed 1.5 h before the flight departure with 532 passengers waiting.

Fig. 15.

Representation of cumulative passengers in case of peak according to scenario 2.

Here we can see that the total number of passengers has been absorbed. Indeed, 30 min before departure there are no more passengers left in the queue. There was therefore good management of the capacity to handle the flow of departing passengers. The higher number of check-in counters made it possible to process the flow.

The simulation program provides a fairly accurate representation of the passenger flow. It provides information on the queue, the management of check-in counters, gives the waiting time and the number of passengers remaining. It also complies with IATA measures for passenger processing. However, despite its effectiveness, the simulation program has limitations in its use. The surface area of the check-in counters is not allocated according to the distribution of flights. This means that flights are treated uniformly without distinction. Passengers are treated for all flights together and it is assumed that the treatment is homogeneous. In addition, since the IATA table distributing the volume of space per passenger is very extensive, the simulation was carried out for a particular parameter present at check-in and not according to all the parameters. Also, the calculation of the surface area of the check-in hall is made according to DGAC standards and not with a real calculation carried out within the terminal in question. Persons with reduced mobility and those with assistance are not included in the simulation. They were considered to be passing through a separate lane specifically assigned to them. Similarly, the time required for additional potential health measures before the check-in area is not taken into account in the calculation. The simulation models used are stochastic and dynamic. They represent a close approximation of the real system and incorporate most of its main features. The analysis of the results obtained attests to the proper use of the proposed passenger flow management solution. In times of health crisis, the tool for setting parameters allows to ensure the application of the required distances while anticipating the saturation of the check-in area. However, its use remains non-exhaustive and limited to a case study related to terminal T1, where the treatment of flights are considered to be uniform, as it is dedicated exclusively to the National Airline. However, this does not necessarily apply to the other terminals.

8. Conclusion

In times of health crisis, the tool for setting parameters allows to ensure the application of the required distances while anticipating the saturation of the check-in area. The simulations showed that it would be possible to support the processing of passengers at the airport using considerable resources (indeed, it would be necessary here to open all positions for check-in). Under this condition alone, it is therefore possible to maintain an acceptable performance in terms of respectability of schedules and an acceptable LOS in terms of waiting times. However, its use remains non-exhaustive and limited to a case study related to terminal T1, where the treatment of flights are considered to be uniform, as it is dedicated exclusively to the National Airline. While this study reveals the weaknesses of traditional passenger flow management and underlines the need for a fully integrated management system to meet service quality requirements, the proposed tool will help to keep ahead of unforeseen events, avoiding bottlenecks and long waiting times, while ensuring that sanitary measures such as social distancing is maintained during an international health crisis. The question arises to know to what extent such an allocation of resources (here we are only looking at recording, but we must think of other crossing points on which it is also necessary to intervene) would be economically bearable and if a possible adjustment of the schedule, or a decrease in the frequency of flights would lead to a decrease in the resource requirements necessary to maintain performance. In addition, this research could also be extended to other areas of the airport facing similar challenges.

CRediT authorship contribution statement

Yassine Dabachine: Conceptualization, Methodology, Software, Writing - review & editing. Hamza Taheri: Resources, Software, Writing - original draft, Conceptualization. Mohamed Biniz: Data curation, Validation, Conceptualization, Methodology, Writing - review & editing. Belaid Bouikhalene: Supervision, Conceptualization, Project administration. Abdessamad Balouki: Methodology, Visualization.