Abstract
Mixed gels of plant proteins are being investigated for use as meat analogues. Juiciness is an important characteristic for the acceptability of meat analogues. The juiciness is assumed to be governed by the hydration properties, or water holding capacity, of the gel (WHC). We analysed the WHC of single-phase gels of respectively soy protein and gluten by applying Flory-Rehner theory. This enabled us to describe the WHC of more the complex mixed gels. The WHC of mixed soy protein - gluten gels is shown not to be a linear combination of their constituents. At high volume fractions, soy forms a continuous network and swells similarly to pure soy without being hindered by gluten. However, increasing gluten content leads to a gradual decrease in soy swelling. This is due to the mechanical interaction between soy and gluten. We propose that gluten-rich gels have a continuous gluten network that entraps soy and hinders its swelling. The elastic moduli of the gluten network were extracted from WHC data, and are in reasonable agreement with experimentally determined moduli. A better understanding of the effect of mixed gel composition on WHC is valuable for the development of the next generation meat analogues.
Keywords: Gel swelling, Water holding capacity, Meat analogues, Water sorption, Gel mechanics, Plant proteins
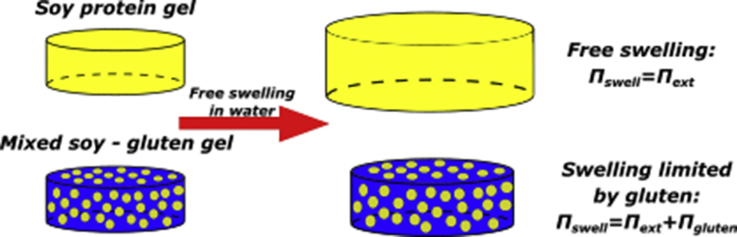
Graphical abstract
The swelling of soy in mixed soy-gluten gels is lowered by a mechanical force exerted by gluten on soy.
Highlights
-
•
Water holding capacity of soy protein gels can be described with Flory-Rehner theory.
-
•
Swelling of mixed soy and gluten gels is not a linear combination of their parts.
-
•
Gluten hinders soy swelling via a mechanical interaction with soy.
1. Introduction
Technological advancements in high moisture extrusion and shear cell technology have enabled the production of fibrous structures from plant proteins (Chiang et al., 2019, Grabowska et al., 2014, Grabowska et al., 2016, Dekkers et al., 2016b). These fibrous structures resemble the texture of muscle fibres but lack the juiciness found in real meat (Hoek, 2010, de Bakker and Dagevos, 2010). The juiciness of meat is related to its water holding capacity (WHC) (Warner, 2017, Aaslyng et al., 2003, Puolanne, 2017, Pearce et al., 2011), and a similar relation is expected for meat analogues. The juice release from meat has a typical temporal profile. Some of the juice should be readily expelled, while the remainder should be more tightly bound to the matrix to prevent the sensation of dryness (Bertram et al., 2005, Yven et al., 2005). Consumers demand a product similar to meat (Hoek et al., 2011), and the lack of juiciness due to inadequate WHC and juice release profile is thus a hurdle for consumer acceptance.
Meat analogues are complex mixed gels, and often contain soy protein isolate (SPI), gluten, or a combination of both (Grabowska et al., 2014, Dekkers et al., 2016a, Liu and Hsieh, 2007, Akdogan, 1999, Chiang et al., 2019). However, the physics governing the WHC of such mixed protein gels is still poorly understood. We apply the concept of Flory-Rehner theory in a phenomenological way to describe the WHC of single-phase and mixed gels as a function of pressure. We aim to improve our understanding of the WHC of such complex mixed systems.
It has been reported that water distributes unevenly between SPI and gluten (Dekkers et al., 2016a, Dekkers et al., 2018), which can be related to differences in polymer-water affinity and cross-link density between the two phases. The uneven distribution of water appears to be essential for obtaining a meat-like structure as the moisture content in the two phases affects their rheological properties (Dekkers et al., 2018). Although the gluten network is known to be affected by the addition of soy in bread doughs (Roccia et al., 2009), a recent study showed that heating mixtures of gluten proteins and soy glycinin, one of the main soy proteins, does not result in cross-linking between the different proteins (Lambrecht et al., 2017). This suggests the two networks can coexist in mixed systems. Studying the mixed systems as well as the two phases separately could, therefore, provide valuable insights into the mixed system.
We investigate the WHC of mixed protein gels as a model system for meat analogues. To reduce the complexity of the system we first characterize the WHC of single-phase SPI and gluten gels before moving towards more complex mixed gels that could be regarded as a rudimentary meat analogue. As is the case for many foods, meat and meat analogues can be regarded as cross-linked polymer networks (Jin et al., 2014, Paudel et al., 2015, van der Sman et al., 2013, van der Sman, 2012, van der Sman, 2007). The WHC of polymer networks can be described using Flory-Rehner theory (Paudel et al., 2015, van der Sman, 2007, van der Sman, 2012, van der Sman, 2013), which describes the swelling of a cross-linked polymer network using two opposing contributions (Flory and Rehner, 1943). These contributions are the osmotic (mixing) pressure and the elastic pressure due to network deformation. At equilibrium, the sum of these contributions is equal to the pressure exerted onto the network. As such, the theory can be used to describe the WHC (and thus moisture content) of a material as a function of the applied pressure.
Flory-Rehner theory has several underlying assumptions which might limit its application to (globular) protein gels. Globular proteins are innately non-linear given their secondary and tertiary structure, which for soy proteins persists after heating [Kim et al., 2004]. The assumption of linear Gaussian chains is therefore void. However, this does not mean the Flory-Rehner theorem is not applicable. The concept of a net swelling pressure as the result of opposing mixing and elastic pressures can still provide insight. In fact, Li et al. (2016) showed that the swelling of fine-stranded (and predominantly globular) whey protein and egg white protein gels can be predicted with FR theory (Li et al., 2016). Similarly, FR theory was used to describe the swelling of complex mixtures such as mushrooms (Paudel et al., 2015). The precise physical meaning of the different parameters may, however, be affected given that not all assumptions are met.
This paper is organized as follows. We study the WHC of single-phase SPI and gluten gels by applying an increasing load via centrifugation. Based on insights from the single-phase gels we describe the WHC of more complex mixed gels. By combining data from large strain compression experiments and data from the WHC experiments we hypothesize about the network structure of mixed SPI-gluten gels. We will briefly discuss the implications for the development of juicier meat analogues.
2. Theory
2.1. Flory-Rehner theory
The WHC of polymer gels is governed by their thermodynamics and can be analysed using Flory-Rehner theory (Flory and Rehner, 1943, Flory and Rehner, 1944). Flory-Rehner theory states that the amount of solvent retained by the polymer network depends on the external pressure . In our experiments we will exert this pressure via centrifugation. Under equilibrium conditions the external pressure will be equal to the swelling pressure :
| (1) |
The swelling pressure is composed of two independent contributions that account for the different interactions between water and polymer. These contributions are the mixing pressure , which accounts for the interaction between the polymer and the solvent, and the elastic pressure , which accounts for the elastic pressure exerted by the polymer network onto the solvent. Note that we assume the contribution of dissolved ions and polymer charges to the swelling pressure to be constant, and of limited magnitude (). The theory assumes a homogeneous network of Gaussian chains that swells uniformly. van der Sman (2015) showed that the behaviour of a range of bio-polymers can be captured with Flory-Rehner theory, and obey to the scaling laws from polymer physics (van der Sman, 2015).
2.1.1. The mixing pressure
can be described with Flory Huggins (FH) theory. We will use water sorption isotherms to estimate the governing parameter of the FH theory, namely the interaction parameter χ. However, as most biopolymers undergo a glass transition during desorption, we will analyse the sorption isotherms with the Free Volume extension of FH theory, so-called FVFH theory, instead (Vrentas and Vrentas, 1991). FVFH theory has already been successfully used to describe the water sorption of various food products such as vegetables (van der Sman et al., 2013), mushrooms (Paudel et al., 2015), broccoli (Jin et al., 2014), meat (van der Sman, 2012), chicken (van der Sman, 2013), and various bio-polymer gels (van der Sman, 2015).
Note that FVFH theory includes an extra term () that is not found in the classical FH theory. is equal to zero above the glass transition temperature. Therefore, when describing WHC data, is equal to zero in our calculation of the mixing pressure. The mixing pressure is related to the water activity, , and is taken as:
| (2) |
where is the molar volume of water, R is the universal gas constant, T is the absolute temperature, ϕ and are the volume fraction of polymer and water respectively, N is the ratio of the molar volume of water and polymer, and χ is the Flory-Huggins interaction parameter between water and polymer. Because of the relatively large size of a polymer, N becomes very large allowing us to simplify the second term on the right hand side to ϕ. accounts for structural relaxation in the glassy state and the changes in hydrogen bonding between water and polymer in the semi-dilute regime (Vrentas and Vrentas, 1991, van der Sman and Meinders, 2011). was calculated according to van der Sman et al. (2013) as (van der Sman et al., 2013):
| (3) |
with
| (4) |
and is calculated according to Couchman-Karasz (Couchman and Karasz, 1978):
| (5) |
Here, is the molar weight of water, is the change in heat capacity at the glass transition, and is the glass transition temperature in the dry state. represents the weight fraction of polymer or water. We have used which appears to be universal for biopolymers (van der Sman, 2012, van der Sman and Meinders, 2011, Pouplin et al., 1999).
As has been shown previously, the interaction parameter for biopolymers and water is composition dependent and can be calculated as (van der Sman and Meinders, 2011):
| (6) |
with and as the interaction parameters under dilute and concentrated conditions respectively. Water is a theta solvent for proteins at very low protein concentrations, and thus is 0.5.
2.1.2. The elastic pressure
We take the elastic contribution to the swelling pressure as originally described in Flory-Rehner theory. It assumes a homogeneous polymer network that consists of linear Gaussian chains that swell isotropically. The Young's modulus E of such gel networks can be described with the power law reported by Horkay and Zrínyi (1982) as function of (Horkay and Zrínyi, 1982), which is based on the theorem (De Gennes, 1979):
| (7) |
in which β is 9/4 and a is a constant (Horkay and Zrínyi, 1982). Higher values of β have also been reported for certain biopolymers (, (van der Sman, 2015). is the ϕ for which and thus describes maximum swelling at . For incompressible materials, E is related to the Shear modulus, G, via:
| (8) |
For the elastic contribution we use the affine network model (van der Sman, 2015):
| (9) |
is the Shear modulus in the reference state. is related to G via:
| (10) |
is defined as:
| (11) |
with as the ϕ at which the polymer network is in the relaxed state and the chains experience zero stress.
It must be noted that the conditions at which the reference state is determined differ greatly between studies (Quesada-Pérez et al., 2011), and the physical meaning of is still under debate (Quesada-Pérez et al., 2011, Khokhlov, 1980). For synthetic polymers is often defined as the ϕ at cross-linking, which often occurs in the dry state (thus ). When cross-linking takes place in the presence of a solvent, as is the case for bio-polymers, the reference state is often chosen in a similar fashion (Hino and Prausnitz, 1996, Shibayama et al., 1997). Khokhlov (1980) argues that should be chosen at theta-conditions at which the individual chains are unperturbed (Khokhlov, 1980). However, since we apply the affine network model (van der Sman, 2015), polymer-solvent and polymer-polymer interaction are omnipresent (Shibayama et al., 1997). van der Sman (2015) showed that for many bio-polymer gels it holds that (van der Sman, 2015). Because of the ambiguous nature of , we will determine it by fitting our WHC data with Eq. (9).
3. Materials and methods
We have prepared single-phase gels from soy protein isolate (SPI) and gluten via heat-induced gelation. By varying the polymer weight fraction at cross-linking, gels with different cross-link densities were obtained. Gels were washed and swollen in water before their WHC as a function of pressure was determined using the centrifugation method (Kocher and Foegeding, 1993, Paudel et al., 2015). The WHC data was fitted with Flory-Rehner theory to obtain and . Water sorption isotherms and glass transition temperatures were measured for the different bio-polymers before and after gelation to obtain using FVFH theory. Based on the WHC of the single-phase gels we analysed the WHC of more complex mixed gels with different SPI: gluten ratios.
3.1. Materials
Soy protein isolate (Supro 500E IP) and vital wheat gluten were obtained from Solae (DuPont, St Louis, MO, USA) and Roquette (Lestrem, France) respectively. Some compositional data is presented in Table 1. Salt content was determined based on the conductivity of a 5 wt% protein dispersion and is expressed in NaCl equivalents. Mili-Q water was used in all experiments.
Table 1.
Compositional information of the protein powders used. Dry matter contents (DMC) as determined by drying at 105°C for 24, protein content according to the Dumas combustion method with Nx5.7 (see e.g. Berghout et al. (2015) (Berghout et al., 2015)), and salt content of the powders based on the conductivity of 5 wt dispersions (as NaCl equivalents).
| DMC (wt) | Protein content (Nx5.7, wt), n = 3 | Salt content (expressed as wt NaCl), n = 3 | |
|---|---|---|---|
| SPI | 93.70.2 | 81.71.1 | 1.33.01 |
| Gluten | 93.40.5 | 77.90.1 | 0.39.01 |
3.2. Gel preparation
3.2.1. Soy gels
SPI gels were prepared by dispersing SPI powder in water, followed by vigorous mixing to achieve a final dry matter content of between approximately 25 and 35 wt. SPI dispersions had an ionic strength of between 0.08 and 0.12 molal and were not adjusted. Dispersions of SPI and gluten were of neutral pH and were not adjusted. Actual dry matter content of the dispersions was determined by drying at for . The obtained dispersions were placed in vacuum bags and exposed to a vacuum of for 15 s to remove any air bubbles. The dispersions were stored overnight at 4°C to ensure an even hydration of the protein. The hydrated dispersions were placed in cylindrical stainless steel gelation vessels with a radius of 12.5 mm and a height of 5 mm. The hermetically sealed vessels were submerged in a shaking water bath (Julabo, Seelbach, Germany) preheated at 95°C for 30 min. The vessels were cooled by submersion in water of 10°C for 15 min. After cooling, the gels were gently removed from their vessels.
3.2.2. Gel washing and swelling
Gel swelling and the removal of solutes was carried out simultaneously by washing in Mili-Q water. Gels were submerged in an excess of Mili-Q water (1/100 wt/wt) immediately after gelation and stored at for . The water was exchanged 3 times during the first at regular intervals. This was sufficient to reach a stable sample weight and constant conductivity of the washing liquid. These signs were taken as confirmation that equilibrium had been reached.
The maximum level of swelling is defined as the polymer volume fraction at maximum swelling and referred to as . was determined based on the dry matter content as determined by drying the swollen gels at 105°C for 24. Polymer and water densities were assumed to be 1330 kg m-3 and 1000 kg m-3 respectively.
3.2.3. Gluten gels
Gluten gels were prepared similarly to SPI gels, with some alterations to the protocol. The gel-like structures obtained after heating hydrated gluten were not uniform in shape and thus not suitable for uniaxial compression testing or centrifugation (for WHC). The use of ethanol can greatly improve the ease of handling of gluten (Lambrecht et al., 2016, Dahesh et al., 2014). We therefore prepared gluten gels in anhydrous ethanol (Sigma Aldrich, Steinheim, Germany) to study their strength and WHC. By mixing gluten with ethanol a particle dispersion is obtained. Gluten dispersions were transferred to the aforementioned gelation vessels, omitting the evacuation and hydration steps. Gelation and the subsequent washing and swelling was carried out as per the protocol for SPI gels. Three water changes were assumed to be sufficient to wash out all ethanol and solutes present. The range in which we could reproducibly prepare gluten gels was narrow () due to issues such as gluten sedimentation and drainage within the gelation vessel.
3.2.4. Mixed gels
Mixed gels were prepared by dispersing SPI in water and vigorous mixing, followed by gluten addition and further mixing. Mixed gels had an ionic strength between 0.09 and 0.04 molal. The mixtures were freed from air, hydrated, and gelled according to the protocol for SPI gels. The overnight hydration at was assumed to be sufficient to reach an equilibrium water distribution.
3.3. Water holding capacity by centrifugation
WHC was determined by centrifugation at different relative centrifugal forces to apply a range of pressures to the equilibrated gels, similar to Kocher and Foegeding (1993), and Paudel et al. (2015) (Kocher and Foegeding, 1993, Paudel et al., 2015). Samples were gently taken from pre-swollen gels using a biopsy punch with a diameter of 4 mm. The samples were placed in centrifugal filters with a pore size of 0.2μm (Pall Centrifugal Devices). An Eppendorf centrifuge with a swinging bucket rotor was used to ensure the pressure was applied perpendicularly to the surface of the sample. A centrifugation time of 1 was found to be sufficient to reach a constant gel weight. During centrifugation, the expelled fluid was collected in the bottom compartment of the tube without being in contact with the sample, and the amount of water released was determined by weighing.
Assuming a linear gradient in ϕ and , the relative centrifugal force can be converted to an average pressure applied on the sample as:
| (12) |
is the mean density of the sample, is the relative centrifugal force at the sample location, and H is the sample height. Since the amount of polymers is assumed to remain constant during centrifugation, the change in sample height as a result of the moisture loss can be calculated as:
| (13) |
is the initial polymer volume fraction, is the initial sample height, and is the average polymer volume fraction.
3.4. Linear compression tests
Elastic Young's moduli E were determined by uniaxial compression of the swollen gels using an Instron texture analyser equipped with a 100N load cell similar to Renkema et al. (2001) (Renkema et al., 2001). In short, gels prepared and swollen according to the protocol in Section 2, 3 were trimmed to a radius of 12.5 mm using a cork borer and placed on the plate of the texture analyser. Gels were compressed at a rate of 1 mms-1. True Hencky strain was calculated as:
| (14) |
in which ε is the Hencky strain and and are the initial height and height after deforming for a certain time t. The stress on the gel σ is calculated as:
| (15) |
in which is the force recorded by the texture analyser and the contact area of the gel after deforming for a certain time t. We assume constant sample volume during deformation, which enables us to calculate the sample area during deformation as:
| (16) |
in which is the initial contact area of the gel. E was determined as the slope of σ versus ε in the linear regime.
3.5. Dynamic vapour sorption
Water vapour sorption isotherms can be used to determine the interaction parameter χ with FVFH theory. Isotherms were determined at 25°C on a ProUmid SPSX-S3-EU01508. Measurements started by drying for 24 at 0%RH, after which the RH was increased with 10% increments up to 90% RH, and lowered again to 0% RH in 10% increments. Equilibrium was assumed when the weight change over a window of 10 min was less than 0.0005min-1 for a period of 120 min. A maximum step duration of 2000 min was used. Isotherms were determined in duplicate.
3.6. Determination of
The glass transition temperature is required to accurately fit sorption isotherms with FVFH theory. Values of were determined using a TA Instruments DSC 250 (modulated Differential Scanning Calorimetry, mDSC). Samples with different moisture contents were prepared by exposing them to water vapour for different lengths of time after which the DSC sample pans were sealed hermetically. The samples were allowed to equilibrate inside of the sample pan for at least 1 week before being analysed. During thermal analysis samples were equilibrated at after which a temperature modulation with an amplitude of with a period of was switched on. Temperature was raised to at a rate of after which the samples cooled back to again, followed by a second heating cycle to . Glass transitions were identified from the shift in the baseline of the reversing heat flow signal of the second scan. Dry matter content of the samples was determined by puncturing the sample pan after measuring and drying at for .
3.7. Statistical analysis
Error bars indicate the confidence intervals of the mean value, as calculated from the standard error of the mean. n indicates the number of measurements. In the case of , error bars represent the absolute deviation from the mean. Fitted values are the result of fitting individual datasets, with error bars indicating the confidence interval of the mean of the fitted values. Where applicable, significant differences were tested with a one-way ANOVA and Tukey-test, with p indicating the significance level.
4. Results and discussion
4.1. Tg and water sorption isotherms
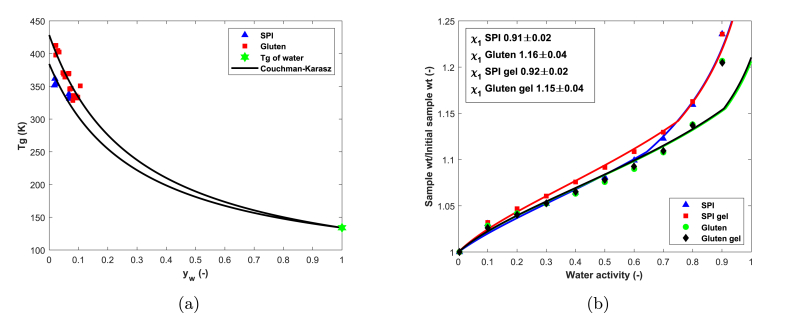
Glass transition temperatures of SPI and gluten were determined via mDSC for different levels of hydration and fitted with Couchman-Karasz with respect to (Fig. 1a). The fitted value for SPI () is in good agreement with the value reported by Morales and Kokini (1997) for 7S soy globulins ( (Morales and Kokini, 1997, Morales and Kokini, 1999); which is remarkable as we used a crude commercial protein isolate. Values reported for the of soy proteins deviate widely between references (Morales and Kokini, 1997, Morales and Kokini, 1999, Mizuno et al., 2000, Kealley et al., 2008), possibly due to variations in experimental methodology, raw materials, and sample preparation. For the sake of consistency we will use our own determined values. The fitted of gluten (428) is in good agreement with literature values (Kalichevsky et al., 1992, Pouplin et al., 1999, Verbeek and Van Den Berg, 2010), although higher values have also been reported (Micard and Guilbert, 2000).
Fig. 1.
Glass transition temperatures of SPI and gluten protein at different moisture weight fractions, as determined via mDSC. Solid lines indicate best fit according to Couchman-Karasz (1a). Water sorption isotherms of SPI and gluten, before and after the gelation process. Error bars overlap with the markers (n = 2). Solid lines indicate best fits with FVFH theory. Fitted values of are presented in the insert (1b).
Water sorption isotherms of SPI and gluten were collected before and after the gelation process using dynamic vapour sorption (Fig. 1b). Gels were lyophilized and ground to a fine powder before sorption analysis. The gelation process increased sorption by SPI at . Additional cross-linking can result in a higher glass transition temperature (Stutz et al., 1990) and, as follows from FVFH theory, increase sorption in the glassy regime. At where , the sorption of gelled and non-gelled SPI is identical. DSC analysis of the lyophilized gels did not reveal a clear glass transition. Therefore, a slightly higher of was fitted which coincides with the of 11S soy glycinin as reported by Morales and Kokini (1997) (Morales and Kokini, 1997). Gluten sorption was not affected by the gelation process. Sorption isotherms were fitted using FVFH theory with respect to (Eq. (2)). Best fits and fitted values for are presented in Fig. 1b. SPI has a lower than gluten, indicating it has more attractive interactions with water compared to gluten.
4.2. Gel swelling and mechanical characterization
4.2.1. Soy protein gels
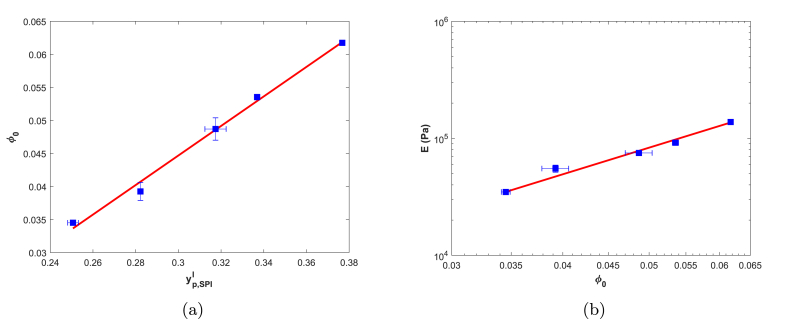
We will use as the polymer weight fraction at gelation of a single-phase () or two-phase () gel, made of polymer j, or of the gel as a whole (). Recall that represents the polymer volume fraction at maximum swelling (when ). Increasing resulted in a linear increase of (Fig. 2a). This indicates that varying is a controllable method to adjust maximum swelling. The elastic Young's moduli E of the swollen SPI gels were determined via uni-axial compression. E increased proportionally as increases (Fig. 2b); E thus also relates directly to . The elastic modulus relates directly to the cross-link density of the gel (van der Sman, 2013). An increased cross-link density results in a greater resistance to deformation (conform Eq. (9)), and explains the reduced swelling as is increased (Fig. 2a).
Fig. 2.
Maximum level of swelling, , of SPI gels as function of (solid line , ; Fig. 2a), and elastic Young's moduli of swollen SPI gels as function of (solid line with and , ; Fig. 2b). n = 3 for , n = 2 for E, and n = 3 for .
The modulus as a function of can be described with a power law with an exponent of 2.28 (Fig. 2b). Note that the moduli were determined in the swollen states. The apparent agreement with the theoretical exponent reported by Horkay and Zrínyi (1982) for networks of Gaussian chains is most probably a deceptive coincidence as the majority of soy proteins are globular (de HHJ de Jongh, 2003). It is unlikely that the heat applied during gelation resulted in a complete loss of protein secondary structure (Kim et al., 2004).
4.2.2. Gluten gels
Wheat gluten proteins are more difficult to handle than soy proteins as they bind little water (Grabowska et al., 2014) and form a network upon hydration (Attenburrow et al., 1990, Ng and McKinley, 2008). Our swelling experiments revealed that non-heated gluten binds water protein, similar to Grabowska et al. (2014) , (Grabowska et al., 2014). Higher levels of swelling have also been reported ( (Bárcenas et al., 2009)). It must be noted that the strength of gluten networks depends on the temperature at hydration (Farahnaky and Hill, 2007), which can affect swelling. In addition, the kneading process can affect the gluten network structure in wheat flour doughs, by changing from a lumped to a strand-like structure (Auger et al., 2008, Ng and McKinley, 2008). During preparation of our gluten doughs the gluten was only hydrated with water, and not kneaded as you would a bread dough, which may explain the difference in swelling.
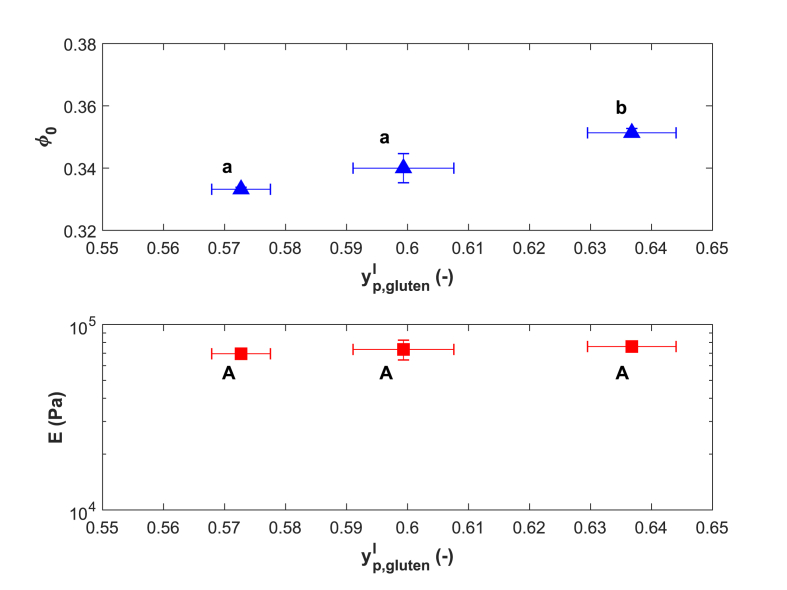
Single-phase gluten gels were prepared in ethanol and swollen in water to study their swelling as function of (Fig. 3 top). The gluten gels bind less water than hydrated gluten (). This could be due to additional cross-linking upon heating. The exposure to ethanol may also induce additional cross-linking as ethanol decreases the denaturation temperature of gluten (Lambrecht et al., 2016) and may facilitate further protein unfolding. increased slightly but significantly with increasing . Elastic moduli of gluten gels swollen in water were not significantly different (Fig. 3 bottom), which suggests similar cross-link densities. This is in line with the similar values of . A similarly limited dependence of swelling on the is expected for gels obtained from hydrated gluten.
Fig. 3.
(top) and elastic Young's moduli (bottom) of gluten gels prepared in ethanol and washed and swollen in water as function of . Different letters indicate significant differences (p; n = 3).
4.3. WHC of single-phase protein gels during centrifugation
4.3.1. Soy protein gels
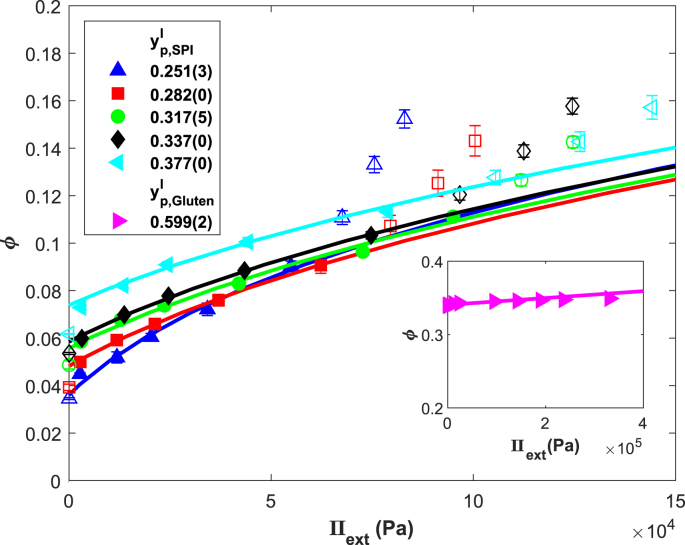
Swollen SPI gels were subjected to an increasing external pressure by centrifugation to determine their WHC as a function of applied pressure. The WHC data was fitted with the Flory-Rehner theory (Fig. 4). We calculate the mixing contribution to the swelling pressure using the interaction parameter, , as obtained from fitting the sorption isotherms with FVFH theory (Fig. 1). This leaves only the shear modulus in the reference state, , and the polymer volume fraction in the reference state, , as unknown parameters. Recall that the reference state refers to the relaxed state of the polymer. Defining as ϕ at gelation did not match the observed swelling and de-swelling. was therefore obtained through fitting. For some gels, gel collapse was observed at higher , which affected the WHC. Data points where collapse occurred were therefore excluded from the fitting process (Fig. 4, open symbols). Fig. 4 shows a strong dependence of ϕ on the applied pressure that can be described qualitatively with Flory-Rehner theory.
Fig. 4.
WHC of swollen SPI and gluten gels expressed as polymer volume fraction as function of the applied pressure as determined via centrifugation. Open symbols were excluded from the fitted procedure due to gel collapse. Solid lines are best fits with Flory-Rehner (). (n = 8).
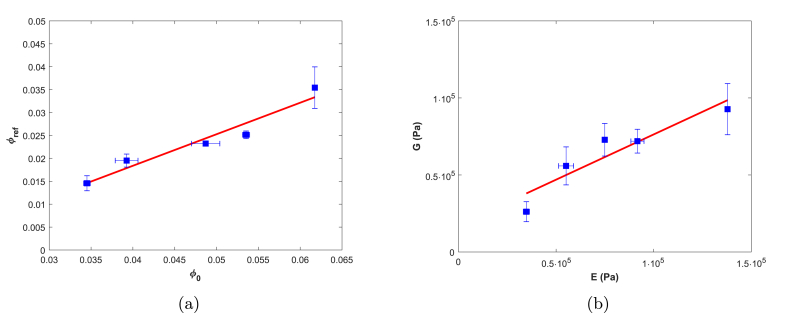
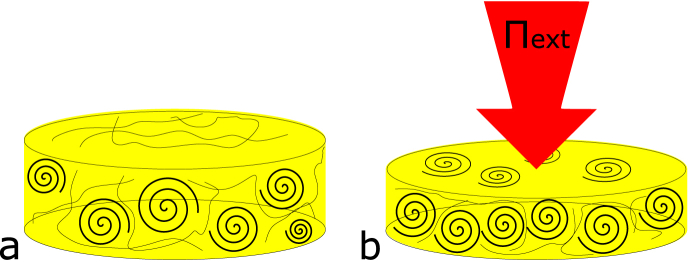
We compare the fitted values with E and from Fig. 2. Fitted values of correlate linearly with the experimentally determined (Fig. 5a). However, the results deviate from the expected result of , as was shown for various other bio-polymers (van der Sman, 2015). The deviation could be the result of the globular (non-Gaussian) nature of soy protein network. Alternatively, it could be due to some inhomogeneity in the distribution of cross-links in the swollen gel. Hydrogel swelling depends on the local cross-link density, as was also addressed in the review by Hoffman (2012) (Hoffman, 2012, Drumheller and Hubbell, 1995). Areas of low cross-link density will swell to a higher level than high cross-link density areas, effectively increasing . Low cross-link density areas will exude more water at lower , after which a homogeneous material is obtained. We have accounted for these inhomogeneities by excluding the first data point from the fits (Fig. 4). A schematic representation of a possible gel structure is presented in Fig. 6.
Fig. 5.
Fitted as function of experimentally determined (Slope: 0.69, ) (5a). Fitted elastic Shear moduli as function of experimentally determined elastic Young's moduli (Slope: 0.59, ) (5b). Solid lines are the result of linear regression. n = 3 for and n = 2 for E.
Fig. 6.
Schematic representation of the SPI gel network before (a) and after (b) the expulsion of water under external load (). Sustained external pressure will induce the initial expulsion of water from the lower cross-link density areas. This results in a compaction of the network and allows for the higher cross-link density patches to overlap. This induces an increase in the elastic modulus of the gel after the exudation of water and a change in the effective . Spirals represent patches with high cross-link density.
We convert the fitted elastic shear modulus in the reference state, , to the Shear modulus, G, using Eq. (10) to enable direct comparison with the experimental Young's modulus E. G correlates linearly with E (Fig. 5b). For incompressible materials a slope of would be expected, while linear regression indicates a slope of 0.59. The deviation could be due to the globular nature of soy. Alternatively, inhomogeneities in cross-link density could account for this deviation. During relatively fast measurements (such as uni-axial compression), moisture losses are negligible and we measure the gel's bulk properties. During sustained deformation (such as during centrifugation) areas of lower cross-link density will exude more water until the higher cross-link density patches overlap (Fig. 6b). The volume fraction of high cross-link density material increases, resulting in a higher modulus.
The physical meaning of the parameters obtained through fitting may be limited given that not all assumptions for Flory-Rehner theory are met. Still, they are practically useful when describing and predicting the WHC.
4.3.2. Gluten gels
Gluten gels prepared in ethanol were firm and showed no signs of collapse during centrifugation, even at the highest pressures applied. WHC as function of pressure was similar for the different values of and therefore only is shown (Fig. 4). Despite binding very little water, gluten gels (prepared in ethanol) bind water very tightly with negligible water losses in the relevant range of . Similarly low losses were reported for hydrated gluten doughs (Roccia et al., 2009) and we expect similar behaviour for gluten gels prepared in water. Gluten is an elastomer (Ng and McKinley, 2008), and thus characterized by a high stretchability and limited polymer-solvent interaction. Although reasonable fits of Flory-Rehner theory could be made, the WHC of gluten gels is characterized by gluten's elastomeric behaviour as indicated by the limited interaction with the solvent.
4.4. WHC of mixed protein gels
4.4.1. Water distribution before gelation
We have prepared mixed gels with different SPI: gluten ratios while keeping the total dry matter content of the gel constant at to study the effect of the SPI: gluten ratio on the WHC. As was shown by Dekkers et al. (2018), two separate phases of soy and gluten can be observed in similar mixed gels using confocal scanning laser microscopy (Dekkers et al., 2018). The two phases are thought to be relatively pure and consisting of SPI or gluten (Grabowska et al., 2014, Dekkers et al., 2016a, Dekkers et al., 2018), While gluten swelling shows only a limited dependence on , the WHC of SPI depends strongly on (Fig. 4). Knowledge of the water distribution between SPI and gluten before gelation is therefore required to understand the WHC of the mixed gels.
Water distribution between polymers without cross-links, like our protein powders, should adhere to Flory-Huggins theory (Eq. (2)). However, gluten spontaneously cross-links upon hydration, which will limit its hydration. Therefore, the full Flory-Rehner theory is required to describe the water partitioning between SPI and gluten before gelation. An experimental study using Time Domain-NMR on the water distribution between SPI and gluten as a function of and SPI:gluten ratio showed that SPI binds more water than gluten (Dekkers et al., 2016a).
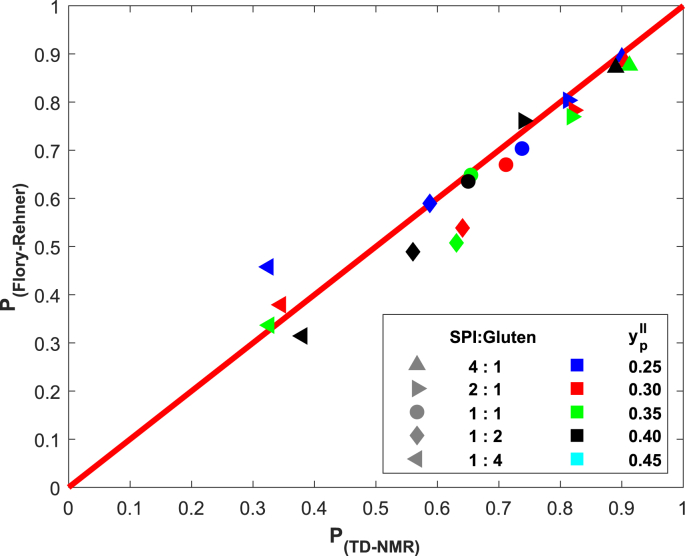
We define the partition coefficient P as the fraction of total water in the SPI phase; is therefore the fraction in the gluten phase. Since SPI is a sol, its swelling depends only on . Gluten is cross-linked and its swelling depends on and . Equilibrium is assumed when . depends on from Fig. 1b, and follows from fitting and to the data from Dekkers et al. (2016a). Predictions based on Flory-Rehner theory match the experimental data from Dekkers et al. (2016a) reasonably well (Fig. 7).
Fig. 7.
Prediction plot of the water partition coefficient, P, using TD-NMR data from Dekkers et al. (2016a), and as predicted with Flory-Rehner theory assuming and . Average difference between experimental and predictions is .
We calculate the polymer weight fraction of the hydrated SPI, before gelation, using the partition coefficient P:
| (17) |
is the weight of SPI and is the total weight of water in the mixture. We derive the expected level of swelling SPI in the mixed gel from and the relation between and in Fig. 2b.
4.4.2. WHC of mixed gels
Mixed gels with different SPI:gluten ratios were swollen until constant weight. We assume gluten to swell to water protein and derive the amount of water in the SPI phase of the mixed gel using a simple mass balance:
| (18) |
where is equal to 0.33. From the result of Eq. (18) we can derive ϕ using and the densities of polymer and water. Now that we have separated the contribution of gluten to the WHC from that of SPI we can study the WHC of SPI separately from gluten.
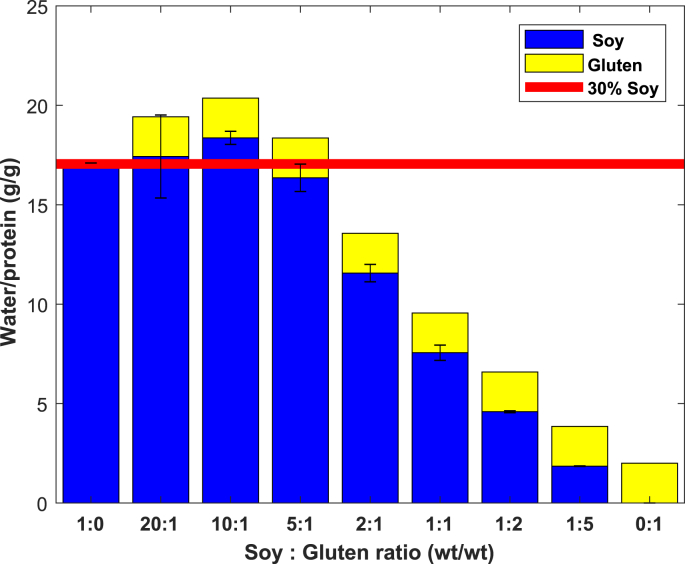
The swelling of the SPI phase strongly depends on the SPI:gluten ratio (Fig. 8). Mixed gels containing primarily SPI (ratios 20:1, 10:1, 5:1) swell to a level similar to single-phase SPI gels, as indicated by the red line for a single-phase SPI gel with . The swelling of SPI decreased gradually as gluten content was increased. Because of the limited water uptake by gluten in the dough before gelation, more water will be available to hydrate SPI, causing (before gelation) to decrease. As was shown in Fig. 2b, the maximum level of swelling increases with decreasing , as a result of the decreased cross-link density. An increased level of swelling of SPI with increasing gluten content was therefore expected, while the opposite is observed. The swelling of mixed SPI-gluten gels is less than the weighted sum of the individual phases, indicating an interaction between SPI and gluten.
Fig. 8.
WHC of mixed SPI-gluten gels at expressed as gram water per gram protein. Gluten is assumed to bind 2 g water per gram protein. Solid line indicates swelling of an SPI gel with (n = 3).
4.4.3. Mixed gel mechanics
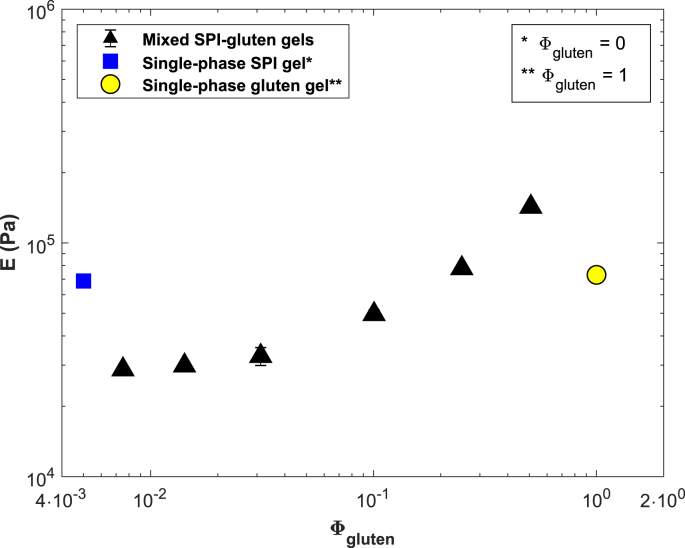
To investigate the interaction between SPI and gluten in mixed gels, we have determined the elastic Young's moduli of swollen mixed gels via uni-axial compression (Fig. 9). We express the modulus as function of the volume fraction of the gluten phase in the mixed gel, .
Fig. 9.
Elastic Young's moduli of swollen mixed gels with different SPI:gluten ratios as determined with uni-axial compression (n = 2). represents the volume fraction of the gluten phase in the swollen gel. Moduli of swollen single-phase SPI and gluten gels were added for comparison. Note that the single-phase SPI gel contains no gluten and thus .
Both single-phase SPI and gluten gels have a considerably higher modulus than mixed gels with low gluten fractions (SPI:gluten ratios 20:1, 10:1, 5:1). Since the modulus increases upon increasing the gluten content, it is unlikely that gluten acts as an inactive filler (Dickinson and Chen, 1999). Gluten and soy proteins have recently been shown not to co-aggregate (Lambrecht et al., 2017). We hypothesize that the inclusion of gluten may have introduced defects in the SPI network, causing the observed weakening.
The modulus of the mixed gels increases with and exceeds the modulus of neat gluten gels (ratios 1:1, 1:2). Gluten networks are known to be strain hardening (Dobraszczyk and Morgenstern, 2003). For gels with a continuous gluten network, gluten may already be strained as a result of SPI swelling, and could consequently have a higher modulus.
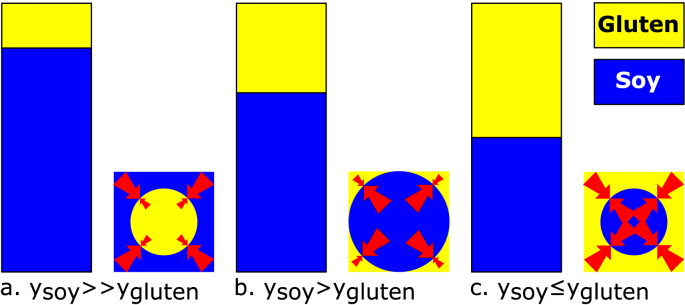
We hypothesize that mixed gels with low gluten fractions are SPI continuous (ratios 20:1, 10:1, 5:1). As the gluten content increases (ratios 2:1, 1:1, 1:2), a continuous gluten network forms that is either entrapping or co-continuous with the SPI network. The mechanism explaining the observed swelling of mixed SPI-Gluten gels is presented in Fig. 10.
Fig. 10.
Proposed mechanism explaining the swelling of mixed SPI-gluten gels. SPI forms the continuous phase with gluten as a dispersed phase when (11a). For intermediate ratios of SPI:Gluten (; ratio), gluten forms a continuous network and hinders SPI swelling (11b). Upon further increasing the amount of gluten the continuous gluten network becomes stronger, which further limits SPI swelling (11c). Here, represents the fraction of polymer i of the total polymer content. Note that the depicted structure merely describes the interaction between gel phases and does not represent the proposed gel micro-structure.
4.4.4. Mechanical interaction between SPI and gluten
The mechanism proposed in Fig. 10 explains the reduced swelling of SPI based on confinement and compression by a continuous gluten network. To quantify this mechanical interaction interaction between SPI and gluten, we analyse the WHC of the SPI phase in the mixed gel as function of applied pressure. We derive the polymer volume fraction in the SPI phase by subtracting the contribution of gluten using Eq. (18). We hypothesize that at higher gluten contents the gluten forms a continuous network and imposes a pressure on the SPI phase during swelling. This will limit SPI swelling, as schematically depicted in Fig. 10. We will call this pressure , which is additive to the external pressure experienced by SPI as:
| (19) |
Since is additive to , we can determine as the difference in pressure between the freely swollen SPI gels and the SPI phase of the mixed gels at the same value of ϕ (Fig. 11). We obtain the pressure dependence of ϕ for a freely swollen SPI gel from and the relations for single phase SPI gels between and and (Fig. 2, Fig. 5a), as indicated by the solid lines in Fig. 11. The difference in between experimental data points and the corresponding solid line indicates the value of :
| (20) |
with as the pressure exerted by the gluten on the SPI phase in the mixed gel, as the external pressure associated with a certain ϕ for a single phase SPI gel, and as the external pressure associated with that same ϕ for the SPI phase of the mixed gel.
Fig. 11.
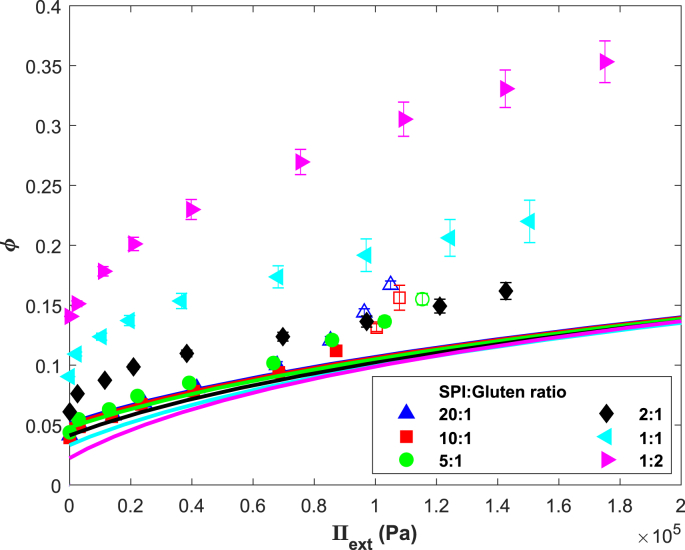
Water holding capacity as measured via centrifugation for mixed SPI-gluten gels, expressed for the SPI phase, assuming gluten binds water protein. Solid lines indicate the expected dependence of ϕ based on the SPI phase composition according to Eq. (17). Open symbols indicate gel collapse (n = 8).
Dekkers et al. (2016a) showed that one cannot easily differentiate between iso-strain, iso-stress, and inter-penetrating networks for SPI-gluten mixtures as they provide similar outcomes over a wide range of sample compositions (Dekkers et al., 2016a). The iso-strain model (Eq. (14)) should therefore provide a good indication of the strain on the network. By expressing as function of strain (ε), we effectively obtain the stress-strain relation for the gluten network. Two distinct regimes can be identified based on the SPI: Gluten ratios (Fig. 12).
Fig. 12.
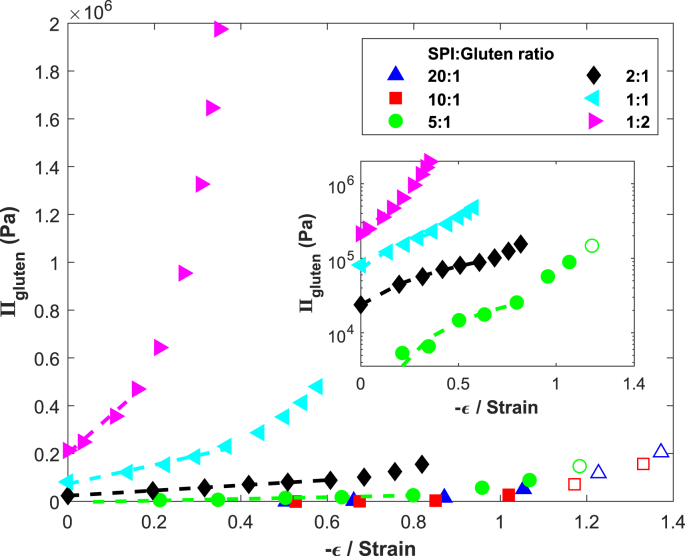
The pressure exerted by the gluten phase on the SPI phase, , as calculated with Eq. (20), as function of the strain, ε. Dashed lines indicate the regime over which the elastic modulus was determined. Open symbols indicate gel collapse occurred during centrifugation. Insert shows the data for ratios 5:1, 2:1, 1:1 and 1:2 on a lin-log scale for clarity.
The first regime covers the gels low in gluten, which swell to a similar level as pure SPI (Fig. 9, ratios 20:1, 10:1, 5:1). These gels have near-zero values of at low strains, indicating similarity in WHC to pure SPI. In line with our earlier hypothesis, SPI will be the continuous phase in gels as they swell and de-swell similarly to pure SPI, with the gluten present as inclusions. The increasingly positive pressures at high strain () are the result of additional water loss associated with gel collapse (Fig. 12, open symbols).
The second regime covers the gels with higher gluten content, which show a gradual decrease in swelling as gluten content is increased (Fig. 8, ratios 2:1, 1:1, 1:2). The markedly lower swelling of the SPI phase compared to pure SPI suggests gluten is a continuous phase. The ratio at which the second regime starts ( 2:1) could be the ratio at which gluten starts forming a space-filling network. becomes higher as gluten content increases, indicating that the pressure exerted onto the SPI phase becomes higher.
At higher strains, we observe an increase in . Gluten networks are strain hardening (Uthayakumaran et al., 2002) which might explain the increasing slope of versus ε.
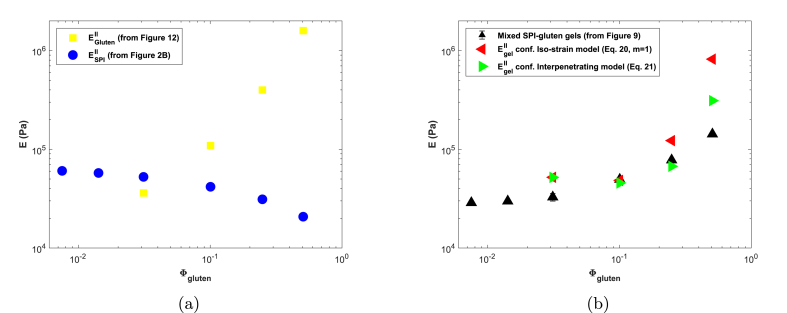
For the gluten-rich gels (ratios 2:1, 1:1, 1:2) we were able to calculate the elastic modulus of the gluten network as the slope in the linear regime in Fig. 12. Naturally, a linear model cannot describe the observed strain hardening of gluten. However, the more sophisticated affine network model (similar to Eq. (8)) also failed to describe the observed non-linear behaviour, suggesting the observed strain hardening is real (fits not shown). The elastic modulus of the gluten phase increases with gluten volume fraction (Fig. 13a), which is in line with the reduced swelling of SPI as the amount of gluten in the mixed gels is increased.
Fig. 13.
Elastic Young's moduli of the gluten and SPI phases in mixed gels (Fig. 13a). Moduli of the mixed gels according to the iso-strain and inter-penetrating network models, and the experimental Young's moduli of mixed gels (Fig. 13b). represents the volume fraction of gluten in the swollen gel.
To test the validity of the gluten moduli obtained from the WHC measurements, we use them to calculate the expected moduli of the mixed gels and compare the result with the experimentally determined moduli. An iso-strain or inter-penetrating network structure is most probable based on the hypothesized structure. The modulus according to the iso-strain network model is given by Eq. (21), (Takayanagi et al., 1963):
| (21) |
is the modulus of the mixed gel, and , , and are the volume fractions and moduli of the individual phases respectively. Exponent m taken as 1 for iso-strain behaviour. The modulus of an isotropic inter-penetrating network is given by (Feng et al., 2003):
| (22) |
where a is:
| (23) |
We take the moduli of the SPI phase from the relation between and from Fig. 2b. We acknowledge that the modulus of SPI appears to be negatively affected by the addition of gluten. However, since the modulus of the composite is dominated by the elasticity of gluten in the relevant range of the influence of the uncertainty in on the modulus of the composite will be limited. Comparison of the moduli calculated for the mixed gels with our experimentally determined moduli shows a reasonable agreement, for both iso-strain and inter-penetrating models, which is in line with Dekkers et al. (2016a). Even though we cannot confirm the exact network structure, these findings support our hypothesis that at sufficiently high gluten contents a continuous gluten network forms which is capable of limiting the swelling of SPI via a mechanical interaction.
The mechanical interaction between SPI and gluten in swollen mixed gels depends on the ratio between the two bio-polymers. Therefore, varying the ratio between SPI and gluten could be used to control the swelling and de-swelling of mixed gels, and possibly meat analogues. How the high shear processes commonly used to produce meat analogue products would affect these findings remains unclear.
4.5. General discussion
We have used Flory-Rehner (FR) theory to better understand the behaviour of mixed SPI-gluten gels. The parameters obtained through fitting of FR theory were not entirely consistent with theory, possibly due to the globular nature of soy protein. Nonetheless, using FR theory provided useful insights on the interaction between SPI and gluten. The results indicate that at sufficiently high gluten contents, a continuous gluten network forms. The gluten network both limits water uptake by SPI, and increases the modulus of the mixed gel. While the limited WHC might be detrimental to the juiciness of a meat analogue product, the improved texture could be beneficial to the product's ‘bite’. Unfortunately, there is currently no experimental method capable of predicting juiciness accurately. The exact effect of SPI:gluten ratio on juiciness thus remains unclear.
Interestingly, the SPI:gluten ratio at which gluten forms a continuous network coincides with the ratios at which fibrous materials can be made (Grabowska et al., 2014, Schreuders et al., 2019), and suggests gluten continuity might be a prerequisite for making meat-like structures with shear-cell technology.
5. Conclusion
We have studied the WHC of single-phase and mixed SPI and gluten gels with Flory-Rehner theory to ultimately enhance the juiciness of meat analogues. WHC of single-phase SPI gels depends on the polymer weight fraction at gelation, , and can be described with Flory-Rehner theory. WHC of mixed SPI - gluten gels is not a linear combination of the WHC of their constituents. Mixed gels low in gluten exhibit similar behaviour to neat SPI gels, although their elastic moduli were lowered by gluten addition. This did not affect the WHC as a function of external pressure, as indicated by the near-zero values of . Increasing the gluten content results in the formation of a continuous gluten network, that limits SPI swelling via an apparent mechanical interaction with SPI. The pressure exerted on the SPI phase by the gluten network depends on the SPI:gluten ratio and the elastic modulus of the gluten network was extracted. The elastic modulus of the mixed gels could be approximated with the polymer blending law and the predicted moduli of soy and gluten. Understanding the interaction between the different phases in bio-polymer blends can help in improving their structuring potential, and aid the development of the next generation meat analogues. This work shows that the gel network structure can be controlled with the SPI-gluten ratio. Therefore, it can be an important tool to control both WHC/juiciness and the mechanical properties of meat analogues.
CRediT authorship contribution statement
Steven H.V. Cornet: Conceptualization, Methodology, Investigation, Formal analysis, Writing - original draft, Writing - review & editing. Atze Jan van der Goot: Writing - review & editing, Supervision. Ruud G.M. van der Sman: Writing - review & editing, Supervision.
Declaration of Competing Interest
There are no conflicts to declare.
Acknowledgements
We acknowledge Stefano Renzetti for his help in performing the DVS experiments. This research is part of the project Plant Meat Matters, which is co-financed by Top Consortium for Knowledge and Innovation Agri & Food by the Dutch Ministry of Economic Affairs; the project is registered under contract number TKI-AF-16011.
Contributor Information
Steven H.V. Cornet, Email: steven.cornet@wur.nl.
Atze Jan van der Goot, Email: atzejan.vandergoot@wur.nl.
Ruud G.M. van der Sman, Email: ruud.vandersman@wur.nl.
References
- Aaslyng M.D., Bejerholm C., Ertbjerg P., Bertram H.C., Andersen H.J. Cooking loss and juiciness of pork in relation to raw meat quality and cooking procedure. Food Qual. Prefer. 2003;14(4):277–288. doi: 10.1016/S0950-3293(02)00086-1. https://www.sciencedirect.com/science/article/pii/S0950329302000861 ISSN 09503293. [DOI] [Google Scholar]
- Akdogan H. High moisture food extrusion. Int. J. Food Sci. Technol. 1999;34(3):195–207. doi: 10.1046/j.1365-2621.1999.00256.x. https://onlinelibrary.wiley.com/doi/abs/10.1046/j.1365-2621.1999.00256.x ISSN 09505423. [DOI] [Google Scholar]
- Attenburrow G., Barnes D.J., Davies A.P., Ingman S.J. Rheological properties of wheat gluten. J. Cereal. Sci. 1990;12(1):1–14. doi: 10.1016/S0733-5210(09)80152-5. ISSN 07335210. [DOI] [Google Scholar]
- Auger F., Morel M.H., Lefebvre J., Dewilde M., Redl A. A parametric and microstructural study of the formation of gluten network in mixed flour-water batter. J. Cereal. Sci. 2008;48(2):349–358. doi: 10.1016/j.jcs.2007.10.006. https://www.sciencedirect.com/science/article/pii/S0733521007001877 ISSN 07335210. [DOI] [Google Scholar]
- Bárcenas M.E., De la O-Keller J., Rosell C.M. Influence of different hydrocolloids on major wheat dough components (gluten and starch) J. Food Eng. 2009;94(3–4):241–247. doi: 10.1016/j.jfoodeng.2009.03.012. ISSN 02608774. [DOI] [Google Scholar]
- Berghout J.A.M., Venema P., Boom R.M., van der Goot A.J. Comparing functional properties of concentrated protein isolates with freeze-dried protein isolates from lupin seeds. Food Hydrocolloids. 2015;51:346–354. doi: 10.1016/j.foodhyd.2015.05.017. http://linkinghub.elsevier.com/retrieve/pii/S0268005X15002180 ISSN 0268005X. [DOI] [Google Scholar]
- Bertram H.C., Aaslyng M.D., Andersen H.J. Elucidation of the relationship between cooking temperature, water distribution and sensory attributes of pork - a combined NMR and sensory study. Meat Sci. 2005;70(1):75–81. doi: 10.1016/j.meatsci.2004.12.002. https://www.ncbi.nlm.nih.gov/pubmed/22063282 ISSN 03091740. [DOI] [PubMed] [Google Scholar]
- Chiang J.H., Loveday S.M., Hardacre A.K., Parker M.E. Effects of soy protein to wheat gluten ratio on the physicochemical properties of extruded meat analogues. Food Struct. 2019;19(September 2018):100102. doi: 10.1016/j.foostr.2018.11.002. ISSN 22133291. [DOI] [Google Scholar]
- Couchman P.R., Karasz F.E. A classical thermodynamic discussion of the effect of composition on glass-transition temperatures. Macromolecules. 1978;11(1):117–119. doi: 10.1021/ma60061a021. https://pubs.acs.org/doi/10.1021/ma60061a021 ISSN 15205835. [DOI] [Google Scholar]
- Dahesh M., Banc A., Duri A., Morel M.H., Ramos L. Polymeric assembly of gluten proteins in an aqueous ethanol solvent polymeric assembly of gluten proteins in an aqueous ethanol solvent. J. Phys. Chem. B. 2014;118(38):11065–11076. doi: 10.1021/jp5047134. https://www.ncbi.nlm.nih.gov/pubmed/25171192 [DOI] [PubMed] [Google Scholar]
- de Bakker E., Dagevos H. Den Haag; Wageningen UR: 2010. Vleesminnaars, vleesminderaars en vleesmijders - Duurzame eiwitconsumptie in een carnivore eetcultuur. Technical report,https://www.wur.nl/nl/Publicatie-details.htm?publicationId=publication-way-333933323534 [Google Scholar]
- De Gennes P.G. Cornell University Press; Ithaca and London: 1979. Scaling Concepts in Polymer Physics. ISBN 080141203X. [Google Scholar]
- Dekkers B.L., de Kort D.W., Grabowska K.J., Tian B., Van As H., van der Goot A.J. A combined rheology and time domain NMR approach for determining water distributions in protein blends. Food Hydrocolloids. 2016;60:525–532. doi: 10.1016/j.foodhyd.2016.04.020. ISSN 0268005X. [DOI] [Google Scholar]
- Dekkers B.L., Nikiforidis C.V., van der Goot A.J. Shear-induced fibrous structure formation from a pectin/SPI blend. Innovat. Food Sci. Emerg. Technol. 2016;36:193–200. doi: 10.1016/j.ifset.2016.07.003. ISSN 14668564. [DOI] [Google Scholar]
- Dekkers B.L., Emin M.A., Boom R.M., van der Goot A.J. The phase properties of soy protein and wheat gluten in a blend for fibrous structure formation. Food Hydrocolloids. 2018;79:273–281. doi: 10.1016/j.foodhyd.2017.12.033. http://linkinghub.elsevier.com/retrieve/pii/S0268005X17311785 ISSN 0268005X. [DOI] [Google Scholar]
- Dickinson E., Chen J. Heat-set whey protein emulsion gels: role of active and inactive filler particles. J. Dispersion Sci. Technol. 1999;20(1–2):197–213. doi: 10.1080/01932699908943787. https://www.tandfonline.com/doi/abs/10.1080/01932699908943787 ISSN 01932691. [DOI] [Google Scholar]
- Dobraszczyk B.J., Morgenstern M.P. Rheology and the breadmaking process. J. Cereal. Sci. 2003;38(3):229–245. doi: 10.1016/S0733-5210(03)00059-6. https://www.sciencedirect.com/science/article/pii/S0733521003000596 ISSN 07335210. [DOI] [Google Scholar]
- Drumheller P.D., Hubbell J.A. Densely crosslinked polymer networks of poly(ethylene glycol) in trimethylolpropane triacrylate for cell-adhesion-resistant surfaces. J. Biomed. Mater. Res. 1995;29(2):207–215. doi: 10.1002/jbm.820290211. https://www.ncbi.nlm.nih.gov/pubmed/7738068 ISSN 10974636. [DOI] [PubMed] [Google Scholar]
- Farahnaky A., Hill S.E. The effect of salt , water and temperature on wheat dough rheology. J. Texture Stud. 2007;38:499–510. doi: 10.1111/j.1745-4603.2007.00107.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1745-4603.2007.00107.x ISSN 0022-4901. [DOI] [Google Scholar]
- Feng X.Q., Mai Y.W., H Qin Q. A micromechanical model for interpenetrating multiphase composites. Comput. Mater. Sci. 2003;28(3–4 SPEC. ISS.):486–493. doi: 10.1016/j.commatsci.2003.06.005. https://www.sciencedirect.com/science/article/pii/S0927025603001320 ISSN 09270256. [DOI] [Google Scholar]
- Flory P.J., Rehner J. Statistical mechanics of cross-linked polymer networks II. Swelling. J. Chem. Phys. 1943;11(11):521–526. doi: 10.1063/1.1723792. ISSN 00219606. [DOI] [Google Scholar]
- Flory P.J., Rehner J. Effect of deformation on the swelling capacity of rubber. J. Chem. Phys. 1944;12(10):412. doi: 10.1063/1.1723884. http://scitation.aip.org/content/aip/journal/jcp/12/10/10.1063/1.1723884 ISSN 00219606. [DOI] [Google Scholar]
- Grabowska K.J., Tekidou S., Boom R.M., van der Goot A.J. Shear structuring as a new method to make anisotropic structures from soy-gluten blends. Food Res. Int. 2014;64:743–751. doi: 10.1016/j.foodres.2014.08.010. https://www.sciencedirect.com/science/article/pii/S0963996914005481? ISSN 09639969. [DOI] [PubMed] [Google Scholar]
- Grabowska K.J., Zhu S., Dekkers B.L., De Ruijter N.C.A., Gieteling J., van der Goot A.J. Shear-induced structuring as a tool to make anisotropic materials using soy protein concentrate. J. Food Eng. 2016;188:77–86. doi: 10.1016/j.jfoodeng.2016.05.010. ISSN 02608774. [DOI] [Google Scholar]
- HHJ de Jongh . Globular proteins. In: Aalbersberg W.Y., Hamer R.J., Jasperse P., de Jongh H.H.J., de Kruif C.G., Walstra P., de Wolf F.A., editors. vol. 23. Elsevier Science B.V.; 2003. http://www.sciencedirect.com/science/article/pii/S0921042303800035 (Industrial Proteins in Perspective). chapter III, pages 31–86. [DOI] [Google Scholar]
- Hino T., Prausnitz J.M. Swelling equilibria for heterogeneous polyacrylamide gels. J. Appl. Polym. Sci. 1996;62(1):1635–1640. ISSN 0021-8995http://onlinelibrary.wiley.com/doi/10.1002/(SICI)1097-4628(19961205)62:10{%}3C1635::AID-APP15{%}3E3.0.CO;2-0/abstract. [Google Scholar]
- Hoek A.C., Luning P.A., Weijzen P., Engels W., Kok F.J., de Graaf C. Replacement of meat by meat substitutes. A survey on person- and product-related factors in consumer acceptance. Appetite. 2011;56(3):662–673. doi: 10.1016/j.appet.2011.02.001. ISSN 01956663. [DOI] [PubMed] [Google Scholar]
- Hoek A.C. PhD thesis; Wageningen UR: 2010. Will Novel Protein Foods Beat Meat? Consumer Acceptance of Meat Substitutes - a Multidisciplinary Research Approach.http://library.wur.nl/WebQuery/clc/1926634 [Google Scholar]
- Hoffman A.S. Hydrogels for biomedical applications. Adv. Drug Deliv. Rev. 2012;64(Suppl. L):18–23. doi: 10.1016/j.addr.2012.09.010. ISSN 0169409X. [DOI] [PubMed] [Google Scholar]
- Horkay F., Zrínyi M. Studies on the mechanical and swelling behavior of polymer networks based on the scaling concept. 4. Extension of the scaling approach to gels swollen to equilibrium in a diluent of arbitrary activity. Macromolecules. 1982;15(5):1306–1310. doi: 10.1021/ma00233a018. https://pubs.acs.org/doi/10.1021/ma00233a018 ISSN 15205835. [DOI] [Google Scholar]
- Jin X., van der Sman R.G.M., van Maanen J.F.C., van Deventer H.C., van Straten G., Boom R.M., Moisture A. J. B. van Boxtel. Sorption isotherms of broccoli interpreted with the flory-huggins free volume theory. Food Biophys. 2014;9(1):1–9. doi: 10.1007/s11483-013-9311-6. https://link.springer.com/article/10.1007/s11483-013-9311-6 ISSN 15571858. [DOI] [Google Scholar]
- Kalichevsky M.T., Jaroszkiewicz E.M., Blanshard J.M.V. Glass transition of gluten. 1: gluten and gluten-sugar mixtures. Int. J. Biol. Macromol. 1992;14(5):257–266. doi: 10.1016/S0141-8130(05)80038-8. https://www.sciencedirect.com/science/article/pii/S0141813005800388 ISSN 01418130. [DOI] [PubMed] [Google Scholar]
- Kealley C.S., Rout M.K., Dezfouli M.R., Strounina E., Whittaker A.K., Appelqvist I.A.M., Lillford P.J., Gilbert E.P., Gidley M.J. Structure and molecular mobility of soy glycinin in the solid state. Biomacromolecules. 2008;9(10):2937–2946. doi: 10.1021/bm800721d. https://pubs.acs.org/doi/10.1021/bm800721d ISSN 15257797. [DOI] [PubMed] [Google Scholar]
- Khokhlov A.R. Swelling and collapse of polymer networks. Polymer. 1980;21(4):376–380. doi: 10.1016/0032-3861(80)90005-1. https://www.sciencedirect.com/science/article/pii/0032386180900051 ISSN 00323861. [DOI] [Google Scholar]
- Kim K.S., Kim S., Yang H.J., Kwon D.Y. Changes of glycinin conformation due to pH, heat and salt determined by differential scanning calorimetry and circular dichroism. Int. J. Food Sci. Technol. 2004;39(4):385–393. doi: 10.1111/j.1365-2621.2004.00795.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1365-2621.2004.00795.x ISSN 09505423. [DOI] [Google Scholar]
- Kocher P.N., Foegeding E.A. Microcentrifuge-based method for measuring water-holding of protein gels. J. Food Sci. 1993;58(5):1040–1046. doi: 10.1111/j.1365-2621.1993.tb06107.x. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1365-2621.1993.tb06107.x ISSN 17503841. [DOI] [Google Scholar]
- Lambrecht M.A., Rombouts I., Delcour J.A. Denaturation and covalent network formation of wheat gluten, globular proteins and mixtures thereof in aqueous ethanol and water. Food Hydrocolloids. 2016;57:122–131. doi: 10.1016/j.foodhyd.2016.01.018. ISSN 0268005X. [DOI] [Google Scholar]
- Lambrecht M.A., Rombouts I., De Ketelaere B., Delcour J.A. Prediction of heat-induced polymerization of different globular food proteins in mixtures with wheat gluten. Food Chem. 2017;221:1158–1167. doi: 10.1016/j.foodchem.2016.11.043. ISSN 18737072. [DOI] [PubMed] [Google Scholar]
- Li H., Zhao L., Chen X.D., Mercadé-Prieto R. Swelling of whey and egg white protein hydrogels with stranded and particulate microstructures. Int. J. Biol. Macromol. 2016;83:152–159. doi: 10.1016/j.ijbiomac.2015.11.018. ISSN 18790003. [DOI] [PubMed] [Google Scholar]
- Liu K.S., Hsieh F.H. Protein-protein interactions in high moisture-extruded meat analogs and heat-induced soy protein gels. JAOCS, J. Am. Oil Chemists’ Soc. 2007;84(8):741–748. doi: 10.1007/s11746-007-1095-8. https://link.springer.com/article/10.1007/s11746-007-1095-8 ISSN 0003021X. [DOI] [Google Scholar]
- Micard V., Guilbert S. Thermal behavior of native and hydrophobized wheat gluten, gliadin and glutenin-rich fractions by modulated DSC. Int. J. Biol. Macromol. 2000;27(3):229–236. doi: 10.1016/S0141-8130(00)00122-7. https://www.ncbi.nlm.nih.gov/pubmed/10828369 ISSN 01418130. [DOI] [PubMed] [Google Scholar]
- Mizuno A., Mitsuiki M., Motoki M. Effect of transglutaminase treatment on the glass transition of soy protein. J. Agric. Food Chem. 2000;48(8):3286–3291. doi: 10.1021/jf9911500. https://www.ncbi.nlm.nih.gov/pubmed/10956103 ISSN 00218561. [DOI] [PubMed] [Google Scholar]
- Morales A., Kokini J.L. Glass transition of soy globulins using differential scanning calorimetry and mechanical spectrometry. Biotechnol. Prog. 1997;13(5):624–629. doi: 10.1021/bp9700519. https://aiche.onlinelibrary.wiley.com/doi/abs/10.1021/bp9700519 ISSN 87567938. [DOI] [Google Scholar]
- Morales A., Kokini J.L. State diagrams of soy globulins. J. Rheol. 1999;43(2):315–325. doi: 10.1122/1.550985. http://sor.scitation.org/doi/10.1122/1.550985 ISSN 0148-6055. [DOI] [Google Scholar]
- Ng T.S.K., McKinley G.H. Power law gels at finite strains: the nonlinear rheology of gluten gels. J. Rheol. 2008;52(2):417–449. doi: 10.1122/1.2828018. http://sor.scitation.org/doi/10.1122/1.2828018 ISSN 0148-6055. [DOI] [Google Scholar]
- Paudel E., Boom R.M., van der Sman R.G.M. Change in water-holding capacity in mushroom with temperature analyzed by flory-rehner theory. Food Bioprocess Technol. 2015;8(5):960–970. doi: 10.1007/s11947-014-1459-7. https://link.springer.com/article/10.1007/s11947-014-1459-7 ISSN 19355149. [DOI] [Google Scholar]
- Pearce K.L., Rosenvold K., Andersen H.J., Hopkins D.L. Water distribution and mobility in meat during the conversion of muscle to meat and ageing and the impacts on fresh meat quality attributes - a review. Meat Sci. 2011;89(2):111–124. doi: 10.1016/j.meatsci.2011.04.007. ISSN 03091740. [DOI] [PubMed] [Google Scholar]
- Pouplin M., Redl A., Gontard N. Glass transition of wheat gluten plasticized with water, glycerol, or sorbitol. J. Agric. Food Chem. 1999;47(2):538–543. doi: 10.1021/jf980697w. ISSN 00218561. [DOI] [PubMed] [Google Scholar]
- Puolanne E. Developments in our understanding of water-holding capacity. In: Purslow P.P., editor. chapter 8. Woodhead Publishing Limited; 2017. pp. 77–113. (New Aspects of Meat Quality). ISBN 9780081007631. [DOI] [Google Scholar]
- Quesada-Pérez M., Maroto-Centeno J.A., Forcada J., Hidalgo-Alvarez R. Gel swelling theories: the classical formalism and recent approaches. Soft Matter. 2011;7(22):10536. doi: 10.1039/c1sm06031g. ISSN 1744-683X. [DOI] [Google Scholar]
- Renkema J.M.S., Knabben J.H.M., Van Vliet T. Gel formation by beta-conglycinin and glycinin and their mixtures. Food Hydrocolloids. 2001;15(4–6):407–414. doi: 10.1016/S0268-005X(01)00051-0. https://www.sciencedirect.com/science/article/pii/S0268005X01000510 ISSN 0268005X. [DOI] [Google Scholar]
- Roccia P., Ribotta P.D., Pérez G.T., León A.E. Influence of soy protein on rheological properties and water retention capacity of wheat gluten. LWT - Food Sci. Technol. (Lebensmittel-Wissenschaft -Technol.) 2009;42(1):358–362. doi: 10.1016/j.lwt.2008.03.002. https://www.sciencedirect.com/science/article/pii/S0023643808000637 ISSN 00236438. [DOI] [Google Scholar]
- Schreuders F.K.G., Dekkers B.L., Bodnár I., Erni P., Boom R.M., van der Goot A.J. Comparing structuring potential of pea and soy protein with gluten for meat analogue preparation. J. Food Eng. 2019;261(May):32–39. doi: 10.1016/j.jfoodeng.2019.04.022. https://linkinghub.elsevier.com/retrieve/pii/S0260877419301803 ISSN 02608774. [DOI] [Google Scholar]
- Shibayama M., Shirotani Y., Hirose H., Nomura S. Simple scaling rules on swollen and shrunken polymer gels. Macromolecules. 1997;30(23):7307–7312. doi: 10.1021/ma970443w. ISSN 00249297. [DOI] [Google Scholar]
- Stutz H., H Illers K.-, Mertes J. A generalized theory for the glass transition temperature of crosslinked and uncrosslinked polymers. J. Polym. Sci. B Polym. Phys. 1990;28(9):1483–1498. doi: 10.1002/polb.1990.090280906. ISSN 10990488. [DOI] [Google Scholar]
- Takayanagi M., Harima H., Iwata Y. Viscoelastic behavior of polymer blends and its comparison with model experiments. Soci Mater Sci. 1963;12(116):389–394. doi: 10.2472/jsms.12.389. ISSN 1880-7488. [DOI] [Google Scholar]
- Uthayakumaran S., Newberry M., Phan-Thien N., Tanner R. Small and large strain rheology of wheat gluten. Rheol. Acta. 2002;41(1):162–172. doi: 10.1007/s003970200015. https://link.springer.com/article/10.1007/s003970200015 ISSN 00354511. [DOI] [Google Scholar]
- van der Sman R.G.M. Moisture transport during cooking of meat: an analysis based on Flory-Rehner theory. Meat Sci. 2007;76(4):730–738. doi: 10.1016/j.meatsci.2007.02.014. https://www.ncbi.nlm.nih.gov/pubmed/22061251 ISSN 03091740. [DOI] [PubMed] [Google Scholar]
- van der Sman R.G.M. Thermodynamics of meat proteins. Food Hydrocolloids. 2012;27(2):529–535. doi: 10.1016/J.FOODHYD.2011.08.016. https://www.sciencedirect.com/science/article/pii/S0268005X11002529 ISSN 0268-005X. [DOI] [Google Scholar]
- van der Sman R.G.M. Modeling cooking of chicken meat in industrial tunnel ovens with the Flory-Rehner theory. Meat Sci. 2013;95(4):940–957. doi: 10.1016/j.meatsci.2013.03.027. ISSN 03091740. [DOI] [PubMed] [Google Scholar]
- van der Sman R.G.M. Biopolymer gel swelling analysed with scaling laws and Flory-Rehner theory. Food Hydrocolloids. 2015;48:94–101. doi: 10.1016/j.foodhyd.2015.01.025. ISSN 0268005X. [DOI] [Google Scholar]
- van der Sman R.G.M., Meinders M.B.J. Prediction of the state diagram of starch water mixtures using the Flory–Huggins free volume theory. Soft Matter. 2011;7:429. doi: 10.1039/c0sm00280a. https://pubs.rsc.org/en/content/articlelanding/2011/sm/c0sm00280a ISSN 1744-683X. [DOI] [Google Scholar]
- van der Sman R.G.M., Paudel E., Voda A., Khalloufi S. Hydration properties of vegetable foods explained by Flory-Rehner theory. Food Res. Int. 2013;54(1):804–811. doi: 10.1016/j.foodres.2013.08.032. https://www.sciencedirect.com/science/article/pii/S0963996913004766 ISSN 09639969. [DOI] [Google Scholar]
- Verbeek C.J.R., Van Den Berg L.E. Extrusion processing and properties of protein-based thermoplastics. Macromol. Mater. Eng. 2010;295(1):10–21. doi: 10.1002/mame.200900167. https://onlinelibrary.wiley.com/doi/full/10.1002/mame.200900167 ISSN 14387492. [DOI] [Google Scholar]
- Vrentas J.S., Vrentas C.M. Sorption in glassy polymers. Macromolecules. 1991;24(9):2404–2412. doi: 10.1021/ma00009a043. https://pubs.acs.org/doi/abs/10.1021/ma00009a043 ISSN 15205835. [DOI] [Google Scholar]
- Warner R.D. Chapter 14 – the Eating Quality of Meat––IV Water-Holding Capacity and Juiciness. 8 edition. Woodhead Publishing Limited; 2017. http://www.sciencedirect.com.ezp.lib.unimelb.edu.au/science/article/pii/B9780081006948000145 ISBN 9780081006948. [DOI] [Google Scholar]
- Yven C., Culioli J., Mioche L. Meat bolus properties in relation with meat texture and chewing context. Meat Sci. 2005;70(2):365–371. doi: 10.1016/j.meatsci.2005.02.002. https://www.ncbi.nlm.nih.gov/pubmed/22063494 ISSN 03091740. [DOI] [PubMed] [Google Scholar]