Physical chemistry of gastric digestion of proteins gels

Abstract

In this paper, we present the rich physics and chemistry of the gastric digestion of protein gels. Knowledge of this matter is important for the development of sustainable protein foods that are based on novel proteins sources like plant proteins or insects. Their digestibility is an important question in the design of these new protein foods.

As polyelectrolyte gels, they can undergo volume changes upon shifts in pH or ionic strengths, as protein gels experience when entering the gastric environment. We show that these volume changes can be modelled using the Flory-Rehner theory, combined with Gibbs-Donnan theory accounting for the distribution of electrolytes over gel and bath. In-vitro experiments of soy protein gels in simulated gastric fluid indeed show intricate swelling behaviour, at first the gels show swelling but at longer times they shrink again. Simulations performed with the Flory-Rehner/Gibbs-Donnan theory reproduce qualitatively similar behaviour. In the final part of the paper, we discuss how the model must be extended to model realistic conditions existing in the in-vivo gastric environment.

Highlights

• •Physical-chemistry of gastric digestion of protein gels is presented.
• •A numerical model based on Flory-Rehner can qualitatively explain swelling of gels.
• •Protein gels in gastric environments can swell and shrink when put in gastric acid.
• •For ion transport it is important to recognize the finite volume of the gastric juice.

1. Introduction

Proteins are one of the essential ingredients in our diet. They are sometimes present as soluble ingredients in a drink, but more often proteins are present in a certain structure or food matrix. The type of structure affects the digestibility of the proteins (Norton et al., 2015, Singh et al., 2015). Due to the interest of new protein sources, e.g. plant or insect proteins, it is essential to have a better understanding of the underlying mechanisms of the digestion of structured protein-rich food. This can help us to understand the relation between food properties and the physiological mechanisms underlying the absorption of nutrients and feelings of satiety or fullness (Veldhorst et al., 2008). Especially structured foods, high in proteins, have shown to be strongly satiating, due to the slow rate of gastric digestion and gastric emptying rate (Zhang and Vardhanabhuti, 2014).

The first step in the digestion of protein gels happens in the stomach. Contrary to other parts of the digestive tract, the gastric secretion is very acidic. This condition has a significant impact on the digestion of foods high in proteins. Protein gels behave as polyelectrolyte gels, whose swelling is very responsive to external pH conditions, leading to either swelling or collapse - which depends on how the internal pH differs from the isoelectric point. It can be expected that the swelling enhances the digestion, as it allows a convective influx of acid and enzymes. Similar to polyelectrolyte gels, the amount of swelling will depend on the charge of the protein, and the amount of crosslinking. The amount of swelling will facilitate the diffusion of digestive enzymes into the gel, while strong crosslinking will hinder the diffusion and consequently the digestion of the gel (Sarkar et al., 2015, Opazo-Navarrete et al., 2018). During digestion, the internal pH will strongly vary. When pH is near the isoelectric point, the gel will strongly contract (Floury et al., 2018). At the edge of the gel, the gel will swell as pH is lower than pI, allowing the pepsin to perform hydrolysis. There is a clear indication of a pH gradient inside the gel.

It is assumed that gastric digestion of protein gels can be steered via the crosslink density or the composition in amino-acid groups, which determine the protein charge as a function of pH. There are ample tools to design protein gel microstructure for improved satiety, as the crosslink density of protein gels can be controlled via environmental conditions during gelation, such as temperature, shear, pH, ionic strength, and concentration of crosslinking agents or enzymes. This is particularly opportune for novel food products like meat replacers based on plant proteins, which receive recently a strong research interest (Dekkers et al., 2018, Jones, 2016). Literature search shows that in the development of novel food products digestibility is rarely evaluated. We argue to take digestibility into account in the development and design of novel protein foods.

In food science, there is knowledge lacking in the interaction between the swelling of protein gels and their gastric digestion. Only in the last decade, in-vitro and in-silico models of food digestion are being developed (Muttakin et al., 2019). Recognizing protein gels as polyelectrolyte gels, one can use the vast collection of knowledge developed in polymer physics describing the swelling of such gels (Horkay et al., 2006, Hong et al., 2010, Quesada-Pérez et al., 2011, Kees de Kruif et al., 2015). Based on this knowledge, this paper will present and discuss the theoretical framework for modelling the behaviour of protein foods in gastric conditions. Using the theory a model is constructed. Simulation results are compared in a qualitative way to the observed behaviour of soy gels, which have been subjected to in-vitro experiments using simulated gastric juice. From this comparison, it has become apparent that a computer model simulating realistic gastric conditions needs to model changes in the gastric fluid too, due to its finite volume and limitation on the secretion rate of gastric juices. We conclude the paper with an outlook on such a model for the gastric environment.

2. Theory

The theoretical framework builds on previous work from several fields. We use the thermodynamic theory for the swelling of polyelectrolyte gels, as developed by Tanaka and coworkers (English et al., 1996), who combine the Flory-Rehner theory with Gibbs-Donnan theory. Flory-Rehner theory has been developed for describing the swelling of neutral gels, expressing the balance between mechanical stress and osmotic pressure. Gibbs-Donnan theory describes the ionic contribution to the osmotic pressure, which is non-zero due to partitioning of free ions over the gel phase and external bath. This partitioning is a consequence of the fixed charges on the polyelectrolyte, as follows also from the Gibbs-Donnan theory.

Protein gels are so-called polyampholyte gels, which are polyelectrolyte gels that carry both positive and negative fixed charges. In proteins, the fixed charges arise from the dissociation of weak acidic or basic side groups of the amino-acid monomers. The dissociation depends on the pH of the gel phase. Several amino-acids are having either an acidic or basic side group, each having a different dissociation constant (pK value). The dissociation of the protein will be modelled as being a collection of different weak acids and bases, each having a different, but fixed pK value. Putting a protein gel, initially at neutral pH, in an acidic bath, leads to an extensive binding of protons to negatively charged, dissociated acidic side groups. It is said that protein gels have a strong buffering capacity. If put in a bath of finite volume, the pH of the bath will strongly increase due to the extensive binding of protons. Therefore, determining the buffering capacity of protein gels is an important step in developing numerical models for the gastric digestion of protein gels. Furthermore, one also needs to determine the isoelectric point, the pH where the total fixed charge of the protein is exactly zero. For many proteins, the isoelectric point is around $pI\approx 5$, which is often in between the initial pH of protein gel, and the pH of the gastric juice ($1<pH<2$).

For the kinetics of swelling and ion transport, we build on the triphasic models as applied to the swelling of cartilage (Lai et al., 1991). In these models the swelling and ion transport is modelled in a thermodynamically consistent way, using the Stefan-Maxwell framework. The triphasic models take the gradients in chemical potential as the driving force for transport. The chemical potentials can be derived from the above model of polyampholyte gel swelling. After some algebraic manipulation, we show the ion transport model can be simplified to a flux law with a convective and diffusive contribution, with the convective contribution due to the water transport in case of swelling or shrinkage of the gel.

Due to the extensive binding of protons by protein gels in the gastric environment, one can compare the ion transport in protein gels with that in ion-exchange resins (Geise et al., 2010). We show that this insight leads to further simplification of the ion transport model.

The literature on ion-exchange membranes (Kamcev et al., 2016) also shows that we have to account for the non-ideality of the activity of free ions in the gel and its bathing fluid. Furthermore, the ionic strength requires a redefinition for ions inside the gel phase. We follow the theory of Maurer for non-ideality of polyelectrolyte solutions (Pessôa Filho and Maurer, 2008), which uses the Debye-Hueckel and Pitzer theory for the non-ideality of the ion and solvent activity, together with a redefinition of the ionic strength.

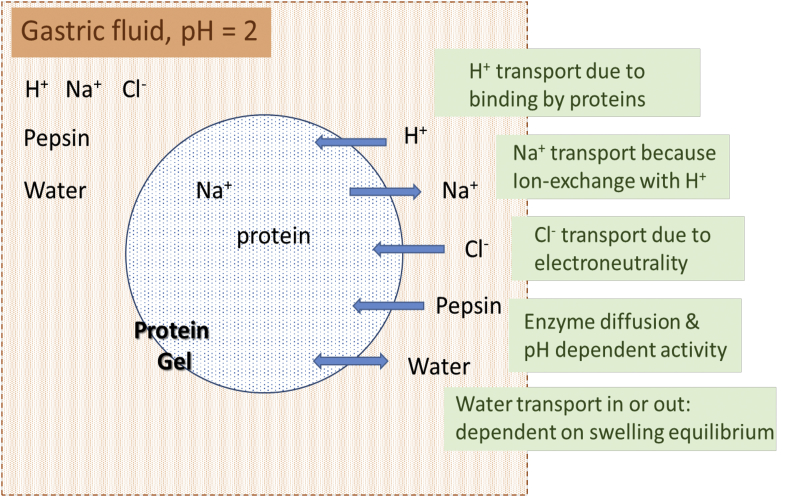
The theory for polyelectrolyte gel swelling will be constructed in several steps. First, we discuss the dissociation of proteins. Secondly, we discuss the Donnan theory, rendering the ionic contribution to the swelling pressure of the gel. Thirdly, we discuss the equilibrium relations governing the swelling of polyelectrolyte gels, where we include the first two theories. Subsequently, we discuss the kinetics of swelling using the triphasic model, and how the ion transport can be simplified to an ion-exchange model. Next, we discuss the non-ideality of (poly)electrolyte solutions. Finally, we discuss how calculations can be simplified via integration of the model over the gel volume, rendering a lumped model for the swelling kinetics and the transport of ions. A schematic of all physico-chemical processes involved is shown in Fig. 1. All these processes will be discussed in detail below. In the numerical model most of these processes will be incorporated, except for the enzyme digestion - which will be incorporated in a later stage.

Fig. 1.

Schematic diagram of physical chemistry happening during gastric digestion of protein gel particles.

2.1. Dissociation of proteins

Proteins have ionizable acidic and basic groups, due to (de)protonation of these groups the protein will carry fixed charges on its polymer chain. Proteins are characterized by their isoelectric point ($pI$), where the sum of positive and negatives fixed charges is zero. If $pH>pI$ the proteins will be negatively charged, and if $pH<pI$ the proteins will be positively charged. For most of the proteins $pI<7$. Hence, under neutral conditions ($pH$=7) most of the proteins will be negatively charged. (Poly)electrolyte solutions are always electroneutral, and the negatively charged protein will be accompanied by positive counter-ions like $N{a}^{+}$.

The acidic and basic groups have each a dissociation equilibrium constant, often expressed by their pK value. Proteins have multiple types of acidic and basic groups, each having its pK value. In the stomach, the pH range is often 2<pH<7. Within this range, one can assume that the basic groups are fully dissociated. Hence, we have to regard only the dissociation of three amino-acids, with pKa<7, which are aspartate (Asp), glutamate (Glu) and histidine (His). Mind that Asp and Glu are acidic, while His is basic, and it will be positively charged when dissociated. For isolated amino-acids the pKa values are: 3.67, 4.25, and 6.54 respectively (Thurlkill et al., 2006). But, in proteins, the local chemical environment (such as nearby charges) lead to shifts of the pKa values (Alexov et al., 2011).

The acidic groups and the basic groups can undergo the following protonation reactions:

$$HA\leftrightarrow H^{+}+A^{-}$$

$$B{H}^{+}\leftrightarrow B+H^{+}$$ (1)

$A^{-}$ and $B{H}^{+}$ represent the charged groups. Protons are also involved in the dissociation of water:

$$H_{2}O\leftrightarrow O{H}^{-}+H^{+}$$ (2)

This reaction must be taken into account in the above dissociation chemistry.

The above reactions have associated reaction constants:

$$K_w=\frac{a_H{a}_{OH}}{a_w}$$

$$K_A=\frac{a_H{a}_A}{a_{HA}}$$

$$K_A^{\text{*}}=\frac{a_B{a}_H}{a_{BH}}$$ (3)

Instead of the reaction constants one defines $pKa={-}^{10}\text{log}\left(K_A\right)$, and $pKw={-}^{10}\text{log}\left(K_w\right)=14$.

$a_i$ is the activity of the ions and neutral groups, which relates to their chemical potential ${\mu }_i=RT\text{log}\left(a_i\right)$. The activity is often rewritten in terms of the activity coefficient ${\gamma }_i$, as $a_i={\gamma }_i{n}_i$. $n_i$ is the molal concentration. For very dilute solutions ${\gamma }_i\approx 1$, otherwise the Debye-Hueckel theory can be used. For high ionic strengths Debye-Hueckel breaks down and the Pitzer theory has to be used.

Assuming ideal solution conditions, the molal concentration of charged amino-groups is given by:

$$\begin{array}{l}{n}_{A,i}^{-}=n_{A,i}\frac{K_{A,i}}{n_H+K_{A,i}}\\ n_{BH,i}^{+}=n_{B,i}\frac{n_H}{n_H+K_{A,i}^{\text{*}}}\end{array}$$ (4)

with $n_H$ the molal concentration of free protons. The pH of the liquid is related to that: $pH={-}^{10}\text{log}\left(n_H\right)$.

Similarly, we can derive the number of bound protons to the acidic/basic groups:

$$\begin{array}{l}{n}_{HA,i}=n_{A,i}^{tot}\frac{n_H}{n_H+K_{A,i}}\\ n_{BH,i}^{+}=n_{B,i}^{tot}\frac{n_H}{n_H+K_{A,i}^{\text{*}}}\end{array}$$ (5)

Note, that $n_{A,i}^{tot}=n_{HA,i}+n_{A,i}^{-}$ and $n_{B,i}^{tot}=n_{BH,i}^{+}+n_{B,i}$.

We assume that basic groups with $pKa>7$, such as lysine (Lys) and arginine (Arg) are fully dissociated. Their molal concentration is denoted as $n_B=n_B^{+}$. At the so-called isoelectric point the total charge on the protein is zero:

$$\sum _i{n}_{A,i}^{-}=\sum _i{n}_{BH,i}^{+}$$ (6)

The isoelectric point is at a specific $n_H$ concentration. The corresponding $pH$ is denoted as $pI$. We note that the buffer capacity of the protein gel is independent of the isoelectric point.

Below, in the Donnan theory, the total fixed charge on the protein is important. We define that here as (with $i=\mathrm{1,2}$ for Asp and Glu, $i=3$ for His, and $n_B^{+}$ for Lys and Arg):

$$\begin{array}{c}{n}_p=n_B^{+}+n_{BH,3}^{+}-n_{A,2}^{-}-n_{A,1}^{-}\\ =n_B^{+}+n_{A,3}\frac{n_H}{n_H+K_{A,3}}-n_{A,2}\frac{K_{A,2}}{K_{A,2}+n_H}-n_{A,1}\frac{K_{A,1}}{K_{A,1}+n_H}\end{array}$$ (7)

Below, we will mainly use the expression $n_p$.

2.2. Donnan theory

Here, we first present the Donnan theory for ideal solutions (Horkay et al., 2000). In a later section, we present how to model non-idealities. We apply the theory to simulated gastric juice, as used in the experiments, which is an aqueous solution of HCl and NaCl. Hence, we consider the following free ions: $H^{+}$, $O{H}^{-}$, $N{a}^{+}$ and $C{l}^{-}$. The first two are always related via the dissociation of water: $n_{OH}=\frac{K_w}{n_H}$. The external ion concentrations of the bath will be denoted as $n_H^{\text{*}}$, $n_{OH}^{\text{*}}$, $n_{Na}^{\text{*}}$ and $n_{Cl}^{\text{*}}$. The free ions concentrations inside the gel are denoted as: $n_H$, $n_{OH}$, $n_{Na}$ and $n_{Cl}$.

For both the bath and the gel electroneutrality holds:

$$n_H^{\text{*}}+n_{Na}^{\text{*}}-n_{OH}^{\text{*}}-n_{Cl}^{\text{*}}=0$$

$$n_H+n_{Na}-n_{OH}-n_{Cl}+n_p=0$$ (8)

Due to the charging of the protein, there will be a partitioning of the free ions between the gel phase and the bath. The difference in ion concentrations will lead to an electrical potential difference, $\text{Ψ}$, the so-called Donnan potential. This potential must be included in the chemical potential of the free ions. The partitioning of ions follows from the equality of the chemical potential inside and outside the gel:

$${\mu }_H=RT\log \left(x_H\right)+F\text{Ψ}$$

$${\mu }_{OH}=RT\log \left(x_{OH}\right)-F\text{Ψ}$$

$${\mu }_{Na}=RT\log \left(x_{Na}\right)+F\text{Ψ}$$

$${\mu }_{Cl}=RT\log \left(x_{Cl}\right)-F\text{Ψ}$$

F is the Faraday constant. In principle the swelling pressure inside the gel should be taken into account in the above chemical potentials, cf. (Jansen et al., 1996, Bellot et al., 1999, Hong et al., 2010, Yu et al., 2017, Galizia et al., 2017). However, for small ions as in our simulated gastric fluid, the swelling pressure contribution is negligible compared to the Donnan potential (Sassi et al., 1996).

The mole fractions $x_i$ are linear with the molar/molal concentration $n_i$ for dilute solutions. One can eliminate the potential $\text{Ψ}$, obtaining the Gibbs-Donnan relations:

$$\begin{array}{l}{n}_H^{\text{*}}{n}_{OH}^{\text{*}}=n_H{n}_{OH}=K_w\\ n_H{n}_{Cl}=n_H^{\text{*}}{n}_{Cl}^{\text{*}}=K_{HCl}\\ n_{Na}{n}_{Cl}=n_{Na}^{\text{*}}{n}_{Cl}^{\text{*}}=K_{NaCl}\end{array}$$ (10)

These relations can be substituted into the electroneutrality condition of the gel, which can be expressed as a function of $n_H$ only:

$$n_H+\frac{n_H{K}_{NaCl}}{K_{HCl}}-\frac{K_w}{n_H}-\frac{K_{HCl}}{n_H}+n_p=0$$ (11)

This equation will be solved numerically in the model using non-linear solvers. It is instructive to derive a simplified equation, in line with the original Donnan theory. In the simulated gastric juice the NaCl concentration is in the order of 100 mM. Hence, if $pH\ge 2$ it follows that $n_{OH}{n}_H\ll n_{Na}$. Hence, the amount of cations in the gels is approximately equal to the amount of sodium ions: $n_{+}\approx n_{Na}$. Similar arguments hold for the bath. We define the ionic strength of the bath $I^2=n_{Na}^{\text{*}}{n}_{Cl}^{\text{*}}$. For this approximation, the solution to the Donnan problem is:

$$n_{+}=-\frac{1}{2}{n}_p+{\left[I^2+{\left(\frac{1}{2}{n}_p\right)}^2\right]}^{\frac{1}{2}}$$ (12)

The ionic contribution to the osmotic pressure is due to the difference in ion concentrations between the gel phase and the bath (with contributions of $O{H}^{-}$ being negligible):

$${\text{Π}}_{ion}=RT\left(n_H+n_{Na}+n_{Cl}-n_H^{\text{*}}-n_{Na}^{\text{*}}-n_{Cl}^{\text{*}}\right)$$ (13)

Substituting the above approximation renders:

$${\text{Π}}_{ion}=2RT\left[\sqrt{I^2+{\left(\frac{1}{2}{n}_p\right)}^2}-I\right]$$ (14)

2.3. Swelling equilibrium

The condition for swelling equilibrium is that the swelling pressure is zero:

$${\text{Π}}_{swell}={\text{Π}}_{mix}+{\text{Π}}_{elas}+{\text{Π}}_{ion}=0$$ (15)

The first two terms we take from the Flory-Rehner theory. For the ionic pressure we take the Donnan expression.

For ${\text{Π}}_{mix}$ and ${\text{Π}}_{elas}$ we will use expressions as developed by Cornet (Cornet et al., 2019). ${\text{Π}}_{mix}$ is modelled following Flory-Huggins:

$${\text{Π}}_{mix}=-\frac{RT}{{\nu }_w}\left[\text{log}\left(1-{\varphi }_p\right)+{\varphi }_p+{\chi }_{ws}{\varphi }_p^2\right]$$ (16)

${\nu }_w$ is the molar volume of water, ${\varphi }_p$ is the polymer volume fraction, and ${\chi }_{ws}$ is the interaction parameter, which depends on composition as follows:

$${\chi }_{ws}={\chi }_0+\left({\chi }_1-{\chi }_0\right){\varphi }_p^2$$ (17)

with ${\chi }_0=0.5$, and ${\chi }_1$ depends on the specific protein used.

${\text{Π}}_{elas}$ follows from the Neo-Hookean model.

$${\text{Π}}_{elas}=-G_{ref}{\tilde{\varphi }}^{\frac{1}{3}}$$ (18)

with $G_{ref}$ the shear modulus under reference conditions ${\varphi }_p={\varphi }_{ref}$, and $\tilde{\varphi }={\varphi }_p/{\varphi }_{ref}$. $G_{ref}$ and ${\varphi }_{ref}$ are properties of the gel, and they are related to the initial concentration of proteins used at gelation. Via this amount the crosslink density is controlled, and thus mechanical properties like $G_{ref}$.

The mixing chemical potential is per definition negative (as $a_w<1$). Hence, the mixing pressure is positive. The elastic pressure counteracts the swelling, and ${\text{Π}}_{elas}<0$. The ionic pressure is always positive, as can be viewed also from the approximations above. The condition for swelling equilibrium, Eq. (15), is to be solved for ${\varphi }_p$, from which the gel volume follows assuming incompressibility of solvent and polymer. Note, that upon change of the gel volume all concentrations in the gel phase will change accordingly.

2.4. Triphasic model for swelling kinetics and diffusion

The ion transport is investigated first using the triphasic model, as pioneered by Lai and Mow for cartilage (Lai et al., 1991). Four components are distinguished: 1) water (with index $i=w$), 2) polymer ($i=p$), and 3) the mobile ions ($i=\pm$). In the derivation below, we first assume that $n_{+}\approx n_{Na}\gg n_H$, and $n_{-}=n_{Cl}$. The derivation of the triphasic model starts with the steady-state momentum equations, similar to Stefan-Maxwell and Kirkwood-Bearman models. The driving forces are gradients in the chemical potential $\nabla {\mu }_i$, which are balanced by friction forces linear in the friction coefficient ${\zeta }_{ij}$ between components i and j. In the momentum balances below, we neglect the friction between ions:

$$0={\varphi }_w\nabla {\mu }_w-{\zeta }_{wp}\left(u_p-u_w\right)-{\zeta }_{w+}\left(u_{+}-u_w\right)-{\zeta }_{w-}\left(u_{-}-u_w\right)$$

$$0={\varphi }_{+}\nabla {\mu }_{+}-{\zeta }_{+p}\left(u_p-u_{+}\right)-{\zeta }_{w+}\left(u_w-u_{+}\right)$$

$$0={\varphi }_{-}\nabla {\mu }_{-}-{\zeta }_{-p}\left(u_p-u_{-}\right)-{\zeta }_{w-}\left(u_w-u_{-}\right)$$

$$0={\varphi }_p\nabla {\mu }_p-{\zeta }_{wp}\left(u_w-u_p\right)-{\zeta }_{+p}\left(u_{+}-u_p\right)-{\zeta }_{-p}\left(u_{-}-u_p\right)$$ (19)

In principle the fourth momentum equation is superfluous, as the deformation is solved via the condition for mechanical equilibrium: $\nabla \cdot \sigma =0$, with σ the mechanical stress. If we assume uniform and isotropic deformation, the condition for mechanical equilibrium $\nabla \cdot \sigma =\nabla {\text{Π}}_{elas}=0$ is satisfied.

The total deformation will follow from the influx of water, using the incompressibility assumption. Furthermore, the concentration and momentum of the ions will be coupled via the electroneutrality condition. Hence, we have to solve the momentum balance equation only for one type of ion. In the momentum balance for water, we neglect the friction of polymers with ions, compared to the friction between polymer and water (as the amount of ions is negligible compared to water).

Summarizing, we need to solve only the momentum equations for the water phase, and the mobile ions. We rewrite their equations in terms of the slip velocities using the framework of the moving polymer network: $w_i=u_i-u_p$, with $i=w,+$. The first two lines in Eq. (19) can be rewritten in terms of $w_i$ only:

$$0={\varphi }_w\nabla {\mu }_w+{\zeta }_{wp}{w}_w$$

$$0={\varphi }_{+}\nabla {\mu }_{+}-{\zeta }_{w+}\left(w_w-w_{+}\right)$$ (20)

Yao and Gu have proposed to transform the above set of equations to a convection-diffusion framework (Yao and Gu, 2007), similar to others (Zhang and Szeri, 2005, Zhang and Szeri, 2008, Abazari et al., 2009). We explore this approach.

We solve the above equations, Eq. (20), explicitly in terms of $w_{+}$:

$$w_{+}=\frac{{\zeta }_{w+}}{\left({\zeta }_{+p}+{\zeta }_{w+}\right)}{w}_w-\frac{1}{\left({\zeta }_{+p}+{\zeta }_{w+}\right)}{\varphi }_{+}\nabla {\mu }_{+}$$ (21)

The convective velocity is defined as:

$$w_c=\frac{{\zeta }_{w+}}{\left({\zeta }_{+p}+{\zeta }_{w+}\right)}{w}_w=h_{+}{w}_w$$ (22)

Hence, the (relative) solute velocity is decomposed in a convective term and a diffusive term, with the latter linear in the gradient of its chemical potential. $h_{+}$ is the so-called convective coefficient, or hindrance factor, as in the work of Deen and coworkers (Deen, 1987, Davidson and Deen, 1988, Johnston and Deen, 1999). The diffusive flux of ions (in the reference frame of the gel) equals:

$$J_{diff,+}={\varphi }_{+}\left(w_{+}-w_c\right)=-\frac{{\varphi }_{+}^2}{{\zeta }_{+p}+{\zeta }_{w+}}\nabla {\mu }_{+}=-\frac{D_{+}}{RT}\nabla {\mu }_{+}$$ (23)

$D_{+}$ is the ion diffusion coefficient inside the gel, which depends on the friction coefficients ${\zeta }_{+p}$, ${\zeta }_{w+}$. The latter are quite difficult to determine experimentally, in contrast to diffusion coefficients.

For the internal solution, we define ${\varphi }_{+}=n_{+}{\varphi }_w$. For dilute solutions the chemical potential is ${\mu }_{+}=RT\text{log}\left(n_{+}\right)$. Hence,

$$\nabla {\mu }_{+}=RT\frac{\nabla n_{+}}{n_{+}}$$ (24)

Hence, the diffusive flux will be similar to Fick's law:

$$J_{diff,+}={\varphi }_{+}\left(w_{+}-w_c\right)=-{\varphi }_w{D}_{+}\nabla n_{+}$$ (25)

The convective flux $w_c=h_{+}{w}_w$ follows from the above momentum equation for water:

$$w_w=-\frac{{\varphi }_w}{{\zeta }_{wp}}\nabla {\mu }_w$$ (26)

which is a generalization of Darcy's law?

The flux of mobile ions, relative to the polymer network, is defined as:

$$J_{+}={\varphi }_{+}{w}_{+}={\varphi }_{+}{w}_c+{\varphi }_{+}\left(w_{+}-w_c\right)=n_{+}{\varphi }_w{h}_{+}{w}_c-{\varphi }_w{D}_{+}\nabla n_{+}$$ (27)

2.5. Ion-exchange model

Contrary to the above triphasic model, we have multiple positive and negative ions, namely $H^{+}$, $O{H}^{-}$, $N{a}^{+}$ and $C{l}^{-}$. Hence, the triphasic approach should be extended to account for that. Recall, that we assume that the digested protein gel starts at neutral pH, with negative fixed charges and $N{a}^{+}$ as counter-ions. Protons from the acidic gastric juice will migrate to the gel, and they will be bound by the dissociated acidic groups: $H^{+}+A^{-}\to HA$. At the end of gastric digestion, the internal pH of the gel will be about pH = 2, with positive fixed charges and $C{l}^{-}$ as counter-ions.

This process is very similar to ion-exchange resins as used in chromatography. The protein gels in the gastric juice will exchange $N{a}^{+}$ for $H^{+}$. Due to the constraint that the electric current is always zero, the cation transport will always be accompanied by the anion, $C{l}^{-}$ (Geise et al., 2010).

A simplified ion-exchange model for ion-exchange resins is described by Paul and coworkers (Geise et al., 2010). They consider a charged resin immersed in a bath containing a monovalent salt MX. It is assumed that polyelectrolyte is negatively charged, with $M^{+}$ as counter-ion. The bath contains less $M^{+}$ ions, but more $X^{-}$ ions. Due to a Donnan potential, combined with electroneutrality, there is a partitioning of ions between bath and membrane.

The authors have derived the ion-exchange model from the Stefan-Maxwell, similar to the above triphasic model. The model is formulated in the framework co-moving with the resin (which can swell in principle). The fluxes of MX are coupled due to the electric potential, and electroneutrality condition. Hence, it is advantageous to define the neutral salt flux:

$$J_s=x_s\left(J_w+J_s\right)+c_T{D}_s\nabla \text{log}\left(a_s\right)$$ (28)

$j_w$ is the water flux, $x_s$ is the molar fraction of the salt MX, $c_T$ is the total molar concentration in the solution, $a_s=a_M{a}_X$ is the mean activity of the salt MX. $D_s$ is the effective salt diffusion coefficient. As above, the flux is decomposed in a convective term, and a diffusive term. The triphasic model and ion-exchange model are consistent with each other if one defines $j_s=J_{+}+J_{-}$.

For a charged resin the effective salt diffusion coefficient is assumed to be equal to the harmonic mean of the diffusion coefficient of the individual ions:

$$\frac{x_s+x_p}{D_s}=\frac{x_p+x_s}{D_M}+\frac{x_s}{D_X}$$ (29)

with $x_p$ the molar fraction of the polyelectrolyte monomers.

Similarly, we can define the fluxes for both HCl and NaCl ion pairs for our case study regarding a protein gel swelling in gastric fluid. Assuming ideal solutions, the diffusive part of the fluxes can be written as:

$$\begin{array}{c}{J}_{NaCl}=-RT{\zeta }_{NaCl}{n}_{NaCl}\nabla \left(\text{log}\left(n_{Na}\right)+\text{log}\left(n_{Cl}\right)\right)\\ J_{HCl}=-RT{\zeta }_{HCl}{n}_{HCl}\nabla \left(\text{log}\left(n_H\right)+\text{log}\left(n_{Cl}\right)\right)\end{array}$$ (30)

with ${\zeta }_i$ the Stefan-Maxwell friction coefficients, accounting for friction with both the polymer and the water phase, similar to the above triphasic model.

Note that an expression consistent with Fick's law follows using the chain rule:

$$\begin{array}{c}{J}_{NaCl}=-RT{\zeta }_{NaCl}{n}_{NaCl}\nabla \left(\text{log}\left(n_{Na}\right)+\text{log}\left(n_{Cl}\right)\right)\\ =-RT{\zeta }_{NaCl}{n}_{NaCl}\left[\frac{\nabla n_{Na}}{n_{Na}}+\frac{\nabla n_{Cl}}{n_{Cl}}\right]\\ =-D_{NaCl}[\nabla n_{Na}+\nabla n_{Cl}]\end{array}$$ (31)

2.6. Non-ideal contributions

Various theories are formulated how to deal with non-ideality in polyelectrolyte gels. Hence, first, we review these theories.

Manning counter-ion condensation phenomenon states that polyelectrolytes line charge density will never exceed $e/l_B=1/z$, with $l_B\approx$ 0.7 nm the Bjerrum length (Andelman, 2006). Compare this to charge density of proteins during titration (as reported in section). The average percentage of charged amino acids in soy is about 40–50% (Ishihara et al., 2003). Around $pI$ the charge density is about zero, no condensation is expected. If $pH\ll pI$ the acidic groups have bound protons, and the charge is due to arginine and lysine, which are about 10–15% (Ishihara et al., 2003). The size of an amino-acid molecule is about 0.35 nm, and hence the average distance between charges is $d_c$ = 3.5 nm, which is much larger than $z{l}_B$. Hence, the positively charged protein will not reach the Manning condensation limit.

The first correction to non-ideality is given by the Debye-Hueckel theory (Andelman, 2006). In polyelectrolyte gel and solution problems, one often sees that non-ideality is taken into account for the activity coefficient of the electrolytes, but not for the osmotic pressure of solvent, as it is said to give too much deviation from experiment (Hasa et al., 1975, Baker et al., 1995, Nguyen et al., 2018).

The expression for the Debye-Huckel activity coefficient ${\gamma }_{\pm }$ (accounting for finite size of ion with radius r) (Baker et al., 1995):

$$\text{log}\left({\gamma }_{\pm }\right)=-\frac{z_i^2{F}^2}{8\pi {\epsilon }_0{\epsilon }_r{N}_{A}RT}\frac{\kappa }{1+\kappa r}$$ (32)

$\epsilon {\epsilon }_r$ is the dielectric constant of the solvent, $N_A$ is Avogrados number, F is the Faraday constant, and κ is the inverse Debye screening length:

$${\kappa }^2=\frac{F^2}{{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{r}RT}I$$ (33)

I is the ionic strength (which is just a summation over all free ions in case of monovalent ions). The activity coefficient is used in the chemical potentials of the ions, and for the non-ideality in the dissociation reactions of the charged amino-acid groups.

Debye-Huckel theory can explain the anti-polyampholyte effect, i.e. the swelling of the polyampholyte gels upon the increase of added salts. It is due to non-ideal contribution to ${\text{Π}}_{ion}$ (Baker et al., 1995, Nguyen et al., 2018). This non-ideal contribution is named ${\text{Π}}_{direct}$, giving an independent addition to the swelling pressure ${\text{Π}}_{swell}$. ${\text{Π}}_{direct}$ is a negative contribution and thus it enhances the swelling of the gel. Its expression is:

$${\text{Π}}_{direct}=-\frac{RT}{N_A}\frac{{\kappa }^3}{24\pi }\frac{3}{{\left(\kappa r\right)}^2}\left(1+\kappa r-\frac{1}{1+\kappa r}-2\log \left(1+\kappa r\right)\right)$$ (34)

$$\text{If}\kappa r\ll 1\sigma =1$$

For a gel the osmotic pressure difference between gel and bath, indicated with index α and β respectively (Goh et al., 2019):

$${\text{ΔΠ}}_{direct}=\frac{RT}{24\pi }\text{Σ}\left(\kappa r\right)$$ (35)

with

$$\text{Σ}\left(\kappa r\right)=\left({\kappa }_{\beta }^3{\sigma }_{\beta }-{\kappa }_{\alpha }^3{\sigma }_{\alpha }\right)$$ (36)

An approximation of $\text{Σ}$ is:

$$\text{Σ}\left(\kappa a\right)=1-\frac{3}{2}\kappa r+\frac{9}{5}{\left(\kappa r\right)}^2$$ (37)

For 1:1 electrolyte solutions r = 0.304 nm (Baker et al., 1995).

Maurer argued that the ionic strength of a polyelectrolyte solution should be modified to include also the (partially) mobile charges on the polymer (Pessôa Filho and Maurer, 2008). For our protein gel, it is defined as:

$$I=\frac{1}{2}(n_{Na+}+n_{Cl-}+n_{H+}+n_{OH-}+n_{A-}+n_{B+}$$ (38)

To calculate the molar concentrations the volume of proteins is excluded from the total volume of the gel, cf. (Pessôa Filho and Maurer, 2008), similar to the Ross equation (van der Sman, 2012).

Andelman has given another definition of ionic strength in weak acidic polyelectrolyte gels (Borukhov et al., 2000):

$$I_{eff}=\frac{1}{2}\left(n_{Na+}+n_{Cl-}+n_{H+}+n_{OH-}+n_{A-}^{eff}+n_{B+}^{eff}\right)$$ (39)

with

$$\begin{array}{l}{n}_{A-}^{eff}=\sum _i{n}_{A,i}2i_{A,i}\left(1-i_{A,i}\right)\\ n_{B+}^{eff}=\sum _i{n}_{B,i}2i_{B,i}\left(1-i_{B,i}\right)\end{array}$$ (40)

with $i_{A,i}=n_{i,A-}/n_{A,i}$, and $i_{B,i}=n_{i,B+}/n_{B,i}$ the degree of ionization of the acidic and basic chargeable groups. $i_A\left(1-i_A\right)$ is a measure of the mobility of bound protons on the polyelectrolyte chain. There is zero mobility if the chain is fully charged or is non-charged.

The next order of non-ideal correction is given by Pitzer theory (Edwards et al., 1978), accounting for short-range interactions. Hence, the activity coefficient of ion a is defined by:

$$\text{log}\left({\gamma }_a\right)=z_a^{2}F\left(I\right)+2\sum _c{m}_c{B}_{ac}+z_a^2\sum _c\sum _{a\prime }{m}_c{m}_{a\prime }B{\prime }_{ac\prime }$$ (41)

The first term of Eq. (41) is the Debye contribution, as given above. In Eq. (41) the subscripts $ac$ represent any anion/cation pair, while $a\text{'}c$ represent anion/cation pairs with $a\prime \ne a$. $B_{ca}$ are called the binary ion-ion parameters.

The binary Pitzer coefficients are a function of the ionic strength I, via:

$$B_{ac}={\beta }_{ac}^{\left(0\right)}+2{\beta }_{ac}^{\left(1\right)}\frac{1-\left(1+\alpha \sqrt{I}-\frac{1}{2}{\alpha }^{2}I\right)\text{exp}\left(-\alpha \sqrt{I}\right)}{{\alpha }^{2}I}$$ (42)

and

$$B{\text{′}}_{ac\prime }=-{\beta }_{ac\prime }^{\left(1\right)}\frac{1-\left(1+\alpha \sqrt{I}+\frac{1}{2}{\alpha }^{2}I\right)\text{exp}\left(-\alpha \sqrt{I}\right)}{{\alpha }^2{I}^2}$$ (43)

The constant is $\alpha =2$. Sometimes for complex mixtures the term in $B_{ac}$ linear with ${\alpha }^{2}I$ is neglected (Edwards et al., 1978, Millero, 1983). In a single electrolyte mixture, or binary mixtures with common ions one finds this term (Pitzer, 1973, P de Lima and Pitzer, 1983).

The ionic pressure of the electrolyte solution is given in terms of the osmotic coefficient $\text{Φ}$, defined as:

$${\text{Π}}_{ion}=\text{Φ}RT\sum _i{n}_i$$ (44)

with $\text{Φ}$ given as (Pitzer, 1973, Edwards et al., 1978):

$$\begin{array}{c}\text{Φ}=-\frac{2A_{\varphi }{I}^{3/2}}{1+b\sqrt{I}}\\ +\sum _a\sum _c{m}_a{m}_c[{\beta }_{ac}^{\left(0\right)}+{\beta }_{ac}^{\left(1\right)}\text{exp}\left(-\alpha \sqrt{I}\right)]\end{array}$$ (45)

The first term is again the Debye contribution.

Data on interaction coefficients ${\beta }_{ca}^{\left(i\right)}$ are shown in Table 1, which are taken from (Kim et al., 1993, Meng et al., 1995). The interaction coefficients between salt and charged acidic or basic groups of proteins ($A^{-}$ and $B^{+}$), are assumed similar to that of amino-acids and salts (De Stefano et al., 2000). Interactions between protons and acidic/basic groups are assumed negligible (De Stefano et al., 2000).

Table 1.

Pitzer interaction coefficients (Kim et al., 1993, Meng et al., 1995).

ion-pair	${\beta }^{\left(0\right)}$	${\beta }^{\left(1\right)}$
$N{a}^{+}C{l}^{-}$	0.0765	0.2664
$H^{+}C{l}^{-}$	0.1775	0.2945
$N{a}^{+}{A}^{-}$	−0.06	0.835
$B^{+}C{l}^{-}$	0.12	0.425

2.7. Volume integrated model

To reduce the complexity of this model of protein gel digestion it is convenient to assume small gradients inside the gel, and integrate all mass balances over the total volume using the Gauss theorem. We illustrate that for the mass balance of water, which holds:

$${\partial }_t{\varphi }_w=-\nabla \cdot J_w$$ (46)

with water flux density $J_w~\nabla {\text{Π}}_{swell}$. After volume integration of the left hand side of Eq. (46), one obtains: $\int {\partial }_t{\Phi }_{w}dV={\partial }_t{V}_{water}$, which is the time derivative of the total amount of water in the gel. For now we assume that there is no loss of proteins due to digestion. Hence, the amount of proteins, $V_p$ remains constant. The total volume of the gel is $V_{gel}=V_{water}+V_p$. Consequently, ${\partial }_t{V}_{gel}={\partial }_t{V}_{water}$. The polymer volume fraction follows from the ratio: ${\varphi }_p=V_p/V_{gel}$.

Via Gauss theorem we convert the volume integral of the flux, into an integral of the flux over the surface:

$${\partial }_t{V}_{gel}=-\int \nabla \cdot J_{w}dV=-\int J_{w,surf}dS$$ (47)

We assume that the water flux has a constant value over the whole surface. The surface flux is:

$$J_{w,surf}=-\frac{k}{\eta }\nabla {\text{Π}}_{swell,surf}$$ (48)

k is the permeability, and η is the viscosity of the solvent, which is assumed to be equal to pure water.

We need to estimate the gradient in the swelling pressure at the surface. We take the ambient pressure in the bath as a reference value, and hence the external pressure is zero. The governing equation for water transport is quite similar to diffusion. Hence, we estimate the internal resistance for water transport similar to our previous work on the (heat) diffusion resistance of a sphere (Van der Sman, 2008):

$$\nabla {\text{Π}}_{swell,surf}=\frac{{\text{Π}}_{swell}}{R_{gel}/5}$$ (49)

$R_{gel}$ is the radius of the spherical gel particle, computed via the volume: $V_{gel}=4/3\pi R_{gel}^3$. The surface area of the gel is: $S_{gel}=4\pi R_{gel}^2$. Hence, the governing equation for the volume of the gel becomes:

$${\partial }_t{V}_{gel}=-J_{w,surf}{S}_{gel}=\frac{4\pi R^2}{R/5}\frac{\kappa }{\eta }{\text{Π}}_{swell}$$ (50)

Similarly, we integrate the mass balances for the ions. The number of moles of sodium and chloride ions in the gel evolves as:

$$\begin{array}{l}\frac{d{N}_{Na}}{dt}=+J_{NaCl}\\ \frac{d{N}_{Cl}}{dt}=+J_{NaCl}+J_{HCl}\end{array}$$ (51)

The charge on the protein follows from electroneutrality:

$$N_p=-N_{Na}+N_{Cl}$$ (52)

The internal pH is computed from $N_p$, from the known titration curve, Donnan relations and electroneutrality. The approximated fluxes follow:

$$\begin{array}{l}{J}_{NaCl}=J_w{n}_{NaCl}^{\text{*}}+\frac{D_{NaCl}}{RT}{S}_{gel}{\hat{n}}_{NaCl}\left({\mu }_{NaCl}-{\mu }_{NaCl}^{\text{*}}\right)\\ J_{HCl}=J_w{n}_{HCl}^{\text{*}}+\frac{D_{HCl}}{RT}{S}_{gel}{\hat{n}}_{HCl}\left({\mu }_{HCl}-{\mu }_{HCl}^{\text{*}}\right)\end{array}$$ (53)

with

$${\mu }_{MX}=RT\text{log}\left({\gamma }_M{\gamma }_X{n}_M{n}_X\right)$$ (54)

The chemical potential of the ions in the bath are indicated with the asterisk *. ${\hat{n}}_{MX}$ is the estimation of the molar concentration at the interface. ${\hat{n}}_{NaCl}\approx n_{Na}+n_{Na}^{\text{*}}$, and ${\hat{n}}_{HCl}\approx n_H+n_H^{\text{*}}$.

Due to the complexity of the model, we think it is instructive to present the algorithm, we have used to solve the swelling model. A flow sheet representing the algorithm is shown in Fig. 2. It represents the main iteration, which is supplemented with initial conditions. The bath is thought to be infinite, and at constant (external) pH: $p{H}_{ext}$, and salt concentration $n_{NaCl}^{\text{*}}$. The gel has initially a neutral pH, $p{H}_{int}=7$, and a certain added salt concentration $n_{NaCl}^0$. The amount of sodium ions is increased with the number of counter-ions needed to balance the negative fixed charge at $p{H}_{int}=7$. Also, the initial gel volume, $V_{gel}^0$, is a given value.

Fig. 2.

Flowsheet for the simulation of protein gel in simulated gastric fluid with reference to used equations.

Furthermore, it is instructive to analyse the time scales of the model, where we follow the earlier analysis of a charged swellable membrane (Jeremy and J Grodzinsky, 1981). We start with the time scale for swelling. The balance equation for water is:

$${\partial }_t{\varphi }_w{V}_{gel}=-\frac{S_{gel}}{R/5}\frac{\kappa }{\eta }\frac{\partial {\text{Π}}_{swell}}{\partial {\varphi }_w}\left({\varphi }_w-{\varphi }_w^{\text{*}}\right)$$ (55)

with the (osmotic) bulk modulus, defined as (De Aguiar et al., 2017):

$$K_{bulk}=\frac{\partial {\text{Π}}_{swell}}{\partial {\varphi }_w}$$ (56)

Hence, the characteristic time scale for swelling is:

$${\tau }_{swell}=\frac{\eta }{\kappa }\frac{15R^2}{K_{bulk}}$$ (57)

Due to the ion exchange character of the protein swelling, while transferred from initial neutral pH to the acidic pH of the bath with simulated gastric juice, there is a single time scale for ion transport, which is governed by the protonation of the protein gel (Jeremy and J Grodzinsky, 1981). As most of the protons are quickly absorbed by the protein, the dynamics will be determined by the slow evolving variable, the total number of free and bound protons in the gel. $n_{H,tot}=n_H+n_{HA}$. The governing equation is:

$${\partial }_t{n}_{H,tot}{V}_{gel}={\partial }_t{C}_H{n}_H{V}_{gel}=D_{HCl}\frac{S_{gel}}{R/5}\left(n_H-n_H^{\text{*}}\right)$$ (58)

$C_H=\partial n_{H,tot}/\partial n_H=1+\partial n_{HA}/\partial n_H$ is the so-called buffer capacity of the protein gel. The value of the buffer capacity follows from the dissociation equilibrium:

$$C_H=1+\sum _i{n}_{A,i}\frac{K_{A,i}^{\text{*}}}{{\left(K_{A,i}^{\text{*}}+n_H\right)}^2}$$ (59)

Note, that the effective buffer capacity $C_H$ is dependent of the ionic strength of the gel phase, via the effective dissociation constant $K_{A,i}^{\text{*}}$, which takes the non-ideality into account.

The time scale for ion transport is given by (Jeremy and J Grodzinsky, 1981):

$${\tau }_H=\frac{15C_H{R}^2}{D_{HCl}}$$ (60)

3. Results

3.1. Buffer capacity of soy protein gel

Titration experiments were conducted to determine the buffer capacity of a 5 wt% solution of soy protein isolate (SPI), which was purchased from Solae (St. Louis, MO, USA). The SPI solution was stirred in water at room temperature (20°C) for 2 hours. A Metrohm Titrator 877 was used with a constant titration rate of 0.05 ml/min. The titrant contained 0.5 M HCl and 0.88 wt% NaCl. The pH of the solution was measured every 40 seconds until a final pH of 2 is reached. The mass of SPI is $m_p$ = 5 g. At the beginning of the experiments, SPI was dispersed into $V_L$ = 100 g of deionized water, which was titrated back to an initial neutral pH, $p{H}_{ext}=7.2$ before adding the soy. After the addition of soy, the titration with acid began for the buffer capacity determination.

Under the acidic conditions in the stomach, the basic Lys and Arg groups are assumed to be fully dissociation. Hence, for the modelling of the buffer capacity, we only have to regard the dissociation of Asp, Glu and His. For isolated amino-acids, the pK values of the side groups are 3.67, 4.25, and 6.54 respectively (Thurlkill et al., 2006). Recall that Asp and Glu are acidic, while His has a basic side group.

Mind that pK and pH are defined for concentrations expressed in molarity (mol/L). For the modelling we have converted them into mol/m3.

The total volume of added titrant is not negligible compared to the initial volume of the bath $V_{init}$. The number of bound protons is determined as a function of the amount of protein, which is independent of the total volume: $N_{HA}=\sum _i{N}_{A,i}{n}_H^{\text{*}}/\left(n_H^{\text{*}}+K_{A,i}\right)$. We use the following proton balance to fit the titration curve:

$$\sum _i{N}_{A,i}\frac{n_H^0}{n_H^0+K_{A,i}}+V_{titr}{c}_{HCl}=\sum _i{N}_{A,i}\frac{n_H^{\text{*}}}{n_H^{\text{*}}+K_{A,i}}+\left(V_{titr}+V_{water}\right)n_H$$ (61)

$n_H^0$ is the pH at the start of the titration, which was pH = 7.2.

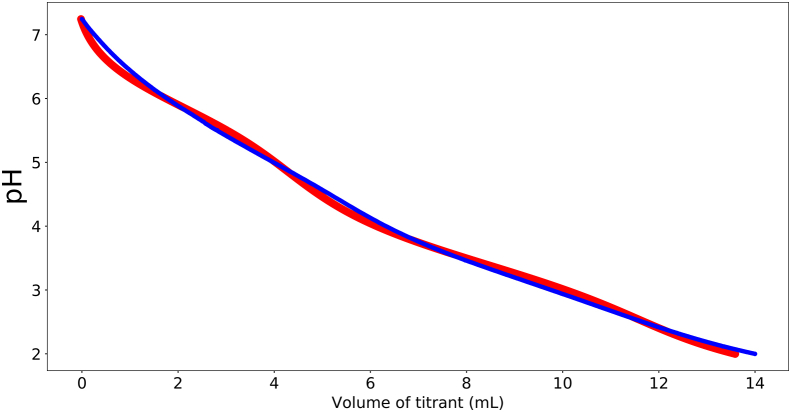
In literature there is quite some variation in pKa values of the amino-acid side groups: Asp: $3.5<pK{a}_1<4.2$, Glu $4.2<pK{a}_2<4.5$, His $6.0<pK{a}_3<6.6$ (Audain et al., 2015). Furthermore, there can be pKa shifts of individual side groups due to electrostatic interactions with nearby charged groups within the protein. pKa shifts can be up to 0.5 points for amino-acids in very specific environments, such as enzyme catalytic centres, but most pKa shifts are modest (Jan et al., 1994). Due to the pKa shifts, we will also estimate individual pKa values, but within the following bounds: Asp $3.4<pK{a}_1<4.3$, Glu $4.1<pK{a}_2<4.6$, and His $5.9<pK{a}_3<6.7$. Our fit to the titration curve is shown in Fig. 3, with estimated pKa values being: $pK{a}_1=3.4$, $pK{a}_2=4.6$, and $pK{a}_3=5.9$, which are all equal to one of the limits. Fitted values are: $N_{A1}/m_p$ = 0.67 mmol/g, $N_{A2}/m_p$ = 0.10 mmol/g $N_{A3}/m_p$ = 0.43 mmol/g. Note, that in the titration experiment we have used $m_p$ = 5 g. Hence, the total amount of protonated amino-acid groups is $N_A=\sum _i{N}_{A,i}$ = 6 mmol. This must be of similar order as the amount of HCl added. The total added volume of the titrant is 14 ml. Hence, about 7 mmol $HCl$ is added, which agrees quite well with the fitted parameters. Hence, the ionic strength of the titrated protein solution is still reasonably low. Consequently, we neglect non-idealities from the fitting, which will complicate the fitting severely.

Fig. 3.

Titration curve of soy protein isolate (blue line) fitted with the model (red line), allowing for some shift in pKA of acidic side-groups.

An important parameter of the model is the isoelectric point $pI$, and the charge at initial pH. For soy protein isolate it is reported that $pI\approx 5.0$ (Yuan et al., 2002). In our model, we tune the pI via the number of basic groups, $n_B$, which are all assumed to be charged at $pH\le 7$. At $pH=pI$ the net charge of His, Asp, Glu groups is:

$$N_{p,I}=-N_{A,1}\frac{K_{A,1}}{K_{A,1}+n_{H,I}}-N_{A,2}\frac{K_{A,2}}{K_{A,2}+n_{H,I}}+N_{A,3}\frac{n_{H,I}}{K_{A,3}+n_{H,I}}$$ (62)

This is balanced by the number of Lys/Arg basic groups: $N_B^{\left(0\right)}=-N_{p,I}$ = 0.306 mmol/g.

The charge on the proteins during the initial pH determines the number of counter-ions present in the gel, as they account for electroneutrality. The initial proton concentration is $n_{H,0}$.

$$N_{p,0}=-N_{A,1}\frac{K_{A,1}}{K_{A,1}+n_{H,0}}-N_{A,2}\frac{K_{A,2}}{K_{A,2}+n_{H,0}}+N_{A,3}\frac{n_{H,0}}{K_{A,3}+n_{H,0}}+N_B^{\left(0\right)}$$ (63)

For $p{H}_i=7.2$ the net protein charge is $N_{p,0}$ = - 0.38 mmol/g. The amount of initial sodium counter-ions is $n_{Na,0}^{+}$ = 0.38 mmol/g.

3.2. Swelling experiments

We will compare simulation results with swelling experiments performed with soy gels, which were prepared similar to reported in our earlier paper (Cornet et al., 2019). Gels were made from soy protein isolate (SPI). SPI was weighed and mixed well with water until the dry SPI powder was fully incorporated to form a loose, dough-like mixture. The dough was then vacuum packed and stored in the fridge for 24 hours. A circle of dough was cut out, cutting off the top and bottom to ensure an even surface, and placed in a gel mould with a height of 5 mm and a diameter of 12.5 mm. After closing and sealing the mould, it was put in a 95^oC water bath for 30 minutes. The mould was then cooled in cold water for 5 minutes, after which the gel was removed from the mould. A 7 mm gel cutter was used to cut samples from the gels.

Gel samples of about 0.5 g were submerged in 1000 ml of simulated gastric fluid (SGF) (without pepsin) at 37^oC. The SGF consisted of a physiological salt at a concentration of 0.88% (weight basis), via adding NaCl to deionized water. The pH is set at different values (pH = 2,4,6) via titration of 2 M HCl or 0.5 M NaOH. Swelling experiments were conducted for approximately 25 hours. Gel samples (in duplo) were removed from the SGF and weighed every 15 minutes for the first hour and then once per hour (accuracy of the scales was 5 mg). After the measurement, the gel is returned to the SGF. Gel samples were kept in individual mesh gaskets, which were hung in the SGF. During swelling the pH is kept constant via titration using a 5 mM to 0.5 M HCl solutions. At different time intervals, the gaskets are taken out of the SGF, and their masses are weighted (after gently removing excess water droplets from gaskets). Assuming a density of ${\rho }_s$ = 1330 kg/m³ the volume of the gel is calculated from the mass and initial moisture content.

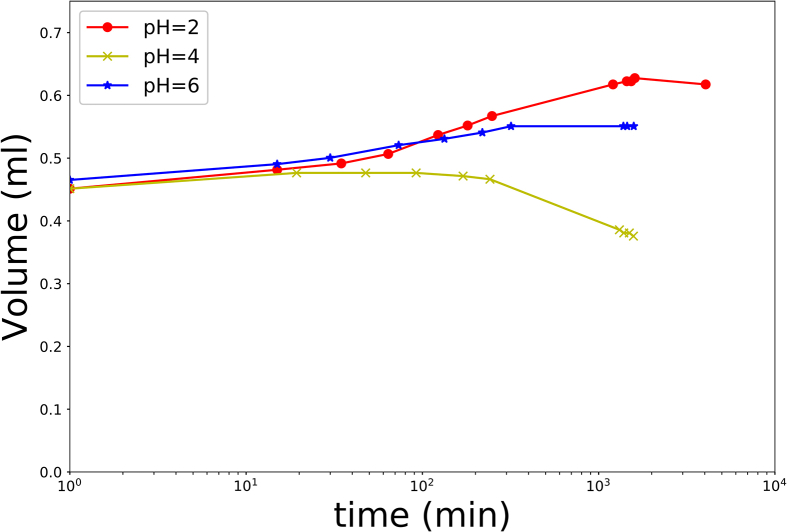
We show the results of swelling experiments of gels with initial protein mass fraction of $y_p$ = 0.30 in Fig. 4. Initially, all gels tended to swell, as the moisture content is far from equilibrium. However, at longer times one observes differences in swelling dynamics depending on the pH of the SGF. Above all, one observes shrinkage after initial swelling for pH = 4, but also slightly for pH = 6.

Fig. 4.

Results of swelling experiments of soy gels with $y_p$ = 30% at $p{H}_{ext}=\left\{\mathrm{2,4,6}\right\}$. Error bars are smaller than symbols, and are not shown.

3.3. Simulation of swelling experiments

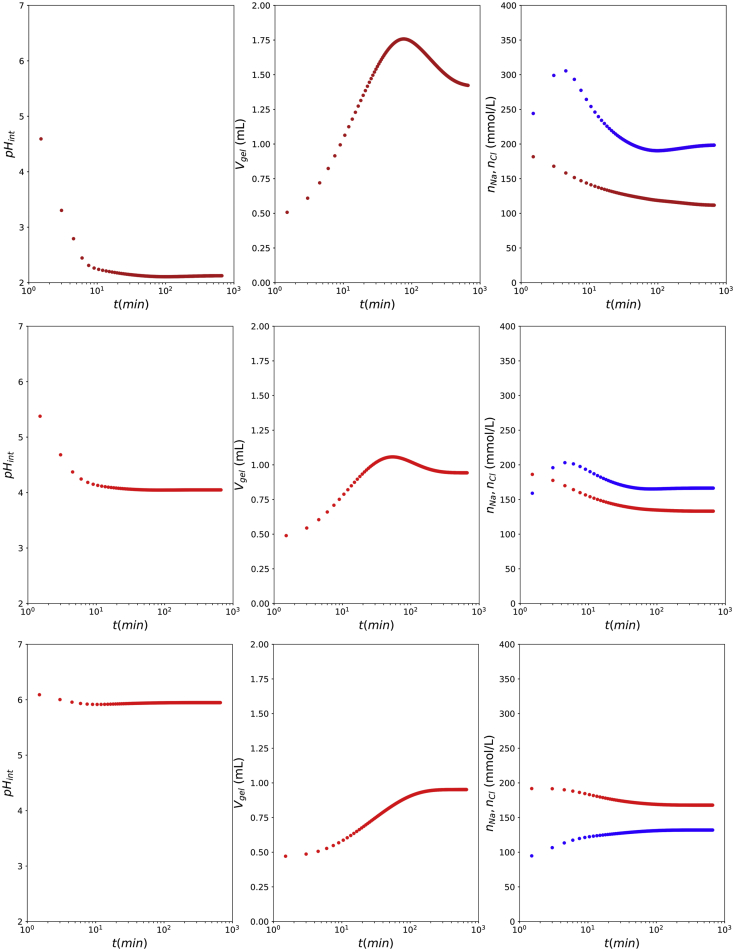
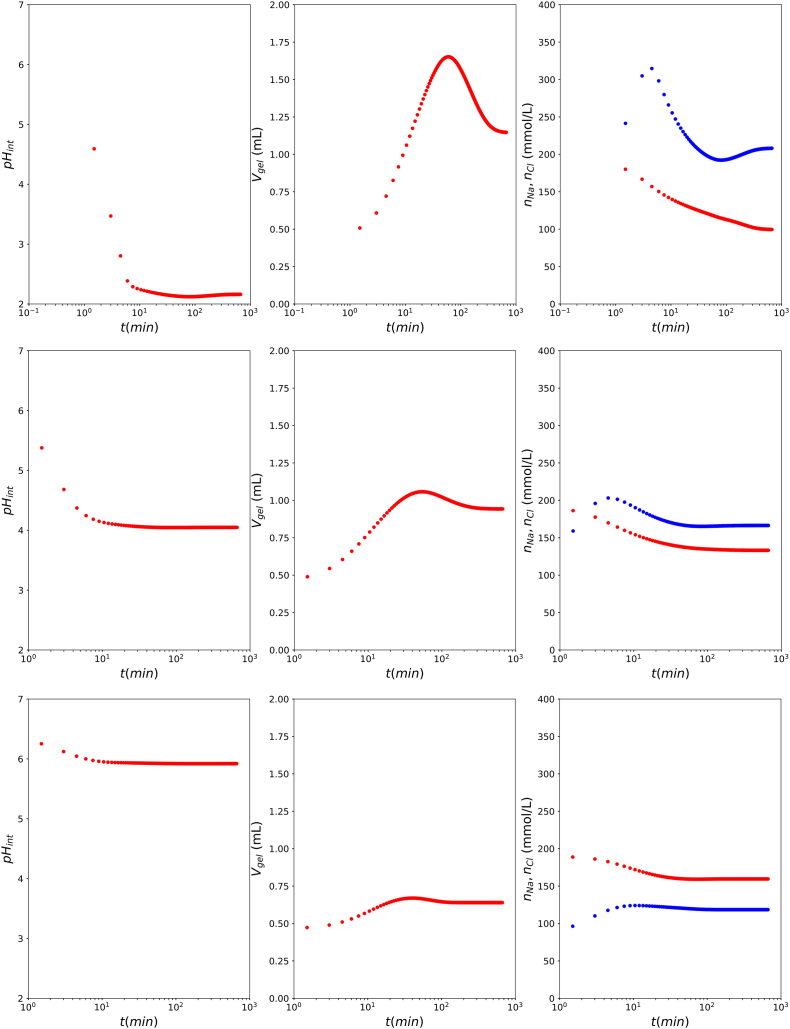
First, we test the model while assuming ideality of the bath and gel phase. Exemplary simulations are shown in Fig. 5, where the external pH is taken from the range: $pH=\left\{\mathrm{2,4,6}\right\}$. Elastic properties depend on the amount of proteins at gelation (Cornet et al., 2019). Simulations are performed for mass fraction of proteins at gelation $y_p=0.30$. Due to the production of SPI one can expect NaCl to be present in the level of 0.3–1%. Hence, we have assumed the initial NaCl concentration (excluding $N{a}^{+}$ counterions) to be 70 mmol/L. Furthermore, we assumed the shear modulus to be related to $y_p$ via: $G_{ref}=5\times {10}^7{\varphi }_{ref}^{9/4}$ (Cornet et al., 2019), with ${\varphi }_{ref}=0.34y_p$. The permeability is taken as $\kappa =8\times {10}^{-18}$ $m^{-2}$, which is comparable to values assumed for water transport in cheese (Dijk et al., 1984). The diffusion coefficient at 37°C for $NaCl$ is assumed to be $D_{NaCl}=0.6\left(1-{\varphi }_p\right){10}^{-9}$ cf. salt diffusion in cheese (Pajonk et al., 2003), and $D_{HC}=2D_{NaCl}$, because of the smaller size of $HCl$. The mass of the gel particle is $m_p$ = 0.5 g. In the figures we show a) the change of the internal pH ($p{H}_{int}$), b) the gel volume $V_{gel}$, and c) the ion concentrations inside the gel $n_{Na}$ and $n_{Cl}$.

Fig. 5.

Simulation results for $pH=\left\{\mathrm{2,4,6}\right\}$ (top to bottom), assuming ideal solutions. We show internal pH, $p{H}_{int}$, the gel volume $V_{gel}$, and ions concentrations inside the gel $n_{Na}$ (red) and $n_{Cl}$ (blue).

Due to the high internal and external ion concentrations, the ideal solution assumption is not valid. We are interested in whether the non-ideality has a significant influence on the protein swelling. Hence, we perform similar simulations, but now with non-ideality of dissolved ions taking into account, as computed with the Pitzer theory - and using the Diamant definition of the ionic strength in polyelectrolyte gels. Results are shown in Fig. 6, which can be compared to simulation using the ideal solution assumption, as shown in Fig. 5. Qualitatively, the results are quite similar, albeit that the swelling is reduced if one assumes non-ideality.

Fig. 6.

Examplary simulation results for $pH=\left\{\mathrm{2,4,6}\right\}$ (top to bottom) using non-ideality models. We show internal pH, $p{H}_{int}$, the gel volume $V_{gel}$, and ions concentrations inside the gel $n_{Na}$ (red) and $n_{Cl}$ (blue).

The simulation results are qualitatively in agreement with expectations based on experiments shown in Fig. 4 when considering pH with respect to the isoelectric point $pI$. At $pH=6$, $pH>pI$ and only part of the sodium counter-ions are exchanged for $H^{+}$, allowing $C{l}^{-}$ to enter the gel phase. As the final pH is near the pI the swelling is small as compared to $pH=2$ treatment. At $pH=4$ a similar picture arises, only $n_{Cl}$ exceeds $n_{Na}$, as $pH<pI$ and the protein is now negatively charged. The final volume is similar as pH = 6, as the distance from $pI$ is similar. At the internal $pH$ crosses the $pI$ there is a reversal of charge, contributing to the elaborate dynamics of the swelling: first the gel swells, and then it shrinks. A similar dynamics of initial swelling followed by shrinkage is observed experimentally, as shown in Fig. 4. At pH = 2, $pH\ll pI$ and the swelling is quite large, due to the large (negative) charge of the protein, and consequently $n_{Cl}\gg n_{Na}$. Also in the swelling experiments, we observe the maximal swelling at $pH=2$, with the tendency to de-swell at long times. The simulation results are still not in quantitative agreement, as the swelling is predicted too large. But it requires more measurements while varying initial and final pH, ionic strength, and bath volume, and also of additional observables like the electrical conductivity of the bath, and mechanical strength at different pH and ionic strengths.

4. Models with realistic gastric conditions

In the above model, it is assumed that the protein gel is immersed in an infinite bath of constant conditions. However, due to meal sizes compared to stomach volume, and high buffer capacity of proteins the assumption in the model above of an infinite bath is a poor approximation of the real gastric conditions in the human body. A better approach is taken in engineering perspectives of digestions. Here, the digestive tract is envisioned as a collection of reactor vessels of finite volume, connected in series, each performing a set of unit operations (M Bornhorst et al., 2016, Lamond et al., 2019). The stomach performs the following unit operations: mechanical breakdown, mixing, pH regulation, enzymatic hydrolysis, and sieving (via the pyloric valve).

The above model has focussed only on the effect of pH and ionic strength of the (simulated) gastric juice on the pH and moisture transport into the protein gel, which is only a small part of the processes going on in the stomach. Our model does show that pH and ionic strength internally the protein gels can be significantly different from the values in the gastric juice. Hence, in the stomach at least two phases must be distinguished: a) the protein gel (or meal) and b) the gastric juice. From the discussion below follows that one might also need to describe a gas phase, to account for CO2 production if gastric acid is neutralized by sodium bicarbonate in the mucous lining of the epithelial cells (Stevens et al., 1987, Goetze et al., 2007).

For each phase, we need to establish balance equations for the total phase volume, moisture content, electrolyte concentrations (including $H^{+}$), and enzyme concentrations. The governing equations for meal volume and gastric juice are the following:

$$\frac{d{V}_{meal}}{dt}=+Intake-Emptying+MoistureUptake-Digestion$$ (64)

The balance of the gastric juice is:

$$\frac{d{V}_{juice}}{dt}=+Secretion-JuiceEmptying-MoistureUptake+Digestion$$ (65)

Meal volume increases via the Intake function, which is distributed over a finite time for a meal containing a protein gel, as it needs mastication. Gastric emptying decreases the volume of both meal and gastric juice. There is moisture transport between juice and gel, as described above via swelling or shrinkage. Enzymatic digestion converts part of the protein gel into soluble peptides, which can be viewed as part of the gastric juice. The gastric juice increases due to secretion, which is regulated by hormones. Such hormonal regulation also holds for the gastric emptying.

In the following subsections, we discuss several of the processes happening in the stomach in more detail. These processes are enzymatic digestion, electrolyte transport, gastric secretion, and emptying. In the discussion of electrolyte transport, we also take into account electrolyte transport across the mucus layer. For gastric secretion and emptying the regulation is important to know.

In the discussion below, we disregard spatial gradients inside the meal particles. In reality, the spatial gradients in pH, electrolyte concentration, moisture content, and enzyme concentration might be quite significant and need to be taken into account in the modelling. Strong gradients in mechanical deformation can be accounted for in the polyelectrolyte gel modelling approach using the approach for Suo and coworkers (Hong et al., 2010), as we have recently applied to water holding capacity of cellular tissue (Van der Sman, 2015). But, a discussion on this aspect is out of the scope of this review.

4.1. Enzymatic digestion

Pepsin is the proteolytic enzyme secreted in the human stomach. Its precursor, pepsinogen is produced by chief cells in the same glands as hydrochloric acids and must pass the mucus layer to enter the gastric environment.

The activity of pepsin has an optimum at $pH\approx 2$. Effect of ionic strength is less known. Commonly, enzyme kinetics are described by Michaelis-Menten kinetics. A recent study shows that pepsin activity at pH = 2 decreases at increasing ionic strength. The enzyme kinetics appears not to follow Michaelis-Menten. Pepsin can attack multiple peptide-bonds, with some more easily than others. Its activity is said to be inhibited by intermediate peptides (Qi et al., 2018). Salivary amylase and gastric lipase can be active in the stomach (Sarkar et al., 2015, Lamond et al., 2019), but their action is irrelevant for meals of protein gels, and hence we disregard further discussion of that.

Recently, the enzyme kinetics of pepsin has been modelled (Kondjoyan et al., 2015, Sicard et al., 2018). There, pepsin is assumed to behave as a diprotic acid, cf. (Lin et al., 1992):

$$E{H}_2\leftrightarrow H^{+}+E{H}^{-}\leftrightarrow 2H^{+}{E}^{2-}$$ (66)

Only the active form of the enzyme $H{E}^{-}$ leads to protein hydrolysis. The dissociation constants are $K_{E1}$ and $K_{E2}$:

$$\begin{array}{l}{K}_{E1}=\frac{E{H}^{-}{H}^{+}}{E{H}_2}\\ K_{E2}=\frac{E^{2-}{H}^{+}}{E{H}^{-}}\end{array}$$ (67)

Substitution of these constants in the relation that the total amount of E remains constant $E(t=0)=E=E{H}_2+E{H}^{-}+E^{2-}$ renders the following relation for the amount of active enzyme (Kondjoyan et al., 2015, Sicard et al., 2018):

$$\frac{E{H}^{-}}{E}=\frac{1}{1+K_{E2}/n_H+n_H/K_{E1}}$$ (68)

$$p{K}_{E1}=2.5\text{,}p{K}_{E2}=1.6$$

First-order kinetics is assumed for protein digestion (Kondjoyan et al., 2015):

$$\frac{dP}{dt}=-P{\theta }_{max}\frac{E{H}^{-}}{E{H}^{-}+L}$$ (69)

The enzyme absorbs at the protein similar to a Langmuir isotherm. P is the undigested protein concentration. It will decrease due to digestion, it will be related to ${\varphi }_p$. L is linked to the maximum amount of enzymes absorbed to the substrate. It is assumed that heating induces protein denaturation and aggregation. Denaturation increases the (relative) amount of binding sites for pepsin ${\theta }_{max}$, while aggregation reduces the reaction speed (i.e. diffusion of enzymes is hindered by the dense protein matrix), but also reduces the accessibility of the substrates for the enzyme.

Pepsin produces amino-acids/peptides, which contribute to the buffer capacity of the gastric juice. For each hydrolysis, an extra carboxyl and amide group is produced (JL Mat et al., 2018), which can be ionized depending on the pH of the gastric juice. The degree of hydrolysis can be obtained via titration but must be corrected for the buffer capacity of the undigested protein. After cleaving most of the hydrolysis products can still be bound to the network. Only after the second cleavage, individual peptides are liberated, which can diffuse from the gel phase to the gastric juice. Diffusion can be slow due to the large size of fragments. Hence, titration is a better measure for the degree of hydrolysis than the amount of hydrolysis products in the juice phase.

Across the mucous layer, there is a pH gradient from pH = 2 at the gastric lumen side to pH = 7 at the side of the epithelial cells. Only at the top of the mucous layer, the pepsinogen ($E{H}_2$) is converted into the active pepsin form ($E{H}^{-}$). However, pepsin acts also on the mucus layer, which needs to be replenished continuously. Campos (Campos and Sancho, 2003) states that there is an intermediate form of pepsin, which binds to mucin, which is transported from the crypts containing the parietal and chief cells to the lumen.

4.2. Enzyme transport and partitioning

The enzyme transport from the gastric juice to the protein gel has to be incorporated in the model. Several studies have already indicated the importance of diffusion of pepsin (Thevenot et al., 2017, Qi et al., 2017, Somaratne et al., 2020), and how it is influenced via the protein gel microstructure via obstruction and decrease of free volume (Axpe et al., 2019). The diffusion of pepsin, or fluorescent molecules of similar size, has been compared to several diffusion models, as reviewed by (Masaro and Zhu, 1999, Amsden, 2002).

However, recent investigations in our research group has shown that convection of pepsin by the gastric fluid imbibing the gel during swelling is an equally important transport mechanism to be accounted for (Deng et al., 2019). Moreover, we have found that there is also a significant partitioning of the enzyme between the gel and the bathing (simulated) gastric juice. Such a partitioning of solutes between gel and bath phase is described by thermodynamic theory (Van Der Sman, 2018). The elastic contribution in the swelling pressure, ${\text{Π}}_{elas}$, also contributes to the chemical potential of the solute, resulting in unequal distribution (i.e. partitioning) of the solute between gel and bath. The partitioning is dependent on the molecular size of the solute and the solute concentration. Partitioning is particular significant at low concentrations, and high molecular sizes - as holds for enzymes.

4.3. Electrolyte transport in the gastric juice

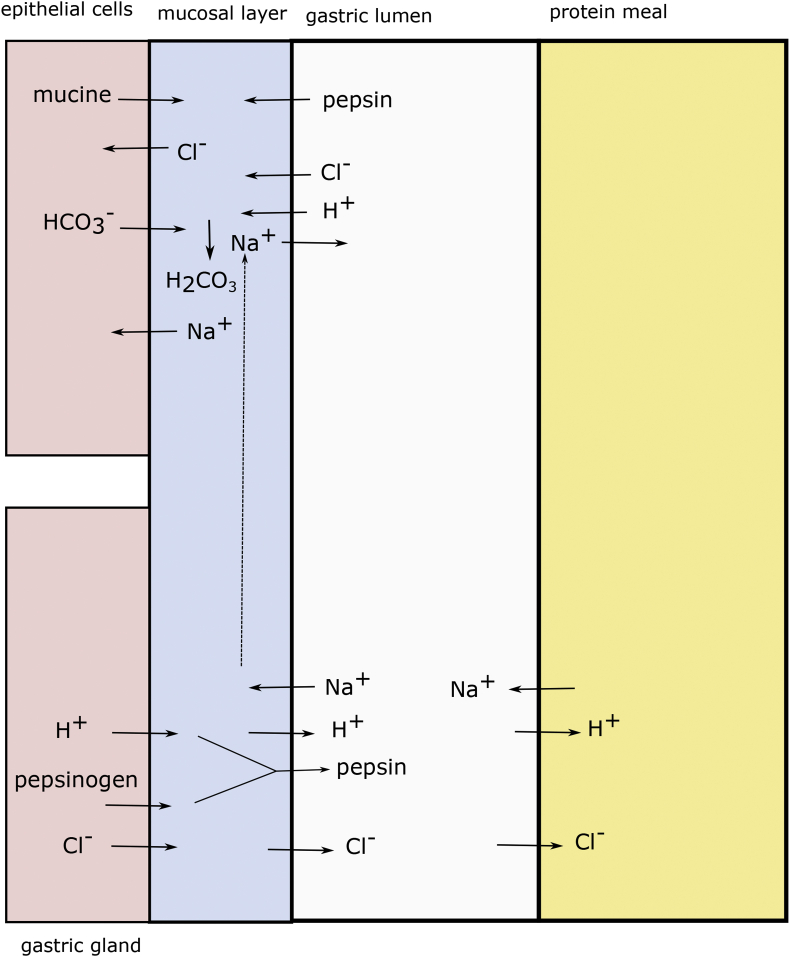
We restrict this discussion to monovalent ions only for the sake of brevity. Gastric juice contains the following monovalent ions $H^{+}$, $O{H}^{-}$, $C{l}^{-}$, $N{a}^{+}$, and $K^{+}$. $HC{O}_3^{-}$ is assumed not to be present in the gastric juice, as it would be neutralized directly by $H^{+}$ to $H_{2}O$ and $C{O}_2$. However, $HC{O}_3^{-}$ transport across the mucus layer is important for the protection of the epithelial cells against the low pH of the gastric lumen.

The electrolyte contents of the gastric juice changes due to ion exchange with the protein gel, and the ion exchange with the cells lining the stomach: during secretion $H^{+}$, $C{l}^{-}$ and $K^{+}$ are secreted (but $K^{+}$ can be cycled back). This exchange of electrolytes between gastric juice and cells is modelled by de Beus (De Beus et al., 1993), who has also included the secretion of $HC{O}_3^{-}$ by the epithelial cells. Furthermore, the transport of electrolytes via the blood vessels is modelled. Acid production by the parietal cells leads to the so-called alkaline tide in the blood, which passes directly to the epithelial cells, which uptake the bicarbonate for the neutralization of acid at the lumen side of their mucosal lining. An important constraint of any digestion model is that the gastric juice remains electroneutral. A remarkable feature of the model by de Beus is that there is no transport of sodium from the gastric lumen to the cellular environment.

The electrolyte transport between cellular environment and gastric lumen is via the mucosal lining. Mucin, the glycoprotein in the mucus layer, is a polyelectrolyte, like proteins, and it swells as function of pH and ion composition (Lewis et al., 2018). Ion transport in the mucus layer is similar to ion-exchange membrane (Lewis et al., 2017). It is hypothesized that protons are sequestered by the mucin, and that they are released by the degradation of mucin by pepsin. A mathematical model is constructed (Lewis et al., 2017, Lewis et al., 2018), which is very similar to models used to describe cartilage swelling, as discussed above. Four ions are considered: $H^{+}$, $N{a}^{+}$, $C{l}^{-}$, and $HC{O}_3^{-}$. $H^{+}$ and $HC{O}_3^{-}$ combine to $H_{2}O$ and $C{O}_2$. Binding/unbinding of $H^{+}$ is not modelled in the mucus layer. An ion exchange of $C{l}^{-}/HC{O}_3^{-}$ and $H^{+}/N{a}^{+}$ at the epithelial surface is assumed (Lewis et al., 2017).

This recent model (Lewis et al., 2017, Lewis et al., 2018) is much in agreement with an earlier (qualitative) model of Schreiber and Scheid (Schreiber and Scheid, 1997, Schreiber et al., 2000). Here, mucus is viewed as a proton/diffusion barrier. There is continuous growth of the mucus layer, which is required because of its degradation by pepsin. Pepsinogen is simultaneously secreted with acid, bicarbonate, and mucus. Near the lumen, pepsinogen is converted into pepsin. Protons are back diffusing in the epithelial mucus layer. Near the gastric acid gland, there is proton release from the mucus. $HC{O}_3^{-}$ transport to the lumen side is coupled to $Cl-$, via a special protein transporter. It is suggested that there is active $N{a}^{+}$ transport via $H^{+}$/$N{a}^{+}$ ion exchange, which appears to be in contradiction with the model of de Beus (De Beus et al., 1993).

In an even earlier model (Allen and Garner, 1980), it is assumed sodium is secreted by epithelial cells together with bicarbonate. Bicarbonate neutralized the protons in the mucus layer, leaving sodium chloride remaining in the mucus layer, of course, free to diffuse. However, later the same author (Allen and Flemström, 2005) shows that $HC{O}_3^{-}$ secretion is coupled to $C{l}^{-}$ via the $HC{O}_3/Cl$ exchanger at the apical membrane (lumen side). At the basolateral side $HC{O}_3^{-}$ is imported via $N{a}^{+}/HC{O}_3^{-}$ co-transporter. $N{a}^{+}$ can be transported via $N{a}^{+}/H^{+}$ exchangers, and $N{a}^{+}/K^{+}$ ATPase. Also, it is proposed there are (apical) $N{a}^{+}$-$K^{+}$-2$C{l}^{-}$ cotransporters, and basolateral $N{a}^{+}$-$C{l}^{-}$-$HC{O}_3^{-}$ cotransporter (White, 2010). Hence, there is ample opportunity for epithelial cells to transport $N{a}^{+}$ across the membrane. $N{a}^{+}/H^{+}$ exchangers are thought to act only at the basolateral side of parietal cells, which are secreting the gastric acid $HCl$ (Ritter et al., 2001). Perhaps, these models can be reconciled if one assumes ionic conduction of $N{a}^{+}$ inside the mucus layer. Polyelectrolyte gels are capable of ion conduction if electric potential differences arise. There can be Donnan potential differences between mucus layer lining epithelial cells and that lining the gastric gland, as shown in Fig. 7.

Fig. 7.

Ion exchange between meal, gastric juice, mucus and cellular environment, where we distinguish parietal and epithelial cells.

4.4. Gastric emptying and secretion models

The gastric secretion and emptying are under hormonal control, receiving signals from the small intestine, gastric juice and the stretching of the stomach wall. A very elaborate model is developed by Joseph (Joseph et al., 2003), having a detailed description of the various hormones involved. Also, it describes the fate of endocrine cell populations. The latter is not significant on the time scale of the digestion of a meal. Hence, the model is later simplified in (Marino et al., 2003), assuming steady cell populations. It models acid and bicarbonate secretion, which can be different in either fundus or antrum (upper and lower part of the stomach). The gastrin hormone diffuses between fundus and antrum, which is simplified with a delay function. However, the model has few links to the signals controlling the hormone levels.

Models with a more engineering perspective are more helpful for extending our digestion model towards realistic gastric conditions. Such models have been developed by Marciani as based on MRI observations (Marciani et al., 2000, Marciani et al., 2001). This model regards two phases in the stomach: a) the meal with volume $V_m$ and b) the gastric juice with volume $V_s$. $V_m$ decreases via gastric emptying, which is assumed to have a constant rate: $d{V}_m/dt=-k_p{V}_m$. The secreted volume evolves as:

$$d{V}_s/dt=S_0+k_m{V}_m-k_p{V}_s$$ (70)

There is a basal secretion rate, $S_0$. Secretion is stimulated by the presence of food, and it is assumed to be linear with $V_m$: the increase of the volume of the stomach leads to stretching of the stomach walls, which is sensed and triggers acid secretion. The last term represents the loss of gastric fluid via gastric emptying (having the same rate p as the meal volume).

Sauter has developed a similar model (Sauter et al., 2012):

$$\begin{array}{l}d{V}_m/dt=-k_p{V}_m+k_s{V}_s\\ d{V}_s/dt=+k_m{V}_m-k_p{V}_s\end{array}$$ (71)

But, there is little physiological justification for the coupling between $V_s$ and $V_m$ via the term linear in $k_s$.

Moxon proposed that the secretion rate is a function of the chyme viscosity (Moxon et al., 2017), which is explained via the meal effect on gastric distension (i.e. the stretching of the stomach wall). We view that elastic properties, as exhibited by protein gels, have a similar effect on gastric distension.

Gastric emptying is largely regulated by digestion in small intestine (Depoortere, 2014, Sarkar et al., 2015, Moxon et al., 2017). Similar to taste sensors in the mouth the small intestine has similar nutrient sensors, feeding information back to the stomach hormone system, which controls the gastric emptying. The feedback from absorbed nutrients in the small intestine is assumed to be the major control mechanism for gastric emptying. Hence, it will be important to incorporate digestion in the small intestine into the gastric digestion model, to have more realistic feedback on gastric emptying, cf. (Moxon et al., 2017).

Gastric emptying is also controlled by the particle size (Moxon et al., 2017). Particles larger than a critical size of 1–2 mm will not pass the pyloric sphincter, which acts as a filter. Particle size can decrease due to enzymatic digestion or mechanical fragmentation due to the antral waves. Thus, a realistic gastric digestion model should also describe the evolution of particle sizes. Effects of swelling and enzymatic digestions are described above. A proper fragmentation model is still lacking in the literature.

5. Conclusions

The gastric digestion of (novel) protein gels has a very rich physics and chemistry due to their polyelectrolyte character of the gels. We have shown that their physical chemistry can be described using models, which have been developed already in the fields of polymer physics and biophysics. In particular, we have described in detail a model for the description of the swelling of protein gels in simulated gastric fluids, which shows qualitative similar behaviour as observed in in-vitro experiments performed with soy gels. This model is assembled from several building blocks, describing a) the charging of proteins at different pH conditions, b) the distribution of ions over gel and gastric juice following Gibbs-Donnan, c) the swelling (kinetics) of the protein gel following Flory-Rehner and Darcy's law, and d) ion transport between gel and gastric juice following Stefan-Maxwell. Considering the high electrolyte concentration in the gastric juice and protein gel, extensions of the above theories with the Debye-Hueckel or Pitzer theories must be used for dealing with the non-ideality of the electrolyte solutions. This hypothesis paper is concluded with an outlook on how the above model must be extended for simulating realistic (in-vivo) gastric conditions. For that the model needs to be extended with the following building blocks: a) enzyme kinetics as function of pH, b) transport of enzyme into the gel, c) exchange of electrolytes between glands/epithelial cells with the gastric juice via the mucus lining the stomach, d) physiology of gastric emptying and gastric secretion. All these submodels need to be integrated into a process model accounting for the finite volume of the stomach, describing volume changes in gastric juice and protein gel, due to food intake, gastric emptying, gastric juice secretion, and gel swelling/shrinkage. We hope this overview gives new directions to the experimental investigation of gastric digestion, and development of in-vitro digestion protocols, which are more compliant with realistic gastric conditions.

Table 2.

List of symbols.

Symbol	Description	Unit
$a_i$	activity of compound i	[-]
$c_T$	total molar concentration	[mol/m3]
$h_i$	convective coefficient	[-]
$i_i$	degree of ionization	[-]
k	permeability	[m2]
$m_i$	molal concentration	[mol/kg]
$n_i$	molar concentration of compound i	[mol/m3]
$pI$	isoelectric point	[-]
$p{K}_i$	logarithm of dissociation reaction constant	[-]
r	mean ion radius	[m]
t	time	[s]
$u_i$	velocity	[m/s]
$w_i$	drift velocity	[m/s]
$x_i$	mole fraction	[-]
$z_i$	valency of ion	[-]
$A_{\varphi }$	Debye coefficient	[-]
$B_{ij}$	Pitzer coefficient	[-]
$C_H$	buffer capacity	[mol/mol]
$D_i$	diffusion coefficient	[m2/s]
F	Faraday constant	[C/mol]
$G_i$	elastic modulus	[Pa]
$K_i$	dissociation reaction constants	[-]
$K_{bulk}$	osmotic bulk modulus	[Pa]
I	ionic strength	[mol/m3]
$J_i$	molar flux density	[mol/s.m2]
L	saturation constant	[mol/m3]
$N_A$	number of avogrado	[-]
$N_i$	number of moles	[mol]
P	amount of proteins	[kg/m3]
R	universal gas constant	[J/mol/K]
$R_{gel}$	radius of gel	[m]
S	Surface area	[m2]
T	temperature	[K]
V	volume	[m3]

Table 3.

List of symbols.

Symbol	Description	Unit
α	Pitzer constant	[-]
${\beta }_{ij}$	Pitzer coefficient	[-]
${\gamma }_i$	activity coefficient	[-]
ε	dielectric constant	[-]
${\chi }_i$	Flory-Huggins interaction parameter	[-]
η	viscosity	[Pa.s]
${\varphi }_i$	volume fraction	[-]
κ	inverse of Debye screening length	[1/m]
${\mu }_i$	chemical potential of compound i	[J/mol]
${\nu }_i$	molar volume	[m3/mol]
${\theta }_{max}$	fraction of enzyme binding sites	[-]
σ	stress	[Pa]
${\tau }_i$	time scale	[s]
${\zeta }_{ij}$ friction coefficient	[kg/mol/s]
$\text{φ}$	osmotic coefficient	[-]
${\text{π}}_i$	pressure	[Pa]
$\text{σ}$	Debye-Hueckell correction factor	[-]
$\text{ψ}$	electric potential	[V]