Applying sorting algorithms to sensory ranking tests – A proof of concept study

Abstract

In a sensory or consumer setting, panelists are commonly asked to rank a set of stimuli, either by the panelist's liking of the samples, or by the samples' perceived intensity of a particular sensory note. Ranking is seen as a “simple” task for panelists, and thus is usually performed with minimal (or no) specific instructions given to panelists. Despite its common usage, seemingly little is known about the specific cognitive task that panelists are performing when ranking samples. It becomes quickly unruly to suggest a series of paired comparisons between samples, with 45 individual paired comparisons needed to rank 10 samples. Comparing a number of elements with regards to a scaled value is common in computer science, with a number of differing sorting algorithms used to sort arrays of numerical elements. We compared the efficacy of the most basic sorting algorithm, Bubble Sort (based on comparing each element to its neighbor, moving the higher to the right, and repeating), vs a more advanced algorithm, Merge Sort (based on dividing the array into sub arrays, sorting these sub arrays, and then combining), in a sensory ranking task of 6 ascending concentrations of sucrose (n = 73 panelists). Results confirm that as seen in computer science, a Merge Sort procedure performs better than Bubble Sort in sensory ranking tasks, although the perceived difficulty of the approach suggests panelists would benefit from a longer period of training. Lastly, through a series of video recorded one-on-one interviews, and an additional sensory ranking test (n = 78), it seems that most panelists natively follow a similar procedure to Bubble Sorting when asked to rank without instructions, with correspondingly inferior results to those that may be obtained if a Merge Sorting procedure was applied. Results suggests that ranking may be improved if panelists were given a simple set of instructions on the Merge Sorting procedure.

Graphical abstract

Highlights

• •Ranking is common in both sensory and consumer testing.
• •Despite its wide adoption, no standard set of procedural instructions exists on how to perform a ranking exercise.
• •This report details 2 approaches, borrowed from computer science, to ensure that all panelists are ranking using the same strategy.
• •In addition, a separate panel were asked to rank the same samples without instruction, with in-depth follow up interviews on a smaller cohort to delineate the natural approach.
• •The strategies are contrasted in terms of ease, speed and accuracy.

1. Introduction

In the sensory analysis of food products, panelists are commonly asked to rank samples, either on their liking of the samples, or the intensity of a specific sensory attribute (i.e. sweetness, thickness, etc). Ranking tests are seen as having the advantage of simple instructions (if any are given at all) that are instinctively understood and easy to follow, as well as being simple with regards to the handling of data. Ranking tasks are often used to infer information on a set of paired comparisons, despite these comparisons not being directly made (Luce, 2012). Usual instructions would resemble something as simplistic as “taste the samples in front of you in whatever order you see fit, and rank from left to right, in order of weakest to strongest.” Thus, panelists taste the samples without a set structure for doing so, and it is up to the panelist to decide how to go about tasting and arranging the samples in their chosen order. Up until now there has not been any existing standard instructions or methods for completing a ranking test in a controlled manner, consistent across participants (see ISO, 2006). The procedure is seen as relatively simple, quick and reliable (Falahee and MacRae, 1997), but the many individual judgements involved in a full set of paired comparisons of every sample in a given set would seem fatiguing to a sensory panelist (Lawless and Heymann, 2010).

The literature on ranking is notably limited (from outside the field, see Luce, 1977, Luce, 2012 for some discussion on contrasting of ranking tasks with the noted Choice Axiom, and Block, 1974 for thoughts on the economics of decisions and response theories). Thurstone (1931) describes ranking as “one of the simplest of experimental procedures”, though still noting the high number of paired comparisons needed to contrast every stimulus with all others. There are also theoretical incompatibilities with Thurstonian models and the concept that ranking direction is reversible (Yellott, 1980), i.e. that ranking from best-to-worst will occur with the same probability as when ranking from worst-to-best, which seems theoretically incompatible when ranking is accomplished by carrying out a sequence of totally independent choices. Marley (1968) relates the ranking probabilities of an element to that element's binary choice probability, again under the assumption that preference functions and aversion functions are not equivalent. The ISO document (ISO, 2006) used to internationally standardize the process of ranking in sensory evaluation also contains no information on the cognitive basis for ranking.

Sorting algorithms are commonly used in computer science. Their purpose is to order numerical elements, thus parallels that of ranking tasks in sensory science. There are many different sorting algorithms, but in this study we chose to focus on the most basic algorithm, and one of the first attempts to improve on it. The simplest method of sorting is Bubble Sort. This method sorts an array of elements by comparing one element with the adjacent element (i.e. a paired comparison) and swapping them if they are in the wrong order. This algorithm moves linearly through the array and keeps making passes through the whole array until no swaps are made, thus the higher elements “bubble” to the top of the array (Astrachan, 2003), in the same way the stronger sample may continually move to the right in a ranking task.

Another sorting method is Merge Sort, a divide and conquer method where the array is first divided into smaller sub-problems. The sub-problems are then sorted, and step-by-step, merged together into a sorted order, until the full order has been established (Knuth, 1998). More information on both Merge and Bubble Sort are found in the methods. As the function of both algorithms is to rank an array from lowest to highest, it should be possible to apply such algorithms to sensory ranking tests. Applying a set algorithm would allow for a more standardized strategy in performing a ranking task. Thus, the aim of this study was to test a pair of tools that could make sensory ranking tests more effective, by adapting methods from algorithmic sorting for the ranking procedure. We evaluate the effectiveness of using Merge and Bubble Sorting algorithms in a sensory ranking test, and to compare the efficacy of such strategies to the native strategy panelists use to rank samples when not provided with instructions. A secondary goal of the project was to determine if one algorithm was more efficient, accurate, or easy to use compared to the other. Finally, we sought to determine the strategies used natively by panelists to rank samples when no explicit instructions were given.

2. Materials and methods

2.1. Participants

All procedures were evaluated and approved by the Cornell University Institutional Review Board for Human Subject Research. Panelists were recruited from the Cornell University sensory listserv, consisting mostly of university students, staff, and faculty. Panelists were not informed of the purpose of the study, but were informed that sugar solutions would be consumed, and screened for allergies. All panelists (total n = 151) gave informed consent, and were compensated for their time. The un-cued ranking task used a separate panel (recruited with matching demographics and ranking experience), to avoid learning effects, or biasing participants’ ranking strategy.

2.2. Samples

Solutions were prepared using food-grade sucrose (Sigma Aldrich, St Louis, MO) and distilled water. For each test participants received six samples of sucrose prepared in the following concentrations: 0 g/l, 5 g/l, 8 g/l, 11 g/l, 14 g/l, 17 g/l (or 0 mol/L, 0.015 mol/L, 0.023 mol/L, 0.032 mol/L, 0.041 mol/L, 0.050 mol/L). The concentration range was adapted from ISO 22935–1:2009 and ISO8586:2012(E) and was chosen to be perceptible as different, based on the pre-test, but not excessively strong to be considered fatiguing for repeated evaluation. 2oz samples were served in 5oz cups with lids, at room temperature. A counterbalanced serving order was used, with RedJade®Sensory Software Suite (RedJade Sensory Solutions LLC, California) used to collect data in the experiment.

2.3. Test setup

The study consisted of three 15–20 min sessions. In the first 2 sessions, a set of 73 participants either completed the Bubble Sorting method or the Merge Sorting method, counterbalanced across the panel, with the other test performed in the following session. The panelists were provided with one of the visual aids in Supplemental Figs. 1 and 2 when completing the Bubble or Merge Sorting tasks, along with instructions also given as online supplemental materials. The same sucrose concentrations were used both days, but were presented with different three digit codes. On a third test day, a non-overlapping set of 78 panelists, recruited with matching demographics and experience of sensory testing, were given identical concentrations of samples and instructed to sort the samples from low to high without further instructions on the method to use. Following the task, panelists were instructed to provide a short explanation for the strategy they used to rank the samples. Panelists also provided demographic information in all tests (age, gender, sweet consumption habits). Participants previous experience with sensory ranking tests was also recorded. Following the un-cued ranking exercise, 10 panelists were invited back to perform video-recorded interviews where they detailed their ranking strategy, and were further compensated for their time.

2.4. Data analysis

The experiment quantified a ranking score representing the success of the participants in ranking the array, the perceived difficulty of the two methods (scored on a 5-pt scale, and referred to as ease) and the time the test took each panelist to complete (collected electronically). The ranking score was quantified from the number of reversals a panelist made, from zero (perfectly sorted) to 15 (completely reversed, i.e. sorted high to low, not low to high), with numerical scores from 0 to 1. Results were non-normally distributed, and thus were analyzed with Wilcoxon matched pairs tests (when comparing Bubble and Merge Sorting, where panelists performed both tasks), and Kruskal-Wallis tests (when including un-cued ranking, where sets of panelists differed). Statistical significance was assumed when p < 0.05.

The open-ended responses from the un-cued ranking test were compiled and first examined via Wordclouds (http://www.wordclouds.com, © Zygomatic, Vianen, The Netherlands), free online software program. The researchers then manually coded them into different semantic theme groups and calculated their frequency counts using XLStat by Addinsoft, Paris, France.

2.5. Bubble Sorting

Panelists were provided with a visual aid as in Supplemental Fig. 1 for the Bubble Sort procedure. The principle of Bubble Sorting is to repeatedly compare pairs of samples, moving the smallest element of the array to the position of lowest index (Knuth, 1998). To sort the sucrose solutions like in this study, the algorithm goes through the array of concentrations, comparing each pair of adjacent elements (concentrations), swapping them if they are in the wrong order. As an example, suppose an array of the following numbers, as in the concentrations in this study: (8, 17, 14, 0, 5, 11). The highest concentration (17 g/l) would by using Bubble Sort gradually “bubble” up to position F, which marks the highest index, like bubbles rising in a glass of soda. The next lowest concentration (14 g/l) would bubble to position E, 11 g/l to position D and so on. The process repeats until all elements are placed in the right order. No swapping can be performed unless a comparison between two adjacent elements is performed, which means that the algorithm often has to run through the full array several times, and comprises many individual paired comparisons, thus may be fatiguing for panelists.

2.6. Merge Sorting

Panelists were provided with a visual aid as in Supplemental Fig. 2 for the Merge Sort procedure. Merge Sorting is a more complex sorting algorithm, termed a divide-and-conquer method. As such, the first step is the divide portion, where the array is divided into its smallest sub-problems. As an example; an array consisting of the values [5, 14, 0, 17, 11, 8] is to be sorted using Merge Sorting. We split the array, so we now have two subarrays [5, 14, 0] and [17, 11, 8]. We then split once again, to get the smallest sub-problem [5, 14]. Now, we compare the first and second sample, and switch if the left side is higher (false in this case). Following this, the third sample is first compared with the first sample [5], and switched if the rightmost sample is smaller. Since [0] < [5] the first three samples are now recombined in the subarray [0,5,14]. Likewise, comparing [17] with [11] determines the order [11,17], with [8] compared with [11]. Since [8]<[11] the new subarray is [8,11,17]. The next step is to arrange the final order of the entire array. In order to do this the samples in the two subarrays [0,5,14] and [8,11,17] are individually compared. In other words [8] is first compared with [0]. Since sample [8] > [0] we know that [0] is our lowest value since it is the lowest of the two lowest samples in the subarrays. Next we compare [8] with [5] and determine that 8 > 5, therefore [5] is the second value in our array. Then we compare [8] with [14], and as [8] < [14], [8] is our third value. Next, we compare [11] with [14] since we already established that [11] is greater than [8] we do not need to compare sample [11] with [0] and [5]. We conclude that [11] < [14] and thus [11] is the fourth value in our array. Finally we compare [17] with [14] and determine that [17] > [14]. We now have our final order of the array [0, 5, 8, 11, 14, 17]. The array is now fully sorted.

3. Results and discussion

3.1. The efficacy of Merge Sorting is greater than that of Bubble Sorting

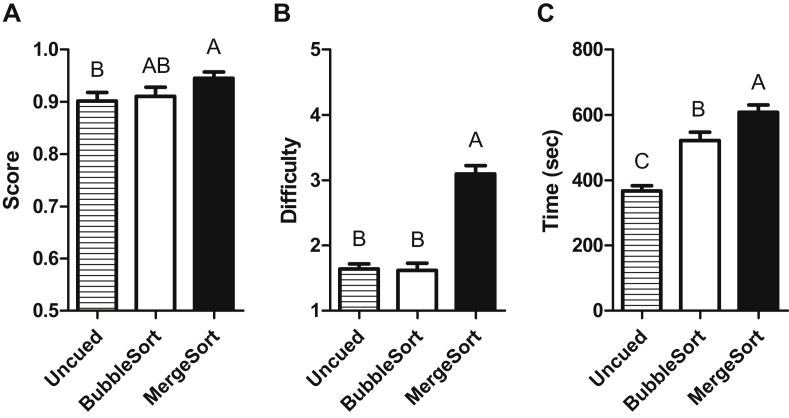
73 panelists (54F) took part in the first session, ranging from 18 to 66 years old (mean = 32.3, SD = 13.2), with 55% having performed a sensory ranking task before, and sweet consumption habits ranging from once a month to multiple times per day. Panelists generally performed well on the ranking tasks, showing they were capable of ranking samples with differences in this range ably (mean ranking scores 0.911 for Bubble Sorting, and 0.945 for Merge Sorting, or a mean of around one reversal per panelist, Fig. 1). However, when comparing the results of the merge and Bubble Sorting procedures, panelists scored higher, that is, were more accurate, when sorting with a Merge Sort procedure (p = 0.030). The Merge Sorting procedure was also perceived as a significantly harder task to perform than the Bubble Sorting setup (p < 0.001), and also took significantly longer to perform (mean 608s, vs 521s for Bubble Sort; p < 0.001). Interestingly, there was a positive correlation between panelist's age and the time taken to complete the tests, with older the participants taking longer to complete either procedure (r = 0.231; p = 0.005). When examining the results in a linear mixed model, no effect on panelist ranking score was observed from panelist age, gender, or sweet consumption, with only the test strategy followed (p = 0.023), and the panelist's experience of sensory ranking (p = 0.023) being significant in the model. Interestingly, those with experience of ranking tests (59% of the panel) performed slightly worse than those without experience, perhaps due to having to stick to an unfamiliar procedure. One further extension of such ranking strategies in future study may be to introduce measures of certainty, such as those associated with R-index approaches (Brown, 1974, O'Mahony, 1979, O'Mahony, 1992). In such a manner, an interaction between a panelist's degree of certainty in ranking order and the perceived difficulty of the test may shed more light on the cognitive tasks performed in cued and un-cued ranking tasks.

Fig. 1.

A. Panelist's ranking score when using Bubble Sorting, Merge Sorting, or an un-cued sorting strategy. Ranking scores of 1.0 imply a perfect ordering, with 0 a complete reversal, i.e. sorted from strongest to weakest. Columns show mean plus SEM, columns with differing letters imply statistical differences. B. Panelist's perceived level of difficulty from the Bubble Sorting, Merge Sorting, and an un-cued sorting strategies, where 1 implies very easy, and 5 implies very difficult. Columns show mean plus SEM, columns with differing letters imply statistical differences. C. Panelist's time to complete the sorting tasks when following a Bubble Sorting, Merge Sorting, or un-cued sorting strategy. Y axis denotes time taken for ordering 6 samples in seconds. Columns show mean plus SEM, columns with differing letters imply statistical differences.

3.2. When un-cued, panelists rank less successfully than with a specific procedure

Following the test, a second panel, similar in size (n = 78) and demographics (p > 0.05 for age, gender, ranking experience and sweet consumption), was recruited to perform a ranking task with the same samples, this time without being given specific instructions. In this case, the scores achieved in the ranking task (mean ranking score = 0.902) were lower than those obtained with Merge or Bubble Sorting (although only statistically lower versus Merge Sorting, Fig. 1A, p = 0.024). While the improvement in ranking scores observed between techniques was small, this is reflective of the task's relative ease, and the panel size. Given a more difficult ranking task (with lower discriminability between samples), or a larger panel, differences between ranking strategies would undoubtedly be more pronounced. Despite lower ranking scores than Merge Sorting, the perceived difficulty of the sorting procedure when not cued was much lower than that of merge Bubble Sorting (Fig. 1B, p < 0.001), while viewed as similar in difficulty to the Bubble Sort procedure. When comparing the time taken for un-cued sorting, the un-cued method was the quickest of the 3 (Fig. 1C, mean 367 s; p < 0.001). Sorting similar data arrays is noted to differ greatly in duration based on sorting strategy (Abbas, 2016). This may also reflect the time to read and digest the instructions involved with each process, a factor less important in a panel that had undergone a period of training. In future studies, it may be of use to improve on the written instructions provided, by demonstrating the principal of the divide and conquer Merge Sort method, which is less intuitive than Bubble Sorting, highlighting the ease of sorting multiple smaller arrays over the full-sized array.

3.3. The most common cognitive task performed in ranking is similar to that of Bubble Sorting

When left un-cued in their strategy to rank the samples, panelists identified a number of approaches when asked to explain after the task. Some chose a single strategy, where others combined several approaches to rank the samples. The most common approach was to compare samples to their neighbor, and move up if stronger, an approach analogous to Bubble Sorting (40% of the panelists). The other most common other approaches were to split into sub-groups, sorting these smaller sets, thus similar to Merge Sorting (16% of the panelists), or some form of internal scaling, whereby the panelist attempted to assign a value to how strong the stimulus was, without explicitly doing this (12% of the panelists), or to assign a particular sample as a reference sample, and judge the distance from the reference sample of each individual test sample (9% of the panelists). The remaining panelists chose a hybrid of these approaches, or could not adequately describe their approach. Following the sensory testing, 10 panelists were asked to return for a video-recorded session, where they would explain their approach to the ranking task in real time, examples of which demonstrating a bubble-like and merge-like procedure are provided online (http://blogs.cornell.edu/sensoryevaluationcenter/2020/01/09/ranking-and-sorting-strategies).

4. Conclusions

The hypothesis for this study was that by applying sorting algorithms to ranking tests for sensory analysis, the efficacy of the task could be improved, highlighting sorting algorithms as potential tools for sensory ranking. The data showed significant improvements in ranking score from Merge Sorting versus either Bubble Sorting or an un-cued strategy. This came at the expense of time, and perceived level of difficulty, both of which may be ameliorated with training. Our secondary goal was to identify the strategies that panelists use to rank samples when no instructions were given, which seem to most closely follow a Bubble Sorting procedure, however interestingly differing approaches were adopted, highlighting inconsistencies in the individual cognitive task being performed by the same panel. The efficiencies offered by a structured ranking procedure may mirror advantages offered by forms of structured sorting or multidimensional scaling, where numerous judgements are made from a large set of data (Rosenberg et al., 1968, Lawless et al., 1995, Pagès et al., 2010).

One source of possible improvement lies in the instructions, which were complex, and could use some refinement, possibly with a better visual (ideally animated) aid. The instructions were written based on two fairly complex mathematical algorithms, and thus may have been perceived by some as confusing, causing them to hurry, or make a mistake. Again, this could be improved with a period of training. Finally, either of the formal ranking strategies undoubtedly add to the time requirements (as much as 66% longer) and panelist burden from the task, however we believe they still offer a more systematic approach to ranking, which may be of utility when accuracy is deemed to be of more importance than speed.

Author contribution

Markus Ekman: Investigation, Writing – original draft

Asa Amanda Olsson: Investigation, Writing – original draft

Kent Andersson: Investigation, Writing – original draft

Amanda Jonsson: Investigation, Writing – original draft

Alina Stelick: Methodology, Supervision, Project administration, Writing – original draft

Robin Dando: Conceptualization, Formal analysis, Methodology, Project administration, Writing – original draft, Writing – review & editing

Appendix A. Supplementary data

The following is the Supplementary data to this article: